Abstract
A lipid vesicle, or simply called a liposome, represents a synthetic compartment for the examination of transmembrane transport and signaling phenomena. Yet, a liposome is always subjected to size and shape fluctuations due to local and global imbalance of internal and external osmotic pressures. Here, we show that an osmotically-stressed liposome placed within a hypotonic spherical bath undergoes cyclic dynamics described by a periodic sequence of swelling and relaxation phases. These two phases are interfaced by the appearance of a transient transmembrane pore through which chemical delivery occurs. An analytical model was formulated for the recurrent differential equations that convey the time-dependent swelling phase of a pulsatory liposome during individual cycles. We demonstrate that the time-dependent swelling phases of the last several cycles of a pulsatory liposome are strongly dependent on the size of the external bath. Furthermore, decreasing the size of the hypotonic medium reduces the number of cycles of a pulsatory liposome. Comparisons and contrasts of an infinite hypotonic bath with finite external baths of varying radius are discussed.
Keywords: External bath, Number of cycles, Laplace pressure, Osmotic pressure, Transmembrane transport, Giant unilamellar vesicle, Analytical model
Graphical Abstract
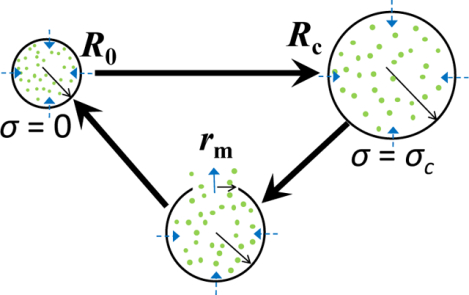
INTRODUCTION
Cellular response to local and global fluctuations in the osmotic pressure of external environment is a fundamental property of living systems. There are numerous mechanisms by which cells operate for regulating the strain of the cellular membrane, including mechanosensitive and water channels. In a much more simplified context, a unilamellar liposome undergoes shape and size fluctuations upon rapid changes in the environmental osmotic pressure. It has already been documented that a liposome undergoes a cyclic activity when it is filled with an aqueous solution of an increased osmotic pressure and it is placed within a finite hypotonic environment.1–3 In each cycle, the osmotic influx of water swells the liposome up to a critical point at which the membrane attains the maximum strain that is characterized by a critical (or lytic) tension, σc (Fig. 1A). In this way, the radius of a spherical liposome expands from an initial value, R0, to a critical value, Rc. At this point, the nucleation of a transient transmembrane pore occurs,4–8 sometimes leading to an irreversible rupture of the liposomal membrane.9–12 This phase, also called the swelling phase,13 is followed by solute extrusion through the transient pore and a fast relaxation (or compression) phase until the liposome reaches its initial size. Then, a new cycle begins and the liposome activity becomes cyclic. This is the reason why we call this liposome a pulsatory liposome. Therefore, a pulsatory liposome operates like a two-stroke engine. The transmembrane gradient of osmotic solute assures the potential energy that generates the functional force of the engine.
Figure 1: Diagrams that show details of the dynamics of a pulsatory liposome during a single cycle.
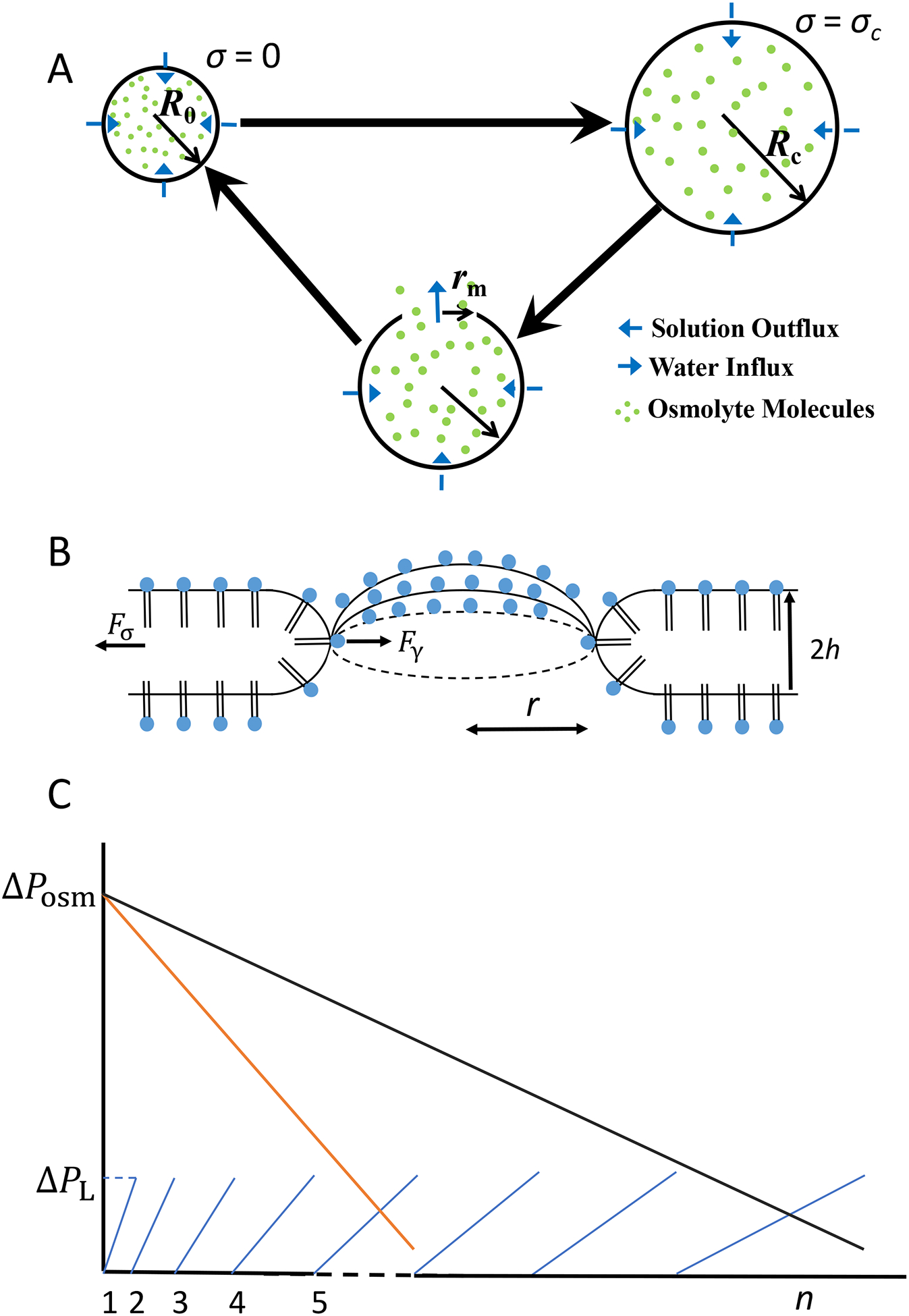
(A) Each cycle encompasses two phases: swelling phase (top) and relaxation phase (bottom). The initial radius of the liposome, R0, is reached when the surface tension is zero. In contrast, the critical radius of the liposome, Rc, is attained at a critical surface tension, σc. At this point, the liposomal membrane undergoes a lytic tension, leading to a transient transmembrane pore. The maximum radius of the transient pore is rm. (B) This model assumes the osmotic stress-induced formation of a single transient pore across the liposomal membrane. The dynamics of the transient pore is affected by the balance between the driving force for the pore opening, Fσ, which corresponds to the mechanical surface tension of the membrane, σ, and the driving force for pore closure, Fγ, which corresponds to edge tension (or line tension), γ. The former force is created by the Laplace pressure, whereas the latter force is created by the strong hydrophobic interactions among the alkyl tails of the liposomal phospholipids. r is the pore radius. h is the thickness of a monolayer of the liposomal bilayer membrane. (C) Schematic that shows the balance of the osmotic and Laplace pressures during the succession of various cycles. ΔPosm and ΔPL are the osmotic and Laplace pressures, respectively. n is the cycle order. A pulsatory liposome becomes active when ΔPL < ΔPosm. The tilted line in black corresponds to a pulsatory liposome located within an infinite hypotonic bath (e.g., a larger number of cycles). The tilted line in orange corresponds to a pulsatory liposome located within a finite hypotonic bath (e.g., a smaller number of cycles).
The succession of swelling and relaxation phases is mediated by the appearance of a transmembrane pore formed in a stretched liposomal membrane (Fig. 1B). A significant number of theoretical,4, 7, 10–11, 14–24 computational,25–27 and experimental5, 11, 28–32 studies have reported the presence of transient pores in liposomes and planar lipid membranes. Moreover, there is an increasing interest in the exploration of these metastable transmembrane pores, because of their pivotal role in the cyclic activity of an osmotically-stressed liposome.1–3, 7, 33–37
In this paper, we put an emphasis on the swelling phase of the cyclic activity of a liposome when it is inserted into a finite hypotonic environment. If the external bath is filled with water, then the external concentration of solute increases in a cyclic fashion.1–2, 37–39 The cyclic activity of the liposome depends on the transmembrane gradient of solute. The relaxation phase is short lived and it does not affect the swelling phase.2 Our expectation is that the size of the hypotonic environment has significant impact on the number of cycles, the swelling time of a pulsatory liposome, as well as the total amount of solute released into the external environment. On the other hand, we expect that other biophysical parameters of a pulsatory liposome, such as the relaxation time, are not significantly affected. Therefore, we wanted to explore the swelling phase of a pulsatory liposome of varying cycle order.
Here, we report that the size of the finite hypotonic bath has substantial impact on the total number of cycles and the amount of solute released during the active life of the liposome. A pulsatory liposome becomes inactive at a point in which the internal osmotic pressure is equal to the Laplace pressure (Fig. 1C). The outcomes of this study represent a theoretical platform for further developments with a practical impact. Specifically, the solute might be substituted by a chemical agent of pharmacological significance for a healthcare application. In this case, a pulsatory liposome can release drugs in a programmable fashion at a strategic location of a targeted tissue.40–41
METHODS
Background.
Let us consider a large liposome filled with a solute-containing aqueous solution and assume that it is located within a sufficiently large, water-filled spherical bath. In the first phase, the liposome expands from the initial state up to a critical state when a single transient transmembrane pore appears. Let us set the initial liposomal radius equal to R0. In this case, the liposomal membrane is unstretched, so that the mechanical surface tension, σ, is zero. In the critical state, the liposomal radius and surface tension are Rc and σc, respectively. In the second phase, the cycle is determined by the appearance of the transmembrane pore. The time trajectory of the transient pore has two phases: in the first part, the pore radius increases up to a maximum value, rm, and in the second part, the pore radius declines up to the pore closure, leading to the recovery of the liposomal membrane (Fig. 1A, Fig. 1B). During this process, some solute amount is extruded through the transient pore.
As soon as the membrane is recovered, the liposome returns to its initial state and a new cycle begins. In our model, we assumed that the critical membrane tension, σc, at which the relaxation phase starts, depends on the intrinsic properties of the liposomal membrane, so that this is assumed unaltered by increasing the cycle order.1, 10–11 Because of the solute release through the transient transmembrane pore, the internal solute concentration is changed at the end of each cycle. The liposomal expansion is mediated by the balance between the osmotic and Laplace pressures. This is the conceptual mechanism by which an osmotically-stressed liposome placed within a finite, hypotonic environment can undergo a cyclic activity as a result of the balance between the osmotic and Laplace pressures (Fig. 1C). Overall, each cycle of a pulsatory liposome is characterized by a differential equation for the liposomal radius during the swelling (expansion) phase and a system of three differential equations for the liposomal radius, transient pore radius, and solute internal concentration during the relaxation (compression) phase.
Analytical model for the swelling phase.
Let us consider that the initial state of the liposome is defined by the surface area, A0, and the volume, V0. At the same time, the initial state of the liposome is characterized by the initial internal concentration of the solute, C01. In a hypotonic environment, the liposomal volume increases because of the osmotic pressure difference between the interior and exterior of the lipid vesicle. The direct outcome of the volume growth is the stretching of the bilayer membrane and the appearance of the Laplace pressure. During liposomal swelling, two pressures occur in directions against each other: osmotic pressure, ΔPosm, and Laplace pressure, ΔPL, corresponding to the transmembrane gradient of solute concentration and surface tension, respectively (Fig. 1B).
The rate of change in the liposomal volume, V, is described by the following equation:
| (1) |
Here, Pw and Vμw denote the water permeability across the liposomal membrane and the water molar volume, respectively. A is the total area of the liposome.
Here,
| (2) |
where NA, kB, and T are the Avogadro number, the Boltzmann constant, and the absolute temperature, respectively. The osmotic pressure, ΔPosm,42–43 and Laplace pressure, ΔPL,29–30 are given by the following equations:
| (3) |
| (4) |
where
| (5) |
is the transmembrane gradient of the solute concentration. R denotes the liposomal radius. Cin and Cout are the solute concentrations inside and outside the liposome, respectively. According to Hooke’s law of elasticity in a two-dimensional formulation, if a closed spherical membrane is stretched by a surface tension, σ, the radius of the swelled state, R(σ), is:
| (6) |
where R0 and R are the liposomal radii in the initial (untensed) state and expanded (tensed) state, respectively. In eqn. (6), E is the elastic modulus for the stretching and compression of liposomal membrane in two dimensions. Therefore, if a liposome is stretched, then the mechanical tension is given by the following formula:
| (7) |
Let us assume a spherical geometry of the liposome. Using eqns. (2–7), we rewrite eqn. (1) in the following form:
| (8) |
Let us consider two cases. In the first case, the liposome is placed within an infinite water bath with a time-independent solute concentration (Cout = 0). In the second case, the liposome is placed within a finite (closed) hypotonic environment with a time-dependent solute concentration. In the latter case, Cout increases during pulsatory solute exchange with the hypotonic environment, whereas Cin decreases. Using the law of mass conservation during the swelling process of the first cycle (Supporting Information, eqns. (S1)–(S7)), eqn. (8) can be analytically solved for the first cycle, as follows:
| (9) |
where
| (10) |
and
| (11) |
Here, C01 is the initial internal solute concentration.
Differential eqn. (9) has a solution that is a bijective function:
| (12) |
where Rc is the critical radius of the liposome. Here, we define the critical swelling ratio, xc, by the following formula:
| (13) |
One might calculate the inverse function R = R(t). Yet, the differential equation of the swelling process of a pulsatory liposome in the n-th cycle is given by the following expression (Supporting Information, eqns. (S8)–(S16)):
| (14) |
where
| (15) |
The differential equations that describe the swelling phases of a pulsatory liposome, except the equation for the first cycle, can be solved using numerical methods.
Comparisons between the first cycle and subsequent cycles.
The major question in this study is how the “finite” nature of the spherical environment with a radius, Rb, impacts the parameters of the liposome. Specifically, we solve the differential equation for the swelling phase of each cycle. For the first cycle, Cout = 0 and the differential equation is provided by eqn. (9). The final form of eqn. (8) for the expansion phase of a pulsatory liposome during the n-th cycle (n ≥ 2, Cout > 0) is eqn. (14). The functional operation of a pulsatory liposome is contingent upon a specific imbalance between competing pressures: the osmotic pressure is greater than the Laplace pressure:
| (16) |
This is the running condition of a pulsatory liposome. During the cyclic activity of the liposome, its osmotic pressure declines continuously until this becomes equal to the Laplace pressure. At this point, the cyclic activity of a pulsatory liposome stops. The number of cycles achieved by a pulsatory liposome is calculated by the following formula:
| (17) |
where
| (18) |
and
| (19) |
RESULTS
Our analytical model can be used to acquire quantitative information regarding the cyclic activity of an osmotically-stressed liposome. Let us consider that such a giant unilamellar vesicle (GUV) has the radius in the initial state, R0 = 19.7 μm, and the radius of the critical state, Rc = 20.6 μm.5 In addition, we consider a liposome that contains a solution of a nonpermeant solute. Let us consider that the initial internal solute concentration is C01= 0.5 M. Using experimentally determined parameters,44 the membrane permeability coefficient for water, Pw, is equal to 3×10−5 m/s and the molecular volume of a water molecule is Vμw = 18.04×10−6 m3/mol. A representative value of the two-dimensional stretch modulus of the lipid bilayer is E = 0.2 N/m.29–30 Typical values for the surface tension, σ, of a phospholipid membrane in a stretched state are in the range of 0.1 – 1 mN/m.28, 33 Yet, GUVs undergo much greater values of their surface tension due to their large spherical surfaces. To examine the effect of a finite water bath on a pulsatory liposome, we considered three closed spherical boxes with a radius, Rb, where Rb values are 4R0, 8R0, and 12R0. We formulate the following parameters that characterize the cyclic activity of a liposome: the number of cycles, the amount of solute released at the end of cyclic liposomal activity, the duration of each cycle, and the total lifetime of cyclic activity.
Using eqn. (17), we found that the total numbers of cycles for finite hypotonic environments with radii 4R0, 8R0, and 12R0, are 30, 42, and 46, respectively. If a liposome is placed into an infinite hypotonic environment, namely for Cout = 0 and an indefinite duration, then the cyclic activity has 47 cycles. This is a value closely similar to the maximum cycle order of a spherical hypotonic bath of radius, Rb = 12R0. This outcome was obtained using eqn. (17) and employing the condition Rb → ∞. Theoretical predictions of this analytical model are in accord with prior experimental observations acquired by Karatekin and colleagues (2003).29–30 They have experimentally detected a succession of 30–40 pores in a giant liposome tensed by intense optical illumination, each of them corresponding to a certain cycle order.
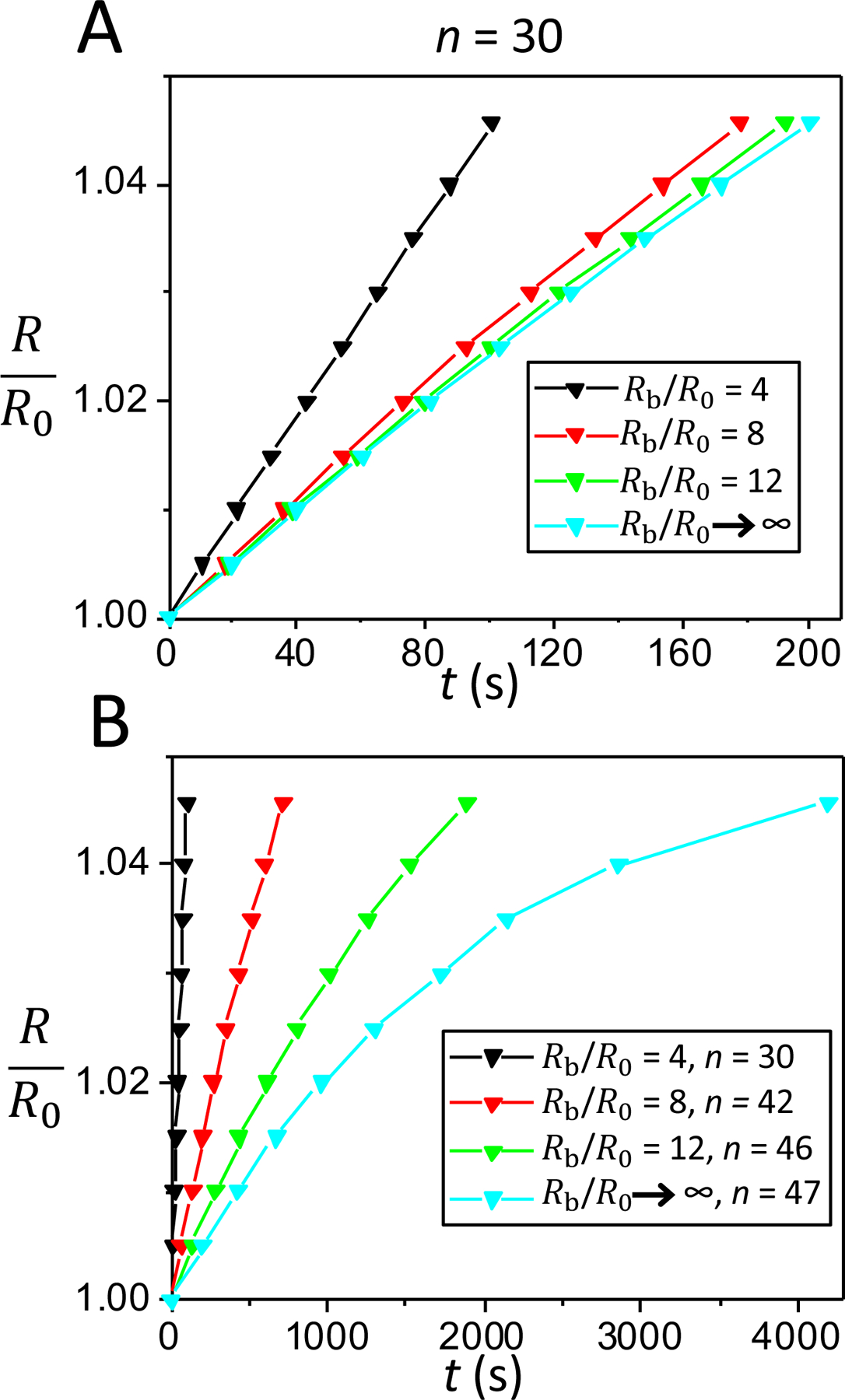
Fig. 2 shows the time dependence of the swelling ratio of a pulsatory liposome, R/R0, for the first part of the cyclic activity of the liposome, which includes 15 cycles. These calculations were performed for finite hypotonic spherical baths with radii Rb = 4R0 (Fig. 2A), Rb = 8R0 (Fig. 2B), and Rb = 12R0 (Fig. 2C), as well as for an infinite hypotonic environment (Rb → ∞ ; Fig. 2D). The swelling phase occurred at a swelling ratio, Rc/R0, in the range of 1 – 1.045. These panels show that the time dependences of the swelling phases for cycles from the beginning cyclic activity are fairly linear and slightly dependent on the size of the external hypotonic environment. For example, for n = 3, the swelling times of a pulsatory liposome were 4.90 s, 5.07 s, and 5.09 s, for the radii of the external bath 4R0, 8R0, and 12R0, respectively. If the liposome was inserted into an infinite hypotonic environment, then the swelling time was 5.10 s, a closely similar value to those acquired for finite hypotonic water baths. On the other hand, for n = 15, the swelling times were 22.46 s, 25.17 s, and 25.47 s, for the radii of the external bath of 4R0, 8R0, and 12R0, respectively. Yet, the swelling time was 25.60 s when the liposome was inserted within an infinite hypotonic environment.
Figure 2: Time dependence of the liposomal radius during the swelling phase for cycles of varying cycle order, n, in the beginning of the cyclic activity.
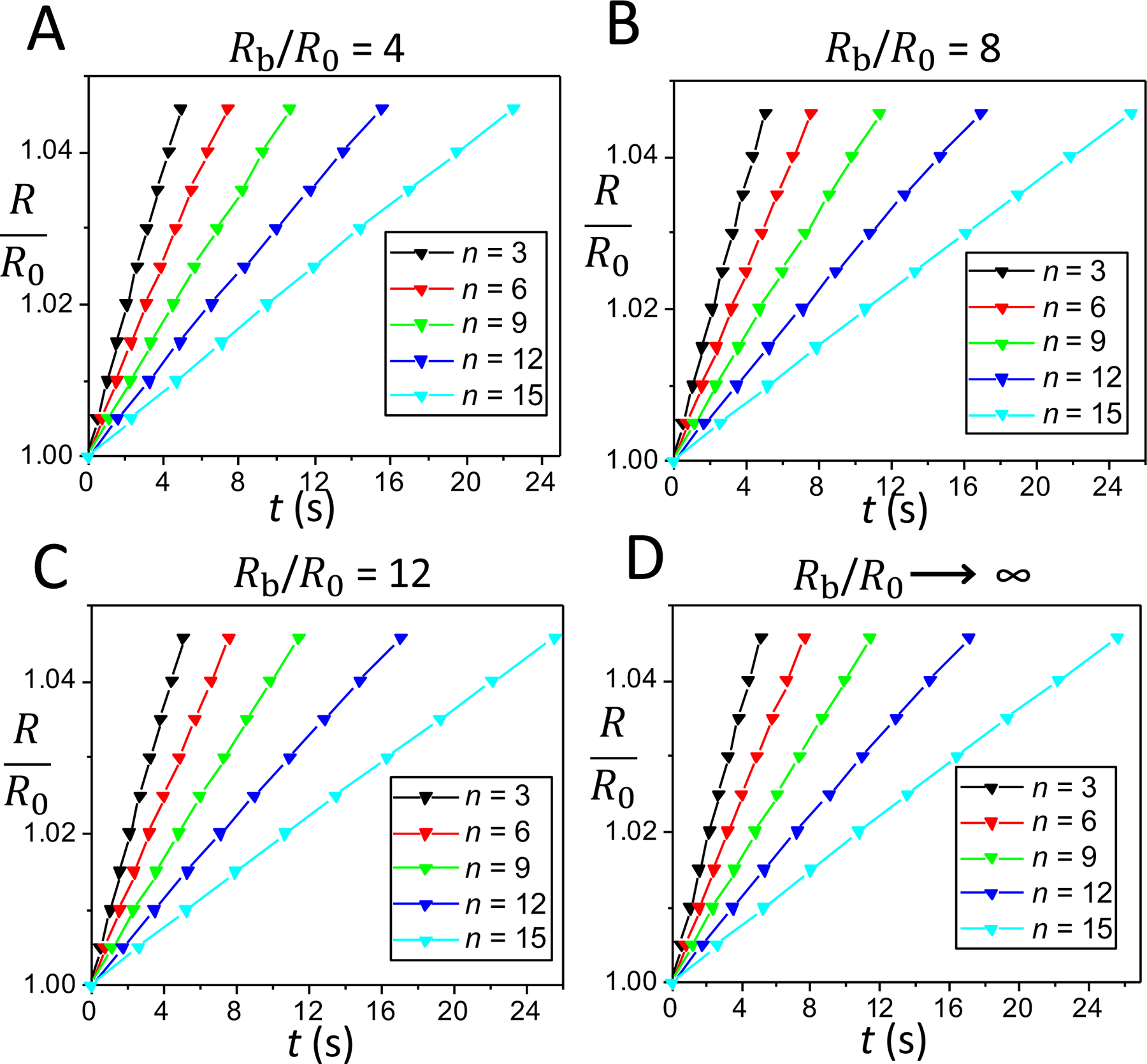
Different panels indicate cases when the liposome was placed within a finite water bath of radius, Rb = 4R0 (A), Rb = 8R0 (B), and Rb = 12R0 (C), as well as when the liposome was placed within an infinite water bath, Rb → ∞ (D). In (A), (B), (C), and (D), the cycle orders of liposomal activity are 3, 6, 9, 12, and 15.
Fig. 3 illustrates the time dependence of the swelling ratio of a pulsatory liposome for the last part of the cyclic activity, which encompasses 12–14 cycles. This data was acquired for the cases presented in Fig. 2, either for a finite spherical bath or an infinite environment under hypotonic conditions (Rb = 4R0, Fig. 3A; Rb = 8R0, Fig. 3B, Rb = 12R0, Fig. 3C; Rb → ∞; Fig. 3D). In both cases, the finite hypotonic medium and opened water bath, the expanded liposomal radius is a linear function on swelling time, except for the last cycles. This observation is highlighted for the case of hypotonic environments of larger sizes, e.g. for n = 46 when Rb = 12R0 as well as for n = 46 and n = 47 when Rb → ∞. Moreover, in contrast to the findings pertaining to Fig. 2, the swelling phases of the last cycles were drastically slower in large external baths (e.g., for Rb = 12R0 and Rb → ∞) with respect to smaller finite environments (e.g., for Rb = 4R0 and Rb = 8R0). This phenomenon was amplified at the highest cycle orders. For instance, the durations of the swelling phases were 16.95 min and 31.42 min for n = 42 and n = 46, respectively, when Rb was 12R0 (Fig. 3C). The slowest swelling phase, in the duration of 69.97 min, was obtained for n = 47 when a pulsatory liposome was placed within an infinite water bath (Fig. 3D).
Figure 3: Time dependence of the liposomal radius during the swelling phases that correspond to the last cycles of the pulsatory activity.
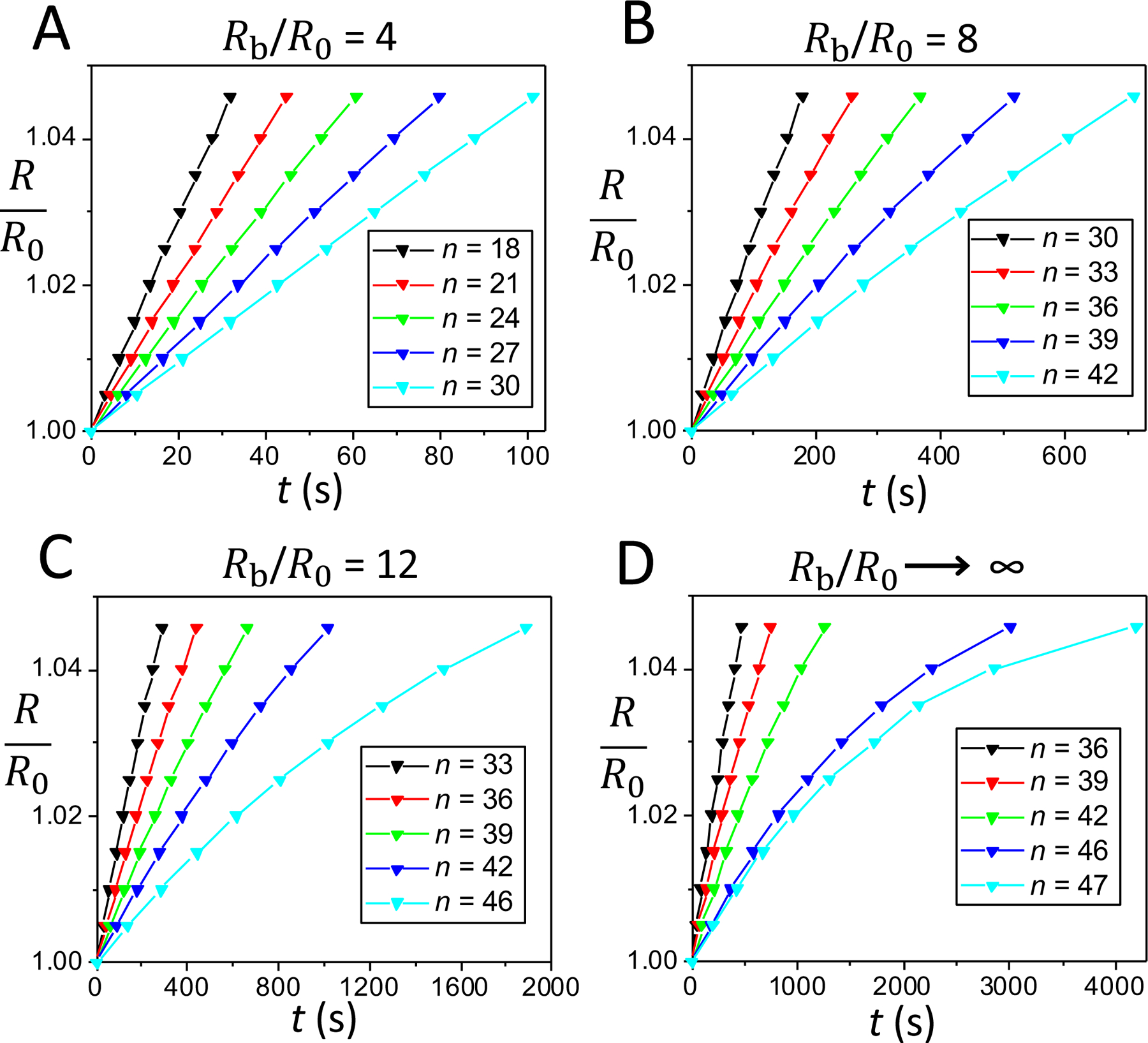
This time dependence is illustrated for three distinct cases of a finite hypotonic environment and an infinite hypotonic water bath, as follows: (A) Rb = 4R0, cycles 18, 21, 24, 27, and 30. (B) Rb = 8R0, cycles 30, 33, 36, 39, and 42; (C) Rb = 12R0, cycles 33, 36, 39, 42, and 46. (D) Infinite hypotonic medium, cycles 36, 39, 42, 46, and 47.
Fig. 4A presents the durations of the swelling phase of the 30th cycle of pulsatory liposomes located in hypotonic water baths of varying radius. One can note a significant distinction between the swelling rate acquired for the external bath with the smallest radius and the others. If we define the swelling rate as the critical swelling ratio divided by the total swelling time, meaning (Rc/R0)/tswell, where tswell is the duration of the swelling phase for a certain cycle order, then its value was 4.52 × 10−4 s−1 for the 30th cycle of a finite bath with Rb = 4R0. In contrast, slower swelling rates of 2.56 × 10−4 s−1, 2.37 × 10−4 s−1, and 2.29 × 10−4 s−1, were determined for external baths with the radii equal to 8R0, 12R0, and infinity, respectively.
Figure 4: Comparisons of the durations of the swelling phase of the 30th cycle and final cycle for distinct sizes of the hypotonic water bath.
(A) The duration of the swelling phase of the 30th cycle for the three sizes of finite hypotonic water baths (Rb/R0 =4; Rb/R0 =8; Rb/R0 =12) and for an infinite hypotonic environment. (B) The duration of the swelling phase of the last cycle for the three sizes of finite hypotonic water baths (Rb/R0 =4; Rb/R0 =8; Rb/R0 =12) and for an infinite hypotonic environment.
Fig. 4B illustrates the time dependence of the swelling ratio, R/R0, of a pulsatory liposome during the last cycle. The durations of the swelling phase of the last cycles were equal to 1.68 min, 11.84 min, and 31.42 min when a pulsatory liposome was inserted into in finite hypotonic media with radii 4R0, 8R0, and 12R0, respectively. Yet, the duration of the swelling phase of the last cycle was equal to 69.97 min when the liposome was placed within an infinite hypotonic environment. These are the durations required for a pulsatory liposome to attain the critical swelling ratio, Rc/R0, of 1.045 during the last cycle. This observation reveals that an increase in the size of the external hypotonic bath drastically declines the swelling rate of a pulsatory liposome in the terminal cycle.
We found that the durations of the first half of the swelling phase of the last cycles (e.g., those corresponding to R/R0 = 0.5×(Rc/R0+1) = 1.0228) were equal to 0.90 min, 5.88 min, and 13.42 min when a pulsatory liposome was inserted within in a finite hypotonic media of radii 4R0, 8R0, and 12R0, respectively. However, the duration of the first half of the swelling phase of the last cycle was equal to 21.77 min when the liposome was placed within an infinite hypotonic bath. Notably, in this case the duration of the second half of the swelling phase of the last cycle was equal to 48.19 min, a significantly longer value than that of the first half of the swelling phase. This outcome results from a strong non-linear time dependence of the liposomal swelling ratio in the last cycle of infinite external bath (Fig. 4B, F → ∞, n = 47).
Fig. 5 shows the duration of the swelling phase as function of the cycle order for hypotonic baths of a smaller sizes (Fig. 5A) and for larger environments (Fig. 5B). It is clear that cycles of low order numbers (n < 15) are significantly shorter than those of high order numbers (n > 30). The duration of the swelling phase drastically increased to tens of minutes for cycles with order number greater than 40. On the contrary, the total swelling time for the maximum cycle order was only 100.95 s in the case of the smallest hypotonic bath.
Figure 5: The duration of swelling phase as a function of the cycle order for a pulsatory liposome.
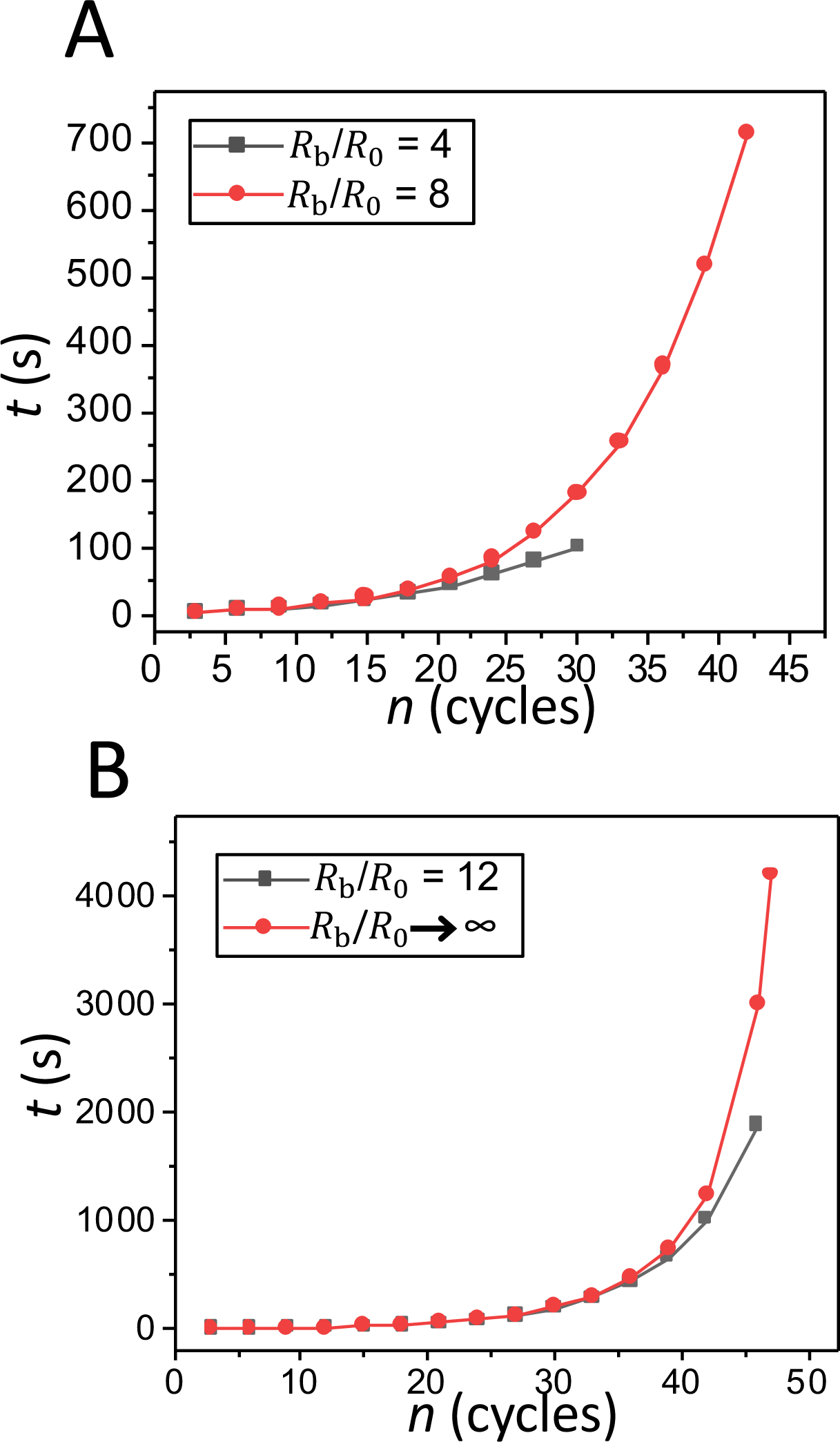
(A) Comparison for hypotonic water baths with Rb=4R0 and Rb=8R0. (B) Comparison for hypotonic water baths with Rb=12R0 and Rb → ∞.
If the pulsating liposome function as a device for the controlled release of a chemical agent, then the most important parameter is the amount of solute released into the external environment during its functional operation. Let us assume that the initial internal concentration of the solute is equal to 0.5 M, so the liposome contains Q01 = C01V0= 9.643 × 1012 molecules. At the end of the cyclic activity, a pulsatory liposome releases the amounts of solute equal to Q30 = 9.4997 × 1012 molecules, Q42 = 9.6083 × 1012 molecules, and Q46 = 9.6227 × 1012 molecules, if this liposome is placed within closed hypotonic environments with radii Rb = 4R0, Rb = 8R0, and Rb = 12R0, respectively. For the case of an infinite hypotonic bath, the amount of delivered solute is equal to Q47 = 9.625 × 1012 molecules, which is ~99.81% of the initial solute amount. We highlight that the amount of solute released during a single cycle of the same order is unchanged regardless of whether a pulsatory liposome is placed into a finite or an infinite hypotonic environment.
DISCUSSION
In the results section, we provided a detailed quantitative description of the swelling phase of a pulsatory liposome when this is placed within a hypotonic bath of varying size. The energy required for the liposomal swelling is provided by the osmotic transmembrane gradient. The swelling phase is an active process of each cycle and is described by a differential equation for the radius of the liposome (eqn. (8)). In contrast, the liposomal relaxation is a passive and fast process,38–39 resulting from the appearance of a transient pore of a pulsatory liposome at a point that reaches a critical radius, Rc, and a critical surface tension, σc. The appearance of the transient pore is a critical event for the cyclic activity of the liposome, because at this point the swelling phase stops and the relaxation phase starts. After this event, some internal solute is released into the external hypotonic bath.
The lifetime of the transient pore is ~1.725 s.45 This value was previously inferred using similar conditions to those employed in this study. The transient pore undergoes two phases, the expansion and shrinkage phases. The durations of these phases are 225 ms and 1500 ms, respectively. The lifetime of the pore is independent of the cycle order of the pulsatile liposome. Kinetics of the two phases of the transient pore depend on the properties of liposomal membranes. Because of the very short duration of the transient pore, we expect that this parameter does not significantly affect the overall dynamics of the liposomal cyclic activity.
The pore energy, Ep, is given by the following formula:46
| (20) |
This shows the balance between the line tension and surface tension. Here, r denotes the pore radius. γ and σ are the line tension and surface tension coefficients, respectively. The only stable energetic minimum of Ep is reached at a radius r = 0. The transient pore undergoes membrane rupture at a pore radius greater than a critical radius, rc = γ /σ. However, this phenomenon is rare, because the activation free energy for this process is high (ΔE=πγ2/σ).47 For smaller tensions, a transient pore can rapidly shrink, evolving toward a closed pore state. On the contrary, for tensions greater than a critical value, a transient pore can rapidly expand until it reaches membrane rupture, leading to liposomal lysis. Therefore, it is not possible to detect stable transmembrane pores with long lifetimes. Yet, Zhelev and Needham (1993) have demonstrated for the very first time the appearance of long-lived quasistable transmembrane pores with a radius of 1 μm in GUVs.48 A giant liposome was aspirated into a micropipette and short-lived electrical stimuli were applied across the vesicle. In this way, the lifetime of relatively stable pores spanned a duration range from tenths of a second to several seconds. These studies enabled the determination of the pore size and pore line tension. In parallel with these studies, Wilhelm and coworkers (1993) have studied the kinetics of pore appearance followed by mechanical rupture using high-voltage, charge-pulse technique.49 A large number theoretical,4–5, 7, 10–11, 14–24, 28–30, 46 computational,7, 16, 21, 23, 25–27, 50 and experimental5, 11, 28–32 studies have documented the existence of these transient pores across bilayer membranes.
Our analytical model involves a spherical symmetry. Yet, in a given experimental context, ample alterations in external mechanical stress can lead to membrane deformations51–53 and thickness fluctuations.7 We considered the case of a spherical liposome, because this geometry represents the equilibrium conformation with an enhanced shape stability of the membrane. This also means that the membrane tension, σ, has a uniform value across the entire liposomal surface. If transient undulations occur,50, 54 then the amplitude of these membrane motions would normally decrease during the liposomal swelling phase. Quantitative assessment of local and global membrane undulations, some of which might be thermally activated, is experimentally challenging. The spherical geometry represents the average experimental substate of the undulatory dynamics of liposomal membrane.2, 36–37 It is also a reason for which the outcomes of our analytical model quantitatively recapitulate experimental results (see below). However, if an amplified out-of-membrane pressure occurs, this would lead to stable membrane deformations. In this case, the membrane tension, σ, has no longer a uniform value across the entire liposomal membrane. In addition, the swelling phase of the liposome is no longer described by a single differential equation. The transient transmembrane pore appears on the liposomal membrane, where the critical surface tension, σc, is reached. Moreover, the liposome may feature a cyclic activity when stable membrane deformations take place.
Here, we highlighted the quantitative aspects of the swelling phases of the cycles of a pulsatory liposome under finite hypotonic conditions for one major reason. Because the duration of the relaxation phase is very short, the alteration in the internal concentration of solute is negligible during this process. Indeed, recent experimental studies of the cyclic activity of GUVs provided evidence for very short-lived relaxation phase38–39 and unchanged initial radius of the vesicle, R0, of a pulsatory liposome for successive cycles.2, 33 Yet, there is experimental evidence that indicates fluctuations in the critical radius, Rc, of a pulsatory liposome for successive cycles.2, 33 This finding suggests a more complex dependence of the lytic tension on the cycle order, which was not included on our analytical model (METHODS). Indeed, Evans and coworkers (2003)55 as well as Chabanon and coworkers (2017)2 have shown that the lytic tension for the pore formation is a function that depends on the load rate. Therefore, we expect that the amplitude of Rc and the time of pore appearance are affected by the cycle order. If the lytic tension depends on the cycle order, then the corresponding critical value of liposome radius, Rc, is introduced in eqns. (14) – (15). Dependence of the lytic tension on the load rate will certainly affect the swelling phase of the liposome. Therefore, this will affect the overall duration of large-order cycles. If the liposomes are exposed to a surfactant-containing environment, then the partitioning of surfactant molecules into the membrane likely changes the lytic tension at which short-lived pores occur.36
The periodic behavior of osmotically-stressed liposomes has been first predicted by Koslov and Markin (1984).9 Later, other groups have developed theoretical approaches for acquiring quantitative information of this fundamental process.1, 38 Our theoretical formulation includes low-amplitude size fluctuations of the swelling and relaxation phases between R0 and Rc, which are characterized by a critical liposomal radius of ~4.5% out of that value of an unstretched lipid vesicle. This assumption is in good accord with the cyclic size fluctuations of GUVs, as previously reported.3, 5, 39 Our model quantitatively recapitulates the number of the swelling-relaxation cycles observed experimentally. For example, we acquired a total number of cycles, nmax, of 47 for our infinite hypotonic bath. This value is close to the numbers of swell/burst cycles noted with GUVs in hypotonic media.38 Furthermore, our model calculations predict long-lived swelling phases of larger-order number cycles, which is in quantitative agreement with recently reported experimental determinations of osmotically-stressed lipid vesicles.2, 37
In summary, we formulated an analytical model that provides quantitative information on the cyclic activity of a lamellar liposome in a finite hypotonic environment. The swelling phase of the last several cycles of a pulsatory liposome is strongly dependent on the size of the external bath. A reduced number of cycles of a pulsatory liposome as well as a lower amount of chemical agent released into the external environment were found by decreasing the size of the external hypotonic medium. Furthermore, the duration of the swelling phase is strongly dependent on the cycle order, which is in good accord with recent experimental explorations of the pulsatory GUVs.2, 33 For example, the swelling phases of the last few cycles last several hundred of seconds, contrasting the cycles of low order numbers, which are in the second range. From a practical point of view, the consumed fuel of this two-stroke liposomal engine might be substituted by an active biotherapeutic agent. Finally, there is great potential for the use of lipid vesicles in clinical applications, specifically for controlled drug release of targeted chemicals at precise locations of diseased tissues. In this case, the osmotically-stressed liposomes would be located within a finite hypotonic environment.
Supplementary Material
ACKNOWLEDGMENTS.
We are grateful to Lauren Mayse and Jiaxin Sun for their comments and stimulating discussions. This work was supported by US National Institutes of Health grants GM088403 (to L.M.) and GM129429 (to L.M.).
Footnotes
SUPPORTING INFORMATION. (i) Determination of the final state of the first cycle of a pulsatory liposome; (ii) Determination of the swelling phase of the n-th cycle of a pulsatory liposome. These materials are available free of charge via the Internet at http://pubs.acs.org
REFERENCES
- 1.Popescu D; Popescu AG, The working of a pulsatory liposome. J. Theor. Biol 2008, 254 (3), 515–9. [DOI] [PubMed] [Google Scholar]
- 2.Chabanon M; Ho JCS; Liedberg B; Parikh AN; Rangamani P, Pulsatile Lipid Vesicles under Osmotic Stress. Biophys. J 2017, 112 (8), 1682–1691. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ixaru LG; Popescu D, A mathematical investigation on the active substance pulsatory release from a solution-charged liposome. Biosystems 2019, 179, 48–54. [DOI] [PubMed] [Google Scholar]
- 4.Popescu D; Rucareanu C, Membrane selfoscillations model for the transbilayer statistical pores and flip–flop diffision. Mol. Cryst. Liquid Cryst 1992, 25, 339–348. [Google Scholar]
- 5.Brochard-Wyart F; De Gennes P-G; Sandre O, Transient pores in stretched vesicles: role of leak-out. Physica A 2000, 278 (1–2), 32–51. [Google Scholar]
- 6.Melikov KC; Frolov VA; Shcherbakov A; Samsonov AV; Chizmadzhev YA; Chernomordik LV, Voltage-induced nonconductive pre-pores and metastable single pores in unmodified planar lipid bilayer. Biophys. J 2001, 80 (4), 1829–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Movileanu L; Popescu D; Ion S; Popescu AI, Transbilayer pores induced by thickness fluctuations. Bull. Math. Biol 2006, 68 (6), 1231–1255. [DOI] [PubMed] [Google Scholar]
- 8.Trick JL; Song C; Wallace EJ; Sansom MS, Voltage Gating of a Biomimetic Nanopore: Electrowetting of a Hydrophobic Barrier. ACS nano 2017, 11 (2), 1840–1847. [DOI] [PubMed] [Google Scholar]
- 9.Koslov MM; Markin VS, A theory of osmotic lysis of lipid vesicles. J. Theor. Biol 1984, 109 (1), 17–39. [DOI] [PubMed] [Google Scholar]
- 10.Idiart MA; Levin Y, Rupture of a liposomal vesicle. Phys. Rev. E 2004, 69 (6 Pt 1), 061922. [DOI] [PubMed] [Google Scholar]
- 11.Peterlin P; Arrigler V, Electroformation in a flow chamber with solution exchange as a means of preparation of flaccid giant vesicles. Colloids Surf. B Biointerfaces 2008, 64 (1), 77–87. [DOI] [PubMed] [Google Scholar]
- 12.Mahendra A; James HP; Jadhav S, PEG-grafted phospholipids in vesicles: Effect of PEG chain length and concentration on mechanical properties. Chem. Phys. Lipids 2019, 218, 47–56. [DOI] [PubMed] [Google Scholar]
- 13.Peterlin P; Arrigler V; Haleva E; Diamant H, Law of corresponding states for osmotic swelling of vesicles. Soft Matter 2012, 8 (7), 2185–2193. [Google Scholar]
- 14.Popescu D; Rucareanu C; Victor G, A Model for the Appearance of Statistical Pores in Membranes Due to Selfoscillations. Bioelectrochem. Bioenerg 1991, 25 (1), 91–103. [Google Scholar]
- 15.Saulis G, Pore disappearance in a cell after electroporation: Theoretical simulation and comparison with experiments. Biophys. J 1997, 73 (3), 1299–1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shillcock JC; Seifert U, Thermally induced proliferation of pores in a model fluid membrane. Biophys. J 1998, 74 (4), 1754–1766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Popescu D; Movileanu L; Ion S; Flonta ML, Hydrodynamic effects on the solute transport across endothelial pores and hepatocyte membranes. Phys. Med. Biol 2000, 45 (11), N157–N165. [DOI] [PubMed] [Google Scholar]
- 18.Popescu D; Ion S; Popescu AI; Movileanu L, Elastic properties of bilayer lipid membranes and pore formation In Planar Lipid Bilayers (BLMs) and Their Applications, 7 ed.; Tien HT; Ottova A, Eds. Elsevier Science Publishers: Amsterdam, 2003; pp 173–204. [Google Scholar]
- 19.Levin Y; Idiart MA, Pore dynamics of osmotically stressed vesicles. Physica A 2004, 331, 578. [Google Scholar]
- 20.Ryham R; Berezovik I; Cohen FS, Aqueous viscosity is the primary source of friction in lipidic pore dynamics. Biophys. J 2011, 101 (12), 2929–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Fournier L; Joos B, Lattice model for the kinetics of rupture of fluid bilayer membranes. Phys. Rev. E 2003, 67 (5). [DOI] [PubMed] [Google Scholar]
- 22.Farago O; Santangelo CD, Pore formation in fluctuating membranes. J. Chem. Phys 2005, 122, 1606–1612. [DOI] [PubMed] [Google Scholar]
- 23.Shillcock JC; Boal DH, Entropy-driven instability and rupture of fluid membranes. Biophys. J 1996, 71 (1), 317–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Winterhalter M; Helfrich W, Effect of Voltage on Pores in Membranes. Phys. Rev. A 1987, 36 (12), 5874–5876. [DOI] [PubMed] [Google Scholar]
- 25.Akimov SA; Volynsky PE; Galimzyanov TR; Kuzmin PI; Pavlov KV; Batishchev OV, Pore formation in lipid membrane II: Energy landscape under external stress. Sci. Rep 2017, 7 (1), 12509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Akimov SA; Volynsky PE; Galimzyanov TR; Kuzmin PI; Pavlov KV; Batishchev OV, Pore formation in lipid membrane I: Continuous reversible trajectory from intact bilayer through hydrophobic defect to transversal pore. Sci. Rep 2017, 7 (1), 12152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tieleman DP; Leontiadou H; Mark AE; Marrink SJ, Simulation of pore formation in lipid bilayers by mechanical stress and electric fields. J. Am. Chem. Soc 2003, 125 (21), 6382–6383. [DOI] [PubMed] [Google Scholar]
- 28.Sandre O; Moreaux L; Brochard-Wyart F, Dynamics of transient pores in stretched vesicles. Proc. Natl. Acad. Sci. U.S.A 1999, 96 (19), 10591–10596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Karatekin E; Sandre O; Brochard-Wyart F, Transient pores in vesicles. Polym. Int 2003, 52 (4), 486–493. [Google Scholar]
- 30.Karatekin E; Sandre O; Guitouni H; Borghi N; Puech PH; Brochard-Wyart F, Cascades of transient pores in giant vesicles: Line tension and transport. Biophys. J 2003, 84 (3), 1734–1749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Srividya N; Muralidharan S; Okumu W; Tripp B, Determination of the line tension of giant vesicles from pore-closing dynamics. J. Phys. Chem. B 2008, 112 (24), 7147–52. [DOI] [PubMed] [Google Scholar]
- 32.Peterlin P; Arrigler V; Kogej K; Svetina S; Walde P, Growth and shape transformations of giant phospholipid vesicles upon interaction with an aqueous oleic acid suspension. Chem. Phys. Lipids 2009, 159 (2), 67–76. [DOI] [PubMed] [Google Scholar]
- 33.Oglecka K; Rangamani P; Liedberg B; Kraut RS; Parikh AN, Oscillatory phase separation in giant lipid vesicles induced by transmembrane osmotic differentials. eLife 2014, 3, e03695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Martinez-Balbuena L; Hernandez-Zapata E; Santamaria-Holek I, Onsager’s irreversible thermodynamics of the dynamics of transient pores in spherical lipid vesicles. Eur. Biophys. J 2015, 44 (6), 473–81. [DOI] [PubMed] [Google Scholar]
- 35.Ho JC; Rangamani P; Liedberg B; Parikh AN, Mixing Water, Transducing Energy, and Shaping Membranes: Autonomously Self-Regulating Giant Vesicles. Langmuir 2016, 32 (9), 2151–63. [DOI] [PubMed] [Google Scholar]
- 36.Chabanon M; Rangamani P, Solubilization kinetics determines the pulsatory dynamics of lipid vesicles exposed to surfactant. Biochim. Biophys. Acta 2018, 1860 (10), 2032–2041. [DOI] [PubMed] [Google Scholar]
- 37.Su WC; Gettel DL; Chabanon M; Rangamani P; Parikh AN, Pulsatile Gating of Giant Vesicles Containing Macromolecular Crowding Agents Induced by Colligative Nonideality. J. Am. Chem. Soc 2018, 140 (2), 691–699. [DOI] [PubMed] [Google Scholar]
- 38.Peterlin P; Arrigler V; Diamant H; Haleva E, Permeability of phospholipid membrane for small polar molecules determined from osmotic swelling of giant phospholipids In Advances in Planar Lipid Membranes and Liposomes, Iglic A, Ed. Elsevier Sciece Publishers: Amsterdam, 2012; Vol. 16, pp 301–335. [Google Scholar]
- 39.Peterlin P; Jaklic G; Pisanski T, Determining membrane permeability of giant phospholipid vesicles from a series of videomicroscopy images. Meas. Sci. Technol 2009, 20 (5), 055801. [Google Scholar]
- 40.Majd S; Yusko EC; Billeh YN; Macrae MX; Yang J; Mayer M, Applications of biological pores in nanomedicine, sensing, and nanoelectronics. Curr. Opin. Biotechnol 2010, 21 (4), 439–476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Winterhalter M, Lipid membranes in external electric fields: kinetics of large pore formation causing rupture. Adv. Colloid Interface Sci 2014, 208, 121–128. [DOI] [PubMed] [Google Scholar]
- 42.Alam Shibly SU; Ghatak C; Sayem Karal MA; Moniruzzaman M; Yamazaki M, Experimental Estimation of Membrane Tension Induced by Osmotic Pressure. Biophys. J 2017, 112 (6), 1290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Alam Shibly SU; Ghatak C; Sayem Karal MA; Moniruzzaman M; Yamazaki M, Experimental Estimation of Membrane Tension Induced by Osmotic Pressure. Biophys. J 2016, 111 (10), 2190–2201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Lawaczeck R, On the permeability of water molecules across vesicular lipid bilayers. J. Membr. Biol 1979, 51 (3–4), 229–261. [Google Scholar]
- 45.Popescu D, The pulsatory lipid vesicle dynamics under osmotic stress. Lambert Academic Publishing and AV Academikerverlag: Saarbruecken, Germany, 2012. [Google Scholar]
- 46.Moroz JD; Nelson P, Dynamically stabilized pores in bilayer membranes. Biophys. J 1997, 72 (5), 2211–2216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Evans E; Rawicz W, Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett 1990, 64 (17), 2094–2097. [DOI] [PubMed] [Google Scholar]
- 48.Zhelev DV; Needham D, Tension-stabilized pores in giant vesicles: determination of pore size and pore line tension. Biochim. Biophys. Acta 1993, 1147 (1), 89–104. [DOI] [PubMed] [Google Scholar]
- 49.Wilhelm C; Winterhalter M; Zimmermann U; Benz R, Kinetics of Pore-Size During Irreversible Electrical Breakdown of Lipid Bilayer-Membranes. Biophys. J 1993, 64 (1), 121–128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Farago O, “Water-free” computer model for fluid bilayer membranes. J. Chem. Phys 2003, 119 (1), 596–605. [Google Scholar]
- 51.Nielsen C; Goulian M; Andersen OS, Energetics of inclusion-induced bilayer deformations. Biophys. J 1998, 74 (4), 1966–1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Nielsen C; Andersen OS, Inclusion-induced bilayer deformations: Effects of monolayer equilibrium curvature. Biophys. J 2000, 79 (5), 2583–2604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Litschel T; Ramm B; Maas R; Heymann M; Schwille P, Beating Vesicles: Encapsulated Protein Oscillations Cause Dynamic Membrane Deformations. Angewandte Chemie (International ed. in English) 2018, 57 (50), 16286–16290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Garcia-Saez AJ; Schwille P, Fluorescence correlation spectroscopy for the study of membrane dynamics and protein/lipid interactions. Methods 2008, 46 (2), 116–122. [DOI] [PubMed] [Google Scholar]
- 55.Evans E; Heinrich V; Ludwig F; Rawicz W, Dynamic tension spectroscopy and strength of biomembranes. Biophys. J 2003, 85 (4), 2342–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


