Assessment of the SARS-CoV-2 basic reproduction number, R₀, based on the early phase of COVID-19 outbreak in Italy

Abstract

As of March 12^th Italy has the largest number of SARS-CoV-2 cases in Europe as well as outside China. The infections, first limited in Northern Italy, have eventually spread to all other regions. When controlling an emerging outbreak of an infectious disease it is essential to know the key epidemiological parameters, such as the basic reproduction number R₀, i.e. the average number of secondary infections caused by one infected individual during his/her entire infectious period at the start of an outbreak. Previous work has been limited to the assessment of R₀ analyzing data from the Wuhan region or Mainland China. In the present study the R₀ value for SARS-CoV-2 was assessed analyzing data derived from the early phase of the outbreak in Italy. In particular, the spread of SARS-CoV-2 was analyzed in 9 cities (those with the largest number of infections) fitting the well-established SIR-model to available data in the interval between February 25–March 12, 2020. The findings of this study suggest that R₀ values associated with the Italian outbreak may range from 2.43 to 3.10, confirming previous evidence in the literature reporting similar R₀ values for SARS-CoV-2.

Highlights

• •The SIR model was applied to the early spread of SARS-CoV-2 in Italy
• •The SIR model fits well the reported COVID-19 cases in Italy
• •We assessed the basic reproduction number R0
• •We compared our results with previous literature findings and found that the basic reproduction number associated with the Italian outbreak may range from 2.43 to 3.10

1. Introduction

Italy joined the list of SARS-CoV-21 -affected countries on 31 January when two people tested positive for coronavirus disease 2019 (COVID-19). A cluster of cases was later detected, starting with 16 confirmed cases in Lombardy on 21 February 2020. As of March 12th, the spread of the coronavirus is mainly concentrated in the North of Italy and more precisely in the regions of Lombardy, Veneto, Emilia Romagna and Piedmont. The largest number of infections is recorded in the cities of Bergamo, Lodi, Cremona, Brescia, Milan and Pavia, while Piacenza and Parma are the most affected cities of Emilia Romagna. The other cities affected by the contagion were found in the Veneto region in the city of Padua mostly. On March 9th nationwide lockdown came into force to prevent SARS-CoV-2 spreading further.

The basic reproduction number, R ₀, is the number of secondary infections resulting from a single primary infection into an otherwise susceptible population. It is used to measure the transmission potential of a disease and is the most widely used estimator of how severe an epidemic outbreak can be. If R ₀ < 1, on average an infectious individual infects less than one person and the contagion is expected to stop spreading. In the present study the R ₀ value for SARS-CoV-2 was assessed analyzing data derived from the early phase of the outbreak in Italy. In particular, the spread of SARS-CoV-2 was analyzed in 9 cities (those with the largest number of infections) fitting the well-established SIR-model to available data.

2. Materials and methods

A well-known mathematical description of the spread of a disease in a population is the SIR model, which divides the population of N individuals into three compartments (varying as a function of time, t): S(t) are those susceptible but not yet infected with the disease, I(t) is the number of infectious individuals and R(t) are those individuals who have recovered from the disease and now have immunity to it. The SIR model describes the change in the population of each compartment in terms of two parameters, β and γ, with β describing the effective transmission rate of the disease and γ is the mean recovery rate. According to the SIR model, new infections occur as a result of contact between infectives and susceptibles. The rate at which new infections occur is β·S·I. When a new infection occurs, the individual infected moves from the susceptible compartment to the infective compartment. The other process that can occur is that infective individuals can enter the removed class at a rate γ·I. Assuming that at the outset of an epidemic nearly everyone is susceptible, the basic reproduction number is given by R ₀ = β / γ.

The SIR model can be expressed by the following set of ordinary differential equations:

$$\frac{\mathit{dS}}{\mathit{dt}}=-\mathit{\beta IS}$$

$$\frac{\mathit{dI}}{\mathit{dt}}=\mathit{\beta IS}-\mathit{\gamma I}$$

$$\frac{\mathit{dR}}{\mathit{dt}}=\mathit{\gamma I}$$

where the disease transmission rate β > 0 and the recovery rate γ > 0 (and with 1/γ representing the duration of the infection). A detailed description of the model is provided elsewhere [1,2].

In this paper the spread of SARS-CoV-2 was analyzed in the cities of Bergamo, Lodi, Cremona, Brescia, Milan, Pavia, Piacenza and Parma fitting the SIR-model to SARS-CoV-2 cases in the population in the interval between February 25 and March 12, 2020. Furthermore, R ₀ was assessed fitting the SIR-model to the reported cases of coronavirus disease 2019 (COVID-19) in the whole country. The coefficient of determination, r ², was used to assess the goodness of fit of the SIR model to data. The number of confirmed cases of COVID-19 cases was collected from the Italian Ministry of Health [3].

3. Results and discussions

Table 1 shows R ₀ values for SARS-CoV-2 assessed in the 9 Italian cities reporting the largest number of cases. The SIR model fits well to the reported COVID-19 data with r ² in the range 0.85–0.99. It is plausible that lower r ² values reflect a poorer fit in the initial data, where official estimates are most likely subject to a large uncertainty. Furthermore, it should be noted that the present study only considers data between February 25 and March 12. This is because the nationwide lockdown established on March 9 is likely to alter the initial R ₀ value in the following days [6].

Table 1.

R₀ values for SARS-CoV-2 assessed analyzing data derived from the early phase of the outbreak in the 9 Italian cities reporting the largest number of cases. Data refer to the interval between February 25 and March 12, 2020. A comparison with recently published R₀ values is also reported.

City	Population	R0	r2
Bergamo	122,161	2.52	0.98
Lodi	45,872	3.09	0.91
Cremona	72,680	2.93	0.94
Brescia	198,536	2.61	0.85
Piacenza	103,942	2.76	0.90
Milano	1,389,834	2.70	0.91
Pavia	73,195	2.43	0.91
Parma	197,499	2.46	0.99
Italy	60,483,973	3.10	0.99
Majumder et al. [4]	–	2.00–3.10	–
Li et al. [5]	–	1.40–3.90	–
Wu et al. [7]	–	2.47–2.86	–
Zhao et al. [8]	–	2.24–3.58	–
Chen et al. [9]	–	3.58	–

Previous work has only focused to the assessment of R ₀ analyzing data collected from the Wuhan region or Mainland China. Our results suggest that R ₀ values associated with the Italian outbreak (at time of writing) may range from 2.43 to 3.10, when using data from February 25, 2020 through March 12, 2020, thus confirming the pandemic potential of SARS-CoV-2. This is consistent with [4], reporting R ₀ values in the range 2.0 to 3.1 and with [5,7] reporting R ₀ values in the range 1.4–3.9 and 2.47–2.86, respectively. In another study Zhao et al. [8] reported similar values, with R ₀ ranging from 2.24 to 3.58 while Chen et al. [9] estimated R ₀ for SARS-CoV-2 to be slightly higher, i.e. 3.58.

Fig. 1 shows the SIR model fitted to the data of infectious and recovered people in the early phase of the outbreak in Italy (February 25–March 12, 2020). The SIR model fits very well reported data, both for the number of infectious people (r ² = 0.99) and for the number of recovered people (r ² = 0.98). The doubling time resulted to be about 3.1 days, in good agreement with the values of 1.4 days, 3 days and 2.5 days reported for the cities of Hunan, Xinjiang, and Hubei, respectively [10]. However, the doubling time in a disease outbreak is not constant and for the outbreak of SARS-CoV-2 it has changed in recent weeks and will continue to change with time.

Fig. 1.

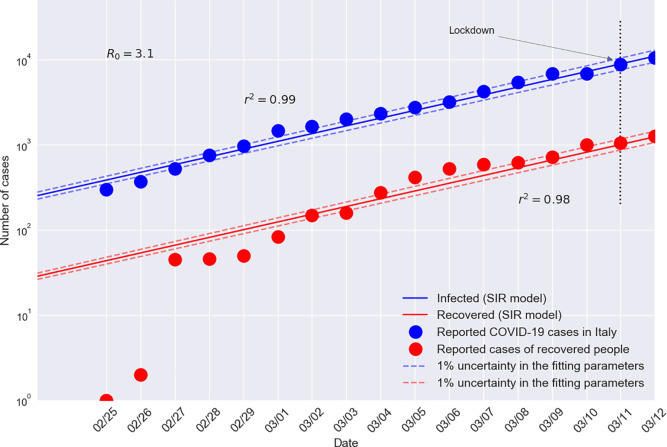
SIR model fitted to reported cases of COVID-19 and to the number of recovered people in the early phase of the outbreak in Italy (February 25–March 12, 2020). Data were collected from [3]. Dotted bands correspond to a 1.0% uncertainty attributed to the fitting parameters, β and γ.

In the present study the date of epidemic outbreak was assessed extrapolating to t = 0 the fitting function associated with the infectious population (Fig. 1), obtaining February 1st as a possible date of epidemic outbreak in Italy.

Ultimately, it is worth noticing that SARS-CoV-2 has a latent phase during which the individual is infected but not yet infectious (median incubation 4.5–5.8 days [11]). This delay between the acquisition of infection and the infectious state can be incorporated within the SIR model by adding a latent population (i.e. SEIR model). Since the latency delays the start of the individual's infectious period, the secondary spread from an infected individual will occur at a later time compared with an SIR model, which has no latency. Therefore, including a longer latency period will result in slower initial growth of the outbreak. However, since the model does not include mortality, the basic reproduction number, R ₀ = β / γ, would not change.

In conclusion, despite the Italian outbreak being the worst in Europe by the end of 12 March 2020, our findings would seem to suggest that the R ₀ value of SARS-CoV-2 is in the range 2.43 to 3.10, consistent with R ₀ values reported for Wuhan or the Chinese Mainland. Mitigation strategies (e.g. social distancing, quarantine measures, travel restrictions) are essential to contrast further epidemic spreading, especially in countries experiencing a lag time behind the Italian outbreak.

Conflict of interest statement

The authors declare that there are no conflicts of interest.