Coordination amongst quadriceps muscles suggests neural regulation of internal joint stresses, not simplification of task performance

Significance

Our study overturns a common hypothesis about how the nervous system produces movement. According to this hypothesis, muscles with complementary contributions to overt task performance (e.g., similar joint torques and endpoint forces) are controlled as a single functional unit, often referred to as a “muscle synergy,” and so the activation of muscles with similar task-related actions should strongly covary. Our results do not support this hypothesis and, instead, suggest that covariation patterns amongst muscles better reflect the control of low-level aspects of limb mechanics, such as the stresses and strains within joints. In addition to arguing against this standard interpretation of muscle covariation patterns, our experiments also highlight the critical role of the nervous system in regulating internal joint mechanics.

Abstract

Many studies have demonstrated covariation between muscle activations during behavior, suggesting that muscles are not controlled independently. According to one common proposal, this covariation reflects simplification of task performance by the nervous system so that muscles with similar contributions to task variables are controlled together. Alternatively, this covariation might reflect regulation of low-level aspects of movements that are common across tasks, such as stresses within joints. We examined these issues by analyzing covariation patterns in quadriceps muscle activity during locomotion in rats. The three monoarticular quadriceps muscles (vastus medialis [VM], vastus lateralis [VL], and vastus intermedius [VI]) produce knee extension and so have identical contributions to task performance; the biarticular rectus femoris (RF) produces an additional hip flexion. Consistent with the proposal that muscle covariation is related to similarity of muscle actions on task variables, we found that the covariation between VM and VL was stronger than their covariations with RF. However, covariation between VM and VL was also stronger than their covariations with VI. Since all vastii have identical actions on task variables, this finding suggests that covariation between muscle activity is not solely driven by simplification of overt task performance. Instead, the preferentially strong covariation between VM and VL is consistent with the control of internal joint stresses: Since VM and VL produce opposing mediolateral forces on the patella, the high positive correlation between their activation minimizes the net mediolateral patellar force. These results provide important insights into the interpretation of muscle covariations and their role in movement control.

The detailed spatiotemporal structure of muscle activations can provide insight into the control strategies used by the central nervous system (CNS) to produce movement (1–4). For instance, muscle activations have been shown to covary during the production of many behaviors. According to one common hypothesis, the covariation between muscle activations reflects a neural strategy in which muscles with similar contributions to task performance are controlled together as a single functional unit, often referred to as a “muscle synergy” (5–8). This strategy might simplify task performance by reducing the number of variables that need to be specified for the production of behavior. For example, the quadriceps muscles VL and VM have very similar contributions to task performance with each muscle producing a similar extension torque at the knee (9–11); in rats, which have knees that can move in both flexion/extension and pronation/supination, VM and VL produce similar actions along all degrees of freedom (11). Consistent with the proposal that covariation patterns reflect muscles’ contribution to task performance (7, 12–15), the activations of VM and VL are strongly correlated (15–18), suggesting that the CNS might control VM and VL as a single functional unit to simplify the achievement of task goals (19).

Alternatively, covariation of muscle activations might reflect aspects of motor control other than achieving task goals. Although VM and VL have similar contributions to task performance, they produce opposing mediolateral forces on the patella (11, 20, 21). The strong correlation between VM and VL might, therefore, reflect minimization of net mediolateral patellar forces to prevent aberrant patellofemoral loading (17, 22). In this interpretation, covariation between these muscles reflects the regulation of low-level biomechanical features that are common across tasks, such as those affecting joint integrity rather than simplification of task performance.

We evaluated these issues by recording the activity in all four quadriceps muscles, including RF and VI, during locomotion across a number of task conditions in the rat. Like VM and VL, RF and VI both produce knee extension, but RF also produces an extra flexion torque at the hip (Fig. 1). If covariation patterns among muscles reflect the similarity of their contributions to task performance, the correlations among the three vastii muscles (VM, VL, and VI) should be equally strong and stronger than their correlations with RF since these three muscles all have the same contribution to task performance. However, unlike VM and VL, neither VI nor RF produces a strong mediolateral force on the patella (23). Therefore, if covariation patterns among muscles reflect regulation of internal joint stresses, the correlation between VM and VL should be higher than the correlation between any other pair of quadriceps muscles, reflecting the need to balance mediolateral forces on the patella. Furthermore, such a low-level control strategy to balance mediolateral patellar forces should be common across variations in task conditions; hence, we expect the correlation between VM and VL to be the highest independent of speed and incline of locomotion. Our results support these latter predictions, suggesting that covariation patterns among quadriceps muscles reflect control of low-level aspects of internal joint mechanics better than simplification of task performance. These results, therefore, call for a reinterpretation of previous studies examining muscle activation covariation and suggest the importance of internal joint stresses and strains when investigating neural control strategies.

Fig. 1.

Quadriceps actions. Quadriceps muscles attach to the patella, which transfers muscle forces to the tibia via the patellar tendon. Forces from VM, VL, VI, and RF produce extension torque at the knee. In addition, RF produces a flexion torque at the hip. Besides joint torques (task variables), VM and VL also produce opposite mediolateral forces on the patella, while RF and VI have minimal effect on mediolateral patellar forces (internal joint variables). Poor regulation of these mediolateral forces might cause aberrant contact stresses within the knee due to patellar loading or displacement.

Results

Stride-Averaged Activities of VM and VL Are Strongly Correlated across Task Conditions.

We first examined the covariation patterns among stride-averaged activity of each quadriceps muscle across task conditions. If covariation patterns reflect simplification of task performance, the activity of VM, VL, and VI should be similar to each other for all task conditions but distinct from the activity of RF. If these patterns reflect control of internal joint stresses, the activity in VM and VL should be similar to each other but distinct from activity in both RF and VI.

An example of the activity in quadriceps muscles for one animal and task condition (upslope locomotion at 20 m/min) is illustrated in the SI Appendix, Fig. S1, demonstrating the good signal to noise ratio of electromyography (EMG) recordings in these experiments and typical muscle activation patterns. In general, all four quadriceps were active starting in the late portion of the swing phase prior to foot contact and maintained activity throughout the stance phase (SI Appendix, Fig. S1). The activity of VI and RF had slightly different activation profiles, or time courses, from that of VL and VM: VI was highly active during early stance, RF activity was slightly shifted toward late stance, and both VI and RF had a prominent burst of activity during swing.

This general pattern of muscle activity was similar across animals and task conditions (Fig. 2). For all speeds and inclines of locomotion, the average activity of quadriceps muscles across animals started in late swing and was maintained throughout the stance phase. However, the detailed time course (i.e., the activation profile or envelope of activation) and intensity (i.e., the overall level of activation) of each muscle activation were different across conditions. Such differences are expected based on the different torque requirements across speeds and inclines of locomotion (24–27). In some behavioral conditions, the activity of multiple quadriceps muscles was very similar; e.g., VM, VL, and RF each had similar activity patterns during downslope walking. Strikingly, only the activity patterns in VM and VL remained similar across all task conditions, even though equivalent task performance could have been accomplished by many other alterations in quadriceps muscle activations (e.g., increasing only VL or only VM or altering all vastii in parallel).

Fig. 2.

Stride-averaged activity of VM and VL are strongly coordinated across task conditions. Stride-averaged quadriceps muscle activity is modulated by speed and incline of locomotion, both in terms of activation time course and in terms of activation intensity. However, the averaged activities of VM and VL are strikingly similar to each other for all task conditions, suggesting a tight coordination between these two muscles. Signals are represented as mean ± SE across stride averages of each animal (number of animals as indicated in the image). Signals from each animal are averaged across strides (n_s = 113 ± 60, mean ± SD, and SD, across animals and conditions). Note that the number of animals varies across conditions and muscles due to the inclusion criteria described in the SI Appendix, Detailed Methods. The activation of each muscle is normalized by its maximum across speeds or inclines for each animal for display purposes; all analyses described in the Results were performed on the unnormalized values.

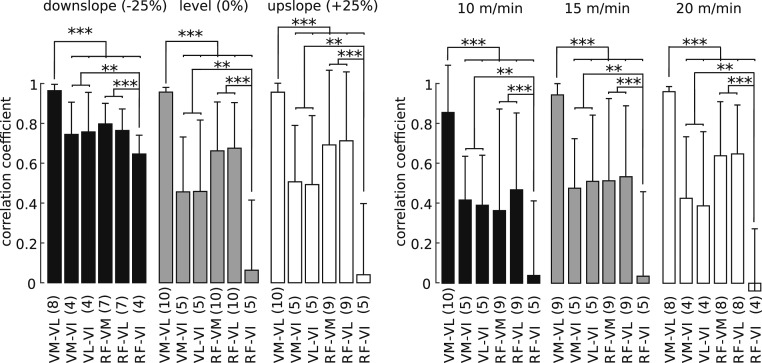
Statistical analyses of stride-averaged activation time courses confirmed these observations (Fig. 3), demonstrating strong correlation between VM and VL in all behavioral conditions (correlation coefficients across inclines: r_incline = 0.96 ± 0.03, P < 0.001; correlation coefficients across speeds: r_speed = 0.92 ± 0.15, P < 0.001). Most importantly, these correlations were higher than the correlations between the stride-averaged activation time courses of any other pair of muscles including those involving VI (all post hoc comparisons, P < 0.001) for all behavioral conditions (global test: p_{incline:muscle} = 0.61, p_speed:muscle = 0.75). We also found that the correlations between stride-averaged activation time courses of RF and VI were the lowest for all inclines (post hoc tests: p_{RFVI = VLVI} = 0.003; p_{RFVI = VMVI} = 0.006; other comparisons: P < 0.001) and speeds (post hoc: p_{RFVI = VLVI} = 0.002; p_{RFVI = VMVI} = 0.002; other comparisons: P < 0.001), reflecting the observation that VI was more active during early stance whereas RF was more active during late stance.

Fig. 3.

Correlation between VM and VL stride-averaged time courses is strongest for all task conditions. Correlations between stride-averaged activation time courses of VM and VL is stronger than correlation between stride-averaged activation time courses of any other pair of muscles for each behavioral condition. Data are shown as mean ± SD across animals (number of animals as indicated in parentheses under the bars; average number of strides for each animal as indicated above). Significance levels: **P < 0.01; ***P < 0.001.

Correlation between VM and VL Time Courses on Individual Strides Is Strongest for All Task Conditions.

If the CNS coordinates quadriceps muscles in order to balance mediolateral forces on the patella not only should the activation time courses of VM and VL be similar on average (Figs. 2 and 3), but also the time courses of these two muscles should be similar on each individual stride. We, therefore, evaluated the correlations between the activation time courses of each pair of muscles for each stride of locomotion. SI Appendix, Fig. S2 illustrates the distributions of the correlation coefficients for one animal and locomotor condition, calculated for each individual stride. In this example, the activation time courses of VM and VL were highly correlated for the vast majority of the strides. Furthermore, VM and VL were more strongly correlated than all other muscle pairs. Note also that the correlation between RF and VI appeared to be lower than the correlation between other muscle pairs, although there was high variability across strides.

These covariation patterns were consistent across animals and task conditions (Fig. 4). The time courses of VM and VL activation were highly correlated on individual strides for all locomotor conditions (r_speed = 0.82 ± 0.07, P < 0.001; r_incline = 0.86 ± 0.04, P < 0.001), and significantly more correlated than those of any other muscle pair for all inclines (global: p_{incline:muscle} < 0.001; post hoc: p_{VMVL = VLVI,−25%} = 0.02; p_{VMVL = VMVI,−25%} = 0.006; other post hoc comparisons: P < 0.001) and for all speeds (global: p_speed:muscle < 0.001; all post hoc comparisons: P < 0.001). These results demonstrate that the correlation between VM and VL was consistently the strongest correlation among quadriceps muscles independent of task conditions, supporting the idea that covariation patterns reflect regulation of internal joint stresses rather than simplification of task performance.

Fig. 4.

Correlation between VM and VL time courses on individual strides is strongest for all task conditions. The correlation between the activation time courses of VM and VL on individual strides is significantly higher than the correlation between the time courses of any other pair of muscles. This result is independent of incline and speed of locomotion. Correlation between RF and VI is the lowest for all speeds and lower than RF–VL and RF–VM for all inclines. Data are represented as mean ± SD across animals (number of animals as indicated in parentheses under the bars; number of strides for each animal, incline: 121 ± 66, speed: 105 ± 56). Significance levels: *P < 0.05; **P < 0.01; ***P < 0.001.

Similar to the results analyzing stride-averaged muscle activity (Fig. 3), we also found that the correlation between the activation time courses of RF and VI on individual strides was lower than the correlations between RF and VM (post hoc P values for downslope: p_{RFVI = RFVM,−25%}< 0.001; level walking: p_{RFVI = RFVM,0%}< 0.001; upslope: p_{RFVI = RFVM,25%}< 0.001) and RF and VL (post hoc: p_{RFVI = RFVL,−25%}= 0.01; p_{RFVI = RFVL,0%}< 0.001; p_{RFVI = RFVL,25%}< 0.001) for all inclines, and lower than the correlations between any other muscle pair for all speeds (all post hoc comparisons: P < 0.001).

Correlation between VL and VM Activation Intensities across Strides Is Strongest for All Task Conditions.

The analysis of the muscle activation time course described in the previous section does not account for covariation in activation intensities across strides: Two muscles can have similar activation time courses in each individual stride but different patterns of intensity covariation across strides (Fig. 5A). If the CNS coordinates the activity of VM and VL, the intensity in these muscles should covary. We, therefore, analyzed the correlation between activation intensities of each pair of quadriceps muscles across strides for each task condition. Fig. 5B illustrates the results of this analysis for an animal in one task condition, showing that the correlation between activation intensities of VM and VL across strides was stronger than the correlation between the intensities of any other pair of muscles.

Fig. 5.

Correlation between the activation intensities across strides. (A) High correlation between activation time courses within the gait cycle does not imply high correlation between activation intensity across strides. The cartoon on the left illustrates an example in which the activation intensities of two muscles (m1 and m2) change independently from each other from one stride to the next, although their activation time courses are highly correlated within the gait cycle. The cartoon on the right shows muscles that have both correlated activation intensities and correlated activation time courses. B illustrates the activation intensities of each pair of quadriceps muscles for each stride of locomotion (each represented by a dot, n_s = 141) and corresponding correlation coefficients (r), for a representative animal and behavioral condition. In this example, the activation intensities of VM and VL are strongly correlated and more strongly correlated than the activation intensities of the other muscle pairs.

Similar results were obtained across animals and behavioral conditions (Fig. 6). The correlation between the activation intensities of VM and VL was strong (r_incline = 0.81 ± 0.13, P < 0.001; r_speed = 0.83 ± 0.10, P < 0.001) and was higher than the correlations between all other muscle pairs (all post hoc comparisons: P < 0.001). The higher correlation between VM and VL was consistent across behavioral conditions (global tests: p_{incline:muscle} = 0.97, p_speed:muscle = 0.30). The correlations between the activation intensities of the other muscle pairs were not significantly different from one another for all inclines (all post hoc comparisons: P = 1) and speeds (post hoc: p_{VMRF = VLVI} = 0.74; all other comparisons: P = 1). These results again demonstrate the preferentially strong covariation between VM and VL activation across task conditions.

Fig. 6.

Correlation between VM and VL activation intensities is strongest for all task conditions. Correlation between intensities of VM and VL is significantly higher than the correlation between any other muscle pair. This result holds for all inclines and speeds of locomotion. The correlations between the other pairs of muscles were not significantly different from one another. Data are represented as mean ± SDs across animals (number of animals as indicated in parentheses under the bars; number of strides for each animal, incline: 121 ± 66, speed: 105 ± 56). ***P < 0.001.

Correlation between VM and VL Activity under Different Patellar Loading Conditions.

If covariation between VM and VL limits mediolateral displacements or aberrant loading of the patella, it might be especially important during the stance phase of locomotion when the knee is subject to potentially unstabilizing ground reaction forces that load the patella as compared to the swing phase when the leg is in the air. We, therefore, compared the correlation between the activity of VM and VL during stance to that during swing.

During stance, the correlations between the activation intensities of VM and VL (Fig. 7A) were significantly higher than during swing (global test: p_{stance–swing} < 0.001) independent of behavioral conditions (global test: p_{incline:stance–swing} = 0.28, p_{speed:stance–swing} = 0.16). On the other hand, the correlations between the activation time courses of VM and VL during stance were not significantly different from those obtained during swing (SI Appendix, Fig. S3A) for any incline (global tests: p_{stance–swing} = 0.2, p_{incline:stance–swing} = 0.12) or speed (global tests: p_{stance–swing} = 0.054, p_{speed:stance–swing} = 0.77).

Fig. 7.

Correlation between VM and VL activation intensities at different patellar loadings. (A) During the stance phase of the gait cycle, when ground reaction forces may destablize the patella, the correlations between VM and VL activation intensities are stronger than during the swing phase for all behavioral conditions. (B) The application of a chronic lateral force on the patella by means of an implanted spring does not alter the correlation between VM and VL activation intensities. Data are represented as mean ± SD across animals (number of animals: 8, 10, and 10 for the three levels of incline, and 10, 9, and 8 for the three levels of speed; number of strides for each animal, incline: 121 ± 66, speed: 105 ± 56; number of animals: 5, 4, and 5 for no spring, spring attached, and spring detached conditions, respectively; number of strides for each animal, 51 ± 11). ***P < 0.001; n.s., not significant, P > 0.05.

To further explore the relationship between patellar loading and covariation of VM and VL activity, we examined whether VM/VL correlation strength changed after applying a lateral force to the patella by means of a chronically implanted spring between the patella and the femur (Fig. 7B). Previous results from our laboratory demonstrated that the CNS adjusts the balance between VM and VL activity to compensate for this lateral patellar force (28). If the CNS regulates joint stresses and strains, the covariation between the activity of VL and VM should be unaffected by this change in balance so that the net mediolateral force on the patella remains consistently low.

The correlation between VL and VM muscle intensity (Fig. 7B) was unaffected by spring attachment and detachment (global test: p_spring = 0.32, Fig. 7B). Similarly, the correlations between the activation time courses of VL and VM before and after spring attachment (SI Appendix, Fig. S3B) were not significantly different from one another (global: p_spring < 0.001; post hoc: p_{no spring = attached} = 1), although correlation strength increased after spring detachment (post hoc: p_{no spring = detached} < 0.001; p_{attached = detached} = 0.02). Taken together, these results suggest that application of a chronic load to the patella has minimal effects on the covariation between VL and VM.

Discussion

We examined the patterns of covariation among quadriceps muscles during locomotion in the rat. The correlation between the activity of VM and VL was stronger than the correlation between the activity of any other pair of quadriceps muscles, and this stronger correlation was consistent across behavioral conditions. In particular, the activities of VM and VL were more strongly correlated than the activity of either of these muscles and VI, even though these three muscles have the same action on task performance. This higher correlation between VM and VL was observed for the stride-averaged time courses of muscle activity, for the time courses of muscle activity on each individual strides, and for the covariation of muscle intensities across strides. These results demonstrate that covariation patterns among quadriceps muscles do not simply reflect simplification of task performance; rather, these results support the idea that these covariations reflect regulation of internal joint mechanics. Consistent with this interpretation, correlation between VM and VL intensities was reduced during the swing phase of locomotion when potential aberrant patellar loading would be less likely.

Evaluating Muscle Covariation Patterns.

We evaluated muscle covariation in terms of the similarity of activation time courses and overall intensities of muscle activity in this study. We used these measures because of their functional interpretability, evaluating whether sets of muscles are activated in similar ways across a variety of task conditions. Although the relationship between EMG and muscle force is complex (29), these measures can also provide information about mechanical consequences of muscle activation strategies; i.e., about the contributions of these muscles to task performance (torques across joints) and their contributions to internal joint mechanics (mediolateral forces on the patella).

Other measures of muscle covariation have been used to provide insight into the strategies underlying the neural control of movement. Dimensionality reduction analyses have been used to identify muscle covariation patterns (muscle synergies) among large numbers of muscles in order to evaluate coordination strategies across entire limbs and bodies (5, 8, 30, 31), although less strict concepts of synergies might not require fixed covariation in muscle activation time courses (32, 33). The measures of muscle covariation we used in this study are clearly related to those analyses since both reflect covariation of EMG time courses and intensities and, in fact, quadriceps muscles often appear as a single synergy when analyzing EMGs during locomotion (34, 35). Our approach is similar to previous analyses examining covariation of muscles occurring spontaneously or across variations in task conditions (36–39). Although dimensionality reduction techniques provide insights into neural control strategies, they can be difficult to perform (e.g., evaluating the correct number of synergies or whether important information is left in the residual variance, but see ref. 40). The measures we used in this study are more straightforward to perform and to interpret in terms of motor function.

A different approach for evaluating muscle covariation is to examine the precise timing of motor units in different muscles, using either time domain cross-correlations or frequency domain coherence analyses (1, 15, 16). These measures provide important information about the neural drive to motor units, evaluating whether they share common inputs from the nervous system. Of particular relevance to the current study, previous experiments showed that there is strong coherence in the activity of motor units in VM and VL (15). Although this result is consistent with the strong correlations in activation time courses and intensities observed here, it is important to note that the two measures are not necessarily related: It is possible to have correlated activations without having strong coherence and to have strong coherence without correlated activity. Although there are difficulties in recording motor unit activity in free behaviors especially for deep muscles, such as VI, it would be interesting to evaluate coherence between motor units in VI and the other quadriceps muscles to determine whether the correlation patterns observed here are mirrored at the level of individual motor units.

Finally, we note that, although the measures of muscle coordination we considered here are related to each other, they reflect different aspects of muscle activation patterns and provide complementary information. For example, in many behavioral conditions, the activation time courses of RF and VI appeared temporally shifted relative to one another (Fig. 2) with VI more strongly activated during early stance and RF more strongly activated during late stance. These distinct activity patterns resulted in correlations between the activation time courses of RF and VI that were lower than those between other muscle pairs (Figs. 3 and 4). However, the correlation between the intensities of RF and VI was similar to the correlation between any other muscle pair (other than VM–VL, Fig. 6), suggesting that, although these muscles have distinct time courses, they have similar modulation of intensity across strides. Similarly, the correlation between VL and VM intensities but not their time courses differed significantly between stance and swing phases. This lack of difference in activation time course correlations likely reflects the fact that the time courses of VM and VL during swing consist of a simple synchronous burst causing knee extension in preparation of foot contact (Fig. 2) leading to high correlation between these muscles and making this measure potentially insensitive to differences in activation due to patellar loading. Despite the potential differences in these measures of covariation, the fact that, for all measures, the correlation between VM and VL was consistently stronger than that between any other pair of muscles demonstrates the robustness of this result.

Functional Role of Muscle Covariation in Quadriceps.

Our results provide important insights about the functional interpretation of the covariation between quadriceps muscle activity. Although previous studies have demonstrated a strong correlation between the activity of VM and VL (10, 41–43), the functional role of this correlation has not been clear. Since VM and VL have the same contribution to task variables and produce opposing mediolateral patellar forces (11), their strong correlation is consistent with both simplification of task performance (16, 19) and regulation of internal joint stresses (41, 44, 45). Similarly, the observation that RF could be controlled more independently than the vasti (43, 46) is also consistent with both interpretations as RF has a different task action from VM and VL (47, 48) and produces minimal mediolateral patellar force (Fig. 1). In order to distinguish between these competing interpretations, we recorded the activity in VI. This muscle has the same task action as VM and VL but has minimal action on mediolateral patellar forces (23). Although these muscles might differ in other properties (e.g., sarcomere operating range and fiber type), if muscle covariation solely reflected simplification in task performance, we would expect the activation of these muscles to be tightly coordinated. Instead, our observation that the correlation between VM and VL was higher than the correlations of either muscle to VI provides strong support that covariation patterns between these muscles best reflect regulation of internal joint stresses. It is important to note that, although the correlation between VM and VL was consistently high in these experiments, it was not perfect. Whether this residual variation in VM and VL activation has functionally relevant consequences or is simply intrinsic variability is unclear. Our results are consistent with previous work suggesting that the CNS actively coordinates quadriceps activity so as to minimize the net mediolateral force on the patella (17, 22, 49–52). Although EMG recordings provide an indirect estimate of muscle force (29), the strong correlations between the time course and the intensity of VM and VL observed here would be expected to limit the net mediolateral patellar force. Consistent with this idea, alterations in the coordination between VM and VL have been associated with the development of patellofemoral pain or patellar maltracking (17, 53). The observation here that correlation between VM and VL was reduced during swing when the chance of unexpected patellar loading is lower is also consistent with this idea. These observations suggest that covariation patterns between muscles and their alteration might provide insights into the development of musculoskeletal disorders. It is not clear, however, whether the observed cocontraction between VM and VL is sufficient to prevent patellar dislocation or maltracking. A differential control of these muscles in response to perturbations (similar to what we demonstrated previously in ref. 28) might be necessary to prevent patellar dislocations in more challenging contexts (e.g., walking on a rough terrain or during changes in running direction in rodent predator evasion or in human sport activities).

A more independent control of VI from the other quadriceps would allow the CNS to regulate other aspects of motor control while balancing VL and VM to minimize patellar loading. For example, VI could be used to stabilize the knee joint during flexion by providing antagonistic cocontractions to the hamstrings (54), consistent with the high level of VI activity we observed during the swing phase of locomotion in all behavioral conditions (Fig. 2) and potentially leaving RF to help flex the hip. Similarly, VI might be used to compensate for reductions in RF activity during fatiguing contractions (18). This strategy is consistent with the idea of uncontrolled manifolds (2) in which the activity of RF and VI would be negatively correlated in order to obtain a stable knee torque, although we did not observe such negative correlations between RF and VI here. Alternatively, activation of VI might help patellar stabilization but in a manner distinct from the coactivation of VM and VL: The relatively constant activation of VI throughout the stance phase of locomotion might ensure the patella is locked firmly within the patellar groove thereby preventing patellar dislocation. Additional experiments will be necessary to clarify the functional role of VI and its relationship to other quadriceps muscles.

The observation that the strong VM–VL correlation was consistent across task conditions might suggest that these patterns are produced by lower-level sensorimotor systems, potentially within the spinal cord. For example, last order spinal interneurons might branch to activate both VM and VL motoneurons (15, 55) or be strongly coordinated by feedback from sensory afferents (56) conveying information about patellar loading via joint receptors (57, 58) or muscle proprioceptors (59, 60). However, previous work has suggested that the strong covariation between VM and VL motor units is due to both cortical and spinal systems (15, 16), suggesting that this covariation may result from distributed processing in multiple areas of the CNS. Further work will be needed to understand the neural systems involved in coordinating these muscles and ensuring joint integrity.

It is important to note that our results do not argue against the existence of neurally specified muscle synergies. The strong and consistent correlation between VM and VL in these and other experiments is consistent with the idea that these muscles are controlled together by the CNS. Similarly, the lower correlation between VI and VM/VL might reflect coordination of VI with other muscles as part of additional synergies, potentially controlling other aspects of limb mechanics. The main contribution of this study is to demonstrate that these coordination patterns cannot simply be explained based on examination of the task related actions of muscles, therefore, arguing against the idea that such synergies serve to simplify task production. Instead, our results suggest that other factors, such as internal joint stresses and strains, might be responsible for this coordination.

Note also that coordination between VM–VL and regulation of internal joint mechanics might indirectly simplify task performance. By ensuring proper control of joint integrity, it would reduce the number of criteria that have to be specified by higher-level systems involved in performing tasks and achieving behavioral goals. This reduction of complexity would be similar to the potential simplification of muscle mechanics by spinal reflexes (59) or synergistic drive to muscles and is consistent with previous suggestions of hierarchical control strategies in the CNS (61).

Interpretation of Muscle Covariation Patterns in Other Systems.

It will be interesting to evaluate whether the results of these experiments extend to other joints and limb structures. Our ability to disambiguate between interpretations of muscle covariation relied on the conceptual simplicity of the knee biomechanics in the rat. The rat knee joint provides a clear separation between the action of quadriceps muscles on task performance and internal joint stresses, allowing us to distinguish between the different interpretations of muscle covariation (11, 22). In other joints and animals, such a separation may not be as clear, and the actions of muscles on these different aspects of motor control may need to be estimated using detailed biomechanical models (62, 63).

It is also possible that covariation patterns among muscles might reflect different processes depending on the joint/limb being considered. For instance, covariation patterns among finger muscles in primates, identified using motor unit coherence analyses, have been suggested to mainly reflect direct cortical inputs to motor units and appear to vary with task conditions (64). It will be interesting in future work to reconsider covariation patterns at other joints and limbs, evaluating whether they reflect regulation of task performance or internal joint mechanics. Regardless of the generalization of these results across limbs and joints, the results of this study, in combination with previous work (65, 66), highlights the potential importance of internal joint mechanics when interpreting muscle covariation patterns and neural control strategies.

Methods

Detailed methods can be found in the SI Appendix, Detailed Methods.

We performed experiments on adult female Sprague–Dawley rats (n = 10 without patellar perturbation, weight = 0.31 ± 0.02 g). All procedures were approved by the Animal Care Committee of Northwestern University.

Experimental Protocol.

Bipolar electrodes were implanted in quadriceps muscles for chronic recording of EMGs. All implantation surgeries were performed under isoflurane (2 to 3%) followed by postoperative analgesics (buprenorphine, 0.2 mg/kg, twice daily; meloxicam, 0.25 mg, once daily). Following recovery, quadriceps EMGs, and hindlimb kinematics (from three-dimensional tracking of markers on the skin) were recorded during, at least, 2 min of treadmill locomotion at a range of speeds (10, 15, and 20 m/min during level locomotion) and inclines (−25, level, and +25%, at 20 m/min).

We also analyzed data from a separate experiment (28) examining the effects of attaching a spring that imposed a lateral load on the patella. Details of the experimental methods can be found elsewhere (28). EMGs in VM and VL were recorded before (no spring), during (attached), and after (detached) attaching the spring. As described in ref. 28, we found that the ratio between VM and VL was altered systematically as the spring was attached and detached, consistent with regulation of the net mediolateral force on the patella (i.e., compensating for the lateral patellar load). Note that VI activity was not recorded in these animals.

Data Analyses.

We segmented EMG envelopes into separate strides, defining the beginning of each stride as the moment of foot strike. We analyzed the strength of coordination between quadriceps muscles using two measures of muscle activation. We first considered the correlation between time courses of muscle activation across the stride, evaluating how similarly each pair of muscles was modulated across the locomotor cycle in each behavioral condition. We calculated this correlation between time courses in two ways: 1) using the stride-averaged activation of each muscle (Fig. 2), and 2) using the activation of each muscle on individual strides. The second measure of coordination strength evaluated the covariation between the overall activation intensities of muscle activations across strides. Activation intensity was calculated by integrating activity separately during stance and swing phases of each individual stride. The correlation between intensities across strides was then calculated for each muscle pair and each behavioral condition.

Statistical Analyses.

We used linear mixed effect models to perform all statistical analyses. All post hoc tests were performed using Bonferroni corrections for multiple comparisons. A detailed explanation of statistical analyses for specific hypotheses can be found in the SI Appendix, Detailed Methods. Tables reporting statistical results are provided in the SI Appendix, Results of Statistical Analyses.

Data and Code Availability.

The data and code used in this study can be found at https://osf.io/m38np/ (67).