Mesoscale bicontinuous networks in self-healing hydrogels delay fatigue fracture

Significance

Muscles, composed of exquisite hierarchical structures, exhibit high fatigue resistance and can resist crack propagation even after injury. The mechanism of the hierarchical structures on suppressing crack advance under reciprocating movement is poorly understood. Tough and self-healing hydrogels are good candidates as simplified model systems for studying the mechanical behaviors of load-bearing biotissues. Here, we report that polyampholyte hydrogels, having a hierarchical structure, demonstrate high fatigue resistance through a synergistic effect between different scales. Such an antifatigue mechanism based on hierarchical structure not only gives important hints to understand fatigue-resistant behavior of biotissues with complex hierarchical structures, but also provides design strategy for tough and fatigue-resistant hydrogels, by forming multiscale network structures using noncovalent bonds as building blocks.

Abstract

Load-bearing biological tissues, such as muscles, are highly fatigue-resistant, but how the exquisite hierarchical structures of biological tissues contribute to their excellent fatigue resistance is not well understood. In this work, we study antifatigue properties of soft materials with hierarchical structures using polyampholyte hydrogels (PA gels) as a simple model system. PA gels are tough and self-healing, consisting of reversible ionic bonds at the 1-nm scale, a cross-linked polymer network at the 10-nm scale, and bicontinuous hard/soft phase networks at the 100-nm scale. We find that the polymer network at the 10-nm scale determines the threshold of energy release rate G₀ above which the crack grows, while the bicontinuous phase networks at the 100-nm scale significantly decelerate the crack advance until a transition G_tran far above G₀. In situ small-angle X-ray scattering analysis reveals that the hard phase network suppresses the crack advance to show decelerated fatigue fracture, and G_tran corresponds to the rupture of the hard phase network.

Suppression and deceleration of crack growth under cyclic loading are observed in load-bearing biological tissues, such as muscles and bones (1, 2). Such antifatigue ability of biotissues, which is essential for their function, should be related to their exquisitely organized hierarchical structures at different scales. For example, skeletal muscles, having a hierarchical structure ranging from folded proteins through noncovalent bonds at the molecular scale to muscle fibers at the micrometer scale (3, 4), sustain repeated stretching and contraction over 1 billion cycles (5, 6) and crack propagation is suppressed even to an injury (7). On the other hand, common synthetic soft materials are unstructured and usually exhibit poor fatigue resistance as a result of strain concentration at crack tip (8) or polymer network imperfection (9). For example, synthetic hydrogels could be made tough and self-healing by introducing noncovalent bonds to dissipate energy (10, 11), but these tough hydrogels show poor fatigue resistance (12, 13). Above a threshold of energy release rate G₀, the crack grows rapidly with the fatigue cycle. It has been revealed that the threshold G₀ is only determined by the primary network structure of the materials, which depends on chemical cross-linking density (13–16). The antifatigue properties of soft materials are found to be effectively improved by introducing additional structures to the primary network structure, such as crystals (17–19), composites (20–22), ordered folded units (23, 24), and so on. These results suggest that hierarchical structures may contribute to reduce the strain/stress concentration at the crack tip and hence be beneficial for fatigue resistance in these kinds of soft materials. However, the mechanism by which well-designed hierarchical structures at microscopic level can mitigate or suppress crack advance remains poorly understood.

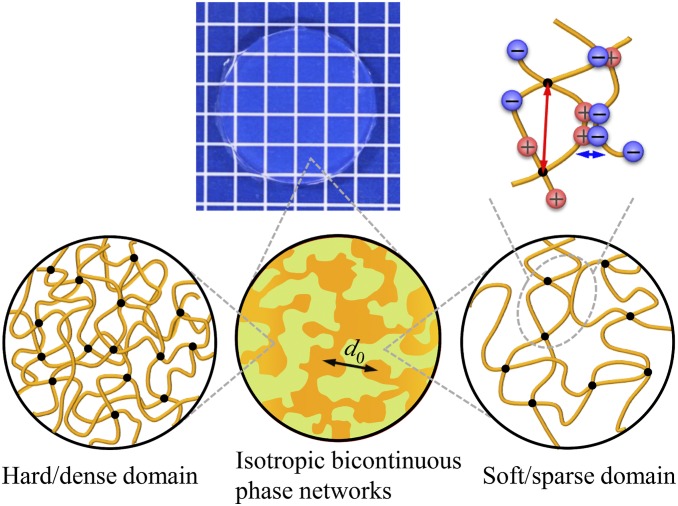
In this work we attempt to elucidate the role of hierarchical structures on the fatigue resistance of self-healing soft materials, focusing on the mechanism of suppression of crack advance and delayed antifatigue-fracture. We chose the recently developed self-healing polyampholyte hydrogels (PA gels) (25–27) as model materials. These PA gels, containing ionic bonds at the 1-nm scale, a cross-linked polymer network at the 10-nm scale, and isotropic bicontinuous hard/soft phase networks at the 100-nm scale (Fig. 1), exhibit a multiscale response to loads and dissipate large amounts of energy to show a very high toughness (28). Such hierarchical structures make the PA gels good candidates as a simple model system to study the effect of hierarchical structures on the fatigue behavior of self-healing materials containing abundant noncovalent bonds. By combining fatigue measurement and time-resolved synchrotron radiation small-angle X-ray scattering (SAXS) we discovered that, upon fatigue cycling, the bicontinuous phase networks in PA gels form a transient oriented structure to induce a pronounced crack blunting and crack deceleration effect, resulting in an extremely slow mode of crack growth above the energy release rate threshold G₀. This mode is maintained until the energy release rate exceeds a transition G_tran that is several times higher than G₀. Above G_tran, the stress-carrying hard phase network ruptures, resulting in an abrupt jump of crack growth to a fast mode. Thus, the 100-nm-scale bicontinuous hard/soft phase networks substantially decelerate the fatigue fracture and remarkably enhance the fatigue resistance of the tough hydrogels.

Fig. 1.

Illustration for hierarchical structures in PA gels. PA gels are composed of hierarchical structures containing ionic bonds (sacrificial bond) at the 1-nm scale (indicated by blue arrow), cross-linked polymer network with mesh size at the 10-nm scale (indicated by red arrow), and bicontinuous hard/soft phase networks with mesh size at d₀ ∼100-nm scale (indicated by black arrow).

Results and Discussion

Tuning Hierarchical Structures in Self-Healing Hydrogels.

PA gels used in this study were obtained from a chemically cross-linked copolymer consisting of the oppositely charged monomers sodium p-styrenesulfonate (NaSS) and methyl chloride quaternized N,N-dimethylamino ethylacrylate (DMAEA-Q) (SI Appendix, Fig. S1). The opposite charges on the polymer chains form ionic bonds when the small counter ions (Na⁺ and Cl⁻) are removed from the PA gels by dialysis of the samples in pure water. The formation of these ionic bonds induces local aggregation of the polymers, and as a result the gels form a dense hard phase and sparse soft phase interconnected at ∼100-nm scale (28). Such a structure acts as bicontinuous hard/soft phase networks. The primary network structure in the 10-nm scale depends on the formulation of monomer and cross-linker concentrations in precursor solution, which controls the cross-linking density of the network from the chemical cross-linker and from trapped polymer entanglement, while the contrast and the size of the hard/soft phase networks depend on the primary network structure as well as the temperature at which the dialysis of the PA gels was performed. In this work, we adopted the samples with the same primary network structure but different phase network structure. For this purpose, the samples were synthesized from the same formulation but dialyzed at different temperatures (see SI Appendix for sample preparation). The samples are coded as PA-T_dial, where T_dial (5 °C, 30 °C, and 60 °C) stands for the dialysis temperature. The water content and thickness of these samples were ∼46 wt % and ∼1.64 mm, respectively, independent of T_dial.

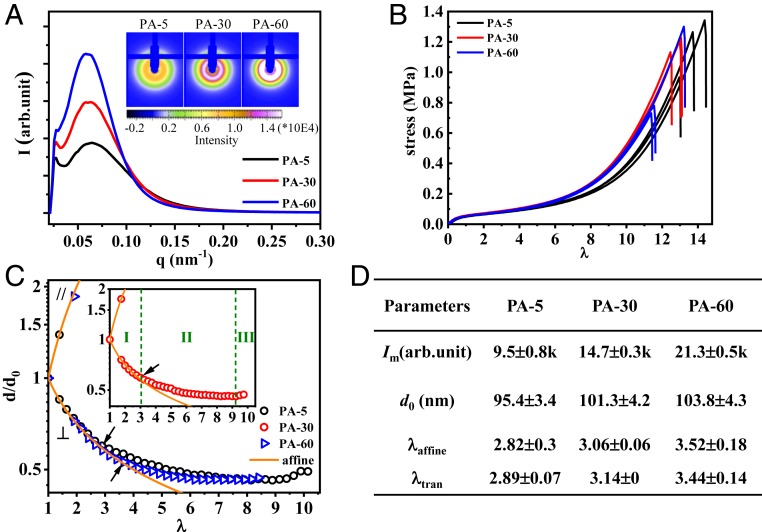
First, we show the structure and mechanical behavior of these PA gels. As shown in Fig. 2A, SAXS images of the samples show an isotropic ring and a peak in one-dimensional (1D) scattering profiles, attributed to the bicontinuous phase networks consisting of a soft network (with a low modulus) and a hard network (with a high modulus) (28, 29). The intensity of the peak I_m significantly increases with the increase of T_dial. Furthermore, the average mesh size of the phase networks, related to the periodicity of the hard and soft phases (d₀), increases slightly with the increase of T_dial (Fig. 2D). These results indicate that a higher dialysis temperature induces stronger phase separation, to form bicontinuous networks with a higher density contrast and slightly larger size. Such a temperature effect should be attributed to an enhanced hydrophobic interaction of the polymers at high temperature. The tensile behaviors of gels with different phase network structure exhibit little difference (Fig. 2B).

Fig. 2.

Structure and tensile behavior of PA gels used in this study. (A) The 1D SAXS profiles of undeformed gels dialyzed at various temperatures T_dial, coded as PA-T_dial. (Inset) The 2D SAXS images. (B) Tensile behaviors of the gels. (C) Phase network deformation ratio in parallel (d_///d₀) and perpendicular (d_⊥/d₀) directions versus global elongation ratio λ. The orange lines stand for the affine deformation of the phase networks. The maximum affine deformation λ_affine for each sample is indicated by arrows. (Inset) For clarity, the data of PA-30 are shown, and three deformation regimes are marked. (D) Summary of SAXS peak intensity I_m, average phase network mesh size d₀, maximum affine elongation ratio of phase networks λ_affine in tensile test, and critical elongation ratio of fatigue test for fast crack growth, λ_tran (extracted from Fig. 3D). a.u., arbitrary unit.

Deformation of Mesoscale Bicontinuous Phase Networks under Tensile Test.

The deformation of the phase networks of PA gels shows three regimes, as observed by in situ time-resolved SAXS during a uniaxial tensile test (SI Appendix, Fig. S3 and Fig. 2C). In regime I, the bicontinuous networks deform affinely, assuming incompressibility. That is, the mesh size of the phase networks in the parallel (d_//) and perpendicular (d_⊥) direction obeys d_///d₀ = λ and d_⊥/d₀ = λ^−1/2, respectively, with the global elongation ratio λ. As previously demonstrated (28), the loading–unloading curves exhibit a fully recoverable hysteresis in the affine deformation regime. During loading, the ionic bonds break, and the polymer chains in a globule conformation are unfolded, contributing to energy dissipation responsible for toughening the materials. During unloading, the entropic elasticity drives the polymer chains back to their original globule conformation. After a certain waiting time, the temporary ionic bonds formed in the deformed state dissociate and the original ionic bonds in the undeformed state are reformed to show full recovery of structure and properties. In regime II, d_⊥/d₀ decreases slowly and deviates from affine deformation. In this regime, the first loading sample softens but fully shrinks back to its original size after a sufficiently long waiting time, which indicates that the hard phase network ruptures, while the soft phase network stays intact, providing the entropic restoring force (28). In regime III, d_⊥/d₀ increases slightly with λ, and the failure of the whole sample occurs soon thereafter, by rupture of the soft phase network. We observe that the maximum stretch ratio for the affine-like deformation of the phase network, λ_affine, slightly increases with the dialysis temperature of the samples (Fig. 2D). This order is consistent with the change in the degree of phase contrast and mesh size d₀ of the two networks that both increase with dialysis temperature.

Suppressed Crack Advance and Delayed Fatigue Fracture.

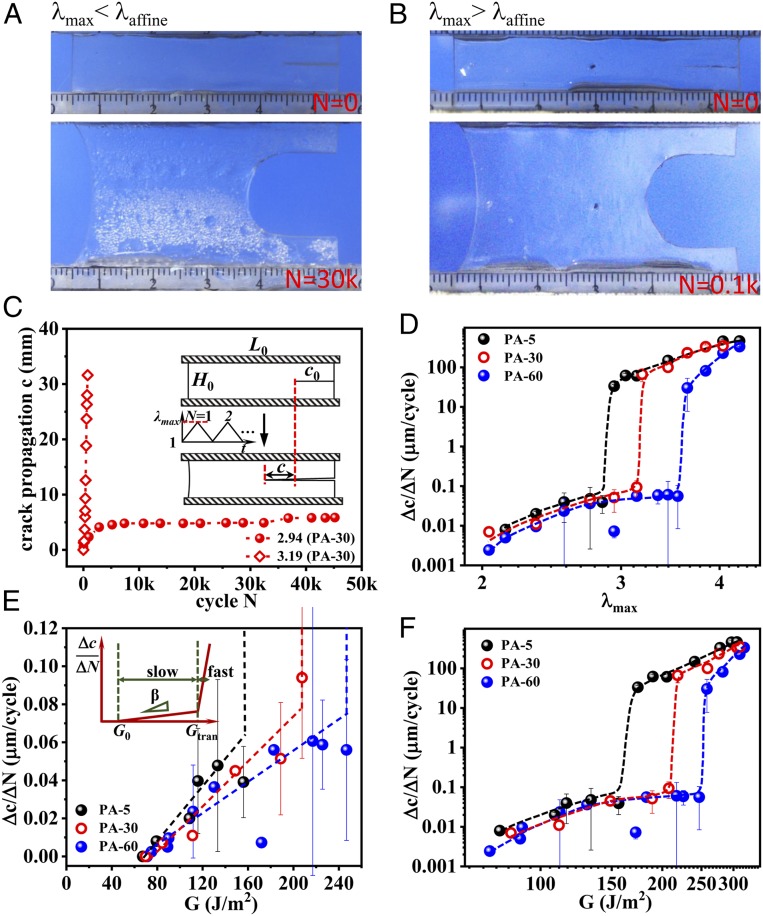
Then, we explored the cyclic fatigue behavior in uniaxial tension of these PA samples with differently tuned bicontinuous phase networks. The fatigue experiments were performed using prenotched samples in the pure shear geometry (Fig. 3C, Inset) in a humidity-controlled box (SI Appendix, Fig. S2A), following the method by Suo and coworkers (30). The cyclic fatigue behaviors are found to be sensitively depended on the relationship between the maximum stretch ratio λ_max applied in the cyclic fatigue test and the maximum affine deformation ratio λ_affine observed in the tensile test. As shown in Fig. 3 A–C for the PA-30 as a representative, we observe a striking difference for λ_max = 2.94 (<λ_affine) and λ_max = 3.19 (>λ_affine). For λ_max = 2.94, a blunt crack tip forms progressively (Fig. 3A). The crack length c initially increases fast, but crack growth slows down soon to a much slower crack propagation rate with increasing cycle N. The average crack advance rate at steady state Δc/ΔN is extremely small (Δc/ΔN = 0.028 μm per cycle; red sphere in Fig. 3C). On the other hand, for λ_max = 3.19, a relatively sharp crack tip is observed (Fig. 3B), and the crack length c always increases fast with the number of cycles N. The samples failed after only 800 cycles, showing a fast crack propagation rate Δc/ΔN (∼59 μm per cycle; red diamond in Fig. 3C), three orders of magnitude larger than that of the sample tested at λ_max = 2.94.

Fig. 3.

Delayed fatigue fracture of PA gels. (A and B) Shape of crack tip for fatigue test under λ_max = 2.94 (<λ_affine) at 30,000 cycles (A) and λ_max = 3.19 (>λ_affine) at 100 cycles (B) for PA-30 as a representative. (C) Crack propagation length c as a function of cycle N at elongation ratio λ_max = 2.94 and 3.19 for PA-30. (Inset) The geometry of the sample applied in the fatigue test (width L₀ = 50 mm, height H₀ =10 mm, initial notch length c₀ = 10 mm). (D) Δc/ΔN as a function of λ_max for gels dialyzed at various temperatures T_dial. A transition for crack propagation from slow to fast mode is observed universally at λ_tran ∼ λ_affine for all of the samples. The comparison of λ_tran and λ_affine is shown in Fig. 2D. (E) The enlarged slow mode regime for Δc/ΔN as a function of energy release rate G. A linear relation Δc/ΔN = β(G − G₀) at G₀ < G < G_tran, is observed (as schemed in Inset). The G₀, β, and G_tran are shown in Table 1. (F) The Δc/ΔN as functions of G in log-log plot. Δc/ΔN jumps from a low plateau (<0.1 µm per cycle) to a high value (>10 µm per cycle) at G = G_tran. The dashed lines are guides for the eyes. The average crack advance velocity Δc/ΔN is estimated from the slope at steady state. The Δc/ΔN values at the boundary of the transition regime in D, E, and F are obtained from the statistical average values of the high probability mode at the corresponding λ_max (see SI Appendix, Fig. S5).

We observed similar behaviors for PA-5 where the crack length c also initially increased fast, slowed down, and finally hardly increased at a representative elongation ratio λ_max = 2.54 (<λ_affine), while it increased rapidly until fracture of the whole sample at λ_max = 2.94 (>λ_affine) (SI Appendix, Fig. S4A). PA-60 also exhibits the same suppression of crack advance (crack blunting) and fast crack extension behavior at λ_max = 2.94 (<λ_affine) and λ_max = 3.84 (>λ_affine), respectively (SI Appendix, Fig. S4B).

The λ_max dependences of the crack growth rate Δc/ΔN for the three materials with different T_dial are shown in Fig. 3D. All three of the materials show no measurable crack growth over 40,000 cycles below a threshold value of λ_max defined here as λ₀. Above λ₀, the crack started to grow slowly at steady state. A transition of Δc/ΔN from a slow crack growth mode to a fast crack growth mode occurred at a value of λ_max that we define as λ_tran. Specifically, the three materials show a similar threshold value λ₀ ∼2, and the crack advances very slowly (Δc/ΔN < 0.1 µm/cycle) at λ₀ < λ_max < λ_tran, as a result of crack blunting. At λ_tran = 2.89 ± 0.07, 3.14 ± 0, and 3.44 ± 0.14 (SI Appendix, Fig. S5) for PA-5, 30, and 60, respectvely, a jump of crack growth rate Δc/ΔN to the fast mode (Δc/ΔN > 10 µm/cycle) occurs (Fig. 3D). The values of λ_tran are almost coincident with the values of λ_affine observed by the tensile test (Fig. 2D). This result suggests that λ_tran corresponds to the limit of affine deformation ratio for the fatigue test, and that the high fatigue resistance is achieved when the hard phase network is intact.

We consider that the coincidence of λ_tran and λ_affine is due to two reasons. One is that the rupture of the hard phase network occurs at similar elongation ratio λ in the fatigue test (in 10 mm × 50 mm pure shear geometry) and in the tensile test (in 16-mm × 7.5-mm strip geometry). In fact, the stress–elongation curves of the uniaxial tensile tests in pure shear geometry and in strip geometry almost overlap with each other at small λ values, where the hard phase network is in the region of affine deformation (SI Appendix, Fig. S6). Another reason is that there is no strong stress concentration around the crack tip before the rupture of the hard phase network, which is seen in Fig. 3A.

The maximum applied energy release rate G was also calculated from the work of extension of the unnotched sample (9, 30, 31). To obtain a meaningful elastic energy release rate, the hysteresis energy U_hys(λ_max) that is dissipated during each cycle by the breaking/reforming of the ionic bonds during loading is excluded from the work of extension, and G was calculated from the equation$G=W_e\left({\lambda }_{\max }\right)H_0$, where H₀ is the initial distance between the two clamps and $W_e\left({\lambda }_{\max }\right)$ is the released elastic strain energy density upon unloading for the unnotched sample up to the stretch ratio λ_max under the 3,000th cycle (at which the sample reached the steady state) (SI Appendix, Fig. S2 B and C). Even after 3,000 cycles the hysteresis loop is still very large (SI Appendix, Fig. S2D), indicating that breaking and reforming of the ionic bonds reaches a dynamic equilibrium for that applied deformation rate. Within the range of applied G, two characteristic crack growth modes are observed on a Δc/ΔN versus G plot: a slow crack growth mode with a linear relation Δc/ΔN = β(G − G₀) at G₀ < G < G_tran (Fig. 3E) and a fast crack growth mode after a jump at G = G_tran (Fig. 3F), where G₀ is the fatigue threshold, below which the crack does not grow, β is the slope of the linear response region, and G_tran is the energy release rate at which the crack growth rate transits from slow to fast mode. G₀ and G_tran correspond to λ₀ and λ_tran, respectively. High G₀ and G_tran as well as low β values mean high fatigue resistance. The parameters G₀, β, and G_tran extracted from Fig. 3 E and F are summarized in Table 1. The β is reduced and G_tran is much increased for gels dialyzed at high temperature, consistent with a high value of λ_affine and a delay in fatigue fracture. The G₀ for these three samples is almost the same (∼68 J/m²). This is consistent with the reports by Suo and coworkers showing that the threshold G₀ is determined by the chemically cross-linked polymer network structure (9, 13, 15), which is the same for the three samples. Furthermore, G₀ has the same order of magnitude as the energy required to rupture the polymer strands across the fracture plane, Γ₀, predicted by the Lake–Thomas model (32). The G_tran is more than twice higher than G₀ for PA-5, and it increases to about three times and 3.5 times for PA-30 and PA-60, respectively. Since G_tran corresponds to the maximum affine elongation ratio λ_affine of the phase networks, the abrupt increase of the crack growth rate at G_tran should be related to the breaking of the hard phase network.

Table 1.

Comparison of fatigue parameters of PA gels with various hydrogels

Sample	E*, MPa	G0 (λ0), J/m2	β, m3/(J·cycle)	Gtran, J/m2
PA-60	0.14	71.1 (1.94)	4.1 × 10−10	236.2 ± 15.0
PA-30	0.14	69.8 (1.94)	6.1 × 10−10	207.6 ± 0
PA-5	0.14	67.3 (2.04)	7.3 × 10−10	165 ± 12.7
Alginate/PAAm (13, 41)	∼0.1	35 (1.9)	(1.3 ∼ 2.3) × 10−9	84
PAAm-PVA (12)	∼0.03	9.5 (1.4)	5.3 × 10−7	40
PAMPS/PAAm DN (14)	∼0.3	200 ∼ 418 (∼1.5)	(1.3 ∼ 4.5) × 10−9	—
PAAm (30, 35)	∼0.04	4.3 ∼ 64.5 (∼1.3)	(0.3 ∼ 3.4) × 10−7	—

^*The Young’s modulus E is tested under the same condition for the fatigue test.

The Role of Bicontinuous Phase Networks in Antifatigue Fracture.

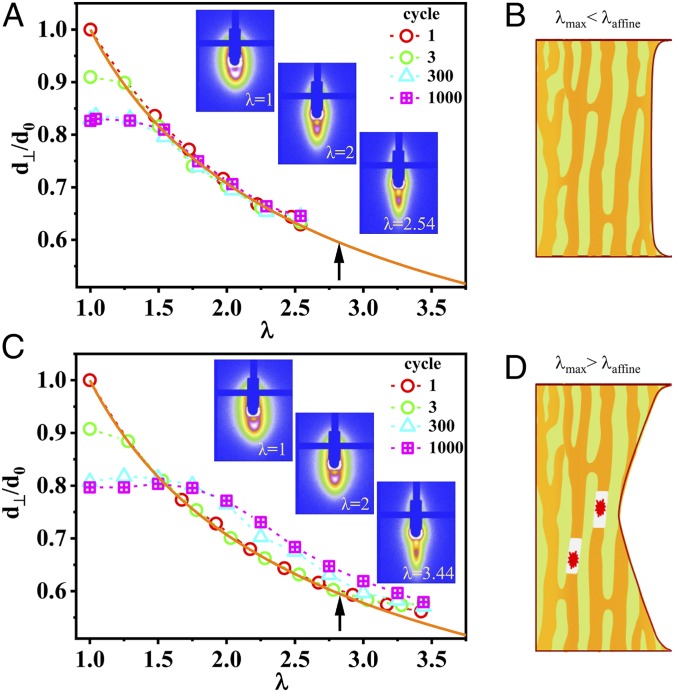
To investigate the effect of the bicontinuous phase networks on the fatigue-resistance behavior, we performed in situ time-resolved SAXS experiments to observe the evolution of the structure of unnotched gels under cyclic tensile deformation with the strip geometry (SI Appendix, Fig. S3A). Fig. 4 A and C show the stretch ratio of the phase networks in the perpendicular direction d_⊥/d₀ versus the maximum applied stretch ratio λ_max at the first, third, 300th, and 1,000th cycles for λ_max = 2.54 (<λ_affine) and λ_max = 3.44 (>λ_affine), respectively. The PA-5 sample was adopted as an example. In the case of λ_max < λ_affine, the d_⊥/d₀ always obeys affine deformation from the first to the 1,000th cycles, except at very small λ (Fig. 4A). The latter should be attributed to the residual strain at unloading state. For our consecutive cyclic tensile test at a strain rate 1 s⁻¹, the sample has not enough time to reach full recovery when the sample approaches full unloading (SI Appendix, Fig. S7). The result suggests that the deformation is reversible under cyclic loading–unloading except for very small λ. This result confirms that the hard network remains intact in cyclic loading. The representative two-dimensional (2D) SAXS patterns at different λ for the 1,000th cycle are shown in Fig. 4 A, Inset. The scattering intensities exhibit a strongly elongated spot in the perpendicular direction at large deformation (λ = 2.54), suggesting the formation of highly anisotropic structure of the phase networks during the cyclic loading. It is also confirmed that no strain-induced crystallization occurs during the cyclic loading. The highly anisotropic hard strands of the intact phase network may carry, rather homogeneously, most of the stress during loading, as suggested by other oriented hard components in composite materials (17, 20, 21), preventing the stress concentration necessary for crack growth as schemed in Fig. 4B. This is similar to the effect of strain-induced crystallization during fatigue test in elastomers, where the hard crystal reinforces crack tip (19, 33, 34). This explains why crack blunting occurs ahead of the crack tip at λ_max < λ_affine during the fatigue test in this work.

Fig. 4.

Structure evolution of PA gels under cyclic tensile deformation. (A and C) Microscopic deformation under cyclic loading at λ_max = 2.54 (<λ_affine) (A) and λ_max = 3.44 (>λ_affine) (C) for unnotched PA-5 gel. (Inset) The SAXS patterns (the stretching is along horizontal direction) at representative λ under the 1,000th cycle. The orange solid line in each figure is for affine deformation. The dashed lines are guides for the eyes. The black arrow in each figure is the maximum λ to show affine deformation λ_affine. (B and D) Illustration of bicontinuous phase network deformation and rupture at λ_max of fatigue test for λ_max< λ_affine (B) and λ_max> λ_affine (D), respectively. The red starburst pattern in D is the rupture of hard phase network.

On the contrary, when cyclic loads are performed up to λ_max > λ_affine (Fig. 4C), d_⊥/d₀ becomes increasingly larger with increasing number of cycles, deviating from the value predicted by the affine deformation. This suggests that the hard strands gradually rupture with increasing number of fatigue cycles, and the force-carrying ability of the hard strands decreases (SI Appendix, Fig. S8). Meanwhile, due to the fracture of hard strands during cyclic loading, the recovery and reassociation ability of ionic bonds with their original pairs of the virgin sample decreases, resulting in a decrease of d_⊥/d₀ at small λ with cycles, as well as a more anisotropic pattern at λ = 1 after cyclic loading at λ_max = 3.44 (>λ_affine) compared with at λ_max = 2.54 (<λ_affine) (Fig. 4 C, Inset), and a much smaller hysteresis loop U_hys at λ_max = 3.14 (>λ_affine) than at λ_max = 2.34 (<λ_affine) (SI Appendix, Fig. S2D). Once the hard strands fracture, the soft strands with sparse polymer density may carry most of the load, leading to a fast crack propagation under fatigue test as schemed in Fig. 4D, similar to a single network system (30, 35). That explains why we see a crack velocity jump when the maximum cyclic λ_max exceeds λ_affine (Fig. 3D).

To further verify the role of the hard strands for the suppression of the fast fatigue crack growth, we turned off the hard strands by preloading the unnotched sample at λ_pre > λ_affine and then performed the fatigue tests immediately at λ_max < λ_affine (Fig. 5A). The sample with ruptured hard strands exhibited the fast crack growth mode even at λ_max < λ_affine (Fig. 5B). We also preloaded the sample at λ_pre < λ_affine, a stretch at which the hard strands are not damaged. This preconditioned sample showed even slightly better fatigue resistance than the pristine sample without preconditioning. These results clearly show that the presence of hard strands suppresses the fast crack growth in fatigue fracture.

Fig. 5.

Turning off the hard phase network and its effect on fatigue behavior. (A) The experimental protocol to turn off the hard phase network: The unnotched PA-5 sample is first preloaded at λ_pre = 3.44 (>λ_affine) for 1,000 cycles, then a notch is made and fatigue test is performed at λ_max = 2.54 (<λ_affine). For comparison, a sample with λ_pre = 2.74 (<λ_affine) is also studied. The hollow arrows indicate cyclic loading. The single-line arrow indicates that fatigue test for notched sample is performed after the cyclic preloading. (B) Fatigue experimental results for samples experienced different preloading: blue, λ_pre = 3.44 (>λ_affine) with ruptured hard phase network; red, λ_pre = 2.74 (<λ_affine) with undamaged hard phase network; and black, pristine sample without preloading.

Once the hard strands rupture, the PA gels with intact soft strands act as a single network gel. If we treat the dependence of Δc/ΔN with G in the fast crack propagation regime (G > G_tran) as a linear relation, the slope β₂ is 3.1 × 10⁻⁶ ∼ 4.3 × 10⁻⁶ m³/(J·cycle) (SI Appendix, Fig. S9), close to the β value observed for single networks of PAAm gel (Table 1). The slope β₂ slightly increases with dialysis temperature of the samples, which could be associated with the increasing degree of phase contrast of the samples prepared at high dialysis temperature (Fig. 2A). A higher phase contrast indicates a higher concentration contrast and a higher modulus ratio between the hard phase network and the soft phase network. The PA-60, having the relatively weaker soft phase network among the three samples, exhibits the largest exponent β₂. This result indicates that the crack grows faster with a weaker soft phase network when the hard phase network has ruptured. Such a mechanism leads to notch sensitivity of the PA gels. The prenotched sample ruptures at much smaller elongation ratio than the unnotched sample when being compared at the same pure shear geometry, due to rupture of the hard phase network (SI Appendix, Fig. S10).

Thanks to the role played by hard phase network in PA gels, the fatigue fracture slowed down dramatically above the threshold G₀. The crack advance rate Δc/ΔN is less than 0.1 µm per cycle and β is as low as 10⁻¹⁰ m³/(J·cycle) below G_tran. To see if this fatigue fracture behavior of PA gels is unique to the self-healing PA gels with mesoscale structure, we summarized the reported fatigue fracture behaviors of various hydrogels (9, 12–14, 35) (SI Appendix, Fig. S11 and Table 1). We see that the single-network PAAm gels and the double-network PAMPS/PAAm gels, free of physical bonds, only exhibit a single mode increase of Δc/ΔN above the threshold G₀, although in the double-network gels the crack growth is significantly suppressed, resulting in a very large G₀. On the other hand, the tough and self-healing gels with physical bonds (PAAm-PVA and Ca-alginate/PAAm) also show multimode-like fatigue behaviors above the threshold G₀, though not as prominently as the PA gels. Especially in the case of Ca-alginate/PAAm gels with ionic cross-links, a relatively clear slow to fast crack growth transition is observed at G_tran = 84 J/m². These results suggest that these gels containing physical bonds may also contain mesoscale structure. In fact, phase separation was observed in PAAm-PVA gels (11, 36). We also see that the β of PA gels and Ca-alginate/PAAm gels with ionic bonds is orders of magnitude smaller than the PAAm-PVA hydrogels without ionic bonds, which suggests that strong physical bonds play a role to suppress the crack growth in the slow mode regime. These results clearly show that the interplay between different scales of the gels substantially delays the fatigue crack growth.

Conclusion

Most amorphous hydrogels exhibit extremely poor fatigue resistance. Above the fatigue threshold G₀, which can be predicted by the classic Lake–Thomas theory, the fatigue crack grows rapidly to cause sample failure. Thus, the fatigue threshold G₀ has been thought of as the most critical parameter for hydrogels under cyclic loading. In this work, we discovered that the self-healing PA hydrogels with a hierarchical structure exhibit high fatigue resistance due to the existence of multimode fatigue behaviors. The 10-nm-scale polymer network structure determines the fatigue threshold G₀ for the onset of crack growth, while the phase networks at the 100-nm scale, having ionic bonds at the 1-nm scale as building blocks, decelerate the advancing of fatigue crack dramatically until reaching a transition G_tran. Above G_tran, which is directly related to the rupture of the hard phase network, fast growth of the fatigue crack occurs. The synergistic effect between the structures at different length scales results in high fatigue resistance. As G₀ and G_tran are related to the energy release rates at rupture of the primary network and the hard phase network, respectively, increasing the network density and rupture elongation ratios of these networks at different length scales should enhance the fatigue resistance of the materials. Furthermore, increasing the hierarchy number should induce high-order G transitions with large values. The role of hierarchical structures on the delay of fatigue crack advancing elucidated in this work should guide the designing of antifatigue soft materials. It also provides clues to understanding the fatigue process of biological tissues, which have a more sophisticated hierarchical structure (37–39).

Materials and Methods

Materials.

The raw materials cationic monomer DMAEA-Q, anionic monomer NaSS, chemical cross-linker N,N-methylenebis(acrylamide) (MBAA), and ultraviolet initiator α-ketoglutaric acid (α-keto) were purchased from Wako Pure Chemical Industries, Ltd and used as received.

Preparation of PA Gels.

PA gels were synthesized by a one-step random copolymerization of precursor aqueous solution containing DMAEA-Q, NaSS, MBAA, and α-keto according to previous work (25, 26, 40). The total monomer concentration is C_m = 2.0 M, and both MBAA and α-keto content are 0.1 mol % (relative to C_m).

All details associated with sample preparations, measurement of water content, tensile tests, fatigue tests, and SAXS measurements are available in SI Appendix.

Data Availability.

All data are included in the main text and SI Appendix.