Heart rate n-variability (HRnV) and its application to risk stratification of chest pain patients in the emergency department

Abstract

Background

Chest pain is one of the most common complaints among patients presenting to the emergency department (ED). Causes of chest pain can be benign or life threatening, making accurate risk stratification a critical issue in the ED. In addition to the use of established clinical scores, prior studies have attempted to create predictive models with heart rate variability (HRV). In this study, we proposed heart rate n-variability (HRnV), an alternative representation of beat-to-beat variation in electrocardiogram (ECG), and investigated its association with major adverse cardiac events (MACE) in ED patients with chest pain.

Methods

We conducted a retrospective analysis of data collected from the ED of a tertiary hospital in Singapore between September 2010 and July 2015. Patients > 20 years old who presented to the ED with chief complaint of chest pain were conveniently recruited. Five to six-minute single-lead ECGs, demographics, medical history, troponin, and other required variables were collected. We developed the HRnV-Calc software to calculate HRnV parameters. The primary outcome was 30-day MACE, which included all-cause death, acute myocardial infarction, and revascularization. Univariable and multivariable logistic regression analyses were conducted to investigate the association between individual risk factors and the outcome. Receiver operating characteristic (ROC) analysis was performed to compare the HRnV model (based on leave-one-out cross-validation) against other clinical scores in predicting 30-day MACE.

Results

A total of 795 patients were included in the analysis, of which 247 (31%) had MACE within 30 days. The MACE group was older, with a higher proportion being male patients. Twenty-one conventional HRV and 115 HRnV parameters were calculated. In univariable analysis, eleven HRV and 48 HRnV parameters were significantly associated with 30-day MACE. The multivariable stepwise logistic regression identified 16 predictors that were strongly associated with MACE outcome; these predictors consisted of one HRV, seven HRnV parameters, troponin, ST segment changes, and several other factors. The HRnV model outperformed several clinical scores in the ROC analysis.

Conclusions

The novel HRnV representation demonstrated its value of augmenting HRV and traditional risk factors in designing a robust risk stratification tool for patients with chest pain in the ED.

Background

Chest pain, which may be caused by life-threatening myocardial infarction (MI) or benign musculoskeletal pain, is one of the most common presenting complaints in the emergency department (ED) [1–3]. Majority of chest pain patients are subjected to extensive diagnostic tests to rule out acute coronary syndrome (ACS), resulting in oftentimes, prolonged and costly ED admission, with only a small proportion of these patients eventually receiving a diagnosis of ACS [3]. This can strain crowded EDs and reduce availability of resources for patients who need urgent medical attention. Hence, early identification of chest pain patients who are at high-risk of developing adverse cardiac events has been a pressing issue to contend with in the ED. Several established clinical scores have been used for risk stratifying chest pain patients in the ED [4, 5], including the History, ECG, Age, Risk factors and Troponin (HEART) [6], the Thrombolysis in Myocardial Infarction (TIMI) [7], and the Global Registry of Acute Coronary Events (GRACE) [8] scores. Of these scores, the HEART score is the most accurate and widely used [5, 9–12], with recent studies focusing on the development of risk score-based clinical pathways for rapid, yet safe discharge of low-risk patients [1, 3, 13, 14].

In a recent review of clinical scores for ED patients with chest pain [5], heart rate variability (HRV) has demonstrated its capability in building predictive models for accurate risk stratification [15–17]. HRV is a widely adopted tool for evaluating changes in cardiac autonomic regulation, and has been shown to be strongly associated with the autonomic nervous system (ANS) [18–20]. HRV analysis characterizes the beat-to-beat variation in an electrocardiogram (ECG) by utilizing time and frequency domains, and nonlinear analyses [19]. Reduced HRV has been found to be a significant predictor of adverse cardiac outcomes [21]. Given the complexity of quantifying HRV representation, several tools such as the PhysioNet Cardiovascular Signal Toolbox [22] and Kubios HRV [23] have been developed to standardize HRV analyses.

Based on the principle of parameter calculation on normal R-R intervals (RRIs; in this paper, RRIs are equivalent to normal-to-normal [NN] intervals, in which abnormal beats have been removed), HRV analysis generates only one set of parameters from a fixed length of ECG record. This limits the amount of information that can be extracted from raw ECG signals. In this paper, we proposed a novel representation of beat-to-beat variation, named as heart rate n-variability (HRnV) [24] to characterize RRIs from a different perspective. With the use of HRnV measures, multiple sets of parameters can be calculated from the same ECG record, which significantly increases the amount of extracted information. Our study is the first clinical application and evaluation of the HRnV representation in risk stratification of chest pain patients in the ED. We hypothesized that HRnV, while closely related to conventional HRV, can provide supplementary information associated with adverse cardiac events. We also investigated the potential use of HRnV parameters to develop risk prediction tools.

Methods

Study design and setting

We conducted a retrospective analysis of data collected in our previous study on risk stratification of chest pain patients in the ED [9]. A convenience sample of patients was recruited at the ED of Singapore General Hospital, a tertiary hospital with around-the-clock primary percutaneous coronary intervention capabilities and a median door-to-balloon time of 101 min [25], between September 2010 and July 2015. At ED triage, patients are classified using the Patient Acuity Category Scale (PACS), with PACS 1 patients being the most critically ill and requiring immediate medical attention and PACS 4 patients being non-urgent cases. In this study, patients > 20 years old who presented to the ED with chief complaint of chest pain and with PACS of 1 or 2 were included. Patients were excluded from the study if they had ST-elevation myocardial infarction (STEMI) or an obvious non-cardiac etiology of chest pain diagnosed by the primary emergency physician. Patients were also excluded if their ECGs had high level of noise or if they were in non-sinus rhythm; these criteria were applied to ensure the quality of HRV and HRnV analyses. Ethical approval was obtained from the Centralized Institutional Review Board (CIRB, Ref: 2014/584/C) of SingHealth, the largest public healthcare system in Singapore that includes the Singapore General Hospital as a key partner. Patient consent was waived for this study.

Data collection

During the data collection period, five to six-minute single-lead (lead II) ECG recordings were retrieved from the X-Series Monitor (ZOLL Medical Corporation, Chelmsford, MA). The first set of vital signs and troponin values from the recruited patients were extracted from the hospital’s electronic health records (EHR). In this study, high-sensitivity troponin-T was used, and an abnormal value was defined as > 0.03 ng/mL [26]; it was further stratified into three groups and coded as 0 if the value was ≤0.03 ng/mL, 1 if the value was between 1 and 3 times the normal limit, and 2 if the value was > 3 times the normal limit. Additionally, patients’ first 12-lead ECGs were interpreted by two independent clinical reviewers. Pathologic ST-elevation, ST-depression, T-wave inversions, and Q-waves were recorded. Patient demographics, medical history, and information required for computing the HEART, TIMI, and GRACE scores were retrospectively reviewed and obtained from EHR.

Proposed HRnV representation of beat-to-beat variation in ECG

HR_nV: a novel measure with non-overlapping RRIs

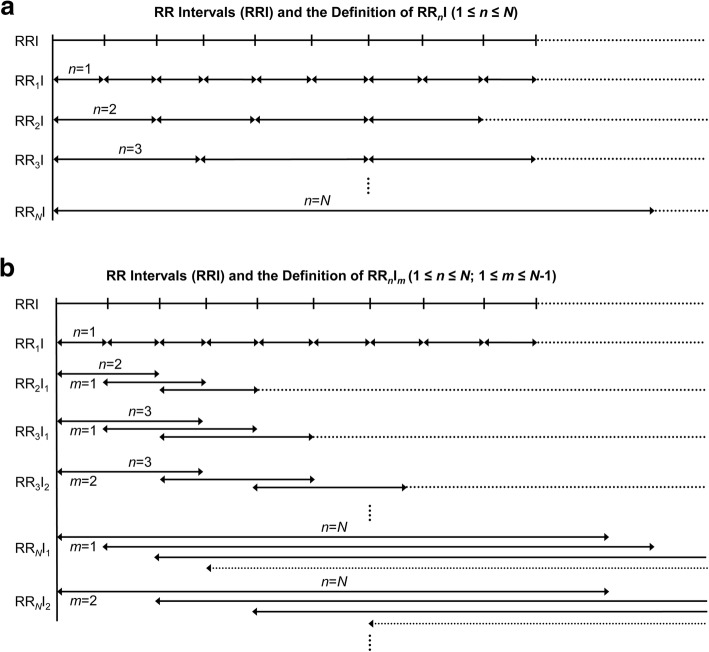
Prior to introducing the new HR_nV measure, we define a new type of RRI called RR_nI, where 1 ≤ n ≤ N, and $N\ll \widehat{N}$; $\widehat{N}$ is the total number of RRIs. The definition of RR_nI is illustrated in Fig. 1a. When n = 1, RR_nI is equivalent to conventional RRI. When n > 1, every n adjacent RRI is connected to form a new sequence of RR_nIs. By using this strategy, we can create a maximum number of (N − 1) new RR_nI sequences from conventional single RRI sequence. With these newly generated RR_nI sequences, the calculation of HR_nV parameters is straightforward and can be accomplished by applying established quantitative methods including time and frequency domain analyses and nonlinear analysis [18, 19]. In describing this new measure, we use the term “HR_nV” prior to parameter names to indicate that these parameters are calculated from RR_nI sequences. As noted in the above, HR_nV is a novel measure based on newly generated, non-overlapping RR_nIs. The computed HR_nV parameters include but are not limited to the following: the average of RR_nIs (HR_nV mean NN), standard deviation of RR_nIs (HR_nV SDNN), square root of the mean squared differences between RR_nIs (HR_nV RMSSD), the number of times that the absolute difference between two successive RR_nIs exceeds 50 ms (HR_nV NN50), HR_nV NN50 divided by the total number of RR_nIs (HR_nV pNN50), the integral of the RR_nI histogram divided by the height of the histogram (HR_nV triangular index), low frequency power (HR_nV LF power), high frequency power (HR_nV HF power), approximate entropy (HR_nV ApEn), sample entropy (HR_nV SampEn), and detrended fluctuation analysis (HR_nV DFA), among others. Notably, two new parameters NN50n and pNN50n are created, where 50 × n ms is set as the threshold to assess the difference between pairs of consecutive RR_nIs.

Fig. 1.

a Illustration of R-R intervals (RRIs) and the definition of RR_nI where 1 ≤ n ≤ N and $N\ll \widehat{N}$. $\widehat{N}$ is the total number of RRIs; b Illustration of RRIs and the definition of RR_nI_m where 1 ≤ n ≤ N, 1 ≤ m ≤ N − 1, and $N\ll \widehat{N}$. $\widehat{N}$ is the total number of RRIs and m indicates the non-overlapping portion between two consecutive RR_nI_m sequences

HR_nV_m: a novel measure with overlapping RRIs

Like RR_nI that is used in HR_nV, to define HR_nV_m measure, we introduce another type of RRI called RR_nI_m, where 1 ≤ n ≤ N, 1 ≤ m ≤ N − 1, and $N\ll \widehat{N}$. In the RR_nI_m sequence, m is used to indicate the level of overlap between consecutive RR_nI_m sequences. As illustrated in Fig. 1b, (n − m) RRIs form the overlapping portions. When m = n, RR_nI_m becomes RR_nI; therefore, the upper limit of m is N − 1. By controlling the overlap among these newly generated RR_nI_m sequences, we can create a maximum number of (N × (N − 1)/2) RR_nI_m sequences (excluding the RR_nI sequence) from conventional single RRI sequence. For each of the newly created RR_nI_m sequences, we apply time and frequency domain analyses, and nonlinear analysis to calculate HR_nV_m parameters. We add the term “HR_nV_m” prior to the parameters to denote that they are computed from RR_nI_m sequences. For example, the average RR_nI_m intervals and the sample entropy are written as HR_nV_m mean NN and HR_nV_m SampEn, respectively. The HR_nV_m measure extracts more information than HR_nV, by adopting a strategy of controlling sequence overlap.

HRnV analysis and parameter calculation

We developed the HRnV-Calc software suite (https://github.com/nliulab/HRnV) to calculate HRnV parameters. The HRnV-Calc software integrates functions from the PhysioNet Cardiovascular Signal Toolbox [22] to perform standardized ECG signal processing and QRS complex detection. Given the short ECG records in this study, the upper limit of n was set as three; thus, six sets of parameters were calculated, namely HRV, HR₂V, HR₂V₁, HR₃V, HR₃V₁, and HR₃V₂.

Clinical outcomes

The primary endpoint in this study was a composite outcome of major adverse cardiac events (MACE) [27], including all-cause death, acute myocardial infarction (AMI), and revascularization (coronary artery bypass graft [CABG] or percutaneous coronary intervention [PCI]) within 30 days of ED presentation.

Statistical analysis

Continuous variables were presented as mean and standard deviation and compared between two categories of the primary outcome (MACE) using two-sample t-test. Categorical variables were presented as frequency and percentage and compared between two categories of the primary outcome (MACE) using chi-square test. A statistically significant difference was defined as p < 0.05. To evaluate the HRnV parameters and other risk factors, we conducted univariable and multivariable analyses and subsequently developed simple prediction models using traditional logistic regression. In building the HRnV prediction model, we selected candidate variables with p < 0.2 in the univariable analysis and fed them into the multivariable stepwise logistic regression. To evaluate the predictive performance, we used leave-one-out cross-validation (LOOCV) to conduct the analysis.

Receiver operating characteristic (ROC) analysis [28] was performed to compare prediction performances among the HRnV model, HEART, TIMI and GRACE scores. The area under the ROC curve (AUC), sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV) were reported as predictive measures. Data preparation, descriptive analysis, and predictive model development were performed in R version 3.6.0 (R Foundation, Vienna, Austria); ROC analysis was conducted in MATLAB R2019a (MathWorks, Natick, MA).

Results

A total of 795 patients were selected from the originally recruited 922 patients [9]. Twenty-eight patients were excluded for ECG recording issues, four were excluded for obvious non-cardiac chest pain, and 95 were excluded for irregular rhythm/artifacts. Among the included 795 patients, 247 (31%) had the primary outcome of 30-day MACE. Table 1 shows patient baseline characteristics. Patients with the primary outcome were older (mean age 61 years vs. 59 years, p = 0.035), with a higher proportion being males (76.1% vs. 64.6%, p = 0.002). There was no statistically significant difference between MACE and non-MACE groups in terms of patient ethnicity. Factors such as history of diabetes and current smoking status were significantly more prevalent in the group with MACE.

Table 1.

Patient baseline characteristics

	Total (n = 795)	MACE (n = 247)	Non-MACE (n = 548)	p-value
Age, mean (SD)	59.63 (12.88)	61.06 (11.38)	58.99 (13.47)	0.035
Male gender, n (%)	542 (68.2)	188 (76.1)	354 (64.6)	0.002
Race, n (%)				0.623
Chinese	492 (61.9)	159 (64.4)	333 (60.8)
Indian	129 (16.2)	34 (13.8)	95 (17.3)
Malay	150 (18.9)	46 (18.6)	104 (19.0)
Other	24 (3.0)	8 (3.2)	16 (2.9)
Medical history, n (%)
Ischemic heart disease	343 (43.1)	115 (46.6)	228 (41.6)	0.22
Diabetes	278 (35.0)	106 (42.9)	172 (31.4)	0.002
Hypertension	509 (64.0)	161 (65.2)	348 (63.5)	0.707
Hypercholesterolemia	476 (59.9)	151 (61.1)	325 (59.3)	0.683
Stroke	58 (7.3)	15 (6.1)	43 (7.8)	0.458
Cancer	29 (3.6)	7 (2.8)	22 (4.0)	0.537
Respiratory disease	31 (3.9)	5 (2.0)	26 (4.7)	0.102
Chronic kidney disease	87 (10.9)	26 (10.5)	61 (11.1)	0.32
Congestive heart failure	38 (4.8)	9 (3.6)	29 (5.3)	0.407
History of PCI	199 (25.0)	68 (27.5)	131 (23.9)	0.316
History of CABG	71 (8.9)	26 (10.5)	45 (8.2)	0.355
History of AMI	133 (16.7)	48 (19.4)	85 (15.5)	0.288
Active smoker	197 (24.8)	73 (29.6)	124 (22.6)	0.003

MACE Major adverse cardiac events, SD Standard deviation, PCI Percutaneous coronary intervention, CABG Coronary artery bypass graft, AMI Acute myocardial infarction

Descriptive analyses of HRV and HRnV parameters are tabulated in Table 2. In this clinical case study, N was set as 3, thus HR₂V, HR₂V₁, HR₃V, HR₃V₁ and HR₃V₂ parameters were calculated. Among time domain parameters such as mean NN, SDNN and RMSSD, the HR_nV and HR_nV_m values were generally incremental with an increase in n. Notably, HR₂V NN50 and HR₃V NN50 were much lower than conventional HRV NN50. Moreover, NN50n and pNN50n are parameters specifically applicable to the HRnV representation. Like time domain parameters, the same trend of changes in frequency domain parameters were observed. The magnitude of increment in VLF power and LF power was larger than that of HF power with increasing n. One exception, however, was the normalized HF power, where HR_nV and HR_nV_m parameters were smaller than that of HRV. In nonlinear analysis, there were marked differences in Poincaré SD2 values between HRV and HRnV parameters. HR₂V SampEn and HR₃V SampEn were considerably larger compared to SampEn parameters of HRV, HR₂V₁, HR₃V₁, and HR₃V₂, as their confidence intervals (CIs) were wide. The wide CI was due to insufficient data points of less than 200 [19], as our ECG recordings were only five to six minutes long. HR₂V₁, HR₃V₁ and HR₃V₂ were free from this issue as they were calculated from overlapping RR_nI_m sequences where more data points were available.

Table 2.

Descriptive analyses of heart rate variability (HRV) and heart rate n-variability (HRnV) parameters

	HRV	HR2V	HR2V1	HR3V	HR3V1	HR3V2
Mean NN (s)	829.40 (169.49)	1656.65 (339.85)	1658.81 (338.99)	2484.80 (509.33)	2488.22 (508.50)	2485.02 (509.84)
SDNN (s)	38.16 (25.49)	62.28 (45.45)	68.81 (47.00)	82.06 (62.47)	97.79 (67.46)	87.77 (64.52)
RMSSD (s)	30.04 (23.07)	32.61 (26.68)	33.79 (25.67)	34.83 (28.86)	36.27 (26.50)	34.98 (27.43)
Skewness	−0.65 (2.34)	−0.41 (1.66)	−0.59 (1.95)	− 0.29 (1.29)	−0.55 (1.69)	− 0.38 (1.42)
Kurtosis	14.59 (26.83)	7.33 (13.58)	10.17 (17.90)	5.15 (8.13)	8.06 (12.92)	5.98 (9.75)
Triangular index	7.68 (4.19)	10.38 (5.10)	12.60 (6.45)	11.47 (5.29)	16.25 (7.94)	13.06 (6.04)
NN50 (count)	21.08 (33.98)	14.46 (20.35)	29.35 (40.03)	11.57 (15.05)	35.29 (44.34)	17.41 (22.51)
pNN50 (%)	6.31 (11.08)	8.66 (13.18)	8.75 (12.97)	10.31 (14.27)	10.38 (13.95)	10.28 (14.20)
NN50n (count)	–	4.16 (9.72)	8.45 (18.76)	1.37 (3.72)	4.37 (10.72)	2.08 (5.48)
pNN50n (%)	–	2.60 (6.67)	2.64 (6.47)	1.32 (3.95)	1.39 (3.86)	1.33 (3.87)
Total power (ms2)	2518.30 (4797.05)	7797.46 (16,947.44)	9156.26 (17,970.75)	13,904.78 (37,182.24)	18,714.67 (37,620.26)	15,706.11 (34,845.52)
VLF power (ms2)	985.18 (1991.52)	3401.42 (6569.37)	3922.74 (7987.46)	6503.53 (14,205.11)	8772.26 (17,986.63)	7567.79 (14,666.32)
LF power (ms2)	732.36 (1841.88)	2626.83 (7593.16)	2782.48 (7212.62)	5091.49 (18,402.20)	5740.99 (15,243.38)	5397.76 (16,001.18)
HF power (ms2)	527.27 (1232.69)	1328.86 (4033.96)	1361.53 (3433.55)	1661.69 (7237.55)	1762.45 (4851.11)	1761.05 (6477.63)
LF power norm (nu)	56.76 (19.20)	66.82 (18.17)	66.42 (17.35)	76.53 (15.32)	77.65 (14.55)	77.93 (14.95)
HF power norm (nu)	43.24 (19.20)	33.18 (18.17)	33.58 (17.35)	23.47 (15.32)	22.35 (14.55)	22.07 (14.95)
LF/HF	1.99 (1.93)	3.24 (2.95)	3.04 (2.73)	5.60 (5.21)	5.79 (4.99)	6.06 (5.18)
Poincaré SD1 (ms)	21.27 (16.34)	23.12 (18.93)	23.92 (18.18)	24.72 (20.50)	25.68 (18.77)	24.80 (19.46)
Poincaré SD2 (ms)	48.82 (33.29)	84.47 (62.15)	93.88 (64.58)	112.87 (86.62)	135.55 (94.02)	121.20 (89.72)
SampEn	1.57 (0.51)	83.84 (2324.24)	1.33 (0.48)	248.48 (4020.64)	1.06 (0.41)	1.14 (0.45)
ApEn	0.99 (0.20)	0.72 (0.18)	0.91 (0.17)	0.60 (0.15)	0.84 (0.17)	0.70 (0.15)
DFA, α1	0.99 (0.31)	1.24 (0.29)	1.23 (0.27)	1.41 (0.27)	1.42 (0.23)	1.42 (0.25)
DFA, α2	0.95 (0.22)	0.98 (0.35)	0.98 (0.22)	0.86 (0.65)	1.01 (0.22)	1.02 (0.36)

HRV Heart rate variability, mean NN Average of R-R intervals, SDNN Standard deviation of R-R intervals, RMSSD Square root of the mean squared differences between R-R intervals; NN50, the number of times that the absolute difference between 2 successive R-R intervals exceeds 50 ms; pNN50, NN50 divided by the total number of R-R intervals; NN50n, the number of times that the absolute difference between 2 successive RR_nI/RR_nI_m sequences exceeds 50 × n ms; pNN50n, NN50n divided by the total number of RR_nI/RR_nI_m sequences; VLF Very low frequency, LF Low frequency, HF High frequency, SD Standard deviation, SampEn Sample entropy, ApEn Approximate entropy, DFA Detrended fluctuation analysis

Table 3 presents the results of univariable analyses of HR_nV and HR_nV_m parameters. Eleven out of 21 conventional HRV parameters were statistically significant. Additionally, 13 HR₂V, six HR₃V, 11 HR₂V₁, seven HR₃V₁ and 11 HR₃V₂ parameters were also significant. Overall, additional 115 HRnV parameters were derived, among which 48 showed statistical significances between patients with 30-day MACE and those without. Among all HRV and HRnV parameters, mean NN, SDNN, RMSSD, NN50, pNN50, HF power, Poincaré SD1 and SD2 were statistically significant in at least five out of six measures (i.e., HRV, HR₂V, HR₂V₁, HR₃V, HR₃V₁, and HR₃V₂). Furthermore, skewness, LF power, SampEn, and ApEn, which did not demonstrate statistical significance in conventional HRV analysis, were statistically significant in HRnV representation. Table 4 presents the results of the multivariable analyses of HR_nV and HR_nV_m parameters by adjusting for age and sex. After adjustment, several parameters such as NN50 of HR₃V and HR₃V₂, and triangular index of HRV, HR₂V, and HR₃V₂, became statistically non-significant, while parameters such as ApEn of HR₂V, HR₂V₁, and HR₃V₂ became statistically significant.

Table 3.

Univariable analysis of HR_nV and HR_nV_m parameters

	HRV		HR2V		HR3V
	OR (95% CI)	p	OR (95% CI)	p	OR (95% CI)	p
Mean NN	0.999 (0.998–1.000)	0.023*	0.999 (0.999–1.000)	0.023*	1.000 (0.999–1.000)	0.023*
SDNN	0.992 (0.986–0.999)	0.023*	0.996 (0.992–1.000)	0.028*	0.997 (0.995–1.000)	0.060
RMSSD	0.990 (0.982–0.998)	0.010*	0.992 (0.985–0.998)	0.011*	0.994 (0.988–0.999)	0.030*
Skewness	1.059 (0.991–1.132)	0.088	1.079 (0.981–1.186)	0.118	1.139 (1.006–1.290)	0.040*
Kurtosis	1.006 (1.000–1.011)	0.038*	1.009 (0.998–1.019)	0.113	1.011 (0.993–1.029)	0.242
Triangular index	0.961 (0.925–0.998)	0.039*	0.967 (0.938–0.997)	0.032*	0.978 (0.950–1.007)	0.133
NN50	0.993 (0.987–0.998)	0.008*	0.989 (0.981–0.998)	0.012*	0.988 (0.977–0.999)	0.031*
pNN50	0.978 (0.962–0.995)	0.009*	0.984 (0.971–0.997)	0.014*	0.987 (0.976–0.999)	0.027*
NN50n	–	–	0.982 (0.964–1.001)	0.065	0.952 (0.905–1.002)	0.059
pNN50n	–	–	0.974 (0.946–1.002)	0.069	0.951 (0.903–1.001)	0.054
Total power	1.000 (1.000–1.000)	0.031*	1.000 (1.000–1.000)	0.021*	1.000 (1.000–1.000)	0.072
VLF power	1.000 (1.000–1.000)	0.132	1.000 (1.000–1.000)	0.070	1.000 (1.000–1.000)	0.133
LF power	1.000 (1.000–1.000)	0.077	1.000 (1.000–1.000)	0.023*	1.000 (1.000–1.000)	0.063
HF power	1.000 (0.999–1.000)	0.002*	1.000 (1.000–1.000)	0.014*	1.000 (1.000–1.000)	0.074
LF power norm	1.001 (0.994–1.009)	0.738	0.999 (0.99–1.007)	0.733	0.994 (0.985–1.004)	0.248
HF power norm	0.999 (0.991–1.007)	0.738	1.001 (0.993–1.01)	0.733	1.006 (0.996–1.015)	0.248
LF/HF	1.034 (0.959–1.116)	0.381	1.014 (0.964–1.066)	0.592	1.001 (0.973–1.031)	0.923
Poincaré SD1	0.986 (0.975–0.997)	0.010*	0.988 (0.979–0.997)	0.011*	0.991 (0.983–0.999)	0.029*
Poincaré SD2	0.995 (0.990–1.000)	0.032*	0.997 (0.994–1.000)	0.032*	0.998 (0.996–1.000)	0.063
SampEn	0.813 (0.604–1.095)	0.173	0.730 (0.545–0.977)	0.035*	1.000 (1.000–1.000)	0.932
ApEn	1.645 (0.752–3.598)	0.213	2.319 (1.003–5.357)	0.049*	1.241 (0.463–3.327)	0.667
DFA, α1	0.953 (0.585–1.552)	0.846	1.031 (0.611–1.741)	0.908	0.968 (0.560–1.672)	0.907
DFA, α2	1.532 (0.773–3.034)	0.221	1.202 (0.782–1.848)	0.401	1.184 (0.934–1.500)	0.163
	HR2V1		HR3V1		HR3V2
	OR (95% CI)	p	OR (95% CI)	p	OR (95% CI)	p
Mean NN	0.999 (0.999–1.000)	0.023*	1.000 (0.999–1.000)	0.023*	1.000 (0.999–1.000)	0.023*
SDNN	0.996 (0.993–1.000)	0.034*	0.997 (0.995–1.000)	0.042*	0.997 (0.995–1.000)	0.034*
RMSSD	0.991 (0.984–0.998)	0.010*	0.992 (0.986–0.999)	0.016*	0.993 (0.986–0.999)	0.016*
Skewness	1.061 (0.980–1.149)	0.144	1.072 (0.978–1.176)	0.139	1.098 (0.982–1.227)	0.100
Kurtosis	1.007 (0.999–1.015)	0.082	1.006 (0.994–1.017)	0.333	1.010 (0.995–1.025)	0.195
Triangular index	0.981 (0.958–1.005)	0.119	0.982 (0.963–1.001)	0.065	0.974 (0.949–0.999)	0.040*
NN50	0.995 (0.991–0.999)	0.018*	0.996 (0.993–1.000)	0.052	0.992 (0.985–0.999)	0.035*
pNN50	0.984 (0.972–0.997)	0.020*	0.988 (0.977–1.000)	0.049*	0.988 (0.976–0.999)	0.035*
NN50n	0.989 (0.979–1.000)	0.043*	0.982 (0.964–1.000)	0.054	0.974 (0.943–1.007)	0.118
pNN50n	0.969 (0.939–0.999)	0.046*	0.947 (0.895–1.002)	0.058	0.960 (0.914–1.009)	0.109
Total power	1.000 (1.000–1.000)	0.048*	1.000 (1.000–1.000)	0.072	1.000 (1.000–1.000)	0.029*
VLF power	1.000 (1.000–1.000)	0.139	1.000 (1.000–1.000)	0.145	1.000 (1.000–1.000)	0.074
LF power	1.000 (1.000–1.000)	0.084	1.000 (1.000–1.000)	0.092	1.000 (1.000–1.000)	0.027*
HF power	1.000 (1.000–1.000)	0.005*	1.000 (1.000–1.000)	0.010*	1.000 (1.000–1.000)	0.022*
LF power norm	1.000 (0.991–1.008)	0.937	0.995 (0.985–1.006)	0.382	0.995 (0.986–1.005)	0.356
HF power norm	1.000 (0.992–1.009)	0.937	1.005 (0.994–1.015)	0.382	1.005 (0.995–1.015)	0.356
LF/HF	1.024 (0.970–1.080)	0.387	1.003 (0.973–1.033)	0.863	0.999 (0.971–1.029)	0.966
Poincaré SD1	0.987 (0.978–0.997)	0.010*	0.989 (0.980–0.998)	0.016*	0.989 (0.981–0.998)	0.016*
Poincaré SD2	0.997 (0.995–1.000)	0.039*	0.998 (0.996–1.000)	0.045*	0.998 (0.996–1.000)	0.037*
SampEn	0.854 (0.623–1.171)	0.328	0.802 (0.553–1.161)	0.242	0.709 (0.500–1.005)	0.053
ApEn	2.065 (0.842–5.064)	0.113	1.207 (0.499–2.922)	0.677	2.558 (0.906–7.222)	0.076
DFA, α1	0.888 (0.514–1.537)	0.672	1.039 (0.547–1.971)	0.907	1.004 (0.549–1.835)	0.991
DFA, α2	1.557 (0.782–3.098)	0.208	1.554 (0.780–3.093)	0.210	1.169 (0.764–1.789)	0.472

HRV Heart rate variability, OR Odds ratio, CI Confidence interval, mean NN Average of R-R intervals, SDNN Standard deviation of R-R intervals, RMSSD Square root of the mean squared differences between R-R intervals, NN50 The number of times that the absolute difference between 2 successive R-R intervals exceeds 50 ms, pNN50, NN50 divided by the total number of R-R intervals; NN50n, the number of times that the absolute difference between 2 successive RR_nI/RR_nI_m sequences exceeds 50 × n ms; pNN50n, NN50n divided by the total number of RR_nI/RR_nI_m sequences; VLF Very low frequency, LF Low frequency, HF High frequency, SD Standard deviation, SampEn Sample entropy, ApEn Approximate entropy, DFA Detrended fluctuation analysis

* p < 0.05

Table 4.

Multivariable analysis of HR_nV and HR_nV_m parameters by adjusting for age and sex

	HRV		HR2V		HR3V
	OR (95% CI)	p	OR (95% CI)	p	OR (95% CI)	p
Mean NN	0.999 (0.998–1)	0.005*	0.999 (0.999–1.000)	0.005*	1.000 (0.999–1.000)	0.005*
SDNN	0.993 (0.986–0.999)	0.035*	0.996 (0.992–1.000)	0.040*	0.998 (0.995–1.000)	0.093
RMSSD	0.990 (0.982–0.998)	0.011*	0.992 (0.985–0.999)	0.016*	0.994 (0.988–1.000)	0.047*
Skewness	1.064 (0.995–1.138)	0.068	1.082 (0.983–1.191)	0.109	1.140 (1.005–1.293)	0.042*
Kurtosis	1.005 (1.000–1.011)	0.047*	1.008 (0.997–1.019)	0.139	1.011 (0.993–1.030)	0.238
Triangular index	0.967 (0.93–1.006)	0.093	0.971 (0.940–1.002)	0.070	0.982 (0.953–1.013)	0.256
NN50	0.993 (0.988–0.999)	0.013*	0.991 (0.982–0.999)	0.030*	0.990 (0.979–1.001)	0.078
pNN50	0.979 (0.963–0.996)	0.015*	0.986 (0.972–0.999)	0.033*	0.989 (0.977–1.001)	0.063
NN50n	–	–	0.983 (0.964–1.002)	0.081	0.954 (0.906–1.005)	0.077
pNN50n	–	–	0.975 (0.947–1.004)	0.086	0.952 (0.903–1.004)	0.069
Total power	1.000 (1.000–1.000)	0.042*	1.000 (1.000–1.000)	0.026*	1.000 (1.000–1.000)	0.104
VLF power	1.000 (1.000–1.000)	0.167	1.000 (1.000–1.000)	0.082	1.000 (1.000–1.000)	0.152
LF power	1.000 (1.000–1.000)	0.093	1.000 (1.000–1.000)	0.033*	1.000 (1.000–1.000)	0.105
HF power	1.000 (0.999–1.000)	0.003*	1.000 (1.000–1.000)	0.016*	1.000 (1.000–1.000)	0.101
LF power norm	1.002 (0.994–1.011)	0.589	0.999 (0.990–1.007)	0.769	0.994 (0.984–1.003)	0.202
HF power norm	0.998 (0.989–1.006)	0.589	1.001 (0.993–1.010)	0.769	1.006 (0.997–1.016)	0.202
LF/HF	1.039 (0.961–1.124)	0.336	1.013 (0.962–1.066)	0.620	0.999 (0.970–1.028)	0.928
Poincaré SD1	0.986 (0.975–0.997)	0.011*	0.989 (0.980–0.998)	0.016*	0.992 (0.983–1.000)	0.047*
Poincaré SD2	0.995 (0.990–1.000)	0.050*	0.997 (0.994–1.000)	0.046*	0.998 (0.996–1.000)	0.098
SampEn	0.852 (0.630–1.152)	0.297	0.752 (0.559–1.010)	0.058	1.000 (1.000–1.000)	0.956
ApEn	1.669 (0.754–3.693)	0.207	2.668 (1.139–6.246)	0.024*	1.507 (0.555–4.096)	0.421
DFA, α1	0.991 (0.593–1.654)	0.971	1.072 (0.622–1.848)	0.802	0.962 (0.550–1.682)	0.891
DFA, α2	1.499 (0.750–2.993)	0.252	1.204 (0.782–1.853)	0.400	1.193 (0.941–1.512)	0.146
	HR2V1		HR3V1		HR3V2
	OR (95% CI)	p	OR (95% CI)	p	OR (95% CI)	p
Mean NN	0.999 (0.999–1.000)	0.005*	1.000 (0.999–1.000)	0.005*	1.000 (0.999–1.000)	0.005*
SDNN	0.996 (0.993–1.000)	0.052	0.998 (0.995–1.000)	0.064	0.997 (0.995–1.000)	0.049*
RMSSD	0.992 (0.985–0.998)	0.015*	0.993 (0.986–0.999)	0.023*	0.993 (0.987–0.999)	0.023*
Skewness	1.066 (0.984–1.156)	0.118	1.079 (0.983–1.185)	0.108	1.099 (0.982–1.229)	0.099
Kurtosis	1.007 (0.999–1.015)	0.096	1.005 (0.994–1.017)	0.377	1.010 (0.994–1.025)	0.218
Triangular index	0.985 (0.960–1.010)	0.234	0.985 (0.965–1.005)	0.137	0.977 (0.951–1.003)	0.088
NN50	0.996 (0.991–1.000)	0.047*	0.997 (0.993–1.001)	0.130	0.993 (0.986–1.001)	0.084
pNN50	0.986 (0.973–1.000)	0.046*	0.990 (0.979–1.002)	0.111	0.989 (0.978–1.001)	0.076
NN50n	0.990 (0.980–1.000)	0.059*	0.982 (0.963–1.001)	0.064	0.975 (0.943–1.008)	0.142
pNN50n	0.971 (0.941–1.002)	0.063	0.947 (0.893–1.004)	0.067	0.962 (0.915–1.012)	0.131
Total power	1.000 (1.000–1.000)	0.064	1.000 (1.000–1.000)	0.096	1.000 (1.000–1.000)	0.035*
VLF power	1.000 (1.000–1.000)	0.173	1.000 (1.000–1.000)	0.180	1.000 (1.000–1.000)	0.086
LF power	1.000 (1.000–1.000)	0.100	1.000 (1.000–1.000)	0.108	1.000 (1.000–1.000)	0.037*
HF power	1.000 (1.000–1.000)	0.006*	1.000 (1.000–1.000)	0.014*	1.000 (1.000–1.000)	0.025*
LF power norm	1.000 (0.991–1.009)	0.960	0.995 (0.984–1.005)	0.324	0.995 (0.985–1.005)	0.329
HF power norm	1.000 (0.991–1.009)	0.960	1.005 (0.995–1.016)	0.324	1.005 (0.995–1.015)	0.329
LF/HF	1.023 (0.968–1.081)	0.428	0.999 (0.969–1.030)	0.940	0.996 (0.967–1.026)	0.786
Poincaré SD1	0.988 (0.979–0.998)	0.015*	0.990 (0.981–0.999)	0.023*	0.990 (0.981–0.999)	0.023*
Poincaré SD2	0.997 (0.995–1.000)	0.059	0.998 (0.997–1.000)	0.068	0.998 (0.996–1.000)	0.052
SampEn	0.870 (0.632–1.197)	0.393	0.842 (0.578–1.227)	0.371	0.716 (0.504–1.019)	0.064
ApEn	2.520 (1.009–6.298)	0.048*	1.413 (0.575–3.471)	0.451	3.461 (1.201–9.971)	0.021*
DFA, α1	0.898 (0.508–1.587)	0.710	1.068 (0.555–2.058)	0.843	1.005 (0.543–1.838)	0.988
DFA, α2	1.507 (0.751–3.025)	0.249	1.500 (0.746–3.014)	0.255	1.172 (0.764–1.798)	0.467

HRV Heart rate variability, OR Odds ratio, CI Confidence interval, mean NN average of R-R intervals, SDNN Standard deviation of R-R intervals, RMSSD Square root of the mean squared differences between R-R intervals, NN50, the number of times that the absolute difference between 2 successive R-R intervals exceeds 50 ms; pNN50, NN50 divided by the total number of R-R intervals; NN50n, the number of times that the absolute difference between 2 successive RR_nI/RR_nI_m sequences exceeds 50 × n ms; pNN50n, NN50n divided by the total number of RR_nI/RR_nI_m sequences; VLF Very low frequency, LF Low frequency, HF High frequency, SD Standard deviation, SampEn Sample entropy, ApEn Approximate entropy, DFA Detrended fluctuation analysis

* p < 0.05

Table 5 lists the 16 variables that were selected through multivariable stepwise logistic regression, among which there were one conventional HRV parameter and seven HRnV parameters. In addition to traditional predictors of adverse cardiac outcomes such as ST segment changes and troponin, HR₂V ApEn (OR = 0.095; 95% CI 0.014–0.628), HR₂V₁ ApEn (OR = 19.700; 95% CI 2.942–131.900) and HR₃V skewness (1.560; 95% CI 1.116–2.181) also demonstrated strong predictive power in assessing the risk of 30-day MACE. Figure 2 shows the ROC curves and Table 6 presents the results of ROC analysis in evaluating the predictive performance of the HRnV model (based on LOOCV), HEART, TIMI, and GRACE scores. The HRnV model achieved the highest AUC value and outperformed HEART, TIMI, and GRACE scores in terms of specificity, PPV, and NPV at the optimal cut-off scores, defined as the points nearest to the upper-left corner of the ROC curves.

Table 5.

Multivariable analysis with stepwise logistic regression (backward selection) on all variables

Variable	Adjusted OR	95% CI
Age	1.021	1.002–1.041
Diastolic BP	1.018	1.003–1.034
Pain score	1.082	1.003–1.168
ST-elevation	6.449	2.762–15.059
ST-depression	4.827	2.511–9.277
Q wave	3.383	1.668–6.860
Cardiac historya	7.838	5.192–11.832
Troponin	4.406	3.218–6.033
HRV NN50	0.981	0.970–0.991
HR2V skewness	0.806	0.622–1.045
HR2V SampEn	0.600	0.348–1.035
HR2V ApEn	0.095	0.014–0.628
HR2V1 ApEn	19.700	2.942–131.900
HR3V RMSSD	1.024	1.008–1.040
HR3V skewness	1.560	1.116–2.181
HR3V2 HF power	1.000	1.000–1.000

BP Blood pressure, HRV Heart rate variability, OR Odds ratio, CI Confidence interval; mean NN, average of R-R intervals; RMSSD, square root of the mean squared differences between R-R intervals; NN50, the number of times that the absolute difference between 2 successive R-R intervals exceeds 50 ms; LF Low frequency, HF High frequency, SampEn Sample entropy, ApEn Approximate entropy

^aCardiac history was a numeric value that was derived from the narrative in the hospital charts. Its value was zero if the patient history contained characteristics of atypical cardiac chest pain; Its value was two if the history contained characteristics of typical cardiac chest pain; Its value was one if the history contained characteristics of both atypical and typical cardiac chest pain

Fig. 2.

The receiver operating characteristic (ROC) curves produced by heart rate n-variability (HRnV) model (performance was based on leave-one-out cross-validation), the History, ECG, Age, Risk factors and Troponin (HEART) score, the Thrombolysis in Myocardial Infarction (TIMI) score, and the Global Registry of Acute Coronary Events (GRACE) score

Table 6.

Comparison of performance of the HRnV model (based on leave-one-out cross-validation), HEART, TIMI, and GRACE scores in predicting 30-day major adverse cardiac events (MACE)

	AUC (95% CI)	Cut-off	Sensitivity (95% CI)	Specificity (95% CI)	PPV (95% CI)	NPV (95% CI)
HRnV Model	0.888 (0.860–0.917)	0.3611a	77.3% (72.1–82.5%)	81.8% (78.5–85.0%)	65.6% (60.2–71.1%)	88.9% (86.1–91.6%)
	–	0.0352	99.2% (98.1–100.0%)	39.6% (35.5–43.7%)	42.5% (38.5–46.6%)	99.1% (97.8–100.0%)
HEART	0.841 (0.808–0.874)	5a	78.9% (73.9–84.0%)	72.8% (69.1–76.5%)	56.7% (51.4–61.9%)	88.5% (85.5–91.4%)
	–	3	99.6% (98.8–100.0%)	35.8% (31.8–39.8%)	41.1% (37.2–45.1%)	99.5% (98.5–100.0%)
TIMI	0.681 (0.639–0.723)	2a	63.6% (57.6–69.6%)	58.4% (54.3–62.5%)	40.8% (35.9–45.7%)	78.0% (74.0–82.1%)
	–	0	98.4% (96.8–100.0%)	19.3% (16.0–22.7%)	35.5% (31.9–39.1%)	96.4% (92.9–99.9%)
GRACE	0.665 (0.623–0.707)	107a	64.0% (58.0–70.0%)	60.8% (56.7–64.9%)	42.4% (37.3–47.4%)	78.9% (75.0–82.8%)
	–	60	98.8% (97.4–100.0%)	8.0% (5.8–10.3%)	32.6% (29.3–36.0%)	93.6% (86.6–100.0%)

AUC Area under the curve, CI Confidence interval, PPV Positive predictive value, NPV Negative predictive value, HEART History, ECG, Age, Risk factors and Troponin, TIMI Thrombolysis in Myocardial Infarction, GRACE Global Registry of Acute Coronary Events

^aOptimal cut-off values, defined as the points nearest to the upper-left corner on the ROC curves

Discussion

HRV has generated significant research interest in the past decades [18, 19, 29], with majority of studies focusing on development of advanced nonlinear techniques to derive novel parameters [30, 31]. There is, however, a paucity of research on alternative approaches to analyze RRIs. Vollmer [32] used relative RRIs to describe the relative variation of consecutive RRIs, with which HRV was analyzed. Likewise, we proposed a novel HRnV representation, providing more HRnV parameters than conventional HRV analysis. In this paper, we introduced two measures of HRnV, namely HR_nV and HR_nV_m. HR_nV was calculated based on non-overlapping RR_nI sequences, while HR_nV_m was computed from overlapping RR_nI_m sequences. HRnV was not developed to replace the conventional HRV but to augment it. It enables the creation of additional parameters from raw ECGs, and thus empowers the extraction of supplementary information.

In our clinical case study, we investigated the predictive value of HRnV parameters in assessing the risk of 30-day MACE for chest pain patients in the ED. In addition to 21 HRV parameters, 115 HRnV parameters were derived, of which 48 were found to be statistically significant in their association with the primary outcome. Notably, even with a small n (three in our study), newly generated HRnV parameters greatly boosted the number of candidate predictors. When longer ECG records are available, more HRnV parameters can be calculated. With HRnV parameters, HRV parameters, vital signs, and several established risk factors, we conducted multivariable logistic regression analysis and selected age, diastolic BP, pain score, ST-elevation, ST-depression, Q wave, cardiac history, troponin, HRV NN50, and seven HRnV parameters. In addition to traditional risk factors such as ST segment changes, HR₂V ApEn, HR₂V₁ ApEn, and HR₃V skewness were found to be strong predictors for 30-day MACE. Compared to the HEART, TIMI, and GRACE scores, the HRnV model achieved the highest AUC, specificity, PPV, and NPV values at the optimal cut-off points in ROC analysis. This demonstrated the clinical utility of HRnV in determining the risk of 30-day MACE for ED patients with chest pain.

Due to the wide differential diagnosis for chest pain, accurate stratification is vital, particularly for preventing low-risk patients from obtaining expensive and unnecessary medical testing and intervention [3]. Although the TIMI and GRACE scores have been validated for risk prediction of patients with chest pain in the ED [4, 33, 34], some criteria used in these scores may be inappropriate for undifferentiated chest pain cohorts in the ED, as they were originally developed for post-acute myocardial infarction patients [1]. In comparison, the HEART score was derived from a population of ED patients with chest pain, and has been extensively validated worldwide [10, 13, 27, 35]. It has demonstrated its utility in identifying both low-risk patients for possible early discharge and high-risk patients for urgent intervention. Built upon established scores, several chest pain pathways [14, 36–38] have been implemented and tested, particularly for the management of low-risk patients. Than et al. [38] evaluated a TIMI score-based accelerated diagnostic protocol (ADP) with a reported sensitivity of 99.3% and NPV of 99.1%. Similarly, a systematic review by Laureano-Phillips et al. [39] reported that the HEART score achieved both sensitivity and NPV of 100% in several validation studies. Furthermore, a cost-effectiveness study conducted in Brisbane, Australia reported economic benefits by adopting an ADP in the ED, with reduction in expected cost and length of stay amongst patients with chest pain [40].

Most established clinical scores use conventional risk factors such as biomarkers, medical history, and presenting vital signs. However, patient history can sometimes be subjective and blood tests, such as troponin, require waiting time. HRV, as a noninvasive measure, can be easily calculated from ECGs; it is an objective tool to assess the activities of the ANS [19]. It also has the advantage of requiring only several minutes to acquire (five to six minutes in our protocol), which is much faster than serum biomarkers. Over the past decades, HRV has been widely investigated in a broad range of clinical applications, particularly in cardiovascular research. Apart from being associated with sudden cardiac death [18], HRV also showed significant correlations with adverse clinical outcomes in prehospital setting [41] and with MACE outcomes in ED patients with chest pain [17]. HRV parameters have been integrated with other risk factors into machine learning algorithms to predict adverse outcomes [42, 43]. These promising results motivated the use of HRV to develop objective and computerized risk stratification tools for chest pain patients [44, 45]. In an updated review of clinical scores for chest pain, Liu et al. [5] summarized several studies which aimed to develop alternative techniques for risk stratification.

This study aimed to present novel HRnV representation and its measures and investigate their association with clinical outcomes. Although HRnV parameters showed promising performance in identifying high-risk chest pain patients, this study was not intended to create a ready-to-use clinical tool. Instead, we demonstrated the feasibility of utilizing HRnV parameters to augment conventional HRV and risk factors in designing a prediction tool/score. These HRnV parameters can be readily calculated without the collection of supplementary data. In this study, with five to six-minute ECG recording and n = 3, five-fold more HRnV parameters were calculated compared to HRV alone. When longer ECG recordings are available and parameter n is larger, more HRnV parameters can be derived. To build a HRnV-based risk stratification tool, a systematic approach is needed to derive a point-based, consistent score to ease its clinical application and practical implementation.

As a natural extension of conventional HRV, HRnV representation creates the opportunity to generate additional parameters. This representation could also serve as a smoother for RRIs, making them less sensitive to sudden changes caused by abnormal heart beats (e.g. very short or very long RRI). However, since HRnV is a novel representation of beat-to-beat variations in ECG, many technical issues need to be addressed in future research. For instance, as shown in Table 2, SampEn became larger when the available number of data points was less than 200 [19], suggesting that additional research is required to investigate its applicability to short ECG records. Moreover, parameters NN50n and pNN50n are newly introduced in HRnV representation only. They characterize the number of times that the absolute difference between two successive RR_nI sequences exceeds 50 × n ms, by assuming that the absolute difference may be magnified when the corresponding RR_nI is n times longer than RRI. Thus, in-depth investigations are required in the selection of appropriate thresholds. More importantly, physiological interpretations of the HRnV parameters and their normal values [29] need to be determined through numerous research. One example is the identification of frequency bands that correlate with certain physiological phenomenon. In the current analysis, the conventional cut-off values were adopted (i.e., ≤0.04 Hz as very low frequency range; 0.04–0.15 Hz as low frequency range; 0.15–0.4 Hz as high frequency range). With the increase in n, frequency domain analysis may need to be changed accordingly.

Beyond its use in risk stratification of ED patients with chest pain, HRnV can potentially be used in other clinical domains, where conventional HRV has been extensively investigated [46–49]. With the augmented RR_nI and RR_nI_m sequences, HRnV could possibly capture more dynamic changes in cardiac rhythms than HRV. This capability enables the extraction of additional information from limited raw ECGs. This study utilized HRnV parameters as independent risk factors and analyzed them with traditional biostatistical methods. There are multiple ways to use HRnV parameters, e.g. each set of HRnV parameters can be analyzed individually and subsequently combined with an ensemble learning [50] (a special type of machine learning algorithm) architecture to reach a decision. However, artificial intelligence and machine learning methods generally create black-box predictive models, making interpretation a challenge [51].

Limitations

This study has several limitations. First, we did not develop a scoring tool for practical clinical use. The primary aim of this study was to demonstrate the feasibility of using HRnV parameters and common risk factors to build predictive models. Second, the HRnV model was evaluated with LOOCV strategy due to the small sample size. Ideally, separate patient cohorts are needed to train and test prediction models. When a new scoring tool is developed, it is necessary to conduct external validations on cohorts with diverse patient characteristics. Furthermore, properly designed clinical pathways are needed as well. Third, the patients included in this study were mainly from the high acuity group, resulting in a higher 30-day MACE rate (i.e., 31%) compared to other similar studies [10, 39]. As a result, the generalizability of the HRnV model developed in this study may be uncertain in other patient cohorts. Fourth, the calculated HRnV and HRV parameters depended on the choice of tools and methods for ECG signal analysis. Thus, the values of these parameters may vary across studies. Last, the physiology of HRnV and interpretations of its measures are mostly unknown; calculation of some parameters also needs to be standardized. All these require future collaborative research efforts between clinicians and scientists to address.

Conclusions

In this study, we proposed a novel HRnV representation and investigated the use of HRnV and established risk factors to develop a predictive model for risk stratification of patients with chest pain in the ED. Multiple HRnV parameters were found to be statistically significant predictors, which effectively augmented conventional HRV, vital signs, troponin, and cardiac risk factors in building an effective model with good discrimination performance. The HRnV model outperformed the HEART, TIMI, and GRACE scores in the ROC analysis. It also demonstrated its capability in identifying low-risk patients, which could potentially be used to build a new clinical pathway. Moving forward, we suggest further development of a point-based, ready-to-use HRnV risk stratification tool. Although some issues remain to be addressed, we hope to stimulate a new stream of research on HRnV. We believe that future endeavors in this field will lead to the possibility of in-depth evaluation of the associations between HRnV measures and various human diseases.

Abbreviations

ACS

Acute coronary syndrome

ADP

Accelerated diagnostic protocol

AMI

Acute myocardial infarction

ANS

Autonomic nervous system

AUC

Area under the curve

ApEn

Approximate entropy

CABG

Coronary artery bypass graft

CI

Confidence interval

DFA

Detrended fluctuation analysis

ED

Emergency department

EHR

Electronic health records

GRACE

Global registry of acute coronary events

HEART

History, ECG, age, risk factors and troponin

HF

High frequency

HRnV

Heart rate n-variability

HRV

Heart rate variability

LF

Low frequency

LOOCV

Leave-one-out cross-validation

MACE

Major adverse cardiac events

Mean NN

Average of R-R intervals

MI

Myocardial infarction

NN50

The number of times that the absolute difference between 2 successive R-R intervals exceeds 50 ms

NN50n

The number of times that the absolute difference between 2 successive RR_nI/RR_nI_m sequences exceeds 50 × n ms

NPV

Negative predictive value

PACS

Patient acuity category scale

PCI

Percutaneous coronary intervention

pNN50

NN50 divided by the total number of R-R intervals

pNN50n

NN50n divided by the total number of RR_nI/RR_nI_m sequences

PPV

Positive predictive value

RMSSD

Square root of the mean squared differences between R-R intervals

ROC

Receiver operating characteristic

RRI

R-R interval

SampEn

Sample entropy

SD

Standard deviation

SDNN

Standard deviation of R-R intervals

STEMI

ST-elevation myocardial infarction

TIMI

Thrombolysis in Myocardial Infarction

VLF

Very low frequency

Authors’ contributions

NL invented the HRnV representation, conceived the study, supervised the project, and wrote the first draft of the manuscript. NL, DG, ZXK, and FX performed the analyses. NL, DG, ZXK, AFWH, FX, TT, JTS, PPP, BC, SHL, JWCT, and MEHO contributed to evaluation of the HRnV measures, interpretation of the results, and revision of the manuscript. NL, DG, ZXK, AFWH, FX, TT, JTS, PPP, BC, SHL, JWCT, and MEHO approved the final manuscript.

Funding

This work was supported by the SHF Foundation Research Grant (SHF/FG652P/2017). The study sponsor was not involved in the study design; in the collection, analysis and interpretation of data; in the writing of the manuscript; and in the decision to submit the manuscript for publication.

Availability of data and materials

The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.

Ethics approval and consent to participate

The ethical approval was obtained from the Centralized Institutional Review Board (CIRB, Ref: 2014/584/C) of SingHealth, in which patient consent was waived.

Consent for publication

Not applicable.

Competing interests

NL and MEHO hold patents related to using heart rate variability and artificial intelligence for medical monitoring. NL, DG, ZXK, and MEHO are currently advisers to TIIM SG. The other authors report no conflicts.