Highlights
-
•
Predictions of NO2 concentrations across Europe at 1 km2 spatial resolution.
-
•
Estimates of population exposed to NO2 levels exceeding WHO and EU thresholds.
-
•
Tropospheric column to-surface conversion of satellite NO2 using GEOS-Chem.
-
•
Column to-surface conversion improved slightly geostatistical predictions of NO2.
-
•
CAMS-Ensemble regional CTM simulations further improved the estimates.
Keywords: Nitrogen dioxide; Bayesian geostatistics; Ozone monitoring instrument (OMI); Chemical transport models (GEOS-Chem, CAMS-Ensemble); Copernicus; Air quality guidelines
Abstract
Bayesian geostatistical regression (GR) models estimate air pollution exposure at high spatial resolution, quantify the prediction uncertainty and provide probabilistic inference on the exceedance of air quality thresholds. However, due to high computational burden, previous GR models have provided gridded ambient nitrogen dioxide () concentrations at smaller areas of investigation. Here, we applied these models to estimate yearly averaged concentrations at 1 spatial resolution across 44 European countries, integrating information from in situ monitoring stations, satellites and chemical transport model (CTM) simulations. The tropospheric values of derived from the ozone monitoring instrument (OMI) onboard the National Aeronautics and Space Administration’s (NASA’s) Aura satellite were converted to near ground concentration proxies using simulations from the 3-D global CTM (GEOS-Chem) at 0.5° 0.625° spatial resolution and surface-to-column ratios. Simulations from the Ensemble of regional CTMs at spatial resolution of 0.1° 0.1° were extracted from the Copernicus atmosphere monitoring service (CAMS). The contribution of these covariates to the predictive capability of geostatistical models was for the first time evaluated here through a rigorous model selection procedure along with additional continental high-resolution satellite-derived products, including novel data from the pan-European Copernicus land monitoring service (CLMS). The results have shown that the conversion of columnar values to surface quasi-observations yielded models with slightly better predictive ability and lower uncertainty. Nonetheless, the use of higher resolution CAMS-Ensemble simulations as covariates in GR models granted the most accurate surface estimates, showing that, in 2016, 16.17 (95% C.I. 6.34–29.96) million people in Europe, representing 2.97% (95% C.I. 1.16% - 5.50%) of the total population, were exposed to levels above the EU directive and WHO air quality guidelines threshold for . Our estimates are readily available to policy makers and scientists assessing the burden of disease attributable to in 2016.
1. Introduction
Ground-level nitrogen dioxide () concentrations represent a serious public health concern. Exposure to elevated levels of are associated with increased cardiovascular, respiratory and all-cause mortality and respiratory morbidity (WHO, 2013, European Environment Agency, 2014). Many early epidemiological studies used measurements from the nearest monitoring sites to estimate exposure (Hesterberg et al., 2009, Latza et al., 2009). This approach introduces exposure misclassification (Jerrett et al., 2005), since it fails to capture the sources of local spatial variability. Air quality related policies require an accurate assessment of the exposures in any given area. In practice, this is difficult to address due to the complexity of the processes involved and due to the sparsity of the monitoring data. In Europe, air quality monitoring is maintained by the European Environment Agency’s (EEA’s) member states, and although there is a relatively dense network of stations, when compared to other areas globally, large parts of the continent remain unmonitored. Therefore, predicting the spatial distribution of the outdoor air pollution is an important research goal for environmental health.
There are a number of methods that have been used to provide gridded estimates on large scales (like continental or global). These include chemical transport models (CTMs) and empirical models based on their outputs (Schaap et al., 2008, Lamsal et al., 2008, Geddes et al., 2015), spatial interpolation, such as kriging (Beelen et al., 2009, Young et al., 2016) and land-use regression (LUR) (Beelen et al., 2009, Novotny et al., 2011, Vienneau et al., 2013, Knibbs et al., 2014, Bechle et al., 2015, De Hoogh et al., 2016, Young et al., 2016, Larkin et al., 2017). Each of these models has both strengths and weaknesses. In particular, the continental or global-scale dispersion models (e.g. CTMs), which follow the principles of chemistry and physics, usually have low spatial resolution, due to limitations related to computational capacity and coarse resolution of the emission inventories. The latter are typically available at 4° 5°, 2.0° 2.5°, 0.500° 0.667° or 0.2500° 0.3125° scales (Di et al., 2017); however, higher resolution inventories, like EDGAR (Emission Database for Global Atmospheric Research - https://edgar.jrc.ec.europa.eu/) are also becoming available in recent time (Crippa et al., 2018). The LUR models are technically less challenging and computationally easy to fit. They can provide predictions of concentration at very high spatial resolution (Vienneau et al., 2013), however, they don’t take into account the spatial correlation present in the air pollution data, thus overestimating the significance of the covariates. Moreover, their predictive ability is lower when compared to more complex geostatistical or geographically weighted regression models (Beloconi et al., 2018). Bayesian geostatistical regression (GR) models capture the spatial correlation present in the pollutant concentrations and provide estimates of the prediction uncertainty. Furthermore, they allow a straightforward assessment of the exposure burden through high-resolution population estimates, since the posterior predictive distributions of can be derived for every pixel within the study domain. However, as for any statistical model, predictions rely on appropriate input data (i.e. monitoring stations), which is available for most of Europe but may not be available for other regions of the world. In addition, as discussed in Shaddick et al. (2013), the prediction of levels using this set of models at high spatial resolution over large scales (e.g. for 15 countries of the European Union (EU)) is computationally complex. The approximate Bayesian inference using the stochastic partial differential equations (SPDE) approach and integrated nested Laplace approximation (INLA) (Rue et al., 2009, Lindgren et al., 2011) has shown to provide yearly-averaged gridded concentrations of particulate matter at spatial resolution across Europe in a reasonable computational time (Beloconi et al., 2018).
Most of the data-driven air-quality assessments incorporate geographical covariates derived from satellite-based observations, since they usually provide spatial coverage over the entire domain of interest. Several previous works have used the tropospheric from the ozone monitoring instrument (OMI), onboard the National Aeronautics and Space Administration’s (NASA’s) Aura satellite (Levelt et al., 2006), to estimate the corresponding surface concentrations (Lamsal et al., 2008, Novotny et al., 2011). However, there are two main issues that should be taken into consideration while using this data for modelling.
First, the satellite instruments measure total tropospheric columns and therefore the proxies derived from OMI may not represent well the corresponding surface concentrations. Aerial measurements reveal that the concentration of in the tropospheric column is determined primarily by in the mixed layer, as well as by in the boundary layer (Martin et al., 2004, Richter et al., 2005, Martin et al., 2006, Boersma et al., 2008, Bucsela et al., 2008). However, the proportion of in these two layers varies in both space and time (Lamsal et al., 2008, Grajales and Baquero-Bernal, 2014). Although recent works suggested that the satellite column abundance (total concentration within a vertical column) may be efficient to track spatial patterns in the ground-level (Bechle et al., 2013, Knibbs et al., 2014, Bechle et al., 2015), in which case conversion of columnar values to surface concentrations becomes unnecessary within a LUR model, the contribution of this conversion within a GR modelling framework to the best of our knowledge has not been evaluated.
Second, although OMI’s spatial resolution (of up to 13 × 24 km at nadir) is the highest among all available space-borne sensors (except of the recently released data from the Sentinel 5 Precursor tropospheric monitoring instrument (S5P/TROPOMI) which provides measurements at 7 × 3.5 resolution (Veefkind et al., 2012) from late 2017 onwards), it is still too coarse to capture near-source (e.g. near-roadway) concentration variability (Novotny et al., 2011). Since many parameters, including local combustion sources, land surface characteristics and atmospheric conditions influence formation and dispersion (Bechle et al., 2015, Young et al., 2016, Larkin et al., 2017), the use of statistical models which incorporate covariates of higher spatial-resolution could allow estimation of the local-scale variation of the pollutant. Additionally, in the view of the new S5P/TROPOMI data, it is of interest to evaluate whether higher resolution CTM simulations will lead to even better predictive ability of the statistical models, when considered as additional covariates.
Here, we applied Bayesian GR models to estimate gridded concentrations at resolution across 44 European countries. For the first time we evaluated the contribution of the tropospheric column-to-suface conversion of satellited-based proxies within a geostatistical modelling framework. We incorporated the vertical distribution of derived from the global 3-D CTM (GEOS-Chem, Bey et al., 2001), to quantify the corresponding tropospheric columns and to infer quasi-observed surface concentrations from the columnar OMI measurements using the estimated surface-to-column ratios. Additionally, we included a large set of high-resolution geo-referenced predictors available at continental scale, such as the novel pan-European Copernicus land monitoring products (CLMS, 2019) and meteorological data and tested the contribution of each predictor through a rigorous model selection procedure. We compared the results with simulations from the Ensemble of regional CTMs available at the Copernicus atmosphere monitoring service (CAMS, 2019) at higher spatial resolution than the OMI/GEOS-Chem estimates. The Bayesian framework allowed us to quantify the uncertainty of the predictions and to determine areas that exceed the air quality guidelines (AQGs) thresholds set by the European Union (EU) and World Health Organization (WHO), as well as to assess the number of people living in such areas. This study provides relevant information for policy and decision-makers in Europe and can contribute to improved estimates of the burden of disease attributable to (Lim et al., 2012, Forouzanfar et al., 2016).
2. Materials and methods
2.1. Study area and data
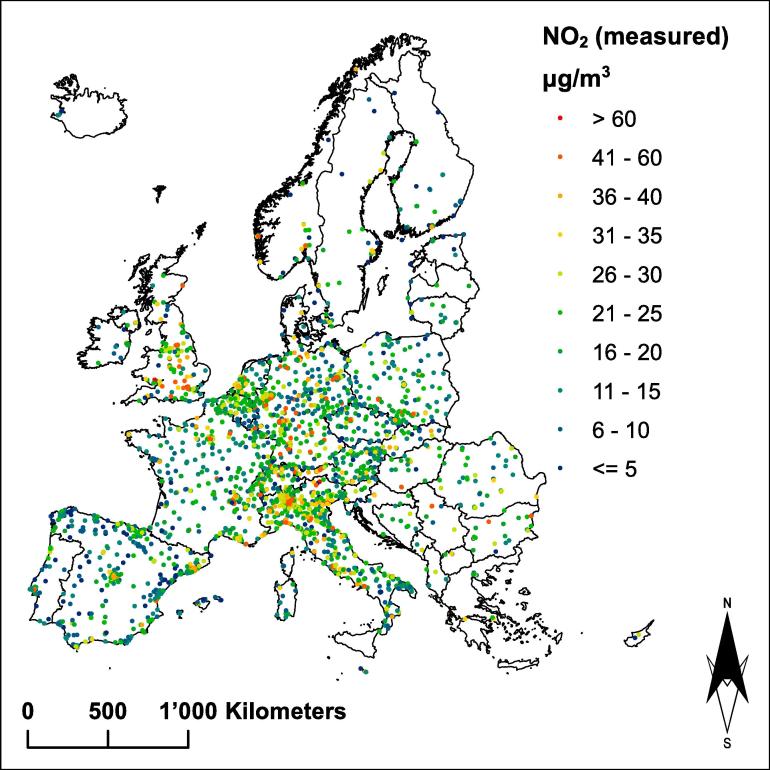
The raw measurements were obtained from the Air Quality e-Reporting database (Air Quality e-Reporting, 2019) maintained through the European environment information and observation network (Eionet). The monitoring network covers up to 38 European Countries, including all EU member states and EEA cooperating countries. The database consists of multi-annual time series of air quality measurements for a number of pollutants together with the meta-information on the monitoring stations involved. Here, the analysis was based on the yearly averaged 24 h data of 2016 at sites with 75% data capture. The station data were used for both, model building and model validation. Fig. 1 illustrates the locations of the monitoring sites used in this work together with the yearly averaged measured concentrations of . All data considered in this study were converted to the Lambert Azimuthal Equal Area (ETRS89-LAEA5210) projection recommended by the EEA (European Environment Agency, 2006) for storing raster data, statistical analysis and mapping purposes.
Fig. 1.
Nitrogen Dioxide. Annual average concentration of in 2016 at 2852 monitoring sites across Europe.
The satellite-derived product of columnar derived from OMI offers near global daily coverage of column abundance at spatial resolution of up to 13 × 24 km at nadir. The level-3 daily data of tropospheric concentration (OMNO2d) (Krotkov, 2013), cloud-screened at 30% and binned into 0.25° 0.25° grids, were accessed from the NASA’s Goddard Earth Sciences Data and Information Services Center (GES DISC) website (GES DISC, 2019). To obtain pollutant concentrations at the surface, the surface-to-column ratios (Lamsal et al., 2008, Lamsal et al., 2010, Bechle et al., 2011) derived from the global 3-D atmospheric model (GEOS-Chem v.11-01, http://acmg.seas.harvard.edu/geos/) were used (see Section 2.2 for details).
Satellite-based estimates reflect contributions from all sources, including e.g. emissions from industry, roads, airports or harbours and are not explicitly included as covariates within statistical models (Novotny et al., 2011). Following our previous work (Beloconi et al., 2018), a number of additional products were used as predictors in our models, to better assess the spatial variability of pollutant’s concentrations across Europe. The choice of variables was guided by literature review and data availability on continental scale. Table 1 summarizes the covariates used in this work. Detailed information on data sources, retrieval and processing is given in the appendix.
Table 1.
Data sources and spatio-temporal resolution of the covariates used in our models
| Product | Temporal Resolution | Spatial Resolution | Source |
|---|---|---|---|
| Tropospheric cloud-screened () | daily (13:00–15:00 LT) | 0.25° 0.25° | OMI |
| Surface estimates () | daily (13:00–15:00 LT) | 0.5° 0.625° | OMI/GEOS-Chem |
| Surface estimates () | year 2016 | 0.1° 0.1° | CAMS - Ensemble |
| Corine Land Cover (LC) | year 2012 | 100 m 100 m | CLMS |
| Tree Cover Density (TCD) | year 2015 | 20 m 20 m | CLMS |
| Imperviousness (IMP) | year 2015 | 20 m 20 m | CLMS |
| Digital Elevation Model (DEM) | year 2000 | 30 m 30 m | EEA |
| Night Time Lights (NTL) | year 2013 | 1 km 1 km | NOAA |
| Land Surface Temperature Day & Night (LST) | 2 acquisitions per day | 1 km 1 km | MODIS Aqua and Terra |
| Normalized Difference Vegetation Index (NDVI) | 2 acquisitions per day | 1 km 1 km | MODIS Aqua and Terra |
| Road Density (RD) | February 2016 | 1 km 1 km | OpenStreet Maps |
| Specific Humidity (SHUM) | every 6 h | 0.2° 0.2° | NCEP/CFSv2 |
| Precipitation (PREC) | every 6 h | 0.2° 0.2° | NCEP/CFSv2 |
| Wind Speed (WS) | every 6 h | 0.2° 0.2° | NCEP/CFSv2 |
| Distance to Sea (DISS) | year 2015 | vector | EEA |
| Distance to Roads (DISR) | February 2016 | vector | OpenStreet Maps |
2.2. Chemical transport models
Conversion of the proxies derived from OMI to surface concentrations require information about the vertical profile in the troposphere. Here we used the nested-grid version of the GEOS-Chem (Wang et al., 2004, Zhang et al., 2012) model which is operated at 0.5° 0.625° spatial resolution with 47 vertical layers and a transport and chemistry time step of 10 and 20 min, respectively. The boundary conditions are updated every 3 h using global simulations from a 2° 2.5° parent model (one-way nesting). We used assimilated meteorological fields (Modern-Era Retrospective Analysis for Research and Application (MERRA2)) provided by the NASA’s Global Modelling and Assimilation Office. One year spin-up for 2015 was performed to produce simulations for 2016. Daily tropospheric columns, using 2 h average between 13:00 and 15:00 local time (LT), corresponding to the time of the Aura satellite overpass, were generated to compare with the OMI retrievals. In particular, the simulated mixing ratios obtained from GEOS-Chem at 47 vertical layers were integrated from the surface (i.e. the lowest layer of the model, which is approximately 60 m above ground) to the modelled tropopause for every pixel and day within the study domain. Ideally for CTMs the inner product of the simulated profiles and the OMI averaging kernels should be taken, before comparing the modeled retrieval equivalents to the OMNO2d product. When the model profile shape is different from the a priori profile used in the satellite retrieval, this comparison could have an impact on the agreement between the estimates using these two approaches (Eskes et al., 2003). However, when averaged over larger regions the averaging-kernel based columns are very similar to the direct columns, showing only a remarkably small bias when not taken into account (Huijnen et al., 2010). Therefore, here the OMI product is directly compared to the modelled total columns.
Additionally, CTM simulations of surface concentration were obtained from the regional production of the Copernicus atmosphere monitoring service (CAMS) reanalysis dataset of atmospheric composition produced by the European centre for medium-range weather forecasts (ECMWF) (Inness et al., 2019). The CAMS regional air quality production (CAMS, 2019) is based on the median value of 7 partner state-of-the-art numerical air quality models (Ensemble) operated by 8 European institutes: CHIMERE from INERIS (France), EMEP from MET Norway (Norway), EURAD-IM from University of Cologne (Germany), LOTOS-EUROS from KNMI and TNO (Netherlands), MATCH from SMHI (Sweden), MOCAGE from METEO-FRANCE (France) and SILAM from FMI (Finland). Common to all models are the meteorological parameters’ settings (coming from the ECMWF global weather operating system), the boundary conditions for chemical species (coming from the CAMS IFS-MOZART global production) and the emissions coming from CAMS (for anthropogenic emissions over Europe and for biomass burning). The CAMS-Ensemble simulations used in this work represent annual averages of surface concentration (in ) at 0.1° 0.1° spatial resolution for the year 2016, and are denoted as in all the further analyses.
2.3. Vertical correction of OMI data
The GEOS-Chem vertical profiles were used to estimate the OMI concentrations at the surface employing the following formula (Lamsal et al., 2008):
| (1) |
where S represents the superficial level concentration, measured in parts per billion volume (ppbv) and - the tropospheric column, measured in . The sub-indices O and G indicate OMI and GEOS-Chem, respectively. The OMI-derived surface concentrations (ppbv) represent the mixing ratio in the lowest layer of the model.
We generated daily estimates of surface , based on the 2 h average (between 13:00–15:00 LT) surface-to-column ratios. Subsequently, annual averages of abundances were calculated for every pixel within the study domain. The raw data obtained from the EEA as well as the AQGs in Europe are based on measurements expressed in mass density () units, therefore, the estimates in ppbv were converted to using the following formula:
| (2) |
where R is the gas constant (), is the molar mass of nitrogen dioxide (), P and T are the grid level surface pressure (in mPa), and temperature (in K), respectively. The EU legislation (EU, 2008) specifies that, for gaseous pollutants the volume must be standardized at a temperature of 293 K (20 °C) and an atmospheric pressure of 101,3 kPa. In this case, the temperature refers to the bench temperature of the instrument and the pressure to the internal pressure in the measurement cell, not to ambient conditions (Sofen et al., 2016). The use of these values resulted in a conversion factor of 1.9125 ().
2.4. Geostatistical modelling
In the geostatistical framework spatial correlation is modelled by location-specific random effects through a Gaussian process. The covariance matrix of this process assumes a correlation decay which is a function of distance between locations. Let represents the log-observed annual average of concentration (calculated using daily averaged station measurements) at site s (). We assumed a stationary, isotropic geostatistical regression (GR) model,
| (3) |
where is the intercept term, the vector of regression coefficients associated with the spatial random effect, and the random error assumed to be i.i.d. from a . All the continuous covariates were standardized by subtracting the mean and dividing by the standard deviation (calculated using the yearly averaged measurements from all the monitoring stations). For the estimation of model parameters, the covariates were extracted at the locations of the stations, while for the prediction at unknown locations each covariate was aggregated within a fixed 1 grid using bilinear or nearest neighbour interpolation methods (for continuous and categorical data, respectively).
We assumed that the spatial random effect arises from a multivariate normal distribution:
| (4) |
with a vector of zeros and is the spatial process variance. is the dense correlation matrix with elements , where is the Matern function given by:
| (5) |
where is the distance between stations i and is a scaling parameter, a smoothing parameter (fixed to 1 in our application) and is the modified Bessel function of second kind. This specification implies that the range r (the distance at which the spatial variance becomes less than 10%) is given by .
The Bayesian model formulation is completed by specifying prior distributions for the parameters and the hyperparameters. We wanted the corresponding posterior distribution to be solely influenced by the data, therefore we considered non-informative priors for each unknown. Particularly, the log-gamma priors were chosen for the and r parametrized on the log-scale, i.e.: and . Normal priors were assigned for the regression coefficients and a vague normal one for the intercept.
We fitted models arising from all possible combinations of the covariates, i.e. 16384 ( distinct models and ordered them according to Bayesian model comparison criteria. Particularly, the models with the best predictive performance were selected based on the lowest logarithmic score (logscore) – a measure of the predictive ability of an individual model (Ntzoufras, 2011), given by: , where the leave-one-out conditional predictive ordinate () is based on the cross-validatory predictive densities for each excluded location s, i.e. . All the models were fitted using the R-INLA package (Rue et al., 2013) available within the R software (R Core Team, 2015). To reduce computational time, the fit of all possible combinations of covariates was done in parallel on an Intel Xeon E5-2697 CPU machine (2 × 2.60 GHz, 128 GB RAM). The fitting of 16384 models took around 2 weeks.
Subsequently, model performance was evaluated using the 5-fold-cross-validation method. The dataset was randomly divided 5 times in 80% (training set) and 20% (validation set) splits of the total number of sites. Then, models were trained on each of the five 80% subsets of the data and used to predict concentrations at the corresponding 20% of the stations. In this case, each of the five 20% subsets is independent to the model building. The following performance metrics were examined for each fold comparing the observed values to the posterior mean estimates (on log-scale) at the validation stations: mean absolute error (MAE), mean absolute prediction error (MAPE), root mean squared error (RMSE) and the coefficient of determination (). The average value of the metrics over the 5 folds was presented.
We assessed the contribution of the OMI tropospheric column-to-surface conversion of (using the surface-to-column ratios from GEOS-Chem) to the predictive ability of the GR models. In particular, two models were fitted: one with tropospheric column densities, i.e. (Model 1 - SAT); and another one with surface estimates based on Eq. 1, i.e. (Model 2 - SAT-CTM), as distinct covariates. The results were compared with the models which don’t include any of the satellite-derived or CTM proxies (Model 0). To evaluate whether higher spatial resolution of the CTM simulations influences the predictive ability of the models, we further fitted GR models with the CAMS-Ensemble predictor, i.e. (Model 3 - ENSEMBLE), as an additional covariate, and compared them to the above-mentioned formulations.
Model fit and prediction was done using the SPDE method and INLA algorithm for the fast approximation of the marginal posterior distributions. In the SPDE/INLA approach, the spatial process is represented as a Gaussian Markov random field (GMRF) with mean zero and a symmetric positive definite precision matrix Q (defined as the inverse of ). First, a GMRF representation of the Matern field was constructed on a set of non-intersecting triangles partitioning the domain of the study area (Lindgren et al., 2011). Subsequently, the INLA algorithm was used to estimate the posterior distribution of the latent Gaussian process and hyperparameters using the Laplace approximation (Rue et al., 2009). More details regarding this methodology are provided elsewhere (Blangiardo and Cameletti, 2015). Prediction was carried out after fitting the models to the full datasets (for a better spatial coverage and therefore for obtaining more accurate parameter estimates and predictions).
We used simulation-based inference to estimate the concentration of over a gridded surface of 1 resolution covering the study area. In particular, 1000 samples from the posterior predictive distribution were drawn at the centroids of each grid cell (approximately 5.8 million pixels). The maps display the sample-based medians, the standard deviations and the coefficients of variation (ratios of the standard deviation to the mean) of the posterior predictive distribution; with the last two representing a measure of uncertainty of the predictions. We determined the most polluted European areas using the first-level Nomenclature of Territorial Units for Statistics (NUTS) (EuroStat, 2019) classification of the EU to define the regions’ borders. To evaluate whether the concentration decreases as we move away from the city centres (SimpleMaps, 2019) of each capital, buffer zones with areas varying from 1 to 30 surrounding the city centres were considered. The high-resolution estimates (pixel-level posterior medians) were first clipped by each region and buffer and then averaged over the resulting sectors. For every capital, spline curves were employed to profile the relationship between pollutant concentration and distance from the city center within each buffer zone.
The Bayesian framework allowed us to make probabilistic statements about areas exceeding the international AQGs. The concentrations exceeding the threshold limit set by the EU and WHO were calculated at pixel level by the proportion of samples drawn from the predictive posterior distributions of that have pollution levels above the threshold. The exceedance maps were used to estimate the total number of population exposed to elevated levels of . In particular, we overlayed the gridded population data at 1 spatial resolution with the threshold map and summed up all the pixels within a particular country that have exceedance probability higher than 50%. Repeating it for each of the 1000 samples drawn from the posterior distribution allowed us to estimate the number of exposed population per country together with the prediction uncertainty.
3. Results
3.1. Evaluation of GEOS-Chem and OMI tropospheric columns
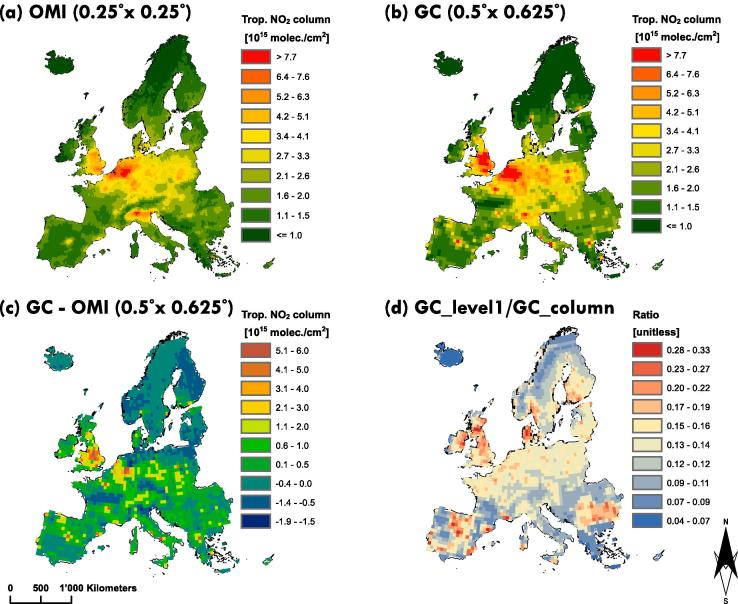
Figs. 2(a)-(b) depict yearly-averaged OMI-observed tropospheric columns and GEOS-Chem nested-grid model simulations in 2016 over the study area. In order to compare the agreement between tropospheric columns for these annual averages, the OMI observations, available at (0.25° 0.25°) spatial resolution, were aggregated to the extent of the nested (0.5° 0.625°) GEOS-Chem grid. Additionally, since the OMI observations include missing data for different days within the year (due to clouds and large solar zenith angles) whereas GEOS-Chem simulations have full daily coverage, for the computation of yearly-averaged values, the GEOS-Chem estimates were extracted only at those times that OMI data is available. Table 2 provides summary statistics for the resulting estimates (over land). There is a good agreement between the products in terms of mean, median, as well as 25% and 75% quantiles. However, the densities of the tropospheric columns obtained from GEOS-Chem are spreading over a wider range of values, as indicated by a larger standard deviation as well as lower minimum and higher maximum. Comparison of the complete GEOS-Chem dataset to the one sampled only at the locations and days when OMI is available shows that the maximum N available is the same, meaning that there is at least one OMI observation within the year for every pixel. However, the mean and the median of the full dataset is slightly higher in case of full coverage.
Fig. 2.
Comparison of yearly averaged tropospheric columns () from OMI and GEOS-Chem (GC) in 2016. a: OMI at original resolution. b: Nested-grid GEOS-Chem model simulations sampled only at the locations and days when OMI data is available c: Difference between GEOS-Chem simulations sampled only at the locations and days when OMI data is available and OMI resampled to the spatial resolution of the GEOS-Chem nested-grid. d: The ratios of integrated over the lowest layer of the GEOS-Chem to the tropospheric column.
Table 2.
Summary statistics for tropospheric annual averages for 2016 derived from OMI, GEOS-Chem nested grid simulations (in ) extracted only at the locations and days when OMI is available and GEOS-Chem simulations with full spatio-temporal coverage (i.e. with no missing).
| Product | N | Mean | Median | SD | Min | Max | ||
|---|---|---|---|---|---|---|---|---|
| OMI () | 2193 | 1.95 | 1.60 | 1.21 | 0.46 | 1.19 | 2.33 | 9.18 |
| GEOS-Chem () | 2193 | 2.07 | 1.60 | 1.81 | 0.19 | 0.90 | 2.64 | 16.62 |
| GEOS-Chem (with no missing) | 2193 | 2.44 | 1.90 | 1.89 | 0.41 | 1.21 | 3.03 | 16.32 |
The spatial patterns of the GEOS-Chem and OMI columnar abundances for the study domain (i.e. over land) are highly consistent (correlation ), however the tropospheric columns simulated in GEOS-Chem tend to be higher than OMI-observations over urban areas, especially over big European cities (Fig. 2(c)). The annual mean ratios of integrated over the lowest layer of GEOS-Chem to the tropospheric column, depicted in Fig. 2(d), suggest that there is a variation in space of the vertical distribution of , when averaged over the entire year; the values across Europe vary between 0.04 and 0.33.
3.2. Surface retrieval
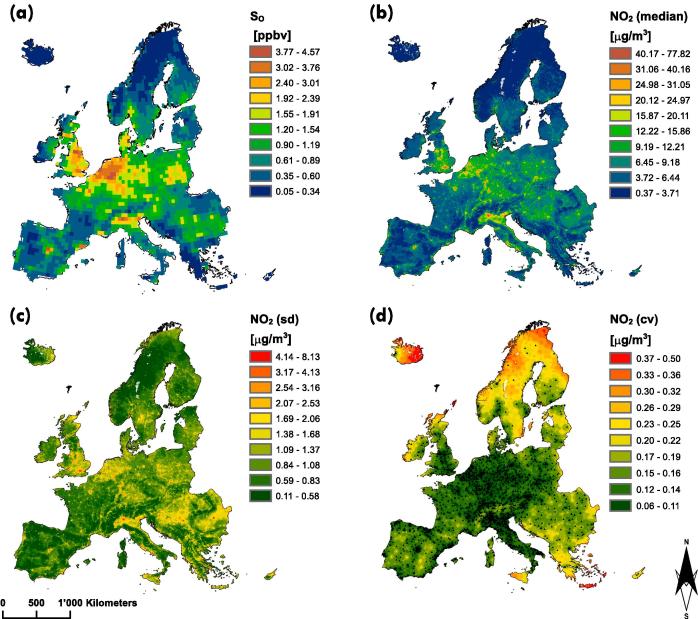
Fig. 4(a) shows the yearly-averaged OMI-derived surface concentrations obtained using Eq. 1 () at the spatial resolution of the nested-grid simulations (0.5° 0.625°). The spatial pattern of the resulting estimate is similar to that observed in the original tropospheric OMI column () (Fig. 2(a)). However, the differences for some regions (e.g. Greater London, Madrid, Be-Ne-Lux region) are also evident. The surface simulations derived from GEOS-Chem and Ensemble models, averaged over the year 2016, are illustrated in Fig. S1 (in the appendix).
Fig. 4.
Surface estimates in Europe in 2016. a: mixing ratios () obtained using Eq. 1 at 0.5° 0.625° spatial resolution. b: Predicted concentrations (i.e. median of the posterior predictive distribution) at 1 spatial resolution. c: Prediction uncertainty in terms of standard deviation (sd) of the posterior predictive distribution of . d: Prediction uncertainty in terms of coefficient of variation (cv) of the posterior predictive distribution of . Locations of the monitoring stations are overlayed on the map.
3.3. Geostatistical model selection
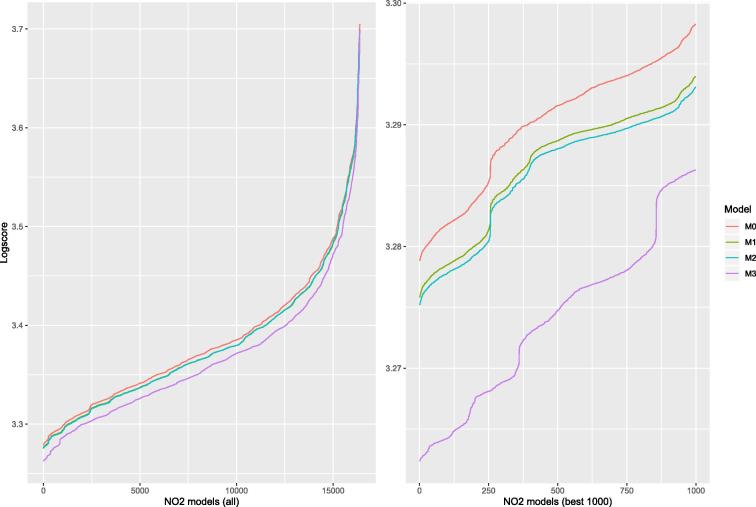
The variable selection process for the estimation of surface concentrations revealed that not all of the tested covariates are needed to achieve optimal predictions. The five best selected combinations of covariates (based on the lowest logscore values) for Model 0, Model 1 (SAT), Model 2 (SAT-CTM) and Model 3 (ENSEMBLE) are shown in Table 3. The model selection indicated that for both of the SAT and SAT-CTM cases, the columnar proxies derived from OMI (i.e. ) and the surface mixing ratios (i.e. ) are among the covariates included in the best models, with SAT-CTM slightly outperforming the SAT formulations in terms of logscore. We also see an improvement in logscore values compared to Model 0, in which neither of the satellite-derived proxies is considered as predictor. The use of the covariate in the models lead to both and becoming non-important predictors. The predictive ability in this case becomes even higher (as indicated by much lower logscore values of Model 3). The additional covariates included in the best five model combinations are similar for all four models (Table 3). Plotting the logscore values for every possible combination of covariates (Fig. 3) reveals that M3, outperforms the other models for any of those combinations, followed by M2, M1 and M0. The same figure shows that the range in improvement for the best model is highest between M3 and M2 and between M1 and M0.
Table 3.
First five covariate combinations with the highest predictive ability (i.e. lowest logscore) for Model 0, Model 1 (SAT), Model 2 (SAT-CTM) and Model 3 (ENSEMBLE).
| Model | Covariates | logscore |
|---|---|---|
| Model 0 | 3.2789 | |
| 3.2789 | ||
| 3.2791 | ||
| 3.2792 | ||
| 3.2792 | ||
| Model 1 (SAT) | 3.2758 | |
| 3.2759 | ||
| 3.2760 | ||
| 3.2760 | ||
| 3.2761 | ||
| Model 2 (SAT-CTM) | 3.2752 | |
| 3.2753 | ||
| 3.2754 | ||
| 3.2754 | ||
| 3.2755 | ||
| Model 3 (ENSEMBLE) | 3.2618 | |
| 3.2619 | ||
| 3.2621 | ||
| 3.2621 | ||
| 3.2621 |
IMP - Imperviousness; DEM - Digital elevation model; NTL - Night time lights; LST - Land surface temperature day & night; NDVI - Normalized difference vegetation index;
RD - Road density; DISS - Distance to sea; DISR - Distance to roads; LC - land cover; TCD - Tree cover density; PREC - Precipitation.
Fig. 3.
Model selection. Predictive performance of the M0, M1, M2 and M3 models (ordered according to the logscore values) arising from all possible combinations of covariates for each formulation. All the 16384 models (left) and zoom in on the best 1000 models (right).
The surface concentrations were positively associated with both and covariates, with similar estimates (i.e. posterior medians) of the regression coefficients but slightly lower uncertainty (i.e. narrower Bayesian credible interval) for and even lower uncertainty for (Table 4). Additionally, we found a significant positive association of concentration with the degree of imperviousness, night-time light intensity, land surface temperature, road density and distance to the sea and a negative association of surface with elevation, normalized difference vegetation index, wind speed and distance to the roads; the concentration was higher for stations situated in areas dominated by urban structures and transport networks (i.e. over land cover category LC1) followed by industrial (LC2), agricultural (LC3) and forest (LC4) areas (Table 4).
Table 4.
Posterior medians, 95% Bayesian credible intervals (BCI) and cross-validation performance metrics of Model 0, Model 1 (SAT), Model 2 (SAT-CTM) and Model 3 (ENSEMBLE) with covariate combinations giving the best predictive ability of surface concentrations in 2016.
| Model 0 | Model 1 (SAT) | Model 2 (SAT-CTM) | Model 3 (ENSEMBLE) | |
|---|---|---|---|---|
| Covariates | Median (95% BCI) | Median (95% BCI) | Median (95% BCI) | Median (95% BCI) |
| Intercept | 2.77 (2.62, 2.89) | 2.91 (2.79, 3.01) | 2.89 (2.78, 3.00) | 2.80 (2.63, 2.94) |
| 0.18 (0.12, 0.24) | ||||
| 0.17 (0.13, 0.22) | ||||
| 0.19 (0.16, 0.22) | ||||
| TCD | – | – | – | – |
| IMP | 0.11 (0.09, 0.12) | 0.11 (0.09, 0.12) | 0.11 (0.09, 0.12) | 0.11 (0.10, 0.13) |
| DEM | −0.17 (−0.20, −0.14) | −0.16 (−0.19, −0.13) | −0.16 (−0.19, −0.14) | −0.16 (−0.19, −0.14) |
| NTL | 0.21 (0.18, 0.23) | 0.20 (0.18, 0.23) | 0.20 (0.18, 0.23) | 0.19 (0.17, 0.22) |
| LST | 0.12 (0.07, 0.16) | 0.11 (0.06, 0.15) | 0.10 (0.06, 0.15) | – |
| NDVI | −0.07 (−0.09, −0.05) | −0.06 (−0.09, −0.04) | −0.06 (−0.09, −0.04) | −0.05 (−0.07, −0.03) |
| RD | 0.06 (0.05, 0.08) | 0.06 (0.05, 0.07) | 0.06 (0.05, 0.07) | 0.05 (0.04, 0.07) |
| SHUM | – | – | – | – |
| PREC | – | – | – | – |
| WS | −0.06 (−0.10, −0.03) | −0.06 (−0.09, −0.03) | −0.06 (−0.09, −0.03) | −0.06 (−0.09, −0.03) |
| DISS | 0.09 (0.00, 0.18) | 0.09 (0.02, 0.16) | 0.09 (0.02, 0.16) | – |
| DISR | −0.04 (−0.06, −0.02) | −0.04 (−0.06, −0.02) | −0.04 (−0.06, −0.02) | −0.03 (−0.05, −0.02) |
| LC: | ||||
| LC2 | −0.11 (−0.15, −0.07) | −0.11 (−0.15, −0.07) | −0.11 (−0.15, −0.07) | −0.11 (−0.15, −0.07) |
| LC3 | −0.15 (−0.21, −0.09) | −0.16 (−0.22, −0.10) | −0.16 (−0.22, −0.10) | −0.16 (−0.22, −0.10) |
| LC4 | −0.34 (−0.42, −0.26) | −0.36 (−0.44, −0.28) | −0.36 (−0.44, −0.28) | −0.38 (−0.46, −0.30) |
| 0.10 (0.09, 0.11) | 0.10 (0.09, 0.11) | 0.10 (0.09, 0.11) | 0.10 (0.10, 0.11) | |
| 0.14 (0.11, 0.20) | 0.11 (0.08, 0.15) | 0.11 (0.08, 0.15) | 0.13 (0.08, 0.20) | |
| (km) | 351.8 (271.4, 462.9) | 286.4 (219.3, 376.5) | 310.1 (236.5, 414.2) | 490.9 (355.0, 684.7) |
| 0.271 | 0.269 | 0.268 | 0.263 | |
| 0.167 | 0.166 | 0.166 | 0.166 | |
| 0.363 | 0.361 | 0.360 | 0.356 | |
| 0.711 | 0.713 | 0.715 | 0.724 |
- variance of the random error; - variance of the spatial process; - range (the distance at which the spatial variance becomes less than 10%);
- Mean Absolute Error; - Mean Absolute Prediction Error; - Root Mean Squared Error; - coefficient of determination.
The ENSEMBLE model provided the highest cross-validated values of 0.724, followed by the SAT-CTM ( = 0.715), the SAT ( = 0.713) and the one which does not include any proxy from satellite or CTM, i.e. Model 0 ( = 0.711). The out-of-sample MAE, MAPE and RMSE metrics of the predictive performance were also the lowest for Model 3. Very similar findings were observed when the 10-fold (instead of 5-fold) cross-validation was performed, or when the metrics were based on the posterior median (instead of mean) point estimates at the validation locations. The estimated range parameters (r) as well as the variances of the spatial process () were lower in Models 1 and 2 when compared to Model 0, indicating that inclusion of either or covariate decreases the spatial variability in the residuals. However, this variability was higher in Model 3, as shown by the higher r and estimates compared to all other models. This is due to the fact that the number of covariates resulting in optimal predictions is lower for Model 3; thus, the LST and DISS covariates become non-important (Table 4) in this case. The separate contributions of the spatial process () as well as of OMI (), OMI_GC () and Ensemble () covariates to the predictive ability of the models is presented in Table A1 in the appendix. The predictive ability using only these inputs as covariates is much lower compared to the final models that include additional climatic and land-use/cover factors.
3.4. High-resolution model-based pollutant maps and exposed population
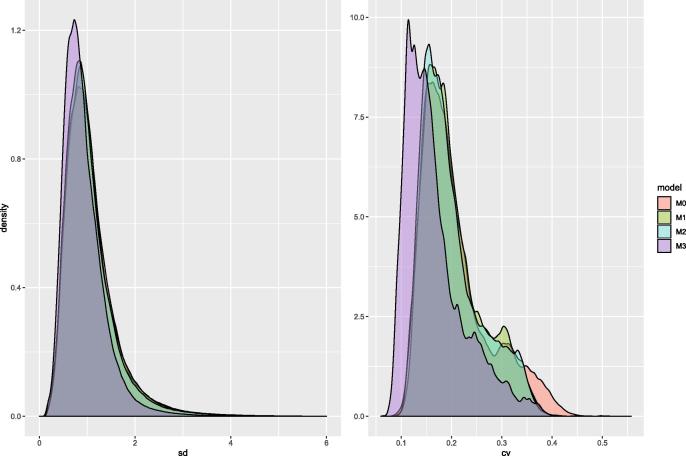
The above results suggest that Model 3 had the best predictive ability. Therefore, statistical inferences (i.e. mapping concentrations, exceedance probabilities and estimates of population exposure) are based on Model 3 with the covariate combination giving the lowest logscore (i.e. 1st among M3 - ENSEMBLE models in Table 3). Figs. 4(b)-(d) depict the predictions and their uncertainty, i.e. the median, the standard deviation and the coefficient of variation of the posterior predictive distribution for at 1 spatial resolution. The most heavily polluted regions in terms of concentration include south-eastern England, north-western Italy, Belgium, Netherlands, Germany (Nordrhein-Westfalen) as well as the big European cities, such as London, Rome and Paris. As one can see from the plots of the standard deviation and of the coefficient of variation, higher uncertainty is estimated at locations with higher estimates and within areas with fewer monitoring stations. Additionally, as a general trend, we found that the concentration of decreases with distance away from the centers of each European capital (Fig. S2 in the appendix). The maps of the medians, the standard deviations and the coefficients of variation of the posterior predictive distributions based on the other three models are presented in the appendix (Figs. S3–S5). Density plots of the prediction uncertainty (both, sd and cv) of the 4 models over the entire study area (i.e. over 5.8 million pixels) show that M3 has the lowest overall uncertainty, followed by M2, M1 and M0 (Fig. 5).
Fig. 5.
prediction uncertainty. Density plot of the standard deviation (left) and the coefficient of variation (right) of the posterior predictive distribution for all the 4 models at each 1 pixel of the prediction grid.
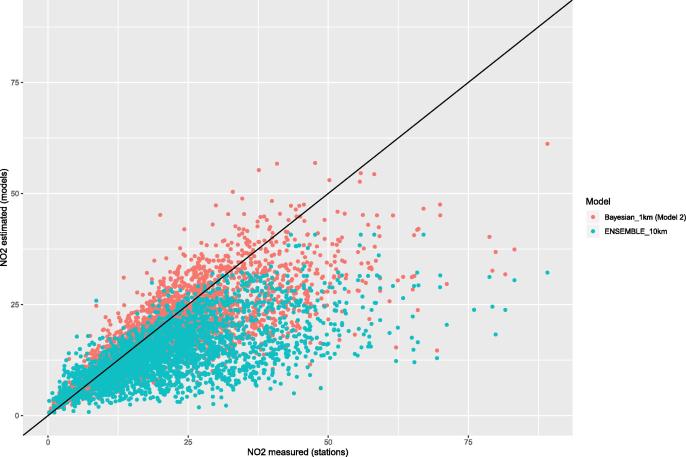
Additionally, we compared estimates obtained from Model 2 with the surface simulations from the Ensemble model. Predictions were aligned by aggregating the higher resolution estimates of Model 2 (at 1 ) to the lower resolution of the Ensemble (at 10 ). The correlation of the predictions based on the two models was R = 0.837 at pixel level. At the monitoring locations, predictions based on the Bayesian GR model (i.e. Model 2) are closer to the measured data than the ones based on the Ensemble (Fig. 6 and Table A2). However, Model 3, that included Ensemble simulations as an additional covariate, has higher predictive ability and even lower uncertainty than Model 2.
Fig. 6.
Comparison between the SAT-CTM GR model estimates and the Ensemble CTM simulations. Scatter plot of the measured versus estimated concentration at the location of the monitoring stations using the Bayesian GR SAT-CTM Model (at 1 resolution) and Ensemble of regional CTMs ( 10 ).
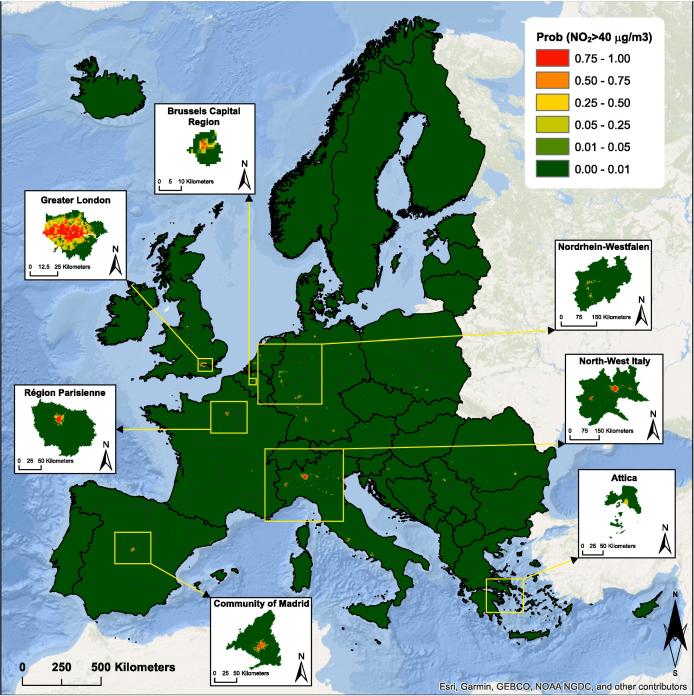
The Bayesian framework allowed us to make probabilistic statements about areas exceeding the international AQGs. Particularly, for concentrations, the yearly threshold set by the European Air Quality Directive and WHO is 40 (EU, 2008, WHO, 2005). This threshold is considered as an achievable objective to minimize the health impact. Fig. 7 depicts the probabilities of concentrations exceeding the threshold for each 1 pixel. The vast majority of the continent meets the requirements of the AQG threshold standards, however, there are some small areas where the limits are still to be reached. The exceedance probability map (i.e. Fig. 7) was used to estimate the number of people exposed to elevated levels of at each pixel. The estimates were aggregated at country levels and presented in Table 5 together with the prediction uncertainty (i.e. median and 95% credible intervals of the posterior predictive distribution). Results show that in 2016, 16.17 (95% C.I. 6.34–29.96) million people were exposed to levels above the thresholds, which represent only 2.97% (95% C.I. 1.16% - 5.50%) of the total number of people living within the study area (Table 5).
Fig. 7.
Exceedance probabilities. Probability that concentration exceeds the EU Directive and WHO air quality threshold of 40 . The zoomed areas represent some of the level 1 subdivisions of the Nomenclature of Territorial Units for Statistics (NUTS 1) classification of the European Union.
Table 5.
Estimated number of people exposed to levels above the EU and WHO thresholds in 2016 (median and 95% credible intervals of the posterior distributions).
| Country | Population1 | Exposed to |
|---|---|---|
| (AD) Andorra | 67 462 | 0 (0, 0) |
| (AL) Albania | 2 925 168 | 0 (0, 6136) |
| (AT) Austria | 8 731 711 | 26 948 (3513, 71 469) |
| (BA) Bosnia and Herzegovina | 3 817 952 | 0 (0, 0) |
| (BE) Belgium | 11 469 758 | 209 841 (24 752, 535 658) |
| (BG) Bulgaria | 7 153 089 | 0 (0, 32 782) |
| (CH) Switzerland | 9 202 540 | 4980 (0, 41 116) |
| (CY) Cyprus | 1 190 214 | 0 (0, 0) |
| (CZ) Czech Republic | 10 618 625 | 2648 (0, 38 496) |
| (DE) Germany | 81 848 649 | 1 148 965 (418 143, 2 558 156) |
| (DK) Denmark | 5 766 524 | 0 (0, 0) |
| (EE) Estonia | 1 349 753 | 0 (0, 0) |
| (EL) Greece | 11 050 816 | 99 697 (0, 1 704 795) |
| (ES) Spain | 44 529 778 | 1 895 762 (581 991, 3 196 598) |
| (FI) Finland | 5 979 902 | 0 (0, 0) |
| (FR) France | 65 346 726 | 3 339 836 (885 080, 5 005 125) |
| (GG) Guernsey | 53 479 | 0 (0, 0) |
| (GI) Gibraltar | 31 233 | 0 (0, 0) |
| (HR) Croatia | 4 221 881 | 4490 (0, 108 244) |
| (HU) Hungary | 10 027 750 | 0 (0, 225 219) |
| (IE) Ireland | 4 814 831 | 0 (0, 0) |
| (IS) Iceland | 330 470 | 0 (0, 0) |
| (IT) Italy | 60 499 999 | 4 620 219 (2 964 773, 6 229 796) |
| (JE) Jersey | 92 559 | 0 (0, 0) |
| (LI) Liechtenstein | 37 363 | 0 (0, 0) |
| (LT) Lithuania | 2 923 123 | 0 (0, 0) |
| (LU) Luxembourg | 570 985 | 0 (0, 0) |
| (LV) Latvia | 2 125 289 | 0 (0, 0) |
| (MC) Monaco | 13 681 | 0 (0, 0) |
| (ME) Montenegro | 664 404 | 0 (0, 0) |
| (MK) North Macedonia | 2 123 204 | 0 (0, 3780) |
| (MT) Malta | 420 872 | 0 (0, 0) |
| (NL) Netherlands | 17 718 000 | 140 468 (25 726, 527 690) |
| (NO) Norway | 5 372 166 | 6015 (575, 15 649) |
| (PL) Poland | 39 149 578 | 70 633 (6204, 457 799) |
| (PT) Portugal | 9 700 000 | 0 (0, 13 646) |
| (RO) Romania | 19 740 811 | 196 024 (0, 1 253 267) |
| (RS) Serbia | 8 995 232 | 96 610 (0, 475 274) |
| (SE) Sweden | 10 521 396 | 0 (0, 0) |
| (SI) Slovenia | 2 112 593 | 0 (0, 17 407) |
| (SK) Slovakia | 5 486 419 | 0 (0, 3972) |
| (SM) San Marino | 30 187 | 0 (0, 0) |
| (UK) United Kingdom | 65 644 463 | 4 304 920 (1 422 934, 7 431 681) |
| (VA) Vatican | 1970 | 1970 (1970, 1970) |
| Whole study area (44 countries) | 544 472 605 | 16 170 026 (6 335 661, 29 955 725) |
| 2.97% (1.16%, 5.50%) | ||
1Estimate obtained via cubic spline interpolation of 2000, 2005, 2010, 2015 and 2020 population data at 1 pixel level.
4. Discussion
Nitrogen dioxide monitors do not provide full data coverage over Europe, which is an obstacle to assess the attributable health effects for the entire continent. This paper is the first to estimate surface concentrations at 1 spatial resolution over 44 European countries using a hybrid approach which combines satellite-based observations, chemical transport model simulations, monitors and additional auxiliary data within a Bayesian geostatistical modeling framework.
The tropospheric columns obtained using the 3-D simulations of concentration from the nested-grid GEOS-Chem model (at 0.5° 0.625° spatial resolution) were found to be highly consistent with OMI observations over the study area (correlation of , ). Huijnen et al. (2010) reported a spatial correlation of () between an ensemble median of regional air quality models and Dutch OMI tropospheric (DOMINO) v1.0.2 product (http://www.temis.nl) for the years 2008–2009, while Vinken et al. (2014) found a higher spatial agreement () between the nested-grid GEOS-Chem tropospheric column simulations and DOMINO v2.0 product in 2005, with both studies performed over a similar domain in Europe.
Comparison between the models M0, M1 and M2 showed that both, the satellite-derived proxies of columnar from OMI () as well as the vertically corrected surface quasi-observations () obtained using surface-to-column ratios from GEOS-Chem, improved estimation of the corresponding surface concentration and reduced prediction uncertainty, despite of missing data present in both products. This important contribution of satellite-derived proxies to the estimation of surface concentrations was also found using LUR models in Europe (Vienneau et al., 2013), US (Novotny et al., 2011) and globally (Larkin et al., 2017). Although the above-mentioned works have not assessed the contribution of the vertical correction itself to the model predictive ability, several recent works (Bechle et al., 2013, Knibbs et al., 2014, Bechle et al., 2015), suggested that the satellite column abundances from OMI () may be sufficient to estimate the spatial patterns of ground-level , therefore conversion of columnar values to surface concentrations becomes unnecessary within a LUR model. In fact, Knibbs et al. (2014) found that the annual models that included tropospheric column as covariate exhibited a slightly better predictive ability compared to those that included estimates of surface obtained by modelling surface-to-column ratios using the Weather Research and Forecasting (WRF-Chem) chemical transport model for a LUR study in Australia. Bechle et al. (2015) reported similar findings using DOMINO tropospheric columns and GEOS-Chem surface-to-column ratios for a LUR study in the US. Our results showed that this conversion improved the predictive ability of the geostatistical models. However, the improvement was marginal when additional predictors were considered in the models, as indicated by the logscore values (differences in the 4th digit) and the cross-validation performance metrics (i.e. and RMSE presented here on the log-scale).
To further evaluate, whether the vertical correction is more important at locations with large variability in the surface-to-column ratio (Fig. 2(d)), we extracted the ratio values at the location of the stations and re-fitted the models M0–M2 on the subset of the data with (i) large variability (i.e. ratio smaller than 0.25th quantile or higher than 0.75th quantile of all the ratio values) and (ii) almost constant values (i.e. ratio higher than 0.25th and lower than 0.75th quantile of all the values). The results (Table A3 in the appendix) revealed that, indeed, the vertical correction using CTM simulations results in a higher predictive performance when the variation in the ratio is high. Therefore, conversion of the columnar values to surface concentrations is more important in cases when a particular spatio-temporal domain of interest ascertains higher variation in the ratio (e.g. in case of daily or weekly, rather than annually averaged data).
Rigorous variable selection indicated that additional high-resolution auxiliary earth observation data such as the novel pan-European Copernicus land monitoring products, including the impervious surfaces and land-use/cover datasets were important predictors in all models. The road density and distance to the roads covariates computed from the OpenStreetMap project as well as the distance to the sea, elevation, night time lights intensity, NDVI, LST and wind speed increased the predictive ability of the best model (based on the logscore). The positive/negative associations of these covariates with surface measurements from monitoring stations generally agree with those reported in the literature. In particular, the important positive associations of surface with impervious surfaces and major roads were also found in Novotny et al., 2011, Knibbs et al., 2014, Bechle et al., 2015, while the negative effect of NDVI was also estimated in Larkin et al. (2017). However, in contrast to studies in the US (Novotny et al., 2011, Bechle et al., 2015), we found a positive effect of the distance to the sea (or coast) on and a negative association with elevation, which is consistent with another European study by Beelen et al. (2009).
The comparison of the simulations from the Ensemble of regional CTMs (i.e. ), available at 10 resolution, with the estimates obtained using Model 2 (SAT-CTM) aggregated at the same scale has shown a good spatial agreement. Extracted at the locations of the stations, the 1 predictions from Model 2 were closer to the measurements than the simulations, implying that the higher the resolution of the estimated concentration is (i.e. of the gridded GR predictions or CTM simulations), the smaller the underestimation of the exposure gets. When was included as a covariate in the GR model (i.e. Model 3), its predictive ability increased and the prediction uncertainty reduced, granting the most accurate surface estimates.
The advantage of the geostatistical models is their ability to provide information in areas where there is no monitoring (i.e. no stations). Traditional statistical approaches that are used to produce gridded estimates (e.g. LUR or GWR) usually fail to quantify the uncertainties in the predictions (which are necessary for studies related to health risks assessments). For a single CTM, sensitivity analyses (Saltelli et al., 2004) quantify uncertainty by e.g. perturbing the emissions and meteorological conditions. For multi-model ensembles of CTMs (Galmarini et al., 2018, Marécal et al., 2015, Potempski et al., 2008), the analyses from different models (varying in number) provide a composite of model simulations (e.g. medians or percentiles). In this case, the final estimates at the various points in space and time are more conservative, filter the single model differences and are usually more consistent with the actual evolution of the process (Galmarini et al., 2004). On the other hand, Bayesian inference treats the unknown concentrations at pixel level as random quantities and estimates their predictive posterior distribution, a probability distribution that incorporates the uncertainty of the predictions via its variance. Sensitivity analysis in the context of Bayesian modelling assesses influence the alternative distributions (for the data or the priors) have on the predictions. By drawing samples from the predictive posterior distribution, we can estimate the mean, median, standard deviation or any other quantity of interest (e.g. probability of exceeding any particular threshold). The assessment of exposure burden also becomes possible by utilizing gridded population data.
Estimates from the posterior predictive distribution show that the most heavily polluted regions in terms of are south-eastern England, north-western Italy, Belgium, Netherlands, Germany (Nordrhein-Westfalen) as well as the big European cities, like London, Brussels, Hamburg, Berlin, Paris and Athens. Similarly to Shaddick et al. (2013), we found that higher uncertainty of the predictions is estimated in areas with elevated pollutant concentrations (as seen in the plot of the predictive standard deviation, i.e. Fig. 4(c)). A plausible explanation is that the number of stations in areas dominated by urban structures and transport networks is usually lower, which leads to higher uncertainty in the coefficient estimates of the land-cover covariates defining these regions, and therefore to higher uncertainties in areas with higher concentration estimates. Additionally, the map of the coefficient of variation (Fig. 4(d)) has shown that the predictive uncertainty is higher in regions (and countries) with fewer monitoring stations. Thus, the results of our study can help identifying areas where new monitoring stations are needed. In terms of population exposure, we found that only about 3% of people living within the study domain were exposed to values exceeding the international AQGs. This result suggest that represents a much smaller threat to Europe, when compared to particulate matter (both fine - and coarse - ) concentrations. For the latter, it was estimated that more than 66% of people within the same area and year were breathing air abvove the WHO thresholds (Beloconi et al., 2018). Our results are comparable to findings put forth in a recent EEA Air Quality report (European Environment Agency, 2019) based on Eionet gridded estimates (using a completely different approach) for 2016 (Eionet, 2018). Indeed, it was reported that 2.8% of population in almost the same area covered by our study were exposed to concentrations above the WHO/EU thresholds.
The EU Directive sets criteria for the minimum number of the sampling points and for the site locations. They require Member States to locate sampling points both ”where the highest concentrations occur” (with traffic or industrial type stations) and in areas which are ”representative of the general population’s exposure” (with background type stations). However, the selection of site locations involves a degree of flexibility, which allows Member States to not necessarily measure air quality near major industries or main urban traffic. Additionally, the Air Quality Directive requires that Member States maintain sampling points that have exceeded , but this obligation does not apply to other pollutants, in particular to (European Court of Auditors, 2018). Statistical models rely on the monitoring data, and therefore they may underestimate the concentration of pollutants, particularly in urban areas.
Our methodology can be applied to estimate concentration and evaluate international AQGs for any specific year or spatial domain. The operational application of the models for a different year or area of investigation although possible, is not straightforward, since it requires re-estimation of the regression parameters and spatial process, based on the availability of the station data and the covariates. The dense in situ network available in Europe allows for an accurate estimation of the spatial correlation structure, especially over shorter distances. In other world regions, except North America and Asia, the station coverage is much lower (Larkin et al., 2017). Reliable estimation of the spatial correlation is not possible due to the large distances between the stations. Therefore, we expect that the satellite/CTM covariates will improve model predictions even more than in Europe.
The number of days with missing OMI varies in space. In particular, higher proportion of missing values is observed in the northern part of the continent and at high altitudes due to the presence of clouds, higher surface reflectance and larger solar zenith angles. Our results have shown, that even with missing values, the annual averaged OMI product was a significant predictor either vertically corrected (Model 2) or not (Model 1). In order to evaluate the impact of missing OMI data on the predictive ability of Models 1 and 2, we re-fitted the models to the subset of stations located in pixels with larger and with lower availability of OMI. We defined the availability of OMI as the proportion of days with complete data and considered that this is ”large” when the proportion is above the median of those across the stations (here ). The results (Table A4 in the appendix) have shown that the contribution of OMI covariate to the predictive ability of the model was higher when models were fitted to data from stations with large availability (i.e. proportion of days with complete data ). Therefore, the number of missing data influences the predictive ability of the models. Methods for missing satellite-data imputation could improve estimates. The frequentist statistical/machine learning methods (e.g. random forests) available for filling the data gaps cannot quantify the uncertainty in the estimates, which propagates to the outcome and therefore complicates results interpretation. Bayesian models can estimate both the missing values and the model parameters within a single hierarchical formulation. However, this is computational not yet feasible for very large surfaces such as our study region. Furthermore, whereas the annual EEA station data were calculated based on the daily averaged values, the daily OMI measurements and GEOS-Chem simulations are confined to the OMI overpass window ( 13–15 LT). This may also explain the small contribution of covariate to the predictive ability of the models, given the diurnal variation (cycle) in concentrations. For specific applications, such as those health related, it is important to estimate the total annual average, rather than average at a particular time within the day. Another drawback is the varying spatial resolution of the covariates. We analysed data at the original georgraphical scales assuming homogeneity of their values within a coarser spatial resolution. Approaches have been proposed to address the fusion of data with different spatial supports (Nguyen et al., 2012, Beloconi et al., 2016) and particularly for statistical downscaling of coarse resolution CTM outputs (Fuentes and Raftery, 2005, Berrocal et al., 2010).
While the OMI’s 15-year dataset (2004-onwards) is suitable for investigating past changes and trends, the high spatial resolution of the recently released Sentinel 5P/TROPOMI (7 3.5 near nadir) (Veefkind et al., 2012) will allow detection of small-scale sources and will increase the fraction of cloud-free observations by an estimated 70% as compared to OMI (Krijger et al., 2007). The results presented here are very promising, especially in view of these new data. As observed in this work, higher resolution CTMs lead to better estimates, therefore we expect that the Sentinel 5P/TROPOMI measurements, either alone, or combined e.g. with the CAMS-Ensemble model will lead to even higher predictive ability.
5. Conclusions
We have shown the benefits of combining data from monitors, satellites and chemical transport models in a rigorous Bayesian geostatistical framework to estimate the spatial distribution of in Europe. We presented the results based on different input data (satellite, global and regional CTMs) and evaluated the contribution of the column-to-surface conversion of satellite products and of the effect of spatial resolution of CTMs to the predictive ability of the GR models. The results indicated that the vertical correction slightly improves the predicted estimates, whereas higher resolution CTMs improve the accuracy of the prediction. Based on the best model and available monitoring data, we evaluated the AQGs and estimated the number of people living in areas exceeding the thresholds. Due to data limitations, such as coarse number of stations in some areas and the complexity of variability in urban environments, the findings might underestimate the population exposure, particularly in urban areas. However, our work is the first to estimate the population exposure to in 44 European countries at 1 resolution based on Bayesian geostatistical modelling, which explicitly quantifies the prediction uncertainty.
CRediT authorship contribution statement
Anton Beloconi: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing - original draft, Writing - review & editing, Visualization. Penelope Vounatsou: Conceptualization, Methodology, Resources, Data curation, Writing - review & editing, Supervision, Project administration, Funding acquisition.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
We would like to acknowledge the financial support of the European Research Council (ERC) Advanced Grant (Project No. 323180). The results of this study have been achieved incorporating data of the Copernicus Land Monitoring Service (CLMS) and of the Copernicus Atmosphere Monitoring Service (CAMS).
Handling Editor: Xavier Querol
Footnotes
Supplementary data associated with this article can be found, in the online version, at https://doi.org/10.1016/j.envint.2020.105578.
Supplementary material
The following are the Supplementary data to this article:
References
- Air Quality e-Reporting, 2019. The European air quality database. European Environment Agency. https://www.eea.europa.eu/data-and-maps/data/aqereporting-8 (accessed 1 March 2019).
- Bechle M.J., Millet D.B., Marshall J.D. Effects of income and urban form on urban NO2: Global evidence from satellites. Environ. Sci. Technol. 2011;45(11):4914–4919. doi: 10.1021/es103866b. [DOI] [PubMed] [Google Scholar]
- Bechle M.J., Millet D.B., Marshall J.D. Remote sensing of exposure to NO2: satellite versus ground-based measurement in a large urban area. Atmos. Environ. 2013;69:345–353. [Google Scholar]
- Bechle M.J., Millet D.B., Marshall J.D. National spatiotemporal exposure surface for NO2: monthly scaling of a satellite-derived land-use regression, 2000–2010. Environ. Sci. Technol. 2015;49(20):12297–12305. doi: 10.1021/acs.est.5b02882. [DOI] [PubMed] [Google Scholar]
- Beelen R., Hoek G., Pebesma E., Vienneau D., de Hoogh K., Briggs D.J. Mapping of background air pollution at a fine spatial scale across the European Union. Sci. Total Environ. 2009;407(6):1852–1867. doi: 10.1016/j.scitotenv.2008.11.048. [DOI] [PubMed] [Google Scholar]
- Beloconi A., Kamarianakis Y., Chrysoulakis N. Estimating urban PM10 and PM2.5 concentrations, based on synergistic MERIS/AATSR aerosol observations, land cover and morphology data. Remote Sens. Environ. 2016;172:148–164. [Google Scholar]
- Beloconi A., Chrysoulakis N., Lyapustin A., Utzinger J., Vounatsou P. Bayesian geostatistical modelling of PM10 and PM2.5 surface level concentrations in Europe using high-resolution satellite-derived products. Environ. Int. 2018;121:57–70. doi: 10.1016/j.envint.2018.08.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berrocal V.J., Gelfand A.E., Holland D.M. A spatio-temporal downscaler for output from numerical models. J. Agric. Biol. Environ. Stat. 2010;15(2):176–197. doi: 10.1007/s13253-009-0004-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bey I., Jacob D.J., Yantosca R.M., Logan J.A., Field B.D., Fiore A.M., Schultz M.G. Global modeling of tropospheric chemistry with assimilated meteorology: Model description and evaluation. J. Geophys. Res. Atmosp. 2001;106(D19):23073–23095. [Google Scholar]
- Blangiardo M., Cameletti M. John Wiley & Sons; 2015. Spatial and Spatio-temporal Bayesian Models with R-INLA. [Google Scholar]
- Boersma K.F., Jacob D.J., Bucsela E.J., Perring A.E., Dirksen R., Yantosca R.M., Cohen R.C. Validation of OMI tropospheric NO2 observations during INTEX-B and application to constrain NOx emissions over the eastern United States and Mexico. Atmos. Environ. 2008;42(19):4480–4497. [Google Scholar]
- Bucsela E.J., Perring A.E., Cohen R.C., Boersma K.F., Celarier E.A., Gleason J.F., Veefkind J.P. Comparison of tropospheric NO2 from in situ aircraft measurements with near-real-time and standard product data from OMI. J. Geophys. Res. Atmosp. 2008;113(D16) [Google Scholar]
- Copernicus Atmosphere Monitoring Service (CAMS), Regional Air Quality, 2019. http://www.regional.atmosphere.copernicus.eu (accessed 1 September 2019).
- Copernicus Land Monitoring Services (CLMS), 2019. http://land.copernicus.eu/pan-european (accessed 1 March 2019).
- Crippa, M., Guizzardi, D., Muntean, M., Schaaf, E., Dentener, F., van Aardenne, J.A., Monni, S., Doering, U., Olivier, J.G.J., Pagliari, V., & Janssens-Maenhout, G., 2018. Gridded emissions of air pollutants for the period 1970–2012 within EDGAR v4.3.2. Earth Syst. Sci. Data, 10, 1987–2013, https://doi.org/10.5194/essd-10-1987-2018.
- De Hoogh K., Gulliver J., Van Donkelaar A., Martin R.V., Marshall J.D., Bechle M.J., Forsberg B. Development of West-European PM2.5 and NO2 land use regression models incorporating satellite-derived and chemical transport modelling data. Environ. Res. 2016;151:1–10. doi: 10.1016/j.envres.2016.07.005. [DOI] [PubMed] [Google Scholar]
- Di Q., Rowland S., Koutrakis P., Schwartz J. A hybrid model for spatially and temporally resolved ozone exposures in the continental United States. J. Air Waste Manage. Assoc. 2017;67(1):39–52. doi: 10.1080/10962247.2016.1200159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eionet Report, 2018. European air quality maps for 2016. ETC/ACM 2018/8. https://www.eionet.europa.eu/etcs/etc-atni/products/etc-atni-reports/etc-acm-report-2018-8-european-air-quality-maps-for-2016.
- Eskes H.J., Boersma K.F. Averaging kernels for DOAS total-column satellite retrievals. Atmos. Chem. Phys. 2003;3:1285–1291. http://www.atmos-chem-phys.net/3/1285/2003/ [Google Scholar]
- European Court of Auditors, 2018. Special report no 23/2018: Air pollution: Our health still insufficiently protected. https://www.eca.europa.eu/en/Pages/DocItem.aspx?did=46723.
- European Environment Agency, January 2006. Guide to geographical data and maps.
- European Environment Agency, 2014. Air quality in Europe – 2014 report. EEA Report No. 5/2014.
- European Environment Agency, 2019. Air quality in Europe — 2019 report. EEA Report No. 10/2019.
- EU (2008). Directive 2008/50/EC of the European Parliament and of the Council of 21 May 2008 on ambient air quality and cleaner air for Europe, OJ L 152, 11.6.2008, p. 1–44. https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:02008L0050-20150918&from=EN (accessed 1 March 2019).
- EuroStat–GISCO service (2019). Eurogeographics for the administrative boundaries. http://ec.europa.eu/eurostat/web/gisco/geodata/reference-data/administrative-units-statistical-units (accessed 1 March 2019).
- Forouzanfar M.H., Afshin A., Alexander L.T., Anderson H.R., Bhutta Z.A., Biryukov S., Brauer M., Burnett R., Cercy K., Charlson F.J., Cohen A.J. Global, regional, and national comparative risk assessment of 79 behavioural, environmental and occupational, and metabolic risks or clusters of risks, 1990–2015: a systematic analysis for the Global Burden of Disease Study 2015. Lancet. 2016;388(10053):1659–1724. doi: 10.1016/S0140-6736(16)31679-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuentes M., Raftery A.E. Model evaluation and spatial interpolation by Bayesian combination of observations with outputs from numerical models. Biometrics. 2005;61(1):36–45. doi: 10.1111/j.0006-341X.2005.030821.x. [DOI] [PubMed] [Google Scholar]
- Galmarini S., Bianconi R., Addis R., Andronopoulos S., Astrup P., Bartzis J.C., Bellasio R., Buckley R., Champion H., Chino M., D’Amours R. Ensemble dispersion forecasting—part II: application and evaluation. Atmos. Environ. 2004;38(28):4619–4632. [Google Scholar]
- Galmarini S., Kioutsioukis I., Solazzo E., Alyuz U., Balzarini A., Bellasio R., Benedictow A.M., Bianconi R., Bieser J., Brandt J., Christensen J.H. Two-scale multi-model ensemble: is a hybrid ensemble of opportunity telling us more? Atmosp. Chem. Phys. 2018;18(12):8727–8744. doi: 10.5194/acp-18-8727-2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geddes J.A., Martin R.V., Boys B.L., van Donkelaar A. Long-term trends worldwide in ambient NO2 concentrations inferred from satellite observations. Environ. Health Perspect. 2015;124(3):281–289. doi: 10.1289/ehp.1409567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goddard Earth Sciences Data and Information Services Center (GES DISC NASA), 2019. Level-3 daily OMI/Aura data. http://disc.sci.gsfc.nasa.gov/ (accessed 1 March 2019).
- Grajales J.F., Baquero-Bernal A. Inference of surface concentrations of nitrogen dioxide (NO2) in Colombia from tropospheric columns of the ozone measurement instrument (OMI) Atmosfera. 2014;27(2):193–214. [Google Scholar]
- Hesterberg T.W., Bunn W.B., McClellan R.O., Hamade A.K., Long C.M., Valberg P.A. Critical review of the human data on short-term nitrogen dioxide (NO2) exposures: evidence for NO2 no-effect levels. Crit. Rev. Toxicol. 2009;39(9):743–781. doi: 10.3109/10408440903294945. [DOI] [PubMed] [Google Scholar]
- Huijnen V., Eskes H.J., Poupkou A., Elbern H., Boersma K.F., Foret G., Sofiev M., Valdebenito A., Flemming J., Stein O., Gross A., Robertson L., D’Isidoro M., Kioutsioukis I., Friese E., Amstrup B., Bergstrom R., Strunk A., Vira J., Zyryanov D., Maurizi A., Melas D., Peuch V.-H., Zerefos C. Comparison of OMI NO2 tropospheric columns with an ensemble of global and European regional air quality models. Atmos. Chem. Phys. 2010;10:3273–3296. [Google Scholar]
- Inness A., Ades M., Agustí-Panareda A., Barré J., Benedictow A., Blechschmidt A.-M., Dominguez J.J., Engelen R., Eskes H., Flemming J., Huijnen V., Jones L., Kipling Z., Massart S., Parrington M., Peuch V.-H., Razinger M., Remy S., Schulz M., Suttie M. The CAMS reanalysis of atmospheric composition. Atmos. Chem. Phys. 2019;19:3515–3556. [Google Scholar]
- Jerrett M., Arain A., Kanaroglou P., Beckerman B., Potoglou D., Sahsuvaroglu T., Giovis C. A review and evaluation of intraurban air pollution exposure models. J. Exp. Sci. Environ. Epidemiol. 2005;15(2):185. doi: 10.1038/sj.jea.7500388. [DOI] [PubMed] [Google Scholar]
- Knibbs L.D., Hewson M.G., Bechle M.J., Marshall J.D., Barnett A.G. A national satellite-based land-use regression model for air pollution exposure assessment in Australia. Environ. Res. 2014;135:204–211. doi: 10.1016/j.envres.2014.09.011. [DOI] [PubMed] [Google Scholar]
- Krijger J.M., Weele M.V., Aben I., Frey R. The effect of sensor resolution on the number of cloud-free observations from space. Atmos. Chem. Phys. 2007;7(11):2881–2891. [Google Scholar]
- Krotkov, N.A., 2013. OMI/Aura NO2 Cloud-Screened Total and Tropospheric Column L3 Global Gridded 0.25 degree x 0.25 degree V3, NASA Goddard Space Flight Center, Goddard Earth Sciences Data and Information Services Center (GES DISC). DOI:10.5067/Aura/OMI/DATA3007.
- Lamsal L.N., Martin R.V., Van Donkelaar A., Steinbacher M., Celarier E.A., Bucsela E., Dunlea E.J., Pinto J.P. Ground-level nitrogen dioxide concentrations inferred from the satellite-borne Ozone Monitoring Instrument. J. Geophys. Res. Atmosp. 2008;113(D16) [Google Scholar]
- Lamsal L.N., Martin R.V., Van Donkelaar A., Celarier E.A., Bucsela E.J., Boersma K.F., Wang Y. Indirect validation of tropospheric nitrogen dioxide retrieved from the OMI satellite instrument: Insight into the seasonal variation of nitrogen oxides at northern midlatitudes. J. Geophys. Res. Atmosp. 2010;115(D5) [Google Scholar]
- Larkin A., Geddes J.A., Martin R.V., Xiao Q., Liu Y., Marshall J.D., Brauer M., Hystad P. Global land use regression model for nitrogen dioxide air pollution. Environ. Sci. Technol. 2017;51(12):6957–6964. doi: 10.1021/acs.est.7b01148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latza U., Gerdes S., Baur X. Effects of nitrogen dioxide on human health: systematic review of experimental and epidemiological studies conducted between 2002 and 2006. Int. J. Hygiene Environ. Health. 2009;212(3):271–287. doi: 10.1016/j.ijheh.2008.06.003. [DOI] [PubMed] [Google Scholar]
- Levelt P.F., van den Oord G.H.J., Dobber M.R., Maelkki A., Visser H., de Vries J., Stammes P., Lundell J.O.V., Saari H. The Ozone Monitoring Instrument. IEEE Trans. Geosci. Remote Sens. 2006;44:1093–1101. [Google Scholar]
- Lim S.S., Vos T., Flaxman A.D., Danaei G., Shibuya K., Adair-Rohani H., AlMazroa M.A., Amann M., Anderson H.R., Andrews K.G., Aryee M. A comparative risk assessment of burden of disease and injury attributable to 67 risk factors and risk factor clusters in 21 regions, 1990–2010: a systematic analysis for the Global Burden of Disease Study 2010. lancet. 2012;380(9859):2224–2260. doi: 10.1016/S0140-6736(12)61766-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindgren F., Rue H., Lindström J. An explicit link between Gaussian fields and Gaussian Markov random fields: the stochastic partial differential equation approach. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2011;73(4):423–498. [Google Scholar]
- Marécal, V., Peuch, V.H., Andersson, C., Andersson, S., Arteta, J., Beekmann, M., Benedictow, A., Bergström, R., Bessagnet, B., Cansado, A. & Chéroux, F., 2015. A regional air quality forecasting system over Europe: the MACC-II daily ensemble production.
- Martin R.V., Parrish D.D., Ryerson T.B., Nicks D.K., Jr, Chance K., Kurosu T.P., Wert B.P. Evaluation of GOME satellite measurements of tropospheric NO2 and HCHO using regional data from aircraft campaigns in the southeastern United States. J. Geophys. Res. Atmosp. 2004;109(D24) [Google Scholar]
- Martin R.V., Sioris C.E., Chance K., Ryerson T.B., Bertram T.H., Wooldridge P.J., Flocke F.M. Evaluation of space-based constraints on global nitrogen oxide emissions with regional aircraft measurements over and downwind of eastern North America. J. Geophys. Res. Atmosp. 2006;111(D15) [Google Scholar]
- Nguyen H., Cressie N., Braverman A. Spatial statistical data fusion for remote sensing applications. J. Am. Stat. Assoc. 2012;107(499):1004–1018. [Google Scholar]
- Novotny E.V., Bechle M.J., Millet D.B., Marshall J.D. National satellite-based land-use regression: NO_2 in the United States. Environ. Sci. Technol. 2011;45(10):4407–4414. doi: 10.1021/es103578x. [DOI] [PubMed] [Google Scholar]
- Ntzoufras I. John Wiley & Sons; 2011. Bayesian Modeling using WinBUGS (vol. 698) [Google Scholar]
- Potempski S., Galmarini S., Addis R., Astrup P., Bader S., Bellasio R., Bianconi R., Bonnardot F., Buckley R., D’Amours R., van Dijk A. Multi-model ensemble analysis of the ETEX-2 experiment. Atmos. Environ. 2008;42(31):7250–7265. [Google Scholar]
- R Core Team . R Foundation for Statistical Computing; Vienna, Austria: 2015. R: A Language and Environment for Statistical Computing. http://www.R-project.org/ (accessed 1 March 2019) [Google Scholar]
- Richter A., Burrows J.P., Nüß H., Granier C., Niemeier U. Increase in tropospheric nitrogen dioxide over China observed from space. Nature. 2005;437(7055):129. doi: 10.1038/nature04092. [DOI] [PubMed] [Google Scholar]
- Rue H., Martino S., Chopin N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 2009;71(2):319–392. [Google Scholar]
- Rue, H., Martino, S., Lindgren, F., Simpson, D., Riebler, A., 2013. R-inla: Approximate Bayesian inference using integrated nested Laplace approximations. Trondheim, Norway. URL: http://www.r-inla.org.
- Saltelli, A., Tarantola, S., Campolongo, F., & Ratto, M., 2004. Sensitivity analysis in practice: a guide to assessing scientific models. Chichester, England.
- Schaap M., Timmermans R.M.A., Roemer M., Boersen G.A.C., Builtjes P.J.H., Sauter F.J., Velders G.J.M., Beck J.P. The LOTOS-EUROS model: description, validation and latest developments. Int. J. Environ. Pollut. 2008;32(2):270–290. [Google Scholar]
- Shaddick G., Yan H., Salway R., Vienneau D., Kounali D., Briggs D. Large-scale Bayesian spatial modelling of air pollution for policy support. J. Appl. Stat. 2013;40(4):777–794. [Google Scholar]
- SimpleMaps Geographic Data Products World Cities Database. 2019. http://simplemaps.com/data/world-cities (accessed 1 March 2019)
- Sofen E.D., Bowdalo D., Evans M.J., Apadula F., Bonasoni P., Cupeiro M., Ellul R., Galbally I.E., Girgzdiene R., Luppo S., Mimouni M. Gridded global surface ozone metrics for atmospheric chemistry model evaluation. Earth Syst. Sci. Data. 2016:41–59. [Google Scholar]
- Veefkind J.P., Aben I., McMullan K., Förster H., De Vries J., Otter G., Van Weele M. TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications. Remote Sens. Environ. 2012;120:70–83. [Google Scholar]
- Vienneau D., de Hoogh K., Bechle M.J., Beelen R., van Donkelaar A., Martin R.V., Millet D.B., Hoek G., Marshall J.D. Western European land use regression incorporating satellite-and ground-based measurements of NO_2 and PM_10. Environ. Sci. Technol. 2013;47(23):13555–13564. doi: 10.1021/es403089q. [DOI] [PubMed] [Google Scholar]
- Vinken G.C.M., Boersma K.F., van Donkelaar A., Zhang L. Constraints on ship NO_x emissions in Europe using GEOS-Chem and OMI satellite NO_2 observations. Atmos. Chem. Phys. 2014;14(3):1353–1369. [Google Scholar]
- Wang Y.X., McElroy M.B., Jacob D.J., Yantosca R.M. A nested grid formulation for chemical transport over Asia: applications to CO. J. Geophys. Res. Atmosp. 2004;109(D22) [Google Scholar]
- WHO, 2006. Air Quality Guidelines. Global update 2005. Particulate matter, ozone, nitrogen dioxide and sulfur dioxide, World Health Organization, Regional Office for Europe, Copenhagen.
- WHO, 2013. Review of evidence on health aspects of air pollution – REVIHAAP project. Technical Report, World Health Organization, Regional Office for Europe, Copenhagen, Denmark. [PubMed]
- Young M.T., Bechle M.J., Sampson P.D., Szpiro A.A., Marshall J.D., Sheppard L., Kaufman J.D. Satellite-based NO2 and model validation in a national prediction model based on universal kriging and land-use regression. Environ. Sci. Technol. 2016;50(7):3686–3694. doi: 10.1021/acs.est.5b05099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L., Jacob D.J., Knipping E.M., Kumar N., Munger J.W., Carouge C.C., van Donkelaar A., Wang Y.X., Chen D. Nitrogen deposition to the United States: distribution, sources, and processes. Atmos. Chem. Phys. 2012;12:4539–4554. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.