Predicting death by suicide following an emergency department visit for parasuicide with administrative health care system data and machine learning

Abstract

Background

Suicide is a leading cause of death worldwide and results in a large number of person years of life lost. There is an opportunity to evaluate whether administrative health care system data and machine learning can quantify suicide risk in a clinical setting.

Methods

The objective was to compare the performance of prediction models that quantify the risk of death by suicide within 90 days of an ED visit for parasuicide with predictors available in administrative health care system data.

The modeling dataset was assembled from 5 administrative health care data systems. The data systems contained nearly all of the physician visits, ambulatory care visits, inpatient hospitalizations, and community pharmacy dispenses, of nearly the entire 4.07 million persons in Alberta, Canada. 101 predictors were selected, and these were assembled for each of the 8 quarters (2 years) prior to the quarter of death, resulting in 808 predictors in total for each person. Prediction model performance was validated with 10-fold cross-validation.

Findings

The optimal gradient boosted trees prediction model achieved promising discrimination (AUC: 0.88) and calibration that could lead to clinical applications. The 5 most important predictors in the optimal gradient boosted trees model each came from a different administrative health care data system.

Interpretation

The combination of predictors from multiple administrative data systems and the combination of personal and ecologic predictors resulted in promising prediction performance. Further research is needed to develop prediction models optimized for implementation in clinical settings.

Funding

There was no funding for this study.

Research in Context.

Evidence before this study

It has been shown that risk scales have limited utility for quantifying suicidality risk. It has also been shown that statistical models have quantified suicidality risk better than clinicians but these models have not been widely implemented. At present, there is no consensus on the preferred performance characteristics required to implement prediction models that quantify the risk of suicide in clinical practice.

Added value of this study

This study is one of the first to show strong enough performance to warrant discussion about the feasibility of implementing prediction models that quantify the risk of suicide in clinical practice. There is promise for quantifying suicide risk in clinical practice and this study provides researchers with direction to develop prediction models that quantify suicide risk. Broad administrative data combined with advanced prediction model classes appear necessary to achieve optimal performance.

Implications of all the available evidence

Following an emergency department visit for parasuicide, there are a number of actions that a clinician can choose from (discharge with routine follow-up, discharge with urgent follow-up, assertive outreach, inpatient hospitalization, etc.) and estimates of suicide risk from prediction models may enhance clinical judgment to select the best action. Although this study demonstrated promising performance, further research is needed to determine the performance characteristics required to implement prediction models that quantify the risk of suicide in clinical practice.

Alt-text: Unlabelled box

1. Introduction

Although death by suicide is a rare event, it is an important cause of death because most deaths by suicide are premature deaths and result in a large number of years of life lost. In the Canadian province of Alberta, between 2000 and 2018, the suicide rate was 14 per 100,000 person-years, and 96 percent of deaths by suicide occurred in persons younger than 75 resulting in 290,490 years of life lost [1]. 84 percent of deaths by suicide occurred in persons younger than 60 and 53 percent occurred in persons younger than 45 [1].

There are a number of risk factors that are widely recognized for death by suicide, including mental illness, substance misuse, parasuicide and lethality of parasuicide, suicidal ideation and intensity of suicidal ideation, social conditions and social interactions, and life events [2]. Although many risk factors for suicide are known, quantifying suicide risk is difficult [3], [4], [5] and this makes suicide prevention a challenge for health care service providers and health care policy providers. Risk scales are often used in clinical settings but it has been shown that risk scales have limited utility for quantifying suicidality risk [6], [7], [8], [9], [10]. Statistical models have been developed to quantify suicidality risk but these models have not been widely implemented, even though the models outperformed clinicians when compared [11,12]. In Canada, large amounts of data are collected during the administration of the health care system. This data provides an opportunity to explore whether quantifying suicide risk with machine learning models using administrative data can achieve performance that is potentially capable of guiding preventive actions.

In earlier studies [13,14], it was found that the feedforward neural network, recurrent neural network, one-dimensional convolutional neural network, and gradient boosted trees classes of machine learning models can improve upon logistic regression when quantifying suicide risk with administrative health care system data in Alberta. The optimal feedforward neural network (AUC: 0.8352), recurrent neural network (AUC: 0.8407), one-dimensional convolutional neural network (0.8419), and gradient boosted trees (AUC: 0.8493) model configurations outperformed logistic regression (AUC: 0.8179). It was found that gradient boosted trees model configurations outperformed the neural network model configurations and required far less computational resources.

Further, although recurrent neural networks and one-dimensional convolutional neural networks are designed to process sequences and there was 10 years (40 quarters) of temporal data in the modeling dataset, the optimal recurrent neural network and one-dimensional convolutional neural network model configurations did not materially outperform the optimal feedforward neural network model configuration, required more data to achieve optimal performance, and were far more computationally expensive. The optimal gradient boosted trees and feedforward neural network model configurations required less than two years (8 quarters) of temporal data for optimal performance.

While the earlier studies were designed to identify the most promising model classes and the temporal period required to achieve optimal performance, they used a case-control study design in order to include as many instances of death by suicide as possible in the modeling dataset. The resulting modeling dataset was not representative of a health care setting where a prediction model may have clinical utility. This study seeks to extend the findings of the earlier studies to a realistic health care setting: emergency department (ED) visits for parasuicide (self-harm that did not result in death, regardless of intent). ED visits for parasuicide present a unique opportunity for suicide prevention because these visits identify persons with a high risk of death by suicide (1 in 125 in this study compared with the overall Alberta 90-day risk of 1 in 29,000) and provide opportunities to reduce the imminent risk of suicide and to establish continuity of care to reduce suicide risk following discharge [15]. If the risk of death by suicide following an ED visit for parasuicide could be quantified, then health care service providers and health care policy providers may be able to better target prevention efforts. For example, inpatient admission can be used as a preventive action, but a number of other treatment options are available (discharge with routine follow-up, discharge with urgent follow-up, assertive outreach, etc.), and being able to quantify suicide risk would help health care service providers decide on the best treatment option.

The objective of this study is to compare the performance of logistic regression and gradient boosted trees (XGB) models for quantifying the risk of death by suicide within 90 days of an ED visit for parasuicide with predictors available in administrative health care system data.

2. Methods

2.1. Data sources

A literature review was carried out for this study. The goal of the literature review was to identify predictors that have been used to predict suicide or parasuicide. The majority of predictors were identified from clinical assessment tools and statistical prediction models. Predictors were selected from administrative data systems if they had been shown to predict suicide or parasuicide in the literature review. A complete listing of the administrative data sources and the selected predictors is available in Appendix B. The data sources contain nearly all of the physician visits, ambulatory care visits, inpatient hospitalizations, and community pharmacy dispenses, of nearly the entire 4.07 million persons in Alberta, Canada [16]. Death by suicide was collected from the vital statistics cause of death database (ICD-10 cause of death codes X60 through X84), and the predictors were collected from physician service payment claims, ambulatory care and inpatient hospitalization records, community pharmacy dispense records, and a registry containing the date of qualification for a number of disease case definitions. The data were linked using the unique Personal Health Number assigned to Albertans for the delivery of health care services.

Parasuicide was defined as an ED visit for self-harm that did not result in death, regardless of intent. The term ‘parasuicide’ is used rather than the term ‘attempted suicide’ because intent cannot be determined with the administrative data used in this study. ED visits coded with a disposition of “death on arrival (DOA): patient is dead on arrival to the ambulatory care service” and “death after arrival (DAA): patient expires after initiation of the ambulatory care visit” were excluded because these were considered deaths by suicide. Persons with a date of death in the vital statistics data on the same day as the most recent ED visit for parasuicide – whatever the cause of death – were also excluded because there would be no opportunity for follow-up and would not be relevant to decisions made by clinicians in the ED.

All persons with an ED visit for parasuicide between 2010 and 2017 were extracted from the ambulatory care data system. The most recent ED visit for parasuicide was selected, and the predictors were assembled for each of the most recent 8 quarters because our earlier work [13,14] showed that only the most recent 8 quarters were required for optimal prediction performance. In total, 101 predictors were selected, and these were prepared for each of the 8 quarters prior to the most recent ED visit for parasuicide. The modeling dataset did not include any information following the most recent ED visit for parasuicide. The predictors selected were primarily related to mental health, but predictors related to physical health were also selected because physical health has been shown to predict suicide [17]. The predictors related to physical health may not be directly related to suicide but they were included in the modeling dataset to allow the models to learn which (if any) contribute to quantifying suicide risk. The total number of predictors for each person was 808 (101 predictors x 8 quarters). The outcome was death by suicide within 90 days of the most recent ED visit for parasuicide.

There were 268 persons that died by suicide within 90 days and 33,426 persons that did not, and so the outcome class distribution was imbalanced. In order to assign equal importance to both outcome classes, the models included class weights of 124 / 125 for persons that died by suicide and 1 / 125 for persons that did not die by suicide.

2.2. Hardware and software

The administrative data were extracted and assembled using SAS 9.4. The analysis was performed on a desktop computer with an Ubuntu 18.04.1 LTS operating system and a GeForce GTX 1080 Ti 12GB graphics processing unit (GPU) using the NVIDIA-SMI 390.87 driver. The analysis was written in the Python programming language in a Jupyter 5.6.0 notebook in Anaconda Navigator 1.8.7. The logistic regression models and calibration curves were developed using scikit-learn 0.20.0 [18]. The XGB models were developed with XGBoost 0.72 [19] with GPU support.

2.3. Model configuration evaluation

In prediction modeling, and particularly in machine learning, the distinction is often not made between prediction in the temporal sense and prediction in the classification sense. In this study, the outcome was indeed in the future as far as the models were concerned. The modeling dataset did not contain any information following the ED visit for parasuicide, and so the models predicted suicide in both the temporal and classification senses.

K-fold cross-validation is a model evaluation approach that uses k validation datasets to obtain a robust estimate of expected performance with unseen data [20]. The 10-fold cross-validation area under the receiver operating characteristic curve (AUC) was chosen as the metric to evaluate model configuration performance. The AUC is not the only performance metric that can be used to evaluate model configuration performance. Other metrics such as sensitivity, specificity, positive prediction value (PPV), negative prediction value (NPV), accuracy, F-beta scores, precision-recall curves, log-loss, and Brier scores can also be used. This study used the AUC because it has the intuitive interpretation that the AUC is the probability that the predicted risk was higher for a person that died by suicide than a person that did not [21], and because it was closely associated with sensitivity, specificity, PPV, and NPV.

The logistic regression and XGB model configurations were evaluated with the most recent 1, 2, 4, 6, and 8, quarters of data. The scikit-learn library used to develop the logistic regression models applies a L2 regularization penalty (often called ‘ridge regression’) by default [22]. The L2 regularization penalty adds the sum of the squared beta parameters to the loss function that the logistic regression model seeks to minimize. This has the effect of penalizing large beta parameter values and can help prevent overfitting. To evaluate the logistic regression model configurations without a regularization penalty (the default in most statistical software), the C parameter in scikit-learn was assigned a value 1,000,000. The C parameter is the inverse of regularization strength, and so a regularization strength of 1 / 1,000,000 essentially disables regularization. The XGB hyperparameters evaluated in this study were the number of classification trees (10 to 200 in increments of 10) and the maximum classification tree depth (1, 2, 3, 4, 5). The learning rate and gamma are also XGB hyperparameters but after preliminary exploration with a range of settings, it was decided to use the default settings in the XGBoost library (gamma = 0, learning rate = 0.1) because adjusting the default settings did not result in performance improvements.

2.4. Role of funding

There was no funding for this study.

3. Results

3.1. Discrimination

The 10-fold cross-validation AUC estimates for logistic regression with the L2 regularization penalty disabled (C parameter = 1 / 1,000,000) using the most recent 1, 2, 4, 6, and 8, quarters were 0.8113, 0.7760, 0.7361, 0.6988, 0.6758, respectively. Logistic regression with the L2 regularization penalty disabled was overfit to the training data, and the overfitting was more severe with additional quarters of temporal data. Conversely, the 10-fold cross-validation AUC estimates for logistic regression with the L2 regularization penalty enabled (the default in the scikit-learn library) using 1, 2, 4, 6, and 8, quarters were 0.8590, 0.8632, 0.8572, 0.8454, 0.8392, respectively.

The 10-fold cross-validation AUC estimate was 0.8786 for the optimal XGB model configuration (2 quarters of data, 70 classification trees, maximum tree depth of 2). The performance of the XGB model configurations with the most recent 2, 4, 6, and 8, quarters was essentially indistinguishable but the XGB model configurations using 2 and 4 quarters tended to have slightly higher optimal AUC estimates.

In addition to the AUC, a number of other 10-fold cross-validation performance metrics were computed and are included in Table 1. The optimal XGB model configuration performed better than the optimal logistic regression model configuration with L2 regularization disabled on every performance metric. The optimal XGB model configuration had a higher sensitivity (0.8912 vs 0.8420) than the optimal logistic regression model configuration with L2 regularization enabled but a lower specificity (0.6876 vs 0.7429).

Table 1.

10-Fold cross-validation performance metrics, mean.

Performance metric	Log. regression mean (1 Quarter)	Log. regression L2 mean (2 Quarters)	XGB mean (2 Quarters)
Area Under the Curve	0.8113	0.8632	0.8786
Accuracy	0.8531	0.8411	0.8895
Balanced Accuracy	0.7628	0.7925	0.7894
Sensitivity	0.6710	0.7429	0.6876
Specificity	0.8547	0.8420	0.8912
Positive Prediction Value	0.0354	0.0359	0.0479
Negative Prediction Value	0.9969	0.9974	0.9971

3.2. Calibration

The calibration of prediction models is often evaluated by comparing predicted probabilities with actual probabilities, commonly called a ‘calibration curve’. The calibration of the optimal logistic regression (2 quarters of data, L2 regularization) and XGB (2 quarters of data, 70 classification trees, maximum tree depth of 2) model configurations from above were evaluated using calibration curves. To evaluate calibration with unseen data, the modeling dataset was divided into a training dataset (80 percent) and a validation dataset (20 percent). With modeling datasets that have a small number of instances of the outcome, random divisions of the modeling dataset into training and validation datasets can sometimes result in a validation dataset with a disproportionate number of instances of the outcome which can result in poor calibration. Stratified random sampling based on the outcome is commonly used to ensure that the validation dataset has a proportionate number of instances of the outcome. The division of the modeling dataset into training and validation datasets was stratified based on the outcome to ensure that both datasets had the same proportion of deaths by suicide as the modeling dataset. The models were developed with the training dataset and evaluated with the validation dataset.

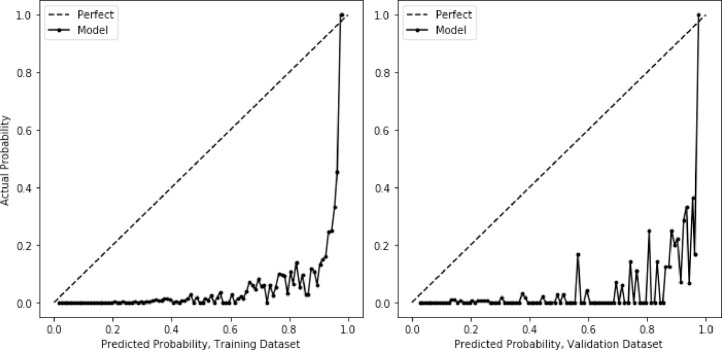
Fig. 1, Fig. 2 show the calibration curves for the logistic regression and XGB models, evaluated on both the training and validation datasets. The predicted probability generally increased as the actual probability increased but the agreement between the predicted and actual probabilities was variable. The variability was mainly due to the small number of instances of death in the modeling dataset. For example, if the XGB model predicted a probability of 80 percent for 100 persons in the validation dataset, it would be expected that the actual number of deaths among those persons would be 80. However, there were only 54 instances of death by suicide in the validation dataset, and as a result, the actual probability was zero for many predicted probabilities. With an increased number of deaths by suicide in the modeling dataset, it is anticipated that the calibration variability would decrease. Even so, the calibration curve for the XGB model was less variable than the calibration curve for the logistic regression model, particularly for predicted probabilities higher than 0.5.

Fig. 1.

Calibration Curve, Logistic Regression, Predicted.

Fig. 2.

Calibration Curve, Gradient Boosted Trees, Predicted.

The models included class weights in order to assign equal importance to both outcome classes, and so the predicted probabilities were calibrated as though the modeling dataset contained balanced outcome classes. To evaluate the models calibrated to the risk of death by suicide in the modeling dataset, Platt calibration was used [23]. Platt calibration uses logistic regression to transform predicted probabilities into calibrated probabilities. Isotonic calibration was also tried but it achieved perfect calibration with the training dataset and poor calibration with the validation dataset. Fig. 3, Fig. 4 show the calibration curves for the logistic regression and XGB models, evaluated on both the training and validation datasets, and calibrated using Platt calibration. As before, the calibration curves were variable, and the calibration curve for the XGB model was less variable than the calibration curve for the logistic regression model, particularly for high predicted probabilities. For the Platt calibrated logistic regression model, predicted probabilities below 0.2 appeared to be well calibrated but predicted probabilities above 0.2 appeared to be poorly calibrated. Similarly, the Platt calibrated XGB model appeared to be well calibrated except for predicted probabilities above 0.2, where the XGB model under-estimated the risk of death by suicide.

Fig. 3.

Calibration Curve, Logistic Regression, Platt Calibration.

Fig. 4.

Calibration Curve, Gradient Boosted Trees, Platt Calibration.

Platt calibration is commonly used to calibrate machine learning models because machine learning models often produce logistic s-shaped calibration curves. The models with outcome class weights did not produce logistic s-shaped calibration curves, and unfortunately, Platt calibration resulted in predicted probabilities of between 0.25 and 0.30 for all actual probabilities over 0.25. As an alternative to Platt calibration, a second XGB prediction model was developed to predict the actual probability of the outcome using the predicted probability of the outcome. The resulting calibration curves for the training and validation datasets (Fig. 5) were better calibrated than the Platt calibration curves, although the validation dataset calibration curve was still variable.

Fig. 5.

Calibration Curve, Gradient Boosted Trees, XGB Calibration.

3.3. Net reclassification improvement

The net reclassification improvement (NRI) for the optimal XGB model compared to the optimal logistic regression model using the models and the training and validation datasets from the calibration section above was 0.5183 (NRI_event = 0.6215, NRI_{no event} = −0.1032) and 0.4644 (NRI_event = 0.5741, NRI_{no event} = −0.1096) respectively.

3.4. Predictor importance

The XGBoost library produces a measure of the importance of each predictor [24], and the 5 predictors with the highest importance from the optimal XGB model configuration (2 quarters of data, 70 classification trees, maximum tree depth of 2) were: the total number of emergency department visits with a parasuicide diagnosis that were classified as triage category 1 (from the most recent quarter); age (from the first quarter); the total number of inpatient days that were classified as maternity (from the most recent quarter); the suicide rate in the Local Geographic Area (community) of residence (from the most recent quarter); and the total cost of physician services (from the most recent quarter).

3.5. Tuning PPV using class weights

Clinicians are often interested in PPV because of its useful interpretation in clinical practice: the probability that a person will die by suicide given that they are identified as being at risk by the prediction model. The PPV of the optimal logistic regression model configuration was 0.0359 and the PPV of the optimal XGB model configuration was 0.0479. A higher PPV can be achieved by reducing the magnitude of the positive class weight configuration, with a decrease in sensitivity being the primary trade-off. The optimal XGB model configuration (2 quarters of data, 70 classification trees, maximum tree depth of 2) was evaluated with the full range of positive class weights from 1 to 125, and achieved a maximum 10-fold cross-validation PPV of 0.2016 using a class weight of 10, with sensitivity of 0.3686, specificity of 0.9884, and NPV of 0.9949. Higher 10-fold cross-validation PPV estimates were achieved with positive class weights below 10 but the estimates were highly variable across cross-validation folds.

4. Discussion

The objective of this study is to compare the performance of logistic regression and XGB models that quantify the risk of death by suicide within 90 days of an ED visit for parasuicide using predictors available in administrative health care system data. It is unlikely that a single prediction model could be developed and implemented everywhere, and so researchers will likely be required to develop prediction models based on the administrative health care system data available to them.

The optimal XGB model configuration (AUC: 0.8786) displayed better discrimination than the optimal logistic regression model configurations with L2 regularization (AUC: 0.8632) and without L2 regularization (AUC: 0.8113). The optimal XGB model configuration also had better overall calibration (particularly following XGB calibration) than the optimal logistic regression model configuration with L2 regularization, particularly for persons at higher risk of death by suicide. The XGB calibration approach seems promising for calibrating machine learning models that do not produce logistic s-shaped calibration curves.

Both the optimal XGB and logistic regression model configurations achieved high 10-fold cross-validation AUC estimates which distinguishes these models from prior efforts to predict death by suicide. This could be because of the combination of predictors from a number of administrative data systems. For example, the 5 most important predictors in the optimal XGB model configuration each came from a different administrative data system: the total number of emergency department visits with a parasuicide diagnosis that were classified as triage category 1, age, the total number of inpatient days that were classified as maternity, the suicide rate in the community of residence, and the total cost of physician services. It seems reasonable that each administrative data system would contribute to a fuller representation of each person, and this would provide prediction models with more information to make better predictions. The combination of personal and ecologic predictors could also be important for the high prediction performance. For example, the fourth most important predictor in the optimal XGB model configuration was the suicide rate in the community of residence.

An interesting finding from this study is that logistic regression without L2 regularization, which is the default in most statistical software, overfit to the training data and overfit more severely as the number of quarters increased. With the default scikit-learn L2 regularization enabled, the optimal logistic regression model configuration achieved a 10-fold cross-validation AUC estimate only slightly lower than the optimal XGB model configurations. This suggests that researchers that prefer logistic regression should consider regularization. Most statistical software includes procedures for regularization, although it might be referred to as ‘penalization’ or ‘shrinkage’.

Another interesting finding from this study that echoes previous work is that only the most recent 2 to 4 quarters (each with all 101 predictors) were needed for optimal performance. Performance increased as temporal data increased until a maximum was reached, after which additional temporal data resulted in decreasing or stationary performance. This suggests that the risk state over the past year is most important for quantifying suicide risk in the current context.

Suicide risk and administrative data differs across jurisdictions, and researchers may need to develop their own prediction models rather than applying prediction models developed in other jurisdictions. Developing optimized models for implementation can be very costly and our studies were designed to provide readers with some direction by identifying the most promising classes of prediction models for quantifying suicide risk and determining the temporal period required for optimal performance. Future research should focus on obtaining as many instances of death by suicide as possible, and these instances may need to come from combining data across jurisdictions in order to obtain as many instances of death by suicide as possible. Future research should also focus on variable reduction to determine the minimal set required for optimal or near-optimal performance. For example, many predictors in the modeling dataset were never used for segmentation by the optimal XGB model configuration and would not be needed in an optimized production model. Predictor engineering is also likely to be important, particularly more refined diagnosis and intervention categories, and perhaps composite predictors.

In this study, good discrimination and calibration were achieved, and the performance seemed to be due more to the data than to the model classes. Although the calibrated XGB model demonstrated better discrimination than the calibrated logistic regression model, it could be argued that the improvement was incremental. The calibrated XGB model demonstrated a material improvement in calibration compared with the calibrated logistic regression model, but still suffered from variable calibration for persons at highest risk. While the calibrated logistic regression model demonstrated high variability in the predicted probabilities for higher risk persons, the calibrated XGB model assigned a small number of predicted probabilities for higher risk persons. The variable calibration for higher risk persons would likely be resolved with larger modeling datasets, particularly with more instances of death by suicide.

The goal of prediction modeling is to furnish health care service providers and health care policy providers with additional information to improve decisions. Prediction models that use administrative data would have access to information a clinician likely would not. For example, a clinician may not be able to access all health service records for a person presenting, and the person presenting may not be able to articulate the full details of their health services history. Further, one of the most important predictors in the optimal XGB model configuration was the suicide rate in the community of residence, and a clinician or person presenting may not be aware of the suicide rate in the community of residence. Also, even if a clinician had access to the same information as a prediction model, it would be unreasonable to expect the clinician to integrate the information into a superior risk estimate, and it has been shown that prediction models outperform clinicians.

In a sense, the utility of predicted probabilities would be to contribute to an informal Bayesian reasoning by clinicians. For example, when a person presents at an emergency department with parasuicide, a clinician would immediately be aware that this is a high-risk situation even before meeting the person, which represents a pretest or prior probability of suicide risk. Then, the prediction model would provide a risk estimate, which may indicate a higher or lower risk. The clinician would update their pretest probability estimate, and meet the person presenting with a more refined prior probability. In meeting with the person presenting, the clinician would again update their probability estimate based on their clinical assessment, and make a better informed clinical judgment.

This study demonstrates that there is promise for realizing the above scenario to quantify the risk of death by suicide within 90 days of an ED visit for parasuicide, but to be clear, this study represents a step towards clinical innovation and not a recommendation for altered assessment. Further research is needed before prediction models can be implemented in clinical practice, including ethical and legal considerations. The calibrated XGB model configuration using a modeling dataset assembled from a number of administrative data systems demonstrated promising discrimination and calibration in a realistic health care setting. But whether furnishing clinicians with predicted probabilities actually leads to better clinical judgment requires further research. Poor predicted probabilities or good predicted probabilities that are integrated poorly have the potential to do harm. Once a prediction model is optimized for a particular clinical setting, clinical studies are necessary to determine how best to use the risk estimates in combination with clinical judgment. Then, once a model is implemented in clinical practice, clinical studies are necessary to determine if furnishing clinicians with predicted probabilities actually leads to better clinical judgment.

Currently, there is no consensus on the performance required for implementation of prediction models that quantify suicide risk in clinical practice. Prediction models can be tuned to seek to achieve preferred performance characteristics, as was done when tuning PPV using class weights above. We invite clinicians to consider and comment on the prediction performance required for implementation in clinical practice, such as the trade-off between PPV and sensitivity, or whether predicted probabilities are preferred to predicted classifications.

5. Limitations

There were three primary limitations in this study: the small number of instances of death by suicide in the modeling dataset, calibration assessment, and the inherent limitations of administrative data. The first two limitations are in a sense related because the Platt and XGB calibration curves seemed to be well calibrated overall but were variable, mainly because there were only 268 instances of death by suicide in the modeling dataset. With a larger number of instances of death by suicide it is anticipated that prediction models would result in calibration curves that would be smoother and better calibrated, particularly for persons with high actual risks of suicide.

The predictors available in the administrative data were not collected for the purposes of quantifying suicide risk and many important predictors were not available. Predictors that were not available in the administrative data but would be important would be direct measures of severity of mental illness, severity of substance misuse, suicidal ideation and intensity of suicidal ideation, social conditions and social interactions, and life events. For example, while the number of health care services with a mental health diagnosis obtained from administrative health care system data can be a proxy for the severity of mental illness, a more direct measure of severity of mental illness would likely provide greater prediction utility. This is likely the most difficult limitation of administrative data to overcome, but this limitation could diminish if electronic health care system data becomes more complete and the ability to link with other data systems improves. Another limitation of developing prediction models with administrative data is that clinicians would not be able to compute risk themselves and would have to rely on the development of an electronic application that would assemble predictors from multiple administrative data systems, quantify the risk of death by suicide using a prediction model, and provide a real-time, user-friendly interface to communicate the risk. Building such an electronic application and incorporating it into existing electronic medical record interfaces is not an impossible task, but the performance of the prediction model would have to warrant such an investment. This study is one of the first to show strong enough performance to warrant discussion about the feasibility of such an investment.

Declaration of Competing Interest

None.

Appendix A:

Table 1

Appendix B: Predictors

Alberta Health Care Insurance Plan (AHCIP) Registry

Residency Flag (0/1)

Sex (0/1)

Age

Social Proxy: Registered First Nations (0/1)

Social Proxy: Income Support (0/1)

Social Proxy: Child Intervention (0/1)

Social Proxy: Other (0/1)

Local Geographic Area: Metropolitan (0/1)

Local Geographic Area: Metropolitan Influence (0/1)

Local Geographic Area: Urban (0/1)

Local Geographic Area: Urban Influence (0/1)

Local Geographic Area: Rural centre (0/1)

Local Geographic Area: Rural (0/1)

Local Geographic Area: Rural Remote (0/1)

Latitude of Residential Postal Code

Longitude of Residential Postal Code

Supplemental Enhanced Service Event (SESE) Physician Service Payment Claims

Total Cost

Total Physician Services: General Practitioner

Total Physician Services: Psychiatrist

Total Physician Services: Other

Total Diagnoses, Category 1 (ICD9: 291* or 292* or 303* or 304* or (305* and not 305.1))

Total Diagnoses, Category 2 (ICD9: 295* or 301.2)

Total Diagnoses, Category 3 (ICD9: 296* or 298.0 or 300.4 or 301.1 or 309* or 311*)

Total Diagnoses, Category 4 (ICD9: 297* or (298* and not 298.0))

Total Diagnoses, Category 5 (ICD9: 308* or (300* and not 300.4))

Total Diagnoses, Category 6 (ICD9: 301* not 301.1 and not 301.2)

Total Diagnoses, Category 7 (ICD9: 302*)

Total Diagnoses, Category 8 (ICD9: 306* or 316*)

Total Diagnoses, Category 9 (ICD9: 307*)

Total Diagnoses, Category 10 (ICD9: 290* or 293* or 294* or 310*)

Total Diagnoses, Category 11 (ICD9: 299* or 312* or 313* or 314* or 315*)

Total Diagnoses, Category 12 (ICD9: 317* or 318* or 319*)

Total Diagnoses, Category 13 (ICD9: Other)

Morbidity and Ambulatory Care Abstract Reporting (MACAR) Ambulatory Care Services

Total Emergency Department Visits, Parasuicide Diagnosis, Triage Category 1

Total Emergency Department Visits, Parasuicide Diagnosis, Triage Category 2

Total Emergency Department Visits, Parasuicide Diagnosis, Triage Category 3

Total Emergency Department Visits, Parasuicide Diagnosis, Triage Category 4

Total Emergency Department Visits, Parasuicide Diagnosis, Triage Category 5

Total Emergency Department Visits, Parasuicide Diagnosis, Triage Category 6

Total Emergency Department Visits, Mental Health Diagnosis, Triage Category 1

Total Emergency Department Visits, Mental Health Diagnosis, Triage Category 2

Total Emergency Department Visits, Mental Health Diagnosis, Triage Category 3

Total Emergency Department Visits, Mental Health Diagnosis, Triage Category 4

Total Emergency Department Visits, Mental Health Diagnosis, Triage Category 5

Total Emergency Department Visits, Mental Health Diagnosis, Triage Category 6

Total Emergency Department Visits, Other Diagnosis, Triage Category 1

Total Emergency Department Visits, Other Diagnosis, Triage Category 2

Total Emergency Department Visits, Other, Diagnosis Triage Category 3

Total Emergency Department Visits, Other Diagnosis, Triage Category 4

Total Emergency Department Visits, Other Diagnosis, Triage Category 5

Total Emergency Department Visits, Other Diagnosis, Triage Category 6

Total Mental Health Department Ambulatory Care Visits, Parasuicide Diagnosis

Total Mental Health Department Ambulatory Care Visits, Mental Health Diagnosis

Total Mental Health Department Ambulatory Care Visits, Other Diagnosis

Total Other Facility Department Care Visits, Parasuicide Diagnosis

Total Other Facility Department Care Visits, Mental Health Diagnosis

Total Other Facility Department Care Visits, Other Diagnosis

Morbidity and Ambulatory Care Abstract Reporting (MACAR) Inpatient Hospitalizations

Total Inpatient Days, Psychiatric

Total Inpatient Days, Maternal

Total Inpatient Days, Other

Pharmaceutical Information Network Community Pharmacy Dispense Records

Total Unique Drug Identification Numbers, Mental Health (ATC: N05* or N06*)

Total Drug Days, Mental Health (ATC: N05* or N06*)

Total Unique Drug Identification Numbers, Non-Mental Health

Total Drug Days, Non-Mental Health

Disease Registry (quarter of diagnosis forward)

Affective Disorder (0/1)

Anorexia (0/1)

Anxiety Disorder (0/1)

Asthma (0/1)

Atrial Fibrillation (0/1)

Chronic Kidney Disease (0/1)

Chronic Obstructive Pulmonary Disorder (0/1)

Congestive Heart Failure (0/1)

Dementia (0/1)

Diabetes (0/1)

End-Stage Renal Disease (0/1)

Epilepsy (0/1)

Gout (0/1)

Guillain-Barré Syndrome (0/1)

Hypertension (0/1)

Inflammatory Bowel Disease (0/1)

Ischemic Heart Disease (0/1)

Liver Cirrhosis (0/1)

Lupus (0/1)

Motor Neuron Disease (0/1)

Multiple Sclerosis (0/1)

Non-Organic Psychosis (0/1)

Organic Psychosis (0/1)

Osteoarthritis (0/1)

Osteoporosis (0/1)

Parkinson's Disease (0/1)

Rheumatoid Arthritis (0/1)

Schizophrenia (0/1)

Shingles (0/1)

Sleep Apnea (0/1)

Stroke (0/1)

Substance Abuse (0/1)

Ecologic

Local Geographic Area: Suicide Rate

Local Geographic Area: Proportion Registered First Nations

Local Geographic Area: Proportion Income Support

Local Geographic Area: Proportion Child Intervention

Local Geographic Area: Proportion Other