Photopolarimetrical properties of coronavirus model particles: Spike proteins number influence

Highlights

• •Coronavirus virions are spherical, 120–160 nm in diameter, with an outer envelope bearing 20-nm-long club-shaped spike proteins.
• •An increasing of spike proteins number makes virus infectivity stronger.
• •The mathematical model that describes the shape of the coronavirus virion having different spikes proteins number is suggested.
• •Based on this model, the characteristics of light scattered by the coronavirus model particles are calculated.
• •Two main features of coronavirus model particles are found in the spectral region near 200 nm: a minimum of intensity and sharp leap of the linear polarization degree.
• •The effect of the spike proteins number on the intensity and polarization properties of scattered light was studied.
• •It was determined that when the spike proteins number decreasing, both intensity minimum and linear polarization leap position shift to shorter wavelengths.
• •Far ultraviolet photopolarimeters are required for a more reliable distinction between viruses and non-viruses.

Abstract

Coronavirus virions have spherical shape surrounded by spike proteins. The coronavirus spike proteins are very effective molecular mechanisms, which provide the coronavirus entrance to the host cell. The number of these spikes is different; it dramatically depends on external conditions and determines the degree of danger of the virus. A larger number of spike proteins makes the virus infectivity stronger.

This paper describes a mathematical model of the shape of coronavirus virions. Based on this model, the characteristics of light scattered by the coronavirus virions were calculated. It was found two main features of coronavirus model particles in the spectral region near 200 nm: a minimum of intensity and a sharp leap of the linear polarization degree. The effect of the spike protein number on the intensity and polarization properties of the scattered light was studied. It was determined that when the number of spike proteins decreases, both the intensity minimum and the position of the linear polarization leap shift to shorter wavelengths. This allows us to better evaluate the shape of the coronavirus virion, and, therefore, the infectious danger of the virus. It was shown that the shorter the wavelength of scattered light, the more reliably one can distinguish viruses from non-viruses. The developed model and the light scattering simulations based on it can be applied not only to coronaviruses, but also to other objects of a similar structure, for example, pollen.

1. Introduction

During 2002–2003, coronavirus SARS-CoV has infected 8000 people at fatality rate about 10% [1]. In 2012, more than 1700 people were infected by coronavirus MERS-CoV at fatality rate about 36% [2]. At the end of 2019 novel coronavirus disease, known as COVID-19 [3], was first reported from Wuhan City of China, and has spread around the 60 countries and territories, threatening tens of millions of people [4].

Coronaviruses cause widespread diseases, threatening human health and causing economic loss [5]. Therefore, health risks from coronaviruses are constant and long-term, with important implications for global health and economic stability. The study of the various properties of coronaviruses, in particular, the characteristics of light scattering by them, can provide new tools for their identification and study.

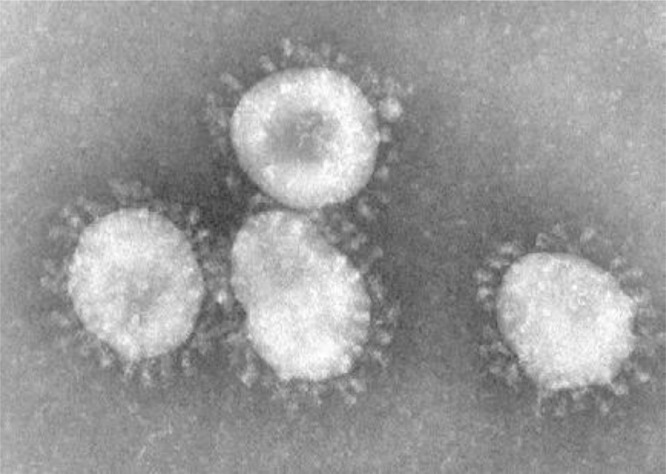
One of the features of the coronavirus is the presence of a certain number of spike proteins on its surface (see Fig. 1 , taken from [6]), forming around the virus a kind of solar corona (due to which coronavirus got its full name). Using these spikes, the coronavirus enter into host cells. The number of these spike proteins is a fairly important characteristic of the danger of the virus. Increasing the spike proteins number per virion increases infectivity [7]. Moreover, adverse conditions such as changes in temperature and pH are leaving large areas of virion relatively free of spike proteins [8].

Fig. 1.

Coronaviruses as seen under an electron microscope [6] (Photo courtesy of CDC/Fred Murphy).

Thus, it is fundamentally important to evaluate the spike proteins number as an indicator of the degree of danger of a given set of virions. But many existing methods, such as real-time fluorescence-based quantitative PCR [9] allow detecting virions number only, without taking into account changes in the virion structure, such as increasing or decreasing spike proteins number. This paper describes a mathematical model that allows simulating the shape of a coronavirus with a given number of spike proteins. Also the effect of the spike proteins number on the scattered light characteristics, such as intensity and the degree of linear polarization, it is studied. This approach can be helpful in the diagnosis of coronaviruses and in assessing the effect of a variety of vaccines on their infectivity.

It should be noted, that the shape of almost all viruses is a sphere with spikes. The difference between different viruses is in the shape, size, and the number of spikes. Moreover, many types of pollen like ragweed have similar structure. So the suggested model may have broader application, not limited by coronaviruses only.

2. Coronavirus virion shape simulation

As known, coronavirus virions are spherical, 120–160 nm in diameter, with an outer envelope bearing 20 nm-long club-shaped spike proteins that collectively resemble a crown or the solar corona [10]. In this paper, the following parameters of model particles are considered: virion has a diameter of 140 nm, surrounded by a set of 20 nm long spike proteins.

First of all, it is necessary to generate the distribution of spike proteins on the surface of the virion. For this, we suggest using the following generation procedure:

• (1)Choose certain angle β _min, which determines the minimal angle between adjacent spike proteins.
• (2)Set a position of first initial spike (θ₀,φ₀). Usually we used north pole of particle (θ₀= 0, φ₀=0) for it.
• (3)Generate a random position of i th spike (θ_i,φ_i) within the limits 0 ≤ θ_i ≤ π; 0 ≤ φ_i ≤ 2π.
• (4)Check the angular distances between i th spike and each of previous i-1 spikes.
• (5)If at least one of the angles is less than β _min, the position of the i th spike is regenerated.
• (6)The procedure is terminated when large number (e.g. 1000) of attempts to create the i th spike is failed.
• (7)As a result of procedure we obtain two arrays Θ and Φ with size N, where Θ contains set of polar angles of spikes positions, and Φ contains azimuthal angles.

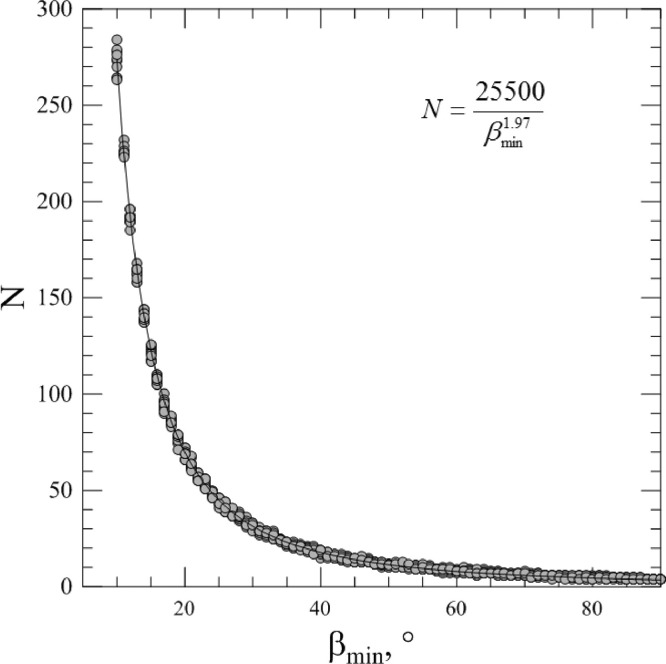
It should be noted that this procedure can produce different spike proteins number N for the same minimum angle β _min. Fig. 2 shows the dependence of the number of spike proteins on angle β _min for 10 different uses of the above procedure (gray dots). It can be seen from the figure that the distribution of the spikes number for different angles β _min obeys a certain regularity expressed by the empirical equation (solid line in Fig. 2):

$$N=\frac{25500}{{\beta }_{\min }^{1.97}},$$ (1)

where β _min should be expressed in degrees. This equation was obtained during searching of the best approximation of the data by function $\frac{a}{{\beta }_{\min }^b}$, where a and b were found with the help of Levenberg–Marquardt method.

Fig. 2.

The dependence of the spike proteins number on angle β_min for 10 different uses of the generation procedure (gray dots). Solid curve is the approximation by empirical Eq. (1).

Using this equation, angle β _min can be calculated for needed N value. After this, the above procedure should be repeated (as a rule, several times) in order to finally obtain the distribution of precisely N spikes on the surface of the coronavirus model particle. We used this procedure for obtain 4 sets of spike proteins: N = 50 (β _min = 23.6°); N = 100 (β _min = 16.6°); N = 150 (β _min = 13.5°) and N = 200 (β _min = 11.7°).

Spike proteins of coronavirus have a complex internal structure [11], [12]. The pillows (S protein) at the end of the spikes are hard to mathematically describe. However, since these objects are much (more than order of magnitude) smaller than the wavelength of light in the spectral range studied in this paper, the effect of the specific shape of the spike protein edge seems to be rather weak. Therefore, we will try to synthesize the spike protein with a fairly smooth algebraic function. In particular, the spike can be described using the following equation:

$$h=\frac{1}{\pi }\arctan \left(\frac{2\pi n}{k}-n\left|\theta -{\theta }_0\right|\right)+\frac{1}{2},$$ (2)

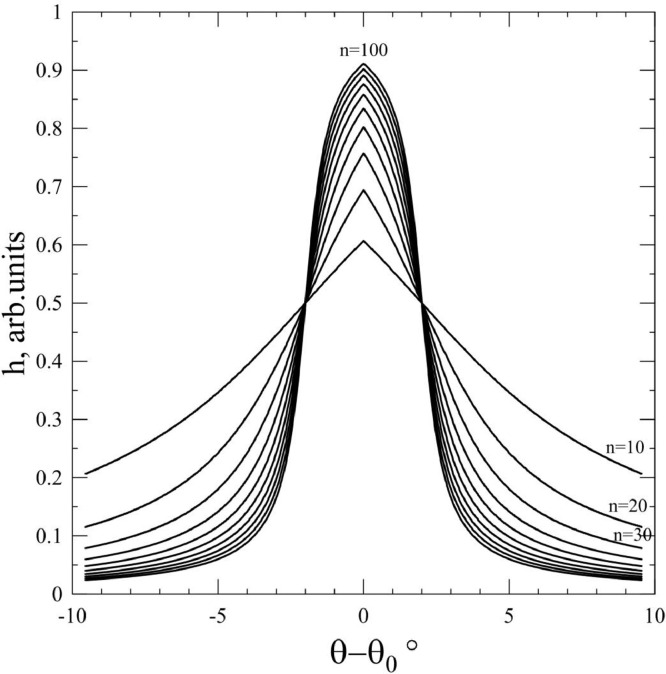
where h is the relative spike height, θ is a polar angle, θ₀ is a position of spike over polar angle (suggesting, that azimuthal angle and azimuthal position are the same φ = φ₀), k is the parameter, determining the width of spike, and n describes how close to the rectangle the spike shape is. Fig. 3 shows changes the spike shapes at k = 180 (providing half-width of spike – 2°) at different values of n. You can see, that at n > 30 spike becomes enough sharp.

Fig. 3.

Shape of individual spike proteins at different values of n.

Note, that Eq. (2) describes the 2D shape of spike, obtained by the cross section of 3-dimensional object by the meridional plane φ = φ₀. In the case of the transition from the two-dimensional case to the three-dimensional, we need to calculate the angle between two vectors (θ;φ) and (Θ_i;Φ_i) in a spherical coordinate system. Value cos β = [cos θcos Θ_i + sin θsin Θ_icos (φ − Φ_i)] is the cosine of angle between two vectors (θ;φ) and (Θ_i;Φ_i) in spherical coordinate system. Such equation provides circular symmetry of i th spike near the direction of (Θ_i;Φ_i).

Now we can suggest an equation, describing the shape of coronavirus model particle with N spike proteins:

$$\begin{array}{ccc}\hfill R\left(\theta ,\varphi \right)& =& R_0+h[\sum _{i=1}^N(\frac{1}{\pi }\arctan (\frac{2\pi n}{k}-n·\arccos [\cos \theta \cos {\Theta }_i\hfill \\ & & +\sin \theta \sin {\Theta }_i\cos \left(\varphi -{\Phi }_i\right)])+\frac{1}{2})],\hfill \end{array}$$ (3)

where R₀ and h parameters, defining the size of spherical part of virion and size of spikes, correspondingly.

In this work, we will use the following parameters: k = 180; n = 50. It should be noted, that arctan function at large values of the argument decreases rather slowly. Therefore, the closer the spikes are to each other, the higher minimal value of the function is obtained. That is why R₀ and h depend on N and was chosen so that the following conditions (determined by the size of the model particle adopted in this work — the radius of the spherical part is 70 nm, the length of the spike proteins is 20 nm) should be satisfied:

$$\{\begin{array}{c}\min \left[R\left(\theta ,\varphi \right)\right]=70\\ \max \left[R\left(\theta ,\varphi \right)\right]=90\end{array}.$$ (4)

Fig. 4 shows examples of coronavirus model particle realizations, calculated with Eq. (3) for N = 50; N = 100; N = 150; N = 200. It will be further demonstrated how a change in the number of spike proteins affects the light scattering characteristics of such particles.

Fig. 4.

An examples of coronavirus model particles with different spike proteins numbers: N = 50; N = 100; N = 150 and N = 200.

3. Light scattering computer simulation

Viruses are often suspended in liquids and may have different concentration. A most high virus concentration in eutrophic regions of world ocean is 10¹⁴ m ^− 3 [13]. At this concentration, using simple calculations, it can be estimated that the average distance between neighboring virions is about 20 μm, while the size of the virion itself is less than 0.2 μm. So, for all viral suspension with such and lower concentrations, multiple scattering between virions is absent, and approaches that calculate scattering by an isolated particle of irregular shape can be used to calculate the scattering properties.

The T-matrix method, developed by Waterman [14] is often used to calculate the light scattering properties of individual scattering particles [15], [16], [17], [18]. The main substance of this method is based on the expansion of the electromagnetic field incident on the particle and scattered by it in a series of vector spherical harmonics. In principle, this method can be used to study the light scattering characteristics of particles of any shape. In this work, calculations were performed by modification of the T-matrix method (the so-called Sh-matrices method, or the shape matrices method). This approach makes it possible to considerably simplify the calculations of arbitrary shape particles. The Sh-matrix technique [19], [20] has been developed to study light scattering of irregular particles, comparable with wavelength, with different shapes. Moreover, analytical expressions for the calculation of Sh-matrix elements of arbitrary shaped particles were found [21], [22], [23], [24], [25]. The Sh-matrix elements depend only on particle morphology and are found by performing surface integrals. Size and refractive index dependences are incorporated through analytical operations on the Sh-matrix to produce the T-matrix.

In this paper we study the intensity and degree of linear polarization of scattered light on scattering angle θ, which is the angle between incident and scattered light. θ = 180° means the scattering in strong backward direction.

The particles can be characterized by the refractive index m₀. In the general case, the refractive index of the particle is complex, m₀ = m_r + i·m_i. The question about viruses refractive index in UV is still open [26], but after studying of the four viruses investigators found, that median relative refractive index (because of virus samples are in water) in visible range is m₀ = 1.06 [13]. Because of it is hard to find information about the refractive index and its spectral change for viruses, calculations were carried out in wavelength range from 10 to 250 nm for constant refractive index m₀ = 1.06. So, this paper is devoted to studying the effects of shape only. Making calculations of scattered light intensity and degree of linear polarization for coronavirus model particles, one can estimate the influence of the spike proteins number on the scattering properties of particles.

4. Results and discussion

4.1. Intensity

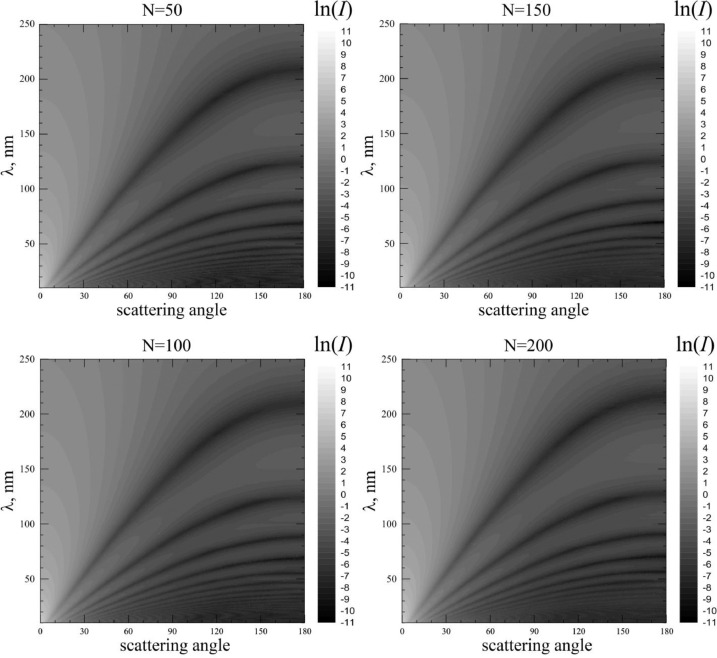
The results of the scattered light intensity calculations are shown on Fig. 5 . On this figure you can see the maps of ln(I), where intensity depends on both scattering angle and wavelength of scattered light, at different numbers of spike proteins: N = 50; N = 100; N = 150 and N = 200. The brighter colors correspond to greater ln(I) values. Note, that calculated scattering angle dependence for each wavelength is normalized according to normalization condition [28]:

$$\frac{1}{2}{\int }_0^{\pi }d\theta \sin \theta ·I\left(\theta \right)=1.$$ (5)

Fig. 5.

Maps of intensity of light scattered by coronavirus model particles distributed over scattering angles (horizontal axis) and wavelength (vertical axis). White color corresponds to high intensity values, black – low ones. Scales are on the right side of figures. Refractive index m₀ = 1.06.

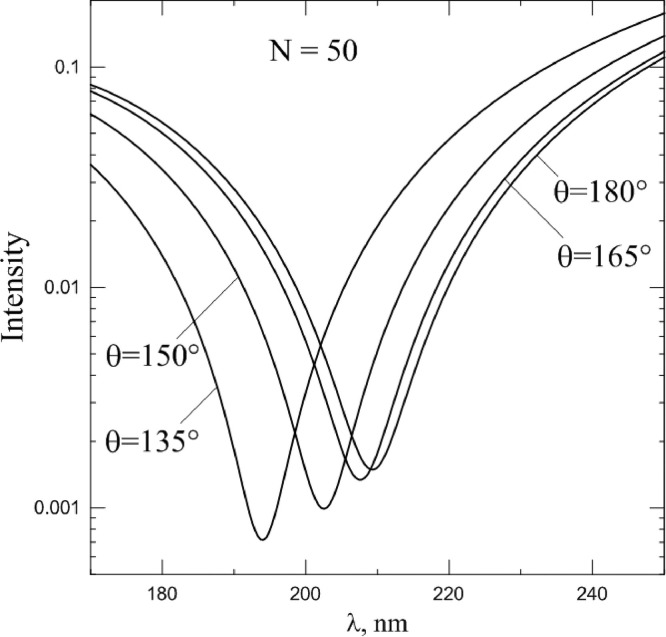
As can be seen from the figure, the scattering pattern has a number of noticeable features, expressed primarily in a sharp drop in the intensity of the scattered light, depending on the scattering angle and wavelength. Moreover, a distinct trend can be noted - with an increase of the spike proteins number, this minimum shifts to the region of larger wavelengths. Fig. 6 demonstrates this, showing spectral dependence of intensity at different scattering angles. It can be seen from the figure that the drop is quite strong - the intensity of the scattered light decreases by more than an order of magnitude in a sufficiently small interval of wavelengths. Therefore, wavelength λ _min, corresponding (at given scattering angle) to the minimum of intensity can serve as a kind of "visiting card" of the particle.

Fig. 6.

Spectral dependence of intensity, scattered by coronavirus model particle with N = 50 spike proteins at different scattering angles. Refractive index m₀ = 1.06.

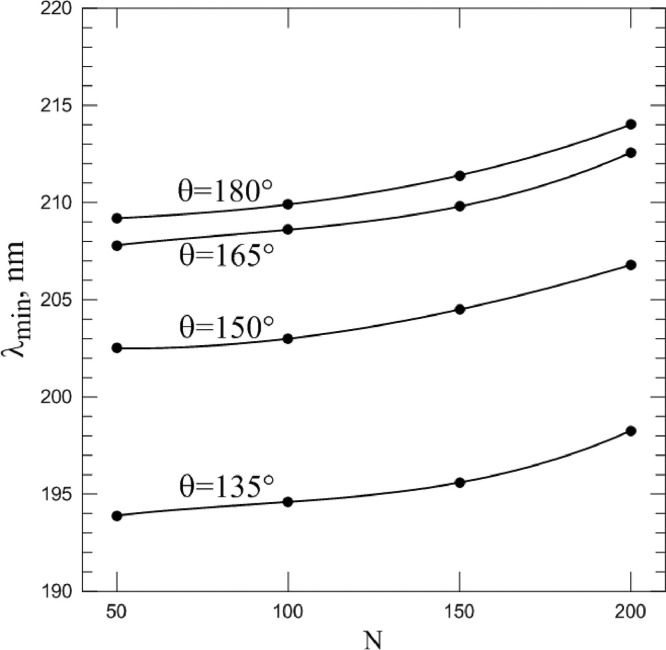
The most important question studied in this paper is how the spike proteins number affects λ _min? The answer is presented in Fig. 7 . Here, the points correspond to the position of the minimum intensity at different scattering angles and the spike proteins number of the model particle. It can be seen from the figure that a decrease in the number of spike proteins at all scattering angles leads to a noticeable shift in the minimum of intensity toward shorter wavelengths. Those, decrease in the infectivity danger of the virus is accompanied by a decreasing of λ _min.

Fig. 7.

Spectral position of intensity minimum at different scattering angles θ and numbers N of spike proteins (points). Lines are the approximation of each set of points by third order polynomial.

4.2. Polarization

The linear polarization of scattered light by is characterized by the following equation:

$$P=\frac{I_{\perp }-I_{\parallel }}{I_{\perp }+I_{\parallel }}$$ (6)

where I _⊥ and I _|| are the intensity of perpendicular and parallel components of scattered light with respect to the scattering plane.

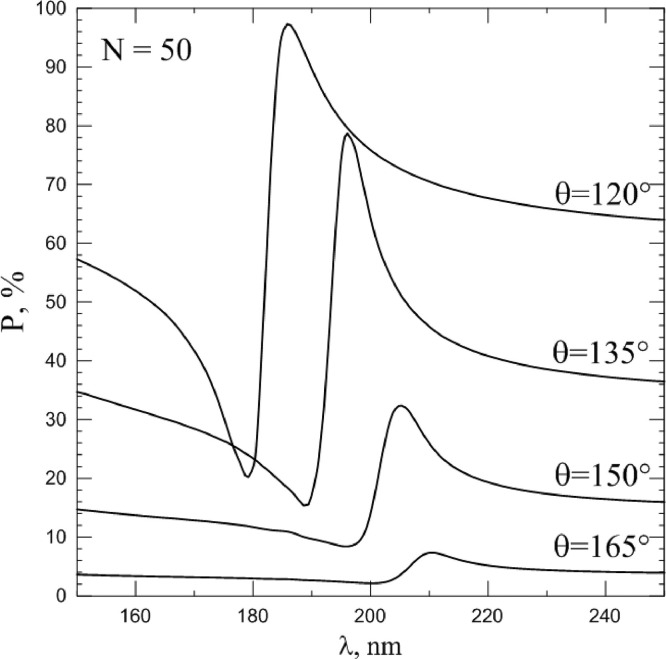
Fig. 8 shows maps of the degree of linear polarization of coronavirus model particles for different values of spike proteins. The X axis corresponds to the scattering angle values, and the Y axis - to the wavelengths. The degree of linear polarization is shown by different shades of gray: darker shades correspond to smaller polarization. An interesting polarization feature is observed in the spectral region of about 200 nm. If we consider it in more detail (see Fig. 9 ), it becomes clear that it consists in a very sharp jump in the degree of linear polarization with increasing wavelength. This feature is clearly manifested in spherical particles and is called the Quasi–Rayleigh polarization leap (QRPL) [29]. QRPL can occur even at refractive indices close to 1, and depends on the scattering angle, on the size, on the refractive index, and on the shape of the scattering particle [30].

Fig. 8.

Maps of degree of linear polarization distributed over scattering angles (horizontal axis) and wavelength (vertical axis). White color corresponds to high polarization values, black – low ones. Scales are on the right side of figures. Refractive index m₀ = 1.06.

Fig. 9.

Spectral dependence of linear polarization degree, scattered by coronavirus model particle with N = 50 spike proteins at different scattering angles. Refractive index m₀ = 1.06.

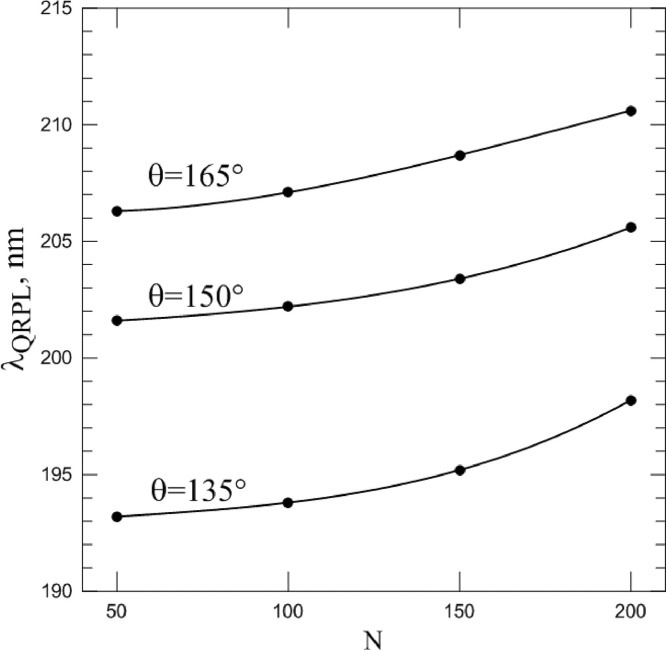
This phenomenon can be characterized by wavelength λ _QRPL at which the rate of polarization change (i.e., the value of the derivative $\frac{dP}{d\lambda }$) is maximal. In this case, we see that the spike proteins number also affects the position of the QRPL. As can be seen from Fig. 10 , the QRPL exhibits a behavior similar in intensity to a change in the spike proteins number. The smaller N, and the less dangerous the virus, the shorter the wavelengths corresponds to QRPL. It should be noted that λ _min and λ _QRPL differ in their values; therefore, they can be used by researchers as two independent sources of information about the spike proteins number.

Fig. 10.

Spectral position of Quasi–Rayleigh polarization leap at different scattering angles and numbers of spike proteins N (points). Lines are the approximation of each point set by third order polynomial.

4.3. Comparison with smooth spheres

The scattering patterns shown on Figs. 5 and 8 are quantitatively similar to the Mie scattering pattern. Both intensity minimum and polarization leap are representative in Mie scattering too. This is not surprising since the particles are based on a sphere, and the refractive index is closed to unity. The interesting question arises: can the scattering features described above be reproduced by a smooth sphere of a specific size? To study this issue, the calculations of λ _min (Fig. 11 a) and λ _QRPL (Fig. 11b) were carried out for smooth spheres with range of sphere radii R_sph from 70 to 90 nm. As can be seen, λ _min and λ _QRPLQuasilinearly depend on R_sph. Consequently, it is formally possible to choose a radius of the sphere that reproduces scattering features described above.

Fig. 11.

Spectral position of intensity minimum (upper panel) and Quasi–Rayleigh polarization leap (lower panel) at different scattering angles and numbers for smooth sphere with radius R_sph. Refractive index m₀ = 1.06.

Fig. 12 a shows the results of Mie calculation for smooth spherical particles of radius R_sph = 72.47 nm (points), whose size provides the best approximation of scattering pattern of coronavirus model particle with N = 150 spike proteins (lines) in spectral region λ = 170…250 nm. Upper part shows the intensity, lower-degree of polarization. As can be seen, smooth spheres provide quantitatively different data, than model particles. This difference is most noticeable in the case of linear polarization degree, where the differences may reach about 10% on absolute value. This feature can be used for distinguishing viruses from non-viruses based on their light scattering in the cases when the size of the objects is not accurately determined.

Fig. 12.

Spectral dependence (λ = 170…250 nm (a); λ = 75…110 nm (b)) of intensity (upper panels) and linear polarization degree (lower panels), scattered by coronavirus model particle with N = 150 spike proteins (lines) at different scattering angles. Points correspond to intensity and polarization of smooth sphere with R_sph = 72.47 nm. Refractive index m₀ = 1.06.

Fig. 12b shows the same as Fig. 12a, but for spectral region λ = 75…110 nm. The figure clearly shows that subsequent resonances in light scattering make the difference with smooth spheres more noticeable. It's because spikes begin to exhibit non-Rayleigh scattering at wavelength decreasing, which means more and more depolarize light. In principle, depolarization of light scattered by model particles is associated with light scattering between the spikes, i.e. with multiple scattering, which always depolarizes light. Moreover, this multiple scattering will be more pronounced for spikes comparable to the wavelength than for those that are much smaller than the wavelength. Those, the shorter the wavelength at which observations are carried out, the more reliably one can distinguish viruses from non-viruses.

5. Concluding remarks

We suggest a method to estimate the spike proteins number of the coronavirus virion. In the region of about 200 nm, two main features are observed for coronavirus model particles-a minimum of intensity and sharp leap of the linear polarization degree. With a decrease in the number of spike proteins (and, consequently, a decrease in the infectious danger of the virus), both of these features exhibit a characteristic tendency to shift to shorter wavelengths. Therefore, this method allows you to evaluate the comparative effect of various external conditions (for example, various vaccines) on the infectious danger of the virus.

There is a fairly wide variety of different coronaviruses. Some publications note that certain varieties of coronaviruses may have the same shape, but somewhat different sizes [31]. So, the main problem is how to differentiate the signal measured from a completely different particle in the same size range, especially when noise is taken into consideration. But, since light scattering depends on the ratio of the particle size to the wavelength (size parameter), all features of model particle scattering, considered in this paper, will appear for particles having other size, manifesting themselves at shorter wavelengths for smaller particles and at larger wavelengths for greater ones. Despite noise and other particles presence, it is possible to detect a tendency to change of λ _min and λ _QRPL and the direction of their changes.

In this work, author tried to limit himself to considering only those scattering features that are in the near ultraviolet region >190 nm. Currently, there are many instruments that allow photometric and polarimetric measurements of biological samples in this spectral range (for example, the spectropolarimeter Jasco J-810 [27]). In addition, there is a Mueller matrix polarimeter, which can carry out measurements at incident angle of light from 0° to near 180° [32]. However, the simulation carried out in the paper shows that far ultraviolet photopolarimeters are required for a more reliable distinction between viruses of non-viruses.

At shorter wavelengths, as can be seen from Figs. 5 and 8, many other features are observed. In the case of using the appropriate measuring technique, the mathematical model suggested in this paper for describing the shape of coronavirus model particles and the calculation of its photopolarimetrical properties can be very useful.

This simulation is applicable not only to coronaviruses, but also to other objects of a similar structure, for example, pollen. Pollen particles are much larger, and therefore is none problem with their measurements right now. In the future, we will certainly apply this model to pollen samples.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.