Abstract
Background
Till 31 March 2020, 105,792 COVID-19 cases were confirmed in Italy including 15,726 deaths which explains how worst the epidemic has affected the country. After the announcement of lockdown in Italy on 9 March 2020, situation was becoming stable since last days of March. In view of this, it is important to forecast the COVID-19 evaluation of Italy condition and the possible effects, if this lock down could continue for another 60 days.
Methods
COVID-19 infected patient data has extracted from the Italian Health Ministry website includes registered and recovered cases from mid February to end March. Adoption of seasonal ARIMA forecasting package with R statistical model was done.
Results
Predictions were done with 93.75% of accuracy for registered case models and 84.4% of accuracy for recovered case models. The forecasting of infected patients could be reach the value of 182,757, and recovered cases could be registered value of 81,635 at end of May.
Conclusions
This study highlights the importance of country lockdown and self isolation in control the disease transmissibility among Italian population through data driven model analysis. Our findings suggest that nearly 35% decrement of registered cases and 66% growth of recovered cases will be possible.
Keywords: COVID-19 outbreak, Forecasting, ARIMA, Italian population, Lock down
Introduction
In the last weeks of 2019, when the world was ready to welcome 2020, many local hospitals in Wuhan, China, were reported unusual number of patients who comes with severe pneumonia without knowing cause and not responds to any kind of vaccine or medicine.1 Besides, these cases were further increased because of human to human transmission, and doctors confirmed that this unknown disease had similar epidemic of Severe Acute Respiratory Syndrome (SARS)2 in 2002 and the agent causing this disease was recognized as a corona virus. Sooner or later World Health Organization (WHO) named this virus as novel corona virus(nCOV-19) or COVID-19. By early January 2020, about 59 suspected cases were identified in province of Wuhan. At the beginning, the disease started as a local epidemic of China, but subsequently it quickly escalated all over the world, being transmitted by international travelers. At the present, there is no any scientific evidence for where it has originated. Currently it is confirmed as a global pandemic and dozens of western countries are alarmed by this severe outbreak of corona virus.
Today (31 March 2020), 854,307 COVID-19 confirmed cases are including of 42,016 deaths were reported worldwide.3 More than 190 countries had been affected, with major outbreaks in the United States (US), Italy, Spain, China, Iran, France, and others. We can imagine the gravity of this pandemic situation by looking into these facts. In Italy, death toll from corona virus jumped over 15,000 deaths since end of February and is still ongoing, whereas the number of infected cases from USA surpass about more than half Million population. Due to easy spreading of COVID-19, most national governments including Italy announced lock down and people are not allowed to come out from their homes. As of this, nearly 3.5 Billion global population went into self isolation.4
The World Health Organization (WHO) confirms that the incubation period (i.e., time elapse between exposure of pathogenic organism to symptom first appearance) of COVID-19 outbreak is 14 days. The basic reproduction number “R naught” or R0 is a contagiousness indicator or infectious transmissibility of parasite agents.5 In epidemic sciences and health literature R0 is highly encountered to understand a slow outbreak of disease. For instance, if R0 is equal to one, this means that average person who got disease could transmit over single individual. According to WHO, R0 for COVID-19 is confirmed around 2.0–2.5. Recent modeling of R0 from Italy confirmed by Lombardy researchers at early outbreak in between 2.76 to 3.25.6
Lombardy region is considered as epicenter of corona virus outbreak in Italy.6 , 7 Most people were died here than anywhere else in the world and later virus spread all over country with more than 98,000 confirmed cases. On 9 March 2020, the Italian prime minister Mr. G Conte had given announcement of imposed national quarantine, restricting the people movement unless for health emergency or unavoidable work needs. Statistics become consciously optimistic and daily number of new registered are becoming constantly stable since last week of March. However, because of both human-to-human and asymptomatic transmission of COVID-19, it is important to understand virus reproduction cases after this Italy lock down. Therefore, we developed a data driven model to forecast COVID-19 outbreak daily registered cases and recovered cases, also estimated the chance of low infected patient cases for next 60 days of Italy quarantine.
Methods
Data
Patient data were obtained from the official website of the Italian Health Ministry (http://www.salute.gov.it/nuovocoronavirus) that reports latest information of COVID-19 infection in Italy. The data model development was done based on the update of 31 March 2020. Patient data consisted of three groups, namely registered cases, recovered cases and death cases. In this study, we excluded the death cases information and forecasted possible number of register and recovered cases in next two months. Rather than observing entire data, we only considered observation from 15 February 2020 because after the first two cases registered on 31 January 2020, no more epidemic was reported in Italy till mid of February. Fig. 1 is the plot of total number of registered and recovered cases trend varied on daily basis.
Figure 1.
Total registered cases progression (left) and Total recovered case progression (right) of COVID-19 in Italy (from mid of February to end of March).
ARIMA model development in R
R is one of the tools that has relevant importance for epidemiologists, and had quick search function can enable users to get many R libraries devoted to outbreak management and analysis. Auto-regressive integrated moving average (ARIMA) and specified by three orderly parameters: (p, d, q); where ‘p’ is an auto aggressive referred to use of ancient values in model,‘d’ is the difference degree of integrated I(d) component, and ‘q’ is model error which is combination of last error terms et.8
By summing above parameters with non-seasonal ARIMA model can be written as linear equation mentioned in equation (1).
| Y t = c+ Ф 1 y d t-1 + Ф p y d t-2 + ……. + Ф n y d t-n +θ 1 e t-1 +θ q e t-q + e t | (1) |
The model equation above mentioned as assumed to be a non-seasonal series. In this study, model specified by two sets of parameter order: (p, d, q) and (P, D, Q) m (i.e., describes the seasonal component of m time intervals). The mathematical equations of ARIMA model were explained in appendix section.
Model evolution and statistical analysis
To calculate the COVID-19 re-production cases among Italy patients, we imported ‘AUTOARIMA’ packages in R. After model exported, simple time series analysis was conducted to understand trends of corona epidemic in Italy. The data available from Italian health ministry website is obtained as day-to-day statistics. Past 45-days patient data were recorded on excel sheet. The command read_excel (“data”) was used to read the excel sheet. When working with time series in R, the data were converted in a time series (ts) for the number of registered cases per day from 15 February 2020 to 31 March 2020 mentioned as:
install. Packages("forecast")
library(forecast)
library(readxl)
worldcovid19 <- read_excel("Italycovid19.xlsx")
View(worldcovid19)
tsworldcovid19 <-ts (Italycovid19$`daily registered Cases’, frequency = 1,start = c(15/02/2020,1))
tsworldcovid19 <-ts (Italycovid19$`daily recovered Cases’, frequency = 1,start = c(15/02/2020,1))
plot(tsworldcovid19)
45 days patient data from 15 February 2020 (i.e., where serious outbreak was about to originated) to 31 March 2020 with one day frequency was considered (Fig. 2 ).
Figure 2.
45-day plot diagram of COVID-19 daily registered cases in Italy (ts = 1).
The plots revealed that the trend in case registered at Italian hospitals was going upwards and peak number of corona cases was registered in the last two weeks of March (Fig. 3 ). This might be caused because of most people are traveled to home lands through public transports before lockdown was officially announced. Through this migration of people, virus could spreads through and expose the symptoms on or after incubation period. In view of this, we conducted simple forecasting of COVID cases if the same trend has been continued for two months. We applied ‘AUTOARIMA’ package in R to evaluate the values of (p, d, q) and forecaste the reproduction of infected cases. Two ARIMA models of COVID-19 daily registered and recovered cases were designed. The possible residuals for these two models to understand the case variance were plotted and statistical analysis was performed using ‘R’ version 1.2.5.
Figure 3.
Weekly box plot diagram of infected Italians of COVID-19.
Results
For data fitting in ARIMA model to develop a model for COVID-19 for both registered and recovered cases, we performed the commands mentioned below.
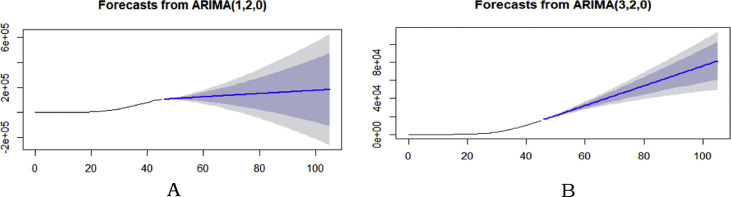
The 60-days COVID-19 forecasting graphs of register along recovery cases (Fig. 4 ), and normalized QQ plots9 were computed (Fig. 5 ). Table 1 presents the model outcomes and accuracy parameters.
Figure 4.
Predictive and confidence intervals (CI) of registered case model (graph A), and recovered case model (graph B) (Black line: actual data, Blue line:60-day forecast, Gray zone: 80% of CI, White zone: 95% of CI).
Figure 5.
Probability plots of registered cases (left), and recovered cases (right).
Table 1.
ARIMA model comparison.
| Model | ar1 | ar2 | ar3 | AIC | AICc | BIC | ME | RMSE | MAE | MPE | MAPE | MASE | ACF1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ARIMA(1,2,0)10 Registered cases | 0.3694 | – | – | 680.41 | 680.7 | 683.98 | 17.84 | 514.74 | 324.46 | 4.26 | 6.25 | 0.1403 | 0.0113 |
| s.e. | 0.1575 | – | – | – | – | – | – | – | – | – | – | – | – |
| ARIMA(3,2,0)10 Recovered cases | −1.14 | −0.74 | −0.48 | 597.18 | 598.21 | 604.32 | 80.80 | 186.85 | 112.27 | 10.57 | 15.60 | 0.3293 | −0.081 |
| s.e. | 0.1296 | 0.1826 | 0.1357 | – | – | – | – | – | – | – | – | – | – |
∗ar1,ar2,….arn are model coefficients; s.e.: standard errors; AIC: Akaike information criteria; AICc: Second order Akaike information criteria; BIC: Bayesian Information criterion; ME: Margin of error; RMSE: Root mean square error of fitted model; MAE: Mean absolute error; MPE: Mean posterior estimate; MAPE: Median absolute prediction error; MASE: Mean absolute scaled error; ACF: Aberrant crypt foci.
The probability of new positive cases and recovered cases in Italy for next two months based on available data were computed. It is evident from Fig. 4, the 60-day forecasting of infected cases might rise in between the range of 105,732–182,757, and recovered cases could increased in between the range of 16,742–81,635 with CI of 80–95%. The regressive distribution of patient cases while two plots had observed to estimate the fitting accuracy. The model validation was assessed by prediction errors.
Based on the ARIMA model accuracy evolution of COVID-19 Italian epidemic data on mentioned time period, we considered mean absolute prediction error (MAPE) parameter. The accuracy (Acc) is defined in equation (2);
| Acc % = 100-MAPE∗100 | (2). |
The models of ARIMA(1,2,0) registered, and ARIMA(3,2,0) recovered cases are validated with an accuracy of 93.75%, 84.4% respectivly.
Discussions
We used existed COVID-19 epidemic data of Italian patients to evaluate the probability of infected and recovered pateint number after having 60-day country lockdown. Simple automatic forecasting package (AUTOARIMA) of ‘R’ was applied to conduct predictive modelling.11 Our data driven model analysis highlights the necessity of country lockdown and self isolation to control disease transmissibility among Italian population at the moment.
At the present, Italy is becoming the worst epidemic corona outbreak center. On 3 March 2020, 11 towns in North Italy announced quarantine after result of 17 deaths and 650 positive cases.12 Unfortunately, in consequence of many Italian citizens continued their daily life routine irrespective of outbreak results epidemic spread all over the country. After about one week, the Italian government announced more than 9000 positive cases with 97 deaths.13 On 9 March 2020 the Italian prime minister announced country lock down and strictly passed regulations to close malls, educational institutions, and sport events in order to stop infection among the other citizens. As mentioned, due to extreme characteristic of COVID-19 is not expose the immediate symptoms while in the incubation time.
After Italy's lockdown, government officials make sure that people were at home. All national administration websites encourages companies to offer free online services. Educational institutions and universities involved e-learning methods, any data or publications on COVID-19 made available for free to general public. COVID-19 response team also conducting screening tests for domicile or long stay in high hit areas like north Italy provinces. Hospitals and medical centers are successfully handling patient flow to local hospitals and addresses individual issues about bed facilities, overcrowding in emergency departments, and patient transfer to other specialized facilities.14
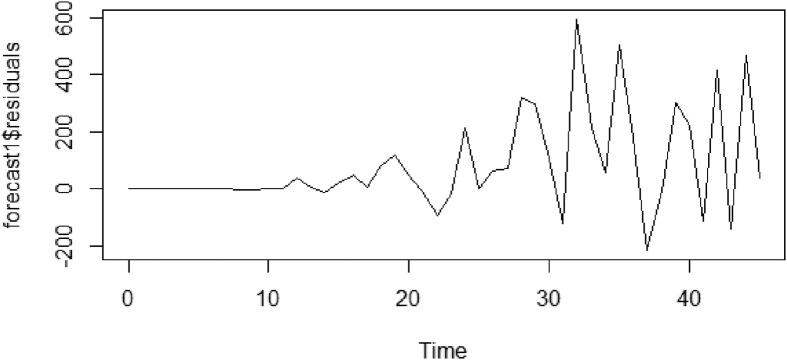
All these critical circumstances were considered to understand what exactly happened in between the period of lockdown (9 March 2020) announcement and incubation period (possibly 23 March 2020). It can be observed in the Fig. 6 , the residual plot of positive COVID-19 cases during the given period. From the plot, it is clear that the first two weeks trend seems normal and after 3 March 2020, a huge spike in case variance can be observed (i.e., 24 to 26th days after quarantine had begun).
Figure 6.
Residual plot of positive registered cases.
One positive sign of this COVID-19 epidemic in Italy is after having established isolation, there is a significant growth of recovered case number, particular with last weeks of March (Fig. 7 ). This could be because of the increased availability of medical devices, medications and health professionals in the most affected areas that might affect lowering of pandemic rates.
Figure 7.
Residual plot of recovered cases.
At present, the Italian citizens are also taking more preventive measures and maintaining social distancing to control speed of infection. As a result, disease transmission is expected to be reduced in the near future. Preliminary results of this study suggest that if Italian government and citizens could continue to be quarantined for another two months there could be chance of low tendency rate in infective cases. Predictions mentioned that another 78,701 infected cases might be the registered in 60 days which is lower than last 45 days.
ARIMA models can forecast the simple up and downs and more predictive than regressive models without change in the overall trend. It is because ARIMA can only look back the data of dependent variables (i.e, registered and recovered cases).15 This represents a primary limitation of this study. Secondly, due to unwillingness to join in hospital, some confirmed cases are not ready to inform the medical authorities. This measure could affect the natural transmission of disease to family members which will also affect the study outcomes. Finally, used data was retrieved from official Italian Health Ministry websites, if any delay or mismatch of data reporting could results incorrect forecasting.
COVID-19 is a severe pandemic that all countries are facing. This results about half of the global population went into lockdown. At the present, Italy is facing serious epidemic of positive and mortality rates. We estimated an increase in the size of registered cases and recovered case number population if the present lockdown could continue for another two months. Results of this study indicate that nearly 35% of decay in positive cases and 66% of growth in recovered cases could be possible.
In addition, present government taking some serious contaminant measures such as suspending training sessions of sports persons, professionals, and non professionals. All emergency issues remained same including to prohibit natural persons to move with public and private means of transport. Advertising of prevention measures such as hand washing, mask wearing and disinfection was done continuously through national media which is largely influences the reproductive number of corona virus cases. The future of COVID-19 diffusion in Italy will largely depend on government regulations and motivation to carry self isolation of individual citizens.
Author contributions
NC: Data analysis, methods, results and study design; GB: Manuscript preparation and statistical analysis; FA: Final revision and study approval.
Declaration of Competing Interest
No author does not have any conflicts of interest.
Acknowledgements
This work was supported by institutional funding of the University of Camerino, Italy. Dr Nalini Chintalapudi and Dr Gopi Battineni were recipients of PhD bursaries from the University of Camerino.
Appendix. ARIMA Mathematics
Autoregressive integrated moving average (ARIMA) model is aims to capture the auto correlation in the series modeling, and generally to do forecasting.
ARIMA model can completely be summarized by three parameters; p: The number of autoregressive terms, d: number of non seasonal differences, and q: number of moving terms. These three parameters (p, d, q) can used to define ARIMA models, thus alternatively it is called as ‘ARIMA (p, d, q)’ model. There are two types of models in ARIMA such as Generalized random walk modes (i.e., well tuned to discard all residual correlations) and Generalized exponential smoothing modes (i.e., which can incorporate the long term trends and seasonality).
The mathematical definitions are well explained below.
If we consider ‘B’ is back shift operator which causes the observation that multiplies to be backward shifting in time by 1 interval.
For any time series Z at any period t is considered as , and for n powers of
ARIMA is joint model of two individual models (autoregressive AR(p) and model average MA(q)) is integrated by difference variable I(d). In ARIMA models non-stationary time series is defined stationary by application of finite difference in data points.
The general multiplicative ARIMA/SARIMA framework can be written:
| (1) |
where B is backshift operator, and
| (2) |
| (3) |
| (4) |
| (5) |
The general setting in equation (1) can also expressed as: ARIMA(p, d, q)x(P,D,Q).
In the ARIMA(2,1,3), we have p = 2, d = 1, q = 3, s = 0, then its mathematical structure can be shown as:
| (6) |
Similarly the structure of ARIMA(1,0,1) (0,1,1)12 where (p = 1,d = 0,q = 1; P = 0, D = 1,Q = 1, S = 12) is:
| (7) |
The mathematical formulation of ARIMA (p, d, q) model with lag polynomials is defined as16
| (8) |
For multiple lag polynomials
| (9) |
The difference integer d controls the differencing levels, usually d = 1 is good enough in highest number of cases, if d = 0 then model turns into ARMA (p, q) model.
References
- 1.Chen Z.-L., Zhang Q., Lu Y., Guo Z.M., Zhang X., Zhang W.J., et al. Distribution of the COVID-19 epidemic and correlation with population emigration from wuhan, China. Chin Med J (Engl). 2020 doi: 10.1097/cm9.0000000000000782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Peiris J.S.M., Poon L.L.M. Encyclopedia of virology. 2008. Severe Acute respiratory Syndrome (SARS) [DOI] [Google Scholar]
- 3.Situation reports. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports
- 4.Which countries are under lockdown - and is it working? https://www.telegraph.co.uk/news/2020/03/29/lockdown-countries/
- 5.Delamater P.L., Street E.J., Leslie T.F., Yang Y.T., Jacobsen K.H. Complexity of the basic reproduction number (R0) Emerg Infect Dis. 2019 doi: 10.3201/eid2501.171901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Grasselli G., Pesenti A., Cecconi M. Critical care utilization for the COVID-19 outbreak in Lombardy, Italy. JAMA. 2020 doi: 10.1001/jama.2020.4031. [DOI] [PubMed] [Google Scholar]
- 7.Tuite A.R., Ng V., Rees E., Fisman D. Correspondence Estimation of COVID-19 outbreak size in Italy. Lancet Infect Dis. 2020 doi: 10.1016/S1473-3099(20)30227-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kalpakis K., Gada D., Puttagunta V. Proceedings - IEEE international conference on data mining. ICDM.; 2001. Distance measures for effective clustering of ARIMA time-series. [DOI] [Google Scholar]
- 9.Loy A., Follett L., Hofmann H. Variations of Q–Q plots: the power of our eyes! Am Stat. 2016 doi: 10.1080/00031305.2015.1077728. [DOI] [Google Scholar]
- 10.Shumway R.H., Stoffer D.S., Shumway R.H., Stoffer D.S. Time series: a data analysis approach using R. 2019. ARIMA models. [DOI] [Google Scholar]
- 11.Zhang P.G. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing. 2003 doi: 10.1016/S0925-2312(01)00702-0. [DOI] [Google Scholar]
- 12.Italy struggled to convince citizens of coronavirus crisis. What can Europe learn? | World news | The Guardian. https://www.theguardian.com/world/2020/mar/23/a-warning-to-europe-italy-struggle-to-convince-citizens-of-coronavirus-crisis
- 13.Novel coronavirus. http://www.salute.gov.it/portale/nuovocoronavirus/homeNuovoCoronavirus.jsp?lingua=english
- 14.Spina S., Marrazzo F., Migliari M., Stucchi R., Sforza A., Fumagalli R. The response of milan's emergency medical system to the COVID-19 outbreak in Italy. Lancet. 2020 doi: 10.1016/S0140-6736(20)30493-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Christodoulos C., Michalakelis C., Varoutas D. Forecasting with limited data: combining ARIMA and diffusion models. Technol Forecast Soc Change. 2010 doi: 10.1016/j.techfore.2010.01.009. [DOI] [Google Scholar]
- 16.Hipel K.W., McLeod A.I. Time series modelling of water resources and environmental systems. Time Ser Model water Resour Environ Syst. 1994 doi: 10.1016/0022-1694(95)90010-1. [DOI] [Google Scholar]