Metals and trace elements in relation to body mass index in a prospective study of US women

Abstract

Background:

Epidemiologic studies on the association between metals and body mass index (BMI) have been cross-sectional and have demonstrated inconsistent associations. Our study prospectively examined whether metals measured at baseline were associated with later BMI. We considered metals individually and as joint exposure to pre-defined metal groupings.

Methods:

We measured concentrations of 16 metals in toenails collected at baseline (2003–2009) in a subset of 1,221 women from the Sister Study. We calculated BMI from height and weight reported on a follow-up questionnaire an average of 5.2 years (range=3.5–8.3) after baseline. Multivariable linear regression was used to estimate β coefficients and 95% confidence intervals (CIs) for associations between BMI and individual metals (with estimates given per interquartile range (IQR) increase or in quartiles). Quantile g-computation was used to examine joint associations between groups of metals and BMI. Groups considered were (1) all metals combined, and metals classified as (2) non-essential or (3) essential.

Results:

In individual metal models we found that, with the exception of cobalt, no single metal was strongly related to BMI. In our mixture analyses, a quartile increase in all non-essential metals was associated with higher BMI (β=0.32; 95%CI: 0.00, 0.63 kg/m²), whereas essential metals were suggestively associated with lower BMI (β= −0.25; 95%CI: −0.58, 0.07 kg/m²).

Conclusions:

In this population of women who were, on average, overweight, essential metals were jointly associated with slightly healthier, lower BMI whereas non-essential metals were jointly associated with slightly higher, unhealthier BMI, after controlling for other health indicators and predictors of metals exposures.

1. INTRODUCTION

Obesity is a significant public health issue with approximately 40% of United States (US) women classified as obese and 67% classified as overweight or obese (NIDDK (National Institute of Diabetes and Digestive and Kidney Diseases), 2017). Overweight or obese individuals are at a higher risk of developing serious adverse health outcomes including type 2 diabetes, heart disease, all-cause mortality, and a number of cancer types, including postmenopausal breast cancer (Aune et al., 2016; Barnes, 2011; Bhaskaran et al., 2014; Poirier et al., 2006; Renehan et al., 2008). Therefore, a better understanding of the factors associated with the development of obesity is of substantial public health importance. Although the roles of diet and lifestyle factors have been well studied, the impact of environmental exposures remains understudied.

It is biologically plausible that metals and trace elements (hereafter referred to together as metals for brevity) may impact BMI. For example, certain metals have been associated with changes in adipose tissue physiology and glucose metabolism (arsenic and cadmium) (Ceja-Galicia et al., 2017; Tinkov et al., 2017), increased oxidative stress (lead, cadmium, arsenic, and mercury) (Ercal et al., 2001; Tinkov et al., 2017), and may act as endocrine disruptors (cadmium, mercury, arsenic, lead, manganese, and zinc) (Iavicoli et al., 2009). Further, in a study of mice, cobalt had a preventative role in dysregulated lipid metabolism as it reduced the size of adipocytes, increased adiponectin, and improved glucose tolerance (Kawakami et al., 2012). We wouldn’t expect all individual metals to have homogenous effects on health outcomes as some are necessary for normal biologic function whereas others are not (Tchounwou et al., 2012). Essential metals, which have a known physiological function and are necessary at certain levels in order to avoid deficiency-related health outcomes, include cobalt, copper, chromium, iron, manganese, molybdenum, nickel, selenium, and zinc. In contrast, non-essential metals have no known physiological function and include antimony, arsenic, cadmium, lead, mercury, tin, and vanadium. Depending on the level of exposure, both classes may cause tissue damage and negative health impacts (Tchounwou et al., 2012).

Prior epidemiologic research on metals and BMI were cross-sectional in design (Bulka et al., 2017; Grashow et al., 2014b; Mendy et al., 2012; Neymotin and Sen, 2011; Padilla et al., 2010; Rothenberg et al., 2015; Scinicariello et al., 2013), so temporality could not be established, which leaves open the possibility that observed associations could be due to the effects of BMI on metals, rather than due to the effects of metals on BMI. The latter question is probably of greater importance to informing public health actions, so some clarity can be gained by studying the problem prospectively. Additionally, these studies largely, with the exception of Wang et al. 2018 (Wang et al., 2018), did not address the fact that individuals are exposed to multiple metals and that those metals are often correlated and may each have small impacts on BMI such that their effects may be missed when studying individual metals, even if the joint impact is larger. Both single metal analyses (unadjusted for other metals) and co-adjusted models could be biased or underpowered due to these phenomena. Consideration of the joint impact of exposure to multiple metals is important for predicting effects of interventions such as remediation, industrial process changes, or dietary changes that would affect multiple metals at once.

The objective of this study was to examine whether toenail-based metal concentrations were associated with prospectively assessed BMI. We examined the associations both with individual metals and with joint exposure to pre-established, essential vs. nonessential-based metal groups.

2. MATERIALS AND METHODS

2.1. Study Design and Population

The Sister Study enrolled a prospective cohort of 50,884 women to study environmental and lifestyle risk factors for breast cancer and other health outcomes (Sandler et al., 2017). Participants were recruited between 2003 and 2009 using a national advertising campaign in English and Spanish. Women were ages 35–74 at enrollment and were eligible for the Sister Study if they had a sister who had been diagnosed with breast cancer but had no prior breast cancer themselves.

At baseline, women completed a computer-assisted telephone interview and written questionnaires to assess demographics; lifestyle factors; occupational, medical, family, and residential history. Trained examiners conducted a home visit where anthropometric data and biospecimens were collected. Toenail clippings from each toe were collected by the participants after removing nail polish. Participants have completed annual health updates and triennial follow-up questionnaires to assess changes in health and risk factor information. Response rates have remained above 91% over follow-up (NIEHS (National Institute of Environmental Health Sciences), 2017).

Metal concentrations were measured in a subset of 1,307 Sister Study participants who were part of a sister-matched case-control study of young-onset breast cancer (O’Brien et al., 2019a). For the analysis presented here, we examined the association between toenail metal levels and BMI in women from this previously selected sample who did not have a history of breast cancer at the time the toenails were collected.

All women provided written informed consent. The Institutional Review Boards of the National Institute of Environmental Health Sciences and Copernicus Group approved the study. The research presented here utilizes data from Sister Study Data Release 7.0.

2.2. Exposure Assessment: Toenail Metal Concentrations

Inductively-coupled plasma mass spectrometry (ICP-MS) was used to assess 16 metals (antimony, arsenic, cadmium, chromium, cobalt, copper, iron, lead, mercury, manganese, molybdenum, nickel, selenium, tin, vanadium, and zinc). The laboratory methods and reliability of the toenail metal measurements have been described previously (O’Brien et al., 2019b). Big toenails were washed, air-dried, and then digested in acid (9:1 HNO₃/HCL) and diluted with de-ionized water. Agilent 8800 ICP-QQQ (Santa Clara, CA) was used to conduct the ICP-MS analyses. Data quality was monitored with continuous calibration verification, analysis of duplicates and spikes, within- and between-batch analyses of laboratory-prepared toenail matrix digest, and comparison with a standard reference material (Japan NIES #13 Hair, n=6 in each digestion batch). Batch effects were corrected for using random effects models. If a concentration was below the limit of quantification, but was still assigned a measured value, that measured value was retained.

2.3. Outcome Assessment: Body Mass Index

Women reported their height and weight on the second detailed follow-up questionnaire completed between January 30^th, 2012 and July 1^st, 2014. This information was used to calculate self-reported BMI (weight in kilograms (kg) divided by squared height in meters (m) (kg/m²)) at follow-up. We excluded 86 women who were missing this follow-up information, leaving 1,221 (93%) women for inclusion in complete-case analysis. Although height and weight were also collected on the first and third follow-up questionnaires only an average of 2.5 years had passed between baseline and the first detailed follow-up which we considered an insufficient interval of time for BMI to measurably change after baseline. At the third follow-up twice as many women (178 vs. 86) were missing information for BMI compared to the second follow-up. Therefore, we used data from the second detailed follow-up. A timeline portraying this information is provided (Supplemental Figure 1).

2.4. Statistical Analysis

2.4.1. Analyses for each metal individually.

For the associations between individual toenail metal concentrations at baseline and self-reported BMI at follow-up, we modeled associations beween BMI and metals both continuously (giving estimates for the change in BMI per interquartile range [IQR] increase in natural log-transformed metal concentration) or categorically based on quartiles of each metal among the study population (for the change in mean BMI in each category of exposure compared to the referent). We used multivariable linear regression with follow-up BMI as the outcome to estimate the regression coefficients (β) and 95% confidence intervals (CIs) (Slinker and Glantz, 2008). Confounders were selected for adjustment based on a directed acyclic graph (DAG) (Greenland et al., 1999; Shrier and Platt, 2008) and included age at baseline (continuous), educational attainment (< high school or high school/some college/college degree or higher), smoking status (never/past/current), race (non-Hispanic white/other), and hours per week of physical activity (continuous). We also adjusted for follow-up time and controlled for baseline examiner-measured BMI to reduce the potential for reverse causation; a DAG and corresponding description showing our framework for this decision is provided in Supplemental Figure 2.

In the individual metal analyses, we examined effect-measure modification by smoking status at baseline. In addition to heavy metals (Caruso et al., 2013), cigarette smoke contains thousands of other chemicals, some of which are endocrine disruptors (Tweed et al., 2012), that could act synergistically with metals to impact BMI. Additionally, the nicotine in cigarettes has been shown to impact metabolic rate and compounds in tobacco smoke may affect susceptibility or the ability to metabolize other chemicals, such as metals (Audrain-McGovern and Benowitz, 2011; Melikian et al., 2007). This was conducted using an interaction term between smoking status (ever vs. never) and metal concentration (> vs. ≤ median) and presented as a stratified analysis with a β coefficient (95% CI) in each stratum of smoking and for the interaction term. Although the focus of our paper is on the prospective results, we did a supplemental analysis to evaluate the cross-sectional associations in our data to compare to the previous literature. This was examined using multivariable linear regression between the metal concentrations and examiner-measured BMI at baseline. We conducted sensitvitiy analyses evaluating the impact of adjusting for (1) pack-years of smoking (among all women; never smokers had 0 pack-years) instead of never/past/current smoking status to assess residual confounding by smoking cumulative dose, (2) baseline menopausal status, which may be related to BMI and could potentially affect measured toenail metals and (3) total caloric intake (calculated based on foods reported on a food frequency questionnaire at baseline; excluding 13 women with missing or implausible intakes (<500 or >5000 kcal) as it is associated with BMI and may impact toenail metals levels through dietary sources. Individual metal analyses were conducted in SAS 9.4 (Cary, NC).

2.4.2. Mixtures Analyses.

Because individual metals may have small effects that are difficult to study, we sought to estimate the joint impact of all metals and groups of metals. We used quantile g-computation to estimate joint impacts of metals. As described in more detail previously (Keil et al., 2019), quantile g-computation is a parametric, generalized-linear-model based implementation of g-computation to estimate the change in the outcome for a one quantile, simultaneous increase in all of the exposures in a specified mixture, which we refer to as a “mixture exposure-response”. Unlike weighted quantile sum, another method for estimating the joint effect of a mixture (Carrico et al., 2015), quantile g-computation does not require a “directional homogeneity” assumption that all exposures have associations with the outcome in the same direction. Additionally, the method generally allows for flexible polynomial functions of the mixture exposure-response, though for simplicity we describe the implementation under linearity assumptions. This model was implemented through categorizing all metals in quartiles, $X_j^q$, coded as 0, 1, 2, and 3, and fitting a linear model $Y_i={\beta }_0+\psi {\sum }_{j=1}^p{w}_j{X}_j^q+{\epsilon }_i={\beta }_0+{\sum }_{j=1}^p{\beta }_j{X}_j^q+{\epsilon }_i$ where ${\sum }_{j=1}^p{\beta }_j=\psi$ (the change in BMI for a one-unit change in all exposures) and each metal is given a negative or positive weight. With the linear model the values of the quartiles are treated continuously. The quantile g-computation estimator of the exposure-response, ψ, is the sum of the regression coefficients across the included exposures. If all β_j are in the same direction, then the weight for mixture component k (e.g. a specific metal) is defined as ${\text{w}}_{\mathrm{k}}={\beta }_k/{\sum }_{j=1}^p{\beta }_j$ which is the proportion of the effect due to that component and sum to 1.0. If metals have different directions of effect, then the weights are interpreted as the proportion of the positive (or negative) partial effect (i.e. the proportion of the total effect of the exposures that have a positive effect on the outcome), and the positive and negative weights together sum to 2.0. We examined three mixture groups: all metals combined, non-essential metals (antimony, arsenic, cadmium, lead, mercury, tin, vanadium), and essential metals (chromium, cobalt, copper, iron, manganese, molybdenum, nickel, selenium, zinc). The non-essential and essential classifications were defined a priori based on the literature (Tchounwou et al., 2012). We conducted a sensitivity analysis where cadmium, a potential proxy for cumulative smoking, was removed from the overall and non-essential metal mixtures, and was instead treated as a confounder in models for each of the three mixture groups. Sample code with examples of quantile g-computation implementation are available (https://cran.r-project.org/web/packages/qgcomp/vignettes/qgcomp-vignette.html).

We also analyzed the joint impact of metals using Bayesian kernel machine regression (BKMR), which allows for the flexible modeling of individual exposures as well as the mixture as a whole (Bobb et al., 2015). The flexibility of BKMR for fitting complex exposure-response curves is based on combining Gaussian process regression, which allows flexible exposure-response functions (Rasmussen and Williams, 2006), with Bayesian variable selection, which improves inference with highly correlated variables (MacLehose et al., 2007). While BKMR does not yield simple regression parameters as in our single pollutant and quantile g-computation models, we used it to graphically check modeling assumptions of those approaches. For example, if non-linearities or interactions are known, quantile g-computation allows for polynomial terms for the exposures or product terms for interactions between exposures to be included in the model. Specifically, we examined exposure-response functions of individual metals while holding all other metals at the median (to address linearity of individual exposures), bivariate exposure-response functions and the association of each metal at selected percentiles of all other metals to evaluate potential interactions (to address potential product term interactions between metals), and the joint exposure-response of increasing all non-essential or essential metals simultaneously by quantiles (similar to quantile g-computation). Mixtures analyses were completed in R 3.6.0.

3. RESULTS

The average time between baseline and the follow-up questionnaire was 5.2 years (range=3.5–8.3). The average examiner-measured BMI at baseline was 26.7 kg/m² and the average self-reported BMI at follow-up was 27.1 kg/m² (Table 1). The 1,221 women were mostly non-Hispanic white (90.4%), never smokers (66.8%), had a college degree or higher (58.1%), and did an average of 2.7 hours/week of recreational physical activity (Table 1). The mean concentrations and quartile cut-points for each metal are shown in Supplemental Table 1. Mean concentrations were highest for zinc (108.39 μg/g), and lowest for cadmium (0.01 μg/g) and molybdenum (0.01 μg/g). The Spearman correlations between metals are shown in Figure 1. The strongest correlation was between iron and manganese (R=0.71).

Table 1.

Baseline characteristics of the 1,221 women with metals measured from toenails, The Sister Study

	N	%
Race/Ethnicity
Non-Hispanic white	1,104	90
All other race/ethnic groups	117	10
Highest level of education
Less than high school, High school graduate or equivalent	130	11
Some college	382	31
College degree or higher	709	58
Cigarette smoking status
Never	815	67
Past	315	26
Current	91	8
Menopause status at baseline
Premenopausal	865	70.8
Postmenopausal	356	29.2
Year of toenail collectiona
2003	5	0
2004	16	1
2005	76	6
2006	192	16
2007	504	42
2008	317	26
2009	100	8
	Mean	SD
Age at baseline (years)	47.0	6.1
Hours per week of physical activity	2.7	2.8
Examiner measured baseline BMI	26.7	6.1
Self-reported baseline BMIa	26.4	5.7
Self-reported follow-up BMI	27.1	6.2
Pack-years of smokinga,b	10.7	11.3

^aYear of toenail collection missing for 9 women; self-reported baseline BMI missing for 4 women; pack-years of smoking missing for 3 women

^bAmong current or past smokers

Figure 1.

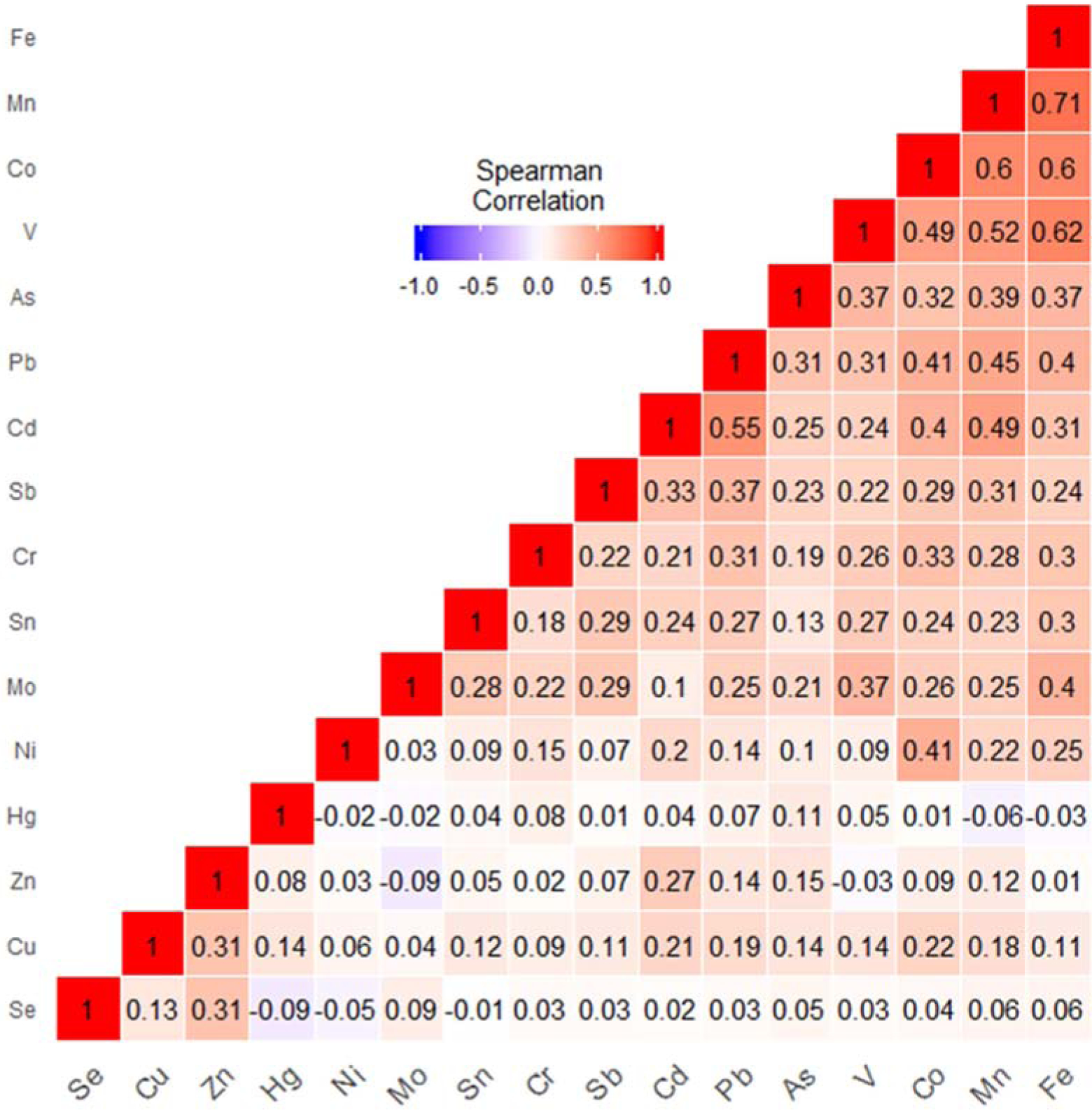
Spearman correlations between metals.

In the single metal models, the 4^th vs 1^st quartile of cobalt was inversely associated with BMI at follow-up (β= −0.41; 95% CI: −0.82, −0.01) (Figure 2 and Supplemental Table 2). The 3^rd vs 1^st quartile of arsenic was also inversely associated with BMI (β= −0.42; 95% CI: −0.83, −0.01), but this association did not persist into the 4^th quartile. Although not statistically significant, a suggestive inverse association was observed for the 4^th vs 1^st quartile of chromium (β= −0.38; 95% CI: −0.78, 0.03) and an IQR increase in zinc (β= −0.15; 95% CI: −0.30, 0.01). Smoking did not modify the associations between individual metals and follow-up BMI except for chromium where an inverse association was observed for never, but not ever smokers (interaction β= 0.71; 95% CI: 0.10, 1.31) (Supplemental Table 3).

Figure 2. Associations (β and 95% confidence intervals) between individual metals at baseline and BMI at follow-up.

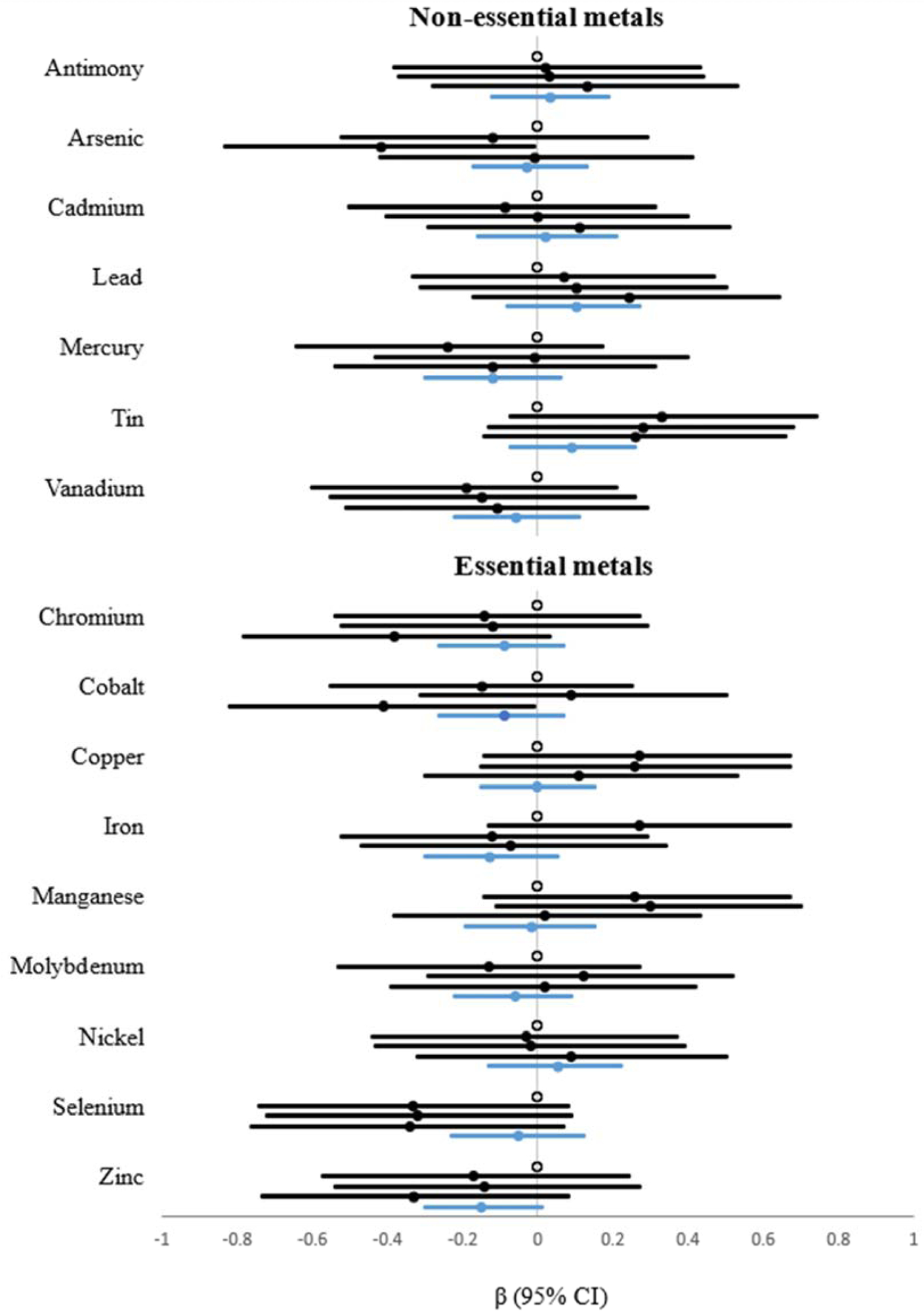
Black, filled circles and bars represent the association for each quartile above the referent (unfilled circle); blue, filled circles and bars represent the association for an interquartile range (IQR) increase in the log-transformed metal concentration.

In sensitivity analyses, adjusting for pack-years of smoking (Supplemental Table 4) or baseline menopausal status (Supplemental Table 5) did not notably change the results. Results were similar when adjusting for daily energy intake, although the suggestive inverse association for the 4^th vs 1^st quartile of chromium and an IQR increase in zinc became statistically significant and the inverse association for the 3^rd vs 1^st quartile of arsenic was slightly attenuated (Supplemental Table 6). In the cross-sectional analysis, higher categories and an IQR increase in copper, arsenic, mercury, and lead were inversely associated with examiner-measured baseline BMI (Supplemental Table 7).

In the quantile g-computation mixtures approach, a negligible association was observed for all metals combined (mean change in BMI per quartile increase= −0.08; 95% CI: −0.39, 0.24) (Table 2). However, a positive association with follow-up BMI was observed for the non-essential metals as a whole; increasing all non-essential metals by one quartile was associated with a 0.32 kg/m² increase in BMI (mean change in BMI per quartile increase= 0.32; 95% CI: 0.00, 0.63). Arsenic and mercury were the only negatively weighted non-essential metals; lead and tin were assigned the largest positive weights (Figure 3). In contrast, a suggestive inverse association was observed for increasing all essential metals by one quartile (mean change in BMI per quantile increase= −0.25; 95% CI: −0.58, 0.07). Within the essential metal quantile g-computation model, cobalt and chromium were assigned the largest negative weights and manganese and nickel were assigned the largest positive weights (Figure 3). In the sensitivity analysis where cadmium was removed from the overall and non-essential metal mixtures, but instead included as a confounder for all three metal groups, the non-essential metal result was slightly attenuated, but the magnitude of the association and conclusions remained similar (Supplemental Table 8).

Table 2.

Quantile g-computation estimates for the change in BMI at follow-up for a one quartile increase in all metals

Metal Group	β (95% CI)a
All metalsb	−0.08 (−0.39, 0.24)
Non-essential metalsc	0.32 (0.00, 0.63)
Essential metalsd	−0.25 (−0.58, 0.07)

Note: BMI, body mass index; CI, confidence interval

^aUnits for β are the change in BMI in kg/m² for a one quartile increase in all metals

^bAdjusted for age, education, physical activity, race, smoking status, baseline BMI, and follow-up time

^cIncludes antimony, arsenic, cadmium, lead, mercury, tin, and vanadium. Adjusted for age, education, physical activity, race, smoking status, baseline BMI, follow-up time, and the essential metals (continuous)

^dIncludes chromium, cobalt, copper, iron, manganese, molybdenum, nickel, selenium, and zinc. Adjusted for age, education, physical activity, race, smoking status, baseline BMI, follow-up time, and the non-essential metals (continuous)

Figure 3.

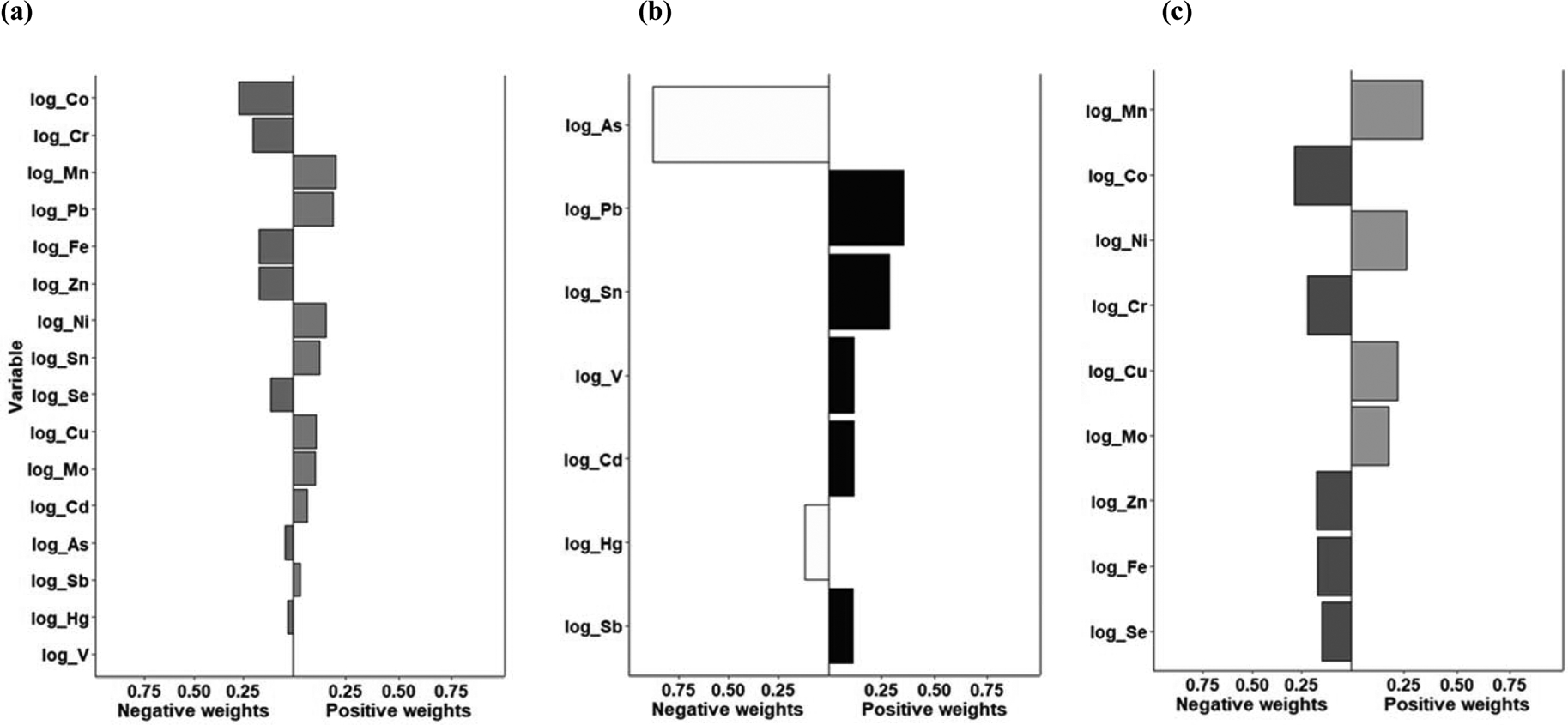
Weights representing the proportion of the positive or negative partial effect for each metal in the quantile g-computation model with (a) all metals, (b) the non-essential, and (c) the essential metals included as exposures.

Results from BKMR indicated that relationships between natural log-transformed values of individual metals and BMI appeared approximately linear (Supplemental Figure 3) and that there was little evidence for additive interactions between the metals (Supplemental Figures 4 and 5). Additionally, the univariate exposure-response curves from BKMR (Supplemental Figure 3) generally mirrored patterns from the single metal, linear regression models. Further, BKMR results examining effects of metal groups suggested a positive, approximately linear relationship across quantiles of non-essential metals and a negative, approximately linear relationship across quantiles of essential metals (Supplemental Figure 6), supporting the results observed in quantile g-computation and suggesting a linear quantile g-computation fit is appropriate.

4. DISCUSSION

In this prospective US-based study of toenail metal mixtures in relation to BMI, we observed that a quartile increase in all non-essential metals was associated with higher BMI whereas a quartile increase in all essential metals was suggestively associated with lower BMI. Although the magnitudes of these associations are modest, these findings are important from a public health standpoint due to the widespread prevalence of metals and the long-term health benefits of maintaining a health body size. The statistical approaches we used here for assessing the joint impact of exposure to multiple metals offer some clear interpretive benefits and reflect the reality that no individuals are exposed to individual metals in isolation. In individual metal models we found that, with the exception of cobalt, no single metal was strongly related to BMI, which is consistent with our mixtures analysis that indicated the overall effects seem to be driven by a number of small effects in which the direction was consistent across metals within a group.

In a study of mice that were fed a high fat diet, the authors concluded that cobalt (as CoCl₂) had a preventative role in dysregulated lipid metabolism as it reduced the size of adipocytes, increased adiponectin, and improved glucose tolerance (Kawakami et al., 2012). This suggests biological plausibility of the inverse association between cobalt and BMI in our study, although, to the best of our knowledge, there have not been in vitro or in vivo studies of cobalt’s effect on human adipose tissue metabolism. Although not significantly associated with BMI in individual metal models, chromium was given a similar, albeit a slightly weaker, negative weight as cobalt in the joint effect analyses, and manganese was given the strongest positive weight overall. Chromium has been shown to increase insulin sensitivity and glucose metabolism (Albarracin et al., 2008; Anderson, 1998) and a meta-analysis of randomized clinical trials concluded that chromium supplementation is associated with decreased body weight (Onakpoya et al., 2013). Manganese has been shown to play an important role in glycolytic and lipogenesis enzymatic pathways and deficiency has been linked to metabolic abnormalities in animal studies (Baquer et al., 1975; Baquer et al., 2003). A few studies have examined manganese and components of metabolic syndrome (including central obesity) in humans, but results have been inconsistent (Li and Yang, 2018). Therefore, the biologic rationale for the positive weight for manganese in our study is unclear. However, these former studies on manganese and chromium have been largely focused on dietary intake or supplementation rather than using biomarkers that integrate over multiple sources, including environmental sources which may be more harmful for health (Li and Yang, 2018).

Certain non-essential metals have been shown to affect adipose tissue and glucose metabolism (arsenic and cadmium) (Ceja-Galicia et al., 2017; Tinkov et al., 2017), increase oxidative stress (lead, cadmium, arsenic, and mercury) (Ercal et al., 2001; Tinkov et al., 2017), and act as endocrine disruptors (lead, cadmium, arsenic, and mercury) (Iavicoli et al., 2009), all potential biological mechanisms through which they could be related to higher BMI. Although our single metal model results suggest that any individual metal contributions are small, there is an overall detectable combined effect. It is possible that while the individual effect of each non-essential metal is minimal, their total combined effect is more relevant for adverse physiological effects. The mixtures analysis also accounted for co-metal confounding between the different metals, which may have been particularly relevant as previous studies of essential and non-essential metals suggest they may interfere with each other metabolically (Abdulla and Chmielnicka, 1989; Lopez Alonso et al., 2004).

In cross-sectional studies the proper temporality of the exposure and outcome relationships is obscured, and it is plausible that an individual’s current BMI could affect their body burden or measurement of metals in biospecimens. Our ability to look at associations between metals measured at baseline and future BMI, while controlling for baseline BMI, mitigates this issue and improves upon previous research. We additionally evaluated the cross-sectional associations in our data by looking at baseline toenails in relation to examiner-measured BMI at baseline in order to compare to the previous literature. In the cross-sectional analyses, copper, arsenic, mercury, and lead were inversely associated with BMI. This contrasts with what we found in our prospective analyses where these individual metals were not associated with BMI. Yet, it mirrors previous cross-sectional studies in the US that reported inverse associations for lead (Padilla et al., 2010; Scinicariello et al., 2013), arsenic (Grashow et al., 2014b), and mercury (Rothenberg et al., 2015) and thus demonstrates the importance of clear temporality.

In addition to looking at all 16 metals combined in quantile g-computation models, we split the metals based on non-essential vs. essential classifications which we hypothesized would be useful groupings from a biological perspective; essential metals are needed for normal physiological processes, while the non-essential metals are not (Tchounwou et al., 2012). From a public health intervention perspective, the general US population exposure to the essential metals derives more from naturally-occurring dietary sources rather than industrial, agricultural, and vehicular contamination of food, water, and air, while the opposite is true for most non-essential metals (with the exception of vanadium) (ATSDR (Agency for Toxic Substances and Disease Registry), 2019; WHO (World Health Organization), 2003). Thus, any potential intervention to affect metals intake would likely act on multiple metals within a given group, but not necessarily all of them (or any individual metal).

We used complimentary mixture methods, quantile g-computation and BKMR, that have different strengths and limitations. We chose quantile g-computation as our primary analytic method for the assessment of the mixture effect because the approach yields parsimonious, interpretable slope estimates that are not possible with BKMR. Quantile g-computation was also advantageous in this context because it can maintain precision despite strong correlations among the exposures (Keil et al., 2019), it is somewhat insensitive to outliers because of the quantization (Czarnota et al., 2015), and it is computationally efficient. Quantile g-computation allows flexible modelling because it is based on generalized linear models and thus allows certain functions, such as splines, polynomials, and product terms. The validity of the quantile g-computation approach relies on accurate model specification, but any non-linearities or interactions must be known and user specified. Because BKMR fits highly adaptive regression functions, we used it to check and inform modeling assumptions of quantile g-computation. The BKMR univariate exposure-response curves were linear for all metals and paired interactions were not identified from the bivariate functions so we maintained the linear form of the model. The positive association for the non-essential metal group and the inverse association for the essential metal group from quantile g-computation was also confirmed in the plots of the overall mixture effect by BKMR. Further, the ranking of the positive and negative weights within the non-essential and essential metal groups generally mirrored the magnitude and direction of the univariate exposure-response functions from BKMR. The results from the mixtures analyses were supported by a few of the trends that were suggested in the single metal models, particularly for the essential metals. The 4^th vs 1^st quartile of cobalt was inversely associated with BMI and cobalt was the most strongly weighted essential metal in the quantile g-computation analysis. A suggestive inverse association was observed for the 4^th quartile of chromium and an IQR increase in zinc and these were also negatively weighted in quantile g-computation for the essential metal group.

Only one other study has formally assessed a mixture-effect of metals in relation to BMI (Wang et al., 2018). Using cross-sectional data from NHANES, an environmental risk score (ERS) was constructed as a weighted sum of predictors (7 non-essential metals [blood lead, cadmium, mercury; urinary monomethylarsonic acid (MMA), barium, mercury, thallium] as main effects, 4 squared metal terms [urinary antimony, tungsten, cadmium; blood cadmium], and 7 pairwise interactions between metals [urinary MMA and blood lead, blood lead and urinary cadmium, blood lead and urinary uranium, urinary cadmium and MMA, urinary tungsten and dimethylarsinic acid, urinary MMA and cobalt, urinary lead and antimony]) selected by adaptive elastic-net. Using linear regression, an increase in the ERS from the 10^th to 90^th percentile was associated with a 4.50 kg/m² increase in BMI. Therefore, the direction of the association for the ERS composed of certain non-essential metals in the NHANES study was in the same direction as the association we observed for the non-essential metals as a whole using quantile g-computation. Future work should continue to emphasize the use of statsitical methods for handling mixures with approaches that, similar to ours, assess effects of the total metal mixture or that explore other aspects of mixtures such as exposure patterns that reflect shared sources. Further, as with any analysis of observational data, our statistical approach for handling mixtures does not overcome issues of unmeasured confounding and does not explicate biologic mechanisms, both of which require confirmation and exploration in controlled, lab environments which could, for example, expose cell lines in vitro to different mixtures of metals.

Another strength of our study was the use of toenails for measuring metals. Toenail measures are thought to reflect 4–6 months of exposure 6–12 months before collection (Grashow et al., 2014a; Yaemsiri et al., 2010) and some studies have observed that levels correlate over even longer periods such as 4–10 (O’Brien et al., 2019b) or 1–7 years (Wu et al., 2018). Therefore, they represent a stable matrix for measuring metals in addition to being easy to collect, ship and store (O’Brien et al., 2019a; O’Brien et al., 2019b). We had a panel of 16 metals that were measured, which allowed us to examine the largest number of individual metals in relation to BMI within a single study, which was beneficial when considering groups of metals.

Toenails that were used for measuring levels of metals were only collected at one time point. Metal exposures can vary over time and BMI is a time-varying outcome that is potentially affected by prior exposure: cumulative effects of these exposures could be more fully captured with multiple measures of both metals and BMI. When evaluating associations between baseline metals and follow-up BMI, the baseline BMI at time of metal measurement matters as it may influence baseline metal concentration measurements and may also affect the BMI that someone can realistically reach during follow-up. Therefore, we adjusted for examiner-measured BMI at baseline. We considered this to be the appropriate choice to attain the least-biased results based on the framework provided by our DAG in Figure S1. However, we acknowledge that the relationship between metals at baseline and BMI at follow-up is complicated and there are likely other causal connections between variables that are unknown based on current literature or are unmeasured, and therefore not included on our DAG or our models. While we posit that we were able to partially control confounding by diet via controlling for BMI at baseline and accounting for multiple diet-related metals, we are nonetheless sensitive to residual confounding by unmeasured dietary factors that may lead to increased essential metals and lower BMI. Future studies could improve on this analysis by collecting more complete data on on dietary sources of metals. Future studies would also benefit from multiple measures of both metals and BMI to capture longitudinal patterns of change in BMI in relation to metals exposure. Additionally, BMI on the follow-up questionnaire was collected by self-report rather than measured by trained examiners. Thus, some measurement error in the outcome is present. However, at baseline, both examiner-measured and self-reported weight and height was available. Self-reported weight and height was found to be highly reliable and accurate in the Sister Study cohort (r=0.99 and 0.96 for self-report vs examiner-measured weight and height, respectively), leading to high correlations (r=0.98) and low mean differences (0.7 kg/m²) between examiner-measured and self-reported BMI at baseline. This strengthens our confidence in the use of self-reported follow-up BMI in this population (Lin et al., 2012). Lastly, women in the Sister Study are mostly non-Hispanic white, well-educated, and have a family history of breast cancer, which may limit how well our results apply to the general population or to groups that may be most highly exposed or susceptible.

In this prospective study, although individual metals except for cobalt demonstrated only weak, non-statisically significant associations with BMI, our findings support an association between groups of metals and BMI and suggest that these associations may vary based on whether the metal is essential or non-essential. Assuming that measured metals represent useful markers of exposure, and that we have at least approximately controlled confounding or selection bias, our results have potential public health implications regarding exposure to both non-essential and essential metals mixtures and support continued efforts to reduce non-essential metal exposure levels in the general population.

HIGHLIGHTS.

• This study prospectively examined whether metals were associated with BMI

• In single metal models cobalt was inversely associated with BMI

• Other metals were not strongly related to BMI individually

• Increasing all non-essential metals jointly was positively associated with BMI

• Results show the importance of a prospective design and examining metal mixtures