Adaptation and visual discomfort from flicker

Abstract

Spatial images with unnatural amplitude spectra tend to appear uncomfortable. Analogous effects are found in the temporal domain, yet discomfort in flickering patterns is also strongly dependent on the phase spectrum (Yoshimoto et al., 2017). Here we examined how discomfort in temporal flicker is affected by adaptation to different amplitude and phase spectra. Adapting and test flicker were square wave or random phase transitions in a uniform field filtered by increasing (blurred) or decreasing (sharpened) the slope of the amplitude spectrum. Participants rated the level of discomfort or sharpness/blur for the test flicker. Before adaptation, square wave transitions were rated as most comfortable when they had “focused” edges, which were defined as characterized by 1/f amplitude spectra, while random phase transitions instead appeared more comfortable the more blurred they were. After adapting to blurred or sharpened transitions, both square wave and random phase flicker appeared more sharpened or blurred, respectively, and these effects were consistent with renormalization of perceived temporal focus. In comparison, adaptation affected discomfort in the two waveforms in qualitatively different ways, and exposure to the adapting stimulus tended to increase rather than decreased its perceived discomfort. These results point to a dissociation between the perceived amplitude spectrum and perceived discomfort, suggesting they in part depend on distinct processes. The results further illustrate the importance of the phase spectrum in determining visual discomfort from flickering patterns.

1. Introduction

Certain visual patterns can produce aversive effects, such as headache, migraine, and even seizures in observers with photosensitive epilepsy, and are typically uncomfortable to view for normal observers. These experiences are referred to as visual discomfort or stress (Wilkins, 1986, 1995, 2016). Examples of visual discomfort are common in the modern visual environment. It has been reported that some artworks evoked such aversive reactions in observers from 1970s–2000s in U.K. (Fernandez & Wilkins, 2008). In 1989, the “Sunday Observer” ran a front-page headline for a newspaper advertisement using swirling stripes that was banned because of its induction of seizures. At around the same period, TV shows or commercials containing rapidly flashing lights for entertainment purposes induced seizures in not only the U.K. but also U.S. and Japan (Fisher, Harding, Erba, Barkley, & Wilkins, 2005). In 1997, when a TV cartoon “Pokémon” was broadcast, many viewers all over Japan complained of headache and discomfort, and more than 700 viewers went to hospital due mostly to seizures. In modern urban life, the probability of seeing artificial visual patterns that can be uncomfortable to look at and can produce aversive effects has thus increased (Le et al., 2017) and more guidelines on image safety are required (So & Ujike, 2010). Therefore, an understanding of the factors related to visual discomfort is an important issue from both scientific and practical viewpoints (Wilkins, 2016).

The spatial properties related to visual discomfort have been studied in many aspects. Fernandez and Wilkins (2008) measured discomfort ratings for a variety of images, including artistic paintings, photographs of natural scenes, and filtered noise patterns, and showed that the images uncomfortable to view often have an excess energy at medium spatial frequencies. In a similar line, Juricevic et al. (2010) found that discomfort for images with filtered noise was rated as most comfortable when the amplitude varied as the reciprocal of spatial frequency, (1/frequency, 1/f) and thus a log-log plot of amplitude versus frequency had a slope of −1. This 1/f spectrum is a common characteristic of natural images, and it has been assumed that our visual system is optimized for such images with encoding that gives an efficient and sparse cortical response (Atick, 1990; Atick & Redlich, 1992; Barlow, 1981; Field, 1987; Lennie, 2003; Olshausen & Field, 2004; Párraga, Troscianko, & Tolhurst, 2000; Srinivasan, Laughlin, & Dubs, 1982). Images with a spatial structure deviating from 1/f might appear uncomfortable because they lead to less efficient and thus stronger responses or overstimulation (Fernandez & Wilkins, 2008; Juricevic et al., 2010). Such a viewpoint is consistent with computational modeling of primary visual cortex (V1), which shows that uncomfortable images cause a non-sparse distribution of neural firing (Hibbard & O’Hare, 2015; Penacchio et al., 2015). On the other hand, there is also evidence that natural spectra can lead to stronger cortical responses, perhaps because they result in a more uniform distribution of responses across different spatial scales (Isherwood, Schira, & Spehar, 2017; Olman, Ugurbil, Schrater, & Kersten, 2004; Tregillus et al., 2014). By either account, discomfort from a wide range of images can therefore be predicted from a simple property of the spatial statistics of the images, and specifically, how much they deviate from natural image statistics.

Visual discomfort and seizures are also known to be induced by periodically flickering patterns (Binnie, Findlay, & Wilkins, 1985; Fisher et al., 2005; Harding & Harding, 1999; Harding & Jeavons, 1994; Lin et al., 2014; Wilkins, 1995). Lin et al. (2014) used an LED display and showed that a flickering light appears most uncomfortable for normal observers at temporal frequencies responsible for headaches or epileptic seizures in photosensitive observers (e.g., Harding & Jeavons, 1994). An intermittent light from lamps or televisions may appear steady but can also induce discomfort; and similarly, flickering lights with frequencies of 100 or 120 Hz are above the critical flicker fusion threshold, but may nevertheless cause aversive effects, potentially because they interact with eye movements to produce artifacts in the visible range (Poplawski & Miller, 2013; Roberts & Wilkins, 2013; Wilkins et al., 1989). The question arises as to whether a relationship between amplitude and frequency analogous to that in the spatial domain would be observed in the temporal domain. Similar to variations over space, variations over time in natural scenes tend to have a characteristic amplitude spectrum in which amplitude falls with increasing temporal frequency (Billock, de Guzman, & Kelso, 2001; Dong & Atick, 1995; Isherwood, Clifford, Schira, & Spehar, 2018; van Hateren & van der Schaaf, 1996). Yoshimoto et al. (2017) measured discomfort for luminance flicker in a 17° uniform field and found that the discomfort increased with deviations from 1/f temporal structure, or with excessive energy at medium or higher temporal frequencies. Discomfort induced by time varying patterns again may be predicted from their temporal amplitude spectra, and may account for the greater discomfort from flicker with an excess energy at medium temporal frequencies (Binnie et al., 1985; Fisher et al., 2005; Harding & Harding, 1999; Harding & Jeavons, 1994; Lin et al., 2014; Wilkins, 1995).

However, the temporal discomfort judgments were also strongly affected by the phase spectra of the flicker, with fixed at a specific phase (e.g., square wave) vs. random spectra producing very different patterns of responses. When the phase was randomized, only higher temporal frequency components induced discomfort. These findings by Yoshimoto et al. (2017) suggest that, like spatial patterns, visual discomfort from time-varying patterns depends in part on how similar they are to the amplitude spectra of temporal variations in the natural visual environment, but also point to the critical role of the phase spectrum in the perceived discomfort of flicker.

In this study, we examined how visual discomfort is affected by adaptation to temporally varying patterns. Adaptation continuously recalibrates visual coding according to the current visual environment the observer is exposed to, and can result in large changes in both sensitivity and perception (Webster, 2015). The adaptation aftereffects have been very widely studied, but few studies have explored how these aftereffects might impact judgments of discomfort. To assess this, we adapted observers to various patterns of flicker, and then examined how this modulated the rating of visual discomfort for subsequently presented flicker. Previous studies have shown that adaptation to temporal luminance contrast strongly biases contrast sensitivity and perceived flicker rate (Anstis, 2014; Krauskopf, Williams, & Heeley, 1982; Pantle, 1971; Webster & Mollon, 1994). This adaptation can also bias the perceived temporal profile of the flicker. Bilson, Mizokami, and Webster (2005), showed that adaptation to flicker with different amplitude spectra alters the perceived blur or sharpness of the flicker. Specifically, they found that adaptation to temporally blurred or sharpened transitions affects the perceived focus of transitions over time. In their experiment, participants adapted to blurred or sharpened transitions created by filtering the temporal amplitude spectrum of a square wave alternation, and then adjusted the amplitude spectrum of a test stimulus until it appeared to match the transitions in a reference stimulus. After adapting to blurred transitions, a physical square wave transition appeared too sharp (i.e. with enhanced temporal “edges”). Conversely, adapting to the physically sharpened patterns caused the same square wave to appear blurred in time. These results suggest that the visual system can rapidly calibrate temporal sensitivity to match the temporal structure in the visual environment, and closely parallel the aftereffects on perceived blur in spatially varying patterns (Webster, Georgeson, & Webster, 2002; Webster & Marcos, 2017)

Here we asked whether adaptation might affect not only the appearance of the flicker but also the associated discomfort, and how the two aftereffects are related. Following Bilson et al. (2005), we measured the effect of adaptation to different temporal spectra on the perception of temporal sharpness/blur, but also assessed the reported changes in the visual discomfort of the stimuli. We also tested how the phase spectrum of the adapting stimuli influences the discomfort. The goal of these experiments was to further reveal the stimulus properties contributing to visual discomfort from flicker.

2. Methods

2.1. Participants

Twenty-two individuals (seven male and 15 female; average age = 21.3 years, range 18–30 years) participated in the experiment. All had normal or corrected to normal vision and were naïve to the purpose of the experiment. The study was reviewed and approved by the Research Ethic Committee of Hiroshima University. The general nature of the experiment was explained to all participants who provided written informed consent before the study began.

2.2. Apparatus

Stimuli were presented on a 21-inch SONY Multiscan 21PS Trinitron CRT monitor at a resolution of 1024 × 768 pixels with a refresh rate of 120 Hz, and controlled by a Cambridge Research Systems ViSaGe MKII. The monitor output was gamma corrected based on calibrations with a Cambridge Research Systems SpectroCAL MKII spectroradiometer. Participants observed the display binocularly from a distance of 57 cm, with their head position maintained by a chin rest. The room was darkened and no other light source was present.

2.3. Stimuli

For the comparisons with our previous study, we used a stimulus that was similar to that used by Yoshimoto et al. (2017). Flicker was displayed in a uniform 17° field, shown on a gray background with the same chromaticity (CIE 1931; x = 0.31, y = 0.33) and mean luminance (40 cd/m²). The luminance of the flickering field was varied according to the waveform obtained by summing the odd harmonics and by filtering in the temporal frequency domain (Fig. 1). The fundamental frequency was set at 1 Hz while the highest harmonic frequency was set at 59 Hz, close to the temporal acuity limit (Kelly, 1961). The first row of Fig. 1a shows a schematic sample of the waveforms and the amplitude spectra of the test stimuli. The phase of each harmonic component was fixed at 0° (2nd row of Fig. 1a) or was randomized from 0°–360° to have a uniform distribution of phases (3rd row of Fig. 1a). The former and latter types of phase spectra were indicated by “square wave” and “random” below, respectively. The amplitude spectrum was multiplied by f ^s, with the value of s ranging from –1.4 to –0.6 in 0.2 steps (–1.4, –1.2, –1, –0.8, and –0.6). The waveform with the phase fixed at 0° and with the amplitude slope of –1 (or 1/f) therefore corresponded to a square wave. Thus, a steeper slope with a value lower than –1 reduced the relative amplitude of higher temporal frequencies leading to blurred transitions; while a shallower slope higher than –1 boosted the higher frequencies leading to sharpened transitions. All the filtered stimuli were adjusted to have a root mean square (RMS) contrast of 0.2. The most blurred transitions (slope = –1.4) and the most sharpened transitions (slope = –0.6) were used not only as test stimuli but also as adapting stimuli.

Fig. 1.

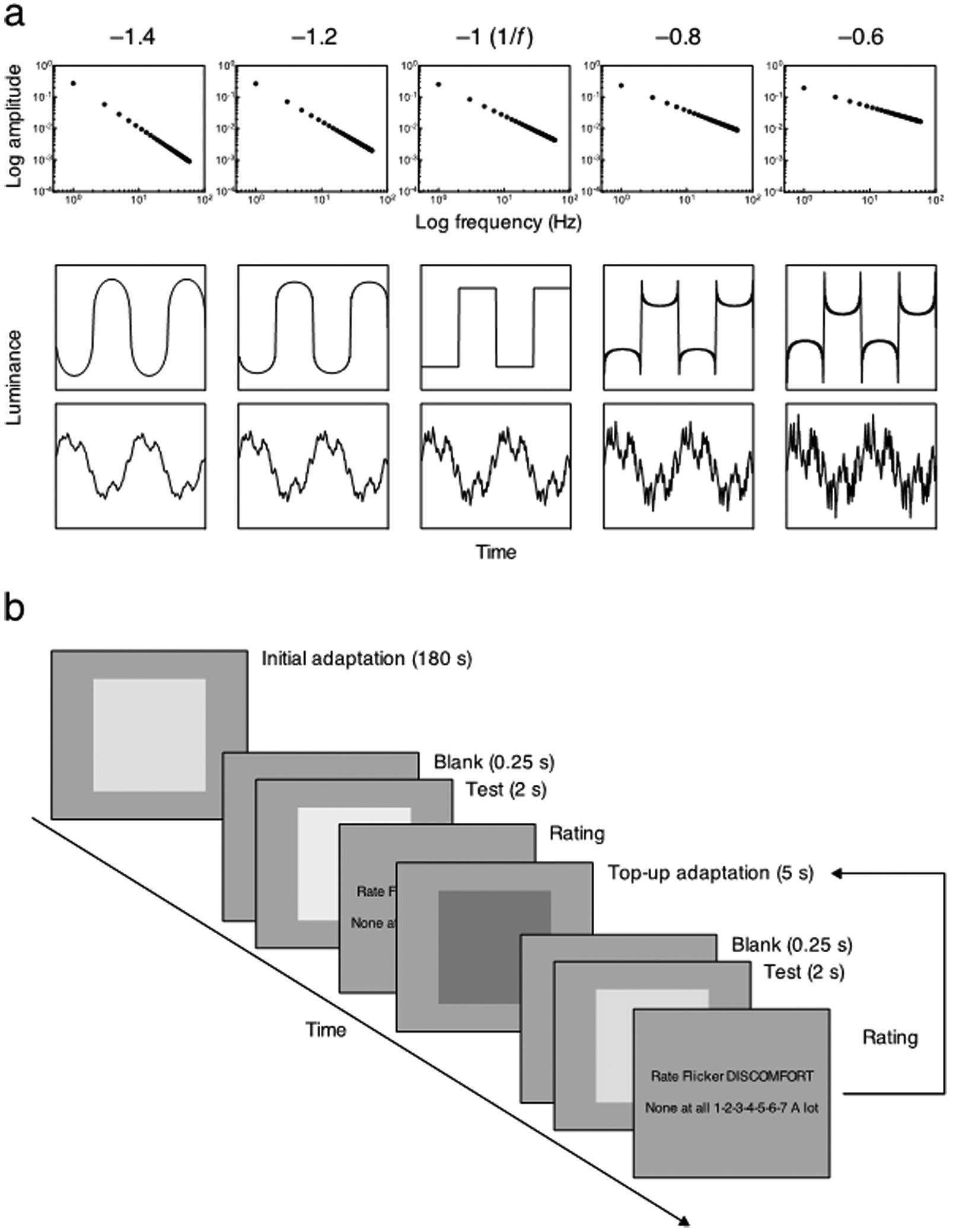
(a) Schematic example of the amplitude spectra (top) and the filtered waveforms with square wave (middle) or randomized phase spectra (bottom). The slope of the amplitude spectrum was –1.4, –1.2, –1, –0.8, or –0.6, from left to right. The amplitude spectrum is plotted as a function of temporal frequency on log-log axes (top). The luminance of the waveform is plotted as a function of time (middle and bottom). (b) Schematic description of the trial sequence with adaptation for the discomfort rating. Participants initially adapted for 180 s and then rated the discomfort from the 2-s test stimulus, as quickly as possible. A top-up adaptation stimulus was displayed for 5 s between each of the tests after participants responded to the previous test stimulus. The adaptation and test stimuli were separated by 0.25-s gaps with a blank screen. The same procedure was applied for the sharpness/blur rating.

Both adapting and test stimuli were presented in a centrally fixated field. Note that in the study by Bilson et al. (2005), the adaptation and test were presented separately in different locations in order to increase sensitivity to changes in the appearance of the test with adaptation. In preliminary observations, we also collected data when the adaptation and test were presented to left and right of center separated by 3°, and vice versa, respectively. No systematic difference was found whether the adaptation and test were presented in side-by side-fields or a single field. In the main experiment, we therefore restricted the measurements only to the single central field condition, as shown in Fig. 1 (b).

2.4. Procedure

Aftereffects on discomfort and sharpness/blur perception were quantified using a rating scale. Visual discomfort represents a perceptual judgment that is intuitive to observers, and has been widely-assessed by subjective methods such as rating (e.g., Fernandez & Wilkins, 2008; Juricevic et al., 2010), ranking (e.g., Fernandez & Wilkins, 2008), paired comparisons (e.g., O’Hare & Hibbard, 2013; Wilkins et al., 1984; Yoshimoto et al., 2017) and questionnaires (e.g., Wilkins & Evans, 2001).

Discomfort rating: participants rated the discomfort from the flickering test stimuli without adaptation. Each test stimulus was presented for 2 s, followed by a gray screen displaying “Rate Flicker DISCOMFORT” with a 7-point scale ranging from 1 “None at all” on the left to 7 “A lot” on the right. The scale format was adopted from Fernandez and Wilkins (2008) and Juricevic et al. (2010). Participants were asked to respond as quickly as possible, by pressing the appropriate number key on the computer keyboard, and typically responded within 1 s. Each session consisted of 10 trials: two trials for each of the five test stimuli with different slopes of amplitude spectra, which were presented in random order. Each participant completed a session for each of the two phase spectra (square wave and random), in random order. Next, the rating protocol was repeated after adapting to the stimulus with the slope of –1.4 (blurred transitions) or –0.6 (sharpened transitions). As shown in Fig. 1b, participants initially adapted for 180 s with a 5 s top-up adaptation after each rating. A 0.25-s blank screen was inserted between the rating and adaptation intervals. The phase spectra of adapting and test stimuli were the same (same-phase adaptation condition: square wave adapt and square wave test or random adapt and random test) or different (cross adaptation condition: random adapt and square wave test or square wave adapt and random test). Each participant completed a session for each of the two amplitude slopes of adapting stimulus and for each of the four pairs of phase spectra (eight sessions in total), in random order. For the random waveforms the phase of the harmonics was randomized on each session. The phase spectra of the adapting and test stimuli were therefore unchanged during each session.

Sharpness/blur rating: the same procedure was applied for rating the temporal sharpness/blur of the test stimulus, except that a gray screen displaying either “Rate Flicker SHARPNESS” with a 7-point scale from 1 “Blurred” to 7 “Sharpened” or “Rate Flicker BLUR” with a 7-point scale from 1 “Sharpened” to 7 “Blurred” followed to a 2-s test presentation. The scales were counterbalanced between participants. The order of ratings (discomfort and sharpness/blur) was also counterbalanced. The discomfort and sharpness/blur for the test stimuli were also rated on separate days to reduce the effect of the former rating.

3. Results

We compared the effects of adaptation to different temporal amplitude spectra on two tasks (perceived temporal blur or sharpness) and for two different phase spectra (square wave or random). Results for each of these conditions are described in the following sections.

3.1. Same-phase adaptation condition

3.1.1. Square wave phase spectra

Fig. 2a shows the rating of sharpness for the stimulus with a square wave phase spectrum before or after adapting to the blurred or sharpened square wave spectra. The figures plot the average of the ratings across observers; patterns for individual observers were generally consistent within and across observers (Yoshimoto et al., 2017). Each participant rated the discomfort and the sharpness/blur twice for each adapt and test condition. To evaluate the intra-rater reliability, we calculated the intraclass correlation coefficient (ICC) based on the mean-rating. The ICC values for the discomfort ranged from .78 to .93; those for the sharpness/blur were ranging from .77 to .92. The participants’ ratings were relatively consistent across times as values above .75 indicate good reliability (Portney & Watkins, 2000). Thus for the subsequent analysis, we used the average point of the two ratings for each participant. Finally, for averaging the values obtained in the scale from 1 “Sharpened” to 7 “Blur” were reversed (1 “Blur” to 7 “Sharpened”). The sharpness rating was then rescaled to range from –3 to 3. Thus, ratings at zero were presumed to represent test stimuli that appeared neither blurred nor sharp and thus appeared as a focused square wave transition in time.

Fig. 2.

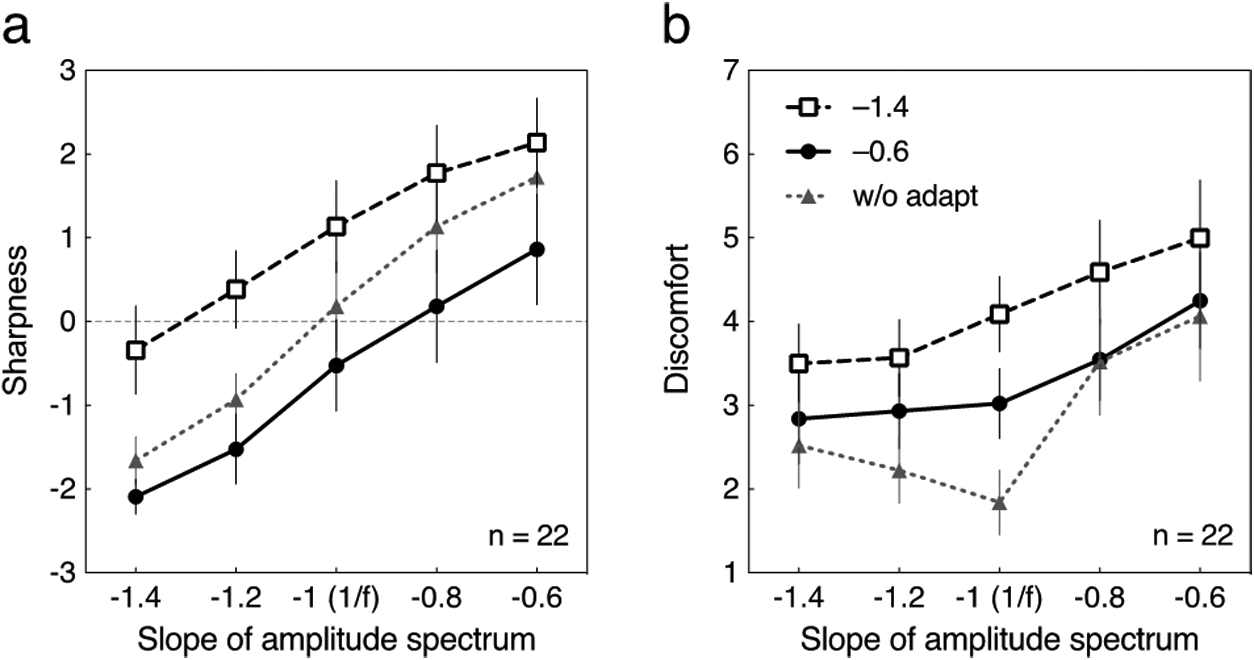
Averaged sharpness and discomfort ratings for the tests with a square wave phase spectrum for the 22 participants in the same-phase adaptation condition. Each curve represents data without adaptation (“w/o adapt”) or after adapting to blurred (–1.4) or sharpened (–0.6) transitions. Error bars represent 95% confidence interval (CI). (a) The sharpness rating is plotted as a function of the slope of amplitude spectrum of the test stimulus. (b) The discomfort rating is plotted as a function of the slope of amplitude spectrum of the test stimulus.

Without adaptation, participants showed good sensitivity to temporal transitions: the shallower the slope of the amplitude spectrum (from –1.4 to –0.6), the sharper the test appeared. The rating for the test with the slope of –1 (1/f) approximated zero. That is, participants correctly described the 1/f transitions as a square wave. After adapting to the blurred transitions (–1.4), all of the test stimuli were rated as sharper; conversely, after adapting to the sharpened transitions (–0.6), the function shifted downward and thus all of the tests appeared more blurred. A repeated-measures two-way ANOVA followed by Tukey’s post-hoc test for multiple comparisons was conducted. The generalized η²_G, which is suggested for analysis of repeated-measures designs (Bakeman, 2005; Olejnik and Algina, 2003), was used to estimate the effect size and interpreted according to Cohen’s definition of .02 for a small effect, .13 for a medium effect, and .26 for a large effect (Cohen, 1988). The main effects of amplitude slope and adaptation on the sharpness rating were significant (F(4, 84) = 79.50, p < .0001, η²_G = .48 for the slope; F(2, 42) = 46.96, p < .0001, η²_G = .27 for the adaptation). The interaction between amplitude slope and adaptation was also significant, but the effect size was small (F(8, 168) = 2.76, p < .01, η²_G = .02). The Tukey’s test revealed significant differences in the sharpness ratings without adaptation (“w/o adapt”) and after adapting to blurred (–1.4) or sharpened (–0.6) transitions (qs ≥ 3.42, ps < .05), except between “w/o adapt” and –1.4 for the test with the slope of –0.6 (q = 3.24, ns).

Fig. 2b shows the averaged rating of discomfort for the square wave phase spectrum for the same adapting and test conditions. The discomfort rating is again plotted as a function of the slope of amplitude spectrum. Without adaptation, the test stimulus with the slope of –1 was rated as most comfortable, and the discomfort rating increased both for steeper and shallower slopes, replicating the pattern we observed previously (Yoshimoto et al., 2017). After adapting to the blurred transitions (–1.4), the discomfort ratings instead increased monotonically as the slope became shallower. A similar increase in discomfort was found after adapting to the sharpened transitions (–0.6), although the effect was weakened. A repeated-measures two-way ANOVA showed that the main effects of amplitude slope and adaptation on the discomfort rating were significant (F(4, 84) = 35.29, p < .0001, η²_G = .22 for the slope; F(2, 42) = 22.78, p < .0001, η²_G = .17 for the adaptation). The interaction between amplitude slope and adaptation was also significant, but the effect size was small (F(8, 168) = 6.49, p < .0001, η²_G = .04). The post-hoc Tukey’s test revealed significant differences in the discomfort ratings among the adapting conditions (qs ≥ 5.31, ps < .001), except between “w/o adapt” and –0.6 for the test with the slopes of –1.4, –0.8, and –0.6 (qs ≤ 2.65, ns).

3.1.2. Random phase spectra

Fig. 3a and 3b show the averaged ratings of sharpness and discomfort for the stimuli with a random phase spectrum. Similar to the square wave phase condition, the shallower the slope of the amplitude spectrum the sharper the test appeared without adaptation (Fig. 3a). The rating for the test with the slope of –1 again approximated zero. Adaptation to the blurred transitions caused the test to appear sharper and vice versa. A repeated-measures two-way ANOVA showed that the main effects of amplitude slope and adaptation on the sharpness rating were significant (F(4, 84) = 138.9, p < .0001, η²_G = .58 for the slope; F(2, 42) = 35.85, p < .0001, η²_G = .22 for the adaptation). The interaction between amplitude slope and adaptation was also significant, but the effect size was small (F(8, 168) = 4.245, p < .001, η²_G = .04). The post-hoc Tukey’s test revealed significant differences in the sharpness ratings among the adapting conditions (qs ≥ 3.50, ps < .05), except between “w/o adapt” and –1.4 for the test with the slopes of –0.8 and –0.6 (qs ≤ 2.24, ns), and between “w/o adapt” and –0.6 for the test with the slopes of –1.4 and –0.6 (qs ≤ 3.22, ns).

Fig. 3.

Averaged sharpness and discomfort ratings for the tests with a random phase spectrum for the 22 participants in the same-phase adaptation condition. Each curve represents data without adaptation (“w/o adapt”) or after adapting to blurred (–1.4) or sharpened (–0.6) spectra. Error bars represent 95% CI. (a) The sharpness rating is plotted as a function of the slope of amplitude spectrum of the test stimulus. (b) The discomfort rating is plotted as a function of the slope of amplitude spectrum of the test stimulus.

As shown in Fig. 3b, the discomfort rating also varied monotonically with the slope of the amplitude spectrum, thus paralleling the sharpness rating while differing from the pattern of ratings for the square wave spectrum (Fig. 2b). This again replicates the discomfort ratings we observed previously for these stimuli (Yoshimoto et al., 2017). Adaptation produced a roughly uniform shift in the discomfort ratings. Thus all test slopes appeared more uncomfortable after adapting to the blurred transitions whereas they appeared more comfortable after adapting to the sharpened transitions. A repeated-measures two-way ANOVA showed that the main effects of amplitude slope and adaptation on the discomfort rating (Fig. 3b) were significant (F(4, 84) = 61.34, p < .0001, η²_G = .44 for the slope; F(2, 42) = 22.22, p < .0001, η²_G = .23 for the adaptation). The interaction between amplitude slope and adaptation was also significant, but the effect size was small (F(8, 168) = 3.28, p < .01, η²_G = .03). The post-hoc Tukey’s test revealed significant differences in the sharpness ratings among the adapting conditions (qs ≥ 3.91, ps < .05), except between “w/o adapt” and –0.6 for the test with the slopes of –1.4 and –0.6 (qs ≤ 3.23, ns).

3.2. Cross adaptation condition

In the preceding condition the adapting and test stimuli had the same phase spectra but different amplitude spectra. The finding that the pattern of results depended on which phase spectrum was tested (random vs. square wave) again demonstrates that the phase was also important in determining the discomfort and adaptation aftereffects. In this condition we assessed this a second way, by comparing cross adaptation between the random and square wave modulations.

3.2.1. Random phase adapt and square wave test

Figs. 4a and 4b show the averaged ratings of sharpness and discomfort when the test stimuli had a square wave phase spectrum while the adapting stimuli had random spectra. The measurements were made for the same 22 observers. ICC values for the discomfort and the sharpness were again calculated in the manner describe previously. The ICC values for the discomfort ranged from .81 to .98 while those for the sharpness ranged from .80 to .91, indicating fair to good intra-rater reliability. Thus, the subsequent analysis was the same as for the prior conditions.

Fig. 4.

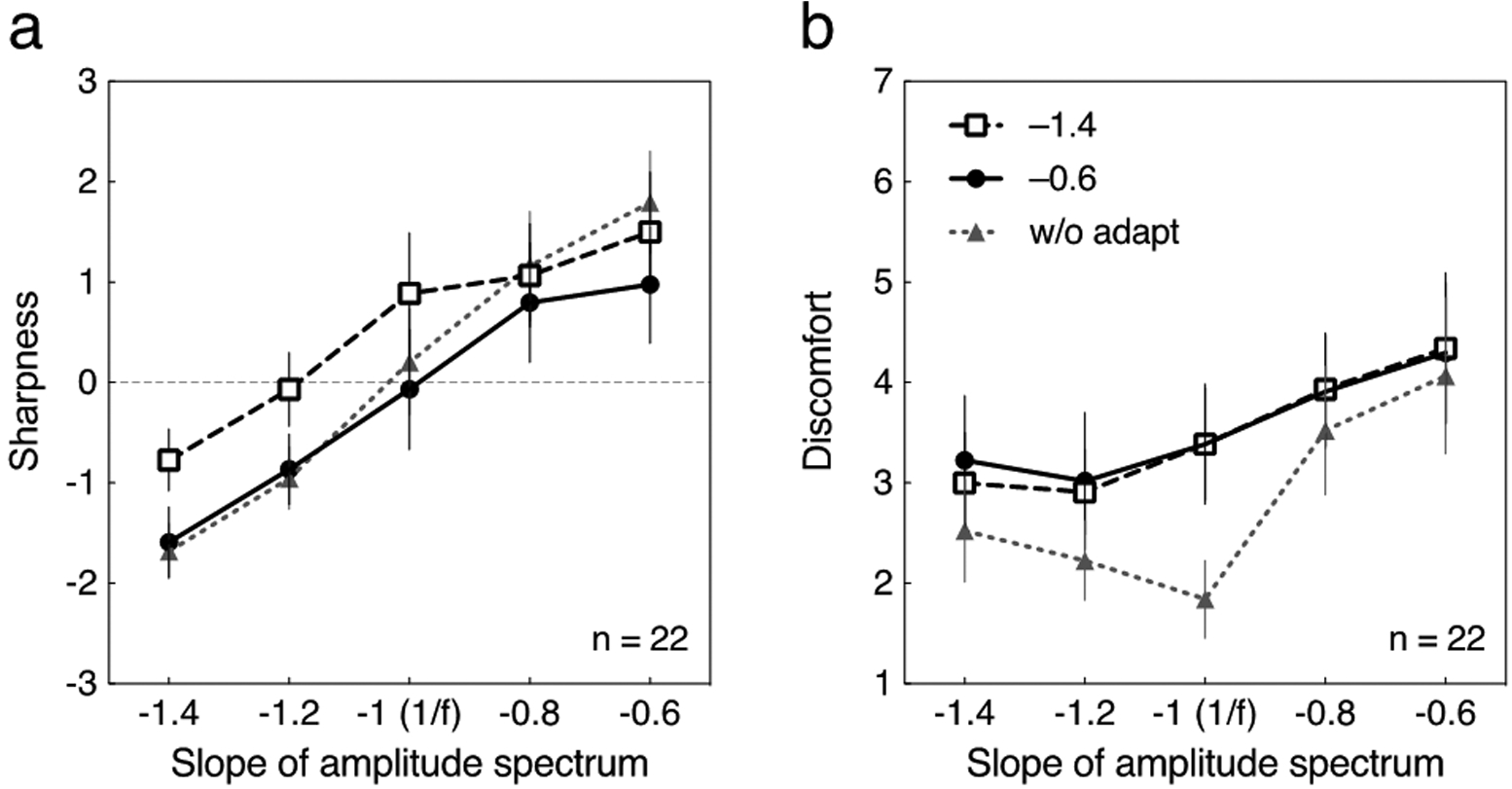
Averaged sharpness and discomfort ratings for the tests with a square wave phase spectrum for the 22 participants in the cross adaptation condition. The adapting stimuli had a random phase spectrum. Each curve represents data without adaptation (“w/o adapt”) or after adapting to blurred (–1.4) or sharpened (–0.6) transitions. Error bars represent 95% CI. Gray dotted line with triangle symbols are re-plots of the data at “w/o adapt” in Fig. 2. (a) The sharpness rating is plotted as a function of the slope of amplitude spectrum of the test stimulus. (b) The discomfort rating is plotted as a function of the slope of amplitude spectrum of the test stimulus.

Ratings indicated by the gray dotted line with triangle symbols are re-plots of the data prior to adaptation (“w/o adapt”) as in Fig. 2. Although the adaptation to blurred (–1.4) random-phase transitions again caused the test to appear sharper, the effect was weaker than for the square wave adaptor. Moreover, in the present cross-adaption condition the sharpened adaptor (–0.6) induced very little change. A repeated-measures two-way ANOVA followed by Tukey’s post-hoc test for multiple comparisons was conducted. The main effect of amplitude slope on the sharpness rating was significant with a large effect size (F(4, 84) = 73.39, p < .0001, η²_G = .48). The main effect of type of adaptation and the interaction were also significant, but the effect sizes were small (F(2, 42) = 11.52, p < .001, η²_G = .06 for the adaptation, F(8, 168) = 5.19, p < .0001, η²_G = .04 for the interaction). The Tukey’s test revealed significant differences in the sharpness ratings between “w/o adapt” and –1.4 (qs ≥ 5.17, ps < .001), except for the test with the slopes of –0.8 and –0.6 (qs ≤ 2.24, ns); conversely, no significant difference was found between “w/o” adapt and –0.6 (qs ≤ 2.76, ns), except for the test with the slope of –0.6 (qs = 6.20, ps < .0001).

The discomfort ratings are shown in Fig. 4b. Both –1.4 and –0.6 adapting stimuli with random phase spectra induced almost the same effect on the test stimuli, which is different from the results of same-phase adaptation condition (Fig. 2b). Also, both adaptation to –1.4 (blurred transitions) and –0.6 (sharpened transitions) increased the discomfort for the test with the slope of –1. A repeated-measures two-way ANOVA showed that the main effect of amplitude slope on the discomfort rating was significant with a medium effect size (F(4, 84) = 23.09, p < .0001, η²_G = .17). The main effect of type of adaptation and the interaction were also significant, but the effect sizes were small (F(2, 42) = 4.553, p < .05, η²_G = .06 for the adaptation, F(8, 168) = 5.75, p < .0001, η²_G = .03 for the interaction). The post-hoc Tukey’s test revealed significant differences in the discomfort ratings between “w/o adapt” and –1.4, and between “w/o adapt” and –0.6, for –1.4, –1.2, and –1 (qs ≥ 3.85, ps < .05); no significant difference was found for other conditions (qs ≤ 3.30, ns)

3.2.2. Square wave adapt and random phase test

Figs. 5a and 5b show the converse condition of random test stimuli and square wave adaptors. Ratings indicated by gray dotted line with triangle symbols are again re-plots of the pre-adapt data (“w/o adapt”) in Fig. 3. The results indicate that the square wave adapting stimuli had very little effect on the random phase test stimuli for both sharpness perception (Fig. 5a) and visual discomfort (Fig. 5b). A repeated-measures two-way ANOVA showed that the main effect of amplitude slope on the sharpness rating (Fig. 5a) was significant (F(4, 84) = 130.2, p < .0001, η²_G = .47). The main effect of type of adaptation and the interaction were not significant (F(2, 42) = 2.78, ns for the adaptation; F(2, 42) = 1.85, ns for the interaction). A repeated-measures two-way ANOVA again showed that the main effect of amplitude slope on the discomfort rating (Fig. 5b) was significant (F(4, 84) = 73.94, p < .0001, η²_G = .53). The main effect of type of adaptation and the interaction was not significant (F(2, 42) = 2.10, ns for the adaptation; F(8, 168) = 1.65, ns for the interaction).

Fig. 5.

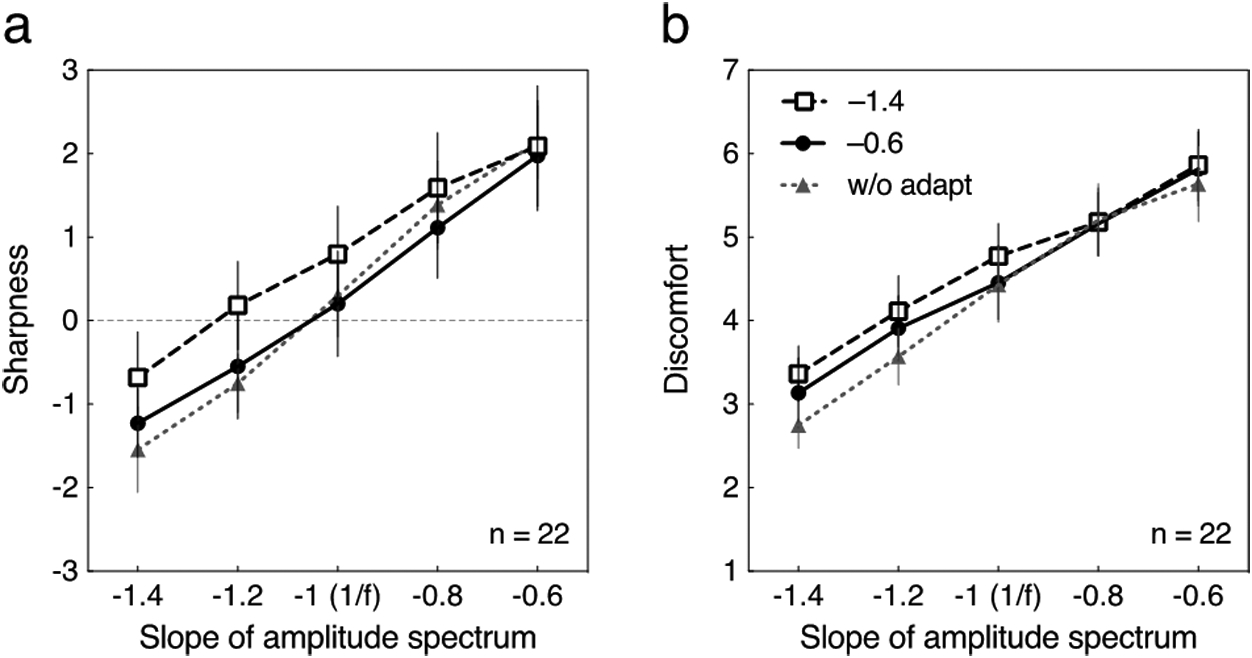
Averaged sharpness and discomfort ratings for the tests with a random phase spectrum for the 22 participants in the cross adaptation condition. The adaptation had a square wave phase spectrum. Each curve represents data without adaptation (“w/o adapt”) or after adapting to blurred (–1.4) or sharpened (–0.6) transitions. Error bars represent 95% CI. Gray dotted line with triangle symbols are re-plots of the data at “w/o adapt” in Fig. 3. (a) The sharpness rating is plotted as a function of the slope of amplitude spectrum of the test stimulus. (b) The discomfort rating is plotted as a function of the slope of amplitude spectrum of the test stimulus.

3.3. Effects of adaptation on the appearance and discomfort of the adapting stimulus

An important question is whether adaptation alters the appearance of the adapting stimulus itself (e.g., so that a blurred adaptor appears more focused, consistent with renormalization of the appearance) or instead produces only a sensitivity loss, so that nearby stimulus levels appear less like the adapting level (consistent with repulsion aftereffects). Spatial blur aftereffects are consistent with renormalization (Elliott et al., 2011). To assess this for temporal spectra and for both appearance and discomfort, we compared the changes in the settings for the adapting levels in each of the preceding conditions, by replotting the ratings from Figs 2–5 for the cases in which the adapting and test stimuli had the same amplitude spectra (–1.4 or –0.6). These re-plots are shown in Figure 6 for both the sharpness/blur ratings (Fig. 6a) and the discomfort ratings (Fig. 6b). Each data point shows the difference in the rating before and after adaption. Positive values indicate a bias to appear more sharpened while negative values indicate a bias to appear more blurred for the sharpness/blur ratings (Fig. 6a). For the discomfort ratings, positive values indicate a bias to appear more uncomfortable while negative values indicate a bias to appear more comfortable (Fig. 6b).

Fig. 6.

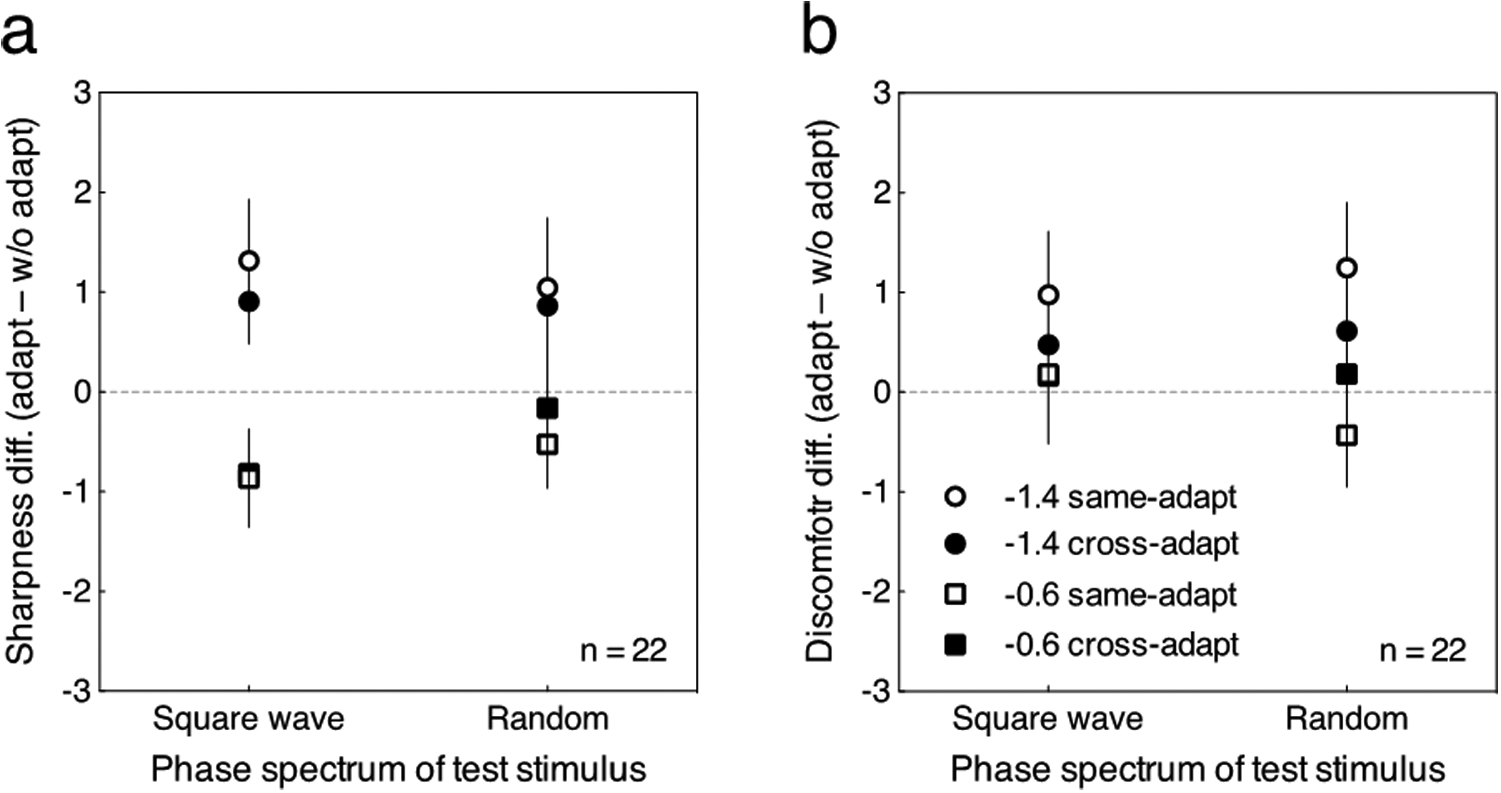
Re-plot of the data in Figs. 2, 3, 4, and 5. Each point represents the change in the rating for the amplitude spectrum that observers adapted to, after adaptation to the same or different phase spectrum. Error bars represent 95% CI. (a) The difference in sharpness ratings (adaptation condition minus pre-adaptation condition) plotted as a function of the phase spectrum of the test stimulus. (b) The difference in discomfort ratings (adaptation condition minus pre-adaptation condition) plotted as a function of the phase spectrum of the test stimulus.

For the sharpness/blur ratings (Fig. 6a), the same-phase adaptation (shown by the unfilled symbols) tended to produce a strong aftereffect on the perception of the adapting stimulus itself, and cause it to appear more focused (less blurred for –1.4 stimulus or sharpened for –0.6 stimulus) irrespective of the phase spectrum (square wave or random). The cross adaptation (shown as the filled marks) also produced aftereffects, though the strength of the aftereffect tended to be reduced compared to the same-phase adaptation. The transfer of the aftereffect between different phase spectra is consistent with Webster et al. (2002) for spatial blur, and suggests that the visual system can adapt directly to the attribute of blur somewhat independently of the stimulus (phase spectrum) carrying that attribute. Conversely, the reduction of the aftereffect in the cross adaptation condition indicates that the aftereffect is also phase selective, and again reinforces the importance of the phase spectrum in determining the temporal blur aftereffects.

For the discomfort ratings (Fig. 6b), when the adapting and test stimuli had a same phase spectrum, the presumed enhancement in higher frequency components after adapting to blurred transitions (–1.4) increased visual discomfort (unfilled circles). This change also occurred though to a weaker extent for the cross adaptation condition for blurred adapting stimulus (filled circles), and these effects were similar for the two phase spectra. When adapting to sharpened transitions (–0.6), the effect of adaptation was generally reduced, irrespective of the phase spectrum or of the same-phase or cross adaptation conditions. Thus for example when the adapting stimulus was the sharpened square wave, perceived blur was modulated while the discomfort rating did not change. These results indicate both that the aftereffects are selective for the phase of the adapting stimulus, and that the discomfort ratings cannot be predicted simply from the changes in perceived blur or sharpness of the images. Moreover, these comparisons show that short-term adaptation to a stimulus does not necessarily cause that stimulus to be perceived as more comfortable.

4. Discussion

To summarize, our pre-adapt settings confirm the results of Yoshimoto et al. (2017) in showing that the discomfort for the stimuli depends on both the amplitude and phase spectra of the stimuli. Square wave spectra are most comfortable when they have focused temporal transitions (1/f) while random spectra instead appear more comfortable the more blurred they are. Adaptation to biased amplitude spectra altered both ratings of discomfort and also the ratings of blur. However, the patterns for these aftereffects differed (Figs. 2 and 3). The aftereffects also showed only partial transfer across different phase spectra (Figs. 4 and 5). In the following we consider the implications of these effects for understanding visual discomfort and temporal processing.

The aim of this study was to explore the stimulus properties associated with discomfort from temporally varying stimuli and how this discomfort is influenced by the observer’s state of adaptation. The results shown in Figs. 2 and 3 illustrate that temporal modulations with the same amplitude spectra but different phase spectra (square wave vs. random) can lead to very different patterns of visual discomfort. In randomly varying modulations discomfort increased monotonically with decreasing slopes (sharper) in the amplitude spectra, so that blurred spectra appeared the most comfortable (Fig 3b). However, for square wave modulations there was instead a minimum in discomfort near a focused slope of 1/f (Fig 2b). In contrast, for both stimuli the perceived blur and sharpness varied in a similar monotonic way with the amplitude slope (Figs. 2a and 3b). These results confirm our earlier findings on the effects of the phase spectrum on discomfort for flicker (Yoshimoto et al., 2017), and further, show that these differential effects cannot be accounted for simply by the level of blur or sharpness perceived in the modulations.

Adaptation to the blurred or sharpened modulations produced changes in the perceived blur for both phase spectra. The aftereffects on perceived focus confirm prior results of Bilson et al. (2005), in showing that blurred temporal modulations cause a focused or 1/f temporal modulation to appear over-sharpened or vice versa. Importantly, the present results also show that this adaptation is consistent with a renormalization of the focus point, since the aftereffects reflect a consistent bias across the different test slopes including the adapting slope. That is, after adaptation, the adapting stimulus itself appeared more focused (less blurred or less sharpened) and there were corresponding shifts in the appearance of all slopes. This pattern of adaptation is similar to the renormalization observed in spatial blur, where again blurred or sharpened patterns appear more focused after adaptation (Elliott et al., 2011; Radhakrishnan et al., 2015). These blur aftereffects are also similar to the aftereffects observed for other visual attributes such as color or faces, which – like the point of subjective focus - may also be coded relative to a null in the continuum or norm (e.g., gray or an average face) (e.g., Webster & MacLeod, 2015). They are inconsistent with an alternative repulsion aftereffect, which is characterized by a local loss in sensitivity to the adapting stimulus without a change in its perceived level (e.g., perceived level of blur), while higher or lower levels appear biased away from the adapting level. This pattern is typical of stimulus attributes that do not have a unique or special neutral point along the attribute dimension (e.g., spatial frequency; Blakemore & Campbell, 1969). Thus our results suggest that, like spatial focus, temporal focus behaves like a norm-based code that can be rapidly recalibrated by adaptation.

Adaptation also affected the perceived discomfort of the images. This raises the question of whether this discomfort aftereffect was driven by the changes in perceived blur/sharpness of the modulations. The aftereffects for the random phase spectra are consistent with this hypothesis. Adaptation for these spectra again produced a roughly constant bias equivalent to a change of approximately 0.2 in the perceived slope (i.e., the post-adapt ratings are consistent with a horizontal shift of the curve left or right by roughly 0.2). The discomfort ratings show a similar general pattern, and thus in this case the change in discomfort could directly reflect the changes in the perceived blur.

However, the aftereffects for the square wave spectra again followed a very different pattern. Here the primary effect of adaptation was to increase the discomfort for the 1/f stimuli relative to the changes induced in the other stimuli, to the extent that the post-adapt settings also now varied monotonically with the test slope. Moreover, both the blurred and sharpened adaptors tended to increase discomfort across the test levels rather than producing opposite effects as with the random stimuli. The change in the shape of the curve cannot be accounted for by a simple lateral shift, and instead suggests that at least in this case the discomfort aftereffects are not a simple consequence of the blur aftereffects.

The basis for the differences between the blur and discomfort aftereffects is not certain. One possibility is that the adaptation induced additional changes in the appearance of the stimuli that were not captured by the sharpness/blur judgments. For example, adaptation also changes the apparent contrast of the stimuli. However, at higher contrasts the losses in apparent contrast tend to be weak (Georgeson, 1985). Further, contrast losses on their own are unlikely to be the source of the discomfort changes since both blurred or sharpened adaptors should reduce contrast relative to the pre-adapt, yet these stimuli induced opposite changes in the random phase stimuli.

As we noted, comfortable stimuli may reflect the stimuli we are adapted to in the natural visual environment. However, this adaptation is normally thought to depend on very long and even evolutionary timescales. It is interesting to ask whether discomfort can be recalibrated over very short timescales such that the stimuli we are currently exposed to become more comfortable. Anecdotally this is often reported to be the case, since many stimuli seem less “jarring” compared to when we first experience them. However, our current results do not support this prediction. For the random-phase patterns, the least discomfort corresponded to the most blurred spectrum, either before or after adaptation and whether adapted to the blurred or sharpened spectrum. For the square wave stimuli, adaptation either increased or did not change the discomfort of the adaptor, while causing the 1/f test to appear less comfortable.

Rather than pointing to a single metric for discomfort from naturalistic temporal variations, the different patterns of adaptation and discomfort we found for random and square wave modulations suggest that there may be several different factors contributing to the ratings. As we have noted previously (Yoshimoto et al. 2017), the random modulations are characterized by frequent and unpredictable transitions, and these increase in salience as the amplitude spectra become shallower. If these fluctuations are themselves uncomfortable, then the most blurred stimulus will result in the least discomfort, regardless of the observer’s state of adaptation, and it may be that the visual system prefers and is perhaps better optimized for more static environments, perhaps because this is the expected state of the environment (Stocker and Simoncelli, 2006). Temporal patterns like a square wave are very different because they reflect stable periodic modulations, with the amplitude spectra varying the profile but not the frequency of the modulation. In this case the most comfortable stimulus might reflect a simple step edge, and this could also reflect an adaptation of visual coding - though for a very different property of the world (e.g., the temporal changes arising from dynamic occlusion). In any event, the different patterns of discomfort and aftereffects for the random and square wave profiles reinforce the conclusion that discomfort from temporal modulations depends not only on the amplitude spectra but also the phase spectra of the stimuli. This conclusion is also supported by the findings that the cross adaptation between square wave and random phase modulations showed phase selectivity and less affected the ratings (Figs. 4 & 5).

Other potential factors affecting discomfort may be related to the oculomotor system. Random modulations can produce more contractions of extraocular muscles than the square wave modulations due to intensive contrast of luminance transitions and could thereby induce more discomfort. Murray, Plainis, and Carden (2002) measured the electromyography and subjective discomfort from glare caused by light sources of excessive brightness or rough luminance variations, and showed a significant correlation between these two measurements. They argued that high intensity lights lead to simultaneous contractions of the levator and orbicularis oculi muscles, resulting in discomfort. The potential basis of discomfort from glare could be related to the discomfort from random phase flicker because of the higher frequency of temporal transitions (Fig. 2a).

The random phase modulations might also produce a large fluctuation of pupil size. It has been reported that discomfort from glare would render the pupil unstable, such that the pupil fluctuations due to the antagonistic actions of the dilator and constrictor muscles might induce discomfort (Hopkinson, 1956; Fry & King, 1975). This finding, however, was challenged by Howarth et al. (1993), who reported no substantial difference in pupil activity between conditions with discomfort versus no discomfort. A more recent study by Lin et al. (2015) pointed out that the discrepancy may be due to measuring absolute pupil size. They recorded the relative pupil size to glare and background illumination, and demonstrated that the relative pupil size can predict the discomfort from glare. It would be valuable for future research to monitor the pupil constrictions caused by the flicker before and after the adaptation in comparison to the discomfort ratings. As pupil response is known to be controlled by central mechanisms including visual areas such as V1 (Barbur, 2004), it would be fruitful to examine the relationship between visual discomfort, pupil response, and cortical activity to reveal the neural basis for discomfort.

Conclusion

Variations in the pattern of temporal flicker produce significant differences in the reported level of visual discomfort. Here we examined how this discomfort is affect by prior adaptation to different temporal spectra. Our results show that both the appearance and perceived discomfort can be strongly biased by adaptation, but in qualitatively different ways, so that perceived discomfort cannot be predicted from perceived blur or sharpness. We have further shown that adaptation renormalizes the perception of temporal blur, yet does not cause the adapting stimuli to appear more comfortable, further dissociating the two measures.