The Temporal Dynamics of Background Selection in Nonequilibrium Populations

Abstract

Neutral genetic diversity across the genome is determined by the complex interplay of mutation, demographic history, and natural selection. While the direct action of natural selection is limited to functional loci across the genome, its impact can have effects on nearby neutral loci due to genetic linkage. These effects of selection at linked sites, referred to as genetic hitchhiking and background selection (BGS), are pervasive across natural populations. However, only recently has there been a focus on the joint consequences of demography and selection at linked sites, and some empirical studies have come to apparently contradictory conclusions as to their combined effects. To understand the relationship between demography and selection at linked sites, we conducted an extensive forward simulation study of BGS under a range of demographic models. We found that the relative levels of diversity in BGS and neutral regions vary over time and that the initial dynamics after a population size change are often in the opposite direction of the long-term expected trajectory. Our detailed observations of the temporal dynamics of neutral diversity in the context of selection at linked sites in nonequilibrium populations provide new intuition about why patterns of diversity under BGS vary through time in natural populations and help reconcile previously contradictory observations. Most notably, our results highlight that classical models of BGS are poorly suited for predicting diversity in nonequilibrium populations.

THE effects of natural selection and demography on neutral genetic diversity within populations have long been of interest in evolutionary and population genetics. Recent efforts in sequencing tens of thousands of genomes across a multitude of species have yielded new and valuable insights into how these two forces of evolution have shaped extant patterns of genomic variation. Yet, while the theoretical underpinnings of the effects of natural selection and demography on genetic diversity have been investigated for decades (Maynard Smith and Haigh 1974; Nei et al. 1975; Maruyama and Fuerst 1984, 1985; Kaplan et al. 1989; Tajima 1989; Charlesworth et al. 1993; Hudson and Kaplan 1995; Nordborg et al. 1996), detailed investigation into how they jointly act to create patterns of diversity in different populations remains lacking.

Both theory and empirical observation have long shown that patterns of neutral genetic variation can vary regionally across the genome as a function of recombination rate (Maynard Smith and Haigh 1974; Begun and Aquadro 1992). This is because natural selection operating on selected sites not only decreases genetic variation at the focal site but can also lead to decreases in nearby neutral genetic diversity due to genetic linkage (Cutter and Payseur 2013). These effects, known as genetic hitchhiking (Maynard Smith and Haigh 1974) (in which neutral variants rise to high frequency with adaptive variants) and background selection (BGS; in which neutral variants are removed along with deleterious variants) (Charlesworth et al. 1993), can be widespread across the genome (Elyashiv et al. 2016). Evidence for selection at linked sites has been found across an array of species, including Drosophila melanogaster (Begun and Aquadro 1992; Charlesworth 1996; Andolfatto 2007; Sella et al. 2009; Comeron 2014; Elyashiv et al. 2016), mice (Keightley and Booker 2018), wild and domesticated rice (Flowers et al. 2011; Xu et al. 2012), Capsella (Williamson et al. 2014), monkeyflowers (Stankowski et al. 2019), flycatchers (Rettelbach et al. 2019), maize (Beissinger et al. 2016), and humans (Sabeti et al. 2002; Reed et al. 2005; Voight et al. 2006; Cai et al. 2009; McVicker et al. 2009; Hernandez et al. 2011; Lohmueller et al. 2011).

Demographic change can also impact patterns of diversity across the genome. For example, neutral theory predicts that the amount of genetic diversity is proportional to a population’s effective population size $\left(N_e\right)$, such that changes in $N_e$ should result in concomitant changes to diversity (Kimura 1983). One of the most common forms of a population size change is a population bottleneck, whereby populations suffer a large decrease in size, often followed by an expansion. Some of the ways bottlenecks can occur include: domestication events (Doebley et al. 2006; Tang et al. 2010; Wiener and Wilkinson 2011; Gaut et al. 2018), seasonal or cyclical fluctuations in population size (Elton 1924; Ives 1970; Itoh et al. 2009; Norén and Angerbjörn 2014), and founder events (David and Capy 1988; Dlugosch and Parker 2008; Henn et al. 2012). Notably, while the rate of loss of diversity in response to a population contraction is quite fast, the recovery of diversity following a population increase can be slow (Charlesworth 2009). As a result, large contemporary populations may still exhibit patterns of low average genetic diversity if their population size was much smaller in the recent past. In humans, this is clearly evident in European and Asian populations due to the out-of-Africa bottleneck (1000 Genomes Project Consortium et al. 2015).

Because selection at linked sites and demography are both pervasive forces across a multitude of species, it is necessary to characterize how these two forces interact with one another to develop a full picture of the determinants of neutral genetic diversity. The efficiency of natural selection scales proportionally with $N_e$ (Ohta 1973) and the impact of selection at linked sites on neutral diversity is likely to be greater in larger populations (Kaplan et al. 1989; Cutter and Payseur 2013; Corbett-Detig et al. 2015) [but see Gillespie (2001) and Santiago and Caballero (2016)]. Further, demographic changes can also increase (in the case of bottlenecks) or decrease (in the case of expansions) the rate of drift. Therefore, it is plausible that the rate at which diversity at a neutral locus is perturbed by selection at linked sites could be highly dependent on both the current, as well as the long-term, $N_e$ of the population. This competition between the strength of selection at linked sites (which increases with the census size N) and genetic drift (which decreases with census N) may be a key contributor to the limited range of diversity observed among species despite much larger observed differences in census size (Lewontin 1974; Gillespie 2001; Leffler et al. 2012; Corbett-Detig et al. 2015; Santiago and Caballero 2016). However, selection at linked sites alone may not be sufficient to explain the discrepancy between observed diversity and census population sizes (Coop 2016), and the action of both demography and selection in concert at linked sites may provide a better model. Moreover, the heterogeneous structure of selection at linked sites across the genome may yield different responses to demography and population splits through time (Burri 2017), and the resulting effects on patterns of differentiation and divergence also remain largely unexplored [but see Stankowski et al. (2019)].

Many models of selection at linked sites were also formulated with the assumption that the population is large enough (or selection strong enough) such that mutation–selection balance is maintained (Charlesworth et al. 1993; Nicolaisen and Desai 2013; Zeng 2013). However, nonequilibrium demographic change may break such assumptions and forces other than selection may drive patterns of variation in regions experiencing selection at linked sites. For example, during the course of a population bottleneck, genetic drift may transiently dominate the effects of selection at many sites, such that traditional models of selection will poorly predict patterns of genetic diversity. Additionally, in regions affected by selection at linked sites, the impact of genetic drift may be exacerbated because of the lower $N_e$ in those regions, resulting in greater losses to diversity than expected by the action of demography alone. A recent review by Comeron (2017) included an initial investigation into the impact of demography on diversity in regions under BGS and suggested a dependency on demographic history. Recent empirical work in maize and humans has also demonstrated a strong interaction between demography and selection at linked sites (Beissinger et al. 2016; Torres et al. 2018). Yet these studies also demonstrate the need for a deeper understanding of the interactions between these forces, as they observe contrasting patterns of diversity in populations that have undergone a bottleneck and expansion.

To more fully explore the joint consequences of demography and selection at linked sites, in this study we conducted extensive simulations of different demographic models jointly with the effects of BGS. We find that the time span removed from demographic events is critical for populations experiencing nonequilibrium demography and can yield contrasting patterns of diversity that may reconcile apparently contradicting results (Beissinger et al. 2016; Torres et al. 2018). Additionally, the sensitivity of genetic diversity to demography is dependent on the frequency of the alleles being measured, with rare variants experiencing more rapid dynamic changes through time.

Our results demonstrate that traditional models of selection at linked sites may be poorly suited for predicting patterns of diversity for populations experiencing recent demographic change and that the predicted forces of BGS become apparent only after populations begin to approach equilibrium. Importantly, even simple intuition about the effect of selection at linked sites may lead to erroneous conclusions if populations are assumed to be at equilibrium. These results should motivate further research into this area, and support the use of models that incorporate the joint effects of both demography and selection at linked sites.

Materials and Methods

Simulation model

We simulated a diploid, randomly mating population using fwdpy11 v0.1.2a (https://github.com/molpopgen/fwdpy11), a Python package using the fwdpp library (Thornton 2014). Selection parameters for simulating BGS followed those of Torres et al. (2018), with deleterious variation occurring at 20% of sites across a 2-Mb locus and the selection coefficient, s, drawn from two distributions of fitness effects (DFEs). Specifically, 13% of sites were drawn from a gamma distribution (parameters: mean = $\alpha /\beta$, variance = $\alpha /{\beta }^2$) with $\alpha =0.0415$ and $\beta =80.11$, and 7% from a distribution with $\alpha =0.184$ and $\beta =6.25$. These distributions mimic the DFEs inferred across noncoding and coding sites within the human genome (Boyko et al. 2008; Torgerson et al. 2009). Fitness followed a purely additive model in which the fitness effect of an allele was 0, $0.5s$, and s for homozygous ancestral-, heterozygous-, and homozygous-derived genotypes, respectively. Per-base pair mutation and recombination rates also followed those of Torres et al. (2018) and were $1.66\times {10}^{-8}$ and $8.2\times {10}^{-10}$, respectively. We included a 200-kb neutral locus directly flanking the 2-Mb deleterious locus to observe the effects of BGS on neutral diversity. For all simulations, we simulated a burn-in period for 10 N generations with an initial population size of 20,000 individuals before simulating under 12 specific demographic models. The demographic models included one demographic model of a constant sized population (model 1), and 11 nonequilibrium demographic models incorporating bottlenecks and expansions (models 2–12; Table 1 and Supplemental Material, Figures S1–S2). For each demographic model, we also conducted an identical set of neutral simulations without BGS by simulating only the 200-kb neutral locus. Each model scenario was simulated 5000 times.

Table 1. Demographic parameters for models 1–12.

Demography type	Model	Ancestral population size (N $\left[N_{anc}\right]$)	Bottleneck/expansion population size (N)	Bottleneck duration ($N_{anc}$ generations)	Expansion duration ($N_{anc}$ generations)a	Final population size (N)
Constant	Model 1	20,000	NA	NA	NA	20,000
Bottleneck	Model 2	20,000	2,000	1	NA	2,000
Bottleneck	Model 3	20,000	400	1	NA	400
Expansion	Model 4	20,000	40,000	NA	1	40,000
Bottleneck expansion (ancient)	Model 5	20,000	2,000	0	1	200,000
Bottleneck expansion (ancient)	Model 6	20,000	400	0	1	200,000
Bottleneck expansion (ancient)	Model 7	20,000	2,000	0.05	0.95	200,000
Bottleneck expansion (ancient)	Model 8	20,000	400	0.05	0.95	200,000
Bottleneck expansion (recent)	Model 9	20,000	2,000	0	0.1	200,000
Bottleneck expansion (recent)	Model 10	20,000	400	0	0.1	200,000
Bottleneck expansion (recent)	Model 11	20,000	2,000	0.05	0.05	200,000
Bottleneck expansion (recent)	Model 12	20,000	400	0.05	0.05	200,000

^aPopulation expansion in models 5–12 is exponential, but in model 4 population expansion is instantaneous.

Diversity statistics and bootstrapping

After the burn-in period, we measured genetic diversity (π) and singleton density (ξ; the number of singletons observed within a window) within 10-kb windows across the 200-kb neutral locus every 50 generations using a random sample of 400 chromosomes. We measured π and ξ for each demographic model by taking the mean of these values across each set of 5000 replicate simulations. For neutral simulations, we annotated π and ξ as ${\pi }_0$ and ${\xi }_0$, respectively. We took the ratio of these statistics (i.e., $\pi /{\pi }_0$ and $\xi /{\xi }_0$) to measure the relative impact of BGS within each demographic model. We bootstrapped the diversity statistics by sampling with replacement the 5000 simulated replicates of each demographic model to generate a new set of 5000 simulations, taking the mean of π and ξ across each new bootstrapped set. We conducted 10,000 bootstrap iterations and generated confidence intervals (CIs) from the middle 95% of the resulting bootstrapped distribution.

Calculations of expected BGS

To calculate the predicted equilibrium $\pi /{\pi }_0$, we first used equation 14 of Nordborg et al. (1996) but modified it to incorporate two gamma DFEs. Additionally, to properly model our simulations, we only calculated the effects of BGS on one side of the selected locus. This resulted in the following modified equation:

$$\frac{N_e}{N}\equiv \frac{\pi }{{\pi }_0}=f\left(U_T,{\alpha }_T,{\beta }_T\right)\times f\left(U_B,{\alpha }_B,{\beta }_B\right)$$

The first term of the equation $\left(f\left(U_T,{\alpha }_T,{\beta }_T\right)\right)$ models the effects of BGS due to selection on noncoding sites according to the gamma DFE inferred by Torgerson et al. (2009), and the second term of the equation $\left(f\left(U_B,{\alpha }_B,{\beta }_B\right)\right)$ models the effects of BGS due to selection on coding sites according to the gamma DFE inferred by Boyko et al. (2008). Each of these is modeled following:

$$\begin{array}{l}f\left(U,\alpha ,\beta \right)=\\ exp\left(-\frac{U}{2R}{\displaystyle {\int }_C^{\mathrm{\infty }}\frac{1}{s}\left\{{\displaystyle {\int }_0^R\frac{dz}{{[1+r\left(z\right)\left(1-s\right)/s]}^2}}\right\}\text{Γ}\left(s,\alpha ,\beta \right)ds}\right)\end{array}$$

Here, R is the total length of the selected locus in base pairs, U is the total deleterious mutation rate across the selected locus, $r\left(z\right)$ is the genetic map distance between a neutral site and a deleterious mutation, and s is the selection coefficient of a deleterious mutation.

Because N is not explicitly included in this model of BGS, we followed previous work (Charlesworth 2012; Comeron 2014) in truncating selection at some value C (represented in the integral ${\int }_C^{\mathrm{\infty }}$). Here, C represents the minimum selection coefficient (s) that is treated as deleterious for the model. This step effectively excludes neutral mutations from the model that should not contribute to BGS and can be modulated to mimic small or large populations (by increasing or decreasing C, respectively). This truncation step also affects the values used for U, resulting in specific values for each DFE. We simulated different population sizes to equilibrium under our BGS simulation model to see how well the modified version of the classic model fitted populations of different N for different values of C (Figure S3). Despite the fact that our simulations potentially break assumptions of the model (e.g., mutation–selection balance, mutant alleles at frequencies rare enough that higher-order terms can be ignored, and multiplicative fitness effects across loci), we observed a generally good fit of our resulting observed $\pi /{\pi }_0$ to the expectations of Nordborg et al. (1996) (Figure S3).

Because no single value of C provided an estimate of BGS that was robust to the population sizes simulated in our demographic models, we also fitted a log-linear model to the observed values of $\pi /{\pi }_0$ for varying sizes of N (Figure S3). The resulting best-fit model to the observed data was:

$$\frac{\pi }{{\pi }_0}=-0.08121ln\left(N\right)+1.39370$$

For each generation of our demographic models, we calculated the long-term effective population size $\left(N_e\right)$ by applying the following equation:

$$N_e=\frac{\pi }{4\mu }$$

Here, we substituted the mutation rate used in our simulations for μ $\left(1.66\times {10}^{-8}\right)$. For π, we used the mean observed per-site diversity across the 200-kb neutral region from each set of 5000 neutral simulations (i.e., ${\pi }_0$).

Using the fitted log-linear model of population size and $\pi /{\pi }_0$ and the calculations of long-term $N_e$ described above, we also estimated $\pi /{\pi }_0$ for each generation in our demographic models by substituting the estimated long-term $N_e$ for N in $-0.08121ln\left(N\right)+1.39370$.

Data availability

Simulation and analysis code are available at https://github.com/RILAB/BGS_sims/. Supplemental material available at figshare: https://doi.org/10.25386/genetics.11854242.

Results

BGS under instantaneous population size change

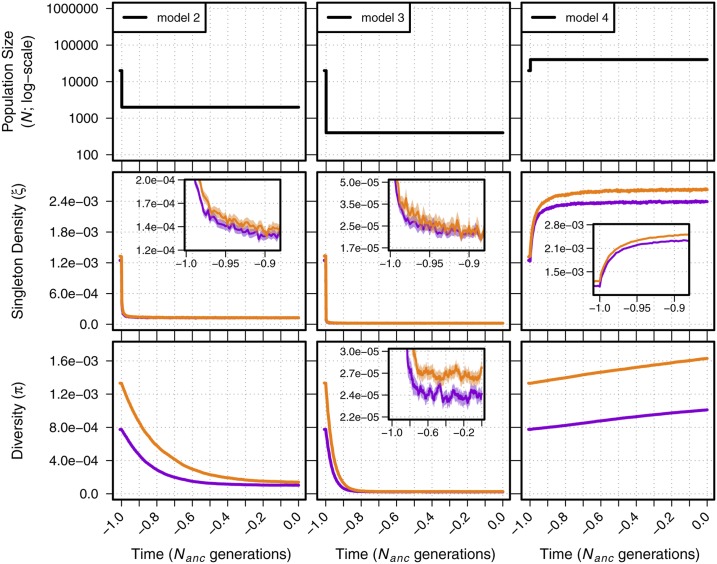
We first present the joint effects of demography and BGS under simple demographic models with a single instantaneous change in size (models 2–4; Figure S1). While our simulations incorporated a 200-kb neutral region, we first focused on patterns of diversity generated within the 10-kb window nearest to the 2-Mb locus experiencing purifying selection, as this is where BGS is strongest. Doing so allowed us to observe any change in the dynamics of ξ and π as they approached new population equilibria resulting from a change in size. In the simple bottleneck models (models 2–3), we observed the expected strong decrease in ξ and π following population contraction in models of both BGS and neutrality (Figure 1). Similarly, we observed the expected rapid increase in ξ compared to π in our model of a simple population expansion (model 4; Figure 1). In all cases, values of ξ and π were lower in models with BGS, and changed more quickly relative to their initial value when compared to the neutral case (Figure S4).

Figure 1.

Singleton density (ξ per site) and diversity (π per site) for models 2–4. The top panel shows each demographic model; time proceeds forward from left to right and is scaled by the N of the population at the initial generation ($N_{anc}$; 20,000 individuals). Diversity statistics are shown for neutral simulations (orange lines) and simulations with background selection (violet lines). Insets show diversity using a log scale for detail. Envelopes are 95% CIs calculated from 10,000 bootstraps of the original simulation data.

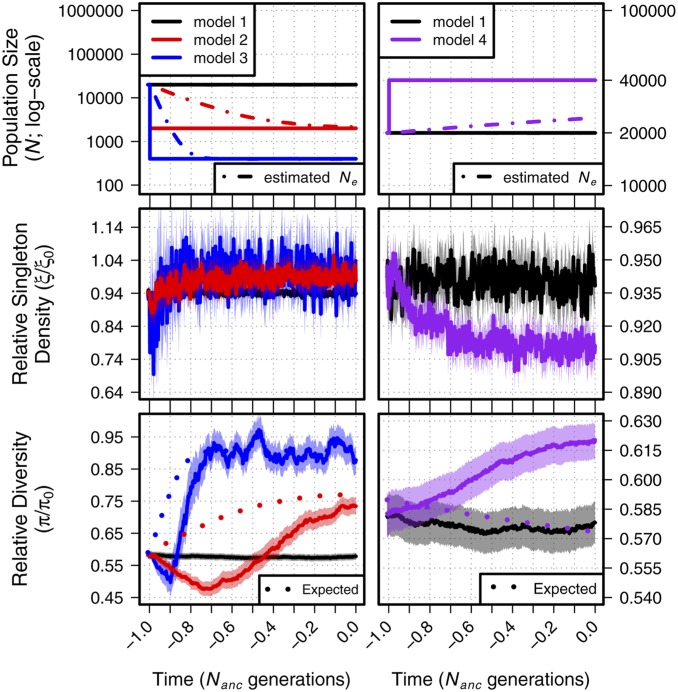
To examine the interaction of demography and selection observed in empirical data (Beissinger et al. 2016; Torres et al. 2018), we normalized π and ξ in models of BGS by their equivalent statistics in models of neutrality (i.e., ${\pi }_0$ and ${\xi }_0$). We observed that $\pi /{\pi }_0$ and $\xi /{\xi }_0$ were dynamic through time in response to demography, with changes occurring to both their magnitude and direction (Figure 2). Moreover, changes to $\xi /{\xi }_0$ occurred more rapidly through time compared to $\pi /{\pi }_0$. For example, in model 2 we observed a dip and rise in the $\xi /{\xi }_0$ statistic relative to equilibrium (model 1) within the first $\approx 0.1N_{anc}$ generations ($N_{anc}$ refers to the size of the ancestral population prior to any demographic change). Yet, for the same model, $\pi /{\pi }_0$ remained depressed for over 0.5 $N_{anc}$ generations. Similar patterns were observed for model 3, which experienced a greater reduction in size, although the pattern is less clear because of the greater sampling variance of $\xi /{\xi }_0$ due to the overall lower number of singletons. In both population contraction models, $\pi /{\pi }_0$ and $\xi /{\xi }_0$ appeared to plateau at levels above that of the equilibrium model (model 1). In contrast, we observed markedly different dynamics in our model of a simple population expansion (model 4). This included a sustained increase in $\pi /{\pi }_0$ but only a transient increase in $\xi /{\xi }_0$, which dropped below the equilibrium model within the first $\approx 0.1N_{anc}$ generations.

Figure 2.

Relative singleton density $\left(\xi /{\xi }_0\right)$ and relative diversity $\left(\pi /{\pi }_0\right)$ across time for demographic models 1–4. The top panel shows each demographic model; time proceeds forward from left to right and is scaled by the N of the population at the initial generation ($N_{anc}$; 20,000 individuals). Dot-dashed lines in the top panels show the estimated $N_e$ from observed ${\pi }_0$. Dotted lines in the bottom panel show the equilibrium expectation of $\pi /{\pi }_0$ from a log-linear model of simulated background selection with the specific selection parameters and the estimated $N_e$ at each time point (see Figure S3). Envelopes are 95% CIs calculated from 10,000 bootstraps of the original simulation data.

Changes in population size should lead to changes in the rate of genetic drift and the efficacy of natural selection and, thus, changes in the magnitude of BGS over time. Indeed, under equilibrium conditions (and if mutations that are effectively neutral can be ignored), the classic model of BGS (Nordborg et al. 1996) predicts weaker BGS (with higher $\pi /{\pi }_0$) for smaller populations and stronger BGS (with lower $\pi /{\pi }_0$) for larger populations (Figure S3). To compare these predictions to those of our simple demographic models, at each generation for each model we calculated $\pi /{\pi }_0$ using a log-linear model fitted to predict $\pi /{\pi }_0$ from N (see Materials and Methods). In all three simple demographic models, we observed that changes in $\pi /{\pi }_0$ over the short-term differed qualitatively from the predicted $\pi /{\pi }_0$ of the log-linear model (Figure 2; bottom panels). While the log-linear model predicts a higher value for $\pi /{\pi }_0$ in a smaller population, we observed a transient drop in $\pi /{\pi }_0$ directly after a contraction (models 2 and 3). Similarly, the log-linear model predicts a decrease in $\pi /{\pi }_0$ in larger populations, but we instead observed an increase in $\pi /{\pi }_0$ with a population expansion (model 4). The trajectory of observed $\pi /{\pi }_0$ changed in our bottleneck models, eventually approaching the higher values predicted by the log-linear model and in line with the overall predictions of the classic model of BGS. In contrast, $\pi /{\pi }_0$ in the expansion model continued to increase over the entire course of the simulation. To test if and when $\pi /{\pi }_0$ for the expansion model reaches the lower value predicted by the log-linear model, we ran a limited set of simulations (2000 total) for 11 $N_{anc}$ generations. We found that, indeed, $\pi /{\pi }_0$ plateaued and then decreased relative to its starting value, eventually approaching the prediction of the log-linear model after ≈ 10 $N_{anc}$ generations (Figure S5). This was because π plateaus more slowly under neutrality when compared to π under BGS (Figure S6). Only once π under neutrality began to approach equilibrium did we begin to observe the prediction of the log-linear model.

To test whether stronger or weaker selection changes the overall patterns we observed from our simulations using two DFEs, we also conducted simulations with s drawn from a point distribution $\left(\gamma =2N_{anc}s=\left\{0.1,0.5,2,5,10,50,100\right\}\right)$ for models 3 and 4. The results displayed broadly similar patterns, but with differing degrees of change in $\pi /{\pi }_0$ or $\xi /{\xi }_0$ depending on the strength of selection (Figure S7). For model 3, $\pi /{\pi }_0$ increased as before when the population approached equilibrium, stabilizing near 1 except under models with the strongest selection. However, the immediate decrease in $\pi /{\pi }_0$ that was seen in Figure 2 directly after a population contraction was much less evident in these simulations and essentially absent in models with stronger selection. For $\xi /{\xi }_0$, patterns were both more dynamic and more closely matched those of Figure 2, with rapid transient decreases and increases occurring shortly after a contraction (model 3) or expansion (model 4), respectively.

BGS under bottleneck-expansion models

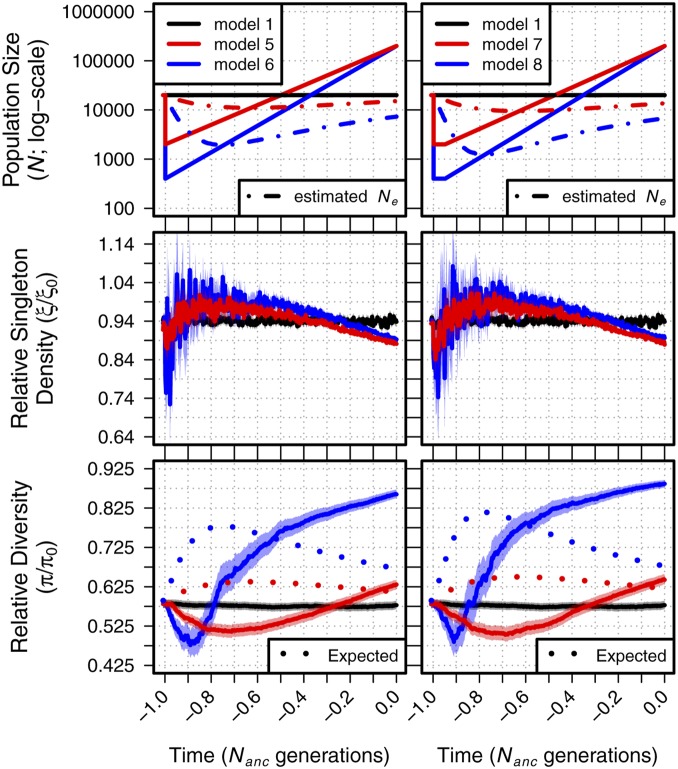
We built upon the simple two epoch demographic models to test more complex scenarios and better understand the relative effects of different events on patterns of diversity under BGS. Specifically, we simulated a population undergoing a contraction similar in size to models 2 and 3 but with a subsequent expansion to 400,000 individuals by the final generation (Figure S2 and Table 1). These bottleneck-expansion models included both ancient (1.0 $N_{anc}$ generations in the past; models 5–8) and recent (0.1 $N_{anc}$ generations in the past; models 9–12) bottleneck events, with either an immediate return to growth (models 5–6 and 9–10) or a sustained contraction (models 7–8 and 11–12).

These models recapitulated several patterns observed in our simple bottleneck models but with added dynamics. In all cases, diversity in models with BGS was both lower (Figures S8 and S9) and changed more rapidly (Figures S10 and S11) than in neutral simulations. Changes in diversity also occurred more quickly in models with a stronger or sustained bottleneck, and ξ again exhibited more rapid dynamics than π. Mirroring results from our simple bottleneck scenarios, models with an ancient bottleneck (models 5–8) showed transient decreases in $\xi /{\xi }_0$ and $\pi /{\pi }_0$ followed by increases to higher values (Figure 3). Longer-term changes in $\pi /{\pi }_0$ contrast with the expectations of the log-linear and classic models, in which BGS is expected to become more efficient in growing populations and result in a decrease in $\pi /{\pi }_0$ through time (Figure 3, dotted lines). While both $\pi /{\pi }_0$ and $\xi /{\xi }_0$ remained elevated in our simple bottleneck models in Figure 2, $\xi /{\xi }_0$ in the bottleneck-expansion models of Figure 3 shifts direction during the course of the expansion and begins to decline, eventually reaching values below that of the equilibrium population. Finally, because of the added complexity of the expansion following the population bottleneck, it is also likely that the increase in $\pi /{\pi }_0$ for these models later in their demographic histories is also recapitulating the similar dynamics witnessed for model 4.

Figure 3.

Relative singleton density $\left(\xi /{\xi }_0\right)$ and relative diversity $\left(\pi /{\pi }_0\right)$ across time for demographic models 1 and 5–8. The top panel shows each demographic model; time proceeds forward from left to right and is scaled by the N of the population at the initial generation ($N_{anc}$; 20,000 individuals). Dot-dashed lines in the top panels show the estimated $N_e$ from observed ${\pi }_0$. Dotted lines in the bottom panel show the equilibrium expectation of $\pi /{\pi }_0$ from a log-linear model of simulated background selection with the specific selection parameters and the estimated $N_e$ at each time point (see Figure S3). Envelopes are 95% CIs calculated from 10,000 bootstraps of the original simulation data.

Though the trajectories of $\pi /{\pi }_0$ and $\xi /{\xi }_0$ were truncated for models in which the bottleneck occurred in the recent past (models 9–12; 0.1 $N_{anc}$ generations), they nonetheless appeared to behave qualitatively similar to the ancient bottleneck models (Figure S12). However, it is worth noting that because of the difference in timescale, the ending values of $\xi /{\xi }_0$ and $\pi /{\pi }_0$ from the recent bottleneck models were in the opposite direction relative to model 1 when compared to models with longer demographic histories (i.e., models 5–8).

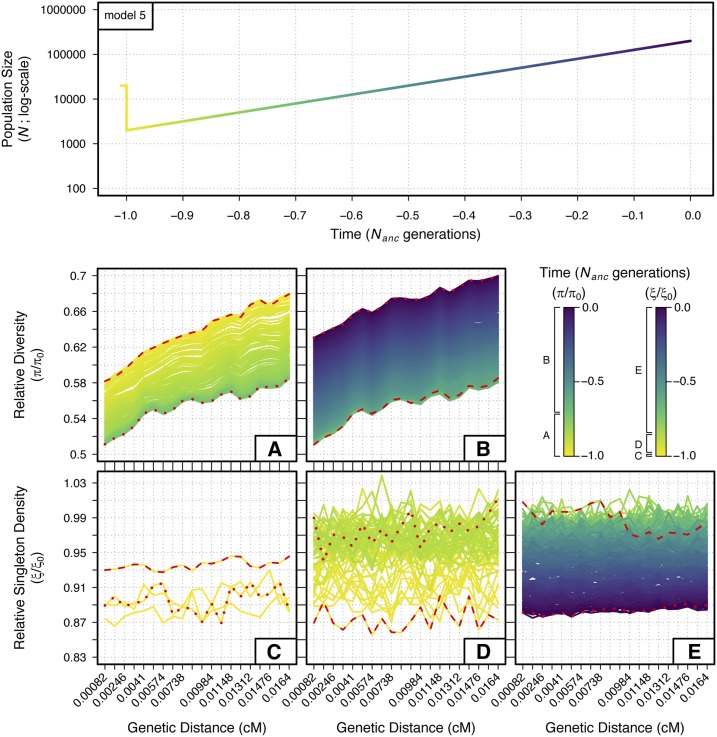
Patterns of diversity across the 200 kb neutral region

We also measured patterns of $\pi /{\pi }_0$ across time for the entire 200-kb neutral region. Doing so showed the characteristic “trough” structure of increasing relative diversity as a function of genetic distance from the deleterious locus (model 5 is shown in Figure 4, see Figure S13 for all models). Change in $\pi /{\pi }_0$ over time generally followed patterns observed in the neutral window closest to the selected region. In all of our ancient bottleneck models (models 2–3 and 5–8), for example, we see a decline in $\pi /{\pi }_0$ across the entire region followed by an increase to levels higher than in the ancestral population. For recent bottlenecks (models 9–12), we see a consistent decline with no recovery, and in our simple expansion model (model 4) $\pi /{\pi }_0$ increases monotonically through time.

Figure 4.

Temporal and spatial dynamics of relative diversity $\left(\pi /{\pi }_0\right)$ and singleton density $\left(\xi /{\xi }_0\right)$ under a bottleneck with expansion (model 5) across a neutral 200-kb region. The genetic distance of each 10-kb bin from the selected locus is indicated on the x-axes of the bottom panels. Each line measuring $\pi /{\pi }_0$ and $\xi /{\xi }_0$ in the bottom panels represents one of the 401 discrete generations sampled from the demographic model; colors follow the demographic model in the top panel (time is scaled as in Figure 1, Figure 2, and Figure 3) and in the figure legend. Multiple plots are given to prevent overlap of the measurements between generations. (A and B) show $\pi /{\pi }_0$ through time from −1.0 to −0.71 $N_{anc}$ (A) and −0.71 to 0.0 $N_{anc}$ (B) generations. (C–E) show $\xi /{\xi }_0$ through time from −1.0 to −0.99 $N_{anc}$ (C), −0.99 to −0.85 $N_{anc}$ (D), and −0.85 to 0.0 $N_{anc}$ (E) generations. Red dashed lines and red dotted lines indicate the first and last generations measured within each plot, respectively.

Yet, these general patterns obscure more subtle changes to the slope of $\pi /{\pi }_0$ in the trough structure. In models with a stronger bottleneck (models 3, 6, and 8), where we expect the efficacy of selection to be most affected in the long-term, we see that the slope $\pi /{\pi }_0$ flattens over time, completely erasing the trough of diversity in the most extreme case without a recovery (model 3).

Finally, while $\xi /{\xi }_0$ across the region largely followed patterns seen in the neutral window most proximal to the selected locus, a closer look across the 200-kb regions of most models yielded no clear patterns. Troughs were slightly apparent for the final generations of some models (models 5 and 7), but the stochasticity among 10-kb windows for $\xi /{\xi }_0$ swamped any other patterns that might otherwise be evident.

Discussion

General patterns of diversity

A long history of both theoretical (Nei et al. 1975; Maruyama and Fuerst 1984, 1985) and empirical (Begun and Aquadro 1992; Cavalli-Sforza et al. 1994; Eyre-Walker et al. 1998) population genetics work has provided a clear picture of the impacts of demographic change on patterns of diversity in the genome. We know, for example, the impact of simple bottleneck and growth models on the allele frequency spectrum (Tajima 1989; Slatkin and Hudson 1991; Griffiths and Tavaré 1994). Theory also offers clear direction on the long-term effects of decreases in effective population size on the efficacy of natural selection (Ohta 1973; Kimura 1983). Likewise, classical theory on BGS provides a solid expectation for the effects of selection at linked sites on diversity in populations at demographic equilibrium (Nordborg et al. 1996). For instance, the reduction in genetic diversity under the influence of BGS increases with increasing population size in equilibrium populations (Nordborg et al. 1996; Figure S3).

Despite these efforts, there have been surprisingly few investigations addressing the expected patterns from the interaction of demography and selection at linked sites in the context of BGS (Nicolaisen and Desai 2013; Zeng 2013; Ewing and Jensen 2016; Comeron 2017; Rettelbach et al. 2019). There also remains substantial confusion in empirical population genetic analyses, with authors often equating long-term predictions of change in effective population size on the efficacy of natural selection to short-term responses under nonequilibrium demography (Brandvain and Wright 2016). Here, we use simulations and analysis of different demographic models, with and without BGS, to show that predictions from such equilibrium models generally fail to hold up over shorter timescales. We find that the predicted impacts of the combined effects of demography and selection at linked sites depend strongly on the details of the demographic model, as well as the timing of sampling.

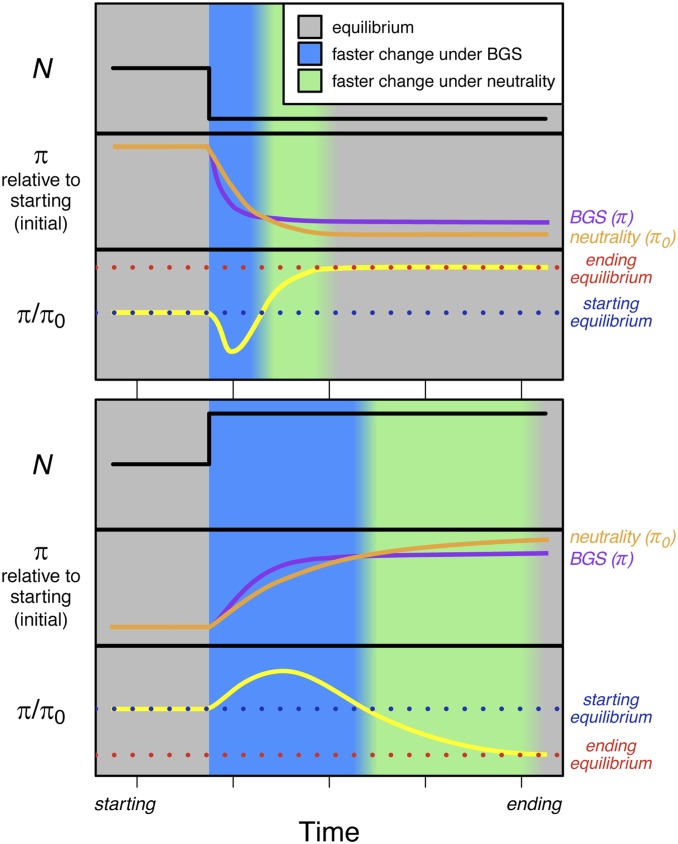
In each of our models, the initial effects observed are driven primarily by the stochastic effects of drift. For example, the loss of relative diversity in the first few generations occurs equally across the entire region after a population decline, independent of the distance from the selected region (Figure S13). This is because the effects of demographic change to diversity occur more rapidly under BGS than under neutrality (Figure 5). Thus, while equilibrium models predict that the effects of BGS should be attenuated in populations with lower $N_e$ due to the decreased efficacy of purifying selection, we instead observed a drop in $\pi /{\pi }_0$ after the bottleneck and a more rapid decrease in models with a stronger bottleneck (Figure 2 and Figure 3). Similarly, while theory predicts a decrease in $\pi /{\pi }_0$ in larger populations, we instead observed that the initial response after a population expansion was an increase in $\pi /{\pi }_0$ (Figure 2), reflecting the more rapid increase in diversity under BGS. These observations make it clear that the combined effects of demography and BGS on $\pi /{\pi }_0$ immediately following a change in $N_e$ are not driven by a change in the efficacy of natural selection, but rather by the more rapid change in diversity under BGS.

Figure 5.

Schematic of the temporal dynamics of diversity under neutrality (${\pi }_0$; orange lines) and BGS (π; violet lines) for a demographic bottleneck and an expansion. Relative diversity ($\pi /{\pi }_0$; yellow lines) is shown in the bottom section of each figure panel, with equilibrium points before demographic change (blue dotted lines) and after demographic change (red dotted lines) shown. Background colors represent epochs of time where the change in diversity is faster under BGS (blue) or neutrality (green). BGS, background selection.

Although the initial changes in diversity are dominated by the impacts of demography, as population size shifts, the efficacy of natural selection begins to change as well. In our simple bottleneck models, $\pi /{\pi }_0$ stops declining and begins to increase, eventually reaching higher values as expected under equilibrium (Figure 2). This change reflects the inability of a smaller population to select against new deleterious mutations, rendering these alleles effectively neutral and decreasing the effects of BGS. These effects are countered in larger, growing populations, which is presumably why we see the rate of increase of $\pi /{\pi }_0$ slow and eventually plateau in models incorporating both bottlenecks and growth (Figure 3). In addition, the rate of change in $\pi /{\pi }_0$ is also diminished, with slower approaches to equilibrium taking place as a function of larger population size. Indeed, in our simple expansion model, patterns of diversity approach equilibrium expectations only after $\approx 10N_{anc}$ generations (Figure S5).

Changes in the efficacy of selection are also readily observed in comparisons of relative diversity across windows varying in recombination distance from the selected region (Figure S13). In the ancestral population, diversity increases with distance from the selected region, as expected under the classic model of BGS at equilibrium (Nordborg et al. 1996) and observed in previous studies (Hernandez et al. 2011; Beissinger et al. 2016). But while the slope of this relationship remains constant in the generations initially following a population size change, for our simple bottleneck models it begins to flatten through time, reflecting a lowered effective population size and a concomitant weakened efficacy of natural selection (Figure S13; models 2–3).

The diversity-reducing effects of BGS have often been modeled as a reduction in $N_e$ (Charlesworth et al. 1993), though we caution that the effects of BGS on the site frequency spectrum (SFS) cannot be simplified to this extent (Cvijović et al. 2018). Like a reduction in $N_e$, BGS also exacerbates the stochastic process of drift. Because the relevant timescale for allele frequency evolution is scaled by the rate of drift (Crow and Kimura 1970), both the reduction and recovery of diversity to equilibrium levels happen over fewer generations in populations with stronger bottlenecks and in regions impacted by BGS. We see this borne out in comparisons of models with stronger (Figure 2) or more sustained (Figure 3) bottlenecks, as well as comparisons of models with BGS to their equivalent neutral scenarios (Figures S4, S6, S10, and S11). This differential scaling also contributes to the observed lag in time in reaching equilibrium for neutrality relative to BGS (Figure 5) and the slower rate of change observed in expanding populations (Figure 3), since increases in the effective size attenuate the rate of drift.

The timing and magnitude of changes in diversity also depend on the range of allele frequencies assayed. We demonstrate this by analyzing changes in singleton density (ξ) along with overall patterns of nucleotide diversity. Because singleton variants represent very recent mutations, changes in $\xi /{\xi }_0$ respond more quickly to changes in N. In our simple expansion model, for example, while $\pi /{\pi }_0$ increases for $\approx 2N_{anc}$ generations (Figure S5), we see a relatively rapid increase in $\xi /{\xi }_0$ followed by a decrease as the larger population size increases the efficacy of selection against new deleterious mutants. And while theoretical predictions for $\xi /{\xi }_0$ are not as straightforward [because of the dependency of distortions to the SFS on sample size (Cvijović et al. 2018)], singleton density in the simple expansion model quickly stabilizes at a new value below that of the ancestral population, consistent with having reached a new equilibrium value. However, signals using rare frequency bins such as ξ are inherently more difficult to capture, partly because they are less affected than π, since BGS perturbs common frequency bins of the SFS more than rare ones (Cvijović et al. 2018). In addition, we observe much higher variance for $\xi /{\xi }_0$ compared to $\pi /{\pi }_0$.

Finally, although we have simulated only one complex DFE under a mixture distribution of selection coefficients for new mutations (see Materials and Methods), this distribution will also play an important role in determining the threshold above which new mutations contribute to the effects of selection at linked sites. For example, while our DFE had a mean of $2N_{anc}s=424$, it is also characterized by an extremely long tail and ≈ 75% of deleterious mutations will only have a $s\le {10}^{-3}$, which is equivalent to $2N_{anc}s=40$. These features add additional complexity to both the initial and long-term dynamics of diversity after demographic change when compared to simulations of BGS using a single value of s (Figure S7). In simulations using our wide DFE, the transient drop in $\pi /{\pi }_0$ following a contraction was stronger than in simulations using a single s, but the long-term qualitative results differed as well: $\pi /{\pi }_0$ was initially higher than models where $2N_{anc}s$ = {2, 5, 10}, but was lower after the population reached its new equilibrium. Thus, it is clear that the details of both the short- and long-term changes in diversity as a result of the interaction of demography and selection will depend on features of the DFE as well.

Conflicting signals in maize and humans

One of the motivations for the work presented here is the fact that empirical analyses evaluating the impact of demography on selection at linked sites have come to conflicting conclusions (Beissinger et al. 2016; Torres et al. 2018). Beissinger et al. (2016) compared domesticated maize to its wild ancestor teosinte, finding higher $\pi /{\pi }_0$ but lower $\xi /{\xi }_0$. In a similar analysis in humans, Torres et al. (2018) found lower $\pi /{\pi }_0$ but higher $\xi /{\xi }_0$ in non-African compared to African populations.

The fact that both maize and non-African human populations have undergone a population bottleneck and expansion over a similar timescale (on the order of $\approx 0.1N_{anc}$ generations) makes the contrasting results from these papers initially somewhat surprising. But despite their qualitatively similar demographies, there are a number of factors that complicate direct comparison between humans and maize, and highlight difficulties in inferring the action of selection at linked sites in empirical data. For example, while the domestication process in maize is widely thought to have led to a population bottleneck and subsequent expansion (Eyre-Walker et al. 1998; Tenaillon et al. 2004; Wright et al. 2005; Beissinger et al. 2016; Wang et al. 2017; Bellon et al. 2018), there is little agreement on the magnitude and timing of these effects, and estimates of the modern maize population vary by several orders of magnitude. And while the estimated demography of African populations is relatively stable compared to that of non-Africans (Torres et al. 2018), the demography of teosinte is not well understood but is likely to include substantial nonequilibrium dynamics (Wang et al. 2017). The distribution of fitness likely differs between the species as well. Compared to the mixture of two DFEs used by Torres et al. (2018), the best-fit gamma distribution for the only published DFE estimated for maize exhibits a nearly 10-fold higher mean (Pophaly and Tellier 2015). Finally, the distribution of functional sites in the genome differs between humans and maize; genes are longer in humans, leading to smaller intergenic spaces and perhaps shorter average distances to the nearest functional site.

Nonetheless, simulations combining demography and BGS highlight plausible scenarios that could result in the differences seen between maize and humans. In models 9–10 (Figure S12), for example, patterns of diversity $\approx 0.1N_{anc}$ generations after the bottleneck qualitatively match those of Torres et al. (2018), with $\pi /{\pi }_0$ lower and $\xi /{\xi }_0$ higher than seen in the ancestral population. In their simulations of a genic region using a single s, Beissinger et al. (2016) found no differences in $\pi /{\pi }_0$ between maize and teosinte, but much lower $\xi /{\xi }_0$, providing some evidence to support their observed findings. As demographic inferences come with uncertainty, it is possible that the population bottleneck during maize domestication was potentially weaker or that the expansion began much sooner. In such a case, something closer to our model 4 (Figure 2) might be a reasonable comparison. Indeed, in that scenario, $0.1N_{anc}$ generations after the expansion we see $\pi /{\pi }_0$ has increased and $\xi /{\xi }_0$ decreased compared to the ancestral population, similar to the observations of Beissinger et al. (2016). However, improved sampling, and more careful modeling of both demography and the DFE, is likely required to demonstrate whether the observed results in maize can be entirely explained by the interaction of BGS and demography.

Implications for empirical data

Combined with our simulation results, the difficulty of interpreting what appear to be straightforward differences between maize and humans suggests that inferences about selection at linked sites from empirical data are likely to be difficult without careful consideration of demography. Most of the work to date using either theory (e.g., Corbett-Detig et al. 2015; Elyashiv et al. 2016; Rettelbach et al. 2019) or simulation (Stankowski et al. 2019) makes use of classic equations that assume populations are at equilibrium. While the rank order of expected diversity in windows along the genome does not change in our models, the magnitude of these differences, and even the relationship between $\pi /{\pi }_0$ and recombination, change over time (Figure S13) and may be further obscured by the stochastic effects of drift, highlighting the importance of incorporating demography into models that use such information to make inference about selection at linked sites.

Given these complexities, what considerations should researchers interested in empirical analysis keep in mind? While simulation results suggest that BGS is unlikely to strongly affect the ability to detect outliers via selection scans using $F_{ST}$ (Matthey-Doret and Whitlock 2019), we argue here against using simple approximations based on equilibrium models to infer the relative importance of demography and selection in patterning diversity along the genome. For researchers interested in assessing the impacts of demography and selection at linked sites, we first recommend estimation of demographic history using regions of the genome in which the effects of BGS are expected to be minimal [using the approach of McVicker et al. (2009), for example], since BGS itself can impact the estimation of demographic history (Pouyet et al. 2018). Using diversity data from such regions, researchers can then estimate a more accurate demographic model. Care should be taken to simulate data under the estimated model to ensure it fits reasonably well with observations. Following the general trends outlined here (e.g., Figure 5) should then allow qualitative predictions about the impacts of demography and selection at linked sites. However, we caution that quantitative predictions will require simulations using a range of plausible DFEs with a genome structure relevant for the species of interest.

Finally, it is worth noting that our results are relevant not just for comparisons of π across regions with strong and weak effects of selection at linked sites, but also apply to comparisons of selected and neutral polymorphisms. Indeed, similar patterns have been observed for comparisons of selected and putatively neutral polymorphisms in both simulations and empirical data (Do et al. 2015; Simons and Sella 2016; Koch and Novembre 2017), and further demonstrate that differential dynamics of diversity in response to demography are ubiquitous across the genome.

Conclusions

Genetic diversity across the genome is determined by the complex interplay of mutation, demographic history, and the effects of both direct and linked natural selection. While each of these processes is understood to a degree on its own, in many cases we lack either theory or sufficient empirical data to capture the effects of their interaction. Selection at linked sites, in particular, is increasingly recognized as perhaps the primary determinant of patterns of diversity along a chromosome (Comeron 2014; Stankowski et al. 2019), but our ability to infer its impact is often complicated by changes in population size. However, many studies interested in these dynamics make the simplifying assumption that selection at linked sites in such nonequilibrium populations can be effectively modeled using classic theory and scaling of the effective population size. Our extensive simulations show that, in the context of purifying selection, this is not the case. We find that the relationship between selection at linked sites and demographic change is complex, with short-term dynamics often qualitatively different from predictions under classic models. These results suggest that inferring the impact of population size change on selection at linked sites should be undertaken with caution, and is only really possible with a thorough understanding of the demographic history of the populations of interest.