Abstract
The propagations of diseases, behaviors and information in real systems are rarely independent of each other, but they are coevolving with strong interactions. To uncover the dynamical mechanisms, the evolving spatiotemporal patterns and critical phenomena of networked coevolution spreading are extremely important, which provide theoretical foundations for us to control epidemic spreading, predict collective behaviors in social systems, and so on. The coevolution spreading dynamics in complex networks has thus attracted much attention in many disciplines. In this review, we introduce recent progress in the study of coevolution spreading dynamics, emphasizing the contributions from the perspectives of statistical mechanics and network science. The theoretical methods, critical phenomena, phase transitions, interacting mechanisms, and effects of network topology for four representative types of coevolution spreading mechanisms, including the coevolution of biological contagions, social contagions, epidemic–awareness, and epidemic–resources, are presented in detail, and the challenges in this field as well as open issues for future studies are also discussed.
Keywords: Complex networks, Coevolution spreading, Critical phenomena, Biological contagions, Social contagions, Resource allocation, Awareness diffusion
1. Introduction
Propagations in many real-world systems can be theoretically described by spreading dynamics, with infectious disease, computer viruses, information, innovation, financial risk, and many others being treated as “epidemics” [1], [2], [3], [4], [5]. When investigating spreading dynamics, scientists wish to understand certain important aspects, such as what are the dynamical mechanisms behind the phenomena, whether there will be an outbreak, how many individuals will be infected, when will an individual be infected, and how to effectively predict and contain the spread. Addressing these problems provides many beneficial aspects for our society. For governments, the situations of epidemics could be apperceived, and effective containment measures could be provided [6]. For e-commerce, certain personalized recommendation strategies could be designed to promote the diffusion of products (e.g., popular clothing) [7]. For economics, financial risks may be perceived at an early stage and thus global economic crises could be evaded to some extent [8].
To address these problems, scientists have already made great efforts since the first mathematical approach to study the spread of an infectious disease by Bernoulli in 1760 [9]. Historically, the single spreading dynamics was placed in a well-mixed population, without any differences among individuals [4], [10]. Following this idea, researchers can theoretically predict the outbreak size, critical threshold, and associated critical phenomena. However, in reality, an individual only has contacts with a limited number of other individuals. This constraint can be characterized by a network , where and are sets of nodes and edges, with nodes representing individuals and edges denoting interactions between individuals. Accordingly, scientists studied the single spreading dynamics on oversimplified networks (e.g., regular networks and Erdös–Rényi (ER) [11] random networks), and analytically obtained the outbreak threshold and epidemic prevalence [12].
The above analytical results are usually far from empirical observations, because real networks are much more complex than the oversimplified models. For example, the node degree (i.e., the number of edges of a node) can vary over a few orders of magnitude, exhibiting a highly heterogeneous nature [13]. Other frequently observed features that cannot be well captured by the oversimplified models include the small-world property [14], community structure [15], multiplexity [16], spatiality [17], temporality [18], and so on. In a pioneering work [19], Pastor-Satorras and Vespignani studied a single infectious virus on networks with power-law degree distribution (named as scale-free (SF) networks), and revealed that there is no epidemic threshold for a specific range of the degree exponent. Following this work, researchers found the spreading dynamics, such as for a global infectious disease, can be better predicted by accounting for more topological features of real networks [20], [21]. Many reviews and books have already summarized the state-of-the-art progress in single dynamics [22], [23], [24], [25], [26], [27], [28], [29].
The propagations of diseases, behaviors, and information in the real world are rarely independent of each other; rather, they are coevolving with strong interactions. Coevolution spreading exists widely, with important practical relevance [30]. For example, HIV results in the lower immunity of virus carriers, who are therefore more susceptible to infectious diseases such as tuberculosis and hepatitis [31], [32]. The propagation of disease-related information in social media could largely suppress the spreading of the corresponding epidemic disease [33]. In an extremely important case, in the early stage of the spreading of the severe acute respiratory syndrome (SARS) in China, an unofficial message entitled “There is a fatal flu in Guangzhou” was sent to tens of millions of individuals [34]. As a result, individuals adopted simple but effective actions (e.g., staying home or wearing face masks) to protect themselves from being infected by SARS, which greatly decreased the final number of infected individuals. Scientists have already made efforts to uncover and understand the interaction mechanisms, spatiotemporal evolution patterns, critical phenomena, and phase transitions of networked coevolution spreading. The complex interactions during the coevolving dynamics lead to rich phase transition phenomena and novel physics, such as coexistence thresholds caused by competitive interactions [35] and discontinuous phase transition caused by synergetic interactions [36]. In addition, the multiscale structure of networks remarkably affects not only the value of thresholds, but also the critical exponents [37] and the type of phase transitions [38] of spreading dynamics. Therefore, the coevolution spreading dynamics on complex networks has attracted increasing attention in recent years.
There are three reasons for us to write this review. First, a large number of papers about coevolution spreading dynamics have emerged recently, but there is still a lack of a comprehensive review to systematically organize these results, discuss major challenges at the current stage, and point out open issues for future studies. Second, the early literature used different expressions to describe essentially the same mathematical problems and methods. It is thus urgent to unify the problem description and the symbolic system. Third, researchers have already tried to find certain potential applications, but these application possibilities are scattered in disparate fields, and lack integration. Accordingly, this review will be helpful to researchers already in the field, those who intend to enter the field, and those who wish to apply the related findings, and it will also contribute to the further development of the field.
In what follows, we will introduce the progress of studying the coevolution spreading on complex networks, including theoretical methods, critical phenomena, phase transitions, interaction mechanisms, effects of network topology, and so on. Four representative types of networked coevolution spreading are considered, including the coevolution of biological contagions, social contagions, awareness–epidemic and resources–epidemic. In Section 2, we introduce the coevolution spreading of biological contagions, in which each contact between susceptible and infected nodes may trigger the transmission of the infection. We mainly focus on the most representative biological contagions, i.e., epidemic spreading. However, in the spreading processes for political information, innovative products, and new drugs, a single contact is insufficient to eliminate the risk of adoption for susceptible individuals, and thus multiple contacts are necessary. The coevolution spreading of social contagions is presented in Section 3, which focuses on the spreading dynamics involving the above social reinforcement effects. To contain the epidemic, certain coevolution spreading strategies are developed. In Sections 4, 5, we respectively introduce the coevolution of awareness and an epidemic, and the coevolution of resources and an epidemic. Finally, in Section 6 we sketch the landscape of this emerging field, summarize representative progress, and make discuss the outlooks of the current challenges and future open issues of the field.
2. Coevolution of biological contagions
Empirically, epidemic spreading, virus spreading, and information diffusion are usually modeled as biological contagions, where a single activated source can be sufficient for infection transmission. Susceptible–infected–susceptible (SIS) and susceptible–infected–recovered (SIR) are the most representative models for biological contagions in networks. For the reversible SIS model, a node can be in the susceptible or infected state. At each time step, each infected node tries to transmit the infection to every susceptible neighbor with rate , and then returns to the susceptible state with rate . For the irreversible SIR model, each infected node also tries to infect every susceptible neighbor with rate , but with the difference that the infected node then becomes recovered with rate . The recovered node does not participate in the remaining spreading process. The effective transmission rate is denoted as . Other well-known models for biological contagions include the susceptible–infected (SI) model, susceptible–infected–recovered–susceptible (SIRS) model, contact process, and so on. Unless specifically stated otherwise, this section focuses on SIS and SIR models (others are similar).
2.1. Single biological contagions
As some reviews have systemically reported the progress of single contagions on complex networks [23], [25], [39], [40], [41], [42], [43], we only briefly emphasize two aspects in the following subsections: (i) the mainstream theoretical approaches and results, and (ii) the effects of network topology.
2.1.1. Theoretical approaches
In 2001, Pastor-Satorras and Vespignani first studied epidemic spreading on SF networks [44]. They analyzed the survival probability of the virus data reported by the Virus Bulletin covering 50 months, and found , where is the characteristic lifetime of the virus strain. Within the traditional framework for well-mixed populations of homogeneous networks (e.g., random networks and regular lattices), such a long lifetime suggested that the effective transmission rate was much larger than the epidemic threshold. However, the average fraction of the infected population was very small, which in contrast suggested a small value of the effective transmission rate in the traditional framework. To understand this seemingly paradoxical phenomenon, Pastor-Satorras and Vespignani studied the SIS model on Barabási–Albert (BA) networks with power-law degree distribution (see Ref. [13] for the construction of BA networks). Using the heterogeneous mean-field theory, the spreading dynamics is described as
| (1) |
where is the density of infected nodes with degree , represents the probability that a randomly selected edge points to an infected node, and is the effective transmission rate. To simplify the analysis, Pastor-Satorras and Vespignani set and , and thus the first term of Eq. (1) implies that all the infected nodes with degree will become susceptible in the next time step, and the second term represents the fraction of susceptible nodes with degree that will be infected by neighbors in this time step. In the steady state, , and the stationary density is
| (2) |
From Eq. (2), one can conclude that the nodes with larger degrees are of higher probability to be infected. Linearizing around the initial conditions , the epidemic threshold can be obtained as
| (3) |
where and are the first and second moments of the degree distribution , respectively. When , there is no global epidemic; otherwise, i.e., when , the global epidemic is possible.
The heterogeneous mean-field theory can accurately capture spreading dynamics on annealed networks; however, it cannot predict the threshold of quenched networks well, because these usually contain very complicated local structures that cannot be characterized only by the degree distribution. For example, BA networks [13] and random Apollonian networks (RANs) [45] are of the same degree distribution but exhibit very different structural features, and thus different epidemic behaviors. In addition, because Eq. (1) assumes that the states of neighbors are independent, the dynamical correlations among the states of neighbors are neglected, resulting in deviations from real dynamics. To address the above shortcomings in the heterogeneous mean-field theory, scientists recently proposed some advanced approaches as follows (see also a recent review [28] about theoretical approaches in networked spreading, as well as the related references therein).
By mapping the transmission probability to the bond occupancy probability, bond percolation is widely used to analyze epidemic spreading on networks for both the SIR and SIS models [46], and to identify influential nodes in epidemic dynamics [27], [47]. The final fraction of recovered nodes goes through a second-order phase transition at the epidemic threshold , which is determined by the network structure. Close to , the final epidemic size behaves as , where the critical exponent for ER networks and SF networks with power-law exponent , and when .
To capture the effects caused by the quenched topology of an undirected network, the quenched mean-field theory [48], discrete-time Markov chain approach [49], and -intertwined approach [50] directly explore the adjacency matrix , where when nodes and are connected, and otherwise. Through these different approaches, they arrived at the same epidemic threshold where is the largest eigenvalue of . For uncorrelated SF networks with a power-law degree distribution , when , suggesting the same threshold as in the heterogeneous mean-field theory. When , , which indicates that there is no epidemic threshold in the thermodynamic limit [51], where is the maximal degree of the network. Further analyses show that the eigenvector corresponding to is localized when , which means that only hubs and their neighbors are infected, and consequently the epidemic grows very slowly and may die out owing to fluctuations.
Although the above approaches more accurately predict the epidemic threshold than the heterogeneous mean-field theory, they still cannot accurately capture the dynamical correlations among the states of neighbors. For example, if there is only one seed node, the dynamical correlations are obvious because the contagion path has the same source, and the epidemic transmission events to one node coming from two neighbors may be correlated [52]. To overcome the weaknesses of the quenched mean-field approach but retain its advantages, i.e., to take into consideration the full network structure, the dynamic message-passing approach was proposed by Karrer and Newman [53] to study the SIR model, and generalized later by Shrestha et al. to describe the SIS model [54]. By disallowing a node in the “cavity” state from transmitting an infection to its neighbors but allowing it to be infected by them, the “echo chamber” [55] (i.e., where a node is reinfected by a neighbor it previously infected) is reduced in the dynamic message-passing approach. The dynamic message-passing approach predicts that the epidemic threshold is , where is the non-backtracking matrix. Note that is a nonsymmetric matrix with rows and columns indexed by directed edges , where is the number of edges. The element of is
| (4) |
where if , and otherwise. Recent studies showed that the dynamic message-passing approach predicts the epidemic spreading dynamics well on uncorrelated locally tree-like networks [56], and it has found wide applications in epidemic containment [52], locating spreading sources [57], and network dismantling [58]. However, the dynamic message-passing approach needs differential equations, which is time-consuming for large networks. Moreover, some simplified approaches have been developed, such as the edge-based compartmental approach, which only uses four differential equations to describe the dynamics, and predicts the dynamics well on configuration networks [43].
The pairwise approximation approach is another well-known approach to capture the dynamic correlations by considering the evolution of pair states, instead of states of individual nodes [59]. It requires equations to describe the dynamics, even assuming that nodes of the same degree are statistically the same, and if it treats every node differently, equations are needed. It is also too complicated for large-scale networks. Another disadvantage is that the pairwise approximation approach usually cannot show an analytical expression of the epidemic threshold, but only a numerical value. Moreover, other approaches were proposed for certain specific dynamics, including the master equations [60] and other generalized ones [61].
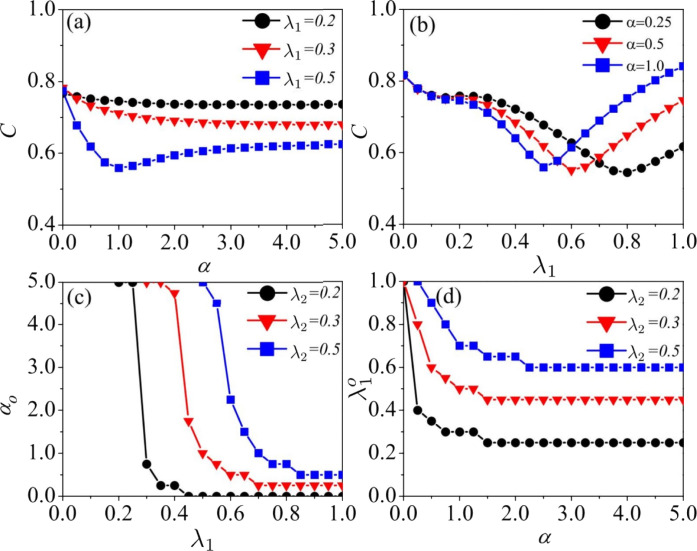
Based on the SIS model, Gleeson et al. [62] compared mean-field predictions with numerical simulation results in 21 real-world networks, and found that the accuracy of the mean-field theory is high when the average degree of the nearest neighbors of a random node is sufficiently large. Wang et al. [56] classified the most widely used approaches into three categories: the (i) mean-field like (MFL), (ii) quenched mean-field (QMF), and (iii) dynamical message passing (DMP) methods. As shown in Fig. 1(a) and (b), the MFL and DMP methods yield identical predictions of epidemic thresholds for the SIR model in uncorrelated configuration networks. As for the 56 real-world networks, as shown in Fig. 1(c), the epidemic thresholds obtained by the DMP method is more accurate, because it incorporates the full network topology information and some dynamical correlations.
Fig. 1.
Predicting the epidemic threshold for the SIR model on uncorrelated SF networks and 56 real-world networks. Theoretical predictions of , , and , and simulation results of versus network size are extensively compared for networks with power-law exponent (a) and (b). Theoretical predictions and simulation results for the 56 real-world networks are shown in (c) .
Reproduced from [56] under CC-BY 3.0.
2.1.2. Effects of network topology
A very important and challenging issue is to reveal the effects of complex topologies on networked epidemic spreading. Here, we briefly review the major progress on this issue, including the effects of degree heterogeneity, degree–degree correlation, clustering, finite network size, community structure, weight distribution, multilayer structure, and time-varying structure.
Early studies on the effects of degree heterogeneity showed that the final epidemic size (i.e., the epidemic prevalence) scales as near the critical point, with the critical exponent for homogeneous networks, such as ER networks and Watts–Strogatz (WS) networks [14]. By comparison, for Barabási–Albert (BA) networks [13], , indicating the absence of an epidemic threshold. Degree–degree correlation is an important feature of networks [63]. In an assortative network (i.e., one with positive degree–degree correlation), large-degree nodes tend to connect with large-degree nodes and small-degree nodes tend to connect with small-degree nodes, whereas in a disassortative network (i.e., one with negative degree–degree correlation), large-degree nodes tend to connect with small-degree nodes and vice versa. Boguñá et al. [64] found that the epidemic threshold vanishes in the thermodynamic limit of SF networks with power-law exponent , whether the two-point degree correlations are assortative or disassortative mixing patterns. Specifically, the epidemic threshold is , where is the largest eigenvalue of the connectivity matrix and is the probability that an edge belonging to a node of degree connects to a node of degree .
Clustering is a widely observed characteristic of disparate networks [65]. Eguíluz and Klemm [66] built a highly clustered SF network model and obtained a finite threshold . Miller [67] also claimed that clustering reduces the epidemic size and increases the epidemic threshold, and network clustering is an important factor in controlling the growth rate of epidemic spreading [68]. However, the effects of clustering seem to be dependent on the underlying network models. For example, studies on random SF networks with high clustering coefficients showed that high clustering cannot restore a finite epidemic threshold [69]. In a solvable model, Newman theoretically proved that higher clustering leads to an even lower epidemic threshold, because redundant paths introduced by triangles in the network provide more opportunities for the susceptible nodes to be infected [70]. Wang et al. [71] revealed that there is a double transition when epidemics spread on networks with cliques.
Most theoretical analyses are under the thermodynamic limit (i.e., assuming the network size is infinite) whereas real-world networks are of finite sizes. Noël proposed an accurate theoretical framework to address the time evolution of epidemic dynamics on finite-size networks [72]. Ferreira et al. proposed a susceptibility method to locate the network-size-dependent epidemic threshold for the SIS model [73], where is the average of the assemble, and is the final epidemic outbreak size. They found , where is the critical exponent. Other methods were developed to determine the epidemic thresholds in finite-size networks, such as variability [74], lifespan [75], and finite-size scaling methods [76].
Community is a mesoscale measurement of networks topology [77]. Generally speaking, nodes within a community are densely connected, whereas nodes between communities are sparsely connected. Liu and Hu [78] studied the epidemic spreading on simplified-community networks and found that the epidemic threshold fulfills , where and respectively stand for the connecting probability of links within a community and between communities, and is the outbreak threshold when there are only edges in the communities. To date, the effects of community structure on spreading dynamics are controversial. Chen et al. [79] found that an overlapping community structure promotes epidemic prevalence. However, Huang and Li [80] claimed that strong community structure suppresses epidemic prevalence.
In simple networks, edges are binary (i.e., edges either do or do not exist), whereas in many real networks, interacting strengths between different node pairs are significantly different, and thus edges are associated with weights to represent their strengths [81]. By treating a simple network as a special weighted network with each edge associated with weight 1, it is obvious that real weighted networks are always of more heterogeneous weight distributions than that of a simple network. Indeed, scientists have demonstrated that the heterogeneity of the weight distribution markedly affects the epidemic dynamics, including both the epidemic threshold and epidemic prevalence [82], [83], [84]. Among the earliest works, Yan et al. [82] showed that nodes with larger strengths (a node’s strength is defined by the sum of the weights of its associated edges) are preferentially infected. To accurately predict the epidemic spreading on weighted networks, Wang et al. [84] developed an edge-weight-based compartmental approach. Their approach shows remarkable agreement with numerical results.
Certain real-world systems are better characterized by multilayer networks (also known as multiplex networks, networks of networks, and interdependent networks in the literature) [85], [86], [87]. A multilayer network consists of a few subnetworks (usually two or three subnetworks, each of which is called a layer), where each has its own organizing rules and functions, different from the others, and nodes in different layers may have strong interactions that can be described by cross-layer edges. Saumell-Mendiola et al. [88] studied the SIS model on interconnected networks. Through a generalized heterogeneous mean-field theory, they found that the global endemic state may occur, even though the epidemics cannot outbreak on each network separately. On the contrary, for the SIR model on interconnected networks, the epidemic occurs on both subnetworks when the coupling is strong enough; otherwise, a mixed phase exists [89]. Arruda et al. [90] found epidemic spreading on multilayer networks shows a localization phenomenon. Recently, Liu et al. [91] constructed two multiplex contact networks from high-resolution sociodemographic data in Italian and Dutch populations, and showed that the classical concept of the basic reproduction number is untenable in realistic populations, owing to the multiplex and clustered contact structure of the populations.
In some real systems, network topologies are time-varying, which can be described by temporal networks [18]. Perra et al. [92] proposed an activity-driven network to model temporal networks, where each node is assigned an activity potential independently drawn from a given probability distribution , and is active with probability in each time step, where is a constant. Each active node generates edges to connect with randomly selected nodes. At the next time step, all existent edges are deleted and the newly active nodes generate edges to form a new network. For the SIS model on the proposed temporal networks, the epidemic threshold is , where and are the first and second moments of , respectively. The results indicated that temporal networks are more robust to epidemic spreading than integrated static networks. Further analysis of this activity-driven model showed that memory inhibits the spreading of the SIR model, whereas it promotes the spreading of the SIS model [93]. Liu et al. [94] studied the SIS spreading process on time-varying multiplex networks, and found that strong multiplexity (i.e., the fraction of overlapping nodes) significantly reduces the epidemic threshold. Starnini et al. [95] revealed that the non-Markovian spreading dynamics can be captured by the effective infection rate.
2.2. Coevolution of two biological contagions
In many real-world scenarios, epidemics spread simultaneously and interact with each other [96]. In this section, we first review two successive contagions, then review some representative models of coevolution epidemic spreading dynamics.
2.2.1. Successive contagions
When two biological contagions spread in the same population, the first contagion may affect the latter one. For example, the hosts may be killed or be provided permanent immunity by the first contagion [97], [98], such that the latter one cannot infect them.
Newman studied two epidemics spreading on the same network [35]. The first and second epidemics are both described by the standard SIR model, but with different transmissibility probabilities given by and , respectively. The recovery probabilities for both models are simply set as 1. Using the bond percolation approach, the threshold of the first epidemic is
| (5) |
denotes the probability that a node is not infected by a neighbor at the end of the epidemic. For this to occur, either the infection does not transmit through an edge with probability , or the infection is transmitted through an edge but the endpoint of this edge is not infected with probability , where is the generating function of the excess degree distribution . Thus, satisfies the following equation: For a randomly selected node with degree , it is not infected with probability . Therefore, the prevalence of the first epidemic is where is the generating function of .
At the ending of the first epidemic, the topology of the residual network (i.e., after deleting the nodes infected by the first epidemic) has obviously changed. The second epidemic cannot transmit the infection to nodes that are infected by the first epidemic, i.e., the second epidemic can only spread on the residual network. For a node that is not infected by the first epidemic on the residual network, it connects to other uninfected nodes with probability , and its generating function can be expressed as
| (6) |
Following the bond percolation theory, the threshold of the second epidemic should fulfill the condition , where . Once , the system undergoes an additional phase transition, and Newman called it a coexistence transition. The threshold of the second epidemic is thus named the coexistence threshold. The corresponding results on ER networks are shown in Fig. 2.
Fig. 2.
Epidemic prevalence of first epidemic or giant connected cluster on residual network versus transmissibility on ER networks with average degree . The parameter is obtained by numerically solving and . The inset shows the two epidemic thresholds as functions of the average degree . The shaded areas denote that both epidemics can spread .
Reproduced from [35].
Newman and Ferrario [99] further considered a different situation, in which the second epidemic can only infect the nodes that are have been infected by the first epidemic. Their model can be used to describe the case in which one disease increases the chance of infection by another. For instance, once a person is infected by syphilis and HSV-2, he/she is more likely to be infected by HIV [100]. With a similar method to Ref. [35], the second epidemic threshold is
| (7) |
where , , and is the transmission probability of the first epidemic. When , one obtains . decreases monotonously with , and . That is to say, the second epidemic threshold is never smaller than the first one.
Bansal and Meyers [101] modeled two consecutive seasonal epidemics, such as influenza, on heterogeneous networks, and the former epidemic inflicts immunity on the latter one. At the end of the first epidemic, a fraction of infected nodes by the first epidemic are immune to the second epidemic, and the remaining infected nodes can be infected by the second epidemic. By using bond percolation theory, they studied both perfect immunity (i.e., ) and partial immunity (i.e., ), and found that the immunity of the first epidemic limits the outbreak of the second epidemic.
Funk and Jansen [102] considered two SIR epidemic dynamics consecutively spread on an overlay network. The overlay network is constructed by two layers, denoted as and . The nodes in the two layers are the same, and the network size is . The overlay network is built according to degree distribution , where and denote the degrees of a node in the two layers. The first epidemic spreads on with effective transmission probability , and then all the nodes infected by the first epidemic are removed from the overlay network. The second epidemic spreads on the residual network with effective transmission probability . The generating function of the residual degree distribution of on is
| (8) |
where is the generating function of the degree distribution , , and is the average degree of network . denotes the probability that an edge does not connect to an infected neighbor, which is obtained by solving , where is the generating function of the excess degree of network . The parameter is the probability for a node arrived at following a random edge on to be infected by the first epidemic. If there is no overlapping between networks and , the second epidemic threshold is
| (9) |
where .
Funk and Jansen [102] further studied networks and with arbitrary overlapping, and determined the second epidemic threshold as
| (10) |
where () is the probability that an edge in network () is also in network (). Obviously, is strictly increasing with , which indicated that overlapping is beneficial for suppressing the second epidemic. Funk and Jansen finally studied a more realistic scenario with partial immunity. They found that once the first epidemic provides partial immunity to the second one, the second epidemic more easily invades the population. However, when two interacting epidemics simultaneously spread on multilayer networks, Zhou et al. [103] found that overlapped links have no effects on the spreading dynamics, whereas the fraction of vulnerable nodes markedly affects the dynamics.
2.2.2. Competing or cross-immunity contagions
Karrer and Newman investigated the behavior of two competing SIR-type epidemics on the same network [104]. The two epidemics are denoted as red and blue epidemics with transmissibilities and , respectively. Each node can only be infected by one of the two epidemics. Initially, a seed node for each epidemic is randomly selected. It is assumed that the blue epidemic evolves with time-step 1, and the red epidemic spreads with time-step . Karrer and Newman developed the competing percolation to study the final state of the two epidemics theoretically. At early time , the average number of nodes infected by the blue epidemic is , where is the reproductive number for the blue epidemic, and . Similarly, the average number of infected nodes by the red epidemic at early time is , where is the reproductive number for the red epidemic. Initially, the two epidemics increase exponentially. is defined as the ratio of the growth rates of the two epidemic, given by
| (11) |
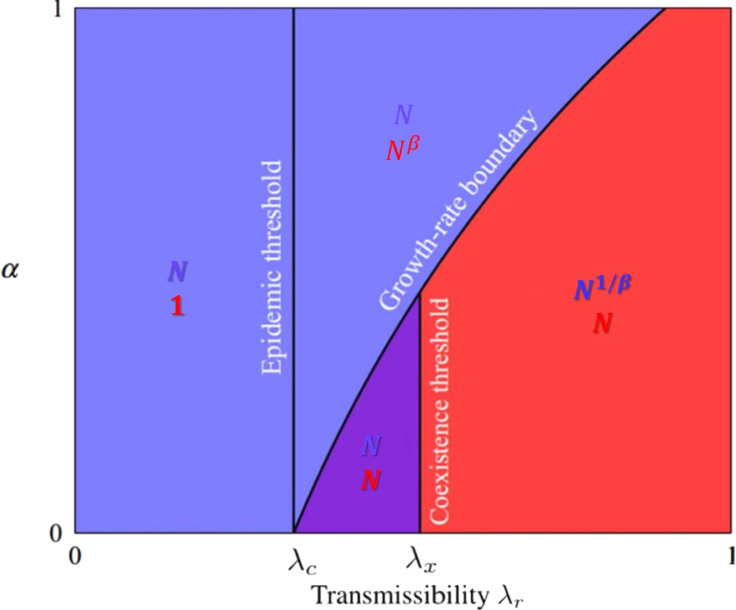
For the case of the red epidemic spreads faster; when , the blue epidemic spreads faster. The growth-rate boundary, i.e., , is thus . In the thermodynamic limit, the faster epidemic spreads on the network first, and the slower one spreads on the residual network. According to the competing percolation theory, the phase diagram of the system is shown in Fig. 3, where .
Fig. 3.
Phase diagram of the system with a given . The colors represent the dominant disease, and the colored symbols represent leading-order scaling of the expected number of individuals infected by each epidemic .
Reproduced from [104].
Miller [105] proposed a different competing spreading model, in which it is not necessary for the initial seed size to be small enough. Miller treated the fast epidemic as completing its spread before the slow epidemic is large enough to warrant consideration, and developed a low-dimensional edge-based compartmental approach to describe the two SIR competing spreading dynamics. Miller found two different situations, which depend on the initial seed sizes and of the two epidemics. If one epidemic has a much larger seed size than the other, the epidemic with larger seeds infects most of the nodes, and the other epidemic cannot spread in the residual network. When and are relatively large, the two epidemics first grow exponentially with rates and . It is assumed that , and is given by . To determine the bounds of the coexistence of two epidemics, Miller assumed that the epidemics exponential growth continues forever, and obtained two critical values and . When , epidemic 1 breaks out before epidemic 2, and vice versa for .
Considering the effects of mobility of individuals, Poletto et al. [106] proposed a novel model with two competing epidemics in a metapopulation network. The metapopulation network is composed of subpopulations, and the edges between the subpopulations are connected according to a given degree distribution. Each subpopulation has a given number of individuals, and each individual moves to a neighboring subpopulation randomly. It is assumed that the two epidemics have different infectious periods, but the same basic reproductive number. Poletto et al. found that the structure of the population and the mobility of hosts across subpopulations affect the infectious period of the dominant epidemic. Poletto et al. [107] further considered a different situation, in which the two epidemics have different basic reproductive numbers and infectious periods. Poletto et al. revealed that mobility can either have no effect on the competition dynamics or play an important role in shaping the dominant epidemic.
The scenario of two competing SIS epidemics on complex networks has also been widely studied. Generally speaking, two epidemics evolve according to the SIS model with infection probabilities and . The recovery probabilities of the two epidemics are and . To include the competing mechanism between two epidemics, scientists assumed that each susceptible node infected by one epidemic decreases its probability of being infected by the other one. For the case of two completely competing SIS epidemics on complex networks, i.e., each susceptible can only be infected by one of the two epidemics, Prakash et al. found that the stronger epidemic completely suppresses the other [108]. Once the two competing SIS epidemics have partial immunizing functions, there is a coexistence region of the two epidemics [109]. Bovenkamp et al. studied two competing SIS epidemics on a complete network [110], and revealed that only one epidemic exists when the transmission probability is above the epidemic threshold, which is markedly different from the observations of competing SIR epidemics. Disallowing epidemic extension by allowing one node to become infected automatically when there are no infected nodes, the dominant and dominated epidemics alternate when the two epidemics are identical. The domination period of an epidemic depends on its initially infected nodes. Yang et al. developed the criteria for the extinction of both epidemics and for the survival of only one epidemic when two competing epidemics have general infection rates [111], [112].
Wang et al. proposed a competing SIS model to describe idea-spreading dynamics [113]. Assuming that the effective transmission rates of the first and second ideas are and , respectively, if node is only surrounded by idea 1 (or 2), it will be infected with rate (or ), where (or ) is the number of neighbors infected by idea 1 (or 2). If node is exposed to both ideas, the infection probabilities are and for ideas 1 and 2, respectively, where . Through a generalized heterogeneous mean-field theory, Wang et al. found that the system has a coexistence region of the two ideas on SF networks, and this region depends on whether the ideas have exclusive or nonexclusive influences.
Different epidemics may transmit on distinct networks. Considering this factor, Sahneh and Scoglio proposed a competitive epidemic spreading model over arbitrary multilayer networks [114]. In this model, each node can be in one of three states: susceptible, (i.e., infected by epidemic 1), and (i.e., infected by epidemic 2). The two epidemics spread on networks and with effective transmission rates and , respectively, where () is the transmission rate of epidemic 1 (epidemic 2), and () is the recovery rate of epidemic 1 (epidemic 2). Note that a node cannot be infected by two epidemics simultaneously. Using the first-order mean-field approximation, the evolutions of the fractions of nodes infected by epidemics 1 and 2 are, respectively,
| (12) |
and
| (13) |
where , () represents the probability that node is in the infected state of epidemic 1 (epidemic 2) in network (network ), and () is the adjacent matrix of network (). In the steady state, and denote the equilibrium probabilities of node being infected by epidemics 1 and 2, respectively. Through a bifurcation analysis of the model, the system has four regions when two competing epidemics spread on multilayer networks. These are the epidemic-free, absolute dominance of epidemic 1, absolute dominance of epidemic 2, and coexistence regions, as shown in Fig. 4. When the two layers are identical, there is no coexistence region. For the epidemic-free region, i.e., , the system is stable when and , where and are the leading eigenvalues of the adjacent matrices and , respectively. For a given , the survival threshold of epidemic 1 is the critical value at which the coexistence equilibrium emerges, say
| (14) |
where is the stable value of at the epidemic 2 absolute-dominance equilibrium, i.e., and . Similarly, another critical point is obtained, where coexistence equilibrium emerges for a given :
| (15) |
where and .
Fig. 4.
Phase diagram of the model on multilayer networks. The plane is divided into the epidemic-free region N, epidemic 1 absolute-dominance region I, epidemic 2 absolute-dominance region II, and coexistence region III .
Reproduced from [114].
2.2.3. Cooperative contagions
Cooperation between two epidemic spreading dynamics means that when a node is infected by one epidemic, the probability increases that this node may become infected by the other epidemic. Such a cooperative effect is also called a synergetic effect. For example, once a person is infected by HIV/AIDS, his/her immune system becomes severely compromised, and thus the probability that he/she may become infected by systemic lupus erythematosus (SLE), syphilis, or hepatitis increases. Conversely, if a person infected by the latter diseases (e.g., SLE) is exposed to HIV, his/her infection probability is increased. Cai et al. [36] proposed a coevolution SIR spreading model with a cooperative effect between two epidemics, in which a node that has not yet been infected will be infected by one of the two epidemics with probability , and a node that has already been infected by one epidemic will be infected by the other with probability . The two epidemics have the same recovery probability. The recovered nodes acquire immunity against the epidemic they had, but not against the other epidemic. Extensive numerical simulations have been performed on ER networks with average degree . Two order parameters, namely the probability of forming a giant infected cluster and the fraction of nodes belonging to the giant connected cluster, are used to describe the phase transition. The system undergoes a hybrid discontinuous transition. At the critical point, the system already has a finite fraction of an infected cluster. The fraction of nodes infected by both epidemics 1 and 2 exhibits a discontinuous phase transition for a given , as shown in Fig. 5. Furthermore, the system undergoes a typical continuous transition on two-dimensional lattices. Specifically, the critical behavior is , where . Grassberger et al. further discussed the roles of network topologies on the phase transition [115], and revealed that loops are crucial for the emergence of a discontinuous transition. For cooperative spreading dynamics on two-dimensional lattices with local contacts or on BA networks, there is no discontinuous transition. However, discontinuous transitions always appear for cooperative contagions on two-dimensional lattices with long-range connections, on four-dimensional lattices, and on ER networks. Chen et al. further investigated the fundamental properties of cooperative contagion processes of two SIS epidemics [116], [117]. It was assumed that a node had a higher rate of infection by one epidemic once it was already infected by another epidemic. Mathematically, it was assumed that the spreading dynamics occurred in well-mixed populations, and the system exhibited a discontinuous phase transition. In a recent study, Chen et al. [118] investigated a model of two interacting SIS epidemics, in which the reproduction number is altered by the interaction introducing a potential change in the secondary infection propensity. When the susceptible nodes move faster than the infected nodes, and the interaction strength is not very strong (i.e., neither too competitive nor too cooperative), there is a nontrivial spatial infection pattern in the system.
Fig. 5.
Cooperative contagions on ER networks with . (a) The mass distribution of infected clusters at threshold and . (b) Phase diagram of versus . The network sizes scale from to . The inset exhibits versus . (c) The peaks of the giant cluster size as a function of at .
Reproduced from [36].
Cui et al. [119] further analyzed two cooperative SIR epidemics proposed in Ref. [36] on uncorrelated SF networks, and developed a generalized heterogeneous mean-field theory to describe the cooperative spreading dynamics. They found that the outbreak threshold is , which is the same as the classical epidemic outbreak threshold. Near the critical point, the auxiliary function can be expressed as
| (16) |
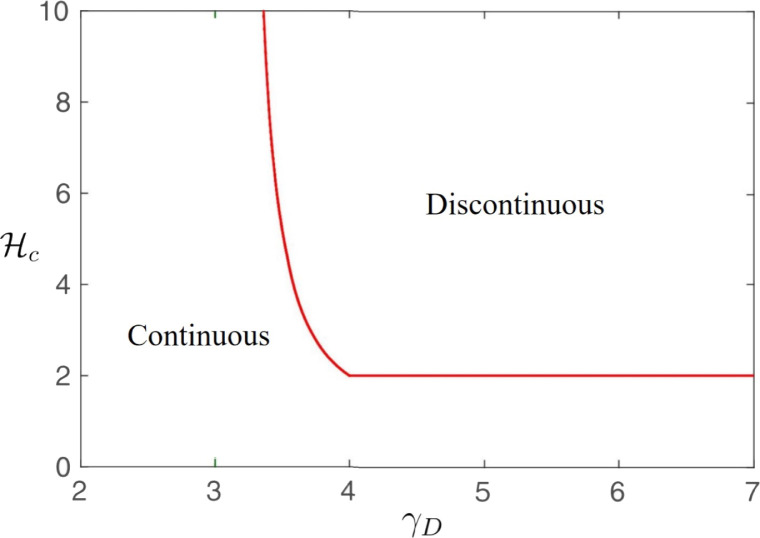
where is the probability that a node with degree is in the recovered state when , and is the critical exponent of the system. The type of phase transition is determined by the values of . (i) For the case in which the degree exponent , there is no epidemic threshold, i.e., , and the phase transition is continuous for any value of the cooperativity . The critical exponent is . (ii) For the case in which , there is a critical value , above which the phase transition is discontinuous, and is always larger than 2. For the continuous phase transition, the critical exponent is . When , . (iii) For the case in which , the critical exponent is , and the phase transition is continuous when ; otherwise, the system exhibits a discontinuous phase transition. The phase diagram is shown in Fig. 6. Cui et al. further demonstrated that the discontinuity decreases with clustering through extensive numerical simulations [120].
Fig. 6.
The minimum cooperativity needed for a discontinuous transition versus degree exponent .
Partially reproduced from [119].
Hébert-Dufresne and Althouse proposed a synergistic coinfection model on clustered networks [38], which is constructed by inducing overlapping communities. In their model, a node that has not yet been infected will be infected by epidemics 1 and 2 with probabilities and , respectively. A node that has already been infected by epidemic 1 (or 2) will be infected by the other with probability (or ). They found that epidemics spread faster on clustered networks than on the equivalent random networks, indicating that clustering has an opposite role on synergistic coinfection spreading dynamics to that on single epidemic dynamics. By investigating the basic reproductive number, Hébert-Dufresne and Althouse gave an accurate estimation of the coupling strength for which epidemics on clustered networks spread faster than the equivalent random networks.
Azimi-Tafreshi [121] considered the effects of multiplexity on cooperative spreading dynamics, and described multiplex networks by using a joint degree distribution , where and respectively denote the number of edges in networks and , and denotes the number of overlapped edges. It is assumed that both epidemics follow the SIR model, denoted as 1 and 2, respectively. Epidemic 1 (2) spreads through edges in network () with transmission probability (), and spreads through overlapped edges with probability , and it is assumed that . By using a generalized percolation theory, the fraction of nodes infected by each epidemic and both epidemics in the final state can be obtained. The system exhibits a tricritical point, and the phase transition changes from continuous to hybrid with the increase in the strength of cooperation. Zhao et al. developed a unified theoretical approach for coevolution spreading dynamics on multiplex networks, which can be used to describe the competitive, cooperative, and asymmetrical interactions between two different dynamics [122].
2.3. Coevolution of multiple biological contagions
In biological systems, the variation of a virus such as influenza [123], HIV [124], meningitis [125], and dengue [126] could lead to thousands of new viruses. Understanding the statistical mechanics, strain structure, and spreading patterns has attracted much attention, especially in the fields of biomedicine and statistical physics. Here, we mainly introduce the progress related to physical science. Abu-Raddad et al. [127] proposed a model consisting of multiple interacting epidemics with the existence of coinfection, cross-immunity, and arbitrary strain diversity. It is assumed that the system has different epidemics, denoted as . Nodes in the recovered and infected states acquire immunity against the epidemic they had, but remain susceptible to the epidemics by which they have not been infected. Mathematically, denotes the set of nodes that have recovered from the set of epidemics and are infected by the set of epidemics . There is no intersection between and . The birth rate of susceptible nodes is and the death rate is . For an epidemic , its transmissibility rate is , recovery rate is , and recovery period is . For each epidemic, the strength of infection can be expressed as . Abu-Raddad et al. assumed the existence of cross-immunity in the system, i.e., the susceptibility of the individuals in should be multiplied by a factor of . The evolutions of the system are
| (17) |
On the right hand of Eq. (17), the third term is the infection rate by epidemic , the fourth term is the rate at which a new node is infected by this epidemic, the fifth term stands for the rate at which nodes recover from an epidemic in , and the last term is the rate at which nodes that have recovered from an epidemic not in will be infected by an epidemic in . Abu-Raddad et al. further analyzed the final state of the spreading dynamics. They assumed that , where is the prior cross-immunity rate of being infected by a new epidemic after exposure by and recovery from different epidemics in the past, and is the cross-immunity rate of being infected by a new epidemic for a node that is currently infected by different epidemics. The further assumed that if , if , if , and if . Under the above assumptions, the total prevalence is as shown in Fig. 7. The cross-immunity against coinfection has a more prominent influence on multiple epidemics than that of the prior exposure cross-immunity.
Fig. 7.
Total prevalence versus and . The number of epidemics is and the effective transmission rate of each epidemic is .
Reproduced from [127].
Gog and Grenfell [128] included the effects of Reduced transmission and polarized immunity into the dynamics of multiple strains. Polarized immunity means that partial cross-immunity renders certain individuals totally immunized. Specifically, Gog and Grenfell assumed that the system has different epidemics, denoted as . For epidemic , its infection and recovery rates are and , respectively. If an individual is infected by epidemic , the probability for to be infected by another epidemic, such as epidemic , is lower than , as given by , which suggests the effect is caused by cross-immunity [129], [130] between epidemics and . In such coevolution dynamics, Gog and Grenfell found that the system has an epidemic cluster. If the infectious period is short, there is only one dominant cluster, whereas for a relatively long infectious period, many clusters coexist and alternate with each other.
Shrestha et al. [131] proposed a novel model to describe the interactions among different epidemics. In their proposed model, they assumed that two epidemics interact with each other when the node has ever been or is currently infected by the two epidemics. For each epidemic, an SICR model is adopted, in which the compartment state (C state) is used to represent the period of convalescence, or a temporal period of immunosuppression or strain-transcending cross-immunity. The SIR part has the same meaning as in classical epidemic dynamics. Furthermore, the host demography is also included. When there are no interactions among the epidemics, the system exhibits damped oscillations. The interactions induce the emergence of sustained oscillations. Shrestha et al. proposed a statistical inference approach to investigate the stochastic temporal variation, under-reporting, and over-aggregation of multiple epidemics.
Juul and Sneppen [132] investigated a multiple-epidemic spreading model on a two-dimensional square lattice with periodic boundary conditions and nodes, which is a generalization of their previous model [133]. At each time step, each node will spawn a new epidemic with probability . If node is infected by more than one epidemic, it can only transmit one of its infected epidemics to a neighbor . If is not infected and immunized against epidemic , it will be infected by . After a period of steps, node recovers. If a node has been infected by different epidemics and not yet recovered from any of them, the probability that it tries to transmit one of its infected epidemics to a given neighbor is , which corresponds to the percolation probability. Numerical simulations indicated that the exponent of cluster mass size versus diameter is close to the fractal dimension of percolation, with diameter 1.896.
Zarei et al. [134] recently developed an exact solution for a cooperative SIR model with epidemics. For a node that has been infected by different epidemics, it is infected by the -th epidemic with probability . The cooperative strength is defined as . At time , the fraction of nodes infected by different epidemics is . The evolution of is
| (18) |
where is the fraction of nodes transferring one specific epidemic. The evolution of can be written as
| (19) |
For well-mixed populations, and setting , Zarei et al. revealed that the critical condition is
| (20) |
where is the fraction of seeds. From the above equation, the minimum value of yields as the discontinuity of the system.
2.4. Summary
In this section, we presented the progress on coevolution spreading biological contagions. For single biological contagions on complex networks, the system always exhibits a continuous phase transition, and the threshold and critical behavior are associated with the network topologies. To describe the spreading dynamics quantitatively, each widely used theoretical approach has limitations and advantages. To summarize, the DMP approach can take into account the full topology of the network and deal with partial dynamical correlations, whereas the heterogeneous mean-field approach, bond percolation theory, edge-based compartmental approach, and quenched mean-field theory only perform well in networks with specific topological properties (e.g., uncorrelated local tree-like networks). For two successive biological contagions, the first epidemic may provide immunity or convenience to the second epidemic, and thus suppress or promote the second one. Generally, the coexistence threshold of two epidemics is larger than the first epidemic threshold. For the coevolution of two epidemics, scientists found that competing or cross-immunity interactions can induce the coexistence phase, and the phase diagram is affected by the network topology. For cooperative epidemics, the discontinuous phase transition and hysteresis loop are included, depending on the network dimensions and spreading dynamics. Finally, when multiple epidemics are simultaneously spreading, epidemic clusters emerge, with the exponent of cluster mass size versus diameter being close to the fractal dimension of percolation. The threshold and phase transition can be analytically solved on well-mixed populations.
3. Coevolution of social contagions
The diffusion of news, innovations, and cultural fads, as well as participation in health behaviors and political protests are all examples of social contagions, in which the state of an individual is not only impacted by interaction with peers, but also strongly influenced by his or her psychological and cognitive factors, as well as social affirmation [135]. In the adoption of a social behavior, multiple confirmation, i.e., the social reinforcement effect, of the credibility and legitimacy of the social behavior is always sought, which has become a key differentiating factor from biological contagions, in which a simple contact is sufficient to trigger the infection. Thus, social contagion processes cannot be described by the biological contagion model. To understand the underlying mechanisms and to make the full use of social contagion, much empirical analysis and modeling work has been devoted to this research area. Therein, Centola’s [136] health behavior experiment on an online social network reveals that the social enforcement effect really exists, the threshold model [137], [138] is a well-known model in studying social contagions, and so on.
As in the case of biological contagions, the main concern of this section regards how different types of interplay impact the coevolution of two or more social contagions, such as the cooperation between two types of behavior adoption. This section is organized as follows. The first part focuses on single social contagions, starting from the empirical studies and the fundamentals of the mathematical models. As a generalization of the classical Watts threshold model [138], we also address the spreading threshold model and introduce the relevant progress. The interest in this part lies in uncovering how the dynamical mechanisms and network structures affect social contagions. The second part is devoted to the interaction of two social contagions. There, we will revisit the models established to capture successive and simultaneous social contagions on complex networks. Our main concern is how the mutual interactions impact the threshold and the type of phase transitions. In the final part, we will generalize the interactions of two social contagions to the interactions of multiple social contagions, empirically and theoretically. This topic will be quite challenging, because their interactions become more complicated, and it is also more important, as they are widely observed in natural, social, and technological systems.
3.1. Single social contagions
One of the key issues in network science is to understand, predict, and finally control the dynamics of social contagion processes on complex networks. As early as 1973, Granovetter showed that information spreading through “weak ties” between casual acquaintances is faster than that diffusing through “strong ties” among close friends [137]. This is because weak ties are usually edges connecting distant nodes, which can accelerate the spreading. The theory of weak ties explained the rapid spread of the HIV disease and information well; however, it cannot give the reason why it fails when using the contagion of preventative measures to stop the HIV disease [139] on the same network. This is mainly because of the difference between the spread of an infectious disease and the contagion of preventative measures, where the former is a simple contagion for which one infected individual is sufficient to reproduce the infection, and the latter is a social contagion that requires multiple sources of activation, as this type of spread is usually uncertain, risky, and costly. In this subsection, we will revisit the progress of empirical analyses that reveal the potential mechanism, i.e., social reinforcement, of social behavior adoption and the established mathematical models for single social contagions on complex networks.
3.1.1. Social reinforcement
The rapid development of Internet technology has enabled large-scale social experiments on online social networks. Centola [136] recruited 1528 participants online and tested the effects of the network structure on the contagion of health behavior. By comparing the spreading of health behavior on a regular clustered network and a random network (as shown in the left panel of Fig. 8), Centola found that the behavior spreads farther and faster across clustered networks than random networks, because the participants can receive social reinforcement from multiple neighbors in the former network (as presented in the right panel of Fig. 8). This is significantly different from the results of biological contagions, where a clustered structure usually suppresses the spreading. To investigate the robustness of Centola’s experiment, Lü et al. [140] proposed an unknown–known–approved–exhausted model, which emphasizes the effect of social reinforcement by incorporating a mechanism by which redundant signals can increase the approval rate. They found that under certain conditions, information spreads faster and more broadly in a regular clustered network than in a random network, which to some extent supports the results of Centola’s experiments. However, increasing the network size tends to favor effective spreading in a random network, which challenges the validity of the abovementioned experiment for larger-scale systems. Moreover, they found that introducing a low degree of randomness into a regular network yields the most effective information spreading. Similar to Ref. [140], Zheng et al. [141] further claimed that increasing the network size or decreasing the average degree enlarges the difference in the final fraction of approved nodes between regular and random networks. Smoking behaviors explicitly inflict the effects on people around the smokers; as a result, they also impact the initiation and cessation of smoking [142]. Christakis and Fowler studied the effects of peer influences on quitting behavior by analyzing a network of 12,067 people who underwent repeated assessments of their smoking behavior and social-network ties over a period of 32 years [143]. They found that the likelihood for a smoker to quit smoking depends on their exposure to multiple contacts with nonsmokers. The social reinforcement in encouraging smokers to abstain is also found online. Myneni et al. [144] found that smokers are more likely to abstain if they are exposed to several abstinent users by examining peer interactions over QuitNet—a social media platform for smokers attempting to quit. A series of other studies also demonstrated that the effects of social reinforcement from the peers were strengthened when the peers come from different social groups, exhibit the value of structural diversity, and share some key characteristics with the ego in the dynamics of social contagion [145].
Fig. 8.
The left panel shows randomization of clustered-lattice and random-network conditions in a single trial of this study (, ). In each condition, the black node shows the focal node of a neighborhood to which an individual is assigned, and the red nodes correspond to that individual’s neighbors in the network. In the clustered-lattice network, the red nodes share neighbors with each other, whereas in the random network, they do not. White nodes indicate individuals who are not connected to the focal node. The right panel presents the fraction of health behavior adoption versus time through the clustered-lattice (solid black circles) and random (open triangles) social networks. (A) to (F) show six independent trials for different network size and average degree . Specifically, (A) shows a trial with parameters , ; (B–D) shows , ; and (E,F) shows , . The speed of the diffusion process is evaluated by comparing the time required for the behavior to spread to the greatest fraction reached by both conditions in each trial .
Reproduced from Ref. [136].
To popularize innovations in the most timely manner, economists and marketers have been focused on how technological innovations diffuse though a population by performing various controlled experiments. In developing countries, the adoption of new agricultural technologies is an important way to help people to escape poverty. Bandiera and Rasul studied the adoption process of a new crop for farmers in Mozambique, and found that the farmers were more likely to adopt the crop when they had a higher number of adopters among their family and friends [146]. In the diffusion of online innovations, Karsai et al. analyzed a dataset recording the adoption process of the world’s largest voice over Internet protocol service, Skype, and found that the probability of adoption via social influence is linearly proportional to the fraction of adopting neighbors [147]. An empirical analysis in recruiting individuals to use Facebook [148] and Twitter [149] indicates that the more exposures an individual receives, the higher the probability that he will adopt the applications.
Social reinforcement effects also occur widely in other types of behavioral adoption processes, such as using menstrual cups [150], adopting seeding strategies [151], taking a new diagnostic method [152], joining social movement activities [153], retweeting politics hashtags [154], and learning a new industry [155].
3.1.2. Threshold model
One early mathematical model established to describe the dynamics of social contagions is the threshold model [138], [156], [157], based on the Markovian process without memory, where the adoption of behaviors depends only on the states of the currently active neighbors (i.e., individuals who have adopted the behavior), and an individual adopts a behavior only when the number or the fraction of his/her active neighbors is equal to or exceeds the adoption threshold. Granovetter [156] proposed the linear threshold model, in which all individuals are in the active or inactive states, and an individual becomes active if and only if the current absolute number of active neighbors is equal to or exceeds the corresponding threshold. As real-world networks are highly heterogeneous, within the linear threshold framework, hub nodes are too vulnerable. To overcome this weakness, Watts takes into account the heterogeneity of individuals’ number of contacts and proposes a novel threshold model (later named the Watts threshold model) [138]. In the model, each node is initially assigned a threshold , randomly drawn from a distribution . When the fraction of active neighbors of a node is equal to or exceeds its threshold , it becomes active. Adopting the fraction of active neighbors instead of the absolute number is the essential difference compared with the linear threshold model. The function can be defined arbitrarily, but satisfies the condition . For an infinite network with finite average degree, the only way that an initial seed node can grow is for at least one of its immediate neighbors to have a threshold such that , where is the degree of this neighbor. These nodes with are called vulnerable nodes, because they become active with only one active neighbor. Specifically, for a node of degree , the probability that it is vulnerable is
| (21) |
where . By using the method of generating functions, the critical condition on an uncorrelated configuration model is [138]
| (22) |
where and respectively represent the degree distribution and the average degree of the network. The critical condition can be explained as follows. When , most of the vulnerable clusters in the network are small and are not connected, and thus the initial seed node cannot induce the global behavior adoption. However, for , there exists a giant vulnerable cluster in the network whose size cannot be neglected when the size of network becomes infinite, and therefore a random initial seed node can trigger a global cascade. A remarkable result is that if all individuals are of the same adoption threshold, the final adoption size first grows continuously and then decreases discontinuously with the increase in the average degree. Meanwhile, a global cascade occurs more easily in a network with a more heterogeneous degree distribution. In modeling the propagation of opinions, the diffusion of innovations, and the adoption of behaviors, the Watts threshold model is well recognized as the fundamental model. Similar to epidemic spreading dynamics, researchers have explored social contagions on complex networks based on the Watts threshold model for two aspects. One is to reveal the effects of network topology and the other is to understand the mechanisms of diffusion at the individual level.
Clustering measures the edge density among the neighbors of an individual, which plays a key role in epidemic spreading. One manifest conclusion is that high clustering suppresses epidemic spreading, leading to an increase in the epidemic threshold and a decrease in the infection size [45]. In investigating the effects of clustering on the adoption of behaviors, Ikeda et al. [158] studied the Watts threshold model on a clustered network generated from a projection of bipartite graphs and compared it with a nonclustered network with the same degree distribution. Similar to the spreading of health behavior [136], [140], [141], global cascades occur more easily on clustered networks than on nonclustered networks [158]. Hackett et al. [159] explored cascades on clustered networks produced by the configuration model with adjustable clustering [70], and found that there exists a range of in which increasing the clustering of the network results in an increase in the mean cascade size, whereas outside of this range it will decrease the mean cascade size [160]. Hackett and Gleeson [161] further explored cascade phenomena on highly clustered clique-based graphs [162] and obtained a closed-form expression for the final fraction of active nodes within a clique of arbitrary size.
Social networks are mostly assortative, whereas technological and biological networks are usually disassortative [63]. Gleeson [163] studied the Watts threshold model on correlated networks and put forward an analytical approach to compute the mean cascade size. Dodds and Payne [164] developed a generating function method that can not only calculate the mean cascade size, but also obtain the probability that a randomly chosen seed will trigger a global cascade. Moreover, they also validated the theoretical results on random networks with bimodal degree distributions. Payne et al. [165] studied the Watts threshold model on degree-correlated random networks by numerical simulations. They found that increasing the positive degree–degree correlation of a network expands the global cascade regions. Moreover, the degree–degree correlations impact the relationship between the initiator’s degree and its ability to trigger a large cascade.
Galstyan and Cohen [166] studied the linear threshold model on a network composed of two loosely coupled communities. They found if the seeds are contained in one of the communities initially, the peaks of the activation dynamics in each community are well-separated in time. Curato and Lillo [167] used the linear threshold model to explore the optimal structure of a network consisting of two communities to maximize the asymptotic extent of the diffusion. They found that the optimal structure can be assortative, core–periphery, or even disassortative when the average degree and the fraction of initiators are constrained. In looking for a minimal fraction of initial seeds needed to trigger a global cascade, they showed that the optimal network is a very dense community linked to a much more sparsely connected periphery. The impact of community structure on the cascade processes based on the Watts threshold model was theoretically studied by Nematzadeh et al. [168]. They constructed a network model with two homogeneous modules, where the internal connectivities of the two communities are the same, and one parameter, i.e., the fraction of edges between the two communities, is used to control the strength of the community structure. There exists an optimal network modularity at which the cascade size is maximized. This study was extended to the case of a network with multiple modular communities [169], which yielded similar results, i.e., that modular structures facilitate the cascade and an optimal modularity exists.
Weighted networks provide meaningful representations of the strengths of interactions between entities in the real world [83]. However, only a limited number of works have studied the Watts threshold model on weighted networks. Hurd and Gleeson [170] studied the Watts threshold model on weighted networks, where the weight of an edge depends on the degrees (e.g., and ) of its nodes and is proportional to . In the case of (), the edge strength decreases (increases) with the increase in the product of the connectivities and . The cascade window (i.e., the range of for which global behavioral adoption occurs) is shifted to higher values when , because highly connected nodes have relatively less influence on their neighbors. Unicomb et al. [171] found that the heterogeneities of the weight distribution show a nonmonotonous effect on the spreading dynamics, which can accelerate or decelerate cascade processes.
In the real world, the interactions that trigger an individual to become active may come from the multiple sources [85]. Brummitt et al. [172] generalized the Watts threshold model to multiplex networks, in which a node becomes active if the fraction of its active neighbors in any channel exceeds a certain threshold, i.e., , where and respectively represent the number of active neighbors and the number of neighbors in channel . Compared with contagions on single networks that have the same topology but without considering multiplexity, Brummitt et al. found that a multilayer network has a higher probability to experience a global cascade. Yağan and Gligor [173] proposed a content-dependent linear threshold model for social contagion in multiplex networks. In this model, each edge type is associated with a content-dependent parameter in that measures the relative bias of type in propagating this content. An inactive node becomes active if the total perceived influences, i.e., , where and respectively represent the number of active neighbors and the number of neighbors in type , exceeds its threshold . The authors showed that the content and edge types are important in characterizing a global cascade. Zhuang et al. [174] studied the content-dependent linear threshold model on clustered multiplex networks, and found that the clustering plays a double-faceted role in cascade processes, where the clustering decreases the cascade size when the average degree of the network is small, and facilitates cascades when the average degree is large. Along this line, Lee et al. [175] studied the effect of individuals’ heterogeneous responses of Watts threshold model in multiplex networks. Two types of responses are introduced. In the first type, an individual becomes active if in at least one layer, a sufficiently large fraction of neighbors is active. In the second type, an individual becomes active only if the fraction of active neighbors is sufficiently large in every layer. They showed that varying the fractions of nodes following either rule facilitates or inhibits cascades. Furthermore, they found that the global cascades become discontinuous near the inhibition regime, and the cascade size grows slowly as the network density increases. Li et al. [176] explored cross-layer cascade processes in multiplex networks. They found that multiplexity accelerates the cascade if the additional layer can provide extra short paths for rapid spreading.
Karimi and Holme [177] modeled the cascade process in temporal networks, where individuals are only influenced by their contacts within a finite time window from the past to the present. The randomization of time stamps makes the cascades larger for the fractional-threshold mechanism [138], whereas it makes the cascades smaller in the case of the absolute-threshold mechanism [156]. Takaguchi et al. [178] also studied the linear threshold model on empirical temporal networks incorporated with a decaying mechanism of the exposures, and showed that burst activity patterns facilitate the contagion. However, in another study of the linear threshold model on empirical temporal networks, Bachlund et al. [179] found that some networks support cascades, and some do not. Their further analysis manifested that there exists competition between the inhibition effect of burst activity patterns and the promotion effect of timing correlations between contacts on adjacent edges.
Some specific models incorporating the underlying mechanisms that affect the behavioral adoption of individuals have also been established. Melnik et al. [180] purposed a multistage social contagion model accounting for the fact that individuals in different stages of the spreading process exert different levels of influence on their neighbors, which can reproduce multistage cascade phenomena. Liu et al. [181] considered a specific situation, in which individuals in the network have several opinion leaders, who affect their behaviors markedly. The impact of opinion leaders makes global cascades occur more easily, which can not only reduce the lowest average degree of the network required for a global cascade, but also increase the highest average degree of a network for which a global cascade can occur. Kobayashi [182] generalized the Watts threshold model with a trend-driven mechanism, which introduces another type of node, global nodes whose states depend on the fraction of activated nodes in the population. When the fraction of activated nodes in the population exceeds a threshold, a trend emerges and the global nodes become active. Kobayshi showed that global nodes accelerate cascades once a trend emerges, whereas their existence reduces the probability of a trend emerging. Accordingly, there exists a moderate fraction of global nodes that maximizes the average size of cascades. The persuasion mechanism, which can strengthen the ability of activated nodes to convince their neighbors to adopt the behavior is also considered in the Watts threshold model purposed by Huang et al. [183]. They found that this introduced mechanism can render networks more vulnerable to global cascades, especially in heterogeneous networks. Ruan et al. [184] generalized the Watts threshold model with mechanisms of spontaneous adoption and complete reluctance to adoption (i.e., immune or blocked nodes). They showed that the speed of spreading depends strongly on the density of blocked nodes. When the fraction of blocked nodes is small, spontaneous adopters are able to generate a large cascade. When the fraction of blocked nodes is large, because spontaneous adopters dominate the spreading, only small cascades can be generated and the spreading becomes slow. Juul and Porter [185] incorporated synergistic effects into the Watts threshold model, and found that constructive synergy (i.e., the peer pressure experienced by a node is larger than in the Watts threshold model) accelerates the contagion process and interfering synergy (i.e., the peer pressure experienced by a node is less than in the Watts threshold model) slows down the contagion process. Oh and Porter [186] accounted for the case in which individuals wait for some period of time before they adopt a behavior. Their results indicated that heterogeneously distributed wait times can change the adoption order of nodes, and either accelerate or decelerate the spread of adoptions.
3.1.3. Memory effects
Social reinforcement resulted from multiple exposures of peer influence is a key feature of social contagions. In the above-discussed models, whether a node becomes active depends only on the number of current exposures from its neighbors, without memory effects. However, the historical records may be relevant; for example, recent exposures may be more important than long-ago exposures. In such cases, memory plays a significant role and the dynamics become non-Markovian. To account for memory effects, Dodds and Watts [187], [188] proposed a generalized threshold model, where each individual contacts with one other individual drawn randomly from the population. If is susceptible and is infected, with probability , node receives a positive dose sampled from a distribution at time step . Each individual maintains a memory of doses received over the previous time steps, recorded by . A susceptible individual becomes infected if , where is a certain threshold initially drawn from the distribution . The probability that a susceptible individual contacts infected individuals in time steps and then becomes infected is
| (23) |
where d, which means the average fraction of individuals infected after receiving positive doses in time steps, and denotes the probability that the sum of doses drawn from exceeds a given . Each infected individual recovers with probability if is smaller than , and the recovered individuals become susceptible with probability in each time step. By adjusting the parameters, such as , , , , and , this generalized threshold model can be reduced to the SIS, SIR, Watts threshold model, and so on. Specifically, when , , and denotes the steady-state fraction of infected individuals, Eq. (23) becomes
| (24) |
By analyzing the fixed points of Eq. (24), three universal classes of equilibrium behavior are found (see Fig. 9). Furthermore, when the length of the memory is fixed, the class to which a particular system belongs is only determined by and , which respectively represent the probabilities that an individual will become infected as a result of one and two exposures.
Fig. 9.
Numerical analysis of Eq. (24). (a) Class I: Epidemic threshold. (b) Class II: Vanishing critical mass. (c) Class III: Pure critical mass. Dose sizes are lognormally distributed with mean 1 and variance 0.433, , and thresholds are uniformly set at (a) , (b) , and (c) . Inset in (a): Example of a more complicated fixed point diagram. Here, , dose size is set to unity, is the delta function, and with probability 0.15 and 6 with probability 0.85 .
Reprinted with permission from AAAS. From [187].
Considering the nonredundancy of received behavior information in social contagions, Wang et al. [189] put forward a non-Markovian susceptible–adopted–recovered (SAR) social contagion model. Initially, a fraction of individuals are randomly chosen as seeds. At each time step, adopted individuals transmit the behavior information to their susceptible neighbors with transmission probability . Once an adopted neighboring individual of individual transmits the behavior information to successfully, the cumulative number of received pieces of information of is increased by 1 and individual cannot transmit the same information to again, i.e., the information transmission is nonredundant. At time step , assume a susceptible individual of degree already has pieces of information, and once receives another piece of information, the probability that it adopts the behavior is whose maximum possible value is one. The adopted individual permanently becomes recovered with probability . An edge-based compartmental theory has been developed, and a variable was adopted to represent the probability that a random neighboring individual had not transmitted the information to individual at the end of the spreading dynamics. The expression of is
| (25) |
where is the probability that an individual has received pieces of nonredundant information. The critical condition for the behavior to be widely adopted is
| (26) |
where . The Heaviside step function is adopted to depict , as when . By using a bifurcation analysis of Eq. (25) in the steady state, one main result is that the transition phase of the final adoption size on can be changed from discontinuous to continuous, as shown in Fig. 10.
Fig. 10.
Non-Markovian SAR model on ER networks. (a) Time evolution of the average densities of susceptible, adopted, and recovered nodes. (b) Final adoption size versus effective transmission rate for different adoption thresholds . (c) Simulation results of NOI (number of iterations) as a function of . The lines in (a) and (b) are the theoretical predictions. The parameters in (a) are set as , , , and ; in (b) and (c), and .
Reproduced from Ref. [189].
Following the work of Ref. [189], researchers considered certain different situations. Zhu et al. [190] investigated the SAR model on weighted networks and found that the heterogeneity of weight distributions always hinders social contagions. Su et al. [191] proposed a reversible social contagion model on community networks, and found an optimal community structure that can maximize spreading processes. Along this line, the SAR model was also studied in time-varying community networks [192], in which hierarchical orders of behavior adoptions are uncovered. Shu et al. [193] explored the social contagion process on interdependent lattice networks, and showed that the phase transition can be changed from continuous to discontinuous by increasing the fraction of dependency links. The SAR model was also studied in multiplex networks [194], [195], [196], [197]. Wang et al. [194] found that multiplex networks can promote the final adoption size. Zou et al. [195] considered that different layers of multiplex networks have distinct reliability for social contagions. They showed that increasing the reliability of one layer can promote the contagion process. Wu et al. [196] found a double transition, whereby a continuous transition occurs first, followed by a discontinuous transition. Chen et al. [197] studied the SAR model on multiplex networks and assumed that a susceptible individual becomes adopted only if the number of adopted neighbors is equal to or exceeds the adoption threshold in every layer. They found the final adoption size increases sharply with the information transmission probability when the adoption threshold is high.
Within the SAR model, there are many factors that potentially impact the behavior adoption. Wang et al. [189] took the limited contact capacity of individuals in transmitting information and suggested that enlarging the contact capacity facilitates global adoption. Considering the heterogeneity of individuals, a binary threshold model is proposed in Ref. [198], in which some individuals have a low adoption threshold (i.e., activists), and the remaining individuals have a high adoption threshold (i.e., bigots). A hierarchical adoption phenomenon is observed, where activists first adopt the behavior and then stimulate bigots to adopt the behavior. Moreover, the model also shows crossover phenomena in the phase transition. Wang et al. [194] also explored the heterogeneous credibility of individuals in social contagion. Zhu et al. [199], [200] studied local trend imitation within a social contagion model, where both tent-like adoption and gate-like adoption probabilities were analyzed. Tent-like adoption means that the adoption probability is an increasing function of (i.e., the fraction of adopted neighbors) when is smaller than a certain value, above which it becomes a decreasing function of . The gate-like adoption, however, means that the behavior adoption probability is equal to 1 when is in a certain range, and it is equal to when is out of this range. For the tent-like case, they showed that the local trend imitation capacity impacts the phase transition, where a second-order phase transition is observed when the capacity is strong, and it becomes a first-order phase transition when the capacity is weak [199]. An optimal imitation capacity is found to maximize the final adoption size in the gate-like case [200]. Su et al. [201] proposed a susceptible–trial–adopted–susceptible (STAS) threshold model, where individuals in the trial state accept the behavior temporarily and can transmit the information. They found that the initial conditions of the dynamics affect the final state of the dynamics, which introduces a hysteresis loop in the system. Wang et al. [202] considered that individuals communicate with multiple channels. When an individual is active in one layer, he/she cannot use other channels to communicate, as individuals cannot simultaneously use all communication channels. Time delays occur and slow down the behavior adoption process; however, this does not affect the final adoption size. Wang et al. [203] proposed a model in which time delays are introduced before an individual adopts a behavior when his/her fraction of adopted neighbors is equal to or exceeds the adoption threshold. They found that long time delays induce a microtransition, which becomes sharper when high-degree individuals have a larger probability of experiencing time delays.
3.1.4. Generalized social contagions
The threshold model [138], [156] and the non-Markovian SAR model [189] only take into account the synergy effects, i.e., the reinforcement effects, of susceptible individuals’ direct neighbors. However, much evidence indicates that other infected individuals around a pair of susceptible–infected individuals would strengthen the transmission rate between them [204]. Pérez-Reche et al. [205] proposed a generalized SIR model, in which the transmission rate between an infected individual (donor) and one of its susceptible neighbors (recipient) depends on the neighborhood of this donor–recipient (d-r) pair, as
| (27) |
where is a positive constant representing the basic rate of infection for an isolated pair without synergy effects. The rate quantifies the degree of synergistic effects. In the absence of synergistic effects, and the model reduces to the simple SIR process. Two types of synergy are introduced in the model, and the expression for depends on the synergy type. When multiple donors challenge a recipient host (i.e., r-synergy type), with representing the number of donors challenging a recipient host at time . The rate measures the strength of the synergy, which is constructive for and interfering for . The other type of synergy (i.e., d-synergy) accounts for the effect of other donors connected to a donor that is challenging a recipient host. For d-synergy type, and represents the number of other donors at time . The rate is of the same meaning as for r-synergy. As shown in Fig. 11, the epidemic threshold is a nonincreasing function of for both r-synergy and d-synergy. Pérez-Reche et al. also showed that constructive synergy induces an exploitative behavior that results in a rapid spreading process, and interfering synergy causes a slower and sparser exploitative foraging strategy that traverses larger distances by infecting fewer hosts. Within this framework, Taraskin and Pérez-Reche [206] found that increasing the connectivity of a lattice enhances the synergistic effects on spreading. Broder-Rodgers et al. [207] investigated the effects of both the r-synergistic mechanism and network topology (by rewiring edges in regular lattices) on the epidemic threshold of the SIR model. They found the network topology markedly impacts the spread. Under strong constructive synergy, the systems become more resilient to the spread of the epidemic after more rewiring. However, rewiring always enhances the spread of epidemics when the synergy is destructive or weakly constructive, if the local connectivity is low.
Fig. 11.
Phase diagram for synergistic epidemics .
Reproduced from Ref. [205].
Gómez-Gardeñes et al. [208] proposed an SIRS model in which recovered individuals can be reinfected. This reinfection mechanism affects the nature of its epidemic transition, which induces an abrupt transition when the transmission rate for reinfection () is larger than a critical value. Gómez-Gardeñes et al. [209] investigated the synergy effects of the neighborhood of the target ignorant receiver by using the SIS model, where the transmission rate from a transmitter to an ignorant/healthy receiver is , and its expression is as follows:
| (28) |
Here, accounts for the intrinsic value of the spreading phenomenon in the absence of the context, represents the number of ignorant/healthy neighbors of the receiver , and is a function of , which captures the effect of the context. Gómez-Gardeñes et al. analyzed both the exponential relation and the linear dependence of on , and found that the inhibitory mechanism (i.e., interfering synergy) leads to an explosive contagion that is not observed in the SIR model.
Liu et al. [210] studied the constructive synergy of the spreader’s context, where the transmission rate between a transmitter and a receiver is , with and respectively representing the number of infected neighbors of the infected node and the strength of the synergy effect, and accounting for the basic transmission rate. Two theoretical methods are established, where a master equation is used to accurately predict the simulation results and the mean-field theory is adopted to give a physical understanding. Liu et al. obtained a critical strength
| (29) |
by the mean-field theory when dynamical processes occur on a random regular network with average degree . When the steady-state density of the infected nodes exhibits explosive growth with respect to the basic transmission rate and a hysteresis loop emerges. Hoffmann and Boguñá [211] proposed a synergistic cumulative contagion model, which takes into account the memory of past exposures and incorporates the synergy effects of multiple infectious sources. They found that the interplay of the non-Markovian feature and a complex contagion produces rich phenomena, including the loss of universality, collective memory loss, bistable regions, hysteresis loops, and excitable phases.
Rumor spreading is another type of social contagion, which rests on the basic idea that a sender continues propagating a rumor as long as it is new for the recipient. Otherwise, he/she loses interest and never spreads it. Daley and Kendall [212], [213] first proposed an ignorant–spreader–stifler model to describe the dynamical process of rumor spreading. In the model, the ignorant, spreader, and stifler states are respectively similar to the susceptible, infected, and removed states in the SIR model. In contrast to the SIR model, the recovery process (spreader becomes stifler) of the rumor model is not spontaneous. Rather, it is the consequence of individuals’ interactions. In detail, both spreaders become stiflers with probability once they contact, and a spreader becomes a stifler with probability once he/she meets an another stifler. Instead of two spreaders becoming stiflers when they contact in the recovery process, Maki and Thompson [214] introduce a slightly distinct version, in which, when a spreader contacts another individual in the spreader state, only turns into a stifler and the state of remains unchanged. Barrat et al. [215] studied the rumor model on the complete graph and found that the final fraction, , of stiflers satisfies the following self-consistent equation
| (30) |
where, is the transmission rate between a spreader and an ignorant. From Eq. (30), it is found that the rumor becomes an outbreak for any , which is different from the finite threshold for the SIR model on homogeneous networks. Moreover, when simulating the Maki–Thompson model on SF networks, Moreno et al. [216], [217] found that the outbreak threshold for rumor spreading is finite. Nekovee et al. [218] found that if the spontaneous recovery process is allowed with a constant rate, the rumor model behaves exactly as the SIR model, such as an infinite threshold on a SF network. These findings show that the dynamic process of rumor spreading is markedly different from the SIR model.
3.2. Coevolution of two social contagions
Real-world social contagions usually interact with each other successively or simultaneously, which are thus named the ecology of contagions [219]. In this section, we will revisit the literature on the interactions between two social contagion processes.
3.2.1. Successive contagions
The studies of two successively interacting epidemics were introduced in the previous section. In comparison, there are very few studies about two successively interacting social spreading processes. Liu et al. [220] proposed a successively interacting social contagion model, in which two behaviors, i.e., behavior 1 and behavior 2, spread successively on a network. The dynamical processes of both behaviors are depicted by a modified version of the SAR threshold model [189], with a different behavioral response function. During the spread of behavior 1, for a susceptible node of degree and with cumulative pieces of behavior information, when this node receives a new piece of information at this time step, the probability that it adopts the behavior is , where is the adopting probability for each reception of behavior information. At the termination of behavior 1, a small fraction of nodes are randomly chosen and set to be in the adopted state for behavior 2. The remaining nodes are in the susceptible state for behavior 2. The spreading dynamics of behavior 2 are mathematically identical to the dynamics of behavior 1, except that the transmission probability and recovery rate are different. For simplicity, we denote the effective information transmission rate as , given by . When a susceptible node of degree receives a piece of information about behavior 2 and the cumulative number of pieces of information about behavior 2 is , then node adopts behavior 2 with a probability
| (31) |
where is the adopting probability for each reception of behavior information 2, denotes the state of node for behavior 1, and quantifies the impact of behavior 1 adoption on adopting behavior 2. When (), the adopting probability for each reception of behavior information 2 is increased (decreased), corresponding to the cooperative (inhibitive) effects of behavior 1. The adoption of behavior 1 has no effect on adopting behavior 2 when , and indicates that if a node has adopted behavior 1, it never adopts behavior 2, which means that behavior 1 completely suppresses the adoption of behavior 2. An edge-based compartmental method was established, and the equation for behavior 2 in the steady state is written as
| (32) |
where () represents that in the final state, a random individual does not successfully transmit the behavior information 1 (2) to his/her neighbor along a random edge. It is useful to define to be the right-hand of Eq. (32) minus the left-hand of Eq. (32). Thus, for a given (i.e., ), combining Eq. (32) and
| (33) |
the critical transmission probability of behavior information 2 is determined and the type of phase transition can be analyzed by the bifurcation theory. To determine the critical condition for the change of phase transition types (from continuous to discontinuous in the presence of inhibition effects, and from discontinuous to continuous in the presence of synergy effects), Eqs. (32), (33), and the second derivative of with respect to equals zero are solved numerically. Liu et al. showed that with the outbreak of behavior 1, the inhibition effects of behavior 1 can cause the continuous phase transition of the spreading of behavior 2 to become discontinuous. Meanwhile, this discontinuous phase transition of behavior 2 can also become continuous when the effects of the adoption of behavior 1 become synergistic (see Fig. 12).
Fig. 12.
Graphical analysis of versus with inhibition and synergy effects on ER networks. (Top panel) versus with inhibition effect (i.e., ). The parameters in (a) are , , and , and in (b) are , , and . (Bottom panel) versus . The parameters in (c) are , , and , and in (d) are , , and .
Reproduced from Ref. [220].
3.2.2. Simultaneous contagions
In real social networks, two behaviors may spread simultaneously and interact with each other. By analyzing the number of tweets versus time in a Twitter music dataset, Zarezade et al. [221] found that the usage of Google Play Music follows the same rhythm as that of YouTube when a new album arrives in both systems, and one URL link becomes popular as the other receives less attention (see Fig. 13). The former implies cooperative contagions that promote the spreading adoption of both services, whereas the latter indicates the competitive contagions, where the adoption of one behavior inhibits that of the other. A correlated cascades model was also proposed to predict users’ product adoption behavior. By evaluating the prediction accuracy, Zarezade et al. claimed that the correlated model performs better than models that do not consider the interaction among spreading processes.
Fig. 13.
Visualization of correlated cascading behavior in real data. (left) Tweets with terms Google and YouTube in Twitter music dataset are synchronized most of the time. (right) Different URL shortening services. and are cooperating, whereas and are competing .
Reproduced from Ref. [221].
Liu et al. [222] proposed a synergistic behavior spreading model on two-layer networks, where the SAR model was adopted to describe the adoption process of each behavior. In this model, behavior 1 and behavior 2 are assumed to spread on layers and , respectively, where the adoption thresholds of the two behaviors are respectively equal to and . The synergistic mechanism is that the adoption of one behavior by a node in one layer enhances its probability of adopting another behavior in the other layer. Mathematically speaking, once node has adopted behavior 1 (2), it generates an increase () in the number of pieces of information about behavior 2 (1). For example, if a node has adopted behavior 2 and has received a cumulative total of pieces of information about behavior 1 from distinct neighbors in layer , this node will adopt behavior 1 if . An edge-based method was established to describe such model, In particular, when the dynamical parameters and network parameters for behaviors 1 and 2 are the same, one has
| (34) |
In the above equation, when and , the bifurcation theory was used to analyze the above equations. One interesting result is that the synergistic interactions can greatly enhance the spreading of the behaviors in both layers. They also found that the synergy effects alter the nature of the phase transition of the behavior adoption processes, where a small (large) value of the transmission rate of behavior 1 (with a low adoption threshold) can lead to a discontinuous (continuous) phase transition in behavior 2 (with a high adoption threshold). Moreover, a two-stage spreading phenomenon is observed with the synergy effects, whereby nodes adopting the low-threshold behavior in one layer are more likely to adopt the high-threshold behavior and further stimulate the remaining nodes to quickly adopt the behavior in the other layer.
Chang and Fu [223] proposed a co-diffusion model for social contagion on a two-layer network, the layers of which are a periodic lattice and a random regular network. The model considers two aspects of the diffusion process. One is inclusive adoption, which allows individuals to adopt two behaviors (i.e., synergy adoption). At first, each naive individual (without adoption of any behaviors) becomes active with probability
| (35) |
where and respectively represent the fractions of neighbors who have adopted behavior 1 and behavior 2, and are constants, and is a free parameter. If it is activated, then with probability
| (36) |
it adopts behavior 1; otherwise, it adopts behavior 2. Once an individual adopts one behavior, it adopts another behavior with probability . The other is stochastic dormancy, which means that an adopted individual becomes dormant at any given time step with a given rate. When an individual is considering adoption, if a neighbor is dormant then this neighbor’s influence is discounted. Chang and Fu found that lower synergy makes contagions more susceptible to a global cascade, especially for those diffusing on lattices. Faster diffusion of one contagion with dormancy may block the diffusion of the other.
Czaplicka et al. [224] explored the competition of the simple (SIS model) and complex adoption processes (Watts threshold model) on interdependent networks. Interdependent networks consist of a simple adoption layer and a complex adoption layer, respectively corresponding to the layers on which the SIS spreading and Watts threshold adoption processes occur. Interconnections between these two layers are added to couple the adoption processes. Czaplicka et al. found that the transition points and the nature of transitions for both single dynamical processes are affected by the coupled dynamics. Specifically, the continuous transition can be observed in the complex adoption layer and the discontinuous transition occurs in the simple adoption layer, whereas in previous studies [25], the SIS and Watts threshold models were found to exhibit continuous and discontinuous transitions, respectively. Srivastava et al. [225] investigated two competing cascades modeled by a generalized threshold model on a signed network, with trust and distrust edges. They developed a pairwise analytical method to approximately calculate the probability of a node being infected at any given time. Srivastava et al. took the advantage of the derived solution to develop a heuristic method for the influence maximization problem, and showed that their proposed method significantly outperforms the state-of-the-art methods, particularly when the network is dominated by distrust relationships.
3.3. Coevolution of multiple social contagions
In the real world, multiple social contagion processes may compete or cooperate with each other and spread simultaneously, such that, with the wide adoption of social media and other socio-technical systems, the abundance of information to which we are exposed is exceeding our limited capacity [226], [227]. The information or ideas in different social media must compete for our limited attention to become popular. To understand the role of the limited attention of individual users in the diffusion of memes, Weng et al. [228] developed an agent-based model and investigated how they shape the spread of information (see Fig. 14 for the illustration of the meme diffusion model). By tuning the length of the time window during which posts are retained in an agent’s screen or memory, they can change the extent of competition. For example, a shorter time window leads to less attention and thus enhances competition, whereas a longer time window allows for paying attention to more memes and thus decreases competition. By modeling the meme spreading on real social networks and random networks, they found that the combination of a social network structure and the competition for finite user attention is a sufficient condition for the emergence of broad diversity in meme popularity, lifetime, and user activity. Gleeson et al. [229] presented an analytically solvable model of selection behavior on a social network. They assumed each screen has capacity for only one meme, corresponding to fierce competition. During each time step (with time increment ), one node is chosen at random. Node then innovates with probability and generates a brand-new meme, which appears on its screen and is retweeted to all ’s followers. Otherwise, node retweets the meme currently on its screen. When a meme is retweeted, its popularity is incremented by 1 and the meme currently on the followers’ screens is overwritten by this meme. They found that the competition among multiple memes for the limited user attention places the system at criticality. For a network of degree distribution , with , they derived the distribution of popularities at age by (i.e., a meme has been retweeted times when its age is ) when as
| (37) |
Here, and are the prefactors (see Ref. [229] for details). From Eq. (37), they showed that the popularity growth of each meme is described by a critical branching process, and an asymptotic analysis predicts power-law distributions of popularities with very heavy tails in the zero-innovation limit (). Gleeson et al. [230] further extended the above simplified model with the inclusion of memory times and heterogeneous user activity rates. Even this generalized model is more complicated; they showed that it is analytically solvable and is able to reproduce several important characteristics of empirical microblogging data on hashtag usage, such as the time-dependent heavy-tailed distributions of meme popularity. In modeling the collective behavior of users’ decisions on adopting different software applications, Gleeson et al. [231] proposed a model that incorporates two distinct mechanisms: one is associated with recent user decisions and the other reflects the cumulative popularity of each application. They found various combinations of the two mechanisms that can yield long-time behavior matched with the data. However, only the models that strongly emphasize the recent popularity of applications over their cumulative popularity can reproduce the observed temporal dynamics.
Fig. 14.
Illustration of the meme diffusion model. Each user has a memory and a screen, both with limited sizes. (a) Memes are propagated along follower links. (b) The memes received by a user appear on their screen. With probability , the user posts a new meme, which is stored in memory. (c) Otherwise, with probability , the user scans the screen. The user then either retweets a meme chosen from the screen with probability , or tweets a meme chosen from memory with probability . (d) All memes posted by the user are also stored in memory .
Reproduced from Ref. [228].
Myers et al. [232] studied URL diffusion on Twitter and proposed a statistical model that allows for the cooperation as well as competition of different contagions in the diffusion of retweeting behaviors. Competing contagions decrease each other’s transmission rates, whereas cooperating contagions help each other. By evaluating the model on 18,000 contagions that are simultaneously spreading through the Twitter network, Myers et al. estimated the probability of a user being infected, given a sequence of previously observed contagions, and also found that the interactions between simultaneous contagions cause a relative change in the spreading probability of a contagion by 71% on average. Valera et al. [233] used continuous-time Hawkes processes to model the adoption of multiple products and conventions. An inference method was developed to estimate the parameters for both synthetic and real data. They found that this data-driven model predicts the adoption and the usage pattern of competing products and social conventions well. Meanwhile, the model reveals that the usage of more popular products and conventions is triggered by cooperation and using a less popular product or convention has a stronger inhibiting effect on future usage of a more popular product or convention than vice versa. Pathak et al. [234] proposed a generalized version of the linear threshold model to simulate multiple cascades on a network. In the model, nodes are allowed to switch their states back and forth. An algorithm was developed to estimate the most likely statistical properties of the cascades’ spread and shown to be of high quality when tested with real data.
3.4. Summary
Social contagions are found in every aspect of the real world, from online to offline behaviors. Experimentally, various types of social contagions, ranging from health behaviors and new crops to Skype adoption, exhibit the social reinforcement effect. That is to say, accumulative multiple contacts between adopted and susceptible individuals are necessary to trigger the infection. When including the social reinforcement effect in social contagions, the order parameter, i.e., the cascade size or final fraction of adopted (activated) individuals, changes discontinuously or continuously, depending on the strength of the social reinforcement. In addition, the network structures and the underlying mechanism incorporated in social contagion models can alter the cascade size and the type of phase transition. For two successive and simultaneous social contagions, the inhibiting or synergistic effects of one spreading behavior can render the discontinuous phase transition of the other behavior as continuous. For the coevolution of multiple competitive and multiple cooperative social contagion processes, the competition induced by limited attention or memory is a sufficient condition for the emergence of broad diversity in meme popularity, and cooperative behaviors mutually promote each other’s contagion.
4. Coevolution of awareness diffusion and epidemic spreading
When an epidemic spreads in a society, information about the disease spreads through various types of communication platforms, such as TV news, Facebook, Twitter, text messages, phone calls, and WeChat. Once healthy individuals obtain information about the epidemic, they will be aware of the epidemic and thus take certain actions (e.g., wearing face masks or staying at home) to protect themselves from being infected by the disease, which will effectively suppress the outbreak of the infectious disease. The search to understand how awareness spreading (also called information spreading in the literature) can mitigate disease outbreaks, and more broadly, the interplay between the two types of spreading dynamics, has led to a novel research domain in network science [30]. When investigating the coevolution of awareness diffusion and epidemic spreading dynamics, scientists assume that susceptible individuals will take certain nonpharmaceutical interventions (NPIs, e.g., hand-washing and social distancing) once they are aware of that they are in dangerous circumstances, and thus the susceptible nodes will have a lower probability of being infected by their neighbors [235], [236], [237]. Usually, the disease outbreak threshold increases and the infected size decreases when such interventions are implemented. Vaccination is another effective measure to suppress the spreading of infectious diseases [238], [239]. In most cases, the effects of vaccination and NPIs on the epidemic spreading have been investigated separately [240]. Andrews and Bauch [241] proposed a model that includes both measures, and revealed that the practice of NPIs decreases as vaccine coverage increases, and vice versa. In the following, we discuss the recent progress on the coevolution of awareness and epidemics on single and multiplex networks.
4.1. Empirical analyses
Google is one the most popular channels for persons to obtain information about epidemics, and thus the volume of related queries or the Google Flu Trends (GFT) should be highly correlated to the number of infected persons [242], [243], [244]. Therefore, Ginsberg et al. [242] found a new way to improve the early detection of influenza-like illness (ILI) by using the data collected by GFT. They can accurately estimate the current level of weekly influenza activity in each region of the United States, with a reporting lag of approximately one day. However, the results reported by Ginsberg et al. [242] were challenged until 2013, as GFT predicted more than double the fraction of doctor visits for ILI [245], [246]. Lazer et al. [247] concluded that two issues, big data hubris and the instability of the algorithm, caused GFT’s errors. On the one hand, GFT developers report that the data are highly correlated with the disease control and prevention (CDC), but not related to the flu. As a result, the data quality is not very high, because certain detailed information about the epidemic issues are ignored. On the other hand, the Google search algorithm is time-varying, which induces an unstable reflection of the prevalence of the flu.
To study the coevolution mechanism in real data about information and epidemics, Wang et al. [248] investigated the weekly series of GFT and ILI epidemics, and their synchronous evolution from 3 January 2010 to 10 December 2013 (nearly 200 weeks) in the United States [244]. Fig. 15 shows the time series of (i.e., the number of ILIs) and (i.e., the volume of search queries). From the macroscopic perspective, ILI and GFT have similar trends, as shown in Fig. 15(a). The time series were further analyzed from a microscopic view. The relative growth rates of and are defined as and , respectively. The growth trends of and are the same, as shown in Fig. 15(b). Furthermore, the cross-correlations between the and time series for a given window size , as defined in Ref. [249], were investigated. As shown in Fig. 15(c), positive and negative cross-correlations are unveiled for and , respectively. Once the susceptible individuals received information through GFT, they adopted certain actions to protect themselves from being infected, and thus the opposite growth was observed. The infected individuals tend to search for information about the disease, which leads to the same growth trends. Furthermore, Wang et al. found that the asymmetric interaction (i.e., the epidemic spreading promotes information diffusion but information diffusion suppresses the epidemic spreading) between information diffusion and epidemic spreading only occurred for a short period, as shown in Fig. 15(d).
Fig. 15.
Weekly outpatient visits and Google Flu Trends (GFT) of influenza-like illness (ILI) in the United States. (a) Fractions of outpatient visits (blue line) and GFT (red line) versus . (b) Relative growth rate (blue line) and (red line) of and versus , respectively. (c) Cross-correlation between the two time series of and for the given window size (blue line) and (red line). (d) Fraction of negative correlations (blue squares) and positive correlations (red circles) as a function of . In (a), and are divided by their respective average values .
Reproduced from Ref. [248]. © 2017 AAAI (www.aaai.org).
Zhan et al. [250] analyzed the coevolution of information and two representative diseases (i.e., H7N9 and Dengue fever). They collected daily data about the two diseases from the Chinese Center for Disease Control and Prevention, and crawled for information about the diseases from Sina Weibo. Individuals who obtained information about the diseases were aware of the diseases, and may take some actions to protect themselves from being infected. Through empirical analyses and mathematical modeling, Zhan et al. claimed that the awareness and epidemic asymmetrically affect each other, i.e., the information diffusion suppresses the epidemic spreading, whereas the epidemic spreading promotes the information diffusion. Similar results are also reported in Refs. [248], [251], [252].
4.2. Coevolution of awareness and epidemic on single networks
Funk and his colleagues investigated a variant SIR model that considers the coevolution of awareness and diseases on well-mixed populations and lattices [33]. In their proposed model, information about the disease is called awareness. An individual with awareness level represents that the awareness has been through individuals before arriving at , and means that individual has first-hand awareness. The awareness level of individual is updated according to the following three rules. (i) A new awareness is generated with probability if individual is in the infected state. (ii) If individual transmits a newer piece of awareness with level to his/her neighbor, individual , with rate , is updated as when . (iii) At each time step, the awareness level of node fades to with probability . For a susceptible node with awareness level , its susceptibility is , where . That is, the older the awareness is (i.e., the higher its level), the weaker the protection power is. In consideration of awareness, the SIR epidemic evolves as follows. An infected node transmits the infection to a susceptible neighbor of awareness level with probability , and recovers with probability . Using a mean-field approach, the authors revealed that the outbreak threshold does not change in a well-mixed population, although the epidemic size is much lower than one without awareness. However, the epidemic outbreak threshold increases on highly structured networks, such as lattices. As shown in Fig. 16, in the snapshot, the infected nodes are surrounded by a cloud of awareness, which greatly suppresses the epidemic spread.
Fig. 16.
Snapshot of awareness and epidemic spreading on triangular lattice. Red represents nodes in the recovered state, light red stands for nodes in the infected state, and darker gray represents nodes with a higher level of awareness .
Reproduced from Ref. [33].
Funk et al. [253] further considered a more complicated case in which the epidemic spreading is characterized by a classical epidemic SIRS model [4] and the awareness spreading is described by a generalized SIS model. In the former, the infection, recovery, and loss of immunity probabilities are , , and ; in the latter, an infected node becomes aware with probability , an aware node transmits the awareness to unaware neighbors with probability , and an aware node loses awareness with probability . The dynamical parameters are dependent on whether nodes are aware of the epidemic information. (i) Reduced susceptibility and infectivity. The awareness suppresses the infectious transmission, as shown in Table 1. (ii) Faster recovery. The recovery probability of an aware–infected node is . (iii) Longer preservation of immunity. For an unaware recovered node, the probability of loss of immunity is , and for an aware recovered node, the probability of loss of immunity is . With the above three modifications, the basic reproductive number of the epidemic is different for distinct situations. If the susceptibility of a susceptible node is reduced, is only dependent on the basic reproductive number of the awareness. Funk et al. [253] computed the corresponding reproduction number for different situations. By reducing infectivity of infected nodes and fixing other parameters, i.e., , the global epidemic outbreak conditions are when , and when . When the faster recovery strategy is implemented, the global epidemic outbreak conditions are if , and if . The epidemic outbreak thresholds for these situations are shown in Fig. 17. To sum up, the epidemic threshold increases if the infection and recovery rates are changed, owing to the diffusion of awareness. Agaba et al. [254] proposed a model in which the awareness is induced by two aspects: direct contacts between aware and unaware nodes and public information, and they revealed distinct dynamical regimes.
Table 1.
Transmission probabilities from an infected node to a susceptible node with different states of awareness, where the two parameters are and .
| Infected node | Susceptible node |
|
|---|---|---|
| Unaware | Aware | |
| Unaware | ||
| Aware | ||
Fig. 17.
Outbreak threshold under reduced susceptibility (), reduced infectivity (), and faster recovery () .
Reproduced from Ref. [253].
Ruan et al. [255] assumed that the awareness can be generated by the information transmission, which is described by the delivery of information packets. A susceptible–infected–recovered–vaccination (SIRV) model was proposed to describe the epidemic spreading dynamics. Mathematically, the SIR component of the spreading dynamics is identical to the classical SIR model, with infection and recovery probabilities of and , respectively. A susceptible node becomes vaccinated with probability . Nodes in the recovery and vaccinated states do not participate in the spreading dynamics. At each time step, there are newly generated packets with randomly chosen origins and destinations, following a shortest-path routing protocol [256]. At time , if a node receives packets from infected neighbors, it becomes vaccinated with probability , where is the strength of the sensitivity to information, and is the degree of the node. Through extensive simulations, Ruan et al. [255] found that the final epidemic size monotonously changes with vaccination , as shown in Fig. 18. Specifically, the epidemic may outbreak globally or locally for low vaccination prevalence, which is markedly different from other classical immunization approaches, e.g., random, degree-based, and betweenness-based approaches.
Fig. 18.
Fraction of nodes in the recovered state versus the fraction of nodes in the vaccinated state under different immunization approaches. The network size is set as , the average degree is , the infection probability is , and the recovery probability is .
Reproduced from Ref. [255].
Mass media, e.g., TV news broadcasts, is an important measure to distribute information about an epidemic, and has observable effects on controlling infectious epidemics [257], [258]. Some studies considered the coevolution of awareness and epidemics on well-mixed populations [259], in which the awareness is generated by mass media. Some interesting phenomena are observed when awareness spreading is induced by mass media. For example, sustained oscillations may occur if the awareness is larger than a threshold [259]. Wang et al. [260] investigated the effects of mass media on the spread of epidemics on complex networks, where the epidemic spreading is described by the SIS model. The mass media density is a linear function of the current epidemic prevalence. By using the approach developed in Ref. [261], Wang et al. found that the basic reproductive number is highly correlated with the volume of mass media. Their results indicate that mass media is an effective tool in controlling global epidemic outbreaks.
Another line about the awareness–epidemic spreading dynamics assumed that the awareness is correlated with neighbors, such as the number of infected neighbors [235], [236]. The nodes that are aware of the epidemic decrease their infectivity probability [235] or activity [262]. In this case, the evolution of awareness is directly determined by the evolution of the epidemic. Thus, we only need to write down the evolution equations of the epidemic. Zhang et al. [236] proposed an awareness–epidemic model, in which the awareness of a susceptible node is determined by the number of its infected neighbors. In this model, a susceptible node with awareness has a smaller infectivity probability, i.e., the infection probability is , where is the basic infection probability, is the reduction factor, and is the number of infected neighbors. Zhang et al. used the heterogeneous mean-field theory to describe the spreading dynamics, and found that the outbreak thresholds of SIS and SIR models are the same, as follows:
| (38) |
From Eq. (38), one can observe that the stronger awareness is, the larger the outbreak threshold is.
To describe the belief and vaccination decision of individuals, Xia and Liu proposed a novel model [263], which assumes that an individual’s belief about the severity and vaccine safety of an epidemic is updated according to the awareness received from their neighbors. Two key factors determine the adoption of vaccination. The first factor is the fraction of nodes infected by the epidemic and vaccinated, and the second factor is the fading of awareness [33]. The authors found that the first factor affects the fraction of vaccinated nodes, and the second factor influences the time when the nodes become vaccinated.
Time delays are pervasive real-world networked dynamics and can radically alter the evolution of dynamic processes in networks [203], [264]. Greenhalgh et al. introduced time delays into awareness–epidemic coevolution spreading dynamics [265]. On the one hand, the awareness of individuals disappears after a certain number of time steps have elapsed. On the other hand, the strength of awareness is dependent on the number of infected individuals at time , because the policy-maker makes decisions based on previous reports about the epidemic. Once time delays are included, the system exhibits limit-cycle oscillation. Agaba et al. [266] assumed that the time delays are induced when nodes became aware and modified their behavior. They analytically studied the stability of disease-free and endemic equilibria, and revealed that the Hopf bifurcation is correlated to the dynamical parameters and the time delay.
4.3. Coevolution of awareness and epidemics on multiplex networks
The previous subsection dealt with the case in which scientists studied the spreading of awareness and an epidemic on the same network. However, a typical case is that in which the epidemic spreads on contact networks, such as sexual webs, and the awareness spreads on various types of social communication platforms, such as Twitter and Facebook. Thus, using multiplex networks to describe the coevolution spreading of awareness and an epidemic is more realistic. In this subsection, we will introduce the progress of the coevolution of awareness and epidemics on multiplex networks.
Granell et al. [267] proposed an unaware–aware–unaware+susceptible–infected–susceptible (UAU+SIS) model on multiplex networks to describe the coevolution of awareness diffusion and epidemic spreading, where nodes in the multiplex networks are matched one-to-one randomly. The awareness spreads through virtual contact following an UAU model, in which each node can be in an unaware or aware state. The evolution of awareness follows three rules: (i) Each unaware node is infected by aware neighbors on the virtual network with probability . (ii) Each unaware node becomes aware if its counterpart in the physical network is infected by the epidemic. (iii) Each aware node forgets the epidemic information or relaxes its vigilance and becomes unaware with probability . The epidemic spreading through physical contacts is described by an SIS model, following two rules. (i) Each susceptible node is infected by infected neighbors with probability if its counterpart in the virtual network is unaware, and otherwise it is infected with probability , where . (ii) Each infected node recovers with probability .
To analyze the model described above, Granell et al. [267] applied a generalized microscopic Markov chain approach (MMCA) [49]. , , and respectively denote the probability that node is in the aware–infected, aware–susceptible, unaware–susceptible state at time . For node , it does not get the awareness from neighbors at time with probability , where represents the adjacent matrix of the virtual network, and is the probability that node is in the aware state. If node is in the aware state, it is not infected by the epidemic at time with probability , where is the adjacent matrix of the physical network. Otherwise, if node is in the unaware state in the virtual network, it is not infected by the epidemic with probability . With the scheme presented in Fig. 19, the generalized MMCA equations of the coevolution dynamics are
| (39) |
In the steady state, linearizing Eq. (39), the epidemic outbreak threshold is
| (40) |
where is the largest eigenvalue of matrix , whose elements are . From Eq. (40), the epidemic threshold is dependent on the topology of the physical network and the awareness outbreak size. If the awareness cannot achieve an outbreak, the epidemic threshold reduces to , which is the same as the classical epidemic outbreak threshold [49]. Granell et al. defined as the metacritical point of epidemic spreading, and the average accuracy of the approximation in the MMCA approach is approximately 98%. The phase diagram of the coevolution dynamics is shown in Fig. 20 for different values of and . The metacritical point is bounded by , where is the largest eigenvalue of matrix .
Fig. 19.
Transition probabilities for the states (a) AI, (b) US, and (c) AS at each time step .
Reproduced from Ref. [267].
Fig. 20.
Epidemic threshold versus awareness transmission probability under different values of and . The shaded rectangle, which represents the metacritical points, is bounded by and .
Reproduced from Ref. [267].
Following the work of Granell et al. [267], many interesting studies have been reported [268], [269], [270]. The model proposed by Granell et al. [267] assumed that (1) the infected nodes immediately become aware, and (2) the aware nodes have a lower susceptibility with a certain probability. What happens when these two assumptions are removed? To this end, Granell et al. [268] proposed a novel model without the two assumptions but including a new aspect, i.e., that the mass media can broadcast awareness. A generalized MMCA approach is developed to describe the proposed model, and it agrees markedly well with numerical simulations. Granell et al. revealed that the first assumption has almost no effect on the epidemic spreading, whereas the second assumption and mass media indeed alter the phase diagram. For instance, the metacritical point disappears if the mass media effect is strong enough. Kan and Zhang included this mechanism in the coevolution of awareness and epidemics, and revealed that self-awareness generation (i.e., an unaware individual becoming aware spontaneously) cannot alter the epidemic outbreak threshold [269]. Starnini et al. [270] found that the temporal correlations slow down the epidemic spreading, and slow down (speed up) the awareness spreading for small (large) values of epidemic transmission probability.
In reality, the awareness spreading is different from the epidemic spreading. When an epidemic outbreaks, the information about the epidemic can spread on various channels such as Twitter, Facebook, and text messages through mobile phones. However, the susceptible nodes may not become aware immediately when they only receive one piece of information from their neighbors [2]. Thus, the awareness spreading exhibits a social reinforcement or herd-like feature [271]. Guo et al. proposed a local awareness-controlled contagion spreading (LACS) model to describe the coevolution of awareness and epidemics on multiplex networks [272]. The Watts threshold model [138] is used to describe the awareness spreading, in which an unaware node becomes aware if (1) the fraction of its aware neighbors exceeds a given threshold , or (2) it is infected by the epidemic. The aware node reverts to unaware when it is susceptible or relaxes its vigilance. For the epidemic spreading dynamics, they adopted the model proposed in Ref. [267] with complete immunization, i.e., . Using a generalized MMCA approach, Guo et al. obtained a highly accurate prediction of the epidemic threshold. Through extensive numerical simulations and theoretical analyses, the epidemic threshold versus exhibits an abrupt decrease at . For the case of , the epidemic size and outbreak threshold remain nearly unchanged with . When , the epidemic threshold does not vary with , but the epidemic size increases with . Huang et al. [273] investigated the coupled contagion of awareness and an epidemic, where the former is depicted by the unaware–aware–unaware (UAU) model on the aware layer and the latter is represented by the threshold model (susceptible–infected) on the contact layer. The interacting mechanisms are introduced such that an unaware individual immediately changes to the aware state if it is infected in the contact layer. A susceptible individual can be infected by each of its infected neighbors with a certain probability if it is in the unaware state. However, an aware and susceptible individual can only be infected by the epidemic when the number of its infected neighbors is equal to or exceeds a threshold. Huang et al. found that such heterogeneous interactions can induce hybrid phase transitions in which a continuous phase transition and bi-stable states coexist.
Node heterogeneity is widely observed in many real-world systems, including different degrees [22], adoption thresholds [194], [198], and waiting times [18]. Different nodes usually exhibit distinct responses when they know information about the epidemic; therefore, the awareness spreading dynamics should be described by using a model with heterogeneous thresholds. Pan and Yan [274] proposed a coevolution model of awareness and epidemics, in which the awareness of nodes comes from three types of information: contact information as well as local and global prevalence of the epidemic. The epidemic threshold increases with the contact-based information, but does not change with the information about the local and global prevalence of the epidemic. Furthermore, the effects of the heterogeneity of individuals’ responses, and the structures of the virtual and contact networks are investigated, and the existence of two-stage effects on the epidemic threshold is demonstrated [274]. Zang considered that the awareness transmission probability equals the fraction of nodes in the aware state, and found that the epidemic spreading is greatly suppressed [275].
Because the transmission probability of epidemic may be time-varying [276], [277], Sagar et al. [278] proposed a generalized UAU+SIS model, in which the transmission probabilities of the awareness and epidemic vary with time. The system can be in one of the sustained oscillatory and damped dynamics. For the case of damped dynamics (i.e., endemic state), the epidemic is greatly suppressed if the awareness spreading is included. Their results were further verified by using a generalized MMCA approach. In addition, the evolution time scale is fatal for the coevolution spreading dynamics [104]. Wang et al. [279] investigated the effects of the time scale on the coevolution of awareness and epidemics on multiplex networks. Compared with the model in Ref. [267], Wang et al. introduced a new parameter to adjust the relative speed of awareness and epidemics, and assumed the infected nodes in the contact network may not become aware instantly in the virtual network. An individual-based mean-field approximation method and MMCA approach were applied to analyze the coevolution dynamics, and they found distinct accuracies for different time scales, suggesting the existence of an optimal time scale, at which the epidemic would be greatly suppressed.
Most previous studies about the coevolution of awareness and epidemics on multiplex networks assumed that the time scale of the network evolution is much longer than the spreading dynamics. Thus, the network topology can be treated as static networks. However, many experimental studies indicated that the network topology varies during the spreading process [18]. Guo et al. [280] assumed that the virtual network varies faster than the awareness spreading, and the contact network varies slower than the epidemic spreading. Therefore, the activity-driven network [92] is used to describe the virtual network, and the contact network is still assumed to be static. Then, the awareness spreads on the temporal network according to the UAU model as proposed in Ref. [267]. The epidemic spreading dynamics on a contact network evolves as the model in Ref. [92]. Through a generalized MMCA approach, Guo et al. found that the metacritical point is bounded by , where and are the first and second moments of the activity potential distribution. If the awareness spreading dynamics follows a threshold model, the epidemic threshold versus exhibits a sharp decrease at , which is similar to the results in Ref. [272]. In addition, the time-variation of the virtual network promotes the epidemic spreading on the contact network.
Different from the reversible SIS model, certain epidemics such as measles and chickenpox should be described by using the irreversible SIR model [1]. Wang et al. [281] assumed that the awareness spreads on a communication network (layer ), and the irreversible epidemic transmits through a contact network (layer ). For the awareness spreading dynamics, they used an SIR-like model. Specifically, each aware (or infected) node transmits the awareness to unaware (i.e., susceptible) neighbors with probability , and recovers with probability . The unaware node becomes aware about the epidemic when its counterpart in the contact network is infected by the epidemic. For the epidemic spreading dynamics, an SIRV model is adopted. The infected nodes transmit the infection to susceptible neighbors with probability , and recover with probability . A susceptible node in layer becomes vaccinated if its counterpart in layer becomes aware. Wang et al. developed a generalized heterogeneous mean-field theory to quantitatively describe the coevolution spreading dynamics. To obtain the outbreak threshold of the awareness spreading, Wang et al. used a linear approximation method, and got
| (41) |
When computing the outbreak threshold of the epidemic in the thermodynamic limit, the competing percolation theory [104] is used. If the awareness does not outbreak, i.e., , the epidemic outbreak threshold is , which is the same as that when there is no awareness spreading [46]. When , there are two different situations: (i) If the epidemic spreads faster than the awareness, i.e., , the threshold is still . (ii) If the awareness spreads faster than the epidemic, i.e., , the threshold is
| (42) |
where is the fraction of the aware nodes in layer , which can be obtained by using the bond percolation theory [46]. In the simulations, the communication network is generated by using the SF uncorrelated configuration model [282], and the contact network is an ER network. This coupled network is hereinafter called a SF–ER network (i.e., the communication network is SF and the contact network is an ER network). As shown in Fig. 21, the theoretical predictions agree well with the simulations. One can observe that the final awareness outbreak size increases with and , whereas the final epidemic outbreak size decreases with .
Fig. 21.
Coevolution of awareness and epidemics on SF–ER networks. (a) The final awareness outbreak size and (b) the final epidemic outbreak size versus and . The other parameter is set as . The lines are theoretical predictions with , and 0.9 in (a) and with , and 0.9 in (b) .
Reproduced from Ref. [281].
Juher and Saldaña investigated the effects of the overlap of two layers on the coevolution of awareness and epidemics [283]. They first proposed an approach to adjust the overlap and the cross-layer correlations in two-layer networks. Juher and Saldaña assumed that the awareness spreads on layer and the epidemic spreads on layer . The coevolution mechanisms of the awareness and epidemic are similar to the model in Ref. [281]. By contrast, for a pair of nodes with susceptible and infected states, the susceptible node reduces its infection probability to . They proposed a variant mean-field theory, where edges are divided into two categories: the ones existing in both networks are called common edges while the ones only in one network are called private edges. The epidemic outbreak threshold fulfills the following condition
| (43) |
where is the overlap coefficient between the two layers, and . For the case of , the epidemic threshold is the same as the classical epidemic threshold. When , the epidemic threshold decreases with , that is, overlap edges promote the epidemic outbreak.
In reality, immunization is always expensive and risky [52]. For rational individuals, they verify the necessity before adopting immunization. Along this line, Wang et al. [248] generalized the model proposed in Ref. [281] and assumed that a susceptible node adopting immunization should consider two aspects: (i) whether its counterpart in the communication network is aware of the epidemic, and (ii) whether the number of its infected neighbors in the contact network is larger than a threshold . Using the heterogeneous mean-field theory, Wang et al. showed that the awareness outbreak threshold is identical to that in Eq. (41). However, the epidemic outbreak threshold is the same as that where there is no awareness spreading on the communication network when , whereas if , the epidemic threshold is identical to that in Eq. (42). Through extensive numerical simulations and theoretical analyses on different types of artificial multiplex networks, Wang et al. found that there is an optimal awareness transmission probability , at which the epidemic is greatly suppressed, as shown in Fig. 22.
Fig. 22.
Coevolution of awareness and epidemic spreading dynamics on different types of multiplex networks. (a) Awareness outbreak size , (b) epidemic outbreak size and (c) vaccination size versus effective awareness transmission probability on ER–ER, ER–SF, SF–ER, and SF–SF multiplex networks with . (d) , (e) , and (f) as functions of with . Other parameters are set as , , and .
Reproduced from Ref. [248].
Most of the previous studies assumed that the adoption by individuals of vaccination or immunization behaviors only depends on their current perceptive awareness of the epidemic. Liu et al. [284] proposed a non-Markovian model that assumes the probability of adopting immunization behavior is dependent on the cumulative awareness, say , where is the basic vaccination probability when a node receives the first piece of awareness on the communication network, and is used to reflect the strength of social reinforcement: a larger corresponds to stronger social reinforcement. By using the heterogeneous mean-field theory, Liu et al. showed that the awareness outbreak threshold is identical to that in Eq. (41), namely the social reinforcement has no effect on the threshold of awareness spreading. For the epidemic outbreak threshold, there are two different situations. (i) If the awareness cannot outbreak on the communication network, the epidemic outbreak threshold is . (ii) If the awareness breaks out and the epidemic spreads faster than the awareness, the epidemic outbreak threshold does not change; otherwise, the epidemic outbreak threshold is
| (44) |
where is the fraction of vaccination nodes with . Because vaccination and infection incur some social cost, Liu et al. defined the social cost of the system as , where means that node is in the vaccination state, otherwise, . Analogously, means that node is in the recovered state, otherwise, . The parameters and denote the social unit cost of vaccination and treatment, respectively. There exists an optimal strength of the social reinforcement effect , at which the social cost is minimized when , as shown in Fig. 23(a). Similarly, in Fig. 23(b), also exhibits a minimum value at . The value of decreases with , and decreases with , as shown in Fig. 23(c) and (d).
Fig. 23.
Social cost of the coevolution of awareness and epidemic spreading on SF–ER multiplex networks. The social cost versus (a) the strength of the social reinforcement effect , and (b) awareness transmission probability (b). (c) The optimal social reinforcement effect versus , and (d) the optimal awareness transmission probability versus .
Reproduced from Ref. [284].
4.4. Summary
In this section, we reported the progress of the coevolution of awareness and epidemics. Empirically, the coevolution of awareness and epidemics exhibits an asymmetric coupling between the two dynamics: the awareness suppresses the epidemic spreading, whereas the epidemic spreading promotes the awareness diffusion. For the coevolution on single networks, the network topology (e.g., degree distribution and clustering) remarkably affects the coevolution spreading dynamics. For the coevolution of awareness and epidemics on multiplex networks, the epidemic threshold of the UAU+SIS model has a critical value (i.e., the metacritical point), which is correlated with the awareness diffusion and the topology of the underlying network. In the SIR+SIR model, there exists an optimal awareness diffusion probability at which the epidemic spreading is maximally suppressed.
5. Coevolution of resource diffusion and epidemic spreading
The treatment and control of epidemics require human intervention, which is infeasible without the resource input from the government or other institutions. Thus, the effect on resource input in coping with the epidemic propagation is an issue of great social significance. A traditional research domain named economic epidemiology [285], is mainly interested in the occurrence of infectious epidemics and the effects of public health interventions designed to control them. The possibility of eradicating epidemics, as well as the welfare loss induced by epidemics are highlighted. In the area of public health, there are some outstanding studies on the government resource input in coping with epidemic spreading [286]. It is found that sharing the resource of antiviral drugs among countries helps to contain the epidemic outbreak at the global level, and the more cooperative the resources, the more effective are the containments in all regions of the world. It has been pointed out that the lack of resource allocation can arouse critical financial crises. For example, the scarcity of a resource is closely related to the susceptibility of the trade network with respect to cascading shocks [287]. However, the study of the field under the framework of network coevolution dynamics has come to the fore only recently. Most importantly, the effects of resources are often critical on this epidemic–resource coevolution process.
5.1. Epidemic spreading dynamics under constant resources
The resources (e.g., vaccines, funding, and human beings) for curing an infectious epidemic are always limited and expensive. Given limited resources, determining how to effectively allocate them is extremely important [288]. For instance, we could randomly allocate resources to infected individuals, or prefer to allocate resources to certain important individuals and areas; in the latter case, how to find the important individuals to allocate the resources becomes a related optimization problem. Moreover, the critical phenomena of epidemic spreading dynamics could be different under different strategies for resource allocation. In this section, we first introduce the progress on the influences of constant resources on the evolution of epidemic spreading dynamics, and then discuss the critical phenomena induced by constant resources.
5.1.1. Optimal allocation of resources
From the perspective of macroscopic resource cost in terms of vaccinations and the social welfare loss associated with epidemics, Francis et al. [289] solved an optimal control problem of suppressing the epidemic through vaccination while minimizing the total cost. The model is a standard SIR model incorporating an extra vaccination rate , such that the susceptible can turn into the recovered state at this rate. Then, Francis et al. solved an optimal control problem to minimize the total cost during the disease process, where the total cost is a weighted summation of the cost of vaccination and the cost from loss of utility when people are infected. The resource regulation effects from both government policy and the market were discussed. In a more realistic scene, the resource allocation is performed on spatial districts. For example, the epidemic outbreaks may occur in different but interconnected regions. Under this setting, Mbah et al. [290] studied an optimal control model to minimize the discounted number of infected individuals during the course of an epidemic with economic constraints, and investigated preferential treatment strategies. Their model is a two-region SIRS model in which the infected can be cured with a cost. The discounted number has the form , where the discount rate aims to give greater emphasis to control in the short rather than the long term. Mbah et al. discuss the optimal control problem to minimize the discounted numbers of the two regions with total budget constraints. Their results indicated that when faced with the dilemma of choosing between socially equitable and purely efficient strategies, the optimal control strategy is not apparent but should be determined by many epidemiological factors, such as the basic reproductive number and the efficiency of the treatment measure. Apart from multiple populations from different regions, the resource allocation can occur over multiple time periods. Zaric et al. [291], [292] studied a dynamic resource allocation model in which a limited budget is allocated over multiple time periods to interventions. The epidemic model is a generalized epidemic model with multiple compartments and the interventions turn to the changes in the model parameters. Through a heuristic numerical study, Zaric et al. found that allowing for some reallocation of resources or funds over the time horizon, rather than allocating resources just once at the beginning of the time horizon, can lead to significant increases in health benefits.
Because the allocation to districts is preliminary and rough, to better quantify the effect of resources, one can further consider the case in which resources are allocated to individuals in networks (such as distributing vaccines and antidotes to individuals throughout the network). A number of studies focus on studying the algorithm of the network distribution problem. Preciado et al. [293] proposed a model in which the infection rate of each individual can be reduced by distributing the vaccination resources to them (such that they become less infective). Thus, individuals in the SIS epidemic model in the network present different levels of susceptibility, depending on how many resources they gain. Considering how to minimize the total cost of the corresponding vaccination and the corresponding outbreak asymptotic exponential decaying rate, a convex framework to find the optimal distribution of vaccinations to contain the epidemics in arbitrary contact networks is proposed. In a similar study, Enyioha et al. [294] considered a linearized SIS epidemic spreading model with the setting that the resources can be used to reduce individual infection rates or/and to increase the recovery rates. Enyioha et al. proposed a distributed alternating direction method of multipliers algorithm to solve this problem, and obtained a distributed solution in which agents in the network were able to locally compute their optimal allocations.
In general, the curing rate of each node is positively correlated to its medical resources, that is, the more resources given, the higher the curing rate. In a more realistic case, the total amount of medical resources is limited and the average curing rate is thus fixed. Chen et al. [295] analyzed how to best allocate limited resources to each node so as to minimize the epidemic prevalence. They formulated the SIS model by the mean-field theory and solved the corresponding optimal control problem by the Lagrange multiplier method, and found counterintuitively that in the strong infection region, the low-degree nodes should be allocated more medical resources than the high-degree nodes to minimize prevalence. The above models assume that resources can be distributed to reduce the infectiousness or increase the recovery of a node. A similar idea can also be conducted on the edges. Nowzari et al. [296] assumed that the epidemic spreading can be suppressed by decreasing the strength or weight of edges when allocating resources. For example, the government might be able to decrease the edge weight by reducing interactions between two nodes, such as by limiting the amount of transportation between two cities. Nowzari et al. considered an SIS epidemic model on time-varying networks and studied how to optimally allocate the budget to best combat the undesired epidemic within a given budget. They showed that this problem can be formulated as a geometric programming and solved in polynomial time.
The optimal allocation can also be formulated from a mathematical perspective. Ogura et al. [297] focused on the mathematical problem of finding the optimal allocation of containment resources to eradicate epidemic outbreaks over models of temporal and adaptive networks, including Markovian temporal networks, aggregated-Markovian temporal networks, and stochastically adaptive networks. For each model, a rigorous and tractable mathematical framework to efficiently find the optimal distribution of control resources to eliminate the epidemic is developed.
5.1.2. Resource-induced critical phenomena
Chen et al. [298] studied an SIS model that incorporates the relationship between the devoted resource and the recovery rate . This is motivated by their finding from the empirical cured rate of cholera that the recovery rate can be formulated in terms of , where indicates the amount of the resource. The infected proportion is governed by the equation
| (45) |
where is the infection rate. In the steady state, Eq. (45) could have multiple stable points, which depend on the initial infected population . Chen et al. found that there is a critical resource value , such that only when will the epidemic be widespread. In real-world networks and artificial networks, Chen et al. found three types of phase transitions: discontinuous, hybrid, and continuous, as shown in Fig. 24. The regions for the three distinct phase transitions are determined by the value of . The three phase regimes are separated by and . When , increasing resource can always eradicate the epidemic spreading. When , the infected fraction changes continuously with , and this region is the continuous phase transition. When , there is a hybrid phase transition. In this region, because , the epidemic can never be totally removed.
Fig. 24.
Nontrivial critical resource amount and multiphase behaviors in real sexual contact network. (a) The size of jump as a function of . When , the catastrophic jump behavior disappears, switching to a continuous phase. (b) versus with . (c) The critical resource versus when . as a function of with (d), (e), and (f) .
Reproduced from Ref. [298].
Jiang et al. [299] generalized the above model to multilayer networks. For a two-layer network, through a discrete-time Markov chain approach, the spreading dynamics on network can be described by the equation
| (46) |
where and respectively represent the probabilities that node in the networks and is infected at time . The epidemic is described by the SIS dynamics in each layer, with () and () being the infectious and recovery probability, respectively, in network (). Note that the recovery process is the same as for the model in Ref. [298]. The parameter () represents the infectious probability from network () to network (). The evolution of epidemic on network can be expressed similarly. Jiang et al. found that a significant fraction of the total population may be infected if the resource amount is below the resource threshold. Moreover, the resource threshold is dependent upon both the inter- and intra-connections of the two networks. It is found that the inter-layer infectious strength can lead to a phase transition from the discontinuous to the continuous phase or vice versa, whereas the internal infectious strength can result in a hybrid phase transition. Thus, the links between the two networks and the edges within a network play different roles in the resource-induced critical phenomena.
Time delay is another important factor that affects the epidemic spread dynamics. In the spreading on multilayer networks, the time delay can arise from the difference in physical properties between the layers. Jiang et al. [300] further studied the effects of time delays between the layers. This model modifies Eq. (46) such that and . Here, and represent the time delays involved of transmitting between the layers. Interestingly, it is found that the time delay can induce discontinuous, continuous, and hybrid phase transitions among them, depending on the resource amount, the infectious strength between the layers, and their internal structures. In addition, there is a critical threshold of the time delay, such that even a small resource amount can effectively control the epidemic spreading if the delay is beyond this threshold, whereas a huge amount of the resource is needed otherwise. Thus, the effect of time delays in the presence of a limited resource is more important.
The resource discussed above is not relevant to the network topology and thus it is a global resource. One can further consider a resource that is provided by the neighboring individuals in the network. Such local resources can induce more abundant effects on the epidemic spreading process. In an SIS model proposed by Bottcher et al. [301], the infected nodes can only recover when they remain connected to a predefined central node, which provides the resources. In other words, there is a single central node in the system that controls healing. An infected node can heal if, and only if, it is connected to the central node via a path involving only healthy nodes. Interestingly, through numerical simulation, a two-phase behavior is observed such that the system converges to only one of two stationary states: either the whole population is healthy or it becomes completely infected. This gives rise to discontinuous jumps of different sizes in the infected population and larger jumps tend to emerge at lower infection rates. The discontinuous jumps can be understood by the fact that at some point, the central node may become surrounded by infected nodes, such that nodes outside cannot be cured, which leads to a sudden jump to a fully infected absorbing state.
5.2. Coevolution of epidemic–resource spreading dynamics
The coevolution process of an epidemic and resources is more realistic in social networks. In the view of global (government) resources, the outbreak of an epidemic will reduce the labor force, as sick workers lose their productivity, and thus decrease the resource output. In the view of individual resources, social individuals may distribute their resources to their sick friends. In all these cases, the amount of resources should be affected by the epidemic process. In other words, the evolution of epidemic spreading is affected by the amount of resources, and at the same time, the amount of resources is also influenced by the epidemic spreading. Unlike the case of constant resources, the dynamical evolution of resources can introduce nontrivial effects on the epidemic spreading. Research on the epidemic–resource coevolution processes has only recently come to the fore. In this coevolution process, the critical outbreak of an epidemic depends on the evolution properties of epidemics and resources, the complex interplay among them, as well as the network topology.
5.2.1. Effects of global resources
If an epidemic becomes more prevalent, it can limit the availability of the resources needed to effectively treat those who have fallen ill, because the recovery of sick individuals may depend on the availability of healing resources that are generated by the healthy population. Bottcher et al. [302] proposed a budget-constrained SIS (bSIS) model, in which healthy individuals produce resources and infected individuals consume resources to recover. The bSIS model modifies the classical SIS dynamic by introducing a global budget that can be increased by the number of healthy individuals per time step. There is a basic recovery process that is independent of the available budget, occurring at a rate . Furthermore, each individual can recover through treatment and this requires a cost . This resource-mediated recovery requires the budget. However, the rate of recovery through treatment is , where is a function of the budget, satisfying for and for . With the mean-field assumption, the dynamics of the fraction of infected individuals is given by
| (47) |
Fig. 25(a) shows an explosive epidemic where the entire population is infected in the steady state []. Furthermore, there is a discontinuous transition in the model parameters. For example, as illustrated in Fig. 25(b), the transition is discontinuous in the basic reproduction number. Therefore, there is a jump, , in the infection level (see Fig. 25(a)). The discontinuity of this jump in the final infected fraction has important implications for the resilience of the healthy system and the control of the epidemic. It implies that small changes in the properties of the epidemic can abruptly increase the infection level, such that the epidemic is harder to control. In short, an insufficient resource production rate would induce the outbreak of the epidemic. Equivalently, the epidemic spreads out explosively if the cost of recovery is above a critical value.
Fig. 25.
Phase behavior of the bSIS model. (a) Coevolution of the proportion of infected individuals and the budget on the friendship network. Other parameters are set to be , and . (b) Asymptotic fraction of the infected individuals on the friendship network, for and , as a function of . The inset shows that in the epidemic regime , where .
Reproduced from Ref. [302].
Another way to contain the spread of an epidemic is to make the population aware of the epidemic and possible self-protection methods. For this purpose, the government can allocate funds to make the public aware through mass media, print media, pamphlets, etc. In this case, Misra et al. [303] proposed an SIS model in which the infectious rate can be decreased by the resource input. The available resource itself evolves in a logistic growth dynamical process. They used a compartmental model to describe this coevolution process, and found that although increasing the funds reduces the number of infected individuals, the delay in providing the funds can destabilize the interior equilibrium and may cause stability switches, resulting in epidemic outbreaks.
The effect of global resources can also be seen from the strategy of the usage of resources. Assume that each individual can choose to use the resource to vaccinate or otherwise not to vaccinate. Without vaccination, there is a possibility that they become infected and this would also result in a cost to treat the epidemic. In this situation, the evolution of the resource is reflected in the evolution of the strategy about how individuals use the resource. Human behavior and the networking-constrained interactions among individuals significantly impact the coevolution of the epidemic and the resource strategy.
Zhang et al. [304], [305] proposed a theoretical framework to study the coevolution of epidemic and the resources game. Taking into account the periodic outbreaks of flu-like epidemics and the limited effectiveness of vaccines, they studied models with seasonal updating and pre-emptive vaccination, in which individuals decide whether or not to get vaccinated before each epidemic season. The strategy for individuals is to determine whether or not they vaccinate. Although it requires a cost to vaccinate, individuals also bear the cost to treat the epidemic if they are infected when they do not receive vaccination. Once the epidemic ends, individuals update their vaccination decisions for the next season by imitating the strategy of their neighbors. The neighbor with a higher payoff has higher probability for their strategy to be learned, which is described by the famous Fermi rule in game theory [306]. By this rule, an individual, say , updates his/her vaccination strategy by randomly choosing one of its immediate neighbors, say , and adopts the strategy of with the following probability determined by the payoff difference
| (48) |
where or denotes the vaccination choice for individual : either vaccinated or not, and is the current payoff of individual at the current season. Without any subsidy, according to the costs of vaccination and infection, we have
| (49) |
where is a parameter characterizing the rationality of the individuals: higher implies more rational. By incorporating evolutionary games into epidemic dynamics, Zhang et al. found that under the partial-subsidy policy, the vaccination coverage depends monotonically on the sensitivity of individuals to payoff difference, , but the dependence is nonmonotonic for the free-subsidy policy, referring to Fig. 26(c) and 26(d). For the case of irrational individuals where , the free-subsidy policy can in general lead to higher vaccination coverage, referring to Fig. 26(a)–(b).
Fig. 26.
Epidemic dynamics with incentive vaccination strategy. Snapshots of the stationary state configuration in square lattices with partial-subsidy (a) and free-subsidy (b) policies. Other parameters are , , , and . The vaccination coverage (c) and epidemic size (d) as a function of in homogeneous small-world network. The insets show the differences in the vaccination coverage and epidemic size between the partial-subsidy and free-subsidy policies, and , respectively .
Reproduced from Ref. [305].
In [307], Zhang et al. further explored the effect of a preferential imitation rule, where individuals choose their imitating neighbors with a tendency rather than randomly selecting them. It is found that the targeted subsidy policy is only advantageous when individuals prefer to imitate the subsidized individuals’ strategy. Otherwise, the effectiveness of the targeted policy is worse. More importantly, under the targeted subsidy policy, preferential imitation causes a nontrivial phenomenon whereby the final epidemic size increases with the increase in the proportion of subsidized individuals. In summary, epidemic-control policy through resource input depends on the complex interplay among the intrinsic mathematical rules of epidemic spreading, governmental policies, and the behavioral responses of individuals. Moreover, this complexity may introduce the so-called Braess’s Paradox [240], such that increasing the effectiveness of the strategy may in contrary lead to worse strategy outcomes (more resource to be consumed).
The increasing level of vaccination in the population helps to inhibit the epidemic spreading, which in turn, however, discourages people from participating in vaccination owing to the cost. Cai et al. [308] studied the impact of some other vaccination strategies on the epidemic spreading. The epidemic and game dynamics are similar to the above process in Eq. (48) and Eq. (49). Individuals randomly choose a neighbor to perform the Fermi rule. Consider three strategies: (i) deterministic (individuals choose to vaccinate or not before the epidemic season), (ii) probabilistic (individuals choose to vaccinate with certain probabilities), and (iii) probabilistic with random mutation (after choosing the vaccinating probability, there is still a random change in the probability). Cai et al. showed that there is a critical value of in Eq. (49), below which, the lower the mutation probability, the higher the vaccination level, and above which the opposite effect takes place. Both the final vaccination level and epidemic size in the continuous-strategy case are less than those in the pure-strategy case when vaccination is cheap.
In terms of the resource strategy game, Wang et al. [309] examined how two countries would allocate resources at the onset of an epidemic when they seek to protect their own populations. They build a two-region SIR model in which infected individuals can transmit between the two regions (countries). Each country can distribute the total resource to itself or to the other country. The effect of the resource is to decrease the initial number of susceptibles. As a game between selfish countries, each country aims to minimize its own outbreak size over the entire time horizon. Wang et al. mathematically analyze the model and show that the best strategy for selfish countries is to allocate all their resources to themselves to decrease their own effective reproduction ratio. Moreover, they further identify the mathematical conditions under which the total number of infected in the whole population is minimized by their the best strategy. In this case, even though each country selfishly seeks their own optimal strategy without communication, the global optimal situation can be achieved such that a major global outbreak may still be avoided.
5.2.2. Effect of individual resources
Long et al. [310] considered an SIS model in which the recovery rate of a node is positively related to the resource provided by its healthy neighbors. That is, , with being the basic recovery rate and a scale factor, where is the resource provided by its healthy neighbors and takes the form
| (50) |
Here, is the connectivity matrix of the networks, are its minimum and maximum degrees, indicates the state of node , which equals 1 if it is healthy and 0 if infected, and is a preference factor. Consider the cases in which the recovery rate of infected nodes is heterogeneous in the sense that nodes with large degree tend to receive more (or less) resources, corresponding to and , respectively. Through analysis and numerical simulations, Long et al. find that the virus spreading can be optimally suppressed if there is no such relation between the node degrees and resource amounts they received. In other words, if each healthy node contributes equal resources to the infected nodes, the virus can be optimally suppressed and there will be a maximum outbreak threshold and minimum fraction of infected nodes. Moreover, they find that in a homogeneous network, the uneven distribution of resources (if the recovery resources of infected nodes mainly rely on nodes with large or small degrees) would lead to a discontinuous phase transition, but the phase transition is continuous under even distribution of resources. However, heterogeneous networks always go through continuous transitions. In a similar scenario, Chen et al. [311] studied another model with a preferential effect. When the transmission rate is small, the resources of the healthy nodes should be allocated preferentially to the highly infectious nodes (nodes with more infected neighbors). When the transmission rate is large, in the early stage, resources should be allocated preferentially to the highly infectious nodes, whereas after the early stage, resources should be allocated to the less infectious nodes. With the individual resource diffusion framework, Chen et al. found that the allocation strategy can adaptively change with the current fraction of infected nodes and the epidemic can be maximally suppressed under the proposed strategy, which gives a novel viewpoint to the optimal epidemic control problem under resource constraints.
In the above model, the epidemic process and resource diffusion occur on the same network. Chen et al. [312] proposed a coevolution spreading model in multilayer networks, where the epidemic and resources separately spread in the contact and social layers, respectively. At each time step, each healthy individual generates one resource unit, which are distributed equally to infected neighbors through the social layer and infected nodes consume all of the received resources to improve their recovery rate. The recovery rate of node is , where are the resources that node receives from its healthy neighbors and is an efficiency coefficient. Mathematically, the epidemic threshold can be approximately computed by a generalized dynamical message-passing approach based on the nonbacktracking matrix of the contact layer. Under this approach, the epidemic threshold is given by
| (51) |
where is the largest eigenvalue of , defined as , with being the Dirac delta function. Chen et al. found that a hybrid phase transition can be observed in SF networks, as shown in Fig. 27(a) and (b). The final infected proportion increases continuously with infection probability at ; a small increase in would induce a sudden jump in at . Here, and are the first and second thresholds, respectively. In addition, there are hysteresis loops in the phase transition. When the seed density is initially low, the epidemic breaks out at the invasion threshold , but at the persistence threshold if it is initially high. When the fraction of edge overlap of the two layers is decreased (e.g., when ), a hybrid phase transition appears (see Fig. 27(c)). Note that when the edges of the two layers overlap completely () the infected density smoothly increases from to (see Fig. 27(d)).
Fig. 27.
Epidemic spreading on multiplex networks with resource allocation. The infected density as a function of epidemic transmission rate . Results in scale-free network with exponent (a) and (b). Results in scale-free network with exponent with edge overlapping fraction (c) and (d) .
Reproduced from Ref. [312].
In this multilayer network framework, Chen et al. [313] further considered the case in which the diffusion of resources has a preferential tendency that the resource tends to spread to the nodes with higher () or lower () degrees, determined by a bias parameter . Specifically, the resource transfer probability from node to , , is
| (52) |
where only when . The model exhibits different types of phase transition, depending on the preference value . This dependence relation is nontrivial and determined by the interlayer degree correlation of the network. Moreover, there is an optimal strategy at any given strength of interlayer correlation, where the threshold reaches a maximum and under which the epidemic can be maximally suppressed.
The coevolution of resources and the network topology is also an interesting problem. Aoki et al. [314] proposed an adaptive model in which resources diffuse over a weighted network with edge weights adaptively varying depending on the resource distribution. The dynamics of node resources are governed by a reaction–diffusion process in which nodes are coupled through the weighted links of the network. Aoki et al. showed that under feasible conditions, the weights of the network robustly acquire SF distribution in the asymptotic state, even when the underlying topology of the network is not a SF degree distribution. Interestingly, in the case in which the system includes dissipation, it asymptotically realizes a dynamical phase characterized by an organized SF network, in which the ranking of each node with respect to the quantity of the resource it possesses changes ceaselessly. Regarding the epidemic dynamics, the weight of edges of a network may indicate the infectious strength, which can adaptively change during the epidemic process. Because the coevolution of resources and the network weight exhibits abundant and various properties, the coevolution of resources, network weight, and epidemic deserves further study.
5.3. Summary
In this section, we reviewed the progress in the study of the effects of resource diffusion on epidemic spreading processes. Resource consumption arises from the resource input to reduce the spreading rate and/or from the medical cost of curing to improve the recovery rate. The optimal solution of resource allocation can be found under constant resources. If the amount of total resources is limited, the epidemic may exhibit abrupt phase transitions at certain critical points, which is different from the traditional understanding that the optimal allocation strategy and its consequential outbreak size changes continuously with the total amount of resources. This critical phenomenon indicates that a slight lack of resource input may result in a catastrophic epidemic outbreak. In the case of coevolution, an inadequate resource production rate may cause an epidemic outbreak through abrupt phase transitions, similar to the case of inadequate constant resources. Individual behavior can induce complex coevolution dynamics with different types of critical phase transitions. This would depend on the complicated interplay among the intrinsic rules of epidemic spreading and behavioral responses of individuals, such as resource allocation strategies and the interlayer degree correlations between two networks.
6. Conclusions and outlooks
Studies of coevolution spreading dynamics are very popular in the field of network science, especially because of recent empirical observations, which indicate that some collective phenomena can hardly be understood by using single contagion models and the ignorance of the coevolving nature may yield misleading results. For instance, why a global epidemic can be contained once the awareness about the epidemic is induced, why a virus grows discontinuously in biology, and why an epidemic outbreak size exhibits bistable states for limited resources. Correct answers to these questions cannot be obtained by analyzing a single spreading process.
In this review, we presented the state of the art of the progress of coevolution spreading dynamics on complex networks. The landscape of the studies on coevolution spreading dynamics is presented in Fig. 28 . The two main classes of spreading dynamics are biological and social contagions, and the two types of coevolution spreading processes related to the control strategies are epidemic–awareness spreading and epidemic–resource spreading. As in the early stage of the progress of evolution spreading studies, many efforts have been made in analyzing various factors that are known to play significant roles in single spreading dynamics. In addition, most theoretical approaches introduced in this review were first developed to analyze single spreading dynamics. This situation will likely persist for years and then completely novel viewpoints and approaches may arise.
Fig. 28.
Landscape of coevolution spreading dynamics.
In the so-called big data era, the increasingly available empirical data on social platforms (such as Twitter and Facebook) and biological systems enables us to build more realistic data-driven coevolution spreading models. For the existing works, most of the known interacting mechanisms between two spreading contagions, such as synergy, competition, and asymmetrical, have not been verified by empirical data. Whether those coevolving mechanisms are sufficient to capture the main properties of real dynamics, or whether we still need more intricate interacting models is not yet clear to us. Therefore, we should first collect as much related data as possible. For example, one could crawl the forwarding time series, network topology, and personal information about news and products, and then analyze the interacting mechanisms between the news and products. To reveal the representative features of real coevolution spreading processes from empirical data (or, more valuably but with more difficulty, from designed experiments) is the most significant task facing the advancement of credible studies on mathematical models.
Another important aspect is that the coevolution spreading dynamics are largely affected by the network topology. To get analytical solutions of the coevolution spreading dynamics, most previous studies made some assumptions about the network topology, such as that the network is large, sparse, local-tree-like, or static. Studies on single spreading dynamics have already indicated that each assumption markedly alters the spreading dynamics; therefore, we should systematically study the effects of network topology on coevolution spreading dynamics from the microcosmic, mesoscopic, and macroscopic views. Furthermore, the spreading on adaptive networks [315] that also incorporates the coevolution of network topology should be investigated.
In addition, studies on human dynamics have revealed some inherent regularities of human behaviors, such as memory and burstiness in temporal activities [316], [317] and heterogeneity in mobility patterns [318], [319], which remarkably influence single spreading dynamics. Once the human dynamics are included, the interaction patterns and transmissibility among nodes will be affected, and thus the coevolution spreading will also be affected. Temporal and spatial network representations [17], as well as Monte Carlo simulations may be useful tools in this direction.
The resilience of coevolution spreading is a potentially interesting topic. The resilience of a system is its ability to maintain its functions when some errors and attacks occur, or some environmental and dynamical parameters are changed [320]. Previous studies mainly focused on the resilience of single dynamics, such as epidemic spreading [321], biological dynamics [322], climate changes [323], and financial dynamics [324]. Pananos et al. [325] studied the critical dynamics in a population with vaccinating behavior by extracting data on measles-related tweets and Google searches. They revealed the critical slowing down and critical speeding up for coevolution dynamics, which are markedly different from single spreading. Because the resilience depends on the dynamical process, do there exist some common characteristics for the resilience of coevolution spreading dynamics? For a given coevolution spreading process, how might its resilience be estimated?
To control the coevolution spreading dynamics, we should identify the most influential nodes, such that we can promote the spreading by letting these influential nodes be infected seeds or suppress the spreading by immunizing these nodes. For single spreading dynamics, some effective measures (e.g., -index [326] and -core [327]) and algorithms (e.g., PageRank [328], LeaderRank [329], collective influence [330], and some heuristic algorithms [331]) have been proposed. More detailed progress on vital node identification is presented in a recent review [27]. We should note that an effective vital node identification algorithm may not work for coevolution spreading dynamics. For instance, the nodes with high -shell values are more likely to be the influential nodes; however, those nodes may inhibit the spreading when there exist asymmetrical interactions between two dynamics. Therefore, the vital node identification problem should be redefined and reanalyzed for coevolution spreading dynamics.
Lastly, to our best knowledge, the existing theoretical approaches were originally designed for single spreading dynamics, and can only deal with certain specific situations in coevolution spreading dynamics. Generally speaking, the dynamical correlations in coevolution dynamics are stronger and more complicated than those in single dynamics, which demand novel theoretical approaches that may be based on but beyond the message passing approaches [53]. According to our intuition, the nonbacktracking matrix [332] and the Hankel matrix [333] may be useful tools for these theoretical analyses.
Acknowledgments
This work was partially supported by the China Postdoctoral Science Foundation (No. 2018M631073), China Postdoctoral Science Special Foundation (No. 2019T120829), and Fundamental Research Funds for the Central Universities, China. Y.H. and J.L. are supported by the National Natural Science Foundation of China Grants (Nos. 61773412 and U1711265), the Program for Guangdong Introducing Innovative and Entrepreneurial Teams, China (No. 2017ZT07X355), Guangzhou Science and Technology Project, China (No. 201804010473), Guangdong Research and Development Program in Key Fields, China under Grant 2019B020214002 and Three Big Constructions-Supercomputing Application Cultivation Projects sponsored by National Supercomputer Center in Guangzhou. T.Z. acknowledges the National Natural Science Foundation of China (No. 61433014) and the Science Promotion Program of UESTC, China (No. Y03111023901014006). We would like to thank J.C. Miller for his meaningful comments.
Editor: H. Orland
References
- 1.Keeling M.J., Rohani P. Princeton University Press; 2008. Modeling Infectious Diseases in Humans and Animals. [Google Scholar]
- 2.Centola D. Princeton University Press; 2018. How Behavior Spreads: The Science of Complex Contagions. [Google Scholar]
- 3.Lehmann S., Ahn Y.-Y. Springer; 2018. Complex Spreading Phenomena in Social Systems. [Google Scholar]
- 4.Anderson R.M., May R.M. Oxford university press; 1992. Infectious Diseases of Humans: Dynamics and Control. [Google Scholar]
- 5.Hethcote H.W. The mathematics of infectious diseases. SIAM Rev. 2000;42:599–653. [Google Scholar]
- 6.Brockmann D., Helbing D. The hidden geometry of complex, network-driven contagion phenomena. Science. 2013;342:1337–1342. doi: 10.1126/science.1245200. [DOI] [PubMed] [Google Scholar]
- 7.Lü L., Medo M., Yeung C.H., Zhang Y.-C., Zhang Z.-K., Zhou T. Recommender systems. Phys. Rep. 2012;519:1–49. [Google Scholar]
- 8.Helbing D. Globally networked risks and how to respond. Nature. 2013;497:51–59. doi: 10.1038/nature12047. [DOI] [PubMed] [Google Scholar]
- 9.Bernoulli D. Avec les Mémoires de Mathematique & de Physique; Paris: 1760. Essai Dune Nouvelle Analyse de la Mortalité CauséE Par la Petite Vérole et des avantages de Linoculation Pour la PréVenir, Histoire de L’Academie Royale Des Sciences; pp. 1–45. [Google Scholar]
- 10.Kermack W.O., McKendrick A.G. Contributions to the mathematical theory of epidemics. Bull. Math. Biol. 1991;53:33–55. doi: 10.1007/BF02464423. [DOI] [PubMed] [Google Scholar]
- 11.Erdös P., Rényi A. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci. 1960;5:17–61. [Google Scholar]
- 12.Marro J., Dickman R. Cambridge University Press; 2005. Nonequilibrium Phase Transitions in Lattice Models. [Google Scholar]
- 13.Barabási A.-L., Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- 14.Watts D.J., Strogatz S.H. Collective dynamics of small-world networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 15.Newman M.E.J. Modularity and community structure in networks. Proc. Natl. Acad. Sci. USA. 2006;103:8577–8582. doi: 10.1073/pnas.0601602103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kivelä M., Arenas A., Barthélemy M., Gleeson J.P., Moreno Y., Porter M.A. Multilayer networks. J. Complex Netw. 2014;2:203–271. [Google Scholar]
- 17.Barthélemy M. Spatial networks. Phys. Rep. 2011;499:1–101. [Google Scholar]
- 18.Holme P., Saramäki J. Temporal networks. Phys. Rep. 2012;519:97–125. [Google Scholar]
- 19.Pastor-Satorras R., Vespignani A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2001;86:3200. doi: 10.1103/PhysRevLett.86.3200. [DOI] [PubMed] [Google Scholar]
- 20.Hufnagel L., Brockmann D., Geisel T. Forecast and control of epidemics in a globalized world. Proc. Natl. Acad. Sci. USA. 2004;101:15124–15129. doi: 10.1073/pnas.0308344101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Belik V., Geisel T., Brockmann D. Natural human mobility patterns and spatial spread of infectious diseases. Phys. Rev. X. 2011;1 [Google Scholar]
- 22.Albert R., Barabási A.-L. Statistical mechanics of complex networks. Rev. Modern Phys. 2002;74:47–97. [Google Scholar]
- 23.Castellano C., Fortunato S., Loreto V. Statistical physics of social dynamics. Rev. Modern Phys. 2009;81:591–646. [Google Scholar]
- 24.Wang Z., Bauch C.T., Bhattacharyya S., d’Onofrio A., Manfredi P., Perc M., Perra N., Salathé M., Zhao D. Statistical physics of vaccination. Phys. Rep. 2016;664:1–113. [Google Scholar]
- 25.Pastor-Satorras R., Castellano C., Van Mieghem P., Vespignani A. Epidemic processes in complex networks. Rev. Modern Phys. 2015;87:925–979. [Google Scholar]
- 26.de Arruda G.F., Rodrigues F.A., Moreno Y. Fundamentals of spreading processes in single and multilayer complex networks. Phys. Rep. 2018;756:1–59. [Google Scholar]
- 27.Lü L., Chen D., Ren X.-L., Zhang Q.-M., Zhang Y.-C., Zhou T. Vital nodes identification in complex networks. Phys. Rep. 2016;650:1–63. [Google Scholar]
- 28.Wang W., Tang M., Stanley H.E., Braunstein L.A. Unification of theoretical approaches for epidemic spreading on complex networks. Rep. Progr. Phys. 2017;80 doi: 10.1088/1361-6633/aa5398. [DOI] [PubMed] [Google Scholar]
- 29.De Domenico M., Granell C., Porter M.A., Arenas A. The physics of spreading processes in multilayer networks. Nat. Phys. 2016;12:901–906. [Google Scholar]
- 30.Bauch C.T., Galvani A.P. Social factors in epidemiology. Science. 2013;342:47–49. doi: 10.1126/science.1244492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ferguson N.M., Galvani A.P., Bush R.M. Ecological and immunological determinants of influenza evolution. Nature. 2003;422:428–433. doi: 10.1038/nature01509. [DOI] [PubMed] [Google Scholar]
- 32.Abu-Raddad L.J., Patnaik P., Kublin J.G. Dual infection with HIV and malaria fuels the spread of both diseases in sub-saharan africa. Science. 2006;314:1603–1606. doi: 10.1126/science.1132338. [DOI] [PubMed] [Google Scholar]
- 33.Funk S., Gilad E., Watkins C., Jansen V.A. The spread of awareness and its impact on epidemic outbreaks. Proc. Natl. Acad. Sci. USA. 2009;106:6872–6877. doi: 10.1073/pnas.0810762106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Tai Z., Sun T. Media dependencies in a changing media environment the case of the 2003 SARS epidemic in china. New Media Soc. 2007;9:987–1009. [Google Scholar]
- 35.Newman M.E.J. Threshold effects for two pathogens spreading on a network. Phys. Rev. Lett. 2005;95 doi: 10.1103/PhysRevLett.95.108701. [DOI] [PubMed] [Google Scholar]
- 36.Cai W., Chen L., Ghanbarnejad F., Grassberger P. Avalanche outbreaks emerging in cooperative contagions. Nat. Phys. 2015;11:936–940. [Google Scholar]
- 37.Noh J.D., Park H. Asymmetrically coupled directed percolation systems. Phys. Rev. Lett. 2005;94 doi: 10.1103/PhysRevLett.94.145702. [DOI] [PubMed] [Google Scholar]
- 38.Hébert-Dufresne L., Althouse B.M. Complex dynamics of synergistic coinfections on realistically clustered networks. Proc. Natl. Acad. Sci. USA. 2015;112:10551–10556. doi: 10.1073/pnas.1507820112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhou T., Fu Z., Wang B.-H. Epidemic dynamics on complex networks. Progr. Natural Sci. 2006;16:452–457. [Google Scholar]
- 40.Dorogovtsev S.N., Goltsev A.V., Mendes J.F. Critical phenomena in complex networks. Rev. Modern Phys. 2008;80:1275–1335. [Google Scholar]
- 41.Zhang Z.-K., Liu C., Zhan X.-X., Lu X., Zhang C.-X., Zhang Y.-C. Dynamics of information diffusion and its applications on complex networks. Phys. Rep. 2016;651:1–34. [Google Scholar]
- 42.Wang L., Li X. Spatial epidemiology of networked metapopulation: An overview. Chin. Sci. Bull. 2014;59:3511–3522. doi: 10.1007/s11434-014-0499-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kiss I.Z., Miller J.C., Simon P. Springer; 2017. Mathematics of Epidemics on Networks: From Exact To Approximate Models. [Google Scholar]
- 44.Pastor-Satorras R., Vespignani A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2001;86:3200. doi: 10.1103/PhysRevLett.86.3200. [DOI] [PubMed] [Google Scholar]
- 45.Zhou T., Yan G., Wang B.-H. Maximal planar networks with large clustering coefficient and power-law degree distribution. Phys. Rev. E. 2005;71 doi: 10.1103/PhysRevE.71.046141. [DOI] [PubMed] [Google Scholar]
- 46.Newman M.E.J. Spread of epidemic disease on networks. Phys. Rev. E. 2002;66 doi: 10.1103/PhysRevE.66.016128. [DOI] [PubMed] [Google Scholar]
- 47.Hu Y., Ji S., Jin Y., Feng L., Stanley H.E., Havlin S. Local structure can identify and quantify influential global spreaders in large scale social networks. Proc. Natl. Acad. Sci. USA. 2018;115:7468–7472. doi: 10.1073/pnas.1710547115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Goltsev A.V., Dorogovtsev S.N., Oliveira J., Mendes J.F. Localization and spreading of diseases in complex networks. Phys. Rev. Lett. 2012;109 doi: 10.1103/PhysRevLett.109.128702. [DOI] [PubMed] [Google Scholar]
- 49.Gómez S., Arenas A., Borge-Holthoefer J., Meloni S., Moreno Y. Discrete-time markov chain approach to contact-based disease spreading in complex networks. Europhys. Lett. 2010;89:38009. [Google Scholar]
- 50.Van Mieghem P., Omic J., Kooij R. Virus spread in networks. IEEE/ACM Trans. Netw. 2009;17:1–14. [Google Scholar]
- 51.Chung F., Lu L., Vu V. Spectra of random graphs with given expected degrees. Proc. Natl. Acad. Sci. USA. 2003;100:6313–6318. doi: 10.1073/pnas.0937490100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Altarelli F., Braunstein A., Dall’Asta L., Wakeling J.R., Zecchina R. Containing epidemic outbreaks by message-passing techniques. Phys. Rev. X. 2014;4 [Google Scholar]
- 53.Karrer B., Newman M.E.J. Message passing approach for general epidemic models. Phys. Rev. E. 2010;82 doi: 10.1103/PhysRevE.82.016101. [DOI] [PubMed] [Google Scholar]
- 54.Shrestha M., Scarpino S.V., Moore C. Message-passing approach for recurrent-state epidemic models on networks. Phys. Rev. E. 2015;92 doi: 10.1103/PhysRevE.92.022821. [DOI] [PubMed] [Google Scholar]
- 55.Castellano C., Pastor-Satorras R. Relating topological determinants of complex networks to their spectral properties: Structural and dynamical effects. Phys. Rev. X. 2017;7 [Google Scholar]
- 56.Wang W., Liu Q.-H., Zhong L.-F., Tang M., Gao H., Stanley H.E. Predicting the epidemic threshold of the susceptible-infected-recovered model. Sci. Rep. 2016;6:24676. doi: 10.1038/srep24676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Altarelli F., Braunstein A., Dall’Asta L., Lage-Castellanos A., Zecchina R. Bayesian Inference of epidemics on networks via belief propagation. Phys. Rev. Lett. 2014;112 doi: 10.1103/PhysRevLett.112.118701. [DOI] [PubMed] [Google Scholar]
- 58.Zhao J.-H., Zhou H.-J. Feedback arcs and node hierarchy in directed networks. Chin. Phys. B. 2017;7 [Google Scholar]
- 59.Eames K.T., Keeling M.J. Modeling dynamic and network heterogeneities in the spread of sexually transmitted diseases. Proc. Natl. Acad. Sci. USA. 2002;99:13330–13335. doi: 10.1073/pnas.202244299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Gleeson J.P. High-accuracy approximation of binary-state dynamics on networks. Phys. Rev. Lett. 2011;107 doi: 10.1103/PhysRevLett.107.068701. [DOI] [PubMed] [Google Scholar]
- 61.Cai C.-R., Wu Z.-X., Chen M.Z., Holme P., Guan J.-Y. Solving the dynamic correlation problem of the susceptible-infected-susceptible model on networks. Phys. Rev. Lett. 2016;116 doi: 10.1103/PhysRevLett.116.258301. [DOI] [PubMed] [Google Scholar]
- 62.Gleeson J.P., Melnik S., Ward J.A., Porter M.A., Mucha P.J. Accuracy of mean-field theory for dynamics on real-world networks. Phys. Rev. E. 2012;85 doi: 10.1103/PhysRevE.85.026106. [DOI] [PubMed] [Google Scholar]
- 63.Newman M.E.J. Assortative mixing in networks. Phys. Rev. Lett. 2002;89 doi: 10.1103/PhysRevLett.89.208701. [DOI] [PubMed] [Google Scholar]
- 64.Boguná M., Pastor-Satorras R., Vespignani A. Absence of epidemic threshold in scale-free networks with degree correlations. Phys. Rev. Lett. 2003;90 doi: 10.1103/PhysRevLett.90.028701. [DOI] [PubMed] [Google Scholar]
- 65.Newman M.E.J. Clustering and preferential attachment in growing networks. Phys. Rev. E. 2001;64 doi: 10.1103/PhysRevE.64.025102. [DOI] [PubMed] [Google Scholar]
- 66.Eguiluz V.M., Klemm K. Epidemic threshold in structured scale-free networks. Phys. Rev. Lett. 2002;89 doi: 10.1103/PhysRevLett.89.108701. [DOI] [PubMed] [Google Scholar]
- 67.Miller J.C. Percolation and epidemics in random clustered networks. Phys. Rev. E. 2009;80 doi: 10.1103/PhysRevE.80.020901. [DOI] [PubMed] [Google Scholar]
- 68.Miller J.C. Spread of infectious disease through clustered populations. J. R. Soc. Interface. 2009;6:1121–1134. doi: 10.1098/rsif.2008.0524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Serrano M.Á., Boguná M. Percolation and epidemic thresholds in clustered networks. Phys. Rev. Lett. 2006;97 doi: 10.1103/PhysRevLett.97.088701. [DOI] [PubMed] [Google Scholar]
- 70.Newman M.E.J. Random graphs with clustering. Phys. Rev. Lett. 2009;103 doi: 10.1103/PhysRevLett.103.058701. [DOI] [PubMed] [Google Scholar]
- 71.Wang W., Wang Z.-X., Cai S.-M. Critical phenomena of information spreading dynamics on networks with cliques. Phys. Rev. E. 2018;98 [Google Scholar]
- 72.Noël P.-A., Davoudi B., Brunham R.C., Dubé L.J., Pourbohloul B. Time evolution of epidemic disease on finite and infinite networks. Phys. Rev. E. 2009;79 doi: 10.1103/PhysRevE.79.026101. [DOI] [PubMed] [Google Scholar]
- 73.Ferreira S.C., Castellano C., Pastor-Satorras R. Epidemic thresholds of the susceptible-infected-susceptible model on networks: A comparison of numerical and theoretical results. Phys. Rev. E. 2012;86 doi: 10.1103/PhysRevE.86.041125. [DOI] [PubMed] [Google Scholar]
- 74.Shu P., Wang W., Tang M., Zhao P., Zhang Y.-C. Recovery rate affects the effective epidemic threshold with synchronous updating. Chaos. 2016;26 doi: 10.1063/1.4953661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Mata A.S., Ferreira S.C. Multiple transitions of the susceptible-infected-susceptible epidemic model on complex networks. Phys. Rev. E. 2015;91 doi: 10.1103/PhysRevE.91.012816. [DOI] [PubMed] [Google Scholar]
- 76.Hong H., Ha M., Park H. Finite-size scaling in complex networks. Phys. Rev. Lett. 2007;98 doi: 10.1103/PhysRevLett.98.258701. [DOI] [PubMed] [Google Scholar]
- 77.Fortunato S., Hric D. Community detection in networks: A user guide. Phys. Rep. 2016;659:1–44. [Google Scholar]
- 78.Liu Z., Hu B. Epidemic spreading in community networks. Europhys. Lett. 2005;72:315. [Google Scholar]
- 79.Chen J., Zhang H., Guan Z.-H., Li T. Epidemic spreading on networks with overlapping community structure. Physica A. 2012;391:1848–1854. [Google Scholar]
- 80.Huang W., Li C. Epidemic spreading in scale-free networks with community structure. J. Stat. Mech. Theory Exp. 2007:P01014. [Google Scholar]
- 81.Barrat A., Barthélemy M., Pastor-Satorras R., Vespignani A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA. 2004;101:3747–3752. doi: 10.1073/pnas.0400087101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Yan G., Zhou T., Wang J., Fu Z.-Q., Wang B.-H. Epidemic spread in weighted scale-free networks. Chin. Phys. Lett. 2005;22:510. [Google Scholar]
- 83.Yang Z., Zhou T. Epidemic spreading in weighted networks: An edge-based mean-field solution. Phys. Rev. E. 2012;85 doi: 10.1103/PhysRevE.85.056106. [DOI] [PubMed] [Google Scholar]
- 84.Wang W., Tang M., Zhang H.-F., Gao H., Do Y., Liu Z.-H. Epidemic spreading on complex networks with general degree and weight distributions. Phys. Rev. E. 2014;90 doi: 10.1103/PhysRevE.90.042803. [DOI] [PubMed] [Google Scholar]
- 85.Boccaletti S., Bianconi G., Criado R., Del Genio C.I., Gómez-Gardeñes J., Romance M., Sendiña-Nadal I., Wang Z., Zanin M. The structure and dynamics of multilayer networks. Phys. Rep. 2014;544:1–122. doi: 10.1016/j.physrep.2014.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Gao J., Buldyrev S.V., Stanley H.E., Havlin S. Networks formed from interdependent networks. Nat. Phys. 2012;8:40–48. doi: 10.1103/PhysRevE.85.066134. [DOI] [PubMed] [Google Scholar]
- 87.Bianconi G. Oxford University Press; 2018. Multilayer Networks Structure and Function. [Google Scholar]
- 88.Saumell-Mendiola A., Serrano M.Á., Boguná M. Epidemic spreading on interconnected networks. Phys. Rev. E. 2012;86 doi: 10.1103/PhysRevE.86.026106. [DOI] [PubMed] [Google Scholar]
- 89.Dickison M., Havlin S., Stanley H.E. Epidemics on interconnected networks. Phys. Rev. E. 2012;85 doi: 10.1103/PhysRevE.85.066109. [DOI] [PubMed] [Google Scholar]
- 90.de Arruda G.F., Cozzo E., Peixoto T.P., Rodrigues F.A., Moreno Y. Disease localization in multilayer networks. Phys. Rev. X. 2017;7 [Google Scholar]
- 91.Liu Q.-H., Ajelli M., Aleta A., Merler S., Moreno Y., Vespignani A. Measurability of the epidemic reproduction number in data-driven contact networks. Proc. Natl. Acad. Sci. USA. 2018;115:12680–12685. doi: 10.1073/pnas.1811115115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Perra N., Gonçalves B., Pastor-Satorras R., Vespignani A. Activity driven modeling of time varying networks. Sci. Rep. 2012;2:469. doi: 10.1038/srep00469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Sun K., Baronchelli A., Perra N. Contrasting effects of strong ties on sir and sis processes in temporal networks. Eur. Phys. J. B. 2015;88:326. [Google Scholar]
- 94.Liu Q.-H., Xiong X., Zhang Q., Perra N. Epidemic spreading on time-varying multiplex networks. Phys. Rev. E. 2018;98 [Google Scholar]
- 95.Starnini M., Gleeson J.P., Boguñá M. Equivalence between non-markovian and markovian dynamics in epidemic spreading processes. Phys. Rev. Lett. 2017;118 doi: 10.1103/PhysRevLett.118.128301. [DOI] [PubMed] [Google Scholar]
- 96.Vasco D.A., Wearing H.J., Rohani P. Tracking the dynamics of pathogen interactions: modeling ecological and immune-mediated processes in a two-pathogen single-host system. J. Theoret. Biol. 2007;245:9–25. doi: 10.1016/j.jtbi.2006.08.015. [DOI] [PubMed] [Google Scholar]
- 97.Castillo-Chavez C., Huang W., Li J. Competitive exclusion in gonorrhea models and other sexually transmitted diseases. SIAM J. Appl. Math. 1996;56:494–508. [Google Scholar]
- 98.Andreasen V., Lin J., Levin S.A. The dynamics of cocirculating influenza strains conferring partial cross-immunity. J. Math. Biol. 1997;35:825–842. doi: 10.1007/s002850050079. [DOI] [PubMed] [Google Scholar]
- 99.Newman M.E.J., Ferrario C.R. Interacting epidemics and coinfection on contact networks. PLoS ONE. 2013;8 doi: 10.1371/journal.pone.0071321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Freeman E.E., Weiss H.A., Glynn J.R., Cross P.L., Whitworth J.A., Hayes R.J. Herpes simplex virus 2 infection increases HIV acquisition in men and women: Systematic review and meta-analysis of longitudinal studies. AIDS. 2006;20:73–83. doi: 10.1097/01.aids.0000198081.09337.a7. [DOI] [PubMed] [Google Scholar]
- 101.Bansal S., Meyers L.A. The impact of past epidemics on future disease dynamics. J. Theoret. Biol. 2012;309:176–184. doi: 10.1016/j.jtbi.2012.06.012. [DOI] [PubMed] [Google Scholar]
- 102.Funk S., Jansen V.A. Interacting epidemics on overlay networks. Phys. Rev. E. 2010;81 doi: 10.1103/PhysRevE.81.036118. [DOI] [PubMed] [Google Scholar]
- 103.Zhou S., Xu S., Wang L., Liu Z., Chen G., Wang X. Propagation of interacting diseases on multilayer networks. Phys. Rev. E. 2018;98 doi: 10.1103/PhysRevE.98.012303. [DOI] [PubMed] [Google Scholar]
- 104.Karrer B., Newman M.E.J. Competing epidemics on complex networks. Phys. Rev. E. 2011;84 doi: 10.1103/PhysRevE.84.036106. [DOI] [PubMed] [Google Scholar]
- 105.Miller J.C. Cocirculation of infectious diseases on networks. Phys. Rev. E. 2013;87 doi: 10.1103/PhysRevE.87.060801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Poletto C., Meloni S., Colizza V., Moreno Y., Vespignani A. Host mobility drives pathogen competition in spatially structured populations. PLoS Comput. Biol. 2013;9 doi: 10.1371/journal.pcbi.1003169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Poletto C., Meloni S., Van Metre A., Colizza V., Moreno Y., Vespignani A. Characterising two-pathogen competition in spatially structured environments. Sci. Rep. 2015;5:7895. doi: 10.1038/srep07895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Prakash B.A., Beutel A., Rosenfeld R., Faloutsos C. Proceedings of the 21st International Conference on World Wide Web. ACM; 2012. Winner takes all: competing viruses or ideas on fair-play networks; pp. 1037–1046. [Google Scholar]
- 109.Beutel A., Prakash B.A., Rosenfeld R., Faloutsos C. Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM; 2012. Interacting viruses in networks: Can both survive? pp. 426–434. [Google Scholar]
- 110.van de Bovenkamp R., Kuipers F., Van Mieghem P. Domination-time dynamics in susceptible-infected-susceptible virus competition on networks. Phys. Rev. E. 2014;89 doi: 10.1103/PhysRevE.89.042818. [DOI] [PubMed] [Google Scholar]
- 111.Yang L.-X., Yang X., Tang Y.Y. A bi-virus competing spreading model with generic infection rates. IEEE Trans. Netw. Sci. Eng. 2018;5:2–13. [Google Scholar]
- 112.Yang L.-X., Li P., Yang X., Wu Y., Tang Y.Y. On the competition of two conflicting messages. Nonlinear Dynam. 2018;91:1853–1869. [Google Scholar]
- 113.Wang Y., Xiao G., Liu J. Dynamics of competing ideas in complex social systems. New J. Phys. 2012;14 [Google Scholar]
- 114.Sahneh F.D., Scoglio C. Competitive epidemic spreading over arbitrary multilayer networks. Phys. Rev. E. 2014;89 doi: 10.1103/PhysRevE.89.062817. [DOI] [PubMed] [Google Scholar]
- 115.Grassberger P., Chen L., Ghanbarnejad F., Cai W. Phase transitions in cooperative coinfections: Simulation results for networks and lattices. Phys. Rev. E. 2016;93 doi: 10.1103/PhysRevE.93.042316. [DOI] [PubMed] [Google Scholar]
- 116.Chen L., Ghanbarnejad F., Brockmann D. Fundamental properties of cooperative contagion processes. New J. Phys. 2017;19 [Google Scholar]
- 117.Chen L., Ghanbarnejad F., Cai W., Grassberger P. Outbreaks of coinfections: The critical role of cooperativity. Europhys. Lett. 2013;104:50001. [Google Scholar]
- 118.Chen L. Persistent spatial patterns of interacting contagions. Phys. Rev. E. 2019;99 doi: 10.1103/PhysRevE.99.022308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Cui P.-B., Colaiori F., Castellano C. Mutually cooperative epidemics on power-law networks. Phys. Rev. E. 2017;96 doi: 10.1103/PhysRevE.96.022301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Cui P.-B., Colaiori F., Castellano C. Effect of network clustering on mutually cooperative coinfections. Phys. Rev. E. 2019;99 doi: 10.1103/PhysRevE.99.022301. [DOI] [PubMed] [Google Scholar]
- 121.Azimi-Tafreshi N. Cooperative epidemics on multiplex networks. Phys. Rev. E. 2016;93 doi: 10.1103/PhysRevE.93.042303. [DOI] [PubMed] [Google Scholar]
- 122.Zhao Y., Zheng M., Liu Z. A unified framework of mutual influence between two pathogens in multiplex networks. Chaos. 2014;24 doi: 10.1063/1.4902254. [DOI] [PubMed] [Google Scholar]
- 123.Ferguson N., Anderson R., Gupta S. The effect of antibody-dependent enhancement on the transmission dynamics and persistence of multiple-strain pathogens. Proc. Natl. Acad. Sci. USA. 1999;96:790–794. doi: 10.1073/pnas.96.2.790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Nowak M.A., May R.M., Phillips R.E., Rowland-Jones S., Lalloo D.G., McAdam S., Klenerman P., Köppe B., Sigmund K., Bangham C.R. Antigenic oscillations and shifting immunodominance in HIV-1 infections. Nature. 1995;375:606–611. doi: 10.1038/375606a0. [DOI] [PubMed] [Google Scholar]
- 125.Richardson A.R., Yu Z., Popovic T., Stojiljkovic I. Mutator clones of neisseria meningitidis in epidemic serogroup a disease. Proc. Natl. Acad. Sci. USA. 2002;99:6103–6107. doi: 10.1073/pnas.092568699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Hughes A.L. Evolutionary change of predicted cytotoxic t cell epitopes of dengue virus. Infect. Genet. Evol. 2001;1:123–130. doi: 10.1016/s1567-1348(01)00013-2. [DOI] [PubMed] [Google Scholar]
- 127.Abu-Raddad L., Van der Ventel B., Ferguson N. Interactions of multiple strain pathogen diseases in the presence of coinfection, cross immunity, and arbitrary strain diversity. Phys. Rev. Lett. 2008;100 doi: 10.1103/PhysRevLett.100.168102. [DOI] [PubMed] [Google Scholar]
- 128.Gog J.R., Grenfell B.T. Dynamics and selection of many-strain pathogens. Proc. Natl. Acad. Sci. USA. 2002;99:17209–17214. doi: 10.1073/pnas.252512799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Abu-Raddad L., Ferguson N. Characterizing the symmetric equilibrium of multi-strain host-pathogen systems in the presence of cross immunity. J. Math. Biol. 2005;50:531–558. doi: 10.1007/s00285-004-0292-4. [DOI] [PubMed] [Google Scholar]
- 130.Kamo M., Sasaki A. The effect of cross-immunity and seasonal forcing in a multi-strain epidemic model. Physica D. 2002;165:228–241. [Google Scholar]
- 131.Shrestha S., King A.A., Rohani P. Statistical inference for multi-pathogen systems. PLoS Comput. Biol. 2011;7 doi: 10.1371/journal.pcbi.1002135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Juul J., Sneppen K. Locally self-organized quasicritical percolation in a multiple-disease model. Phys. Rev. E. 2011;84 doi: 10.1103/PhysRevE.84.036119. [DOI] [PubMed] [Google Scholar]
- 133.Sneppen K., Trusina A., Jensen M.H., Bornholdt S. A minimal model for multiple epidemics and immunity spreading. PLoS ONE. 2010;5 doi: 10.1371/journal.pone.0013326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Zarei F., Moghimi-Araghi S., Ghanbarnejad F. Exact solution of generalized cooperative usceptible-infected-removed (SIR) dynamics. Phys. Rev. E. 2019;100 doi: 10.1103/PhysRevE.100.012307. arXiv:1901.02702. [DOI] [PubMed] [Google Scholar]
- 135.Rogers E.M. Simon and Schuster; 2010. Diffusion of Innovations. [Google Scholar]
- 136.Centola D. The spread of behavior in an online social network experiment. Science. 2010;329:1194–1197. doi: 10.1126/science.1185231. [DOI] [PubMed] [Google Scholar]
- 137.Granovetter M.S. The strength of weak ties. Am. J. Sociol. 1973;78:1360–1380. [Google Scholar]
- 138.Watts D.J. A simple model of global cascades on random networks. Proc. Natl. Acad. Sci. USA. 2002;99:5766–5771. doi: 10.1073/pnas.082090499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Coates T.J., Richter L., Caceres C. Behavioural strategies to reduce hiv transmission: how to make them work better. Lancet. 2008;372:669–684. doi: 10.1016/S0140-6736(08)60886-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Lü L., Chen D.-B., Zhou T. The small world yields the most effective information spreading. New J. Phys. 2011;13 [Google Scholar]
- 141.Zheng M., Lü L., Zhao M. Spreading in online social networks: The role of social reinforcement. Phys. Rev. E. 2013;88 doi: 10.1103/PhysRevE.88.012818. [DOI] [PubMed] [Google Scholar]
- 142.Powell L.M., Tauras J.A., Ross H. The importance of peer effects, cigarette prices and tobacco control policies for youth smoking behavior. J. Health Econom. 2005;24:950–968. doi: 10.1016/j.jhealeco.2005.02.002. [DOI] [PubMed] [Google Scholar]
- 143.Christakis N.A., Fowler J.H. The collective dynamics of smoking in a large social network. N. Engl. J. Med. 2008;358:2249–2258. doi: 10.1056/NEJMsa0706154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Myneni S., Fujimoto K., Cobb N., Cohen T. Content-driven analysis of an online community for smoking cessation: Integration of qualitative techniques, automated text analysis, and affiliation networks. Am J Public Health. 2015;105:1206–1212. doi: 10.2105/AJPH.2014.302464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Aral S., Nicolaides C. Exercise contagion in a global social network. Nature Commun. 2017;8:14753. doi: 10.1038/ncomms14753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Bandiera O., Rasul I. Social networks and technology adoption in northern mozambique. Econ. J. 2006;116:869–902. [Google Scholar]
- 147.Karsai M., Iñiguez G., Kaski K., Kertész J. Complex contagion process in spreading of online innovation. J. R. Soc. Interface. 2014;11 doi: 10.1098/rsif.2014.0694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Ugander J., Backstrom L., Marlow C., Kleinberg J. Structural diversity in social contagion. Proc. Natl. Acad. Sci. USA. 2012;109:5962–5966. doi: 10.1073/pnas.1116502109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Toole J.L., Cha M., González M.C. Modeling the adoption of innovations in the presence of geographic and media influences. PLoS ONE. 2012;7 doi: 10.1371/journal.pone.0029528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Oster E., Thornton R. Determinants of technology adoption: Peer effects in menstrual cup take-up. J. Eur. Econom. Assoc. 2012;10:1263–1293. [Google Scholar]
- 151.Banerjee A., Chandrasekhar A.G., Duflo E., Jackson M.O. The diffusion of microfinance. Science. 2013;341 doi: 10.1126/science.1236498. [DOI] [PubMed] [Google Scholar]
- 152.Weiss C.H., Poncela-Casasnovas J., Glaser J.I., Pah A.R., Persell S.D., Baker D.W., Wunderink R.G., Amaral L.A.N. Adoption of a high-impact innovation in a homogeneous population. Phys. Rev. X. 2014;4 doi: 10.1103/PhysRevX.4.041008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Bond R.M., Fariss C.J., Jones J.J., Kramer A.D., Marlow C., Settle J.E., Fowler J.H. A 61-million-person experiment in social influence and political mobilization. Nature. 2012;489:295–298. doi: 10.1038/nature11421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Romero D.M., Meeder B., Kleinberg J. Proceedings of the 20th International Conference on World Wide Web. ACM; 2011. Differences in the mechanics of information diffusion across topics: Idioms, political hashtags, and complex contagion on twitter; pp. 695–704. [Google Scholar]
- 155.Gao J., Jun B., Pentland A., Zhou T., Hidalgo C.A. 2017. Collective learning in China’s regional economic development. arXiv:1703.01369. [Google Scholar]
- 156.Granovetter M. Threshold models of collective behavior. Am. J. Sociol. 1978;83:1420–1443. [Google Scholar]
- 157.Miller J.C. Equivalence of several generalized percolation models on networks. Phys. Rev. E. 2016;94 doi: 10.1103/PhysRevE.94.032313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Ikeda Y., Hasegawa T., Nemoto K. CaScade dynamics on clustered network. J. Phys.: Conf. Ser. 2010;221 [Google Scholar]
- 159.Hackett A., Melnik S., Gleeson J.P. CaScades on a class of clustered random networks. Phys. Rev. E. 2011;83 doi: 10.1103/PhysRevE.83.056107. [DOI] [PubMed] [Google Scholar]
- 160.Miller J.C. Complex contagions and hybrid phase transitions. J. Complex Netw. 2015;4:201–223. [Google Scholar]
- 161.Hackett A., Gleeson J.P. Cascades on clique-based graphs. Phys. Rev. E. 2013;87 doi: 10.1103/PhysRevE.87.062801. [DOI] [PubMed] [Google Scholar]
- 162.Gleeson J.P. Bond percolation on a class of clustered random networks. Phys. Rev. E. 2009;80 doi: 10.1103/PhysRevE.80.036107. [DOI] [PubMed] [Google Scholar]
- 163.Gleeson J.P. Cascades on correlated and modular random networks. Phys. Rev. E. 2008;77 doi: 10.1103/PhysRevE.77.046117. [DOI] [PubMed] [Google Scholar]
- 164.Dodds P.S., Payne J.L. Analysis of a threshold model of social contagion on degree-correlated networks. Phys. Rev. E. 2009;79 doi: 10.1103/PhysRevE.79.066115. [DOI] [PubMed] [Google Scholar]
- 165.Payne J.L., Dodds P.S., Eppstein M.J. Information cascades on degree-correlated random networks. Phys. Rev. E. 2009;80 doi: 10.1103/PhysRevE.80.026125. [DOI] [PubMed] [Google Scholar]
- 166.Galstyan A., Cohen P. Cascading dynamics in modular networks. Phys. Rev. E. 2007;75 doi: 10.1103/PhysRevE.75.036109. [DOI] [PubMed] [Google Scholar]
- 167.Curato G., Lillo F. Optimal information diffusion in stochastic block models. Phys. Rev. E. 2016;94 doi: 10.1103/PhysRevE.94.032310. [DOI] [PubMed] [Google Scholar]
- 168.Nematzadeh A., Ferrara E., Flammini A., Ahn Y.-Y. Optimal network modularity for information diffusion. Phys. Rev. Lett. 2014;113 doi: 10.1103/PhysRevLett.113.088701. [DOI] [PubMed] [Google Scholar]
- 169.Wu J., Du R., Zheng Y., Liu D. Optimal multi-community network modularity for information diffusion. Internat. J. Modern Phys. C. 2016;27 [Google Scholar]
- 170.Hurd T.R., Gleeson J.P. On Watts’ cascade model with random link weights. J. Complex Netw. 2013;1:25–43. [Google Scholar]
- 171.Unicomb S., Iñiguez G., Karsai M. Threshold driven contagion on weighted networks. Sci. Rep. 2018;8:3094. doi: 10.1038/s41598-018-21261-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Brummitt C.D., Lee K.-M., Goh K.-I. Multiplexity-facilitated cascades in networks. Phys. Rev. E. 2012;85 doi: 10.1103/PhysRevE.85.045102. [DOI] [PubMed] [Google Scholar]
- 173.Yağan O., Gligor V. Analysis of complex contagions in random multiplex networks. Phys. Rev. E. 2012;86 doi: 10.1103/PhysRevE.86.036103. [DOI] [PubMed] [Google Scholar]
- 174.Zhuang Y., Arenas A., Yağan O. Clustering determines the dynamics of complex contagions in multiplex networks. Phys. Rev. E. 2017;95 doi: 10.1103/PhysRevE.95.012312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175.Lee K.-M., Brummitt C.D., Goh K.-I. Threshold cascades with response heterogeneity in multiplex networks. Phys. Rev. E. 2014;90 doi: 10.1103/PhysRevE.90.062816. [DOI] [PubMed] [Google Scholar]
- 176.Li Z., Yan F., Jiang Y. Cross-layers cascade in multiplex networks. Auton. Agents Multi-Agent Syst. 2015;29:1186–1215. [Google Scholar]
- 177.Karimi F., Holme P. Threshold model of cascades in empirical temporal networks. Physica A. 2013;392:3476–3483. [Google Scholar]
- 178.Takaguchi T., Masuda N., Holme P. Bursty communication patterns facilitate spreading in a threshold-based epidemic dynamics. PLoS ONE. 2013;8 doi: 10.1371/journal.pone.0068629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179.Backlund V.-P., Saramäki J., Pan R.K. Effects of temporal correlations on cascades: Threshold models on temporal networks. Phys. Rev. E. 2014;89 doi: 10.1103/PhysRevE.89.062815. [DOI] [PubMed] [Google Scholar]
- 180.Melnik S., Ward J.A., Gleeson J.P., Porter M.A. Multi-stage complex contagions. Chaos. 2013;23 doi: 10.1063/1.4790836. [DOI] [PubMed] [Google Scholar]
- 181.Liu Q.-H., Lü F.-M., Zhang Q., Tang M., Zhou T. Impacts of opinion leaders on social contagions. Chaos. 2018;28 doi: 10.1063/1.5017515. [DOI] [PubMed] [Google Scholar]
- 182.Kobayashi T. Trend-driven information cascades on random networks. Phys. Rev. E. 2015;92 doi: 10.1103/PhysRevE.92.062823. [DOI] [PubMed] [Google Scholar]
- 183.Huang W.-M., Zhang L.-J., Xu X.-J., Fu X. Contagion on complex networks with persuasion. Sci. Rep. 2016;6:23766. doi: 10.1038/srep23766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 184.Ruan Z., Iniguez G., Karsai M., Kertész J. Kinetics of social contagion. Phys. Rev. Lett. 2015;115 doi: 10.1103/PhysRevLett.115.218702. [DOI] [PubMed] [Google Scholar]
- 185.Juul J.S., Porter M.A. Synergistic effects in threshold models on networks. Chaos. 2018;28 doi: 10.1063/1.5017962. [DOI] [PubMed] [Google Scholar]
- 186.Oh S.-W., Porter M.A. Complex contagions with timers. Chaos. 2018;28 doi: 10.1063/1.4990038. [DOI] [PubMed] [Google Scholar]
- 187.Dodds P.S., Watts D.J. Universal behavior in a generalized model of contagion. Phys. Rev. Lett. 2004;92 doi: 10.1103/PhysRevLett.92.218701. [DOI] [PubMed] [Google Scholar]
- 188.Dodds P.S., Watts D.J. A generalized model of social and biological contagion. J. Theoret. Biol. 2005;232:587–604. doi: 10.1016/j.jtbi.2004.09.006. [DOI] [PubMed] [Google Scholar]
- 189.Wang W., Tang M., Zhang H.-F., Lai Y.-C. Dynamics of social contagions with memory of nonredundant information. Phys. Rev. E. 2015;92 doi: 10.1103/PhysRevE.92.012820. [DOI] [PubMed] [Google Scholar]
- 190.Zhu Y.-X., Wang W., Tang M., Ahn Y.-Y. Social contagions on weighted networks. Phys. Rev. E. 2017;96 doi: 10.1103/PhysRevE.96.012306. [DOI] [PubMed] [Google Scholar]
- 191.Su Z., Wang W., Li L., Stanley H.E., Braunstein L.A. Optimal community structure for social contagions. New J. Phys. 2018;20 [Google Scholar]
- 192.Liu M.-X., Wang W., Liu Y., Tang M., Cai S.-M., Zhang H.-F. Social contagions on time-varying community networks. Phys. Rev. E. 2017;95 doi: 10.1103/PhysRevE.95.052306. [DOI] [PubMed] [Google Scholar]
- 193.Shu P., Gao L., Zhao P., Wang W., Stanley H.E. Social contagions on interdependent lattice networks. Sci. Rep. 2017;7:44669. doi: 10.1038/srep44669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 194.Wang W., Cai M., Zheng M. Social contagions on correlated multiplex networks. Physica A. 2018;499:121–128. [Google Scholar]
- 195.Zou Y., Xiong Z., Zhang P., Wang W. Social contagions on multiplex networks with different reliability. Physica A. 2018;506:728–735. [Google Scholar]
- 196.Wu J., Zheng M., Wang W., Yang H., Gu C. Double transition of information spreading in a two-layered network. Chaos. 2018;28 doi: 10.1063/1.5038853. [DOI] [PubMed] [Google Scholar]
- 197.Chen L.-J., Chen X.-L., Cai M., Wang W. Complex contagions with social reinforcement from different layers and neighbors. Physica A. 2018;503:516–525. [Google Scholar]
- 198.Wang W., Tang M., Shu P., Wang Z. Dynamics of social contagions with heterogeneous adoption thresholds: Crossover phenomena in phase transition. New J. Phys. 2016;18 [Google Scholar]
- 199.Zhu X., Wang W., Cai S., Stanley H.E. Dynamics of social contagions with local trend imitation. Sci. Rep. 2018;8:7335. doi: 10.1038/s41598-018-25006-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 200.Zhu X., Wang W., Cai S., Stanley H.E. Optimal imitation capacity and crossover phenomenon in the dynamics of social contagions. J. Stat. Mech. Theory Exp. 2018 [Google Scholar]
- 201.Su Z., Wang W., Li L., Xiao J., Stanley H.E. Emergence of hysteresis loop in social contagions on complex networks. Sci. Rep. 2017;7:6103. doi: 10.1038/s41598-017-06286-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202.Wang W., Tang M., Stanley H.E., Braunstein L.A. Social contagions with communication channels alternation on multiplex networks. Phys. Rev. E. 2018;98 [Google Scholar]
- 203.Wang W., Stanley H.E., Braunstein L.A. Effects of time-delays in the dynamics of social contagions. New J. Phys. 2018;20 [Google Scholar]
- 204.Ludlam J.J., Gibson G.J., Otten W., Gilligan C.A. Applications of percolation theory to fungal spread with synergy. J. R. Soc. Interface. 2012;9:949–956. doi: 10.1098/rsif.2011.0506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 205.Pérez-Reche F.J., Ludlam J.J., Taraskin S.N., Gilligan C.A. Synergy in spreading processes: From exploitative to explorative foraging strategies. Phys. Rev. Lett. 2011;106 doi: 10.1103/PhysRevLett.106.218701. [DOI] [PubMed] [Google Scholar]
- 206.Taraskin S.N., Pérez-Reche F.J. Effects of variable-state neighborhoods for spreading synergystic processes on lattices. Phys. Rev. E. 2013;88 doi: 10.1103/PhysRevE.88.062815. [DOI] [PubMed] [Google Scholar]
- 207.Broder-Rodgers D., Pérez-Reche F.J., Taraskin S.N. Effects of local and global network connectivity on synergistic epidemics. Phys. Rev. E. 2015;92 doi: 10.1103/PhysRevE.92.062814. [DOI] [PubMed] [Google Scholar]
- 208.Gómez-Gardeñes J., de Barros A.S., Pinho S.T., Andrade R.F. Abrupt transitions from reinfections in social contagions. Europhys. Lett. 2015;110:58006. [Google Scholar]
- 209.Gómez-Gardeñes J., Lotero L., Taraskin S., Pérez-Reche F. Explosive contagion in networks. Sci. Rep. 2016;6:19767. doi: 10.1038/srep19767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 210.Liu Q.-H., Wang W., Tang M., Zhou T., Lai Y.-C. Explosive spreading on complex networks: The role of synergy. Phys. Rev. E. 2017;95 doi: 10.1103/PhysRevE.95.042320. [DOI] [PubMed] [Google Scholar]
- 211.Hoffmann X.R., Boguná M. 2018. Synergistic cumulative contagion in epidemic spreading. arXiv:1802.02757. [Google Scholar]
- 212.Daley D.J., Kendall D.G. Epidemics and rumours. Nature. 1964;204:1118. doi: 10.1038/2041118a0. [DOI] [PubMed] [Google Scholar]
- 213.Daley D.J., Kendall D.G. Stochastic rumours. IMA J. Appl. Math. 1965;1:42–55. [Google Scholar]
- 214.Maki D.P., Thompson M. Prentice-Hall Englewood Cliffs; 1973. Mathematical Models and Applications: With Emphasis on the Social, Life, and Management Sciences. [Google Scholar]
- 215.Barrat A., Barthélemy M., Vespignani A. Cambridge University Press; 2008. Dynamical Processes on Complex Networks. [Google Scholar]
- 216.Moreno Y., Nekovee M., Pacheco A.F. Dynamics of rumor spreading in complex networks. Phys. Rev. E. 2004;69 doi: 10.1103/PhysRevE.69.066130. [DOI] [PubMed] [Google Scholar]
- 217.Moreno Y., Nekovee M., Vespignani A. Efficiency and reliability of epidemic data dissemination in complex networks. Phys. Rev. E. 2004;69 doi: 10.1103/PhysRevE.69.055101. [DOI] [PubMed] [Google Scholar]
- 218.Nekovee M., Moreno Y., Bianconi G., Marsili M. Theory of rumour spreading in complex social networks. Physica A. 2007;374:457. [Google Scholar]
- 219.Guilbeault D., Becker J., Centola D. Springer; 2018. Complex Contagions: A Decade in Review, in: Complex Spreading Phenomena in Social Systems; pp. 3–25. [Google Scholar]
- 220.Liu Q.-H., Zhong L.-F., Wang W., Zhou T., Eugene Stanley H. Interactive social contagions and co-infections on complex networks. Chaos. 2018;28 doi: 10.1063/1.5010002. [DOI] [PubMed] [Google Scholar]
- 221.A. Zarezade, A. Khodadadi, M. Farajtabar, H.R. Rabiee, H. Zha, Correlated cascades: Compete or cooperate, in: Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence 2017, pp. 238–244.
- 222.Liu Q.-H., Wang W., Cai S.-M., Tang M., Lai Y.-C. Synergistic interactions promote behavior spreading and alter phase transitions on multiplex networks. Phys. Rev. E. 2018;97 doi: 10.1103/PhysRevE.97.022311. [DOI] [PubMed] [Google Scholar]
- 223.Chang H.-C.H., Fu F. Co-diffusion of social contagions. New J. Phys. 2018;20 [Google Scholar]
- 224.Czaplicka A., Toral R., San Miguel M. Competition of simple and complex adoption on interdependent networks. Phys. Rev. E. 2016;94 doi: 10.1103/PhysRevE.94.062301. [DOI] [PubMed] [Google Scholar]
- 225.Srivastava A., Chelmis C., Prasanna V.K. Computing competing cascades on signed networks. Soc. Netw. Anal. Min. 2016;6:82. [Google Scholar]
- 226.Dunbar R.I. The social brain hypothesis. Evol. Anthropol. 1998;6:178–190. [Google Scholar]
- 227.Gonçalves B., Perra N., Vespignani A. Modeling users’ activity on twitter networks: Validation of dunbar’s number. PLoS ONE. 2011;6 doi: 10.1371/journal.pone.0022656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 228.Weng L., Flammini A., Vespignani A., Menczer F. Competition among memes in a world with limited attention. Sci. Rep. 2012;2:335. doi: 10.1038/srep00335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 229.Gleeson J.P., Ward J.A., O’sullivan K.P., Lee W.T. Competition-induced criticality in a model of meme popularity. Phys. Rev. Lett. 2014;112 doi: 10.1103/PhysRevLett.112.048701. [DOI] [PubMed] [Google Scholar]
- 230.Gleeson J.P., O’Sullivan K.P., Baños R.A., Moreno Y. Effects of network structure competition and memory time on social spreading phenomena. Phys. Rev. X. 2016;6 [Google Scholar]
- 231.Gleeson J.P., Cellai D., Onnela J.-P., Porter M.A., Reed-Tsochas F. A simple generative model of collective online behavior. Proc. Natl. Acad. Sci. USA. 2014;111:10411–10415. doi: 10.1073/pnas.1313895111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 232.Myers S.A., Leskovec J. Data Mining (ICDM), IEEE 12th International Conference on. IEEE; 2012. Clash of the contagions: Cooperation and competition in information diffusion; pp. 539–548. [Google Scholar]
- 233.Valera I., Gomez-Rodriguez M., Gummadi K. 2014. Modeling adoption of competing products and conventions in social media. arXiv:1406.0516v3. [Google Scholar]
- 234.Pathak N., Banerjee A., Srivastava J. Data Mining (ICDM), 2010 IEEE 10th International Conference on. IEEE; 2010. A generalized linear threshold model for multiple cascades; pp. 965–970. [Google Scholar]
- 235.Zhang H.-F., Xie J.-R., Chen H.-S., Liu C., Small M. Impact of asymptomatic infection on coupled disease-behavior dynamics in complex networks. Europhys. Lett. 2016;114:38004. [Google Scholar]
- 236.Zhang H.-F., Xie J.-R., Tang M., Lai Y.-C. Suppression of epidemic spreading in complex networks by local information based behavioral responses. Chaos. 2014;24 doi: 10.1063/1.4896333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 237.Litvinova M., Liu Q.-H., Kulikove E.S., Ajelli M. Reactive school closure weakens the network of social interactions and reduces the spread of influenza. Proc. Natl. Acad. Sci. USA. 2019 doi: 10.1073/pnas.1821298116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 238.Bauch C.T. Imitation dynamics predict vaccinating behaviour. Proc. R. Soc Lond. Ser. B. 2005;272:1669–1675. doi: 10.1098/rspb.2005.3153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 239.Bauch C.T., Earn D.J. Vaccination and the theory of games. Proc. Natl. Acad. Sci. USA. 2004;101:13391–13394. doi: 10.1073/pnas.0403823101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 240.Zhang H.-F., Yang Z., Wu Z.-X., Wang B.-H., Zhou T. Braess’s paradox in epidemic game: better condition results in less payoff. Sci. Rep. 2013;3:3292. doi: 10.1038/srep03292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 241.Andrews M.A., Bauch C.T. Disease interventions can interfere with one another through disease-behaviour interactions. PLoS Comput. Biol. 2015;11 doi: 10.1371/journal.pcbi.1004291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 242.Ginsberg J., Mohebbi M.H., Patel R.S., Brammer L., Smolinski M.S., Brilliant L. Detecting influenza epidemics using search engine query data. Nature. 2009;457:1012–1014. doi: 10.1038/nature07634. [DOI] [PubMed] [Google Scholar]
- 243.Carneiro H.A., Mylonakis E. Google trends: A web-based tool for real-time surveillance of disease outbreaks. Clin. Infect. Dis. 2009;49:1557–1564. doi: 10.1086/630200. [DOI] [PubMed] [Google Scholar]
- 244.Preis T., Moat H.S. Adaptive nowcasting of influenza outbreaks using google searches. Roy. Soc. Open Sci. 2014;1 doi: 10.1098/rsos.140095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 245.Butler D. When google got flu wrong. Nat. News. 2013;494:155. doi: 10.1038/494155a. [DOI] [PubMed] [Google Scholar]
- 246.Olson D.R., Konty K.J., Paladini M., Viboud C., Simonsen L. Reassessing google flu trends data for detection of seasonal and pandemic influenza: A comparative epidemiological study at three geographic scales. PLoS Comput. Biol. 2013;9 doi: 10.1371/journal.pcbi.1003256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 247.Lazer D., Kennedy R., King G., Vespignani A. The parable of google flu: traps in big data analysis. Science. 2014;343:1203–1205. doi: 10.1126/science.1248506. [DOI] [PubMed] [Google Scholar]
- 248.Wang W., Liu Q.-H., Cai S.-M., Tang M., Braunstein L.A., Stanley H.E. Suppressing disease spreading by using information diffusion on multiplex networks. Sci. Rep. 2016;6:29259. doi: 10.1038/srep29259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 249.Podobnik B., Stanley H.E. Detrended cross-correlation analysis: A new method for analyzing two nonstationary time series. Phys. Rev. Lett. 2008;100 doi: 10.1103/PhysRevLett.100.084102. [DOI] [PubMed] [Google Scholar]
- 250.Zhan X.-X., Liu C., Zhou G., Zhang Z.-K., Sun G.-Q., Zhu J.J., Jin Z. Coupling dynamics of epidemic spreading and information diffusion on complex networks. Appl. Math. Comput. 2018;332:437–448. doi: 10.1016/j.amc.2018.03.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 251.M. Smith, D.A. Broniatowski, M.J. Paul, M. Dredze, Towards real-time measurement of public epidemic awareness: Monitoring influenza awareness through twitter, in: AAAI Spring Symposium on Observational Studies through Social Media and Other Human-Generated Content, 2016.
- 252.Gao J., Zhang Y.-C., Zhou T. Computational socioeconomics. Phys. Rep. 2019;817:1–104. [Google Scholar]
- 253.Funk S., Gilad E., Jansen V., disease Endemic., awareness G.-Q. Endemic disease awareness and local behavioural response. J. Theoret. Biol. 2010;264:501–509. doi: 10.1016/j.jtbi.2010.02.032. [DOI] [PubMed] [Google Scholar]
- 254.Agaba G., Kyrychko Y., Blyuss K. Mathematical model for the impact of awareness on the dynamics of infectious diseases. Math. Biosci. 2017;286:22–30. doi: 10.1016/j.mbs.2017.01.009. [DOI] [PubMed] [Google Scholar]
- 255.Ruan Z., Tang M., Liu Z. Epidemic spreading with information-driven vaccination. Phys. Rev. E. 2012;86 doi: 10.1103/PhysRevE.86.036117. [DOI] [PubMed] [Google Scholar]
- 256.Yan G., Zhou T., Hu B., Fu Z.-Q., Wang B.-H. Efficient routing on complex networks. Phys. Rev. E. 2006;73 doi: 10.1103/PhysRevE.73.046108. [DOI] [PubMed] [Google Scholar]
- 257.Tchuenche J.M., Dube N., Bhunu C.P., Smith R.J., Bauch C.T. The impact of media coverage on the transmission dynamics of human influenza. BMC Public Health. 2011;11:S5. doi: 10.1186/1471-2458-11-S1-S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 258.Rahman M.S., Rahman M.L. Media and education play a tremendous role in mounting aids awareness among married couples in bangladesh. AIDS Res. Ther. 2007;4:10. doi: 10.1186/1742-6405-4-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 259.Samanta S., Rana S., Sharma A., Misra A., Chattopadhyay J. Effect of awareness programs by media on the epidemic outbreaks: A mathematical model. Appl. Math. Comput. 2013;219:6965–6977. [Google Scholar]
- 260.Wang Y., Cao J., Jin Z., Zhang H., Sun G.-Q. Impact of media coverage on epidemic spreading in complex networks. Physica A. 2013;392:5824–5835. doi: 10.1016/j.physa.2013.07.067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 261.Van den Driessche P., Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002;180:29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- 262.Rizzo A., Frasca M., Porfiri M. Effect of individual behavior on epidemic spreading in activity-driven networks. Phys. Rev. E. 2014;90 doi: 10.1103/PhysRevE.90.042801. [DOI] [PubMed] [Google Scholar]
- 263.Xia S., Liu J. A belief-based model for characterizing the spread of awareness and its impacts on individuals’ vaccination decisions. J. R. Soc. Interface. 2014;11 doi: 10.1098/rsif.2014.0013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 264.Olfati-Saber R., Murray R.M. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Automat. Control. 2004;49:1520–1533. [Google Scholar]
- 265.Greenhalgh D., Rana S., Samanta S., Sardar T., Bhattacharya S., Chattopadhyay J. Awareness programs control infectious disease–multiple delay induced mathematical model. Appl. Math. Comput. 2015;251:539–563. [Google Scholar]
- 266.Agaba G., Kyrychko Y., Blyuss K. Dynamics of vaccination in a time-delayed epidemic model with awareness. Math. Biosci. 2017;294:92–99. doi: 10.1016/j.mbs.2017.09.007. [DOI] [PubMed] [Google Scholar]
- 267.Granell C., Gómez S., Arenas A. Dynamical interplay between awareness and epidemic spreading in multiplex networks. Phys. Rev. Lett. 2013;111 doi: 10.1103/PhysRevLett.111.128701. [DOI] [PubMed] [Google Scholar]
- 268.Granell C., Gómez S., Arenas A. Competing spreading processes on multiplex networks: awareness and epidemics. Phys. Rev. E. 2014;90 doi: 10.1103/PhysRevE.90.012808. [DOI] [PubMed] [Google Scholar]
- 269.Kan J.-Q., Zhang H.-F. Effects of awareness diffusion and self-initiated awareness behavior on epidemic spreading-an approach based on multiplex networks. Commun. Nonlinear Sci. Numer. Simul. 2017;44:193–203. doi: 10.1016/j.cnsns.2016.08.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 270.Michele S., Baronchelli A., Pastor-Satorras R. Effects of temporal correlations in social multiplex networks. Sci. Rep. 2017;7:8597. doi: 10.1038/s41598-017-07591-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 271.Borge-Holthoefer J., Baños R.A., González-Bailón S., Moreno Y. Cascading behaviour in complex socio-technical networks. J. Complex Netw. 2013;1:3–24. [Google Scholar]
- 272.Guo Q., Jiang X., Lei Y., Li M., Ma Y., Zheng Z. Two-stage effects of awareness cascade on epidemic spreading in multiplex networks. Phys. Rev. E. 2015;91 doi: 10.1103/PhysRevE.91.012822. [DOI] [PubMed] [Google Scholar]
- 273.Huang Y., Tang M., Zou Y., Zhou J. Hybrid phase transitions of spreading dynamics in multiplex networks. Chinese J. Phys. 2018;56:1166–1172. [Google Scholar]
- 274.Pan Y., Yan Z. The impact of individual heterogeneity on the coupled awareness-epidemic dynamics in multiplex networks. Chaos. 2018;28 doi: 10.1063/1.5000280. [DOI] [PubMed] [Google Scholar]
- 275.Zang H. The effects of global awareness on the spreading of epidemics in multiplex networks. Physica A. 2018;492:1495–1506. [Google Scholar]
- 276.Stone L., Olinky R., Huppert A. Seasonal dynamics of recurrent epidemics. Nature. 2007;446:533–536. doi: 10.1038/nature05638. [DOI] [PubMed] [Google Scholar]
- 277.Liu H., Zheng M., Wu D., Wang Z., Liu J., Liu Z. Hysteresis loop of nonperiodic outbreaks of recurrent epidemics. Phys. Rev. E. 2016;94 doi: 10.1103/PhysRevE.94.062318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 278.Sagar V., Zhao Y., Sen A. 2018. Effect of time varying transmission rates on coupled dynamics of epidemic and awareness over multiplex network. arXiv:1805.08947. [DOI] [PubMed] [Google Scholar]
- 279.Wang H., Chen C., Qu B., Li D., Havlin S. Epidemic mitigation via awareness propagation in communication networks: the role of time scales. New J. Phys. 2017;19 [Google Scholar]
- 280.Guo Q., Lei Y., Jiang X., Ma Y., Huo G., Zheng Z. Epidemic spreading with activity-driven awareness diffusion on multiplex network. Chaos. 2016;26 doi: 10.1063/1.4947420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 281.Wang W., Tang M., Yang H., Do Y., Lai Y.-C., Lee G. Asymmetrically interacting spreading dynamics on complex layered networks. Sci. Rep. 2014;4:5097. doi: 10.1038/srep05097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 282.Catanzaro M., Boguná M., Pastor-Satorras R. Generation of uncorrelated random scale-free networks. Phys. Rev. E. 2005;71(2) doi: 10.1103/PhysRevE.71.027103. [DOI] [PubMed] [Google Scholar]
- 283.Juher D., Saldaña J. Tuning the overlap and the cross-layer correlations in two-layer networks: Application to a susceptible-infectious-recovered model with awareness dissemination. Phys. Rev. E. 2018;97 doi: 10.1103/PhysRevE.97.032303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 284.Liu Q.-H., Wang W., Tang M., Zhang H.-F. Impacts of complex behavioral responses on asymmetric interacting spreading dynamics in multiplex networks. Sci. Rep. 2016;6:25617. doi: 10.1038/srep25617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 285.Philipson T. Economic epidemiology and infectious diseases. Handb. Health Econ. 2000;1:1761–1799. [Google Scholar]
- 286.Colizza V., Barrat A., Barthélemy M., Valleron A.-J., Vespignani A. Modeling the worldwide spread of pandemic influenza: Baseline case and containment interventions. PLoS Med. 2007;4 doi: 10.1371/journal.pmed.0040013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 287.Klimek P., Obersteiner M., Thurner S. Systemic trade risk of critical resources. Sci. Adv. 2015;1 doi: 10.1126/sciadv.1500522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 288.Nagel J. Resource competition theories. Am. Behav. Sci. 1995;38:442–458. [Google Scholar]
- 289.Francis P.J. Optimal tax/subsidy combinations for the flu season. J. Econom. Dynam. Control. 2004;28:2037–2054. [Google Scholar]
- 290.Mbah M.L.N., Gilligan C.A. Resource allocation for epidemic control in metapopulations. PLoS ONE. 2011;6 doi: 10.1371/journal.pone.0024577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 291.Zaric G.S., Brandeau M.L. Resource allocation for epidemic control over short time horizons. Math. Biosci. 2001;171:33–58. doi: 10.1016/s0025-5564(01)00050-5. [DOI] [PubMed] [Google Scholar]
- 292.Zaric G.S., Brandeau M.L. Dynamic resource allocation for epidemic control in multiple populations. Math. Med. Biol. 2002;19:235–255. [PubMed] [Google Scholar]
- 293.V.M. Preciado, M. Zargham, C. Enyioha, A. Jadbabaie, G. Pappas, Optimal vaccine allocation to control epidemic outbreaks in arbitrary networks, in: Decision and Control, CDC, IEEE 52nd Annual Conference on IEEE 2013, pp. 7486–7491.
- 294.Enyioha C., Jadbabaie A., Preciado V., Pappas G. Control Conference, ECC, 2015 European. IEEE; 2015. Distributed resource allocation for control of spreading processes; pp. 2216–2221. [Google Scholar]
- 295.Chen H., Li G., Zhang H., Hou Z. Optimal allocation of resources for suppressing epidemic spreading on networks. Phys. Rev. E. 2017;96 doi: 10.1103/PhysRevE.96.012321. [DOI] [PubMed] [Google Scholar]
- 296.Nowzari C., Ogura M., Preciado V.M., Pappas G.J. Signals, Systems and Computers, 2015 49th Asilomar Conference on. IEEE; 2015. Optimal resource allocation for containing epidemics on time-varying networks; pp. 1333–1337. [Google Scholar]
- 297.Ogura M., Preciado V.M. Temporal Network Epidemiology. Springer; 2017. Optimal containment of epidemics in temporal and adaptive networks; pp. 241–266. [Google Scholar]
- 298.Chen X., Zhou T., Feng L., Yang C., Wang M., Fan X., Hu Y. 2016. Critical amount of resource in containing catastrophic epidemics. arXiv:1611.00212. [Google Scholar]
- 299.Jiang J., Zhou T. Resource control of epidemic spreading through a multilayer network. Sci. Rep. 2018;8:1629. doi: 10.1038/s41598-018-20105-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 300.Jiang J., Zhou T. The influence of time delay on epidemic spreading under limited resources. Physica A. 2018;508:414–423. [Google Scholar]
- 301.Böttcher L., Woolley-Meza O., Goles E., Helbing D., Herrmann H.J. Connectivity disruption sparks explosive epidemic spreading. Phys. Rev. E. 2016;93 doi: 10.1103/PhysRevE.93.042315. [DOI] [PubMed] [Google Scholar]
- 302.Böttcher L., Woolley-Meza O., Araújo N.A., Herrmann H.J., Helbing D. Disease-induced resource constraints can trigger explosive epidemics. Sci. Rep. 2015;5:16571. doi: 10.1038/srep16571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 303.Misra A., Rai R.K., Takeuchi Y. Modeling the effect of time delay in budget allocation to control an epidemic through awareness. Int. J. Biomath. 2018;11 [Google Scholar]
- 304.Zhang H.-F., Wu Z.-X., Xu X.-K., Small M., Wang L., Wang B.-H. Impacts of subsidy policies on vaccination decisions in contact networks. Phys. Rev. E. 2013;88(1) doi: 10.1103/PhysRevE.88.012813. [DOI] [PubMed] [Google Scholar]
- 305.Zhang H.-F., Wu Z.-X., Tang M., Lai Y.-C. Effects of behavioral response and vaccination policy on epidemic spreading-an approach based on evolutionary-game dynamics. Sci. Rep. 2014;4:5666. doi: 10.1038/srep05666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 306.Perc M., Szolnoki A. Coevolutionary games: A mini review. BioSystems. 2010;99(2):109–125. doi: 10.1016/j.biosystems.2009.10.003. [DOI] [PubMed] [Google Scholar]
- 307.Zhang H.-F., Shu P.-P., Wang Z., Tang M., Small M. Preferential imitation can invalidate targeted subsidy policies on seasonal-influenza diseases. Appl. Math. Comput. 2017;294:332–342. [Google Scholar]
- 308.Cai C.-R., Wu Z.-X., Guan J.-Y. Effect of vaccination strategies on the dynamic behavior of epidemic spreading and vaccine coverage. Chaos Solitons Fractals. 2014;62:36–43. doi: 10.1016/j.chaos.2014.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 309.Wang S., de Véricourt F., Sun P. Decentralized resource allocation to control an epidemic: A game theoretic approach. Math. Biosci. 2009;222:1–12. doi: 10.1016/j.mbs.2009.08.002. [DOI] [PubMed] [Google Scholar]
- 310.Long L., Zhong K., Wang W. Malicious viruses spreading on complex networks with heterogeneous recovery rate. Physica A. 2018;509:746–753. [Google Scholar]
- 311.Chen X.-L., Cai S.-M., Tang M., Wang W., Zhou T., Hui P.-M. Controlling epidemic outbreak based on local dynamic infectiousness on complex networks. Chaos. 2018;28 doi: 10.1063/1.5053911. [DOI] [PubMed] [Google Scholar]
- 312.Chen X., Wang R., Tang M., Cai S., Stanley H.E., Braunstein L.A. Suppressing epidemic spreading in multiplex networks with social-support. New J. Phys. 2018;20 [Google Scholar]
- 313.Chen X., Wang W., Cai S., Stanley H.E., Braunstein L.A. Optimal resource diffusion for suppressing disease spreading in multiplex networks. J. Stat. Mech. Theory Exp. 2018 [Google Scholar]
- 314.Aoki T., Aoyagi T. Scale-free structures emerging from co-evolution of a network and the distribution of a diffusive resource on it. Phys. Rev. Lett. 2012;109 doi: 10.1103/PhysRevLett.109.208702. [DOI] [PubMed] [Google Scholar]
- 315.Gross T., Blasius B. Adaptive coevolutionary networks: A review. J. R. Soc. Interface. 2008;5:259–271. doi: 10.1098/rsif.2007.1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 316.Barabasi A.-L. The origin of bursts and heavy tails in human dynamics. Nature. 2005;435:207–211. doi: 10.1038/nature03459. [DOI] [PubMed] [Google Scholar]
- 317.Zha Y., Zhou T., Zhou C. Unfolding large-scale online collaborative human dynamics. Proc. Natl. Acad. Sci. USA. 2016;113:14627–14632. doi: 10.1073/pnas.1601670113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 318.Brockmann D., Hufnagel L., Geisel T. The scaling laws of human travel. Nature. 2006;439:462–465. doi: 10.1038/nature04292. [DOI] [PubMed] [Google Scholar]
- 319.X.-Y. Yan, T. Zhou, Destination Choice Game: A Spatial Interaction Theory on Human Mobility, arXiv:1802.04966. [DOI] [PMC free article] [PubMed]
- 320.Gao J., Barzel B., Barabási A.-L. Universal resilience patterns in complex networks. Nature. 2016;530:307–312. doi: 10.1038/nature16948. [DOI] [PubMed] [Google Scholar]
- 321.Fu C., Gao Y., Cai S., Yang H., Yang C. Center of mass in complex networks. Sci. Rep. 2017;7:40982. doi: 10.1038/srep40982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 322.Carpenter S.R., Cole J.J., Pace M.L., Batt R., Brock W., Cline T., Coloso J., Hodgson J.R., Kitchell J.F., Seekell D.A. Early warnings of regime shifts: a whole-ecosystem experiment. Science. 2011;332:1079–1082. doi: 10.1126/science.1203672. [DOI] [PubMed] [Google Scholar]
- 323.Lenton T.M., Held H., Kriegler E., Hall J.W., Lucht W., Rahmstorf S., Schellnhuber H.J. Tipping elements in the earth’s climate system. Proc. Natl. Acad. Sci. USA. 2008;105:1786–1793. doi: 10.1073/pnas.0705414105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 324.May R.M., Arinaminpathy N. Systemic risk: The dynamics of model banking systems. J. R. Soc. Interface. 2010;7:823–838. doi: 10.1098/rsif.2009.0359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 325.Pananos A.D., Bury T.M., Wang C., Schonfeld J., Mohanty S.P., Nyhan B., Salathé M., Bauch C.T. Critical dynamics in population vaccinating behavior. Proc. Natl. Acad. Sci. USA. 2017;114:13762–13767. doi: 10.1073/pnas.1704093114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 326.Lü L., Zhou T., Zhang Q.-M., Stanley H.E. The h-index of a network node and its relation to degree and coreness. Nature Commun. 2016;7:10168. doi: 10.1038/ncomms10168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 327.Kitsak M., Gallos L.K., Havlin S., Liljeros F., Muchnik L., Stanley H.E., Makse H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010;6:888–893. [Google Scholar]
- 328.Brin S., Page L. The anatomy of a large-scale hypertextual web search engine. Comput. Netw. ISDN Syst. 1998;20:107–117. [Google Scholar]
- 329.Lü L., Zhang Y.-C., Yeung C.H., Zhou T. Leaders in social networks, the delicious case. PLoS ONE. 2011;6 doi: 10.1371/journal.pone.0021202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 330.Morone F., Makse H.A. Influence maximization in complex networks through optimal percolation. Nature. 2015;524:65–68. doi: 10.1038/nature14604. [DOI] [PubMed] [Google Scholar]
- 331.Chen W., Wang Y., Yang S. Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM; 2009. Efficient influence maximization in social networks; pp. 199–208. [Google Scholar]
- 332.Martin T., Zhang X., Newman M.E.J. Localization and centrality in networks. Phys. Rev. E. 2014;90 doi: 10.1103/PhysRevE.90.052808. [DOI] [PubMed] [Google Scholar]
- 333.Zhang H.-T., Fan M.C., Wu Y., Gao J., Stanley H.E., Zhou T., Yuan Y. Ultrafast synchronization via local observation. New J. Phys. 2019;21 [Google Scholar]