Ambident Nucleophilic Substitution: Understanding Non‐HSAB Behavior through Activation Strain and Conceptual DFT Analyses

Abstract

The ability to understand and predict ambident reactivity is key to the rational design of organic syntheses. An approach to understand trends in ambident reactivity is the hard and soft acids and bases (HSAB) principle. The recent controversy over the general validity of this principle prompted us to investigate the competing gas‐phase S_N2 reaction channels of archetypal ambident nucleophiles CN⁻, OCN⁻, and SCN⁻ with CH₃Cl (S_N2@C) and SiH₃Cl (S_N2@Si), using DFT calculations. Our combined analyses highlight the inability of the HSAB principle to correctly predict the reactivity trends of these simple, model reactions. Instead, we have successfully traced reactivity trends to the canonical orbital‐interaction mechanism and the resulting nucleophile–substrate interaction energy. The HOMO–LUMO orbital interactions set the trend in both S_N2@C and S_N2@Si reactions. We provide simple rules for predicting the ambident reactivity of nucleophiles based on our Kohn–Sham molecular orbital analysis.

Two‐Faced Nucleophiles! We provide intuitive design rules to predict ambident reactivity for S_N2@C and S_N2@Si reactions, based on detailed quantum‐chemical activation strain analyses. Our approach overcomes issues that arise from the use of the widely employed HSAB principle and constitutes a more comprehensive predictive model.

Introduction

Shortly after it was introduced, the hard and soft (Lewis) acids and bases (HSAB) principle was widely accepted as a method for understanding ambident reactivity in organic chemistry,1, 2, 3 even many years before a thorough theoretical foundation for the chemical hardness was proposed.4 The success of this theory, which states that hard acids prefer to interact with hard bases and soft acids prefer soft bases, is due to the simplicity of the concept of chemical hardness, and the fact that it is in agreement with other theories, such as the Klopman–Salem principle of charge and orbital controlled reactions,5 as well as Kornblum's rule, which rationalizes products in ambident substitution reactions in relation to their S_N1 or S_N2 character.6

Recently, the controversy on the applicability of the HSAB principle in organic chemistry has peaked, with the central criticism being the model's oversimplification of chemical reactivity and the failure of this principle to describe the reactivity of archetypal nucleophiles, such as CN⁻ and SCN⁻.7 Furthermore, an extensive experimental study, as well as numerous other examples in literature, showed no hard–hard or soft–soft preference for ambident nucleophiles.8 Instead, the intrinsic and thermodynamic contributions in Marcus theory10, 11 were proposed as a more reliable approach for rationalizing the regioselectivity of ambident nucleophiles in kinetically controlled reactions.7b–7c, 9, 12 In an alternative approach, Seitz et al. rationalized the competing ambident character of the enolate anion (a π‐conjugated ambident nucleophile) using gas‐phase DFT calculations and found that resonance effects, more so than inductive effects, govern the preference for O‐methylation over C‐methylation for attack at fluoromethane.13

Among the vast number of chemical reactions, the bimolecular nucleophilic substitution (S_N2) is undeniably one of the most important and best understood.14, 15 The S_N2 reaction generally proceeds via a backside approach of the nucleophile, rather than a front‐side attack, leading to a concerted expulsion of the leaving group. S_N2 reactions at carbon (S_N2@C) in the gas phase proceed via the well‐known double‐well potential energy surface (PES) (Figure 1 a).16 The PES associated with S_N2@Si reactions, on the other hand, is a single‐well shape in the gas phase, as determined by the steric properties around the Si atom (Figure 1 b).17

Figure 1.

Typical gas phase reaction profiles (energy ΔE vs. reaction coordinate ζ): (a) double‐well and (b) single‐well. R=reactants, RC=reactant complex, TS=transition state, TC=transition complex, PC=product complex, and P=products.

In order to shed light on the importance of charge transfer (soft‐soft) and electrostatic (hard‐hard) interactions, we quantum chemically assess the gas‐phase reactivity of three classical ambident nucleophiles (CN⁻, SCN⁻ and OCN⁻) and two electrophiles of variable hardness regarding their central atom (CH₃Cl and SiH₃Cl; see Scheme 1). This research also highlights the limitations and delineates the field of applicability of single‐molecule approaches, such as the HSAB principle, for predicting the outcome of chemical reactions. We do so using the activation strain model (ASM), also known as distortion/interaction model,18 in conjunction with quantitative molecular orbital (MO) theory as contained in Kohn–Sham density functional theory.19 In MO theory, hard nucleophiles correspond to small, negatively charged species with a low‐energy HOMO, while soft nucleophiles are larger weakly negatively charged species with a high‐energy HOMO.

Scheme 1.

Model ambident S_N2 reaction mechanisms of AB⁻+XH₃Cl (X = C, Si; AB⁻ = CN⁻, SCN⁻, OCN⁻).

We complement our activation‐strain and quantitative MO analysis by scrutinizing also the Fukui function and the molecular electrostatic potential (MEP). The Fukui function is a local descriptor in conceptual density functional theory which probes soft sites, prone to soft‐soft interactions; whereas the MEP probes hard sites, inclined to hard‐hard interactions. Hardness increases from the bottom left to the top right in the periodic table, pinpointing a trend of increasing hardness along the elements C<N<O which occur in the nucleophiles of this study.20 Both, Fukui function and MEP, have been applied to qualitatively understand the intrinsic reactivity of ambident nucleophiles in terms of HSAB theory.21

Conceptual DFT offers mathematical definitions of chemical concepts such as electronegativity.22 Although the notion of chemical hardness is well established within the framework of conceptual DFT, its relevance for predicting chemical reactivity is much debated.23 The use of chemical hardness as an interpretative tool is limited by the fact that also other factors have a strong influence on reactivity, such as the Lewis basicity and acidity of the reactants. Nevertheless, the chemical hardness and softness have a physical relevance, also successfully probing global as well as local reactivity properties in many cases.24 Recent research has also revealed the interpretive and predictive significance of other reactivity descriptors, such as the dual descriptor25 and the linear response function.26 While the HSAB principle is being challenged nowadays for the treatment of ambident reactivity, conceptual DFT descriptors offer insight into this special type of reactivity.

Theoretical Methods

Computational details

All quantum chemical calculations were carried out using the Amsterdam Density Functional (ADF) program.27 The OLYP functional, consisting of the optimized exchange (OPTX) functional proposed by Handy and co‐workers and the Lee–Yang–Parr (LYP) correlation functional was used in all calculations.28 The all‐electron TZ2P basis set was used for all calculations. Ab initio benchmark studies confirmed that this level of theory is in satisfactory agreement with highly correlated methods.17b, 29 Relativistic effects were accounted for using the zeroth‐order regular approximation (ZORA).30 Harmonic vibrational analysis confirmed that equilibrium structures had all real frequencies, whereas transition states had one imaginary frequency.31 Intrinsic reaction coordinate (IRC) calculations were performed to unambiguously connect reactant and product complexes with transition state structures.32 Optimized structures were illustrated using CYLview.33

The energy of the stationary points (SP) was computed with respect to the separated reactants, denoted with the subindex R, according to Equation (1).

$${\displaystyle \Delta E{}_{\mathrm{SP}}=E{}_{\mathrm{SP}}-E{}_{\mathrm{R}}}$$ (1)

In this equation, the index SP represents a reactant complex (RC), transition state/complex (TS/TC), product complex (PC) or separated products (P). Because the ambident nucleophiles AB⁻ in our study have two competing reactive sites, A and B, both PESs for attack via A and via B, respectively, were computed for each combination of one ambident nucleophile and one electrophile. Accordingly, in Equation (2), we define ΔΔE _SP(ζ) as the difference between stationary point energies of the two reaction channels, A or B, of an ambident nucleophile reacting with an electrophilic substrate.

$${\displaystyle \Delta \Delta E{}_{\mathrm{SP}}=\Delta E{}_{\mathrm{SP},\mathrm{A}}-\Delta E{}_{\mathrm{SP},\mathrm{B}}=E{}_{\mathrm{SP},\mathrm{A}}-E{}_{\mathrm{SP},\mathrm{B}}}$$ (2)

 

Activation strain analysis

To understand the origin of the activation barriers associated with different ambident reactions, the computed PESs along the reaction coordinate ζ were analyzed using the activation strain model (ASM) of chemical reactivity.18 The ASM is a fragment‐based approach applied to understand chemical reactions, in particular, the height of reaction barriers, in terms of the original reactants. Thus, the potential energy surface, ΔE(ζ), is decomposed into two terms along the reaction coordinate, ζ: the strain energy, ΔE _strain(ζ), which is associated with the energy required to deform the separated reactants, and the interaction energy, ΔE _int(ζ), which is the energy gain by bringing the deformed reactants together [see Equation (3)].

$${\displaystyle \Delta E\left(\zeta \right)=\Delta E{}_{\mathrm{strain}}\left(\zeta \right)+\Delta E{}_{\mathrm{int}}\left(\zeta \right)}$$ (3)

In graphical representations, the reaction coordinate ζ was projected onto the stretching of the central atom‐leaving group bond (C−F, C−Cl or Si−Cl) relative to its value in the equilibrium structure of the substrate, as this reaction coordinate undergoes a well‐defined change throughout the reaction.

Molecular orbital and energy decomposition analysis

The interaction energy, ΔE _int(ζ), between the strained reactants is decomposed into three physically meaningful terms within the Kohn–Sham molecular orbital (KS‐MO) model [Eq. (4)].34

$${\displaystyle \Delta E{}_{\mathrm{int}}\left(\zeta \right)=\Delta V{}_{\mathrm{elst}}\left(\zeta \right)+\Delta E{}_{\mathrm{Pauli}}\left(\zeta \right)+\Delta E{}_{\mathrm{oi}}\left(\zeta \right)}$$ (4)

In Equation (4), ΔV _elst(ζ) corresponds to the classical electrostatic interaction between the unperturbed charge distributions of the deformed fragments A and B, and is usually attractive. The Pauli repulsion, ΔE _Pauli(ζ), accounts for the destabilizing interaction between occupied orbitals (more precisely, between same‐spin electrons) and is responsible for steric repulsion.34 The orbital interaction energy, ΔE _oi(ζ), accounts for donor–acceptor interactions of occupied orbitals on one fragment with unoccupied orbitals on the other (such as the HOMO–LUMO interaction) and polarization, that is, the mixing of empty and occupied orbitals on one fragment due to the presence of the other. A detailed step‐by‐step protocol on how to perform and interpret the activation strain and energy decomposition analysis can be found in reference 35.

Conceptual density functional theory

Reactivity descriptors from conceptual DFT36 were employed to rationalize the chemical reactivity of nucleophiles and substrates and to assess the HSAB principle in our ambident reactions. The Fukui function was calculated within a finite difference approximation and is defined as the second‐order mixed derivative of the electronic energy with respect to the total number of electrons, N, and the external potential, v(r), as stated in Equation (5).37

$${\displaystyle f\left(\mathbf{r}\right)=\frac{\partial \delta \mathrm{E}\left[\mathrm{N},\mathrm{v}\left(\mathbf{r}\right)\right]}{\partial \mathrm{N}\delta \mathrm{v}\left(\mathbf{r}\right)}={\left(\frac{\partial \rho \left(\mathbf{r}\right)}{\partial \mathrm{N}}\right)}_{\mathrm{v}\left(\mathbf{r}\right)}={\left(\frac{\delta \mu }{\delta \mathrm{v}\left(\mathbf{r}\right)}\right)}_{\mathrm{N}}}$$ (5)

Due to the integer discontinuity for N, the Fukui function is split into a left‐ (electron removal from the system) and a right‐hand‐side (addition of an electron to the system) derivative—also known as the nucleophilic and electrophilic Fukui functions, f  ⁻(r) and f  ⁺(r), respectively.38 The Fukui function might be approximated by the frontier orbital density if orbital relaxation is neglected [Eq. (6), Eq. (7)].

$${\displaystyle f{}^{-}\left(\mathbf{r}\right)=\rho {}_N\left(\mathbf{r}\right)-\rho {}_{N-1}\left(\mathbf{r}\right)\approx \left|\Psi {}_{\mathrm{HOMO}}\right|{}^2}$$ (6)

$${\displaystyle f{}^{+}\left(\mathbf{r}\right)=\rho {}_{N+1}\left(\mathbf{r}\right)-\rho {}_N\left(\mathbf{r}\right)\approx \left|\Psi {}_{\mathrm{LUMO}}\right|{}^2}$$ (7)

Application of the chain rule for mathematical derivatives allows f (r) to be interpreted as a function that redistributes the total softness S of a molecule in space [Eq. (8)].39

$${\displaystyle s\left(\mathbf{r}\right)={\left(\frac{\partial \rho \left(\mathbf{r}\right)}{\partial \mu }\right)}_{\mathrm{v}\left(\mathbf{r}\right)}={\left(\frac{\partial \rho \left(\mathbf{r}\right)}{\partial \mathrm{N}}\right)}_{\mathrm{v}\left(\mathbf{r}\right)}{\left(\frac{\partial \mathrm{N}}{\partial \mu }\right)}_{\mathrm{v}\left(\mathbf{r}\right)}=f\left(\mathbf{r}\right)S}$$ (8)

The local softness s(r) is the local analogue of the total softness, S, and it contains very similar information as the Fukui function. The definition of the Fukui function in Eq. (6) and (7) allows for a comprehensive assessment of the electron transfer process in ambident S_N2 reactions based on isolated reactants. Additionally, the molecular electrostatic potential was computed to evaluate the hard sites in the different compounds investigated in this work.

Results and Discussion

The trends in chemical reactivity of isolated reactants arising from the molecular electrostatic potentials (MEPs) and Fukui functions (Figure 2) are first analyzed. These molecular properties allow for an interpretation of the local hardness/softness of the reactive species. The agreement between the HSAB principle and the Klopman–Salem theorem originates from the idea that the reactivity of hard reactive sites is ruled by electrostatics, whereas the reactivity of soft sides is determined by (frontier) orbital interactions.23d–23e, 24h, 40

Figure 2.

Conceptual DFT analyses of ambident nucleophiles and substrates computed at ZORA‐OLYP/TZ2P: (a, b) Molecular electrostatic potentials plotted on an electron‐density isovalue of 0.05 a.u. (c, d) Fukui functions plotted at their 0.004 a.u. isosurface (blue=positive, red=negative). (d) Solid isosurfaces (0.004 a.u.) correspond to σ* orbital density. Meshed isosurfaces (0.01 a.u.) correspond to the σ* orbital density multiplied by the global softness.

The Fukui functions model the electron transfer process in a chemical reaction, thus probing the orbital interaction. That is, when one electron is removed from (added to) the nucleophile (electrophile), the largest change in the electron density is where the Fukui function is greatest. Because ambident entities have two distinctive reactive sites within the same molecule, the Fukui function and local softness are identical except for a system‐dependent constant, which is the global softness, according to Equation (8).

The MEP of CN⁻ and SCN⁻ reveals that the more negatively charged side of the nucleophiles, which is the N‐atom in both cases, does indeed correspond to the expected hard site (Figure 2 a). For OCN⁻, the electrostatic potential on both reactive sides is similar, according to Figure 2 a, and the hard and soft side cannot be assigned using these isosurfaces.

Our conceptual DFT analyses of MEP and Fukui functions show that the hardness of a reactive site increases from bottom‐left to top‐right in the periodic table leading to the following sequence of increasing hardness: S<C<N<O. For example, the Fukui function of CN⁻ has its largest amplitude on the C‐atom which is, therefore, the softer and more strongly charge‐donating site of CN⁻ (Figure 2 c). Analogously, the S‐atom in SCN⁻ can be identified as the soft side because of the larger Fukui function on this end, whereas the N‐atom represents the hard site, in agreement with its more negative MEP. In OCN⁻, however, the Fukui function is larger at the N‐atom, which is then considered softer than the O‐atom. The softness of the acceptor atoms in the electrophiles is illustrated in Figure 2 d.41 The substitution of the C‐atom in CH₃Cl by a Si‐atom in SiH₃Cl has a considerable effect on both electrostatics and orbital size around the acceptor atom. Particularly, the larger local softness in Figure 2 d (mesh isosurface) indicates that the Si‐atom in SiH₃Cl is softer than the C‐atom in CH₃Cl. As discussed later in the manuscript, the HSAB principle and conceptual DFT prove incomplete in correctly predicting the ambident reactivity of the model S_N2 reactions.

Trends in reactivity of S_N2@C and S_N2@Si

The results of our ZORA‐OLYP/TZ2P computations are collected in Table 1 (energies) and Figure 3 (structures). Our computed trends in ambident reactivity at ZORA‐OLYP/TZ2P are the same as those computed using a “popular” meta‐hybrid functional at ZORA‐M06‐2X/TZ2P//ZORA‐OLYP/TZ2P (Table S1) and when dispersion effects are included at ZORA‐OLYP‐D3(BJ)/TZ2P//ZORA‐OLYP/TZ2P (Table S2). Cartesian coordinates for all stationary points are provided in Table S3 of the electronic Supporting Information.

Table 1.

Energies [in kcal mol⁻¹] relative to separated reactants of stationary points computed for the backside S_N2 reactions in the gas phase together with relative stationary point energies (ΔΔE) for two ambident reaction channels.^[a]

		Electrophile
Nucleophile	Side[b]	CH3Cl (1)				SiH3Cl (2)
		ΔE RC	ΔE TS	ΔE PC	ΔE P	ΔE TC	ΔE P
CN−	C (a)	−11.3	−5.9	−51.0	−37.0	−36.6	−9.4
	N (b)	−9.3	0.5	−25.1	−12.2	−31.6	−3.1
	ΔΔE [c]	−2.0	−6.4	−25.9	−24.8	−5.0	−6.3
OCN−	N (c)	−7.5	3.6	−18.6	−7.7	−28.5	−5.7
	O (d)	−7.7	12.2	9.1	25.2	−17.7	23.3
	ΔΔE [c]	0.2	−8.6	−27.7	−32.9	−10.8	−29.0
SCN−	S (e)	−6.0	9.7	0.3	16.4	−10.7	30.8
	N (f)	−6.0	11.6	−7.2	6.3	−19.1	9.9
	ΔΔE [c]	0.0	−1.9	7.5	10.1	8.4	20.9

[a] Computed at ZORA‐OLYP/TZ2P. [b] The soft side of the ambident nucleophile is represented by the former letter in the alphabet (a, c, e). [c] For a particular ambident nucleophile, a more negative value of ΔΔE denotes a stronger preference for the soft side, whereas a more positive value of ΔΔE denotes a stronger preference for the hard side.

Figure 3.

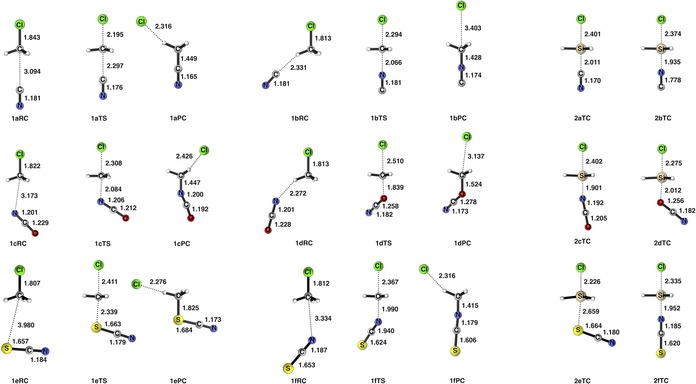
Optimized structures and selected bond lengths (in Å) of the stationary points along our model ambident S_N2 reactions with CH₃Cl (reactions 1 a through 1 f) and SiH₃Cl (reactions 2 a through 2 f) computed at ZORA‐OLYP/TZ2P.

First, we examine the S_N2@C reactions 1 a–f. These S_N2@C reactions proceed through the characteristic double‐well PES (see Figure 1 a), where the reactant complex (RC) and the product complex (PC) are separated by a central barrier via a transition state (TS).13 ΔE _TS for reactions 1 a–1 f range from −5.9 to 12.2 kcal mol⁻¹. In each case, attack via the soft side of the nucleophile on the hard electrophile is preferred kinetically, where ΔΔE _TS is −6.4, −8.6, and −1.9 kcal mol⁻¹ for attack by CN⁻, OCN⁻, and SCN⁻, respectively. We refer to the kinetically preferred pathway as the reaction channel with the lowest energy barrier. Additionally, nucleophilic attack by the soft side is also favored thermodynamically for CN⁻ and OCN⁻, but not for SCN⁻.

The change from the typical double‐well PES (Figure 1 a) to the single‐well PES (Figure 1 b) associated with S_N2@Si reactions is in line with previous reports.14a The studied S_N2@Si reactions proceed from the reactants to a stable central transition complex (TC) via a barrierless process and then finally to the products. ΔΔE _TC values for reactions 2 a–f range from −10.8 to 8.4 kcal mol⁻¹. Attack on the soft Si center by the softer side of the nucleophile is favored with CN⁻ and OCN⁻ both kinetically and thermodynamically. In all cases, except one, the less electronegative and softer nucleophilic side leads to the lower barrier of TS and more stable TC. The exception being reaction 2 f, where the harder N‐side of SCN⁻ is preferred.

According to the HSAB principle, nucleophilic attack at a central C‐atom (hard) and Si‐atom (soft) should proceed preferentially with the hard and soft side of the nucleophile, respectively. A negative ΔΔE denotes a preference for the soft side of the nucleophile [see Eq. (2)]. Reactions obeying the HSAB principle should exhibit a decrease of ΔΔE upon going from CH₃Cl to SiH₃Cl, that is, ΔΔE _TC<ΔΔE _TS. Inversion of the sign of ΔΔE indicates a reversal of the reactivity of one nucleophile with respect to an electrophile.

Our calculations reveal a fundamental inconsistency between this theory and stationary point energies. Specifically, for CN⁻ and SCN⁻, in which ΔΔE _TS is more negative than ΔΔE _TC, indicating the energetic preference for attack via the soft side of the nucleophile does not become more favored when moving to the softer electrophile. In fact, for SCN⁻, the ΔΔE _TS is negative and the ΔΔE _TC is positive, revealing that the attack by sulfur (soft) is preferred at CH₃Cl (hard), and the attack by nitrogen (hard) is preferred at SiH₃Cl (soft). These results thus reveal anti‐HSAB behavior. Only with OCN⁻ do we see HSAB behavior since ΔΔE _TC is more negative than ΔΔE _TS.

Analysis of both relative transition species energies (either ΔΔE _TS and ΔΔE _TC) and relative product energies (ΔΔE _P) shows significant anti‐HSAB behavior upon the exchange of CH₃Cl by SiH₃Cl. HSAB would suggest an energetic preference for the soft side of the nucleophile to a larger degree when moving to a softer electrophile, thus ΔΔE _TC should be more negative than ΔΔE _TS for the same side of the nucleophile reacting with the different electrophiles. Therefore, one should exercise caution when solely using the intrinsic reactivity of an isolated molecule, such as its “hardness” or “softness”, to predict the outcome of chemical reactions where many other interactions between reactants exist.

In the Supporting Information of this article, we also provide an analysis of S_N2@C reactions with CH₃F. In this particular case, the reactivity of the substrate with respect to nucleophilic additions is only affected by a change in leaving group compared to CH₃Cl, resulting in a very similar local softness of the electrophilic C‐atom. Accordingly, relative stationary point energies were found to be very similar for both electrophiles.

Activation strain analyses

To reveal the origin of the differences in ambident reactivity for the nucleophiles, we have performed activation strain (ASM) and canonical energy decomposition analyses (EDA). The activation strain analysis decomposes the total ΔE(ζ) of the ambident reactions along the reaction coordinate ζ, into both the ΔE _strain(ζ) component associated with the deformation of the respective reactants and the actual interaction ΔE _int(ζ) between the deformed reactants. Furthermore, the energy decomposition analysis decomposes ΔE _int(ζ) into three physically meaningful terms: (1) ΔV _elst(ζ), the classical electrostatic interactions; (2) ΔE _Pauli(ζ), which quantifies closed‐shell repulsions (steric effect); and (3) ΔE _oi(ζ), charge transfer, including HOMO–LUMO interactions, and polarization. The activation strain and energy decomposition analysis diagrams for each particular reaction are presented in Figure 4 and Figure 5, respectively. In all cases, the color of the line corresponds to the attacking side of the nucleophile using the following color‐code: carbon (black), nitrogen (blue), oxygen (red), and sulfur (yellow). Additionally, the position of the transition state is indicated by the dot on the ΔE(ζ) curve.

Figure 4.

Activation strain analysis diagrams for the a, b, c) S_N2@C reactions and d, e, f) S_N2@Si ambident reactions computed at ZORA‐OLYP/TZ2P. The color of the line indicates the side of the ambident nucleophile reacting with the substrate (black: C, blue: N, red: O, and yellow: S) and the dot (•) indicates the position of the transition state/complex.

Figure 5.

Energy decomposition analysis diagrams for the a, b, c) S_N2@C reactions and d, e, f) S_N2@Si ambident reactions computed at ZORA‐OLYP/TZ2P. The color of the line indicates the side of the ambident nucleophile reacting with the substrate (black: C, blue: N, red: O, and yellow: S). The dot (•) indicates the position of the transition state/complex. The style of the line indicates Pauli repulsion (⋅⋅⋅), electrostatic interaction (– – –), or orbital interaction (—).

From Figure 4, it is clear that the observed trends in ΔE(ζ) are mostly associated with differences in ΔE _int(ζ) and not differences in ΔE _strain(ζ) (see the relative ordering of the curves in for example, Figure 4 a: attack via the C‐atom is preferred over the N‐atom due to the more stabilizing interaction energy as the strain curves are overlapping). Differences in the interaction energy curves along the entire reaction coordinate determine the kinetically preferred side of the ambident nucleophile in attacking the electrophiles, the only exception being the S_N2@Si reaction of OCN⁻ with SiH₃Cl where the trend in ΔE seems to be governed by the strain energy (see Figure 4 e). The physical factors giving rise to the trends in ΔE _int(ζ) are analyzed in the next section and are summarized in Figure 5, which reveals something very interesting: whereas the ΔE _int(ζ) curves of the S_N2@C reactions are controlled by ΔE _oi(ζ), the ΔE _int(ζ) curves of the S_N2@Si reactions are determined by ΔE _Pauli(ζ).

Energy decomposition analyses

Differences in the ΔE _int(ζ) curves for the S_N2@C reactions at CH₃Cl were traced back to differences in orbital interaction energies for CN⁻ and OCN⁻ leading to lower activation barriers for attack by C and N, respectively (Figures 5 a–b). This preference is caused by the differences in orbital overlap between the HOMO of the nucleophile and the LUMO of CH₃Cl, whereas the associated orbital energies and thus HOMO–LUMO gaps are nearly identical for ambident reaction channels. For CN⁻, attack by carbon is preferred over nitrogen, due to the larger axial lobe of the σ_HOMO on C than on N (similar to the σ_HOMO of the well‐known CO ligand).42 This larger amplitude of the HOMO on the carbon atom results in a more efficient σ_HOMO−σ*_LUMO orbital overlap (see Figure S5 for the key HOMOs of the nucleophile). A similar situation occurs for OCN⁻, in which the highest occupied orbitals are two degenerate π_HOMOs with a nodal plane between the O and C that goes with a large amplitude with π bonding character on the CN moiety and a smaller π amplitude on O. This larger amplitude of the π_HOMO on N results in greater π_HOMO−σ*_LUMO overlap for attack by N and leads to more stabilizing ΔE _oi(ζ) than for attack by O (smaller π_HOMO−σ*_LUMO overlap). In line with these findings, the nucleophilic Fukui function in Figure 2 c shows a larger change in electron density for these reactive sites (i.e. C in CN⁻ and N in OCN⁻), corresponding to the soft sides of the ambident nucleophiles. In the case of SCN⁻, the ΔE _oi(ζ) preference for nitrogen is nearly completely offset by the destabilizing ΔE _Pauli(ζ) resulting in very similar ΔE _int(ζ) curves.

The EDA diagrams for the S_N2@Si reactions in Figure 5 d–f reveal the role of ΔE _Pauli(ζ) in determining the trends in ΔE _int(ζ) and, thus, the total energy ΔE(ζ) (see the relative ordering of the curves in for example, Figure 5 d: the interaction energy corresponding to attack via the C‐atom is more stabilizing than for attack by the N‐atom due to the less destabilizing Pauli repulsion). Note that Pauli repulsion is about steric effects which are out of the scope of HSAB theory. The causal factor behind the magnitude of the ΔE _Pauli(ζ) is, however, the orbital interactions ΔE _oi(ζ). The donor–acceptor orbital interaction determines the approach, either “linear” or “tilted”, of the incoming nucleophile, as shown in the optimized geometries displayed in Figure 3. The nucleophile attacks on the side with the largest HOMO amplitude: large σ_HOMO leads to “linear” and large π_HOMO leads to “tilted” approach. For attack of SCN⁻ on SiH₃Cl, the nucleophile is “linear” for approach via N (large σ_HOMO, 2 fTC) and “tilted” for approach via S (large π_HOMO, 2 eTC). A “linear” attack is favored over “tilted” due to the less destabilizing Pauli repulsion for the former, which originates from the less unfavorable overlap of filled molecular orbitals between the nucleophile and substrate.43, 44 This is illustrated by the fact that the kinetically preferred “linear” attack by N of both OCN⁻ and SCN⁻ is set by a key σ_HOMO−σ*_LUMO donor–acceptor interaction (Scheme 2 a) and goes with a less destabilizing ΔE _Pauli(ζ) along the entire reaction coordinate. On the contrary, the unfavorable attack by O of OCN⁻ and by S of SCN⁻ proceeds via a “tilted” approach of the nucleophile due to a π_HOMO−σ*_LUMO donor–acceptor interaction and leads to a more destabilizing ΔE _Pauli(ζ). The effect of the relative orientation of the nucleophile and electrophile remains hidden in reactivity models based on isolated reactants. Note also that Pauli repulsion between closed shells does not play a role in the Fukui function. These deficiencies preclude HSAB theory and conceptual DFT from being applicable for accurately predicting ambident reactivity.

Scheme 2.

Simplified MO diagram depicting the a) σ_HOMO−σ*_LUMO donor–facceptor interaction causing a “linear” and b) π_HOMO−σ*_LUMO donor–acceptor interaction causing a “tilted” attack of S/OCN⁻ at SiH₃Cl. The “linear” (“tilted”) approach is favored for attack by N (S/O) when the σ_HOMO−σ*_LUMO (π_HOMO−σ*_LUMO) overlap is better than the π_HOMO−σ*_LUMO (σ_HOMO−σ*_LUMO) overlap for the same side of the ambident nucleophile.

Conclusions

Striking deviations from HSAB theory occur in the S_N2 reactions of archetypal ambident nucleophiles (CN⁻, OCN⁻ and SCN⁻) with CH₃Cl (S_N2@C) and SiH₃Cl (S_N2@Si), as follows from our DFT computations. In all S_N2@C reactions, nucleophilic attack at the hard‐electrophilic carbon center proceeds via the soft side of the nucleophile. When moving to the softer silicon electrophilic center, in S_N2@Si, the preference for the soft side of the nucleophile is actually diminished for CN⁻ and SCN⁻. Unexpectedly, the preferred reactive side of SCN⁻ even shifts from soft (S) to hard (N) when going from S_N2@C to S_N2@Si.

Our activation strain analyses yield a clear picture of the physical factors behind the above trends in ambident reactivity. The energetically preferred reactive side of the ambident nucleophile is set by the HOMO–LUMO orbital interactions. For S_N2@C reactions, when orbital overlap between the nucleophile π‐ or σ_HOMO and σ*_LUMO of the substrate is maximized, more stabilizing orbital interactions lead to an enhanced reactivity. Therefore, a general rule‐of‐thumb is: the side of the nucleophile's π‐ or σ_HOMO that has a larger HOMO coefficient will indicate the energetically preferred reactive side of the ambident nucleophile for S_N2@C reactions. For S_N2@Si reactions, when the key donor–acceptor interaction involves the nucleophile's σ_HOMO and σ*_LUMO of SiH₃Cl, it leads to a “linear” approach. By contrast, when the interaction involves the nucleophile's π_HOMO, it leads to a more side‐on or “tilted” approach. In all cases, the “linear” approach goes with a less steric (Pauli) repulsion compared to the “tilted” approach due to significantly less overlap of filled molecular orbitals between the nucleophile and substrate. Therefore, one need only inspect the geometry of the TS for S_N2@Si reactions to determine the preferred side of the ambident nucleophile: the “linear” approach of the nucleophile is always preferred over the “tilted” approach due to less Pauli repulsion.

Finally, the fact that HSAB theory accounts neither for Pauli repulsive nor non‐frontier orbital interactions constitutes a fundamental limitation for correctly predicting reactivity. Our findings highlight the need to move beyond the HSAB principle, MEP maps, and Fukui functions for the prediction of the reactivity of ambident nucleophiles.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supplementary

T. Bettens, M. Alonso, F. De Proft, T. A. Hamlin, F. M. Bickelhaupt, Chem. Eur. J. 2020, 26, 3884.