Abstract
How should managers take into account the propagation of supply chain disruptions and risks (i.e. the ripple effect) when they design their inventory policies? For over 60 years, various extensions and applications to the popular newsvendor model have been suggested, where cost/profit are often the focal objective. We propose a new version of the traditional single-period newsvendor model – the ”Rippled Newsvendor” – with supply chain severity (i.e. risk propagation) as the primary objective while taking into account network structure. Our model considers exogenous and endogenous risk(s) of disruption while exploring the tension between under-supply and ”wear-and-tear” (i.e system breakdown). To model the intricacies of this trade-off whilst minimizing the potential spread of risk, we leverage a Bayesian Network whereby the conditional probability distributions are functions of the inventory ordering decisions. We use a simulation study to understand the nature of our objective function as well as to gain insight into the potential optimal ordering policies of this new model. Furthermore, the simulation seeks to understand how the various factors in our system impact total risk severity, and if they do so in different ways. Our simulations indicate that local exogenous risk is of greater importance than non-local exogenous risk. Furthermore, we show that the type of risk, as well as the structural characteristics of the supply chain and inventory system, impact risk severity differently.
Keywords: Supply chain risk structure, Supply chain risk propagation, Newsvendor, Inventory management, Bayesian networks, Ripple effect
1. Introduction
The popular press is replete with examples demonstrating the importance of supply chains as the primary mechanisms to source, manufacture, store, and deliver products to consumers. This process from raw materials to end consumer looks very different today than just 30 years ago. Today, a typical supply network spans across multiple continents, often operating on 24-hour continuous cycles, all the while intermingling natural, social, economic, and geo-political environments into one cohesive operation. Given just how interconnected modern supply networks are, it is no surprise that these supply networks are at a heightened risk of disruption. Various events across the globe impact the firm’s ability to effectively match its supply with the demand. More recently, we can see clear examples of these risks leading to disruptions in the network such as attacks on oil supply (Turak and Ellyatt, 2019), the implementation of tariffs (Wursthorn, 2019), the call for labor strikes (Ip, 2019), and even the discovery of important social issues such as human rights violations (Smith, 2019). Taken together, it is clear that when firms design their supply networks, they need to be mindful not only of the potential risks to which their supply chains are susceptible, but also how these risks propagate throughout these complex and highly integrated networks.
One important activity of supply chain management is the design of inventory policy. For over 60 years, the newsvendor model has been the bedrock of the design of various inventory policy and systems. Despite the thousands of papers that have been written on the matter, few have attempted to address a pressing concern in modern inventory systems: the presence of the ripple effect (Ivanov et al., 2014, Hosseini et al., 2019b). The ripple effect is defined as the spread of disruption and the resulting impact on performance throughout a supply network (Ivanov, 2017). While it is similar to the bullwhip effect, the ripple effect is often characterized by low-frequency/high-impact events, a lasting impact on supply chain performance, as well as permanent and temporary structural changes to the network (Ivanov et al., 2017a). Put simply, the ripple effect is a propagation of disruption throughout a supply network.
While stochastic elements are often used to model and characterize the results and antecedents of the ripple effect, some distinguish the ripple effect from risk propagation (DuHadway et al., 2019, Garvey et al., 2015), where the difference lies in the perception of a disruption versus a risk. A supply chain disruption is any event that prevents the supply chain from operating at it’s normal or expected state (Kleindorfer and Saad, 2005). On the other hand, a supply chain risk is any event that can manifest into a disruption (DuHadway et al., 2018). Put differently, supply chain disruptions are the manifestations of supply chain risks. While supply chain risk may not inherently result in a cost or loss of some nature, it can lead to a disruptive event that will.
Given the recent call in the literature to theoretically distinguish between supply chain disruptions and supply chain risks (DuHadway et al., 2019, Garvey et al., 2015), it would also be logical, and useful, to theoretically distinguish between disruption propagation and risk propagation. The ripple effect (i.e. disruption propagation) results from a sequence of known events based on the structural design of the supply chain (Ivanov et al., 2014), which is a phenomena that can be objectively studied given that the view of structure is often objectively measured. Contrast this with risk propagation, where supply chain risk is viewed in the eye of the beholder through a “sense-making” process (Ellis et al., 2011). Risk propagation would therefore be dependent on not only the structural characteristics of the supply network, but also how the supply chain manager views and measures “risk”.
Early work in supply chain disruption and risk management primarily focused on models and managerial frameworks that were primarily limited to the focal firm as well as the environment within which the focal firm operates (Kleindorfer and Saad, 2005). Such work advocated for the need to adequately classify and measure risk, as well as understand it’s antecedents and consequences (Peck, 2005). One proposed method for characterizing supply chain disruption was the construct of supply chain severity. Supply chain severity is defined as the number of nodes, locations, or events that are impacted as a result of a supply chain disruption (Craighead et al., 2007). This early work laid the foundation for the literature on the concept of propagation, generally. However, despite the suggestion of multiple frameworks to incorporate the idea of propagation, few have focused on the concept of severity from the lens of risk and risk propagation.
Supply chain risk severity is an important consideration for multiple reasons. First, supply chain risk management is an inherently subjective process, since what one may consider “risky”, another may not. This is due to the firm’s perception of the environment within which they operate (Ellis et al., 2011, DuHadway et al., 2018, DuHadway and Carnovale, 2019). It can equally be argued that “risk” is measured in various ways, many of which are dependent on the decision maker’s preferences and perceptions (Garvey et al., 2015, Zsidisin and Ritchie, 2009). While one may view the minimization of “risk” by minimizing expected cost, another may prefer to instead minimize total spread of risk (i.e. severity). This is simply a matter of preference. A second reason why supply chain risk severity is an important consideration to be studied, is because of the potential financial consequences that the total spread of disruption may have on the focal firm as well as the supply chain (Craighead et al., 2007).
Despite the call from some in the literature for research into the resulting impact of a disruption or risk propagation (Ivanov, 2017), few studies have been conducted focusing on risk severity in this important area. More specifically, the literature has yet to address the design of optimal inventory policies when the objective is to minimize supply chain risk severity, rather than the traditional view of cost minimization. This gap in the extant literature leads to the following research questions:
-
•
How can supply chain risk severity be analytically modeled?
-
•
How do exogenous and endogenous risks to production and inventory affect the overall risk severity in the network?
-
•
Which factors should firms direct most of their attention to in order to help reduce supply chain risk severity?
We address these questions by proposing an updated version of the single-period newsvendor model, based on the use of Bayesian Networks, when the supply chain manager’s objective is to minimize the supply chain risk severity under the guise of risk propagation and the ripple effect. We henceforth construct a simulation study to better understand the optimal nature of our inventory-production system. The remainder of this paper is structured as follows. First, we review the relevant literature on supply chain disruption and risk, the ripple effect and risk propagation, supply chain risk severity, and the fundamentals of Bayesian Networks. Next, we describe our “Rippled Newsvendor” model by first showing how supply chain severity can be analytically modeled leveraging concepts from Bayesian Networks, Models of The Ripple Effect, and Supply Chain Risk Propagation. We then conduct three numerical experiments by simulating various risk structures in a simple linear supply chain so as to implement and approximate, as well as better understand, the “Rippled Newsvendor” model. Last, we discuss our findings, the relevant managerial implications, our limitations, and avenues for future research.
2. Literature review
2.1. Supply chain disruption and risk
A supply chain disruption (SCD) is an “unplanned and unanticipated event that disrupts the normal flow of goods and materials within a supply chain” (Craighead et al., 2007, Kleindorfer and Saad, 2005). In other words, it is any event that prevents the supply chain from operating at an expected or planned state. Due to the proliferation of global sourcing and the level of perceived importance from practitioners (Craighead et al., 2007), academics have given special attention to understanding the various ontologies and methods of analysis to study SCDs. The extant literature on the matter has found that SCDs have a significant impact on a firm’s manufacturing and inventory performance (Tomlin, 2006). As such, some have proposed a general managerial process of identifying, assessing, and mitigating against supply chain disruptions (Kleindorfer and Saad, 2005). Some of the proposed frameworks for designing mitigation strategies include (but are not limited to) the use of primary suppliers, pre-positioned warehouses, or dual sourcing (Yang et al., 2012). In addition, there have been many attempts to optimize decision making within supply chain risk management (SCRM) and SCD management via analytical models (Saghafian and Van Oyen, 2016).
Distinct from a SCD, a supply chain risk (SCR) is often considered to be the antecedent of a SCD (DuHadway et al., 2019). There is, however, much debate over a precise definition of “supply chain risk”. Some authors characterize it in terms of a consequence (Hendricks and Singhal, 2005), whereas others characterize it as a likelihood (Garvey et al., 2015), although these two dimensions are often used together to measure risk (Tang and Tomlin, 2008). Regardless of their definition, SCRs have been shown to have impacts on firm performance, contingent on detection efforts, perception, and implemented mitigation strategies (Garvey et al., 2015, Kleindorfer and Saad, 2005, Zsidisin and Wagner, 2010). The extant literature views Supply Chain Risk Management (SCRM) as both a strategic (Chopra and Sodhi, 2004) and tactical (Ho et al., 2015) activity, which lies at the intersection of Supply Chain Management and Risk Management (Khojasteh-Ghamari and Irohara, 2018). Furthermore, many have proposed managerial frameworks that include several dimensions and related concepts, including assessment, measurement (Kleindorfer and Saad, 2005), mitigation strategies (Tang and Tomlin, 2008), risk classification (Ho et al., 2015), as well as drivers and consequences due to various firm characteristics and decisions (Ang et al., 2016).
2.2. The ripple effect and supply chain risk propagation
While many authors in the supply chain risk management literature have greatly expanded our understanding of the nature of risk, most of this research is limited within the boundaries or horizon of the firm (Garvey et al., 2015). There is currently a need for supply chain scholars to look “beyond the horizon” so as to better understand how various externalities impact strategic and tactical policy at the focal firm level (Carter et al., 2015). Early work in supply chain disruptions suggested how to model the events beyond the horizon of the focal firm (Craighead et al., 2007). For example, [36] proposed a model to study supplier selection in centralized and decentralized supply chain systems. [48] studied the resilience of supply networks under disruptions at multiple echelons in the network. The idea of interconnections between events was proposed by [2], who suggested the use of Petri-Nets in a reachability analysis to determine which specific areas of the network can be affected by a supply chain disruption.
One of the most important contributions in this body of the literature has been the formalization of supply chain disruption propagation by [27], who suggested that such disruption propagation should be termed the “ripple effect”, which is a generalized version of the bullwhip effect. Through a series of papers, the ripple effect has been studied with respect to several decisions, measurements, analysis methods, and phenomena, including but not limited to distribution (Ivanov et al., 2015), recovery and resilience (Ivanov et al., 2016), performance measurement (Sokolov et al., 2016), reverse logistics (Ivanov et al., 2017b), and simulation methods (Ivanov, 2017). The common element in this body of work has been how one element on the supply chain is “connected” to another element of the supply chain. For example, [19] used dynamic Bayesian networks with integrated Markov chains to study and quantify the ripple effect. Extending off of this notion, research has also uncovered optimal strategies for supplier selection and optimal order allocation (Hosseini et al., 2019c). Recent work has also incorporated disruption and recovery considerations into supply chain risk assessments using the ripple effect, developing new measures to identify high-risk suppliers (Hosseini and Ivanov, 2019). The concept of disruption in this literature is not isolated to study at a single location, but rather, to multiple locations and firms; primarily driven by the structure of the network (Hosseini et al., 2019a).
Despite the impressive progress on the disruption propagation front, there still exist only a handful of papers that discuss its distinction from risk propagation. Unlike disruption propagation, where the potential sequence of disruption is solely dependent on the structure of the supply network, risk propagation is more general and describes non-structural as well as structural related events that can lead to disruptions, ripple effects, or other risk propagations. Risk propagation is the sequence of inter-dependent risks in the supply network which may or may not lead to a disruption or ripple effect. Risk propagation is often modeled using conditional probability theory (Garvey et al., 2015) by trying to ascertain which events within and outside the firm will lead to a disruption (such as weather, labor strikes, tariffs, etc.). Some preliminary work in this body of literature exists.
The first known study can be attributable to [39], who proposed the use of Bayesian Networks to model the various inter-dependent risks in a supply chain. [50] proposed a similar methodology by observing various paths of possible risk. One of the first known full frameworks of risk propagation measures based on the use of Bayesian Networks was proposed by [13], who constructed a generic framework of measuring risk based on a general “utility” or “cost”. A similar methodology was also proposed by [43] but for the study of supply chain resilience. Risk propagation has also emerged within analytical models such as facility location (Luo and Chen, 2017). Furthermore, the reverse flow of risk (from downstream to upstream) has been explored from a variation in payment perspective (Serrano et al., 2018). More recently, [38] extended the work of Garvey et al., 2015, Shin et al., 2012, and [42] by proposing another framework of measures more specific to traditional supply chain performance metrics such as fragility, inventory costs, and service levels.
2.3. Supply chain risk and newsvendor models
Some in the extant literature have incorporated supply chain disruptions and risk into the standard newsvendor model with the objective of minimizing cost or maximizing profit. For example, [34] considered a modification to the newsvendor model which included a multi-echelon supply chain with two supply channels. [45] considered a sourcing problem by using a newsvendor model to determine optimality conditions for single vs. multi-sourcing when supplier disruption is possible. [60] found optimal solutions for a dual-sourcing newsvendor problem with suppliers subject to disruption risk with service level constraints. [44] conducted a mean–variance analysis on multi-sourcing with unreliable suppliers. Other newsvendor models that have incorporated disruption include the inclusion of random capacity disruptions (Chen and Xiao, 2015), competitive factors (Li et al., 2010a), random pricing (Zhu, 2013), multiple sourcing strategies (Silbermayr and Minner, 2014), periodic review (Wang et al., 2014), and redundancy (Kamalahmadi and Parast, 2017).
However, to the best of our knowledge, there are no studies that have analytically fused the newsvendor model together with the objective of minimizing supply chain severity. In addition, from a methodological perspective, we also argue that there exist no studies, to the best of our knowledge, that define the parameters (i.e. conditional probabilities) of a Bayesian Network in terms of decisions. Put differently, an overwhelming majority of the literature on Bayesian Networks fit the parameters of the model either by analyzing or simulating data. Yet, as far as we are aware, there exist no studies that have defined a Bayesian Network as a function of decision making in the context of supply chain risk propagation. This research seeks to fill that gap.
2.4. A review of Bayesian networks
Since we will leverage Bayesian Networks in our simulation and our model, a brief review of them is necessary. A more thorough review is conducted in [14] as well as [38]. Bayesianism rests on the general principle that probability is inherently a subjective belief regarding an event that one holds, measured on a 0 to 1 scale (0 being not likely, 1 being certain). The idea is that every individual has a collection of observations and concepts often referred to as knowledge. This knowledge, often represented as , represents all the beliefs that one has about the world surrounding them, and is often referred to as a priori knowledge, or prior belief (Heckerman, 1998). This is commonly modeled with the use of conditional probability. Conditional probability transcends the concept of belief updating. For example, if represents the amount of income we will earn next year, then an individual initially holds a belief that will be equal to with a value of belief . When an individual observes a new event , say, such as a new boss entering the company, this belief is then updated to a posterior belief, namely . To compute this, the standard definition of conditional probability along with Bayes Theorem is often employed:
In probability, random variables can be understood to be independent if they do not exhibit a dependence on each other. Mathematically, if we have variables and , then they are independent if . In addition, two variables are said to be conditionally independent with respect to a variable if they happen to both be dependent on (and hence, they themselves may not be independent), but become independent when knowledge of is known. For example, if causes () and , then we say that and are conditionally independent with respect to if . In other words, the knowledge of in this instance is useless knowledge.
This idea of dependent random variables can be easily extended to form a network of random variables, each of which is dependent on the other in a specific manner, to model all of the dependencies between the random variables. A Bayesian Network is a directed acyclic graph, where the nodes represent the random variables under consideration and the directed arcs represent probability dependencies between the variables. A Bayesian Network is essentially a cause and effect diagram with no circular causality. This is one reason why the resulting network must be acyclic. If we had a directed cycle, the notion of endogeneity would enter into our model of dependency, which would cause problems of inference. That is, we essentially would have a chicken and egg problem (i.e. which came first?).
Bayesian Networks are formed by first determining which random variables should be modeled and what are the causal links that need to be drawn between them. Constructing this network is known as specifying the structure of the dependency model. We then must specify the conditional probability distributions for each variable, which is dependent on the specific assignment of values to the parent random variables. If a node in the network has parents, then the number of conditional distributions we must assign to the random variable is (assuming all the variables are binary). Once the structure and conditional probabilities have been specified (either by definition or estimated from data), the resulting Bayesian Network is said to have been specified. Once this is complete, the network can then be used for probabilistic inference by leveraging Bayes Theorem as well as the Expansion Rule for Probability. However, as the size of the network grows, exact probabilistic inference becomes NP-HARD (Pearl, 2014, Heckerman, 1998). Hence, inference in practical application tends to be conducted using simulation methods (Garvey et al., 2015). While it is outside the scope of this manuscript to provide a comprehensive review of the theory of Bayesian networks, we refer the reader to (Heckerman, 1998) for an in-depth treatment of the subject.
3. A review of supply chain risk propagation measurement
3.1. Supply chain risk propagation measurement
The focus of our study is on determining optimal production–inventory policies when risk propagation is considered. However, in order to measure risk propagation, we will need to choose a framework of metrics to leverage. Some initial frameworks have been proposed in the literature (Blackhurst et al., 2008, Zhao et al., 2019, Qazi et al., 2018, Ojha et al., 2018). However, we decided to leverage the [13] framework for several reasons. First, their framework is the most general, and allows for any measure of “cost” or “utility” to be included. Second, their measures do not rest on specific paths of causality as other BN models do (Qazi et al., 2015).
A major drawback in existing studies that leverage Bayesian Networks is that their analysis rests on the assumption that a disruption cannot “continue” if it is stopped at a location. However, looking at only paths, rather than general scenarios, ignores situations where two simultaneous disruptions occur, one indirectly dependent on the other, that a typical path model cannot capture. For example, if we have three firms such that , many BN models assume that the disruption scenario of is impossible, since the disruption was assumed to be stopped and cannot continue to progress from to . However, this is myopic, since this can occur in practice due to either a limitation of knowledge (firm assumes that will not self-disrupt, and does not have knowledge of the disruption at ) or due to pure coincidence. In addition, much of the extant literature assumes that Bayesian Networks only comprise of two states, scilicet “occurred” and “not occurred”. However, the [13] allows for the possibility of a third state, namely that of “unknown”, which is more natural to the inherent model of Bayesian Networks. Last, the [13] model provides a clear and unambiguous algorithm for constructing the structure of the Bayesian Network, where other models do not. The construction of the network is based on the structure of the supply network itself, which makes the modeling process more realistic and easier to construct.
3.2. A review of the risk graph model
We will now briefly review the risk graph model, which was proposed by [13]. The risk graph is a Bayesian Network that is constructed under a set of assumptions using the structure of the supply network itself and fusing it together with the variety of supply chain risks that are present within each element of the network (either within a node or within a link). They argue that it is illogical to presume that risk “flows” directly from one risk in a location to another risk in a different location where there is no direct connection between the locations, despite the fact that the parameters in the Bayesian Network allow for such an instance. Put differently, their assumption allows for the simplification of modeling the inter-dependency of risks, while allowing for the possibility of risk to flow through non-disrupted events, which allows for the capture of more realistic scenarios without the additional burden of data or computation.
Some of the notation they used in their paper has been altered herein, but we will endeavor to be transparent where such changes have been made. First, the model of risk propagation measurement begins with a set of nine fundamental assumptions behind the model (for explicit enumeration of these assumptions we direct the reader to pg. 621 Garvey et al., 2015). Given the assumptions, we use a procedure which takes as it’s input (1) the structure of the supply network, (2) the collection of all identified risks at each location in the network, (3) the conditional probability distributions between risks, and (4) a procedure that can determine if two risks are causally related (this is somewhat of a corollary of (3)).
More formally, let denote the set of nodes in the supply network and let denote the set of connections in the supply network. The supply network is then the union of these two sets . Now, let denote the set of risks at location of the network. Here, it is assumed that represents the th risk at location and is itself a binary random variable with a sample space of . In addition, represents the number of risks at location . Next, let the set of all random variables (i.e. set of all risks present at all locations) be denoted as . In other words,
The next step is to create the collection of connections between the identified risks. This is done by leveraging the structure of the supply network and the definition of a function which takes as input the location in the supply network and will return the neighbors of that location. We will define it here as:
To clarify our notation above, we have . Put simply, represents the set of suppliers and customers of as well as the respective links if is a firm. In addition, while we have indexed the edge set of the supply network, we have not defined these elements as they usually are defined in graph theoretic language (an ordered pair of vertices, where the first entry represents the tail (source) node and the second entry represents the head (sink) node). Hence, it should be assumed that if , then . .
An assumption that the model makes is that there exists a function, denoted by , that will determine if there is a causal connection between risk at location and risk at location . [13] defines this function to be at the discretion of the analyst and such that adding a proposed causal dependency will result in a directed acyclic graph. Hence, when we use the notation , it will simply represent the result of a query that has been posed to an “analyst” whom has determined if causes . We will simplify their definition here as:
Last, [13] proposes an algorithm to construct the collection of causalities between the risks in the network. We will forgo a description of the algorithm, since it can be expressed more compactly as a mathematical set. To do so, we will define one more function, which will return if one risk at a location in the supply network is a “neighbor” of another risk at a different location in the supply network when given two risks:
Therefore, the edge set in the Risk Graph is defined as:
Put differently, the dependencies between risks in the supply network necessitate two fundamental conditions. First, the locationswherein the risks are defined and exist are neighbors of each other in the supply network. Second, the two events, as determined by some type of analyst, must be causally related. If one of these conditions fail, then we do not model the dependency in the resulting Bayesian Network. The Risk Graph is a directed acyclic graph (DAG) of nodes, which represent binary random variables (which themselves represent risks of disruption), of whose dependencies are determined based on if the risks lie within the same location of the supply network , or, if the locations of where the risks lie are neighbors of each other in the supply network , and if the risks are causally related, as determined by some form of “analyst”. Once the risk graph is specified, it can then be used in a variety of ways.
[13] suggests the use of a measure that can determine the expected descendent cost of a location in the supply network which they term the expected location risk contribution factor. It is defined as follows. First, they define a metric called the expected risk contribution factor of a scenario at a location in the supply network, where is an tuple and is the number of risks at location . To be clear, we use the set notation to represent the Cartesian product of times, scilicet . Let be a location in the supply network (node or link), be the set of risks that are descendants of any of the risks in , and represent the cost, or utility, if the risk were to manifest at location (i.e., the cost is 0 if and any real number if ). Then
In other words, when given an assignment of the random variables representing the risks at location to binary values, we compute the conditional expected value of the total costs of the descendent risks of all the risks at location (i.e. those in ). When given a scenario, the probabilities are propagated through the Bayesian Network, and so the expected descendent cost at the location for a given scenario will be different for each scenario. Once the is computed for every scenario , we then combine them to together by finding the expected ERCF, a measure called the Expected Location Risk Contribution Factor, which is defined as
4. The Rippled Newsvendor model
We consider the problem of designing an analytical framework within which the study of optimal ordering quantity subject to random demand in a single time period can be conducted. Since our model combines two analytical methodologies, namely Bayesian Networks and Stochastic Optimization, our goal in presenting this new framework is to be as parsimonious as possible. Such parsimony is what will allow us to focus our attention on the nuances of how Bayesian Networks can be used within optimal decision making with respect to inventory and production systems (Wacker, 1998). However, where we differ in our approach from the conventional newsvendor model is in the objective of minimizing the supply chain disruption severity rather than the cost/profit. First, we must determine how to measure supply chain disruption severity if we seek to minimize it. We leverage the [13] model reviewed above to measure the severity, as well as to model the various risks present in the supply chain. Once we have the measurement portion of the model specified, we move to the optimization model specification. We will consider a handful of common risks in a basic production–inventory system, and consider the dependencies between them. In order to model the risks, we need a definition of what it means to have the system “disrupted”. We will assume that the “normal” operating state is that the system will be able to fulfill all demand at all firms throughout the supply chain.
If any demand exceeds any order quantity, we will consider this event to be “disrupted”. Furthermore, we consider a natural tendency for portions of the inventory system to “disrupt”. That is, we model the inherent probability to disrupt either the inventory or the production as a linear function of the quantity chosen to be stored in inventory as well as the quantity produced, respectively. While the disruption of a system is commonly modeled with exponential and logistic functions, we made the decision to use a linear function to model this “wear and tear” in the system as a starting point so as to keep the model as parsimonious as possible. This allows for an interesting and more realistic trade-off, between ordering too much and ordering too little. In order to minimize the severity (i.e. risk propagation), we need to satisfy demand in full, and so we will naturally need to produce or hold more in inventory. However, as we increase our production and/or inventory levels, the conditional probability of “disruption” increases as a result of the machines or inventory storage experiencing increased levels of “wear and tear”. This increased level of wear and tear may lead to a breakdown of the system, and hence, a supply chain disruption. Therefore, the natural trade-off in the Rippled Newsvendor Model is between the ability to meet demand and the ability to not cause a total breakdown of the machine or inventory system, all of which is subject to both exogenous and endogenous risk of disruption.
4.1. Measurement model of disruption severity
Recall that disruption severity is defined as the number of nodes or locations that are affected by a disruption. More generally, we consider severity as the number of events that could occur as a result of a supply chain disruption. The risk propagation measurement model reviewed above has a natural fit to measure severity. If we let for all risks at all locations in the supply network, then the measures reviewed above measure the expected number of events that occur as a result of a disruption (or no disruption) relative to a location in the network. However, we also would like to have a relative measure so that severity across locations can be compared. We can do this by taking the ELRCF and dividing it by the sum of risks at the location and the number of descendent risks of any risk in the location. Therefore, for any location and any scenario at that location we have
and
We can see that by finding the expected summation of the random variables in the equation for , we obtain the expected number of events that will occur as a result of a scenario at the location. For the equation of the ELRCF, we can see that the measure is an expectation of the summation of total events over all scenarios of risks at a location. The first part of the inner summation sums the random variables together, which would be a count of the number of events that occurred at the location, while the ERCF of the scenario at the location would be the expected summation of events that occurred in the descendants of the risks at the location. Hence, the ELRCF is a measure of the expected number of events that can occur at a location at any given time. When we find the proportion of this to the total number of events that could occur, we obtain a relative measure of “how many events” to expect at a location. Naturally, given that this measure reflects the expected number of events at a location, it is by definition a relative measure of the severity of the location, which can be used to determine, as well as optimize, “risky” locations.
4.2. Assumptions
Our Rippled Newsvendor Model rests on 5 categories of assumptions regarding, respectively, the supply network structure and dynamics, the decision making within the network, the risk dependency structure, the definition and dynamics of supply chain disruptions, as well as the strategic objective of decision making. We outline each set of assumptions in the below subsections.
4.2.1. Supply network assumptions
Given that we need a simple single time period base model to build upon, our basic “Rippled Newsvendor” will remain as simple as possible. First, let us consider the structural model itself. We consider a fixed number of firms in a network, where the “network” is assumed to be simple chain. In addition, we assume that the entire supply chain is only contributing to the production of a single final product, and to be parsimonious, we assume a single unit delivered from a supplier will be used to manufacture a single unit for the buyer, if the buyer is a firm. We also assume all entities are owned by the same firm, or, all firms have perfect information symmetry and are in complete cooperation with each other. That is, all firms know the structure of the network, and all firms know the ordering and inventory policy of the other firms, as well as the risk structure of the network.
4.2.2. Decision making assumptions
With respect to decision making, we assume that the very bottom firm faces random demand with a known probability distribution that “trickles up” in an instantaneous manner during the same time period. The product, if the entire chain has no disruption, then “trickles down” the chain. It is assumed that all firms are capacitated based on the reliability of the machines and inventory system, but no other factor. In addition, we assume that all firms in the chain have the same beginning inventory of their version of the final product that is to be delivered to the purchasing firm/consumer. In other words, each firm’s inventory holds only the product they provide, rather than the resources they use to manufacture the product. We assume that when any firm places an order to their supplier, the supplier either instantaneously produces it or uses their own inventory and delivers it to the purchasing firm. The purchasing firm then uses this delivery to “manufacture” a new product, all within the same time period.
As mentioned earlier, a single unit of the product that the supplier manufactures is delivered and then used by the purchasing firm to manufacture a single unit of their own product. All firms in the chain agree to hold the same level of initial inventory, but each firm must individually choose their production quantity. Any order that a firm faces can only be satisfied by production or their inventory. If they need to manufacture the product, it is assumed that they place an order to their own supplier, and after doing so, they receive their full order from their supplier (if there is no disruption, more on this soon). The firm who has no supplier is assumed to have two different inventories: their infinite sized inventory of resources to manufacture the product and a fixed size of initial inventory of their final product, which is equal to every other firm’s initial inventory level. We assume that this firm’s resource inventory is not at risk for disruption.
4.2.3. Risk structure assumptions
With respect to the risk structure of the network, we make a few simplifying assumptions. First, every firm’s production and inventory is at risk. The firm’s production is at risk of disruption due to some endogenous reason inherent in the process of production (i.e. machine breakdown, etc.), and we assume this probability of breakdown is dependent on the number of units produced in the current time horizon. Furthermore, production is further at risk of disruption due to a disruption in the firm’s supplier’s inventory or the supplier’s production. We also assume that production is at risk of disruption due to exogenous reasons (hurricane, etc.). The inventory for any firm is at risk of disruption also due to endogenous reasons (i.e. spoiling, etc.) and the probability is dependent on the initial level of inventory held. The inventory is also at risk due to the same exogenous reasons that production faces. We assume that the exogenous risk to a firm is dependent on the exogenous risk of the firm’s supplier. In addition, we assume that the delivery to the final consumer in the chain is at risk of disruption due to exogenous reasons, the last firm’s production, or the last firm’s inventory being disrupted. The top firm’s production is only at risk due to endogenous reasons or exogenous reasons, but not due to the disruption of production or inventory of another firm (since it is the top most firm in the chain).
4.2.4. Disruption assumptions
With respect to the nature of disruptions, we assume that if the production of a firm is disrupted, then the purchasing firm’s order can only be satisfied by the inventory. If the firm’s inventory is disrupted, then the purchasing firm’s order can only be satisfied by production. If both production and inventory are disrupted, we assume that the order cannot be fulfilled. We further assume that if the inventory of a firm is disrupted, then none of it can be used to fulfill orders. If the production of a firm is disrupted, then again, none of production can be used to fulfill orders. We assume that it is impossible for the delivery of the product to be disrupted. That is, if a firm’s production and inventory are both not disrupted, and the total sum of them exceed the order size of the buying firm, then there is no disruption and the order is fulfilled. Again, it should be emphasized, that if a firm’s order is not satisfied, we consider this event to be a “disruption”. We furthermore assume that the transportation of product between any two firms is not at risk of disruption.
4.2.5. Assumptions regarding the objective
Given all of this, we last assume that the objective of any firm in the supply chain is to choose the agreed inventory level and individual production quantities so as to minimize the average supply chain severity via our relative contribution measures described above. In our model, we will consider only one objective pertaining to the overall supply chain severity, which we measure as the mean severity of all firms.
4.3. Decisions
Let be a collection of firms. Let be the “top most” firm and be the bottom most firm, and let firm be the supplier for firm . Let be a random variable that denotes the consumer demand for the product, which is distributed by the probability density function and the cumulative probability function . Let denote the beginning inventory level for firm , denote the number of units to produce for firm , and denote the order quantity of firm . Given our assumptions, we simply assume that , however, future models may seek to not assume this if the network structure under consideration is different than a simple chain. These variables represent the decision variables.
4.4. Risk structure formulation
We now will describe the risk structure of the network. First, let be a binary random variable which represents an exogenous risk to firm , where it is assigned to a value of 1 if the risk manifests and 0 if it does not (this is how we define all of the binary random variables). Let be a binary random variable which represents the risk of production being disrupted for firm . Let be a binary random variable which represents the risk of inventory being disrupted for firm . Let be a binary random variable which represents the final delivery of the product to the ultimate consumer.
To model the risk propagation, we first need to model the risks location by location, with each risk belonging to a location. Since we assumed that no risks of disruption are on the links between the locations, we only need to concern ourselves over the risks that we modeled above at each location. The next step is to determine the conditional probability tables for each risk, as well as how the risks are dependent on each other. Our assumptions help guide us in this. Since we are assuming for our base model that the conditional probabilities between the events are the same across all firms, we can standardize some of our notation in our model. With this said, we have three types of locations to consider within the construction of the risk graph. First, we have the risks within the firm . Then we have the risks in firm . Last, we have all the risks in firms .
4.4.1. Risk probabilities for firm
Recall that firm is the bottom most firm. We have four risks in this location, scilicet the exogenous disruption risk , the production disruption risk , the inventory disruption risk , and any other risk involved that may disrupt the final delivery to the end consumer. Since we need to model the inter-dependencies and the probabilities between these risks, we will go risk by risk and construct the conditional probability table (CPT) of each one. We first have the CPT for disruption to the delivery of the final product to the consumer. There are a few ways in which this can occur. Either the exogenous risk has impacted in some fashion the prevention of delivering to the final end consumer, the inability to have production satisfy the demand, or the inability to have inventory satisfy the demand. Hence, the parents of the random variable would be . Given that these are all binary random variables, there are only eight (8) instantiations of the parent variables.
When there is no exogenous risk (i.e. ), then the only ways for a disruption to occur at the end consumer would be (1) if there is no disruption in production or inventory, but there is insufficient total quantity between these two in order to satisfy demand, (2) if there is a disruption in production and insufficient inventory, (3) if there is a disruption in inventory but insufficient production, or (4) if there is a disruption in both inventory and production. In the first case, it is assumed that no exogenous risk has manifested (), no production risk has manifested (), and no inventory risk has manifested (). However, we can still observe a disruption if it so happens that our decisions were insufficient to cover demand (). Therefore, we should have . If inventory is disrupted (), then we can only use production to satisfy demand so as to prevent a disruption since all inventory is assumed to be wiped out. Therefore, we should have .
If inventory is not disrupted () but production is disrupted (), then by the same reasoning with inventory, we must have . Finally, if both inventory and production are disrupted, then there is no product to deliver to the consumer, and hence we must have a disruption. Thus, we have . By similar reasoning presented previously, when both inventory and production are disrupted, it does not matter if there is an exogenous event, since we already will know, in this instance, that there will be a disruption. Hence, we also will have .
Now if we do have an exogenous event occur (), then the chances of our demand fulfillment being satisfied could be attributable to either the exogenous event or the event that occurs with production and inventory. If there is only an exogenous event, but there is no disruption to inventory or production, we need to specify the probability of a disruption at demand fulfillment, which we denote as . We assume this is the same for all firms in the chain for all of their exogenous events. If we have inventory disrupted (), then the probability of this impacting the demand is based on either the exogenous event impacting all of the demand, or, it does not impact demand but there is insufficient production to satisfy demand. Put differently, the demand cannot be fulfilled if the exogenous event “trickled down” to the demand fulfillment, or if . For the sake of parsimony, we assume these two events are independent (the exogenous event does not impact the ability to satisfy demand with production if production is not disrupted, and likewise, the ability to satisfy demand with production does not impact an exogenous event). Hence, we have
By similar reasoning and assumptions with inventory, we should have:
Summarizing our probabilities, we have the following probability distribution table:
|
| |||
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 | |
Now we move to the production event, , and find the conditional probability table for this variable. First, production can be impacted, based on our assumptions, by an exogenous event (), the disruption in production of the firm’s supplier (), or disruption in inventory of the firm’s supplier (). Hence, the parents for the risk of disruption to production in firm would be , , and . Notice, however, that these are similar risks to what we studied in our previous conditional probability table. Therefore, we can apply much of the same logic here as we did there so as to obtain the following CPT, with some slight alterations. First, since the decision variables are known, we have no need for a probability distribution on them. However, the outcome of a disruption manifesting as a result of insufficient production or inventory is easier to characterize with an indicator function to indicate if a disruption “trickles down” as a result of insufficient supply. This happens when demand/order quantity is larger than total supply. Hence, we will let
Using this, we know then that production is disrupted () when there is something inherent within production that “goes wrong”. We assumed that the probability of this occurring is dependent on the amount of which is produced. Hence, we will let denote the probability of an endogenous disruption to production as a result of producing units. We assume that this function is linear, and we characterize it using the equation . Here, represents a “wear and tear” constant, and it denotes the probability of the machine failing if we produce nothing. This constant takes into consideration all of the wear and tear from previous runs before the current time-period. The constant is the marginal probability of decay. Put differently, it represents the increase in probability of the machine breaking down as a result of producing one additional unit.
In addition to the endogenous possibility of the machine breaking, we also could have the machine breaking as a result of something exogenous to the production system occurring (like a hurricane). We assume that this probability is the same that we discussed earlier, scilicet . Also, we can experience a disruption in production at if production and inventory of does not meet ’s order quantity . In the case of production when an exogenous event manifests, production can be disrupted due to three reasons: (1) the exogenous event led to the machine to break down, (2) the production quantity led to the machine to break down, or (3) the production and inventory were insufficient to cover the order quantity. Using a similar reasoning as with our disruption to delivery to the final consumer, and using our activation function together with the probabilities formed above, we can form the following conditional probability table:
|
| |||
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 | |
The only remaining probabilities we need to find are for the occurrence of an exogenous event and the disruption of inventory. Inventory can be disrupted when something endogenous occurs. Again, we assumed that the probability of this is a function of the initial inventory held. Similar to production, we assume this function is linear, defined as , with the same interpretation on the coefficients as that of production. Inventory can also be disrupted as a result of an exogenous event . The only dependency that inventory disruption has is the exogenous event, which is unlike our production (which depends on not only the exogenous event, but also the inventory and production of the firm’s supplier). We assume that the disruption to inventory as a result of an exogenous event is also , equal to that of production and delivery.
Hence, we have and since we assume that the endogenous and exogenous events are independent of each other. Last, the probability that an exogenous event occurs is dependent on whether or not an exogenous event occurred in the supplier for . For example, a hurricane at the location of firm may have influenced the occurrence of an electrical outage at the location of firm . Hence, and , where denotes the probability of occurring when no other exogenous event has occurred at firm , and denotes the probability of occurring when another exogenous event has occurred at firm . Hence, we have a full specification of the conditional probability tables for all the risks at firm .
4.4.2. Risk probabilities for firm ,
For any firm in between the first firm and the top most firm , we assumed that there are only three risks: exogenous risk , risk of production disruption , and risk of inventory disruption . The dependencies and probabilities for the disruption of these are the same as for the disruption of these for firm . Hence, and . Likewise, we have and . Last, we should also have:
|
| |||
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 | |
4.4.3. Risk probabilities for firm
Recall that firm is the “top-most” firm in the supply chain. We assume once again that this firm has only three risks: exogenous, inventory, and production. Unlike the other firms, however, the risk to production and exogenous disruption are slightly different, since they do not depend on another firm’s risks. The only risk to production at this firm is assumed to be endogenous and exogenous risk. That is, it has only a single parent (). Hence, we have the endogenous risk of production failing and the exogenous risk . As for the inventory, again, we have the same situation as the other firms, and so little changes here: and . Last, the risk of an exogenous event is not dependent on another endogenous event. We will hence let this probability be denoted as , and so (the same as our other exogenous events when we know an exogenous event in the supplier has not occurred).
4.5. Individual firm severity and average supply chain severity objective function
Individually, each firm seeks to set it’s production level . We assume that the inventory level is the same across all firms. First, we will specify the expected severity for each firm. For firm , we have 16 possible scenarios that can occur, since there are four (4) binary random variables . This location has no descendants. Hence, it’s expected relative severity will be :
Intuitively, this represents the expected percentage of events to occur due to risks at firm . We will illustrate the calculation for only one of these 16 terms in the summation. For example, suppose the scenario is . Then we have for :
Notice that the terms are incomplete at this point. We still would need to compute , which can be done by expanding the probability via conditioning over and so that we can obtain a term for which we have an equation:
We subsequently would need to condition on all of the over . For example:
This process of course continues up until we reach firm . As we can see, this computation is very complex, whose terms exponentially grow as we continue up the chain. This is why inference in Bayesian Networks is an NP-HARD problem (Heckerman, 1998, Pearl, 2014). To be clear, we do not resort to computing these exactly given the nature of the complexity of the problem of inference (i.e. the computation of the probabilities). Hence, we resort to approximate inference by way of simulation. This in part is the reason for our simulation study in the following section.
The relative severity function for any firm larger than will have descendents. Firm will have 4 descendants, while any other firm with will have descendants. If we are on firm , then it will have four (4) risks in firm , three risks in firms . Hence, the total number of risks would be . Therefore, our relative severity function for firm would be
Furthermore, for the ERCF, we would have the descendants of be
and the formula for ERCF would be:
Once again, the computation of these necessitates a simulation, since computing all of the probabilities in the expectations would be an NP-HARD problem. Finally, the objective of our model for the entire supply chain would simply be to minimize the mean of all of the individual firm’s relative severity functions:
This basic model with the firms in a chain structure is what we call the Single-Period, Single-Chain, Rippled Newsvendor Model. This is a no-cost model, and rather than optimize based on cost/profit, it is to be optimized based on supply chain severity. While we admit the model has a simplified structure, the base model can be easily extended to more complex structures in future research.
4.6. Summary of variables and notation
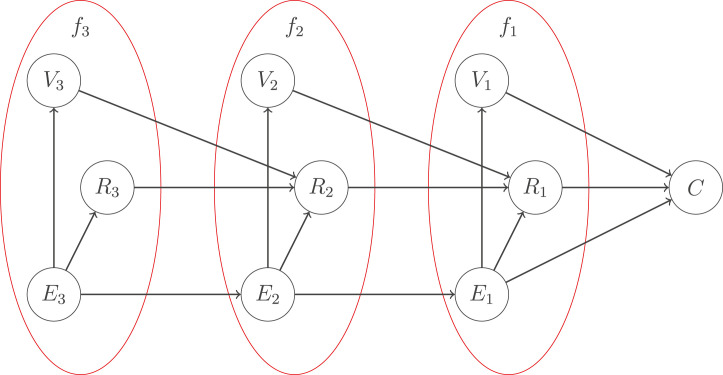
We have organized the collection of variables and notation in Table 1. In addition, please refer to Fig. 1 for an illustration of our model in the case of three firms.
Fig. 1.
The rippled newsvendor Bayesian network for three firms.
Table 1.
List of Variables and Notation for the Rippled Newsvendor Model.
| Variable | Meaning |
|---|---|
| Constants | |
| The firm index | |
| The firms in the supply chain | |
| The bottom-most firm in the chain | |
| The top-most firm in the chain | |
| The probability that production fails given no units have been produced | |
| The marginal probability that production fails with a unit increase in production | |
| The probability that inventory fails given no units have been stored in inventory | |
| The marginal probability that inventory fails with a unit increase in inventory holding | |
| The probability of an exogenous event causing a disruption | |
| The probability of the manifestation of an exogenous event at a firm when no exogenous event has manifested at the firm’s supplier. | |
| The probability of the manifestation of an exogenous event at a firm when an exogenous event has manifested at the firm’s supplier. | |
| Functions | |
| The probability that production will fail producing units at firm | |
| The probability that inventory will fail storing units at firm | |
| An indicator function which returns 1 if , 0 otherwise. | |
| The list of all risks that are pure descendents of risks at firm | |
| The expected number of risks that are descendents of all risks at firm to manifest given the manifestation and non-manifestation () of risks at firm . | |
| The expected number of risks that are to manifest at firm and risks that are descendents of risks at firm . | |
| The number of risks at firm | |
| Decisions | |
| The beginning inventory for firm | |
| The amount that firm decides to produce | |
| The amount that firm decides to order | |
| Random variables | |
| The demand distribution | |
| A Bernoulli variable that represents an exogenous disruptive event at firm | |
| A Bernoulli variable that represents a disruption in production at firm | |
| A Bernoulli variable that represents a disruption in inventory at firm | |
| A Bernoulli variable that represents a disruption to product delivery to final consumer from firm | |
5. Simulation design
5.1. Computing environment and tools used
Given the complexity of our model, we design and run several simulation experiments so as to better understand the nature of the objective function as well as some indication of potential optimality in our model. We did so in R Studio Server that operated on multiple Amazon EC2 Virtual Machines in a distributed computing environment. In total we had 7 machines, one of which was a master machine and the other 6 designated as “worker” machines. The master machine sent various types of commands down to the 6 worker machines so as to compute in parallel. The master machine had 32 Virtual CPUs while each worker machine had 8 Virtual CPUs. To construct the risk graph models (i.e. the Bayesian Networks), we used the bnlearn package, which has the ability to model Bayesian Networks as well as perform approximate inference. Given the complexity of our model, exact inference would not have been feasible, even in small instances. Hence, we used bnlearn’s likelihood weighting sampling algorithm to conduct approximate inference in order to compute the risk severity metrics outlined in the previous section.
5.2. Computation of the objective function
As we illustrated above, the computation of the objective value for a given solution of a stated model instance requires a fully specified Bayesian network. The specification of this Bayesian network is dependent upon the parameters of the specific model instance, and the solution for which we seek to compute the objective value. Recall that the objective function is dependent upon the computations of the ERCF and the ELRCF, both of which are computed using the conditional probabilities of the specified Bayesian network. In order to conduct these computations, we wrote customized code that leveraged R’s bnlearn package. This package uses a pre-defined likelihood weighted sampling method to compute the probabilities of queries provided to the Bayesian networks. The queries themselves, depend on knowing the descendants of a given risk. We therefore wrote a custom function to return the descendants for a given node in the Bayesian network. For further details on the construction of these queries, please refer to Section 3.2 above, as well as (Garvey et al., 2015). The computation of a value for the objective function at a given point was approximately 5 s for a single point, which is why we needed to conduct our simulation in a distributed computing environment so that multiple objective values can be computed in parallel for differing solutions.
5.3. Synopsis of experiments
We conducted three experiments. First, we proposed a base model and used a genetic algorithm to find an approximate optimal solution. Based on the results, we sampled various points in the solution space near the suggested approximate optimal solution to obtain a visual of the objective function across varying dimensions of the model. Our second experiment comprised of methodically changing each parameter from the base model with the others fixed to understand how our model affected the approximate optimal solution. Our last experiment was focused on understanding which decisions and parameters affected the risk severity the most via a sensitivity analysis. We explain the details and results of each experiment below.
6. Numerical experiments
6.1. Experiment 1: Understanding the objective function
In order to understand some properties of the objective function, we first solved a base model using a genetic algorithm, and plotted the objective function over combinations of every two variables in three-dimensions. Our base model had the following configuration: , , , , , , , , . Since there were only three firms, and since we assumed that inventory levels are all the same across all firms, this meant that we had four decisions in this problem instance: production at firm 1 (), production at firm 2 (), production at firm 3 (), and the initial inventory level all firms should set ().
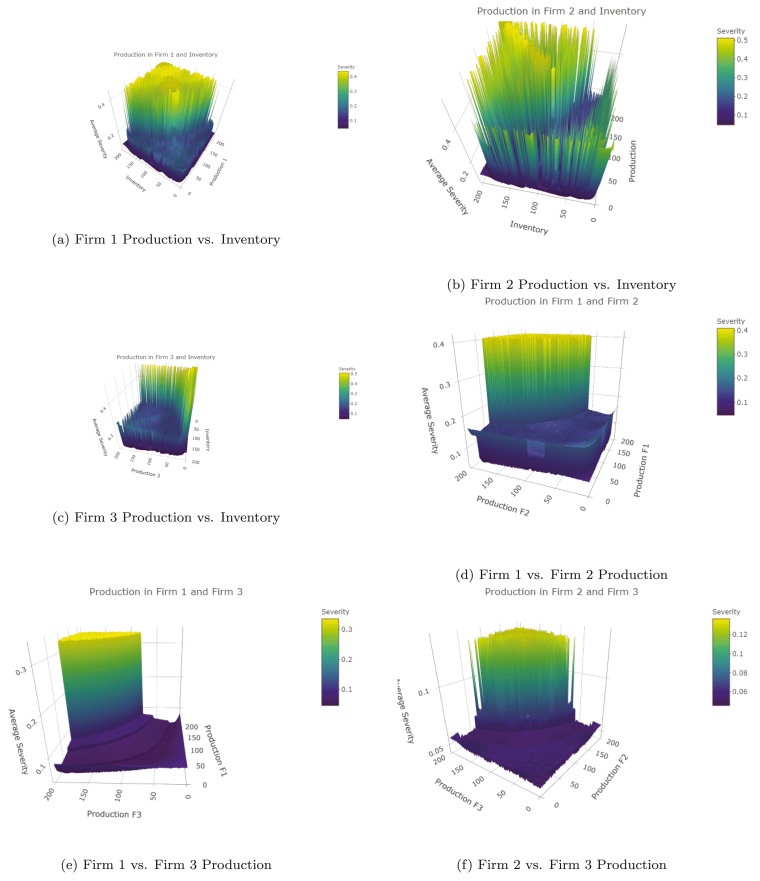
We first ran a genetic algorithm to solve this instance with the fitness function being the negative of the objective function, the cross over probability being 0.8, the mutation probability of being 0.1, a population size of 100 chromosomes, and a total of 1000 iterations. The algorithm ran on a cluster of the 7 machines and took a total of 1 h and 41 min to complete all iterations. Of all iterations of the genetic algorithm with these parameters set, we found the best solution to be , , , with a fitness value (i.e. risk severity) of 0.04589431. Put differently, we can expect on average 4.589% of risks at and below any firm to manifest. We ran the genetic algorithm with varying parameters, and found other solutions with similar fitness values to confirm our first run of the algorithm. We used this point in the solution space as a reference so that we can visualize the objective function. We next leveraged the plotly package to render 6 plots, which are shown in Fig. 2, Fig. 2, Fig. 2, Fig. 2, Fig. 2, Fig. 2, Fig. 2. The plots involved the risk severity plotted against , , , , , over the range of on integers. Given the complexity in computation of each point for our objective function, computing the objective function of the points to plot took approximately 10 h.
Fig. 2.
The Objective Function with two variables fixed at the point , , , and the other two variables that vary between 0 and 200.
6.2. Experiment 2: Understanding the optimal solution
We next wanted to see the effect that varying parameters of the model would have on the optimal solution. We decided to vary all of the parameters from the base model to gain a better understanding as to how the parameters impact the optimal solution’s severity metric, and the optimal solution itself. First, for each parameter, we varied its value while keeping all other parameters in the base model fixed. For each value assigned to each parameter, we ran a genetic algorithm with a population size of 25 and 25 iterations to solve for a sub-optimal solution. We also seeded the algorithm with an initial population of solutions near and within 1 standard deviation of the average demand so as to help the algorithm find sub-optimal solutions faster. Once the sub-optimal solution was found, it was recorded along with all other parameters for the model instance.
First, we fixed all parameters in our base model and varied the probability of a disruption in inventory or production due to the manifestation of an exogenous event (). We varied this parameter from 0 to 1 by every 0.01. We next fixed all the parameters in the base model but only varied the probability of a manifestation of an exogenous event given that an exogenous event did not manifest in the supplier (). We again varied this from 0 to 1 by every 0.01. Subsequently, we repeated this experiment but by varying the probability of a manifestation of an exogenous event given that an exogenous event did manifest in the supplier (). We also varied the number of firms () from 4 to 33. We chose a small number of firms to ensure tractability. Furthermore, we varied the initial endogenous probabilities of disruption in production and inventory () from 0 to 1 by every 0.01.
The marginal endogenous probabilities of disruption in production and inventory () also were varied, respectively. These quantities varied based on the values of , respectively. They varied as follows. When given the value for , we computed and divided this by 1000. The result was the upper limit of the slope. We then varied from 0 to by every . Our reasoning for doing so was based on the fact that setting the slope too high would result in a probability of shutdown for much smaller quantities of production/inventory for higher values of and . The results from this experiment are shown in Fig. 3, Fig. 3.
Fig. 3.
The severity of the optimal solution of the base model with varying levels of the parameters.
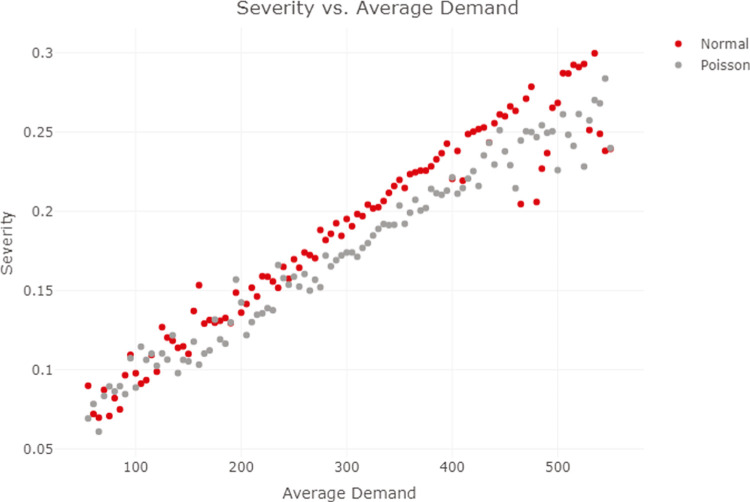
Next, we wanted to understand how the demand distribution, as well as varying levels of demand, affected the severity. We chose to test two different yet common demand distributions: the normal distribution and the Poisson distribution. We left all the parameters the same in the base model, but changed the average demand for the normal distribution between 50 and 500 by every 5. Taking into account the fact that relative variation will depend on the value of the mean, and that the variance of the Poisson distribution is equal to the mean, we also varied the standard deviation of the normal distribution so that the coefficient of variation was the same as in our base model (namely, that of 0.2). In other words, we varied the mean demand from 50 to 550 by every 5 and set it’s standard deviation to . We repeated this procedure for the Poisson distribution, but only varying the mean, since it’s variance is equal to the mean by definition. The results are shown in Fig. 4.
Fig. 4.
Severity vs. average demand.
6.3. Experiment 3: Sensitivity analysis
Our last experiment comprised of a sensitivity analysis on the parameters of our model as well as the decisions for our test instances. Our goal with this experiment was to determine which of the parameters and decisions were most sensitive so as to lead to error in the objective function. We conducted the sensitivity analysis as follows. First, for each model generated in Experiment 2, we kept all decisions and parameters fixed at the optimal value as determined by the genetic algorithm. For each parameter, we computed its value at a certain percentage above and below the original value of the parameter. To do so, we generated a vector of percentages, ranging by every 5%, from −100% to 100%. Each new value of the chosen parameter was then generated by multiplying a factor (which was the percentage plus 1) by the value of that parameter at the optimal solution. Each adjusted parameter’s corresponding objective value was then computed. The percentage error of this value compared to the objective value of the optimal solution was then computed.
After all percentage errors were computed, we subsequently conducted a linear regression of those percentage errors against the percentage errors in the corresponding parameter of interest. The coefficient on the percentage error in the parameter of interest was then recorded, as this quantity represents the percentage error of the objective function for every 1% error in the parameter of interest. We conducted this analysis for the probability of an exogenous event causing a disruption (), the probability of the manifestation of an exogenous event at a firm when no exogenous event has manifested at the firm’s supplier (), and the probability of the manifestation of an exogenous event at a firm when an exogenous event has manifested at the firm’s supplier (). This process was applied for our decisions only where the instances had 3 firms. The results of this analysis can be found in Table 2.
Table 2.
The ratios of the average objective value percentage error to parameter/decision percentage error relative to the optimal solution for all problem instances considered.
| Parameter | Average ratio of percentage error |
|---|---|
| 0.1834% | |
| 0.3661% | |
| 0.0865% | |
| 0.0051% | |
| 0.0120% | |
| 0.0052% | |
| 0.9731% |
7. Discussion
As we can observe from the plots from the three experiments we can gain some insight as to how the parameters of our model impact the risk severity at the optimal (or in our case, sub-optimal) solution. From experiment 1, we can see that the objective function exhibits convexity properties. This should be expected due to the construction of our model, as well as involving the trade-off between disrupting due to not ordering enough, and disrupting due to over-production. The plots convey the idea that when ordering quantities are too high, or if inventory quantities are too high, the risk severity is higher. This is due to our assumption of increased probability of disruption in production or inventory as these quantities rise. We also can observe that if too little is ordered, across the plots, the severity also increases. This is due to the assumption that when demand exceeds total supply, a disruption, by definition, occurs. The apparent convexity properties in our objective function mirror those of more traditional newsvendor models that observe the trade-offs between underage and overage costs (Ray and Jenamani, 2016a).
As one may expect, when firms are higher in the supply network, their decision’s impact to severity appears more sensitive than firms lower in the supply chain. This is in congruence with extant literature that have addressed disruptions and service levels for multi-echelon systems (Schmitt et al., 2017). We also notice that severity is lower when firms produce more than what is ordered, but not too much so as to lead to a disruption in production. The shape of the objective function, however, differs for decisions mixed with inventory rather than those with production. We notice that in the plots with production and inventory, there is a trade-off (higher production necessitates lower inventory, and vice versa). While in the plots with only production between the firms, we notice that such a trade-off has less of an effect on the severity. Overall, however, the biggest take-away from our plots is the convex nature of the objective function, which may indicate that optimal solutions do exist for our model, and reflect the trade-off between producing too little or too much so as to minimize severity.
Turning to our second experiment, we can see that the probability of a disruption at inventory/production due to an exogenous event (), as well as probability of the manifestation of an exogenous event due to the manifestation of the supplier’s exogenous event (), impact the severity in a linear manner, ceteris paribus. From Fig. 3(a) we can see that the probability of a manifestation of an exogenous event at a firm’s location conditional on no manifestation of an exogenous event at the firm’s supplier’s location () has a much greater impact on the risk severity than the other sources of exogenous risk. Essentially what we can gather from this observation is that the exogenous risk itself within the firm’s boundaries poses a greater threat to severity than exogenous risks outside of the firm’s boundaries.
However, when we turn our attention to Fig. 3(d), we observe that the endogenous risks impact the severity in roughly the same manner as the exogenous risk. This observation underscores the importance to distinguish between firm performance and risk severity as well as how risk propagation impacts both. While others in the literature have suggested that there is a greater impact to firm performance due to endogenous risks when compared to exogenous risks (DuHadway and Carnovale, 2019), our results indicate that there is no such difference in magnitude to severity. Rather, there is a distinction of magnitude of impact based on whether the risk had manifested within a firm’s boundaries (yet, the risk itself still being considered as “exogenous”) or from outside. Our results indicate that severity is greater when risk emanates within the firm’s boundaries rather than from outside. Hence, our results can be considered as an extension of the extant literature with respect to the consequences of endogenous/exogenous risk and disruption.
From Fig. 3(b), we observe that as the number of firms increase, ceteris paribus, the severity decreases. This result is congruent with the extant literature which suggests that the complexity of the supply network structure is related to the level of severity (Schmitt et al., 2017). We further emphasize the reasoning for this with two primary explanations with respect to our study. First, the structure of the supply chain is itself linear, and so the number of “paths” for risk to “flow” is greatly reduced in our risk graph than if we were to have a more complex network. Second, all of our parameters remained fixed, and the probabilities of disruption were fairly low. However, if this result holds in general, we can conclude that firms may want to seek more linear structures (single suppliers), as this would naturally help reduce the number of events that could occur.
We therefore have further illustrated that an “unplanned event that disrupts a complex supply chain would be more likely to be severe than the same supply chain disruption occurring within a relatively less complex supply chain” (Craighead et al., 2007 pg. 141). This result also further emphasizes the importance to theoretically distinguish between risk propagation (i.e. severity) and risk. With risk propagation, we have confirmed the findings of other studies that suggest simpler structures lead to decreased risk propagation (Craighead et al., 2007, Schmitt et al., 2017). On the other hand, some in the traditional risk literature have suggested that supply chain risk (not propagation) is related to the complexity of the network in a positive curvilinear manner (Choi and Krause, 2006). Put simply, complexity impacts risk differently than it impacts risk propagation, which further underscores the importance of distinguishing between these constructs.
In addition, we can see that Fig. 4 indicates that Poisson distribution, for the same average demand, tends to result in lower severity compared to the Normal Distribution. However, interestingly enough, despite all parameters remaining constant, an increase in average demand leads to an increase in risk severity. The reason, however, is fairly straightforward. Since the average demand is higher, we will need to either produce more, or, hold more in inventory. This underscores the importance of proper capacity management and management of the aforementioned trade-offs. These results are also consistent with more traditional profit-based newsvendor models (Khouja, 1999).
Last, in experiment 3, we can see which parameters of the model tend to be more sensitive to changes. The production of the lowest firm in our model were the least sensitive, while the inventory was the most sensitive. However, this can be explained due to our simplifying assumption of equal inventories across all firms. With respect to the probabilities of disruption, we can see that the probability of the manifestation of an exogenous event at a firm when no exogenous event has manifested at the firm’s supplier is the most sensitive of our parameters. This is in line with our earlier observation of this probability having the most impact on the optimal severity in the network. Furthermore, we can observe that the probability of the manifestation of an exogenous event at a firm when an exogenous event has manifested at the firm’s supplier is the least sensitive of the parameters in our model. Interestingly enough, of the production decisions, we notice that the production of firm 2 tends to be the most sensitive.
In summary, our results are not only congruent with well established literature in profit-based newsvendor models with respect to convexity properties of our objective function, but also illustrates that our model highlights the importance to distinguish between risk and risk propagation. Furthermore, some in the literature have suggested that when a disruption occurs, it has a natural tendency to trickle down and throughout a supply network, an event which is often referred to as the ripple effect. Our model can be considered an extension of this idea. More appropriately, the Rippled Newsvendor can be viewed as the precursor to various ripple effects, and how the presence of various risks eventually lead to the disruption propagation itself. Hence, our research also illustrates the need to theoretically distinguish between disruption propagations such as the ripple effect, and risk propagations, such as the recent COVID-19 outbreak (Ivanov, 2020), which could eventually lead to a ripple effect.
8. Conclusion
We argue that our new model, the Rippled Newsvendor, is the first major study to explore the optimal inventory and production policy through the lens of a risk severity objective. Our findings lead us to three major contributions of note. First, we designed a model that radically reshapes the traditional newsvendor model. While cost and profit are always objectives of concern, today’s modern supply chains have led supply chain managers to redirect their attention to supply chain disruption, risk propagation, and severity (Craighead et al., 2007, Ivanov et al., 2017a, Hosseini et al., 2019b). As far as we are aware, this is the first major study to clarify and measure the construct of risk severity through the lens of risk propagation and the ripple effect. We further argue, given our construction, that risk severity is more of a risk propagation construct than it is a risk or disruption construct. One way to view risk severity is as a more generalized version of service level. Put differently, we argue severity is a construct that represents the network’s generalized service level, rather than individual firm-specific levels.
Second, while the objective function of our model is highly complex due to it’s specification reliant on the structure and conditional probabilities of a Bayesian Network, we have made great strides in characterizing this highly complex function through visual experimentation. As far as we are aware, while our function is highly complex, our study is the first major study to integrate decision making into the definition of the conditional probability tables of the Bayesian Networks for the purpose of supply chain risk propagation. Put differently, most if not all studies in supply chain risk propagation that leverage a Bayesian Network modeling approach assume that the structure of the network is static (Garvey et al., 2015, Qazi et al., 2018, Ojha et al., 2018). Our study is the first of it’s kind that attempts to understand the nature and dynamics of risk propagation through the lens of decision-dependent and risk-interdependent Bayesian Networks, where the probabilities are not held constant or determined by data-driven methods, but rather are a function of specific decisions.
Last, our study sheds light, at least in the case of simple supply network structures, on how various probabilities of disruption impact optimal decision making under the guise of risk severity. We observed that certain probabilities have more impact on severity than others.
8.1. Managerial implications
In light of all of these observations, we can take away a few managerial implications that our results bring to the fore. At a general level, our findings lead to a better understanding of how not only inventory and production policies should be structured when the objective is severity-based, but also which portions of the supply network (with respect to disruption risk) should be given the most attention and mitigation efforts. Additionally, managers need to have the appropriate management of exogenous events. This of course has been emphasized in the prior literature through proper risk management methodologies, namely that of identification, assessment, and mitigation (Kleindorfer and Saad, 2005), or the detection, mitigation, recovery viewpoint (DuHadway et al., 2019, DuHadway and Carnovale, 2019). Our results, however, indicate that managers should focus more of their attention on control or mitigation of exogenous events that directly impact their own firm, and spend less of an effort and resources on mitigating the propagation of exogenous risk from a supplier to an exogenous risk of the firm itself.
Furthermore, our results indicate that firms should emphasize strict reliability policy of their machines and inventory systems, and to further ensure that these policies are in line with their market demand. Last, if the firm is in a linear structure (which we contend is not a very realistic assumption), they should aim to contract with suppliers that have longer chains. This may seem counter intuitive, since longer chains may expose the firm to more susceptibility of risk. However, our results indicate that when the firm has a single supplier, and suppliers subsequent to them also have single suppliers, when the chain is longer, the average severity is lower. The reasoning behind this observation is simple. Chains can stop disruptions in their path due to the simplicity of the structure, while networks allow for other paths for the disruption to propagate (Kim et al., 2011). If the supply chain structure is a pure linear structure, and one of the firms exposed to the risk managed to mitigate it, it is less likely for the disruption to continue downstream. The only other way in which a disruption can occur in a firm lower than the firm that mitigated the disruption would be due to (1) pure coincidence or (2) due to some unknown path of causality, as we argued above.
9. Limitations and future research
While our research has made great strides, it is not without it’s limitations. First, we only studied a simple chain structure. Future research is needed to understand how multiple suppliers, as well as how general network structure, will impact optimal decision making with respect to minimizing risk severity. Second, while we focused on risk severity, we did not include any profit or budgetary constraints. Future research will need to re-examine our model from either a constrained budget lens, or, a multi-objective optimization problem. In addition, we assume that all firms have the same inventory levels with varying production levels. While this was an initial consideration, we decided that varying both the inventory levels and production levels across all firms would add unnecessary complexity and would be outside the scope of this study. Future research should examine this limitation. Furthermore, we assumed that the probabilities of exogenous events were all the same across all firms. This of course is a threat to the external validity of our results. Future research will need to better understand how the Rippled Newsvendor is to respond when the probabilities of exogenous events differ across firms. Last, our model only was studied from a single-period perspective. The decision for us to do so was mainly motivated by the design of the original newsvendor model and to restrict our attention as to how the risk structure impacts the severity. Future studies will need to address how our optimal policies of the Rippled Newsvendor change as a result of the system changing over time.
While our research has been able to address an understudied area in the risk propagation literature, we also argue that our study raises more questions than answers that necessitate future research. First, we have studied risk propagation and inventory policy with respect to risk severity. However, how would our model change when the manager’s preference is to craft policy based on expected cost of disruption rather than number of events? Even if we were to remain in the severity framework of study, another important consideration to take into account is the manager’s risk preference and response (DuHadway et al., 2018). Some events that manifest may not be as grave of a concern as others. Furthermore, our study only relies on measures of averages without taking into account variation. While the optimal policies characterized herein portend great concern over certain parameters, how would this change when the manager has the competing objective to minimize the variance of the number of events? Future research is required to answer this question. Additionally, future studies could address an extension of the Rippled Newsvendor from a mean–variance perspective.
Last, we assume herein that policy is crafted for a single time-period and that the decisions are static. That is, it is assumed that the ordering policies are crafted from a preventative lens. How can policies be crafted from a reactive mitigation lens, and how would these policies differ from our results of the Rippled Newsvendor? We argue that these questions merit further investigation for future research. Nonetheless, we argue that the Rippled Newsvendor Model is a natural transcendence of operations and supply chain modeling into a modern era of complex networks. While more antiquated inventory models may be appropriate for firms that operate in a more traditional inventory system, we argue that the Rippled Newsvendor model is an appropriate first step in studying systems in our new, complex, and highly adaptable world of supply chain network structures.
CRediT authorship contribution statement
Myles D. Garvey: Conceptualization, Methodology, Software, Validation, Formal analysis. Steven Carnovale: Methodology, Investigation, Resources, Project administration.
References
- Ang E., Iancu D.A., Swinney R. Disruption risk and optimal sourcing in multitier supply networks. Manage. Sci. 2016;63(8):2397–2419. [Google Scholar]
- Blackhurst J., Craighead C.W., Elkins D., Handfield R.B. An empirically derived agenda of critical research issues for managing supply-chain disruptions. Int. J. Prod. Res. 2005;43(19):4067–4081. [Google Scholar]
- Blackhurst J., Wu T.T., Craighead C.W. A systematic approach for supply chain conflict detection with a hierarchical Petri Net extension. Omega. 2008;36(5):680–696. [Google Scholar]
- Carter C.R., Rogers D.S., Choi T.Y. Toward the theory of the supply chain. J. Supply Chain Manage. 2015;51(2):89–97. [Google Scholar]
- Chen K., Xiao T. Outsourcing strategy and production disruption of supply chain with demand and capacity allocation uncertainties. Int. J. Prod. Econ. 2015;170:243–257. [Google Scholar]
- Choi T.Y., Krause D.R. The supply base and its complexity: Implications for transaction costs, risks, responsiveness, and innovation. J. Oper. Manage. 2006;24(5):637–652. [Google Scholar]
- Chopra S., Sodhi M. Supply-chain breakdown. MIT Sloan Manag. Rev. 2004;46(1):53–61. [Google Scholar]
- Craighead C.W., Blackhurst J., Rungtusanatham M.J., Handfield R.B. The severity of supply chain disruptions: design characteristics and mitigation capabilities. Decis. Sci. 2007;38(1):131–156. [Google Scholar]
- DuHadway S., Carnovale S. Revisiting supply chain risk. Springer; 2019. Malicious supply chain risk: a literature review and future directions; pp. 221–231. [Google Scholar]
- DuHadway S., Carnovale S., Hazen B. Understanding risk management for intentional supply chain disruptions: risk detection, risk mitigation, and risk recovery. Ann. Oper. Res. 2019;283(1):179–198. [Google Scholar]
- DuHadway S., Carnovale S., Kannan V.R. Organizational communication and individual behavior: implications for supply chain risk management. Journal of Supply Chain Management. 2018;54(4):3–19. [Google Scholar]
- Ellis S.C., Shockley J., Henry R.M. Making sense of supply disruption risk research: A conceptual framework grounded in enactment theory. J. Supply Chain Manage. 2011;47(2):65–96. [Google Scholar]
- Garvey M.D., Carnovale S., Yeniyurt S. An analytical framework for supply network risk propagation: A Bayesian network approach. European J. Oper. Res. 2015;243(2):618–627. [Google Scholar]
- Heckerman D. Learning in Graphical Models. Springer; 1998. A tutorial on learning with Bayesian networks; pp. 301–354. [Google Scholar]
- Hendricks K.B., Singhal V.R. An empirical analysis of the effect of supply chain disruptions on long-run stock price performance and equity risk of the firm. Prod. Oper. Manage. 2005;14(1):35–52. [Google Scholar]
- Ho W., Zheng T., Yildiz H., Talluri S. Supply chain risk management: a literature review. Int. J. Prod. Res. 2015;53(16):5031–5069. [Google Scholar]
- Hosseini S., Ivanov D. A new resilience measure for supply networks with the ripple effect considerations: A Bayesian network approach. Ann. Oper. Res. 2019:1–27. [Google Scholar]
- Hosseini S., Ivanov D., Dolgui A. Review of quantitative methods for supply chain resilience analysis. Transp. Res. E. 2019;125:285–307. [Google Scholar]
- Hosseini S., Ivanov D., Dolgui A. Ripple effect modelling of supplier disruption: integrated Markov chain and dynamic Bayesian network approach. Int. J. Prod. Res. 2019:1–20. [Google Scholar]
- Hosseini S., Morshedlou N., Ivanov D., Sarder M., Barker K., Al Khaled A. Resilient supplier selection and optimal order allocation under disruption risks. Int. J. Prod. Econ. 2019;213:124–137. [Google Scholar]
- Ip G. Oil spikes, auto strikes join list of supply shocks. Wall Str. J. 2019 URL: https://www.wsj.com/articles/oil-spikes-auto-strikes-join-list-of-supply-shocks-11568805115?mod=searchresults&page=1&pos=3. [Google Scholar]
- Ivanov D. Simulation-based ripple effect modelling in the supply chain. Int. J. Prod. Res. 2017;55(7):2083–2101. [Google Scholar]
- Ivanov D. Predicting the impacts of epidemic outbreaks on global supply chains: A simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp. Res. E. 2020;136:1–14. doi: 10.1016/j.tre.2020.101922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ivanov D., Dolgui A., Sokolov B., Ivanova M. Literature review on disruption recovery in the supply chain. Int. J. Prod. Res. 2017;55(20):6158–6174. [Google Scholar]
- Ivanov D., Hartl R., Dolgui A., Pavlov A., Sokolov B. Integration of aggregate distribution and dynamic transportation planning in a supply chain with capacity disruptions and the ripple effect consideration. Int. J. Prod. Res. 2015;53(23):6963–6979. [Google Scholar]
- Ivanov D., Pavlov A., Pavlov D., Sokolov B. Minimization of disruption-related return flows in the supply chain. Int. J. Prod. Econ. 2017;183:503–513. [Google Scholar]
- Ivanov D., Sokolov B., Dolgui A. The ripple effect in supply chains: trade-off ‘efficiency-flexibility-resilience’in disruption management. Int. J. Prod. Res. 2014;52(7):2154–2172. [Google Scholar]
- Ivanov D., Sokolov B., Solovyeva I., Dolgui A., Jie F. Dynamic recovery policies for time-critical supply chains under conditions of ripple effect. Int. J. Prod. Res. 2016;54(23):7245–7258. [Google Scholar]
- Kamalahmadi M., Parast M.M. An assessment of supply chain disruption mitigation strategies. Int. J. Prod. Econ. 2017;184:210–230. [Google Scholar]
- Khojasteh-Ghamari Z., Irohara T. Supply Chain Risk Management. Springer; 2018. Supply chain risk management: A comprehensive review; pp. 3–22. [Google Scholar]
- Khouja M. The single-period (news-vendor) problem: literature review and suggestions for future research. Omega. 1999;27(5):537–553. [Google Scholar]
- Kim Y., Choi T.Y., Yan T., Dooley K. Structural investigation of supply networks: A social network analysis approach. J. Oper. Manage. 2011;29(3):194–211. [Google Scholar]
- Kleindorfer P.R., Saad G.H. Managing disruption risks in supply chains. Prod. Oper. Manage. 2005;14(1):53–68. [Google Scholar]
- Ledari A.M., Pasandideh S.H.R., Koupaei M.N. A new newsvendor policy model for dual-sourcing supply chains by considering disruption risk and special order. J. Intell. Manuf. 2018;29(1):237–244. [Google Scholar]
- Li J., Wang S., Cheng T. Competition and cooperation in a single-retailer two-supplier supply chain with supply disruption. Int. J. Prod. Econ. 2010;124(1):137–150. [Google Scholar]
- Li Y., Xie E., Teo H.-H., Peng M.W. Formal control and social control in domestic and international buyer–supplier relationships. J. Oper. Manage. 2010;28(4):333–344. [Google Scholar]
- Luo J., Chen X. Risk hedging via option contracts in a random yield supply chain. Ann. Oper. Res. 2017;257(1–2):697–719. [Google Scholar]
- Ojha R., Ghadge A., Tiwari M.K., Bititci U.S. Bayesian network modelling for supply chain risk propagation. Int. J. Prod. Res. 2018:1–25. [Google Scholar]
- Pai R.R., Kallepalli V.R., Caudill R.J., Zhou M. Systems, Man and Cybernetics, 2003. IEEE International Conference on, Vol. 5. IEEE; 2003. Methods toward supply chain risk analysis; pp. 4560–4565. [Google Scholar]
- Pearl J. Elsevier; 2014. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. [Google Scholar]
- Peck H. Drivers of supply chain vulnerability: an integrated framework. Int. J. Phys. Distrib. Logist. Manage. 2005;35(4):210–232. [Google Scholar]
- Qazi A., Dickson A., Quigley J., Gaudenzi B. Supply chain risk network management: A Bayesian belief network and expected utility based approach for managing supply chain risks. Int. J. Prod. Econ. 2018;196:24–42. [Google Scholar]
- Qazi A., Quigley J., Dickson A. Industrial Engineering and Operations Management. IEOM, 2015 International Conference on. IEEE; 2015. Supply chain risk management: Systematic literature review and a conceptual framework for capturing interdependencies between risks; pp. 1–13. [Google Scholar]
- Ray P., Jenamani M. Mean-variance analysis of sourcing decision under disruption risk. European J. Oper. Res. 2016;250(2):679–689. [Google Scholar]
- Ray P., Jenamani M. Sourcing decision under disruption risk with supply and demand uncertainty: A newsvendor approach. Ann. Oper. Res. 2016;237(1–2):237–262. [Google Scholar]
- Saghafian S., Van Oyen M.P. Compensating for dynamic supply disruptions: Backup flexibility design. Oper. Res. 2016;64(2):390–405. [Google Scholar]
- Schmitt T.G., Kumar S., Stecke K.E., Glover F.W., Ehlen M.A. Mitigating disruptions in a multi-echelon supply chain using adaptive ordering. Omega. 2017;68:185–198. [Google Scholar]
- Schmitt A.J., Singh M. A quantitative analysis of disruption risk in a multi-echelon supply chain. Int. J. Prod. Econ. 2012;139(1):22–32. [Google Scholar]
- Serrano A., Oliva R., Kraiselburd S. Risk propagation through payment distortion in supply chains. J. Oper. Manage. 2018;58:1–14. [Google Scholar]
- Shin K., Shin Y., Kwon J.-H., Kang S.-H. Risk propagation based dynamic transportation route finding mechanism. Ind. Manage. Data Syst. 2012;112(1):102–124. [Google Scholar]
- Silbermayr L., Minner S. A multiple sourcing inventory model under disruption risk. Int. J. Prod. Econ. 2014;149:37–46. [Google Scholar]
- Smith J. Today’s logistics report: Tangled supply chains; walmart stocking up; targeting soybeans. Wall Str. J. 2019 URL: https://www.wsj.com/articles/todays-logistics-report-tangled-supply-chains-walmart-stocking-up-targeting-soybeans-11558103675. [Google Scholar]
- Sokolov B., Ivanov D., Dolgui A., Pavlov A. Structural quantification of the ripple effect in the supply chain. Int. J. Prod. Res. 2016;54(1):152–169. [Google Scholar]
- Tang C., Tomlin B. The power of flexibility for mitigating supply chain risks. Int. J. Prod. Econ. 2008;116(1):12–27. [Google Scholar]
- Tomlin B. On the value of mitigation and contingency strategies for managing supply chain disruption risks. Manage. Sci. 2006;52(5):639–657. [Google Scholar]
- Turak N., Ellyatt H. CNBC; 2019. Iran Responsible for ‘Attack Against the World’ After Strikes on Oil Facilities, Saudi Official Says. URL: https://www.cnbc.com/2019/09/21/irans-warnings-to-saudi-arabia-are-laughable-saudis-al-jubeir-says.html. [Google Scholar]
- Wacker J.G. A definition of theory: research guidelines for different theory-building research methods in operations management. J. Oper. Manage. 1998;16(4):361–385. [Google Scholar]
- Wang D., Tang O., Zhang L. A periodic review lot sizing problem with random yields, disruptions and inventory capacity. Int. J. Prod. Econ. 2014;155:330–339. [Google Scholar]
- Wursthorn M. Tariffs could push down amazon, wayfair shares. Wall Str. J. 2019 URL: https://www.wsj.com/articles/tariffs-could-push-down-amazon-wayfair-shares-11567628143?mod=&page=1&pos=8. [Google Scholar]
- Xanthopoulos A., Vlachos D., Iakovou E. Optimal newsvendor policies for dual-sourcing supply chains: A disruption risk management framework. Comput. Oper. Res. 2012;39(2):350–357. [Google Scholar]
- Yang Z., Aydın G., Babich V., Beil D.R. Using a dual-sourcing option in the presence of asymmetric information about supplier reliability: Competition vs. diversification. Manuf. Serv. Oper. Manag. 2012;14(2):202–217. [Google Scholar]
- Zhao K., Zuo Z., Blackhurst J. Modelling supply chain adaptation for disruptions: An empirically grounded complex adaptive systems approach. J. Oper. Manage. 2019;65(2):190–212. [Google Scholar]
- Zhu S.X. Dynamic replenishment, production, and pricing decisions, in the face of supply disruption and random price-sensitive demand. Int. J. Prod. Econ. 2013;146(2):612–619. [Google Scholar]
- Zsidisin G.A., Ritchie B. Supply Chain Risk. Springer; 2009. Supply chain risk management–developments, issues and challenges; pp. 1–12. [Google Scholar]
- Zsidisin G.A., Wagner S.M. Do perceptions become reality? The moderating role of supply chain resiliency on disruption occurrence. J. Bus. Logist. 2010;31(2):1–20. [Google Scholar]