Abstract
Stenosis is the primary complication of current tissue-engineered vascular grafts used in pediatric congenital cardiac surgery. Murine models provide considerable insight into the possible mechanisms underlying this situation, but they are not efficient for identifying optimal changes in scaffold design or therapeutic strategies to prevent narrowing. In contrast, computational modeling promises to enable time- and cost-efficient examinations of factors leading to narrowing. Whereas past models have been limited by their phenomenological basis, we present a new mechanistic model that integrates molecular- and cellular-driven immuno- and mechano-mediated contributions to in vivo neotissue development within implanted polymeric scaffolds. Model parameters are inferred directly from in vivo measurements for an inferior vena cava interposition graft model in the mouse that are augmented by data from the literature. By complementing Bayesian estimation with identifiability analysis and simplex optimization, we found optimal parameter values that match model outputs with experimental targets and quantify variability due to measurement uncertainty. Utility is illustrated by parametrically exploring possible graft narrowing as a function of scaffold pore size, macrophage activity, and the immunomodulatory cytokine transforming growth factor beta 1 (TGF-β1). The model captures salient temporal profiles of infiltrating immune and synthetic cells and associated secretion of cytokines, proteases, and matrix constituents throughout neovessel evolution, and parametric studies suggest that modulating scaffold immunogenicity with early immunomodulatory therapies may reduce graft narrowing without compromising compliance.
Keywords: vascular graft, polymeric scaffold, inflammation, stenosis, Bayesian estimation
Insight Box
This paper proposes a mechanistic computational bio-chemo-mechanical model of in vivo neotissue development in tissue-engineered vascular grafts and establishes a framework for model parameter estimation in the presence of uncertainty. The model captures experimentally available molecular and cellular profiles of immune cells, pro- and anti-inflammatory cytokines, vascular cells, and matrix constituents following scaffold implantation. Utility is demonstrated further by hypothesis-driven parametric studies that explore in vivo graft narrowing as a function of scaffold design parameters as well as targeted pharmacological interventions such as modulating macrophage and TGF-β activity, with the aim of improving long-term patency, avoiding compliance mismatch, and maintaining graft cellularity.
INTRODUCTION
Treatment strategies for vascular diseases often rely on replacement conduits, but the lack of suitable autologous vessels and high rates of failure of synthetic materials significantly limit surgical outcomes [1]. Tissue engineered vascular grafts (TEVGs) represent a promising alternative, particularly in the pediatric population where growth capacity is important. The first TEVG used to treat children consisted of a biodegradable scaffold of a woven poly(glycolic) acid (PGA) felt and a 50:50 copolymer sealant of poly(ε)-caprolactone and L-lactide (P(CL/LA)); these grafts were seeded with autologous bone marrow-derived mononuclear cells before implantation as extracardiac cavopulmonary conduits in children who underwent a Fontan operation to palliate their single ventricle physiology [2, 3]. There were no cases of graft-related mortality, aneurysmal dilatation, rupture, infection, or ectopic calcification during a long-term follow-up (mean of 11.1 years), but imaging revealed asymptomatic narrowing, or stenosis, in 16% of the patients at a mean of 5.8 years and 28% at the last follow-up. This rate of stenosis is greater than that reported for synthetic graft materials [4–6]. Hence, even though stenosis was successfully treated with percutaneous transluminal balloon angioplasty, with one patient also requiring an intra-graft stent, there is a pressing need to understand and better control mechanisms that give rise to TEVG narrowing.
Toward this end, we first implanted similar scaffolds as interposition grafts in the abdominal inferior vena cava (IVC) of mice for up to two years [7–9]. Scaffolds are transformed into functional neovessels via a process involving polymer degradation, immune cell infiltration, vascular cell recruitment, and extracellular matrix deposition, remodeling, and degradation (Fig. 1). We observed a bimodal distribution of outcomes: narrowed grafts had extensive monocyte/macrophage infiltration into the scaffold, with neotissue formation within the lumen composed primarily of smooth muscle cells (SMCs) and myofibroblasts. In contrast, patent grafts had reduced monocyte/macrophage infiltration and three mural layers structurally resembling the native IVC [8], though some had either stiffer or more compliant mechanical behaviors [9]. Importantly, although neotissue formation requires an immune response to the polymeric scaffold, the incidence of TEVG narrowing was proportional to the degree of macrophage infiltration [10]. Graft narrowing could be prevented either by seeding the grafts with bone marrow-derived mononuclear cells or by providing controlled release of an inhibitor to the TGF-β type 1 receptor [7, 8]. Given the myriad possible design modifications and potential pharmacological therapies that could be explored to improve graft patency further, an empirical trial-and-error search for an optimal scaffold design or specific clinical interventions quickly becomes impractical.
Figure 1.
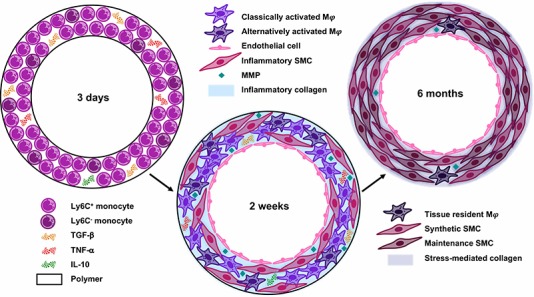
Mechanisms for transformation of implanted biodegradable polymeric scaffolds into vascular grafts. At early times, Ly6C+ and Ly6C− monocytes infiltrate the porous scaffold and release pro-inflammatory (TNF-α), anti-inflammatory (IL-10), and immunomodulatory (TGF-β) signaling molecules. The relative quantities of these cytokines determine monocyte differentiation into classically or alternatively activated macrophages (Mφ) at two weeks. The infiltrating monocytes also release multiple angiogenic cytokines and growth factors to recruit ECs and inflammatory SMCs from the adjacent vessel, which deposit stiff inflammatory collagen as part of the foreign body response. Six months post-implantation, the polymer is replaced with neotissue: only tissue-resident macrophages remain, and the vascular cells have appropriately organized into a mature blood vessel structure. The inflammatory collagen has been degraded by MMPs, and stress-mediated collagen dominates the extracellular matrix.
Recent advances in computational modeling promise time- and cost-efficient simulations that can reduce the experimental search space [11]. We previously developed a computational model of neovessel development from an implanted polymeric scaffold using a growth and remodeling (G&R) theory that incorporates immuno-driven and mechano-mediated turnover of neotissue [11, 12]. This model successfully describes and predicts the evolving geometry and mechanical properties of murine TEVGs, but its basis is phenomenological [9]. There is, therefore, a need for complementary models that incorporate molecular and cellular processes that drive TEVG development. Such models could provide insights into adaptive processes and enable parametric evaluations of consequences of key scaffold parameters and targeted pharmacological interventions. Herein we propose a model that includes interactions among the polymeric scaffold, multiple cell types, key cytokines, growth factors and proteases, the primary structural constituents, and mechanical stimuli (Fig. 2). We benchmark the model against prior data from our IVC interposition mouse model and then parametrically explore the potential for graft narrowing as a function of scaffold pore size, macrophage depletion, and the immunomodulatory cytokine TGF-β.
Figure 2.
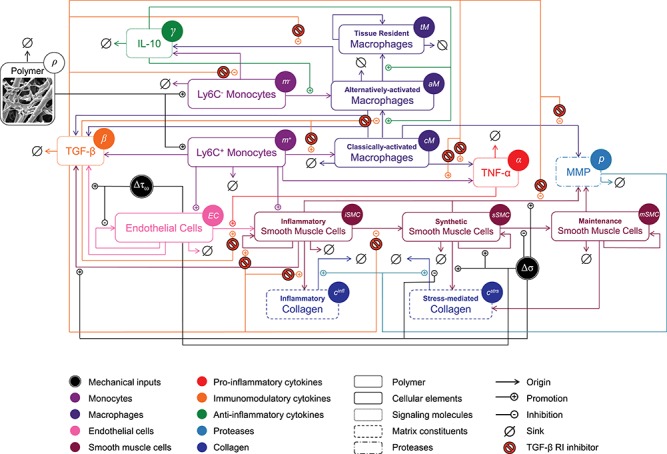
The BCM model of TEVG development, represented graphically using a schematic similar to that originally developed by [13]. The model is shown following pharmacological intervention with a TGF-β R1 inhibitor. Legend and color scheme for the mechanistic pathways are below the figure, and variables used in the governing equations can be found within circles next to the name of each element in the diagram. See text for further details.
METHODS
Our proposed bio-chemo-mechanical (BCM) model builds upon prior models for soft tissue G&R that include molecular and cellular kinetics [13–15], but focuses on the unique problem of in vivo neovessel development from a polymeric scaffold; it consists of 15 coupled ordinary differential equations (ODEs, in time) that govern spatially homogenized interactions that relate the scaffold design and mechanical stimulus to key immune cells, synthetic cells, cytokines, proteases, and matrix constituents that define the adaptation. The model includes 43 parameters, the values of which were tuned against 18 measurements from in vivo and in vitro experimental studies. Bounds on the parameters were chosen consistent with the literature [8, 16–19] or simply to be biologically reasonable when data were lacking. Although such models can increase predictive capability, their complexity necessarily renders the associated parameter estimation nontrivial. Manual parameter tuning has been used in the past [13–15], but it is time-consuming, operator-dependent, and not scalable and does not account for uncertainty in the experimental data. Indeed, tuning parameters in the presence of uncertainty makes manual approaches intractable.
Hence, we employed formal parameter estimation techniques that should scale and translate across users. Various automatic approaches are available [20–27]. While deterministic optimization is convenient for parameter estimation, it provides point estimates and cannot account for uncertainty in parameters or measurements. In other words, although well-suited for initially probing a small subset of problems, such approaches are insufficient for complex biological systems that are stochastic and lack complete measurements in most scenarios. We thus used a Bayesian estimation framework for parameter estimation in data-poor systems with uncertainty that employs an adaptive Markov chain Monte Carlo (MCMC) approach to sample from the joint posterior distribution of the unknown parameters, treated as random variables [28]. This estimation process was complemented with an identifiability analysis to determine unimportant parameters. The maximum a posteriori estimate was then determined on the identifiable parameters using simplex optimization [29], with the maximum a posteriori estimate from MCMC used as the initial guess for optimization. By combining identifiability analysis with Bayesian estimation and simplex optimization, we determined non-identifiable parameter combinations and estimated optimal values that matched experimental measurements in the presence of uncertainty. We then fixed the estimated optimal parameters and, to illustrate the utility of the model in hypothesis testing, simulated the effect of reducing scaffold pore size to that of grafts used in clinical trials or administering pharmacological treatments including clodronate (to deplete macrophages) and an inhibitor of TGF-βR1.
Model formulation
Model inputs
Because we formulated our molecular–cellular model independent of models at the scale of a tissue or organ, prescribed inputs included experimental data from a polymer degradation study and tissue-level computational predictions of mechanical stress [30]. Specifically, inputs included measured temporal changes in normalized mass density 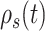 and pore radius
and pore radius 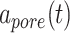 of a PGA/P(CL/LA) scaffold as it degrades (Fig. 3A and B) and computed changes in intramural
of a PGA/P(CL/LA) scaffold as it degrades (Fig. 3A and B) and computed changes in intramural 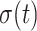 and wall shear
and wall shear 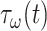 stresses, both over a 2-year implantation in a murine model (Fig. 3C and D). These prescribed intramural and wall shear stresses were computed from a spatially homogenized, membrane model of G&R [30], consistent with prior modeling of neovessel development [11, 12]. The initial pore radius was set at 20 μm consistent with current scaffolds implanted as interpositional grafts in the murine IVC. As the scaffold degrades over time
stresses, both over a 2-year implantation in a murine model (Fig. 3C and D). These prescribed intramural and wall shear stresses were computed from a spatially homogenized, membrane model of G&R [30], consistent with prior modeling of neovessel development [11, 12]. The initial pore radius was set at 20 μm consistent with current scaffolds implanted as interpositional grafts in the murine IVC. As the scaffold degrades over time  in vivo, pore radius can increase up to 25 μm, after which it is assumed that pore size no longer limits cellular infiltration into the scaffold [31, 32].
in vivo, pore radius can increase up to 25 μm, after which it is assumed that pore size no longer limits cellular infiltration into the scaffold [31, 32].
Figure 3.
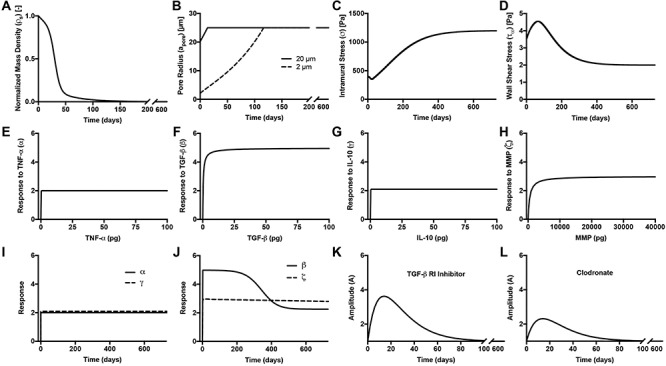
(A–D) Inputs for the BCM model. (A) Normalized polymer mass density (ρs (t)), which captures the degradation of the PGA felt in the first 6 weeks and the loss of the P(CL/LA) sealant over 6 months. (B) Evolving pore size (apore (t)) for two different scaffold designs with an initial pore radius of 20 μm (solid line) or 2 μm (dashed line). (C) Intramural stress (σ(t)) and (D) wall shear stress (τω (t)) profiles were generated using our previous phenomenological G&R framework [30]. (E) Response to TNF-α (parameter α) as a function of the quantity of TNF-α. (F) Response to TGF-β (parameter β) as a function of the quantity of TGF-β. (G) Response to IL-10 (parameter γ) as a function of the quantity of IL-10. (H) Response to MMPs (parameter ζ) as a function of the quantity of MMPs. (I) Values of parameters α and γ throughout the baseline simulation; both parameters are fixed. (J) Values of parameter β and parameter ζ throughout the baseline simulation. Notice that the MMP response function (dashed line) remains maximally activated throughout the baseline simulation, whereas the TGF-β response function (solid line) decays following degradation of the polymeric scaffold. (K) Gamma function used to model the administration of TGF-β RI inhibitor. (L) Gamma function used to model the administration of clodronate.
Equation assembly
The rate equations were developed based on simple principles that govern the behavior of each model constituent [13, 15, 33–37]. Terms with a positive sign indicate production of a constituent, which for cellular species can result from infiltration (e.g. first term in Equations 1 and 2), differentiation (e.g. first term in Equations 5–7), or proliferation (e.g. second term in Equation 7). Removal of a cellular species, represented by terms with a negative sign, can result from differentiation into a different cell type (e.g. second term in Equations 1 and 2), apoptosis, or emigration from the scaffold (e.g. third term in Equations 5 and 7). To facilitate direct comparisons with our available data (e.g. fluorescence-activated cell sorting (FACS)), the calculated numbers of cells represent total numbers per graft. For non-cellular species, their production depends on each cell type that is able to synthesize the given constituent (e.g. the first term for collagen production; Equations 17 and 18), while their degradation occurs by natural clearance modulated by the concentration of cytokines and signaling molecules (e.g. the second term for the inflammatory collagen; Equation 17). The rates of each of these kinds of processes for cellular species, structural proteins, and soluble factors can be modified by cytokines, growth factors, or mechanical stimuli. Population-specific modifications to the equations are elaborated below.
Immune cell infiltration
Secretion of monocyte chemoattractant protein-1 (MCP-1) from seeded bone marrow-derived mononuclear cells enhances early monocyte recruitment to the scaffold [38]. We focused on inflammatory Ly6C+ and patrolling Ly6C− monocytes as the two primary subpopulations [8], which differentiate into classically and alternatively activated macrophages, respectively. Temporal changes (i.e. rates of change) in the numbers of infiltrating Ly6C+ monocytes 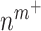 and Ly6C− monocytes
and Ly6C− monocytes 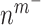 throughout the volume of the graft are modeled by
throughout the volume of the graft are modeled by
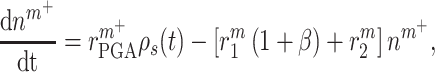 |
(1) |
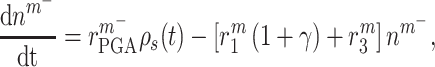 |
(2) |
where 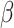 accounts for concentration-dependent cellular responses to the immunomodulatory cytokine TGF-β (Fig. 3F) and
accounts for concentration-dependent cellular responses to the immunomodulatory cytokine TGF-β (Fig. 3F) and 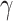 similarly accounts for responses to the anti-inflammatory cytokine IL-10 (Fig. 3G). The parameter
similarly accounts for responses to the anti-inflammatory cytokine IL-10 (Fig. 3G). The parameter 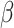 evolves during the implantation period (Fig. 3J), whereas
evolves during the implantation period (Fig. 3J), whereas 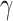 is constant (Fig. 3I). Here and below,
is constant (Fig. 3I). Here and below, 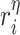 (
(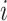 =1,2,3, …;
=1,2,3, …; 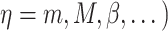 denote fixed rate parameters, specific descriptions of which are in Table 1 along with estimated/prescribed values [34, 35, 39–42]. For example,
denote fixed rate parameters, specific descriptions of which are in Table 1 along with estimated/prescribed values [34, 35, 39–42]. For example, 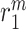 denotes a rate of differentiation and
denotes a rate of differentiation and 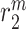 a rate of emigration or death of Ly6C+ monocytes, both of which decrease local cell number
a rate of emigration or death of Ly6C+ monocytes, both of which decrease local cell number 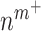 . In contrast, the rate of Ly6C+ monocyte infiltration into the polymeric scaffold
. In contrast, the rate of Ly6C+ monocyte infiltration into the polymeric scaffold 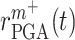 is limited by pore radius and given by an experimentally motivated hyperbolic function [13, 33]:
is limited by pore radius and given by an experimentally motivated hyperbolic function [13, 33]:
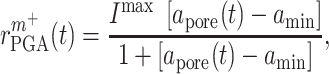 |
(3) |
where 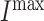 is the maximum rate of infiltration (
is the maximum rate of infiltration (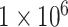 cells/day) [36] whereas
cells/day) [36] whereas 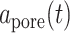 is the current scaffold pore radius and
is the current scaffold pore radius and 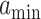 is the minimum pore radius that allows cell infiltration (assumed here to be 2 μm [43]). The rate of Ly6C− monocyte infiltration into the polymeric scaffold
is the minimum pore radius that allows cell infiltration (assumed here to be 2 μm [43]). The rate of Ly6C− monocyte infiltration into the polymeric scaffold 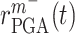 is similarly given by
is similarly given by
 |
(4) |
where 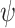 is a scaling factor, set to 0.167 based on experimental observations [19].
is a scaling factor, set to 0.167 based on experimental observations [19].
Table 1.
Model parameter definitions and values for mechanical inputs, inflammatory cells, signaling molecules, vascular cells, matrix constituents, and proteases. Estimated parameters are maximum a posteriori estimates from optimization and are highlighted in gray. The unidentifiable parameters in the model were informed by values in the literature. Note that references [7–10, 16–19, 49] are relevant to the murine IVC interposition graft model.
| Parameter | Description [unit] | Value | References | |
|---|---|---|---|---|
| Mechanical inputs | ||||
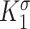
|
Scaling parameter for intramural stress above homeostatic target [−] | 0.0017 | Estimated | [46] |
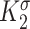
|
Scaling parameter for intramural stress below homeostatic target [−] | 0.0017 | Estimated | [46] |

|
Scaling parameter for wall shear stress below homeostatic target [−] | 0.0017 | Estimated | [46] |
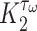
|
Scaling parameter for wall shear stress above homeostatic target [−] | 0.0017 | Estimated | [46] |
| Inflammatory cells | ||||
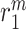
|
Ly6C+/Ly6C− monocyte differentiation rate [day−1] | 0.0485 | Estimated | [8, 19, 39] |
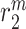
|
Ly6C+ monocyte emigration/death rate [day−1] | 0.5229 | Estimated | [8, 19, 40] |
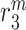
|
Ly6C− monocyte emigration/death rate [day−1] | 0.5848 | Estimated | [8, 19, 40] |
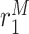
|
Classically activated macrophage differentiation rate [day−1] | 0.5 | Prescribed | [8, 19] |
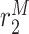
|
Macrophage emigration/death rate [day−1] | 0.7555 | Estimated | [8, 19, 34] |
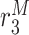
|
Alternatively activated macrophage differentiation rate [day−1] | 0.0025 | Prescribed | [8, 19] |
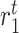
|
Tissue resident macrophage proliferation rate [day−1] | 0.0033 | Estimated | [9] |
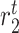
|
Tissue-resident macrophage emigration/death rate [day−1] | 0.0033 | Prescribed | [9] |
| Signaling molecules | ||||
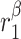
|
TGF-β secretion rate, classically activated macrophages [pg cell−1 day−1] | 0.0934 | Estimated | [34, 35] |
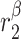
|
TGF-β secretion rate, alternatively activated macrophages [pg cell−1 day−1] | 0.001 | Prescribed | [34, 35] |
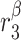
|
TGF-β secretion rate, inflammatory SMCs [pg cell−1 day−1] | 0.01 | Prescribed | [34, 35] |
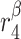
|
TGF-β secretion rate, ECs [pg cell−1 day−1] | 0.0001 | Prescribed | [34, 35] |
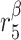
|
TGF-β degradation rate [day−1] | 16.6 | Prescribed | [34, 35] |
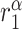
|
TNF-α synthesis rate, classically activated macrophages [pg cell−1 day−1] | 0.0101 | Estimated | [35, 37] |
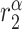
|
TNF-α degradation rate [day−1] | 12.8 | Prescribed | [35, 37] |
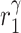
|
IL-10 secretion rate, alternatively activated macrophages and Ly6C− monocytes [pg cell−1 day−1] | 0.0653 | Estimated | [35, 37] |

|
IL-10 degradation rate [day−1] | 4.6 | Prescribed | [35, 37] |
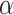
|
Response to TNF-α [−] | 2 | Prescribed | [50] |

|
Response to TGF-β [−] | 0 to 5 | Prescribed | [50] |
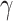
|
Response to IL-10 [−] | 2.0998 | Estimated | [50] |
| Vascular cells | ||||
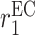
|
EC recruitment rate [day−1] | 0.0017 | Estimated | [10] |
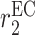
|
EC proliferation rate [day−1] | 0.007 | Prescribed | [10] |
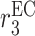
|
EC death rate [day−1] | 0.001 | Prescribed | [10] |

|
Inflammatory SMC recruitment rate [day−1] | 0.1963 | Estimated | [19, 10] |
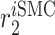
|
Inflammatory SMC proliferation rate [day−1] | 0.0822 | Estimated | [19, 69] |
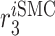
|
Endothelial-to-mesenchymal transition rate [day−1] | 0.0011 | Estimated | [8, 7] |
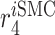
|
Inflammatory SMC to synthetic SMC differentiation rate [day−1] | 0.0973 | Estimated | [19, 66] |
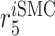
|
Inflammatory SMC death rate [day−1] | 1 | Prescribed | [19] |
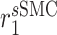
|
Synthetic SMC proliferation rate [day−1] | 0.5003 | Estimated | [19] |
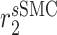
|
Synthetic SMC to maintenance SMC differentiation rate [day−1] | 0.002 | Prescribed | [19, 39] |
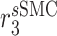
|
Synthetic SMC death rate [day−1] | 0.5 | Prescribed | [19] |
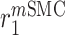
|
Maintenance SMC proliferation rate [day−1] | 0.0013 | Estimated | [69] |
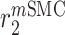
|
Maintenance SMC death rate [day−1] | 0.002 | Prescribed | [69] |
| Matrix constituents | ||||
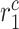
|
Inflammatory collagen secretion rate by inflammatory SMCs [pg cell−1 day−1] | 50 | Prescribed | [17] |
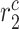
|
Collagen degradation rate due to classically activated macrophages [day−1] | 0.1042 | Estimated | [41, 42] |
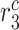
|
Stress-mediated collagen secretion rate by synthetic SMCs [pg cell−1 day−1] | 20 | Prescribed | [66] |
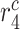
|
Stress-mediated collagen secretion rate by maintenance SMCs [pg cell−1 day−1] | 20 | Prescribed | [17] |
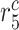
|
Collagen degradation rate due to SMCs [day−1] | 0.0093 | Estimated | [41, 42] |
| Proteases | ||||
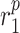
|
MMP secretion rate due to classically activated macrophages [pg cell−1 day−1] | 0.2429 | Estimated | [18] |
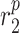
|
MMP secretion rate due to inflammatory SMCs [pg cell−1 day−1] | 0.2169 | Estimated | [18] |
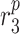
|
MMP secretion rate due to synthetic SMCs [pg cell−1 day−1] | 0.1027 | Estimated | [18] |
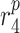
|
MMP secretion rate due to maintenance SMCs [pg cell−1 day−1] | 0.027 | Prescribed | [18] |
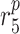
|
MMP degradation rate [day−1] | 0.875 | Prescribed | [34] |
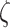
|
Response to MMPs [−] | 0–3 | Prescribed | [49] |
In similar fashion, numbers of classically activated macro-phages 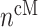 , alternatively activated macrophages
, alternatively activated macrophages 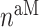 , and tissue-resident macrophages
, and tissue-resident macrophages 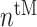 that remain in the graft following monocyte infiltration [33] are computed via
that remain in the graft following monocyte infiltration [33] are computed via
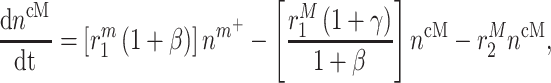 |
(5) |
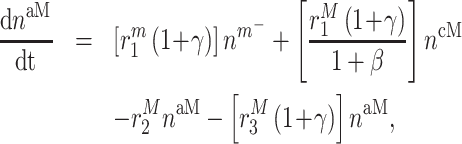 |
(6) |
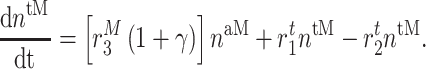 |
(7) |
As an example, Equation (5) specifies that the rate of differentiation of recruited Ly6C+ monocytes 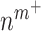 into classically activated macrophages
into classically activated macrophages 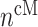 is enhanced by TGF-β through the response parameter
is enhanced by TGF-β through the response parameter 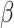 [8], while Equation (6) specifies that TGF-β also inhibits the differentiation of these monocytes to alternatively activated macrophages
[8], while Equation (6) specifies that TGF-β also inhibits the differentiation of these monocytes to alternatively activated macrophages 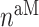 [8]; moreover, this latter differentiation is enhanced by the anti-inflammatory cytokine IL-10 through parameter
[8]; moreover, this latter differentiation is enhanced by the anti-inflammatory cytokine IL-10 through parameter 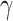 [8].
[8].
Vascular cell recruitment
Infiltrating monocytes secrete multiple cytokines and growth factors that recruit vascular cells into the graft that contribute to neotissue development. For example, SMCs and endothelial cells (ECs) are recruited from adjacent vessel segments as migrating and proliferating cells [16]. These vascular cell populations, calculated over the volume of the graft, are modeled by the following rate equations:
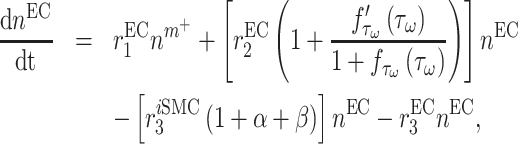 |
(8) |
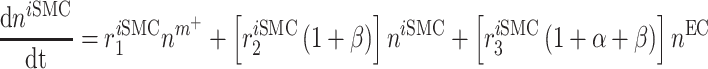 |
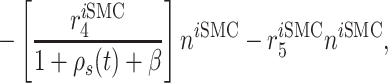 |
(9) |
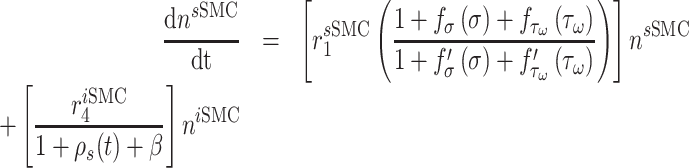 |
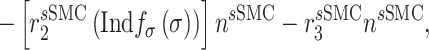 |
(10) |
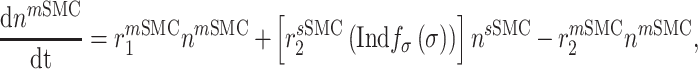 |
(11) |
where 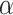 captures cellular responses to the pro-inflammatory cytokine TNF-α (Fig. 3E) and is fixed throughout the simulation (Fig. 3I);
captures cellular responses to the pro-inflammatory cytokine TNF-α (Fig. 3E) and is fixed throughout the simulation (Fig. 3I); 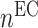 is the number of ECs throughout the volume of the graft;
is the number of ECs throughout the volume of the graft; 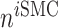 is the number of SMCs that phenotypically promote inflammation, which arise from ECs via endothelial-to-mesenchymal transition (endo-MT) and are recruited to the polymer during the foreign body response [7, 8];
is the number of SMCs that phenotypically promote inflammation, which arise from ECs via endothelial-to-mesenchymal transition (endo-MT) and are recruited to the polymer during the foreign body response [7, 8]; 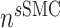 is the number of synthetic SMCs, which sense mechanical stresses and deposit matrix accordingly; and
is the number of synthetic SMCs, which sense mechanical stresses and deposit matrix accordingly; and 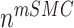 is the number of maintenance SMCs, which represent a more quiescent, sensing, and synthetic phenotype that differentiates from actively synthetic SMCs under homeostatic intramural stresses, as regulated by the binary indicator function:
is the number of maintenance SMCs, which represent a more quiescent, sensing, and synthetic phenotype that differentiates from actively synthetic SMCs under homeostatic intramural stresses, as regulated by the binary indicator function:
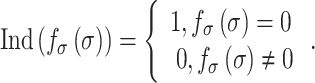 |
(12) |
Noting that both wall shear stress (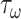 ) and intramural wall stress (
) and intramural wall stress (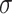 ) elicit myriad changes in gene expression in ECs and SMCs [44, 45], consider normalized differences in
) elicit myriad changes in gene expression in ECs and SMCs [44, 45], consider normalized differences in 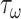 and
and 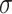 from their homeostatic values (
from their homeostatic values (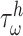 and
and 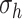 , respectively) given by
, respectively) given by
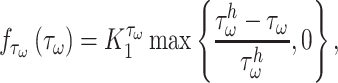 |
(13) |
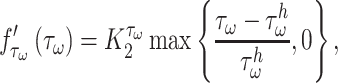 |
(14) |
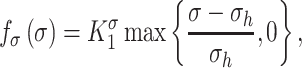 |
(15) |
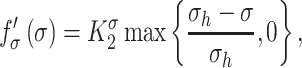 |
(16) |
where 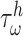 is ~ 2 Pa and
is ~ 2 Pa and 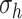 ~ 100 kPa for the native mouse IVC [11]. Here,
~ 100 kPa for the native mouse IVC [11]. Here, 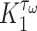 ,
, 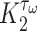 ,
,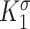 , and
, and 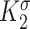 are gain-type scaling parameters, set equal to each other due to lack of data (also same as K in Fig. 5). These functional forms are motivated by the following biological observations: values of wall shear stresses above or below the homeostatic value
are gain-type scaling parameters, set equal to each other due to lack of data (also same as K in Fig. 5). These functional forms are motivated by the following biological observations: values of wall shear stresses above or below the homeostatic value 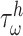 enhance or inhibit EC proliferation, respectively (Equation 8) [46, 47]. Similarly, synthetic SMC proliferation is augmented by intramural stresses above those observed in the native mouse IVC (
enhance or inhibit EC proliferation, respectively (Equation 8) [46, 47]. Similarly, synthetic SMC proliferation is augmented by intramural stresses above those observed in the native mouse IVC (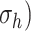 and inhibited by lower values (Equation 10) [12, 46]. Moreover, differentiation of inflammatory SMCs to actively synthesize SMCs is impeded by the presence of both the polymeric scaffold
and inhibited by lower values (Equation 10) [12, 46]. Moreover, differentiation of inflammatory SMCs to actively synthesize SMCs is impeded by the presence of both the polymeric scaffold 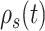 and the immunomodulatory cytokine TGF-β, the latter through
and the immunomodulatory cytokine TGF-β, the latter through 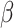 (Equations 9 and 10) [7, 48].
(Equations 9 and 10) [7, 48].
Figure 5.
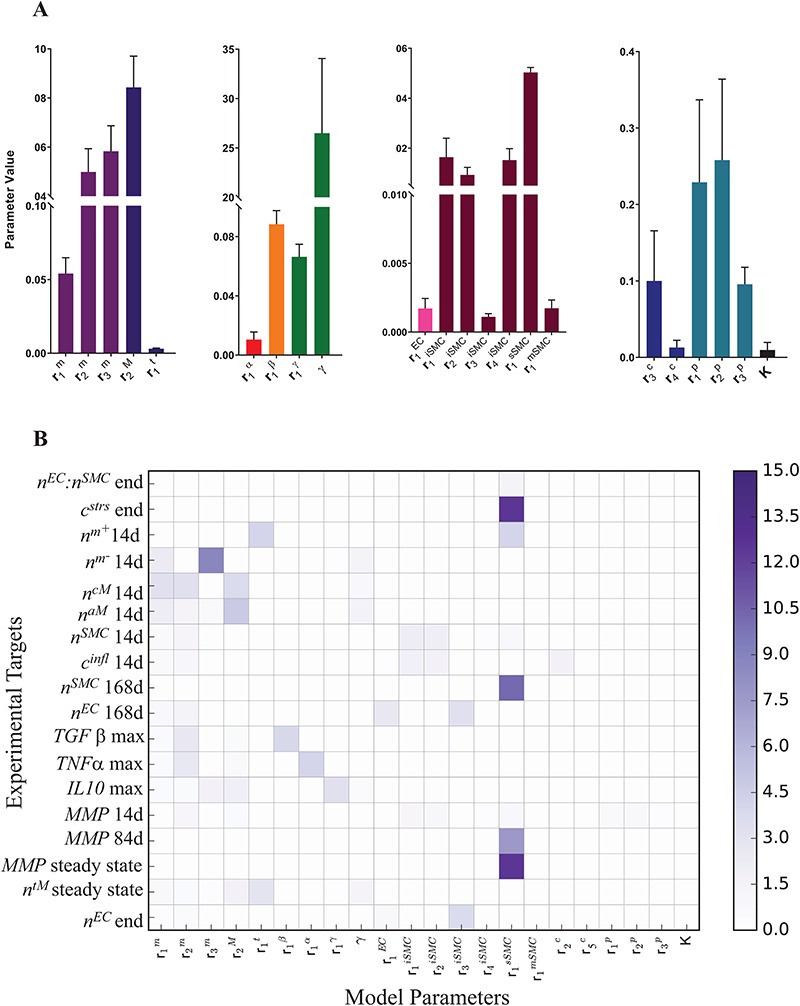
(A) Mean parameter values and their associated standard deviations, computed from the converged DREAM samples, for the set of 22 identifiable parameters that can completely recover the targets within error. (B) Average LSI of the 18 targets to 22 identifiable model parameters. The LSI is averaged over multiple local perturbations (<10%) of the maximum a posteriori estimate.
Matrix synthesis, remodeling, and degradation
As part of the foreign body response, inflammatory SMCs synthesize a more fibrotic collagen (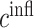 ), the total mass of which is
), the total mass of which is
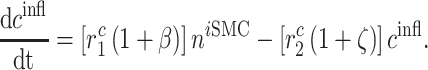 |
(17) |
where 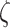 parameterizes the effects of matrix metalloproteinases (MMPs), explained below. This inflammatory collagen is characterized as densely packed, stiff, and scar-like, with a high type I:III ratio [9, 12]. Synthetic SMCs produce natural mechano-sensing-mediated collagen (
parameterizes the effects of matrix metalloproteinases (MMPs), explained below. This inflammatory collagen is characterized as densely packed, stiff, and scar-like, with a high type I:III ratio [9, 12]. Synthetic SMCs produce natural mechano-sensing-mediated collagen (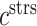 ), which is less densely packed and more compliant, with a lower type I:III ratio [9]. The total mass of stress-mediated collagen is given by
), which is less densely packed and more compliant, with a lower type I:III ratio [9]. The total mass of stress-mediated collagen is given by
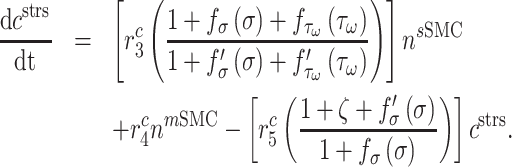 |
(18) |
That is, the rate of mechano-mediated collagen production depends on differences in intramural and wall shear stresses from their target, or homeostatic, values. 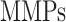 , which degrade inflammatory and stress-mediated collagen, are secreted by classically activated macrophages and SMCs [18], as modeled by
, which degrade inflammatory and stress-mediated collagen, are secreted by classically activated macrophages and SMCs [18], as modeled by
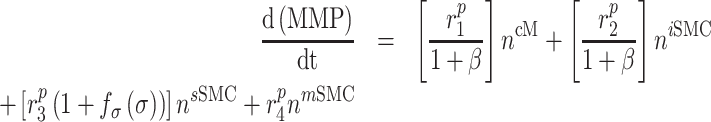 |
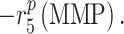 |
(19) |
MMPs and collagen degrade at rates reflected by their respective half-lives. The response to MMPs (parameter 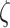 ; see Fig. 3H) was modeled via
; see Fig. 3H) was modeled via
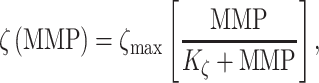 |
(20) |
where 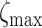 = 3 and
= 3 and 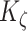 = 500, with
= 500, with 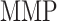 denoting the mass (in pg) of active MMPs [49]. The evolution of
denoting the mass (in pg) of active MMPs [49]. The evolution of 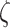 throughout the two-year implantation period is shown in Fig. 3J.
throughout the two-year implantation period is shown in Fig. 3J.
Signaling molecules
Cytokines, including pro-inflammatory (e.g. TNF-α), anti-inflammatory (e.g. IL-10), or immunomodulatory (e.g. TGF-β), are differentially secreted by inflammatory and vascular cells; they regulate cell proliferation, differentiation, and activation [7, 8]. The evolving concentrations of these signaling molecules are given by
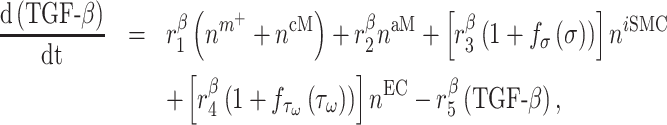 |
(21) |
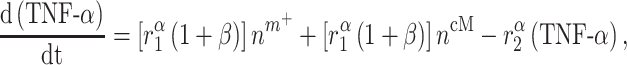 |
(22) |
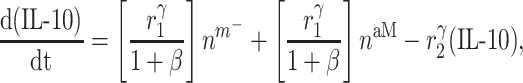 |
(23) |
where each cytokine also degrades at a rate determined by its half-life. Descriptions and values for the rate constants are summarized in Table 1.
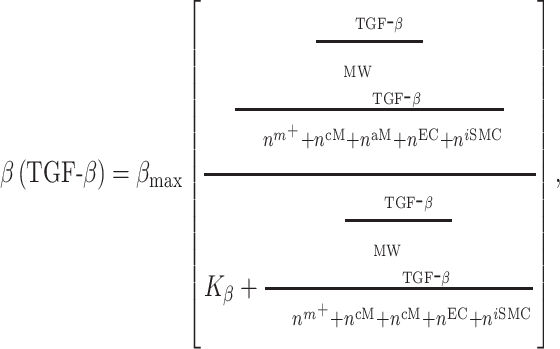
The response to TGF-β (parameter 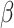 ) was modeled to fit a previously published dose-dependent response profile [50], namely,
) was modeled to fit a previously published dose-dependent response profile [50], namely,
 |
(24) |
with 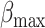 ~ 5 and
~ 5 and 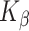 ~ 102.5, where
~ 102.5, where 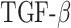 is the mass of TGF-β (in pg).
is the mass of TGF-β (in pg). 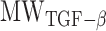 is the molecular mass of a single TGF-β molecule (4.15 × 10−8 pg) with, as before,
is the molecular mass of a single TGF-β molecule (4.15 × 10−8 pg) with, as before, 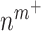 the number of Ly6C+ monocytes,
the number of Ly6C+ monocytes, 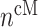 the number of classically activated macrophages,
the number of classically activated macrophages, 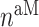 the number of alternatively activated macrophages,
the number of alternatively activated macrophages, 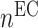 the number of ECs, and
the number of ECs, and 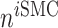 the number of inflammatory SMCs (all of which secrete TGF-β).
the number of inflammatory SMCs (all of which secrete TGF-β).
Targeted pharmacological therapy
Pharmacological interventions in mice using clodronate liposomes (600 μL/day) [10] or the TGF-βR1 kinase inhibitor SB431542 (10 mg/kg twice daily) [7, 8] were modeled phenomenologically over the first few weeks following graft implantation using modified gamma functions, with dose 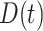 given by
given by
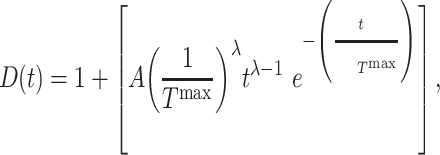 |
(25) |
with 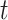 the simulation time in days,
the simulation time in days, 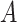 the rate parameter (50 for the TGF-βR1 inhibitor and 100 for clodronate),
the rate parameter (50 for the TGF-βR1 inhibitor and 100 for clodronate), 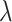 the shape parameter for the function (~2), and
the shape parameter for the function (~2), and 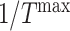 the scaling parameter, with highest drug concentration at 14 days [7, 8, 10] (Fig. 3K and L).
the scaling parameter, with highest drug concentration at 14 days [7, 8, 10] (Fig. 3K and L).
Parameter estimation and sensitivity analysis
Given our system of governing ODEs (i.e. the BCM model represented by Equations 1–24) and the associated model parameters (Table 1), we identified 18 experimentally measured target quantities that should be matched by model outputs following optimal parameterization (Table 2). Fifteen of these targets were determined using our previously published murine IVC interposition graft model: monocyte and macrophage populations were quantified using FACS [8], vascular cells by immunofluorescence analysis [19], collagen content from a hydroxyproline assay [17], and MMPs from immunohistochemical analysis [18]. As system-specific measurements are lacking on the temporal and spatial profiles of key immunomodulatory cytokines known to be involved in graft stenosis, targets for these signaling molecules were determined using in vivo and in vitro measurements reported in the literature [7, 34, 35, 50–52]. Model agreement with all measured targets is found in Table 2. Standard deviations for these targets came from the literature or were assumed to be 10% of the measured value when data were lacking.
Table 2.
Agreement between experimental targets and predicted model outputs. Simulation outputs are the outputs from the maximum a posteriori parameter estimates. Note that 15 of the 18 experimentally measured targets were determined using data from our previously published murine IVC interposition graft model. Targets for key signaling molecules (TGF-β, TNF-∝, and IL-10) were determined from in vivo and in vitro experimental studies from the literature.
| Target definition [unit] | Target value | Reference | % Uncertainty | Simulation output | % Deviation |
|---|---|---|---|---|---|
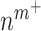 at 14 days [cells] at 14 days [cells] |
1.10 × 106 | [8, 38] | 10 | 1.13 × 106 | 3.02 |
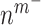 at 14 days [cells] at 14 days [cells] |
2.00 × 105 | [8, 38] | 10 | 2.08 × 105 | 4.11 |
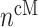 at 14 days [cells] at 14 days [cells] |
3.20 × 105 | [8, 38] | 10 | 3.22 × 105 | 0.81 |
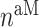 at 14 days [cells] at 14 days [cells] |
1.40 × 105 | [8, 38] | 10 | 1.49 × 105 | 6.50 |
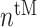 at steady state [cells] at steady state [cells] |
4.14 × 104 | [9, 40] | 10 | 4.12 × 104 | −0.34 |
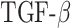 max in the first 50 days [pg] max in the first 50 days [pg] |
8.48 × 103 | [7, 34, 50] | 10 | 8.43 × 103 | −0.58 |
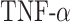 max in the first 50 days [pg] max in the first 50 days [pg] |
6.78 × 103 | [51, 35] | 10 | 6.87 × 103 | 1.26 |
| IL-10 max in first 50 days [pg] | 8.48 × 102 | [52, 35] | 10 | 8.43 × 102 | −0.56 |
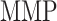 at 14 days [pg] at 14 days [pg] |
3.85 × 104 | [18, 49] | 10 | 3.85 × 104 | −0.16 |
 at 84 days [pg] at 84 days [pg] |
2.14 × 104 | [18, 49] | 10 | 2.15 × 104 | 0.49 |
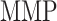 at steady state [pg] at steady state [pg] |
7.00 × 103 | [18, 49] | 10 | 6.88 × 103 | −1.75 |
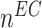 at 168 days [cells] at 168 days [cells] |
4.60 × 105 | [19, 10, 16] | 10 | 4.40 × 105 | 3.55 |
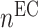 at the end of simulation [cells] at the end of simulation [cells] |
3.10 × 104 | [19, 10, 16] | 10 | 3.17 × 104 | 2.41 |
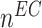 : : 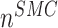 at end of simulation [−] at end of simulation [−] |
2.65 × 10−1 | [19, 10, 16] | 25 | 2.50 × 10−1 | −5.80 |
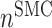 at 14 days [cells] at 14 days [cells] |
4.60 × 105 | [19, 10, 16] | 10 | 4.75 × 105 | 3.29 |
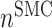 at 168 days [cells] at 168 days [cells] |
1.90 × 105 | [19, 10, 16] | 10 | 1.82 × 105 | −4.14 |
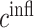 at 14 days [pg] at 14 days [pg] |
3.00 × 108 | [17, 18, 9] | 10 | 2.96 × 108 | −1.24 |
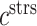 at the end of simulation [pg] at the end of simulation [pg] |
7.50 × 107 | [17, 18, 9] | 30 | 7.29 × 107 | −2.85 |
Statistical model
Consistent with previously published statistical models, consider a set of p random inputs 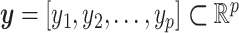 with joint probability distribution
with joint probability distribution 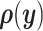 , and let
, and let 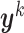 be its kth realization [53, 54]. The present BCM model of TEVG development relates the p input parameters and m outputs
be its kth realization [53, 54]. The present BCM model of TEVG development relates the p input parameters and m outputs 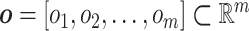 , that is,
, that is, 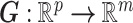 . In other words,
. In other words, 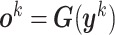 , with
, with 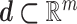 the set of experimental measurements and
the set of experimental measurements and 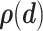 the corresponding joint probability distribution we seek to match. The error between the experimental findings and model outputs is
the corresponding joint probability distribution we seek to match. The error between the experimental findings and model outputs is
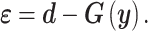 |
(26) |
Model (or epistemic) uncertainty is not explicitly considered but included in the selected standard deviation for the observables.
The target covariance matrix 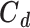 is assumed to be diagonal, as experimental data are obtained from multiple unrelated experiments. The statistical model [53] induces a likelihood of observables of the form,
is assumed to be diagonal, as experimental data are obtained from multiple unrelated experiments. The statistical model [53] induces a likelihood of observables of the form,
 |
(27) |
where 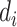 is the ith experimental measurement and
is the ith experimental measurement and  the corresponding model output,
the corresponding model output, 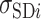 the standard deviation associated with
the standard deviation associated with 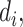 and the weights
and the weights  introduced for target prioritization. Note that
introduced for target prioritization. Note that 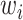 were tuned from MCMC simulations with synthetic targets and included to modulate our ability to match certain targets [53]. The synthetic targets, in turn, represent a set that can be represented exactly by the BCM model and generated from a known parameter set within the permissible range. Once we have determined the likelihood for a given parameter realization, the parameter posterior is computed using the Bayesian conjunction of likelihood and prior as
were tuned from MCMC simulations with synthetic targets and included to modulate our ability to match certain targets [53]. The synthetic targets, in turn, represent a set that can be represented exactly by the BCM model and generated from a known parameter set within the permissible range. Once we have determined the likelihood for a given parameter realization, the parameter posterior is computed using the Bayesian conjunction of likelihood and prior as
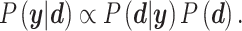 |
(28) |
Optimal parameter estimates are obtained by maximizing 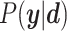 . Since we have no prior knowledge on the parameters, we use uninformative uniform priors
. Since we have no prior knowledge on the parameters, we use uninformative uniform priors 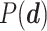 within the permissible range.
within the permissible range.
MCMC with DREAM algorithm
Optimization of overparameterized differential models based on scarce experimental evidence is typically associated with non-convex posterior distributions having multiple local extremes. Hence, we considered this possibly complicated posterior using MCMC to ‘sense’ local and global extremes, thus determining a convenient initial guess for an optimizer. Specifically, based on past experience with similar data-poor, high-dimensional problems [53, 54], we use a DiffeRential Evolution Adaptive Metropolis (DREAM) algorithm [28] that is well suited for nonlinear models and overcomes the slow convergence exhibited by classic Metropolis–Hastings MCMC. DREAM combines differential evolution and self-adaptive randomized subspace sampling, improving over other methods when sampling from heavily tailed or multimodal distributions [55, 56]. Moreover, adopting parallel Markov chains improves computational performance and offers better metrics to assess convergence. Convergence to a stationary distribution is monitored through the Gelman–Rubin (GR) convergence metric [57]. A GR metric < 1.2 for all Markov chains guarantees satisfactory convergence.
Identifiability
Limited experimental data is typically responsible for lack of identifiability of model parameters, that is, when certain parameters cannot be identified uniquely from system outputs and multiple combinations of unidentifiable parameters can yield the same likelihood [58]. It is thus important to recognize unimportant parameters or their unidentifiable combinations to avoid misinterpretations of Bayesian estimation. We used multiple tools to address identifiability. Using local sensitivities, 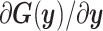 (i.e. derivatives of targets with respect to the parameters), we define the Fisher information matrix (FIM) as [59]
(i.e. derivatives of targets with respect to the parameters), we define the Fisher information matrix (FIM) as [59]
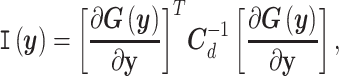 |
(29) |
where 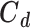 is the diagonal covariance matrix of the targets, as previously described. The rank of this FIM is a measure of local identifiability; for example, a full rank indicates a locally identifiable system given the available set of experimental observations, while dominant contributions to null eigenvectors reveal unimportant parameters, which can be removed.
is the diagonal covariance matrix of the targets, as previously described. The rank of this FIM is a measure of local identifiability; for example, a full rank indicates a locally identifiable system given the available set of experimental observations, while dominant contributions to null eigenvectors reveal unimportant parameters, which can be removed.
Additionally, we use the marginal variance as a measure of global identifiability by defining a learning factor 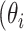 ) as
) as
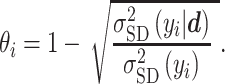 |
(30) |
This metric is a measure of the ability of the Bayesian framework to ‘learn’ a parameter 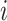 by comparing its prior and posterior marginal variance [53]. So-called well-learned parameters associate with a value of
by comparing its prior and posterior marginal variance [53]. So-called well-learned parameters associate with a value of  close to one, while poorly learned parameters have a resulting variance close to the prior, hence
close to one, while poorly learned parameters have a resulting variance close to the prior, hence  close to zero. Poorly learned parameters, characterized by a ‘flat’ marginal posterior, are also considered unimportant and can be removed, thus reducing the dimensionality of the estimation problem.
close to zero. Poorly learned parameters, characterized by a ‘flat’ marginal posterior, are also considered unimportant and can be removed, thus reducing the dimensionality of the estimation problem.
Unimportant parameters were also identified using a subsystem analysis where similar analyses, as above, were performed for parameters associated with subsystems of inflammatory cells, signaling molecules, vascular cells, and matrix constituents, keeping other subsystems fixed. Note that MCMC merely generates samples from a distribution for which point-wise evaluations of the posterior distribution are available up to a constant. While the density of samples is expected to be larger on the posterior peaks, MCMC need not provide the maximum of this posterior distribution. Hence, we used Nelder–Mead optimization with restarts [29, 60], a simplex-based method, to determine the local maximum a posteriori estimate. The DREAM MCMC algorithm provides the parameter sample with the maximum a posteriori value as a robust initial guess for successive optimization through the Nelder–Mead algorithm. In summary (Fig. 4), we combined FIM analysis and learning factors from MCMC simulations and reduced the initial set of 43 parameters to a set of 22 identifiable parameters that can completely recover the synthetic targets. These 22 parameters were then estimated to match the desired experimental targets (Table 2).
Figure 4.
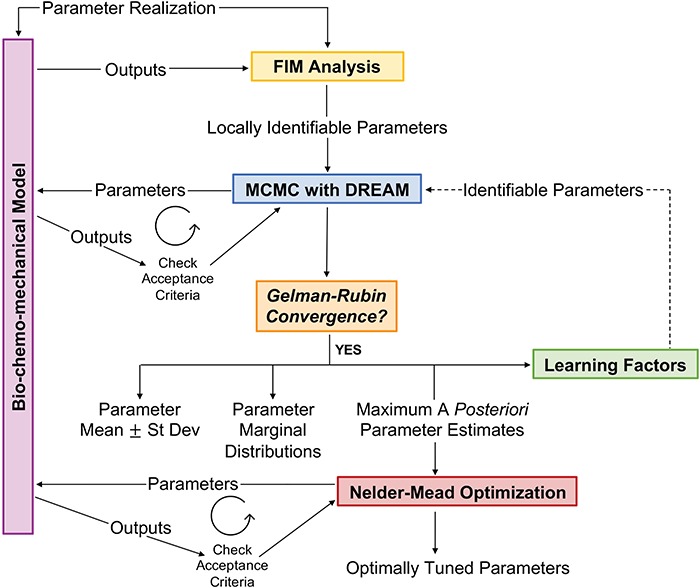
Framework for parameter estimation, consisting of FIM identifiability analysis, adaptive MCMC algorithm, and Nelder–Mead optimization. Using this framework, we report estimates for identifiable parameters in the BCM model in the presence of uncertainty in experimental measurements. See text for further details.
Local sensitivity analysis
Finally, we computed variability in the model predictions due to small perturbations of the inputs. Following parameter estimation, local parameter sensitivity was determined by calculating the local sensitivity index (LSI), defined as the percent change in an output (target) for a percent change in input (parameter) [61]. The LSI was averaged over multiple perturbations (<10%) in the neighborhood of the maximum a posteriori estimate.
RESULTS
Model parameterization captures salient aspects of neovessel development in vivo
We began with a polymeric scaffold having an initial pore radius of 20 μm and calibrated the model parameters (Fig. 5A) to yield outputs consistent with experimental observations (Fig. 6A–D and Table 2); the percent deviation between experimental targets and simulation outputs ranged from 0.16 to 6.5% (Table 2). Specifically, the BCM model captured the available experimental data on molecular and cellular counts of total immune cells per graft, pro- and anti-inflammatory cytokines, total vascular cells, and matrix constituents following the simulated surgical implantation of the scaffold. Marked monocyte infiltration, numerous classically activated macrophages, and many inflammatory SMCs were collectively responsible for an early burst in production of stiff collagen (Fig. 6A–D). Such inflammation-driven collagen adversely affects neovessel distensibility in comparison to the more desirable stress-mediated collagen that is produced after a scaffold loses load-bearing integrity and no longer stress-shields the intramural synthetic cells [9, 12]. Recall, too, that classical activation of monocytes contributes to graft stenosis, with experimental studies in C57BL/6 mice revealing a 48% patency rate for unseeded scaffolds of this design 6 months post-implantation [8].
Figure 6.
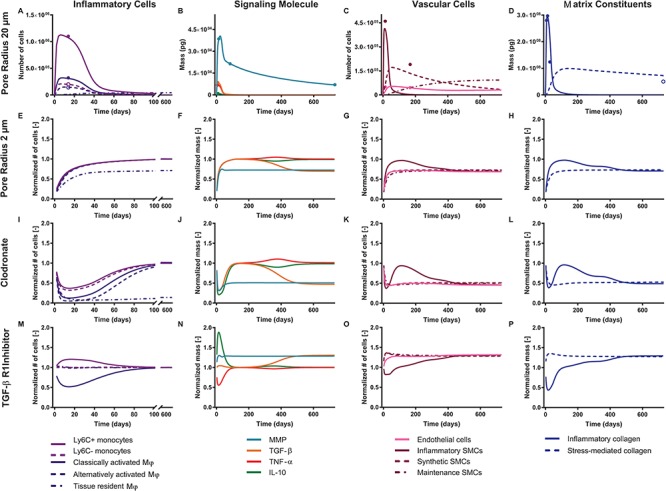
Baseline simulations for a scaffold with an initial pore size of 20 μm, showing the natural evolution of inflammatory cells (A), signaling molecules (B), vascular cells (C), and matrix constituents (D) over the course of 2 years. (A) FACS data of immune cells 14 days post-implantation are shown for Ly6C+ monocytes (solid light purple circle), Ly6C− monocytes (open light purple circle), classically activated macrophages (solid dark purple circle), and alternatively activated macrophages (open dark purple circle) [8]. (B) MMP immunohistochemical quantification is shown 2 weeks, 12 weeks, and 2 years post-implantation (solid teal circles) [18]. Targets for the cytokines TGF-β (solid orange circle), TNF-α (solid red circle), and IL-10 (solid green circle) are derived from literature [50]. (C) Immunofluorescence quantification of SMCs (solid maroon circles) and ECs (solid pink circles) is shown 2 weeks and 24 weeks post-implantation [19, 10, 16]. (D) Hydroxyproline assay data is shown for the graft 7, 14, and 28 days post-implantation (solid blue circles) and for the native IVC at the end of the simulation (open blue circle) [17]. Illustrative studies were then performed to explore these cellular and biochemical variables as a function of reduced initial pore radius (2 μm to simulate the graft used clinically) (E–H), administration of clodronate for 2 weeks following scaffold implantation (I–L), and administration of a TGF-β R1 inhibitor for 2 weeks following scaffold implantation (M–P). All outputs are normalized to baseline simulations for a scaffold with an initial pore size of 20 μm; see Supplementary Fig. 1 for the original simulations.
An analysis of the average LSI for the 22 identifiable parameters revealed that the model has a dominant downwind behavior (Fig. 5B). Parameters that govern the upstream differential equations for the initial inflammatory response to the scaffold and subsequent recruitment of vascular cells affect multiple model outputs to varying degrees, but parameters that govern the downstream equations for matrix constituents, cytokines, and proteases only influence those specific corresponding outputs (Fig. 5B). For example, the proliferation rate for the synthetic SMCs (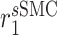 ) affects the number of Ly6C+ monocytes at 14 days (
) affects the number of Ly6C+ monocytes at 14 days (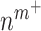 14 days), the number of SMCs at 168 days (
14 days), the number of SMCs at 168 days (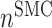 168 days), the mass of stress-mediated collagen at the end of the simulation (
168 days), the mass of stress-mediated collagen at the end of the simulation (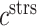 end), and the concentration of MMPs at both 84 days (
end), and the concentration of MMPs at both 84 days (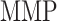 84 days) and steady state (
84 days) and steady state (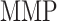 steady state); in contrast, the rate of collagen degradation due to classically activated macrophages (
steady state); in contrast, the rate of collagen degradation due to classically activated macrophages (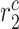 ) only affects the mass of inflammatory collagen at 14 days (
) only affects the mass of inflammatory collagen at 14 days (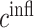 14 days). This suggests that the process of neovessel development from an implanted biodegradable scaffold may be open-loop, governed less by positive and negative BCM feedback and more by the inherent immunogenicity of the scaffold, which emphasizes the importance of scaffold selection and the associated need to control responses early after implantation.
14 days). This suggests that the process of neovessel development from an implanted biodegradable scaffold may be open-loop, governed less by positive and negative BCM feedback and more by the inherent immunogenicity of the scaffold, which emphasizes the importance of scaffold selection and the associated need to control responses early after implantation.
Once the baseline simulation was calibrated against experimental data, we performed hypothesis-driven parametric studies to explore possible changes in the in vivo development of graft constituents, cells, and signaling molecules as a function of modifications to scaffold design as well as targeted pharmacological interventions, with the overall aim of pointing to possible measures to maintain graft cellularity, improve long-term patency, and minimize compliance mismatch.
Reducing scaffold pore size may improve TEVG distensibility at the cost of patency
Physical parameters characterizing a particular scaffold can modulate the host inflammatory response by altering the inherent immunogenicity [11]. We previously identified scaffold pore size as a critical regulator of monocyte infiltration and determinant of stenosis [11]. Reducing pore size from 20 to 2 μm dramatically reduced infiltration and patency [43]. We hypothesized that this lower patency is secondary to the inability of circulating monocytes to infiltrate the scaffold, with an associated lack of paracrine-stimulated synthetic cells migrating into the scaffold and depositing matrix interstitially, thus leading to appositional growth of neotissue at the graft lumen and consequent narrowing (which could be exacerbated by thrombosis, which we do not model). Indeed, reducing pore radius from 20 to 2 μm in our BCM model decreased the number of monocytes and macrophages that entered the scaffold, which reduced the number of recruited vascular cells that could populate and remodel the graft. This decrease in SMCs reduced both the immuno-driven and stress-mediated synthesis of collagen (Fig. 6E–H, Supplementary Fig. 1E–H). Hence, we suggest that, although a reduction in pore size could potentially improve distensibility by reducing the early peak in inflammatory collagen (Supplementary Fig. 1E–H), the inability of immune cells to enter the scaffold immediately after implantation could drastically compromise graft patency and reduce long-term cellularity, suggesting a need to explore alternative solutions.
Macrophage depletion reduces TEVG stenosis but compromises neotissue formation
Our initial therapy for reducing graft stenosis in our murine model targeted macrophages. Clodronate liposomes are a well-described method for depleting macrophages by apoptosis [10]. Treatment with clodronate liposomes by intraperitoneal injection for the first 2 weeks following graft implantation in mice significantly decreased macrophage infiltration and, in turn, TEVG stenosis [10]. Unexpectedly, however, clodronate also dramatically reduced graft cellularity, suggesting that inhibiting macrophage infiltration also reduces vascular neotissue formation. That is, the inflammatory response is a double-edged sword: excessive macrophage infiltration causes stenosis, while severely attenuated infiltration results in insufficient vascular cell recruitment and matrix synthesis, both of which jeopardize long-term graft performance. Indeed, prescribing increased apoptosis of monocytes and macrophages in our BCM model (using a modified gamma function to simulate clodronate administration; Fig. 3L) led to a markedly reduced recruitment of vascular cells into the TEVG and reduced inflammatory and stress-mediated collagen production—all consistent with empirical observations [10] (Fig. 6I–L, Supplementary Fig. 1I–L). Thus, we suggest that, although clodronate (and similar) treatment may ameliorate compliance mismatch by diminishing the peak inflammatory collagen deposition and decrease the incidence of stenosis by reducing luminal neotissue formation, it can also compromise graft cellularity and matrix production, which can have catastrophic consequences once the polymer loses load-bearing integrity.
TGF-βR1 inhibition improves patency, maintains cellularity, and minimizes compliance mismatch
We have shown experimentally that inhibiting TGF-β signaling in mice either by early short-term systemic treatment or local drug elution with the TGF-βR1 kinase inhibitor SB431542 improves graft patency [7, 8]. Specifically, this treatment targets the otherwise significantly higher levels of TGF-β1 expression in occluded murine grafts, with a significant proportion of the cells within the stenotic lesions appearing to arise from endo-MT, a process exacerbated by TGF-β1 [7]. Again, a modified gamma function was used to simulate the administration of this inhibitor in the BCM model. Unlike treatment with clodronate, administration of the TGF-βR1 inhibitor did not disrupt monocyte infiltration or consequent neotissue formation, thus maintaining cellularity of the graft [8]. Rather, treatment with this inhibitor significantly decreases the number of classically activated macrophages, which secrete pro-inflammatory cytokines that exacerbate endo-MT [8]. Both of these effects were captured by the computational model (Fig. 6M–P, Supplementary Fig. 1M–P). Importantly, the model predicted a marked reduction of stiff inflammatory collagen at early times, which could translate to an increase in graft distensibility at a tissue level (not modeled here). Administration of this inhibitor was the only simulated intervention considered that could potentially improve patency and reduce compliance mismatch between the implanted polymeric scaffold and the adjacent native vessel while still maintaining graft cellularity. This promising possibility merits testing in future experiments.
Preferred window and duration of TGF-βR1 inhibitor treatment
While the duration of TGFBR1 inhibitor treatment clearly plays a role in graft outcome, the onset of administration could also modulate these effects. Thus, we next simulated the potential impact of a delayed (by 7 or 14 days) administration of a TGF-βR1 inhibitor on the evolution of model variables throughout the simulation (Supplementary Fig. 2). This strategy blunted the initial reduction in the number of classically activated macrophages (Supplementary Fig. 2E, I, and M), resulting in an early peak of inflammatory collagen production similar to baseline simulations with no pharmacological intervention (Supplementary Fig. 2H, L, and P). We also examined the impact of shortened or prolonged administration of the TGF-βR1 inhibitor; rather than achieving the maximum drug concentration 14 days post-implantation, coinciding with the peak in immune cell infiltration, we modified the gamma function such that the maximum inhibitor concentration was achieved at 7, 21, or 28 days post-implantation (Supplementary Fig. 3). A shortened (7 days) course of therapy did not suppress the immune response and associated production of inflammatory collagen as effectively as did the 14 days of inhibition performed experimentally in the murine model (Supplementary Fig. 3A, D, E, and H). Although prolonged administration of the inhibitor more effectively blunts the residual immune response that persists past the early post-implantation period (Supplementary Fig. 3I and M), it exacerbates a rebound-like phenomenon in TGF-β levels (Supplementary Fig. 3J and N), which in turn chronically elevates the inflammatory collagen when compared to baseline (Supplementary Fig. 3L and P).
One goal is to minimize the total number of classically activated macrophages, which, by secreting TGF-β1 exacerbate endo-MT, and in turn increases the number of inflammatory SMCs in stenotic lesions. In place of the more favorable stress-mediated collagen, these SMCs produce stiff inflammatory collagen, which accumulates due to TGF-β-mediated MMP inhibition and decreases graft distensibility. Further illustrated in Fig. 7A–C, administration of the TGF-βR1 inhibitor immediately after scaffold implantation minimizes the number of classically activated macrophages and inflammatory SMCs and thus the total mass of inflammatory collagen; it also maximizes the total mass of stress-mediated collagen and MMPs through the simulated adaptation period. As such, the simulations suggest that delaying administration of the TGF-βRI inhibitor post-implantation could reduce its efficacy in preventing graft stenosis. Moreover, the reduction in the number of classically activated macrophages and associated inflammatory collagen mass plateaus following 21 days of TGF-βR1 inhibitor therapy (Fig. 7D–F), suggesting that prolonged inhibitor administration may not have added benefits. Indeed, there appears to be a preferred initial window of targeted therapy, for 3 weeks immediately following scaffold implantation, that maximally blunts the immune response to the polymer and minimizes the consequent peak in inflammatory collagen. Identification of such a therapeutic window is critical since prolonged administration of this inhibitor could have adverse effects systemically and on long-term graft biomechanical outcomes. Finally, although tissue-level distensibility, compliance, stenosis, and patency were not explicitly modeled in this study, our hypothesized explanations are based on prior correlations between these geometric/functional metrics and graft composition [7–12, 17–19]. Hence, the present results can guide future experiments and data collection.
Figure 7.
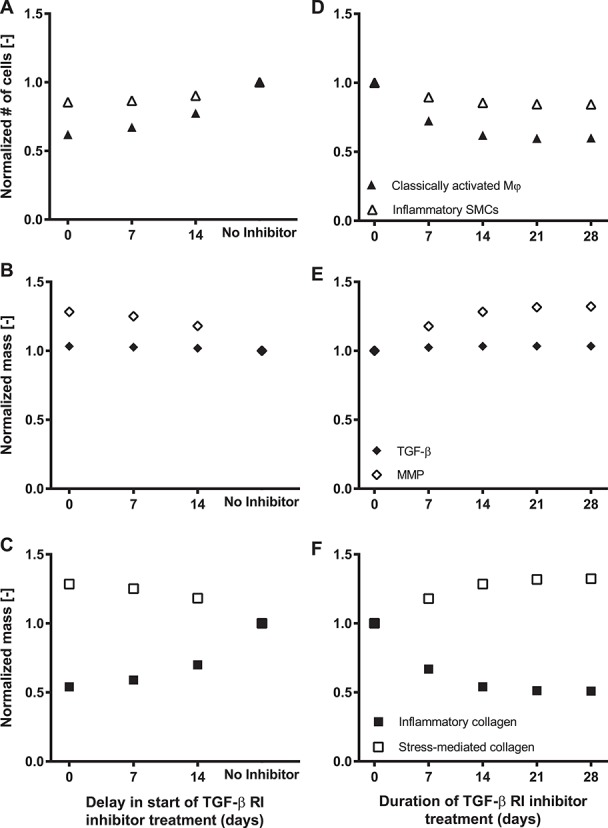
(A–C) Parametric studies showing the evolution of the total number of classically activated macrophages and inflammatory SMCs (A), total mass of TGF-β and MMPs (B), and total mass of inflammatory and stress-mediated collagen (C) through the adaptation period as a function of the delay in the start of TGF-β R1 inhibitor treatment. Variables are normalized to their respective values in the absence of inhibitor treatment. (D–F) Parametric studies showing the evolution of the total number of classically activated macrophages and inflammatory SMCs (D), total mass of TGF-β and MMPs (E), and total mass of inflammatory and stress-mediated collagen (F) through the adaptation period as a function of the duration of TGF-β R1 inhibitor treatment. Variables are normalized to their respective values in the absence of inhibitor treatment. There appears to be an optimal window and duration of TGF-β R1 inhibitor treatment.
DISCUSSION
Several BCM models of vascular adaptation exist [13, 62–65], but few consider neotissue development leading to luminal narrowing. Most studies of stenosis focus on vein grafts using agent-based modeling [36, 66, 67], though biomechanical modeling [68], including hemodynamics [69], has been pursued. Clearly, there is move toward more integrative modeling approaches that consider mechanical factors as well as cellular and molecular mechanisms underlying stenosis, but to our knowledge our BCM model is the first to explore mechanistically the in vivo formation of a neovessel from an implanted biodegradable polymeric scaffold. Previous computational simulations from our group employed a constrained mixture theory of G&R that accounts phenomenologically for immuno-driven and mechano-mediated matrix turnover in TEVGs, with good descriptive and predictive capability [9, 11, 12, 30]. Nevertheless, phenomenological models cannot address the roles of specific classes of cells or biomolecules, which limits one’s ability to simulate particular pharmacological strategies.
Herein, we presented a mechanistic BCM model that complements our prior G&R model by incorporating the complex interplay between biomechanical and biochemical factors that occur throughout neovessel development from an implanted polymeric scaffold. We also propose a framework for the assimilation of experimental data and assessment of associated uncertainty that overcomes problems of manual tuning by automatically determining an optimal parameter set that produces results consistent with observed measurements, in this case for our murine IVC interposition TEVG and experimental values obtained from the literature. This well-parameterized model captured experimentally observed profiles of immune cells, pro- and anti-inflammatory cytokines, vascular cells, and matrix constituents following scaffold implantation.
We then used this BCM model to parametrically explore the in vivo evolution of wall constituents as a function of scaffold pore size, macrophage depletion by clodronate liposomes, and immunomodulation via the growth factor TGF-β1. Notably, the model suggested that treatment with a TGF-βR1 inhibitor not only inhibits endo-MT and prevents TGF-β-induced classical activation of infiltrating monocytes, it also reduces inflammatory collagen production during early scaffold remodeling while preserving neotissue formation and graft cellularity. Interestingly, however, the model suggests that temporal reductions in the level of the TGF-βR1 inhibitor may allow a rebound-like phenomenon, with an increase in TGF-β levels increasing the number of inflammatory SMCs, which results in a chronic (albeit minor) elevation of inflammatory collagen relative to stress-mediated collagen when compared to the baseline simulation (Fig. 6). It appears, then, that an initial suppression of TGF-β signaling, while favorable in the short-term, may not be sufficient to block all adverse effects in the long term. It also appears that there is a preferred window and duration when the TGF-βR1 inhibitor treatment is most effective (Fig. 7). The difficulty in predicting complex temporal effects due to highly coupled molecular and cellular mediators reveals a potential advantage of integrative computational models, as, for example, in overcoming the current challenge of optimizing clinical interventions in vascular tissue engineering.
This study further emphasized the need for focused data collection and carefully designed experiments, which must increase the number and diversity of the experimental targets. The proposed BCM model has 43 parameters, which were tuned herein against available (18 in this case) measurements from in vivo and in vitro experimental studies. As such we were able to uniquely recover only 22 identifiable parameters. Most unidentifiable parameters arose from either overly parameterized systems or systems that have multiple functions and few relevant measurements. As our model was motivated by biological observations and has a high fidelity in its constituent populations, it has identified gaps in the available experimental data. For example, system-specific data are sorely lacking on both the magnitudes and the temporal and spatial profiles of key pro-inflammatory, anti-inflammatory, and immunomodulatory cytokines in TEVGs. Multiplex immunoassays, when performed longitudinally for multiple markers and multiple scaffold designs and pharmacological interventions, could help establish reliable experimental targets and allow us to move away from often unrelated literature values, which are less accurate due to unavoidable differences in animal models and experimental design. Moreover, although we had some data on monocyte/macrophage phenotype, vascular cell populations, protease expression, and collagen synthesis and degradation, many of these data sets need to be extended. For example, FACS analysis could be performed longitudinally rather than at a single end point (currently two weeks), the extent of SMC differentiation and maturation could be identified by careful selection of markers for immunofluorescence staining or lineage tracing, MMP activity could be quantified in addition to its expression, and collagen cross-link density, alignment, and fibrillar ratio could be evaluated during the inflammatory response to the polymeric scaffold and following its resolution. Increasing the number of ‘quality’ experimental targets should increase the number of identifiable parameters.
It is interesting that our model has a dominant downwind behavior; that is, it is an open-loop formulation. Although many biological systems function in closed-loop and are governed by positive (e.g. fibrosis) or negative (homeostatic) feedback, neovessel development from an implanted biodegradable scaffold may be an exception. Variations in graft physical properties and immunogenicity may have far-reaching effects on the local degradation characteristics of the polymer and the elicited inflammatory response, which could change the biochemical environment and biomechanical stimuli experienced by the infiltrating cells, thus influencing local immune cell phenotype, vascular cell differentiation, and matrix production. In essence, the immune response to the polymer is dictated by scaffold physical parameters and can strongly influence the eventual patency and functionality of the remodeling graft. This could explain why early intervention with immunomodulatory therapies has proven effective in reducing the incidence of stenosis [8, 10]. Indeed, as noted above, our BCM model suggested that the best therapeutic window (of those considered) for the TGF-βR1 inhibitor was for 21 days immediately following scaffold implantation, with no observable benefit of prolonged drug administration after this period. Such a downwind behavior also raises challenges in estimating the parameters, especially those that are downstream in the network, as they need to be estimated against fewer measurements.
We started the parameter estimation process with uniform priors and ended up with Gaussian-like marginal histograms for most parameters (not shown). In this way, we overcame bias. Informative priors can accelerate convergence and improve identifiability in Bayesian estimation. Hence, it may be worthwhile to pursue multilevel estimation, that is, updating the parameter prior through submodel analysis. Multilevel estimation can take advantage of the compartmental structure of the BCM model to further reduce the parameter marginal posterior variance and improve parameter learning [53].
We submit that this BCM model and approach to parameter estimation represent an important step forward in computationally modeling neovessel development in vivo. Nevertheless, much remains to be done, including overcoming the current modeling limitations. First, the input parameters (Fig. 3) were fixed and unconnected to the mechanistic BCM model, and we did not account for their uncertainty. Coupling to continuum models of G&R will be a natural next step. Second, we had to mine the literature which represents varying methods, scales, and systems to identity experimental targets against which the parameters were estimated. Third, the proposed system focused mostly on a cellular scale and thus lacks spatial fidelity, namely, luminal versus interstitial versus abluminal cell behaviors or concentration gradients. In designing novel scaffolds to improve outcomes, it is critical to consider that degradation could occur preferentially at the surface of the scaffold [70]. Indeed, polymer degradation for the associated G&R framework was assumed to occur volumetrically; however, some preferential erosion from the graft surface would likely occur, particularly if cells are slow to penetrate the full thickness. Fourth, we did not incorporate platelets into the model, which play roles in determining the short-term patency of small-caliber TEVGs.
There is, therefore, a pressing need for continuing experimentation and integration of this mechanistic model into tissue-level models to create more comprehensive, coupled multiscale BCM models of neovessel formation, well informed and validated by experimental observations. In addition to predictions, good models help to identify specific experimental needs. These include detailed characterizations of scaffold physical parameters and their effects on the elicited immune response, quantification of pro- and anti-inflammatory cytokines and growth factors using multiplex immunoassays, and documentation of the evolution of specific cellular species and matrix constituents, particularly during rapid periods of neovessel formation. Once established for a few diverse scaffold designs, the true merit of a mechanistic model will emerge—to enable extensive time- and cost-efficient parametric studies to identify optimal scaffold parameters as well as optimal concentrations and clinical courses of targeted pharmacological therapies for improving short- and long-term biomechanical outcomes such as graft patency, distensibility, and cellularity. In this way, we can reduce the vast experimental search space and hopefully arrive much sooner at approaches that can be evaluated experimentally in fewer preclinical animal models and validated in clinical trials. We submit that the present model is a critical step toward this long-term goal of the tissue engineering community.
Disclosures
C.K. Breuer receives support from Gunze Limited, the commercial manufacturer of the TEVG scaffold used in the clinic. None of that funding was used to support this research.
Supplementary Material
Acknowledgements
Dr Pedro Aparicio provided guidance and valuable feedback during early model formulation and Dr Justin Tran provided useful guidance on using the tulip framework.
Funding
This work was supported by grants from the US National Institutes of Health (R01 HL098228, R01 HL128602, R01 HL128847, R01 HL139796, and MSTP TG T32GM07205), a Pre-doctoral Fellowship from the American Heart Association and the Children’s Heart Foundation (R.K.), and a Graduate Student Research Fellowship from the National Science Foundation DGE1122492.
References
- 1. Patterson JT, Gilliland T, Maxfield MW et al. Tissue-engineered vascular grafts for use in the treatment of congenital heart disease: from the bench to the clinic and back again. Regen Med 2012;7:409–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Hibino N, McGillicuddy E, Matsumura G et al. Late-term results of tissue-engineered vascular grafts in humans. J Thorac Cardiovasc Surg 2010;139:431–6.e2. [DOI] [PubMed] [Google Scholar]
- 3. Shin’oka T, Matsumura G, Hibino N et al. Midterm clinical result of tissue-engineered vascular autografts seeded with autologous bone marrow cells. J Thorac Cardiovasc Surg 2005;129:1330–8. [DOI] [PubMed] [Google Scholar]
- 4. Giannico S, Hammad F, Amodeo A et al. Clinical outcome of 193 extracardiac Fontan patients: the first 15 years. J Am Coll Cardiol 2006;47:2065–73. [DOI] [PubMed] [Google Scholar]
- 5. Nakano T, Kado H, Tachibana T et al. Excellent midterm outcome of extracardiac conduit total cavopulmonary connection: results of 126 cases. Ann Thorac Surg 2007;84:1619–26. [DOI] [PubMed] [Google Scholar]
- 6. Kim S-J, Kim W-H, Lim H-G et al. Outcome of 200 patients after an extracardiac Fontan procedure. J Thorac Cardiovasc Surg 2008;136:108–16. [DOI] [PubMed] [Google Scholar]
- 7. Duncan DR, Chen P-Y, Patterson JT et al. TGFβR1 inhibition blocks the formation of stenosis in tissue-engineered vascular grafts. J Am Coll Cardiol 2015;65:512–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Lee Y-U, Dios Ruiz-Rosado J, Mahler N et al. TGF-β receptor 1 inhibition prevents stenosis of tissue-engineered vascular grafts by reducing host mononuclear phagocyte activation. FASEB J 2016;30:2627–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Khosravi R, Miller KS, Best CA et al. Biomechanical diversity despite mechanobiological stability in tissue engineered vascular grafts two years post-implantation. Tissue Eng Part A 2015;21:1529–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Hibino N, Yi T, Duncan DR et al. A critical role for macrophages in neovessel formation and the development of stenosis in tissue-engineered vascular grafts. FASEB J 2011;25:4253–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Miller KS, Khosravi R, Breuer CK et al. A hypothesis-driven parametric study of effects of polymeric scaffold properties on tissue engineered neovessel formation. Acta Biomater 2015;11:283–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Miller KS, Lee Y-U, Naito Y et al. Computational model of the in vivo development of a tissue engineered vein from an implanted polymeric construct. J Biomech 2014;47:2080–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Aparício P, Thompson MS, Watton PN. A novel chemo-mechano-biological model of arterial tissue growth and remodelling. J Biomech 2016;49:2321–30. [DOI] [PubMed] [Google Scholar]
- 14. Dale PD, Sherratt JA, Maini PK. A mathematical model for collagen fibre formation during foetal and adult dermal wound healing. Proc Royal Soc London Series B: Biol Sci 1996;263:653–60. [DOI] [PubMed] [Google Scholar]
- 15. Aparicio P. Modelling Signalling Pathways and Cellular Dynamics in Vascular Mechanobiology: a Theoretical, Experimental and Computational Study. Ph. D. Dissertation University of Oxford, 2016. [Google Scholar]
- 16. Hibino N, Villalona G, Pietris N et al. Tissue-engineered vascular grafts form neovessels that arise from regeneration of the adjacent blood vessel. FASEB J 2011;25:2731–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Naito Y, Williams-Fritze M, Duncan DR et al. Characterization of the natural history of extracellular matrix production in tissue-engineered vascular grafts during neovessel formation. Cells Tissues Organs 2012;195:60–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Naito Y, Lee Y-U, Yi T et al. Beyond burst pressure: Initial evaluation of the natural history of the biaxial mechanical properties of tissue-engineered vascular grafts in the venous circulation using a murine model. Tissue Eng Part A 2013;20:346–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Tara S, Kurobe H, de Dios Ruiz Rosado J et al. Cilostazol, not aspirin, prevents stenosis of bioresorbable vascular grafts in a venous model. Arterioscler Thromb Vasc Biol 2015;35:2003–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. DeGroff C. Modeling the Fontan circulation: where we are and where we need to go. Pediatr Cardiol 2008;29:3–12. [DOI] [PubMed] [Google Scholar]
- 21. Pennati G, Migliavacca F, Dubini G et al. Modeling of systemic-to-pulmonary shunts in newborns with a univentricular circulation: State of the art and future directions. Prog Pediatr Cardiol 2010;30:23–9. [Google Scholar]
- 22. Ursino M. Interaction between carotid baroregulation and the pulsating heart: a mathematical model. Am J Physiol-Heart Circ Physiol 1998;275:H1733–47. [DOI] [PubMed] [Google Scholar]
- 23. Spilker RL, Taylor CA. Tuning multidomain hemodynamic simulations to match physiological measurements. Ann Biomed Eng 2010;38:2635–48. [DOI] [PubMed] [Google Scholar]
- 24. Revie JA, Stevenson DJ, Chase JG et al. Validation of subject-specific cardiovascular system models from porcine measurements. Comput Methods Programs Biomed 2013;109:197–210. [DOI] [PubMed] [Google Scholar]
- 25. Sankaran S, Humphrey JD, Marsden AL. An efficient framework for optimization and parameter sensitivity analysis in arterial growth and remodeling computations. Comput Methods Appl Mech Eng 2013;256:200–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Wang J-X, Hu X, Shadden SC. Data-augmented modeling of intracranial pressure. Ann Biomed Eng 2019;47:714–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Akintunde AR, Miller KS, Schiavazzi DE. Bayesian inference of constitutive model parameters from uncertain uniaxial experiments on murine tendons. J Mech Behav Biomed Mater 2019;96:285–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Vrugt JA, Ter Braak C, Diks C et al. Accelerating Markov chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling. Int J Nonlinear Sci Numer Simul 2009;10:273–90. [Google Scholar]
- 29. Dennis J, Woods DJ. Optimization on microcomputers: the Nelder-Mead simplex algorithm. New Computing Environments: Microcomputers in Large-Scale Computing 1987;11:6–122. [Google Scholar]
- 30. Szafron J, Khosravi R, Reinhardt J et al. Immuno-driven and Mechano-mediated Neotissue formation in tissue engineered vascular grafts. Ann Biomed Eng 2018;46:1938–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Sanders J, Lamont S, Mitchell S et al. Small fiber diameter fibro-porous meshes: tissue response sensitivity to fiber spacing. J Biomed Mater Res A 2005;72:335–42. [DOI] [PubMed] [Google Scholar]
- 32. Sussman EM, Halpin MC, Muster J et al. Porous implants modulate healing and induce shifts in local macrophage polarization in the foreign body reaction. Ann Biomed Eng 2014;42:1508–16. [DOI] [PubMed] [Google Scholar]
- 33. Wang Y, Yang T, Ma Y et al. Mathematical modeling and stability analysis of macrophage activation in left ventricular remodeling post-myocardial infarction. BMC Genomics 2012;13:S21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Jin Y-F, Han H-C, Berger J et al. Combining experimental and mathematical modeling to reveal mechanisms of macrophage-dependent left ventricular remodeling. BMC Syst Biol 2011;5:60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Nagaraja S, Chen L, Zhou J et al. Predictive analysis of mechanistic triggers and mitigation strategies for pathological scarring in skin wounds. J Immunol 2017;198:832–41. [DOI] [PubMed] [Google Scholar]
- 36. Hwang M, Garbey M, Berceli SA et al. Rule-based model of vein graft remodeling. PLoS One 2013;8:e57822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Hao W, Schlesinger LS, Friedman A. Modeling granulomas in response to infection in the lung. PLoS One 2016;11:e0148738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Roh JD, Sawh-Martinez R, Brennan MP et al. Tissue-engineered vascular grafts transform into mature blood vessels via an inflammation-mediated process of vascular remodeling. Proc Natl Acad Sci 2010;107:4669–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Cilla M, Pena E, Martinez MA. Mathematical modelling of atheroma plaque formation and development in coronary arteries. J Royal Soc Interface 2014;11:20130866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Italiani P, Boraschi D. From monocytes to M1/M2 macrophages: phenotypical vs. functional differentiation. Front Immunol 2014;5:514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Nissen R, Cardinale GJ, Udenfriend S. Increased turnover of arterial collagen in hypertensive rats. Proc Natl Acad Sci 1978;75:451–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Bashey RI, Cox R, McCann J et al. Changes in collagen biosynthesis, types, and mechanics of aorta in hypertensive rats. J Lab Clin Med 1989;113:604–11. [PubMed] [Google Scholar]
- 43. Best CA, Szafron JM, Rocco KA et al. Differential outcomes of venous and arterial tissue engineered vascular grafts highlight the importance of coupling long-term implantation studies with computational modeling. Acta Biomater 2019;94:183–194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Davies PF. Hemodynamic shear stress and the endothelium in cardiovascular pathophysiology. Nat Rev Cardiol 2009;6:16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Haga JH, Li Y-SJ, Chien S. Molecular basis of the effects of mechanical stretch on vascular smooth muscle cells. J Biomech 2007;40:947–60. [DOI] [PubMed] [Google Scholar]
- 46. Valentin A, Cardamone L, Baek S et al. Complementary vasoactivity and matrix remodelling in arterial adaptations to altered flow and pressure. J Royal Soc Interface 2008;6:293–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Humphrey JD. Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. Springer-Verlag, New York, Inc., New York, NY, USA, 2013. ISBN-13: 978-0387951683, ISBN-10: 0387951687. [Google Scholar]
- 48. Ostriker A, Horita HN, Poczobutt J et al. Vascular smooth muscle cell–derived transforming growth factor-β promotes maturation of activated, Neointima lesion–like macrophages. Arterioscler Thromb Vasc Biol 2014;34:877–86. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Stacy MR, Naito Y, Maxfield MW et al. Targeted imaging of matrix metalloproteinase activity in the evaluation of remodeling tissue-engineered vascular grafts implanted in a growing lamb model. J Thorac Cardiovasc Surg 2014;148:2227–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Zi Z, Feng Z, Chapnick DA et al. Quantitative analysis of transient and sustained transforming growth factor-β signaling dynamics. Mol Syst Biol 2011;7:492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Baze MM, Hunter K, Hayes JP. Chronic hypoxia stimulates an enhanced response to immune challenge without evidence of an energetic tradeoff. J Exp Biol 2011;214:3255–68. [DOI] [PubMed] [Google Scholar]
- 52. Tan RP, Chan AH, Wei S et al. Bioactive materials facilitating targeted local modulation of inflammation. JACC Basic Transl Sci 2019;4:56–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Schiavazzi DE, Baretta A, Pennati G et al. Patient-specific parameter estimation in single-ventricle lumped circulation models under uncertainty. Int J Numer Methods Biomed Eng 2017;33:e02799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Tran JS, Schiavazzi DE, Ramachandra AB et al. Automated tuning for parameter identification and uncertainty quantification in multi-scale coronary simulations. Comput Fluids 2017;142:128–38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55. Laloy E, Vrugt JA. High-dimensional posterior exploration of hydrologic models using multiple-try DREAM (ZS) and high-performance computing. Water Resour Res 2012;48. doi: 10.1029/2011WR010608. [DOI] [Google Scholar]
- 56. Storn R, Price K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J Global Optimiz 1997;11:341–59. [Google Scholar]
- 57. Gelman A, Rubin DB. Inference from iterative simulation using multiple sequences. Statist Sci 1992;7:457–72. [Google Scholar]
- 58. Rannala B. Identifiability of parameters in MCMC Bayesian inference of phylogeny. Syst Biol 2002;51:754–60. [DOI] [PubMed] [Google Scholar]
- 59. Rothenberg TJ. Identification in parametric models. Econometrica 1971;577–91. [Google Scholar]
- 60. McKinnon KI. Convergence of the Nelder-Mead simplex method to a nonstationary point. SIAM J Optimiz 1998;9:148–58. [Google Scholar]
- 61. Hamby D. A review of techniques for parameter sensitivity analysis of environmental models. Environ Monit Assess 1994;32:135–54. [DOI] [PubMed] [Google Scholar]
- 62. Marino M, Pontrelli G, Vairo G et al. A chemo-mechano-biological formulation for the effects of biochemical alterations on arterial mechanics: the role of molecular transport and multiscale tissue remodelling. J Royal Soc Interface 2017;14:20170615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63. Baek S, Valentin A, Humphrey J. Biochemomechanics of cerebral vasospasm and its resolution: II. Constitutive relations and model simulations. Ann Biomed Eng 2007; 35:1498. [DOI] [PubMed] [Google Scholar]
- 64. Kim J, Wagenseil JE. Bio-chemo-mechanical models of vascular mechanics. Ann Biomed Eng 2015;43:1477–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65. Keshavarzian M, Meyer CA, Hayenga HN. Mechanobiological model of arterial growth and remodeling. Biomech Model Mechanobiol 2018;17:87–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66. Boyle CJ, Lennon AB, Prendergast PJ. In silico prediction of the mechanobiological response of arterial tissue: application to angioplasty and stenting. J Biomech Eng 2011;133:081001. [DOI] [PubMed] [Google Scholar]
- 67. Garbey M, Berceli SA. A dynamical system that describes vein graft adaptation and failure. J Theor Biol 2013;336:209–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68. Budu-Grajdeanu P, Schugart RC, Friedman A et al. A mathematical model of venous neointimal hyperplasia formation. Theor Biol Med Modell 2008;5:2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69. Donadoni F, Pichardo-Almarza C, Bartlett M et al. Patient-specific, multi-scale modeling of neointimal hyperplasia in vein grafts. Front Physiol 2017;8:226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70. Gade PS, Lee K, Pfaff BN et al. Degradation and erosion mechanisms of bioresorbable porous acellular vascular grafts: an in vitro investigation. J Royal Soc Interface 2017;14:20170102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


