Order-disorder transition of intrinsically disordered kinase inducible transactivation domain of CREB

Abstract

Transcription factor cyclic Adenosine monophosphate response-element binding protein plays a critical role in the cyclic AMP response pathway via its intrinsically disordered kinase inducible transactivation domain (KID). KID is one of the most studied intrinsically disordered proteins (IDPs), although most previous studies focus on characterizing its disordered state structures. An interesting question that remains to be answered is how the order-disorder transition occurs at experimental conditions. Thanks to the newly developed IDP-specific force field ff14IDPSFF, the quality of conformer sampling for IDPs has been dramatically improved. In this study, molecular dynamics (MD) simulations were used to study the order-to-disorder transition kinetics of KID based on the good agreement with the experiment on its disordered-state properties. Specifically, we tested four force fields, ff99SBildn, ff99IDPs, ff14IDPSFF, and ff14IDPs in the simulations of KID and found that ff14IDPSFF can generate more diversified disordered conformers and also reproduce more accurate experimental secondary chemical shifts. Kinetics analysis of MD simulations demonstrates that the order-disorder transition of KID obeys the first-order kinetics, and the transition nucleus is I127/L128/L141. The possible transition pathways from the nucleus to the last folded residues were identified as I127-R125-L138-L141-S143-A145 and L128-R125-L138-L141-S143-A145 based on a residue-level dynamical network analysis. These computational studies not only provide testable prediction/hypothesis on the order-disorder transition of KID but also confirm that the ff14IDPSFF force field can be used to explore the correlation between the structure and function of IDPs.

INTRODUCTION

A transcription factor is a protein that specifically binds to the minor or major groove of DNA to control gene transcription,¹ which is very important to all living organisms. Cyclic AMP (cAMP) response-element binding (CREB) protein and its coactivator CREB binding protein (CBP) play essential roles in cAMP signaling pathways.² Mutations of CBP may cause human diseases such as cancer, leukemia, and neurological disorders.³ CREB can also interact with the kinase-inducible domain interacting (KIX) domain of CBP via its phosphorylated kinase inducible domain (p-KID), an intrinsically disordered protein (IDP).⁴ p-KID forms two stable helices upon binding with KIX.^5,6 Specifically, phosphorylation of Ser-133 was found to be vital to the binding of CREB and CBP,^5,7 which increases the affinity by two orders of magnitude.⁸

The effect of phosphorylation upon the conformational change in p-KID was investigated by both NMR experiments⁹ and molecular dynamics (MD) simulations.¹⁰ In addition, Bomblies et al. investigated the binding mechanism of p-KID/KIX in MD simulations.¹¹ However, existing generic protein force fields were known to be limited when applied to IDP simulations for the lack of consideration of the intrinsically disordered state. Indeed, simulations with generic protein force fields usually do not agree well with NMR observables. To address this problem, we have developed several generations of special-purpose Assisted Model Building with Energy Refinement (AMBER) force fields ff99IDPs,^12,13 ff14IDPs,¹⁴ and ff14IDPSFF¹⁵ to improve the modeling of the disordered state of IDPs. In these special-purpose force fields, grid-based energy correction map (CMAP) terms are applied to correct the backbone dihedral terms for better sampling of IDPs. In our previous generations of IDPs-specific force fields, ff99IDPs and ff14IDPs, only backbone dihedrals of eight disorder-promoting amino acids were corrected, while in the latest generation force field, ff14IDPSFF, all 20 naturally occurring amino acids were corrected to further optimize the force field, which was found to lead to an excellent agreement with NMR experiments for a range of IDPs.¹⁵

KID is one of the most extensively characterized IDPs and can serve as a paradigm for understanding the relationship between the structure and function for IDPs.⁴ Previous computational studies mainly focus on characterizing its disordered state structures with either simulated annealing or replica exchange simulation.^4,16 An interesting question that remains to be answered is how the order-disorder transition occurs at experimental conditions. Thus room temperature MD simulation was used in this study to reveal the order-disorder transition kinetics of KID. Specifically, we simulated KID starting from the folded structure as in its complex with KIX. We characterized its disordered state with four different force fields, ff99SBildn,¹⁷ ff99IDPs, ff14IDPs, and ff14IDPSFF, and compared their performances in reproducing experimental observables of KID. This is followed with an analysis of the order-disorder transition kinetics with the trajectories in the best-performing force field.

MATERIAL AND METHODS

Molecular dynamics simulations

The initial structure of KID was downloaded from the Protein Data Bank (PDB) database (PDB code: 1KDX¹⁸). Molecular dynamics simulations were set up and performed by AMBER12.¹⁹ Hydrogen atoms were added to the crystal structure. Counter-ions were also added to maintain system neutrality. A buffer of 10 Å of TIP3P water molecules was used to solvate the free KID.²⁰ Direct Coulomb and van der Waals interactions were computed with a cutoff distance of 8 Å. Long-range electrostatic interactions were treated with the Particle Mesh Ewald (PME) method.²¹ The ff99SBildn, ff99IDPs, ff14IDPs, and ff14IDPSFF force fields were used to model the intramolecular interactions. Before starting the MD simulations, the solvated system was relaxed first by the steepest descent minimization and then by the conjugate gradient minimization up to 2000 steps. Next 400 ps MD was used to heat up the system to 298 K in the constant volume and with the Langevin thermostat. This is followed by 200 ps equilibration in the NPT ensemble at 298 K. The equilibration and production simulations were simulated in the Berendsen thermostat.²² In order to sufficiently sample the disordered conformers of KID, ten independent trajectories of 300 ns each were simulated in each of the four tested force fields, ff99SBildn, ff99IDPs, ff14IDPs, and ff14IDPSFF. A total of 12 μs production trajectories were collected. NVIDIA^® Tesla K20 was used to accelerate all MD simulations.

Basic data analysis

The Amber12/PTRAJ module was used to calculate Cα root-mean-square deviations (RMSDs).²³ The Multiscale Modeling Tools for Structural Biology (MMTSB) toolset was used to perform the conformer cluster based on phi/psi dihedral.²⁴ In-house tools were used to calculate native contacts.^25–27 The assignment of secondary structures was based on the Definition of Secondary Structure of Proteins (DSSP) algorithm.²⁸ The secondary chemical shift data were calculated with SPARTA 1.01.²⁹ Experimental chemical shifts were taken from Radhakrishnan et al.⁶ PyMOL 1.7 was used to visualize all structures.

Dynamical correlation network analysis

In our dynamical correlation network analyses, one node represents one residue. Equation (1) was first used to calculate the fluctuation covariance matrix element between a pair of nodes i and j as

$$C_{ij}=\frac{⟨\Delta \overrightarrow{r_i}\left(t\right)\cdot \Delta \overrightarrow{r_j}\left(t\right)⟩}{\sqrt{\left(⟨\Delta \overrightarrow{r_i}{\left(t\right)}^2⟩⟨\Delta \overrightarrow{r_j}{\left(t\right)}^2⟩\right)}},$$ (1)

where $\Delta \overrightarrow{r_i}\left(t\right)=\overrightarrow{r_i}\left(t\right)-⟨\overrightarrow{r_i}\left(t\right)⟩$ and $\overrightarrow{r_i}\left(t\right)$ is the position of node i at time t. With the matrix defined in (1) as input, the dynamical correlation network method has been successfully used in multiple systems in many previous studies with more details explained therein.^30–35 Briefly, all trajectories were used to calculate the matrix elements. An edge is defined to exist between any two nodes if they are not covalently bonded and their heavy atoms are closer than 4.5 Å over 75% of the sampling time.^30–35 The strength of the edge is defined as the absolute value of the matrix element (C_ij). Network topological parameters were calculated with Cytoscape 3.1.1.³⁶ The Floyd-Warshall algorithm was used to identify the shortest path between two nodes.³⁷

RESULTS

Disordered state properties: Validation of force fields against experiment

To validate the performance of selected force fields in MD simulations of KID, we studied their performance in reproducing experimental observables (i.e., NMR secondary chemical shift and helicity) for KID. Additional structural prosperities were also monitored via the backbone root mean square deviation (RMSD), conformer clustering, helical content, and other thermodynamic parameters to evaluate the performance of these force fields.

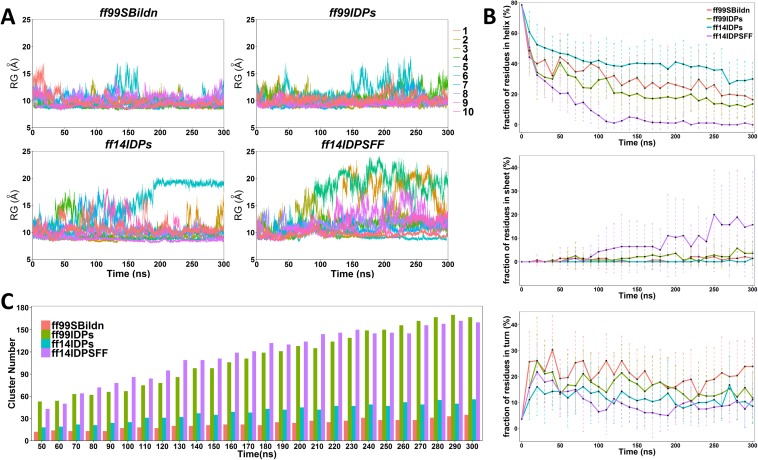
Backbone RMSD profiles were first calculated to check if the simulations of four force fields reached equilibration starting from KID’s folded structure as in the complex. Figure 1 shows the RMSDs from four force fields. Figure 1 suggests that the sampling amount of 10 independent trajectories of 300 ns each is sufficient for the transition to equilibration and equilibrium sampling afterwards.

FIG. 1.

RMSD for MD simulations under ff99SBildn, ff99IDPs, ff14IDPs, and ff14IDPSFF force fields.

To evaluate the sampling convergence under different force fields, the radius of gyration (Rg), the fraction of secondary structures, and the numbers of clusters that occupy 70% of all simulated conformers were calculated. As shown in Fig. 2(a), the values of Rg are stable during the simulation under these four force fields, except several fluctuating trajectories of ff14IDPSFF. In Fig. 2(b), the fraction of helix in KID under four force fields are decreasing to their converged values, which indicates the process of unfolding. The increasing fraction of β strands was only observed in the simulation under ff14IDPSFF, where some disordered conformers were converted into β strands after 80 ns. In addition, the cluster numbers reach plateaus within 300 ns, although ff99SBildn and ff14IDPs reach the plateau much earlier than other two [shown in Fig. 2(c)]. This indicates that sampling was converged in our simulation setup.

FIG. 2.

The convergence analysis of molecular dynamic simulations under four ff99SBildn, ff99IDPs, ff14IDPs, and ff14IDPSFF force fields. (a) Rg of KID protein for MD simulations under four force fields. (b) Fractions of the secondary structure for MD simulations under four force fields. (c) Accumulated numbers of unique clusters for MD simulations under four force fields.

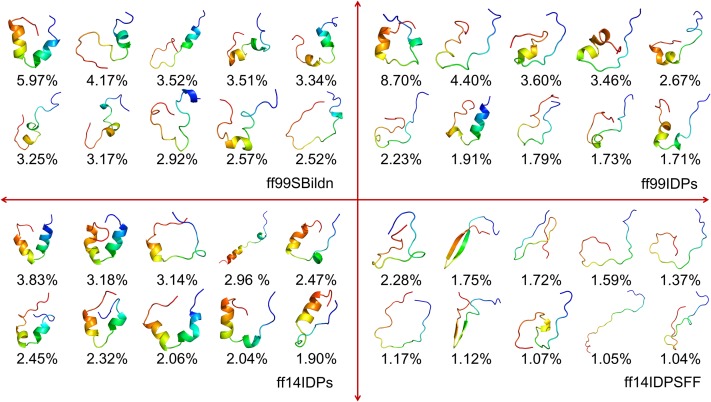
Top 10 conformer clusters and their populations were identified and are shown in Fig. 3. Overall, they each occupy 38.44%, 32.20%, 26.34%, and 14.16% in the ff99SBildn, ff99IDPs, ff14IDPs, and ff14IDPSFF simulations, respectively. The results show that the ff14IDPSFF snapshots are the most diversified among the tested force fields, and the ff99SBildn snapshots are the least diversified. Most top clusters from the ff14IDPSFF simulations include high populations of disordered structures and little native helical elements, especially in the terminal regions.

FIG. 3.

Top 10 cluster confomers and their populations under four ff99SBildn, ff99IDPs, ff14IDPs, and ff14IDPSFF force fields.

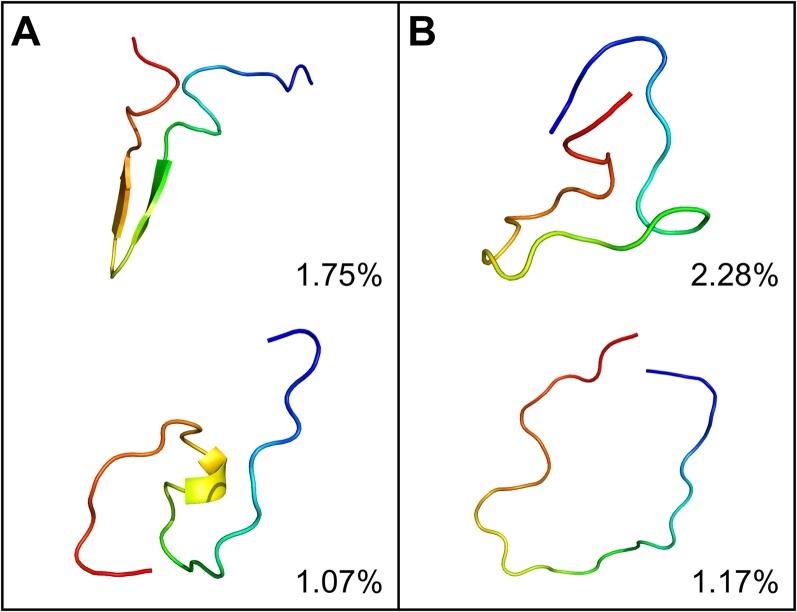
In order to understand the characteristics of the disordered KID conformers, it is also interesting to see how much of the disordered conformers can be clustered into the native random coil state, native pre-molten globule state, or native molten globule state as proposed in the literature.³⁸ Based on the conformer clustering and the secondary structure analysis, the clusters were classified into the two suggested types and are shown in Fig. 4. The pre-molten globule state is with partly disordered and helical or beta-sheet conformers, and the native random coil state is full of intrinsically disordered conformers. This indicates that the distribution of KID conformer is different from that as proposed in the literature.

FIG. 4.

Representative conformers of intrinsically disordered KID simulated in ff14IDPSFF. (a) native pre-molten globule state. (b) native random coil state.

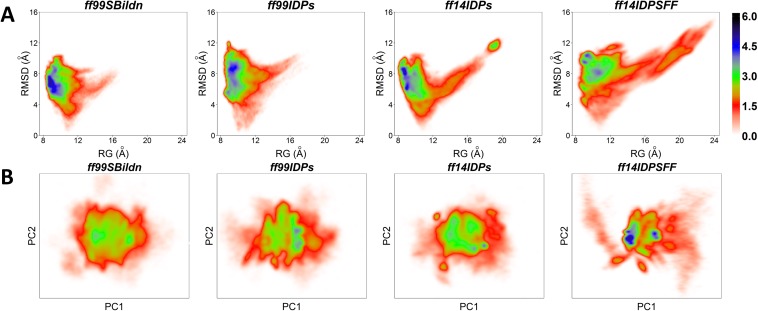
In order to investigate the conformational sampling space of the KID protein, the Potential Means of Force (PMF) free energy landscapes were calculated for the four tested force fields with respect to the backbone RMSD, Rg, and the principal component analysis (PCA) of the interresidue contact map. In recent studies,^39,40 the contact PCA method was successfully applied to two well-established proteins and proven to be useful in studying protein dynamics. Figure 5(a) indicates that sampled conformers in ff99SBildn are with RMSD in the range of 2–10 Å and Rg in the range of 8–16 Å, those in ff99IDPs are with RMSD of 4–12 Å and Rg of 8–12 Å, those in ff14IDPs are with RMSD of 3–10 Å and Rg of 8–20 Å, and those in ff14IDPSFF are with RMSD of 4–12 Å and Rg of 8–22 Å. In addition, Fig. 5(b) shows landscape maps in terms of first and second principal components. It is obvious that ff14IDPSFF leads to more diversified sampling than other three force fields. This suggests that the sampling space is the largest in ff14IDPSFF, in agreement with the RMSD and clustering analyses.

FIG. 5.

PMF free energy landscapes. (a) Landscapes of RMSD and Rg. (b) Landscapes of PC1 and PC2 of native contact.

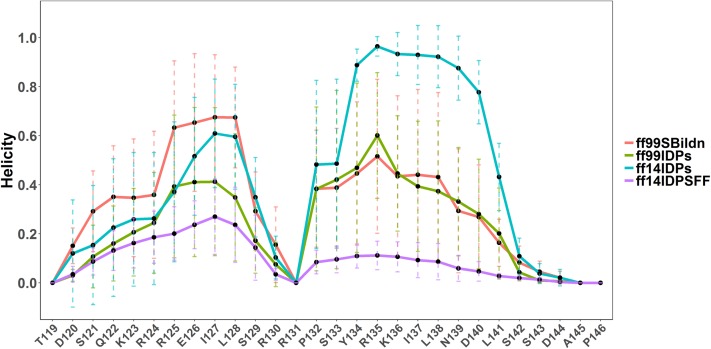
The average helicity of each residue was next calculated, as shown in Fig. 6. The average helicity αA of in ff99SBildn is much higher than those in the other three force fields, while the average helicity of αB in ff14IDPs ranks the highest. According to the report of Radhakrishnan et al., the estimated helical population of KID for helix αA (residues 120-129) is 50%–60%, while that for helix αB (residues 134-144) is only 10%–15%.⁶ As shown in Table I, the average helical content of KID for αA under ff99SBildn, ff99IDPs, ff14IDPs, and ff14IDPSFF is 44.17%, 24.95%, 24.60%, and 16.89%, respectively, while that for αB is 28.57%, 28.68%, 62.62%, and 6.13%, respectively. This shows that ff14IDPSFF best reproduces the helicity of αB, although ff99SBildn best reproduces the helicity of αA.

FIG. 6.

Helicity profiles in simulations with ff99SBildn, ff99IDPs, ff14IDPs, and ff14IDPSFF force fields.

TABLE I.

Average helicity for αA and αB.

	αA (%)	αB (%)
Expt.	50–60	10–15
ff99SBildn	44.17 ± 14.97	28.57 ± 16.55
ff99IDPs	24.95 ± 15.66	28.68 ± 11.90
ff14IDPs	34.60 ± 20.18	62.62 ± 6.96
ff14IDPSFF	16.89 ± 6.5	6.13 ± 2.48

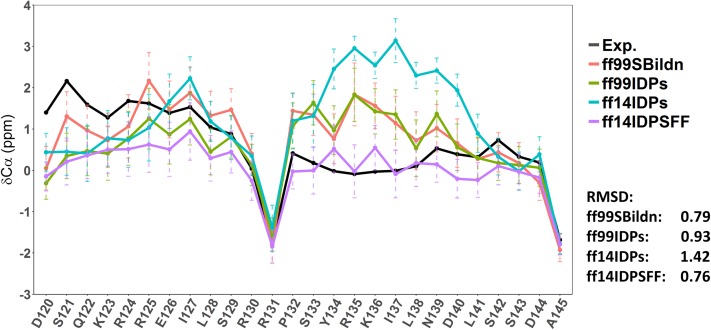
To evaluate the performance of different force fields, the secondary Cα chemical shifts were also calculated and compared with the experiment, as shown in Fig. 7. The RMSDs between experiment and simulations in ff99SBildn, ff99IDPs, ff14IDPs, and ff14IDPSFF are 0.79 ppm, 0.93 ppm, 1.42 ppm, and 0.76 ppm, respectively. These results indicate that the performance of ff14IDPSFF is the best one among the four tested force fields for sampling the disordered conformers of KID.

FIG. 7.

Secondary chemical shifts from experiments and simulations in ff99SBildn, ff99IDPs, ff14IDPs, and ff14IDPSFF.

DISCUSSION

Order-disorder transition kinetics analysis

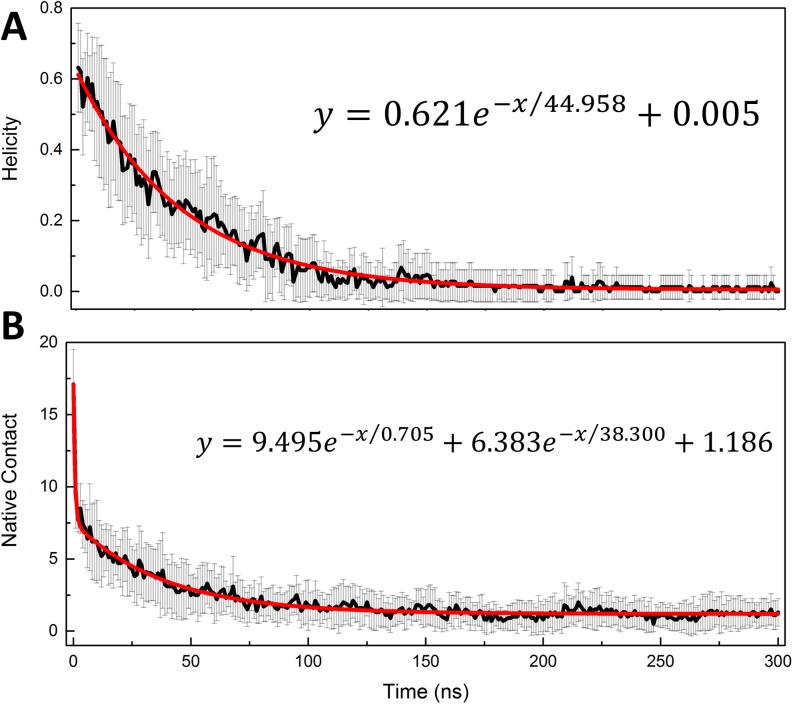
Our above analysis shows that the overall ff14IDPSFF reproduces the observed structural properties better than other tested force fields. Therefore, the trajectories in ff14IDPSFF were chosen to study the order-disorder transition kinetics for KID. First, the native helical content (Qh) and native tertiary contacts (Qf) were used to measure the transition time scales of secondary and tertiary structures, respectively. The regression analysis of Qf and Qh for KID is shown in Fig. 8. The figure shows that a bi-exponential function can be used to fit the tertiary and a single exponential function for secondary transition kinetics curves. The kinetics parameters from the nonlinear regression are listed in Table II. The analysis indicates that the transition processes obey the second-order kinetics at the room-temperature simulation conditions for tertiary structures and first-order kinetics for secondary structures. This is similar with the findings in unfolding simulations at high temperature.^{25–27,41,42} The kinetic analysis also demonstrates that the transition half times are 0.705 ± 0.064 ns and 38.300 ± 1.074 ns for tertiary contacts and 44.958 ± 0.756 ns for helical structures. This indicates that the unfolding of the secondary structure is slower than that of the tertiary contacts, supporting the findings that noticeable secondary components exist in the disordered state in the clustering analysis.

FIG. 8.

Order-disorder transition kinetics of KID in ff14IDPSFF simulations: (a) helicity content and (b) native contact.

TABLE II.

Kinetics parameters for KID.

Native contact		Helicity
$y=A_1{e}^{-x/{\tau }_1}+A_2{e}^{-x/{\tau }_2}+B$		$y=A_1{e}^{-x/{\tau }_1}+B$
A1	9.495 ± 0.314	A1	0.621 ± 0.006
τ1	0.705 ± 0.064	τ1	44.958 ± 0.756
A2	6.383 ± 0.111
τ2	38.300 ± 1.074
B	1.186 ± 0.024	B	0.005 ± 0.002
R2	0.969	R2	0.983

Residue-level dynamical network analysis

Dynamical fluctuation correlation networks were also constructed to monitor the transition kinetics of KID. To construct a fluctuation correlation network, we first calculated fluctuation covariance matrices and constructed the fluctuation correlation networks as in our previous studies.^{30,31,33,34,43–45} According to the half times of tertiary and secondary structures, the transition process of KID can be classified into four stages. Here the last 150 ns represents the equilibrated disordered state based on the kinetics time scale (three times the longest time decay constant involved). Therefore, we constructed four correlation networks for all four stages and utilized the analysis tools in the social network and associated algorithms to compare the different networks.

We first analyzed the topological parameters for the four networks. Specifically, the clustering coefficient is a ratio of the number of edges between the neighbors of node and the maximum number of edges that could possibly exist between the neighbors of node. Network centralization indicates how centralized the central nodes are within a network. The average number of neighbors indicates the average degree of a node. Network density quantifies the proportion of actual edges out of all possible edges, which indicates how easily the information can be transferred in the network. Heterogeneity measures the uniformity of the network, with a higher heterogeneity value indicating that the network consists of different components. These network topology parameters are listed in Table III.

TABLE III.

Topology parameters for four correlation networks.

Parameter	0–38 ns	38–45 ns	45–150 ns	150–300 ns
Clustering coefficient	0.123	0.206	0.077	0.230
Network centralization	0.131	0.140	0.083	0.168
Average no. of neighbors	3.714	3.500	1.929	3.786
Network density	0.138	0.130	0.071	0.140
Network heterogeneity	0.454	0.486	0.498	0.609

Table III shows that the average number of neighbors and the density of the first-stage network are the largest, while the third-stage network is the most heterogeneous during the order-disorder transition. Interestingly the disordered state network was observed to have higher topological parameters than the three networks during the transition. This is due to the formation of beta strands in this state, even if the overall conformers are quite disordered, as shown in the clustering analysis of Fig. 3. Overall the four networks are quite different from each other, and their differences indicate different inter-residue dynamical correlation in the process of order-disorder transition.

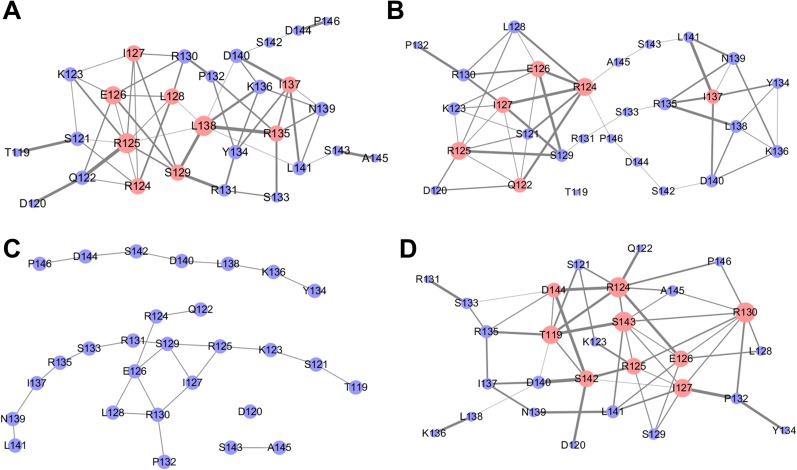
The four dynamical networks are shown in Fig. 9. The protein dynamical networks can be viewed as scale-free networks that have many nodes with low degrees but also allow nodes with high degrees. These high-degree nodes play key roles in inter-residue information transfer.⁴⁶ In this study, nodes with degrees higher than 5 are termed hub nodes. There are 9 hub nodes in the first-stage network: R124, R125, E126, I127, L128, S129, R135, I137, and L138. There are 6 hub nodes in the second-stage network: Q122, R124, R125, E126, I127, and I137, where nodes L128, S129, R135, and L138 are downgraded into non-hub nodes, although node Q122 becomes a new hub node. The third-stage network was found to disintegrate into several isolated sub-networks with little information transfer. There are no hub nodes any more although R125-R130 are still important in this fragmented network. The low information flow in the third-stage network suggests that the order-disorder transition of KID is almost finished. Interestingly, refolding was also observed during the last 150 ns of the trajectories, leading to 9 hub nodes in the last-stage network: T119, R124, R125, E126, I127, R130, S142, S143, and D144. Given the strong presence of nodes R125-R130 in all four networks, these residues may act as a nucleus in the order-disorder transition of KID.

FIG. 9.

Dynamical correlation networks of KID for the four stages: (a) 0–38 ns, (b) 38–45 ns, (c) 45–150 ns, and (d) 150–300 ns. The nodes with degree higher than 5 are marked in pink.

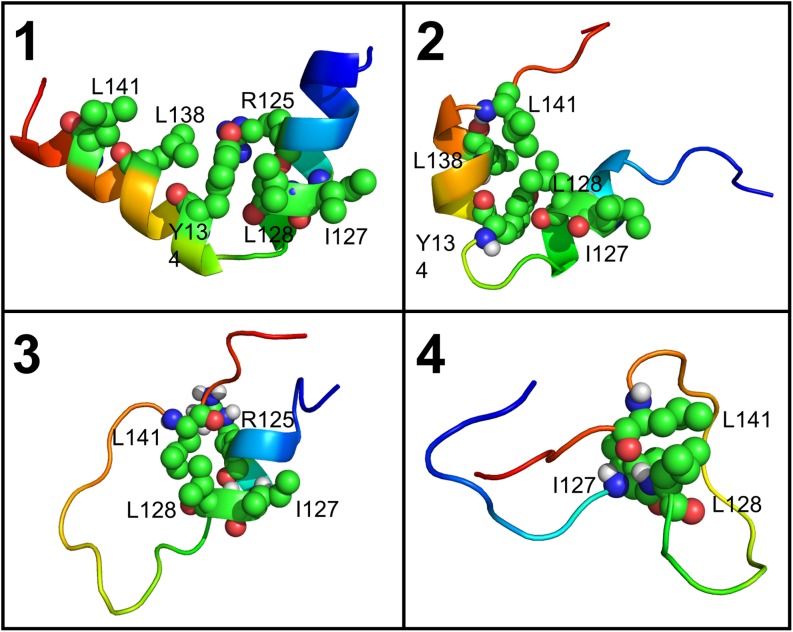
In order to confirm the nucleus in the order-disorder transition, we analyzed the representative conformers in each kinetic stage defined in Table III. Here the representative conformers were chosen to be snapshots closest to the mean main-chain structure in each stage. The representative conformers can be used to illustrate the transition pathway of KID (Fig. 10). It is clear that residues with native contacts are hub nodes in the dynamical network analysis, and there is a noticeable nucleus surrounding I127, L128, and L141; this is consistent with the dynamical network analysis above. The nucleus apparently is important for the KID stability and may also be involved in additional biological functions in the binding interactions of KID to its partners. For example, the previous experiment shows that L128A increases the binding to KIX by over 10-fold and L141 interacts with the groove of KIX;⁴⁷ both are important for the functions of KID.

FIG. 10.

The order-disorder transition pathway of KID.

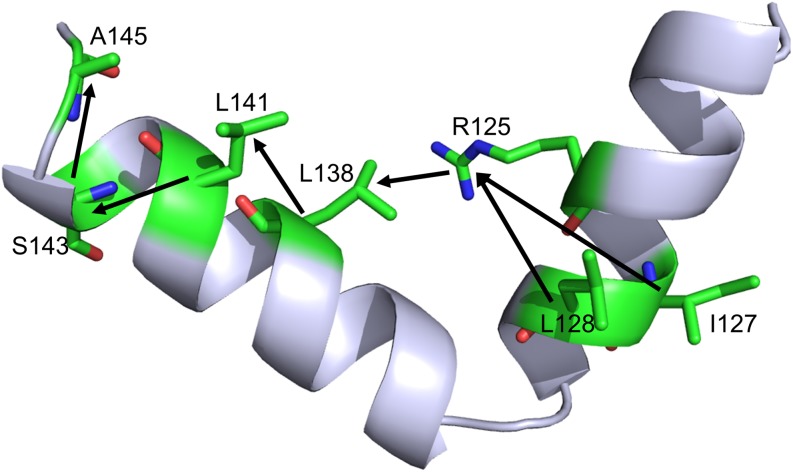
Finally, we identified the shortest pathways from the transition nucleus to the last folded residues in the first-stage network, using the shortest pathway algorithm in the social network analysis. The shortest pathways are shown in Fig. 11, as I127-R125-L138-L141-S143-A145 and L128-R125-L138-L141-S143-A145. It is clear that I127, L128, and L141 share the same shortest path and almost all these residues are hub nodes in the dynamical networks and are involved in native contact interaction networks (Fig. 10).

FIG. 11.

The shortest paths from the transition nucleus to the latest folded residues.

CONCLUSION

In this study, we conducted extensive MD simulations with ff14IDPs, ff99IDPs, ff14IDPSFF, and ff99SBildn force fields to quantify the intrinsically disordered state of KID. Our simulations show that ff14IDPSFF can produce more disordered and diverse conformers of KID than the other tested force fields. In addition, the calculated secondary chemical shift based on the ff14IDPSFF simulation agrees the best with experiment. It is interesting to note that the ff14IDPSFF simulation samples typical IDP conformers such as molten globule, pre-molten globule state, and random coil conformers, as proposed in the literature. Kinetic analysis indicates that the order-disorder transition of KID proceeds via a two-state process and the tertiary transition happens first. This is followed by the helical transition. It is worth pointing out that a few key residues play important roles in stabilizing the disordered state and are also found to be important in binding to their partner proteins. In summary, the computational studies reported here not only provide testable prediction/hypothesis on the order-disorder transition of KID but also confirm that the ff14IDPSFF force field can be used to explore the correlation between the structure and function of IDPs.