Adaptively Optimized Combination (AOC) of Magnetic Resonance Spectroscopy Data from Phased Array Coils

Abstract

Purpose

MR spectroscopy (MRS) can benefit from multi-element coil arrays with enhanced signal-to-noise ratio (SNR). However, how to combine the MRS data in an optimized way from a multi-element coil array has been studied much less than MRI. A recently published method and routine combination methods have detrimental effects on SNR. We present herein a new method for optimal combination of multi-coil MRS data.

Methods

Based on an analytical solution for maximizing the SNR of the combined spectrum, a new method called “adaptively optimized combination (AOC)” of MRS data from phased array coils was developed in which the inversion of the full noise correlation matrix was incorporated into the coil weighting coefficients. Simulations were carried out to demonstrate the superior performance of the proposed AOC method in various noise scenarios. Validation experiments on human subjects were performed with different voxel locations and sizes on a 3T MRI scanner using an eight-element phased array head coil.

Results

Compared with a recently published method (i.e., weighting with the ratio of signal to the square of noise) and routine methods, our proposed AOC method adaptively and robustly produced significant SNR improvement in the combined spectra.

Conclusion

The simulation and human experiments demonstrate that the proposed AOC method represents the theoretical optimal combination of MR spectroscopic data from multi-element coil arrays.

INTRODUCTION

Since the concept of MR phased array coils was first reported about 30 years ago (1,2), phased array coils have been commonly used in magnetic resonance imaging (MRI). Imaging data from multiple coils were first used to increase signal-to-noise ratio (SNR) (2-4), and Roemer et al. proposed the sum-of-squares (SOS) solution for the combination (2). Although these methods focused on increasing SNR, parallel imaging techniques such as simultaneous acquisition of spatial harmonics (SMASH) (5), sensitivity encoding (SENSE) (6), and generalized autocalibrating partially parallel acquisitions (GRAPPA) (7) have been developed to improve imaging speed. These parallel imaging techniques exploited spatial sensitivity information contained in the component coils of an array to partially replace phase encoding, thereby reducing imaging time. MR spectroscopy (MRS) offers a unique window to examine the biochemical composition of a subject in a noninvasive manner (8-11), which can also benefit from using a receiving coil array for an enhanced SNR. However, how to combine the MRS data in an optimized way has been studied much less than MRI.

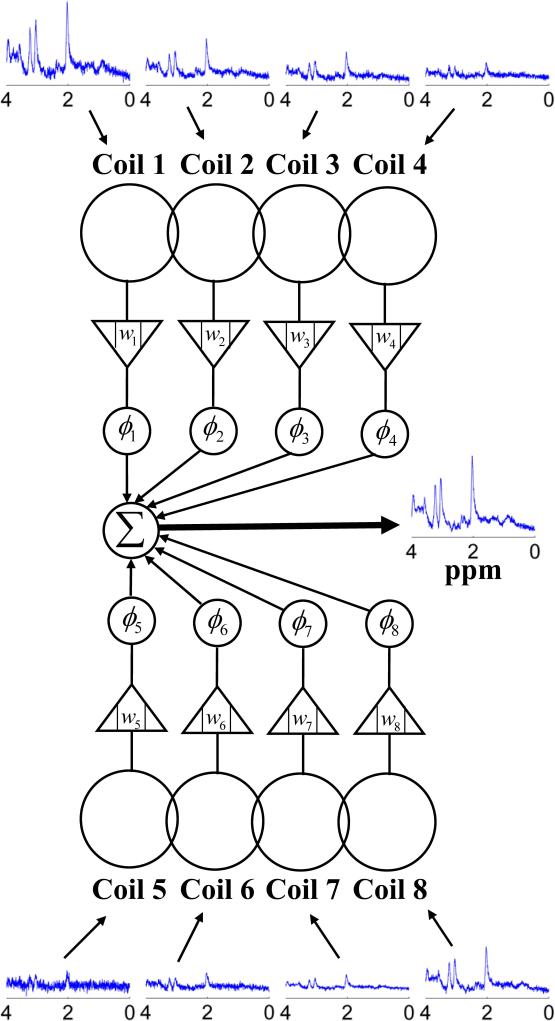
An example of an eight-element phased array coil for MRS is shown in Figure 1. Each coil element of a phased array received MR spectroscopic signal from the voxel of interest with different magnitudes and phases because of different coil sensitivities, phase shifts relative to a common phase reference, and coil/channel noise characteristics. In order to optimize the SNR of the combined spectrum, the relative amplitude and phase of the signal received at each element should be adjusted before summation. The relative amplitude and phase can be expressed as a complex weighting coefficient (e.g., w_i = |w_i|e^jϕ_i). The general question herein is how to determine the complex weighting coefficients for maximizing the SNR of the combined spectrum.

Fig. 1.

Diagram of an 8-element phased array coil used for MRS. The individual spectra received by each element were shown along with a combined spectrum. Each element in the phased array coil received spectroscopic signals from the voxel of interest with different magnitudes and phases because of different coil sensitivities, phase shifts relative to a common phase reference, and coil/channel noise characteristics. The weighting coefficients w_i = |w_i|e^jϕ_i (i =1,2,...,8) were designed to optimize the SNR of the combined spectrum. Note that the combined spectrum exhibited a significant SNR improvement compared with those from individual elements.

A few methods have been proposed, which are summarized in Table 1. Some methods, such as the equal weighting and signal weighting methods (12-16), rely on the assumption of an ideal scenario that the receiving coil elements are completely decoupled from each other and subject to additive, uncorrelated, and identically distributed Gaussian noise. In the equal weighting scheme, phase alignment in the time (12) or frequency domain using unsuppressed water or highly abundant metabolite (e.g., N-acetyl aspartate, NAA) signal is performed first and the phased spectroscopic data from individual coil elements are then summed equally. Alternatively, it is more reasonable to use the signal weighting method, in which each coil element is weighted by the magnitude of unsuppressed water (12-14) or prominent metabolite signal (15) received on respective coil element after the phase is compensated. It should be noted that the singular value decomposition method (16) is one variation of the signal weighting method. This method decomposes the received spectroscopic data matrix to obtain the principal component as the signal weighting vector, which usually brings about a more reliable combination of MRS data from a multi-element coil array. However, the idea noise occurs rarely in practice, and detrimental effects on SNR will be observed.

Table 1.

Summary of existing approaches for combining multi-element MRS data.

Methods		Brief description
Assumption of ideal noise characteristics	Equal weighting	Adding equally after aligning phase
	Signal weighting (12-16)	Weighting with the signal of the unsuppressed water peak or abundant metabolite peak present in water-suppressed spectra
	SVD (16)	Extracting the principal component from the received spectroscopic data matrix using singular value decomposition (SVD)
Consideration of real noise characteristics	S/N weighting (17-20)	Weighting with the SNR of the unsuppressed water peak or abundant metabolite peak present in water-suppressed spectra
	S/N2 weighting (21)	Weighting with the ratio of signal to the square of the noise (S/N2) of the unsuppressed water peak
	Noise decorrelation (26,27)	Noise decorrelation prior to a weighted summation

In contrast, there are a few more advantageous methods in which the real noise characteristics are considered in determining the elemental weighting coefficients. The coil combination method by weighting each element with the ratio of signal to noise (i.e., S/N² weighting) exploits the SNR of the unsuppressed water (17,18) or prominent metabolite peak (19,20) to determine the weighting coefficients. However, it is not an optimal combination method. The recently published method by weighting with the ratio of signal to the square of noise (i.e., S/N2 weighting) represents the theoretical optimal combination if the noise on different coil elements is uncorrelated (21). Although a multi-element coil array is designed with minimal mutual coupling (22,23), residual noise correlation between coil elements is not uncommonly observed in reality (24,25). In this scenario, the aforementioned methods will have a risk of compromising the SNR of the combined spectrum. In order to alleviate this limitation, some schemes were proposed such as whitening the noise prior to the weighted combination (26,27). However, the method introduced by Martini et al. (26) and the method proposed by Rodgers and Robson (27) underestimate those peaks with low SNRs. Therefore, there is a need to develop an adaptively optimized MRS combination method that can perform the best in various scenarios of coil/channel noise.

In the present study, we developed a new analytical solution for maximizing the SNR of the combined spectrum from a multi-element coil array. The performance of the proposed method was demonstrated by simulation of various scenarios of coil/channel noise and human experiments with different voxel locations and sizes performed on a 3T MRI scanner using an eight-element phased array head coil. The results were also compared with those of the recently published method (21) (i.e., S/N² weighting) and routine methods including the equal weighting, signal weighting (12-16), and S/N weighting methods (17-20), which demonstrated that our proposed method had significantly improved performance in terms of adaptivity and robustness for an enhanced SNR of the combined spectra.

METHODS

Multi-Element MRS Combination for Optimal SNR

Generally, the individual elements of a phased array coil have different sensitivities as well as phase shifts due to different geometrical positions of the coil elements relative to the voxel of interest. In addition, the free induction decay (FID) received from each coil element is inevitably contaminated by noise, which depends on both the receiving coil/channel characteristics (e.g., coil mutual coupling, coil sensitivity, and the preamplifier noise figure) and the sequence parameter setting (e.g., receiver bandwidth). Thus, the FID y_i(t) received from the ith element can be expressed as

$$y_i\left(t\right)=b_{i}x\left(t\right)+n_i\left(t\right)$$ [1]

where x(t) is the signal from the voxel of interest; b_i = |b_i|e^jθ_i represents complex data in which |b_i| and θ_i correspond to the coil sensitivity and phase shift of the ith element, respectively; and n_i(t) represents the noise contribution on the ith element. With the sampling frequency f_s, the sampled spectroscopic data can be written as

$$y_i\left(p\right)=b_{i}x\left(p\right)+n_i\left(p\right)$$ [2]

where p = f_st indexes the samples. In the frequency domain, it becomes

$$Y_i\left(k\right)=b_{i}X\left(k\right)+N_i\left(k\right)$$ [3]

where Y_i(k) is the kth spectral component of the FID received by the ith element, X(k) corresponds to the spectral component of the signal, and N_i(k) is the noise. In matrix/vector form, the FID, or spectral data, received by the phased array coil can be expressed as

$$\mathit{Y}=\mathit{bx}+\mathit{N}$$ [4]

where Y and N are M × P matrices with M being the number of coil elements and P being the number of sampled FID or spectral points; N represents the noise; x is a 1×P vector denoting the signal from the voxel of interest in the time or frequency domain; and b is an M×1 vector corresponding to the coil sensitivities and phase shifts.

In the case that the voxel of interest is small relative to the rate of variation of the magnetic flux density of individual coil elements, the derived weighting coefficients for combination should be common to all FID or spectral points. Thus, most of the reported methods (12-21,26,27) use weighted linear combinations of the FID or spectral data and ensure constructive summation of signal, which can be modeled as

$$\mathit{z}={\mathit{w}}^{\mathrm{H}}\mathit{Y}$$ [5]

where z is a 1×P vector denoting the combined data, w is an M×1 complex weighting vector, and H denotes conjugate-transpose.

According to Equations 4 and 5 and the SNR of the combined data can be calculated with

$$SNR=\frac{{\mathit{w}}^{\mathrm{H}}{\mathit{R}}_{\mathit{S}}\mathit{w}}{{\mathit{w}}^{\mathrm{H}}{\mathit{R}}_{\mathit{N}}\mathit{w}}$$ [6]

where R_s = bxx^Hb^H is the signal correlation matrix and R_N = NN^H is the noise correlation matrix. In order to maximize the SNR using the weighting vector w, the method of Lagrange multipliers (28) is employed

$$L\left(\mathit{w}\right)={\mathit{w}}^{\mathrm{H}}{\mathit{R}}_{\mathit{S}}\mathit{w}+\lambda (\mathit{I}-{\mathit{w}}^{\mathrm{H}}{\mathit{R}}_{\mathit{N}}\mathit{w})$$ [7]

The differential with respect to w* (* denotes conjugate) produces

$$\frac{\partial L\left(\mathit{w}\right)}{\partial {\mathit{w}}^{\ast }}={\mathit{R}}_{\mathit{S}}\mathit{w}-\lambda {\mathit{R}}_{\mathit{N}}\mathit{w}$$ [8]

Setting Equation 8 to a zero vector yields

$${\mathit{R}}_{\mathit{S}}\mathit{w}=\lambda {\mathit{R}}_{\mathit{N}}\mathit{w}$$ [9]

Substituting R_S = bxx^Hb^H yields

$$\mathit{w}=\alpha {\mathit{R}}_{\mathit{N}}^{-1}\mathit{b}$$ [10]

where α is a scalar defined as λ⁻¹b^Hw(xx^H). Equation 10 indicates that in order to combine the multi-element MRS data for an optimized SNR, there are three pieces of information of primary importance about each element of the phased array coil: the coil sensitivity, the phase shift, and the coil/channel noise characteristics. Each coil element at different distance and angle with respect to the excitation volume has different sensitivity and phase shift. Thus, simple summation of FID or spectral data received from different coil elements would unconstructively lead to a cancellation or loss of the signal. For these reasons, it is necessary to perform adequate magnitude and phase compensation of the FID or spectral data received at different coil elements prior to summation, in which the coil/channel noise characteristics should also be considered (17-21,26,27).

It is recognized that the noise dominates in the later part of the FID or spectral region that is free of any metabolite resonance peaks, from where the samples of the noise can be obtained. The unsuppressed water signal was selected as the reference for computing the coil sensitivities and phase shifts of individual coil elements in this study (12-14,17,18,21), that is,

$$\mathit{b}=\beta \mathit{s}$$ [11]

where s is an M×1 complex vector associated with the unsuppressed water signal received from the respective coil element and β is a scalar. Ignoring the universal scaling coefficient αβ, the weighting vector is given by

$$\mathit{w}={\mathit{R}}_{\mathit{N}}^{-1}\mathit{s}$$ [12]

where the inversion of the full noise correlation matrix ${\mathit{R}}_N^{-1}$ is incorporated into the weighting coefficients. In the present study, we proposed using Equation 12 as the coil element weighting coefficients for optimal combination of MR spectroscopic data received from phased array coils. The performance of the proposed method is demonstrated herein by comparing it with the recently reported combination method (21) and routine methods (12-20).

Performance in Various Scenarios of Coil/Channel Noise

Compared with the recently published “S/N² weighting” method, which represents the theoretical optimal combination provided that the noise is uncorrelated across different coil elements (21), the proposed new method does not have any assumption or restriction on the coil/channel noise characteristics. To analyze the performance of the proposed method and compare it with the existing methods, it is necessary to consider various coil/channel noise characteristics of a phased array coil (2,22,29-34).

In the ideal scenario that the noise is uncorrelated and identically Gaussian distributed, R_N in Equation 12 becomes an identity matrix timed by a constant that can be absorbed into the universal scaling coefficient, and the weighting is reduced to the aforementioned “signal weighting” scheme, that is,

$$\mathit{w}=\mathit{s}$$ [13]

However, the assumption of an identical noise variance across coil elements seldom holds in practice. In fact, the noise variance, which is associated with the coil sensitivity, varies across coil elements. Brown observed the difference in background noise from individual coil elements of a phased array coil and recommended using the noise variance of each coil element as the estimation of the relative coil sensitivity (12). Therefore, the scenario that the noise has different variances at different coil/channel elements is closer to the reality than the scenario of an identical noise variance across coil elements. In this case, R_N in Equation 12 is reduced to a diagonal matrix and the weighting is equivalent to the recently reported S/N² weighting (21), that is,

$$w_i=s_i∕{\sigma }_i^2$$ [14]

where s_i corresponds to the unsuppressed water signal received at the ith element of a phased array coil, and ${\sigma }_i^2$ represents the noise variance measured from the ith coil element.

Whereas the aforementioned scenarios of coil/channel noise are based on the assumption that the noise is uncorrelated, noise correlation between coil elements is not uncommonly observed in practice, and therefore is a critical issue that cannot be ignored. Noise correlation can be classified into two subtypes: extrinsic and intrinsic (30,32). In the scenario of extrinsic noise correlation (commonly referred to as “cross-talk”), coupling of signal and noise between coil elements occurs. There are three common methods to minimize extrinsic noise correlation: overlapping the coil pair, using low input impedance preamplifiers, and employing decoupling networks (30,31). Intrinsic noise correlation is different in nature from extrinsic noise correlation because the former originates from eddy currents induced in the sample. There are no methods that can reduce the detrimental effects of intrinsic noise correlation without compromising any other performance. In the case of both extrinsic and intrinsic noise correlations present, the FID received from the ith coil element can be modeled as

$$y_i\left(t\right)=b_{i}x\left(t\right)+\underset{\text{noise}}{\underbrace{n_i\left(t\right)+\sum _j{k}_{ij}\left[b_{j}x\left(t\right)+n_j\left(t\right)\right]}}$$ [15]

where k_ij denotes the extrinsic coupling coefficient between the ith and jth coil elements, and the noise n_i from the ith element is intrinsically correlated with the noise n_i from the jth element. It should be noted that a similar model was also introduced by Duensing et al. (32). It has been shown that the noise contains the contribution from part of the signal due to extrinsic noise correlation. If the term ${\sum }_j{k}_{ij}{b}_{j}x\left(t\right)$ from the extrinsic coupling is comparable to the term n_i(t), the S/N weighting and S/N² weighting methods will likely reduce the SNR of the combined spectra compared with the signal weighting method. This is because both methods suppress the noise along with part of the signal. Furthermore, because the S/N² weighting method uses the noise variance in the weighting coefficient, which leads to a larger level of suppression compared with the S/N weighting method, the S/N² weighting method will comprise more SNR than the S/N weighting method in this case. In contrast, because both extrinsic and intrinsic noise correlations correspond to the off-diagonal components in the full noise correlation matrix, our proposed new method, which incorporates the inversion of the noise correlation matrix in the weighting coefficients instead of only the diagonal components as used in (21), will reduce all types of noise and improve the SNR adaptively and robustly. Therefore, our proposed new method is more than just a generalized version of existing coil combination methods. It provides adaptively optimized combination (AOC) of MRS data from phased array coils in various scenarios of coil/channel noise.

Simulation-Based Evaluation of Different Combination Methods

In order to evaluate the performance of the proposed method and compare it with the recently reported method (21) and other routine methods (12-20), we used in vivo spectroscopic data with high SNR, acquired from the rostral anterior cingulate cortex (ACC) of a human subject, as the basis to generate a set of simulation data (see the in vivo spectroscopic data acquisition in the following subsection). The simulated spectroscopic data for each of eight coil elements were obtained by scaling and shifting the complex in vivo spectroscopic data with selected amplitudes and phases and adding simulated multi-coil/channel noise. To simulate various characteristics of noise, the multi-coil/channel noise matrix is modeled as follows

$$\mathit{N}=(\mathit{A}+\mathit{B})\tilde{\mathit{N}}$$ [16]

where Ñ is an M×P matrix associated with M uncorrelated and identically distributed Gaussian noises (at each coil/channel element) with P sampled points, B is an M×M diagonal matrix whose diagonal element denotes the respective simulated noise variance at each coil element, and A is an M×M matrix with appropriate non-zero off-diagonal elements which correspond to the simulated intrinsic noise correlation. In addition, the extrinsic coupling coefficients (e.g., k_ij) in Equation 15 were also taken into account to simulate the extrinsic noise correlation. Four scenarios of noise were simulated: 1) uncorrelated noise with identical variances (A = 0, B = I_M, and k_ij = 0), 2) uncorrelated noise with different variances (A = 0, B ≠ I_M, and k_ij = 0), 3) intrinsic correlated noise with different variances (A ≠ 0, B ≠ I_M, and k_ij = 0), and 4) extrinsic correlated noise with different variances (A = 0, B ≠ I_M, and k_ij ≠ 0).

The simulated spectroscopic data at each coil element were combined using the following five methods: 1) equal weighting, 2) signal weighting, 3) S/N weighting, 4) S/N² weighting, and 5) the proposed AOC method (i.e., ${\mathit{R}}_N^{-1}\mathit{s}$ weighting). To evaluate the different combination methods, the SNR of each combined spectra was quantified. Specifically, the SNR of each combined spectrum was calculated based on the amplitude of the NAA peak divided by the noise level determined from the root mean square of the 256 data points in a spectral region that was free of any metabolite resonance peaks.

Evaluation of Different Combination Methods in Human Experiments

Human experiments were carried out on two volunteers. The study was approved by our Institutional Review Board and written informed consent was obtained from each subject. ¹H-MRS scans were performed on a Philips Achieva 3T scanner (Philips Medical Systems, Best, Netherlands) with an eight-element phased array head coil. A single-voxel PRESS sequence was applied using the following parameters: repetition time (TR)/echo time (TE)=3000/35ms, complex data points acquired = 2048, spectral bandwidth = 2000 Hz, number of averages on each ¹H-MRS scan = 128, 16-step phase cycling, and unsuppressed water data acquired at the beginning for eddy current correction. The voxels were placed in rostral ACC (2×2×2 cm³), left and right dorsolateral frontal white matter (FWM) (2×1×2 cm³), and a subcortical region encompassing the head of left caudate nucleus (Caud) (1×2×2 cm³).

Raw data from each coil element were processed offline using MATLAB (Mathworks, Natick, Massachusetts, USA). The individual in vivo spectroscopic data from each element were first averaged within each phase cycle before being aligned in phase and averaged through different phase cycles (35). The resultant data on each individual element were then combined using the five different methods. The performances of difference combination methods were evaluated using the aforementioned SNR metrics.

RESULTS

Simulated Experiments

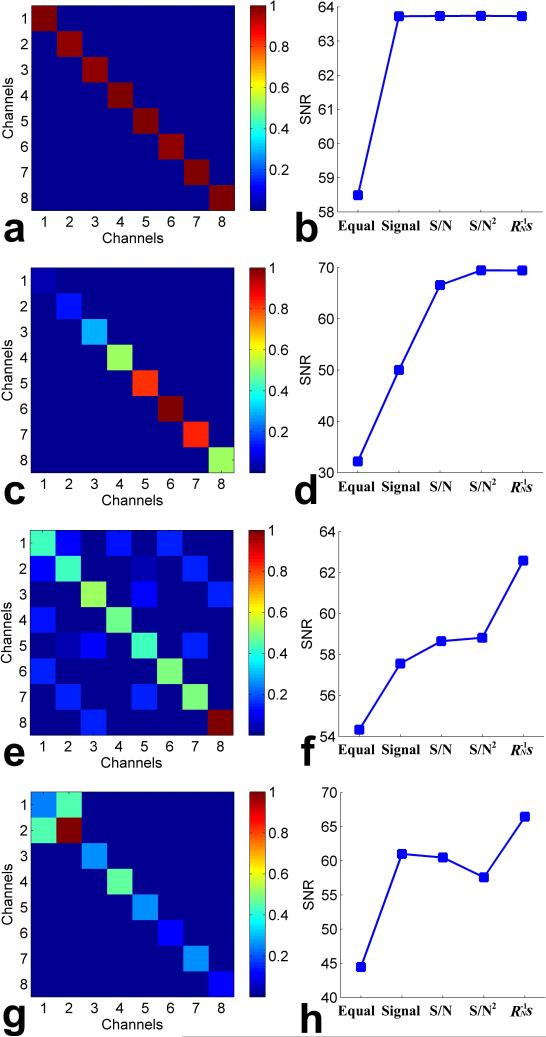
Figure 2 shows the comparison of the proposed AOC method with the recently published method and routine methods in the presence of various characteristics of simulated multi-coil/channel noise. Figure 2a and 2b show the results in the scenario of uncorrelated noise with identical variances across coil elements. Figure 2a shows the noise correlation matrix, which indicates that the noise from each coil element is uncorrelated (so the off-diagonal elements are zero) and identically Gaussian distributed (so the diagonal elements have the same value). Figure 2b shows the SNRs of the combined spectra obtained by the five methods, which yielded an SNR of 58.49 for the equal weighting, 63.73 for the signal weighting, 63.73 for the S/N weighting, 63.74 for the S/N² weighting, and 63.73 for the proposed AOC method (i.e., ${\mathit{R}}_N^{-1}\mathit{s}$ weighting), respectively. The SNR of the combined spectrum using the proposed AOC method was the same as those of the signal weighting, S/N weighting, and S/N² weighting methods but greater than that of the equal weighting method, which verified that the proposed weighting scheme is equivalent to the signal weighting, S/N weighting, and S/N² weighting methods in the ideal scenario that the noises across the coil elements are uncorrelated and have identical variances.

Fig. 2.

Comparison of the proposed method with the recently published method and routine methods in the presence of various characteristics of simulated noise: (a, b) uncorrelated noise with identical variances, (c, d) uncorrelated noise with different variances, (e, f) intrinsic correlation noise with different variances, and (g, h) extrinsic correlation noise with different variances. In each row, the noise correlation matrix and the SNRs of the combined spectra obtained by the ${\mathit{R}}_N^{-1}\mathit{s}$ weighting, equal weighting, signal weighting, S/N weighting, and S/N² weighting methods were illustrated. Color bar beside the noise correlation matrix indicates the normalized noise correlation coefficients.

Figure 2c and 2d show the results in the presence of uncorrelated noise (so the off-diagonal elements are zero) but with different variances across coil elements (so the diagonal elements have different values). The corresponding noise correlation matrix is shown in Figure 2c. Figure 2d shows the SNRs of the combined spectra obtained by the five methods, which yielded an SNR of 32.19 for the equal weighting, 50.04 for the signal weighting, 66.57 for the S/N weighting, 69.45 for the S/N² weighting, and 69.43 for the proposed AOC method (i.e., ${\mathit{R}}_N^{-1}\mathit{s}$ weighting), respectively. The proposed AOC method had the same performance with the S/N² weighting method, which verified that the proposed scheme is equivalent to the S/N² weighting scheme if the noise is uncorrelated across the coil elements. The SNR of the combined spectrum obtained by the proposed AOC method was significantly greater than those by the equal weighting and signal weighting methods but slightly greater than that by the S/N weighting method, which suggested that it is necessary to take the real noise characteristics into account when developing an MRS combination method.

Figure 2e and 2f show the results in the scenario of intrinsic correlated noise with different variances across coil elements. Figure 2e shows the noise correlation matrix, in which some non-zero off-diagonal elements indicate the intrinsic noise correlations between coil elements. Figure 2f shows the SNRs of the combined spectra obtained by the five methods, which yielded an SNR of 54.33 for the equal weighting, 57.56 for the signal weighting, 58.65 for the S/N weighting, 58.82 for the S/N² weighting, and 62.58 for the proposed AOC method (i.e., ${\mathit{R}}_N^{-1}\mathit{s}$ weighting), respectively. The proposed AOC method produced the highest SNR of the combined spectrum compared with the other four methods, which verified that the proposed AOC method has the optimal performance, in the presence of intrinsic correlated noise between coil elements. The signal weighting, S/N weighting, and S/N² weighting methods had similar performance because in this case the noise variances had relatively small differences across coil elements.

Figure 2g and 2h show the results in the presence of extrinsic correlated noise with different variances across coil elements. The noise correlation matrix with extrinsic coupling between coil element 1 and coil element 2 is shown in Figure 2g (so the off-diagonal elements at cross-point of element 1 and 2 are not zero). Figure 2h shows the SNRs of the combined spectra obtained by the five methods, which yielded an a SNR of 44.44 for the equal weighting, 61.00 for the signal weighting, 60.48 for the S/N weighting, 57.57 for the S/N² weighting, and 66.44 for the proposed AOC method (i.e., ${\mathit{R}}_N^{-1}\mathit{s}$ weighting), respectively. In this scenario, the S/N weighting and S/N² weighting methods yielded lower SNRs compared with the signal weighting method, and more SNR was compromised using the S/N² weighting method than the S/N weighting method. This unusual phenomenon is due to the aforementioned extrinsic coupling. In contrast, the proposed AOC method adaptively and robustly provided the highest SNR.

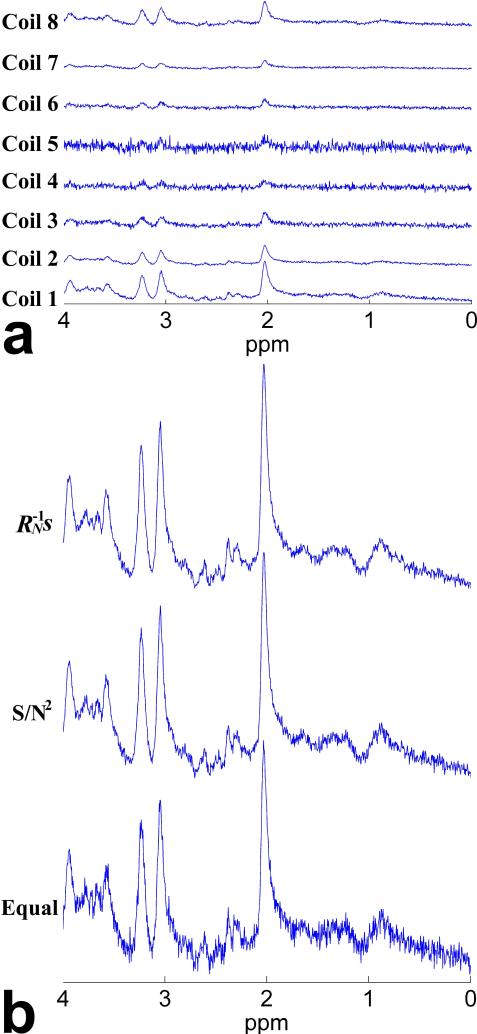
Figure 3 shows individual spectra on each of eight coil elements and the combined spectra in the scenario of simulated intrinsic correlation noise with large differences on the variances. Figure 3a shows the individual spectra, which exhibited a variety of coil sensitivities and noise contributions across coil elements. Figure 3b shows the combined spectra obtained by the proposed AOC method (i.e., ${\mathit{R}}_N^{-1}\mathit{s}$ weighting) along with the S/N² weighting and equal weighting methods. The SNRs of the combined spectra were 70.25, 59.96 and 36.52 for the proposed ${\mathit{R}}_N^{-1}\mathit{s}$ weighting, S/N² weighting, and equal weighting methods, respectively. It is clear that the proposed AOC method yielded a significantly increased SNR compared with the other two methods.

Fig. 3.

Individual and combined spectra in the simulated scenario of intrinsic correlation noise with large difference on the variances: (a) individual spectra received on each of eight coil/channel elements, (b) combined spectra obtained by the proposed ${\mathit{R}}_N^{-1}\mathit{s}$ weighting method along with the S/N² weighting and equal weighting methods. The three methods produced a SNR of 70.25, 59.96, and 36.52, respectively.

Human Experiments

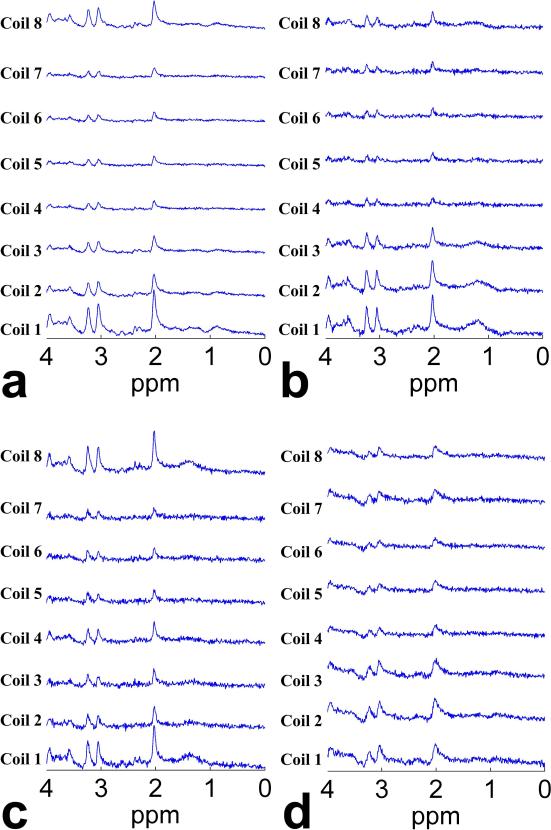
Figure 4 shows the individual spectra received by each coil element of an eight-element phased array head coil, in which each subset of spectra was acquired from one of four voxels in the brain of a human subject: 1) rostral ACC, 2) left dorsolateral FWM, 3) right dorsolateral FWM, and 4) left Caud. For each voxel, the individual spectra had very similar spectral patterns, but the amplitude response varied across coil elements, which depended on the coil location relative to the voxel. Specifically, the individual spectra from rostral ACC (Fig. 4a) exhibited the most heterogeneous amplitude response across coil elements, whereas those from left Caud (Fig. 4d) had a relatively more homogeneous amplitude response. The individual spectra from the left and right dorsolateral FWM (Fig. 4b and 4c) showed intermediate heterogeneity in amplitude response across coil elements.

Fig. 4.

Individual spectra received by each coil element of an 8-element phased array head coil, acquired from four voxels in the brain of a human subject: (a) rostral ACC, (b) left dorsolateral FWM, (c) right dorsolateral FWM, and (d) left Caud. Of note, for each voxel the individual spectra had very similar spectral pattern, but the amplitude response varied across coil elements, which depended on the coil location relative to the voxel. Specifically, the most heterogeneous amplitude response across coil elements was in rostral ACC, the most homogeneous amplitude response in left Caud, and left and right dorsolateral FWM exhibited intermediate heterogeneity in amplitude response across coil elements.

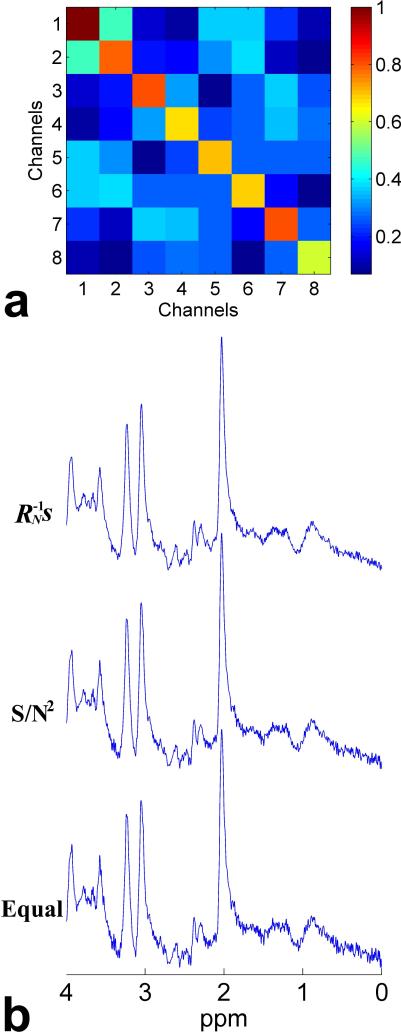
Figure 5 shows the experimental results on a voxel encompassing rostral ACC of a human subject. Figure 5a shows the noise correlation matrix of the spectroscopic data received on an eight-element phased array head coil. It illustrates that the characteristics of noise in the spectroscopic data actually included all the scenarios that we examined in the simulated experiments. The noise on the eight coil elements had different variances (corresponding to different diagonal values). Furthermore, although the largest values were still on the diagonal, some off-diagonal elements. This indicated the noise correlations, were nonnegligible, which justified the use of the full noise correlation matrix in constructing the weight coefficients for combination rather than only using the diagonal values (i.e., noise autocorrelation coefficients) as introduced in the recently reported S/N² weighting (21). Figure 5b shows the combined spectra obtained by the proposed AOC method (i.e., ${\mathit{R}}_N^{-1}\mathit{s}$ weighting) along with the S/N² weighting and equal weighting methods. Compared with the other two methods, the noise in the combined spectrum was reduced substantially using the proposed AOC method, which would potentially improve the quantification of metabolites, especially those with low concentration or MRS sensitivity (21).

Fig. 5.

Noise correlation matrix and combined spectra of the spectroscopic data acquired from a voxel encompassing rostral ACC on one human subject using an 8-element phased array head coil: (a) noise correlation matrix, (b) combined spectra obtained by the proposed ${\mathit{R}}_N^{-1}\mathit{s}$ weighting method along with the S/N² weighting and equal weighting methods, with a SNR of 81.81, 59.62 and 50.87 for the three methods, respectively. Color bar beside the noise correlation matrix indicates the normalized noise correlation coefficients. Note that the characteristics of noise in the real data actually included all the scenarios that we investigated in the simulated experiments.

Figure 6 demonstrates the SNRs of the combined spectra from the four different voxels in the brain of a human subject. Figure 6a shows the locations of the four voxels: rostral ACC, left and right dorsolateral FWM, and left Caud. Figure 6b shows the SNRs of the combined spectra acquired from the four voxels by the proposed AOC method (i.e., ${\mathit{R}}_N^{-1}\mathit{s}$ weighting) as well as the equal weighting, signal weighting, S/N weighting, and S/N² weighting methods. Compared with the existing four methods, the proposed new method adaptively and robustly improved the SNR across four voxels. The signal weighting, S/N weighting, and S/N² weighting methods had similar performance across four voxels, which is one of the reasons that we named the proposed method as the “adaptively optimized combination (AOC)” method and yielded an SNR improvement compared with the equal weighting method. Of note, the improvement on SNR using the proposed AOC method depended on the voxel locations. The rostral ACC benefited the most, followed by the left and right dorsolateral FWM, and the left Caud. It is intriguing that there was unusual performance degradation using the S/N weighting and S/N² weighting methods compared with the signal weighting method, and actually more SNR was compromised using the S/N² weighting method than the S/N weighting method. These unusual decreases of SNR in the combined spectra are due to the extrinsic coupling, which results in partial suppression of signal along with suppression of noise, as explained earlier.

Fig. 6.

SNRs of the combined spectra from the four voxels in the brain of one human subject: (a) locations of the four voxels encompassing rostral ACC (2×2×2 cm³), left and right dorsolateral FWM (2×1×2 cm³), and left Caud (1×2×2 cm³), and (b) SNRs of the combined spectra obtained by the proposed ${\mathit{R}}_N^{-1}\mathit{s}$ weighting method as well as the equal weighting, signal weighting, S/N weighting, and S/N² weighting methods. Colors represent the different voxels. Note that the proposed method consistently produced the highest SNR across the four different voxels.

DISCUSSION

We proposed a method for adaptively optimized combination of MR spectroscopic data from multi-element phased array coils, which incorporated the inversion of the full noise correlation matrix into the coil weighting coefficients for combination. Compared with the recently published method (21) and routine methods (12-20), the proposed AOC method adaptively and robustly produced the best SNR enhancement in various scenarios of coil/channel noise as seen in practice.

This new method requires reliable estimations of the coil sensitivities, phase shifts and noise correlation matrix to construct the coil weighting coefficients. In the present study, the unsuppressed water signal was exploited to estimate the coil sensitivities and phase shifts of the coil elements. Alternatively, when the unsuppressed water signal is not available, the coil sensitivities and phase shifts can still be obtained by estimating the principal component of the received water-suppressed data matrix using singular value decomposition (16). In addition, according to the theory of statistics, sufficient noise samples are required to accurately estimate the noise correlation matrix, which can be achieved by increasing the acquisition bandwidth but without altering the length of acquisition time.

The proposed AOC method (i.e., ${\mathit{R}}_N^{-1}\mathit{s}$ weighting) was compared with the recently reported S/N² weighting method (21) as well as routine methods including the equal weighting, signal weighting (12-16), and S/N weighting methods (17-20). Specifically, we evaluated the performance, in terms of SNR, of these methods in the presence of various characteristics of multi-coil/channel noise. The proposed AOC method had the same performance with the S/N² weighting method in the scenario of uncorrelated noise. However, the proposed AOC method outperformed the other methods by significant SNR improvement in the presence of correlated noise across coil elements, which was not uncommonly observed in practice. The inversion of the full noise correlation matrix in the weighting coefficients of coil elements in the proposed AOC method provided distinct advantages of adaptivity and robustness for an enhanced SNR of the combined spectrum.

It should be noted that we examined the effects of intrinsic and extrinsic noise correlations. Although the S/N weighting and S/N² weighting methods usually outperform the signal weighting method, it is interesting to find in our simulated experiments that the extrinsic noise correlation likely degraded the performance of the S/N weighting and S/N² weighting methods compared with that of the signal weighting method, and more SNR would be compromised using the S/N² weighting method than the S/N weighting method, which were consistent with the theoretical analysis in this study. Of note, similar results were also reported in the recently published article that introduced the S/N² weighting method (21), but the reason underlying this interesting phenomenon was analyzed and verified in the present study for the first time.

In addition to validation through simulations, the proposed AOC method was also evaluated in human brain experiments, in which MRS data were acquired from four voxels at different locations and of different sizes. It is shown that the proposed AOC method consistently provided the maximum SNR enhancement in the combined spectra for all four voxels compared with the other methods, but the degree of the SNR improvement depended on the voxel location. The voxel encompassing rostral ACC benefited the most while the voxel in the left Caud benefited the least. It is probably because certain coil elements were located closer to the rostral ACC voxel than the left Caud voxel, which resulted in a large variation in the amplitude response across coil elements. Of note, similar phenomena were also reported in other published articles (21,26). Furthermore, the interesting phenomenon of the performance degradation of the S/N weighting and S/N² weighting methods compared with the signal weighting method was also observed in the human brain experiments of the present study, which further validated our analysis on this phenomenon.

This study was performed using an eight-element phased array coil at 3T. However, the proposed AOC method can also be applied at higher field strengths and with larger numbers of coil elements.

CONCLUSIONS

We have introduced a new method for adaptively optimized combination of multi-element MRS data from phased array coils and validated this method via simulation and human experiments. Compared with the recently published method (i.e., the S/N² weighting method) and routine methods (i.e., the equal weighting, signal weighting, and S/N weighting methods), the proposed AOC method adaptively and robustly produced significant SNR improvement of the combined spectra, which represented the theoretical optimal combination of multi-element MRS data.