Pharmacometrics and Machine Learning Partner to Advance Clinical Data Analysis

Abstract

Clinical pharmacology is a multidisciplinary data sciences field that utilizes mathematical and statistical methods to generate maximal knowledge from data. Pharmacometrics (PMX) is a well‐recognized tool to characterize disease progression, pharmacokinetics, and risk factors. Because the amount of data produced keeps growing with increasing pace, the computational effort necessary for PMX models is also increasing. Additionally, computationally efficient methods, such as machine learning (ML) are becoming increasingly important in medicine. However, ML is currently not an integrated part of PMX, for various reasons. The goals of this article are to (i) provide an introduction to ML classification methods, (ii) provide examples for a ML classification analysis to identify covariates based on specific research questions, (iii) examine a clinically relevant example to investigate possible relationships of ML and PMX, and (iv) present a summary of ML and PMX tasks to develop clinical decision support tools.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ Currently, pharmacometrics (PMX) models are almost exclusively utilized in drug development and clinical pharmacology. However, for increasing amounts of data, the computational effort for these models significantly increases.

• WHAT QUESTION DID THIS STUDY ADDRESS?

☑ This study investigates how PMX can partner with machine learning (ML) to advance clinical data analysis.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ This study investigates possible intersections to combine PMX and ML and demonstrates commonalities and differences of both methods. Furthermore, it suggests applying ML classification as an initial step for a covariate analysis.

• HOW MIGHT THIS CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE?

☑ Combination of ML and PMX might strongly decrease computational efforts for analysis of clinical datasets and consequently advance clinical data science.

Data science is defined as a multidisciplinary field that deals with the extraction of knowledge from data.1 Dhar et al.1 stated that “a data scientist requires an integrated skill set spanning mathematics, machine learning, artificial intelligence, statistics, databases and optimization, along with a deep understanding of the craft of problem formulation to engineer effective solutions.”

Clinical pharmacology is a multidisciplinary data science field. In the 1950s, pharmacologists/clinicians2 started to apply a mathematical linear one‐compartment model to characterize drug concentrations in patients. Obviously, from a mathematical perspective, such models were not new. As such, the need to advance pharmacology with mathematical modeling emerged from clinical pharmacologists and not from mathematicians. The combination of clinical pharmacology and mathematical modeling, the so‐called pharmacokinetic modeling, was brought to the next level by applying statistical mixed‐effects methods, as introduced by Sheiner,3 and Sheiner and Beal4 in the 1970s. With such approaches, not only can individual pharmacokinetic profiles be described, but the pharmacokinetic behavior of many individuals could also be characterized by simultaneously quantifying its sources of variabilities.

The application of mathematical models and statistical methods are our current basis for data sciences in clinical pharmacology, drug research, and development.5, 6, 7, 8, 9 Currently, we call this pharmacokinetics/pharmacodynamics modeling and quantitative data analysis pharmacometrics (PMX). Over the years, mathematical models became more complex, and, as such, a mathematical and computational special interests group was formed10 within the International Society of Pharmacometrics, with the aim to advance clinical pharmacology using sophisticated mathematical methods. However, game‐changing improvements, which may bring PMX as a discipline to a next level, have not yet materialized.

Current PMX models are constructed with differential equations and, therefore, rely on (semi‐) mechanistic knowledge based on biological and pharmacological principles. This allows biological interpretation of model parameters and provides the capability to simulate “what‐if” scenarios with different parameters. However, PMX models are often quite complex and, therefore, solving them numerically can be time‐consuming, resulting in huge computational effort for large populations. Covariate selection is especially laborious and is usually the most time‐consuming part. Therefore, combining PMX with more computationally powerful data science tools might be the next game‐changing milestone in clinical pharmacology for precision medicine utilizing “big data” sets.11

Machine learning (ML), which lies at the intersection of computer science and statistics, provides such computationally powerful tools for the analysis of large and heterogeneous data sets and has become increasingly popular in different domains in the last decade, including medicine.12, 13, 14, 15, 16, 17 These methods are capable of analyzing large datasets almost in real time. This provides the opportunity to leverage ML in clinical pharmacology, and the combination of ML with PMX might lead to great scientific achievements. Recently, ML was recognized by the American Conference on Pharmacometrics in 2018 with a preconference. The major advantage of ML is its data‐driven approach, thereby eliminating the need for mechanistic assumptions. However, from a PMX perspective this might be considered as black‐box and, therefore, clinical pharmacologists may be reluctant to embrace this opportunity.

In this paper, we have four core components. The first aim is to provide a brief introduction to supervised ML classification methods (called classifiers), such as decision trees and random forests. We will show that it is necessary to first formulate a specific research question and to define a target variable that contains the data labels. Based on these labels, we will demonstrate how a classifier is trained to differentiate between different labels. The second aim is to present examples for a ML classification analysis to identify covariates based on specific research questions. We will show how an ML classifier is applied to answer specific research questions, which will demonstrate the difference when compared to a PMX model. A one‐compartment pharmacokinetic model will be utilized to show how the formulated research question affects the identified features. Furthermore, a maximum effect E_max‐model will be applied to illustrate how a time‐dependent component can be included in an ML classifier. These examples will help us to investigate the possibility of applying ML as an initial step for a subsequent PMX covariate analysis. The third aim is to examine a clinically relevant example to investigate possible relationships between ML and PMX, namely applying ML to perform an initial covariate selection for a more complex PMX example. The fourth aim is to present a summary of the ML and PMX tasks required to develop clinical decision support tools.18

Overall, the goal of this article is to identify intersections and differences between PMX modeling and ML classification. Understanding these relationships may help us in the future to (i) maximize the generated knowledge from available data, (ii) decrease computational time in data analysis, and (iii) allow possible integration of both methods.

Materials and Methods

Brief introduction to supervised ML classification methods

ML models, in general, cover data‐driven modeling for data analysis. ML can be broadly divided into two sub‐areas: supervised and unsupervised learning. In supervised learning, not only the input data but also the corresponding target values, such as disease classes, are observed. Typically, an expert (e.g., a physician) assigns an annotation (the “label“) to every patient (e.g., diseased or healthy). Hence, a specific research question is necessary from the beginning of the data analysis process. The aim is then to find the model that best distinguishes between those classes, in order to either correctly assign the label to new patients, or to identify relevant covariates. In unsupervised learning, the training data consists of a set of variables without any corresponding target values. The goal in unsupervised learning problems is to find patterns and to extract hidden structures from data, in an entirely data‐driven manner, without any expert‐labeling. In this paper, we focus on supervised ML models.

A main question in clinical applications is: What are the risk factors that a patient will be above or below a predefined clinically relevant threshold? In neonatology, time (i.e., postnatal age) plays an additional important role because of fast changing maturation processes in the first days of life.19, 20 Hence, the question is often extended to: What are the risk factors that a patient will be above or below a threshold within a certain time frame (e.g., 24 hours)? Such questions are typical classification tasks to predict a probability for the occurrence of a specific incident. In addition to binary labels, ML can also be used to predict a real‐valued target (that is, perform regression), but for this brief introduction we will only consider classification methods, especially tree‐based classification methods.

Decision trees and random forest

A decision tree is a tree‐structured classifier (see Figure 1 for a simple schematic). The tree is iteratively built by selecting variables according to their relevance for discriminating between classes, where relevance can be measured in terms of information gain or drop in misclassification error. There are several decision tree algorithms (e.g., CART21 or ID322), which use different methods to construct the rules that are represented by individual branches in the tree. The algorithms are similar in that they all recursively apply new rules to discriminate between classes until the classes can be perfectly distinguished (on the data that the tree has already seen), or until a predefined stopping criterion is met. To make a prediction for a new observation, the algorithm proceeds through the decision tree, branching based on the variable values of the observation. This process ends when a terminal node is reached, which determines the prediction of the decision tree. The random forest classifier23 generalizes this concept by building an ensemble of decision trees, a decision forest (see Figure 1 for a simple schematic).

Figure 1.

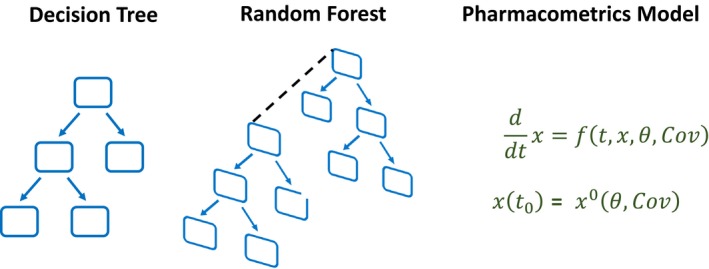
Schematic visualization of a decision tree, an ensemble of several decision trees (the random forest), and the pharmacometrics modeling approach. [Colour figure can be viewed at http://wileyonlinelibrary.com]

In general, for the evaluation of classification methods it is common to divide the dataset into training and test sets, where the former is used to learn the parameters of the model and the latter for its evaluation. It is important that evaluation data is not used for training, this division is used to safeguard against overfitting (i.e., against finding parameters that fit the training data perfectly), but do not generalize well to unseen observations (see Figure 2 for an example illustrating overfitting). Special care must be taken when dealing with multiple measurements from the same patient: If a prediction is required for each measurement, then all measurements of a single patient should be either in the training or test dataset (stratification by patient), because otherwise one would violate the independence of training and test sets. The evaluation of a classifier is typically done based on a metric (e.g., accuracy, sensitivity, and specificity) or with the help of a confusion matrix. A confusion matrix contrasts the predictions of the classifier with the actual classes and can be used to compute different metrics.

Figure 2.

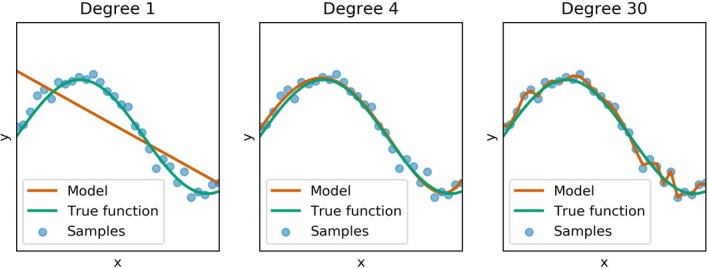
Illustration of the problem of underfitting and overfitting based on a polynomial regression. Different models (red curves) are fit to a set of noisy samples (blue points) from the function y = sin(5x) (green curve). Each subplot present the results from a regression model of degree n (i.e., a model f(x) = β₀ + β₁ x ₁ + β₂  x ₂ + … + β_nx_n with scalar regression coefficients β₀, …, β_n). Underfitting (left subplot) occurs when the model has too little capacity to capture the complexity of the data, whereas overfitting (right subplot) fits the data points well, but is unlikely to generalize well to new samples from the underlying function. The central subplot shows a fit that is “just right” in that it closely approximates the true function given a set of samples.

While training a random forest, all samples in the training set (in our case neonates) are in addition randomly divided into a training (bag) set and a test (out‐of‐bag) set using resampling techniques. The random forest has become extremely popular because it is a straightforward learning algorithm, it has few parameters to tune, and it performs well in practice even when the sample size is small and the number of variables is large. Furthermore, the random forest can identify the features (risk factors) that are most important for differentiating between the different classes. This is especially important in the medical domain, where we need explainable solutions, and where we aim to reduce our model to few explainable features. The feature importance in the random forest can for example be obtained by computing the mean decrease in accuracy. The underlying idea of this measure is, if a feature is important, a random permutation of this feature will change the result of the classifier. See the Supplementary Material for more information.

Results

Examples for an ML classification analysis to identify covariates based on specific research questions

We investigate two detailed examples to demonstrate how a dataset needs to be organized based on a specific research question to allow the application of an ML classifier. In these two examples, the goal is to investigate the possibility of applying an ML classifier as an initial step for a subsequent PMX covariate analysis. In the first example, we omit a time component, which means that we are only interested if a certain incident will happen, not when it will happen. In the second example, such a time component will be included to demonstrate differences in dataset preparation.

The work flow is as follows. We start with a PMX model describing disease progression over time. Individual disease progressions are realized by including the effect of covariates on the model parameters. The PMX model is then applied to simulate patient profiles. Additionally, fake covariates without any effect on the model parameters were included in the dataset. The developed dataset then has the typical PMX form. To train an ML classifier, we need to further process the dataset by labeling the data according to the formulated research questions.

The ML classifier is trained in the software R (R Foundation for Statistical Computing, Vienna, Austria, 2019) with the package “rpart” (4.1‐15). Parts of the code are presented in the Supplementary Material.

Example of a time‐independent ML analysis based on a one‐compartment model

Simulation of artificial data

Pharmacometrics model

We apply a linear one‐compartment pharmacokinetic model to characterize drug concentration $C$ with absorption rate k _a, elimination rate k _el and volume of distribution is V (see Supplementary Material). For simplicity, every patient received the same dose.

Let i = 1,…,n be the i‐th individual in a population of n subjects. We apply standard pharmacology assumptions, such as log‐normal distributions, for the model parameters and covariate effects described with a power function. In this example, two covariates Cov1_i and Cov3_i modulate the elimination rate by:

$$k_{\text{el},i}=k_{\text{el,pop}}{\left(\frac{\text{Cov}{1}_i}{\text{Cov}{1}_{\text{Ref}}}\right)}^{{\beta }_1}{\left(\frac{\text{Cov}{3}_i}{\text{Cov}{3}_{\text{Ref}}}\right)}^{{\beta }_3}\exp \left({\eta }_i\right)\text{with}{\eta }_i\sim \mathcal{N}\left(0,{\omega }_{\text{kel}}^2\right).$$

Additionally, a covariate Cov2_i acts on the volume of distribution

$$V_i=V_{\text{pop}}{\left(\frac{\text{Cov}{2}_i}{\text{Cov}{2}_{\text{Ref}}}\right)}^{{\beta }_2}\exp \left({\eta }_i\right)\text{with}{\eta }_i\sim \mathcal{N}\left(0,{\omega }_V^2\right).$$

with ${\text{CovX}}_{\text{Ref}}=\text{mean}\left({\text{CovX}}_i\right)$ for X = 1,…,3. A proportional residual error model was applied.

Set‐up of the covariate effects

We consider n = 500 patients with m = 7 measurements at the time points (0, 2, 4, 6, 8, 12, and 24). The time points > 0 were additionally perturbed by adding a normal distributed time variation $\mathcal{N}\left(0,0.25\right)$. For simplicity, we produced uniformly distributed covariates $\text{CovX}\sim \mathcal{U}\left(a_{\mathrm{X}},b_{\mathrm{X}}\right)$ (see Supplementary Material) and added two randomly produced fake covariates.

Simulation of drug concentration profiles

The produced dataset in the standard PMX style consists of d = 10 columns (ID, TIME, AMT, DV, MDV, COV1, COV2, COV3, FAKE1, and FAKE2) where ID is the individual patient number, TIME the time point (e.g., postnatal age (PNA)) of the measurement, AMT the administered dose, DV the actual measurement, and MDV a flag indicating a missing DV. Because drug administration is at t = 0, we follow the typical PMX style and have two rows for this time point, one with the dose and one with the measurement. Hence, the size of the PMX dataset is ((m + 1))·n, d). With the chosen simulation set‐up, a .csv file of (4,000, 10) = 40,000 entries was produced (size 522 KB).

Training a decision tree to identify risk factors based on specific research questions

We put ourselves in the realistic situation that only a dataset is available (i.e., no knowledge about the applied model (or the system) that produced the data or any knowledge about an existing PMX analysis is available). Visual inspection of the data showed a linear trend and therefore a noncompartmental analysis was performed to produce the labels for two different research questions.

The first research question is: What are the risk factors that a patient will have a half‐life higher than a given threshold? To answer this question, the dataset is extended with a label that provides for every patient a yes (1) or no (0). The half‐life was computed from the data after the maximal concentration was reached (see Supplementary Material). Two hundred twenty‐three patients were assigned the LABEL = 1 (half‐life above the predefined threshold t _halfTSH = 7 hours) and the rest were assigned the LABEL = 0. Because we have no time component in this research question, only one row per patient is necessary for the labeled classification dataset, see Table 1. Hence, the entire labeled dataset has the size (n, d‐4) = (500, 6) = 3,000 (.csv file = 45 KB), which is tremendously smaller than the PMX dataset. Note that no information about the ID, TIME, AMT, the DV itself, or MDV is necessary.

Table 1.

Example of a labeled classification dataset for three patients

COV1	COV2	COV3	FAKE1	FAKE2	LABEL
9.74	0.73	1.16	9.07	−0.27	0
4.44	0.40	1.71	4.99	0.10	0
3.60	0.48	1.46	9.30	−0.26	1

COV, covariate; FAKE, covariate without any effect; LABEL, assigned label (0 or 1).

A decision tree was trained with the entire labeled dataset, which resulted in a feature importance (presented in parentheses) of COV1 (65%) and COV3 (27%). We are not interested in developing a prediction tool in this example, therefore, the dataset was not divided into training and test sets. The first node was the decision COV1 with a split at value 5.7, which is close to Cov1_Ref = 6.6. Hence, the results from the decision tree confirm the covariates affecting the elimination rate in the model. Furthermore, the decision tree predicted a higher feature importance for COV1 compared to COV3, which also corresponds to the covariate effects included in the model.

The second research question is: What are the risk factors that a patient will have a drug concentration above a given threshold? To answer this question, the maximal concentration was first identified and then compared to the threshold $C_{max}^{\text{TSH}}$ = 3.5. Similar to the above example, the labeled dataset was prepared and resulted in 232 patients being assigned LABEL = 1, and a decision tree was trained. The covariate COV2 (78%) was identified as the most important feature with a value for the first split of 0.47, which is close to Cov2_Ref = 0.50. Hence, the result confirms the covariate that most affects the volume of distribution.

Pushing it to the limit—analyzing one million patients

With the above settings, a PMX dataset consisting of n = 1,000,000 patients with m = 24 measurements each at the same time points was constructed. This pure PMX simulation step needed several hours and produced a PMX dataset with a .csv file of size 2.9 GB. Again, the data were labeled to answer the first research question. The resulting labeled dataset consisted of a 110 MB .csv file. Training a decision tree for these one million patients took only 45 seconds on a standard laptop. Results were similar to the previous example with n = 500 patients.

Example of a Time‐Dependent ML Analysis Based on an E_MAX‐Model

Simulation of artificial data

Pharmacometrics model

We consider an E_max‐model (see Supplementary Material) with the maximal value E_max and the time ET₅₀ of the half‐maximal value. Log‐normally distributed individual model parameters

$${\mathrm{E}}_{max,i}={\mathrm{E}}_{max,\text{pop}}{\left(\frac{\text{Cov}{1}_i}{\text{Cov}{1}_{\text{Ref}}}\right)}^{{\mathrm{\beta }}_1}\exp \left({\eta }_i\right)\text{with}{\eta }_i\sim \mathcal{N}\left(0,{\omega }_{{\mathrm{E}}_{max}}^2\right).$$

$${\text{ET}}_{50,i}={\text{ET}}_{50,\text{pop}}{\left(\frac{\text{Cov}{2}_i}{\text{Cov}{2}_{\text{Ref}}}\right)}^{{\mathrm{\beta }}_2}\exp \left({\eta }_i\right)\text{with}{\eta }_i\sim \mathcal{N}\left(0,{\omega }_{{\text{ET}}_{50}}^2\right).$$

are assumed. Again, a proportional error model was applied.

Set‐up of the covariate effects

We consider n = 1,000 patients with m = 6 measurements each and uniformly distributed covariates, together with two additional fake covariates.

Simulation of patient profiles

The produced PMX dataset consists of d = 7 columns (ID, PNA, DV, COV1, COV2, FAKE1, and FAKE2), where PNA is the postnatal age, which relates to TIME. Hence, the size of the PMX dataset is (m·n, d) = (6 000, 7), which corresponds to a .csv file of 355 KB. Exemplarily, the first two patients are shown in Table 2.

Table 2.

Two patients in the PMX dataset for the time‐dependent E_max‐model example

ID	PNA	DV	COV1	COV2	FAKE1	FAKE2
1	0	0	1.67	10.9	0.28	−0.19
1	24	0.46	1.67	10.9	0.28	−0.19
1	48	0.50	1.67	10.9	0.28	−0.19
1	72	0.59	1.67	10.9	0.28	−0.19
1	96	0.60	1.67	10.9	0.28	−0.19
1	120	0.71	1.67	10.9	0.28	−0.19
2	0	0	2.22	11.7	6.79	−0.16
2	24	0.59	2.22	11.7	6.79	−0.16
2	48	0.87	2.22	11.7	6.79	−0.16
2	72	1.06	2.22	11.7	6.79	−0.16
2	96	1.00	2.22	11.7	6.79	−0.16
2	120	1.03	2.22	11.7	6.79	−0.16

COV, covariate; DV, the actual measurement; E_max, maximum effect; FAKE, covariate without any effect; LABEL, assigned label (0 or 1); PMX, pharmacometrics; PNA, postnatal age.

The research question is: What are the risk factors that a neonate will have measurements greater than a predefined threshold of g ^TSH = 0.75 in the next 24 hours? Now, the construction of the labeled classification dataset becomes more complex because PNA, corresponding to time since birth, is included. Let us consider Table 2 again. As an example, at PNA = 0 the DV value in the future at PNA = 24 is 0.46. This is smaller than the threshold and, therefore, a row with LABEL = 0 is generated. Similarly, at PNA = 24 the DV value in the future (PNA = 48) is smaller than the threshold. This holds for all values of patient ID = 1. The situation is different for ID = 2. At PNA = 0 the DV value in the future (PNA = 24) is smaller than the threshold as well, but for the next values we get at PNA = 24 that the DV value in the future (PNA = 48) is greater than the threshold. Therefore, this row in the dataset is labeled with LABEL = 1. All other DVs of this patient are above the threshold as well. The labeled dataset is shown in Table 3. We kept the ID in the table for a possible division into training and test set. Hence, every patient has five rows in the labeled dataset and the size is ((m‐1)·n, d) = (5 000, 7) and, therefore, comparable to the PMX dataset.

Table 3.

Labeled classification dataset for the time‐dependent E_max‐model example

ID	PNA	COV1	COV2	FAKE1	FAKE2	LABEL
1	0	1.67	10.9	0.28	−0.19	0
1	24	1.67	10.9	0.28	−0.19	0
1	48	1.67	10.9	0.28	−0.19	0
1	72	1.67	10.9	0.28	−0.19	0
1	96	1.67	10.9	0.28	−0.19	0
2	0	2.22	11.7	6.79	−0.16	0
2	24	2.22	11.7	6.79	−0.16	1
2	48	2.22	11.7	6.79	−0.16	1
2	72	2.22	11.7	6.79	−0.16	1
2	96	2.22	11.7	6.79	−0.16	1

COV, covariate; E_max, maximum effect; FAKE, covariate without any effect; LABEL, assigned label (0 or 1); PNA, postnatal age.

Training a decision tree to identify risk factors based on the research question

In the labeled dataset, we have 2,034 rows (from the 5,000) with LABEL = 1. A decision tree was trained with the entire dataset and the three most important features were PNA (49), COV1 (47), and COV2 (3). This shows that now the time component (i.e., the PNA, plays an important role). As expected, COV1 is of importance as well.

Clinically Relevant Example to Investigate Possible Relationships of ML and PMX

We focus on an example from neonatology and investigate whether ML can be used to perform an initial covariate selection for a more complex PMX example. Available data has already been analyzed with an ML classifier and published,14 therefore, our focus is on the relationships with PMX rather than on the ML development process.

Clinical context of hyperbilirubinemia in neonates and available data

Neonatal jaundice due to hyperbilirubinemia is the most common pathology in neonates and one of the major reasons for hospitalization in the first year of life. Almost 10% of newborn infants develop significant hyperbilirubinemia and a substantial number require phototherapy treatment. Data from n = 368 neonates (98 had phototherapy treatment) was available for up to 6 days. In total, 44 covariates were available from every patient.14

ML component

The research question was: What is the probability that a newborn will need phototherapy in the next 48 hours? Note that obtaining phototherapy is equivalent to being above a certain bilirubin threshold. Hence, the formulated research question is similar to the time‐dependent example and the time component was included in the dataset as previously presented. Because ML is computationally efficient, we can even test whether ratios of covariates improve the prediction performance.

It was demonstrated that the bilirubin/weight ratio has the highest feature importance.14 In descending order, bilirubin, weight, gestational age, and PNA were additionally identified as risk factors. The final model had a prediction accuracy above 90%. This result was derived not only from a random forest, but also from other ML methods, which are not in the scope of this paper.

PMX component

The structural model for bilirubin progression B driven by PNA t, maturation processes, and effect of phototherapy reads

$$\begin{array}{cc}& \frac{\mathrm{d}}{\mathrm{d}t}\mathrm{B}=k_{\mathrm{AD}}+k_{\mathrm{in}}\exp (-k_{\mathrm{PNA}}t)-((k_{\mathrm{elMax}}·t^h)/(T_{50}^h+t^h)+k_p\mathrm{PT}(t))\mathrm{B}\hfill \\ & \mathrm{B}(0)={\mathrm{B}}^0\hfill \end{array}$$ (1)

where the effect of the phototherapy PT(t) is described as an on‐off switch [Correction added on 5th March, 2020, after first online publication: Spacing issue in Equation 1 is corrected as above]. Hence, Eq. 1 is a typical indirect response model24, 25 but with time‐dependent production and elimination.26, 27 In Eq. 1, k _AD is the adult bilirubin production rate and k _in the basal neonatal production rate that decreases for increasing PNA. The maximal stimulation of bilirubin elimination is k _elMax and T₅₀ is the time when the half‐maximal stimulation is reached. The additional effect of phototherapy at the bilirubin elimination is described by the rate k _p. Log‐normally distributed interindividual variability was utilized on the model parameters k _in, k _elMax, T₅₀, k _PNA, k _p, and B⁰.

Covariate analysis was performed at different levels: (i) Initial screening of possible correlations within covariates, (ii) assessment of covariates for their clinical relevance, and (iii) capability to be part of a decision support tool. Finally, standard step‐wise forward/backward selection was performed, and identified covariates were further assessed based on their ability to affect an identified model parameter.

Comparison of the ML classification and PMX modeling approaches

Interestingly, bilirubin and PNA (i.e., the time), identified as important features by ML, are the structural components of the PMX model, refer to Eq. 1. Obviously, without these two components, a PMX model cannot be developed. However, from the ML perspective, PNA is simply one feature among many and does not necessarily need to be included in the final classifier. The feature weight (time‐varying) was also identified by the PMX model as acting nonlinearly on T ₅₀. The feature gestational age (time‐independent) is highly correlated with delivery mode, and the PMX model identified delivery mode acting on k _in to be more important. For more details, see the Supplementary Material. The interpretation of the bilirubin/weight ratio in the context of a PMX model is challenging. In PMX modeling, such a bilirubin/weight ratio would probably never be accepted as a covariate because it is strongly related to the dependent variable in the PMX model, which is bilirubin. Furthermore, it is also correlated to weight, which is already included as covariate. Nevertheless, from a clinical perspective, the bilirubin/weight ratio can be interpreted as a marker for the bilirubin elimination capacity. In fact, because weight acts on the elimination in Eq. 1, this is somewhat comparable to the feature bilirubin/weight ratio.

ML and PMX Tasks to Develop Clinical Decision Support Tools

To summarize the commonalties and differences of the necessary tasks to develop and apply an ML classifier and a PMX model, we focus on three main components: Dataset preparation, model building process, and prediction capability, as shown in Figure 3. The latter is especially important for developing a decision support tool and understanding the possibilities such a tool provides for each method. Roughly speaking, the ML classifier predicts a probability that a certain incident will happen within the next hours, as in the hyperbilirubinemia example, whereas the PMX model predicts the bilirubin progression over time and, furthermore, can be used to perform “what‐if” simulations.

Figure 3.

Comparison of the machine learning (ML) classification and pharmacometrics (PMX) modeling approach with respect to dataset preparation, model building, and prediction capability. [Colour figure can be viewed at http://wileyonlinelibrary.com]

Discussion

In every interdisciplinary collaboration, it is important to develop a common vocabulary because often similar things have different names (features vs. variables vs. covariates), whereas identical terms are used but with different meanings (e.g., “model”). In addition, in ML one “trains a model” whereas PMX scientists “develop a model.” At first glance, this might mean the same but it does not, because ML is a data‐driven approach and in PMX the model is developed based on some mechanistic assumptions.

ML is an umbrella for many different methods and, therefore, “the” ML tool does not exist. For several reasons, ML has the image of being a “black‐box.” One reason might be that the functionality of the underlying algorithms is not as obvious as in PMX modeling. Another reason might be that the training is entirely data‐driven, without consideration given to biological/pharmacological mechanisms. However, this clean data‐driven perspective might even be an advantage because no human bias impacts data analysis.

The first aim was to provide a brief introduction to supervised ML classification methods, where we explained the functionality of such classifiers. A fundamental difference between a supervised ML classifier and a PMX model is that the classifier solves a predefined prediction task based on a specific research question and the corresponding data labels, which have to be provided. Hence, the research question is built into the labeled dataset. In PMX modeling, it is obviously also important to have the research question in mind when building the model, however, it is not essential.

The second aim was to present examples for an ML classification analysis to identify covariates based on specific research questions. We showed how an ML classifier is applied to answer specific research questions. With a one‐compartment pharmacokinetic model it was demonstrated how the research question is related to the computed feature importance. With an E_max‐model it was illustrated how a time‐dependent component is included in an ML classifier and how this impacts the size of the labeled dataset. However, once the dataset is accordingly labeled, we demonstrated the computational advantage of utilizing ML. Hence, the time expenses of a data analysis are shifted more to the dataset preparation rather than training the model.

The third aim was to examine a clinically relevant example, to investigate possible relationships of ML and PMX (i.e., the application of ML to perform an initial covariate selection for a more complex PMX example). On one hand, the identified features from the ML classifier are closely related to the PMX model structure and the identified covariates. On the other hand, ratios of features might be difficult to interpret from a PMX perspective.

The fourth aim was to present a summary of the ML and PMX tasks to develop decision support tools (refer to Figure 3). Most notably, the obvious differences are (i) that the random forest classifier that we introduced in this work predicts the probability for an incident for a given time point, whereas a PMX model predicts the disease progression for any time point and additionally is able to simulate “what‐if” scenarios for varying model parameters, and (ii) the tremendous difference in computational efficacy for analyzing “big‐data.”

We identified intersections between PMX modeling and ML classification that have the potential to advance data sciences. Our clinical example illustrates how PMX can partner with ML methods. In another recent example, ML was utilized to supplement a population pharmacokinetic/pharmacodynamic model of tumor growth inhibition. This model was used to understand the various sources of between patient variability, thereby improving model predictions for drug development support.28

In this paper, we discussed opportunities where ML may be utilized as an initial step to investigate a dataset for possible covariate effects. Let us partner across scientific and clinical disciplines to identify new opportunities for leveraging and integrating ML and PMX approaches, with the ultimate goal to innovate and advance clinical data science.

Funding

No funding was received for this work.

Conflict of Interest

All authors declared no competing interests for this work.

Author Contributions

G.K., M.P., I.D., M.W., S.W., and J.V. wrote the manuscript. G.K., M.P., I.D., M.W., S.W., and J.V. designed the research. G.K., M.P., I.D., M.W., S.W., and J.V. performed the research. G.K., I.D., and J.V. analyzed the data.

Supporting information

Supplemental Material.