The unexplained success of stentplasty vasospasm treatment - Insights using mechanistic mathematical modeling

Abstract

Background

Cerebral vasospasm (CVS) following subarachnoid hemorrhage occurs in up to 70% of patients. Recently, stents have been used to successfully treat CVS. This implies that the force required to expand spastic vessels and resolve vasospasm is lower than previously thought.

Objective

We develop a mechanistic model of the spastic arterial wall to provide insight into CVS and predict the forces required to treat it.

Material and Methods

The arterial wall is modelled as a cylindrical membrane using a constrained mixture theory that accounts for the mechanical roles of elastin, collagen and vascular smooth muscle cells (VSMC). We model the pressure diameter curve prior to CVS and predict how it changes following CVS. We propose a stretch-based damage criterion for VSMC and evaluate if several commercially available stents are able to resolve vasospasm.

Results

The model predicts that dilatation of VSMCs beyond a threshold of mechanical failure is sufficient to resolve CVS without damage to the underlying extracellular matrix. Consistent with recent clinical observations, our model predicts that existing stents have the potential to provide sufficient outward force to successfully treat CVS and that success will be dependent on an appropriate match between stent and vessel.

Conclusion

Mathematical models of CVS can provide insights into biological mechanisms and explore treatment approaches. Improved understanding of the underlying mechanistic processes governing CVS and its mechanical treatment may assist in the development of dedicated stents.

Introduction

Balloon angioplasty is a recognised treatment option for patients with delayed cerebral vasospasm (CVS) secondary to subarachnoid haemorrhage (SAH); however, the exact mechanism by which angioplasty results in long lasting vasodilatation remains unknown. Honma et al. [1] suggested that the mechanism of action of balloon angioplasty involves the disruption of both the degenerative muscle and the proliferative non-muscle components, mainly in the media of the vasospastic vessels. Indeed, it is generally believed that, in order for balloon angioplasty to resolve CVS, damage to the underlying collagenous extracellular matrix (ECM) is required [2]. However, there are many studies that have demonstrated resolution of vasospasm but without evidence of damage to the underlying ECM [3–6]. Therefore, the results of previous work have not provided a conclusive answer to the question of whether disruption of the ECM is required in order to achieve long lasting vasodilatation.

In recent previous publications [7,8], several members of this group documented their initial experience with the use of stent-retrievers to treat medically refractory symptomatic CVS, so called stentplasty. It was noted that stents can resolve CVS, however the efficacy is variable with more consistent vasodilatation seen in smaller arteries such as the M2 and A2 branches. Given that these stents provide an outward pressure (approx. 0–23kPa, depending on model and diameter, see Appendix C) which is up to an order of magnitude lower than balloon angioplasty (up to 300kPa [2]), our experience seems at odds with the commonly held belief that damage to the ECM is necessary to resolve CVS.

The variability in the effectiveness of stents points to the need for a mechanistic understanding of the effects of these stents in order to guide future treatment. Differences in outcome are conjectured to be dependent on the outward force exerted by the stents and their ability or lack thereof to reach a dilatation threshold, i.e. a critical diameter beyond which a stent must expand the artery in order to successfully resolve vasospasm. This raises the questions: what determines the dilatation threshold of an artery in vasospasm? Can we predict whether a stent will be successful in resolving the disease (i.e. expanding the artery beyond the dilatation threshold)?

In this article, we propose a mathematical model focused on the mechanobiology of soft tissue with the aim of providing insight into the mechanism of action behind the mechanical treatment of CVS. In particular, our model captures the changing roles of the active and passive vascular smooth muscle cells following CVS and after treatment with stents. The work ends with a comparison of the success of currently available stents for treating vasospasm. Our model predictions are consistent with our recent clinical observations that it is not necessary to damage the ECM to successfully treat CVS.

Methods

We introduce a mathematical model for a cerebral artery and use this to describe its pressure-diameter (p-d) curve and predict how this curve changes following CVS. Assuming a stretch-based damage criterion for vascular smooth muscle cells (VSMCs), this allows us to estimate the (minimum) pressure an interventional device needs to apply to the vessel wall to resolve CVS.

Mathematical Model of the Arterial Wall: pre-vasospasm

We utilise existing mathematical approaches which model the arterial tissue as a constrained mixture [9,10] and attribute its load bearing to the distinct contributions from elastin [11], distributions of collagen fibres [12–14] and VSMCs [15]. Here we overview the key features that the mathematical model captures; further details are provided in Appendix A for the interested reader.

The Law of Laplace is a simple force balance on a vessel, which, when applied to an elastic cylinder model of an artery relates the transmural pressure p to the deformed wall thickness h, the diameter d and the circumferential intramural stress σ as follows (see Fig. 1a):

$$p=\frac{2h\sigma }{d}.$$ (1)

Figure 1:

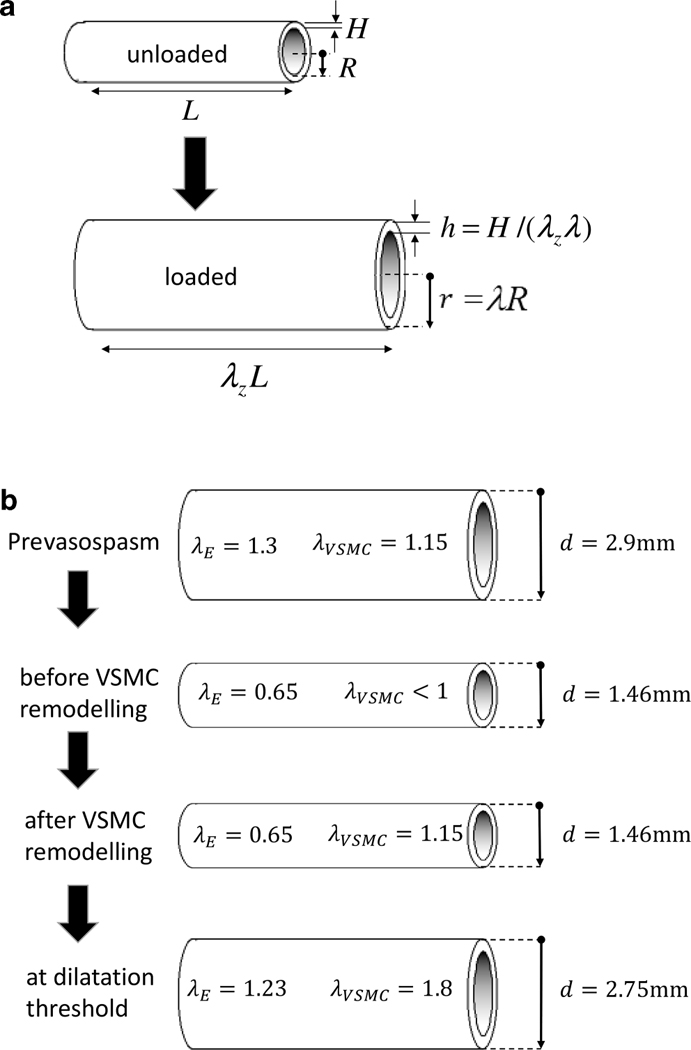
Figure 1a: The arterial geometry is approximated as a nonlinear elastic cylinder with unloaded radius R and thickness H (left) which is pressurized and axially pre-stretched to mimic in vivo conditions (right). Figure 1b: Diameters, internal pressures and constituent stretches at different phases of our model of vasospasm. In the pre-vasospasm phase (1), arterial diameter at systolic blood pressure is 2.9mm, VSMC stretch equals its attachment stretch. In the early phase of vasospasm (2), the constriction is chemically driven and VSMCs haven’t remodelled yet. Following remodelling (3), VSMCs have returned to their attachment stretch while elastin hasn’t remodelled so its stretch hasn’t changed from phase (2). Finally, if a stent provides enough pressure to exceed a critical value, a dilatation threshold (4) is reached at which VSMCs are brought to mechanical failure and incapacity to bear the pressure load. This signifies successful treatment of CVS.

This law is useful to capture aspects of the mechanical behaviour of the whole wall, but it does not capture its layered structure or describe how the individual constituents contribute to bearing the pressure load. However, with a subtle sophistication, we can write a modified Law of Laplace as:

$$p=\frac{2h}{d}({\sigma }_E+{\sigma }_{CM}+{\sigma }_{CA}+{\sigma }_{VSMCp}+{\sigma }_{VSMCa}),$$ (2)

where the wall stress σ is additively split into the stress contributions from the individual load bearing constituents of the arterial wall: elastin, medial and adventitial collagen, and, passive and active VSMC; these are denoted σ_E, σ_CM, σ_CA, σ_VSMCp and σ_VSMCa, respectively.

Of great importance for the normal functioning of the arterial wall is that at a given expanded state of the artery, these wall components experience different stretches from one another. This is possible because they are manufactured (produced and configured) with different physical conformations, dependent on their mechanical role. Hence we model the stress responses as functions of the stretches that individual constituents experience. We can represent this dependence mathematically for each wall component as

$$\begin{gathered} {\sigma }_E={\sigma }_E({\lambda }_E);{\sigma }_{CM}={\sigma }_{CM}({\lambda }_{CM});{\sigma }_{CA}={\sigma }_{CA}({\lambda }_{CA}); \\ {\sigma }_{VSMCp}={\sigma }_{VSMCp}({\lambda }_{VSMC});{\sigma }_{VSMCa}={\sigma }_{VSMCa}({\lambda }_{VSMC}) \end{gathered}$$ (3)

where λ_E, λ_CM, λ_CA, λ_VSMC denote the circumferential stretches of elastin, medial and adventitial collagen and VSMCs. The stretch for each component is defined as the current length of the component divided by its unloaded length. Hence, for example, when a medial collagen fibre is not stretched, λ_CM = 1 and when the artery further expands, the fibre will also stretch so that λ_CM > 1. It is understood in Eq. 2 that a passive wall component will not experience stress until it is stretched (e.g. σ_CM = 0, until λ_CM > 1).

We assume constituents are integrated into the arterial wall in the loaded configuration with a preferred stretch which we refer to as the attachment stretch [9]. For example, we model VSMCs to have an attachment stretch of 1.15 at systolic pressure (see Fig. 1b). The choice of attachment stretches for adventitial and medial collagen are motivated by the experimental observations [13,16] that:

1. medial collagen contributes to load bearing in homeostatic configuration whilst adventitial collagen acts as a protective sheath.

2. both medial and adventitial collagen appear with different levels of waviness and are thus recruited to load bearing at different stretches (i.e. wavier fibres at higher stretches.

In order to capture these features, in the systolic configuration: medial collagen fibres are prescribed to have attachment stretches ranging from 1 to 1.07 (thus all fibres of the distribution are bearing load); adventitial collagen fibres are prescribed to have attachment stretches between 0.8 and 1 (thus no fibres are mechanically engaged until the vessel is enlarged further).

In summary, this modelling approach enables us to:

• account for how the total mechanical behaviour of the artery relates to the mechanical response (and stretches) of its individual constituents;

• predict how changes in quantity (growth) and organisation (remodelling) of these constituents during healthy adaption, aging and disease affect the mechanical behaviour of the wall;

• predict how damage to these constituents affects the mechanical function of the artery – for example after treatment with stents or balloon angioplasty.

Results

Mechanical Model of Arterial Wall

The pressure-diameter (p-d) curve for our model of a healthy cerebral artery is shown in Figure 2. It depicts how the wall components (constituents) contribute to the overall load bearing of the arterial wall. At systolic pressure (16KPa), the arterial diameter is 2.9mm (indicated by red dot) and it can be seen that the p-d curve (solid curve) is the sum of the p-d curves of the individual constituents (non-solid). In essence, this figure illustrates the contributions of each wall component to support the transmural pressure:

$$p=p_E+p_{CM}+p_{CA}+p_{VSMCp}+p_{VSMCa},$$

which is obtained simply from Equation 2 by using the relationship between pressure and stress for each component, e.g. $p_E=2h{\sigma }_E/d$ and analogously for the other terms, consistent with (1). Note, the implications of distinct constituent attachment stretches are visible in Fig. 2 where it can be seen that the individual wall components begin to be recruited to load bearing at different arterial diameters (elastin at ~1.95mm, VSMCs at ~2.25mm and collagen at ~2.65mm).

Figure 2.

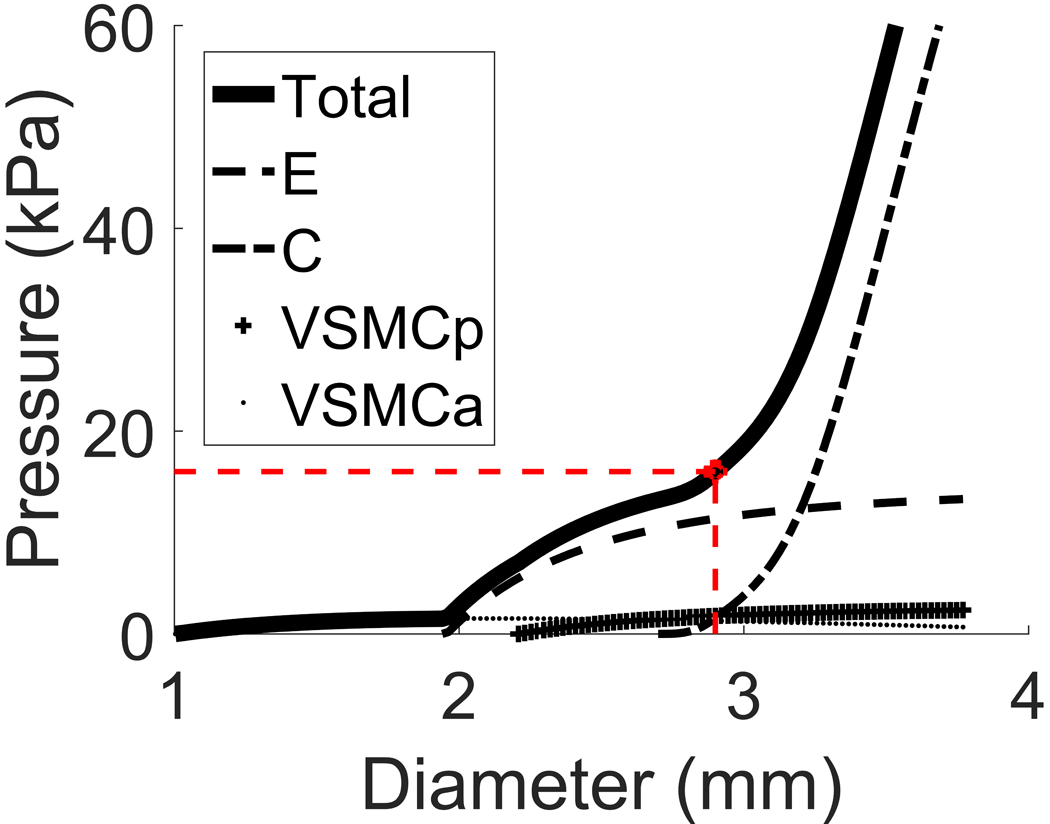
Pressure-diameter curve for a middle cerebral artery (solid curve). Physiological systolic blood pressure of 16kPa corresponds to healthy diameter of 2.9mm (red dashed lines). The non-solid curves represent the contributions of the individual load-bearing constituents: elastin, collagen (medial+adventitial), passive response of VSMCs and active response of VSMCs.

Mechanical Model of arterial wall: post vasospasm

Based on reports in the literature, we model CVS in the following manner. At the onset of vasospasm, the VSMCs contract and as a result the diameter at systolic pressure is decreased (Fig. 1b); for purposes of illustration, we simulate a 50% reduction in systolic diameter so that the arterial diameter at systolic pressure is reduced to 1.46mm. Following this initial constriction, the following changes are conjectured to occur over a time scale on the order of days to weeks (much larger than the cardiac cycle) whilst the diameter is maintained:

• VSMCs remodel to restore their stretch towards their preferred value (VSMC attachment stretch) on the vasospastic vessel (via remodelling [9,10]: this is achieved through reconfiguration of their internal cytoskeleton and/or of their attachments to the ECM [17,18])

• As VSMCs remodel their stretch, to maintain force balance, VSMCs’ cell stiffness increases, captured by increasing material parameters of σ_VSMCp and σ_VSMCa [18,19];

• extra-cellular matrix components (elastin and collagen) do not remodel; elastin production ceases after puberty and we assume collagen turnover rate is long compared to the timescale of CVS.

These model-features enable us to predict how the p-d curve is altered by CVS (see Fig. 3). For our illustrative example, we prescribed increases of material parameters for σ_VSMCp and σ_VSMCa by 20% and 47.5% respectively (we refer to Appendix B for more details and a parameter study). Notice that the loading curves for the VSMCs have shifted to the left (to maintain VSMC attachment stretch) and upwards (increased stiffness of VSMC to maintain mechanical equilibrium at systolic pressure). The solid line reflects the additive effect of these changes on the total response of the wall; note, given that we assume elastin and collagen do not remodel, their curves do not change.

Figure 3.

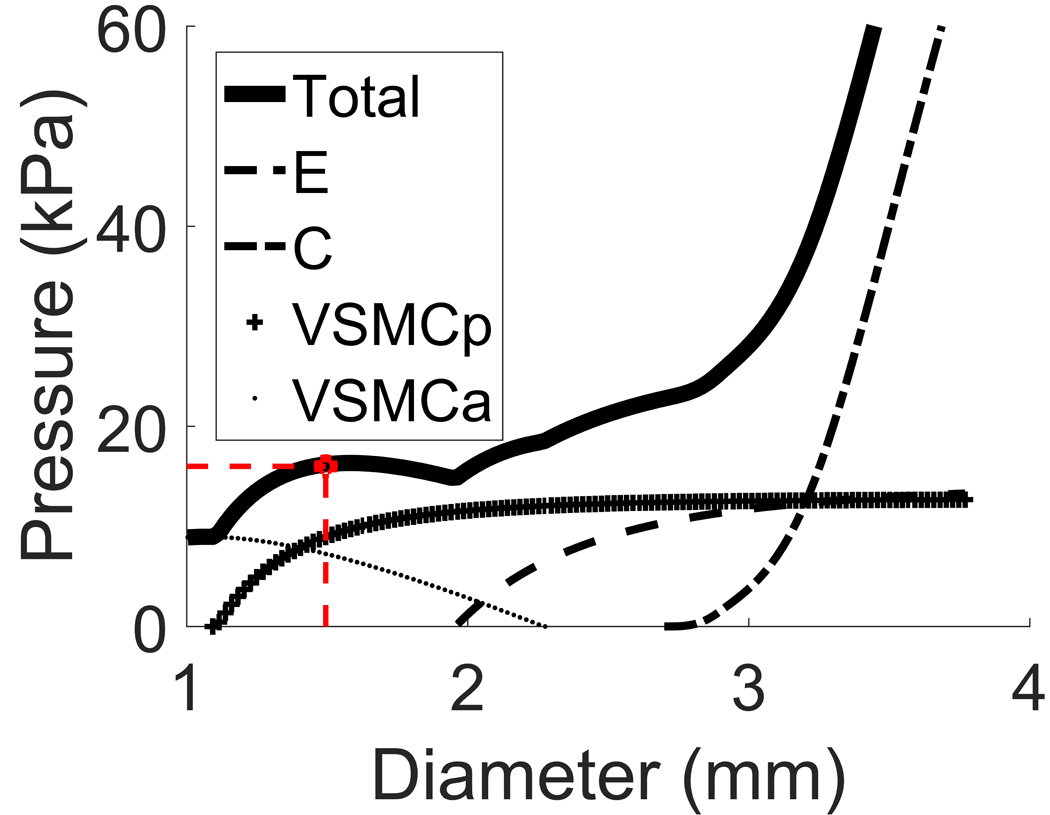
Pressure-diameter curve for a vasospastic middle cerebral artery with original systolic diameter 2.9mm that contracted to a systolic diameter of 1.46mm. The non-solid curves represent the contributions of the individual load-bearing constituents.

Damaging the arterial wall: dilatation threshold

Our model explicitly represents the stretches of the individual constituent and thus we can explicitly define damage criteria for each constituent; where by damage we mean cessation of mechanical contribution to load bearing. VSMC damage could arise from either rupture of the cell’s internal cytoskeleton or cell detachment from the ECM or both.

We define a clinically relevant dilatation threshold as the critical stretch at which VSMCs are damaged. Here, we assume that once the VSMCs are damaged, they not only cease to contribute to load bearing but also no longer generate active tension. Hence, if a stent can provide sufficient outward pressure to expand the artery beyond the dilatation threshold, CVS is successfully treated. A reasonable upper bound for the critical VSMC stretch is 1.8 [20]. Given that we assume VSMCs have a stretch of 1.15 in the post-vasospasm state (1.46mm diameter for this illustrative model), this implies a dilatation threshold diameter of 2.75mm (Fig. 1b).

We predict that a stent will be successful in treating CVS if the total pressure that is exerted on the arterial wall (sum of blood pressure plus stent pressure) remains above the p-d curve for the artery (solid curve) up until the dilatation threshold is reached: the biomechanical explanation of this being that the stent is applying enough force onto the vessel wall to expand it until VSMCs are damaged. For this illustrative example, it can be seen that the sum of the pressure provided by the stent plus the systolic blood pressure must exceed 23kPa at the dilatation threshold diameter to treat the vasospasm. Hence for a systolic blood pressure of 16kPa, this implies a stent would need to provide at least an additional 7kPa of pressure to the arterial wall up to a diameter of 2.75mm.

Observe that the dilatation threshold is slightly lower than the original vessel diameter at systolic pressure and thus the collagen and elastin fibres are not damaged. Therefore, once the dilatation threshold is reached, the pressure relationship (2) becomes, (see Fig. 4),

$$p=\frac{2h}{d}({\sigma }_E+{\sigma }_{CM}+{\sigma }_{CA}).$$ (4)

Figure 4.

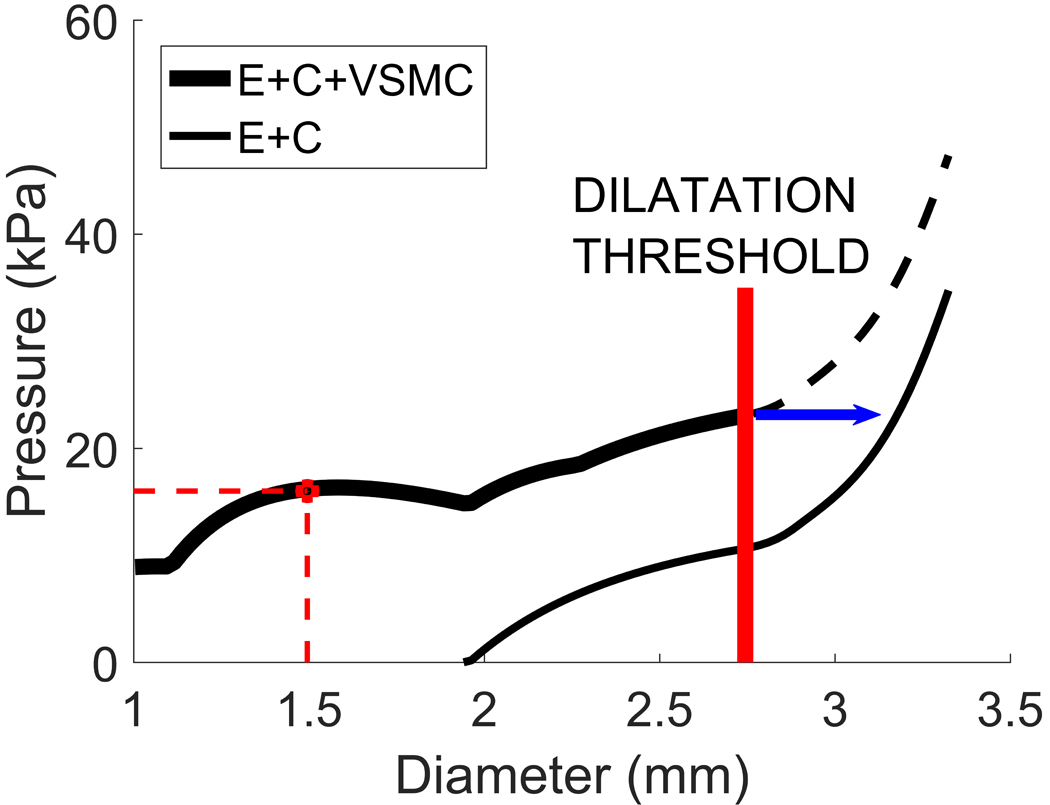
Pressure-diameter curve for the vasospastic artery before and after VSMC damage. When the dilatation threshold is reached, VSMCs cease to contribute to load bearing and only elastin and collagen are bearing the pressure load (thinner solid curve).

Modelling treatment of vasospasm

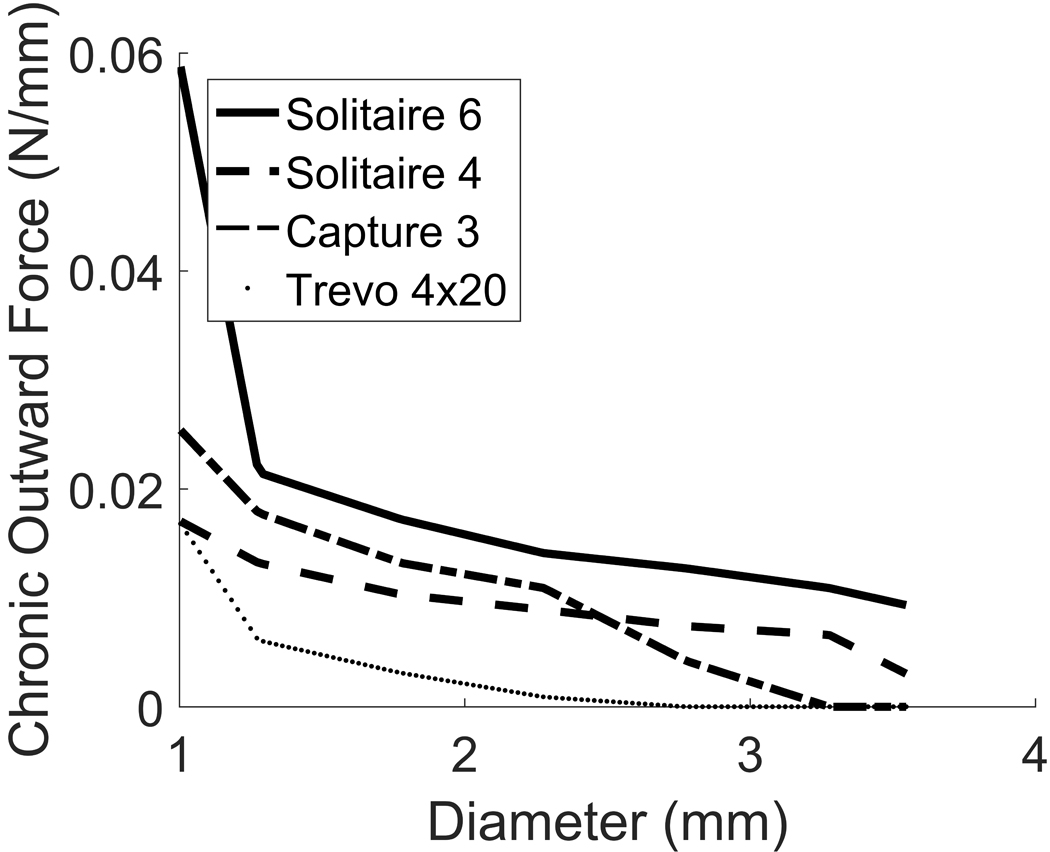
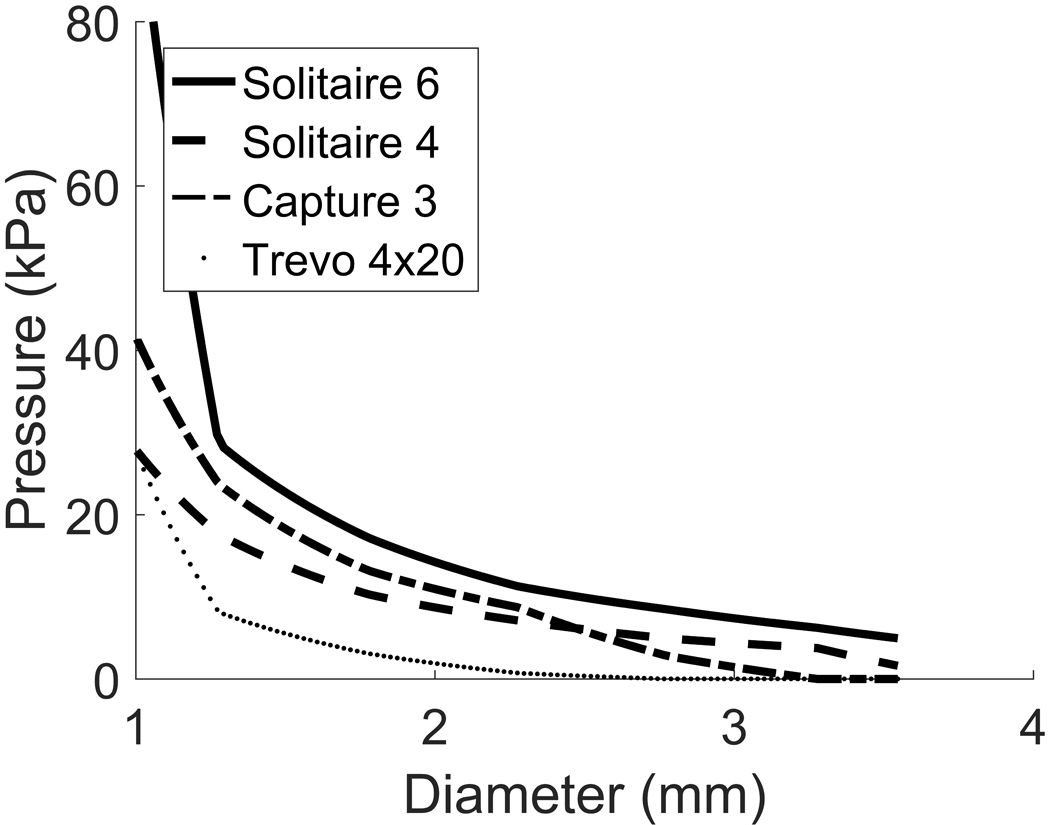
We now apply our mechanistic model to test whether a given stent would provide sufficient force to dilate the vessel beyond the dilatation threshold and thus resolve CVS. To do this, we first convert the chronic outward force data available for commercial stents into stent pressures (see Appendix C), [21]. An important observation to make about the mechanics of stents is that the pressure they exert on the wall decreases as they unfold to larger diameters (Appendix C, Figs 9 & 10), in contrast to the mechanics of balloon angioplasty.

Figure 9.

Chronic outward force vs diameter relationships for four commonly available stents: Solitare 6mm, Solitaire 4mm, Capture 3mm and Trevo 4mm. Note the forces rapidly fall to zero as the stent expands.

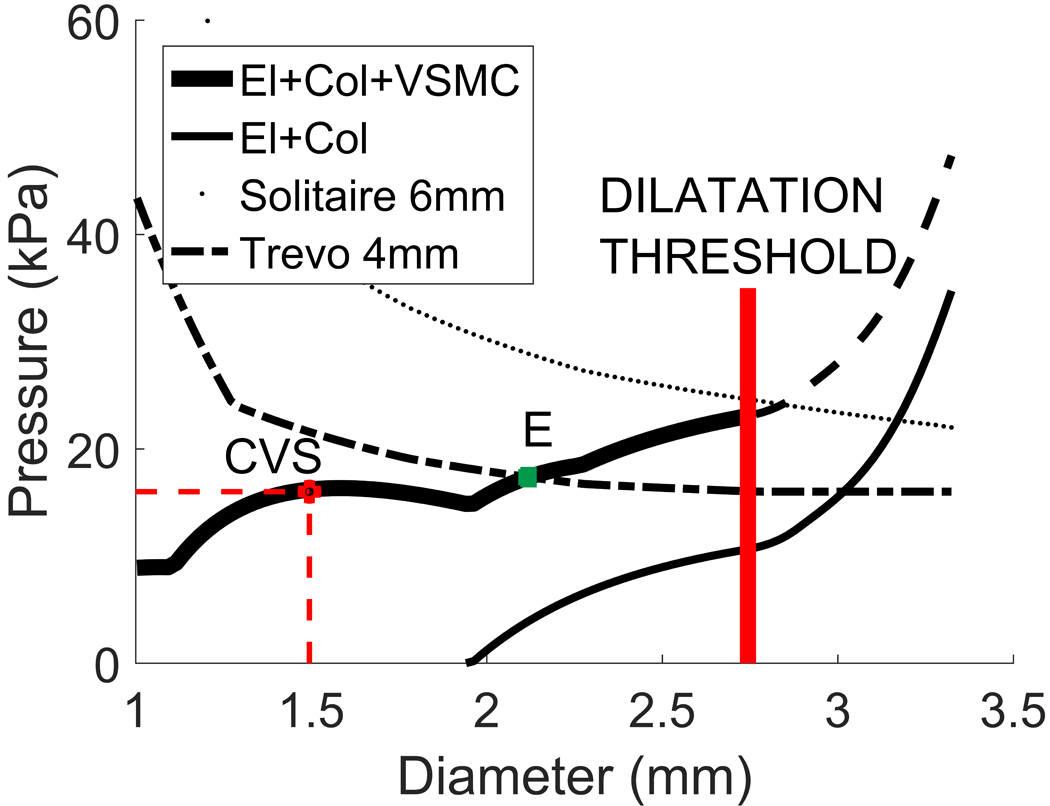
Figure 10.

Pressure-diameter curves for four commonly available stents: Solitaire 6mm, Solitaire 4mm, Capture 3mm and Trevo 4mm.

Figure 5 illustrates how the total pressure curve (systolic blood pressure + stent pressure) of two example stents, Solitaire 6mm and Trevo 4mm, is related to their deployed diameter. The p-d curve (solid curve, Fig. 5) is the same as the one given in Figs. 3, 4 and provides information about which diameter corresponds to which internal pressure, in this case for a vasospastic middle cerebral artery at 50% stenosis.

Figure 5.

Effectiveness of two stent-retrievers in resolving vasospasm in a middle cerebral artery with 50% stenosis. The stent is effective if its related curve remains above the solid curve up until the dilatation threshold. In this example, Solitaire 6mm would be successful, whereas Trevo 4x20mm would not because mechanical equilibrium would be reached at point E, which is well before the dilatation threshold.

As seen in Fig. 5, the Solitaire 6mm stent can apply more than sufficient pressure to dilate the stenosed vessel above the dilatation threshold. In contrast, the Trevo 4mm can only dilate the vessel a few millimetres before a new mechanical equilibrium is reached at a diameter (point E) lower than the dilatation threshold. The thinner solid line shows the mechanical response curve for the vessel after treatment with the Solitaire 6mm, i.e. following damage to VSMCs and having only elastin and collagen contributing to load bearing: the diameter at systole has increased from 1.46mm (vasospastic) to 3.2mm. Note that the initial systolic diameter prior to CVS was 2.9mm (see Fig. 2).

Next we model arteries of several different representative diameters (1.5, 2, 2.9 and 4mm) at 50% stenosis and simulate treatment with the following stents: Solitaire 6mm (Covidien); Solitaire 4mm (Covidien); Capture 3mm (Mindframe); Trevo 4mm (Stryker). It can be seen that all stents are effective in resolving CVS for the smaller arteries whilst none are successful for the larger arteries (Fig. 6). However, even when the stents fail to resolve CVS, notice that the magnitude of pressure necessary to resolve the disease is much smaller than the maximum possible pressure exerted by balloon angioplasty (300KPa). Hence, our model predicts that stronger stents would be able to overcome the dilatation threshold and treat CVS with limited risk of damage to the underlying ECM.

Figure 6.

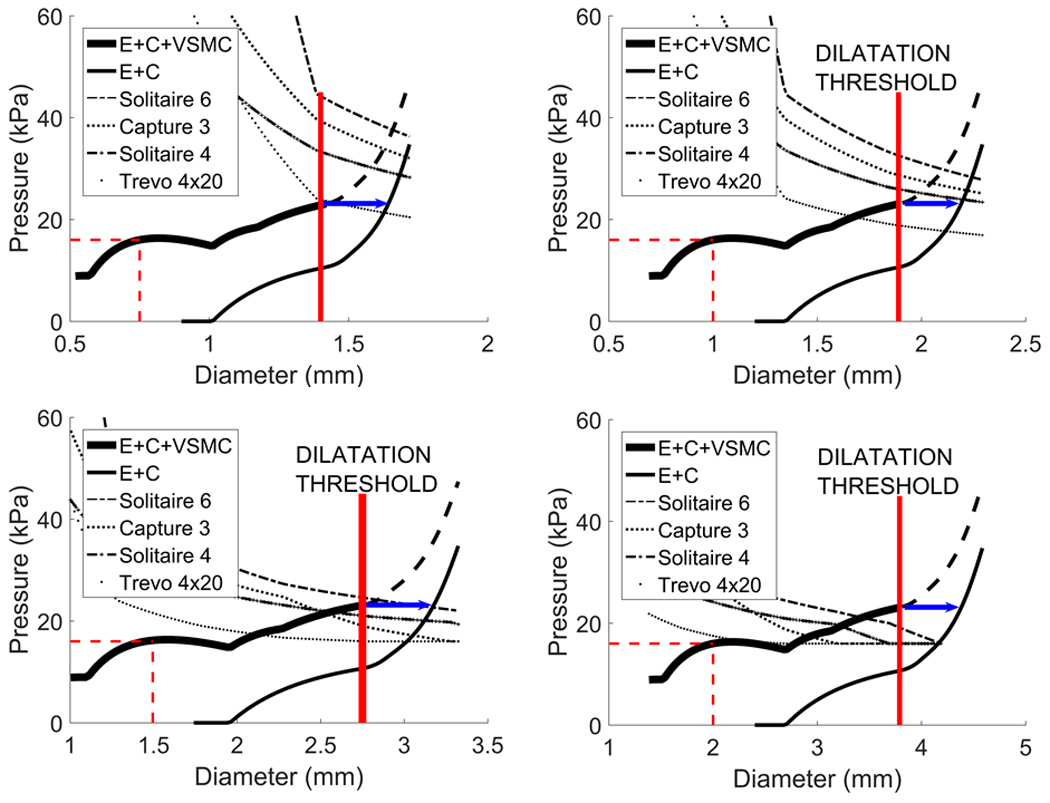
Effectiveness of four stent-retrievers in vasospastic arteries of physiological diameters 1.5mm (Fig. 6a), 2mm (Fig. 6b), 2.9mm (Fig. 6c) and 4mm (Fig. 6d), at 50% stenosis. In the 1.5mm artery all the stents expand the wall beyond the dilatation threshold. In the 4mm artery, they open the artery to new diameters, which are less than the dilatation threshold and are therefore not effective in treating vasospasm.

Discussion

Prior clinical results from our group have demonstrated the tremendous potential of vascular stents in treating vasospasm of cerebral vessels. However, the success has been uneven so far, thus pointing to the need for a mechanistic understanding of changes to the arterial wall during stent deployment in vasospastic arteries. In this paper we present a mathematical model for this process, which demonstrates that the substantially lower forces generated by properly chosen stents compared with balloon angioplasty, can effectively treat vasospasm by altering the VSMCs, even without damage to the ECM.

We believe the importance of the mathematical model is its accurate replication of our clinical experience regarding the use of stents to treat cerebral vasospasm following sub-arachnoid haemorrhage. Whilst we have seen good results in smaller vessels such as spastic M2 and A2 branches, we have seen mixed results in the M1 segment and we are yet to see a successful dilatation of the terminal ICA. Based on the current studies, we believe that this is due to a lack of sufficient outward radial force exerted by the existing stents, which have been designed for a different task, i.e. to perform mechanical thrombectomy in acute thromboembolic stroke. In particular, consistent with these recent clinical observations, the model predicts that stents provide sufficient outward force to treat small diameter arteries but may not provide sufficient force with larger diameter arteries. Hence specifically designed stents may offer a viable alternative to balloon angioplasty for the mechanical resolution of cerebral vasospasm. The advantages of such treatment (over angioplasty) include a lower risk of damage to the ECM and thus a decrease in the risk of rupture of the arterial wall.

In this modelling approach, we assume that the resolution of CVS is achieved by disrupting the VSMCs sufficiently to eliminate their contribution to load bearing. The model predicts that damage to the matrix is not a pre-requisite for successful mechanical treatment of CVS. This is supported by other observations in the literature. For example, Kobayashi et al [3] studied vasospastic primate cerebral arteries that were successfully treated with angioplasty and did not report any significant ECM damage. Similarly, Loch Macdonald et al [4] have shown in a rabbit model that successful angioplasty resulted in damage to the VSMCs but not the ECM.

A key assumption in this work is the existence of a dilatation threshold, that once reached renders the VSMC unable to generate vasoconstriction. It is hypothesized that this level is associated with the VSMCs being detached from the ECM and/or having their stress fibres ruptured. Furthermore, it is assumed that this threshold is too low to damage collagen and elastin fibres. This assumption is supported by experimental observations. Chan et al.’s [5] in vitro study of vasospastic canine basilar arteries assessed the arteries both morphologically and pharmacologically: in congruence to Kobayashi et al. [3] and MacDonald et al. [4], they observed no difference between the ECM collagen fibres and elastin even in vasospastic vessels that were subjected to balloon angioplasty compared to those that were not, i.e. they saw no fibre breakage following balloon angioplasty. Hence this suggests no damage would be expected at the much lower loads achieved during stent deployment. Interestingly, they observed that the response of both normal, non-spastic vessels and vasospastic vessels to vasoconstricting substances following balloon angioplasty was significantly decreased. Loch Macdonald and colleagues [6] also demonstrated a similar decrease in constriction following balloon angioplasty and they proposed that balloon angioplasty somehow decreases the contractility of VSMCs. It remains to assess changes in vasoconstriction response during the much lower loads associated with stent deployment. The paralysis and loss of contractility of VSMCs has been observed in experimental dilatation studies of peripheral arteries [22–25]. However, the exact cellular and/or intracellular mechanism has not yet been determined and more experimental studies on the problem are advised.

In 1990, Fischell et al. [20] observed that, following balloon angioplasty in both relaxed and contracted arteries, an ‘arterial paralysis’ was seen, but that this did not have a relationship with prolonged balloon inflation. They demonstrated that the same degree of balloon dilatation in relaxed vessels produced significantly less, if any, arterial paralysis compared to contracted vessels. Therefore, we conjecture that contraction of VSMCs predisposes them to arterial paralysis when subjected to stretch and balloon angioplasty. This may help explain the frequent finding of arterial paralysis seen in spasm prone rabbit arteries in vivo [25–28]. The question remains, though, as to why contraction of the VSMCs predisposes them to arterial paralysis following angioplasty: is it due to breakage of the VSMCs’ internal contractile cytoskeleton, could it be associated with their detachment from the ECM or is it a combination of both? Either way, they will no longer contribute to the bearing of the pressure load nor will they be able to contract and cause the spasm to return.

We believe that one of the most important points of our work is that the success of mechanical dilatation appears to be related to the degree of contraction. According to our model deployment of the stent is more likely to result in successful dilatation of the vessel is contracted and hence relaxation with vasodilators prior to stentplasty should not be performed. Kwon et al. [29] demonstrated a 60% recurrence of vasospasm if nicardipine was infused prior to stentplasty compared to 0% recurrence if stentplasty was performed prior to nicardipine infusion have recently demonstrated this in their retrospective clinical analysis.

The mathematical model presented is a conceptual representation of the mechanics of the arterial wall, CVS and its treatment. It has many simplifications and does not represent the full biological complexity of the arterial wall. For instance, we model mechanics of the arterial wall using a thin-wall assumption. This hypothesis requires that the strain perceived by the constituents in the arterial wall is constant throughout its thickness. While this holds true for a healthy artery, radial gradients may be important following vasospasm. Additional studies using a thick-walled model [30] and guided by additional experiments can be performed. Another limitation is the assumption that collagen does not remodel following vasospasm. This choice is motivated by the long half-life of the collagen fibre (about 72 days) compared to the time-scale of vasospasm. Nevertheless, it is straightforward to include partial remodelling in a more sophisticated version of the present model.

We assume that the stiffness of VSMCs increases in the vasospastic state. This is consistent with observation that VSMC remodelling of the cytoskeleton modulates the cell stiffness and contractility through signalling pathways; increased cell stiffness leads to an increase in the overall vascular stiffness [31]. However, it is unclear how this increase in stiffness is apportioned between the passive and active stress contributions. In the absence of data to inform the modelling, a parametric study was run (details in Appendix B) covering the range of possible combinations of active and passive stress contributions. These studies showed, the minimum amount of pressure a stent needs to mechanically resolve vasospasm varied between 5kPa and 11kPa, as a result of this uncertainty in load proportioning. Even with this variability, the general conclusion still holds, i.e. that the applied pressure required for a stent to resolve CVS is an order of magnitude lower than that provided by balloon angioplasty. However, this parameter study highlights the need for continued data driven studies to improve our understanding of the mechanobiology of VSMCs in the spastic artery.

The mathematical model provides insight into the underlying mechanisms of vasospasm and its resolution. However, it incorporates a simplified representation of the mechanics, biology and mechanobiology of the arterial wall and there is a need for in vivo/in vitro experiments to quantify model parameters and evaluate the consistency of modelling hypotheses. In particular, experimental guidance is needed to quantify how remodelling of the SMC influences their passive and active stress responses and how resolution of vasospasm is related to disruption of the VSMCs cytoskeleton and/or attachment to the ECM. In vitro experimental investigations on individual cells combined with investigation of tissue samples obtained from animal models of vasospasm will guide the development of more sophisticated mathematical models with improved predictive abilities.

Despite its relative simplicity, the authors believe the current model contains the essential features needed to guide future experiments on the pathophysiology and improved treatment of vasospasm. Understanding the biomechanical mechanisms of CVS would seem to be essential for designing improved therapeutic and interventional treatment options.

Conclusion

Improved understanding of the underlying mechanistic processes governing CVS and its mechanical treatment may assist in the development of dedicated stents. The model presented here supports our clinical experience that currently available stents can successfully resolve CVS in smaller arteries but not in larger, more proximal arteries. The development of dedicated stents targeted to damaging VSMC in a larger range of cerebral arteries, may provide a viable, reproducible and safe treatment option to treat delayed cerebral vasospasm.

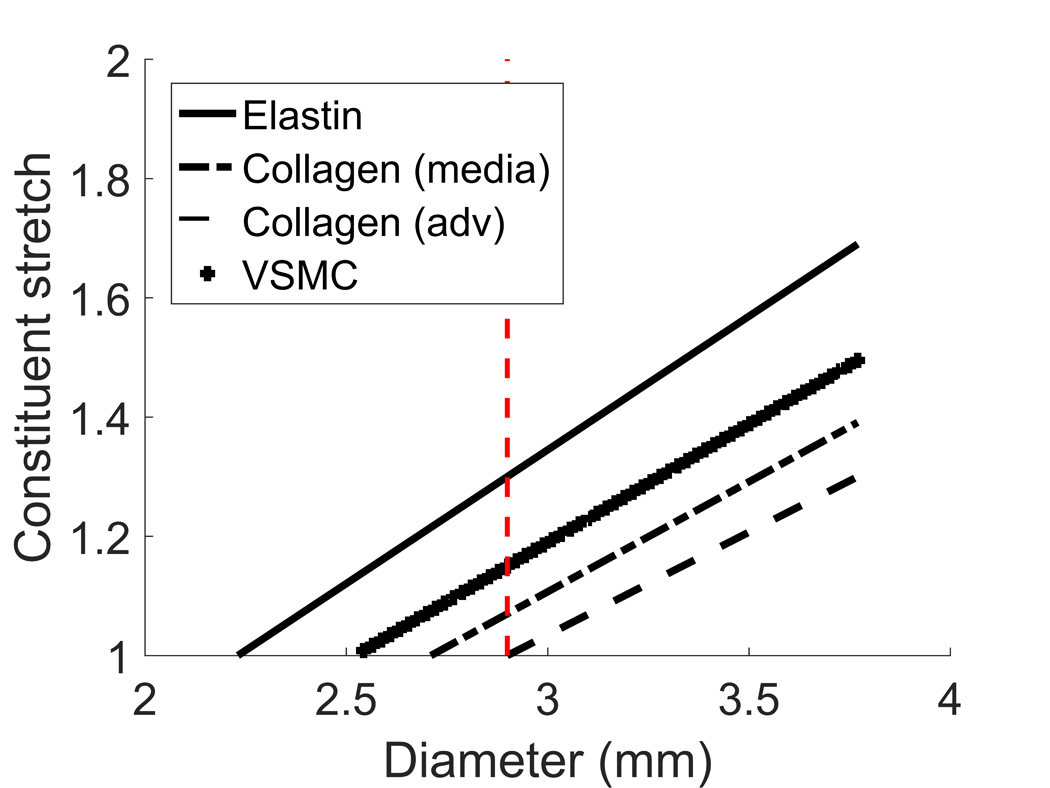
Figure 11.

Constituent stretch vs diameter relationship for elastin, medial collagen, adventitial collagen and VSMCs. Given the different mechanical roles, constituents begin to bear the pressure load at different diameters and are configured at different stretches at the physiological diameter (vertical dashed line).

Appendix A

The arterial wall is modelled as a nonlinear elastic cylindrical membrane [10] with thickness $H$ and radius $R$ in its unloaded configuration. In vivo, it is subject to an internal pressure $p$ and axial stretch ${\lambda }_Z$. The governing equation describing the balance of forces for mechanical equilibrium is:

$$p=\frac{h\sigma }{r}$$

Where the deformed radius r is given by $r=\lambda R$ with λ the circumferential tissue stretch the deformed thickness of the arterial wall is $h=H/{\lambda }_z\lambda ,$ and σ denotes the circumferential Cauchy stress. The arterial wall constituents are modelled as a constrained mixture, so that the total (Cauchy) stress $\sigma$ component for the arterial wall is the sum of stress contributions from the individual constituents, i.e.

$$\sigma ={\sigma }_E(\lambda )+{\sigma }_{CM}({\lambda }_{CM})+{\sigma }_{CA}({\lambda }_{CA})+{\sigma }_{VSMCp}({\lambda }_M)+{\sigma }_{VSMCa}({\lambda }_M)$$

Where ${\sigma }_E,{\sigma }_{CM},{\sigma }_{CA},{\sigma }_{VSMCp}\text{and}{\sigma }_{VSMCa}$ denote the circumferential Cauchy stress contributions of elastin (E), medial collagen (CM), adventitial collagen (CA), passive and active VSMCs, respectively. We exclude the mechanical role of endothelial cells due to their negligible role in the mechanical behaviour of the vessel [30].

We utilise a strain energy function for the collagen that accounts for the recruitment distribution of collagen fibres [13,16]

$${\Psi }_{C_J}\left(\lambda \right)=\underset{1}{\overset{\lambda }{\int }}{\tilde{\Psi }}_{C_J}\left({\lambda }_{C_J}\right)\rho \left({\lambda }_{R_J}\right)d{\lambda }_{R_J},$$

where the distribution of recruitment stretches $\rho \left({\lambda }_{R_J}\right)$ is taken to be a triangular distribution function [12,14] and the mechanical response of an individual fibre is linear, i.e.

$${\tilde{\Psi }}_{C_J}\left({\lambda }_{C_J}\right)=\frac{k_{C_J}}{2}{\left({\lambda }_{C_J}-1\right)}^2$$

Analytical expressions for the collagen Cauchy stresses (see 12) can then be obtained via,

$${\sigma }_{C_J}=\lambda \frac{\partial }{\partial \lambda }{\Psi }_{C_J}(\lambda ),$$

The mechanical responses of elastin and passive VSMCs are modelled using neo-Hookean constitutive models [9] and it follows that

$${\sigma }_E=k_E{\lambda }^2\left(1-\frac{1}{{\lambda }_z^2{\lambda }^4}\right),$$

$${\sigma }_{VSMCp}=f_p{k}_M^{pass}{{\lambda }_M}^2\left(1-\frac{1}{{\lambda }_z^2{\lambda }_M^4}\right),$$

whilst the active response of VSMCs follows [31,32]

$${\sigma }_{VSMCa}=f_a{c}_v{k}_M^{act}{\lambda }_M\left[1-{\left(\frac{{\lambda }_M^{\mathit{mean}}-{\lambda }_M}{{\lambda }_M^{\mathit{mean}}-{\lambda }_M^{max}}\right)}^2\right]$$

The material parameters $k_E,k_M^{pass},k_M^{act},k_C$ are inferred by prescribing the proportion of load borne by the constituent in the initial homeostatic configuration [33–35]. We assume that at systolic pressure the stretch $\lambda =1.3,$ the elastin bears 70% of the load, passive VSMC bears 10% of the load, active VSMC bears 10% of the load medial collagen bears 10% of the load; adventitial collagen is unrecruited so doesn’t bear any load. Note f_p, f_a are dimensionless parameters for increasing the passive and active stress responses following vasospasm to maintain mechanical equilibrium.

Natural reference configurations

The mechanical responses are defined as functions of the stretches that individual constituents experience, i.e.

$${\lambda }_J=\frac{\lambda }{{\lambda }_{R_J}},$$

where $\lambda$ denotes the tissue stretch, ${\lambda }_J$ denotes the stretches of medial and adventitial collagen $(J=C_M,C_A)\mathrm{and}\text{VSMC}(J=S);$ the recruitment stretches ${\lambda }_{R_J}$ define the onset of load bearing. Initial values for recruitment stretches are obtained by prescribing the attachment stretches of constituents (or VSMC) in the (pre-vasospasm) loaded configuration, i.e.

$${\lambda }_{R_J}={\frac{\lambda }{{\lambda }_I}|}_{p_{sys},{\lambda }_z}$$

For collagen, each (symmetric) triangular distribution of fibres requires specification of maximum/minimum fibre attachment stretches, i.e. ${\lambda }_{C_J}^{max}\text{and}{\lambda }_{C_J}^{min},$ respectively. We model distinct distributions so that medial collagen bears load in homeostatic configuration, while adventitial collagen is modelled as playing a purely protective role, i.e. begins to bear load after systole.

Table 1.

Model parameters used for the simulations.

Parameter	Meaning	Value
psys	systolic pressure	16kPa
H/R	ratio of unloaded thickness to unloaded radius	0.2
${\lambda }_{z }$	axial stretch	1.3
kE	material parameter elastin	93.14kPa
$k_M^{pass}$	material parameter VSMC (passive)	22.09kPa
$k_M^{act}$	material parameter VSMC (active)	18.07kPa
$k_{C_M}$	material parameter medial collagen	639.5kPa
$k_{C_A}$	material parameter for adventitial collagen	5115.6kPa
$f_p$	passive stiffness factor (before vasospasm)	1
$f_a$	active stiffness factor (before vasospasm)	1
${\lambda }_M^{mean}$	cell stretch at which VSMC’s active response is maximal	1.1
${\lambda }_M^{max}$	maximum cell stretch at which VSMC’s active response is zero	1.8
${\lambda }_{M_{AT}}$	VSMC attachment stretch	1.15
${\lambda }_{C_M}^{max}$	Maximum Medial collagen fibre attachment stretch	1.07
${\lambda }_{C_M}^{min}$	Minimum Medial collagen fibre attachment stretch	1.0
${\lambda }_{C_A}^{max}$	Maximum Adventitial collagen fibre attachment stretch	1.0
${\lambda }_{C_A}^{min}$	Minimum Adventitial collagen fibre attachment stretch	0.8

Appendix B

In vasospasm, the contraction of the VSMC reduces the vessel cross section, removing load from the ECM components as the stretch of these components drops below one. As a result, the VMSC must bear all of the load, albeit at a smaller diameter. We assume that in the time between vasospasm onset and treatment, that the mechanical contribution from collagen and elastin remains negligible in comparison to the VSMC contributions (despite possible remodelling of collagen fibres). Although the VSMCs must bear the entire transmural load, the relative contributions of the active and passive components may shift in time. The degree and timing of this shift will depend on a number factors involving the damage to the VSMC during treatment as well as the VSCM remodelling process for the individual patient. In this Appendix, we do not directly model these changes, but rather perform a parametric study to conservatively explore the possible impact that the largest possible variation in relative load bearing would have on predicted stent requirements.

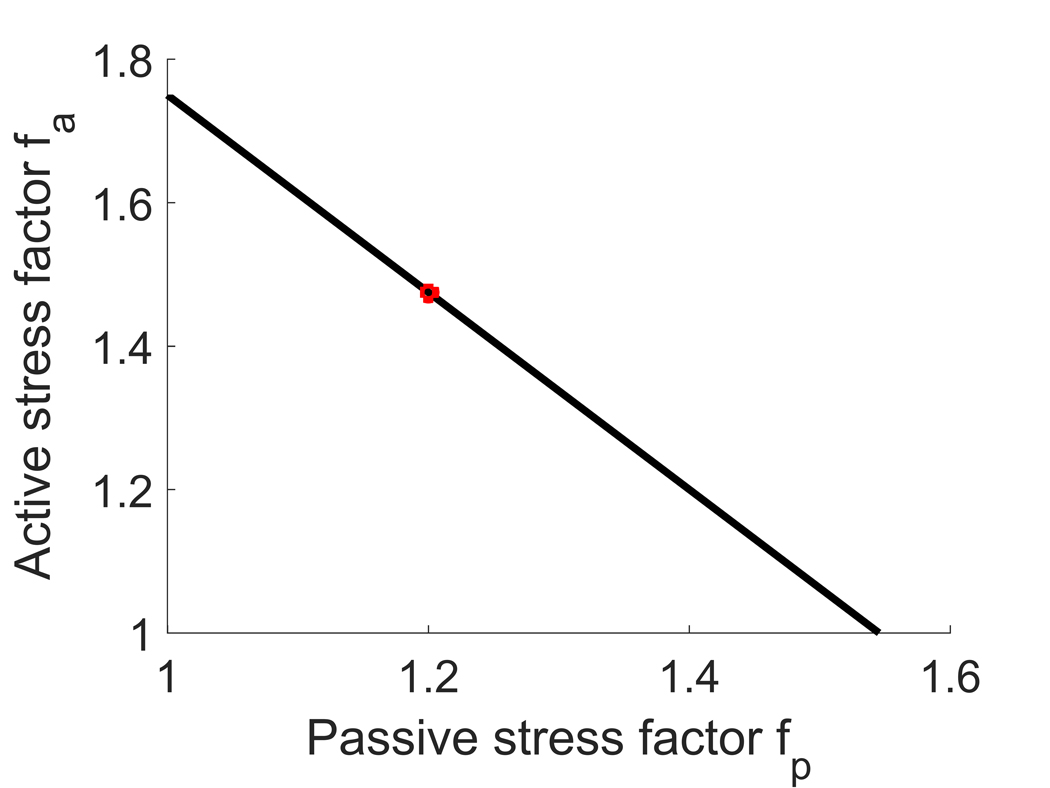
In the parametric study, the relative roles of active and passive VSMC are controlled by varying parameters $f_p$ and $f_a$ (see Discussion for a biological interpretation of these changes). Both parameters are greater than or equal to one and are coupled in that their combined influence maintains equilibrium of the vessel. In the main body of the text, a specific case ($f_p=1.2$, $f_a=1.475$) was considered. Here results are obtained over the entire parameter space. To do so, we first obtained the solutions for the two extremal cases with $f_p$ = 1, and $f_a=1$, respectively. In particular, if the passive response is not affected ($f_p=1$), then $f_a$ must increase by 75%; conversely, if $f_a=1$, then $f_p$ increases by 55%, Figure 7. We then gradually increased f_p from 1 to 1.55 (with f_p = 1.55 corresponding to $f_a=1$) by small constant increments and solved the equation of mechanical equilibrium to obtain the relationship between f_a and f_p shown in Fig. 7.

Figure 7.

Plot of the parameter pairs f_a vs f_p that solve mechanical equilibrium for a vasospastic middle cerebral artery at 50% stenosis. The represented values cover all possible solutions.

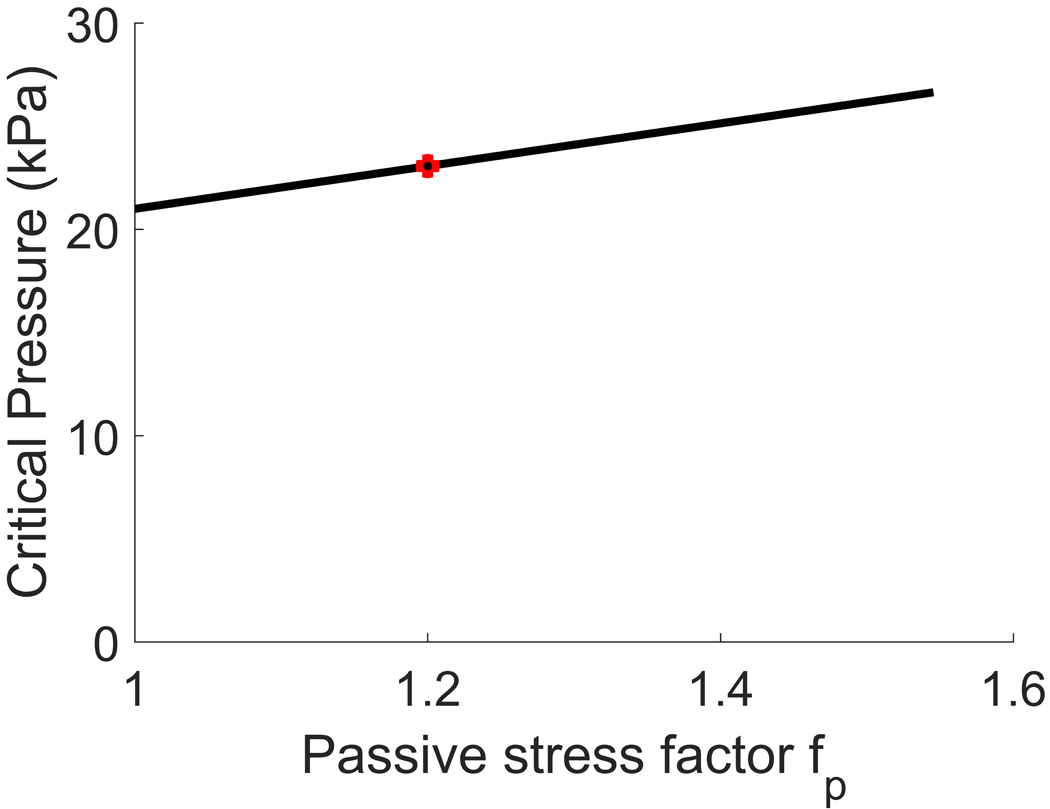
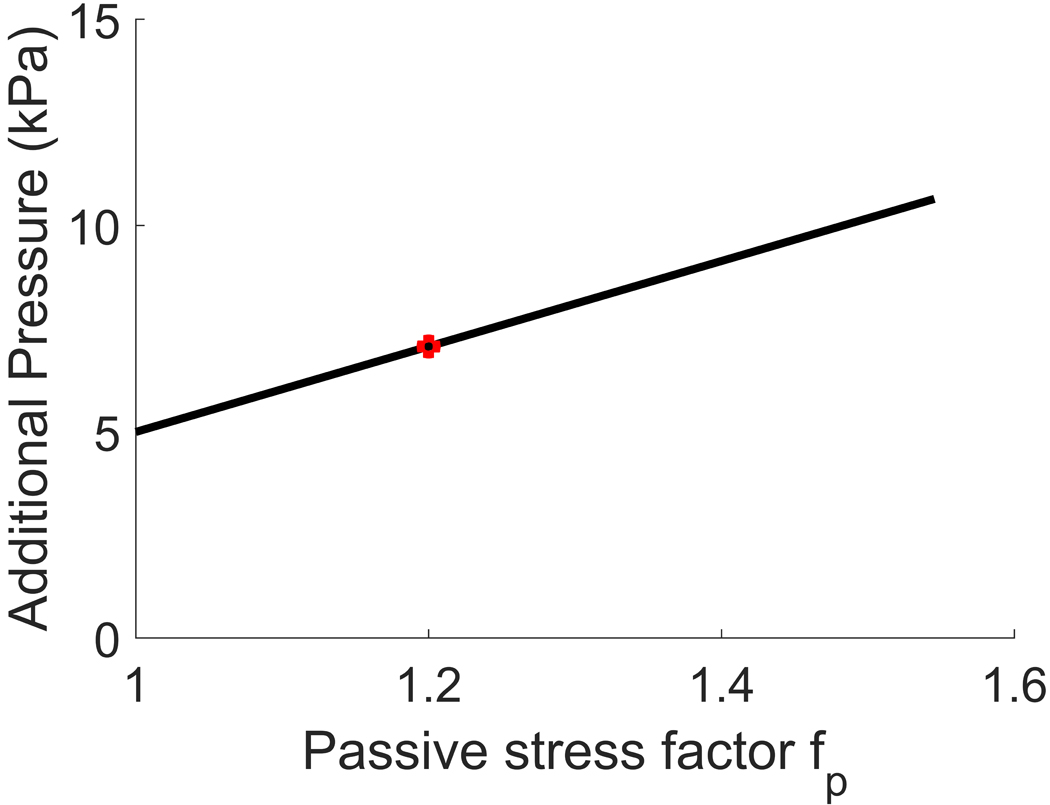
For each pair of values, we then computed the critical pressure, i.e. the pressure that should be applied to the arterial wall to cross the failure threshold of VSMCs (Fig. 8, above). Subtracting systolic blood pressure (16kPa) from the critical pressure, we obtained the additional pressure, namely the amount of pressure an interventional device should provide in order to treat vasospasm (Fig. 8, below).

Figure 8.

Plot of the critical pressure (above) and additional pressure (below) vs increase in passive response in vasospasm at 50% stenosis. The critical pressure is defined as the amount of pressure necessary to be applied to the arterial wall to reach the dilatation threshold, while the additional pressure is the amount of pressure an interventional device should provide to reach such dilatation threshold. Equivalently, the additional pressure equals the critical pressure after subtraction of systolic blood pressure (16 kPa). The case considered in the main text is shown in red.

The results show that the minimum additional pressure a device should provide is about 5kPa, while the maximum is about 11kPa. Therefore, at most, the predictions for required stent pressure would increase to 11kPa. Hence, the conclusion that pressures needed to treat vasospasm are attainable by stents, and are an order of magnitude below the pressure used during balloon angioplasty treatment still holds.

Appendix C

We start from a table of measurements of the chronic outward force (COF) exerted by the stents, expressed in N/mm; this represents the hoop force exerted by the stent divided by its length. Since the hoop force is measured in the circumferential direction, we use the identities in [20] to obtain:

$$P=\frac{COF}{lr},$$

where $P$ is the pressure exerted by the stent, $l$ the length of the stent and $r$ the radius. We illustrate the COF-diameter relationship for the considered stents in Fig. 9, and the corresponding pressure-diameter curves in Fig. 10.