Summary
Cell size homeostasis is often achieved by coupling cell cycle progression to cell growth. Growth has been shown to drive cell cycle progression in bacteria and yeast through ‘sizers’, wherein cells of varying birth size divide at similar final sizes [1-3], and ‘adders’, wherein cells increase in size a fixed amount per cell cycle [4-6]. Intermediate control phenomena are also observed, and even the same organism can exhibit different control phenomena depending on growth conditions [2,7,8]. While studying unicellular organisms in laboratory conditions may give insight into their growth control in the wild, this is less apparent for studies of mammalian cells growing outside the organism. Sizers, adders, and intermediate phenomena have been observed in vitro [9-12], but it is unclear how this relates to mammalian cell proliferation in vivo. To address this question, we analyzed time-lapse images of the mouse epidermis taken over one week during normal tissue turnover [13]. We quantified the 3D volume growth and cell cycle progression of single cells within the mouse skin. In dividing epidermal stem cells, we found that cell growth is coupled to division through a sizer operating largely in the G1 phase of the cell cycle. Thus, while the majority of tissue culture studies have identified adders, our analysis demonstrates that sizers are important in vivo and highlights the need to determine their underlying molecular origin.
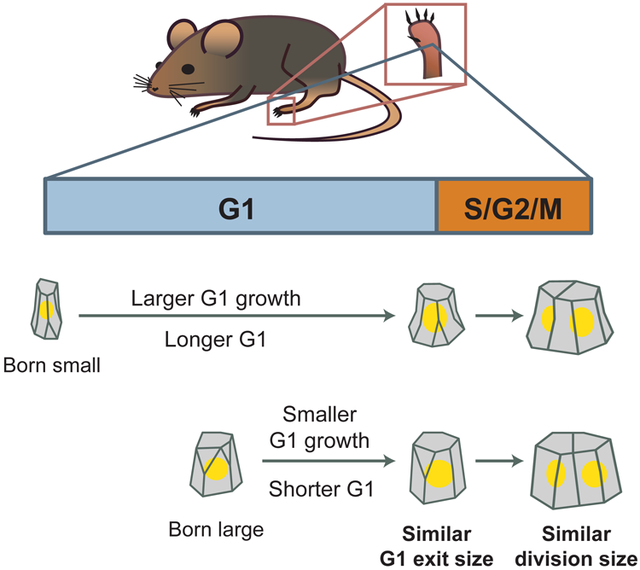
Graphical Abstract
eTOC blurb
Xie and Skotheim quantify single cell growth from longitudinal imaging of mouse epidermal stem cells over one week. Epidermal stem cells grow faster than linearly in vivo, and couple cell growth and cell cycle progression using a G1 sizer.
Results
Measuring cell volume growth in epidermal stem cells during normal tissue turnover
To determine which cell size homeostasis mechanism operates in vivo, we examined epidermal stem cells growing and dividing during normal tissue turnover. Mouse skin is an ideal system to study in vivo cell size control because it has a high frequency of cell divisions [14]. The epidermis is a multilayered epithelium with suprabasal layers of differentiated keratinocytes residing above a basal layer of stem cells (Figure 1A). The epidermal stem cells in the basal layer are the only source of new cells during normal tissue turnover [15]. As they proliferate, these epidermal stem cells can either self-renew and remain in the basal layer or differentiate into the suprabasal layers.
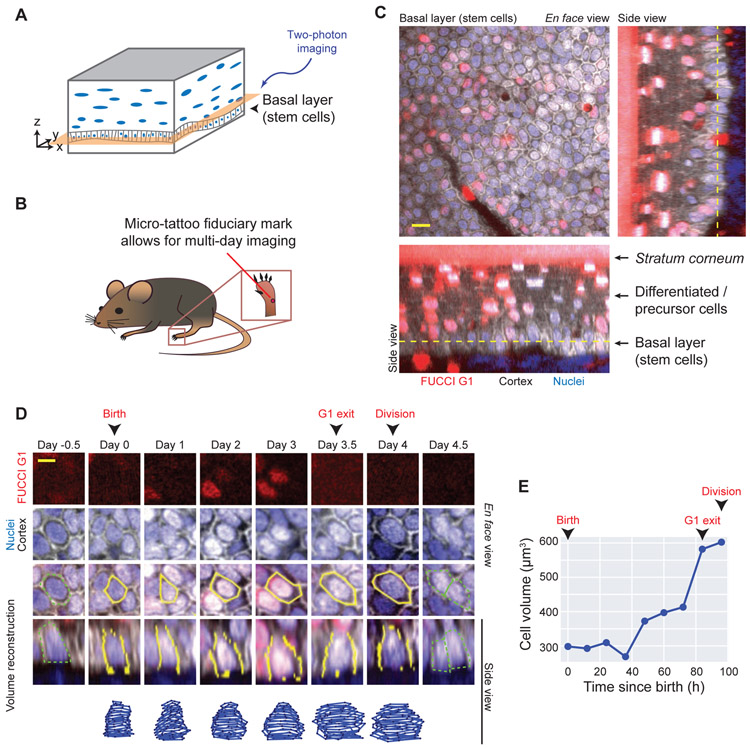
Figure 1. Quantifying cell volume and cell cycle phase of epidermal stem cells growing in vivo.
A. Schematic of mouse non-hairy plantar skin. The epidermal tissue is a stratified epithelium, where stem cells reside in the basal layer. During tissue homeostasis, the basal layer contains the cycling cells.
B. Dataset from [13]. Videos of cells in the mouse hind paw skin were generated by re-visiting a micro-tattooed region with two-photon microscopy every 12h for up to 7 days.
C. Epidermal stem cells in a mouse expressing reporters for G1 phase (red, CMV-mKO2-hCdt1(30/120)), cell cortex (gray, K14-actin-GFP), and nucleus (blue, K14-H2B-Cerulean). The en face view as well as two side views are shown. Dotted lines denote the z-position of the en face view shown. Scale bar is 10 μm.
D. Example of the volume reconstruction of a single epidermal stem cell. The FUCCI G1 reporter is shown in red, the nucleus in blue, and the actin cortex in gray. The manually segmented cell outlines are shown in yellow on top of the merged images showing en face and side views. The reconstructed 3D shape is shown in the bottom track. The cell cycle landmarks birth, G1 exit, and division are annotated. Note the presence of the parent cell at day −0.5 and daughter cells at day 4.5 outlined in dotted green. Scale bar is 5 μm. See Figure S1 for more examples. See Video S1 and Video S2 for videos of cell tracking in time and in 3D.
E. The volume growth curve for the cell shown in (D). Birth, G1 exit, and division are marked.
To measure cell growth and division in vivo, we analyzed images previously acquired by [13]. Micro-tattoos on the mouse hindpaw served as fiducial marks to allow revisiting of the same regions over time (Figure 1B). Single cells were imaged with two-photon microscopy every 12 hours for up to 7 days (Figure 1C). Since the mice were not wounded and allowed to return to normal activity between imaging, these videos capture stem cell growth dynamics during unperturbed tissue turnover.
To quantify cell volume, we reconstructed 3D cell shapes by manually segmenting videos from mice expressing Histone-2B-Cerulean (nuclear reporter), Actin-GFP (cortex reporter), and FUCCI G1 mKO2-hCdt1(30/120) (G1 reporter) (Figure 1D-E, Figure S1). We could track cells over an entire cell cycle and use the G1 reporter to distinguish G1 from S/G2/M phases. We restricted our analysis to dividing stem cells within the basal layer. Similar 4D reconstruction strategies have been used to quantify in vivo epithelial cell volume and shape change in Drosophila and Arabidopsis [16,17].
We measured cell volume growth over entire cell cycles for 197 cells from 3 independent tissue regions in 2 different mice (Figure 2A, Figure S2A-C; Video S1-2). Cells cycled every 71 ± 21h, with the majority of time spent in G1 phase (Figure 2B-D). This estimate is consistent with previous estimates of hindpaw cell cycle durations [18]. Notably, cell cycles in vivo are much longer than cell cycles in vitro, where cell lines typically divide once a day. To assess the error in our 3D segmentation, we fitted our data to smoothing splines since cell volume is expected to increase gradually over time (Method S1, Figure i A-F). The average residual is <10% of the estimated volume (Method S1, Figure i G-H). We performed independent repeat segmentations and found that the average user error is similar in magnitude (9.1± 8.6%) (Method S1, Figure i I-J). Next, we compared the volume growth curves with cross-sectional area growth curves, a common cell size proxy in epithelial cells (Method S1, Figure ii A-B). Area growth curves, while correlated with volume growth (Method S1, Figure ii C), are significantly noisier with larger relative residuals when fit to smoothing splines (Method S1, Figure ii D). These analyses suggest that our volume growth data have low error and better reflect cell size than cross-sectional cell area measurements. To reduce error in subsequent analyses, we present spline-smoothed data in the main text. Similar analyses on raw data yielded qualitatively similar conclusions and are shown in the supplemental figures.
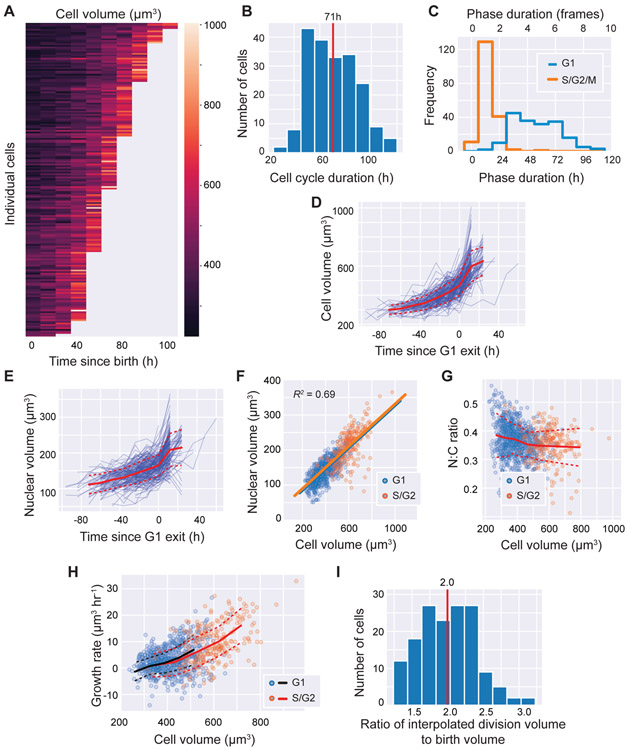
Figure 2. Epidermal stem cells grow faster than linearly and maintain a constant nuclear to cytoplasmic ratio.
A. Heatmap of volume growth curves of epidermal stem cells (N = 197; 3 independent regions from 2 mice). Growth curves are sorted by increasing length.
B. The distribution of cell cycle durations.
C. The distribution of the duration of G1 (blue) and S/G2/M (orange) phases.
D. Volume growth curves aligned by the time of G1 exit.
E. Nuclear volume growth curves aligned by the time of G1 exit.
F. The correlation between cell and nuclear volumes (N = 1,159). Straight lines show linear regression for G1 cells (blue) or S/G2 cells (orange).
G. The nuclear-to-cytoplasmic volume ratio (N:C ratio) for cells of varying volumes. Blue dots denote G1 cells, orange dots denote S/G2 cells.
H. The cell volume growth rate plotted as a function of cell volume (N = 946). The binned mean values are shown for G1 (black) and S/G2 (orange) cells. Dotted lines denote standard deviations corresponding to their color.
I. The distribution of the ratio of the interpolated division volume to the birth volume (N = 167).
Means or binned mean values are shown in red solid lines. Dotted lines denote standard deviations. See also Figure S2 for data broken down by imaging region and mouse.
Nuclear-to-cytoplasm ratio remains constant throughout the cell cycle
Nuclear volume has been shown to be proportional to cell volume (constant N:C ratio) in different cell lines. While the N:C ratio may vary across cells of different types and/or species, within the same cell type it is typically independent of cell size and cell cycle phase [19]. To test if this remains true in vivo, we quantified nuclear volume by segmenting the nucleus using a labeled histone, H2B-Cerulean (Method S1, Figure iii). We observed that the N:C ratio remains relatively constant throughout both G1 and S/G2 phases (Figure 2E-G; Figure S2D-E). In bivariate regression analysis using cell volume or cell phase to predict nuclear volume, cell volume is clearly a significant predictor (P < 10−10) while cell cycle phase is not (P > 0.05). Thus, the N:C ratio remains relatively constant throughout the cell cycle in vivo.
Cells grow faster than linearly in vivo
Next, we examined the volume growth dynamics of epidermal stem cells in vivo. In vitro, cells have been reported to grow linearly (accumulating a constant volume per unit time), exponentially (accumulating volume in proportion to their current volume), or with intermediate dynamics [10, 12,20-22]. However, there is no comparable data in mammalian tissues in vivo, where single-cell growth rates are especially difficult to measure. We quantified the absolute growth rate as a function of cell volume by taking the difference in cell volume between one time-point and its previous time-point, divided by the frame interval. Stem cells grow faster the larger they become and growth curves better fit exponential or bilinear models than linear models, suggesting supra-linear growth (Figure 2H, Figure S2F-G). However, we note that we do not have enough resolution to distinguish the precise form of this nonlinear growth (see Discussion). In addition, we find little difference in growth rates between G1 and S/G2/M cells of the same size. In bivariate regression analysis where cell volume and cell cycle phase were used to predict growth rate, cell volume is a significant predictor (P < 10−10), whereas cell cycle phase is not (P > 0.9). Similarly, cell size-dependent growth rates were similar in early G1 (first 3 frames) and the rest of G1 (P > 0.9). Taken together, these results suggest that size rather than cell cycle phase is the dominant factor determining cell growth dynamics, which is faster than linear in G1 and S/G2/M.
Estimating the final cell division size
To estimate the final division size we averaged the size at the last frame with the sum of the sizes of the daughter cells in the subsequent frame (Methods S1, Figure iv A-C). Stem cell divisions result in daughters of high symmetry (Methods S1, Figure S2H). We observed that the interpolated division size is on average 35 ± 57 μm3 larger than the sampled final size before division (Figure S2I). Importantly, the interpolated volume is likely a better estimate of the division volume because it is closer to twice the average birth volume (1.9-fold for uninterpolated vs 2.0-fold for interpolated; P < 10−13, one-sided paired T-test) (Figure 2I; Figure S2J).
Evidence for swelling during mitosis
Recent studies showed that cells in vitro rapidly swell up to 20% in volume when entering mitosis, and this swelling is quickly lost during anaphase [23,24]. For an epithelial cell, osmotically-driven swelling can push away its neighbors to achieve a spherical geometry during mitosis, which is thought to support spindle formation and accurate chromosome segregation [25]. Interestingly, we have 11 growth curves where the final frame before division captured cells in mitosis as evident in their spherical shape and chromatin condensation (Figure S2K). Consistent with the mitotic swelling model, we found that the volume of mitotic cells is larger than the sum of the two daughter volumes following division (Figure S2L).
G1 and S/G2/M durations adjust to birth size variation
To determine how cell size is controlled in epidermal stem cells, we first examined the relationship between cell size and cell cycle phase durations. Cells born smaller are much more likely to spend longer in G1, suggesting that the G1/S transition is important for cell size control (Figure 3A; R = −0.54, P < 10−15). Cells born in the smallest size bin (233-291 μm3) on average spend 70h ± 19 in G1, whereas cells born in the largest bin (398-496 μm3) spend 40h ± 13 in G1. We note that cells exiting G1 with smaller volumes also spend on average longer in S/G2/M (Figure 3B; R = −0.47, P < 10−10). Cells exiting G1 in the smallest size bin (290-432 μm3) spend 20h ± 12 in S/G2/M, while cells exiting G1 in the largest size bin (530-671 μm3) spend 11h ± 4 in S/G2/M. However, there is poor sampling of the S/G2/M phases, which typically only last 1-2 video frames (Figure 2C). This low sampling may introduce artifacts in correlations between S/G2/M duration and G1 exit size (see Discussion; Methods S1, Figure v). Notably, the coefficient of variation (CV) of the G1 exit volume is smaller than the CV of cell size at birth or at cell division (Figure S2M; P < 0.05, bootstrap test). Taken together, these data suggest that there is size control occurring at the G1/S transition in vivo.
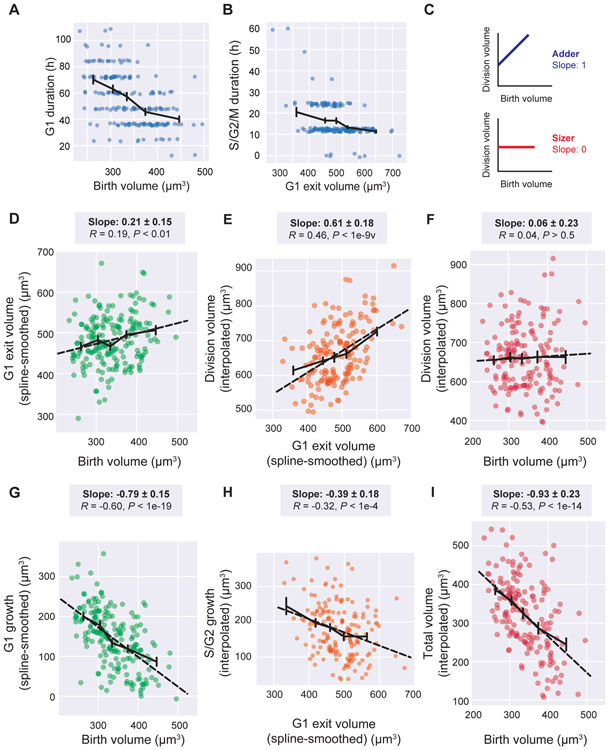
Figure 3. Epidermal stem cells exhibit sizers.
A. Cell birth volume is plotted against the duration of G1 phase (N = 197). Small jitter was added in the plot to avoid overlapping data so all points can be seen.
B. The volume at which cells exit G1 is plotted against with the total duration of S/G2/M phases (N = 197).
C. Schematic of cell size control correlations. For the adder model, the linear regression slope between birth and division volume is 1. For the sizer model, the slope is 0.
D. The cell birth volume is plotted against the G1 exit volume (N = 197).
E. The G1 exit volume is plotted against the volume at division (N = 167).
F. The birth volume is plotted against the volume at division (N = 167).
G-I. The amount of volume grown during the respective phases are plotted against the cell volume at the beginning of the indicated phase (G, H) or the entire cell cycle (I).
Solid black lines show the binned mean ± SEM. For D-I, dotted black lines show the linear regression. Linear regression slopes are reported above the plots with 95% confidence intervals. R values are Pearson’s correlations, with P-values reported against the null-hypothesis of R = 0. See also Figure S3.
Epidermal stem cells grow as sizers
That smaller cells spend more time in G1 phase suggested that they would be able to compensate for their small initial size by growing more during their cell cycle. If the G1/S transition were a ‘sizer’, the linear regression slope (m) between birth size and G1 exit size would be m = 0. Conversely, if G1/S were an adder, then the slope would be m = 1 (Figure 3C). We find that for epidermal stem cells, the slope of the linear regression between birth volume and G1 exit volume is m = 0.21 ± 0.15 (95% confidence interval), indicating a near-sizer mechanism coupling cell birth size to G1 exit (Figure 3D). During S/G2/M, the correlation between G1 exit volume and growth during S/G2/M is intermediate between a sizer and adder with m = 0.61 ± 0.18 (Figure 3E). Over the entire cell cycle, the slope between birth volume and division volume is m = 0.06 ± 0.23, which corresponds to an almost perfect sizer (Figure 3F). The same data can be replotted to view the inverse correlation between cell size and the amount grown in a specific cell cycle phase or over the entire cell cycle (Figure 3G-I, Figure S3).
Cell size predicts timing of G1 exit
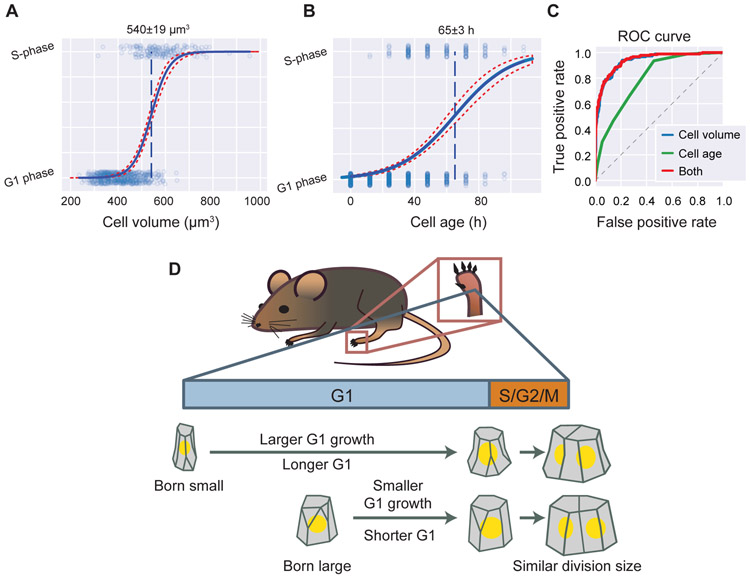
Since cell growth during G1 exhibits a near-sizer, we sought to quantify which factors most affect the rate of G1/S progression. We performed logistic regression using cell size, age, and growth rate as predictors of the timing of G1 exit. We found that both cell size (P < 10−10) and cell age (P < 10−5) were significant factors, while growth rate was not (P > 0.05). Logistic regression with cell volume yields a sharp separation between G1 and S phase cells (Figure 4A), while logistic regression with cell age yields a much shallower slope (Figure 4B). We quantified the accuracy of using cell volume, cell age, or both to predict G1 exit, by calculating the receiver operating characteristic (ROC) curve for all three sets of predictors (Figure 4C). We found that ROC curves obtained using cell volume or using both cell volume and cell age were nearly identical, with the area under the ROC curve being 0.93 for cell volume alone and 0.94 for cell volume and age. This indicates that while cell age is statistically significant, it is a small factor relative to cell volume in determining the timing of G1 exit.
Figure 4. Size-dependent G1/S transition model for in vivo cell size control.
A-B. The logistic regression predicting the exit from G1 into S phase using cell volume (A) or cell age (B). Dots are individual time-points (N = 1,024). Solid blue line is the logistic model, with 95% confidence intervals in dotted red. Dashed blue line is the midpoint. Midpoint intervals are 95% confidence intervals estimated by bootstrap.
C. The ROC curve from logistic regression models predicting G1 exit using cell volume (blue), cell age (green), or both (red). The dotted line is the null model of a random predictor.
D. Model of skin cell size control in vivo. For epidermal stem cells, variation in birth volume are compensated by the size-dependent transition from G1 to S-phase, such that cells born small will spend longer in G1 and grow more in G1. While the control mechanism is insufficiently resolved for S/G2/M, the overall size control is a sizer, where cells divide at a size uncorrelated with their birth size.
See also Figure S4.
Discussion
Keeping cell size homeostasis during proliferation is crucial for maintaining optimal cell physiology, and may also be important for proper tissue function [26-32]. One way that cell size can be controlled is by coupling cell cycle progression to cell growth through a sizer, in which growth over a single cycle compensates for variation in birth size. This way, all cells reach a similar size at division. However, the size control exhibited by a variety of animal cell lines grown in vitro approximates an adder, in which cells grow a constant amount over a single cycle independent of birth size. Here, in contrast to expectations from in vitro studies, we show that mouse epidermal stem cells exhibit a sizer in vivo, and variation in cell birth size is compensated for within one cell cycle. Most of this compensation takes place in the G1 phase, but there may also be some compensation during the remainder of the cell cycle (Figure 4D). To our knowledge, this work is the first study examining how cell size control is operating in a mammalian tissue in vivo. Furthermore, our work highlights that cell birth size is an important factor in determining the timing of stem cell division.
Our analysis of the growth and division of adult epithelial stem cells in vivo has implications for in vitro studies of mammalian cell size control. Of the quantitative mammalian cell size control studies to-date, the majority have reported near-adder phenotypes (including HeLa, RPE, HT29, Raji, MDCK, and two primary fibroblasts) [9,10], while a minority showed near-sizers (HMECs) [12,33]. The observation of a sizer in vivo suggests that more attention should be paid to studying in vitro models that exhibit G1 sizer control. However, an analysis similar to that presented here has yet to be done for any other mammalian cell type in vivo, which limits the strength of this recommendation.
Interestingly, there is a dramatic difference between the duration of cell cycle phases in vitro and in vivo that may relate to the different size control phenomena. While the S/G2/M phase of the cell cycle is similar in duration in vitro and in vivo at ~12h, the G1 phase extends 5-fold from ~10h in vitro to ~50h in vivo. G1 also accounts for ~50% of total cell growth in vivo (Figure S4), while only accounting for ~25% of total cell growth in vitro in HeLa and HT29 cells [10]. Thus, G1 growth contributes more to overall growth and size control in vivo than in vitro, at least for these cell lines. The faster growth rate in vitro may relate to the predominance of adders. In fact, in E. coli, slower and faster growth rates correspond to sizers and adders, respectively [7,34], and it is possible something similar occurs in mammalian cells.
While our work definitively identifies a G1 sizer in vivo, it gives us limited information about the underlying regulatory network. Yeast cells employ the same G1 regulatory network to produce sizers for small-born cells and adders for large-born cells [2,8,35]. This is similarly found in rat leukemia cells [11]. We expect that either of the currently proposed molecular G1 size control mechanisms, Rb dilution or p38 activation [33,36], could theoretically yield sizers or adders depending on parameter values. In addition, an important experimental limitation is the 12h sampling frequency. This low sampling frequency precludes a more careful analysis of growth during S/G2/M phases of the cell cycle. To quantify the effect of poor temporal sampling, we down-sampled data of cell growth and cell cycle progression in human mammary epithelial cells (HMECs) growing in vitro [12] (Methods S1, Figure v A-B). While we saw that size control correlations in G1 were largely unaffected by lowering the sampling rate, the same was not true for the shorter S/G2/M phases (Methods S1, Figure v C-F). We observed that a spurious negative correlation between size at G1/S and S/G2/M duration can emerge as a result of low temporal sampling, suggesting uncertainty in our estimation of S/G2/M dynamics (Methods S1, Figure v G). Additionally, the low sampling frequency prevents accurate estimation of the growth function, i.e., how rapidly cells grow as a function of their size or cell cycle position. At this point, we can conclude that cell growth is not linear, meaning that cells are not increasing their size at a constant rate through the cell cycle. Larger cells grow faster than smaller cells, and this relationship between size and growth rate is similar in G1 and S/G2/M. However, higher temporal resolution is required to more precisely determine the cell growth function and its relationship to exponential, bilinear, or another form of nonlinear growth, which may have implications for cell size control [9,21,22,37].
We have here analyzed cell growth and division at the level of single cells and neglected potential contributions related to tissue geography. In multicellular tissues, cells experience complex chemical or mechanical feedback from neighboring cells and are regulated by pathways controlling organ size. Certainly, regardless of these multicellular considerations, our observation that cell growth in G1 is clearly coupled to the timing of the G1/S transition is inconsistent with a previous model in which cell growth proceeds linearly while division timing occurs at a constant frequency [20].
An important open question is how cell autonomous size control is integrated in the context of a multicellular organ. One attractive model is that total cellular growth within a tissue is determined by organ size control mechanisms, and cell size control mechanisms operate at the cell level to quantize that total growth into individual cells. Specifically, for the epidermis, local changes in cell density lead to stem cell growth [13]. This growth can then be coordinated with cell division by our observed size-dependent G1/S transition. This model is consistent with the corpus of studies showing that mutations affecting G1/S control have generally little effect on organ size, but impact cell size and number within the organ [38-40]. We anticipate it will be exciting to see if and how specific cell-autonomous size control mechanisms interact with organ size control pathways.
STAR Methods
Lead Contact and Materials Availability
Further information and request for the raw dataset should be directed to and will be fulfilled by the Lead Contact, Jan Skotheim (skotheim@stanford.edu). This study did not generate new unique reagents.
Experimental Model and Subject Details
Mice and in vivo imaging
All videos used in this study were previously published [13]. Briefly, cells from non-hairy plantar skin were imaged with two-photon microscopy every 12h for 4 to 7 days. Regions were revisited in independent imaging sessions using micro-tattoo fiducial marks for orientation and intrinsic idiosyncratic features of each skin region for alignment. In between imaging time-points, mice were returned to normal activity. Three datasets used in this study were of mice expressing CMV-mKO2-hCdt1(30/120) [41], K14-actin-GFP [42], and K14-H2B-Cerulean [13], where K14 is the human K14 promoter expressed only within the keratinocyte lineage. Two regions were used from Mouse 1, which was imaged for 7 days (168 h). A third region from Mouse 2 was imaged for 4 days (96 h). Data acquired from both animals were similar (Figure S2B-C), although the shorter video duration in Mouse 2 limited our sampling of longer cell cycles in Region 3.
Method Details
Cell volume reconstruction and cell cycle annotation
All cell volumes were manually segmented in FIJI using PolygonRois [43]. Automatically tracked lineages from Mesa, Kawaguchi, & Cockburn, et al. (2018) were filtered for cells that are born and divide within the duration of the video [13]. A custom FIJI applet was built to display automatically tracked cell centroids on the video to facilitate manual segmentation. Mistakes made by the automatic tracking were fixed manually. Cell volume was calculated by summing the cell area throughout all z-slices and multiplying by the z-step size. Custom JPython scripts were used to automate ROI measurement and export in FIJI. Repeated volume reconstructions were made to quantify intra-user variation in segmentation. Repeat growth curves were generated for 8 cells (N = 48 time-points) chosen at random and the agreement between the original and the repeat measurements were quantified (Methods S1, Figure i I-J). Daughter cell volumes were quantified in the same way as mother cell volumes. Cells whose daughter volumes could not be estimated were excluded from the analysis involving interpolated division volumes (N = 30). For comparison of cell volume to cross-sectional cell area, the z-position of the cross-section was determined by [13] to be the z-position corresponding to the largest projected nuclear area.
Cell cycle transitions were annotated manually based on the fluorescent FUCCI G1 reporter mKo2-hCdt1(30/120). Because the illumination was not constant throughout the video, the total intensity of the G1 reporter was not comparable across time-points. Therefore, the G1 exit frame was annotated as the frame at which the G1 reporter within the cell nucleus became indistinguishable from the local background (Figure S1). The G1 reporter also had variable expression in the basal layer cells so that a subset of cells never had visible expression throughout their cell cycle. These cells were excluded from the analysis. Mitotic cells were manually identified by their rounded cell shapes and chromatin condensation (Figure S2K). The fidelity of the segmentation and tracking was assessed by examining the 3D segmentation overlaid on the original video images (Video S1-2).
Volume growth analysis
Cell volume growth curves and cell cycle annotations were collated in Python using pandas [44]. We fitted cell volume growth curves to smoothing cubic splines using numpy and scipy [45,46]. A high smoothing factor (105) was used to ensure relatively stiff spline fits (Methods S1, Figure i A-F). We used the smoothed data for analysis because we expect volume growth to be both smooth and generally to be monotonically increasing through the cell cycle. Error in individual time-points was estimated as the magnitude of residuals (absolute difference between volume time-points and fitted curves) (Methods S1, Figure i H). Growth curves with fewer than 4 points were kept as unsmoothed. Volume growth curves were also fitted to linear and exponential models and fits were compared using their residuals. Growth rates were estimated from the smoothed growth curves using backwards difference (window size = 1). Confidence intervals for CVs and P-values for differences in CVs were calculated from bootstrap analyses.
Nuclear volume reconstruction
To quantify nuclear volume, the H2B-Cerulean channel was automatically segmented by thresholding pixels that were above the 50th percentile in intensity within a 31-pixel local neighborhood using the scikit-image module in Python (Methods S1, Figure iii) [47]. Small holes and small objects in the thresholded nuclear masks removed by binary erosion and dilation. The nuclear volume was calculated as the number of above-threshold pixels within the manual cell outline segmentation, multiplied by the pixel:μm conversion ratio and z-step size. Nuclear volumes calculated for cells in mitosis were discarded because of nuclear envelope breakdown.
Analysis of framerate limitations
We analyzed in vitro human mammary epithelial cell (HMEC) growth data from [12], who acquired time-lapse phase and fluorescence images of asynchronously growing and dividing cells expressing fluorescent reporters of cell size and cell cycle phase marking the G1/S transition. We examined the time-series from these data, which were taken at 10 minute time intervals. HMECs in these conditions had a ~20 hour cell division cycle and exhibited substantial size control at the G1/S transition, but not during S/G2/M phases. The data were down-sampled to quantify how lowering temporal resolution can affect cell size control correlations. The data decimation factor was determined by down-grading the time resolution in [12] until it had the same average number of frames per cell cycle as we have analyzed here for epidermal stem cells in vivo (Figure 2C; Methods s1, Figure v A-B). For each cell, we down-sampled its time-series starting with a randomly selected time-point and the process was repeated 500 times. The resulting randomized distributions of correlations were compared to the correlations in the original data (Methods S1, Figure v C-E). While the G1 size control correlations are similar between original and down-sampled data, growth during S/G2 is systematically underestimated and a larger error in the correlation between G1 exit size and growth during S/G2 is introduced (Methods S1, Figure v F). To further examine the effect of low temporal resolution on S/G2 dynamics, we used successively larger data decimation factors and observed that a spurious negative correlation between size at G1/S and S/G2 duration could result from poor temporal sampling (Methods S1, Figure v G).
Quantification and Statistical Analysis
All statistical analyses were done in Python using numpy/scipy and statsmodels [48]. Multivariate regression analysis was done using OLS and Logit from statsmodels. All correlation coefficients (R) reported in the text are Pearson's correlation. P-values reported for Pearson's correlation are tested against the null-hypothesis of R = 0. All intervals are given in the text as mean ± SD, unless otherwise noted.
Data and Code Availability
All code used in the study is available at https://github.com/xies/mouse_skin_size_control/.
Supplementary Material
Methods S1. Details of cell and nuclear volume quantification and analysis of low temporal resolution on cell size control correlations. Related to STAR Methods.
Video S1. Tracking epidermal stem cells through 7 days of growth and division. Related to Figure 1.
A single z-slice through time from the time-lapsed in vivo 4D imaging of mouse epidermal stem cells. Actin-GFP (cell cortex) is shown in gray, H2B-Cerulean (nucleus) is shown in blue. Manually segmented cell outlines are shown in yellow. The cell's identifying index is overlaid on the cell, demonstrating the fidelity of cell tracking.
Video S2. 3D reconstruction of epidermal stem cells. Related to Figure 1.
A single time-frame from the time-lapsed in vivo 4D imaging of mouse epidermal stem cells. Z-slices are shown from apical (where differentiated cells reside) to basal slices (where stem cells reside). Actin-GFP (cell cortex) is shown in gray, H2B-Cerulean (nucleus) is shown in blue. Manually segmented cell outlines are shown in yellow. The cell's identifying index is overlaid on the cell.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Bacterial and Virus Strains | ||
| Biological Samples | ||
| Chemicals, Peptides, and Recombinant Proteins | ||
| Critical Commercial Assays | ||
| Deposited Data | ||
| Experimental Models: Cell Lines | ||
| Experimental Models: Organisms/Strains | ||
| Mouse: K14-actinGFP | [42] | N/A |
| Mouse: K14-H2BCerulean | [13] | N/A |
| Mouse: mKO2-hCdt1(30/120) | [41] | N/A |
| Oligonucleotides | ||
| Recombinant DNA | ||
| Software and Algorithms | ||
| FIJI | [43] | https://fiji.sc/ |
| pandas | [44] | https://pandas.pydata.org/ |
| numpy | [45] | https://numpy.org/ |
| scipy | [46] | https://www.scipy.org/ |
| scikit-image | [47] | https://scikit-image.org/ |
| statsmodels | [48] | https://www.statsmodels.org/stable/index.html |
| Python and FIJI scripts | This study | https://github.com/xies/mouse_skin_size_control |
| Other | ||
Highlights.
Quantification of mammalian single cell growth during tissue turnover over a week
Epidermal stem cell growth is faster than linear in vivo
Epidermal stem cells couple growth and cell cycle progression using a G1 sizer
Acknowledgements
We thank members of the Skotheim lab, Shuyuan Zhang, Evgeny Zatulovskiy, Daniel Berensen, Kurt Schmoller, and Clotilde Cadart, for discussion and comments on the manuscript. We thank Valentina Greco and Katie Cockburn for discussions, comments, and facilitating our understanding of the data from Mesa, Kawaguchi, Cockburn, et al. (2018). This work was supported by the NIH through R01 GM115479 (JMS) and F32 GM129878 (SX).
Footnotes
Declaration of interests
The authors declare no competing interests.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.di Talia S, Skotheim JM, Bean JM, Siggia ED, and Cross FR (2007). The effects of molecular noise and size control on variability in the budding yeast cell cycle. Nature 448, 947–951. [DOI] [PubMed] [Google Scholar]
- 2.Sveiczer A, Novak B, and Mitchison JM (1996). The size control of fission yeast revisited. J Cell Sci 109, 2947–2957. [DOI] [PubMed] [Google Scholar]
- 3.Schmoller KM, Turner JJ, Kõivomägi M, and Skotheim JM (2015). Dilution of the cell cycle inhibitor Whi5 controls budding-yeast cell size. Nature 526, 268–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Taheri-Araghi S, Bradde S, Sauls JT, Hill NS, Levin PA, Paulsson J, Vergassola M, and Jun S (2015) Cell-Size Control and Homeostasis in Bacteria. Current Biology 25, 385–391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Campos M, Surovtsev IV, Kato S, Paintdakhi A, Beltran B, Ebmeier SE, and Jacobs-Wagner C (2014). A constant size extension drives bacterial cell size homeostasis. Cell 159, 1433–1446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Soifer I, Robert L, and Amir A (2016). Single-Cell Analysis of Growth in Budding Yeast and Bacteria Reveals a Common Size Regulation Strategy. Curr Biol 26, 356–361. [DOI] [PubMed] [Google Scholar]
- 7.Wallden M, Fange D, Lundius EG, Baltekin Ö, and Elf J (2016). The Synchronization of Replication and Division Cycles in Individual E. coli Cells. Cell 166, 729–739. [DOI] [PubMed] [Google Scholar]
- 8.Delarue M, Weissman D, and Hallatschek O (2017). A simple molecular mechanism explains multiple patterns of cell-size regulation. pLoS ONE 12, e0182633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ginzberg MB, Chang N, D'Souza H, Patel N, Kafri R, and Kirschner MW (2018). Cell size sensing in animal cells coordinates anabolic growth rates and cell cycle progression to maintain cell size uniformity. eLife 7, 7729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cadart C, Monnier S, Grilli J, Sáez PJ, Srivastava N, Attia R, Terriac E, Baum B, Cosentino-Lagomarsino M, and Piel M (2018). Size control in mammalian cells involves modulation of both growth rate and cell cycle duration. Nat Commun 9, 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Varsano G, Wang Y, and Wu M (2017). Probing Mammalian Cell Size Homeostasis by Channel-Assisted Cell Reshaping. Cell Rep 20, 397–410. [DOI] [PubMed] [Google Scholar]
- 12.Berenson DF, Zatulovskiy E, Xie S, and Skotheim JM (2019). Constitutive expression of a fluorescent protein reports the size of live human cells. Mol Biol Cell 30, 2985–2995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mesa KR, Kawaguchi K, Cockburn K, Gonzalez D, Boucher J, Xin T, Klein AM, and Greco V (2018). Homeostatic Epidermal Stem Cell Self-Renewal Is Driven by Local Differentiation. Cell Stem Cell 23, 677–686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Perez-Losada J, and Balmain A (2003). Stem-cell hierarchy in skin cancer. Nat Rev Cancer 3, 434–43. [DOI] [PubMed] [Google Scholar]
- 15.Blanpain C, and Fuchs E (2009). Epidermal homeostasis: a balancing act of stem cells in the skin. Nat Rev Mol Cell Biol 10, 207–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gelbart MA, He B, Martin AC, Thiberge SY, Wieschaus EF, and Kaschube M (2012). Volume conservation principle involved in cell lengthening and nucleus movement during tissue morphogenesis. Proc Natl Acad Sci 109, 19298–19303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Willis L, Refahi Y, Wightman R, Landrein B, Teles J, Huang KC, Meryerowitz EM, and Jönsson H (2016). Cell size and growth regulation in the Arabidopsis thaliana apical stem cell niche. Proc Natl Acad Sci 113: 8238–8246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Piedrafita G, Kostiou V, Wabik A, Colom B, Fernandez-Antoran D, Herms A, Kasumi M, Hall BA, and Jones PH (2019). The single-progenitor model as the unifying paradigm of squamous epithelial maintenance. bioRxiv. doi: 10.1101/716639. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cantwell H and Nurse P (2019). Unravelling nuclear size control. Curr Genet. 65, 1281–1285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Conlon I, and Raff M (2003). Differences in the way a mammalian cell and yeast cells coordinate cell growth and cell-cycle progression. J Biol 2, 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Son S, Tzur A, Weng Y, Jorgensen P, Kim J, Kirschner MW, and Manalis SR (2012). Direct observation of mammalian cell growth and size regulation. Nat Methods 9, 910–912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kafri R, Levy J, Ginzberg MB, Oh S, Lahav G, and Kirschner MW (2013). Dynamics extracted from fixed cells reveal feedback linking cell growth to cell cycle. Nature 494, 480–483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Son S, Kang JH, Oh S, Kirschner MW, Mitchison TJ, and Manalis SR (2015). Resonant microchannel volume and mass measurements show that suspended cells swell during mitosis. J Cell Biol 211, 757–763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Zlotek-Zlotkiewicz E, Monnier S, Cappello G, Le Berre M, and Piel M (2015). Optical volume and mass measurements show that mammalian cells swell during mitosis. J Cell Biol 211, 765–774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lancaster OM, Le Berre M, Dimitracopoulos A, Bonazzi D, Zlotek-Zlotkiewicz E, Picone R, Duke T, Piel M, and Baum B (2013) Mitotic rounding alters cell geometry to ensure efficient bipolar spindle formation. Dev Cell 25, 270–283. [DOI] [PubMed] [Google Scholar]
- 26.Chan Y-HM, and Marshall WF (2010). Scaling properties of cell and organelle size. Organogenesis 6, 88–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Miettinen TP, and Björklund M (2016). Cellular Allometry of Mitochondrial Functionality Establishes the Optimal Cell Size. Dev Cell 39, 370–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Neurohr GE, Terry RL, Lengefeld J, Bonney M, Brittingham GP, Moretto F, Miettinen TP, Vaites LP, Soares LM, Paulo JA, et al. (2019). Excessive Cell Growth Causes Cytoplasm Dilution And Contributes to Senescence. Cell 176, 1083–1097. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Miettinen TP, Pessa HKJ, Caldez MJ, Fuhrer T, Diril MK, Sauer U, Kaldis P, and Björklund M (2014). Identification of transcriptional and metabolic programs related to mammalian cell size. Curr Biol 24, 598–608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Turner JJ, Ewald JC, and Skotheim JM (2012). Cell Size Control in Yeast. Curr Biol 22, 350–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Schmoller KM, and Skotheim JM (2015). The Biosynthetic Basis of Cell Size Control. Trends Cell Biol. 25, 793–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ramanathan SP, Krajnc M, and Gibson MC (2019). Cell-Size Pleomorphism Drives Aberrant Clone Dispersal in Proliferating Epithelia. Dev Cell 51, 49–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zatulovskiy Ee, Berenson DF, Topacio BR, and Skotheim JM (2018) Cell growth dilutes the cell cycle inhibitor Rb to trigger cell division. bioRxiv. doi: 10.1101/470013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Grilli J, Cadart C, Micali G, Osella M, and Cosentino-Lagomarsino M (2010). The Empirical Fluctuation Pattern of E. coli Division Control. Front Microbiol. 9, 1541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Chandler-Brown D, Schmoller KM, Winetraub Y, and Skotheim JM (2017). The Adder Phenomenon Emerges from Independent Control of Pre- and Post-Start Phases of the Budding Yeast Cell Cycle. Curr Biol 27, 2774–2783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Liu S, Ginzberg MB, Patel N, Hild M, Leung B, Li Z, Chen Y-C, Chang N, Wang Y, Tan C, et al. (2018). Size uniformity of animal cells is actively maintained by a p38 MAPK-dependent regulation of G1-length. eLife 7, 47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tzur A, Kafri R, LeBleu VS, Lahav G, and Kirschner MW (2009). Cell growth and size homeostasis in proliferating animal cells. Science 325, 167–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Fero ML, Rivkin M, Tasch M, Porter P, Carow CE, Firpo E, Polyak K, Tsai L-H, Broudy V, Perlmutter RM, et al. (1996). A Syndrome of Multiorgan Hyperplasia with Features of Gigantism, Tumorigenesis, and Female Sterility in p27Kip1-Deficient Mice. Cell 85, 733–744. [DOI] [PubMed] [Google Scholar]
- 39.Ehmer U, Zmoos A-F, Auerbach RK, Vaka D, Butte AJ, Kay MA, and Sage J (2014). Organ size control is dominant over Rb family inactivation to restrict proliferation in vivo. Cell Rep 8, 371–381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Neufeld TP, de la Cruz AFA, Johnston LA, and Edgar BA (1998). Coordination of Growth and Cell Division in the Drosophila Wing. Cell 93, 1183–93. [DOI] [PubMed] [Google Scholar]
- 41.Sakaue-Sawano A, Kurokawa H, Morimura T, Hanyu A, Hama H, Osawa H, Kashiwagi S, Fukami K, Miyata T, Miyoshi H, et al. (2008). Visualizing Spatiotemporal Dynamics of Multicellular Cell-Cycle Progression. Cell 132, 487–98. [DOI] [PubMed] [Google Scholar]
- 42.Vaezi A, Bauer C, Vasioukhin V, and Fuchs E (2002). Actin Cable Dynamics and Rho/Rock Orchestrate a Polarized Cytoskeletal Architecture in the Early Steps of Assembling a Stratified Epithelium. Dev. Cell 3, 367–381. [DOI] [PubMed] [Google Scholar]
- 43.Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, et al. (2012). Fiji: an open-source platform for biological-image analysis. Nat Methods 9, 676–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.McKinney W (2010). Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, van der Walt S and Millman J, ed. (Austin, TX: SciPy Organizers; ), pp. 51–56. [Google Scholar]
- 45.van der Walt S, Colbert SC, and Varoquaux G (2011). The NumPy Array: A Structure for Efficient Numerical Computation. Comput Sci Eng 13, 22–30. [Google Scholar]
- 46.Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckersser W, Bright J, et al. SciPy 1.0--Fundamental Algorithms for Scientific Computing in Python 2019. arXiv:1907.10121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.van der Walt S, Schönberger JL, Nunez-Iglesias J, Boulogne F, Warner JD, Yager N, Gouillart E, Yu T, the scikit-image contributors. (2014). scikit-image: image processing in Python. PeerJ 2, e453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Seabold S, and Perktold J (2010). Statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, van der Walt S and Millman J, ed. (Austin, TX: SciPy Organizers; ), pp 57–61. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Methods S1. Details of cell and nuclear volume quantification and analysis of low temporal resolution on cell size control correlations. Related to STAR Methods.
Video S1. Tracking epidermal stem cells through 7 days of growth and division. Related to Figure 1.
A single z-slice through time from the time-lapsed in vivo 4D imaging of mouse epidermal stem cells. Actin-GFP (cell cortex) is shown in gray, H2B-Cerulean (nucleus) is shown in blue. Manually segmented cell outlines are shown in yellow. The cell's identifying index is overlaid on the cell, demonstrating the fidelity of cell tracking.
Video S2. 3D reconstruction of epidermal stem cells. Related to Figure 1.
A single time-frame from the time-lapsed in vivo 4D imaging of mouse epidermal stem cells. Z-slices are shown from apical (where differentiated cells reside) to basal slices (where stem cells reside). Actin-GFP (cell cortex) is shown in gray, H2B-Cerulean (nucleus) is shown in blue. Manually segmented cell outlines are shown in yellow. The cell's identifying index is overlaid on the cell.
Data Availability Statement
All code used in the study is available at https://github.com/xies/mouse_skin_size_control/.