Abstract
The tragic events of 9/11 and the concerns about the potential for a terrorist or hostile state attack with weapons of mass destruction have led to an increased emphasis on risk analysis for homeland security. Uncertain hazards (natural and engineering) have been successfully analyzed using probabilistic risk analysis (PRA). Unlike uncertain hazards, terrorists and hostile states are intelligent adversaries who can observe our vulnerabilities and dynamically adapt their plans and actions to achieve their objectives. This article compares uncertain hazard risk analysis with intelligent adversary risk analysis, describes the intelligent adversary risk analysis challenges, and presents a probabilistic defender–attacker–defender model to evaluate the baseline risk and the potential risk reduction provided by defender investments. The model includes defender decisions prior to an attack; attacker decisions during the attack; defender actions after an attack; and the uncertainties of attack implementation, detection, and consequences. The risk management model is demonstrated with an illustrative bioterrorism problem with notional data.
Keywords: Bioterrorism, defender–attacker–defender, intelligent adversary risk analysis, risk management, terrorism risk analysis
1. INTELLIGENT ADVERSARY RISK ANALYSIS IS DIFFERENT THAN HAZARD RISK ANALYSIS
Risk analysis has helped public and private organizations assess, communicate, and manage the risk posed by uncertain hazards (i.e., natural hazards and engineered systems).( 1 , 2 , 3 ) Public and private decisionmakers have been informed on the risk of natural events and engineered system failures by credible and timely risk analysis. In probabilistic risk analysis (PRA), the uncertain hazards have been modeled using probability distributions for threats, vulnerabilities, and consequences. The data have been obtained from statistical analysis of past events, tests, models, simulations, and assessments from subject matter experts. Risk analysts have used PRA techniques, including event trees, fault trees, attack trees, systems dynamics, and Markov models, to assess, communicate, and manage the risk of uncertain hazards.
The nuclear power industry, perhaps more than any other risk application area, has integrated the use of PRA for risk assessment, risk communication, and risk management. The original PRA process was developed in the commercial nuclear power industry in the 1970s.( 4 ) The U.S. Nuclear Regulatory Commission and the nuclear power industry jointly developed procedures and handbooks for PRA models.( 5 , 6 ) Today, the nuclear power industry is moving toward risk‐based regulations, specifically using PRA to analyze and demonstrate lower cost regulations without compromising safety.( 7 , 8 ) Research in the nuclear industry has also supported advances in human reliability analysis, external events analysis, and common cause failure analysis.( 9 , 10 , 11 )
More recently, leaders of public and private organizations have requested risk analyses for problems that involve the threats posed by intelligent adversaries. For example, in 2004, the president directed the Department of Homeland Security (DHS) to assess the risk of bioterrorism.( 12 ) Homeland Security Presidential Directive 10 (HSPD‐10): Biodefense for the 21st Century, states that “[b]iological weapons in the possession of hostile states or terrorists pose unique and grave threats to the safety and security of the United States and our allies” and charged the DHS with issuing biennial assessments of biological threats to “guide prioritization of our on‐going investments in biodefense‐related research, development, planning, and preparedness.” A subsequent Homeland Security Presidential Directive 18 (HSPD‐18): Medical Countermeasures Against Weapons of Mass Destruction directed an integrated risk assessment of all chemical, biological, radiological, and nuclear (CBRN) threats.( 13 ) The critical risk analysis question addressed in this article is: Are the standard PRA techniques for uncertain hazards adequate and appropriate for intelligent adversaries? As concluded by the NRC (2008) study on bioterrorism risk analysis, we believe that new techniques are required to provide credible insights for intelligent adversary risk analysis. We will show that treating adversary decisions as uncertain hazards is inappropriate because it can provide a different risk ranking and may underestimate the risk.
In the rest of this section, we describe the difference between natural hazards and intelligent adversaries and demonstrate, with a simple example, that standard PRA applied to attacker's intent may underestimate the risk of an intelligent adversary attack. In the second section, we describe a canonical model for resource allocation decision making for an intelligent adversary problem using an illustrative bioterrorism example with notional data. In the third section, we describe the illustrative analysis results obtained from the model and discuss the insights they provide for risk assessment, risk communication, and risk management. In the fourth section, we describe the benefits and limitations of the model. Finally, we discuss future work and our conclusions.
1.1. Intelligent Adversary Risk Analysis Requires New Approaches
We believe that risk analysis of uncertain hazards is fundamentally different than risk analysis of intelligent adversaries.( 14 , 15 ) Some of the key differences are summarized in Table I.( 16 ) A key difference is historical data. For many uncertain events, both natural and engineered, we have not only historical data of extreme failures or crises, but many times we can replicate events in a laboratory environment for further study (engineered systems) or analyze using complex simulations. Intelligent adversary attacks have a long historical background, but the aims, events, and effects we have recorded may not prove a valid estimate of future threat because of changes in adversary intent and capability.
Table I.
Uncertain Hazards Versus Intelligent Adversaries
| Uncertain Hazards | Intelligent Adversaries | |
|---|---|---|
| Historical Data | Some historical data: | Very limited historical data: |
| A record exists of extreme events that have already occurred. | Events of September 11, 2001, were the first foreign terrorist attacks worldwide with such a huge concentration of victims and insured damages. | |
| Risk of Occurrence | Risk reasonably well defined: | Considerable ambiguity of risk: |
| Well‐developed models exist for estimating risks based on historical data and experts’ estimates. | Adversaries can purposefully adapt their strategy (target, weapons, time) depending on their information on vulnerabilities. Attribution may be difficult (e.g. anthrax attacks). | |
| Geographic Risk | Specific areas at risk: | All areas at risk: |
| Some geographical areas are well known for being at risk (e.g., California for earthquakes or Florida for hurricanes). | Some cities may be considered riskier than others (e.g., New York City, Washington), but terrorists may attack anywhere, any time. | |
| Information | Information sharing: | Asymmetry of information: |
| New scientific knowledge on natural hazards can be shared with all the stakeholders. | Governments sometimes keep secret new information on terrorism for national security reasons. | |
| Event Type | Natural event: | Intelligent adversary events: |
| To date, no one can influence the occurrence of an extreme natural event (e.g., an earthquake). | Governments may be able to influence terrorism (e.g., foreign policy; international cooperation; national and homeland security measures). | |
| Preparedness and Prevention | Government and insureds can invest in well‐known mitigation measures. | Attack methodologies and weapon types are numerous. Local agencies have limited resources to protect potentially numerous targets. Federal agencies may be in a better position to develop better offensive, defensive and response strategies. |
Both uncertain hazard risks of occurrence and geographical risk can be narrowed down and identified concretely. Intelligent adversary targets vary by the goals of the adversary and can be vastly dissimilar between adversary attacks.
Information sharing between the two events differs dramatically. After hurricanes or earthquakes, engineers typically review the incident, publish results, and improve their simulations. Sometimes after intelligent adversary attacks, or near misses, the situation and conduct of the attack may involve critical state vulnerabilities and protected intelligence means. In these cases, intelligence agencies may be reluctant to share complete information even with other government agencies.
The ability to influence the event is also different. Though we can prepare, we typically have no way of influencing the natural event to occur or not occur. On the other hand, governments may be able to affect the impact of terrorism attacks by a variety of offensive, defensive, and recovery measures. In addition, adversary attacks can take on so many forms that one cannot realistically defend/respond/recover/etc. against all types of attacks.
Although there have been efforts to use event tree technologies in intelligent adversary risk analysis (e.g., BTRA), many believe that this approach is not credible.( 19 ) The threat from intelligent adversaries comes from a combination of both intent and capability. We believe that PRA still has an important role in intelligent adversary risk analysis for assessment of the capabilities of adversaries, the vulnerabilities of potential targets, and potential consequences of attacks. However, intent is not a factor in natural hazard risk analysis. In intelligent adversary risk analysis, we must consider the intent of the adversary. The adversary will make future decisions based on our preparations, its objectives, and information about its ability to achieve its objectives that is dynamically revealed in a scenario. Bier et al. provides an example of addressing an adversary using a defender–attacker game theoretic model.( 20 ) NRC provides three examples of intelligent adversary models.( 16 ) We believe it will be more useful to assess an attacker's objectives (although this is not a trivial task) than assigning probabilities to their decisions prior to the dynamic revelation of scenario information.
We believe that modeling adversary objectives will provide greater insight into the possible actions of opponents rather than exhaustively enumerating probabilities on all the possible actions they could take. Furthermore, we believe the probabilities of adversary decisions (intent) should be an output of, not an input to, risk analysis models.( 16 ) This is a principal part of game theory as shown in Aghassi et al. and Jain et al.( 21 , 22 )
1.2. An Illustrative Bioterrorism Example
To make our argument and our proposed alternative more explicit, we use a bioterrorism illustrative example. In response to the 2004 HSPD, in October 2006, the DHS released a report called the Bioterrorism Risk Assessment (BTRA).( 19 ) The risk assessment model contained a 17‐step event tree (18 steps with consequences) that could lead to the deliberate exposure of civilian populations for each of the 27 most dangerous pathogens that the Center for Disease Control tracks (http://emergency.cdc.gov/bioterrorism) plus one engineered pathogen. The model was extremely detailed and contained a number of separate models that fed into the main BTRA model. The BTRA resulted in a normalized risk for each of the 28 pathogens, and rank‐ordered the pathogens from most risky to least risky.
The National Research Council (NRC) conducted a review of the BTRA model and provided 11 specific recommendations for improvement to the model.( 16 ) In our example, we will use four of the recommendations: model the decisions of intelligent adversaries, include risk management, simplify the model by not assigning probabilities to the branches of uncertain events, and do not normalize the risk. The intelligent adversary technique we developed builds on the deterministic defender–attacker–defender model and is solved using decision trees.( 16 ) Because the model has been simplified to reflect the available data, the model can be developed in a commercial off‐the‐shelf (COTS) software package, such as the one we used for modeling, DPL (http://www.syncopation.org). Other decision analysis software may work as well. 4 ( 23 )
1.3. Event Trees Underestimate Intelligent Adversary Risk
Event trees have been useful for modeling uncertain hazards.( 24 ) However, there is a key difference in the modeling of intelligent adversary decisions that event trees do not capture. As Norman C. Rasmussen, the director of the 1975 reactor safety study that validated PRA for use in nuclear reactor safety, states in a later article, while the basic assumption of randomness holds true for nuclear safety, it is not valid for human action.( 25 ) The attacker makes decisions to achieve his or her objectives. The defender makes resource allocation decisions before and after an attack to try to mitigate vulnerabilities and consequences of the attacker's actions. This dynamic sequence of decisions made by first the defender, then an attacker, then again by the defender should not be modeled solely by assessing probabilities of the attacker's decisions. For example, when the attacker looks at the defender's preparations for their possible bioterror attack, it will not assign probabilities to its decisions; it chooses the agent and the target based on perceived ability to acquire the agent and successfully attack the target that will give it the effects it desires to achieve its objectives.( 15 )
Representing an attacker decision as a probability may underestimate the risk. Consider the simple bioterrorism event tree given in Fig. 1 with notional data. Using an event tree, for each agent (A and B) there is a probability that an adversary will attack, a probability of attack success, and an expected consequence for each outcome (at the terminal node of the tree). The probability of success involves many factors, including the probability of obtaining the agent and the probability of detection during attack preparations and execution. The consequences depend on many factors, including agent propagation, agent lethality, time to detection, and risk mitigation; in this example, the consequences range from 0 or no consequences to 100, the maximum consequences (on a normalized scale of consequences). Calculating expected values in Fig. 1, we would assess expected consequences of 32. We would be primarily concerned about agent B because it contributes 84% of the expected consequences (30 × 0.9 = 27 for B out of the total of 32). Looking at extreme events, we would note that the worst‐case consequence of 100 has a probability of 0.05.
Figure 1.

Event tree example.
However, adversaries do not assign probabilities to their decisions; they make decisions to achieve their objectives, which may be to maximize the consequences they can inflict.( 26 ) If we use a decision tree as in Fig. 2, we replace the initial probability node with a decision node because this is an adversary decision. We find that the intelligent adversary would select agent A, and the expected consequences are 50, which is a different result than with the event tree. Again, if we look at the extreme events, the worst‐case event (100 consequences) probabilities are 0.5 for the agent A decision and 0.6 for the agent B decision.
Figure 2.
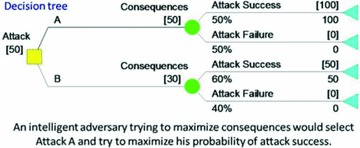
Decision tree example.
The expected consequences are greater and the primary agent of concern is now A. In this simple example, the event tree approach underestimates the expected risk and provides a different risk ranking. Furthermore, the event tree example underestimates the risk of the extreme events. However, while illustrating important differences, this simple decision tree model does not sufficiently model the fundamental structure of intelligent adversary risk.
2. CANONICAL INTELLIGENT ADVERSARY RISK MANAGEMENT MODEL FOR HOMELAND SECURITY
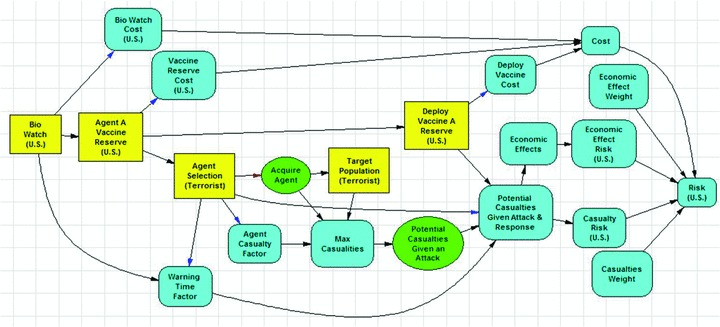
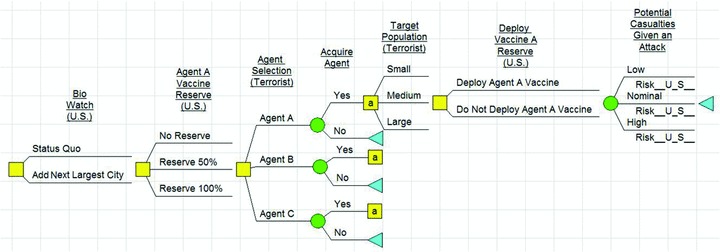
This model has a large number of applications for Homeland Security. For example, it would be easy to see the use of this canonical model applied to a dirty bomb example laid out in Rosoff and von Winterfeldt( 27 ) or any other intelligent adversary scenario. In this article, we show a use of a bioterrorism application. We believe that the canonical risk management model must have at least six components: the initial actions of the defender to acquire defensive capabilities, the attacker's uncertain acquisition of the implements of attack (e.g., agents A, B, and C), the attacker's target selection and method of attack(s) given implement of attack acquisition, the defender's risk mitigation actions given attack detection, the uncertain consequences, and the cost of the defender actions. From this model, one could also conduct baseline risk analysis by looking at the status quo. In general, the defender decisions can provide offensive, defensive, or information capabilities. We are not considering offensive decisions such as preemption before an attack; instead, we are considering decisions that will increase our defensive capability (e.g., buy vaccine reserves)( 28 ) or provide earlier or more complete information for warning of an attack (add a Bio Watch city).( 29 ) In our defender–attacker–defender decision analysis model, we have the two defender decisions (buy vaccine, add a Bio Watch city), the agent acquisition for the attacker is uncertain, the agent selection and target of attack is another decision, the consequences (fatalities and economic) are uncertain, the defender decision after attack to mitigate the maximum possible casualties, and the costs of defender decisions are known. The defender risk is defined as the probability of adverse consequences and is modeled using a multiobjective additive model similar to multiobjective value models.( 30 ) We have assumed that the defender minimizes the risk and the attacker maximizes the risk. 5 We implemented this model as a decision tree (Fig. 3) and an influence diagram (Fig. 4) using DPL. The mathematical formulation of our model and the notional data are provided in the Appendix
Figure 3.
Canonical bioterrorism decision tree.
Figure 4.
Canonical bioterrorism influence diagram.
2.1. Defender
The illustrative decision tree model (Figs. 3 and 4) begins with decisions that the defender (United States) makes to deter the adversary by reducing the vulnerabilities or be better prepared to mitigate a bioterrorism attack of agents A, B, or C. We modeled and named the agents to represent notional bioterror agents using the CDC's agent categories in Table II. For example, agent A represents a notional agent from category A. Table III provides a current listing of the agents by category. There are many decisions that we could model; however, for our simple illustrative example, we chose to model notional decisions about the Bio Watch program for agents A and B and the BioShield vaccine reserve for agent A.
Table II.
CDC BioTerror Agent Categories( 31 )
| Category | Definition |
|---|---|
| A | The U.S. public health system and primary healthcare providers must be prepared to address various biological agents, including pathogens that are rarely seen in the United States. High‐priority agents include organisms that pose a risk to national security because they: can be easily disseminated or transmitted from person to person; result in high mortality rates and have the potential for major public health impact; might cause public panic and social disruption; and require special action for public health preparedness. |
| B | Second highest priority agents include those that: are moderately easy to disseminate; result in moderate morbidity rates and low mortality rates; and require specific enhancements of CDC's diagnostic capacity and enhanced disease surveillance. |
| C | Third highest priority agents include emerging pathogens that could be engineered for mass dissemination in the future because of: availability; ease of production and dissemination; and potential for high morbidity and mortality rates and major health impact. |
Table III.
| National Institutes of Health National Institute of Allergy and Infectious Diseases (NIAID) Category A, B, and C Priority Pathogens | ||
|---|---|---|
| Category A | Category B | Category C |
| • Bacillus anthracis (anthrax) | • Burkholderia pseudomallei | Emerging infectious disease threats such as Nipah virus and additional hantaviruses. |
| • Clostridium botulinum toxin (botulism) | • Coxiella burnetii (Q Fever) | |
| • Brucella species (brucellosis) | ||
| • Yersinia pestis (plague) | • Burkholderia mallei (glanders) | NIAID priority areas: |
| • Variola major (smallpox) and other related pox viruses | • Chlamydia psittaci (Psittacosis) | • Tickborne hemorrhagic fever viruses |
| • Ricin toxin (from Ricinus communis) | • Crimean‐Congo hemorrhagic fever virus | |
| • Francisella tularensis (tularemia) | • Epsilon toxin of Clostridium perfringens | • Tickborne encephalitis viruses |
| • Staphylococcus enterotoxin B | • Yellow fever | |
| • Viral hemorrhagic fevers | • Typhus fever (Rickettsia prowazekii) | • Multi‐drug resistant TB |
| • Arenaviruses | • Food and waterborne pathogens | • Influenza |
| • LCM, Junin virus, Machupo virus, Guanarito virus | • Bacteria | • Other Rickettsias |
| • Diarrheagenic E. coli | • Rabies | |
| • Lassa Fever | • Pathogenic Vibrios | • Prions |
| • Bunyaviruses | • Shigella species | • Chikungunya virus |
| • Hantaviruses | • Salmonella | • Severe acute respiratory syndrome associated coronavirus (SARS‐CoV) |
| • Rift Valley Fever | • Listeria monocytogenes | |
| • Flaviruses | • Campylobacter jejuni | |
| • Dengue | • Yersinia enterocolitica) | |
| • Filoviruses | • Viruses (Caliciviruses, Hepatitis A) | |
| • Ebola | • Protozoa | |
| • Marburg | • Cryptosporidium parvum | |
| • Cyclospora cayatanensis | ||
| • Giardia lamblia | ||
| • Entamoeba histolytica | ||
| • Toxoplasma | ||
| • Microsporidia | ||
| • Additional viral encephalitides | ||
| • West Nile virus | ||
| • LaCrosse | ||
| • California encephalitis | ||
| • VEE | ||
| • EEE | ||
| • WEE | ||
| • Japanese Encephalitis virus | ||
| • Kyasanur Forest virus | ||
The list of potential bioterrorism agents was compiled from both CDC and NIH/NIAID websites.
Bio Watch is a program that installs and monitors a series of passive sensors within a major metropolitan city.( 29 ) The BioShield program is a plan to purchase and store vaccines for some of the more dangerous pathogens.( 28 ) The defender first decides whether or not to add another city to the Bio Watch program. If that city is attacked, this decision could affect the warning time, which influences the response and, ultimately, the potential consequences of an attack. Of course, the Bio Watch system does not detect every agent, so we modeled agent C to be the most effective agent that the Bio Watch system does not sense and provide additional warning. Adding a city will also incur a cost in dollars for the United States.
The second notional defender decision is the amount of vaccine to store for agent A. Agent A is the notional agent that we have modeled with the largest probability of acquisition and potential consequences. The defender can store a percentage of what experts think we would need in a large‐scale biological agent attack. The more vaccine the United States stores, the fewer consequences we will have if the adversaries use agent A and we have sufficient warning and capability to deploy the vaccine reserve. However, as we store more vaccine, the costs for purchasing and storage increase. For simplicity's sake, each of the defender decisions cost the same amount; therefore, at the first budget level of US$ 10 million, the defender can only choose to one decision.
2.2. Attacker
After the defender has made its investment decisions, which we assume are known to the attacker, the attacker makes two decisions: the type of agent and the target. We will assume that the attacker has already made the decision to attack the United States with a bioterror agent. In our model, there are three agents it can choose, although this can be increased to represent the other pathogens listed in Table III. As stated earlier, if we only looked at the attacker decision, agent A would appear to be the best choice. Agents B and C are the next two most attractive agents to the attacker, respectively. Again, agents A and B can be detected by Bio Watch whereas agent C cannot. The attacker has some probability of acquiring each agent. If the agent is not acquired, the attacker cannot attack with that agent. In addition, each agent has a lethality associated with it, represented by the agent casualty factor. Finally, each agent has a different probability of being detected over time. Generally, the longer it takes for the agent to be detected, the more consequences the United States will suffer.
The adversary also decides what size of population to target. Generally, the larger the population targeted, the more potential consequences could result. The attacker's decisions affect the maximum possible casualties from the scenario. However, regardless of the attacker's decisions, there is some probability of actually attaining a low, medium, or high percentage of the maximum possible casualties. This sets the stage for the next decision by the defender.
2.3. Defender
After receiving warning of an attack, the defender decides whether or not to deploy the agent A vaccine reserve. This decision depends upon how much of the vaccine reserve the United States chose to store, whether the attacker used agent A, and the potential effectiveness of the vaccine given timely attack warning. In addition, there is a cost associated with deploying the vaccine reserve. Again, for simplicity's sake, the cost for every defender decision is the same, thus forcing the defender to only choose the best option(s) for each successive US$ 10 million increase in budget up to the maximum of US$ 30 million.
2.4. Consequences
In our model (Fig. 4), we have two types of consequences: casualties and economic impact. Given the defender–attacker–defender decisions, the potential casualties and the economic impact are assessed. Casualties are based on the agent, the population attacked, the maximum potential casualties, the warning time given to the defender, and the effectiveness of vaccine for agent A (if the agent A is the agent and the vaccine is used). Economic effects are modeled using a linear model with a fixed economic cost that does not depend on the number of casualties and a variable cost of the number of casualties multiplied by the cost per casualty. Of course, the defender would like potential consequences (risk) given an attack to be low, whereas the attacker would like the potential consequences (risk) to be high.
Our economic consequences model was derived using a constant and upper bound from Wulf et al.( 34 ) The constant cost we used is $10 billion, and from the upper bound, also given in Wulf et al., we derived the cost per casualty.( 34 ) We believe this fixed cost is reasonable because when looking at the example of the anthrax letters of 2001, experts estimate that although there were only 17 infected and five killed, there was a US$ 6 billion cost to the United States.( 35 ) In this tragic example, there was an extremely high economic impact even when the casualties were low.
2.5. Budget
Each U.S. defender decision incurs a budget cost. The amount of money available to homeland security programs is limited by a budget determined by the president and Congress. The model will track the costs incurred and only allows spending within the budget (see the Appendix). We considered notional budget levels of US$ 0 million, US$ 10 million, US$ 20 million, and US$ 30 million.
2.6. Risk
Normally, a decision tree is solved by maximizing or minimizing the expected attribute at the terminal branches of the tree. In our model however, the defender risk depends on the casualty and economic consequences given an attack. We use multiple objective decision analysis with an additive value (risk) model to assign risk to the defender consequences. 6 The defender is minimizing risk and the attacker is maximizing risk. We assign a value of 0.0 to no consequences and a value of 1.0 to the worst‐case consequences in our model. We model each consequence with a linear risk function and a weight (see the Appendix). The risk functions measure returns to scale on the consequences. Of course, additional consequences could be included and different shaped risk curves could be used.
2.7. Assumptions
Some of the key assumptions in our model are listed in Table IV (the details are in the Appendix) along with some possible alternative assumptions. Given different assumptions, the model may produce different results.
Table IV.
Modeling Assumptions
| Categories | Our Assumptions | Possible Alternative Assumptions |
|---|---|---|
| Uncertain Variables | Probability of acquiring the agent, detection time varies by agent | Other indications and warning |
| Decisions | Add Bio Watch city for agents A and B | Additional detection and warning systems |
| Increase vaccine reserve stocks for agent A | Increase stocks of multiple agents | |
| Deploy vaccine A | Other risk mitigation decisions | |
| Consequence Models | One casualty model for all three agents | Different casualty models for different agents |
| Risks | Casualties and economic consequences | Additional risk measures |
| Defender minimizes risk and attacker maximizes risk | Other defender and attacker objectives | |
| Solve decision tree at various budget levels | Other solution approaches |
We model the uncertainty of the attacker's capability to acquire an agent with a probability distribution and we vary detection time by agent. Clearly, other indications and warnings exist to detect possible attacks. These programs could be included in the model.
We model three defender decisions: add a Bio Watch city for agents A and B, increase vaccine reserve for agent A, and deploy agent A. We assume limited decision options (i.e., 100% storage of vaccine A, 50% storage, 0% storage), but other decisions could be modeled (e.g., other levels of storage, storing vaccines for other agents, etc). We used one casualty model for all agents. Other casualty and economic models could be used.
Finally, our model makes some assumptions about objectives. In the first of these we assume that the risks important to the defender are the number of casualties and the economic impact, but additional measures could be used. Second, we assume defenders and attackers have a diametrically opposed view of all of the objectives. Clearly, we could model additional objectives. In addition, we made some budget assumptions, which could be improved or modified. We assumed a fixed budget, but this budget could be modeled with more detailed cost models (e.g., instead of a set amount to add a city to the Bio Watch program, the budget could reflect different amounts depending upon the city and the robustness of the sensors installed). Finally, our model results in a risk of a terrorist attack; the same methodology for a defender–attacker–defender decision tree can be used to determine a utility score instead of a risk; an example of this is in Keeney.( 15 ) One thing to consider when altering or adding to the assumptions is the number of strategies the model evaluates. Currently, the canonical model has 108 different strategies to evaluate (Table V). With more complexity, the number of strategies that would need to be evaluated could grow significantly. Large‐scale decision trees can be solved with Monte Carlo simulation.
Table V.
Total Number of Strategies
| Owner | Decision | No. of Strategies |
|---|---|---|
| United States | Bio Watch | 2 |
| United States | BioShield | 3 |
| Attacker | Agent selection | 3 |
| Attacker | Target | 3 |
| United States | Deploy reserve | 2 |
| Total No. of Strategies | 108 | |
3. ILLUSTRATIVE DECISION ANALYSIS RESULTS
After modeling the canonical problem, we obtained several insights. First, we found that in our model economic impact and casualties are highly correlated. Higher casualties result in higher economic impact. Other consequences, for example, psychological consequences, could also be correlated with casualties. Second, a bioterror attack could have a large economic impact (and psychological impact), even if casualties are low.
The major risk analysis results are shown in Fig. 5. Risk shifting occurs in our decision analysis model. In the baseline (with no defender spending), agent A is the most effective agent for the attacker to select and, therefore, the agent against which the defender can protect if the budget is increased. As we improve our defense against agent A, at some point the attacker will choose to attack using agent B. The high‐risk agent will have shifted from agents A to B. As the budget level continues to increase, the defender adds a city to the Bio Watch program and the attackers choose to attack with agent C, which Bio Watch cannot detect. We use notional data in our model, but if more realistic data were used, the defender could determine the cost/benefit ratios of additional risk reduction decisions. This decision model uses COTS software to quantitatively evaluate the potential risk reductions associated with different options and make cost–benefit decisions.
Figure 5.
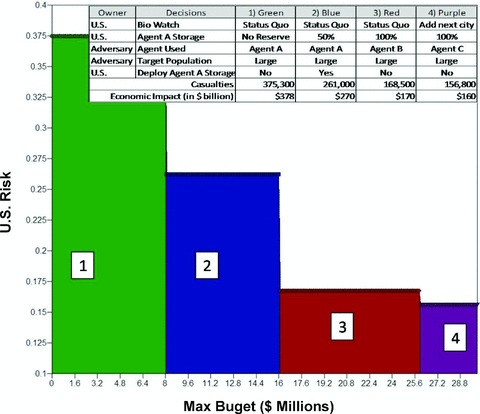
Budget versus U.S. risk.
Fig. 5 provides a useful summary of the expected risk. However, it is also important to look at the complementary cumulative distribution (Fig. 6) to better understand the likelihood of extreme outcomes. For example, the figure shows that spending US$ 0 or US$ 10 million gives the defender a 10% chance of zero risk, whereas spending US$ 20 or US$ 30 million gives the defender an almost 50% chance of having zero risk. The best risk management result would be that option 4 deterministically or stochastically dominates (SD) option 3, option 3 SD option 2, and option 2 SD option 1. The first observation we note from Fig. 6 is that options 2, 3, and 4 stochasically dominate 1 because option 1 has a higher probability for each risk outcome. A second observation is that while option 4 SD option 3, option 4 does not SD option 2 because option 4 has a larger probability of yielding a risk level of 0.4. Along the x‐axis, one can see the expected risk (ER) of each alternative. This expected risk corresponds to the expected value of risk from the budget versus risk rainbow diagram in Fig. 5. This example illustrates a possibly important relationship necessary for understanding and communicating how the budget might affect the defender's risk and choice of options.
Figure 6.
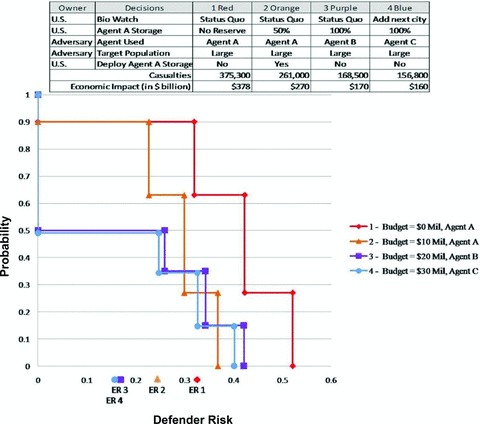
Complementary cumulative distribution.
Risk managers can run a value of control or value of correlation diagram to see which nodes most directly affect the outcomes and which are correlated (Fig. 7). Because we only have two uncertainty nodes in our canonical model, the results are not surprising. The graphs show that the ability to acquire the agent is positively correlated with the defender risk. As the probability of acquiring the agent increases, so does defender risk. In addition, the value of control shows the amount of risk that could be reduced given perfect control over each probabilistic node, and that it is clear that acquiring the agent would be the most important variable for risk managers to control. Admittedly, this is a basic example, but with a more complex model, analysts could determine which nodes are positively or negatively correlated with risk and which uncertainties are most important.
Figure 7.
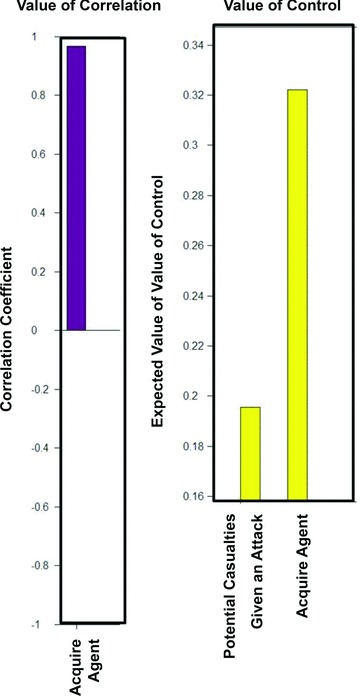
Value of correlation and value of control.
Using COTS software also allows us to easily perform sensitivity analysis on key model assumptions. From the value of correlation and control above, the probability of acquiring the agent was highly and positively correlated with defender risk and had the greatest potential for reducing defender risk. We can generate sensitivity analysis such as rainbow diagrams. The rainbow diagram (Fig. 8) shows the decision changes as our assumption about the probability of acquiring agent A increases. The different shaded regions represent different decisions, for both the attacker and the defender. This rainbow diagram was produced using a budget level of US$ 20 million, so in the original model, the defender would choose not to add a city to Bio Watch, store 100% of vaccine for agent A, but not choose to deploy it because the attacker chose to use agent B. If the probability of acquiring agent A was low enough (in section A from Fig. 8), we see that the attacker would choose to use agent C because we have spent our money on adding another city to Bio Watch, which is the only thing that affects both agents A and B, but not agent C. As the probability of acquiring agent A increases, both the attacker's and the defender's optimal strategies change. Our risk management decision depends on the probability that the adversary acquires agent A.
Figure 8.
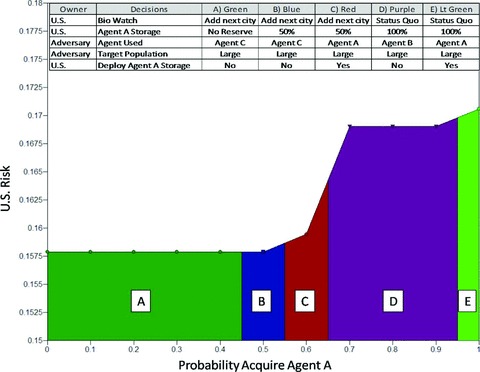
Rainbow diagram probability of acquiring agent A versus U.S. risk.
4. BENEFITS AND LIMITATIONS OF DEFENDER–ATTACKER DECISION ANALYSIS MODEL
4.1. Benefits
Risk analysis of intelligent adversaries is fundamentally different than risk analysis of uncertain hazards. As we demonstrated in Section 1.3, assigning probabilities to the decisions of intelligent adversaries can underestimate the potential risk. Decision tree models of intelligent adversaries can provide insights into the risk posed by intelligent adversaries.
The defender–attacker–defender decision analysis model presented in this article provides four important benefits. First, it provides a risk assessment (the baseline or status quo) based on defender and attacker objectives and probabilistic assessment of threat capabilities, vulnerabilities, and consequences. Second, it provides information for risk‐informed decision making about potential risk management options. Third, using COTS software, we can provide a variety of very useful sensitivity analysis. Fourth, although the model would be developed by a team, the risk analysis can be conducted by one risk analyst with an understanding of decision trees and optimization and training on the features of the COTS software.
The application of risk assessment and risk management techniques should be driven by the goals of the analysis. In natural hazard risk analysis, there is value in performing risk assessment without risk management. Some useful examples are “Unfinished Business,” a report from the EPA and the 2008 U.K. National Risk Register.( 36 , 37 ) In intelligent adversary risk analysis, the defender–attacker–defender decision analysis can provide essential information for risk management decision making. In our example, risk management techniques are important, and this type of model provides insights about resource allocation decisions to reduce or shift risk. In addition, with budget set to US$ 0, the model can be used to assess the baseline risk. As the budget increases, the model clearly shows the best risk management decisions and the associated risk reduction.
This model enables the use of COTS risk analysis software. In addition, the use of COTS software enables the use of standard sensitivity analysis tools to provide insights into areas in which the assumptions are critical or where the model should be improved or expanded.
Currently, many event tree models including the DHS BTRA event tree require extensive contractor support to run, compile, and analyze.( 16 ) Although one would still need a multidisciplinary team to create the model, once completed the defender–attacker–defender decision analysis model is usable by a single risk analyst who can provide near real‐time analysis results to stakeholders and decisionmakers as long as the risk analyst understands the risk management options, decision trees, optimization, and has training in the COTS tool.
4.2. Limitations
The technique we advocate in this article has limitations. Some of the limitations of this model are the same as those of event trees. There are limitations on the number of agents used in the models. We easily modeled 28 bioagents with reasonable run times, but more agents could be modeled. In addition, there are challenges in assessing the probabilities of uncertain events, for example, the probability that the attacker acquires agent A. Next, there is a limitation in the modeling of the multiple consequences. Another limitation may be that to get more realistic results, we may have to develop “response surface” models of more complex consequence models. These limitations are shared by event trees and decision trees.
However, decision trees also have some limitations that are not shared by event trees. First, only a limited number of risk management decisions can realistically be modeled. Therefore, care must be used to choose the most appropriate set of potential decisions.( 15 , 18 ) In addition, there may be an upper bound on the number of decisions or events that can be modeled in COTS software. It is important to note that it may be difficult to determine an objective function for the attacker. As mentioned before, there is a tradeoff in replacing the probabilities assigned to what an attacker might do (event tree approach) with attacker objectives (decision tree approach). We believe it is easier to make informed assessments about the objectives of adversaries than to assess the probabilities of their future actions. However, we need more research on assessing the robustness of risk management decisions to assumptions about adversary objectives. Finally, successful model operation and interpretation requires trained analysts who understand decision analysis and defender–attacker–defender optimization.
5. CONCLUSION
This article has demonstrated the feasibility of modeling intelligent adversary risk using defender–attacker–defender decision analysis. Table IV and Section 2.7 identified several alternative modeling assumptions that could be considered. We can modify and expand our assumptions to increase the complexity and fidelity of the model. The next step is to use the model with the best data available on the agents of concern and a proposed set of potential risk management options.
Use of our defender–attacker–defender model does not require a major intelligent adversary research program; it requires only the willingness to change.( 16 ) Much of the data used for event tree models can be used in the decision analysis model. Assessing probabilities of attacker decisions will not increase our security but defender–attacker–defender decision analysis models can provide a sound assessment of risk and the essential information our nation needs to make risk‐informed decisions.
ACKNOWLEDGMENTS
G.S.P. is grateful for the many helpful discussions on intelligent adversary risk analysis with his colleagues on the 2008 NRC committee and the defender–attacker–defender research of Jerry Brown and his colleagues at the Naval Postgraduate School. The authors are grateful for the DPL modeling advice provided by Chris Dalton of Syncopation. The authors thank Roger Burk at the United States Military Academy for his useful reviews and suggestions. Finally, the authors thank the area editor and reviewers for very detailed comments and suggestions that have helped us improve our article.
APPENDIX: MODEL FORMULATION
This model is a multiobjective decision analysis/game theory model that allows for risk management at the U.S. governmental level in terms of budgeting and certain bioterror risk mitigation decisions. The values for probabilities as well as factors are notional and could easily be changed based on more accurate data. It uses the starting U.S. (defender) decisions of adding a city to the Bio Watch program (or not) and the percent of storing an agent in the nation's vaccine reserve program to set the conditions for an attacker decision. The attacker can choose which agent to use as well as what size of population to target. There is some unpredictability in the ability to acquire the agent as well as the effects of the agent given the defender and attacker decisions. Finally, the defender gets to choose whether to deploy the vaccine reserve to mitigate casualties. The model tracks the cost for each U.S. decision and evaluates them over a specified budget. The decisions cannot violate the budget without incurring a dire penalty. The objectives that the model tracks are U.S. casualties and impact to the U.S. economy. They are joined together using a value function with weights for each objective.
We outline our model using a method suggested by Brown and Rosenthal.( 38 )
Indicies
-
1
w = add Bio Watch city {0, 1}
-
2
v = store vaccine A at percent {0%, 50%, 100%}
-
3
a = agent {A, B, C}
-
4
t = target population {small—0.0001 million, medium—0.1 million, large—1 million}
-
5
c = potential casualties given an attack {low, nominal, high}
-
6
d = deploy reserve vaccine {0, 1}
-
7
i = risk measure {1, 2}
Data
-
1
aca= agent acquired {0, 1}
-
2
wi= weight of i value measure {w 1, 1 − w 1}
Probability Data
-
1
P(aca) = probability acquire agent a
-
2
P(pcac) = probability of potential casualties c with agent a
Casualty Data
-
1
bwf = Bio Watch factor {0.9}
-
2
arv= agent A reserve factor
-
3
wfa= warning time factor
-
4
afa= agent casualty factor
-
5
popt= target population factor
-
6
mpop = max population targeted {1 million people}
-
7
pcfc= potential casualties factor
Economic Impact Data
-
1
eif = economic impact of attack (fixed) {US$ 10 billion}
-
2
dtc = dollars to casualty effect ratio {US$ 1 million/person}
Cost Data
-
1
mbw = maximum Bio Watch cost {US$ 10 million}
-
2
mcvr = maximum cost for vaccine reserve {US$ 10 million}
-
3
vrcfv= vaccine reserve cost factor
-
4
mcd = maximum cost to deploy 100% of vaccine agent A {US$ 10 million}
-
5
mb = maximum budget (United States) {US$ 30 million or variable}
-
6
cbp = cost greater than budget penalty = 1
Equations
Casualty Equations
-
1wtaw= warning time factor (U.S.)
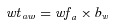
-
2mcat= maximum casualties given an attack
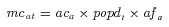
-
3pcatc= potential casualties given attack
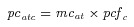
-
4drfvd= deploy reserve factor
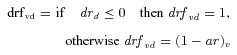
-
5x 1= U.S. casualties due to bioterrorism attack given response

Economic Impact Equations
-
1mei = maximum economic impact
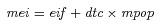
-
2x 2= U.S. economic effects due to a bioterrorism attack
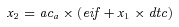
Cost Equations
-
1bwcw= Bio Watch cost (United States)
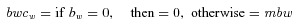
-
2vrcv= vaccine reserve cost (United States)
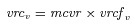
-
3drcfav= deploy reserve cost factor

-
4cdavd= deploy vaccine cost (United States)
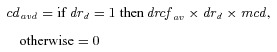
-
5costawvd= U.S. cost to prepare and mitigate a potential bioterrorism attack
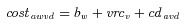
Decision Variables
-
1
bw= Bio Watch decision (United States)
-
2
rv= vaccine reserve decision (United States)
-
3
agenta= agent selection decision (terrorist)
-
4
popdt= target population decision (terrorist)
-
5
drd= deploy reserve decision (United States)
Objectives
-
1r 1(x 1) = risk function for U.S. casualties due to bioterrorism attack
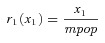
-
2r 2(x 2) = risk function for U.S. economic effects due to a bioterrorism attack
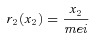
-
3
r(x) = risk to the United States
-
4r(x) = if costawvd≤ mb then
 , else cbp
, else cbp
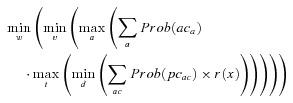
Footnotes
A useful reference for decision analysis software is located on the ORMS website (http://www.lionhrtpub.com/orms/surveys/das/das.html).
This is a key assumption and other assumptions are possible. We will discuss other assumptions later in the article.
Here we define risk to be a weighted expected value using an additive value model instead of the probability of a bad outcome.
REFERENCES
- 1. Henley E, Kumamoto H. Probabilistic Risk Assessment: Reliability Engineering, Design, and Analysis, 2nd ed New York : IEEE Press, 1996. [Google Scholar]
- 2. Ayyub B. Risk Analysis in Engineering and Economics. London , UK : Chapman and Hall, 2003. [Google Scholar]
- 3. Haimes Y. Risk Modeling, Assessment, and Management. Hoboken , NJ : John Wiley and Sons, Inc., 2004. [Google Scholar]
- 4. U.S. Nuclear Regulatory Commission (USNRC) . Reactor Safety Study: Assessment of Accident Risk in U.S. Commercial Nuclear Plants. Washington , DC : U.S. Nuclear Regulatory Commission, WASH‐1400 (NUREG‐75/014), 1975. [Google Scholar]
- 5. U.S. Nuclear Regulatory Commission (USNRC) . PRA Procedures Guide. Washington , DC : U.S. Nuclear Regulatory Commission, NUREG/CR‐2300, 1983. [Google Scholar]
- 6. Vesely WE. Fault Tree Handbook. Washington , DC : Office of Nuclear Regulatory Research, 1981. [Google Scholar]
- 7. Davison M, Vantine W. Understanding Risk Management: A Review of the Literature and Industry Practice. European Space Agency Risk Management Workshop, ESTEC, 1998 March 30April; 2:253–256. [Google Scholar]
- 8. Frank M. A Survey of Risk Assessment Methods from the Nuclear, Chemical, and Aerospace Industries for Applicability to the Privatized Vitrification of Hanford Tank Wastes. Report to the Nuclear Regulatory Commission, August, 1998.
- 9. U.S. Nuclear Regulatory Commission (USNRC) . Procedural and Submittal Guidance for the Individual Plant Examination of External Events (IPEEE) for Severe Accident Vulnerabilities. Washington , DC : U.S. Nuclear Regulatory Commission, NUREG‐1407, 1991. [Google Scholar]
- 10. Mosleh A. Procedure for Analysis of Common‐Cause Failures in Probabilistic Safety Analysis. Washington , DC : U.S. Nuclear Regulatory Commission, NUREG/CR‐5801, 1993. [Google Scholar]
- 11. U.S. Nuclear Regulatory Commission (USNRC) . A Technique for Human Error Analysis (ATHEANA). Washington , DC : U.S. Nuclear Regulatory Commission, NUREG/CR‐6350, 1996. [Google Scholar]
- 12. The White House . Homeland Security Presidential Directive 10 [HSPD‐10]: Biodefense for the 21st Century, 2004. Available at: http://www.fas.org/irp/offdocs/nspd/hspd-10.html, Accessed on January 30, 2009.
- 13. The White House . Homeland Security Presidential Directive 18 [HSPD‐18]: Medical Countermeasures against weapons of mass destruction. 2007. Available at: http://www.fas.org/irp/offdocs/nspd/hspd-18.html, Accessed January 30, 2009.
- 14. Willis H. Guiding resource allocations based on terrorism risk. Risk Analysis, 2007; 27(2):597–606. [DOI] [PubMed] [Google Scholar]
- 15. Keeney RL. Modeling values for anti‐terrorism analysis. Risk Analysis, 2007; 27(2):585–596. [DOI] [PubMed] [Google Scholar]
- 16. National Research Council . Department of Homeland Security's Bioterrorism Risk Assessment: A Call for Change, Committee on Methodological Improvements to the Department of Homeland Security's Biological Agent Risk Analysis. National Research Council of the National Academies . Washington , DC : National Academy Press, 2008. [Google Scholar]
- 17. Kunreuther H, Michel‐Kerjan E. Insurability of (Mega)‐Terrorism Risk: Challenges and Perspectives. Report prepared for the OECD Task Force on Terrorism Insurance, Organization for Economic Cooperation and Development , March 25, 2004.
- 18. Parnell GS, Dillon‐Merrill RL, Bresnick TA. Integrating Risk Management with Homeland Security and Antiterrorism Resource Allocation Decision‐Making Chapter 10 in Kamien D. (ed). The McGraw‐Hill Handbook of Homeland Security. New York : McGraw‐Hill, 2005. [Google Scholar]
- 19. U.S. Department of Homeland Security . Bioterrorism Risk Assessment (BTRA). Fort Detrick , MD : Biological Threat Characterization Center of the National Biodefense Analysis and Countermeasures Center, 2006. [Google Scholar]
- 20. Bier V, Oliveros S, Samuelson L. Choosing what to protect: Strategic defensive allocation against an unknown attacker. Journal of Public Economic Theory, 2007; 9(4):563–587. [Google Scholar]
- 21. Aghassi M, Bertsimas D. Robust game theory. Mathematical Programming, 2006; 107(1):231–273. [Google Scholar]
- 22. Jain M, Ordonez F, Pita J, Portway C, Tambe M, Western C, Paruchuri P, Kraus S. Robust Solutions in Stackelberg Games: Addressing Boundedly Rational Human Preference Models. Association for the Advancement of Artificial Intelligence Workshop: 55‐60. Available at: http://www.aaai.org/Papers/Workshops/2008/WS-08-09/WS08-09-010.pdf, 2008, Accessed on July 2, 2009.
- 23. Syncopation Software . Available at: http://www.syncopationsoftware.com/, Accessed on January 30, 2009.
- 24. Pate‐Cornell E, Guikema S. Probabilistic modeling of terrorist threats: A systems analysis approach to setting priorities among countermeasures. Military Operations Research, 2002; 7(4):5–23. [Google Scholar]
- 25. Rasmussen NC. Probabilistic risk assessment: Its possible use in safeguards problems. Presented at the Institute for Nuclear Materials Management meeting, Fall 1976, 66–88.
- 26. Golany B, Kaplan EH, Marmur A, Rothblum UG. Nature plays with dice—Terrorists do not: Allocating resources to counter strategic versus probabilistic risks. European Journal of Operational Research, 2007; 192(1):198–208. [Google Scholar]
- 27. Rosoff D, Von Winterfeldt D. A risk and economic analysis of dirty bomb attacks on the ports of Los Angeles and Long Beach. Risk Analysis, 2007; 27(3):533–546. [DOI] [PubMed] [Google Scholar]
- 28. Meadows M. Project BioShield: Protecting Americans from Terrorism. FDA Consumer Magazine, 2004 November–December. Available at: http://www.fda.gov/fdac/features/2004/604_terror.html, Accessed on January 30, 2009. [PubMed]
- 29. Shea D, Lister S. The Bio Watch Program: Detection of Bioterrorism. Washington , DC : Congressional Research Service Report, RL 32152, November 19, 2003. [Google Scholar]
- 30. Kirkwood C. Strategic Decision Making: Multiobjective Decision Analysis with Spreadsheets. Belmont , CA : Duxbury Press, 1997. [Google Scholar]
- 31. U.S. Center for Disease Control (CDC) . Bioterrorist Agents/Diseases Definitions by Category. Available at: http://www.bt.cdc.gov/agent/agentlist-category.asp, Accessed on February 10, 2009.
- 32. U.S. Center for Disease Control (CDC) . Listing of Biological Agents A‐Z. Available at: http://www.bt.cdc.gov/agent/agentlist.asp, Accessed on January 30, 2009.
- 33. National Institute of Allergy and Infectious Diseases (NIAID) . Emerging and Re‐emerging Infectious Diseases. Available at: http://www3.niaid.nih.gov/topics/emerging/list.htm, Accessed on January 30, 2009.
- 34. Wulf W, Haimes Y, Longstaff T. Strategic alternative responses to risks of terrorism. Risk Analysis, 2003; 23(3):429–444. [DOI] [PubMed] [Google Scholar]
- 35. Commission on the Prevention of Weapons of Mass Destruction Proliferation and Terrorism . World at Risk: Report of the Commission on the Prevention of WMD Proliferation and Terrorism. New York : Vintage Books, 2008. [Google Scholar]
- 36. U.S. Environmental Protection Agency . Unfinished Business: A Comparative Assessment of Environmental Problems. Washington , DC : U.S. Environmental Protection Agency, EPA Number 230287025a, February, 1987. [Google Scholar]
- 37. U.K. Cabinet Office . National Risk Register, 2008. Available at: http://www.cabinetoffice.gov.uk/reports/national_risk_register.aspx, Accessed on July 2, 2009.
- 38. Brown G, Rosenthal R. Optimization tradecraft: Hard‐won insights from real‐world decision support. Interfaces, 2008; 38(5):356–366. [Google Scholar]


