3D Tracking-Free Approach for Obtaining 3D Super-Resolution Information in Rotationally Symmetric Biostructures

Abstract

Currently, it is highly desirable but still challenging to obtain high-resolution (<50 nm) three-dimensional (3D) super-resolution information on structures in fixed specimens as well as for dynamic processes in live cells. Here we introduce a simple approach, without using 3D super-resolution microscopy or real-time 3D particle tracking, to estimate 3D sub-diffraction-limited structural or dynamic information in rotationally symmetric biostructures. This is a postlocalization analysis that transforms 2D super-resolution images or 2D single-molecule localization distributions into their corresponding 3D spatial probability distributions on the basis of prior known structural knowledge. This analysis is ideal in cases where the ultrastructure of a cellular structure is known but the substructural localization of a particular (usually mobile) protein is not. The method has been successfully applied to achieve 3D structural and functional sub-diffraction-limited information for 25–300 nm subcellular organelles that meet the rotational symmetry requirement, such as nuclear pore complex, primary cilium, and microtubule. In this Article, we will provide comprehensive analyses of this method by using experimental data and computational simulations. Finally, open source code of the 2D to 3D transformation algorithm (MATLAB) and simulations (Python) have also been developed.

Graphical Abstract

1. INTRODUCTION

Since stated by Ernst Abbe in 1873, the resolution of conventional light microscopy has been limited to approximately 200 nm laterally (x, y) and 600 nm axially (z) due to light diffraction from the microscope objective.^1,2 Currently, super-resolution light microscopy techniques break this limitation and allow for the capture of static or dynamic images with subdiffraction resolution (<200 nm) in all three axes. The techniques generally fall into two broad categories: optical based approaches such as stimulated emission depletion (STED) microscopy, which generate a subdiffraction illumination volume due to the nonlinear optical response of fluorophores in samples through laser modifications, and single-molecule-based mathematical approaches such as photo-activated light microscopy (PALM) and stochastic optical reconstruction microscopy (STORM). PALM and STROM utilize mathematical functions to localize the emitting fluorophores and then reconstitute these localizations to form super-resolution images.^1–4 Although these superresolution techniques have revolutionized imaging of biological samples via unprecedented spatial resolution, they are still limited in acquisition time (seconds to hours) and axial spatial resolution (typically >50–100 nm).^1–4 Meanwhile, fast, three-dimensional (3D) super-resolution imaging is critical for obtaining structural or dynamic information in live cells, which are inherently 3D objects. Moreover, many biological functions in bacteria^5–7 and subcellular organelles are near or below the spatiotemporal resolution limit of current 3D super-resolution imaging techniques, such as nucleocytoplasmic transport through 50 nm nuclear pore channels with millisecond transport times.^8–10

Typically, 3D super-resolution imaging is more technically demanding than 2D super-resolution imaging. This is due to the fact that the point spread function (PSF) of the emitting fluorescent probe in the axial dimension is much larger than that in the lateral dimension at the focal plane of the light microscopy objective.¹ Several methods have been developed to improve axial resolution in fluorescence microscopy. One category is to alter the shape of the PSF of the fluorescent probe along the optical axial position and then determine the probe’s axial information by referencing a predetermined relationship (set up through control experiments) between the shape of the PSF and the corresponding locations in the z dimension.^11–15 The other is to use two objectives to improve the axial resolution after comparing fluorescent signals of the probes from these objectives with or without interference.¹⁶ Typically, the above approaches involve expensive and complex optical implements.

Here we reintroduce an alternative and simple approach, with a new comprehensive analysis, that does not require unique optics for overcoming this axial dimension resolution limitation in rotationally symmetric biostructures. Instead of modifying the microscopy setup, this approach is a postlocalization analysis that transforms 2D super-resolution images or 2D single-molecule localization distributions into a corresponding 3D probability distribution by imaging biological structures that are inherently symmetrical in the axial and at least one of the lateral dimensions. In cases where the symmetry assumption is true, the distribution of information in the axial dimension may be inferred from the corresponding symmetrical axis or axes in the lateral dimension. In this Article, we will first introduce the mathematical concept and demonstrate the algorithm’s applications in determining the 3D density distribution of 2D single-molecule localizations in subcellular submicrometer organelles that have rotational symmetry,^17,18 such as the nuclear pore complex and the primary cilia.^8,9,19–21 These data will demonstrate that the 2D-to-3D transformation process can be extended to convert 2D super-resolution images obtained from currently existing 2D super-resolution light microscopy techniques, by using STORM-based 2D super-resolution data of microtubules as an example. Finally, a detailed analysis of the 2D-to-3D transformation process, which aims to estimate the capabilities and resolution of the 3D reconstructed density probability distribution, will be presented. Open source code for the 2D-to-3D transformation algorithm and the simulations will be provided online at https://github.com/andrewruba/YangLab.

2. METHODS

Calculating the Regions of the Area Matrix.

In the 2D-to-3D density transformation process, we use an area matrix to reflect the contribution of each ring to the 2D distribution. Then, we essentially count the number of localizations that fall in each region of the area matrix. Finally, we calculate the density as the number of localizations per cross-sectional area of the area matrix. A more thorough discussion of this topic can be found in the Supporting Information.

Single-Molecule Localization Precision.

For immobile molecules or fluorescent nuclear pores, the fluorescent spot was fitted to a 2D symmetrical or an elliptical Gaussian function, respectively, and the localization precision was determined by the standard deviation (SD) of multiple measurements of the central point. Therefore, the precision is presented as mean ± SD. However, for moving molecules, the influence of particle motion during image acquisition should be considered in the determination of localization precision. In detail, the localization precision for moving substrates (σ) was determined by the formula

$$\sigma =\sqrt{F\left[\frac{16\left(s^2+a^2/12\right)}{9N}+\frac{8\pi b^2{\left(s^2+a^2/12\right)}^2}{a^2{N}^2}\right]}$$

where F is equal to 2, N is the number of collected photons, a is the effective pixel size of the detector, b is the standard deviation of the background in photons per pixel, and $s=\sqrt{{s_0}^2+\frac{1}{3}D\Delta t}$ , where s₀ is the standard deviation of the point spread function in the focal plane, D is the diffusion coefficient of the substrate, and Δt is the image acquisition time.^22–26 In our experiments, more than 1100 signal photons were collected from each targeted moving molecule. As a result, using the NPCs as an example, the localization precision for transiting molecules through the NPCs is calculated to be <10 nm on the basis of the above equations, while the parameters were determined experimentally (N > 1100, a = 240 nm, b ≈ 2, s₀ = 150 ± 50 nm, Δt = 0.4 ms, and D is <0.1 μm²/s for the tested substrates in the central channel of the nuclear pores).^17,18

Code Availability.

The code for the simulations is available online at github.com/andrewruba/YangLab.

3. RESULTS

3.1. Mathematical Concept and Detailed Process for the 2D-to-3D Transformation Algorithm.

It is known that many biological structures are symmetrical along multiple axes. As shown in Figure 1A–D and the Methods section, radial symmetry in biological structures (typically determined by using electron microscopy and partially validated by bilateral symmetry of the y-dimensional data) such as nuclear pore complexes (NPCs), primary cilium, and microtubules permits the development of an area matrix in the radial dimension (y and z dimensions in Figure 1E). As molecules locate in or travel through these structures, their 3D locations can be projected into the xy or the yz plane, depending on whether microscopy imaging of the structure is conducted at the lateral or the axial dimension, respectively (Figure 1F). After further projection of the 2D molecular spatial locations into the y dimension from either the xy or the yz plane, the obtained two y-dimension histograms in principle are identical, as demonstrated in Figure 1G–J. Then, on the basis of the two identical y-dimensional histograms, each column in the y-dimension histogram projected from the xy plane will be equal to the areas times the densities for each radial bin in the yz plane (Figure 1G–J). Typically, in practice, it is much easier to obtain 2D super-resolution data of these targeted molecules in the xy plane than the yz plane because of the much limited radial dimension resolution compared to that of the axial dimension in these structures shown in Figure 1A–C. To finally achieve the 3D super-resolution information in these structures, as detailed in the mathematical calculation shown in the flowchart in Figure 2 and Figure S1, the densities in the radial dimension can be obtained by solving the matrix equations, which eventually reconstitute the corresponding 3D density information for the structure (Figure 1I–L). It is important to note that the resulting 3D density distribution represents the average density along each radial bin rooted in the known rotational symmetry of these biostructures and any deviations from the perfect rotational symmetry will be averaged in the 3D density distribution.

Figure 1.

An area matrix can be developed for radially symmetric biological structures that reflects 2D single-molecule data. (A) 3D electron tomography image of the nuclear pore complex averaged rotationally with 8-fold symmetry.^55,56 Scale bar = 20 nm. (B) Transverse slice of the primary cilia using transmission electron microscopy.^56–58 From left to right, the red lines indicate cross sections of the basal body, transition zone, and ciliary shaft of the primary cilium. Scale bar = 100 nm. (C) 3D electron tomography image of a microtubule averaged rotationally with 13-fold symmetry.^56,59,60 Scale bar = 10 nm. (D) Structures from parts A, B, and C may be simplified as a radially symmetric circle in the y and z dimensions. (E) An area matrix may be designed where the radially symmetrical simplified model is divided along the y dimension due to the fact that the projection of 2D single-molecule data is along the y dimension even though it came from the y and z dimensions. (F) Simulated single-molecule data in the x, y, and z dimensions from a cylinder with an ideal radius of 25 nm and a localization error of 5 nm for demonstration of the 2D-to-3D density transformation. Dotted lines represent the ideal structure from which the simulated data originated. (G) Single-molecule data from part F in the y and z dimensions superimposed with the area matrix from part E. (H) Histogram of the single-molecule data from part G along the y dimension to model the effects of 2D microscopy, from which a y-dimensional histogram can also be obtained. (I) Single-molecule data from part F in the x and y dimensions. (J) Histogram of the single-molecule data from part I along the y dimension. (K) The resultant radial density map of the single-molecule data from part G determined by dividing the number of points in each radial bin by the area of each radial bin as well as the resultant radial density map of only the y-dimensional histogram from part I determined by using the 2D-to-3D density transformation. (L) Radial density map from part K expressed as a cartoon reconstruction of the density of single molecules through the original 3D structure. The intensity of rings, from black to white, indicates highest to lowest normalized density.

Figure 2.

Flowchart illustrating the 2D-to-3D density transformation algorithm. The 2D-to-3D transformation algorithm converts the y-dimensional histogram into r-dimensional density information. This process is based on the area matrix that was developed for the given structure from which the y-dimensional information was obtained.

3.2. SPEED Microscopy.

Our lab has previously developed SPEED microscopy to fill the technique niche of capturing single molecules transporting through sub-diffraction-limit biochannels at high spatial [<10 nm in lateral dimensions (Figure S3)] and temporal (<1 ms) resolution.^18,19 We achieve this through four main technical modifications on traditional epifluorescence or confocal light microscopy. (1) A small inclined or vertical illumination PSF is used for the excitation of single transiting molecules through biochannels in the focal plane. This greatly increases the allowable detection speed (up to 0.2 ms per frame for the CCD camera we used) by reducing the number of camera pixels required for detection. Also, it significantly avoids out-of-focus fluorescence with an inclined illumination PSF in a similar way as total internal reflection microscopy.²⁷ (2) The high-speed detection enables us to capture hundreds or thousands of fast moving molecules in submicrometer organelles within a few seconds, which also reduces the systematical errors in localizing these transiting molecules induced by stage drift, cell movements, and molecular diffusion during the detection^23,28 (Methods). (3) A high optical density (100–500 kW/cm²) in the small illumination volume, similar to confocal microscopy, causes a high number of photons from the fluorophores to be emitted. (4) Pinpointed illumination in live cells causes negligible photoinduced toxicity.^29–31 Thus, SPEED microscopy meets the needs of high 2D spatiotemporal resolution for in vivo single-molecule tracking in dynamic biochannels such as single NPCs. However, SPEED does not directly obtain any 3D information. As demonstrated below, we have employed SPEED microcopy to obtain 2D single-molecule data in glass nanocapillary tubes, the NPC, and primary cilia. However, other single-particle tracking or super-resolution microscopy approaches may be employed to obtain similar 2D data sets for processing by the 2D-to-3D transformation. It is important to emphasize that SPEED microscopy obtains 2D localizations for mobile particles and, thus, is less constrained by labeling efficiency compared to the fixed sample super-resolution approaches, such as STORM or PALM. However, the cost is that SPEED microscopy is unable to localize fixed particles. While there is no theoretical upper limit to the 2D-to-3D transformation algorithm, the strength of this approach is to determine the 3D density map of subdiffraction biological structures (<250 nm). Therefore, a typical high NA objective will safely accommodate the biological structure without significant influence from out of focus emitters and periphery localizations such that the 2D projection plane accurately reflects the 3D distribution of molecules in the biological structure. Also, 2D single-molecule localizations should be selected from biological structures that are parallel in the x and y dimensions, which can be assessed by z scanning.

3.3. Experimental Validation of the 2D-to-3D Transformation Process in Several Systems: Glass Nanocapillary Tube, Nuclear Pore Complex, Primary Cilia, and Microtubules.

Since the 2D-to-3D transformation algorithm requires radial symmetry, we first used an ideal artificial glass nanocapillary to test the algorithm’s accuracy when coupled with SPEED microscopy for data acquisition. The glass nanocapillaries (GNCs) were fabricated using laser-assisted capillary-pulling of quartz micropipettes which can generate pore diameters ranging from 20 to 300 nm. The dimensions of GNCs used in this study were determined by helium scanning transmission ion microscopy to have an inner radius of ∼35 nm.^32,33 With that parameter in mind, the dimensions of the GNC were remeasured by determining the 3D density map of 1 nM Alexa Fluor 647 that was pumped into the inner lumen of the GNC. After thousands of 2D spatial locations for Alexa Fluor 647 were collected with a single-molecule localization precision of ≤5 nm, the final 3D density map revealed a radius of 37 ± 2 nm (a width at the two standard deviations of the Gaussian function), agreeing well with the 35 nm inner radius of the GNC imaged by helium ion microscopy with a reproducibility rate of 100% and a route localization error of 0.25 nm determined by inputting the experimental parameters (localization precision, radius, and number of localization) into the following simulations (Figure 3A–D). Reproducibility rate was defined as the number of experimental peak fittings from all simulation runs that fell within an acceptable range of the ground truth peak location, while route localization error was defined as the standard deviation of the experimental peak fittings from all of the simulation runs (Figure S2E). This value is a measure of the error one may expect given a certain level of localization precision and single-molecule localizations in one trial during an experiment.

Figure 3.

3D density maps accurately reconstruct the locations of labeled molecules in various structures. (A) Schematic of the glass nanocapillary tube with dimensions of 35 nm inner radius. (B) x- and y-dimensional single-molecule data from the tracking of Alexa Fluor 647 inside the glass nanocapillary tube. (C) 3D density map of part B showing the width at 2 standard deviations from the mean is ∼37 nm. Parts A–C were reproduced from ref 29 with permission. Copyright 2002 Wiley. (D) Radial density map from part C. (E) Schematic of the nuclear pore complex with a model trajectory for Alexa Fluor 647-labeled Importin β1. Scale bar = 50 nm. (F) x- and y-dimensional single-molecule data from the tracking of Alexa Fluor 647-labeled Importin β1 in the nuclear pore complex. (G) 3D density map of part F showing the peak fitting of the Importin β1 transport route is ∼23 nm. (H) Radial density map from part G. (I) Schematic showing the Alexa Fluor 647 externally labeled SSTR3 in the shaft of a primary cilium. (J) x- and y-dimensional single-molecule data from the tracking of externally labeled SSTR3 in the primary cilium. (K) 3D density map of part J showing the peak fitting of the SSTR3 transport route is ∼127 nm. (L) Radial density map from part K. (M) 2D STORM data showing the reconstructed super-resolution image of tubulin labeled with a primary and secondary antibody attached to Alexa Fluor 647. Scale bar = 1 μm. (N) x- and y-dimensional single-molecule data from the section of 2D STORM data in the dashed white box from part M. (O) 3D density map of part K showing the peak fitting of the labeled tubulin from part N to be ∼32 nm. (P) Radial density map from part O.

After the inner diameter of the GNC was confirmed by the application of the 2D-to-3D transformation algorithm, we moved to two different types of macromolecular trafficking in subcellular organelles: Importin β1 (a major transport receptor in nucleocytoplasmic transport^34–36) moving through the NPC and externally labeled SSTR3 (a major transmembrane protein in primary cilia^37–39) on the surface of primary cilia on the ciliary shaft. Previously, our lab has revealed that Importin β1 assists the movement of protein cargo via interactions at the periphery of the NPC, a selective gate between the cytoplasm and nucleus.^17,18 In this analysis, we present a total of 450 2D spatial locations with a single-molecule localization precision of <10 nm at the NPC’s scaffold region for Importin β1 within the NPC. The corresponding 3D density map clearly shows a high density region for Importin β1 at 23 ± 1 nm along the radius of the NPC with a 100% reproducibility rate and a route localization error of ∼1 nm (Figure 3E–H). Similarly, in primary cilia, SSTR3 was externally labeled with Alexa Fluor 647⁴⁰ and tracked using SPEED microscopy along the length of the primary cilia, a cellular projection ∼125 nm in radius determined by electron microscopy (EM).^19–21 Agreeing well with the EM-determined diameter, 260 externally labeled SSTR3 molecules with a single-molecule localization precision of ≤10 nm were determined to have a high density region at 127 ± 2 nm along the radius of primary cilia, with a 97% reproducibility rate and a route localization error of ∼2 nm (Figure 3I–L).

Lastly, to test whether the 2D-to-3D density transformation algorithm could be applied beyond SPEED microscopy, we measured the diameter of microtubules,^41–43 in which tubulins were labeled by a primary and secondary antibody conjugated to Alexa Fluor 647 and then imaged by 2D-STORM.⁴⁴ By converting the published 2D super-resolution image for a microtubule (112 single-molecule locations) into its 3D structure by our 2D-to-3D transformation algorithm, we determined the diameter of microtubules in this specific sample to be 64 ± 1 nm with a reproducibility rate of 90% and a route localization error of ∼1 nm (Figure 3M–P). This result agrees well with previous determinations by using EM⁴² and 3D super-resolution microscopy.¹

3.4. Monte Carlo Simulation Demonstrates the Parameters Required for Accurate 3D Density Map Reconstruction.

Next, we used Monte Carlo simulation^45,46 to demonstrate that two critical parameters, the single-molecule localization error of targeted molecules²² and the number of single-molecule locations,^4,22 determine the reproducibility of obtaining accurate 3D super-resolution information in biological structures with rotational symmetry. Typically, the spatial localization of individual targeted molecules labeled with fluorophores or fluorescent proteins is determined with nonzero localization error because of, primarily, background noise and limited photon collection in real experiments.²² To mimic typical transport routes of proteins in the NPC or primary cilia, our Monte Carlo simulations were performed where varying numbers of single-molecule locations were randomly simulated on an ideal radius (R_I) (Figure S2A,B). Then, single-molecule localization error (σ_LE) was added to R_I by sampling an error value from a normal distribution with a standard deviation of σ_LE (Figure S2C). Subsequently, the 2D-to-3D transformation algorithm was performed on only the y-dimensional data of the simulated single-molecule localization distribution around R_I to model the loss of z-dimensional information during the 2D microscopy projection process. The peak position of the transformed 3D density histogram was then determined by Gaussian fitting to produce a measured mean radius (R_M) which may deviate from the R_I due to the limited number of simulated locations and nonzero single-molecule localization error (Figure S2D). We conducted 10,000 iterations of this process and obtained 10,000 R_M values, in which the mean of the R_M values converges on R_I as expected (Figure S2E). With this many iterations, the error of our measurements and the resulting interpretations never exceeded 0.1 nm. To quantify how reproducible a single experimental data set is, we set out to determine how many individual R_M values from the whole distribution of R_M fell within an acceptable range of R_I. The acceptable range was defined as R_I ± σ_LE because, in principle, any single R_M value can only be accurately localized within the range of approximately two standard deviations of its Gaussian fitting, similar to the concept of resolution stated by the Rayleigh criterion⁴⁷ (Figure S2F). We expect that a high number of simulated single-molecule locations or low single-molecule localization errors would increase the number of iterations that fall within the acceptable range, thus resulting in a high reproducibility rate. To determine the reproducibility rate, we found that two critical steps should be correctly followed first in the process: The first step is to optimize the bin size for each set of simulation parameters. This is accomplished by determining the smallest bin size that produces no statistical difference by Chi square analysis between the original 2D histogram and the back-calculated 2D histogram obtained by multiplying the 3D density histogram by the corresponding area matrix (Figure S4). The second step is to account for the slightly increased sensitivity of the inner bins of the area matrix when determining the accurate R_M peak fitting. This phenomenon is due to the fact that the area of the inner bins is slightly smaller compared to the area of the outer bins, making them more sensitive to noise (Figure S5).

3.4.1. Reproducibility of Obtaining an Accurate 3D Density Map Reconstruction.

First, to test the effects of single-molecule localization error on the final R-dimensional peak fitting obtained for the 3D transformed density histogram, Monte Carlo simulations were performed with an R_I value of 25 nm, a data point number of 1,000,000 to control point number and represent the ideal case, and σ_LE ranging from 0 to 30 nm (Figure 4A–D). In principle, as the single-molecule localization error becomes excessively large, the peaks in the 3D density map will become heavily overlapped on the y-dimensional axis and, subsequently, the radial axis after the transformation algorithm. This will obscure the peak at R_I and make it indistinguishable. A ratio between the error of a bimodal Gaussian fitting and the error of a single Gaussian fitting is used to determine the indistinguishable overlap (Figure 4E–H). As shown in Figure 4I, a series of tests indicate that the bimodal fitting error becomes much larger than the single peak fitting error beyond a 21 nm localization error. This suggests that the experimental localization error cannot exceed 21 nm for any structure containing a transport route with a radius of 25 nm. This is smaller than the theoretical single-molecule localization error of 25 nm predicted by the Rayleigh criterion, mainly due to the aforementioned sensitivity of the inner bins of the area matrix in this 2D-to-3D transformation process (Figure S5). Moreover, the above results can be generalized by using a radius/precision (R/P) ratio to estimate whether the transport route can be distinguished before computational simulations or real experiments. As shown in Figure 4C,G, the threshold case of a R/P ratio of 1.19 (25 nm/21 nm) presents the minimally distinguishable transport route in the R dimension, corresponding to a separation of ∼68% of the single-molecule density around the radius. As mentioned above, 1.19 represents the case where the radius is approximately equal to the precision or standard deviation of the transport route; thus, separation of the radial distribution by ∼1 standard deviation results in ∼68% of single-molecule density separation. Meanwhile, when the R/P ratio is ≥2.0, a much higher degree (correspondingly ≥95% of single-molecule density) of peak separation and a well distinguished transport route can be achieved (Figure 4B,F).

Figure 4.

Varying the simulated precision shows the resolution limit of the 3D transformation algorithm. (A–D) 1,000,000 locations were simulated on an ideal radius (R_I) of 25 nm with localization errors (σ_LE) of 0, 10, 21, and 35 nm, respectively. Scatter plots were down-sampled to 2000 locations for visualization. (E–H) The corresponding 3D transformed density histogram of each simulation from parts A, C, E, and G, respectively. To determine whether the density peaks could be distinguished after a given localization error had been added to the ideal data, the ratio between the fitting error of a bimodal Gaussian distribution (PRFE) and a single Gaussian distribution was used (CRFE). If the bimodal fitting error was less, then the peaks in the 3D transformed distribution could likely be distinguished. If the single peak fitting error was less, the localization error was too great and the two peaks were indistinguishable. (I) Up to 21 nm, the PRFE was much less than the CRFE. Above 21 nm, the CRFE was much less than the PRFE. Therefore, the maximum localization error allowed to distinguish a 25 nm ideal radius is ∼21 nm. The results are generalized as precision/radius.

Next, using an R/P ratio of ≥2.0, we sought to determine the effects of the quantity of single-molecule locations on reconstituting an accurate 3D transformed structure. To accomplish this, Monte Carlo simulations were performed with an R_I value of 25 nm, a σ_LE value of 10 nm (an R/P ratio of 2.5), and data point numbers ranging from 50 to 1000. Representative simulations are shown for 50, 100, 500, and 1000 points, and the corresponding reproducibility percentages were calculated for each point number after 10,000 iterations (Figure 5A–H). Remarkably, only 100 and 350 points are sufficient to achieve 90 and 99% reproducibility, respectively (Figure 5I). It is highly feasible to obtain 100– 1000 points experimentally, although the number of points is higher than the minimum Nyquist sampling theorem estimation of 38 single-molecule locations²⁸ (Supporting Information). This is resultant from a nonuniform distribution of locations through the area matrix, which causes deviations from the requirement of radial symmetry. Stated in another way, it is necessary to achieve a reasonable level of radial bin uniformity—through sufficient collection of single-molecule localizations—to accurately reconstruct the 3D density distribution. Of note, we found that 1000 single-molecule locations can already result in an accuracy of 1 nm in obtaining the mean location of the 3D transformed density map (Figure 5D,H,I). In a similar way, we can also determine the accuracy of other parameters of the 3D transformed density map, such as the width of the distribution (Figure S6). In theory, given enough single-molecule data, the accuracy could be unboundedly small as long as the R/P ratio is above 2. Finally, in some cases, we noticed that, if the width of the transport route (2σ_w, the width at one standard deviation of its Gaussian distribution) is significantly bigger than the single-molecule localization precision, the above R/P ratio should be modified as R/P_W (P_W = σ_w) before determining the final radius of the transport route and the number of single-molecule locations needed for a high reproducibility rate. This discrepancy between the single-molecule localization precision and σ_w is due to a non-negligible width of the biological transport route, as is the case in Figure 3I–L where the localization precision of SSTR3 molecules was 10 nm but the width of the transport route was 35 nm.

Figure 5.

Varying the number of simulated points shows the effect of sampling error on the peak fitting of the 3D transformed data. (A–D) 50, 100, 500, and 1000 locations were simulated on an ideal radius (R_I) of 25 nm with a localization error (σ_LE) of 10 nm. (E–H) The average 3D transformation of 10,000 simulated data sets for each number of simulated locations. Error bars indicate the standard deviation of each histogram bin value, while R_I ± σ_TR indicates the average peak fitting ± the standard deviation of the peak fittings, that is, the standard deviation (σ_TR) of the R_M distribution outlined in Figure 1E. The reproducibility percentage, the number of peak fittings that fell within the localization error, is shown beneath each 3D transformed density histogram. (I) The plot of reproducibility percentage for 10,000 iterations of each number of points up to 1000. The simulation parameters were the same as those in parts A, B, C, and D except for the varying point number.

3.4.2. Reliability of the 2D-to-3D Transformation Algorithm to Distinguish Multiple Transport Routes in the NPC.

Third, there are experimental instances where there may be a mixture of transport modes that a protein may use as it traverses a rotationally symmetric organelle. For example, in the NPC, our previous work has shown that passively diffusing molecules <40 kDa pass through the central axis of the NPC while transport receptors such as Importin β1 pass through the NPC closer to the scaffold region, ∼23 nm along the NPC’s radial cross section.^17,18 As the transit of molecules is studied, it is conceivable that they could traverse the NPC at one or both of these transport routes. To test the ability of the 2D-to-3D transformation algorithm to distinguish between these potential cases, we simulated data sets from the three distinct distributions [peripheral only, central only, and bimodal (peripheral + central)] and then compared the reconstructed distributions to the ground truth input distributions via a categorization routine (Figure 6) that calculates the sum of the absolute-valued residuals (SAR) between each trial and the ground truth input distributions (Figure 6E). With these measures used in our simulations, ∼100 locations allowed us to reach >90% successful categorization for peripheral and central distributions when the single-molecule localization precision was set to 5 nm. A bimodal distribution requires more localizations for accurate categorization, but still only ∼200 locations were sufficient to achieve >90% successful categorization (Figure 6G–P). When the simulation was applied to the 10 nm localization precision case which is typical of experimental cases, ∼100–300 points were sufficient to distinguish the three distributions with >90% success (Figure 6Q). Of course, this approach has limitations. We can only assess the distribution against hypotheses and determine which hypothesis is the most likely result.

Figure 6.

Route categorization simulation. (A) For each set of simulation parameters (distribution type, localization precision, peripheral radius, central radius, and number of single-molecule locations), 1000 data sets were generated in the y, z dimensions. Displayed here is a representative data set from a peripheral distribution, localization precision of 5 nm, peripheral radius of 23 nm, central radius of 0 nm, and 500 single-molecule locations to clearly visualize the distribution from the y, z scatter data. y, z coordinates can also be transformed to analogous R, θ coordinates. (B) The bin size optimization algorithm was performed in the same way as Figure S4 with the exception that the first bin with a p-value >0.99 was selected. In this simulation, larger bin sizes made the simulation perform better; however, in the simulations in Figures 4 and 5, a smaller bin size was more ideal due to necessity of Gaussian fitting. (C) The y-dimensional histogram was obtained with the optimized bin size for every data set. (D) The 2D-to-3D transformation algorithm was performed on every data set. (E) The resultant 3D density histograms were compared via SAR to the central, peripheral, and bimodal ground truth distributions, which were obtained by simulating a data set with all of the same parameters except for 1,000,000 single-molecule locations. The lowest SAR indicates which distribution a given data set is most similar to and, thus, which ground truth distribution it is classified as. (F) The count of all classifications for the ground truth peripheral parameters set of 5 nm localization precision, 23 nm peripheral radius, 0 nm central radius, and 100 single-molecule locations. (G–I) Sample data sets from simulation runs for the peripheral, central, and bimodal distributions, respectively, using the same parameters as those in part A. (J–L) y-dimensional histograms from parts G–I. (M–O) 3D density histograms calculated from parts J–L. (P) Resultant success rates for the different distributions. (Q) Simulation results for the peripheral, central, bimodal, and uniform distributions with parameters of 10 nm localization precision, 23 nm peripheral radius, 0 nm central radius, and 10–20 nm bin sizes obtained from the optimization algorithm.

3.4.3. Effects of Deviations from the Radial Symmetry on 3D Density Map Reconstruction.

In addition, we explored how deviations from the radial symmetry assumption at various rotation angles affected the final 3D probability density distribution. First, we looked at compression of the radial symmetry which may occur from a lateral force on the subdiffraction biological structure of interest, using the NPC as an example. Currently, it is challenging to assess how radial symmetry of the NPC may be affected due to the possible distortion effects in the sample preparation technique for in vitro studies⁴⁸ as well as the natural distortion of the NPC in live cell imaging,⁴⁹ Beck et al. have minimized these effects using cryo-fixation and visualized single NPCs using electron tomography which show a high degree of regularity.⁵⁰ They found that natural distortion of the NPC’s symmetry may have an approximate ratio of the long (a) and short (b) axis of 1.3⁵⁰ (Figure 7). Therefore, while holding the circumference of the biological structure constant, we varied the a/b ratio and the rotation of the structure in relation to the orientation of these axes. For the case of a 25 nm radius, 10 nm simulated localization precision, 1,000,000 simulated localizations, and an a/b ratio of 1.3 (Figure 7A–H), we found that the mean peak in the 3D density distribution can range up to 4.4 nm from the actual mean (Figure 7I–L). Overall, the deviation from the a/b ratio of 1 grows linearly as the a/b ratio grows (Figure 7M); however, variation in the biological range easily permits the distinction between peripheral and central routes, which our lab has previously shown.^17,18 Second, we explored how labeling efficiency affected the ability to reconstruct an accurate 3D density map distribution. For super-resolution techniques that used fixed cells and antibody labeling, this is an important factor to consider. Therefore, we looked at how unequal distributions around the radius at various rotation angles affected the final 3D probability density distribution. Indeed, there were negative values that occurred in some situations, typically an artifact of undersampling or unequal labeling. However, in several of the distributions, the majority of the cases were unaffected for a 25 nm radius, 10 nm localization precision, 1,000,000 localizations, and various sections missing from the distribution at different rotation angles (Figure 8A–X). This robustness is likely caused by the z-averaging that occurs during the microscopy projection process and the y-averaging that occurs during our data analysis process. The results are summarized in Figure 8Y. While these simulations represent the deviations that may occur from any single experimental data set, typically we average at least five such data sets to minimize the effects of these deviations to our results and have not seen significant deviations in overall distribution type. If such a case were to occur, it is advisible to report the different classes of distributions that may arise separately so as not to improperly average the results. However, the NPC structure has been shown to have great regularity.⁵⁰ Furthermore, it is advisible, as we do in our experiments, to use a fluorophore-labeled nucleoporin as a marker for the NPC.^17,18 In this way, the labeling efficiency and, thus, the proper formation of the NPC may be assessed via the total fluorescence of the NPC compared to the total fluorescence of a single fluorophore.^17,18

Figure 7.

Varying the compression and rotation of the radial symmetry shows minimal effects under biological conditions. (A) Ideally, the radial symmetry is perfect with both the a and b axes being equal in the y and z dimensions. (B–D) In some cases, compression may occur where the a and b axes are unequal and rotated at any angle relative to the compression axis. (E–H) Single-molecule data simulated from an ideal distribution of 25 nm radius, 10 nm localization precision, and an a/b ratio of either 1.0 or 1.3 at 0, 45, and 90° rotation. While 1,000,000 were used for the simulation, only 1000 are shown here for ease of visualization. (I–L) 3D density distributions calculated from the data in parts E–H, respectively, with deviations from the ideal radius noted above the 3D density histogram. (M) Summary of a/b ratios ranging from 1.0 to 1.5 using the same simulation parameters as those in parts E–L.

Figure 8.

Varying the labeling ratio and rotation shows minimal affects beyond half labeling efficiency. (A–D) Single-molecule distributions simulated from an ideal radius of 25 nm radius, 10 nm localization precision, and various labeling ratios are simulated. While the simulations used 1,000,000 points, only 1000 are shown here for ease of visualization. (E–L) Rotation angles of 45 and 90° were also simulated for the simulation conditions in parts A–D. (M–X) 3D density histograms from parts A–L with deviations from the ideal radius noted above the 3D histogram. (Y) Summarized results from parts M–X.

3.4.4. Effects of Fold Symmetry and Rotation on 3D Density Map Reconstruction.

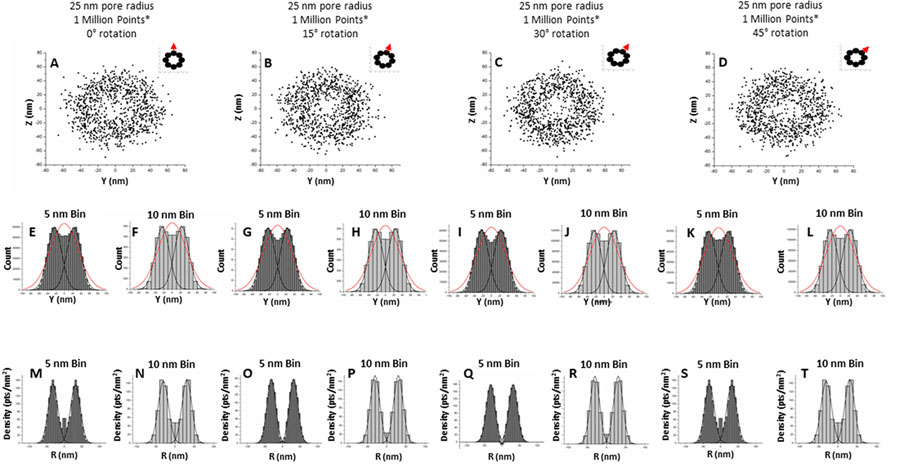
Lastly, we evaluated whether the 8-fold symmetry and rotation of the NPC structure would affect the reconstruction of the 3D density map. To interrogate this, a separate simulation was created to mimic the 8-fold rotational symmetry of the NPC (Figure 9A–D). As an NPC has an ideal interior pore radius of 25 nm and an external radius of 45 nm,⁵¹ the simulation was created to have a radius of 35 nm. The eight probability lobes have a central point on the circular radius in 45° increments. The probability lobes were generated to be as close to one another as possible without overlapping as well as mimicking an NPC with an average internal pore radius of ∼25 nm and an external pore radius of ∼45 nm. Localization precision of 10 nm was then applied to each point. A 2D histogram of the simulated data set of 1,000,000 points was then created using a 5 or 10 nm bin size (Figure 9E–L). Different bin sizes were employed to interrogate the small localized differences that may arise between different rotational conformations, with smaller bin sizes being more susceptible to changes than larger bin sizes. The resulting histograms were then fit to single and bimodal Gaussian curves in order to identify the mean radius R_M of the peaks. In general, there were no statistically significant differences between the resultant histograms from different rotational conformations. The 3D density map was then generated for the four rotational conformations with bin sizes of 5 or 10 nm (Figure 9M–T). Density maps for rotations at 0 and 45° were observed to be identical, as would be expected of a perfectly rotationally symmetrical object. A negative value near 0 nm was observed in Figure 9Q, the 30° rotation conformation with a bin of 5 nm. These negative values are most likely small artifacts resulting from rotation and do not appear to undermine the validity of the 3D density histogram, as the R_M of the histogram did not change as a result of the negative values. In addition, increasing the bin size to 10 nm removed the negative values and a bimodal Gaussian was fit to both the 5 bin and 10 bin histograms with an R² value greater than 0.99. This strongly indicates that such artifacts from rotation can be resolved with appropriate binning but are unlikely to impact the R_M of the 3D histogram. As was anticipated, the results of the evaluated rotational conformations indicate the 2D-to-3D transformation algorithm can sufficiently interpret density maps from rotationally different conformations.

Figure 9.

8-Fold symmetry and rotation does not significantly impact reconstruction of the 3D density map. (A–D) Simulation of 1,000,000 points with an internal pore radius of 25 nm, 10 nm localization precision, and probability lobe radius of 13.394 nm. The inset is the rotation of the probability lobe as the rotation is applied in 15° increments. (E–L) 2D density histogram of scatter plots A–D with a bin size of 5 and 10 nm. The histogram was fit to a bimodal Gaussian curve (R² ≥ 0.99) as well as a standard Gaussian (R² ≤ 0.9). (M–T) 3D density maps of scatter plots A–D with a bin size of 5 or 10 nm. Each histogram was fit to a bimodal Gaussian curve (R² ≥ 0.95).

4. DISCUSSION

In this paper, we presented a detailed analysis of the 2D-to-3D transformation algorithm that enabled us to obtain 3D superresolution information from 2D super-resolution images or 2D single-molecule localization data without using 3D light microscopy setups. The roles that two critical factors played in reproducing the accurate 3D super-resolution information, the single-molecule localization error, and the number of single-molecule locations have been fully discussed. We also discussed a general rule that a transport route can be well distinguished if it has a radius/precision ratio greater than 2 and the ratio-based minimum number of single-molecule locations (Figure S7). The successful applications in various systems, including the GNC, the NPC and primary cilia in live cells, and microtubules in fixed samples, prove the robustness of achieving accurate 3D super-resolution information by combining 2D experimental data and the 2D-to-3D transformation algorithm.

It is noteworthy that one prerequisite of the algorithm is that the density of the molecules of interest is constant along a given radial bin for the biological structure. As a result, the rotational symmetry cannot be determined by our algorithm but, rather, must be determined by another technique. Normally, transmission electron microscopy, especially since the development of freezing techniques for specimen fixation which reduces distortion,⁵² is appropriate for determining the ground truth structure and its rotational symmetry with high spatial resolution. Another alternative approach is expansion microscopy, by which the size of a specimen can be enlarged 4.5–20 times without significant distortion and the enlarged structure can be labeled and imaged by epi-fluorescence or confocal light microscopy.^53,54 As demonstrated, with the known structures of the NPC, primary cilia, and microtubules, area matrices have been developed for the cylindrical structures based on their rotational symmetry for the 2D-to-3D transformation algorithm. Furthermore, area matrices could also be developed for other regular or even irregularly shaped, radially symmetric structures, with the only prerequisite being constant density of the molecules of interest along a given radial bin.