Evaluating the Portability of Satellite Derived Chlorophyll-a Algorithms for Temperate Inland Lakes using Airborne Hyperspectral Imagery and Dense Surface Observations

Abstract

This study recreated and reevaluated the performances of twenty-nine satellite derived chlorophyll-a algorithms for temperate inland lakes to serve as a proxy for algal bloom detection. The performances of these algorithms were compared over two study areas, Harsha Lake in Southwest Ohio and Taylorsville Lake in central Kentucky. The datasets utilized for an estimation of chlorophyll-a concentrations were the airborne derived CASI-1500 hyperspectral imagery, and the spatially resampled and spectrally binned synthetic datasets designed to mimic the configurations of WorldView-2/3, Sentinel-2, Landsat-8, MODIS, and MERIS. This study demonstrates promising results for the use of CASI and Sentinel-2, and to a lesser degree WorldView-2 and Landsat-8 for the identification of algal blooms with r² values 0.678, 0.707, 0.499, and 0.317, respectively for correlations tested with coincident lake surface chlorophyll measurements in Taylorsville Lake, Kentucky. The results confirm the portability and efficacy of utilizing a suite of algorithms across multiple sensors in order to detect potential hotspots for algal blooms through the use of chlorophyll-a as a proxy. Furthermore, the strong performance of the Sentinel-2 algorithms is exceptionally promising, due to the recent launch of the second satellite in the constellation, which will provide higher temporal resolution for temperate inland water bodies susceptible to algal blooms. In addition, much of the data processing has been automated using the open-source statistical software R, resulting in reduced processing time, and allowing for the integration of numerous algorithms across multiple sensors for the near real-time monitoring required for detecting algal blooms and mitigating their adverse impacts.

1. Introduction:

Over the last several decades, there has been a noticeable increase in the frequency and extent of freshwater harmful and nuisance algal blooms (HNABs) in the United States (Reif, 2011; USEPA, 2012). Exact environmental mechanisms have yet to be determined (Graham, 2006; Linkov, Satterstrom, Loney, & Steevans, 2009), although, high nutrient concentrations and algae available insolation appear to be significant contributing factors (Dokulil and Teubner, 2000; Ohio EPA, 2012). Freshwater HNABs have become a global concern affecting forty-five countries worldwide and have resulted in animal deaths in at least twenty-seven US states (Graham, 2006, USEPA, 2012; WHO, 2003). What makes these blooms “harmful” is that the algae comprising the bloom can produce toxic compounds including, dermatoxins, hepatoxins, and neurotoxins to humans and animals (USEPA, 2012). Although the World Health Organization and state agencies such as, The Ohio Department of Health, have set safety standards for the consumption and contact of these toxins (ODH 2017), their monitoring in every small body of water is difficult, time intensive, and costly (Backer, 2002; Pitois et., 2000). Remote sensing using satellite imagers of HNABs is possible because of photo reactive pigments produced by algae allowing for photosynthesis. The pigments have reflective properties that can be ‘sensed’ by analyzing the images. The toxins produced by algae are not directly detectable by the imagery, but toxin concentration is often correlated with algal biomass density, which in turn, is directly related to the concentration of photopigments (Gitelson et al., 1986; Gitelson et al., 2003; Kudela et al., 2015; Morel and Prieur, 1997; Stumpf et al., 2012; Stumpf et al. 2016; Vos et al., 1986; Wynne et al., 2012). One of the most abundant photopigments produced by all types of algae is chlorophyll-a. Using satellite imagery to estimate the concentrations of chlorophyll-a in inland surface waters, therefore, can serve as an indicator of the presence of an algal bloom. Subsequent water sampling for toxin analysis has to be conducted to evaluate the nature of the high chlorophyll-a concentration; determining if the bloom is harmful or not.

To reduce costs and increase coverage of algal bloom monitoring the use of remote sensing, especially from satellite platforms, are currently being utilized to address the risk management challenges associated with HNABs including, the monitoring of smaller fresh water lakes, rivers, and reservoirs, long-term studies of individual bodies of water, and the development of techniques for early detection (Shen, Xu, & Guo, 2012). The most effective way to accomplish these goals are through the continual use of high temporal resolution satellites with spatial resolutions significantly less than the size of the water body being observed (Beck et al. 2016). Temporal resolution is of the utmost importance, especially in temperate regions, where the highest probability of freshwater HNABs occurring is during the summer, corresponding to the most frequent chances of heavy cloud cover, which influences the effectiveness of the satellite imagers. Therefore, the ability to maximize the number of satellites to image algal blooms in inland water bodies is especially important (Veryla, 1995). Remote imaging systems allow for quicker turnaround time for officials to notify the public about potential HNAB occurrence (Blondeau-Patissier, Gower, Dekker, Phinn, & Brando, 2014; Klemas, 2012; Stumpf & Tomlinson, 2005).

There has been some success in the global monitoring of algal blooms using satellites systems with high return times and swath widths of sensors such as the Moderate Resolution Imaging Spectroradiometer (MODIS), Ocean and Land Colour Instrument (OLCI) or the Medium Resolution Imaging Spectrometer (MERIS) (Augusto-Silva et al., 2014; Blondeau-Patissier et al., 2014; Klemas, 2012; Stumpf et al., 2012). Since MERIS is no longer operational, the similarly configured sensor, OLCI on the ESA’s Sentinel-3, will essentially take MERIS’s place for data sets after the launch date of February 16^th, 2016 (ESA, 2018). Unfortunately, these are less useful for the monitoring of inland lakes that typically have widths of less than a few kilometers, and the satellites that have high enough spatial resolution have too low temporal resolution to offer a less than or equal to weekly monitoring frequency of HNABs, that is needed to account for algal growth dynamics in surface waters. Beck et al. (2016) suggest the use of a suite of sensors in order to optimize the successful acquisition of a cloud-free scene and provide effective monitoring of small freshwater lakes for minimal cost. This study recreates and reevaluates the efficacy and transferability of the synthetic satellite reflectance algorithms studied by Beck et al. (2016) for quantification of chlorophyll-a in two temperate reservoirs. It extends the work of Augusto-Silva et al. (2014) and Beck et al. (2016) using airborne hyperspectral imagery and dense coincident in-situ observations.

The increase in frequency and extent of algal blooms, especially the rise of harmful algal blooms (HABs), has pushed for the further development of effective and accurate satellite-based algorithms to estimate chlorophyll-a. This is mainly due to the fact that chlorophyll-a is a spectrally active compound in phytoplankton that is commonly used as a proxy for phytoplankton biomass (Morel & Prieur, 1977; Vos, Donze, & Bueteveld, 1986; Gitelson, Nikanorov, Sabo, & Szilagyi, 1986; Gitelson, Gritz, & Merzlyak, 2003; Wynne, Stumpf, Tomlinson, & Dyble, 2012; Stumpf, Wynne, Baker, & Fahnenstiel, 2012; Kudela et al., 2015) and is a reliable proxy for water quality (Verdin, 1985; Ekstrand, 1992; Reif, 2011; Mishra & Mishra, 2012). Augusto-Silva et al. (2014) provide a review of the satellite reflectance algorithms, including two-band-algorithm (2BDA) (Dall’Olmo & Gitelson, 2005), three band-algorithm (3BDA) (Gitelson et al., 2003), and the Normalized Difference Chlorophyll Index (NDCI) algorithm (Mishra & Mishra, 2012), while Beck et al. (2016) added the Fluorescence Line Height algorithms (FLH) for the approximation of chlorophyll-a concentrations in inland lakes. The findings of these studies demonstrate the accuracy of sensor-based chlorophyll-a estimates (Sauer, Roesler, Werdell, & Barnard, 2012).

Due to differing band spacing and sensor configurations, it is important to note that not all algorithms can be applied to all sensors, and direct measurements of chlorophyll-a and phytoplankton communities in surface waters are highly variable due to nutrient, wind, and temperature fluxes, as well as a host of other bio-physical factors (Hunter, Tyler, Willby, & Gilvear, 2008; Sawaya et al., 2003; Stumpf et al., 2016; Wang, Xia, Fu, & Sheng, 2004). Another issue conflating the direct detection of HABs over other algal blooms, is that most current sensors lack the narrow band at 620nm corresponding to the phycocyanin absorption feature. Phycocyanin is more directly related to gauging harmful algal risk because it is a pigment produced by the cyanobacteria algal taxa types most frequently responsible for toxin production in fresh waters. Here the focus is solely on chlorophyll-a algorithms as proxies for any algal bloom as a method of early detection. The comparison of multiple sensors is again complicated by the varying atmospheric and surface conditions that result from differing overpass schedules (Thonfeld, Feilhauer, & Menz, 2012). These issues are addressed by upscaling and spectral binning one hyperspectral image in order to mitigate the effects of differing acquisition times. This resulted in the need for the collection of only one set of dense coincident surface observations.

This research recreated the twenty-nine algorithms used to derive and estimate chlorophyll-a content for each of the following sensors: Compact Airborne Spectrographic Imager (CASI), WorldView-2, Sentinel-2, Landsat-8, MODIS, and MERIS. Each of these algorithms were evaluated against in-situ water samples collected during a multi-agency/investigator field campaign that included the United States Army Corp of Engineers (USACE), U.S. Environmental Protection Agency (USEPA), Kentucky Division of Water, and the University of Cincinnati. The CASI hyperspectral imager (HSI) data was used to upscale and resample the images to develop synthetic images for the sensors listed above. Following the methodology of Beck et al. (2016), this study evaluated the 1-meter airborne CASI-HSI imagery, and the resampled 1.8-, 20-, 30-, 250- and 300-meter multispectral imagery designed to mimic current and future operational satellite imagers. The interest in on expanding the use of remote sensing satellite systems as an accurate and cost-effective way to monitor and quantify the water quality of inland water bodies. To this end, an automated approach using the R open source software was applied (R Core Team, 2017). Beck et al. (2016) demonstrated a high statistical correlation between NOAA CI, FLH, NDCI, 2BDA and 3BDA chlorophyll-a algorithms and the in-situ observations, but was limited to only one lake in Southwest Ohio. Given the findings of Beck et al (2016), it is hypothesized that the algorithm performances of this study would result in the same order: MERIS, WorldView-2, Sentinel-2, MODIS, and Landsat-8. It should be noted, that Landsat-8 performed rather poorly with the previously developed algorithms, but performs moderately well with the advent of the fluorescence line height (FLH) algorithms.

This research provides a technique that attempts to evaluate the portability of these algorithms by reproducing the methods of Beck et al. 2016 in order to examine how site-specific variations, such as geography, atmospheric conditions, and lake bio-chemistry will impact the performances of each sensor-algorithm pair. This research also aimed at confirming the use of these moderate resolution satellite imagers as a “red flag” detection system to identify potential problem areas that can be then verified by in situ measurements. This study defines a red flag event at 25μg/L, which is derived from the reference data on ambient water quality for ecoregion VI level III ecoregion 55 (EPA, 2000). The use of red flag event is flexible and dependent on the water use and environmental health standards. These standards vary by state, but generally follow the threshold guidelines outlined by the World Health Organization (WHO, 1999). Since toxicity levels cannot be detected directly via current remote sensing instruments, this approach is designed to be an early detection of high concentrations of chlorophyll-a, which in turn would alert local officials or managers to test for toxicity level with traditional in situ techniques, such as ELISA kits.

2. Methods

2.1. Study area

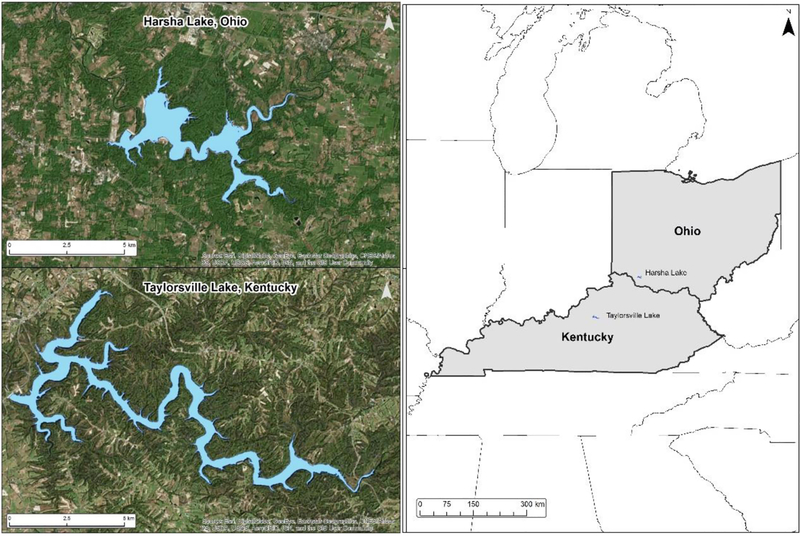
The study focuses on Taylorsville Lake in Central Kentucky, roughly 150 kilometers southwest of Harsha Lake (aka East Fork Lake), Ohio, which was the focal water body in Beck et al. (2016). Taylorsville Lake has an approximate water surface area of 11.88km², while Harsha’s is 7.99km² (Fig. 1). These lakes were chosen because they are both sites of recent and reoccurring algal blooms (including HABs), they share similar geography, and are subject to routine monitoring by the USEPA and USACE. In addition to being a source of drinking water, these lakes are recreation areas containing beaches, host open water swimming, and are used for recreational fishing. Both lakes are reservoirs that were created in the late 1970’s by the USACE for flood control.

Fig 1.

Map of the locations of the two studies, Harsha Lake near Cincinnati, Ohio and Taylorsville Lake in Central Kentucky.

2.2. Datasets

The datasets used in this research were the following: 1) Compact Airborne Spectrographic Imager (CASI) hyperspectral imagery (HSI), 2) coincident surface spectral observations collected using an ASD brand spectroradiometer, and 3) in situ measurements made using in-vivo water sensors and analyzing surface water grab samples using laboratory and microscopy methods. These same datasets were used in Beck et al. (2016) for Harsha lake only. Data was acquired for Taylorsville on 6/18/2014, while the Harsha flyover and sampling event occurred on 6/27/2014. The USACE Joint Airborne Lidar Bathymetry Technical Center of Expertise (JALBTCX) supported the CASI-1500 airborne surveys while the USACE, USEPA, Kentucky Division of Water, and the University of Cincinnati all helped to acquire water quality and phytoplankton community measurements within one hour of the image acquisition time.

2.3. Hyperspectral Imagery Acquisition

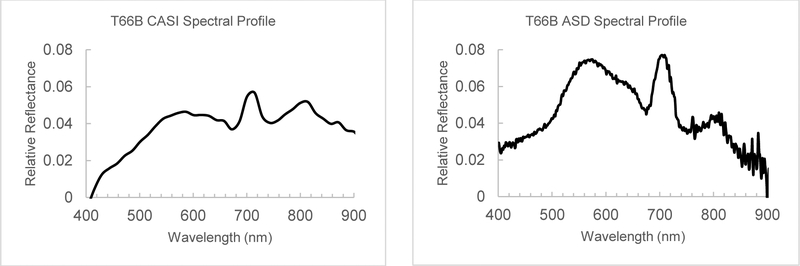
The acquisition of the CASI-1500 VNIR airborne HSI and radiometer collected coincident surface observations for Taylorsville lake took place on the morning of June 18, 2014. The system was flown at an altitude of approximately 2000 meters where it collected a 48-band hyperspectral image with 1,466-meters wide at 1-meter spatial and 14-nanometer Full Width Half Maximum (FWHM) spectral resolution over a wavelength range of 371 to 1042 nanometers (Fig. 2). The detailed description of the hyperspectral image acquisition and pre-processing are available in Beck et al. (2016) section 2.4. Tests with extracted water pixel FLAASH reflectance spectra after atmospheric correction are similar to water field spectral measurements and display a strong peak at 714 nm associated with chlorophyll-a (Fig. 2).

Fig. 2.

Spectral profile of water at sample location T66B (Fig. 3) of Taylorsville Lake, KY, exhibiting a strong chlorophyll-a reflectance peak at 714 nanometers from atmospherically corrected CASI HSI data (left) and the same location measured at the water surface with a spectroradiometer in the field within one hour of the overflight (right). Y-axis is reflectance relative to calibration standards and the X-axis is scaled from 400 nm to 900 nm in both graphs.

2.4. Coincident surface observation procedures

An in-depth literature review reveals a consensus that accepts chlorophyll-a approximations as a reasonable proxy for algal blooms (Alawadi, 2010; Allee and Johnson, 1999; Brivio et al., 2001; Cannizzaro and Carder, 2006; Choubey, 1994; Dekker and Peters, 1993; Dall’Olmo et al., 2003; Fraser, 1998; Frohn and Autrey, 2009; Gitelson, 1992; Gower et al., 2008; Han et al., 1994; Klemas, 2012; Kneubuhler et al., 2007; Matthews et al., 2001; Quibell, 1992; Rundquist et al., 1996; Schalles et al., 1997; Stumpf et al., 2012; Thiemann and Kaufmann, 2002: Vos et al., 1986; Wynne et al., 2012; Zhao et al. 2010). The Taylorsville surface water sampling campaign included the use of four research boats to acquired seventy coincident surface observations on a 400-meter grid point spacing with YSI water quality sondes cross-calibrated following manufacturer guidelines. Surface observation collection was coordinated with the imaging aircraft via an air-to-ground radio. Each boat’s crew collected the following:

1. Surface water grab samples from each sample point for subsequent laboratory measurements of general water quality constituents, algal pigments, and a subset of samples were processed for algae identification and enumeration.

2. ASD brand spectroradiometer spectral signature to evaluate atmospheric correction of CASI imagery.

3. In situ sensor measurements using YSI brand chlorophyll, phycocyanin, turbidity, specific conductance, pH, water temperature, and dissolved oxygen sensor suite of a YSI 6600 data sonde (YSI Instruments, Yellow Springs, Ohio).

4. Secchi depth measurements.

5. GPS location- and date/time-referenced photos of surface water conditions at each sample point. All data were referenced to the WGS84 map datum and converted to the Universal Transverse Mercator (UTM) Zone 16 North map projection (Fig. 3).

Fig. 3.

Sampling scheme implemented on June 18^th, 2014 for Taylorsville Lake in order to acquire water quality information from seventy sites within 1 h of image acquisition. (Source: United States Army Corps of Engineers).

Note, only the algal pigment and I&E information obtained from the grab samples are pertinent to this manuscript.

Grab samples were measured for chlorophyll-a by extraction and spectrophotometric detection according to Standard Method 10200H2.b (APHA et al., 2012). The summed values for pheophytin corrected chlorophyll-a and pheophytin (i.e., a so-called measure of uncorrected chlorophyll-a) and abbreviated this variable as SUMReCHL (μg/L)). This measure of total chlorophyll pigment more likely aligns with the reflectance of the in vivo chlorophyll pigments measured by the imagers.

2.5. Synthetic satellite imagery

The original CASI Hyperspectral bands were spectrally averaged with equal weight using band math in the raster package (Hijmans, 2016) for R to produce synthetic satellite image bands for Landsat-8, Sentinel-2, MERIS/OLCI, MODIS, and WorldView-2/3, according to published specifications (DigitalGlobe, 2009, 2014; ESA, 2012, 2013; USGS, 2015; Lindsey and Herring, 2001). Since the results from the spectral binning process are generated from the same original reflectance data set as well as the same series of dense coincident surface observations this approach eliminates the errors that arise from co-registration, atmospheric conditions, and surface fluxes that complicate the comparison of real imagery acquired at different times (Beck et al., 2016; Thonfeld et al., 2012). After spectral resampling, these data were then spatially resampled to the appropriate resolution of each sensor (Table 1). This approach is not without uncertainty, the linear spectral resampling can introduce error of up 1–3% RMS and up to 6–8% relative error, and similarly the spatial resampling process may produce 10–32% (Schlapfer et al. 1999; Schlapfer et al. 2002). Given the trade-offs associated with signal to noise ratio (SNR), sampling interval, and band configuration this research followed the recommendation set forth by Broge and Mortensen (2002) to spectrally and spatially resample hyperspectral imagery to mimic coarser sensors. This approach has been successfully applied to OLCI by Augusto-Silva et al. (2014), MERIS by Koponen et al. (2002), and expanded to include additional sensor configurations in Beck et al. (2016).

Table 1.

Original CASI and synthetic sensor band configurations

IMAGER	ORIGINAL RANGE (NM)	CENTER (NM)	BANDWIDTH (NM)	SYNTHETIC RANGE (NM)	SYNTHETIC CENTER (NM)		BAND WIDTH (NM)
WORLDVIEW-2/3				Resampled to 1.8 m
B1	400–450	425	50	400.3–444.4		428.9	44
B2	450–510	480	60	457.8–515.1		486.5	57
B3	510–580	545	70	515.1–586.5		550.8	71
B4	585–625	605	40	586.5–629.3		607.9	43
B5	630–690	660	60	629.3–686.2		657.75	57
B6	705–745	725	40	700.4–743.1		721.75	43
B7	770–895	832.5	125	771.5–899.7		835.6	128
B8	860–1040	950	180	856.9–1042.7		949.8	186
SENTINEL-2				Resampled to 20 m
B1	433–453	443	20	429.0–457.8		443.4	29
B2	458–523	490.5	65	457.8–529.4		493.4	72
B3	543–578	560.5	35	543.7–572.2		557.9	29
B4	650–680	665	30	643.5–686.2		664.8	43
B5	698–713	705.5	15	700.4–714.6		707.5	14
B6	733–748	740.5	15	728.9–757.3		743.1	28
B7	773–793	783	20	771.5–800.0		785.7	29
B8	785–900	842.5	115	785.8–899.7		842.7	114
B8B	855–875	865	20	856.9–885.4		864.0	26
B9	935–955	945	20	928.2–956.8		942.5	29
LANDSAT-8				Resampled to 30 m
B1	430–450	440	20	429.0–457.8		443.4	28
B2	450–510	480	60	457.8–500.8		479.3	43
B3	530–590	560	60	529.4–586.5		557.9	57
B4	640–670	655	30	643.5–672.0		657.7	29
B5	850–880	865	30	842.7–885.4		864.0	43
MERIS/OLCI				Resampled to 300 m
B1	402–412	407	10	400.3–414.7		407.5	14
B2	438–448	443	10	429.0–457.8		443.4	29
B3	485–495	490	10	486.5–500.8		493.6	14
B4	505–515	510	10	500.8–515.1		507.9	14
B5	555–565	560	10	558.0–572.2		565.1	14
B6	615–625	620	10	615.0–629.3		622.1	14
B7	660–670	665	10	657.7–672.0		664.8	14
B8	678–685	681.5	7	672.0–686.2		679.1	14
B9	704–714	709	10	700.4–714.6		707.5	14
B10	750–757	753.5	7	743.1–757.3		750.2	14
B11	757–762	759.5	5	757.3–771.5		764.4	14
B12	772–787	779.5	15	771.5–785.8		778.5	14
B13	855–875	865	20	856.9–871.2		864.0	14
B14	880–890	885	10	871.2–899.7		885.4	29
B15	895–905	900	10	885.4–913.9		899.6	29
MODIS				Resampled to 250 m
B1	620–670	645	50	615.0–672.0	643.5		57
B2	841–876	858.5	35	842.7–871.2	856.9		29

Sensor spatial resolution and lake geometry must be considered because the acquisition of water only pixels is critical for evaluating the algorithm performance via regression analysis. A minimum of three pure water pixels are required to perform a linear regression, but at least ten points are recommended for a more robust analysis. For a full description of this methodology see Beck et al. (2016) section 2.6. A deviation from the original study is the transition from Environment for Visualizing Images (ENVI) to R, which allows for the easier automation of all aspects of this research. This is also a step toward operational systems, and for complete R script details see Johansen (2017). To ensure there were no differences between the methods, pixel values from both studies were evaluated at multiple randomly chosen points for each of the chlorophyll-a algorithms. All of the pixels evaluated displayed the same values regardless of which software was chosen to do the computation, so no further modifications were needed to transfer the methods from the original ENVI formats to the R scripts used in this study (data not shown). Table 1 displays the band combinations of the original sensors as well as modified synthetic configurations. The objective was to recreate the original sensors using the CASI band configurations to keep the synthetic band widths and centers a close as possible.

2.6. Image analysis

The theme of reproducibility is continued by following the methodology set forth by Beck et al. (2016) who further extended the work of Augusto-Silva et al. (2014) in which airborne hyperspectral imagery was used in the place of surface measurements collected via spectroradiometer (Mittenzwey, Ulrich, Gitelson, & Kondratiev, 1992; Kallio, 2000; Koponen et al., 2002). The advantage of the synthetic version approach is that all configurations or synthetic sensors are compared to one set of surface observations as detailed by Reif (2011). This research applied all of the algorithms used in Augusto-Silva et al. (2014) and the more recent set of hybrid algorithms developed my Beck et al. (2016), which include the following: Cyanobacterial Index (CI), Maximum Chlorophyll Index (MCI), series of Fluorescence Line Height (FLH/FLH Blue/FLH Violet), and Surface Algal Bloom Index (SABI) algorithms, two band-algorithms (2BDA), three band-algorithm (3BDA), and 3BDA-like (KIVU) (Alawadi, 2010; Beck et al., 2016; Binding et al., 2013; Brivio et al., 2001; Chipman, Olmanson, & Gitelson, 2009; Dall’Olmo & Gitelson, 2005; Gitelson et al., 2003; Mishra & Mishra, 2012; Wynne et al., 2012; Zhao et al., 2010;). Table 2 contains the full list of chlorophyll-a algorithms, their abbreviations, and the band math for each algorithm used for this study.

Table 2.

Band math and wavelengths in nm for each algorithm used for chlorophyll-a estimation at Harsha Lake. Float refers to floating point values.

Chlorophyll-a index algorithms by satellite/sensor	Spatial res. (m)	Band math/wavelengths (nm)
CASI CI	1	−1*((CASI[[23]])−(CASI[[22]]−(CASI[[25]]−CASI[[22]])))
CASI CI	1	−1*(((float(686))−(float(672))−((float(714))−(float(672)))))
CASI MCI	1	((CASI[[23]])−(CASI[[22]]−(CASI[[25]]-CASI[[22]])))
CASI MCI	1	(((float(686))−(float(672))−((float(714))−(float(672)))))
CASI FLH	1	(CASI[[25]]−(CASI[[27]]+(CASI[[23]]−CASI[[27]])))
CASI FLH	1	(float(714))−[float(743) + (float(686)−float(743))]
CASI NDCI	1	(CASI[[25]]−CASI[[23]])/(CASI[[25]]+CASI[[23]])
CASI NDCI	1	(float(714)−float(686))/(float(714) + float(686))
CASI 2BDA	1	(CASI[[25]])/(CASI[[22]])
CASI 2BDA	1	(float(714))/(float(672))
CASI 3BDA	1	((1/CASI[[22]])−(1/CASI[[25]]))*(CASI[[28]])
CASI 3BDA	1	((1/float(672))−(1/float(714)))*(float(757))
WorldView-2 and −3 NDCI	1.8	(WV2[[6]]−WV2[[5]])/(WV2[[6]]+WV2[[5]])
WorldView-2 and −3 NDCI	1.8	(float(722)−float(658))/(float(722) + float(658))
WorldView-2 and −3 FLH violet	1.8	(WV2[[3]])−(WV2[[5]]+(WV2[[1]]−WV2[[5]]))
WorldView-2 and −3 FLH violet	1.8	((float(551))−[float(658) + (float(429)−float(658))])
WorldView-2 2BDA	1.8	(WV2[[6]])/(WV2[[5]])
WorldView-2 2BDA	1.8	(float(722))/(float(658))
WorldView-2 3BDA	1.8	((1/WV2[[5]])−(1/WV2[[6]]))*(WV2[[7]])
WorldView-2 3BDA	1.8	((1/float(658))−(1/float(722)))*(float(836))
Sentinel-2 NDCI	20	(S2[[5]]−S2[[4]])/(S2[[5]]+S2[[4]])
Sentinel-2 NDCI	20	(float(708)−float(665))/(float(708) + float(665))
Sentinel-2 FLH violet	20	(S2[[3]])−(S2[[4]]+(S2[[2]]−S2[[4]]))
Sentinel-2 FLH violet	20	((float(558))−[float(665) + (float(493)−float(665))])
Sentinel-2 2BDA	20	(S2[[5]])/(S2[[4]])
Sentinel-2 2BDA	20	(float(708))/(float(665))
Sentinel-2 3BDA	20	((1/S2[[4]])−(1/S2[[5]]))*(S2[[9]])
Sentinel-2 3BDA	20	((1/float(665))−(1/float(708)))*(float(864))
*Landsat-8 NIR band is far from chlorophyll-a peak Landsat-8 NDCI	30	(L8[[5]]−L8[[4]])/(L8[[5]]+L8[[4]])
Landsat-8 NDCI	30	(float(864)−float(658))/(float(864) + float(658))
Landsat-8 SABI	30	(L8[[5]]−L8[[4]])/(L8[[2]]+L8[[3]])
Landsat-8 SABI	30	(float(864)−float(658))/(float(479) + float(558))
Landsat-8 FLH blue	30	(L8[[3]])−(L8[[4]]+(L8[[2]]−L8[[4]]))
Landsat-8 FLH blue	30	(float(558))−[float(657) + (float(480)−float(658))]
Landsat-8 FLH violet	30	(L8[[3]])−(L8[[4]]+(L8[[1]]−L8[[4]]))
Landsat-8 FLH violet	30	(float(558))−[float(658) + (float(443)−float(658))]
Landsat-8 2BDA	30	(L8[[5]])/(L8[[4]])
Landsat-8 2BDA	30	(float(864))/(float(658))
Landsat-8 KIVU (3BDA-like)	30	(L8[[2]]−L8[[4]])/(L8[[3]])
Landsat-8 KIVU (3BDA-like)	30	(float(479)−float(658))/(float(558))
Landsat-8 3BDA	30	((1/L8[[2]])−(1/L8[[4]]))*(L8[[3]])
Landsat-8 3BDA	30	((1/float(479))−(1/float(658)))*(float(558))
MODIS NDCI	250	(MODIS[[2]]−MODIS[[1]])/(MODIS[[2]]+MODIS[[1]])
MODIS NDCI	250	(float(857)−float(644))/(float(857) + float(644))
MODIS 2BDA	250	(MODIS[[2]])/(MODIS[[1]])
MODIS 2BDA	250	(float(857))/(float(644))
MERIS CI	300	(−1*((MERIS[[8]])−(MERIS[[7]])−((MERIS[[9]])−(MERIS[[7]]))))
MERIS CI	300	−1*(((float(679))−(float(665))−((float(708))−(float(665)))))
MERIS MCI	300	((MERIS[[9]])−(MERIS[[8]])−((MERIS[[10]])−(MERIS[[8]])))
MERIS MCI	300	(((float(708))−(float(679))−((float(750))−(float(679)))))
MERIS FLH	300	(MERIS[[9]])−(MERIS[[10]]+(MERIS[[8]]−MERIS[[10]]))
MERIS FLH	300	(float(708))−[float(750) + (float(679)−float(750))]
MERIS NDCI	300	(MERIS[[9]]−MERIS[[7]])/(MERIS[[9]]+MERIS[[7]])
MERIS NDCI	300	(float(708)−float(665))/(float(708) + float(665))
MERIS 2BDA	300	(MERIS[[9]])/(MERIS[[7]])
MERIS 2BDA	300	(float(708))/(float(665))
MERIS 3BDA	300	((1/MERIS[[7]])−(1/MERIS[[9]]))*(MERIS[[11]])
MERIS 3BDA	300	((1/float(665))−(1/float(708)))*(float(764))

The standard Type-1 regression test (Pinero, Perelman, Guerschman, & Paruleo, 2008; Kudela et al., 2015; Beck et al., 2016) was used for the 70 laboratory observations of chlorophyll-a (SumReChl (μg/L)) that corresponded to seventy pixels for each of the following sensors: CASI, synthetic WorldView-2, synthetic Sentinel-2, synthetic Landsat-8, synthetic MODIS, and synthetic MERIS. Each pair of pixels and surface observations were compared and evaluated using the Pearson’s r correlation and are shown in Table 3 with their corresponding Pearson’s r² value, p-value, slope, and intercept. A standard Type-1 regression was applied to test the chlorophyll-a algorithms against measured chlorophyll-a (i.e. SUMReCHL) values in order to normalize all of the values and create a fair comparison of the performance of each of the indices. For this study, a critical p-value of 0.001 was used for all Pearson’s r Type-1 regression tests in Tables 3 and 4. In order to accommodate that certain researchers prefer the use of the Type-2 geometric mean method which is designed to test correlations in natural systems (Peltzer, 2015) was applied to the chlorophyll-a estimations at Taylorsville Lake (Table 6) and then normalized to calculated chlorophyll-a values for all of the algorithms from the Type-1 regression tests (Beck et al., 2016; Kudela et al., 2015) (Table 7). The detailed combined error budget for this analysis is stipulated in section 2.8 of Beck et al. (2016).

Table 3.

Performance of algorithms for chlorophyll-a estimation at Taylorsville Lake using chlorophyll-a indices according to Pearson’s r test (Type-1) linear regressions.

ALGORITHMS	NO. OF POINTS	PEARSON’S R	PEARSON’S R2	P_VALUE	SLOPE	INTERCEPT
CASI CI	70	0.823	0.678	<0.001	0.642	21.677
CASI MCI	70	0.693	0.481	<0.001	0.539	21.745
CASI FLH	70	0.823	0.678	<0.001	0.642	21.677
CASI NDCI	70	0.758	0.575	<0.001	401.211	21.34
CASI 2BDA	70	0.811	0.658	<0.001	146.489	−131.003
CASI 3BDA	70	0.777	0.604	<0.001	169.812	15.953
WV2 NDCI	70	0.699	0.488	<0.001	504.827	32.776
WV2 FLHVIOLET	70	0.434	0.188	<0.001	0.558	−86.486
WV2 2BDA	70	0.706	0.499	<0.001	244.43	−212.303
WV2 3BDA	70	0.665	0.442	<0.001	225.43	32.479
S2 NDCI	69	0.836	0.698	<0.001	554.162	7.204
S2 FLH VIOLET	69	0.478	0.228	<0.001	1.489	30.850
S2 2BDA	69	0.841	0.707	<0.001	239.526	−230.765
S2 3BDA	69	0.767	0.588	<0.001	256.550	9.001
L8 NDCI	69	0.108	0.012	0.375	−53.498	39.285
L8 SABI	69	0.130	0.017	0.288	−44.960	39.789
L8 FLH BLUE	69	0.563	0.317	<0.001	0.972	−23.625
L8 FLH VIOLET	69	0.555	0.308	<0.001	0.696	−51.341
L8 2BDA	69	0.095	0.009	0.437	−21.212	60.267
L8 KIVU	69	0.315	0.099	0.008	80.752	71.521
L8 3BDA	69	0.345	0.119	0.004	−74.272	78.442
MODIS NDCI	10	0.089	0.008	0.804	−34.494	28.393
MODIS 2BDA	10	0.109	0.012	0.758	−20.866	49.409
MERIS*	3	N/A	N/A	N/A	N/A	N/A

^*The MERIS configuration only produced three usable water only pixels, which did not meet the minimal requirements to derive Pearson’s r statistical correlations.

Table 4.

Normalized performance of algorithms for chlorophyll-a estimation at Taylorsville Lake using chlorophyll-a indices according to Pearson’s r test (Type-1) linear regressions. This test is used to normalize the slope and intercepts to facilitate a direct comparison between algorithms following the method of Kuedela et al. (2015).

ALGORITHMS	NO. OF POINTS	PEARSON’S R	PEARSON’S R2	P_VALUE	SLOPE	INTERCEPT
CASI CI_CHLA	70	0.823	0.678	<0.001	1.000	0.004
CASI MCI_CHLA	70	0.694	0.481	<0.001	1.001	−0.017
CASI FLH_CHLA	70	0.823	0.678	<0.001	1.000	0.004
CASI NDCI_CHLA	70	0.759	0.575	<0.001	1.000	0.000
CASI 2BDA_CHLA	70	0.811	0.658	<0.001	1.000	0.000
CASI 3BDA_CHLA	70	0.777	0.604	<0.001	1.000	0.000
WV2 NDCI_CHLA	70	0.699	0.488	<0.001	1.000	0.000
WV2 FLH VIOLET_CHLA	70	0.434	0.188	<0.001	1.000	0.009
WV2 2BDA_CHLA	70	0.706	0.499	<0.001	1.000	0.001
WV2 3BDA_CHLA	70	0.665	0.442	<0.001	1.000	0.000
S2 NDCI_CHLA	69	0.836	0.698	<0.001	1.000	0.000
S2 FLH VIOLET_CHLA	69	0.478	0.228	<0.001	1.000	0.009
S2 2BDA_CHLA	69	0.841	0.707	<0.001	1.000	0.001
S2 3BDA_CHLA	69	0.767	0.588	<0.001	1.000	0.000
L8 2NDCI_CHLA	69	0.108	0.012	0.375	1.000	0.000
L8 SABI_CHLA	69	0.130	0.017	0.288	1.000	0.000
L8 FLH BLUE_CHLA	69	0.563	0.317	<0.001	1.000	−0.009
L8 FLH VIOLET_CHLA	69	0.555	0.308	<0.001	1.000	0.012
L8 2BDA_CHLA	69	0.095	0.009	0.437	1.000	−0.001
L8 KIVU_CHLA	69	0.315	0.099	0.008	1.000	−0.001
L8 3BDA_CHLA	69	0.345	0.119	0.004	1.000	0.000
MODIS NDCI_CHLA	10	0.090	0.008	0.804	1.000	0.000
MODIS 2BDA_CHLA	10	0.112	0.013	0.758	1.000	−0.002
MERIS_CHLA*	3	N/A	N/A	N/A	N/A	N/A

^*The MERIS configuration only produced three usable water only pixels, which did not meet the minimal requirements to derive an accurate Pearson’s r statistical correlations.

Table 6.

Performance of algorithms for chlorophyll-a estimation at Taylorsville Lake using chlorophyll-a indices according to Peltzer (2015) Type 2 Geometric Mean Tests. Included for completeness because type-2 Geometric Mean Test is designed to evaluate the correlations values in natural systems, which some researchers prefer over the Type-1 method above.

ALGORITHMS	PEARSON’S R	PEARSON’S R2	SLOPE	INTERCEPT	STD_SLOPE	STD_INTERCEPT
CASIWY08CI	0.823	0.678	0.779	18.439	0.056	2.381
CASIMCI	0.694	0.481	0.778	15.105	0.074	3.323
CASIFLH	0.823	0.678	0.779	18.439	0.056	2.381
CASIMM12NDCI	0.759	0.575	528.902	16.426	44.569	2.882
CASIDA052BDA	0.811	0.658	180.594	−170.065	13.459	15.551
CASIGI033BDA	0.777	0.604	218.475	9.985	17.683	3.107
WV2MM12NDCI	0.699	0.488	722.538	31.049	68.019	2.643
WV2BE16FLHVIOLET	0.434	0.188	1.286	−247.371	0.166	36.840
WV2MI092BDA	0.706	0.499	346.165	−315.974	32.184	32.896
WV23BDA	0.665	0.442	339.094	30.311	33.669	2.804
S2MM12NDCI	0.836	0.698	663.210	1.328	46.464	3.163
S2BE16FLHVIOLET	0.478	0.228	3.116	24.055	0.389	3.808
S2SI052BDA	0.841	0.707	284.769	−281.353	19.611	22.010
S2BE163BDA	0.767	0.588	334.700	0.452	27.943	3.827
L8MM12NDCI	0.108	0.012	−493.140	57.535	80.447	5.604
L8AL10SABI	0.130	0.017	−346.854	58.084	55.909	5.590
L8BE16FLHBLUE	0.563	0.317	1.725	−70.685	0.197	12.700
L8BE16FLHVIOLET	0.555	0.308	1.254	−122.189	0.145	18.625
L8DA032BDA	0.095	0.009	−223.199	281.200	36.685	40.381
L8KN07KIVU	0.315	0.099	256.065	146.324	36.607	16.110
L8GI033BDA	0.345	0.119	−215.088	156.891	30.068	17.189
MODISMMNDCI12	0.090	0.008	−381.906	31.128	182.126	8.444
MODISSY002BDA	0.112	0.013	−186.502	218.386	87.880	90.029
MERIS*	N/A	N/A	N/A	N/A	N/A	N/A

^*The MERIS configuration only produced three usable water only pixels, which did not meet the minimal requirements to derive an accurate Pearson’s r statistical correlations.

Table 7.

Normalized performance of algorithms for chlorophyll-a estimation at Taylorsville Lake using chlorophyll-a indices according to Peltzer (2015) Type 2 Geometric Mean Tests.

ALGORITHMS	PEARSONS R	PEARSONS R2	SLOPE	INTERCEPT	STD SLOPE	STD INTERCEPT
CASIWY08CI_CHLA	0.823	0.678	1.214	−7.880	0.087	3.779
CASIMCI_CHLA	0.694	0.481	1.443	−16.268	0.137	5.671
CASIFLH_CHLA	0.823	0.678	1.214	−7.880	0.087	3.779
CASIMM12NDCI_CHLA	0.759	0.575	1.318	−11.705	0.111	4.697
CASIDA052BDA_CHLA	0.811	0.658	1.233	−8.563	0.092	3.952
CASIGI033BDA_CHLA	0.777	0.604	1.287	−10.540	0.104	4.429
WV2MM12NDCI_CHLA	0.699	0.488	1.431	−15.862	0.135	5.591
WV2BE16FLHVIOLET_CHLA	0.434	0.188	2.305	−47.983	0.298	11.499
WV2MI092BDA_CHLA	0.706	0.499	1.416	−15.307	0.132	5.476
WV2BE163BDA_CHLA	0.665	0.442	1.504	−18.544	0.149	6.134
S2MM12NDCI_CHLA	0.836	0.698	1.197	−7.294	0.084	3.660
S2BE16FLHVIOLET_CHLA	0.478	0.228	2.093	−40.511	0.261	10.281
S2SI052BDA_CHLA	0.841	0.707	1.189	−7.000	0.082	3.580
S2BE163BDA_CHLA	0.767	0.588	1.305	−11.291	0.109	4.648
L8MM12NDCI_CHLA	0.108	0.012	9.218	−304.591	1.504	55.917
L8AL10SABI_CHLA	0.130	0.017	7.715	−248.877	1.244	46.304
L8BE16FLHBLUE_CHLA	0.563	0.317	1.775	−28.757	0.203	8.149
L8BE16FLHVIOLET_CHLA	0.555	0.308	1.802	−29.682	0.208	8.323
L8DA032BDA_CHLA	0.095	0.009	10.522	−352.947	1.729	64.262
L8KN07KIVU_CHLA	0.315	0.099	3.171	−80.469	0.453	17.259
L8GI033BDA_CHLA	0.345	0.119	2.896	−70.273	0.405	15.493
MODISMMNDCI12_CHLA	0.090	0.008	11.072	−283.231	5.280	148.712
MODISSY002BDA_CHLA	0.112	0.013	8.938	−223.237	4.212	118.725
MERISMCI_CHLA*	N/A	N/A	N/A	N/A	N/A	N/A

^*The MERIS configuration only produced three usable water only pixels, which did not meet the minimal requirements to derive an accurate Pearson’s r statistical correlations.

3. Results

Each image derived chlorophyll-a index had a single-band output calculated (Table 2) that was compared with the seventy coincident surface observations of chlorophyll-a at Taylorsville Lake. To evaluate the performance of each algorithm standard Type-1 regression test (Pearson’s r), of the chlorophyll-a algorithms derived from the atmospherically corrected imagery following Pinero et al. (2008) and Kudela et al. (2015) with a p-value threshold of 0.001 was undertaken, the result of which are in Table 3. Pixels that were not pure water pixels were excluded in order to mitigate the algorithm from conflating land vegetation with aquatic vegetation or algae. The summary of algorithm performances for both Harsha Lake and Taylorsville Lake are displayed in Table 5.

Table 5.

Algorithm performance comparison, shown as Pearson’s r² values, for Harsha Lake in Cincinnati, Ohio (Beck et al. 2016) and Taylorsville Lake in Central Kentucky.

Algorithms	HARSHA	TAYLORSVILLE
CASI
CASI CI	0.668	0.678
CASI MCI	0.588	0.481
CASI FLH	0.668	0.678
CASI NDCI	0.687	0.575
CASI 2BDA	0.717	0.658
CASI 3BDA	0.729	0.604
World-View 2
WV2 NDCI	0.724	0.488
WV2 FLH Violet	0.530	0.188
WV2 2BDA	0.711	0.499
WV2 3BDA	0.741	0.442
Sentinel-2
S2 NDCI	0.794	0.698
S2 FLH Violet	0.358	0.228
S2 2BDA	0.799	0.707
S2 3BDA	0.692	0.588
Landsat-8
L8 NDCI	0.125	0.012
L8 SABI	0.123	0.017
L8 FLH Blue	0.381	0.317
L8 FLH Violet	0.548	0.308
L8 2BDA	0.156	0.009
L8 KIVU	0.098	0.100
L8 3BDA	0.158	0.119
MODIS
MODIS NDCI	0.301	0.008
MODIS 2BDA	0.256	0.013
MERIS
MERIS CI	0.841	*
MERIS MCI	0.158	*
MERIS FLH	0.841	*
MERIS NDCI	0.845	*
MERIS 2BDA	0.845	*
MERIS 3BDA	0.832	*

^*The MERIS (Taylorville Lake) configuration only produced three usable water only pixels, which did not meet the minimal requirements to derive an accurate Pearson’s r statistical correlations.

3.1. Real Aircraft and Synthetic Satellite Imagery Results

CASI Imagery (Real):

Six algorithms (CI, MCI, FLH, NDCI, 2BDA and 3BDA) were evaluated using the atmospherically corrected CASI-1500 hyperspectral imagery. All six algorithms performed strongly and are ranked in order of highest to lowest Pearson’s r² value, CASI CI, CASI FLH, CASI 2BDA, CASI 3BDA, CASI NDCI, and CASI MCI (Fig. 4). These high r² values are expected given the band configurations of the CASI HSI and the well-placed bands of 700 nm and 714 nm that highly correlate with spectral signatures of chlorophyll-a (Gitelson, 1992; Zhao et al., 2010). Although there is a change in the ranking order for these algorithms from Harsha Lake (Beck et al 2016), the Pearson’s r² values are all very high with a range of 0.588–0.729 and 0.481–0.678 at Harsha Lake and Taylorsville Lake, respectively.

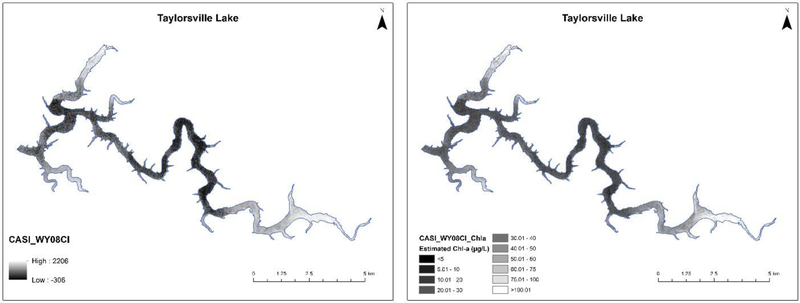
Fig. 4.

A Results of the best performing CASI algorithm, CASI_Wy08CI, as the algorithm index values as applied to original CASI HSI imagery (shoreline in Blue) with brighter pixels indicating higher chlorophyll-a concentrations. Pearson’s r² = 0.678, p-value <0.001, N = 70. B Estimated cholorphyll-a content (μg/L) by applying the slope and intercept from table 3 (0.642x + 21.667) to the raw CASI_Wy08CI algorithm values.

WorldView-2 (Synthetic):

Four algorithms (NDCI, FLH Violet, 2BDA and 3BDA) were evaluated using the synthetically created WorldView-2 image. There was a noticeable decline in their performance, especially with the WV2 FLH Violet algorithm. The remaining WV2 NDCI, WV2 2BDA, and WV2 3BDA algorithms had r² values of 0.442–0.499, and were significantly lower compared to the r² results obtained from the Harsha Lake study (Table 5). A t-test indicated that these correlation values show a significant difference between the performance of WorldView-2 algorithms across the two lakes.

Sentinel-2 (Synthetic):

Four algorithms (NDCI, FLH Violet, 2BDA and 3BDA) were evaluated using the synthetically created Sentinel-2 image. The results showed high portability across study areas. Only a single pixel/sample location pair was excluded (T38), because of land/water mixing. Three of the Sentinel-2 algorithms performed very well with r² values ranging from 0.5875–0.707, again slightly lower than the original study of Harsha Lake where the r² values ranged from 0.6922–0.799 (Beck et al., 2016). The FLH Violet algorithms performed well below the other three algorithms with r² values of 0.2281 at Taylorsville and 0.3576 at Harsha Lake, indicating this algorithm should not be used for water bodies similar to those studied in this paper.

Landsat-8 (Synthetic):

Seven algorithms (NDCI, SABI, FLH Blue, FLH Violet, 2BDA, KIVU, and 3BDA) were evaluated using the synthetically created Landsat-8 image, and produced relatively poor results with the noted exception of the FLH algorithms. A single pixel and sample location pair was excluded (T38) because of land/water mixing. As stated by Beck et al. (2016), the band configuration of Landsat-8 affects its ability to detect the peak wavelength of chlorophyll-a, and subsequently diminishes the applicability and transferability of these algorithms. The newly developed FLH Blue and Violet algorithms were able to capture some of the visible green peak and overcome these limitations with low to moderate success. Again, the Taylorsville Lake algorithms consistently exhibited lower r² values than Harsha for both the FLH Blue and FLH Violet algorithm, with Taylorsville r² of 0.317 and 0.308 and Harsha r² values of 0.3807 and 0.5476, respectively. Given the relatively low accuracy of the Landsat-8 algorithms, it is proposed that the FLH algorithms should be used solely as qualitative or “red flag” indicator of potential areas of concern and not as a quantitative indicator of concentration.

MODIS (Synthetic)

Two algorithms (NDCI and 2BDA) were evaluated using the synthetically created MODIS imagery, but were only able to use ten pixel/sample site locations due to the 250-meter pixel spatial resolution (T05, T12, T14, T16, T30, T40, T44, T47, T51B, and T70B). The large spatial resolution of MODIS coupled with Taylorsville Lake’s thin width, roughly 300–500 meters across, makes the acquisition of a pure water pixel difficult. The two algorithms evaluated, performed very poorly with r² values only 0.090 and 0.112, respectively. MODIS might be an appropriate choice for some larger inland water bodies, but due to the band spacing and spatial resolution it is not a good candidate for Taylorsville Lake.

MERIS (Synthetic)

Six algorithms (CI, MCI, FLH, NDCI, 2BDA and 3BDA) were evaluated using the synthetically created MERIS imagery. Due to MERIS’s coarse spatial resolution of 300 meters, only three pixels (T32, T54, and T59) were considered “pure”, which was deemed insufficient to accurately measure any statistical correlation.

4. Discussion

This research utilized atmospherically corrected CASI-1500 VNIR hyperspectral imagery to develop synthetic WorldView-2, Sentinel-2, Landsat-8, MODIS, and MERIS imagery coupled with dense coincident water surface observations in order to reevaluate and assess the transferability of the chlorophyll-a algorithms for temperate inland water bodies as proposed by Beck et al. (2016) and Augusto-Silva et al. (2014). The results demonstrate a high-level of confidence in the portability of certain algorithm-sensor pairs proposed in this study. A special focus should be placed on three highly performing Sentinel-2 algorithms (S2NDCI, S22BDA, and S23BDA), because of the availability of Sentinel-2 products through the European Space Agency’s (ESA) data hub, the band configurations, and a revisit time of 5–10 days (ESA, 2017). Although the CASI algorithms performed well, it is not expected that these algorithms would be implemented in routine monitoring due to the high cost and intensive labor required for aircraft acquisition. Instead the CASI dataset was utilized as a baseline to study the portability of these algorithms under varying conditions.

The Taylorsville Lake results confirm the findings of Beck et al. (2016) for Harsha Lake and support the use of NDCI, 2BDA, and 3BDA algorithms as the highest performing of all sensors (Table 5). Due to the unique configuration of band spacings on the Landsat-8 sensor, the only algorithms to perform moderately well for Landsat-8 were the newly developed FLH Blue/Violet algorithms with r² values greater than 0.3. Another important finding is the poor performance of both MODIS and MERIS sensors. The larger pixel sizes of MODIS and MERIS imagers were acknowledged, but were still evaluated because the potential acquisition of enough water-only pixels was a possibility. Unfortunately, the image resulted in only three water-only points for MERIS, making it statistically unusable. These results suggest that these sensors require a lake width of over a kilometer across in order to offer any assistance in the monitoring of the water quality of inland lakes and reservoirs. Given the success of MERIS in previous studies (Augusto-Silva et al., 2014; Beck et al., 2016; Gower et al., 2008; Koponen et al., 2002), the authors of this paper still feel confident that these algorithms will perform strongly and greatly improve the ability to monitor algal blooms as a “red flag” in water bodies with widths large enough for the acquisition of pure water pixels.

The normalized chlorophyll-a indices for the highest performing algorithm-imager combinations allow for similar prediction of chlorophyll-a values across algorithms and sensors (Table 4). For example, any of the normalized indices with a value of 10 would correspond to an estimated chlorophyll-a concentration to 10μg/L. Although it is expected that there will be some variation in the slopes and intercepts of the real imagers, these would be easily corrected with the acquisition of the real satellite imagery. This research offers a step forward in the operational use of a multi-sensor approach. This will increase the chance of successful (i.e. cloud-free) image acquisition, which subsequently will increase the monitoring of dynamic algal bloom conditions.

The highest performing sensors, CASI and Sentinel-2, demonstrate a high level of portability for the atmospherically corrected original (non-synthesized) CASI imagery, which had high levels of correlation for both lakes. All CASI-based algorithms performed at least moderately well with r² values over 0.5 and p-values well below the threshold of 0.001. Most operational satellites were designed for terrestrial applications and it is acknowledged that the signal to noise ratios may be reduced for aquatic studies. This issue has been discussed at length in the literature and there is general consensus that the application of these terrestrial satellites for inland water studies are still appropriate (Kallio, 2000; Kudela et al., 2015; Mishra and Mishra, 2012; Reif, 2011; Stumpf et al 2012; Stumpf et al., 2016).Stumpf et al. (2016) further addressed the many challenges of using remote sensing for mapping cyanotoxins, including biological, environmental, and even pigment detection method. This paper follows that approach, by offering options in terms of sensor-algorithm pairs to better assist local decision makers. Given those variables, the high correlations observed for both lakes give us confidence that these algorithms suggest a degree of portability, with focus on the CASI CI, CASI FLH, CASI 2BDA, S2 NDCI, and S2 2BDA algorithms for the detection of chlorophyll-a in inland water bodies.

Counter to the results for Harsha Lake where the WorldView-2 algorithms performed the same amongst themselves and had slightly higher r² values than CASI, the performance of WorldView-2 algorithms were significantly lower at Taylorsville Lake (Table 5). This is clearly shown in 2BDA and 3BDA algorithms, where Harsha Lake had r² values of 0.711 and 0.741 respectively and Taylorsville had r² values of 0.499 and 0.442, respectively. It is expected that this is due in part at least to the spectral binning process, where slightly different band configurations where applied to mimic the original WorldView-2 band centers as close as possible. For exact band configurations see Table 1 of Beck et al. (2016) and Table 1 of this paper. The exact mechanism that resulted in a ~30% difference in performance is not yet known. Although more investigation is needed to determine the cause of the performance difference, the four algorithms were able to estimate the chlorophyll-a content at a moderate level in turbid waters with differing algal content (table 8) supporting the idea of portability and serving as a “red flag” indicator for algal blooms in under varying conditions, and it is suggested that MODIS could still be useful for the monitoring of inland water bodies subject to blooms.

Table 8.

A comparison of the algae taxonomy differences between Harsha Lake and Taylorsville Lake as described by algae divisions.

ALGAE DIVISION	TAYLORSVILLE	HARSHA
	Average Relative Abundance (%)
BACILLARIOPHYTA	2.695	0.077
CHLOROPHYTA	15.429	1.059
CHRYSOPHYTA	0.030	0.000
CRYPTOPHYTA	7.366	1.527
CYANOBACTERIA	72.443	97.320
EUGLENOPHYTA	0.068	0.000
PYRROPHYTA	0.294	0.018
TOTAL	98.325	100.000

The results for Sentinel-2 and its algorithms are the most promising for inland algal bloom monitoring purposes because not only are the r² values very high, but the performances of each algorithm are nearly identical between the lakes studied, which indicate a high degree of portability across water bodies., There was a slight decline in the performance for all Sentinel-2 algorithms applied to Taylorsville as compared to Harsha lake (Table 5). The exception was the S2 FLH Violet algorithm, which performed well below the other three algorithms in both studies, which signifies it is unlikely to play a major role for the detection of chlorophyll-a in turbid inland water bodies. At the time the Harsha Lake data was being processed and interpreted the authors were unaware of the exact band configuration of Sentiniel-2 because the satellite was not yet launched. This might explain some of the differences in performance as noted in Table 1 of each study and the results shown in Table 5. To reiterate the fact that inland water body are highly variable and spectrally altered due to local variations in the algal content, turbidity, and atmospheric conditions, it is expected that algorithm performances and ranking order for each algorithm with change to some degree. In order to overcome this issue, this study automated much of the procedures using scripts in R to provide a suite of algorithms so individual water managers may decide which works best for their specific scenario (Johansen, 2017).

The performance of the NDCI and 2BDA algorithms with Sentinel-2 in both studies appear as the most promising for inland algal bloom monitoring. The significance of these highly consistent findings is that unlike CASI or WorldView-2, Sentinel-2 has the spatial resolution of 10–20 meters for the bands required for these chlorophyll-a algorithms. Given Sentinel-2’s lower spatial resolution than CASI and WorldView-2 it is assumed the results will be more accurate as a “red flag” detection system because the areas detected will be less susceptible to pixel value noise at the meter level. Another advantage of using Sentinel-2 for evaluating water quality is that the data are open source, making it highly accessible to any researcher or resource manager. Sentinel-2 with a swath width of 290km is ideal for small to mid-sized water bodies but poses challenges to the study of large water bodies such as the Great Lakes or Gulf of Mexico. For large area studies, it would be recommended to utilize the MERIS/OLCI-like sensors, with swaths of 1270km. Another issue continues to be satellite revisit time, which for sentinel-2 is on the order of 10–20 days (currently), but as this paper is being written, the ESA has announced the launch of Sentinel-2B, which will reduce the revisit time to as little as 5- days. Although this is still not ideal, because algal blooms can appear very rapidly, it is a significant step forward in the ability to real-time monitor many lakes, rivers, and reservoirs cost-effectively and in significantly less time.

The results of this portability study are promising because of their ability to help address the three research needs suggested by Graham (2006); 1) create quantitative tools for evaluating for monitoring algal blooms in general in temperate reservoirs; 2) contributing directly to the long-term study HAB formation in individual water bodies and; 3) assist in the development of methods for early algal bloom detection (“red flags”) and to allow more time for resource managers to respond to potentially harmful algal blooms.

The results shown here support the view of Beck et al. (2016) in suggesting that future satellite imaging systems for inland water quality monitoring of water bodies smaller than a few kilometers will require spatial resolutions of 30 m or finer to capture the spatial heterogeneity observed during this experiment and spectral resolutions equal to or better than Sentinel-2 if they are to leverage the shape metric algorithms for the chlorophyll-a peak near 710 nm. Another area of great potential for the advancement of algal bloom monitoring with future satellite systems is the launching of constellations of systems, such Sentinel-2 A&B. The recent launch of S2B will increase the number of annual overpasses by two-fold which will allow for twice as many opportunities for cloud-free acquisition, which are necessary for operational water quality monitoring systems due to frequent cloud cover in mid-latitude temperate climates. Finally, the adaption of sensors with a band configuration that takes advantage of the phycocyanin absorption feature near 620 nm would allow for the delineation between general algal blooms and blooms dominated by cyanobacteria, which tend to be the algal division most responsible for toxin production in inland waters.

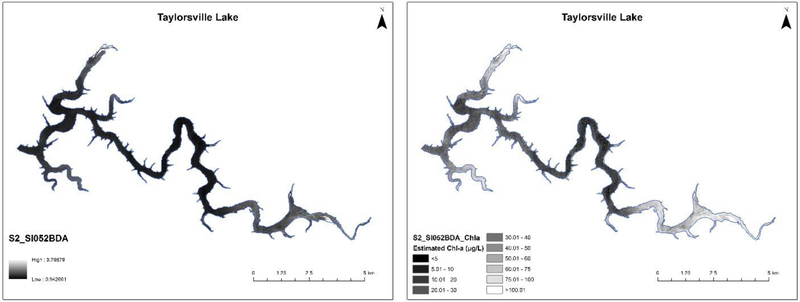
Fig. 5.

A Results of the best performing Sentinel-2 algorithm, S2_SI052BDA, as algorithm index values as applied to synthetic Sentinel-2 imagery (shoreline in Blue) with brighter pixels in the indicating higher chlorophyll-a concentrations. Pearson’s r² = 0.707, p-value <0.001, N = 69 (to avoid shoreline). B Estimated chlorophyll-a content (μg/L) by applying the slope and intercept from table 3 (239.526x – 230.765) to the raw S2_SI052BDA algorithm values.