Spectral and entropic features are altered by age in the electroencephalogram in patients under sevoflurane anesthesia

Abstract

Background:

Pre-existing factors such as age and cognitive performance can influence the electroencephalogram (EEG) during general anesthesia. Specifically, spectral EEG power is lower in the elderly as compared to younger subjects. Here we investigate age-related changes in EEG architecture in patients undergoing general anesthesia through a detailed examination of spectral and entropic measures.

Methods:

We retrospectively studied 180 frontal EEG recordings from patients undergoing general anesthesia, induced with propofol/fentanyl and maintained by sevoflurane at the Waikato Hospital in Hamilton, New Zealand. We calculated power spectral density and normalized power spectral density, the entropic measures approximate and permutation entropy, as well as the beta ratio and spectral entropy as exemplary parameters used in current monitoring systems from segments of EEG obtained prior to the onset of surgery; i.e. with no noxious stimulation.

Results:

The oldest quartile of patients had significantly lower 1/f characteristics (p<0.001; AUC= 0.84 [0.76 0.92]), indicative of a more uniform distribution of spectral power. Analysis of the normalized power spectral density revealed no significant impact of age on relative alpha (p=0.693; AUC=0.52 [0.41 0.63]) and a significant but weak effect on relative beta power (p=0.041; AUC= 0.62 [0.52 0.73]). Using entropic parameters, we found a significant age-related change towards a more irregular and unpredictable EEG (permutation entropy: p<0.001, AUC=0.81 [0.71 0.90]; approximate entropy: p<0.001, AUC=0.76 [0.66 0.85]). With approximate entropy, we could also detect an age-induced change in alpha-band activity (p=0.002, AUC=0.69 [0.60 78]).

Conclusions:

Like the sleep literature, spectral and entropic EEG features under general anesthesia change with age revealing a shift towards a faster, more irregular, oscillatory composition of the EEG in older patients. Age-related changes in neurophysiological activity may underlie these findings however the contribution of age-related changes in filtering properties or the signal to noise ratio must also be considered. Regardless, most current EEG technology used to guide anesthetic management focus on spectral features, and improvements to these devices might involve integration of entropic features of the raw EEG.

Introduction

We are experiencing a strong shift in population demographics towards an aging society.¹ This shift is going to result in an increased number of surgeries in geriatric patients.² Older patients are at higher risk of developing adverse outcomes like delirious episodes after surgery with general anesthesia.^3,4 Electroencephalographic (EEG) monitoring devices may help to estimate the patients’ level of neurophysiologic activity and to prevent episodes of excessively high administered doses of anesthesia as characterized by EEG burst suppression. The presence of these episodes seem to represent an independent risk factor for cognitive impairments after anesthesia,^5,6 however some controversy exists regarding strategies designed to reduce the duration of burst suppression.^3,7

Despite these possible advantages, the current generation of monitoring devices does not account for age-related changes in EEG characteristics. In general, EEG characteristics during general anesthesia vary greatly among patients of different age and cognitive performance.^8–10 Older patients exhibit lower EEG amplitudes (and consequently, lower power) during wakefulness,¹¹ sleep,¹² and general anesthesia.^8,9 Previous publications have described age-related changes in power spectral density under general anesthesia to some degree,^8,9 but a detailed description of age-related differences in other aspects of quantitative EEG analysis is still missing. We investigated age-related changes in the EEG recorded from patients from 18 to 90 years under general anesthesia with the goal to (i) characterize the EEG of older patients in more detail to further understand the neurophysiological changes that occur with advanced age and to (ii) estimate the influence of these changes on current EEG -based monitoring systems. We analyzed power spectral density, normalized power spectral density, the 1/f characteristics of the power spectrum, as well as the entropic measures permutation entropy¹³ and approximate entropy¹⁴ to investigate age-related changes in the EEG activity. The 1/f characteristic and information extracted from power spectral density and normalized power spectral density analysis help to get a good (more broad-band) overview of age-related changes. The entropic measures can help to identify subtler changes in the EEG. These analytical parameters were originally developed to characterize the complexity of a time-series signal and are reported as good measures to estimate the anesthetic level of a patient.^15–17 We also used two parameters beta-ratio¹⁸ and spectral entropy,¹⁹ that are incorporated in current monitoring systems to estimate possible impact of age on the index these systems generate to reflect the (hypnotic) level of anesthesia.

Methods

We used frontal EEG records from 180 patients during general anesthesia, collected at the Waikato District Health Board Hospital in Hamilton, New Zealand. These patients gave written informed consent, and had contributed to an earlier observational study.²⁰ The ethical approval was specifically for the establishment of an anonymous EEG database that could be used for various post-hoc analyses. We selected those patients who had received propofol for induction, and sevoflurane for maintenance of anesthesia. For each patient, we selected ten seconds of artifact-free, non-burst-suppression EEG, recorded five to two minutes prior to the onset of surgery, which represent a clinical level of general anesthesia without any surgical stimulation. We recorded the EEG with either the BIS (Medtronic, Dublin, Ireland) or the Entropy Module (GE Healthcare, Helsinki, Finland) monitors at 128 and 100 Hz respectively. Raw EEG from the BIS was then resampled to 100 Hz for ease of comparison.

We estimated effect-site concentrations of sevoflurane, opioid, and propofol using standard pharmacokinetic models. We calculated the effect-site sevoflurane concentration (in minimum alveolar concentration (MAC), C_eMAC) using a simple end-tidal to brain delay model with a diffusion half-time constant (K_eo) of 144 seconds.²¹ Based on these values, we calculated age-adjusted MAC values (referenced to 1 MAC in a 40 year old, i.e. MAC₄₀) as described by Mapleson.²² Opioid concentration (in fentanyl-equivalents; 1 ng/ml of fentanyl equals 20 ng/ml of morphine) was calculated using the two-compartment model parameters in Mazoit, Butscher et al. 2007²³ for morphine, and in Shafer and Varve²⁴ for fentanyl. We estimated effect-site propofol concentrations according to the model and parameters described by Wiczling et al.²⁵

EEG analysis

Spectral analysis

We calculated the power spectral density using Thompson’s multitaper power spectral density estimate. We used the MATLAB R2015a (The MathWorks Inc., Natick, MA) pmtm function (default settings and NFFT=256). Based on power spectral density, we calculated the power in the 0.5–30 Hz range, the alpha-band power (7.8–12.5 Hz), and the beta-band power (12.5–25 Hz) as well as the lower frequency delta-band (0.4–3.9 Hz) and theta-band (3.9–7.8 Hz). We also computed a normalized power spectral density by dividing the power spectral density by the sum from 0.4 to 30.5 Hz. We used the Python based fitting oscillations & one over f toolbox using the provided MATLAB-wrapper²⁶ to identify periodic activity as well as the aperiodic component of the EEG. The fitting oscillations & one over f algorithm decomposes the power spectral density into periodic components as well as an aperiodic component that reflects 1/f like characteristics. The aperiodic component is fitted according to L=b-log(F^a) with b being the (broadband) offset, F being the frequency vector, and a being the slope. We did not consider a “knee” parameter and hence used the “fixed model” as described in the original publication.²⁶ We defined the range to detect possible oscillatory components from 1 to 30 Hz and focused on the detection of these peaks in the alpha range.

Furthermore, we obtained the relative alpha- and beta-band power by dividing the sum of power spectral density in the 8–12 Hz (alpha) or 12–25 Hz range (beta) by the sum of power spectral density in the 0.4–30 Hz range.

Entropy analysis

Entropic measures constitute a straightforward, time-domain approach to evaluate EEG features. We individually calculated approximate entropy and permutation entropy for the EEG 0.5–30 Hz range, the EEG alpha-band, and the EEG beta-band. We applied an adaptive filtering routine (Butterworth filter, order 3–5) using the MATLAB filtfilt functions that preserves the phase of the signal. So as not to include edge effects caused by filtering, we applied the filter to a 30 s EEG segment and used the central 10 s to calculate the entropies for the different frequency ranges.

For approximate entropy we used a custom routine, for permutation entropy, we adapted the my_permutation_entropy function from MATLAB Central. We chose an embedding dimension m=3 and a time delay τ=1 for permutation entropy¹⁵ and m=2 / τ=1 together with tolerance r=0.2SD for approximate entropy.²⁷ These parameter settings are commonly used for EEG analyses.^15,16,27,28 A detailed description of how to calculate the parameters can be found in the papers initially presenting the methods by Steven M Pincus for approximate entropy¹⁴ and Bandt and Pompe for permutation entropy.¹³ Approximate entropy searches for similar amplitude patterns (of length m) in the EEG and calculates the probability of the patterns remaining similar if it is extended to a length of m+1. Similar in this context means that the amplitude values between the patterns do not differ by more than the defined tolerance r. permutation entropy as an ordinal measure codes small segments of length m according to their ranks, with the highest amplitude in the segment having the highest rank. permutation entropy presents the Shannon entropy²⁹ of the probability distribution of the possible patterns (here 6, if m=3). A graphical explanation for approximate entropy and permutation entropy can be found here³⁰.

Phase-randomized surrogate analysis

In order to clearly delineate the specific contribution of extracting information from the entropic measures vs the spectral measures of a signal we used phase-randomized surrogate data. We calculated 200 phase-randomized surrogates for each of the 180 EEG episodes and compared the entropic measures to the spectral EEG band powers. For surrogate generation we used a modified version of the surrogate function for phase randomization of the PhysioNet Toolkit³¹. We modified this function, so that no amplitude transformation, but only a phase randomization was performed. We then calculated the approximate entropy and permutation entropy for the alpha and beta range as well as the relative alpha- ad beta band power for the surrogates.

Parameters for comparison to available monitors

In order to estimate the influence of age on available monitoring systems like the BIS and Entropy module we calculated the beta ratio=log(sum(power spectral density_30–47Hz)/sum(power spectral density_11–20Hz)) as proxy for the sub-parameter BetaRatio of the BIS.³² We further calculated the spectral entropy of the normalized power spectral density for settings mimicking the state entropy (to 32 Hz) and response entropy (47 Hz) for different lower band limits of 0.8 and 1.1 Hz.¹⁹ For 168 of the 180 patients we also had BIS indices available. In order to evaluate the influence of age on BIS, we used the last index value displayed within the 10 s analysis window we used for spectral and entropic analysis.

Statistical analysis

Because of the retrospective nature of our investigation, no statistical power calculation was conducted prior to the study and the sample size was based on the available number of patient EEG. Our spectral analyses (except the spectral entropy with the 1.1 Hz lower limit were a priori and the entropic analyses (approximate entropy, permutation entropy) were post hoc analyses after evaluating different parameter settings.

Regression analyses

We generated models using the least squares method for linear regression analysis for each dependent variable with respect to age. For each linear model, we generated the regression curve and performed a one-sample t-test comparing the slope coefficient against a slope of zero. Additionally, we determined the strength of the correlation, or rather the fit of the model as an R² value.

Evaluation of interaction between sevoflurane concentration and EEG parameters

In order to evaluate if the EEG parameters (i.e., permutation entropy and approximate entropy, differ significantly based on an interaction between age and age-adjusted MAC at a 5% significance level, we calculated the linear model interaction terms using the MATLAB fitlm function.

Comparison of the youngest versus the oldest quartiles

For each parameter, we compared the youngest 25% (n=46, 1^st quartile, Y25) and the oldest 25% (n=46, 4^th quartile, O25) of patients using a Mann-Whitney U test at a confidence level of 95% together with the area under the receiver operator characteristics curve (AUC) and 10000-fold bootstrapped 95% confidence intervals (CI) as effect size. We used the MATLAB-based MES toolbox for AUC and 95% CI calculation.³³ By including all subjects of a certain age our youngest and oldest quartiles each contained 46 subjects (not 45). Our excluded middle age range (44 to 72 years old) contained 88 instead of the expected 90 subjects. According to the traditional academic point system, AUC values can be interpreted as excellent: 1≥AUC≥0.9; good: 0.9>AUC≥0.8; fair: 0.8>AUC≥0.7; poor: 0.7>AUC≥0.6; or fail: AUC<0.6. For the (normalized) power spectral density comparison, we only defined significant results if at least two neighboring frequencies showed significant differences between the young and old group. This procedure has been applied for similar studies , by other groups.³⁴

All tests applied were two-tailed tests and we considered p<0.05 being significant.

Results

Of 234 patients undergoing surgical intervention with propofol induction and sevoflurane maintenance, 54 patients were excluded from analysis due to missing EEG or incomplete volatile anesthetic concentrations data in the period prior to surgery onset, resulting in 180 patients being included in the final analysis. The subject ages ranged from 18 to 90 years (mean (SD) = 56.7(18.4) years). The age range for the youngest 25% (Y25) was from 18 to 43 years and for the oldest 25% (O25) from 73 to 90 years. Figure 1 presents a flow chart of patient and group selection. The results of all linear regressions as well as all the comparisons between the youngest 25% and the oldest 25% are presented in Table 1.

Figure 1:

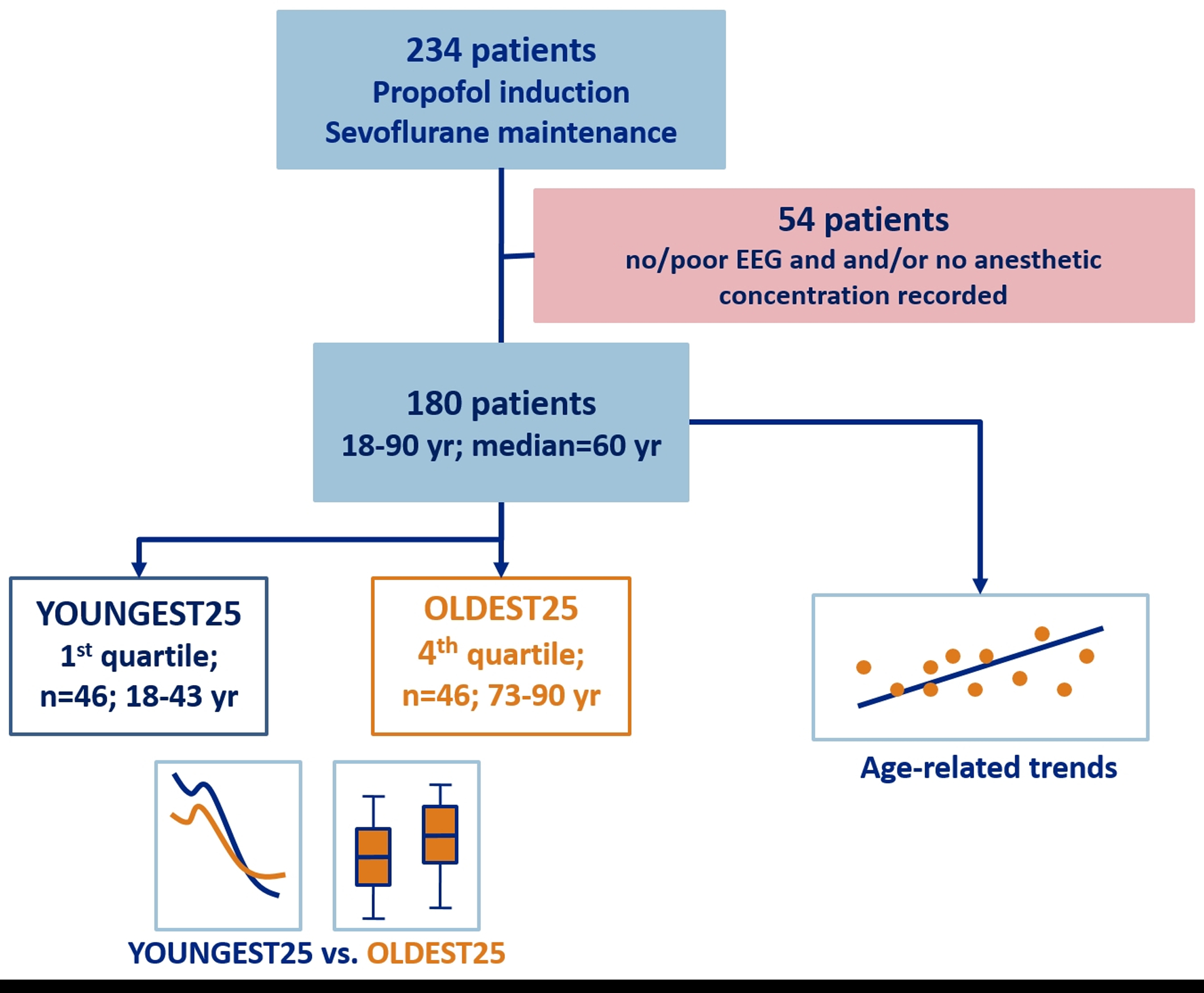
Flow chart of the excluded patients and groups defined for analysis

Parameter	Intercept	Slope	95% CI Slope	t-Stat	p Slope	R2	Youngest 25%	Oldest 25%	p (Ranksum)	AUC
EEG Band Power
Absolute Delta	37.66	−0.15	[−0.18 −0.13]	−10.99	<0.001	0.40	32.72 [30.80 35.87]	5.98 [23.90 28.36]	<0.001	0.94 [0.89 0.98]
Absolute Theta	29.82	−0.17	[−0.20 −0.15]	−13.13	<0.001	0.49	24.13 [22.33 26.93]	16.02 [13.85 19.27]	<0.001	0.93 [0.86 0.98]
Absolute Alpha	30.71	−0.18	[−0.20 −0.15]	−12.25	<0.001	0.46	24.81 [21.85 28.19]	17.77 [15.31 19.72]	<0.001	0.92 [0.86 0.98]
Absolute Beta	23.02	−0.13	[−0.16 −0.10]	−9.74	<0.001	0.35	18.30 [16.29 21.04]	13.75 [10.02 15.24]	<0.001	0.90 [0.83 0.96]
Relative Delta	0.69	0.000	[−0.001 0.002]	0.53	0.599	0.00	0.76 [0.69 0.82]	0.75 [0.63 0.83]	0.806	0.52 [0.40 0.63]
Relative Theta	0.11	0.000	[−0.001 0.000]	−0.77	0.445	0.00	0.10 [0.07 0.12]	0.09 [0.06 0.13]	0.375	0.55 [0.43 0.68]
Relative Alpha	0.17	−0.001	[−0.002 0.000]	−1.36	0.176	0.01	0.10 [0.08 0.17]	0.10 [0.07 0.17]	0.693	0.52 [0.42 0.63]
Relative Beta	0.02	0.000	[−0.000 0.001]	1.78	0.077	0.02	0.03 [0.02 0.04]	0.04 [0.02 0.06]	0.041	0.62 [0.52 0.73]
Fitting Oscillations & One Over f
Exponent	2.65	−0.009	[−0.011 −0.007]	−8.14	<0.001	0.27	2.36 [2.19 2.60]	2.00 [1.89 2.16]	<0.001	0.84 [0.76 0.92]
Offset	−0.43	−0.008	[−0.009 −0.006]	−8.27	<0.001	0.29	−0.59 [−0.90 −0.48]	−0.96 [−1.15 −0.85]	<0.001	0.81 [0.71 0.89]
Entropic Measures
Permutation Entropy 0.5–30 Hz	1.97	0.002	[0.001 0.003]	7.04	<0.001	0.22	2.02 [1.98 2.07]	2.11 [2.06 2.15]	<0.001	0.81 [0.71 0.90]
Permutation Entropy Delta	1.34	0.000	[−0.000 0.001]	1.67	0.097	0.02	1.35 [1.32 1.37]	1.36 [1.34 1.38]	0.129	0.59 [0.48 0.70]
Permutation Entropy Theta	1.72	0.000	[−0.000 0.000]	1.12	0.263	0.01	1.72 [1.70 1.75]	1.73 [1.71 1.75]	0.219	0.57 [0.44 0.71]
Permutation Entropy Alpha	1.92	0.000	[−0.000 0.000]	0.69	0.489	0.00	1.92 [1.91 1.95]	1.93 [1.91 1.95]	0.384	0.55 [0.43 0.67]
Permutation Entropy Beta	2.21	0.001	[0.001 0.001]	4.95	<0.001	0.12	2.24 [2.20 2.27]	2.27 [2.24 2.29]	<0.001	0.71 [0.61 0.80]
Approximate Entropy 0.5–30 Hz	0.76	0.002	[0.001 0.003]	4.87	<0.001	0.12	0.83 [0.77 0.89]	0.93 [0.84 0.99]	<0.001	0.76 [0.66 0.85]
Approximate Entropy Delta	0.41	−0.001	[−0.001 −0.001]	−2.20	0.029	0.03	0.40 [0.34 0.44]	0.37 [0.33 0.41]	0.088	0.60 [0.50 0.70]
Approximate Entropy Theta	0.62	0.000	[−0.000 0.000]	−1.95	0.052	0.02	0.61 [0.61 0.62]	0.61 [0.60 0.62]	0.143	0.59 [0.46 0.71]
Approximate Entropy Alpha	0.55	0.001	[0.000 0.001]	4.18	<0.001	0.09	0.57 [0.56 0.59]	0.60 [0.57 0.62]	0.002	0.69 [0.60 0.78]
Approximate Entropy Beta	1.01	0.001	[0.001 0.001]	2.44	0.016	0.03	1.05 [1.00 1.08]	1.08[1.03 1.12]	0.007	0.66 [0.55 0.77]
Monitoring Parameter
BIS	33.96	0.16	[0.078 0.24]	3.84	<0.001	0.08	42 [32 44]	45 [40 51]	0.026	0.65 [0.52 0.76]
Beta Ratio	−4.74	0.02	[0.01 0.02]	5.00	<0.001	0.12	−4.20 [−4.63 −3.71]	−3.61 [−4.02 −3.27]	<0.001	0.73 [0.63 0.82]
Spectral Entropy (1.1–32 Hz)	2.73	0.007	[0.005 0.01]	5.81	<0.001	0.16	3.02 [2.78 3.17]	3.25 [3.13 3.46]	<0.001	0.79 [0.70 0.87]
Spectral Entropy (1.1–47 Hz)	2.73	0.007	[0.005 0.010]	6.08	<0.001	0.17	3.02 [2.79 3.18]	3.29 [3.18 3.47]	<0.001	0.80 [0.71 0.88]
Spectral Entropy (0.8–32 Hz)	2.64	0.002	[−0.002 0.005]	0.79	0.433	0.00	2.72 [2.31 2.91]	2.78 [2.50 3.16]	0.202	0.58 [0.47 0.68]
Spectral Entropy (0.8–47 Hz)	2.64	0.002	[−0.002 0.006]	0.37	0.372	0.00	2.73 [2.31 2.91]	2.79 [2.51 3.16]	0.161	0.58 [0.47 0.69]

Abbreviations:; BIS: bispectral index; CI: confidence interval;

Medications

Despite the lack of any prescribed anesthetic protocol, the delivered sevoflurane concentration was lower in the older patients. We could eliminate this trend by age-adjusting the MAC according to Mapleson.²² Similarly, the estimated propofol concentration decreased with age. By contrast, our data did not reveal any age-related difference in the opioid concentrations, measured in fentanyl equivalents. Supplemental Figure S1 presents the details and corresponding plots for describing the drug dose to age relationships. While the relationships for propofol and sevoflurane and age were statistically significant, the R²-values were rather low (R²≤0.06), indicating substantial contribution by other unmeasured factors. These results may reflect that the providers in our study consider age in their titration of dosages of propofol and sevoflurane but other nuanced factors go into decisions on opioid administration (e.g., surgery type, hemodynamic changes).

Older patients exhibit a more uniform distribution of relative spectral power

We obtained very similar age to power spectral density relationships as presented in a previous study⁹ and provide the results and the corresponding plots as supplemental data in Figure S2 and Figure S3. The normalized power spectral density showed significant differences only in the low (0.5–5 Hz) and high (>21 Hz) frequency ranges when comparing the youngest 25% versus the oldest 25% patients (Figure 2A). Figure 2B presents exemplary traces from the youngest 25% and the oldest 25% group.

Figure 2: normalized power spectral density exemplary raw EEG traces, and the aperiodic (1/f) component from young and old patients.

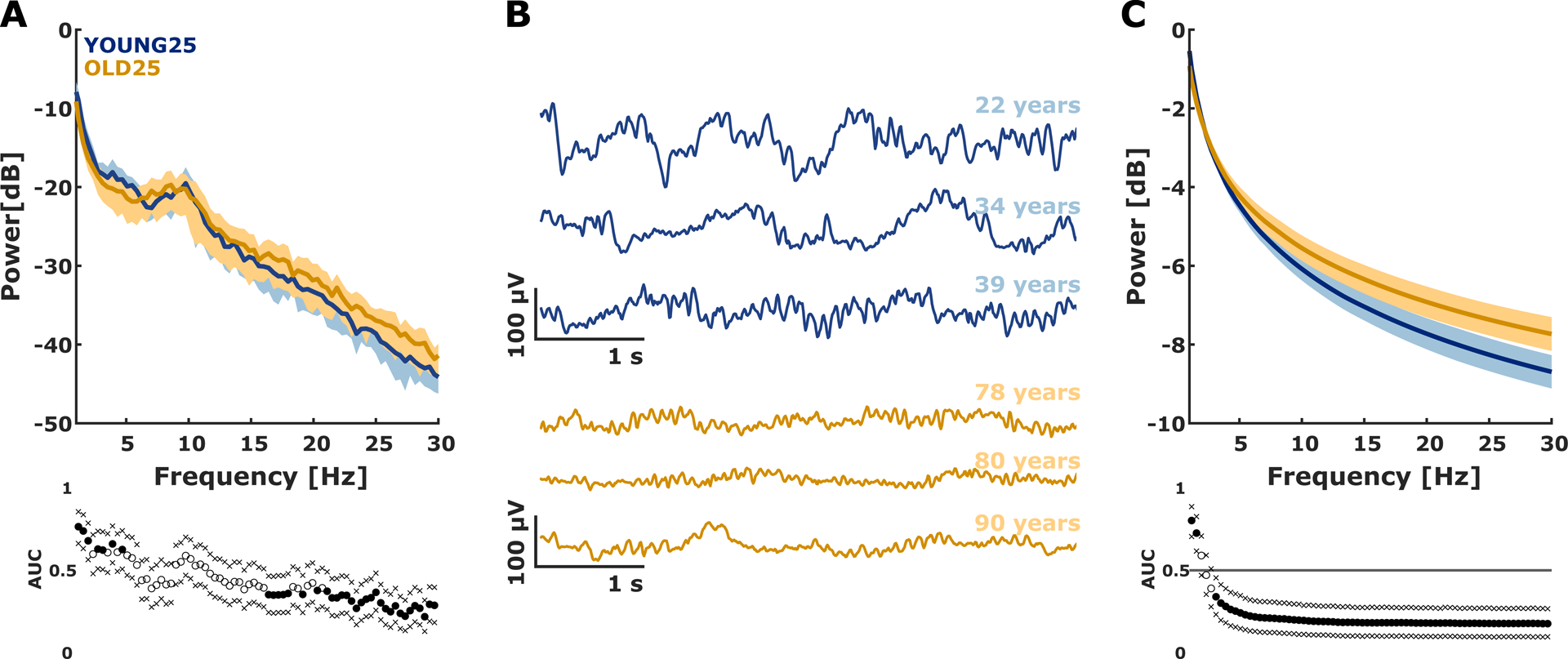
A) Median (±median absolute deviation) normalized power spectral density plots of EEG derived from the Y25 (blue) and O25 (orange) patients of the data set. power spectral density is presented with corresponding AUC values and bootstrapped 95% confidence intervals. The relative power spectral density indicated a more uniform distribution of the EEG from the old group with lower relative power at low frequencies (0.5–5 Hz) and higher relative power at high frequencies (>21 Hz).

B) Exemplary raw EEG traces from patients in the Y25 group (blue) and O25 group (orange). These traces highlight the age-induced differences on the EEG, especially fewer slow oscillations and an increased amount of high frequent activity.

C) Median (±median absolute deviation) of the exponential fit of the aperiodic (background) 1/f component between the Y25 (blue) and O25 (orange) patients. In addition, the AUC values and 95% bootstrapped confidence intervals are presented. In general, the aperiodic component of the power spectral density was more uniformly distributed in the old patients.

Filled circles indicate a significant difference, between Y25 and O25 evaluated by AUC confidence intervals excluding 0.5. The areas of light colors indicate the median absolute deviation. In the boxplots, the circles indicate outliers as defined by the MATLAB plotting routine. They were not excluded from analysis. Y25: youngest 25% O25: oldest 25%

We did not find significant differences between the youngest 25% and the oldest 25% in normalized power spectral density in the EEG alpha range (p=0.693; AUC=0.52 [0.42 0.63]) (Figure 3A) but a “poor” and significant effect (p=0.041; AUC= 0.62 [0.52 0.73]) in the EEG beta range (Figure 3B) as we did not observe a linear relationship of age with relative alpha and beta power and the difference in relative beta power. We take these results as evidence that age induces a change in the EEG, but that these changes may not be reliably detected by using the power in the classical frequency ranges. The evaluation of the relative power in the lower frequency delta and theta band did not show any age induced effects as well (Figure S4).

Figure 3: Linear regression and box plots of the youngest vs. the oldest quartile for (A) the relative (normalized) EEG alpha power, (B) the relative EEG beta power, and (C) the slope of the aperiodic 1/f component with corresponding box plots.

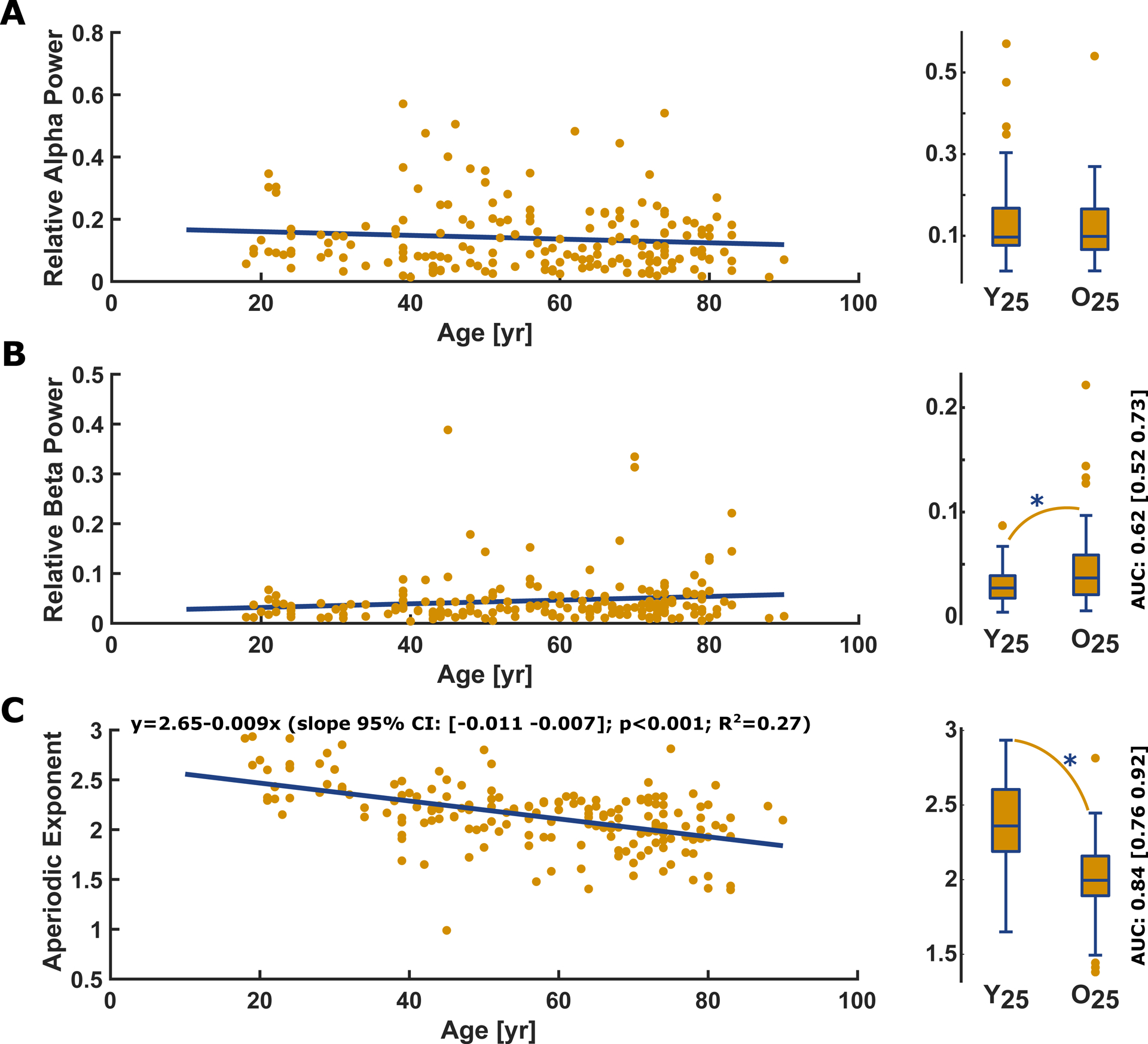
A) Relative power in the alpha-band EEG did not significantly (p= 0.176, t-statistic: −1.36) change with age. There was no significant difference (p= 0.693, AUC= 0.52 [0.42 0.63]) in relative alpha power between Y25 (0.10 [0.08 0.17]) and O25 (0.10 [0.07 0.17]).

B) Relative EEG beta power did not significantly (p=0.077, t-statistic: 1.78) change with age, but there was a significant difference (p= 0.041) in relative beta power between Y25 (0.03 [0.02 0.04]) and O25 (0.04 [0.02 0.06]). The AUC=0.62 [0.52 0.73] as effect site indicated a “poor” effect

C) The slope of the aperiodic 1/f component derived by the fitting oscillations & one over f algorithm significantly decreased with age (p<0.001, t-statistic: −8.14). The box plot indicates a significant flatter (p<0.001) slope in O25 patients (median [1^st 3^rd quartile]: 2.00 [1.89 2.16]) compared to the Y25 (2.36 [2.19 2.60]). The AUC=0.84 [0.76 0.92] as effect site indicated a “good” effect.

In the regression plots, the yellow dots present the single patients and the blue line the linear fit. Y25: youngest 25% O25: oldest 25%; yr: year

The fitting oscillations & one over f analysis revealed that in 174/180 patients (97%) at least one oscillatory component in the 8–12 Hz alpha range could be observed. Because the six patients without such a periodic component were distributed over the age range, we decided to keep these patients included. The parameters of the aperiodic component of the normalized power spectral density changed with age (Figure 3C). For the comparison between the youngest 25% and the oldest 25% the exponent was affected significantly and strongly (p<0.001, AUC= 0.84 [0.76 0.92]) by age as was the offset (p<0.001, AUC=0.81 [0.71 0.89]. Figure 2C shows the more uniform distribution of the aperiodic 1/f component of the power spectral density in the old patients.

Age related changes can be observed using entropy-based analyses

permutation entropy increased with age in the 0.5–30 Hz range as well as in the EEG beta range, but not in the EEG alpha range EEG (Figure 4A–C). Comparing the youngest 25% and the oldest 25%, we found a strong and significant (p<0.001, AUC=0.81 [0.71 0.90]) effect of age on the (0.5–30 Hz) filtered EEG and a fair and significant (p=0.0006, AUC=0.71 [0.61 0.81]) effect on the beta band EEG. We found no significant difference for the alpha band EEG (AUC=0.55 [0.43 0.67], p=0.384). These results signify that permutation entropy tracks the shift towards higher-frequency EEG activity with age.

Figure 4: Permutation entropy (m=3, τ=1): Linear regression and box plots of the youngest vs. the oldest quartile for the (A) 0.5–30 Hz range, (B) the alpha range, (C) and the EEG beta range.

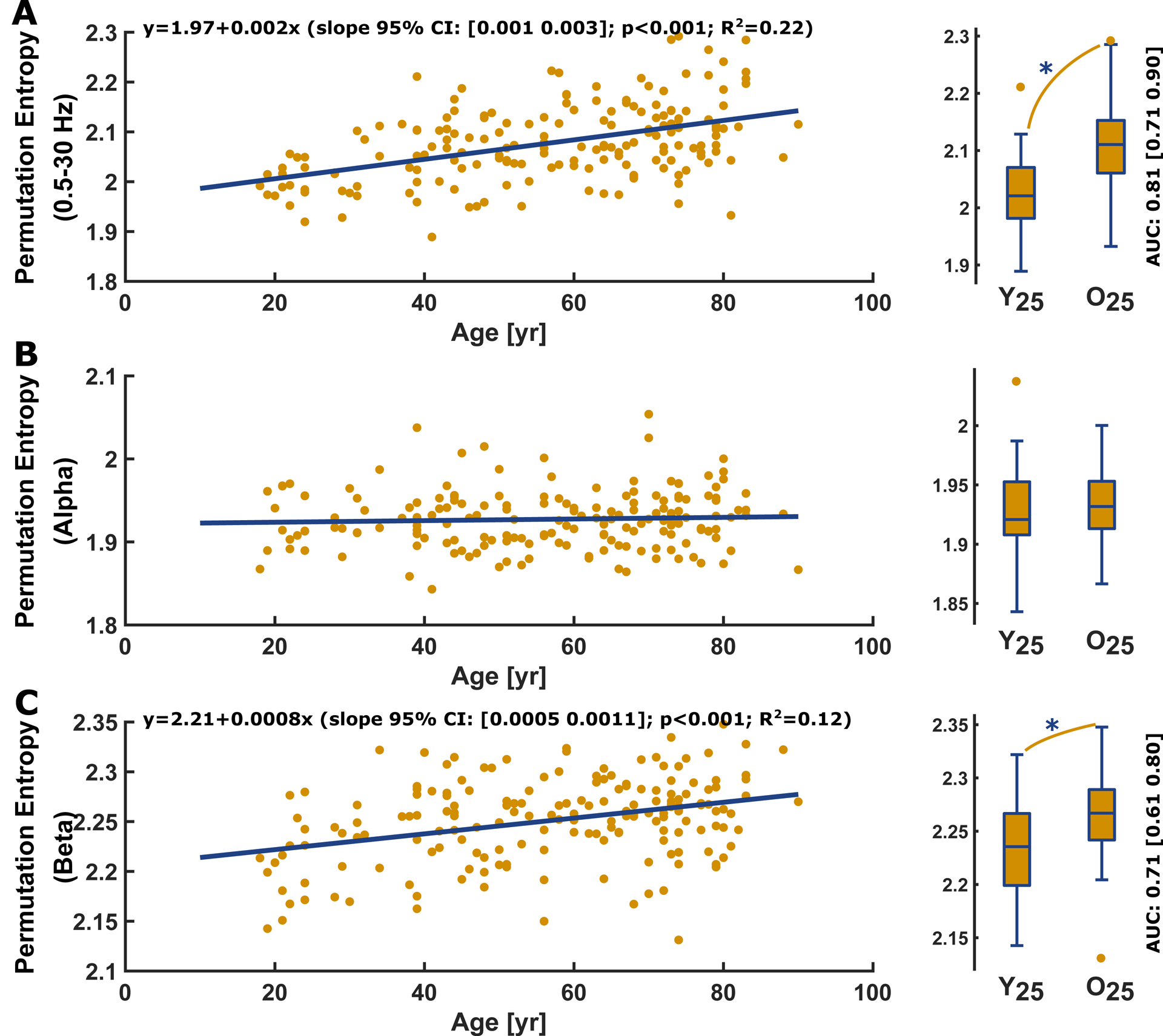
A) Permutation entropy of the 0.5–30 Hz filtered EEG significantly increased (p<0.001, t-statistic: 7.04) with age. Age had a “good” and significant (p<0.001; AUC=0.81 [0.71 0.90]) effect on permutation entropy as depicted in the comparison between Y25 (2.02 [1.98 2.07]) and O25 (2.11 [2.06 2.15]).

B) Permutation entropy of the alpha-band EEG showed no significant age-related effect (p=0.489, t-statistic: 0.69) and the AUC for the comparison between Y25 and O25 indicated no effect (p=0.384; AUC=0.55 [0.43 0.67]).

C) Permutation entropy of the beta-band EEG significantly (p>0.001, t-statistic: 4.95) increased with age. Age had a “fair” and significant (p<0.001; AUC= 0.71 [0.61 0.80]) effect on permutation entropy as depicted in the comparison between Y25 (2.24 [2.20 2.27]) and O25 (2.27 [2.24 2.29]).

In the regression plots, the yellow dots present the single patients and the blue line the linear fit. In the boxplots, the circles indicate outliers as defined by the MATLAB plotting routine. They were not excluded from analysis. Y25: youngest 25% O25: oldest 25%; yr: year

approximate entropy of all three frequency ranges increased with age (Figure 5A–C). The comparisons of approximate entropy for the youngest 25% and the oldest 25% patients revealed a significant and moderate to strong effect of age in the 0.5–30 Hz range (p<0.001, AUC=0.76 [0.66 0.85]), in the EEG alpha range (p=0.002, AUC=0.69 [0.60 0.78]), as well as in the EEG beta range (p=0.007, AUC=0.66 [0.55 0.77]). The fact that approximate entropy, in contrast to permutation entropy, revealed an effect on the alpha-band possibly indicates a higher sensitivity of approximate entropy to lower frequencies.

Figure 5: Approximate entropy (m=2, r=0.2SD, τ=1) vs. age and corresponding youngest vs. oldest quartile box plot for the (A) 0.5–30 Hz EEG range, (B) the EEG alpha range, (C) and the EEG beta range.

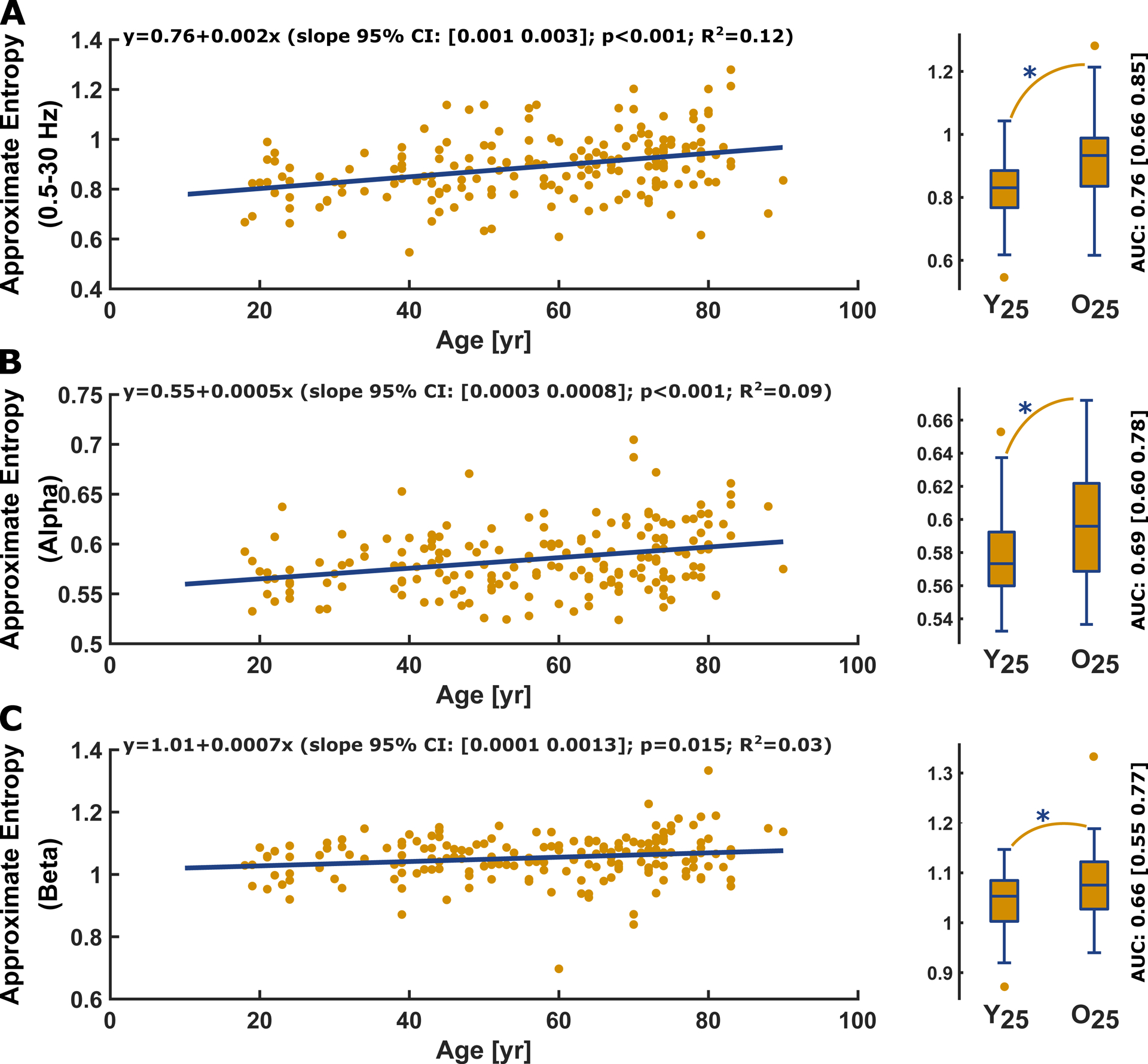
A) Approximate entropy of the 0.5–30 Hz filtered EEG significantly (p<0.001, t-statistic: 4.87) increased with age. Age had a “fair” and significant (p<0.001; AUC= 0.76 [0.66 0.85]) effect on approximate entropy as depicted in the comparison between Y25 (0.83 [0.77 0.89]) and O25 (0.93 [0.84 0.99]).

B) Approximate entropy of the alpha-band EEG significantly (p<0.001, t-statistic 4.18) increased with age. Age had a “poor”/”fair” and significant (p=0.002; AUC= 0.69 [0.60 0.78]) effect on approximate entropy as depicted in the comparison between Y25 (0.57 [0.56 0.59]) and O25 (0.60 [0.57 0.62])

C) Approximate entropy of the beta-band EEG significantly increased with age (p=0.015; AUC=0.66 [0.55 0.77]). Age had a “fair” and significant effect on approximate entropy as depicted in the comparison between O25 (1.08[1.03 1.12]) and Y25 (1.05 [1.00 1.08]) of the data set.

In the regression plots, the yellow dots present the single patients and the blue line the linear fit. In the boxplots, the circles indicate outliers as defined by the MATLAB plotting routine. They were not excluded from analysis. Y25: youngest 25% O25: oldest 25%; yr: year

The entropic parameters did not undergo an age-related change in the slower dynamics, i.e., when applied to the EEG filtered to the delta and theta range. We present the detailed statistical parameters in Table 1 and the corresponding regression and box plots in the supplemental Figure S5.

Surrogates

The surrogate analysis revealed a lower regression line for approximate entropy in the alpha and beta band as well as for permutation entropy in the beta band for the original signals. The phase randomization had no influence on the relative alpha- and beta band power. The supplemental Figure S6 shows the corresponding plots.

Monitoring parameters show age-related changes

We used the beta ratio and spectral entropy to estimate a possible influence of age on neurophysiological measures as implemented in commonly used monitoring systems. The BIS revealed a strong dependence on age as did the spectral entropy for the 1.1 to 32 Hz and 1.1 to 47 Hz range (Table 1 and Figure S7). The comparison of the youngest 25% and the oldest 25% revealed significant and fair effects of age on beta ratio (p<0.001, AUC=0.73 [0.63 0.82]) and spectral entropy (1.1–32 Hz: p<0.001, AUC=0.79 [0.70 0.87]; 1.1–47 Hz: p<0.001, AUC=0.80 [0.71 0.88]. For the 0–8 to 32 Hz (p=0.202; AUC=0.58 [0.47 0.68]) or 47 Hz (p=0.161; AUC=0.58 [0.47 0.69]), we could not observe a significant difference with age. These results indicate an influence of age on the (sub-) parameters that are used to track neurophysiological changes in EEG-based monitoring systems which seems strongly dependent on the frequency range. For the sample of 168 patients we could observe an increase of the recorded BIS with age (linear regression: p>0.001, t-statistic: 3.84; youngest 25% vs. the oldest 25%: P=0.026, AUC=0.65 [0.52 0.76])

Discussion

Our results show that age-dependent changes in EEG characteristics during general anesthesia extend beyond a mere decrease in EEG amplitude. Our demonstrable changes in power spectral density of the EEG recorded under general anesthesia have been reported by other groups.^8,9 The absolute power decreases with age in every frequency range. After normalization, we found that delta oscillations contributed less to total power with age, while (high) beta oscillations contributed more. The change in the 1/f characteristics as revealed by the fitting oscillations & one over f analysis confirm this finding. We did not observe a significant change in the relative power in the specific bands, but the additional usage of entropic parameters revealed that these parameters are capable of tracking subtler changes in the oscillatory composition of the EEG that are not detected by power spectral density based approaches, also in the alpha- and beta band. The entropic parameters seem to analyze additional content in the signal as shown by surrogate analysis. The higher entropies in the surrogates point towards a loss in deterministic signal properties, as has been also reported earlier.³⁵ The monitoring parameters BIS, BetaRatio, and spectral entropy were also affected by age, a finding highlighting that age adjustments should be considered for monitoring.

Influence of age on EEG amplitude and power spectral density

Reductions in grey matter, including cortical thinning,^36–40 or a decrease in skull conductance⁴¹ with age cause a decrease in EEG amplitude, and hence lower power spectral density. Furthermore, the EEG amplitude also depends somewhat on neuronal synchrony, but it is unknown at present to what extent this is altered by aging.⁴²

Age influences EEG spectral power

Our power spectral density analyses are in line with previously published findings, i.e., power spectral density decreases with age⁹. The body of knowledge we can add to these results is the more uniformly distributed normalized power spectral density that is reflected by a flatter (aperiodic) 1/f slope. Schultz et al.⁸ reported changes in relative band power for propofol anesthesia and other groups for non-rapid eye movement sleep.^12,43 Age-related cortical activation during non-rapid eye movement sleep seems to increase relative beta power,¹² a scenario that sounds plausible for our findings under general anesthesia as well. Further, aged women had lower relative EEG delta-band and higher beta-band power during wakefulness and rapid eye movement sleep compared to a middle-aged group.⁴⁴ In general, there may be a number of potential explanations that cause the observed shift in the relative power spectrum. An increase of neural noise may be one of them. Older test subjects had a flatter 1/f slope during visual tasks, due to increased neural noise.^42,45 This increase does not have to represent a more aroused brain state since recent research found increased higher beta-frequencies to be associated with poorer memory test outcome in geriatric women.⁴⁶ Volunteers with eyes closed exhibited higher beta-coherence with age, indicative of higher synchrony in this frequency range.⁴⁷ But, besides a possible increase in neural noise, the changes in spatiotemporal filtering properties may be due to a change of age-related, physiological changes affecting the cortex⁴⁰ for instance the extracellular space, which can act as 1/f filter.⁴⁸ Further, age, and the decline in EEG power also reduces the signal to noise ratio, as e.g. shown in experiments with event-related potentials.⁴⁹ Our findings may either reflect increased cortical neural noise, i.e., spiking not correlated to oscillatory activity in the elderly brain, the age-induced change of physiological 1/f filtering properties, or changes in the signal to noise ratio of the EEG with age, or a combination of these factors. Our observational study was not designed to closely investigate the cause for the flatter slope. The results further showed that the relative alpha and beta-band power was not affected by age. This information could become important for the design of future monitoring devices but does also question the use of this approach to investigate age-related changes. Entropic measures in the time domain, like approximate entropy and permutation entropy, provide information separate from spectral features.^15–17,27 An understanding of both spectral and entropic features may broaden our clinical model of estimations regarding consciousness in patients under general anesthesia

Older patients express higher signal entropy

Our findings showed increasing approximate entropy and permutation entropy (except in the alpha-band) values with age. The results of approximate entropy and permutation entropy differ to some degree, because both parameters may target different EEG characteristics.⁵⁰ permutation entropy is regarded as superior to approximate entropy in distinguishing conscious from unconscious EEG,^16,17,51 while approximate entropy performs better than permutation entropy in tracking different levels of anesthesia.¹⁷ These differences are in accordance with the strong effect of age on permutation entropy in the high frequencies (beta-band), as well as the ability of approximate entropy to identify differences in the alpha band – where permutation entropy showed no contrast. The age-related increase in entropic measures seem to apply to other vigilance states and encephalographic modalities as well: in a magnetoencephalography study, permutation entropy increased with age in volunteers that were awake with their eyes closed.⁵² In general, the increase of entropic measures with age probably reflects the effect on the 1/f slope by indicating a more uniform distribution of ordinal EEG patterns (permutation entropy), and a decreased signal predictability (approximate entropy) in the elderly. In this regard, an association between permutation entropy (for m=3) and the spectral centroid of the (weighted) power spectral density was recently described.⁵³ This proposition may eventually add a general link between spectral analytical approaches and permutation entropy, such that ordinal irregularity may become usable as a proxy for changes in the oscillatory EEG composition. Admittedly, this link is still missing for approximate entropy, though. But these measures seem to track deterministic properties in the signal, in contrast to power spectral density measures. Although other settings of permutation entropy could have tracked age-related changes with higher precision, we do not know the underlying cause for that and hence we refrained from presenting the results in this manuscript. Since using lags of τ>1 could lead to unintended distortions in the signal,⁵³ we chose to apply permutation entropy with τ=1 to EEG filtered to the different frequency bands. In any case, our analyses demonstrate the sensitivity of entropic measures to subtle changes in the EEG.

Reasons for altered EEG characteristics

There is evidence that the aged brain reacts to general (sevoflurane) anesthesia differently than the young brain. In young brains, usually, a peak in the EEG alpha range develops under general anesthesia³⁴ as a marker of adequate anesthesia. This peak in the EEG alpha-band, as well as strong interhemispheric EEG alpha-band coherence³⁴ most probably is associated with thalamocortical pacemaker cells and their activity spreading to the cortex.⁵⁴ Older and cognitively impaired patients express lower alpha power and alpha coherence during general anesthesia.^9,10,55 We did not observe an influence of age using the relative alpha-band power, a finding that is in line with Schultz et al., who found age related differences in relative alpha power only at very profound levels of propofol anesthesia.⁸

Hence, the described decrease in alpha power may be due to the general decrease in EEG amplitude with age.

Although we did not see an influence of age in relative alpha-band power in our results, approximate entropy of the alpha-band revealed a significant change. Because strong and synchronous (i.e., low approximate entropy) alpha oscillations may correlate with good cognitive function and better outcomes after general anesthesia,^10,56,57 this parameter may be useful to identify patients with a ‘frail’ brain using EEG recordings during general anesthesia in the future. For both entropic parameters we observed changes in the EEG beta range. This frequency range seems associated with an activated cortex and intracortical as well as corticocortical information processing.^54,58 Hence our findings of a flatter 1/f slope may reflect a state of higher cortical activation in the elderly, or a higher influence of noise. During visual tasks the flatter 1/f slope may represent a decoupling of (cortical) population spiking activity from an oscillatory regimen.⁴² Furthermore, findings from sleep research indicate that the EEG of older subjects during sleep may be closer to the wake state than in middle-aged to young subjects.⁴⁴ At the same time, age seems to affect thalamocortical regulatory mechanisms during sleep as expressed by lower sleep spindle density, duration, and amplitude.⁵⁹ In general, the EEG of older patients may have a smaller dynamic range. During the awake state, the EEG is slower in the older population⁸ and it shows increased relative beta power during general anesthesia. Hence, the aged brain may not be capable of expressing activated or synchronized activity to the same degree that the young adult brain is capable of. In conclusion, a difference between chronologic vs. functional brain age should be considered to reveal functional-age-related differences in the EEG in more detail. Young patients with potential for having a frail brain can express EEG activity typical for an old patient.⁵⁵ Furthermore, (mild) cognitive impairments like early-stage Alzheimer’s seem to change the EEG architecture in a similar fashion as aging.⁶⁰

Implications for titration of anesthesia

We utilized BIS, beta ratio and spectral entropy to estimate the presumed behavior of existing monitoring systems. In general, these parameters exhibited an increase with age. Consequently, our results hint at a possible influence of age on the indices of commonly used EEG monitors (BIS and GE Entropy) towards a lower dose. But the presented BIS values may not correlate with our analyzed EEG segments because of a considerable time delay of up to 60 s.^61,62 Still, recent findings from Ni et al. show higher BIS in older adults, hence emphasizing our results.⁶³ At least some of the commercially available monitors were developed using data from rather young adult subjects.⁶⁴ A study found that at the propofol-induced loss of consciousness, older patients expressed higher BIS and state entropy values, projecting a “more awake” EEG by means of the indices.⁶⁵ These and our own findings imply that future EEG -based “depth of anesthesia” monitoring systems should account for patient age, or use parameters not affected by age. In our data limited to EEG during unstimulated unconsciousness, relative alpha and beta power did not change with age but showed considerable variability. Hence, a possible use for monitoring purposes has to be investigated more thoroughly.

Limitations

General anesthesia was not conducted by any strict protocol but navigated by best clinical practice. For sevoflurane, we could overcome a possible limitation of age and drug requirement by using age-adjusted MAC estimates.²² While we did find a decrease in residual propofol concentration with age, lower propofol requirements with age have been reported previously.⁶⁶ Some patients also received opioids, but these concentrations did not show any age-related trend. We did not evaluate the EEG characteristics during general anesthesia with surgical stimulation. We also cannot make a statement regarding age-related EEG changes for other anesthetic drugs triggering different EEG patterns and having different receptor targets – like ketamine or dexmedetomidine. Although, we did not observe any consistent age-related differences in the sevoflurane MAC and the opioid concentration, we cannot completely exclude a complex confounding relationship between age and anesthetics or opioids. To tease out these relationships would require some, specific, tightly controlled, prospective interventional studies. Another limitation is that we only recorded single channel EEG. We could thus not evaluate the influence of age on multivariate parameters, and cannot add information to reported changes in spectral coherence with age.⁹ And ultimately, the EEG is a signal originating from a large number of (mainly) cortical neurons and transmitted through layers of cerebrospinal fluid, bone, skin, and hair.⁶⁷ Hence, we refrain from drawing mechanistic conclusions on the receptor level. Still, an age-related influence on inhibitory network activity is highly likely.

In conclusion, we could show that the EEG under general anesthesia changes with age towards activity patterns of higher frequencies that cause a flatter 1/f slope of power spectral density as well as an increase of entropic measures. These changes may be due to changes in neurophysiological filtering properties or the signal to noise ratio. But in general, patient age should be taken into account when using the EEG. Current, EEG -based monitoring approaches do not seem to correct for it.

Supplementary Material

Revised, with caption_1

Figure S1: Different drug concentrations versus age; yr: year

A) There was a significant linear trend between sevoflurane MAC and age, before age adjustment.

B) After age adjustment according to Mapleson¹⁹ there was no significant trend for sevoflurane MAC and age.

C) There was a significant trend with residual propofol and age.

D) There was no significant trend between opioids delivered and age.

In the regression plots, the yellow dots present the single patients and the blue line the linear fit. In the boxplots, the circles indicate outliers as defined by the MATLAB plotting routine. They were not excluded from analysis; yr: year

Revised, with caption_2

Figure S2: Power spectral density of the youngest and oldest quartile and the entire data set

A) Median (±median absolute deviation) power spectral density plots of EEG derived from the 46 youngest (blue) and 46 oldest (yellow) patients of the data set. power spectral density is presented with corresponding AUC values and bootstrapped 95% confidence intervals. Solid dots indicate a significant difference between old and young.

B) Absolute power spectral density for each single patient, sorted by age displayed as heat map or spectral array. With age the colors tend to become colder in all frequencies, reflecting the age-dependent decrease in spectral power. In the boxplots, the circles indicate outliers as defined by the MATLAB plotting routine. They were not excluded from analysis; yr: year

Revised, with caption_3

Figure S3: Power spectral density measures vs. age: Power vs. age and corresponding youngest vs. oldest quartile box plot for the delta power(A), the theta power (B), EEG alpha power (C) and the EEG beta power (D).

A) Delta power decreased with age (p<0.001, t-statistic −10.99) and age had an excellent and significant (p<0.001, (AUC=0.94 [0.89 0.98])) effect as depicted in the Y25 vs. O25 boxplot.

B) Theta power decreased with age (p<0.001, t-statistic −13.13) and age had an excellent and significant (p<0.001, (AUC=0.93 [0.86 0.98])) effect as depicted in Y25 vs. O25 boxplot.

C) Power in the alpha-band significantly (p<0.001, t-statistic −12.25) decreased with age. Age had had an excellent and significant (p<0.001, AUC=0.92 [0.86 0.98]) effect on absolute alpha-band power as depicted in Y25 vs. O25 boxplot

D) EEG beta power significantly (p<0.001, t-statistic −9.74) decreased with age. had an excellent and significant (AUC=0.90 [0.83 0.96]) and significant (p<0.001) effect as depicted in Y25 vs. O25 boxplot.

In the regression plots, the yellow dots present the single patients and the blue line the linear fit. Y25: youngest 25% O25: oldest 25%; yr: year

Revised, with caption_4

Figure S4: Linear regression and box plots of the youngest vs. the oldest quartile for the (A) relative EEG delta power and the (B) relative EEG theta power. Neither of them showed an age-related trend.

In the regression plots, the yellow dots present the single patients and the blue line the linear fit. Y25: youngest 25% O25: oldest 25%; yr: year

Revised, with caption_5

Figure S5: Age-induced change of approximate entropy and permutation entropy in the slow dynamics, i.e., the delta and theta range of the EEG.

A) Approximate entropy decreased with age (p=0.029, t-statistic: −2.20), but the fit was quite poor with R2=0.03. The comparison of Y25 vs. O25 did not reveal a significant difference

B) Approximate entropy did not show a n aged-induced trend in the EEG theta range

C) Age did not influence permutation entropy, when applied to the EEG filtered to the delta range.

D) Age did not influence permutation entropy, when applied to the EEG filtered to the theta range.

In the regression plots, the yellow dots present the single patients and the blue line the linear fit.

In the boxplots, the circles indicate outliers as defined by the MATLAB plotting routine. They were not excluded from analysis. Y25: youngest 25% O25: oldest 25%; yr: year

Revised, with caption_6

Figure S6: Results from the phase-randomized surrogate analysis of the parameter settings showing significant changes with age, i.e., for the approximate entropy in the alpha- (A) and beta-band (B), the permutation entropy in the beta-band (C), as well as for the relative alpha- (D) and beta-band power (E). yr: year

Revised, with caption_7

Figure S7: Age induced-change of (A) bispectral index (BIS), (B) BetaRatio, and spectral entropy for (C) the 0.8–32 Hz and (D) the 1.1–32 Hz range.

A) BIS values increased with age (p<0.001, t-statistic 3.84) and age had a “poor” but significant (p=0.026, AUC=0.65 [0.52 0.76]) effect as depicted in Y25 vs. O25 boxplot.

A) The beta ratio as proxy for the bispectral index increased (p<0.001, t-statistic 5.00) with age. Age had a “fair” (AUC=0.73 [0.63 0.82]) and significant (p<0.001) effect on beta ratio as depicted in Y25 vs. the O25 boxplot.

B) The beta ratio as subparameter of the BIS increased (p<0.001, t-statistic: 5.00) with age. Age had a “fair” and significant (p<0.001, AUC=0.73 [0.63 0.82]) effect on beta ratio as depicted in Y25 vs. O25 boxplot.

C) Spectral entropy for the 1.1–32 Hz range as proxy for the state entropy index from the Entropy Module increased (p<0.001, t-statistic: 5.81) with age. Age had a “fair” to “good” and significant (p<0.001, AUC=0.79 [0.70 0.87]) effect as depicted in the youngest 25% Y25 vs. the oldest 25% O25 boxplot.

D) Spectral entropy for the 0.8–32 Hz range as proxy for the state entropy index from the did not show a significant influence of age on spectral entropy (p=0.433, t-statistic: 0.79) with age. Age no effect (p=0.201, AUC=0.58 [0.47 0.68]) effect as depicted in Y25 vs. O25 boxplot.

In the regression plots, the yellow dots present the single patients and the blue line the linear fit. Y25: youngest 25% O25: oldest 25%; yr: year