Personalized Dosimetry for Liver Cancer Y-90 Radioembolization Using Computational Fluid Dynamics and Monte Carlo Simulation

Abstract

Yttrium-90 (Y-90) transarterial radioembolization uses radioactive microspheres injected into the hepatic artery to irradiate liver tumors internally. One of the major challenges is the lack of reliable dosimetry methods for dose prediction and dose verification. We present a patient-specific dosimetry approach for personalized treatment planning based on computational fluid dynamics (CFD) simulations of the microsphere transport combined with Y-90 physics modeling called CFDose. The ultimate goal is the development of a software to optimize the amount of activity and injection point for optimal tumor targeting.

We present the proof-of-concept of a CFD dosimetry tool based on a patient’s angiogram performed in standard-of-care planning. The hepatic arterial tree of the patient was segmented from the cone-beam CT (CBCT) to predict the microsphere transport using multiscale CFD modeling. To calculate the dose distribution, the predicted microsphere distribution was convolved with a Y-90 dose point kernel.

Vessels as small as 0.45 mm were segmented, microsphere distribution between the liver segments using flow analysis is predicted, and volumetric microsphere and resulting dose distribution in the liver volume are computed. The patient was imaged with positron emission tomography (PET) 2 hours after radioembolization to evaluate the Y-90 distribution. The dose distribution was found to be consistent with the Y-90 PET images. These results demonstrate the feasibility of developing a complete framework for personalized Y-90 microsphere simulation and dosimetry using patient-specific input parameters.

1. Introduction

Transarterial radioembolization (TARE) with yttrium 90 (⁹⁰Y), is a type of radionuclide therapy increasingly used for hepatocellular carcinoma (HCC) and liver metastases. It consists of injecting radioactive ⁹⁰Y resin or glass microspheres through the patient’s hepatic artery using a catheter to irradiate liver tumors internally. The targeted radiation delivery achieved with a minimally invasive procedure makes radioembolization attractive to treat an increasing number of liver cancer patients ³¹.

The potential of TARE in terms of patient outcome improvement is still limited by the lack of reliable treatment planning. The major obstacle is the dose calculation used to select the ⁹⁰Y activity to inject, which leads physicians to lower the ⁹⁰Y activity to limit toxicity at the expense of the dose to the tumor. Clinical dosimetry provides a single dose value for the whole liver without accounting for non-uniform microsphere distribution, tissue heterogeneity, and critical parameters such as the injection point^19,38. For example, the activity of resin microspheres (SIR-Spheres, Sirtex) is computed with the body surface area model (BSA) assuming a correlation between liver volume and BSA, which is often incorrect for liver cancer patients ²². The calculation of the prescribed activity is in fact not based on a target dose to the tumor, but simply on the BSA and the tumor volume manually determined from CT images. Alternatively, the ⁹⁰Y activity of glass microspheres (TheraSphere^®, BTG) is computed based on a single target dose encompassing tumor and liver tissue per the manufacturer instructions ¹⁶. The partition model¹⁷ has been developed to refine this calculation by separating the tumor, liver, and lungs but its accuracy is still strongly limited by the incorrect assumption of a uniform microsphere distribution in each region. These models also suffer from uncertainty added by operator-dependent steps and do not make consistent recommendations of the activity to inject to a patient. As a result, interventional radiologists do not have reliable methods to personalize the treatment, leading to an increased risk of insufficient tumor dose or severe side-effects²⁹. Recent research on radioembolization planning focuses on image-based dosimetry, using the ^99mTc macro-aggregated albumin (MAA) scan routinely done to monitor toxicity with single photon emission computed tomography (SPECT) ^5,18. However the ^99mTc-MAA SPECT spatial resolution is limited to 12 mm or larger¹² and MAA does not consistently predict the behavior of ⁹⁰Y microspheres accurately ^20,28,42.

Here, we are implementing a method that includes minimal changes to TARE clinical workflow and is based on computational fluid dynamics (CFD) simulations to predict the ⁹⁰Y microsphere 3D distribution. Using generic structures with 1-2 bifurcations, other works have demonstrated the potential of CFD to study the distribution of microspheres ^4,21. The central hypothesis of our approach is that carrying out the CFD simulations for the hepatic artery anatomy of each patient is necessary. This accounts for the large variations of anatomical features across the population¹⁴ and their complex effect on the microsphere transport, which results in non-uniform distribution of the microspheres. This has recently been demonstrated in patient-specific hepatic arterial trees approximating the blood flow with Poiseuille’s law ^10,34.

We have developed a CFD dosimetry tool, named CFDose, based on individual patient angiograms. These planning angiograms are performed to study the liver blood supply in preparation for TARE. CFDose is based on the following three steps: (1) segment the hepatic arterial tree from the patient’s planning cone-beam CT (CBCT) angiogram, (2) predict the microsphere distribution using patient-specific CFD, and (3) calculate the absorbed dose based on the microsphere distribution with ⁹⁰Y physics modeling. CFDose can be used to optimize both the quantity and injection site of ⁹⁰Y microspheres, to ensure each tumor receives a sufficient dose to eradicate it ^15,41. Alternatively, optimizing the activity and delivery can be directed at limiting the exposure of healthy liver tissues to preserve hepatic function. Recent work on microsphere transport modeling for chemo- or radio- embolization has illustrated the potential of simulation to improve the catheter design for microsphere delivery ^1-3 and suggested the importance of using patient-specific CFD to predict the microsphere transport.

In this paper, we describe the CFD-based dosimetry and demonstrate its proof-of-concept from the acquisition of the hepatic CBCT to the dose distribution map for one patient. The patient was also scanned with positron emission tomography (PET) immediately after treatment to image the distribution of the microspheres through the ⁹⁰Y activity. We are showing the dose distribution computed by CFDose with the same injection point and activity used by the physician and the acquired PET data.

2. Materials and Methods

2.1. General framework

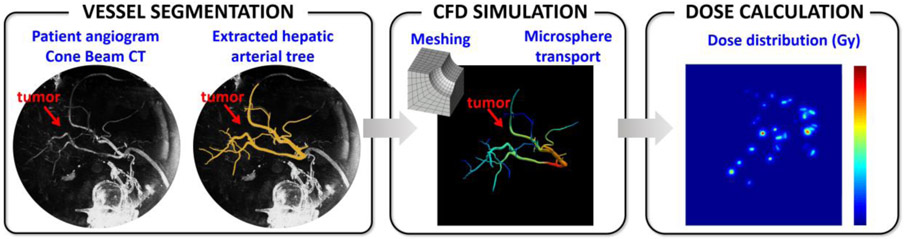
The first step is to collect the standard-of-care angiograms acquired during treatment planning to get a full picture of the liver anatomy, and segment the hepatic artery (HA) from the CBCT (Figure 1). The second step is to mesh the segmented hepatic arterial tree in order to carry out patient-specific CFD simulations to model the blood flow and microsphere transport. The end point is to estimate the microsphere distribution after the injection is completed (typically done over 15 cardiac cycles in ~12 s), when the microspheres have reached their final location to deliver most of the radioactive dose.

Figure 1. CFD-based dosimetry.

From left to right: the hepatic artery is segmented from the cone beam CT images acquired in Interventional Radiology; the segmented hepatic artery is meshed and used to carry out CFD simulations to predict the microsphere distribution; the microsphere distribution is convolved with the ⁹⁰Y dose deposition kernel to calculate the absorbed dose distribution.

The third step is the dosimetry itself, consisting in calculating the dose deposited by the microspheres from their volumetric distribution in the vasculature using a dose point kernel method.

2.2. Data collection

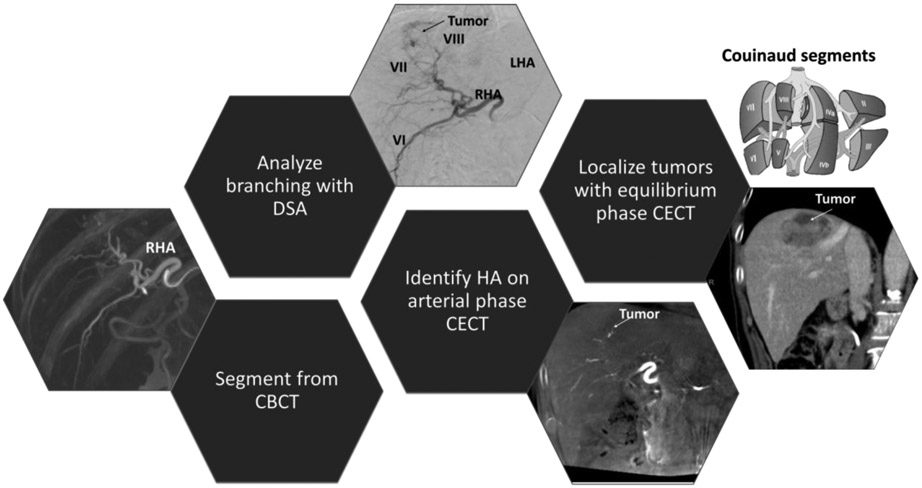
Patients enrolled in our study were referred for radioembolization after being diagnosed with liver cancer. The patient whose images are shown in Figure 2 was diagnosed with HCC in segments 7 and 8 (according to the Couinaud classification⁹) based on a 4-phase contrast-enhanced CT (CECT) obtained prior to treatment planning.

Figure 2. Multimodal imaging for hepatic artery segmentation.

Vessels are segmented from the CBCT and labelled using digital subtraction angiography (DSA) and contrast-enhanced CT (CECT) in arterial phase. The right and left hepatic arteries (RHA and LHA) and Couinaud segments (e.g. VI, VII, and VIII) are labelled using CECT and CBCT. The contrast in the tumor is higher in the equilibrium phase.

2D and 3D hepatic angiograms were acquired during standard-of-care ⁹⁰Y mapping (treatment planning) in the Interventional Radiology suite. 2D digital subtraction angiography (DSA) images were acquired at different times during the planning and were used to label the different branches and the injection sites. A radio-opaque contrast agent (Omnipaque 300) was injected in the proper hepatic artery to image the complete liver arterial tree through a catheter inserted into the femoral artery. 3D CBCT angiograms were obtained under breath-hold using a Siemens Artis Zeego angiography system (6s, 198° coverage with a 0.5° angular sampling). Images were exported as a 3D axial volume consisting of 1024 x 1024 images (pixel size of ~0.25 mm, slice thickness of 1 mm) covering the abdominal region with an axial field of view of 185 mm.

The study protocol for standard-of-care DSA and CBCT collection and post-processing was approved by the UC Davis Institutional Review Board (IRB) as a single-site, retrospective study at UC Davis Health. A separate single-site, prospective study (20 patients) was also approved by the IRB to collect CBCT, DSA, and PET images for each patient in the study at UC Davis Health. This paper demonstrates the feasibility of the full dosimetry calculation for one patient enrolled in the prospective study, and the segmentation of two patient CBCT datasets.

2.3. Hepatic artery segmentation from CBCT

2.3.1. Segmentation method

The hepatic arterial tree segmentation was done using the open-source Vascular Modeling Toolkit vmtk (www.vmtk.org). A marching cubes algorithm ²³ was employed to initialize the segmentation of hepatic arterial tree at a grey level corresponding to the isovalue of interest (~ 250-400 HU) from CBCT images (Figure 2). In order to avoid segmenting other irrelevant tissues with the same isovalue, only the largest connected region of that isosurface was considered.

Surfaces created using the marching cubes algorithm were first smoothed using Taubin’s algorithm (30 iterations with a passband filter of 10⁻²). The centerlines and maximum inscribed radii, r_max, of the smoothed surface were then calculated from the Voronoi diagram. The centerlines and r_max values were smoothed using smoothing filters. A tubular surface with a radius of r_max was finally created around the centerline trajectory (Figure S1) in Matlab R2018b, (The MathWorks, Inc., USA).

2.3.2. Meshing of the segmented hepatic arterial tree

The mesh size was chosen based on a mesh independency test performed in a separate study according to the ASME recommendation for CFD studies⁷. Three mesh sizes with a refinement factor of 2.29 were used and the discretization error was calculated for the global maximum velocity. Based on the mesh independency study, a final linear tetrahedral mesh consisted of 8,784,761 elements and 1,532,979 nodes with regional refinement to resolve the boundary layer was used to prepare the computational domain.

2.4. CFD modeling

2.4.1. Fluid dynamics governing equations

As the diameter of hepatic artery ranged from 4.3 to 12.4 mm, blood could be modelled as an incompressible Newtonian fluid [22–24] with a density of 1.06 g.cm⁻³ and viscosity of 0.04 g.cm⁻¹.s⁻¹. The blood flow was considered laminar, since the Reynolds number was below 900. To calculate the 3D flow field, Navier-Stokes conservation of mass and momentum equations were solved using a finite element method:

$$\frac{\partial u_i}{\partial x_i}=0;\rho \left(\frac{\partial u_i}{\partial t}+u_j\frac{\partial u_i}{\partial x_j}\right)=-\frac{\partial P}{\partial x_i}+\mu \frac{{\partial }^2{u}_i}{\partial x_j^2}+\rho F_B$$ Eq. 1

where u, P, F_B, ρ, and μ are velocity, pressure, body forces, density, and viscosity, respectively. Subscripts i and j represent the Cartesian tensor notation where the repeated subscripts stand for summation over the three coordinates. For each patient, the CFD simulation was carried out over six cardiac cycles until a periodically stable state was achieved, using the open-source software SimVascular ³⁷.

The Stokes number for the microspheres and blood is given by Eq. 2 where ρ_MS, Ø_MS, and Ø_vessel are the microsphere density, diameter, and blood vessel diameter, respectively. For 25 μm diameter microspheres representing the glass microspheres used in this study (e.g. TheraSphere^®) and 500 μm vessels segmented from CBCT (Ø_MS =25 μm and Ø_vessel= 500 μm), the Stokes number was about 1, which indicated that the microsphere transport could be approximated by the blood flow streamlines.

$$\mathit{Stk}=\frac{{\rho }_{MS}.{{Ø}_{MS}}^2}{18\mu {Ø}_{\mathit{vessel}}}u$$ Eq. 2

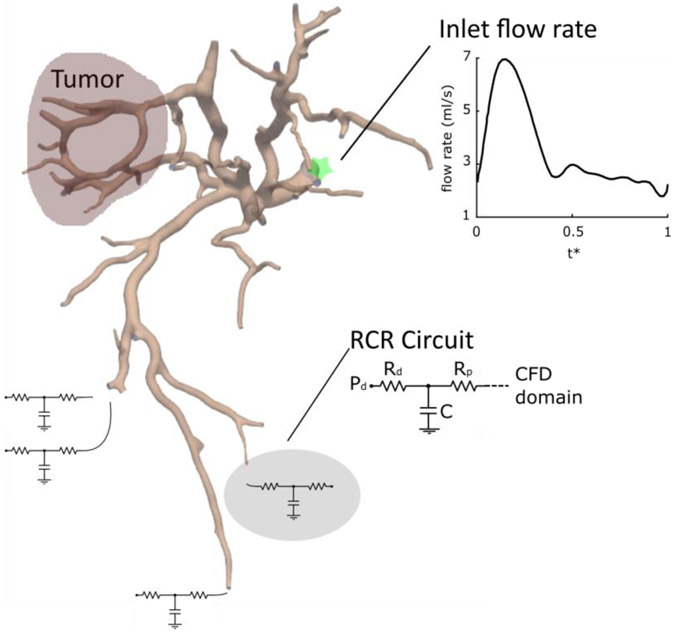
2.4.2. Patient-specific boundary conditions

A pulsatile flow rate waveform with a parabolic velocity profile was used as the inlet boundary condition (Figure 3) and the microspheres were considered to be delivered over ~15 cardiac cycles, corresponding to the clinical protocol. The inlet flow rate is normalized by the duration of the cardiac cycle and is given as a function of dimensionless time t*. Because the outlet boundary conditions (i.e. flow rate and pressure) cannot be directly measured in vivo, the vasculature downstream of the smallest segmented vessels was approximated by a lumped parameter RCR circuit (Figure 3). The distal pressure in this parameter network was obtained from a whole body lumped parameter network³⁹ and tuned based on the patient’s measured heart rate, systolic pressure, and diastolic pressure (72 bpm, 80 mmHg, and 110 mmHg, respectively). The resistance and capacitance values were adjusted to obtain a physiological pressure drop of 4.5-9 mmHg between the computational domain and the distal vasculature, with R_d = R_p ²⁴. The resistance and capacitance values of the arterial branches feeding each liver segment were split between the outlets belonging to that segment using Murray’s law with a coefficient of 2²⁷.

Figure 3. Multiscale modeling for blood flow simulation.

The inlet flow rate waveform is a function of dimensionless time t*. The computation domain segmented from CBCT is coupled with a lumped parameter RCR circuit. Rd, Rp, C, and Pd are the distal and proximal resistances, capacitance, and distal pressure.

2.5. Dose calculation

2.5.1. MIRD equation for ⁹⁰Y microspheres

The dose reported by the physician for the administered activity was calculated using the formalism adapted for ⁹⁰Y microspheres^6,16:

$$\mathit{AD}(\mathit{Gy})=49.7\ast \frac{A_{\mathit{MBq}}}{m_{liver}}$$ Eq. 3

Where AD is the absorbed dose in Gy, A_MBq is the activity in MBq, and m_liver the liver mass in g.

2.5.2. From microsphere distribution to dose map

Based on the dimensions of arterial trees segmented from our patient datasets, the microspheres travel a total distance of ~25 cm in the blood flow. With an average velocity of 30-50 cm/s ⁴³, this corresponds to a travel time of less than 1s for an individual microsphere. Considering the ⁹⁰Y half-life of 2.67 days together with a unit activity of 50 Bq and 2500 Bq for resin and glass microspheres, one microsphere can produce approximately 50-2500 events along its path and more than 3.5x10⁶ – 8x10⁸ events in its final destination, indicating that the number of events during the transport is negligible. In addition, the activity decay of each microsphere during the short transport time is negligible. All microspheres will therefore have the same unit activity at the inlet and outlets after traveling in the arterial tree.

The ⁹⁰Y dose distribution in the liver is determined by the number of injected microspheres and their volumetric distribution in the hepatic artery. All simulations assumed that the microspheres were transported with the blood flow, based on the Stokes number (Eq. 2). Therefore the number of microspheres reaching each outlet was proportional to the cumulative blood flow at the outlet after the injection is completed.

Each ⁹⁰Y microsphere deposits a certain amount of energy per volume of tissue determined by the ⁹⁰Y decay physics and the microsphere unit activity. The dose corresponding to the energy deposited in tissue was calculated using a dose kernel method for ⁹⁰Y ¹¹. The 86 x 105 x 132 cm³ volume of interest was selected to contain all outlets and microspheres. The distribution of the microspheres in the volume of interest was voxelized with a voxel size of 1 mm x 1 mm x 1 mm in order to be convolved with the ⁹⁰Y dose kernel.

2.5.3. Dose kernel computation

The dose kernel was computed with the opensource Monte Carlo simulation toolkit GATE ³², using a ⁹⁰Y point source placed in water ^25,36 . 5x10⁵ events were simulated for the electron dose kernel.

⁹⁰Y is a pure beta emitter which decays to ⁹⁰Zr with a maximum energy Q of 2.28 MeV and mean energy of 930 keV, corresponding to a maximum and mean electron range of 11 mm and 2.5 mm in water, respectively ³⁰. The ⁹⁰Y energy spectrum was calculated based on the Fermi theory of beta decay:

$$N(E)=\sqrt{E^2+2m_e{C}^2\cdot E}\cdot (Q-E{)}^2\cdot (E+m_e{C}^2)\cdot F(Z,E)\cdot S(E)$$ Eq. 4

Where E is the electron energy, m_e is the electron mass, c is the speed of light, Q is the maximum energy for ⁹⁰Y, F(Z,E) the Fermi function, and S the shape correction factor to account for forbidden decays ⁸. The peak energy is 860 keV (Figure S2a). There is also a significant contribution of low energy events (47% of events are below 860 keV) that will affect the dose point kernel.

The size of the kernel was 1 mm, matching that of the voxelized microsphere distribution (Figure S2b). There is a radial symmetry, as the kernel is computed for a point source located at the center of a homogenous medium. The maximum energy deposition occurs closest to the ⁹⁰Y point source and rapidly decreases at the distance increases, as shown in Figure S2c.

2.6. Patients

2.6.1. ⁹⁰Y microsphere injection

The patient enrolled in the PET study received two injections of TheraSphere^® glass microspheres with a total activity of 2.85 GBq to the right lobe, which mass was 1028 g. The first injection site aimed at a selective targeting of the tumor, while the second injection site located in the RHA resulted in a lobar injection intended to shrink the right lobe before future lobectomy. The selective and lobar injection activities were 1.37 GBq (547,200 microspheres) and 1.63 GBq (654,800 microspheres), respectively.

2.6.2. ⁹⁰Y PET clinical study

Aside from its 99.98% decay through β- emission, ⁹⁰Y has a small branching ratio of pair production leading to a 0.0032% fraction of a positron emission. The positron emission distribution can be imaged using PET with better image quality than standard-of-care Bremsstrahlung imaging ¹³. The patient was scanned for 2x15 minutes (2 bed positions, 15 minutes per bed position) with a GE Discovery 690 PET/CT (GE Healthcare) to measure the ⁹⁰Y microsphere activity in the liver after radioembolization. The reconstruction was performed with 3D OSEM with 24 subsets, 2 iterations, and a voxel size of 3.645 mm. A standard Gaussian filter of 12 mm FWHM was applied. The vendor resolution recovery algorithm with time-of-flight was applied, as well as CT-based attenuation correction.

3. Results

3.1. Hepatic artery segmentation and CFD domain computation

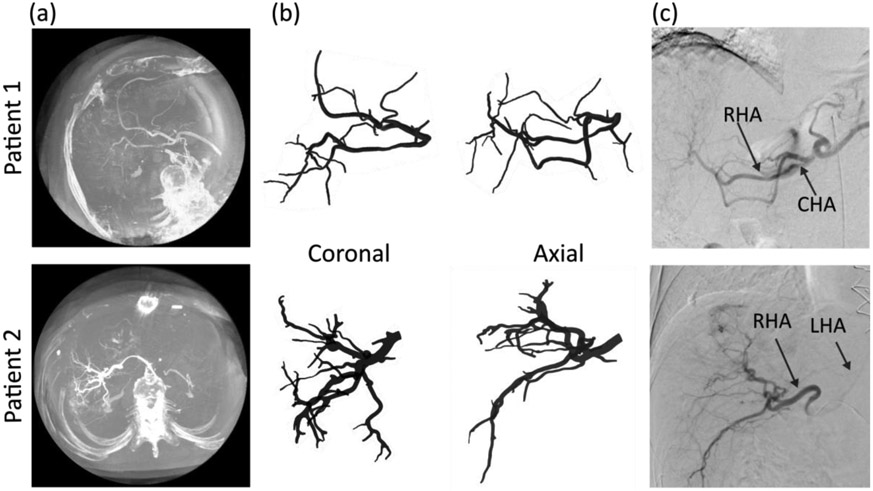
Figure 4a shows two patient CBCT datasets acquired with a multilobar contrast injection during treatment planning. The hepatic arterial trees segmented from these CBCT volumes are shown in coronal and axial views in Figure 4b. For each subject, the diameter of the common hepatic artery (CHA) was 4.7 mm and 4.6 mm, respectively, which is consistent with values from the literature ³³. The main arterial branches (common, left, and right hepatic arteries) were labelled using the corresponding 2D DSA (Figure 4c). The CHA was labelled as inlet, while 7 and 13 vessel generations were identified leading to 23 and 46 outlets, respectively (Table 1). The smallest detected outlet diameter was 0.45 mm, indicating the ability of our method to segment small vessels. The anatomy of the first patient was unconventional with a left-replaced artery and a non-trivial branching pattern. The proposed algorithm successfully segmented the hepatic arterial tree, regardless of the branching pattern.

Figure 4. Hepatic arterial tree segmentation from CBCT for 2 patients.

(a) CBCT for each patient. Patient 1 has a left replaced artery; patient 2 has a conventional anatomy. (b) Coronal and axial views of the segmented hepatic arterial trees. 7 and 13 generations of vessels were segmented for patient 1 and 2, respectively. (c) The hepatic arteries segmented from CBCT can also be visualized on digital subtracted angiography, providing a qualitative verification of the segmentation.

Table 1.

Morphology of segmented arterial trees

	Inlet diameter	Number of generations	Number of outlets	Outlet diameter range	Average outlet diameter
Patient 1	4.6 mm	7	23	0.75-1.54 mm	1.23 mm
Patient 2	4.7 mm	13	46	0.45-1.84 mm	1.04 mm

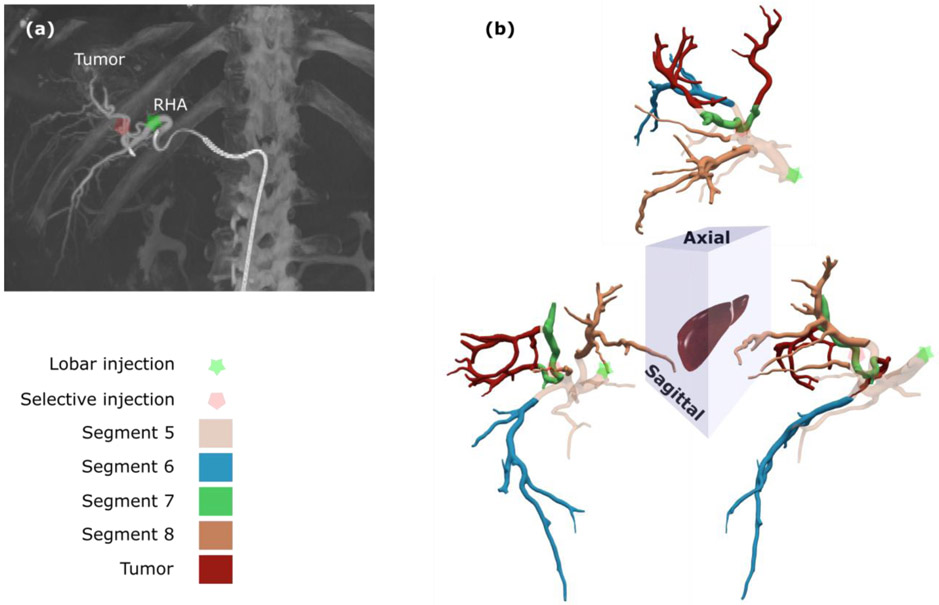
The CHA of patient 2 was identified on the arterial phase of the diagnostic CECT and used to link the RHA branches to the different liver segments and the tumor on the CFD computational domain (Figure 5). The labels were used in the CFD simulation to set the outlet and inlet conditions. The lobar and selective injection sites used for patient 2 are indicated in Figure 5a.

Figure 5. CFD simulation computational domain.

(a) The two injection sites for patient 2 are indicated on the CBCT image. (b) Each outlet was associated with a Couinaud segment and the corresponding branches are shown in the 3D views of the hepatic arterial tree. The tumor was located mostly in segment 7 with some involvement in segment 8.

3.2. Fluid dynamics analysis

3.2.1. Blood flow analysis

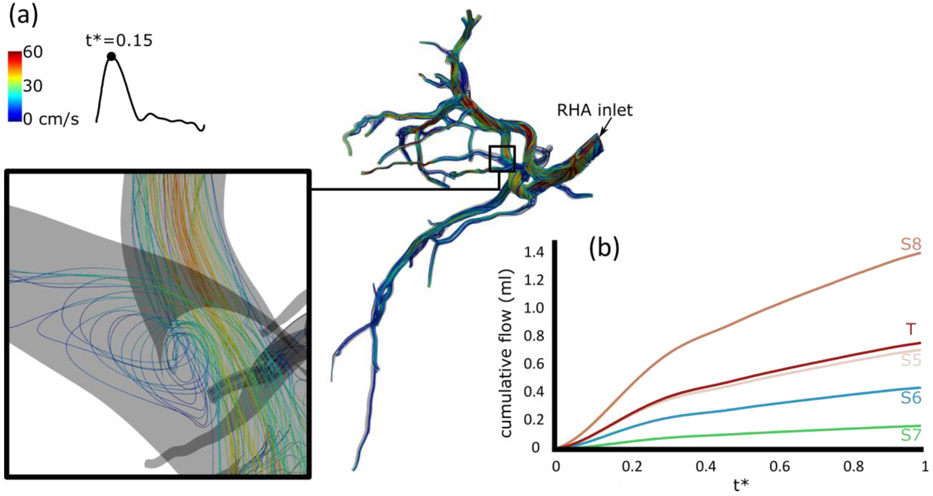
The flow streamlines color-coded with the velocity are shown in Figure 6a for the lobar injection at the peak of the cardiac cycle (t*=0.15). A detailed view of a bifurcation is given in the left inset. Generally, the velocity decreased in branches closer to the tumor outlets, although a limited number of high-velocity and flow recirculation regions was also observed (see inset). Figure 6b shows the cumulative flow in each segment, calculated as the total flow of all outlets belonging to the segment. As expected the cumulative flow rises in all segments as the injection progresses, with segment 8 receiving the largest volume. No significant difference in the trends was observed. The selective injection reached the tumor and segment 7 only and the blood flow in the other segments was not affected.

Figure 6. Blood flow analysis for the lobar injection.

(a) Velocity streamlines. (b) Cumulative blood flow after the lobar injection.

3.2.2. Microsphere distribution

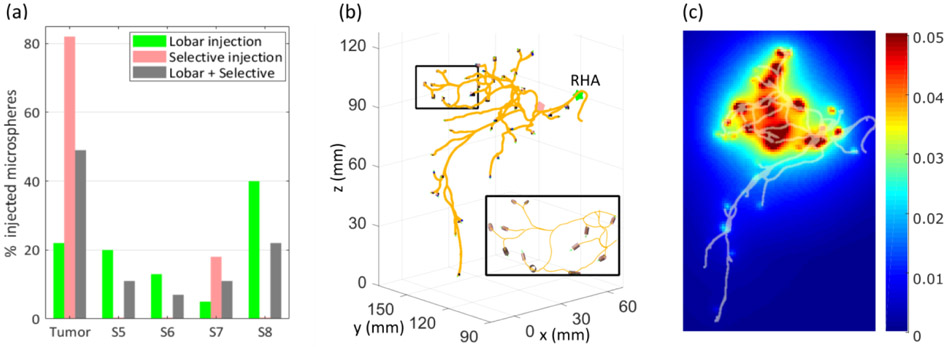
The number of microspheres at each outlet is proportional to the cumulative flow. The selective injection targeted only segment 7 and the tumor (Figure 7a) and delivered 82% of the microspheres to the tumor, as measured by the cumulative flow at the outlets. Small variations of the flow rate distribution over time among segments were observed in the case of the lobar injection (not shown here). Although the variations were limited to 1-3% for this patient, they could be larger for other patients and indicate the need for unsteady state CFD simulations. For the lobar injection, the cumulative flow was distributed among four right hepatic segments and the tumor. Finally, when combining both injections, the tumor received 49% of the cumulative flow.

Figure 7. Microsphere distribution.

(a) The selective injection delivered 82% of the injected microspheres to the tumor and all the rest to segment 7. The lobar injection delivered microspheres to all segments. The combination of both injections resulted in 49% of microspheres in the tumor. (b) At the outlets, the microspheres were arranged in small cylinders. Z axis corresponds to the axial direction. (c) Coronal projection of dose distribution (Gy/voxel) with hepatic arterial tree superimposed. The dose distribution is consistent with the microsphere distribution, with most of the dose deposited in the tumor (mostly in segment 7), and segments 7 and 8.

The selective injection delivered an average of ~32,000 microspheres at the outlets, while the lobar injection delivered 14,200 microspheres per outlet in average. The number of microspheres at the outlets can then be used to calculate the dose distribution. At each outlet, the microspheres were arranged in a cylinder which diameter and axis were given by the diameter of the blood vessel and its orientation (Figure 7b).

3.3. ⁹⁰Y dose and activity distribution

3.3.1. CFD-predicted dose distribution

Figure 7c shows the coronal projection of the dose distribution for both injections combined. The total dose predicted was 125.3 Gy, 9% lower than the dose of 137.7 Gy given by the MIRD formalism (Eq. 3) for a liver activity of 2.85 GBq and liver mass of 1028 g. One of the major findings is the large non-uniformities of the dose distribution; even if more outlets were segmented resulting in a more diffuse distribution, the dose would remain concentrated around clusters of microspheres and would not be fully characterized by a single value. The distribution between segments is consistent with the microsphere distribution (Figure 7a), with a dose of 22 Gy in segments 5 and 6 (bottom part of the vasculature), and 41 Gy in segments 7 and 8 (top part).

Here the simulation allowed us to separate the two injections to predict the dose distribution for each case separately, which could be used to optimize the injection sites and the injected activity at each site (Figure S3). The selective injection delivered a total of 58.3 Gy (48 Gy to the tumor and 10.3 Gy to segment 7), while the lobar injection delivered only 15 Gy to the tumor. Most of the lobar dose (67 Gy) was delivered to segment 8.

3.3.2. Post treatment ⁹⁰Y PET/CT

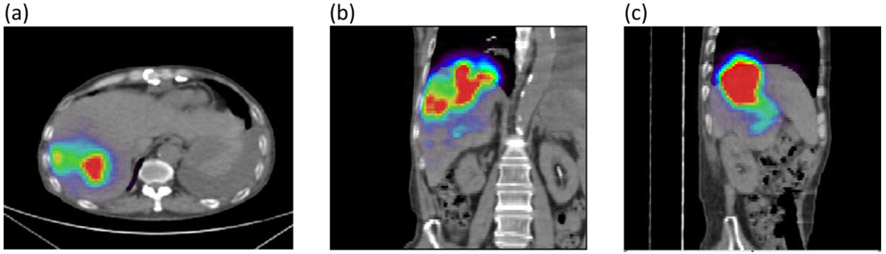
The ⁹⁰Y activity distribution was imaged after radioembolization (after the two injections) using PET/CT. Images were reviewed by a board-certified radiologist (CF). The axial, coronal, and sagittal views shown in Figure 8 indicate that the microspheres were successfully administered, with the activity concentrated in segments 7 and 8 predominantly (superior portion of right hepatic lobe) and some activity in segments 5 and 6. A possible small focus in segment 4b (left lobe) was also noted by the radiologist. Qualitatively, the activity distribution measured post-treatment is consistent with the dose distribution predicted by our CFD simulations.

Figure 8. ⁹⁰Y PET/CT data acquired 1 hour post radioembolization.

(a) Axial view showing most of the activity in segments 7 and 8. (b) Coronal view confirms lodging of the microspheres in segments 7 and 8 where the tumor is located, with some activity in segment 6. (c) Sagittal view.

4. Discussion

The primary goal of this study is to present a proof-of-concept method (CFDose) for personalized dosimetry of liver cancer ⁹⁰Y radioembolization. Simulations presented here were conducted with CFDose using a combination of CFD and ⁹⁰Y physics modeling (dose point kernel) for the clinical case of a patient who received two ⁹⁰Y microsphere injections in different locations of the right lobe. The liver dose predicted by CFDose was consistent with that calculated using the MIRD formalism for ⁹⁰Y microspheres within 10%. This discrepancy is expected and can partially be explained by the fact that we calculated the dose point kernel with the full energy spectrum for ⁹⁰Y (Figure S2) instead of a monoenergetic value of 930 keV as approximated in the MIRD equation (Eq. 3). Most importantly, personalized CFD simulations showed a highly non-uniform dose distribution and different patterns between the lobar and selective injections, which could not be inferred from the single value produced by the MIRD equation. These results confirm our initial hypothesis and suggest that CFDose could be used to predict and analyze the complex dose distribution. In fact, gaining more insight on the heterogenous distribution of the microspheres would allow for a better understanding of the dose-limiting liver structures, as suggested by small-scale dosimetry studies such as Stenvall et al³⁵.

Based on the results of a separate study we conducted, the blood flow in the liver vasculature is modelled with CFD coupled to a lump parameter model. Approximations of the blood flow such as Poiseuille’s law used in other published works cannot account for some geometrical complexities of the hepatic arterial tree that affect the microsphere distribution differently for each patient, resulting in less accurate prediction of the flow distribution between arterial branches. We used a whole body lumped parameter taken from the literature to calculate the distal pressure of our lumped parameter RCR model. These values need to be validated in future studies. We will also include more personalized boundary conditions using direct measures of the pressure and blood flow conditions at the inlet obtained with clinical methods such as Doppler ultrasound or more advanced methods such as 4D flow MRI ²⁶. Here the microspheres were assumed to be transported by the blood flow, which is valid for the size of vessels segmented from the CBCT (~0.5 mm). Since most of the vasculature in the segmented arterial tree had a diameter > 1mm, we assumed a Newtonian behavior for blood flow based on previous studies^4,10,34. If smaller vessels are segmented in the future, the non-Newtonian behavior of blood as well as the interaction of the microspheres with the arterial wall may have to be considered to account for viscoelastic property of blood and potential clogging of small arterioles. To our knowledge, the effect of these interactions has not been characterized and it is unclear at which scale it changes the dose distribution.

To produce higher resolution absorbed dose distributions, the microsphere distribution obtained at the segmented outlets (46 in this patient case) needs to be augmented. Potential strategies include using the high-resolution DSA images to infer downstream microsphere distribution from the blood flow, or assuming an isotropic distribution of decreasing vessel size around the outlet location.

One of the major challenges with ⁹⁰Y radioembolization is the difficulty to image it, as it is almost a pure beta emitter. Here we present the ⁹⁰Y PET data acquired for the patient after treatment. The superiority of ⁹⁰Y PET/CT to Bremsstrahlung gamma imaging or SPECT to assess the treatment performance has been reported in several studies ^15,40. ⁹⁰Y PET dosimetry is the most promising strategy to validate CFDose in patients and will be used to quantitatively compare CFD-predicted and measured dose distributions. This will require the quantification of the PET images and their registration with the CFDose distribution, a non-trivial task relying on the registration of both dose distributions within the liver volume. The same strategy could also be applied to compute the MAA-based dose distribution.

In conclusion, we present the proof-of-concept of a new dosimetry computational method for ⁹⁰Y liver radioembolization, CFDose, which we are developing and validating with a pilot clinical study at UC Davis (20 patients). For the first time, ⁹⁰Y PET images corresponding to the predicted dose distribution are presented, illustrating the potential of our work to combine dose prediction and dose verification.

Supplementary Material

10439_2020_2469_MOESM3_ESM

Figure S1. Hepatic artery segmentation pipeline. CBCT images with a resolution of 0.25 mm and slice thickness of 1 mm are segmented to extract blood vessels using a semi-automatic approach.

10439_2020_2469_MOESM2_ESM

Figure S2. ⁹⁰Y dose kernel. (a) ⁹⁰Y beta energy spectrum with a maximum energy of 2.28 MeV and peak at 860 keV. (b) Projection of the 1mm dose point kernel computed with the ⁹⁰Y spectrum shown in (a). (c) The energy deposited is highest close to the ⁹⁰Y point source (located at 0 mm) and decreasing rapidly with increasing distance from the point source (note the log scale).

10439_2020_2469_MOESM1_ESM

Figure S3. Predicted dose distribution for the lobar and selective injections separately, which are shown combined in Figure 7c. (a) Selective injection, coronal view, with a total dose of 58.3 Gy. (b) Lobar injection, coronal view, with a total of 67 Gy.