Inherent Fibrin Fiber Tension Propels Mechanisms of Network Clearance During Fibrinolysis

Abstract

Proper wound healing necessitates both coagulation (the formation of a blood clot) and fibrinolysis (the dissolution of a blood clot). A thrombus resistant to clot dissolution can obstruct blood flow, leading to vascular pathologies. This study seeks to understand the mechanisms by which individual fibrin fibers, the main structural component of blood clots, are cleared from a local volume during fibrinolysis. We observed 2-D fibrin networks during lysis by plasmin, recording the clearance of each individual fiber. We found that, in addition to transverse cleavage of fibers, there were multiple other pathways by which clot dissolution occurred, including fiber bundling, buckling, and collapsing. These processes are all influenced by concentration of plasmin utilized in lysis. The network fiber density influenced the kinetics and distribution of these pathways. Individual cleavage events often resulted in large morphological changes in network structure, suggesting that the inherent tension in fibers played a role in fiber clearance. Using images before and after a cleavage event to measure fiber lengths, we estimated that fibers are strained ~23% beyond their equilibrium length during polymerization. To understand the role of fiber tension in fibrinolysis we modeled network clearance under differing amounts of fiber polymerized strain (prestrain). The comparison of experimental and model data indicated that fibrin tension enables 35% more network clearance due to network rearrangements after individual cleavage events than would occur if fibers polymerized in a non-tensed state. Our results highlight many characteristics and mechanisms of fibrin breakdown, which have implications on future fibrin studies, our understanding of the fibrinolytic process, and the development of thrombolytic therapies.

Graphical abstract

1. Introduction

Blood clots stop the flow of blood at the site of vascular injury. They are composed of a fibrin network that surrounds and intertwines a mass of cells and extracellular matrix components. This same fibrin-cell system can also comprise an occlusive thrombus, which impedes the flow of blood within the vasculature leading to strokes, pulmonary embolism and other pathologies. In hemostasis, the fibrinolytic system digests the fibrin network upon the completion of wound healing, thereby dissolving the clot and recanalizing the blood vessel. However, in many pathologies the fibrinolytic system is ineffective at completely dissolving the clot components [1,2], and the mechanisms impeding fibrinolysis in these circumstances are unclear. To better understand what regulates the lysis of blood clots and thrombi, we have taken a bottom up approach by studying the mechanisms governing the clearance of individual fibrin fibers during the fibrinolytic process.

Fibers, the focus of this study, form the “intermediate scale” of the fibrin structural hierarchy, and are composed of roughly 10,000 individual fibrin molecules. Fibrin molecules originate from the cleavage by the enzyme thrombin of fibrinopeptides A and B from the N-termini of fibrinogen molecules’ α- and β-chains. After the conversion of fibrinogen to fibrin, fibrin molecules polymerize into protofibrils, which further bundle laterally into fibers. The fibers, finally, branch into the 3-D network, which holds the blood clot together. The process of polymerization, even in the absence of flow, creates tension on the fibers in the network, such that they appear taut and straight in fluorescent microscopy images [3,4] and will elastically recoil back into a taut conformation if stretched [5]. This is a contrast with other semiflexible biopolymers such as actin, whose fibers can appear loose and floppy depending on crosslinking conditions [6]. Although the mechanisms generating the tension in polymerized fibrin fibers are poorly understood [7,8], it was recently suggested that the tension in fibers may help to regulate their fibrinolytic susceptibility [9].

The conversion of fibrinogen to fibrin by thrombin and the subsequent fiber polymerization exposes binding sites for fibrinolytic molecules including plasminogen, plasmin, and tissue plasminogen activator (tPA), thereby upregulating the fibrinolytic process [10-12]. The primary fibrinolytic enzyme is plasmin, a serine protease that cleaves fibrin at multiple sites [13]. Plasmin’s activation and activity are tightly regulated by enzymatic factors including activators, inhibitors, cofactors, and receptors. Plasmin activators tPA (tissue-type) and uPA (urokinase-type) convert the zymogen plasminogen into plasmin by cleaving the R560-V561 bond. Once activated, plasmin specifically cleaves the carboxyl side of lysine or arginine, so there are many potential cleavage sites on the fibrin molecule. However, fibrin degradation occurs in a kinetically specific manner. The C-termini of the fibrin α-chains (the αC regions) are removed first, with the primary cleavage points at αK206 and αK230 [13]; however, over ten potential cleavage sites in the αC region have been identified, so other degradation pathways are possible [14]. Plasmin then cleaves residues in the coiled coil region, eventually cutting the α-, β-, and γ-chains and splitting off the C-terminal portions of the β- and γ-chains from the central portion of the molecule. Thus, the lysis of an entire blood clot hinges on the ability of individual plasmin molecules to degrade fibrin molecules inside fibers.

Although fibrinolysis has been studied for decades, details are sparse regarding the process of network degradation at the fiber-level. Experiments in which tPA or plasmin are added to the outside of an already polymerized network show that networks are degraded by a “lysis front”, where the fibrinolytic enzymes digest the outer fibers first and then work inward into the network [4,15]. A longstanding debate involves whether plasmin digests fibers uniformly along their radius, causing fibers to get thinner and then dissolving [16-18], or whether plasmin cuts transversely across fibers, so that they are cleaved at a specific point [4,9]. Regardless of the mechanism, recent work has shown that the fibers initially break at a single point during lysis [9]. How fibers are digested after this initial cleavage event has not been studied in detail, but some evidence suggests that cleaved fibers bundle together prior to being degraded further [4,19]. Also debated is the way in which plasmin molecules move through the fiber during lysis: either diffusing between protofibrils [20,21] or "crawling" from one binding site to the next [15,20].

The spacing between fibers (network pore size) and the thickness of fibers influences the kinetics of fibrin lysis. Some studies show that thick fibers lyse more slowly than thin fibers, but that sparse networks composed of thick fibers lyse more rapidly than densely packed networks composed of thin fibers [4,22,23], but other studies show contradictory results [18,24]. Recent modeling efforts suggest that these competing results can be reconciled, in part, by considering the number of tPA molecules available to initiate lysis on individual fibers [15].

In this study, the lysis of small, 2-D fibrin networks was investigated to carefully study the mechanisms by which fibrin fibers are cleared out of a local region. Surprisingly, the lysis of individual fibers was not the only mechanism by which fibers were removed. Because fibers polymerize under tension, the lysis of even one fiber within a network had a profound influence on the conformation and digestion pathways of all other local fibers. These other fibers often buckled, bundled with surrounding fibers, or collapsed, suggesting that lysis progresses through more mechanisms than just the transverse cleavage or digestion of individual fibers. The results show that fiber connectivity and inherent tension profoundly influence the digestion of individual fibers. Moreover, the lytic susceptibility of individual fibrin fibers depended on the density of the local fibrin network. Similarly, the time at which the initial transverse cleavage event in a network occurred was influenced by local network density. To further study the effect of tension on lysis, the lytic process was modeled using a mass-spring system. The models showed that fiber tension played an important role in enhancing secondary lysis clearance mechanisms (i.e. mechanisms other than the direct digestion of fibers by plasmin) such as fiber reorientation and collapse, which would not occur in the absence of tension. Moreover, our models show that tension greatly reduces the number of fibers that must be cleaved in order to clear fibrin from a region. Thus, our results highlight the dynamic nature of fibrinolysis and emphasize that the modeling of blood clot dissolution needs to account for network density and tension to fully capture the fibrinolytic process.

2. Methods and Materials

2.1. Polymerization and Lysis of 2-Dimensional Fibrin Networks

A PDMS stamp (Polydimethylsiloxane: Sylgard 184; Dow Corning Corp., Midland, MI, 48686) and an optically curable glue (Optical Adhesive 81, Norland Products Inc., Cranbury, NJ) cured with ultraviolet light was used to form substrates with ridges measuring 20 μm apart and 10 μm high on glass coverslips as previously described [5,9] (See Fig. 1). Aliquots of fibrinogen (Peak 1 human fibrinogen, pH 7.4, Enzyme Research Labs (ERL), Indianapolis, IN) diluted to 0.6 mg/ml using a HEPES Buffered Saline (HBS; 20 mM HEPES, 150 mM NaCl, pH 7.4) were thawed from −80.0°C, and 30 μl was placed onto the ridged surface. Aliquots of human alpha thrombin (ERL) diluted to 2.35 U/ml (twice the final concentration required) using 10 mM CaCl₂ in HBS were thawed from −80.0°C and mixed in equal volumes with fibrinogen (30 μl each) on the ridged surface to give a final fibrinogen concentration of 0.3 mg/ml and thrombin concentration of 1.18 U/ml. Samples were placed into a closed petri dish with wet paper to create a humidified container and were allowed to polymerize for one hour at 37°C. Each sample was prepared for fluorescence microscopy following the protocol described in section 2.2. Human plasmin (ERL; 16.7 U/mL/1.48 mg/mL stock concentration in 50 mM HEPES, 50mM Sodium Acetate pH 8.5/50% glycerol) was diluted to 2x the final concentration (either 2.0 U/ml or 0.2 U/ml) using 10 mM CaCl₂ HBS buffer. Aliquots were thawed from −20.0°C and 30 μL was added to each fibrinogen sample after polymerization to give final plasmin concentrations of either 1.0 U/ml or 0.1 U/ml, as indicated. Ten trials at each plasmin concentration were conducted and images were taken for each trial over a 24-hour period. Final sample on the ridges had a volume of 60 μL and a buffer containing HBS, 5 mM CaCl₂, and trace amounts of glycerol and Sodium Acetate due to the plasmin dilutions. Note that the 1.0 U/mL plasmin and 0.1 U/mL plasmin will have slightly different glycerol concentrations after dilution (3% vs 0.3%). In previous work, looking at the lysis of individual fibers [9], we showed an exponential rate of decay for cleavage time as a function of plasmin concentration. There was no apparent deviation from this behavior despite slight differences in glycerol content, indicating that small differences in glycerol content do not alter fibrinolytic outcomes. To further test plasmin activity, we performed a receding clot assay [25], in 3.0% and 0.3% glycerol. There was no decrease in the plasmin activity at higher glycerol concentrations (data not presented). Thus, the slight differences in buffer conditions should not affect the lysis outcomes observed in this study.

Figure 1. Depiction of Experimental Set-up Used to Observe Fibrin Networks.

A stamp was used to cure optically clear adhesive ridges, and fibrin was polymerized between the gaps. Networks were washed and labelled with fluorophores for viewing using fluorescent microscopy.

2.2. Fluorescent Microscopy

Once polymerization was completed, buffer was carefully removed from the sample using a pipette to avoid removing the fibrin network. Fibers were gently washed three times using 30 μl of bead solution (FluoSpheres™ carboxylate-modified, 0.02 μm, red, Life Technologies, Eugene, OR, 1/10,000 dilution from stock concentration) in HBS and washed again using 30 μl of plain HBS three times to remove excess beads; 30 μl of HBS was added to each sample after washing to allow the suspension of fibers in solution. FluoSphere-based fiber labeling has previously been used to label fibrin fibers during fibrinolysis assays [9,25]. Fluorospheres enable single fiber fluorescent imaging over long time-periods and are much brighter and more photostable than fluorescent dyes, which are commonly used for labeling fibrin fibers in bulk lysis assays [25]. Samples were placed face-up on a Leica DMi8 epifluorescent microscope (Leica Microsystems Inc., Buffalo Grove, IL) and imaged with a 63x oil objective. Images were taken using a Leica DFC9000GT SCMOS 4 Megapixel monochrome camera. Areas (211 μm²) were chosen, based on the presence of local fiber networks, for imaging on each sample and images (2048x2048 pixels) were taken before gently adding plasmin. Images were acquired every 30 seconds (starting with the addition of plasmin) for the first hour and once more at 24 hours. For samples treated with a plasmin concentration of 1.0 U/ml, images were acquired every 3 seconds for the initial 30 seconds, followed by every 30 seconds for the next hour. After the first hour of imaging, the samples were put back into a closed petri dish with wet paper at 37°C until they were imaged once again at the 24-hour mark. In between image exposures, the excitation light was turned off to minimize sample photodamage.

2.3. Image analysis

Images were manually segmented into smaller areas containing small fibrin networks (isolated clusters of fibrin fibers); an individual network was defined as a connected cluster of fibers with no direct fibrin connections to adjacent clusters. An image processing software (ImageJ [26]) was utilized to record the area and number of fibers present for each fibrin network. Images were equally and minimally brightened using the brightness/contrast tool in imageJ to increase fiber identification. Image time series of fibrinolysis were manually tracked, and individual fiber outcomes were categorized over time during the network lysis. These outcomes include cleavage, buckling, bundling, and/or collapse and are shown in Figure 2 and described in detail in section 4.1. The fibrinolytic mechanism observed in each fiber was recorded at specific time points after the addition of plasmin: 0 seconds, 1 minute, 3 minutes, 5 minutes, 10 minutes, 15 minutes, 30 minutes, and 24 hours. Trials using a plasmin concentration of 1.0 U/ml were also analyzed at 6 seconds, 12 seconds, 21 seconds, and 30 seconds to increase data resolution for quickly lysing networks. These observations were made to determine possible differences or patterns in fibrin behavior over time due to plasmin concentration and network density. The timing of each initial transverse cleavage event (with 3 second time resolution) was recorded in every network to further analyze how the lytic susceptibility of fibrin is affected by local network density. The relative total of each fibrinolytic mechanism observed at 24 hours (defined as the end of network lysis) was compared between each of the two plasmin concentrations to determine the influence of plasmin concentration on fibrinolytic behavior (see 3.2 for statistical methods).

Figure 2. Micrographs Showing the Different Processes of Fibrin Observed During Fiber Degradation.

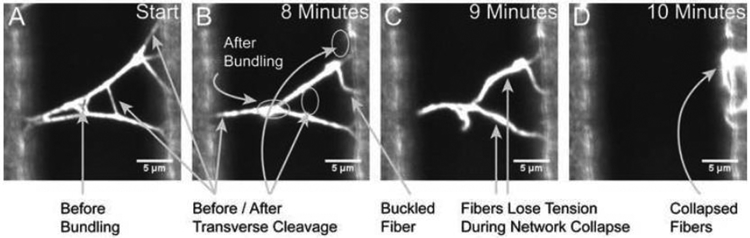
Image A depicts a 2-D fibrin network prior to the addition of plasmin. Arrows indicate fibers that will be cleared through transverse cleavage or bundling. Image B depicts the same network, but restructured after 8 minutes of digestion, with arrows indicating the space where fibers have been cleaved, bundled, or buckled. Image C captures the network collapsing, caused by cleavage of the last fiber attached to the left ridge. Note that fibers lose tension and often appear bent or “floppy” during the collapse event, highlighting the semiflexible polymer nature of fibrin fibers. All fibers that that fall onto the ridge without being cleaved are counted as “collapsed” for categorization purposes. Image D depicts the appearance of fibers that have collapsed into the ridge.

To measure the network area, the ImageJ polygon tool was used to trace the perimeter around the exterior fibers and the wall attachment points for each network analyzed. This was performed for both experimental networks and simulated networks where images of equilibrium network structures were screen captured and imported into ImageJ. Three measurements were made for each area and the results were averaged. Network area was calculated from the polygon using the “measure” tool. Fiber density was calculated as the number of fibers contained in the network divided by the area.

To measure fiber lengths for prestrain analysis, the ImageJ line segment tool was used to measure the length of fibers and fiber segments. Three measurements were made for each segment and the results were averaged for a final length estimate. Care was taken to choose fibers and fiber segments that were in focus both before and after cleavage, however because fiber segments are loose and floppy, there is inherently more uncertainty in their length estimates than the pre-cleavage lengths.

2.4. Network lysis modeling to understand the effects of tension

Network lysis under differing tension conditions was simulated using Webslinger 4.1 (http://www.cismm.org/), a quasi-static mass-spring simulation, which was previously used to analyze network strain distributions using different fibrin force-extension behaviors [27]. Webslinger approximates fibrin fibers as springs and uses Euler integration with small time steps and damping to solve the system of partial differential equations governing the network. After each step, the system relaxes to equilibrium, and that solution is used for the initial conditions of the next step. For lysis analysis, the original webslinger program was upgraded to allow the user to select springs to remove from the network (simulating the transverse cleavage of a fiber). After the removal of a fiber, the spring system relaxed to new equilibrium positions and the new network geometry was captured as an image. From the images, network areas were calculated using ImageJ (in the same manner as described in section 2.3). Webslinger does not account for buckling or bundling of springs (fibers), so those aspects of lysis are unaccounted for in these simulations.

Webslinger does not assume a specific unit system, but rather requires the user to input parameters that are defined in consistent units. Experimental wall attachment points were simulated as immovable (mass = 10¹⁰⁰), but freely rotating pivot positions, and fiber junctions were simulated as moveable (mass = 1.0) and freely rotating pivot joints between the springs. A mass damping term of 3.0 was used to govern the system relaxation times; because we only considered equilibrium network structures, this term does not affect our results. For simplicity we assumed that every fiber in a network had the same spring constant and was under the same amount of initial prestrain. These are reasonable approximations as fibers that form under the same thrombin concentration have roughly the same diameter [28], however given the dependence of fiber elastic modulus on fiber diameter [29], further studies could investigate how different amounts of tension in each fiber would affect our results. We utilized a linear spring constant of 10.0 in these simulations. Fibrin fibers do exhibit strain stiffening (non-linear spring constants), when stretched to more than double their polymerized lengths [30,31], but fibers in our experiments experience no stretching beyond their polymerized lengths, and hence a linear spring constant was reasonable. Because all fibers were assumed to have the same spring constant, and we only considered equilibrium network structures when calculating the network area, the results are independent of spring constant. As a test, we tried spring constants ranging over 5 orders of magnitude, but the network structure and calculated area enclosed by the structure were within 0.2%.

Network geometries for the webslinger simulations were matched to experimental fibrin network geometries using custom Matlab R2018b (The MathWorks, Natick, MA) code (webslinger_inputfile_creator.m in the downloadable webslinger source code). The code allows the user to open an image of an experimental network, and define simulated networks with the same fibers, orientations, and connections as observed in the experimental network.

Tension in the network was simulated using the webslinger rest_length_fraction parameter, which determines the extent to which springs are initially stretched. For example, a rest length fraction of 0.5 means that the springs in their initial equilibrium position are stretched to L_o/0.5=2L_o (100% fiber strain from an equilibrium position), where L_o is the rest length of the spring. A rest length fraction of 1.0 means that the springs were not stretched at all beyond their equilibrium position in their initial configuration, and hence not initially under tension (0% prestrain). Every network geometry was subjected to lysis simulations using fiber rest_length_ fraction values of 1.0, 0.8, 0.7, 0.5, and 0.3 (corresponding to prestrain values of 0%, 25%, 43%, 100%, and 233%).

Lysis simulations were carried out using the following procedure. A webslinger network with a specific fiber prestrain value (e.g. 0% fiber prestrain), was generated to mimic an experimental geometry. A frame by frame analysis of experimental lysis images was performed to identify which fibers were transversely cleaved in the network in each frame (Note that fibers recoil in millisecond timescales [5], so a camera frame rate of 3s should capture an equilibrium network state unless a cleavage event occurred within 1ms of an image capture). For each identified experimental cleavage event, the corresponding springs were removed from the webslinger network, the network re-equilibrated to a new conformation, and an image was taken of the new network geometry. This process proceeded until all springs corresponding to cleaved fibers in the experimental data were removed from the simulated network. At this point the lysis simulation was considered complete. The entire process was repeated for every fiber prestrain value to determine how fiber prestrain influenced the lysis process for each network geometry.

3. Statistical Methods

3.1. Fiber Density Tests

Fiber lysis data were categorized into five groups: transversely cleaved, bundled, buckled, collapsed, and straight. The percent of fibers that fell into each category was tracked for each network over time. For the cleaved, bundled, collapsed, and straight categories, time series data were fit using the sigmoidal function SSlogis using the fitting model nlsLM in R programing language (See Supplemental Fig. 1) [32,33]. SSlogis is a nonlinear least-squares model that uses the Levenberg-Marquardt algorithm for improved fit parameter predictions [33]. The fit solves for the three sigmoidal function parameters: asymptote, inflection point, and scale. The asymptote represents the proportion of fibers that will eventually be affected (cleaved, bundled, etc.); the inflection point designates the time at which half of the fibers that will be affected are affected. This timepoint represents a time when the network is actively being lysed, while the asymptote represents the end timepoint when lysis is complete. Scale is the scaling parameter on the time axis. The proportion of straight fibers was inverted to be able to fit the sigmoidal function to the data. Time series of the buckling data were fit using a gaussian function, since the fibers were only temporarily in this category and thus a sigmoidal function was not appropriate. Starting parameters were picked for both functions based on a Monte Carlo method. Random numbers were generated for the starting parameters asymptote, inflection point, and scale between 0-15, 0-3, and, 0-3, respectively. Starting parameters were first optimized for ability to fit a maximum number of bins by trying to use them to fit the sigmoidal function to the data and checking for singular gradient (local minima) errors. Once a maximum number of bins was achieved, the starting parameters were checked to assure they were not outliers by averaging both the resulting standard error of each bin and the slope calculated by the method detailed below. To enable smoother fitting (which was sometimes prohibited by discrete jumps in the number of fibers lysed between frames), data was binned to include three networks of similar density.

Visually, it appeared that networks of more densely packed fibers were digested more rapidly. To test whether this was statistically true, we plotted data points for the time at which half of the fibers in a binned set of networks that were going to undergo a process (cleavage, bundling, etc.) had done so vs the fiber density of the binned set of networks. For the buckling data the center value of the gaussian fit was plotted vs the fiber density of the binned set of networks. A linear least squares model fit was used in R in order to get the average variance of the data from the fit line. The data was then fit again with each datapoint having a weight of the reciprocal of the summed average data variance and the standard error of sigmoidal fit parameter. This weighted fit showed the relationship between the sigmoidal/gaussian parameter and the density of the network represented by the slope of the relationship (See Supplemental Fig. 2 and Supplemental Table 1). The fit’s associated p-value indicates the probability of getting the calculated slope if there was no correlation. The same method was used for the two different plasmin concentrations.

3.2. Comparison of Means and Sum of Squared Errors

Statistical analysis investigating differences in fibrinolytic mechanisms at different plasmin concentrations was done using Minitab 18.1.0.0 (Minitab, LLC, State College, PA). To determine whether the percent of fibers that were cleared via a specific lysis mechanism (transverse cleavage, bundling, etc.) depended on the plasmin concentration, we considered the data taken 24 hours after the addition of plasmin (See Fig. 3). The mean and standard deviation of the percentage of fibers that experienced each lytic mechanism were calculated (See Supplemental Table 2). We then performed two-sample t-tests to determine the difference of means between the two plasmin concentrations for each lytic mechanism. A reported 95% confidence interval that does not overlap with zero, or a p-value less than 0.05, indicates a significant difference between the means being compared (See Supplemental Table 3).

Figure 3. Box and Whisker Charts Showing the Fraction of Fibers in Each Pathway Over Time.

Fibrin networks were dissolved by administering plasmin at a final concentration of either 0.1 U/ml or 1.0 U/ml. The number of fibers in each category was recorded at specific time intervals, which represent time passed after the addition of plasmin. Each point on a plot represents a different network, and each time interval displays all networks. Results from 0.1 U/ml plasmin concentration include 22,151 fibers across 255 networks and results from 1.0 U/ml plasmin concentration include 13,199 fibers across 156 networks. Trials taken at 1.0 U/ml contain extra intervals below 1 minute to increase plot resolution for quickly lysing networks. Completion of lysis is represented by boxes plateauing in later intervals. Data points located outside the whiskers are outliers that deviate from the 1^st or 3^rd quartile by over 1.5 times the interquartile range.

Network area measurements were acquired by tracing the periphery of a network for both experimental and simulated network images. Uncertainties in individual network areas were calculated by measuring the area three times and calculating the standard deviation. Percent differences between the mean area values at two different points in lysis (% Area difference; Supplemental Table 4) were calculated as:

$$\%Areadifference=(InitialArea-FinalArea{)}^{\ast }100\%∕InitialArea$$ (1)

Uncertainties in the differences between network areas were calculated using propagation of error of the individual uncertainties of each mean area measurement. The average percent area difference, standard deviations, and standard errors of all ten experimental fibrin networks and webslinger simulations at varying levels of fiber tension were determined using Minitab (See Supplemental Table 5).

To estimate which amount of prestrain in the simulations best replicated the experimental results, we used a sum of squared errors metric. We define the sum of squared errors as:

$$SSE={\sum }_{i=1}^N(ExptAre{a}_i-SimAre{a}_i{)}^2$$ (2)

Where N is the number of network geometries evaluated; ExptArea_i is the % Area difference in the lysis experiment corresponding to the i^th geometery; and SimArea_i is the % Area cleared in the webslinger simulation corresponding to the i^th geometery. SSE was determined for each prestrain value at both the lysis midpoint and the lysis endpoint, and the data are in Supplemental Table 5.

3.3. Calculating Probabilities of a First Fiber Cleavage Time given a Certain Number of Fibers in the Network

From the first fiber lysis data, we were able to make an estimate of the probability of observing a first cleavage time for a network composed of an arbitrary number (k) of fibers. For a k-fiber network, the probability of obtaining a particular first fiber cleavage time (“t”, in the following equations) was calculated from the experimental data as follows:

$$\begin{gathered} P(tsec\mid k-fibernetwork)fort=3,6,9,12,15,18,21,24,27,30,60,210 \\ =P(cleavagetime\ge t\mid k-fibernetwork)-P(cleavagetime>t\mid k-fibernetwork) \\ =P(alltimesforkfibers\ge t)-P(alltimesforkfibers>t) \\ =[P(cleavagetime\ge t\mid singlefiber){]}^k-[P(cleavagetime>t\mid singlefiber){]}^k \end{gathered}$$ (3)

As an example, for a 10-fiber network this is calculated as:

$$\begin{gathered} P(tsec\mid 10-fibernetwork)fort=3,6,9,12,15,18,21,24,27,30,60,210 \\ =P(cleavagetime\ge t\mid 10-fibernetwork)-P(cleavagetime>t\mid 10-fibernetwork) \\ =P(alltimesfortensinglefibers\ge t)-P(alltimesfortensinglefibers>t) \\ =[P(cleavagetime\ge t\mid singlefiber){]}^{10}-[P(cleavagetime>t\mid singlefiber){]}^{10} \end{gathered}$$

Probabilities were calculated using Microsoft Excel (Microsoft, Redmond, WA).

3.4. Antitonic regresion

An antitonic regression identifies the non-increasing function possessing the smallest sum of square residuals with the data. An antitonic regression was performed using a custom-built script written in the R programing language [32]. The script uses the technique by which a cumulative sum diagram is formed and its greatest convex minorant obtained. The estimates of the antitonic regression are the left-hand slopes associated with the greatest convex minorant.

4. Results

4.1. Pathways of fiber clearing

By analyzing the lysis of small networks, we determined multiple different pathways by which individual fibers can be cleared from a region of space. The pathways are: 1) Transverse cleavage, which is characterized by the cleavage of a fibrin fiber at a single point. 2) Buckling (or structural elongation), which occurs when one or more fibers undergoes transverse cleavage and the remaining fibers reorient and bend due to changes in the tension distribution in the network. 3) Fiber bundling, which is characterized by an un-cleaved fiber physically moving into another un-cleaved fiber and binding to it, forming a new, thicker fiber. And 4) Fiber collapse, which occurs when the transverse cleavage of one fiber results in the recoil of other un-cleaved fibers, with the eventual result being the un-cleaved fibers folded onto a ridge, effectively disappearing from view. See Figure 2 and Supplemental Movies 1, 2, and 3 for examples of each of these pathways.

We observed a general order of these pathways for the degradation of fibrin. Fibers began in a straight, taut conformation, appearing stationary and under tension, before they were affected by plasmin. In every network observed, transverse cleavage of a single fiber was the first mechanism that occurred during the lysis of a network. This served as the starting point for all other degradation pathways and triggered downstream effects, including bundling and buckling, for the remaining fibers in each network. For this reason we refer to bundling, buckling, and collapsing as secondary mechanisms. Each cleavage event resulted in a redistribution of the tension and physical location of all connected fibers (See Supplemental Movies 1, 2, and 3). Thus, inherent fiber tension necessitates that the cleavage of any single fiber in the network will result in secondary clearance mechanisms (See Fig. 2).

Many (~10-20% of the total fibers observed; See Fig. 3) un-cleaved fibers buckle (lose their tension and bend) due to conformational changes in the network caused by transverse cleavage of one or more fibers. Buckling is usually a temporary state, as further transverse cleavage events will redistribute the tension in the network again, and buckled fibers can restraighten if they are no longer under a compressive tension. Therefore, fibers could move between the “straight” and “buckled” categories as lysis progressed, before being either cleaved, bundled, or collapsed in their final state.

Bundling of un-cleaved fibers was observed shortly after the first fibers underwent transverse cleavage; the redistribution of tension within the network caused fibers to move and re-orient, leading some fibers to stick together and form a thicker, single fiber. Fiber bundling was usually permanent, suggesting that bonds holding bundled fibers together were stronger than the forces exerted on them from subsequent tension redistribution events as the network continued to lyse.

As the lysis process progressed, the networks typically reached a state where only a few remaining fibers were holding the network between the ridges (for simplicity, we’ll call these “critical attachment fibers”). In this situation, when the critical attachment fibers are cleaved, the remaining fibers dependent on that attachment will recoil back (due to the tension), collapse onto the opposite ridge, and stick there. All fibers in the network that crumple onto the ridge during this process without being cleaved, are categorized as “collapsed” (See Figs. 2 and 3) for our analysis. These fibers are now considered cleared from the gap and no other degradation pathways can be distinguished. Thus, fiber collapse is a terminal degradation pathway. Fibers that are categorized as “collapsed” usually (but not always) coincide with whole or partial collapse of the entire network. In a large fibrin network, collapsed fibers would likely bundle with other fibers, but in our experimental setup, we are able to identify the collapse event as its own distinct category. Ultimately, all fibers after the completion of fibrinolysis were either transversely cleaved, collapsed, or bundled (bundled fibers are cleaved or collapse with the fiber they are bundled with).

Lysis experiments were performed using two different plasmin concentrations (0.1 U/ml and 1.0 U/ml) to test the effects of plasmin concentration on the fibrinolytic mechanisms. Fibers that undergo cleavage, buckling, bundling, and collapse were categorized over time and are shown in Fig. 3. Similar patterns were observed for the lysis of fibrin networks in both plasmin concentrations, although the 1.0 U/ml samples were cleared more rapidly. At the time that plasmin was delivered, all fibers were straight; subsequently, the number of straight fibers decreased, and the number of cleaved fibers increased until the network area was completely cleared of fibrin (all fibers are cleaved, bundled, or collapsed and the ridge gap is empty). Fiber buckling was predominantly seen during mid-lysis; buckled fibers were eventually cleaved, bundled, collapsed, or occasionally re-straightened, causing a decrease in the number of buckled fibers as lysis approached completion (See Fig. 3). Fiber bundling was seen early during network clearance, and the number of fibers bundled increased until lysis was complete. We saw a similar pattern for fiber collapse, though collapsing was delayed when compared with cleavage and bundling (Fig. 3).

The two plasmin concentrations exhibited different rates of fibrinolysis and statistically significant differences in the percentage of fibers that experienced each fibrinolytic mechanism. Networks in the lower plasmin concentration typically had their first fiber lysed one to three minutes after the addition of plasmin, while many networks in the higher plasmin concentration were observed to begin dissolution within 6 seconds after adding plasmin (Fig. 3). After the clearance of individual networks was completed, in the lower plasmin concentration we found that 54 ± 16% of fibers were removed by transverse cleavage, 23 ± 15% of fibers were removed by bundling, and 23 ± 16% of fibers were removed through collapsing. In the higher plasmin concentration, we found that 43 ± 17% of fibers were removed by transverse cleavage, 30 ± 17% of fibers were removed by bundling, and 28 ± 19% of fibers were removed through collapsing. Using a two sample t-test, we confirmed the statistical significance of these differences; 8.3 – 14.8% less fibers were cleaved in the higher plasmin concentration. We also found that in the higher plasmin concentration, fiber bundling occurred in 3.6 – 10.0% more fibers and fiber collapsing in 1.5 – 8.6% more fibers than for the lower concentration. Comparisons using two sample t-tests showed strong statistical significance (See Supplemental Table 3) for each category, indicating that the plasmin concentration alters the degradation pathways taken.

4.2. Modeling the Effect of Tension on Fibrin Network Clearance

Because the pathways of network clearance seemed to be influenced by the redistribution of tension within the network, we sought to model the effects of tension in fiber reorientation and the clearance of an area of fibers. Additionally we sought to determine how the results would change if networks were under different amounts of tension. We used the program Webslinger, which has previously been used to model fibrin network stretching [27], to simulate fibrin lysis of ten representative networks from our experiments. For each experimental network geometry, we modeled the lysis of fibers with an imposed prestrain of 0%, 25%, 43%, 100%, and 233% (corresponding to Webslinger rest_length_fraction values of 1.0, 0.8, 0.7, 0.5, and 0.3). Note that we refer to this as “prestrain” because the fibers are stretched beyond their equilibrium length, and hence under tension, strictly from the polymerization process. Further strain can be applied to fibers from mechanical stretching, but that is not what we are considering in these experiments [25]. Supplementary Movies 4-8 show side-by-side comparisons of experimental results and the corresponding webslinger simulations at each prestrain value.

In the recanalization process, the fibrinolytic enzymes must clear a blood clot out of a volume of space within the vasculature in order for full blood flow to resume. The 2-D analog to volume is area, so the parameter that we considered in these simulations was the area covered by the 2-D fibrin network (See Fig. 4) at different timepoints in the lysis process. Webslinger does not account for fiber buckling or bundling but does allow for the transverse cleavage and collapse of fibers. By modeling the clearance of multiple fibrin networks at varying levels of tension, we found that the area cleared of fibrin during clot digestion was greatly influenced by tension present in the network. We determined that for experimental networks, 95 ± 5% of the area initially encompassed by a network, was no longer covered by fibrin at the end of the lysis process (See Fig. 4). Simulations of network fibrinolysis using a prestrain of 0% showed an average area clearance of only 60 ± 17% at the end of lysis (See Supplemental Table 5). The main reason that these networks showed much lower clearance than experimental was the absence of any fiber movement due to tension redistribution and the lack of fiber collapse after transverse cleavage events (Fig. 4, Supplemental Movie 8). Repeating each simulation using prestrains of 25%, 43%, 100%, and 233% showed average network area clearances of 71 ± 14%, 77 ± 12%, 90 ± 5%, and 96 ± 2% respectively. Thus, a greater amount of tension increases the effect of fiber collapse and fiber reorientation after cleavage events, resulting in a greater clearance of fibrin (Fig. 4).

Figure 4. Comparison of Experimental Network Lysis and Network Models at Varying Levels of Tension.

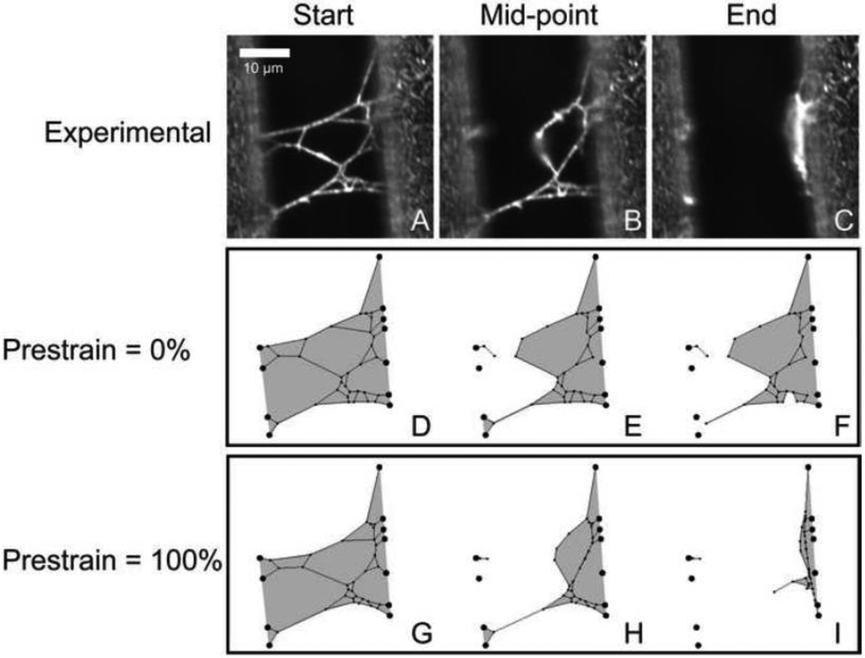
The experimental micrographs depict a fibrin network stretched between ridges prior to lysis (A), when half of the fibers that experienced cleavage have been cut (B), and after lysis is complete (C). Model networks created from the micrographs using Webslinger 4.1 depict lysis at the same stages of fibrin clearance using prestrain values of 0% and 100% (D – I). Gray shaded regions highlight the area covered by the network.

The clearance of each network was also analyzed at the “mid-point” of lysis, the timepoint at which 50% of the fibers that ultimately experience transverse cleavage were cut. The average area clearance in experimental networks at the mid-point of lysis was 45 ± 25%. The average clearance of simulated networks at the mid-point of lysis were determined to be 35 ± 24%, 41 ± 25%, 44 ± 27%, 48 ± 30%, and 52 ± 32% when modeled with prestrains of 0%, 25%, 43%, 100%, and 233%, respectively (See Supplemental Table 5).

Taken together, these results strongly suggest that inherent fiber prestrain and tension must be taken into account when modeling fibrinolysis. To estimate which simulated prestrain value best approximated the experimental area clearance, we utilized a sum of squared errors metric (SSE), summing up the squared difference between experimental and simulated network clearance (See Methods). At the lysis midpoint, the lowest SSE between experiment and simulations came from the 43% prestrain simulations, while at the endpoint the lowest SSE was from the 233% prestrain simulations (See Supplemental Table 5).

4.3. Network Density Effects on Lysis Events

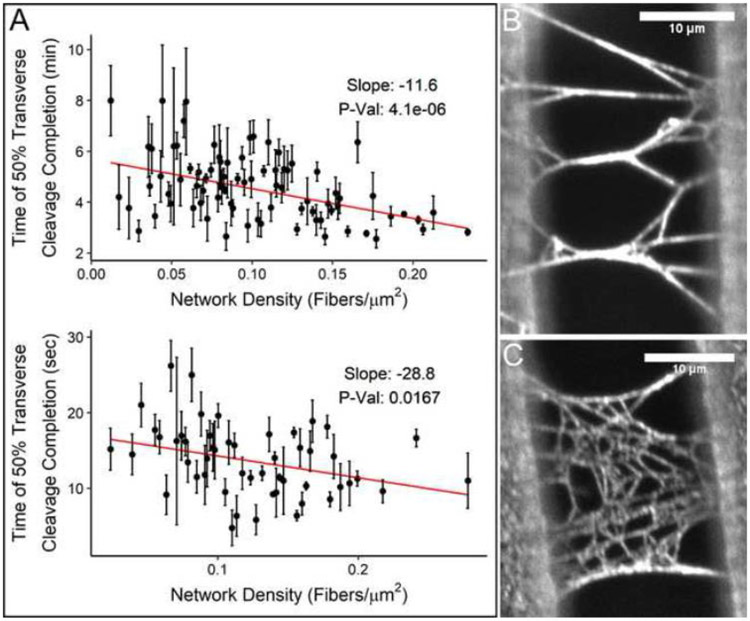
Our experiments offer a unique look at the effect of network fiber density on the rate of fiber lysis. Using a benchmark of 50% of the cleavage events (the lysis midpoint), Figure 5A shows an inverse relationship between the time of 50% fiber cleavage and the network density for both concentrations of plasmin used. Time of 50% transverse cleavage completion is defined as the point at which half of the fibers that will ultimately be cleaved during fibrinolytic network clearance are cleaved (For example, in a 50 fiber network, if 26 fibers are ultimately cleaved, the time of 50% transverse cleavage completion is the time at which half of the 26 fibers (13 fibers for this example) are cleaved. This timepoint captures a time of active network lysis, when the network is half-digested, and is therefore a good point to compare the rate of network lysis across different networks. Thus, the data suggest that networks with higher density lyse more rapidly than less-dense networks. While both plasmin concentrations show this downward trend, the time it takes for 0.1 U/ml plasmin treated networks to reach the 50% cleavage benchmark is approximately 18-20 times longer than the time needed for 1.0 U/ml plasmin treated networks. Figure 5B-C show representative images of “higher” and “lower” density networks. Supplemental Movie 9 shows a side-by-side comparison of the lysis of the two networks shown in Figure 5B-C.

Figure 5. Scatter Plot of Transverse Cleavage and Micrographs Representing Differing Network Densities.

The graphs represent density (x-axis) vs the time at which 50% of the fibers that will be cleaved are cleaved (y-axis) (A). The top graph represents trials taken at a plasmin concentration of 0.1 U/ml, and the bottom graph at 1.0 U/ml. The slope is calculated and plotted based on a weighted least squared linear fit (See Statistical Methods 3.1 for details). For ease of visualization, data points with error bars larger than the scale of a plot were not included in the figure (6 points total between the two plots), but all data points were included in the fit and statistical analysis. Note the different time scales on the y-axis. The micrographs depict a lower density network at 0.06 fibers/micron² (B) and a higher density network at 0.17 fibers/micron² (C). Scale par is 10 μm. Graphs plotted with ggplot2 [44].

4.4. Timing of the First Transverse Cleavage Event

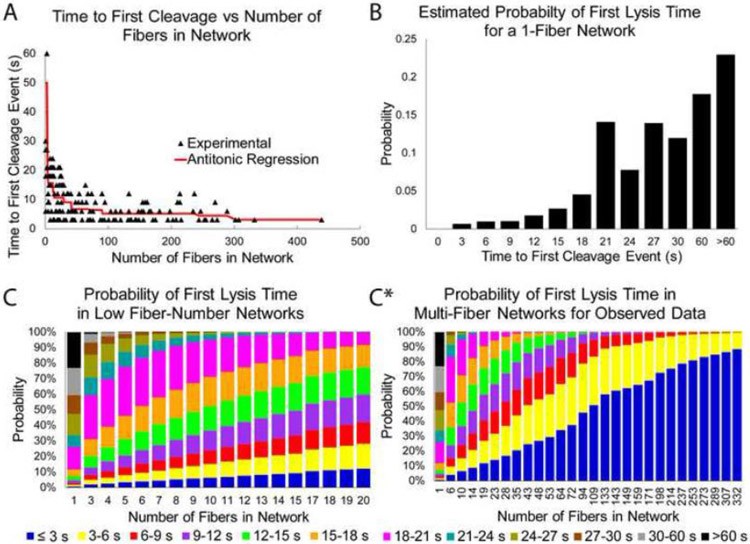
Considering the discovery of secondary lysis mechanisms detailed in this publication, it is likely that the timing of the initial fiber cleavage event in a network will impact the timing of all subsequent fiber outcomes. Figure 6A shows a plot of the time of the first cleavage event versus the number of fibers in the network for the experimental data using 1.0 U/ml plasmin. The antitonic regression shows a trend where networks with lower fiber numbers have an average first lysis event that is slower than for networks with higher numbers of fibers. Intuitively, this isn’t too surprising, since more fibers provide more locations for the first lysis event to occur. If we assume that every fiber in the network has an associated “cleavage time” (CT; the time it would take plasmin to cleave the fiber, if the fiber was isolated), then we can model the time to first lysis in a k-fiber network as the minimum cleavage time for k independent fibers. Doing so, allows us to estimate the probability distribution of cleavage times for individual fibers as seen in Figure 6B. This distribution was estimated by choosing probabilities so that the theoretical distribution of times across all 156 networks (fiber counts ranging from 1 to 439) matched the empirical proportions. For example, in 156 networks, the time to first lysis was observed to be 3 seconds (or less) 54 times or 34.66%. If k-fiber networks behave as we assume, then we would expect to get that percentage of <3s first fiber cleavage times in our data only if the probability of an individual fiber cleavage time less than 3s (P(CT<3s) is 0.65%.

Figure 6. Time of First Fiber Lysis.

A) Experimental data showing the time of first lysis as a function of the number of fibers in the network. Antitonic regression identifies the non-increasing function possessing the smallest sum of square residuals, similar to how linear regression identifies the linear function possessing the smallest sum of square residuals. The downward trend indicates that networks with more fibers tend to begin lysing more rapidly. The figure is zoomed in on the fibers that lyse in 60s or under, to emphasize the downward trend, but this cropping cut only one (210s) data point, which occurred for a 3-fiber network. B) Estimated probability distribution of lysis time for an individual fibrin fiber. Note that insufficient data prevents more accurate probabilities for times greater than 60s. C) and C*) Probability distributions for observing a first lysis event within a certain time period for a network consisting of a certain number of fibers. C contains the same data as C* but is zoomed in to emphasize the probabilities in low fiber number networks. As fiber numbers grow larger the probability that at least one fiber will lyse in under three seconds approaches 100%.

Using this same line of reasoning, we can also calculate the probability of observing a first fiber cleavage time for a k-fiber network. These were calculated using equation 3 described in the statistical methods section and are displayed in Fig. 6C and C*

Note that Figure 6C shows the probabilities only up to a 20-fiber network, while Figure C* shows the same data, but includes networks up to 332 fibers. The trends in the probabilities show how, for low fiber number networks, the first fiber lysis times could range from <3s to >60s, with an expected mean somewhere in the 20-30s range, while for higher fiber networks the odds of having a slow first lysis event go down dramatically, with most networks expected to have a first lysis event occur in under 6s. This is in general agreement with what is seen in Figure 6A, but the presence of networks with > 200 fibers with first lysis times of 12s indicate that other factors (including fiber diameter, the uniformity of fiber diameter [is the fiber the same diameter along its entire length], and fiber tension) may play a role as well.

4.5. Experimental Estimates of the Inherent Fiber Prestrain and tension values

We identified thirteen fibers where the initial fiber cleavage occurrence transpired in such a way that two fiber fragments were clearly identifiable in the image directly following the event. In these cases we measured the fiber length before cutting (L), and the fiber fragment lengths (L₁ and L₂) after cutting (See Fig. 7). Assuming that L₁ and L₂ approximate the relaxed length of the fiber strands, we can define the relaxed fiber length as:

$$L_o=L_1+L_2$$ (4)

Figure 7. Fiber Prestrain Estimate.

Top (A) and Bottom (B) panels show a fiber before and after cleavage. The difference in fiber segment locations in B highlight how much the network recoils backwards after the cleavage event, emphasizing the role of inherent fiber tension. Measuring the polymerized length (L) and segment lengths (L₁ and L₂), enables an estimate of the fiber prestrain. Note that the cleavage point occurs in an area of lower fluorescence intensity. The 5 μm scale bar applies to both Panel A and B.

And prestrain as:

$$\epsilon =\frac{L-L_o}{L_o}x100\%$$ (5)

Averaging the 13 fiber prestrain values, we find < ε >= 23 ± 11% (See Supplemental Table 6). Thus, we arrive at an estimate of how much fibers are inherently stretched beyond their initial length due strictly to polymerization processes. Assuming an elastic modulus (E) of ~ 1MPa, in agreement with previously published results [3,30,31], yields an inherent fiber tension (σ) of:

$$\sigma =E\epsilon =1MPax0.23=0.23MPa$$

5. Discussion

Previous studies on fibrinolytic processes have focused on transverse cleavage of individual fibers as the primary mechanism for clearing a space of fibrin [4,19,34]. Similar to these studies, our results suggest that lysis of individual fibers is accomplished by cleavage at a single point. Other studies have suggested that fibers thin radially as plasmin digests the fibers inward [16-18]. We attempted to look for fiber thinning by looking at the fluorescence intensity profile in cross-sections of fibers but did not see clear evidence of a decrease in cross-section fluorescent intensity prior to cleavage (data not shown). It is interesting to note, as observed in Fig. 7, that fiber cleavage often occurred at points of lower fluorescence intensity when compared with other regions of the fiber. Whether cleavage occurring at these points is related to lower fiber thickness in these regions will be the subject of future investigations. Our fluorescent labeling method (beads added after polymerization) may not lead to uniform fiber labeling, so our fluorescence data cannot be directly correlated to fiber thickness and thus cannot be used to rule out fiber thickness/thinning as lysis mechanisms. In either case, the transverse cleavage of a single fiber always led to dramatic changes in network architecture, suggesting that the cleavage events (rather than fiber thinning) play the dominant role in network clearance.

Our results also indicate the importance of lesser-appreciated secondary mechanisms involved in fibrin clot dissolution that occur because of the transverse cleavage of individual fibers; these mechanisms include the buckling, bundling, and collapsing of fibers. In our experiments, a substantial percentage of fibers progress through fibrinolysis using these secondary mechanisms rather than experiencing transverse cleavage (Fig. 3). This suggests that buckling, bundling, and collapsing also play a significant role in clearing fibrin out of a volume during lysis. The presence of fibrin bundling during lysis is consistent with other studies, which have reported bundling in the form of lysed fragments and ends associating laterally to create thick bundles [19,34]. However, in our experiments we observe fully intact fibers bundling with other intact fibers due to fiber reorientation during the tension redistribution that arises from individual fiber cleavage events. The bundling of fibers is mostly permanent, which is consistent with other studies of fiber cohesion, which have shown that a large amount of force is required to pull fibers apart that are stuck together at a junction [27,35,36]. Intact fiber bundling is a novel mechanism by which fibers are cleared during lysis, to our knowledge. Intriguingly, our results suggest that fibers can be cleared from an area with only 40-50% of the fibers undergoing transverse cleavage (Fig. 3). Thus, we propose that secondary fiber clearance mechanisms (bundling and collapsing) contribute a great deal to the recanalization of the vasculature during fibrinolysis and should be considered in future studies on the behavior of individual fibers during lysis.

Understanding what happens to fibrin after collapse and bundling is an important next step in continuing this research. Recent modeling and confocal microscopy studies looking at the overlay of tPA and fibrin at the lysis front indicate that digested fibrin “pieces” can be expelled from the clot during degradation [15]. This mechanism serves to regulate the local concentration of tPA. The time resolution of their experiments was likely too rapid to capture fiber collapse, but it will be important to look for fiber collapse in 3-D gels going forward. In our experiments, remnants of collapsed fibers persisted for up to 24 hours without obvious further degradation, so collapsed fibers have some resistance to further lysis. It would be interesting to know whether the collapsed fibers in our experiment correspond to the digested fibrin “pieces” of the confocal experiments. Further experiments could investigate this.

The concentration of plasmin used to initiate fibrinolysis plays a role in determining the digestion pathways that fibers take. A higher percentage of fibers were cleaved in trials using a lower concentration of plasmin than in the trials using a higher concentration. The higher concentration trials exhibited more fiber collapsing and bundling (Fig. 3). The mechanism responsible for the difference in fiber digestion pathways is unclear, though network areas are typically completely cleared of fibrin in either plasmin concentration. A possible explanation is that fibers exposed to a lower concentration of plasmin have more time to re-straighten after they buckle, resulting in more lysis-prone fibers. Future studies should focus on the lytic susceptibility of buckled fibers, since previous studies have suggested the fibers that lose tension may not lyse [9,25].

Our findings also indicate that the density of the local fibrin network affects lytic susceptibility. Most significantly, an increase in local fiber density greatly increases the rate at which fibrin is cleaved (See Fig. 5). At first glance, these results seem to be at odds with previous studies that indicate dense networks of thin fibers lyse more slowly [22,23]; however in those experiments the delayed lysis of the networks is likely due to the slower entrance of fibrinolytic agents into the dense networks. In our experiments, plasmin should diffuse onto all the fibers at the same time, so our results reflect the direct influence of density on the rate at which fibers are cleared from an area, rather than on the rate at which plasmin arrives at the fibers. Fibrin density also seems to affect the rate at which secondary fibrinolytic mechanisms occur, but this relationship holds less statistical significance (See Supplemental Fig. 2 and Supplemental Table 1). The exact mechanism causing this increase in fibrinolytic susceptibility is unclear. A possible explanation is that denser networks contain thinner fibers, which are transected at a faster rate than thicker fibers [19]. In these studies, we were unable to quantify the fiber thickness prior to digestion due to our fluorescent labeling method, but this hypothesis could possibly be tested in the future using other methods to measure fiber diameter. We do note, as seen in Fig. 5, that less dense networks have some fibers that appear thicker according to fluorescence intensity, so fiber thickness likely plays some role. Another hypothesis is that the fiber tension could be different in dense and less dense networks. Fibrin polymerizes under tension [7-9], but the mechanism for this is not well understood, thus future studies could try to quantify the inherent fiber tension in dense and less dense networks to see if that plays a role in lytic susceptibility.

A third hypothesis is that denser networks just have more fibers that have the possibility of undergoing transverse cleavage events. Since the first transverse cleavage event initiates all the secondary lysis mechanisms, the timing of the first cleavage event would likely play an important role in the timing of all the other events. To test this hypothesis, we plotted the time of the first cleavage event of a fiber in every network vs the number of fibers in the network (Figure 6A). The antitonic regression shows a decreasing trend where networks with more fibers have increasingly faster 1^st lysis times. To determine whether this trend could come from the fact that there are more fibers available to be cleaved in higher density networks, we also developed a simple model based on probability distributions of observing a cleavage event. The model uses our experimental data to estimate the probability as a function of time for observing a single fiber to lyse (Figure 6B). We show that if one treats a network of fibers as if it was made up of k- independently lysing fibers, then based on the probability distribution of seeing a single fiber lyse, one can develop a probability distribution of observing the first lysis event in that k-fiber network (Figure 6C & C*). The results of this work show that indeed, as the number of fibers increases, the probability of at least one of the fibers lysing early also increases, so higher density networks with more fibers would be expected to have an earlier first lysis event.

To our knowledge, this is the first time anyone has considered the effect of the raw number of fibers available to be lysed on fibrinolytic outcomes. These results point out that because of the tension in fibers, lytic enzymes merely need to cleave the most “rapidly lysable fiber” in order to initiate all of the secondary lysis mechanisms. Thus, lysis may progress more rapidly than might be expected through models that only consider enzyme diffusion and a uniform lysis time for individual fibers.

Our model does not completely describe the data, as some large fiber-number networks, have slower-than predicted lysis times, suggesting additional factors (fiber thickness, fiber density, etc.) may also be in play. A more detailed model involving the cleavage of fibers by individual plasmin molecules, which includes fiber density, tension, and different fiber thicknesses is important to further understand these results. It is important to be aware of the limitations of the first cleavage time probability estimates (Fig. 6B) for large times (> 60s), given that we only have eight networks of three fibers or fewer in our data. As can be seen in Fig. 6C&C*, the probability of observing a high cleavage time in high-fiber count networks is negligible, so the exact probabilities for first lysis times >60s would require many more low fiber number networks. Further characterization of the lysis times of low fiber-count networks would enable a more complete probability distribution for individual fibers and would enhance future modeling efforts.

Our results have important implications for the idea that fibers polymerize under tension, even under static conditions. First, we’ve shown that fiber tension is important for secondary lytic mechanisms in clearing an area of fibrin. Simulated networks with 0% prestrain (no tension) showed no fiber collapse and no fiber movement in response to cleavage events. Conversely, a high level of initial tension in fibers increases the space cleared through fibrinolysis by enhancing the effect of these secondary mechanisms (Fig. 4). From our analysis of model networks half-way through lysis, we also found that higher tension reduces the number of fibers that must be cleaved to observe a significant network clearance. The influence of fiber tension on fibrin removal varies due to network geometry; in some networks, the cleavage of just one or two crucial fibers may cause a significant clearance of fibrin from an area.

We attempted to estimate the amount of prestrain in fibers using two methods. Using the lengths of cut and uncut fibers, we estimated that fibers are under ~ 23% prestrain, which would correspond to a tension of 0.23 MPa. The drawbacks to this approach are that there are large uncertainties in the length measurements of the cleaved fiber ends, because they are loose after cleavage. We also assume that the lengths of the cut fiber segments that are observed one image frame after the cleavage event correspond the equilibrium lengths, which may not be true (See Fig. 7). Therefore, while 23% seems like a reasonable first estimate, more work should be done on intact fibers to determine their prestrain. One other point to note is we often saw fibers cleaved at locations of lower fluorescent intensity. This could suggest that fiber cleavage occurs at locations of fiber thinness, but a better measurement of fiber diameter is necessary to confirm this.

We also can estimate the inherent fiber prestrain values using our sum of squared errors metric for comparing the simulation and experimental area clearance. Surprisingly, the best match at the lysis midpoint came from the 43% prestrain simulations, while at the endpoint the best match was the 233% prestrain simulations. The endpoint value, in particular, seems high, given the experimental estimate. Real fibers are semiflexible polymers, which can both buckle, bundle, and even fold on to themselves in response to changes in tension. Additionally, fibrin fibers can have different thicknesses, and thus different spring constants, and potentially different amounts of tension. The springs in the simulation can only get shorter or longer, have the same spring constant, and do not buckle or bundle. Where these differences likely manifest themselves the greatest is in the “collapse event”, after the last critical fibers holding the network together are cleaved. When this occurs in experiments, the fibers rapidly fold up onto the ridge, while in the simulations, the springs relax to their equilibrium lengths. Thus, the simulations need much shorter equilibrium lengths to replicate the collapse event, and this may explain why the high prestrain value gives the best SSE match at the endpoint (this effect can be observed in Supplemental Movies 4-8). Thus, while our simulations highlight the important role that fiber tension plays in clearing an area of fibrin during lysis, future models should incorporate the semiflexible nature and inherent “stickiness” of fibrin to replicate the collapse events.

The mechanism from which fiber tension is derived is still under consideration; one study proposed that fibers and protofibrils polymerize in a twisted structure, and consequently, protofibrils that bind laterally to the surface of a fiber are further stretched than those near the center [7]. Other studies suggest that many fibrin structures polymerize under tension without any twist [8]. Our data can help to constrain models on the origin of fibrin fiber tension, and further experimental studies on the prestrain of individual fibers can help to quantify fiber tension further. Though the mechanism causing the inherent tension in fibrin is still under study, it undoubtedly plays a significant role in fibrin removal, especially through secondary fibrinolytic mechanisms.

Further tension can be applied to fibers through mechanical stretching. This can occur due to external mechanical forces from fluid flow, movement of cells through the network, or blood clot contraction [37,38]. Recent studies have shown that fibrin stretching alters its fibrinolytic susceptibility [25,39,40]. In particular, stretched fibers and clots are typically more resistant to fibrinolysis. Stretched clots likely expel fibrinolytic agents as water is expelled, which could explain some of these results [40], but even stretched individual fibers lyse more slowly [25]. Intriguingly, a study on the lysis of contracted clots showed a 4-fold decrease in lysis speed for clots where the lytic enzyme is introduced from the outside, but a 2-fold increased lysis rate for internal fibrinolysis [41]. Our results could help explain why internal lysis is increased due to clot contraction, as the tension in contracted fibers could help to clear the network more rapidly due to secondary lytic mechanisms. The interplay between inherent fiber tension and tension from mechanical stretching needs to be investigated further to understand their respective contributions to lysis.

The goal of this study is to tease out mechanisms regulating fibrinolysis that may be overlooked in studies of larger clot structures. We believe that has indeed been the case, but great care must be taken in interpreting the results into a more physiological context. Our networks contain a small number of fibers and are only two-dimensional, we did not consider the effects of FXIIIa crosslinking, we only initiated lysis with plasmin (not plasminogen and its activators), our system consists of only purified fibrinogen, while physiological clots contain many other plasma proteins and even blood cells and platelets, and the concentrations of both fibrinogen and plasmin are not physiological. In spite of these limitations, starting with a basic experimental setup and building stepwise to more complicated models should reveal the interactions that each clotting component has on overall network characteristics (polymerization, mechanical properties, fiber connectivity, lytic susceptibility, and more). Studying individual fibrin fiber mechanical properties, led to the realization of their remarkable extensibility [42], and studying the lysis of small networks of fibers has the potential to reap similar gains in knowledge. To do so, it will be important to investigate hypotheses generated from our research, such as the role of fiber tension and secondary clearance mechanisms in fibrinolysis, in both 3-D in vitro and in vivo models.

Additional steps to expand this research could focus on studying secondary lytic mechanisms in fibrinolysis initiated using plasminogen and plasminogen activators (rather than plasmin). FXIIIa crosslinking is also known to impact fibrinolysis [13,43] and its influence on fiber tension and these secondary mechanisms should be elucidated. Further characterizing the influence of fiber network density on fibrinolysis mechanisms is also important, with an emphasis on the role of the “most rapidly lysable fiber” on network clearance. The observation that collapsed fibers on ridges are resistant to further degradation could have important implications for fibers that collapse on blood vessel walls. It would be interesting to know if a) collapsed fibers which are not rapidly cleared could serve as nucleation points for thrombosis and b) enzymes other than plasmin are required to digest collapsed fibers in vivo.

6. Conclusion

Taken together our results have implications for understanding fibrinolytic mechanisms. First, the transverse cleavage of individual fibers influences the structure of many other fibers near the cleavage event due to the tension in the network. Second, only 40-50% of the fibers in a network need to undergo transverse cleavage for an area to be cleared of fibrin due to secondary clearance mechanisms including fiber bundling, buckling, and collapse. Finally, our results show that fiber density influences the rate at which fibers are cleared, but in a way that is different than previously anticipated from studies of bulk network lysis. By studying the lysis of small networks, we have uncovered mechanisms that have previously been undiscovered in studies of large 3-D networks. Fibrinolysis is thus a dynamic process with many competing factors that influence the clearance of fibers from a local volume. We anticipate that careful future studies of small networks will help to unravel the influence of the varying factors contributing to the lytic susceptibility of fibrin clots.

Supplementary Material

1

Movie 1-3: Micrograph Movies Depicting Fibrinolysis of Various 2-D Example Fibrin Networks. Timestamps in the lower left corner indicate the amount of time that has passed since the addition of plasmin to the sample of fibrin. A scale bar is located in the upper left corner. Once lysis reaches completion, collapsed fibers rarely experience fibrinolytic activity or rearrangement. Movie 1 depicts the lysis of a network that results in collapsed fibers settling into the ridge over the span of several minutes. Movie 2 depicts a network where individual cleavage events cause dramatic shifts in network geometry, leading to bundling and collapsing. Movie 3 depicts multiple fibers that do not experience cleavage, collapsing, or bundling, and continue to occupy a small area an hour after plasmin administration.

4

Movie 4: Micrograph Movie comparing Experimental Lysis Data and a Webslinger simulation with 233% prestrain.

5

Movie 5: Micrograph Movie comparing Experimental Lysis Data and a Webslinger simulation with 100% prestrain.

6

Movie 6: Micrograph Movie comparing Experimental Lysis Data and a Webslinger simulation with 43% prestrain.

7

Movie 7: Micrograph Movie comparing Experimental Lysis Data and a Webslinger simulation with 25% prestrain.

8

Movie 8: Micrograph Movie comparing Experimental Lysis Data and a Webslinger simulation with 0% prestrain.

9

Movie 9: Micrograph Movie with a side-by-side comparison of a dense network (right) and a sparse network (left). The networks are the same representative networks shown in the main text in figure 5. The lower density network is at 0.06 fibers/micron² and the higher density network is at 0.17 fibers/micron².

Statement of Significance.

Fibrin fibers serve as the main structural element of blood clots. They polymerize under tension and have remarkable extensibility and elasticity. After the cessation of wound healing, fibrin must be cleared from the vasculature by the enzyme plasmin in order to resume normal blood flow: a process called fibrinolysis. In this study we investigate the mechanisms that regulate the clearance of individual fibrin fibers during fibrinolysis. We show that the inherent tension in fibers enhances the action of plasmin because every fiber cleavage event results in a redistribution of the network tension. This network re-equilibration causes fibers to buckle, bundle, and even collapse, leading to a more rapid fiber clearance than plasmin alone could provide.