Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Mar 13;32(7):3245–3253. doi: 10.1021/acs.chemmater.0c00453

GeSe: Optical Spectroscopy and Theoretical Study of a van der Waals Solar Absorber

Philip A E Murgatroyd ‡, Matthew J Smiles ‡, Christopher N Savory ¶,§, Thomas P Shalvey ‡, Jack E N Swallow ‡, Nicole Fleck ‡, Craig M Robertson ∥, Frank Jäckel ‡, Jonathan Alaria ‡, Jonathan D Major ‡, David O Scanlon ¶,§,⊥, Tim D Veal ‡,*
PMCID: PMC7161679  PMID: 32308255

Abstract

graphic file with name cm0c00453_0006.jpg

The van der Waals material GeSe is a potential solar absorber, but its optoelectronic properties are not yet fully understood. Here, through a combined theoretical and experimental approach, the optoelectronic and structural properties of GeSe are determined. A fundamental absorption onset of 1.30 eV is found at room temperature, close to the optimum value according to the Shockley–Queisser detailed balance limit, in contrast to previous reports of an indirect fundamental transition of 1.10 eV. The measured absorption spectra and first-principles joint density of states are mutually consistent, both exhibiting an additional distinct onset ∼0.3 eV above the fundamental absorption edge. The band gap values obtained from first-principles calculations converge, as the level of theory and corresponding computational cost increases, to 1.33 eV from the quasiparticle self-consistent GW method, including the solution to the Bethe–Salpeter equation. This agrees with the 0 K value determined from temperature-dependent optical absorption measurements. Relaxed structures based on hybrid functionals reveal a direct fundamental transition in contrast to previous reports. The optoelectronic properties of GeSe are resolved with the system described as a direct semiconductor with a 1.30 eV room temperature band gap. The high level of agreement between experiment and theory encourages the application of this computational methodology to other van der Waals materials.

Introduction

Conventional commercial solar cells based upon Si, Cu(In,Ga)Se2, and CdTe present both high stability and high device efficiency.1 Solar power based on such inorganic absorbers has now reached a levelized cost of electricity below that of fossil fuels in many countries. However, these materials are not without issues. The production of high-quality silicon is energy-intensive, giving a high energy pay-back time and environmentally damaging waste products;2,3 cadmium is a toxic heavy metal; and both indium and tellurium are scarce.2,4 From a materials’ design perspective, three-dimensional crystal structures unavoidably result in dangling bonds residing at the grain boundaries leading to a reduction in device performance via recombination losses; this deficiency can be minimized by producing single crystalline material, which in turns results in additional cost and complexity of synthesis.

Van der Waals (vdW) materials, such as the transition metal dichalcogenides, have been the focus of intensive study in recent years because of a plethora of potential applications.5 Commonly cited examples include the molybdenum dichalcogenides: MoS2 has successfully been incorporated for the intercalation of Li in batteries, while MoSe2 has been used as an ultrathin layer in transistors. Despite the wide-reaching potential of layered vdW materials, the accurate prediction of properties from ab initio calculations is nontrivial. The limiting factor for first-principles calculations of vdW systems is the accurate description of the dispersion forces involved in the bonding.6 The development and experimental verification of first-principles methods pertaining to vdW materials are crucial to accelerate the discovery of new materials within this class.

The fundamental nature of the intermolecular bonding of vdW systems makes them an attractive class of materials for photovoltaic application; offering a solution to the dangling bond issue that afflicts conventional solar absorbers.7 Sb2Se3 is the seminal example of a vdW solar absorber and belongs to the orthorhombic structural family Pnma (space group 62). Sb2Se3 is a relatively low-toxicity, low-cost material which has rapidly presented reasonably high device efficiency (9.2%).8 It has been suggested that through the growth of highly oriented films, one-dimensional ribbons are developed which lead to superior transport properties within the absorber layer coupled with benign grain boundaries. Because of the fairly complex crystal structure of Sb2Se3, these benefits are only achievable if the films are grown with preferred orientation in the [00l] direction, a requirement which leads to an unavoidable constraint in production. Sb2Se3 clearly presents itself as a promising candidate for photovoltaic purposes and demonstrates that research on isomorphous compounds is imperative.

GeSe has a stable orthorhombic Pnma phase at room temperature (space group 62), presenting vdW bonding (different orientations are shown in Figure 1). The compound has low-toxicity, a lower raw cost than Sb2Se3, and germanium is over 6 times more earth-abundant than antimony.10 Solar cells incorporating GeSe as the absorber, deposited by thermal sublimation, have been reported with a power conversion efficiency of 1.48%,11 an impressive result for such an understudied material. It has been reported for single crystal electrical transport measurements that conductivity exhibits weak anisotropy and p-type transport character.12,13 Unfortunately, the literature available on GeSe regarding optical properties is highly conflicted with neither the nature nor magnitude of the fundamental band gap being reconciled. This issue is further compounded when considered in unison with results from computational studies, especially those which predate the use of hybrid functionals, leading to misconceptions regarding the fundamental properties of the material.

Figure 1.

Figure 1

Open in a new tab

Different crystal orientations for GeSe drawn using VESTA9 using the crystallographic information files generated by our single crystal X-ray diffraction. The (a) [001], (b) [010], and (c) [100] directions are pointing out of the page for the space group Pnma. Each box represents one unit cell. In the [001] and the [100] directions, the nanosheets can be seen clearly, and the van der Waals interactions between these sheets can be distinguished.

A commonly cited value of the GeSe band gap comes from a study on cleaved single crystals with thicknesses ranging between 25 μm to 2.25 mm.14 This study claims indirect energy gaps of 1.075 and 1.080 eV for polarization parallel to the a- and c- crystallographic axis respectively (space group Pbnm), with reported absorption coefficients on the order of 5 cm–1. Further studies on single crystals supported this polarization dependence of the band gap.15,16 However, other studies have found no polarization dependence and an indirect band gap of 1.10 eV.17,18 It has also been reported that the 1.10 eV band gap is indirect forbidden.19 Studies on both thin films and nanobelts have found similar indirect band gaps of 1.14 eV.13,20 Studies on amorphous thin films have found indirect band gaps of 1.01 eV21 and 1.16 eV (with a direct forbidden band gap of 1.53 eV).22 In addition to these optical studies, Mishra et al.23 concluded that GeSe has an indirect band gap using angle-resolved ultraviolet photoemission spectroscopy (ARUPS). The validity of conclusions from ARUPS come with considerable doubts. ARUPS is a surface-sensitive technique, and the data had to be double differentiated before being interpreted. This collection of contradictory experimental data demonstrates the necessity for the nature and size of the band gap to be resolved to inform the development of photovoltaic devices.

Uncertainty also arises because of the wide range of computational results available for GeSe. Despite the extensive literature available for monolayer GeSe, our work focuses on the bulk properties. The calculated values of the band gap for the bulk vary widely. One study found a direct band gap of 1.59 or 1.50 eV depending on the light polarization, while another found an indirect band gap of 1.45 eV independent of polarization.24,25 Both of these studies, however, used semiempirical methods, with the former constructing an effective-orbital linear combination of atomic orbitals (EO-LCAO) Hamiltonian and the latter using empirically derived pseudopotentials fitted to optical data of GeS and SnSe.26 These methods are highly sensitive to the data used to fit them and have difficulty accurately reproducing conduction band states, leading to significant uncertainty in the magnitude of the gap. An ab initio study for GeSe revealed a band gap of 1.08 or 1.05 eV dependent on whether spin–orbit coupling was included.27 This study uses the generalized gradient approximation (GGA), which is known to inherently underestimate band gaps by around 30%, and so must be considered a lower-bound on the magnitude of the gap but does demonstrate the minimal effect of spin–orbit coupling on both the size of the gap and the shape of the band edges.

Chen et al. performed a combined experimental-theoretical study on GeSe films.28 Optical absorption measurements were analyzed under the assumption of an indirect band gap, giving a room-temperature value of 1.25 eV. First-principles calculations using a hybrid functional found an indirect band gap of 1.24 eV. These two values should not be compared directly; the band gap varies with temperature, while DFT gives a prediction of the value at 0 K. This brief summary of the literature illustrates obvious uncertainty regarding the fundamental properties of GeSe both experimentally and theoretically.

In this work, single crystals and thin films of GeSe were produced by chemical vapor transport (CVT) and thermal evaporation, respectively. The phase purity of all samples was confirmed by X-ray diffraction (XRD) and Raman spectroscopy. Lattice parameters were extracted from the refinement of single crystal XRD. Optical properties were studied by Fourier-transform infrared spectroscopy (FTIR) at room temperature on cleaved single crystals, and films of varying thickness. The temperature dependence of the band gap was studied on a film between 70 and 400 K. Density functional theory (DFT), of varying computational expense, was used to calculate the band structure for comparison with the experimentally obtained results and address the question of the nature and magnitude of the fundamental band gap of GeSe. The spectroscopic limited maximum efficiency was theoretically calculated to assess the appropriateness of GeSe as a solar absorber. The combination of experiment and theory enables the fundamental optical properties of GeSe to be understood and offers an explanation regarding the potential limitations of this system from a PV perspective.

Experimental and Computational Details

Single crystals of GeSe were grown via chemical vapor transport (CVT). A stoichiometric mixture of Ge and Se (totalling a mass of 1 g) both of 5N purity (Alfa Aesar) was sealed under vacuum in an evacuated quartz tube of pressure ≤10–4 Torr with iodine used as the transport agent (5 mg cm–3). The reaction was carried out in a two-zone furnace with a temperature gradient of 790 to 680 K with the charge placed at the hot end for 7 days. Powder GeSe was produced by melting of stoichiometric amounts of the Ge and Se at 800 K, allowed to dwell for 2 days and slowly cooled to room temperature, with the solid ingot pulverized to a fine powder in an agate pestle and mortar.

Polycrystalline GeSe films were deposited on SnO2:F-coated soda lime glass substrates (TEC15, NSG Group) via thermal evaporation at a rate of ∼2 Å/s with no substrate heating. Film thickness was monitored using a quartz crystal microbalance (QCM) calibrated with an Ambios XP-200 surface profilometer and further verified by infrared reflectivity. Films were then annealed on a hot plate in a N2 environment for 20 min at 623 K. Four-point probe measurements were performed using an Advanced Instrument Technology CMT-SR2000N to measure sheet resistances of the deposited films.

The phase and purity of polycrystalline GeSe powder and polycrystalline films were confirmed using a Rigaku Smartlab X-ray diffractometer, with a rotating copper anode, under ambient conditions. Monochromated incident radiation (Cu Kα1) was used to perform θ:2θ scans carried out between 20° and 80° at 0.5° min–1 in parallel beam geometry for both powder and film measurements.

Lattice parameters were extracted from single-crystal XRD measurements. Single crystals of GeSe were carefully selected under a microscope and mounted on a “Bruker D8 Venture” diffractometer with a Photon 100 detector. The crystal was kept at 250.7 K during data collection. Using Olex2,29 the structure was solved with the ShelXT30 structure solution program using Intrinsic Phasing and refined with the ShelXL31 refinement package using least-squares minimization.

Raman spectroscopy was performed using 532 nm laser illumination in backscattering configuration on a Renishaw inVia microscope. The laser power was kept below 0.2 mW to prevent sample damage. Infrared transmission and specular reflection spectra were acquired at an 11° angle of incidence at ambient temperature in the range of 0.9–1.8 eV using a Bruker Vertex 70 V Fourier-transform infrared spectrometer with a combined reflection–transmission accessory. A tungsten near-infrared source and CaF2 beam splitter were used for all measurements. For single-crystal measurements, a liquid-nitrogen-cooled mercury–cadmium–telluride (MCT) detector was used. For thin-film measurements, both a room temperature silicon (Si) and the MCT detector were used. For temperature-dependent optical measurements, the samples were cooled in an Oxford Instruments CFV2 continuous-flow cryostat using liquid nitrogen.

Periodic DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP).32−35 The interaction between valence and core electrons was described by the projector augmented wave method.36 Ge 3d electrons were included in the valence band, and all pseudopotentials were scalar-relativistic. In order to fully assess the electronic and optical behavior of bulk GeSe, multiple theoretical methods were applied. Both the functional of Perdew, Burke, and Ernzerhof (PBE)37 and Heyd, Scuseria, and Ernzerhof (HSE06)38,39 were used as exchange-correlation functionals for the optimization of the GeSe structure to its equilibrium geometry—as neither DFT nor hybrid DFT is able to fully describe dispersion forces. Both methods also included the D3 dispersion correction of Grimme et al.6 Adding such a dispersion correction has been shown to improve the structural description of layered and lower-dimensionality post-transition metal chalcogenides: PBE+D3 has recently been used to calculate the Sn(S,Se) solid solution,40 while HSE06+D3 has been shown to reproduce the experimental structure of the pseudo-1D chalcogenide Sb2Se3, as well as its electronic properties.41−43 For both functionals, the total energy of GeSe was found to be converged to within 1 meV per atom using a plane-wave energy cutoff of 500 eV, and a Γ-centered k-point mesh of 6 × 6 × 3. Geometry optimizations used a higher plane-wave cutoff of 650 eV to avoid the effects of Pulay stress and were considered to be converged when the forces on each atom were reduced to less than 0.01 eV Å–1. To ensure accurate calculations of the band gap, electronic calculations such as densities of states, band structures, and optical absorption were all performed using HSE06 on top of both the PBE+D3 and HSE06+D3 relaxed geometries. Phonon calculations were also performed on a 4 × 4 × 2 (256 atom) supercell of each of the PBE+D3 and HSE06+D3 relaxed structures of GeSe, using their respective functionals, to confirm dynamic stability through the supercell method within the Phonopy package.44 The calculations on displaced supercells used the 650 eV plane wave cutoff, together with convergence criteria of 1 × 10–8 eV on the total energy and 1 × 10–4 eV Å–1 on the forces per atom to ensure sufficient accuracy in the calculation of the second-order force constants.

To further check the accuracy of band gaps calculated at the HSE06 level, additional calculations of the electronic band structures for each relaxed geometry were performed using the quasiparticle self-consistent GW (qsGW) method of Kotani et al.45 within the Questaal package.46 Questaal implements qsGW and DFT methods within a full-potential linear muffin-tin orbital (FP-LMTO) basis—for these calculations, the automatically generated augmentation spheres and interstitial smoothed Hankel function basis sets were used for each structure, with a l-cutoff of 4 used for both Ge and Se. The electronic structure was not observed to change significantly on the inclusion of Ge 3d as local orbitals, and so these were not included in the valence band. A k-mesh of 6 × 6 × 3 and was also used for qsGW calculations, with recommended G-vector cutoff for the interstitial density of 5.5 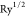Inline graphic, and the qsGW method was iterated until the root-mean-square (RMS) change in the self-energy, Σ0, was below 1 × 10–5 Ry. qsGW, while demonstrating excellent agreement with experimental band gaps for a variety of semiconductor systems, is known to systematically overestimate band gaps slightly due to usage of the random phase approximation (RPA). To quantify the effect of this error, after a fully self-consistent qsGW calculation, a correction to the screened Coulomb interaction W was calculated through solution of the Bethe–Salpeter equation (BSE), allowing the inclusion of ladder diagrams—this too was self-consistently iterated until the RMS change in the qsGW+BSE Σ0 was below 1 × 10–5 Ry. Such qsGW+BSE has previously been shown to replicate the band gaps of semiconductors with exceptional accuracy.47,48 Plotting of the electronic band structures from both VASP and Questaal, and phonon dispersion curves, made use of the sumo package.49

Results and Discussion

Because of the previously reported anisotropic nature of the optical properties in GeSe and potential for forming impurity phase GeSe2, X-ray diffraction (XRD) was performed to confirm phase purity and to assess the existence of preferred orientation in the polycrystalline powder and films. Figure 2a presents the XRD patterns for the powder, thermally evaporated film, and the TEC-15 substrate. These results show that no impurity phase is incorporated into the film through deposition with strongly preferred (001) orientation. The 004 peak of the powder and film are minimally displaced in 2θ indicating negligible strain on the film with respect to the powder (difference in lattice parameter values is <0.08%). Raman spectra from both a single crystal and the deposited film are shown in Figure 2b and confirm that all samples are composed of GeSe. The peaks at 150, 175, and 188 cm–1 are consistent with α-GeSe50−52 and no contamination or secondary phase peaks were identified. The combination of results from these structural characterization techniques indicates that the samples are of high phase purity. Four point probe measurements indicate a sheet resistance of several MΩ/□ for the GeSe films deposited on highly conductive TEC-15 (15 Ω/□). Such a large resistance measured for the GeSe film, in spite of the highly conductive substrate, is indicative of a nondegenerate semiconductor with the Fermi level residing within the band gap. Due to the nondegeneracy, all optical measurements can be considered without Burstein–Moss shifts,53,54 with the measured absorption onset being the fundamental direct band gap between the valence band maximum and conduction band minimum. The nondegenerate transport properties and absence of phase impurities suggest high phase purity and negligible nonstoichiometry. The Pnma structure shown in Figure 1 was confirmed through single crystal X-ray diffraction (Supplementary Tables S1–S5.55). The lattice parameters extracted are a = 10.833(2) Å, b = 3.8355(7) Å, and c = 4.3954(9) Å which are consistent with previously reported results.56,57

Figure 2.

Figure 2

Open in a new tab

(a) X-ray diffraction patterns of GeSe powder, thermally evaporated film, and TEC glass. Strong preferred (001) orientation exists in the film and no impurity phases are apparent. Dashed line included as a guide to the eye to demonstrate the minimal displacement of the 004 peak of the GeSe powder and film. (b) Raman spectra of GeSe bulk crystal and GeSe film, showing the same features, confirming phase purity is retained through deposition of the film.

The absorption spectra, (αhν)2 versus hν, are shown in Figure 3a for the temperature range of 70 to 280 K. Details of how these measurements were taken can be found in the Supporting Information. By extrapolation to the (αhν)2 = 0, an optical transition of 1.301 ± 0.004 eV is found at 300 K. This suggests a maximum solar cells power conversion efficiency of 32.6% based on the SQ-limit.58,59 Identification of the initial relatively weak absorption onset with absorption coefficient rising to ∼1.5 × 104cm–1 by ∼1.5 eV (as shown in the inset of Figure 3a) was informed by comparison with the calculated joint density of states (JDOS), which will be discussed below, as shown with the 70 K experimental data in Figure 3b. There is a stronger absorption onset at ∼1.6 eV for which the absorption coefficient rises to ∼6 × 104 cm–1 by ∼1.8 eV. This strong onset is apparent in both the experimental absorption data and the calculated JDOS using the HSE06+D3 level of theory. This is an interesting finding for photovoltaic applications—while the direct nature and size of the band gap appears to be optimal based on the SQ-limit, the weakness of the initial absorption onset suggests that GeSe has nonideal optical properties for solar cells. The steepness of the absorption onset is often not considered when screening for potential photovoltaic absorbers, but is a key property; the experimentally determined absorption is compared to the theoretically calculated JDOS in Figure 3b and discussed further below.

Figure 3.

Figure 3

Open in a new tab

(a) Optical absorption spectra of the 400 nm GeSe thin film for the temperature range 70–280 K, plotted as (αhν)2 versus hν. The inset shows the weak initial absorption onset. (b) The 70 K experimental absorption data, showing the weak absorption onset at ∼1.33 eV followed by the strong absorption onset at ∼1.6 eV, along with the calculated joint density of states (JDOS) derived from the HSE06+D3 band structure—both are plotted with a logarithmic y-axis. To account for the difference between HSE06+D3 and qsGW+BSE fundamental band gaps, the JDOS is shifted to 0.05 eV lower energy. (c) The variation of the direct band gap as a function of the temperature between 70 and 400 K fitted by the Varshni relation. The fundamental direct band gaps calculated with successively higher levels of theory are shown as horizontal lines. Note that PBE+D3 predicts an indirect band gap, but the smallest direct transition from that level of theory has been included here for comparison.

In Figure 3c the temperature dependence of the band gap, Eg(T), is analyzed with the Varshni relation:60

graphic file with name cm0c00453_m002.jpg 1

where Eg(0), α, and β are fitting parameters. The typical Varshni-like temperature dependence of the band gap is observed due to thermal expansion and electron–phonon interactions.60 The Varshni fit yields Eg(0), α, and β parameters of 1.333 ± 0.003 eV, 2.3 × 10–4 eV K–1, and 478 K respectively. The different values of the direct band gaps found from different theoretical calculations are also presented on the figure. These results will be discussed further below, but it can be seen that the value of Eg(0) is in excellent agreement with the fundamental direct band gap found by qsGW+BSE.

In spite of previous reports suggesting an indirect band gap, the Tauc-like analysis in Figure 3a is performed under the assumption that the direct allowed transition dominates the absorption. For many conventional III–V, II–VI compound semiconductors (e.g., GaAs and CdTe) and elemental group IV semiconductors (e.g., Si),61,62 the nature of the band gap can be determined by plotting (αhν)m versus hν where m = 2 and m = 1/2 give a linear onset for the cases of direct and indirect fundamental band gaps, respectively. In these cases, the manifestation of the fundamental transition in optical spectra is unencumbered by other transitions which occur at significantly higher energies. For many other semiconductor materials, such as GeSe, there are many direct and indirect transitions within a few hundred meV of the fundamental band gap. Therefore, determining whether the fundamental band gap is direct or indirect is extremely challenging from optical absorption measurements. In such a scenario, the direct transitions will dominate absorption spectra due to their much greater probability. We, therefore, do not make any claims to have experimentally determined the nature of the fundamental band gap of GeSe. Additionally, this approach is supported by the theoretical results reported below which all indicate direct and indirect transitions within close energy proximity.

The absorption spectra of the single crystal (see Supplementary Figure S3) reveals a much weaker absorption feature, with an onset that begins around 1.0 eV and an absorption coefficient of 150 cm–1 by 1.4 eV. This is consistent with other aforementioned reports of single crystals within the literature,15,16 which are often cited as the band gap for GeSe. However, we suggest the absorption onset manifests itself at a lower photon energy for the single crystals (here and in the literature) due to subgap phenomena such as Urbach tailing and defect-related absorption. In this lower energy region, due to the low absorption coefficient, a portion of photons are permitted to transmit through a thick sample. However, the higher energy photons will be very efficiently absorbed making it impossible, for thick samples, to probe the direct onset at 1.3 eV (see Supplementary Figure S4); this is an obvious benefit of our work focusing primarily on thin films. This, therefore, supports our interpretation that the fundamental band gap is higher than previously reported and the lower energy onsets found for bulk crystals are due to the fact that no light can be transmitted through thick crystals in the high-absorption-coefficient region of the spectrum.

The GeSe lattice parameters obtained from DFT relaxations with the PBE+D3 and HSE06+D3 methods differ from those determined experimentally; these are summarized for the two methods in Table 1. Both calculation methods show some difference from the 250.7 K experimental values—both give b parameter values over 2% higher than experiment, with HSE06+D3 differing more than PBE+D3. The other two calculated lattice parameters are closer to the experimental values. HSE06+D3 reproduces a within 1%, while PBE+D3 overestimates by just more than 1%; however, in c, HSE06+D3 more closely reproduces the experimental parameter. Neither geometry optimization appears to more closely replicate the experimental structure overall, and hence electronic band structures were calculated using both relaxed structures. To ensure that the optimized structures are indeed the dynamic ground state, and no instabilities exist that could lead to a transition to the other respective structure, phonon dispersion curves were calculated for each structure with their respective functional , and the resultant plots are depicted in Supplementary Figure S5. In both cases, the structures are found to be dynamically stable, with no imaginary modes at Γ; the small (<0.1THz) imaginary mode off-Γ for the PBE+D3 structure is likely an artifact of numerical noise in the compilation of the interatomic force constants, rather than a genuine instability. As such, hybrid DFT and GGA DFT fundamentally disagree on the equilibrium structure of GeSe—we may consider that the inclusion of exact exchange, as opposed to the approximate exchange and correlation of PBE, in HSE06 means it is more likely to represent a more “complete” theoretical description of the electronic ground state of GeSe; however, as above, the comparison to experiment leaves this judgment unclear.

Table 1. Calculated Lattice Parameters of GeSe, with Percentage Differences from the Experimental Lattice Parameters Obtained in This Work from Refinement of the Experimental XRD Data Collected at 250.7 K.

  a (Å) b (Å) c (Å)
PBE+D3 3.884 4.486 11.014
  +1.265% +2.061% +1.671%
HSE06+D3 3.811 4.451 10.950
  –0.64% +3.31% +1.08%
Open in a new tab

The HSE06 band structures on each of the two relaxed structures are depicted in Figure 4. The majority of the band structure of GeSe is very similar regardless of the geometry optimization, with the conduction band minimum occurring at Γ in both, except for a key difference in the crucial Γ to Y path (corresponding to the c direction in the Pnma cell). In the PBE+D3-optimized structure, the valence band maximum (VBM) occurs away from the high symmetry points and GeSe is predicted to be an indirect semiconductor, in line with previous GGA calculations; however, with the HSE06+D3 structure, the VBM occurs at Γ, meaning the fundamental band gap is direct. Nevertheless, in both cases, the magnitude of the fundamental band gap of bulk GeSe is similar to each other and higher than previously assessed by GGA-DFT; specifically, with Egi = 1.34 eV for the PBE+D3 structure, with the lowest direct transition at Γ only slightly higher at 1.43 eV, while Eg = 1.38 eV for the HSE06+D3 structure.

Figure 4.

Figure 4

Open in a new tab

HSE06 electronic band structures of GeSe on the structures relaxed using (a) PBE+D3 and (b) HSE06+D3. Valence band is in blue, conduction band in orange, and E = 0 eV is set to the valence band maximum.

To confirm that HSE06 is accurate in its determination of the band gap, we further compare to high-level qsGW calculations performed within the Questaal package at a similar k-point density. In both cases, the qsGW band structure (Figure 5) is found to compare very closely (with the indirect/direct band gaps within 20 meV) to the HSE06 electronic structure calculated at that same geometry. The direct band gap feature in the HSE06+D3 band structure is retained in the qsGW calculation, further confirming that this feature is structurally driven. The resultant band gap here is found to be direct with a value of 1.36 eV. Further, the error within qsGW quasiparticle band gaps is systematic. For simple semiconductors, like GeSe, without large spin fluctuations, its primary error arises from the omission of higher-order “ladder” diagrams when determining the contributions of the screened Coulomb interaction, W. To quantify this effect, GeSe was calculated (at the HSE06+D3 structure alone, due to the significant computational cost) with qsGW+BSE; the resultant band gap was found to be 1.33 eV, only 30 meV lower than the original qsGW gap. Encouragingly, the calculated ground state direct band gaps converge to the 0 K experimental value, as the computational cost increases, as demonstrated in Figure 3c.

Figure 5.

Figure 5

Open in a new tab

qsGW electronic band structures of GeSe on the structures relaxed using (a) PBE+D3 and (b) HSE06+D3. Valence band is in blue, conduction band in orange, and E = 0 eV is set to the valence band maximum.

While the fundamental band gap of GeSe is optimal for a solar absorber, as mentioned above, the weak initial absorption onset is not ideal for photovoltaics. The weak absorption onset observed in Figure 3b is due to the low joint density of states associated with the dispersive band extrema of both the conduction and valence bands, as is apparent in the calculated band structures shown in Figures 4 and 5. The validity of the theoretical findings is supported by the agreement between the experimental and theoretical results shown in Figure 3, and a comparison is also shown in Table 2.

Table 2. Experimental and Calculated Fundamental Band Gap, Eg, and Strong Absorption Onset Energy.

  Eg (eV) strong absorption onset energy (eV)
experiment, thin film (70K) 1.329 ± 0.004a 1.56 ± 0.03
HSE06+D3 1.38 1.60
qsGW+BSE 1.33 1.55
Open in a new tab
a

A very weak onset was measured at ∼1.0 eV for the bulk GeSe crystals, with the absorption coefficient not exceeding 150 cm–1 below the fundamental band gap at 1.3 eV (supplementary Figure S4)—it is not fundamental and, as discussed, comes from Urbach tailing/defects.

The success of the theoretical approach employed here for GeSe suggests that using a combination of the HSE06+D3 method to calculate the structure and the qsGW+BSE level of theory for optical properties is an appropriate procedure for obtaining accurate first-principles descriptions of vdW materials. Additional equivalent studies on a range of semiconducting vdW materials would be desirable to evaluate this procedure further.

Conclusion

In conclusion, the optical and structural properties of the vdW material GeSe have been studied both experimentally and theoretically in the context of photovoltaic application. The Pnma orthorhombic structure of GeSe was confirmed through single crystal X-ray diffraction with the lattice parameters extracted being a = 10.833(2) Å, b = 3.8355(7) Å, and c = 4.3954(9) Å. In terms of optical properties, the theoretical study suggests the fundamental band gap is direct. Under the assumption of a direct band gap, experimental absorption spectra from thin films indicate a value of 1.301 ± 0.004 eV at 300 K, somewhat larger than the widely quoted value of 1.1–1.2 eV for the fundamental band gap. Previous optical absorption results, suggesting lower band gaps with low absorption coefficients have been understood to be artifacts of measurements of very thick crystals for which light is not transmitted in the direct absorption onset region of the spectrum. Hybrid density functional theory calculations (HSE06), with the Grimme correction (D3) used to account for the vdW interactions, suggest a band gap that is direct with a value of 1.38 eV at 0 K. Additionally, quasiparticle self-consistent GW approximations (using the structure from the HSE06+D3 calculations) also give a fundamental direct band gap but with a value of 1.36 eV. Further to this, when the BSE correction is applied to the qsGW, a smaller direct band gap of 1.33 eV is calculated. With increasing computational cost, the different theoretical approaches converge toward the experimentally obtained value of 1.333 ± 0.003 eV for the 0 K fundamental band gap. As well as this, the shape of the theoretical JDOS is consistent with the low-temperature experimental optical absorption spectra, with both exhibiting an onset ∼0.3 eV above the initial absorption edge.

Acknowledgments

Engineering and Physical Sciences Research Council (EPSRC) are acknowledged for funding studentships for M.J.S., T.P.S., and J.E.N.S. with the Centre for Doctoral Training in New and Sustainable Photovoltaics (Grant No. EP/L01551X/1) and for P.A.E.M. and N.F. within the Doctoral Training Partnership (EP/N509693/1). The XRD facility used was supported by EPSRC (Grant No. EP/P001513/1). J.D.M., D.O.S., and T.D.V. acknowledge EPSRC funding (Grant nos EP/N014057/1, EP/N01572X/1 and EP/N015800/1, respectively). The use of the UCL Legion, Myriad and Grace High Performance Computing Facilities (Legion@UCL, Myriad@UCL and Grace@UCL) are acknowledged in the production of this work. Computational work was also performed on the ARCHER UK National Supercomputing Service, via our membership of the UK’s HEC Materials Chemistry Consortium, funded by EPSRC (EP/L000202/1 and EP/R029431/1). Phil King is acknowledged for discussions about the relevant angle resolved photoemission literature. Laurence Hardwick is thanked for access to the Raman spectrometer.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.chemmater.0c00453.

  • GeSe SXRD (CIF)

  • Single-crystal XRD results, methodology to obtain absorption coefficient, bulk crystal optical absorption data, further information relating to the optical absorption in Figure 3, DFT-calculated phonon dispersion curves, DFT band structure diagrams for the HSE06 functional without dispersion correction and for the PBE functional with D3 dispersion correction (PDF)

Author Contributions

† P.A.E.M., M.J.S., and C.N.S. contributed equally to this work.

The authors declare no competing financial interest.

Supplementary Material

cm0c00453_si_001.cif (42.8KB, cif)
cm0c00453_si_002.pdf (782KB, pdf)

References

  1. Green M. A.; Hishikawa Y.; Dunlop E. D.; Levi D. H.; Hohl-Ebinger J.; Yoshita M.; Ho-Baillie A. W. Y. Solar cell efficiency table (Version 53). Prog. Photovoltaics 2019, 27, 3–12. 10.1002/pip.3102. [DOI] [Google Scholar]
  2. Battersby S. The solar cell of the future. Proc. Natl. Acad. Sci. U. S. A. 2019, 116, 7–10. 10.1073/pnas.1820406116. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Yang H.; Huang X.; Thompson J. R. Tackle pollution from solar cells. Nature 2014, 509, 563. 10.1038/509563c. [DOI] [PubMed] [Google Scholar]
  4. Candelise C.; Winskel M.; Gross R. Implications for CdTe and CIGS technologies production costs of indium and tellurium scarcity. Prog. Photovoltaics 2012, 20, 816–831. 10.1002/pip.2216. [DOI] [Google Scholar]
  5. Das S.; Robinson J. A.; Dubey M.; Terrones H.; Terrones M. Beyond Graphene: Progress in Novel Two-Dimensional Materials and van der Waals Solids. Annu. Rev. Mater. Res. 2015, 45, 1–27. 10.1146/annurev-matsci-070214-021034. [DOI] [Google Scholar]
  6. Grimme S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. 10.1002/jcc.20078. [DOI] [PubMed] [Google Scholar]
  7. Zhou Y.; Wang L.; Chen S.; Qin S.; Liu X.; Chen J.; Xue D.-J.; Luo M.; Cao Y.; Cheng Y.; Sargent E. H.; Tang J. Thin-film Sb2Se3 photovoltaics with oriented one-dimensional ribbons and benign grain boundaries. Nat. Photonics 2015, 9, 409–415. 10.1038/nphoton.2015.78. [DOI] [Google Scholar]
  8. Li Z.; Liang X.; Li G.; Liu H.; Zhang H.; Guo J.; Chen J.; Shen K.; San X.; Yu W.; Schropp R. E. I.; Mai Y. 9.2%-efficient core-shell structured antimony selenide nanorod array solar cells. Nat. Commun. 2019, 10, 125. 10.1038/s41467-018-07903-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Momma K.; Izumi F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. 10.1107/S0021889811038970. [DOI] [Google Scholar]
  10. Kaye G. W. C.; Laby T. H.; Noyes J. G.; Phillips G. F.; Jones O.; Asher J. Tables of Physical & Chemical Constants (16th edition, 1995). Section 3.1.3 Abundances of the elements. Kaye & Laby Online. Version 1.0 (2005). https://web.archive.org/web/20190518224615/http://www.kayelaby.npl.co.uk/chemistry/3_1/3_1_3.html (accessed Mar 11, 2020).
  11. Xue D.-J.; Liu S.-C.; Dai C.-M.; Chen S.; He C.; Zhao L.; Hu J.-S.; Wan L.-J. GeSe Thin-Film Solar Cells Fabricated by Self-Regulated Rapid Thermal Sublimation. J. Am. Chem. Soc. 2017, 139, 958–965. 10.1021/jacs.6b11705. [DOI] [PubMed] [Google Scholar]
  12. Kyriakos D. S.; Anagnostopoulos A. N. Electrical conductivity of layered GeSe related to extended faults. J. Appl. Phys. 1985, 58, 3917–3920. 10.1063/1.335613. [DOI] [Google Scholar]
  13. Vaughn D. D.; Patel R. J.; Hickner M. A.; Schaak R. E. Single-Crystal Colloidal Nanosheets of GeS and GeSe. J. Am. Chem. Soc. 2010, 132, 15170–15172. 10.1021/ja107520b. [DOI] [PubMed] [Google Scholar]
  14. Elkorashy A. M. Indirect Forbidden Fundamental Absorption Edge in Germanium Selenide Single Crystals. Phys. Status Solidi B 1986, 135, 707–713. 10.1002/pssb.2221350230. [DOI] [Google Scholar]
  15. Elkorashy A. M. Photoconductivity in Germanium Selenide Single Crystals. Phys. Status Solidi B 1989, 152, 249–259. 10.1002/pssb.2221520128. [DOI] [Google Scholar]
  16. Vlachos S. V.; Lambros A. P.; Thanailakis A.; Economou N. A. Anisotropic Indirect Absorption Edge in GeSe. Phys. Status Solidi B 1976, 76, 727–735. 10.1002/pssb.2220760234. [DOI] [Google Scholar]
  17. Kim Y.; Choi I. Optical and electrical properties of GeSe and SnSe single crystals. J. Korean Phys. Soc. 2018, 72, 238–242. 10.3938/jkps.72.238. [DOI] [Google Scholar]
  18. Vaughn D. D.; Sun D.; Levin S. M.; Biacchi A. J.; Mayer T. S.; Schaak R. E. Colloidal Synthesis and Electrical Properties of GeSe Nanobelts. Chem. Mater. 2012, 24, 3643–3649. 10.1021/cm3023192. [DOI] [Google Scholar]
  19. Lukeš F. Optical and photoelectric properties of GeSe in the energy range 0.5–1.5eV. Czech. J. Phys. 1968, 18, 784–794. 10.1007/BF01696140. [DOI] [Google Scholar]
  20. Liu S.-C.; Mi Y.; Xue D.-J.; Chen Y.-X.; He C.; Liu X.; Hu J.-S.; Wan L.-J. Investigation of Physical and Electronic Properties of GeSe for Photovoltaic Applications. Advanced Electronic Materials 2017, 3, 1700141. 10.1002/aelm.201700141. [DOI] [Google Scholar]
  21. Katti V. R.; Govindacharyulu P. A.; Bose D. N. Electrical and optical properties of amorphous semiconducting GeSe and GeSbSe films. Thin Solid Films 1972, 14, 143–148. 10.1016/0040-6090(72)90376-8. [DOI] [Google Scholar]
  22. Kannewurf C. R.; Cashman R. J. Optical absorption and photoconductivity in germanium selenide. J. Phys. Chem. Solids 1961, 22, 293–298. 10.1016/0022-3697(61)90274-8. [DOI] [Google Scholar]
  23. Mishra P.; Lohani H.; Kundu A. K.; Patel R.; Solanki G. K.; Menon K. S. R.; Sekhar B. R. Electronic structure of germanium selenide investigated using ultra-violet photoelectron spectroscopy. Semicond. Sci. Technol. 2015, 30, 075001. 10.1088/0268-1242/30/7/075001. [DOI] [Google Scholar]
  24. Gashimzade F. M.; Guliev D. G.; Guseinova D. A.; Shteinshrayber V. Y. Band-structure calculation for A4B6 layered crystals by the equivalent-orbit linear combination of atomic orbitals method. J. Phys.: Condens. Matter 1992, 4, 1081–1091. 10.1088/0953-8984/4/4/018. [DOI] [Google Scholar]
  25. Valiukonis G.; Gashimzade F. M.; Guseinova D. A.; Krivaitė G.; Kulibekov A. M.; Orudzhev G. S.; Šileika A. Reflectance and Thermoreflectance Spectra and Energy Band Structure of GeSe Crystals. Phys. Status Solidi B 1983, 117, 81–92. 10.1002/pssb.2221170108. [DOI] [Google Scholar]
  26. Ciucci G.; Guarnieri A.; Masserini G.; Quartapelle L. Atomic pseudopotentials for orthorhombic IV–VI compounds. Solid State Commun. 1979, 29, 75–80. 10.1016/0038-1098(79)91106-2. [DOI] [Google Scholar]
  27. Makinistian L.; Albanesi E. A. Ab initio calculations of the electronic and optical properties of germanium selenide. J. Phys.: Condens. Matter 2007, 19, 186211. 10.1088/0953-8984/19/18/186211. [DOI] [PubMed] [Google Scholar]
  28. Chen B.; Ruan Y.; Li J.; Wang W.; Liu X.; Cai H.; Yao L.; Zhang J.-M.; Chen S.; Chen G. Highly orientated GeSe thin film_ self-assembly growth via the sandwiching post-annealing treatment and its solar cell performance. Nanoscale 2019, 11, 3968–3978. 10.1039/C8NR09836K. [DOI] [PubMed] [Google Scholar]
  29. Dolomanov O. V.; Bourhis L. J.; Gildea R. J.; Howard J. A. K.; Puschmann H. OLEX2: a complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. 10.1107/S0021889808042726. [DOI] [Google Scholar]
  30. Sheldrick G. M. SHELXT – Integrated space-group and crystal-structure determination. Acta Crystallogr., Sect. A: Found. Adv. 2015, A71, 3–8. 10.1107/S2053273314026370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Sheldrick G. M. Crystal structure refinement with SHELXL. Acta Crystallogr., Sect. C: Struct. Chem. 2015, C71, 3–8. 10.1107/S2053229614024218. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  33. Kresse G.; Hafner J. Ab initio molecular-dynamics simulation of the liquid-metal amorphous-semiconductor transition in germanium. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 49, 14251–14269. 10.1103/PhysRevB.49.14251. [DOI] [PubMed] [Google Scholar]
  34. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  35. Kresse G.; Furthmüller J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  36. Blöchl P. Projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  37. Perdew J.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  38. Heyd J.; Scuseria G. E.; Ernzerhof M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. 10.1063/1.1564060. [DOI] [Google Scholar]
  39. Krukau A. V.; Vydrov O. A.; Izmaylov A. F.; Scuseria G. E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. 10.1063/1.2404663. [DOI] [PubMed] [Google Scholar]
  40. Ektarawong A.; Alling B. Stability of SnSe1–xSx solid solutions revealed by first-principles cluster expansion. J. Phys.: Condens. Matter 2018, 30, 29LT01. 10.1088/1361-648X/aacb9c. [DOI] [PubMed] [Google Scholar]
  41. Phillips L. J.; Savory C. N.; Hutter O. S.; Yates P. J.; Shiel H.; Mariotti S.; Bowen L.; Birkett M.; Durose K.; Scanlon D. O.; Major J. D. Current Enhancement via a TiO2 Window Layer for CSS Sb2Se3 Solar Cells: Performance Limits and High Voc. IEEE J. Photovoltaics 2019, 9, 544–551. 10.1109/JPHOTOV.2018.2885836. [DOI] [Google Scholar]
  42. Savory C. N.; Scanlon D. O. The complex defect chemistry of antimony selenide. J. Mater. Chem. A 2019, 7, 10739–10744. 10.1039/C9TA02022E. [DOI] [Google Scholar]
  43. Birkett M.; Linhart W. M.; Stoner J.; Phillips L. J.; Durose K.; Alaria J.; Major J. D.; Kudrawiec R.; Veal T. D. Band gap temperature-dependence of close-space sublimation grown Sb2Se3 by photo-reflectance. APL Mater. 2018, 6, 084901. 10.1063/1.5027157. [DOI] [Google Scholar]
  44. Togo A.; Tanaka I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. 10.1016/j.scriptamat.2015.07.021. [DOI] [Google Scholar]
  45. Kotani T.; van Schilfgaarde M.; Faleev S. V. Quasiparticle self-consistent GW method: A basis for the independent-particle approximation. Phys. Rev. B: Condens. Matter Mater. Phys. 2007, 76, 165106. 10.1103/PhysRevB.76.165106. [DOI] [Google Scholar]
  46. Pashov D.; Acharya S.; Lambrecht W. R. L.; Jackson J.; Belashchenko K. D.; Chantis A.; Jamet F.; van Schilfgaarde M. Questaal: a package of electronic structure methods based on the linear muffin-tin orbital technique. Comput. Phys. Commun. 2020, 249, 107065. 10.1016/j.cpc.2019.107065. [DOI] [Google Scholar]
  47. Cunningham B.; Grüning M.; Azarhoosh P.; Pashov D.; van Schilfgaarde M. Effect of ladder diagrams on optical absorption spectra in a quasiparticle self-consistent GW framework. Phys. Rev. Mater. 2018, 2, 034603. 10.1103/PhysRevMaterials.2.034603. [DOI] [Google Scholar]
  48. Buckeridge J.; Scanlon D. O. Electronic band structure and optical properties of boron arsenide. Phys. Rev. Mater. 2019, 3, 051601. 10.1103/PhysRevMaterials.3.051601. [DOI] [Google Scholar]
  49. Ganose A. M.; Jackson A. J.; Scanlon D. O. sumo: Command-line tools for plotting and analysis of periodic ab initio calculations. Journal of Open Source Software 2018, 3, 717. 10.21105/joss.00717. [DOI] [Google Scholar]
  50. Chandrasekhar H. R.; Zwick U. Raman Scattering and Infrared Relectivity in GeSe. Solid State Commun. 1976, 18, 1509–1513. 10.1016/0038-1098(76)90381-1. [DOI] [Google Scholar]
  51. Fukunaga T.; Sugai S.; Kinosada T.; Murase K. Observation of new Raman line in GeSe and SnSe at low temperatures. Solid State Commun. 1981, 38, 1049–1052. 10.1016/0038-1098(81)90015-6. [DOI] [Google Scholar]
  52. Taube A.; Łapińska A.; Judek J.; Wochtman N.; Zdrojek M. Temperature induced phonon behaviour in germanium selenide thin films probed by Raman spectroscopy. J. Phys. D: Appl. Phys. 2016, 49, 315301. 10.1088/0022-3727/49/31/315301. [DOI] [Google Scholar]
  53. Burstein E. Anomalous Optical Absorption Limit in InSb. Phys. Rev. 1954, 93, 632–633. 10.1103/PhysRev.93.632. [DOI] [Google Scholar]
  54. Moss T. S. The Interpretation of the Properties of Indium Antimonide. Proc. Phys. Soc., London, Sect. B 1954, 67, 775–782. 10.1088/0370-1301/67/10/306. [DOI] [Google Scholar]
  55. CSD 1971854 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge from FIZ. Karlsruhe via www.ccdc.cam.ac.uk/structures (accessed Feb 10, 2020).
  56. Okazaki A. The Crystal Structure of Germanium Selenide GeSe. J. Phys. Soc. Jpn. 1958, 13, 1151–1155. 10.1143/JPSJ.13.1151. [DOI] [Google Scholar]
  57. Wiedemeier H.; Siemers P.-A. The Thermal Expansion and High Temperature Transformation of GeSe. Z. Anorg. Allg. Chem. 1975, 411, 90–96. 10.1002/zaac.19754110110. [DOI] [Google Scholar]
  58. Shockley W.; Queisser H. J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. 10.1063/1.1736034. [DOI] [Google Scholar]
  59. Rühle S. Tabulated values of the Shockley-Queisser limit for single junction solar cells. Sol. Energy 2016, 130, 139–147. 10.1016/j.solener.2016.02.015. [DOI] [Google Scholar]
  60. Varshni Y. P. Temperature Dependence of the energy gap in semiconductors. Physica 1967, 34, 149–154. 10.1016/0031-8914(67)90062-6. [DOI] [Google Scholar]
  61. Zanatta A. Revisiting the optical bandgap of semiconductors and the proposal of a unified methodology to its determination. Sci. Rep. 2019, 9, 11225. 10.1038/s41598-019-47670-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Lingg M.; Spescha A.; Haass S. G.; Carron R.; Buecheler S.; Tiwari A. N. Structural and electronic properties of CdTe1–xSex films and their application in solar cells. Sci. Technol. Adv. Mater. 2018, 19, 683–692. 10.1080/14686996.2018.1497403. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

cm0c00453_si_001.cif (42.8KB, cif)
cm0c00453_si_002.pdf (782KB, pdf)

Articles from Chemistry of Materials are provided here courtesy of American Chemical Society

RESOURCES