Development and Reporting of Prediction Models: Guidance for Authors From Editors of Respiratory, Sleep, and Critical Care Journals

Supplemental Digital Content is available in the text.

Abstract

Prediction models aim to use available data to predict a health state or outcome that has not yet been observed. Prediction is primarily relevant to clinical practice, but is also used in research, and administration. While prediction modeling involves estimating the relationship between patient factors and outcomes, it is distinct from casual inference. Prediction modeling thus requires unique considerations for development, validation, and updating. This document represents an effort from editors at 31 respiratory, sleep, and critical care medicine journals to consolidate contemporary best practices and recommendations related to prediction study design, conduct, and reporting. Herein, we address issues commonly encountered in submissions to our various journals. Key topics include considerations for selecting predictor variables, operationalizing variables, dealing with missing data, the importance of appropriate validation, model performance measures and their interpretation, and good reporting practices. Supplemental discussion covers emerging topics such as model fairness, competing risks, pitfalls of “modifiable risk factors”, measurement error, and risk for bias. This guidance is not meant to be overly prescriptive; we acknowledge that every study is different, and no set of rules will fit all cases. Additional best practices can be found in the Transparent Reporting of a multivariable prediction model for Individual Prognosis Or Diagnosis (TRIPOD) guidelines, to which we refer readers for further details.

Prediction is the bedrock of clinical practice. Inherent in every diagnosis is a prediction about the course of illness, and every prescription invokes a prediction about a response to treatment. For the most part, clinical predictions are made on a case-by-case basis based on a combination of experience and evidence. More recently, the uptake of electronic health records (EHRs), adoption of genomics technologies, and the advent of data science and machine learning have accelerated the development and publication of data-driven prediction models throughout medicine. Respiratory, sleep, and critical care medicine are no exception; prediction modeling has strong foundations in these fields, and they continue to be influential in its refinement and uptake.

Journals are witnessing an increase in submissions related to prediction modeling. This stands to seed rapid advancement in research and practice but also comes at the risk of pursuing false leads. As statistical editors, associate editors, and editors-in-chief at leading pulmonary, sleep, and critical care journals (Appendix 1), we believe it is important to provide guidance on how to maximize the usefulness of prediction modeling to capitalize on the opportunities that modern statistics and data science afford our fields.

INTENDED PURPOSE

This document is intended for both readers and authors of studies that describe prediction models. It borrows from expert reviews (1–5) and the Transparent Reporting of a multivariable prediction model for Individual Prognosis or Diagnosis (TRIPOD) guidelines, a comprehensive set of recommendations on current best practices for publishing prediction models, to which we direct readers for more information (6, 7).

Our aim is to provide an accessible summary of best practices and recommendations on prediction modeling, rather than to prescribe editorial policy for participating journals. We hope this guidance will enhance the overall quality and scientific merit of submissions to our various journals, provide consistency and common ground, and support readers of these studies in their critical appraisal of the prediction literature. Although exhaustive discussion of all the salient aspects of prediction modeling are beyond our scope, we attempt to address specific issues that we most commonly encounter in the review process at our various journals. We also acknowledge that every study is different, and depending on the overall goals, some may not conform to the guidance herein. We further recognize that this guidance may require updates as the fast-moving field of prediction modeling evolves over time.

DEFINITIONS AND SCOPE

The goal of prediction is to use information currently available to forecast a future outcome (Fig. 1). A prediction model is any construct that uses known variables (often called independent variables, features, or inputs) to estimate the value of this outcome (often called the dependent variable, response, or output) before it is observed. This is distinct from causal inference modeling, which aims to determine how a dependent variable will change as a direct result of altering an independent variable (often called an exposure). Causal inference studies, which we discuss in more detail elsewhere (8), require careful consideration of confounding and other potential biases.

Figure 1.

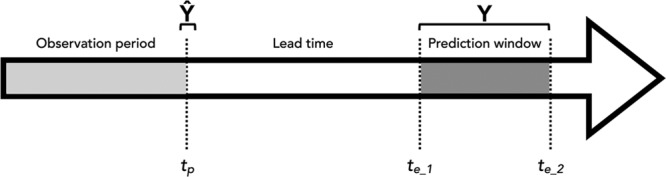
The chronology of information is critical in prediction. A prediction, Ŷ, is made at time, t_p, based on data collected up to and including that time, but no later. Ŷ is the estimate of Y, which cannot be observed until a time in the future. The times at which we can observe Y (rather than just Ŷ) fall within a prediction window (t_{e_1} to t_{e_2}), which occurs after a certain amount of lead time has elapsed. The width of observation, lead time, and prediction intervals will influence the usefulness of any prediction model.

Some prediction models may include causal factors (e.g., smoking is both predictive and causative of lung cancer), but in the strictest sense, such causal relationships are not required (e.g., a rising creatinine may predict impending renal failure, but does not itself cause renal failure). Therefore, prediction models are developed using different methods and should not be used for drawing causal inferences. Doing so can lead to logical fallacies. For example, a study may find endotracheal intubation predicts mortality, but this certainly does not mean patients with a compromised airway should not be intubated. In fact, sometimes the best predictors are interventions that counteract a causal process. Removing causal expectations means fewer restrictions on the variables a model can include, so long as the goal is properly understood to be an accurate and generalizable prediction, and not a deeper understanding of its biological significance (9).

A useful prediction model should, therefore, satisfy three core criteria:

• 1) It must provide a model whereby known variables estimate the value of the event of interest (e.g., for a binary outcome, it must have a classifier function),

• 2) The predictors must be known prior to knowing the outcome state, and

• 3) The model should retain accuracy when applied to new observations (i.e. it must be generalizable).

Some prediction models allow for clear identification of key predictors. Others may obscure the precise factors on which they most heavily rely, as well as the precise mechanisms by which they arrive at predictions. Although this is obviously of concern in causal inference exercises, it is sometimes less important in prediction modeling exercises, so long as the explanation underlying the prediction is felt to be unimportant.

Another important consideration is the intended purpose of any given prediction model. This generally falls into one of two categories. First are clinical prediction models intended for bedside use to inform the care of individual patients. For example, a rapid shallow breathing index calculated during a spontaneous breathing trial may predict whether a mechanically ventilated patient will be successfully extubated. Second are system prediction models intended for deployment across populations for research, benchmarking, and other administrative purposes. For example, an Acute Physiology and Chronic Health Evaluation IV score applied to a particular ICU cohort compares its overall predicted mortality risk with that of another cohort (10). The first type of predictive model is typically applied prospectively to forecast individual events, whereas the latter is typically deployed to characterize an overall population. Nonetheless, both should respect the temporal requirements necessary for an unbiased prediction. Though related in methodology, these two types of prediction models differ in how they should be evaluated and reported. Specifically, applying a model in clinical practice may require higher precision, making characteristics like positive predictive value more relevant than overall measures of discrimination, such as the area under the receiver operator characteristics curve (AUROC).

MODEL ARCHITECTURE

Considering Potential Predictor Variables

How researchers decide on variables to include in a prediction model (also referred to as “features”) is equally if not more important than the specific variables themselves. The large datasets increasingly used in biomedical research, such as those captured from EHRs, administrative systems, and high-dimensional “omics” platforms, include features that may number in the hundreds to thousands.

Not all features available in modern datasets are practical or effective choices. There is a trade-off between the number of features included in a model and its capacity to generalize. This risk becomes particularly important when considering that associations between predictor and outcome may be idiosyncratic. A single center study may show bronchoscopies done on Tuesdays are predictive of lung cancer diagnosis, but this may simply reflect local practice in which the lung nodule clinic has access to the endoscopy suite on certain days.

As noted above, for clinical prediction modeling the only allowable predictor variables are those that will be known at the time the prediction is made. Consider a model to predict whether a chronic obstructive pulmonary disease (COPD) patient with pneumonia and respiratory failure in the emergency department will subsequently develop hypotension. Positive blood cultures may be highly predictive of this outcome, but blood cultures typically take hours to days to be reported. This variable cannot be included in a model intended to assist decision making for a patient’s disposition from the emergency department because the information would never be available to decision-makers at the time they will use the prediction.

Authors should also consider how readily a variable can be obtained—including the cost, invasiveness, and risk of obtaining it—as well as how ubiquitously it is encountered in routine practice. The growing pervasiveness of smartphones and other devices, which can calculate complex scores automatically, has lessened the premium on “simple” scores with few variables, but clear trade-offs between parsimony and accuracy remain. For example, a prediction model for lung cancer that uses smoking history alone may be easy to use in any setting but may underperform compared with one based on smoking history, an exhaustive occupational history, and whole genome sequencing.

Modern datasets may lack representation from demographic groups historically under-represented in biomedical research. Prediction models based on such datasets may lead to bias in real world applications (11). Relatedly, including dimensions such as race as predictors inherently reflects assumptions of difference that are often tenuous, particularly when modeling a physiologic response. The complex issues and history surrounding prediction models creating or reinforcing biases are discussed elsewhere in-depth (11–15). Generally, we caution against arbitrarily including these variables in prediction models. Instead, we suggest careful consideration of what information they add in the context of specific study questions. We discourage their inclusion without reasonable suspicion that they contribute important predictive information.

Procedures for Predictor Selection

Usually, we approach prediction problems with prior knowledge about what features are likely to be predictive. In these cases, candidate variables can (and usually should) be preselected based on theory or prior evidence. The converse approach, selecting variables solely on strength of association, leads to problems. For example, suppose we select variables to predict the risk of future intubation. Lactate level may not initially appear associated with intubation in a population that includes many patients with asthma and COPD in whom lactate may be elevated on the basis of high-dose inhaled β-agonist therapy. Lactate may in fact be highly associated with intubation in patients presenting with pulmonary sepsis and shock. Here, β-agonists are effect modifiers: the predictive relationship between lactate and intubation depends on β-agonist use. This example is one of many reasons why experts have long recommended against using bivariable association to guide feature selection (16).

Another commonly used but problematic methodology is “stepwise” selection (17). Stepwise selection refers to procedures where decisions to include a predictor are based solely on p values associated with that predictor throughout multiple iterations of a model. For example, a study that enters 20 candidate variables into a model and continuously removes those meeting a threshold (e.g., p > 0.10 or >0.05) until all remaining terms are “statistically significant” uses backward-selection. By deciding to include variables based on p values, stepwise selection essentially amounts to multiple comparisons without appropriate correction. Further, unlike prespecified models, where all potential relationships are grounded in plausibility, stepwise models have no “prior” about what to include, making them highly prone to overfitting. Overfitting occurs when a model contains too many variables for the dataset to support. This results in a close fit to the data on which it was trained, but poor generalization to other datasets (18), undermining a key criterion of useful prediction. Any process that rigidly adheres to p value thresholds for variable selection poses similar risks of spurious conclusions (19, 20). In the vast majority of scenarios, p value based feature selection methods are strongly discouraged (21).

Underscoring the rationale to eschew stepwise and p value screening, modern statistical approaches to feature selection (e.g., penalized regression) avoid these pitfalls and can also inherently improve overall accuracy (22). For these reasons, TRIPOD guidelines explicitly recommend these alternative procedures for prediction studies (6). These methods have their own caveats and are comparatively more complex. Accordingly, they may not be amenable to all studies. Ultimately, the balance of prior knowledge about which factors are likely predictive and the need for data-driven discovery of novel predictors should guide a specific study’s approach to feature selection. Fully prespecified theory-based feature selection may be appropriate when there is extensive prior knowledge, whereas penalization methods may be preferred when prior knowledge is lacking or in discovery exercises. Table 1 presents an overview of feature selection techniques for statistical prediction models.

TABLE 1.

Approaches to Feature Selection in Prediction Models

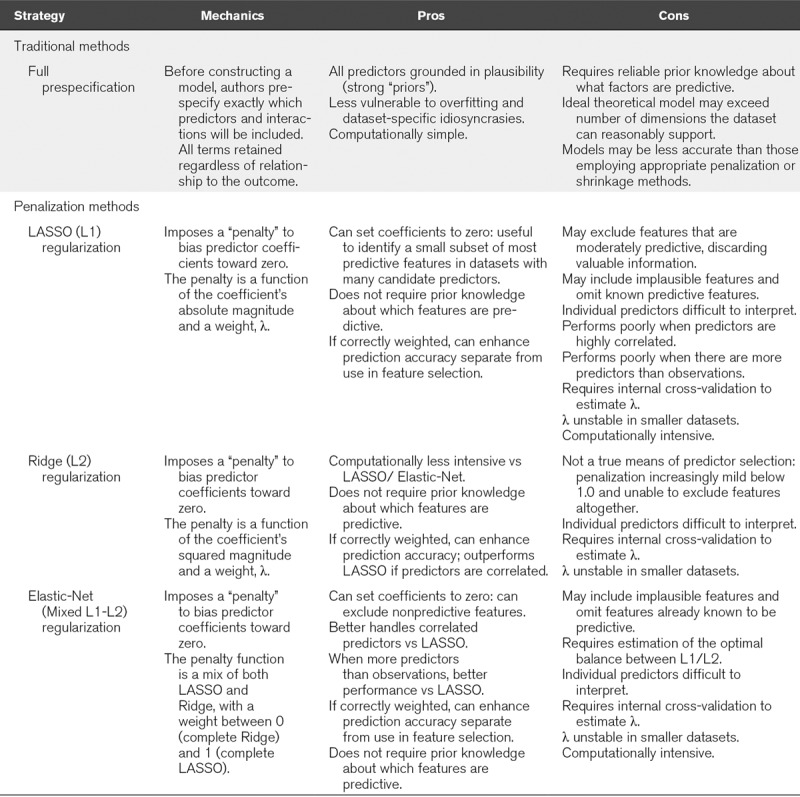
Finally, we note that the number of outcome events, not simply sample size, influences how many predictor terms can be included without overfitting. Large models (e.g., 50+ predictors) are often imposed on smaller datasets (e.g., n = 300, with 30 outcomes) that cannot support them. Methods to determine how many predictors a model can accommodate are discussed elsewhere, and we encourage authors to consider what their datasets can actually support. For sample size guidance, we direct readers to methodological papers based on the type of outcome being predicted—continuous (23, 24), binary (25, 26), or time-to-event (25)—and recommend authors clearly indicate how they determined whether their dataset could support the chosen model.

MODEL CONSTRUCTION

In addition to identifying predictor variables, prediction model development involves decisions about how to operationalize the predictors, define outcomes, handle missing data, and select a method to generate predictions.

Operationalizing Predictor Variables

One practice often employed in preprocessing data is to split continuous variables into dichotomous ones (27, 28). This practice risks discarding information and replacing it with assumptions that rarely have biological plausibility. For example, we might want to include respiratory rate (RR) in a model predicting the need for positive pressure ventilation. Consider four patients with RRs of 12, 29, 31, and 40, respectively. A logical interpretation is that the first patient has the lowest (RR-attributable) risk, the second and third patients have higher but similar risk, and the fourth has the highest risk. Suppose we instead split the population into two groups: RR greater than or equal to 30 and less than 30. This makes several illogical assumptions and discards useful predictive information, as described in Figure 2.

Figure 2.

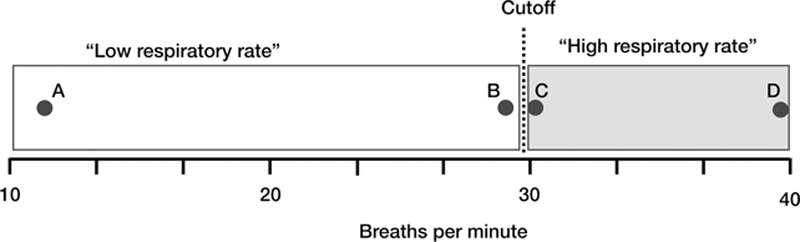
Problems with categorizing continuous variables. Consider the example of splitting respiratory rate (RR) values into “high” and “low” based on a cut-off of 30 breaths per minute. Note this makes several assumptions, namely: 1) that there is no difference between a RR of 12 and a RR of 29 (points A and B); 2) that there’s no difference between a RR of 31 and a RR of 40 (points C and D); and 3) that RRs of 29 and 30 are categorically different (points B and C).

Investigators sometimes create categorical groupings because they suspect a nonlinear relationship (e.g., a threshold rather than a dose-response effect). Although using nonlinear terms in a prediction equation might better accommodate this relationship than categorizing continuous data, using a linear term to model a suspected “J-shaped” curve would also be inappropriate. These issues should underscore the importance of thinking about predictor relationships ahead of time when feasible.

Although avoiding categorization is generally preferred, thresholds may, at times, be useful to formulate prediction scores that can be easily calculated at the bedside. As with other choices in prediction modeling, this involves trade-offs between usability and accuracy. For example, imposing thresholds might be more reasonable if a score is intended as a simple and easily remembered tool but less so when deployed in an electronic risk calculator.

Specifying the Outcome

One of the most important steps in developing prediction models is to determine what precisely to predict. This sounds obvious, but confusion or misspecification here can lead to concerns about the model’s applicability. For example, a model predicting the onset of sepsis should specify whether the labels “sepsis” and “non-sepsis” are assigned based on International Classification of Diseases (ICD) codes, Sequential Organ Failure Assessment scores derived from EHR data, expert opinion after manual chart reviews, or some other methodology. Transparency is important, especially when surrogate endpoints are used. For instance, a model might use a blood culture order and a prescription for IV antibiotics as a proxy for infection. Readers should recognize that the model therefore predicts the proxy state, rather than state of interest directly, and that overlap of the two may vary.

Authors should fully specify criteria used to adjudicate outcomes. Those criteria should consider ease of use, veracity, and consistency. For instance, ICD coding may be ubiquitous in some jurisdictions, but practices for coding any given condition may differ between institutions. Last, the timing of the outcome must be clearly specified. The outcome must be known only after all predictor variables have been collected, ideally with lag time that respects the realities of clinical practice. A model that predicts the onset of clinical deterioration 24 hours in advance is likely more useful than one that provides only 10 minutes of advanced warning.

Data Preprocessing

Missing data frequently complicate prediction modeling. This is especially true when models are built with existing datasets, rather than those collected specifically for the purpose of model development. The former, though convenient, may contain gaps where key variables were not routinely collected or reliably recorded. Missing data can introduce bias, especially if not missing completely at random. Suppose we want to predict bleeding risk during an inpatient stay, and choose to include the admission international normalized ratio (INR) as a predictor. Our dataset includes this measure for 65% of patients. Is the remaining 35% missing completely at random? Since clinical presentation likely dictates whether the INR is measured at admission, the mere presence of an INR value (regardless of its result) carries information (29). If we include only patients with an admission INR measured, we may select a group with higher bleeding risk; these patients are likely on anticoagulants, or deemed by the clinician at high enough risk that an INR was ordered. By omitting patients without an INR we may bias the prediction model.

Several strategies can address missing data. The approach using only patients with complete data (complete case analysis) can introduce bias and decreases sample size. This practice is therefore discouraged (30). Another strategy is multiple imputation of missing values using methods described elsewhere (31). The success of these approaches will depend on the methods used, the amount of missing data, and why the data are missing to begin with. Sometimes too much data are missing to support the proposed prediction modeling. Regardless of the methods chosen, the quantity of missing data, along with the methods used to deal with it, should be reported.

Other types of data preprocessing include the identification and removal of outliers, physiologically implausible values, or features that do not vary across patients and therefore contribute no information. The methods used in these preprocessing steps should be fully outlined (perhaps as a supplement), as they may introduce important biases in the ensuing models.

MODEL EVALUATION

Once developed, a prediction model must be evaluated to determine how useful it might be, and under what circumstances it might be used (32). This requires appropriate validation and quantification of model performance.

Model Validation

Evaluating a model’s predictive performance can be helpful during derivation in the fine tuning of its variables. However, such evaluation does not constitute justification for the model’s adoption. This is because models overly adapted to the idiosyncrasies of a particular dataset may perform well in that dataset, despite having poor accuracy for new observations (33). Many of the pitfalls described above will lead to overly optimistic performance models that fail to generalize.

Validation refers to the process of confirming whether a prediction model generalizes to data that were not used in its development. Internal validation involves determining whether model performance is reproducible in the same underlying population (as distinct from the same specific sample) used to derive it (33). External validation determines whether a model is transportable by evaluating its performance in a population that is somehow distinct from the one used for derivation (33).

Generally, prediction models perform worse in new datasets compared with the sample in which they were developed. Models that perform without large decrements in accuracy in new datasets are more likely to generalize to other contexts we might care about—for example, clinical practice. Conversely, substantial decrements in performance suggest the model is overfitted. Emerging frameworks evaluate both the magnitude of and reasons for performance degradation (34–36); such as the validation cohort being inherently different from the derivation cohort (36). However, determining how much of a decrease in performance during validation is too much proves difficult and will likely depend on the specific study (35).

The typical lifecycle of a prediction model thus involves progression through various stages of derivation and validation. Often, initial model descriptions may be based on validation in archival datasets. When entirely separate datasets are not available, a common compromise approach is to split a single dataset into two parts: a derivation cohort, and a separate validation cohort that is not used in developing the model itself. There are several strategies to handle a single dataset in this way, each with their own drawbacks and benefits (Supplemental Table 1, Supplemental Digital Content 1, http://links.lww.com/CCM/F343) (37). We acknowledge that the distinction between internal and external validation is not always concrete, and will depend on study context. Nevertheless, a compelling validation must use the exact same model obtained from the derivation exercise. Retraining on external data will yield an entirely new model, potentially leading to the same risks of overfitting that validation is meant to overcome.

In the near future, we may see a new approach in which models are deliberately re-trained on local data (38). This strategy might improve accuracy in the specific venue where the method is applied and may become more feasible as more health systems accrue the large datasets and computing infrastructure needed to support such a strategy. Local implementations of any given method may differ in the features selected, and the weights assigned within each local model. In these cases, the prediction method must be shown to generalize, rather than the model itself (38). Nonetheless, validation of the specific method under study is still necessary.

While precise approaches can vary between applications, the most important element of any validation is that the model’s performance is interrogated among observations that were not used in its development or fine tuning. An appropriate validation is the most critical component of assessing model performance. Without it, even models that appear highly accurate are simply quantitative hypotheses.

Performance Metrics

There are numerous ways to quantify a prediction model’s performance (Table 2). These measures are reviewed in detail elsewhere (39). Generally, the appropriateness of any given metric will depend on how we intend to use a model and the nature of the data it describes. For binary outcomes, the often-used AUROC (also known as the C-statistic) measures discrimination—the ability to separate events from nonevents. Indeed prediction models that cannot discriminate are useless, but when discrimination is reasonable, usefulness may become dependent on calibration, which is the ability to specify the probability of the outcome correctly (40). Separating two patients with 1% versus 5% risk has different implications than separating patients with 5% versus 25% risk, yet both correspond to a five-fold risk difference.

TABLE 2.

Selected Measures to Evaluate Prediction Model Performance

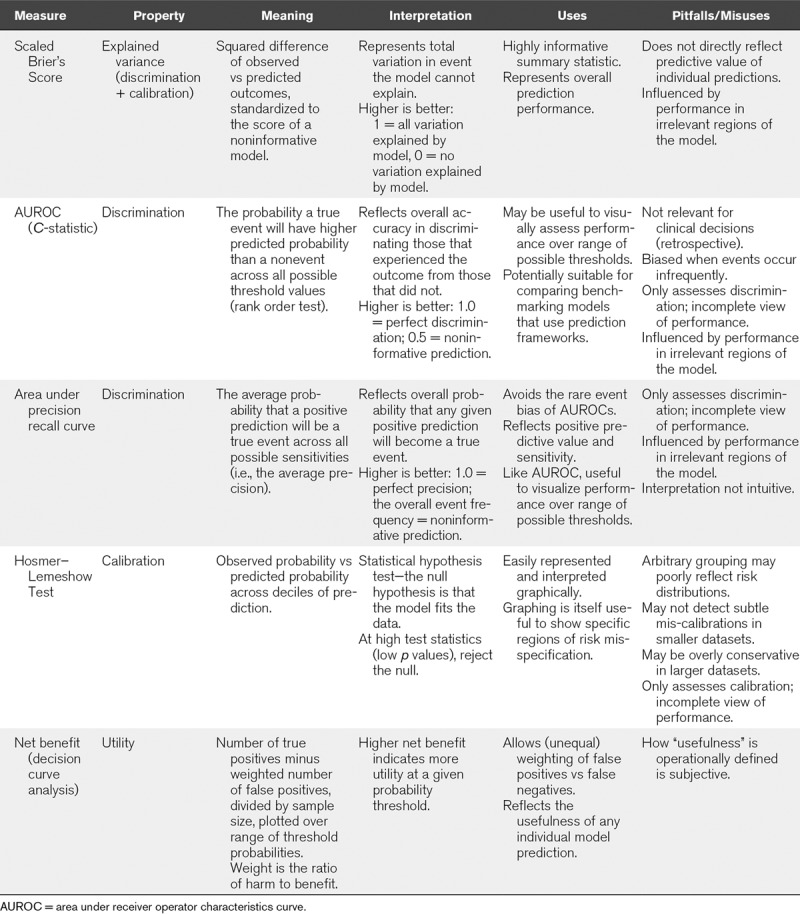
When outcomes occur infrequently, measures of overall accuracy can have misleadingly strong discrimination if they prioritize specificity: if only 5% of patients experience an outcome, a model that predicts zero outcomes can attain 95% accuracy (41). Sensitivity and specificity, reflected by AUROC, are inherently retrospective properties (the number of correct predictions among cases versus noncases, respectively). This may be appropriate for benchmarking indices (e.g., severity of illness scoring), but bedside prediction models are better judged by properly contextualized positive and negative predictive values (how many correctly predicted outcomes among the positive and negative predictions, respectively). These measures also have caveats; predictive values vary with the underlying outcome prevalence and therefore can vary considerably between populations.

Priorities for prediction are context-specific but invariably involve trade-offs determined by the potential consequences of false positives (i.e., overtreatment), and false negatives (i.e., missed cases). For example, in predicting poor neurologic recovery following cardiac arrest, we may wish to know the performance at a false positive rate of 0; we never want to wrongly predict a poor outcome, as this is likely to lead to the withdrawal of life-sustaining therapies. In other cases, it may be more important to accurately predict as many positive outcomes as possible, with less regard to “false alarms.”

Interpreting Performance

It is very rare that a novel prediction model does not require comparison to an existing one. We should seek these comparisons because it is hard to interpret a model’s usefulness in isolation. A prediction model that discriminates with 75% accuracy might be useful if currently used frameworks are little better than a coin flip. Another model with 80% accuracy might not be useful if clinical judgment is right 90% of the time. Similarly, a model might accurately predict the onset of a condition at a given time, but this will only be useful if the diagnosis has not already been made. Considerations beyond standard performance metrics may therefore be important. For example, a model that accurately predicts the onset of infection may have limited clinical usefulness if the majority of patients identified are already receiving antibiotics at the time of the alert.

In the era of big data, the distinction between clinical and statistical significance becomes particularly important. The width of CIs and the size of p values are both inversely proportional to the sample size of a dataset. As models developed from datasets with thousands of patients become more common, it is important to consider what a “significant” difference really means. In such datasets, a complex, 40-variable model with 85% accuracy may well be statistically distinguishable from a simple, two-variable model with 84% accuracy. We must then ask whether that difference is meaningful, and worth all the added complexity.

Additional Considerations

We encourage readers to review additional considerations related to assessing model bias, competing risks, measurement error, algorithm generalization, and so-called “modifiable risk factors” in the accompanying Supplemental Materials (Supplemental Digital Content 1, http://links.lww.com/CCM/F343).

GUIDANCE FOR REPORTING

Table 3 provides key components that must be present for readers to properly evaluate a prediction model. More detailed guidance for reporting prediction modeling studies is widely available. We encourage authors to refer to the TRIPOD checklist (https://www.tripod-statement.org) and ensure they include all recommended elements. Studies that leverage EHR derived datasets present unique considerations, and for these, we also encourage authors to refer to the Reporting of studies Conducted using Observational Routinely-collected Data (RECORD) checklist (https://www.record-statement.org). Including these checklists in submissions is highly recommended. In general, reporting should be as transparent as possible, and should include full specification of statistical models and their diagnostics. Though making data and statistical code available is not required at most journals, it is certainly encouraged.

TABLE 3.

Key Reporting Metrics for Prediction Models (Adapted From the Transparent Reporting of a Multivariable Prediction Model For Individual Prognosis or Diagnosis Checklist) (5)

FINAL COMMENTS—CONSIDERING IMPACT

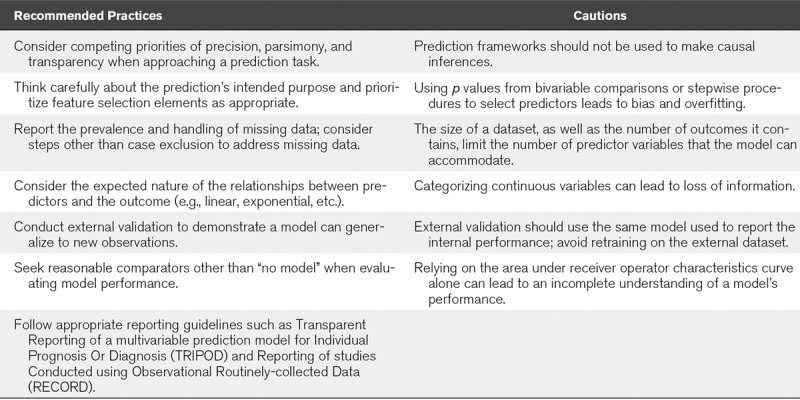
Above, we outline what prediction models do, and offer recommendations for their use (summarized in Table 4). However, considering why a new prediction model is needed may supersede all these considerations. Many published prediction models will never be used. Therefore, our final guidance is to consider what unmet need a prediction model confronts. Perhaps a model has novelty, addressing diseases or outcomes where no data currently exist. Perhaps it shows clinical usefulness, flagging occultly high-risk patients or improving discrimination compared with current practice. Perhaps a model facilitates enrolling enriched populations in clinical trials, or provides an administrative index to make institutional comparisons equitable. We challenge authors to reflect on how their models will benefit patients both when designing their studies and preparing their manuscripts. For example, do authors of a bedside tool now plan to use the model in their own practice?

TABLE 4.

Summary of Guidance for Prediction Models

APPENDIX 1. CONTRIBUTING AUTHORS AND JOURNALS

Core writing group: Daniel E. Leisman (Editorial Board, Critical Care Medicine), Michael O. Harhay (Statistical Editor, Annals of the American Thoracic Society), David J. Lederer (Former Editor-in-Chief, Annals of the American Thoracic Society), David M. Maslove (Associate Editor, Critical Care Medicine).

Contributing authors: Michael Abramson (Statistical Review Board, Respirology), Alex A. Adjei (Editor-in-Chief, Journal of Thoracic Oncology), Jan Bakker (Editor-in-Chief, Journal of Critical Care), Zuhair K. Ballas (Editor-in-Chief, The Journal of Allergy & Clinical Immunology), Esther Barreiro (Editor-in-Chief, Archivos de Bronconeumologia), Scott C. Bell (Editor-in-Chief, Journal of Cystic Fibrosis), Rinaldo Bellomo (Editor-in-Chief, Critical Care & Resuscitation), Jonathan A Bernstein (Editor-in-Chief, Journal of Asthma), Richard D. Branson (Editor-in-Chief, Respiratory Care), Vito Brusasco (Editor-in-Chief, COPD: Journal of Chronic Obstructive Pulmonary Disease), James D. Chalmers (Deputy Chief Editor, European Respiratory Journal), Sudhansu Chokroverty (Editor-in-Chief, Sleep Medicine), Giuseppe Citerio (Editor-in-Chief, Intensive Care Medicine), Nancy A. Collop (Editor-in-Chief, Journal of Clinical Sleep Medicine), Colin R. Cooke (Editor-in-Chief, Annals of the American Thoracic Society), James D. Crapo (Editor-in-Chief, Journal of the COPD Foundation), Gavin Donaldson (Associate Editor, American Journal of Respiratory and Critical Care Medicine), Dominic A. Fitzgerald (Editor-in-Chief, Paediatric Respiratory Reviews), Emma Grainger (Editor, The Lancet Respiratory Medicine), Lauren Hale (Editor-in-Chief, Sleep Health), Felix J. Herth (Editor-in-Chief, Respiration), Patrick M. Kochanek (Editor-in-Chief, Pediatric Critical Care Medicine), Guy Marks (Editor-in-Chief, International Journal of Tuberculosis and Lung Disease), J. Randall Moorman (Editor-in-Chief, Physiological Measurement), David E. Ost (Editor-in-Chief, Journal of Bronchology and Interventional Pulmonology), Michael Schatz (Editor-in-Chief, The Journal of Allergy & Clinical Immunology: In Practice), Aziz Sheikh (Editor-in-Chief, NPJ: Primary Care Respiratory Medicine), Alan R. Smyth (Joint Editor-in-Chief, Thorax), Iain Stewart (Statistical Editor, Thorax), Paul W. Stewart (Associate Editor, Pediatric Pulmonology), Erik R. Swenson (Editor-in-Chief, High Altitude Medicine & Biology), Ronald Szymusiak (Editor-in-Chief, SLEEP), Jean-Louis Teboul (Editor-in-Chief, Annals of Intensive Care), Jean-Louis Vincent (Editor-in-Chief, Critical Care), Jadwiga A. Wedzicha (Editor-in-Chief, American Journal of Respiratory and Critical Care Medicine).