Development and Testing of an Abbreviated Numeracy Scale: A Rasch Analysis Approach

ABSTRACT

Research has demonstrated that individual differences in numeracy may have important consequences for decision making. In the present paper, we develop a shorter, psychometrically improved measure of numeracy—the ability to understand, manipulate, and use numerical information, including probabilities. Across two large independent samples that varied widely in age and educational level, participants completed 18 items from existing numeracy measures. In Study 1, we conducted a Rasch analysis on the item pool and created an eight‐item numeracy scale that assesses a broader range of difficulty than previous scales. In Study 2, we replicated this eight‐item scale in a separate Rasch analysis using data from an independent sample. We also found that the new Rasch‐based numeracy scale, compared with previous measures, could predict decision‐making preferences obtained in past studies, supporting its predictive validity. In Study, 3, we further established the predictive validity of the Rasch‐based numeracy scale. Specifically, we examined the associations between numeracy and risk judgments, compared with previous scales. Overall, we found that the Rasch‐based scale was a better linear predictor of risk judgments than prior measures. Moreover, this study is the first to present the psychometric properties of several popular numeracy measures across a diverse sample of ages and educational level. We discuss the usefulness and the advantages of the new scale, which we feel can be used in a wide range of subject populations, allowing for a more clear understanding of how numeracy is associated with decision processes. Copyright © 2012 John Wiley & Sons, Ltd.

Decision making today involves making sense of a morass of information from various sources, such as insurance companies, financial advisors, and marketers (Hibbard, Slovic, Peters, Finucane, & Tusler, 2001; Thaler & Sunstein, 2003; Woloshin, Schwartz, & Welch, 2004). Today's consumers need an understanding of numbers and basic mathematical skills to use numerical information presented in text, tables, or charts. However, consumers differ considerably in their ability to understand and use such information (Peters, Dieckmann, Dixon, Hibbard, & Mertz, 2007). Numbers are generally provided to facilitate choices, but they can be confusing or difficult to understand and use for even the most motivated and skilled individual, and appear to be more so for those who are less skilled.

Research has demonstrated that individual differences in numeracy, the ability to comprehend and manipulate probabilistic and other numeric information, may have important consequences for decision making (Estrada, Barnes, Collins, & Byrd, 1999; Reyna, Nelson, Han, & Dieckmann, 2009). An estimate from the National Adult Literacy Survey (Educational Testing Service, 1992) suggests that approximately half of the US population has only very basic or below basic quantitative skills (Kirsch, Jungeblut, Jenkins, & Kolstad, 2002). The National Assessment of Adult Literacy (Kutner, Greenberg, Jin, & Paulsen, 2006; NCES, 2003) demonstrated similar results. In addition, these problems may be particularly acute for older adults. For example, Hibbard et al. (2001) found that a large proportion of older adults (more than half of those over age 65) had substantial difficulty using numerical information to compare Medicare health plans.

Although there are several numeracy measures available to researchers (e.g., Lipkus, Samsa, & Rimer, 2001; Peters, Dieckmann et al., 2007; Schwartz, Woloshin, Black, & Welch, 1997), the distributional characteristics of these scales previously reported suggest that the items in these measures may possess a limited range of difficulty (Cokely & Kelley, 2009; Cokely, Galesic, Schulz, Ghazal, & Garcia‐Retamero, 2012). Administering a measure that does not match the range of ability level of the population of interest, which may be the case for highly numerate populations such as college students or ones that are less numerate (e.g., older adults or those with lower educational levels), potentially limits the test's ability to discriminate ability level. Put differently, the items in the measure essentially become redundant as respondents answer all items correctly in the former case and incorrectly in the latter. Therefore, a numeracy measure with a greater range of difficulty would be desirable. In the current study, we developed such a measure by adopting an item response theory (IRT) approach. Using scaling procedures developed by Rasch (1960/1993), we created a measure of numeracy derived from existing measures shown to be related to decision‐making behavior.

Existing measures of numeracy

Researchers have measured numeracy in various ways often because of differences in their specific research interests and domains of study (Reyna et al., 2009). Some scales have focused on subjective perceptions of one's own numerical abilities (Fagerlin et al., 2007; Woloshin et al., 2004; Zikmund‐Fisher, Smith, Ubel, & Fagerlin, 2007) in an attempt to measure numeracy without directly asking participants to make any mathematical computations. These scales, at the face level, appear to measure individual differences in confidence to effectively utilize numeric information in and ability to conduct mathematical operations. One subjective test, the Subjective Numeracy Scale (SNS, Fagerlin et al., 2007; Zikmund‐Fisher et al., 2007), has been found to correlate with objective measures of numeracy. However, self‐assessments of confidence are influenced by factors in addition to true ability level (Dunning, Heath, & Suls, 2004), leading to potential concerns about the validity of such assessments. Other numeracy measures have focused on objective performance, testing individuals' ability to make correct computations and understand probabilistic information. These abilities are particularly important in understanding the risk and benefit information presented in many “real‐world” decision‐making contexts (e.g., health and financial contexts; Burkell, 2004). Although both methods to assess individual differences in numeracy provide valuable insights, the current study focuses on the objective performance scales that have been used in the literature.

Schwartz et al. (1997) developed one of the first performance‐based numeracy measures. The measure was comprised of three items that included one question assessing participants' understanding of chance (i.e., How many heads would come up in 1000 tosses of a fair coin?) and two questions asking the participants to convert a percentage to a proportion and vice versa (i.e., the chance of winning a car is 1 in 1000; what is the percentage of winning tickets for the lottery?). Lipkus et al. (2001) further expanded this scale by adding eight questions to the Schwartz et al. numeracy scale; the additional items were designed to assess a participant's ability to understand and compare risks (e.g., Which of the following numbers represents the biggest risk of getting a disease: 1%, 10%, or 5%?) and to accurately work with decimal representations, proportions, and fractions. Moreover, Peters, Hibbard, Slovic, and Dieckmann (2007) further expanded the Lipkus et al. numeracy scale, introducing four additional items in an attempt to expand the range of difficulty; these additional items assess the understanding of base rates as well as the ability to make more complex likelihood calculations.

Similarly, Frederick (2005) developed a three‐item measure, the cognitive reflection test (CRT), which includes items that involve mathematical ability. Although the CRT was not explicitly defined as a numeracy test and only speculation exists about the underlying dimensions of the CRT, the items appear to require understanding, manipulating, and using numbers to solve them. Prior research has supported this assertion. For instance, Obrecht, Chapman, and Gelman (2009) found that the CRT was moderately correlated with SAT quantitative scores (r = .45; see Toplak, West, & Stanovich, 2011 for similar findings). In a smaller study, Cokely and Kelley (2009) reported a significant (r = .31) correlation between numeracy and CRT performance. Moreover, Liberali, Reyna, Furlan, Stein, and Pardo (2011) reported a moderate to strong correlation (r = .51 and r = .40 in Brazilian and US samples, respectively; Cohen, 1992) between the 11‐item Lipkus et al. (2001) scale and the CRT. Finally, in a large sample including individuals from across the adult lifespan, Finucane and Gullion (2010) also reported a similar effect size (r = .53) between the CRT and numeracy. These findings give us an a priori basis to test whether the CRT items may also serve as valid indicators of the latent construct of numeracy.

Although both the Schwartz‐based numeracy scales and the CRT are predicted to be indicators of numeracy, evidence suggests that these scales may differ in their ability to assess performance at different levels of the latent trait. For instance, even in very numerate populations, such as college students from highly selective universities, a substantial proportion of participants score only 0 or 1 on the three‐item CRT. Frederick (2005) reported that approximately one‐third of this total sample scored 0 on the CRT and another 28% answered only one question correctly. Further, the modal score of nearly half of the sub‐samples collected was 0. In contrast, median scores on the Lipkus et al. (2001) measure approach the maximum range of scores (e.g., Peters, Västfjäll, Slovic, Mertz, Mazzocco, & Dickert, 2006). The skewness of each of these measures may limit the measure's ability to discriminate numeracy level in many populations and may provide a disadvantage when assessing any linear effects of numeracy.

Associations between individual differences in numeracy and decision making

Individual differences in numeracy have been shown to have important associations with judgment and decision making. Recent reviews of the numeracy literature have found that compared with highly numerate individuals, those lower in numeracy are more likely to have difficulty judging risks and providing consistent assessments of utility, are worse at reading graphs, show larger framing effects, and are more sensitive to the formatting of probability information (for reviews, see Peters, Hibbard et al., 2007; Reyna et al., 2009). Although numeracy typically leads to better decision making, there is evidence that the increased numerical processing observed in the highly numerate can lead to increased affective reactions to numbers, or number comparisons, which, in turn, can result in optimal or sub‐optimal decision making. In an optimal example, Peters et al. (2006) asked participants to complete a ratio bias task. They were offered a chance to win a prize by drawing a red jellybean from a bowl. When provided with two bowls from which to choose, participants often elected to draw from a large bowl containing a greater absolute number, but smaller proportion, of red beans (9 in 100, 9%) rather than from a small bowl with fewer red beans but a better winning probability (1 in 10, 10%) even with the probabilities stated beneath each bowl. Peters et al. (2006) found that 33% and 5% of less and more numerate adults, respectively, chose the larger inferior bowl. Controlling for SAT scores, the choice effect remained significant. In addition, compared with the highly numerate, the less numerate reported less affective precision about Bowl A's 9% chance (“How clear a feeling do you have about [its] goodness or badness?”); their affect to the inferior 9% odds (“How good or bad does [it] make you feel?”) was directionally less negative. Peters et al. (2006) concluded that affect derived from numbers and number comparisons may underlie the highly numerate's greater number use (cf. the “Bets” experiment in the present paper's Study 2 and Peters et al., 2006).

Frederick (2005) also found that individuals who performed well on his CRT were more likely to choose a future reward of greater value than a smaller immediate reward. Further, these individuals demonstrated evidence of weaker reflection effects (i.e., risk taking to avoid losses is greater than risk taking to achieve gains; Kahneman & Tversky, 1979), compared with individuals scoring low in cognitive reflection. High‐CRT individuals also were less likely to show risk‐averse preferences towards gambles when the relative expected value between choice options favored choosing an uncertain option. Moreover, Toplak et al. (2011) found that greater CRT performance was significantly associated with an index of rational decision making comprised of a collection of classic heuristics and biases tasks.

Development of an abbreviated numeracy scale

A common problem with traditional methods of short‐form scale construction has been the reliance on item–total correlations to guide item selection for short forms (i.e., choosing items with the highest item–total correlations). Using such an approach renders the researcher unable to ascertain whether the short form has removed error variance or narrowed the construct (Smith, McCarthy, & Anderson, 2000). In turn, scales developed in this manner are often less able to fully assess the scope of the construct in question, thus posing a threat to predictive validity of the measure despite retaining levels of internal consistency similar to the long form (Smith & McCarthy, 1996).

Alternative scaling methods can allay such concerns. Using these techniques, which can be classified as IRT‐based scaling, one can develop more efficient psychological tests, in the sense that fewer items are needed to measure a latent construct while concurrently maintaining the scale's range of difficulty. Importantly, these methods largely preserve psychometric indices such as mean inter‐item correlations despite reductions in the number of items, upon which calculations of coefficient α are based.1

One IRT‐based scaling approach was developed by Rasch (1960/1993) and has been successfully used to develop shorter instruments for a wide range of constructs (e.g., Cole, Kaufman, Smith, & Rabin, 2004; Hibbard, Mahoney, Stockard, & Tusler, 2005; Prieto, Alonso, & Lamarca, 2003; Simon, Ludman, Bauer, Unützer, & Operskalski, 2006). In a Rasch model, responses are viewed as outcomes of the interaction between a test taker's standing on a latent trait or ability level and the difficulty of the test item. According to this model, the probability that an individual will correctly answer an item is a logistic function of the difference between the individual's trait level and the extent to which the trait is expressed in the item. Put differently, the higher a person's ability relative to the difficulty of an item, the higher the probability of a correct response on that item. When a person's location on the latent trait is equal to the difficulty of the item, there is, by definition, a .5 probability of a correct response in the Rasch model. Thus, for each item, Rasch analyses can characterize a curve that describes the ability level at which the item maximally discriminates.

Overview of the present paper

In Study 1, we focused on the development of a Rasch‐based numeracy measure. For our item pool, we used items from the existing scales: the Schwartz et al. (1997) three‐item measure, the Lipkus et al. (2001) expanded 11‐item numeracy scale, further expansion of that scale by Peters, Hibbard et al. (2007), and Frederick's (2005) CRT. In contrast to a typical short‐form scale construction that attempts to reduce a single existing scale, our primary objective was to retain the range of difficulty shown across the scales and to develop a shorter numeracy measure (relative to the entire item pool and to individual measures as possible). The former point will allow a broader use of the scale for populations who show limited variability on the existing measures. To achieve these goals, we incorporated items from all four measures that encompass a greater range of difficulty than any one of the scales. In Study 2, we confirmed the Rasch analysis results on an independent sample and tested the predictive validity of the scale by replicating findings that have been obtained in previous studies. Additionally, we compared the predictive validity of our scale with that of the CRT and the Lipkus et al. measure. Finally, in Study 3, we further tested the predictive and comparative validity of the Rasch‐based numeracy scale by examining its associations with risk likelihood judgments.

STUDY 1

Method

Participants

Participants were 1970 subjects collected from three separate samples. The first sample consisted of 302 community members, equally divided between those with higher education and those with lower education. Participants were recruited through online and newspaper advertisements. The second sample consisted of 163 undergraduates in an introductory psychology class. Finally, the third sample was an online study of adults using the American Life Panel (n = 1505). These three samples were merged into a single dataset.

The sample included 894 women (45.3%) and 1076 men (54.7%). The median age for this sample was 48 years (range = 18–89). Highest educational level attained was as follows: 3% of participants did not graduate from high school, 16.3% received a high school diploma, 9.2% attended a vocational/trade school or community college, 31.7% had completed some college (including those currently enrolled in a 4‐year program), 21.5% received a bachelor's degree, and 17.5% had an advanced degree. The college sample received course credit for their participation, and individuals in both community samples were financially compensated for participation.

Numeracy scales

All participants completed the following measures of numeracy: the 11‐item Lipkus numeracy scale (Lipkus et al., 2001), which also included the three items from Schwartz et al. (1997), four additional items developed by Peters, Hibbard et al. (2007), and three CRT items (Frederick, 2005).

Results and discussion

Numeracy scales

For the Schwartz et al. three‐item scale, Cronbach's α = .58, mean inter‐item r = .31. Adding the additional eight items of Lipkus et al. to the Schwartz et al. scale resulted in the 11‐item Lipkus numeracy measure with Cronbach's α = .76, mean inter‐item r = .23. When adding the four additional items of Peters et al. to the Lipkus measure, Cronbach's α = .76, mean inter‐item r = .19. For the CRT, Cronbach's α = .60, mean inter‐item r = .34.

In the current sample, the Peters, Hibbard et al. (2007) and CRT measures were significantly correlated (r = .49). Further, examination of Cronbach's α of the omnibus 18‐item scale (α = .75) and the mean inter‐item correlation (r = .19) for the combined items provides initial evidence that the decision to combine these scales was warranted.

Confirmatory factor analysis

Because Rasch analysis assumes that the latent construct is unitary in nature, the most important threat to this assumption would occur if the CRT and the items from the other numeracy scales represented separate factors. Such a finding would suggest that the item pool that we intended to use would not tenably represent a coherent, unitary construct. To test whether the CRT and numeracy items load on a unitary factor, we compared two separate confirmatory factor analysis (CFA) models: (i) a single‐factor model in which all numeracy and CRT items loaded on a unitary factor and (ii) a correlated two‐factor model with CRT items loading on one dimension and numeracy items loading on another factor. CFA is widely regarded in the broader psychological assessment literature to be the strongest test for unidimensionality, compared with exploratory factor analysis methods. CFAs were conducted using mplus version 6.1 software. A variance‐adjusted weighted least squares estimation was used to estimate dichotomous variables in CFA.2 Path parameters were freely estimated. Both the one‐factor and two‐factor solutions showed nearly identical fit statistics (see Table 1 for fit statistics and factor loadings). Given that the two‐factor model does not offer an appreciably better model fit and the between‐factor correlation was high (r = .85), the more parsimonious explanation of the data favors adopting a one‐factor model. The data suggest that the assumption that the item pool represented a coherent, unitary construct is a tenable one; hence, Rasch‐based scaling is appropriate.

Table 1.

Fit statistics and unstandardized and standardized coefficients for one‐factor and two‐factor confirmatory factor analysis solutions—Study 1

Item number	One‐factor solution		Two‐factor solution
			Factor 1		Factor 2
	Ustd (SE)	Std (SE)	Ustd (SE)	Std (SE)	Ustd (SE)	Std (SE)
Q1. Imagine that we roll a fair, six‐sided die 1000 times. Out of 1000 rolls, how many times do you think the die would come up as an even number?	1.0 (.00)	1.0 (.00)	.67 (.02)	.64 (.02)
Q2. In the BIG BUCKS LOTTERY, the chances of winning a $10.00 prize are 1%. What is your best guess about how many people would win a $10.00 prize if 1000 people each buy a single ticket from BIG BUCKS?	1.10 (.05)	.70 (.02)	1.1 (.05)	.70 (.02)
Q3. In the ACME PUBLISHING SWEEPSTAKES, the chance of winning a car is 1 in 1000. What percent of tickets of ACME PUBLISHING SWEEPSTAKES win a car?	1.17 (.05)	.76 (.02)	1.18 (.05)	.77 (.02)
Q4. Which of the following numbers represents the biggest risk of getting a disease? (1 in 100, 1 in 1000, or 1 in 10)	1.13 (.06)	.73 (.03)	1.12 (.06)	.73 (.03)
Q5. Which of the following numbers represents the biggest risk of getting a disease? (1%, 10%, or 5%)	1.07 (.06)	.69 (.03)	1.07 (.06)	.69 (.03)
Q6. If Person A's risk of getting a disease is 1% in 10 years, and Person B's risk is double that of A's, what is B's risk?	1.16 (.05)	.75 (.02)	1.17 (.05)	.76 (.02)
Q7. If Person A's chance of getting a disease is 1 in 100 in 10 years, and person B's risk is double that of A, what is B's risk?	1.11 (.05)	.72 (.02)	1.12 (.05)	.72 (.02)
Q8b. Out of 1000?	.92 (.06)	.60 (.03)	.92 (.06)	.60 (.03)
Q9. If the chance of getting a disease is 20 out of 100, this would be the same as having a _____% chance of getting the disease.	1.03 (.05)	.67 (.03)	1.03 (.05)	.67 (.03)
Q10. The chance of getting a viral infection is .0005. Out of 10 000 people, about how many of them are expected to get infected?	.77 (.05)	.49 (.03)	.77 (.05)	.50 (.03)
Q11. Which of the following numbers represents the biggest risk of getting a disease? (1 in 12 or 1 in 37)	1.14 (.07)	.74 (.04)	1.14 (.07)	.74 (.04)
Q12. Suppose you have a close friend who has a lump in her breast and must have a mammography … The table below summarizes all of this information. Imagine that your friend tests positive (as if she had a tumor), what is the likelihood that she actually has a tumor?	.74 (.07)	.48 (.04)	.74 (.07)	.48 (.04)
Q13. Imagine that you are taking a class and your chances of being asked a question in class are 1% during the first week of class and double each week thereafter (i.e., you would have a 2% chance in Week 2, a 4% chance in Week 3, an 8% chance in Week 4). What is the probability that you will be asked a question in class during Week 7?	1.05 (.05)	.67 (.02)	1.05 (.05)	.68 (.02)
Q15 (CRT). A bat and a ball cost $1.10 in total. The bat costs $1.00 more than the ball. How much does the ball cost?	1.20 (.05)	.77 (.02)			1.16 (.05)	.85 (.02)
Q16 (CRT). If it takes five machines 5 minutes to make five widgets, how long would it take 100 machines to make 100 widgets?	1.06 (.05)	.68 (.02)			1.0 (.00)	.74 (.03)
Q17 (CRT). In a lake, there is a patch of lily pads. Every day, the patch doubles in size. If it takes 48 days for the patch to cover the entire lake, how long would it take for the patch to cover half of the lake?	.91 (.05)	.58 (.03)			.87 (.05)	.64 (.03)
Fit statistics
X 2/df	9.980		9.628
CFI	.912		.917
TLI	.900		.903
RMSEA	.068		.066

Note. Standard errors are reported in parentheses.

CFI, comparative fit index; RMSEA, root mean square error of approximation; SE, standard error; TLI, Tucker–Lewis index.

Rasch analysis

Table 2 shows the item difficulty statistics for all items (i.e., the proportion of participants correctly answering each item). On average, the Lipkus et al. numeracy items were less difficult, whereas the CRT items were more difficult. Next, we conducted a Rasch analysis on all numeracy and CRT items, following the procedure of Hibbard et al. (2005). Initially, items were assessed for fit. In general, fit statistics should range from .5 to 1.5 (Linacre, 2002). One item was deleted because of a poor outfit statistic. All other items met this criterion. To reduce the item pool further, items were deleted sequentially on the basis of the extent to which the deletion minimally reduced the person reliability. Person reliability is a measure of the ability of the scale to discriminate the sample into different levels of ability and, therefore, is a key construct in measure development using the Rasch technique. After each item was deleted, Rasch analysis was rerun to determine the decrease in person reliability for that deletion. The item that decreased person reliability the least was deleted, and the process was repeated. In the case of ties, items that were most similar to remaining items in difficulty were deleted. The process was stopped when further deletions resulted in unacceptably low levels of person reliability (Hibbard et al., 2005).

Table 2.

Item difficulties for individual items—Study 1

Item	Item difficulty
Q11. Which of the following numbers represents the biggest risk of getting a disease? (1 in 12 or 1 in 37)	96.1
Q5. Which of the following numbers represents the biggest risk of getting a disease? (1%, 10%, or 5%)	94.5
Q4. Which of the following numbers represents the biggest risk of getting a disease? (1 in 100, 1 in 1000, or 1 in 10)	92.7
Q8a. If the chance of getting a disease is 10%, how many people would be expected to get the disease? Out of 100?	91.2
Q8b. Out of 1000?	88.1
Q9. If the chance of getting a disease is 20 out of 100, this would be the same as having a _____% chance of getting the disease.	84.3
Q1. Imagine that we roll a fair, six‐sided die 1000 times. Out of 1000 rolls, how many times do you think the die would come up as an even number?	74.9
Q13. Imagine that you are taking a class and your chances of being asked a question in class are 1% during the first week of class and double each week thereafter (i.e., you would have a 2% chance in Week 2, a 4% chance in Week 3, an 8% chance in Week 4). What is the probability that you will be asked a question in class during Week 7?	74.3
Q6. If Person A's risk of getting a disease is 1% in 10 years, and Person B's risk is double that of A's, what is B's risk?	71.2
Q2. In the BIG BUCKS LOTTERY, the chances of winning a $10.00 prize are 1%. What is your best guess about how many people would win a $10.00 prize if 1000 people each buy a single ticket from BIG BUCKS?	70.6
Q10. The chance of getting a viral infection is .0005. Out of 10 000 people, about how many of them are expected to get infected?	58.4
Q7. If Person A's chance of getting a disease is 1 in 100 in 10 years, and person B's risk is double that of A, what is B's risk?	55.3
Q14. Suppose that 1 out of every 10 000 doctors in a certain region is infected with the SARS virus; in the same region, 20 out of every 100 people in a particular at‐risk population also are infected with the virus. A test for the virus gives a positive result in 99% of those who are infected and in 1% of those who are not infected. A randomly selected doctor and a randomly selected person in the at‐risk population in this region both test positive for the disease. Who is more likely to actually have the disease?	52.8
Q3. In the ACME PUBLISHING SWEEPSTAKES, the chance of winning a car is 1 in 1000. What percent of tickets of ACME PUBLISHING SWEEPSTAKES win a car?	34.5
Q16 (CRT). If it takes five machines 5 minutes to make five widgets, how long would it take 100 machines to make 100 widgets?	32.3
Q17 (CRT). In a lake, there is a patch of lily pads. Every day, the patch doubles in size. If it takes 48 days for the patch to cover the entire lake, how long would it take for the patch to cover half of the lake?	31.9
Q15 (CRT). A bat and a ball cost $1.10 in total. The bat costs $1.00 more than the ball. How much does the ball cost?	18.7
Q12. Suppose you have a close friend who has a lump in her breast and must have a mammography … The table below summarizes all of this information. Imagine that your friend tests positive (as if she had a tumor), what is the likelihood that she actually has a tumor?	9.8

The final scale consisted of eight items, five from the original Lipkus et al. scale (including the three original Schwartz et al. items), two from the CRT scale, and one of the Peters et al. items. Difficulty structure and fit statistics are shown in Table 3. Fit statistics for all items were deemed to be adequate, and person reliability was .63. Cronbach's α for the eight‐item scale was .71 and mean inter‐item was r = .24.3 Consistent with the psychological assessment literature, which suggests that the mean inter‐item correlation is a more useful index of internal consistency, the observed mean inter‐item correlation was acceptable for measuring a broad, higher‐order construct (Briggs & Cheek, 1986; Clark & Watson, 1995). Combined with the CFA results, these results suggest that the Rasch‐based numeracy scale measures the construct in a coherent, unitary, and internally consistent manner.

Table 3.

Difficulty structure and fit statistics for the eight‐item numeracy scale—Study 1

Item	Difficulty	Infit	Outfit
Q12	89.0	1.10	.90
CRT1	73.5	.95	.72
CRT3	60.2	.87	.75
Q3	57.9	.84	.76
Q2	39.6	1.24	1.61
Q1	29.8	.90	.77
Q9	26.2	1.02	1.16
Q8b	15.2	1.05	.79

Descriptive statistics

Figure 1 shows frequency distributions for the separate measures used: the Lipkus et al. measure (Panel A), Frederick's CRT (Panel B), the Peters et al. measure (Panel C), and the Rasch‐modeled scale (Panel D). Table 4 shows the descriptive statistics for each scale. As expected, the CRT was positively skewed, whereas the Peters et al. measure and especially the Lipkus et al. measure were negatively skewed. These findings suggest that both the Lipkus et al. measure and the CRT do not adhere to a normal distribution. On the contrary, performance scores for the Rasch‐based numeracy scale were roughly normally distributed (M = 4.12, SD = 1.87, median = 4, mode = 4), and the distribution was not significantly skewed (.07, z = 0.11, ns). Taken together, these results strongly suggest that the CRT, Lipkus et al., and Peters et al. scales, taken separately, may be too difficult or too easy, which may limit the sensitivity of the test to accurately detect an individual's true ability level on the latent construct.

Figure 1.

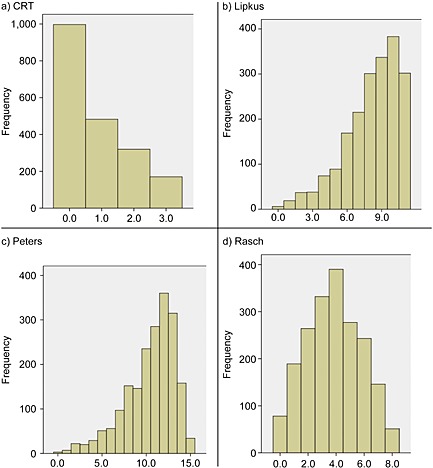
Frequency distributions of individual scales—Study 1. We present the frequency distributions of the cognitive reflection task (CRT; Panel a), the Lipkus et al. numeracy measure (Lipkus; Panel b), the Peters et al. numeracy measure (Peters; Panel c), and the new reduced Rasch‐derived model developed in the current study (“Rasch”; Panel d).

Table 4.

Descriptive statistics for numeracy measures—Study 1

Scale	Mean (SD)	Median	Mode	Skewness
CRT (three items)	0.83 (.99)	0	0	.88
Schwartz et al. (three items)	1.8 (1.01)	2	2	–.36
Lipkus et al. (11 items)	8.15 (2.36)	9	10	–.94
Peters et al. (15 items)	10.48 (2.81)	11	12	–.98
Rasch‐based (eight items)	4.13 (1.87)	4	4	.00

Associations between Rasch‐based numeracy scale and demographic variables

Somewhat surprisingly, we found no significant negative correlation between age and numeracy (r = −.02, ns). With respect to gender, we found that men performed better than women (point biserial r = .28, p < .001). We also investigated how educational level was associated with numeracy performance. As shown in Table 5, we observed that a disproportionate number of individuals with a high school/trade school or less educational level (low education group) scored 0 on the CRT (64%). In fact, even among those with a bachelor's degree or greater (high‐education group), the modal response was still 0. In contrast, we observed that the Lipkus et al. measure showed a greater negative skew as a function of participants' educational level. Nearly 69% of all individuals scored 9 or higher on the Lipkus et al. measure. The Rasch‐based measure, in comparison, maintained a relatively normal distribution across different educational levels. For this scale, the majority of respondents scored in the middle of the distribution, with predictably more individuals in the lower‐education group scoring worse on the scale, whereas in the higher‐education group, more individuals scored towards the higher end of the distribution. To further examine these educational level differences with the Rasch‐based numeracy measure, we conducted a one‐way analysis of variance for educational level (three levels: high school/trade school education or less, some college, and 4‐year college graduate or greater). As expected, we found a significant main effect for educational level (F(2, 1965) = 169.20, p < .001). Those holding a college degree or greater performed best on the Rasch‐based numeracy measure (M = 4.90, compared with 4.02 and 3.06 for the some college and high school/trade school or less education groups, respectively).

Table 5.

Distribution of correct answers for the CRT, Schwartz et al., Lipkus et al., and Rasch‐based measures as a function of educational level—Study 1

Scale score	Educational level
	High school/trade	Some college	College grad
Cognitive reflection test
0	64.1	55.8	36.1
1	22.3	24.8	25.5
2	9.5	13.7	23.1
3	4.2	5.8	15.3
Schwartz et al.
0	22.6	12.4	4.1
1	32.3	27.7	17.1
2	29.7	36.5	35.9
3	15.4	23.5	43.0
Lipkus et al.
0–4	16.9	7.7	2.8
5–8	53.0	47.4	28.4
9–11	37.7	44.9	68.8
Peters et al.
0–4	6.5	3.1	0.8
5–8	35.9	21.2	7.7
9–12	46.0	57.3	51.0
13–15	11.6	18.3	40.4
Rasch‐based
0–2	37.4	20.8	8.5
3–5	50.8	61.2	53.1
6–8	11.8	17.9	38.4

Convergent validity

Participants from the community sub‐sample also completed the Fagerlin et al. (2007) eight‐item SNS (α = .86). As expected, we found that the Rasch‐based numeracy measure was significantly correlated with individuals' subjective perceptions of numeracy (r = .55, p < .001). This correlation did not differ from the Lipkus et al. measure (r = .55) or the Peters et al. 15‐item measure (r = .57). It was stronger than both the Schwartz et al. three‐item measure (r = .44) and the CRT (r = .43).

Taken together, these results indicate that the Rasch‐based measure was able to reduce the item pool from 18 to eight items, while maintaining the psychometric qualities of the larger item pool and the composite scales. Additionally, we found evidence of convergent validity and largely replicated previously reported correlations with demographic variables.

STUDY 2

Overview

The purpose of Study 2 was both to confirm the Rasch results from Study 1 on an independent sample and to test the predictive validity of the eight‐item Rasch‐based numeracy scale. We tested performance on three decision‐making paradigms that previously have been associated with individual differences in numeracy (Peters et al., 2006). Specifically, we tested whether performance on the Rasch‐based numeracy measure predicted the following: (i) the extent of framing effects; (ii) how individuals rated the attractiveness of bets in a “less is more” effect paradigm (Slovic, Finucane, Peters, & MacGregor, 2002); and (iii) the extent of denominator neglect in a ratio bias task. We also compared the predictive validity of the Rasch‐based scale with that of two of the component measures, namely the CRT and the Lipkus et al. measures. One well‐established criteria of successful short‐form development is that an abbreviated measure should not result in significant decrements to validity (Smith et al., 2000). By definition, short‐form development attempts to reduce a construct that prior researchers concluded required a more lengthy assessment. If a full‐length scale contains much irrelevant or invalid content, then one could expect that the validity of the short‐form scale would increase. However, if the items contained in full‐length assessment are largely valid, then one would expect that a short‐form measure would result in reduced validity. In this sense, the Rasch‐based measure does not necessarily have to demonstrate increased validity compared with other assessments but should, at least, show comparable validity with that observed with the other measures.

Method

Participants

The sample consisted of 899 participants who consented to be part of an ongoing opt‐in Web panel administered by Decision Research. The panel members are 65% women and have a mean age of 38.7 years. Two percent had less than a high school education, 33% had completed high school or a trade school, 53% had completed some college or had a college degree, and 13% had completed schooling beyond a 4‐year degree. A subset of this sample (n = 723, 70% women) was used for testing the predictive validity of the Rasch‐based measure. The mean age of the sample was 39.5 years. One percent had less than a high school education, 26% had completed high school or a trade school, 57% had completed some college or had a college degree, and 14% had completed schooling beyond a 4‐year degree. The Decision Research Web panel participants are compensated $15 per hour (prorated).

Decision‐making tasks

Ratio bias task

As explained earlier, in the ratio bias task (Denes‐Raj & Epstein, 1994), participants are offered a chance to win a prize by drawing a red jellybean from one of two bowls. One bowl has a greater absolute number of red beans (i.e., 9 in 100), and the other bowl has a smaller absolute number but a greater proportion of red beans (i.e., 1 in 10). Peters et al. (2006) predicted and found that less numerate adults drew more often from the affectively appealing bowl with less favorable objective probabilities whereas the highly numerate drew more often from the objectively better bowl. Participants responded on a 13‐point bipolar scale (1 = strongly prefer 9% bowl, 7 = no preference, 13 = strongly prefer 10% bowl). We predicted that the new measure would also replicate the findings of Peters et al.

“Bets” task

Peters et al. (2006) concluded from the ratio bias task discussed earlier that an affective process may underlie the greater number use of numbers by the highly numerate. If correct, then highly numerate individuals (who are thought to be more likely to draw affective meaning from number comparisons) may sometimes overuse numbers and respond less rationally than the less numerate. As a replication of the work of Peters et al. (2006), the bets task was conducted in a between‐subjects design. One group of participants rated the attractiveness of a no‐loss gamble (7/36 chances to win $9; otherwise, win $0) on a 0–20 scale; a second group rated a similar gamble with a small loss (7/36 chances to win $9; otherwise lose 5¢). Peters et al. (2006) hypothesized and found that highly numerate participants rated the objectively worse bet as more attractive and reported more precise affect and more positive affect to the $9 in the loss' presence. Thus, although greater numeracy is generally thought to lead to better decisions when numeric information is involved, it appears associated sometimes with an overuse of number comparisons, which may subsequently lead to sub‐optimal judgments despite higher ability levels. These results were consistent with the highly numerate accessing a richer affective “gist” from numbers (Reyna et al., 2009). Thus, we predicted a significant bet condition × numeracy interaction.

Framing

Participants were presented with the exam scores and course levels (200, 300, or 400—indicating varying difficulty levels of classes) of three psychology students and were asked to rate the quality of each student's work on a 7‐point scale (−3 = very poor to +3 = very good). Framing was manipulated between subjects as percent correct or percent incorrect so that “Paul,” for example, was described as receiving either 74% correct on his exam or 26% incorrect. Consistent with prior research (Peters et al., 2006), we predicted the difference in ratings for the positive versus negative frames would be greatest among less numerate participants. Put differently, participants lower in numeracy were expected to show more pronounced framing effects than those higher in numeracy. More numerate individuals were expected to transform the provided frame into the normatively equivalent alternative frame so that they would have both frames of information available (Cokely & Kelley, 2009; Peters et al., 2006).

All participants completed the framing and bets decision tasks. A subset (n = 218) also completed the ratio bias task.

Results and discussion

Rasch analysis

Rasch analysis was conducted in the same manner as in Study 1. We found that the results matched those obtained in Study 1, both in terms of the items retained as well as their relative difficulties (Table 6). Person reliability for this scale was .65, and Cronbach's α was .71; the mean inter‐item correlation for the retained items was .24.

Table 6.

Difficulty structure and fit statistics for the Rasch‐based numeracy scale—Study 2

	Difficulty	Infit	Outfit
Q12	90.5	1.24	.74
CRT1	76.6	.96	.94
CRT3	60.5	.91	.67
Q3	54.2	.84	.80
Q2	30.5	.96	.84
Q1	29.7	1.07	1.27
Q9	17.4	.91	.62
Q8b	14.2	1.07	.98

Note. Higher difficulty scores indicate greater difficulty.

Descriptive statistics

As predicted, the scores for the Rasch‐based numeracy scale were roughly normally distributed (M = 4.07, SD = 1.83, median = 4, mode = 4), and the distribution was not significantly skewed (.07, z = 0.83).

Associations between Rasch‐based numeracy and demographic variables

We found the expected negative correlation between age and numeracy (r = −.17, p < .001). Additionally, we found that men performed better than women (point biserial r = .31, p < .001). Moreover, we conducted a one‐way analysis of variance to determine differences in numeracy as a function of educational level and the association between educational level (three levels: high school/trade school education or less, some college, and 4‐year college graduate or greater). As expected, we found a significant main effect for educational level (F(2, 720) = 35.57, p < .001), in that those with a 4‐year college degree or greater performed better on the Rasch‐based numeracy measure (M = 4.60, compared with 4.11 and 3.27 for the some college and high school/trade school or less education groups, respectively). Overall, these findings replicate the results reported in Study 1.

Predictive validity

We report the analyses based on the Rasch‐derived measure in the following sections and then discuss the issue of comparative validity.

Ratio bias task

We also replicated the findings from the ratio bias task (Peters et al., 2006). Consistent with Peters et al. (2006), more numerate participants had a stronger preference for the objectively better bowl (10% bowl) than those lower in numeracy (r(218) = 0.16, p < .01). This result also is consistent with Stanovich and West's (2008) finding that cognitive ability was significantly associated with a similar ratio bias problem.

Bets task

We regressed the rated attractiveness of the gamble condition (coded −1 = no loss, 1 = small loss), the individual differences in numeracy (mean deviated), and the interaction between numeracy level and condition. Consistent with prior research (Bateman, Dent, Peters, Slovic, & Starmer, 2007; Slovic et al., 2002; Stanovich & West, 2008), participants rated the gamble as more attractive in the small loss condition (F(1, 719) = 60.40, p < .001, β = .92). Participants higher in numeracy also rated the gamble to be more attractive overall than those lower in numeracy (F(1, 719) = 16.11, p < .001, β = .26). Replicating Peters et al. (2006), the hypothesized interaction was also significant, such that participants higher in numeracy were more strongly affected by the small loss in the task (F(1, 719) = 6.50, p < .01, β = .17).

Framing task

We regressed the average rated student's work quality on frame condition (coded −1 = negative, 1 = positive), numeracy (mean deviated), and a frame × numeracy interaction. Subjects who did not respond to all stimuli (n = 29) were excluded from the analyses. As expected, we replicated the findings from the framing task reported earlier (Peters et al., 2006). We found a significant effect for frame (F(1, 690) = 245.07, p < .001, β = .48) and additionally found a significant main effect for numeracy (F(1, 690) = 4.59, p < .05, β = −.04). Most importantly, we found a significant frame × numeracy interaction (F(1, 690) = 8.34, p < .001, β = −.05), in which less numerate participants showed larger framing effects. These findings replicate the work of Peters et al. (2006) and, moreover, are consistent with research suggesting that less numerate decision makers focus on non‐numeric sources of information when constructing preferences (Dieckmann, Slovic, & Peters, 2009; Peters, Dieckmann, Västfjäll, Mertz, Slovic, & Hibbard, 2009).

Comparative validity

Table 7 shows the results for the three behavioral tasks as a function of different numeracy assessment. Overall, the Rasch‐based scale demonstrates comparable validity with that observed with the Lipkus et al. and CRT scales. For the ratio bias task, the Rasch‐based measure was more strongly associated with preference for the normatively correct bowl than the CRT; associations of the Rasch‐based scale and the longer Lipkus et al. scale were about the same.

Table 7.

Comparative validity analyses regressing decision performance on numeracy scales—Study 2

	Ratio bias task	Bets task				Framing task
	Pearson r	Bets condition	Numeracy scale	Interaction	R 2	Framing condition	Numeracy scale	Interaction	R 2
CRT	.11	0.91**	0.57**	0.24*	.11	0.47**	−0.03	−0.1**	.27
Lipkus et al.	.14	0.92**	0.15	0.11*	.09	0.47**	−0.03*	−0.02	.26
Rasch‐ based	.16	0.92**	0.26**	0.16**	.10	0.48**	−0.04*	−0.05**	.27

Note. CRT, cognitive reflection test.

^* p < .05,

^** p < .01. Each row reflects a separate regression analysis. Unstandardized coefficients and effect sizes are shown for each independent variable.

For the bets task, we found that the numeracy × bet condition interaction was significant using all three numeracy measures. To test the extent to which this effect was stronger for the Rasch‐based numeracy measure, we calculated and compared the effect size estimates for the differences between bet conditions (i.e., bets effect) as a function of both numeracy level (i.e., either high or low numeracy) and specific numeracy measure. Essentially, these analyses compare the simple effects of the interaction in terms of a linear contrast for numeracy, as construed by the different measures. For the Rasch‐based measure, the effect size of the bets effect for those scoring highest in numeracy (seven to eight items correct; d = 1.06) was nearly four times as large as the effect size observed for those scoring lowest on the Rasch‐based numeracy measure (zero to two items correct; d = .27). Similarly, those who scored 0 on the CRT showed weaker effect sizes (d = .42) than those who answered all three CRT items correctly (d = .70). We also observed a stronger effect size for those scoring highest on the Lipkus et al. measure (9–11 items correct, d = .65) than for individuals scoring the lowest on numeracy (zero to four items correct, d = .06). Thus, although we found the significant predicted interaction effect for all three scales, these results suggest that these effects were strongest when assessed with the Rasch‐based numeracy scale.

For the framing task, we observed interaction effects for both the CRT and Rasch‐based measures, but not for the Lipkus et al. measure. To explore these interaction effects in greater depth, we again calculated and compared effect size estimates of framing effects for high and low scorers on the CRT and Rasch‐based measures. Individuals who scored lowest on the Rasch‐based measure showed very strong framing effects (d = 1.42) even more so than those scoring 0 on the CRT (d = 1.33). In contrast, we found that individuals scoring highest on the CRT showed about the same framing effects (d = .67) as did those scoring the highest on the Rasch‐based numeracy scale (d = .65). Thus, compared with results of the CRT, these results provide evidence that using the Rasch‐based measure showed a slight advantage over the CRT when predicting framing effects for the less numerate, which was in the predicted direction of the interaction.

Together, these results provide evidence that the Rasch‐based numeracy scale shows comparable validity with both the Lipkus et al. measure and the CRT. The Rasch‐based measure showed better distributional qualities than the CRT or the Lipkus et al. measure and also demonstrated some evidence for stronger predictive validity than these existing measures. However, we acknowledge that this evidence is somewhat mixed. Compared with the Lipkus et al. measure, we found the Rasch‐based measure to show stronger simple effects when we decomposed the framing and bets task interactions, but it showed roughly equal predictive validity for the ratio bias task. Compared with the CRT, the Rasch‐based measure showed stronger effects with respect to the bets task and the ratio bias test but only showed modest effect size differences for the framing task. It is possible that the use of a more general population, not to mention one collected over the Internet, dampened expected relationships between numeracy and decision effects, thus reducing the chances of finding stronger scale‐based differences. For example, the materials in the framing task were originally developed to be meaningful to the undergraduate population tested by Peters et al. (2006), but the course level information (which was provided without further explanation) may have been confusing for the more general population studied here. Second, although Internet data collection is a valid means of obtaining psychological data, data from Internet samples are often noisier because of the lack of environmental control (Gosling, Vazire, Srivastava, & John, 2004).

Although these results are encouraging, they may raise a potential question regarding the advantages of the Rasch‐based numeracy scale. As we have demonstrated in the past two studies, the primary advantage of the Rasch‐based scale is that it offers a normal distribution in the general population, compared with the Lipkus et al. measure and the CRT, both of which are significantly skewed. Because skewness can attenuate linear associations between variables, we predicted that the Rasch‐based scale would be a stronger linear predictor than either of the component scales. Our Study 2 results suggest that this will not always be the case. In Study 3, we examine this issue further within the context of risk perception.

STUDY 3

In this study, we wanted to further explore the comparative predictive validity of the Rasch‐based scale using two additional tasks. We turned our attention to understanding how numeracy may predict perceived risks. Recent work has demonstrated that numeracy is related to likelihood and risk perceptions. For instance, when presented with numerical probability information, less numerate participants tend to think that negative low‐probability events are more likely to occur, compared with more numerate participants (e.g., Dieckmann et al., 2009; also Lipkus, Peters, Kimmick, Liotcheva, & Marcom, 2010). This typical finding may be due to the less numerate responding more to non‐numeric and often emotional information about risks such as cancer (Peters, 2012; Reyna et al., 2009).

For this study, we examined whether the Rasch‐based measure would be a stronger linear predictor for outcomes related to the explicit understanding and use of probabilistic estimation than is afforded by either the CRT or the Lipkus et al. 11‐item measure. The association between understanding risk information and numeracy appears to be a very robust phenomenon (see Reyna et al., 2009, for a review). Understanding how numeracy is associated with risk perceptions is important in many domains, including financial and health decisions. For instance, if individuals lower in numeracy misinterpret the risks of treatment options, they may act in a suboptimal way. Similarly, being able to accurately identify true numeracy abilities may enable risk communicators to develop more customized and effective communication messages.

Method

Participants

The sample (N = 165) was drawn from the Decision Research Web Panel and was 57.6% women (mean age = 39.53 years). Approximately 25% of the sample had a high school education or less, 4% had some vocational training, 28% had attended some college, 33% were college graduates, and 10% had attended graduate or professional school after college.

Procedure

In a previous session, participants completed the CRT, the Lipkus et al. numeracy measure, and the additional items from the Peters et al. measure. Participants each read two different scenarios that included a narrative discussion of available evidence relating to an event as well as a numerical probability assessment made by an expert. The first scenario described a potential terrorist attack, and the second scenario described the possible extinction of salmon in a Pacific Northwest river. The likelihood of each event was presented as either 5% or 20%. Each participant read both scenarios (their order was counterbalanced across subjects), and the numerical probability attached to each scenario was counterbalanced separately across subjects (i.e., numerical probability was a within‐subject manipulation). After reading each scenario, participants reported their own perceptions of the likelihood of the attack or salmon extinction on a scale ranging from 0% to 100%. Because the goal of this analysis was to examine the associations between the different numeracy scales and likelihood perceptions in the two scenarios, we do not report the effect of the within‐subject condition but instead focus on the correlational analyses for this study.

Results and discussion

Table 8 shows the correlations between perceived likelihood and the three different numeracy scales for the full sample, and for the lower‐education (vocational school or less) and higher‐education (some college or more) groups. For both scenarios, the full‐sample correlations were higher with the Rasch‐based measure, although each of the numeracy scales is significantly negatively correlated with perceived likelihood, as expected. However, we anticipated the primary benefit of the Rasch‐based measure to be in identifying linear effects across a range of educational levels. In particular, given the difficulty of the CRT, we expected attenuated correlations in the lower‐education group. As predicted, the results demonstrate that the CRT showed the smallest correlations across both scenarios, with the Lipkus et al. and Rasch‐based measures showing comparable effect sizes. In the higher‐education group, all of the numeracy scales were inversely correlated with risk perceptions; the Rasch‐based measure shows the largest effect size for both scenarios.

Table 8.

Correlations between risk perceptions and numeracy in the full sample and as a function of educational level—Study 3

	Full sample	Lower‐education group	Higher‐education group
Terrorist attacks
CRT (three items)	–.24**	–.13*	–.21*
Lipkus et al. (11 items)	–.34**	–.34*	–.29**
Rasch (eight items)	–.41**	–.38**	–.36**
Salmon extinction
CRT (three items)	–.35**	–.11	–.33**
Lipkus et al. (11 items)	–.38**	–.31*	–.35**
Rasch‐based (eight items)	–.44**	–.27+	–.43**

Note. CRT, cognitive reflection test.

⁺ p < .10,

^* p < .05,

^** p < .01.

As expected, the Rasch‐based measure showed the strongest and most consistent effects in the full sample and across the two education groups. The CRT consistently demonstrated low correlations in the lower‐education group. Moreover, both the Lipkus et al. measure and the CRT showed lower correlations with risk perceptions than did the Rasch‐based measure in the higher‐education group.

Study 3 demonstrates some distinct advantages of the new Rasch‐based measure. First, the Rasch‐based measure demonstrates the most consistent level of correlations across various educational levels. We attribute this advantage to the fact that performance on the Rasch‐based measure is normally distributed in the general population. Second, and perhaps more importantly, the Rasch‐based measure overall shows stronger predictive validity in these judgments and decisions, compared with the other two measures. Compared with the Rasch‐based measure, the CRT showed limited predictive validity, especially in the lower‐education sample. In contrast, the Lipkus et al. measure showed evidence of reduced predictive validity in higher‐education samples.

GENERAL DISCUSSION

A growing body of research has demonstrated that individual differences in numeracy are associated with how individuals perceive risks, understand charts and graphs, and ultimately make decisions. However, measurement of this construct has varied. To our knowledge, this study is the first to present the psychometric properties of several popular numeracy measures across a diverse sample in terms of age and educational level (although see Liberali et al., 2011 for a similar examination with Brazilian and US college‐age samples, which adds to the literature from a cross‐cultural perspective). Inspection of the distributional characteristics of these measures demonstrates that the previously used measures are very skewed, which may limit their ability to discriminate an individual's trait level of numeracy. In general, the CRT appears to be very difficult, whereas the Lipkus et al. (2001) measure appears to be too easy for most individuals, leading to non‐normal score distributions, an issue that prior research has largely addressed by using median splits or extreme group designs. We do not mean to either diminish or criticize the contributions that have been made using these scales. In fact, these studies reinforce past research efforts supporting and strengthening the validity of extant measures.

In the current study, we used Rasch analysis to develop a scale that offers researchers an alternative means to assess individual differences in numeracy, compared with classic test theory approaches (Embretson, 1996). The items retrieved, as well as the relative difficulty scaling of these items, were identical across two large independent samples of individuals ranging from 18 to 89 years of age. Moreover, the Rasch‐based numeracy scale retained a wide range of item difficulties. Further, we found that this scale approached a normal distribution in both samples, which we believe will ultimately lead researchers to treat numeracy as a continuous variable rather than as a dichotomous variable. We feel that this is an important contribution, given the potential limitations involved with dichotomizing variables (MacCallum, Zhang, Preacher, & Rucker, 2002).

Cronbach and Meehl's (1955) classic article first identified construct validity (i.e., how trustworthy is the score and its interpretation) as the most important form of validity in psychological tests. Construct validity of a measure should be treated as a continual process that involves researchers testing the predictive validity of the measure, as well as assessing convergent and discriminant validity. The Rasch‐based measure demonstrates predictive validity comparable with that obtained in previous numeracy studies. In fact, when directly comparing the Rasch‐based scale with its predecessors, we found that the Rasch‐based measure predicted as well as or better than the CRT and the Lipkus et al. measure across two separate studies.

We also found that the Rasch‐based numeracy measure was strongly correlated with the SNS of Fagerlin et al. (2007), supporting the convergent validity of the measure. Although the SNS was not intended to be a substitute for assessing precise numeracy abilities, this finding reinforces prior research supporting a link between subjective and objective assessments of numeracy (Fagerlin et al., 2007; Zikmund‐Fisher et al., 2007; although see Reyna et al., 2009, p. 955, for an excellent discussion regarding concerns about the accuracy of individual's subjective assessments of their own numeracy). Because the SNS was administered after the objective numeracy measures, we cannot rule out the possibility that individuals reflected on the perceived ease/difficulty of the numeracy items, which, in turn, may have inflated the correlation between numeracy and SNS. However, our results are consistent with those reported by Fagerlin et al. (2007), who had subjects complete the SNS first. Finally, our data cannot directly speak to any differences in predictive power between objective and subjective numeracy scales, but we believe that this is an important question that future research should address.

We acknowledge that this scale may not include a complete range of difficulty. Because of our study's design, our results are limited by the number of items that were included in the initial item pool. In fact, examination of the Rasch‐based item difficulties would suggest that more items could be added to more finely differentiate individuals' numeracy ability. Cokely et al. (2012), for instance, applied a decision tree approach to develop a computer‐adaptive test for the highly numerate. Future research using IRT principles can help to create adaptive tests that may assess numeracy across a wider range of ability levels.

Another implication of only using existing measures is that it restricts our ability to conduct a more extensive analysis of potential multidimensionality of the numeracy construct (Liberali et al., 2011). If we had started with a much larger initial item pool, it might be reasonable to expect multiple correlated facets of numeracy to be extracted that would represent sub‐competencies of numeracy. Although previous research has typically added items on the basis of their face validity, we recommend that future scale construction efforts be based instead on accepted scale construction guidelines widely used in the assessment literature (e.g., Clark & Watson, 1995). This process begins with the generation of an item pool based on theoretical considerations, such as those discussed in literature reviews and empirical inquiries (see Dehaene, 1997, and Reyna et al., 2009, for influential reviews). Briefly, researchers should develop an over‐inclusive item pool of various items and difficulty levels. Numeracy skills range from, but are not limited to, simple mathematical operations (e.g., addition, multiplication) to logic and quantitative reasoning, as well as comprehension of probabilities, proportions, and fractions. From this item pool, researchers would subsequently conduct multiple administrations of the items, refining the measure by removing ambiguous/poorly constructed and misfit items along the way. Scale development in this manner can result in the ability to make more fine‐grained distinctions in numeracy across persons and to more extensively identify sub‐competencies/facets of numeracy. From there, researchers will be able to better test if certain sub‐competencies of numeracy are differentially important to particular types of judgment and decision problems. Understanding the multiple potential facets of numeracy is an important and necessary future research direction that would be most properly examined within the context of the scale construction/factor analytic methods that we have outlined.

However, we offer one important caveat with respect to the assessment of multidimensionality. As a consequence of adequately developing measures that assess numeracy sub‐competencies in the manner that we have outlined, this method would add many more items to a numeracy scale. It would especially be the case if one wanted to adequately scale item difficulty and ability levels for each sub‐competency. At the expense of being more comprehensive, it would undoubtedly add more time to assessments than even the longest numeracy measure that currently exists. Thus, researchers who may have limited assessment time or resources available (e.g., researchers interested in assessing numeracy in large nationally representative surveys) may opt for a shorter instrument, sacrificing construct fidelity for a broader bandwidth. We stress that it is vital for researchers to have both types of measures in their assessment arsenal; ultimately, though, the use of each is dependent on the inquiry at hand.

We believe that our Rasch‐based measure provides a valuable advance in the assessment of numeracy. Our results reinforce that our reduced‐item scale measures numeracy in a coherent, unitary manner, across a wide range of ability levels. Of particular interest, we used CFA to directly test whether the CRT and the numeracy items comprised different underlying factors. We did not find this to be the case. At the surface, these results appear to be in contrast with those reported by Liberali et al. (2011), who, across two samples, concluded that items from the scales of Lipkus et al. (2001) and Frederick (2005) produced four to five factors based on exploratory factor analysis.4 Moreover, in one of their two studies, the CRT and objective numeracy items loaded onto different factors. Because the single‐factor un‐rotated solutions, a direct measure of the common construct defined by the item pool, were not reported, we cannot directly compare results of the current study with those of Liberali et al. (2011). However, given that reported correlations between the CRT and the Lipkus et al. numeracy measure by Liberali et al. (2011) were indicative of a moderate to large effect size (range = .40–.51; mean r = .45), it seems reasonable that a one‐factor solution may also have been observed in confirmatory factor analyses of their data as well.

In contrast to exploratory factor analysis as a data reduction tool, the Rasch analysis identifies a hypothetical unidimensional line on which items and persons are scaled on the basis of item difficulty and ability level. In turn, misfit items represent items that do not contribute to better identification of the construct. Hence, the reduced scale requires fewer items to estimate the latent construct with the same range of ability level as the full item pool. In our study, we were able to substantially reduce an item pool from 18 to eight items, creating a measure that is comparable, or even better, in terms of predictive validity and internal consistency with that which would have been obtained by administering either all 18 items or one of the component scales.

As the study of numeracy in the decision‐making literature continues to grow, the importance of being able to appropriately discriminate individual differences in numeracy also increases. The current study offers a measure that researchers interested in the associations between numeracy and human decision processes can use to assess individual differences across a wider range of target populations compared with previous measures.

Biographies

Joshua A. Weller is currently a research scientist at Decision Research (Eugene, OR). His research focuses on how the ability to make advantageous decisions develops throughout the lifespan. Additionally, Dr. Weller is interested in understanding how individual differences relate to risk taking and decision making.

Nathan F. Dieckmann is a research scientist at Decision Research (Eugene, OR). He conducts basic and applied research in decision making, risk communication, and statistical methodology.

Martin Tusler is a research specialist in the Psychology Department at The Ohio State University. He studies medical decision making, scale construction, and numeracy.

C. K. Mertz is a data analyst at Decision Research (Eugene, OR). Her research interests include multivariate statistical methods, risk perception, and affect.

William J. Burns is a research scientist at Decision Research (Eugene, OR), whose current work focuses on modeling public response and the subsequent economic impacts of disasters (special emphasis on terrorism) on urban areas.

Ellen Peters is an associate professor in the Psychology Department at The Ohio State University. She studies decision making as an interaction of characteristics of the decision situation and characteristics of the individual. Her research interests include decision making, affective and deliberative information processing, emotion, risk perception, numeracy, and aging.