Mechanistic Study of the Reaction of Thiol‐Containing Enzymes with α,β‐Unsaturated Carbonyl Substrates by Computation and Chemoassays

Abstract

We investigated the reactions between substituted α,β‐unsaturated carbonyl compounds (Michael systems) and thiols by computations as well as chemoassays. The results give insight into variations in the underlying mechanisms as a function of the substitution pattern. This is of interest for the mechanisms of inhibition of the SARS coronavirus main protease (SARS‐CoV M^pro) by etacrynic acid derivatives as well as for the excess toxicity of substituted α,β‐unsaturated carbonyl compounds. This study compares possible reaction courses including 1,4‐addition followed by a ketonization step, and underscores the importance of a base‐catalyzed step for the reactivity of thiol groups in enzymes. Phenyl and methyl substituents at the Michael system decrease the reactivity of the electrophilic compound, but chlorophenyl substituents partly recover the reactivity. Computations also indicate that electron‐pushing substituents lead to a change in the reaction mechanism. The conformation of the Michael system is also found to significantly influence reactivity: the s‐cis conformation leads to higher reactivity than the s‐trans conformation. The computed data explain the trends in measured inhibition potencies of substituted α,β‐unsaturated carbonyl compounds and of reaction rates in chemical assays. They also indicate that the reversibility of inhibition does not stand in contrast to the formation of a new covalent bond between inhibitor and protease.

Reactions between thiol‐containing enzymes and Michael systems were studied to investigate new agents against viral proteases and to analyze the excess toxicity of Michael systems. Our results explain the trends in inhibition and toxicity and explain why some Michael systems are irreversible inhibitors of the SARS coronavirus main protease, whereas others are only reversible.

Introduction

In 2002, a hitherto unknown plague emerged from the Guangdong province in southern China. Within a few weeks it affected more than 8000 people in 25 countries.1, 2 This atypical form of pneumonia had an overall fatality rate of 10–15 %. It was termed severe acute respiratory syndrome (SARS).3 The etiological agent for the epidemic was identified as the previously unknown coronavirus SARS‐CoV, which contains the largest viral RNA genome known so far.4

The SARS‐CoV main protease (SARS‐CoV M^pro) was found to be a suitable target for antiviral drugs because it controls viral replication and transcription.5 Furthermore, the structure of the SARS‐CoV M^pro is highly conserved among other coronaviruses, which makes it attractive for rational drug design.6

The perspective of limiting or preventing the replication of the SARS coronavirus led to the development of various inhibitors against the SARS‐CoV M^pro. Because of its similarity to picornavirus 3C proteases, it was thought that SARS‐CoV M^pro could be targeted by a drug that inhibits picornavirus 3C protease activity: AG70887 (Ruprintrivir®, Figure 1) was in clinical trials against the common cold, and was proposed as a promising lead structure against coronaviral infections as well. AG7088 itself was found to be inactive in enzyme assays with SARS‐CoV M^pro; however, modifications to the peptidomimetic scaffold lead to significant inhibition potencies.8, 9 The electrophilic building block of these active‐site‐directed inhibitors consists of an α,β‐unsaturated ester function, which undergoes nucleophilic attack by the thiol group of the cysteine residue.

Figure 1.

Two examples of inhibitors containing Michael systems as the electrophilic warhead. The arrows indicate the positions attacked or thought to be attacked by a cysteine residue of the enzyme.

Another approach starts from substituted etacrynic acid,10, 11 which possesses an α,β‐unsaturated ketone moiety as an electrophilic building block (Figure 1). While the vinylogous esters lead to irreversible inhibition, the etacrynic acid derivatives show only reversible inhibition of proteases.12 The underlying reason for the difference is yet unknown.

The rational design of improved inhibitors requires detailed knowledge about the inhibition process and especially about the interplay between the various effects. Of particular interest is the distinction between effects that influence the reversible versus the irreversible step. The former is influenced by noncovalent interactions between inhibitor and enzyme. The latter may also be influenced by such effects, as they may orient the inhibitor in the right arrangement. However, it also relies on the chemical reactivity of the electrophilic warhead which is influenced by substituent effects. Such information can be provided by chemoassays. To elucidate such effects for the inhibition potency of three‐membered heterocycles we employed a thiophenol assay. It proved to be a good model for the active site of cysteine proteases, as it represents a rather acidic thiol (pK _a=7.4–7.8) with half the concentration being deprotonated at the pH used (pH 7.6).13c,d In the work reported herein this assay was applied to gain insight into the reactivity of the studied etacrynic acid derivatives. To analyze the inherent reactivity of electrophiles against thiol‐containing enzymes Schultz and co‐workers14 and Schüürmann and co‐workers15 developed assays based on glutathione. They were employed to quantify the electrophilic reactivity of S_N2 electrophiles such as aliphatic, allylic, and benzylic halides as well as α‐halogenated carbonyls. Because these assays were also used to study the reactivity of α,β‐unsaturated carbonyls acting as Michael acceptors, they are of significant interest to the goals of the present study.

To disentangle the various effects that determine the reactivity of Michael systems, the reactions were also modeled by quantum chemical computations. Earlier theoretical investigations16, 17 predict that the reaction of a thiolate with a Michael system leads to quite stable covalent bonds between the thiolate and the α,β‐unsaturated carbonyl moiety. Thus, they predict an irreversible inhibition of thiol‐containing enzymes by inhibitors containing such electrophiles as warheads. However, the theoretical model systems used completely neglected solvent effects and did not consider substituent effects. Additionally, they assumed the attack of a negatively charged thiolate moiety, while the catalytic active cysteine residue within the SARS‐CoV M^pro 18 or other enzymes represents a neutral thiol. Computations are challenging because various reaction paths are conceivable, and a strong influence of the environment can be expected.

Hence, we developed model systems which can be used to extract the influence of the substitution pattern on the inhibition mechanism. The computed models include the addition step of the thiol to the Michael system via a base‐catalyzed mechanism. Possible addition mechanisms include reaction courses that run across enol intermediates and also consider direct addition pathways. For the former, the subsequent enol–keto tautomerization was also taken into account, as the corresponding activation barriers are expected to be similar or even higher than the barriers of the addition step.

The work is organized as follows: after a brief description of the theoretical and experimental approaches the computed reaction courses are discussed as a function of the different substitution patterns. After describing the experimental results, experiment and theory are compared in order to gather insight as to how the substitution pattern influences the potency of inhibitors that possess substituted Michael systems as an electrophilic warhead. The resulting information also provides insight into the excess toxicity of unsaturated carbonyls acting as Michael acceptors.

Results and Discussion

Model systems

Inhibition mechanisms in which covalent bonds are formed can be formally divided into two steps (Scheme 1).19 The first step consists of the formation of a noncovalent enzyme–inhibitor complex (EI). Within this complex, the attacking enzyme moiety is oriented in such a way that the covalent bond (E—I) can be formed, e.g., by attack of a nucleophilic center of the enzyme at the electrophilic center of the inhibitor. The resulting reaction represents the second step of the overall inhibition. Within this step the bond formation is mainly influenced by enthalpic effects, as all entropic contributions which are associated with the formation of the enzyme–inhibitor complex are already included in the first step.13a Furthermore, entropy effects are quite uniform for similar reactions and hence do not change the relative trends.

Scheme 1.

Two‐step model for the irreversible inhibition of proteases: E=enzyme, EI=noncovalent enzyme–inhibitor complex, E—I=covalently and irreversibly blocked enzyme.

The work presented herein focuses on the second step. In the present context it involves the formation of a covalent bond between a thiol residue (e.g., of the cysteine residue of the SARS‐CoV M^pro) and the electrophilic building block of the inhibitor. Models that aim to describe this step in all details must account for the influence of the protein and the solvent environment. This can be achieved with quantum mechanical/molecular modeling (QM/MM) approaches that take enzyme and solvent explicitly into account. They are even able to describe effects such as regio‐ or stereoselectivity of the inhibition process.20 However, as shown recently by investigations into the inhibition of papain‐like proteases,13 valuable insights into the influence of the substitution pattern of the warhead are already possible from simpler models. These mimic all important parts of the considered system by truncated model compounds in combination with a continuum model such as COSMO.21 These models approximate the cysteine residue by a methyl thiolate, while the environment is modeled either by two water molecules (pK _s≈15) to mimic a low proton‐donating ability of the environment, or by two ammonium ions (pK _s≈9.3) to simulate a higher proton‐donating ability. These explicit solvent molecules were employed in combination with the continuum model COSMO which accounts for the overall polarizability of the solvent and the protein environment. From the inhibitor, only the electrophilic warhead and its directly attached substituents were taken into account. Information about the kinetics and thermodynamics of the irreversible step of inhibition were obtained through potential energy surfaces of the inhibition process which were computed by employing the B3LYP/TZVP//BLYP/TZVP level of theory. Because such approaches are considerably less expensive than QM/MM computations they allowed a scan of a large number of substituents to test changes in the inhibition potencies of epoxides and aziridines. Such model calculations are also important to distinguish between influences of the enzyme environment and inherent effects resulting from the electronic structure of the inhibitor itself. That the prediction of the computations could be proven experimentally underscores the reliability of the simple approach.13

To transfer such models to the situation in thiol‐containing enzymes in reaction with etacrynic acid derivatives, the following approximations were adopted (see Figure 2). The thiol‐containing residue of the enzyme is mimicked by methyl thiol. Possible proton‐accepting groups (e.g., the histidine residue of the SARS‐CoV M^pro) are assumed to play the role of the proton acceptor in the base‐catalyzed process. To evaluate the importance of base catalysis, such groups are modeled by an ammonia molecule, which has been shown to be a good approximation.13 This is shown by comparison between simpler QM13a,b and more elaborate QM/MM20a approaches. The former used an ammonium ion, whereas the latter employed a histidine group.

Figure 2.

Sketch of the model systems used to compute the potential energy surfaces shown in Figure 4. The varied internal coordinates are also given.

The similarity may result because the pK _a value of ammonia (9.3) is not too different from that of histidine residues in thiol proteases (pK _a 8–9).20 Additionally, to investigate the influence of the substitution pattern of the α,β‐unsaturated carbonyl derivates on the reaction mechanisms, we modeled the reactions of compounds 1–11 shown in Figure 3.

Figure 3.

List of α,β‐unsaturated carbonyl compounds (Michael systems) studied in this work.

The possible reaction paths of the overall addition of thiols to Michael systems are depicted in Scheme 2. For the reactions under physiological conditions, thiols are present in protonated (R‐SH) and deprotonated (R‐S⁻) form, but as discussed below, only the reactivity of the thiolate seems to be sufficiently high for an efficient attack at the α,β‐unsaturated carbonyl moiety. Hence, the proton must be transferred to a proton acceptor, that is, a base‐catalyzed reaction has to take place. For the resulting thiolate the reaction can proceed along two pathways. In the direct addition mechanism the thiolate attacks C3 (Figure 2) and at the same time the proton is transferred from the base to C2 (direct E2‐like addition). If the proton is instead transferred to the carbonyl oxygen atom, the enol form of the 1,4‐addition is obtained. A comparison between both pathways was computationally performed by Weinstein and co‐workers,22 who studied the addition of ammonia to α,β‐unsaturated carbonyl compounds. They computed a direct addition as well as the 1,4‐addition. However, they did not consider the base‐catalyzed reactions discussed in Figure 2. In contrast, for the direct addition they assumed an intermolecular proton transfer from the ammonium group to C2. For the 1,4‐addition an intramolecular proton transfer from the nitrogen atom to the carbonyl oxygen was considered. They found that in such cases the 1,4‐addition is favored over direct addition. Both reactions are catalyzed by a single water molecule, but 1,4‐addition remains the favorable reaction course. For acrolein the barrier of the 1,4‐addition is ∼70 kJ mol⁻¹ lower than the corresponding barrier of the direct addition (96 kJ mol⁻¹ vs. 27 kJ mol⁻¹). For acrylic acid the difference is only ∼5 kJ mol⁻¹ (59 kJ mol⁻¹ vs. 54 kJ mol⁻¹), but the 1,4‐addition is still favored. Tezer and Ozkan23 came to similar conclusions.

Scheme 2.

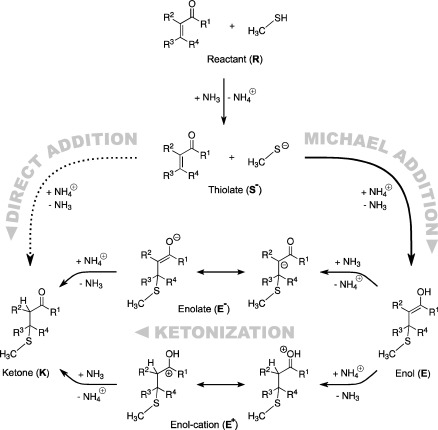
Conceivable reaction mechanisms for the addition of methylthiol to α,β‐unsaturated carbonyl compounds.

If the reaction proceeds along the 1,4‐addition the final product is only reached after a ketonization of the enol form. In the studies mentioned above the influence of possible barriers of this step was not considered. Experimentally, the barrier of the acid‐catalyzed ketonization of acetone enol in water was determined to ΔH ₀ ^≠=40 kJ mol⁻¹. The energy difference between the enol and the keto form was measured to ΔH ₀=−43 kJ mol⁻¹.24 Comparison with gas‐phase data show that ΔH ₀ depends little on the surroundings, but the actual course of the reaction and the kinetics are strongly influenced.25 Recent computations reveal that the barrier of the ketonization strongly depends on the nature of a water bridge, which facilitates the proton transfer. If the bridge consists of three water molecules the computed barrier height is ∼73 kJ mol⁻¹, while a value of >210 kJ mol⁻¹ is computed for the direct transfer. A similar value was also computed by Lien and co‐workers.26 If more than three water molecules are added, the water bridge is solvated itself and the barrier increases again. Notably, the computations did not consider proton catalysis. Further work also showed that in some cases the energy differences between keto and enol forms depend on the molecular structure of the solvent.27

Due to the strong dependence on the actual number of water molecules, computation of the activation energy for this complicated process is too involved for the goal of the present work which is to study the influence of various substitution patterns. Nevertheless, since the corresponding barriers are similar or perhaps even higher than the barriers of the addition step, the ketonization can be expected to influence the inhibition potency of a given inhibitor significantly.

In our model the influence of this part of the reaction path is estimated by the enolate intermediate E⁻ and the enol cation E⁺ (see Scheme 2). The enolate E⁻ represents the most important intermediate if the reaction takes place in basic solution (first deprotonation, then addition). The cation E⁺ is important for an acidic environment in which the deprotonation and the protonation steps interchange. More information about our approach is given in the Supporting Information.

The determination of relative energies that are not biased due to hydrogen bonding networks is quite complicated. Because we are only interested in trends that arise from the substitution pattern it is necessary to compute relative energies without the influence of the network. A suitable reference for all energy considerations is E ₀, which represents the energy of the model system in which all reactants and all explicitly accounted solvent molecules are infinitely separated so that no hydrogen bonding network exists. Because the s‐trans form is slightly lower in energy, E ₀ is defined as:(1)

(1)

The energies of ammonia and the ammonium ion are necessary for the comparison with the computed potential energy surface (PES). Relative energies with respect to E ₀ which also do not account for the influence of the hydrogen bonding network arising due to the explicit solvent molecules are abbreviated with E _0(X). As an example, the relative energy of the enol form E (see Scheme 2) without considering the influence of the hydrogen bonding network is given as:(2)

(2)

Corresponding computations were performed for all other intermediates depicted in Scheme 2. The actual formulas are given in the Supporting Information. The resulting energies computed for compounds 1–11 are summarized in Table 1. The s‐trans and the s‐cis isomers are depicted in Figure 5 below. More information is given in the Supporting Information.

Table 1.

The publisher did not receive permission from the copyright owner to include this object in this version of this product. Please refer either to the publisher's own online version of this product or the printed product where one exists.

Figure 5.

Definition of s‐trans and s‐cis isomers.

Computations

In the first model the inhibitor is represented by acrolein (1), which represents the simplest Michael system. The PES for the reaction branch up to the enol form is depicted in Figure 4 A. It was computed as a function of the distances between the center of methyl thiol and the C3 center of the inhibitor (r(S—C), see Figure 2), and between the sulfur and the proton of the ammonium ion (r(S—H)).

Figure 4.

Potential energy surfaces (PES) computed to characterize the reaction branch up to enol formation for the acrolein model system 1. The internal coordinates are defined in Figure 2. A) PES obtained as a function of r(S—H) and r(S—C); B) PES computed as a function of r(S—H) and the r(O—H) distance.

Both coordinates were varied independently, as the relationship between them was unknown. The S–H distance (r(S—H), see Figure 2) ranges from 1.0 to 3.0 Å, while the C3–S distance (r(S—C), see Figure 2) varied between 1.7 and 3.7 Å. For each point of the PES, r(S—C) and r(S—H) were kept fixed at certain values while all other internal degrees of freedom were optimized. Transition states were identified as maximum points on the potential curves. Frequency analysis of transition states confirmed their nature.

In this PES the r(O—H) distance (see Figure 2) was not treated as an independent variable. It represents the main coordinate of the protonation of the emerging intermediate, but during the optimization of the remaining internal degrees of freedom this coordinate smoothly adjusted for varying distances r(S—C) and r(S—H). To investigate the influence of r(O—H) in greater detail we also computed a two‐dimensional PES for which r(O—H) is varied together with the r(S—C). The corresponding PES (Figure 4 B) indeed shows that r(O—H) smoothly adjusts. More information is given in the Supporting Information.

The PES of the addition reaction (Figure 4 A) gives the qualitative picture of a two‐step mechanism. As the first step, deprotonation of the thiol reactant R occurs leading to a zwitterionic state that consists of a thiolate anion H₃C‐S⁻ which interacts with an ammonium ion (NH₄ ⁺⋅⋅⋅⁻S‐CH₃). In the following this state is abbreviated as S⁻. It lies 12 kJ mol⁻¹ higher than the reactants. The deprotonation process has a barrier (TS1) that is computed to 18 kJ mol⁻¹. Figure 4 A shows that the shape of the potential energy curve describing the deprotonation step is nearly independent from the second reaction coordinate R_CS for R_CS>3 Å. For smaller distances the barrier flattens. Nevertheless, such paths remain energetically less favorable than deprotonation paths with R_CS>3 Å because they start from considerably higher energies. The approach of the protonated thiol to the Michael system is repulsive (Figure 4 A). The subsequent conjugated addition reaction at the C3 atom of the inhibitor proceeds to the enol intermediate E without passing a second transition state (TS2), that is, the prior deprotonation step is the rate‐determining step. During this reaction step, the carbonyl oxygen atom of acrolein (1) is simultaneously protonated by the proton donor ammonium. This is also shown by the PES that is obtained if r(S—H) and r(O—H) are varied (Figure 4 B). The whole reaction to the enol possesses an exothermicity of only −45 kJ mol⁻¹. For the addition of the deprotonated thiolate to the Michael system, a reaction energy of −57 kJ mol⁻¹ is predicted. The reverse reaction is, in both cases, easily possible.

An analysis of selected bond parameters within the Michael system at the characteristic points of the PES is given in Table 2. The bond lengths within the nearly undisturbed Michael system, referring to a C–S distance of 3.7 Å, agree well with the experimentally determined counterparts,28 reported as 1.22 Å for the C1—O carbonyl bond, 1.49 Å for the C1—C2 single bond, and 1.35 Å for the C2=C3 conjugated double bond. The product of the conjugated addition shows the typically observed bond lengths referring to a sulfur–carbon bond C1—S, a C2—C3 single bond, a C1=C2 double bond, and a C1—O single bond.

Table 2.

The publisher did not receive permission from the copyright owner to include this object in this version of this product. Please refer either to the publisher's own online version of this product or the printed product where one exists.

The exothermicity of the reaction strongly depends on the proton donor molecule in the vicinity of the inhibitor's carbonyl oxygen atom. If the ammonia molecule is replaced by a water molecule the inhibitor is not protonated during the addition reaction, and the exothermicity lowers by ∼40 kJ mol⁻¹. Furthermore, the conjugated addition step possesses a barrier (TS2) of ∼3 kJ mol⁻¹; that is, the deprotonation remains the rate‐determining step. While the energies change considerably, the corresponding geometrical parameters resemble those found before. They are summarized in the Supporting Information. Without any proton donor, the conjugated addition becomes the rate‐determining step with a barrier height of 24 kJ mol⁻¹ for the second transition state (TS2). The reaction energy of the complete reaction is +5 kJ mol⁻¹; that is, the reaction becomes endothermic. The geometric parameters again resemble those found for the previous systems; these are also given in the Supporting Information. The strong influence of the proton donor underscores the importance of a proper orientation of the carbonyl oxygen atom of the Michael system toward a stabilizing group, such as the oxyanion hole.

The influence of the hydrogen bonding network is reflected by the relative energies from the PES scan (Figure 4 A) compared with those calculated by Equation (2) (Table 1). If the influence of the hydrogen bonding network is switched off, the energy difference between the reactant and the intermediate S⁻ increases to ∼40 kJ mol⁻¹. The enol form is predicted to lie ∼−20 kJ mol⁻¹ below the reactants. These values can be compared with the relative energies for the ketonization step (enolate or enol cation) to get information about the complete 1,4‐addition mechanism. The enolate is found to lie ∼10 kJ mol⁻¹ below the S⁻ intermediate. Hence, our computations predict that for acrolein the proton transfer leading to the S⁻ intermediate represents the rate‐determining step. This is in line with previous findings.22, 23, 26 For the addition of ammonium to acrolein, previous computations also indicate that the 1,4‐addition mechanism takes place and that the addition step is rate determining. This also supports that our approach is sufficiently accurate.

Substituents are known to influence the inhibition potency of Michael‐system‐based inhibitors. In order to study such effects we investigated the influence of various substituents of the Michael system on the relative position of the intermediates depicted in Scheme 2. The results obtained for the compounds depicted in Figure 3 are summarized in Table 1. The s‐cis form of acrolein (1) (Figure 5) is ∼10 kJ mol⁻¹ higher in energy than the s‐trans form. The corresponding barriers are very similar so that acrolein is expected to react in the s‐trans form. The addition of thiolate to the α,β‐unsaturated carbonyl compound with R¹=methyl possesses an additional barrier of 10–15 kJ mol⁻¹, which was not present for acrolein. Together with the energy necessary to form the thiolate, the total barrier for reaching the enol form increases to ∼60 kJ mol⁻¹. The relative energy of the enolate is computed to ∼50 kJ mol⁻¹. Hence the ketonization is also predicted to be slower than for acrolein, but the addition of the thiolate remains the rate‐determining step. The increase with respect to the unsubstituted acrolein can be explained by the +I effect of the methyl group. This effect also explains why the enol cation becomes more stable by about the same degree, but it is still considerably higher in energy than the enolate. The barriers computed for the s‐trans and s‐cis isomers are virtually identical which represents an additional difference to the unsubstituted counterpart. In summary, the methyl substituent decreases the reactivity of the α,β‐unsaturated moiety, but the overall mechanism is not expected to change.

For compound 3 (R¹=phenyl) similar effects are observed. In contrast to 2, however, the s‐cis form becomes slightly more stable than the s‐trans form. Furthermore, while the addition step for the s‐trans form possesses a barrier (TS2=59 kJ mol⁻¹), no barrier for the s‐cis form is computed. This could result from mesomeric effects, but the phenyl group is rotated with respect to the α,β‐unsaturated moiety so that mainly the inductive effect of the phenyl group remains. The size seems to be similar to the effects observed for R¹=methyl. The differences to compound 2 result from steric effects which are mainly present in the s‐trans form. Going from compound 3 to 4 the +I effects should be diminished due to the electron‐withdrawing effects of the chlorine substituents. Such effects are observed mainly for the s‐trans form, for which the barrier of the addition step disappears. Furthermore, the enol and enolate forms become more stable. The steric effects strongly increase in going from compound 4 to 5. The s‐cis form lies even higher in energy, and the barriers of the addition step increase as well as the enolate intermediate. In summary, 5 is expected to have similar reactivity as 3; that is, the advantages gained through the chlorine substituents are lost due to the additional methyl group. This indicates that many of the effects are additive.

Despite these variations, the overall mechanism remains the same for compounds 1–5. In all cases the formation of the thiolate in combination with the addition to the Michael system represents the rate‐determining step. The ketonization process has lower‐lying intermediates and seems to proceed across the enolate, which is considerably lower in energy than the enol cation. This does not appear to be the case for the remaining compounds. For compound 6 the barrier for the addition step is similar to the other systems, but the necessary ketonization process seems to be impossible. The enol is already considerably less stable than the reactants (+55 kJ mol⁻¹), and the enolate is predicted to be instable. The enol cation lies at ∼+100 kJ mol⁻¹ so that a possible ketonization would represent the rate‐determining step. However, test computations performed for the direct E2‐like addition in which the proton donor was placed in the vicinity of C2 indicated considerably lower barriers at ∼60–70 kJ mol⁻¹.29 Hence, for R¹=methoxy our computations indicate a direct addition. This switch in the mechanism is in line with previous experimental findings of Miyata et al.,30 who explained stereospecific nucleophilic additions of thiols to derivatives of α,β‐unsaturated carboxylic acids by a fast protonation of the arising enolate at C2.

A ketonization across the enolate form is also quite unfavorable for compound 7. In this case, however, the electron‐pushing properties of the N,N‐dimethylamine group stabilize the enol cation in such a way that the ketonization should be easily possible. For compound 8 the addition step is also predicted to represent the rate‐determining step, and the ketonization will proceed across the enol cation. Due to its high stability, the enol cation is expected to be formed directly. In general, compound 8 represents an outlier due to its different electronic structure. Compound 9 was characterized in order to investigate, in combination with compound 3, how R³=methyl influences the reactivity. According to our computations this substitution should lower the reactivity because the barriers associated with the 1,4‐addition and the ketonization step become higher. Compounds 10 and 11 were investigated to distinguish experimentally between the reactivity of the s‐cis and s‐trans forms. The computations predict that the s‐cis form (compound 10) reacts considerably faster than the s‐trans form. However, the difference results mainly from the ketonization step; while it should proceed quite rapidly for 10, it should not take place for 11.

The computations point to three different mechanisms, which are depicted in Figure 6. For acrolein (1) the formation of the thiolate is the rate‐determining step, whereas for its addition to the α,β‐unsaturated carbonyl, no additional energy barrier has to be overcome. Compound 2 represents a prototype for a mechanism in which the barrier of the addition step represents the highest point on the total reaction path. This reaction type is found for various alkyl‐substituted compounds. Finally, for compounds such as the α,β‐unsaturated carboxylic ester 6, the ketonization step is so unfavorable that a direct addition is assumed to take place.

Figure 6.

Sketch of the three different mechanisms found for the reaction of α,β‐unsaturated carbonyl compounds with thiols. Prototypical compounds for the different situations are also shown.

Experimental Results

All tested model compounds showed appropriate solubility and stability in the reaction medium. The signals of the C=C double bond could be monitored for each compound without any overlap with signals originating from the thiol or other reaction products, as illustrated by the ¹H NMR spectra of etacrynic acid (13) (Figure 7).

Figure 7.

¹H NMR reference spectrum of etacrynic acid (13) in buffer solution.

For the reaction with 4‐methoxythiophenol the signals of the C=C double bond and the ethyl side chain of etacrynic acid (13) were expected to be affected (Scheme 3).

Scheme 3.

Model reaction of the NMR test series illustrated for etacrynic acid (13).

Data analysis of the time‐dependent NMR experiments showed that after the first spectrum recorded (t=12 min) >60 % of the etacrynic acid had already reacted with the thiol. Within 60 min the turnover was >95 %. Figure 8 shows the decrease in the signals of the C=C double bond and the ethyl group of etacrynic acid (13) as well as of the thiophenol.

Figure 8.

¹H NMR spectra monitoring the reaction of etacrynic acid (13) with 4‐methoxythiophenol.

The decrease of the inhibitor and the formation of the product could be quantified independently by integration of the signals of the ethyl groups. Relevant signals are the triplet of the methyl group of the etacrynic acid side chain (reactant: δ=1.11 ppm; product: δ=0.86 ppm). The product increase and reactant decrease followed an exponential curve as illustrated in Figure 9.

Figure 9.

Progress curves of the addition of 4‐methoxythiophenol to etacrynic acid (13).

Quantification for the thiol was performed in the same way using the decrease in the signal of the aromatic proton (δ=6.75 ppm, Figure 8) in ratio to the sum of the integration values of the singlet of the methoxy group of the thiol reactant and the product. With constant sums of the integration values of the respective signals of reactant and product, it was possible to calculate concentrations of both reactants etacrynic acid [A] and 4‐methoxythiophenol [B]. Considering the initial concentrations [A]₀=1.25 mm and [B]₀=2.50 mm, the second‐order rate constant k ₂ could be calculated with the following equation:(3)

(3)

Plotting ln([A]/[B]) against time (t) resulted in a linear correlation. From the slope, the second‐order rate constant was calculated from ([A]₀−[B]₀)k _2. For etacrynic acid (13) a second‐order rate constant of k ₂=25.6 m ⁻¹ min⁻¹ was determined. For the other compounds this calculation was not possible owing to reaction rates that were too rapid. Therefore only the percentage turnover rates could be obtained.

Regarding the structural features of compounds 12 and 10, these were expected to show a higher reactivity than etacrynic acid (13). This could be confirmed by the NMR experiments. For both compounds the double bond signals had already disappeared completely in the first recorded spectra (t=12 min) of the series. Because reference spectra of 12 and 10 without thiophenol approved solubility and stability of the compounds, this means that addition of the 4‐methoxythiophenol to the Michael system had already reached completion within 12 min.

For compound 9 containing an endo‐double bond, reactivity was similar to that of etacrynic acid (13). After 12 min, a turnover rate of 88 % was detected. The reaction reached near quantitative completion (99 %) after 42 min.

Compound 11 (s‐trans isomer) was chosen for direct comparison with 10 (s‐cis). In both compounds the s‐cis or s‐trans conformation of the Michael system is fixed by a bicyclic structure. However, in contrast to compound 10, no reaction with the thiophenol was detected for 11. Even after two days the starting material was still present in almost full amount. The results of all NMR test series are summarized in Table 3, which also contains data reported by Schultz et al.14

Table 3.

The publisher did not receive permission from the copyright owner to include this object in this version of this product. Please refer either to the publisher's own online version of this product or the printed product where one exists.

Discussion

The data measured in the present work are collected in Table 3 together with some selected values reported by Schultz and colleagues.14 Further experimental data are available from the work of Schüürmann and co‐workers15 and from the studies of Schultz et al.14 An understanding of the relationships between molecular structure and the reactivity against thiols is important for the comprehension of excess toxicity of α,β‐unsaturated carboxylic derivates and the development of inhibitors of cysteine‐containing proteases. To achieve such an understanding a comparison of the experimental and computed data (Table 1) was performed. Furthermore, this comparison provides information about whether the chosen theoretical model captures the main effects that determine the reactivity of α,β‐unsaturated carbonyl compounds.

According to our computations an alkyl substitution at C3 increases the reaction barrier of the addition step to the enol form (+15 kJ mol⁻¹) and also shifts the enolate intermediate to higher energies (+16 kJ mol⁻¹). This is reflected in the measured decrease of the turnover found in going from compound 13 to 12 (Table 3). This trend is also manifested in the work of Schüürmann and co‐workers in two examples.15 Comparing 2‐cyclopentene‐1‐one and 2‐methyl‐2‐cyclopenten‐1‐one, the RC₅₀ values increase from 0.58 to 8.40, and in going from methyl acrylate to methyl methacrylate, the value increases from 0.42 to 74.1. Similar trends are also reported by Schultz et al.14

As a second trend our computations predict that a terminal alkyl substituent (3 vs. 9) will decrease the reactivity of the α,β‐unsaturated carbonyl compound again, as both the barrier of the addition (+27 kJ mol⁻¹) and the relative energy of the enolate (+21 kJ mol⁻¹) increase. This finding explains the decrease in the RC₅₀ values going from 1‐pentene‐3‐one to 4‐hexene‐3‐one.15 A similar effect is also described by Schultz et al.,14 who observed that a methyl substitution at the olefin moiety decreases activity.

The well‐known experience that aldehydes are more reactive than the corresponding ketones is reflected in the difference computed between compounds 1 and 2. It is also reflected in the investigations of Schultz et al.14 Another important finding of our computations is the prediction that derivatives of α,β‐unsaturated carboxylic esters are less reactive, because the ketonization step is so strongly hampered that a direct addition may take place. This is in line with the explanation provided by Miyata et al.30 for stereospecific nucleophilic additions of thiols to derivatives of α,β‐unsaturated carboxylic acids. An experimental proof of the predicted decrease in reactivity is given by Schüürmann and colleagues.15 They found decreasing RC₅₀ values for 1‐pentene‐3‐one (0.09) and methyl acrylate (0.42).

In many cases the computations predict that the s‐cis forms possess higher reactivity than their s‐trans counterparts. Compounds 10 and 11 were synthesized to prove this prediction experimentally. Indeed, as expected, 10 is very reactive. However, for 11 no reaction takes place. The computations explain the astonishing stability of 11 through very high energy barriers for the ketonization step. Because the addition leading to the enol is strongly endothermic, no reaction will take place. That our model can explain even this unexpected behavior indicates that it does indeed capture the main aspects that govern the reactivity of α,β‐unsaturated carbonyl compounds with respect to thiol‐containing enzymes.

Experimental inhibition assays for SARS‐CoV M^pro and related enzymes show that some agents inhibit the thiol‐containing enzymes irreversibly, whereas for others only reversible inhibition is observed. This is surprising, as all agents possess α,β‐unsaturated carbonyl derivatives as electrophilic warheads. For this unexpected finding our investigations provide two possible explanations. In some cases, for example, compound 5 or 9, the reaction energy is estimated to be only ∼30 kJ mol⁻¹. In such cases the reverse reaction is much slower than the forward reaction but may still occur. In other cases the reaction energies are sufficiently high to impede any reverse reaction. But also in such cases a reversible inhibition may occur because complicated multistep inhibition mechanisms must occur to reach the final keto form. For all compounds, base catalysis is necessary since only the thiolate is sufficiently reactive for the addition. In most cases, the second step consists of a 1,4‐addition leading to the enol intermediate. The final keto form is then obtained through a ketonization of the enol form. This ketonization, as shown in previous investigations, is only possible if the necessary proton transfer is catalyzed by an efficient water bridge, for example. Because such catalysis cannot take place in the active site of many enzymes, the reaction might get stuck at the enol intermediate. Alternatively, if no proton donor is available the reaction might become stuck in an enolate intermediate, which is strongly stabilized by available oxyanion holes. In such cases our computations predict considerably smaller reaction energies. Hence the reverse reaction can take place easily, and only reversible inhibition is observed. Particularly for derivatives of α,β‐unsaturated carboxylic acids the enol form is so high in energy that a direct addition to the olefinic double bond becomes more favorable than 1,4‐addition. For direct addition an efficient proton donor is necessary because the reaction proceeds in an E2‐like manner. However, as shown by various Protein Data Bank (PDB) structures, this role could be played by histidine residues, which would also serve as the base in the first step of the overall reaction. Therefore, providing that a histidine residue can serve as an acceptor and donor and that the electronic structure of the warhead steers the reaction toward direct addition, the keto form can be reached without the ketonization process. Only in such cases is an irreversible inhibition found. In other cases the reaction proceeds only up to the enolate form and only reversible inhibition is observed.

According to our computations such a direct addition is more favorable for α,β‐unsaturated carboxylic esters as provided in AG7088.7 For alkyl or phenyl substituents the 1,4‐addition is predicted to be more favorable. In line with this finding, AG7088 performs an irreversible inhibition of the picornavirus 3C protease,7 whereas agents including alkyl or phenyl substituents indeed inhibit the SARS‐CoV M^pro reversibly.12

Summary and Conclusions

The work presented herein involved the development of a simplified model system to describe the reaction of α,β‐unsaturated carbonyl derivates with thiol‐containing enzymes. The computed PES of the addition of thiols to acrolein is only possible with a base‐catalyzed process. It showed that such catalysis is necessary for an efficient addition. The computations can also explain various trends found in chemoassays which were performed to estimate the excess toxicity of this important class of compounds.

Finally, our investigations provide an explanation for why, depending on agent and enzyme, reversible or irreversible inhibition of thiol‐containing active sites are observed despite the fact that all agents possess α,β‐unsaturated carbonyl derivates as warheads.

Irreversible inhibition is observed only if the reaction steers directly to the final keto form. The computations predict this behavior for unsaturated carbonyl esters. If the reaction proceeds across the 1,4‐addition, which is predicted for most derivatives, the reaction will get stuck in the enol or in a stabilized enolate because the necessary ketonization is strongly hindered in the active sites of the proteins. In such cases the inhibition is reversible because the enol is not sufficiently stabilized with respect to the reactant to hinder the reverse reaction.

Experimental Section

Computational methods

The points of the potential energy surfaces were computed with density functional theory (DFT) employing the TURBOMOLE software package31 with standard settings. The PES scans were performed with a resolution of 0.1 Å for the respective grid points. Optimization of the geometrical parameters (except the two characteristic bond distances) that define the PES was performed with the BLYP exchange correlation functional,32 the resolution of identity approximation (RI),33 and the triple zeta basis set TZVP,34 which includes three sizes of contracted functions and further p‐functions to take polarization into account. The electronic energies of all obtained geometries were recalculated by additional single‐point calculations, employing Becke's three‐parameter hybrid functional B3LYP32 and TZVP basis set. As in previous computations, solvent effects were taken into account within the conductor‐like screening model (COSMO),21 which was used for all calculations (geometry optimizations and single‐point calculations). The dielectric constant of the polarizable environment was set to 78.39, which is the corresponding value for water. For cavity radii, standard settings were used. DFT is well known to describe many properties with an excellent cost–benefit value.35 Nevertheless, this is often based on an error compensation that does not work in all cases,36 and indeed in many cases multi‐reference approaches are necessary to obtain reliable potential energy surfaces.37 However, because we are only interested in trends, DFT should be sufficiently accurate for the present work.

Chemoassays

Within the experimental test series, five different model compounds were treated with 4‐methoxythiophenol: etacrynic acid (13, synthesized according to ref. 11), its norethyl derivative (12, for synthesis, see the Supporting Information), trans‐(1‐phenyl)but‐2‐en‐1‐one (9, Sigma–Aldrich), 3‐methylenechroman‐4‐one (10, synthesized according to ref. 38), and 6‐chloro‐4H‐chromen‐4‐one (11, Maybridge). The structures of these compounds are shown in Figure 3.

The choice of the substances reflected the various substitution patterns of the Michael system treated computationally. Reactions of inhibitors 9–13 with the model thiol 4‐methoxythiophenol were performed and followed by ¹H NMR spectroscopy. Due to the aromatic and symmetric structure of the thiol, only few well‐defined signals in ¹H NMR spectra were expected from the aromatic protons (δ>6.7 ppm) as well as from the signal of the methoxy group (δ<3.8 ppm). For both groups an overlap with the characteristic signals of the Michael systems (δ≈5.5–6.5 ppm) of compounds 9–13 could be ruled out.

For the NMR experiments stock solutions of the thiol (SH, 100 mm) and the inhibitor model compounds 9–13 (I, 100 mm) were prepared in [D₆]DMSO. As reaction medium a phosphate buffer (KH₂PO₄/K₂HPO₄, 100 mm, pH 7.6) in D₂O was used. For the reaction, 10 μL inhibitor stock solution, 770 μL phosphate buffer solution, and 20 μL thiol stock solution (SH) were subsequently transferred into an NMR tube and mixed well, reaching a final volume of 800 μL and concentrations of [I]=1.25 mm and [SH]=2.50 mm. With respect to the pK _a value of the thiol and the pH used, the concentrations refer to second‐order reaction conditions.

¹H NMR experiments were performed on a Bruker Avance 400 spectrometer at 400.13 MHz (25 °C, 64 scans per spectra) directly after mixing the reaction partners. The mixing of the reactants was regarded as the starting point of the reaction (t=0 min). Spectra were recorded continuously for 60 min at first, afterward with increasing intervals depending on the reactivity of the reactants. To assure stability of the model compounds during the measurement, reference spectra of a solution of the single model compounds in buffer at the respective concentration were recorded before and afterward.

Supporting information

Detailed facts of importance to specialist readers are published as ”Supporting Information”. Such documents are peer‐reviewed, but not copy‐edited or typeset. They are made available as submitted by the authors.

miscellaneous_information