Ebola—challenge and revival of theoretical epidemiology: Why Extrapolations from early phases of epidemics are problematic

At the beginning of the second half of the 20th century, there was a widespread belief that science and in particular medicine had progressed so far that Nature could be brought under complete control. It seemed that healthcare and pharmacology were in the position to prevent or to cure almost all diseases. In the 1980s, for example, the pharmaceutical industry stopped the search for new antibiotic drugs that would be badly needed nowadays in the light of the universal capabilities of bacteria to develop resistance factors. At about the same time previously unknown or unnoticed virus transmitted infectious human diseases appeared: acquired immunodeficiency syndrome caused by human immunodeficiency virus (HIV), Ebola caused by Ebola virus (EBOV) and four related other strains of filoviridae, as well as severe acquired respiratory syndrome (SARS) brought about by SARS coronavirus. Caused by prions and not by a virus is been bovine spongiform encephalopathy (BSE). Nevertheless, it gave rise to an equally serious new epidemic. These and other cases as well as the consequences of the “antivaccination movement” 1, 2, for example, the recent reoccurrence of pertussis and measles, revived a need of reliable models in epidemiology. In particular, the recent Ebola epidemic starting in December 2013 in West Africa 3 initiated a new boom in theoretical work on infectious disease dynamics 4. In PLoS Currents Outbreaks I counted 27 articles between the first publication on the recent Ebola epidemics on May 02, 2014 until March 09, 2015. In December 2014, researchers became aware that the predictions made 3 months earlier, in Fall 2014, apparently overstated the numbers of cases and deaths. A recent theoretical paper aims at an analysis of the prediction errors and provides suggestions how to make better forecasts 5. In this essay, we shall be concerned with the predictive power of one frequently used model denoted as susceptible‐exposed‐infectious‐removed (SEIR) model, and try to analyze typical general problems of predictions from early stages of exponentially growing systems to the final outcomes of the processes. In the focus are the model inherent limitations of reliabilities and not the lack of information or external problems like insufficient data or the uncertainty about the effectiveness of intervention strategies or countermeasures.

Before considering epidemiological models, we illustrate the problem of predicting the longtime behavior of a process that starts with exponential growth and later on goes into saturation by means of a well‐known simple example: the logistic equation introduced by Pierre‐François Verhulst 6 in 1838. The equation describes growth of a multiplying population in a world of finite resources. The model is formulated in the language of ordinary differential equations and can be solved by the standard analytical techniques of calculus

$$\frac{dN}{dt}\hspace{0.17em}=\hspace{0.17em}r N \left(1 - \hspace{0.17em}\frac{N}{C}\right)\hspace{0.17em};\hspace{1em}N(t)\hspace{0.17em}=\hspace{0.17em}{N}_0\hspace{0.17em}\frac{C}{N_0\hspace{0.17em}+\hspace{0.17em}(C\hspace{0.17em}-\hspace{0.17em}{N}_0)\hspace{0.17em}{e}^{-\hspace{0.17em}r t}}.$$ (1)

Herein, N(t) is the number of multiplying individuals or the population size as a function of time, N ₀ = N(0) is the initial value, r is the growth or Malthus parameter, and C is called the carrying capacity and represents a parameter, which determines the maximum number of individuals that can be sustained by the ecosystem (Figure 1).

Figure 1.

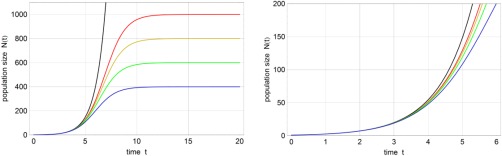
Solution curves of the logistic Eq. (1). Shown is the population size N(t) as a function of time with different carrying capacities C = ∞ (black), 1000 (red), 800 (yellow), 600 (green), and 400 (blue). The black curve evidently represents pure exponential growth. The figure on the r.h.s. is an enlargement of the l.h.s. figure. Further parameters: r = 1 [t ⁻¹] and N(0) = N ₀ = 1.

The initial phase of the process (t < 3) yields practically the same curves for all values of C within the line width. It is straightforward to calculate an approximate expression for N(t) at short times by means of series expansions that has the following two first terms:

$$N(t)\hspace{0.17em}\approx \hspace{0.17em}{N}_0\hspace{0.17em}\left(1\hspace{0.17em}+\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}\frac{N_0}{C}\hspace{0.17em}\right)\hspace{0.17em} r t\hspace{0.17em}--\hspace{0.17em}\hspace{0.17em}\left(1\hspace{0.17em}-\hspace{0.17em}\frac{N_0}{C}\hspace{0.17em}\right)\left(\frac{3}{2}\hspace{0.17em}-\hspace{0.17em}\frac{N_0}{C}\right)\hspace{0.17em}\hspace{0.17em}{r}^2{t}^2\right)\hspace{0.17em}\hspace{1em}$$ (2)

for small t

Equation (2) illustrates well the problem of parameter fitting to data from the initial phase: In cases where N ₀ is small and C is large and N ₀/C << 1, the growth parameter r can be determined from the slope of the linearized growth curve, N(t) ≈ N ₀ + N ₀ r t, as N ₀/C is only a small correction. The determination of the second parameter C is tricky, in particular for small N ₀/C because the first and the second coefficient of the series expansion are needed and the equations for the fit of C are commonly ill‐conditioned. Unfortunately small N ₀ and large C, being tantamount to a few infected individuals—in extreme but not uncommon cases we have N ₀ = 1—and a comparatively large population of susceptible individuals, are almost always the case in the spread of epidemics. For very good reasons, Aaron King et al. 5 emphasize the requirement of highly reliable data and sophisticated high‐level stochastic methods for parameter estimations and potential error predictions from the early phase of an exponentially growing system to a final situation when the process is under control. The problem is very general and not restricted to epidemiology. The politically reasonable but scientifically unacceptable flaw in the predictions of the famous Club of Rome 7 is precisely of the same kind: You cannot extrapolate from the initial phase of an exponentially growing process to the final situation unless additional information is or additional data are available.

The SEIR model of epidemiology is very popular and despite relative simplicity it has interesting dynamical features that are highly relevant for prediction. The model describes infection dynamics in a population of initially susceptible individuals and attributes four different states to the people: S means susceptible to infection, E implies exposed and infected but not yet showing the symptoms and not being infectious, I stands for being infected, showing the symptoms and being infectious, and eventually R stands for the number of individuals being out of the game by either being recovered and immune to further infection or being dead. For population dynamics, the SEIR model can be casted into equations of chemical kinetics:

$$\mathrm{S} + \mathrm{I}\to \mathrm{E} + \mathrm{I}$$ (3a)

$$\mathrm{E}\to \mathrm{I}$$ (3b)

$$\mathrm{I}\to \mathrm{R}$$ (3c)

The rate parameters commonly attributed to the three steps are denoted by β/C, k, and γ. As a matter of fact, the epidemiological mechanism (3) is nothing but a chemical reaction consisting of three consecutive steps, and it can be cast into the differential equation

$$\frac{ds}{dt}\hspace{0.17em}=\hspace{0.17em}-\hspace{0.17em}\frac{\beta }{C}\hspace{0.17em}s \cdot i\hspace{0.17em},\hspace{0.17em}\frac{de}{dt}\hspace{0.17em}=\hspace{0.17em}\frac{\beta }{C}\hspace{0.17em}s \cdot i\hspace{0.17em}-\hspace{0.17em}k \cdot e\hspace{0.17em},\hspace{0.17em}\frac{di}{dt}\hspace{0.17em}=\hspace{0.17em}k \cdot e\hspace{0.17em}-\hspace{0.17em}\gamma \cdot \hspace{0.17em}i\hspace{0.17em},\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\frac{dr}{dt}\hspace{0.17em}=\hspace{0.17em}\gamma \cdot \hspace{0.17em}i\hspace{0.17em}.$$ (4)

Herein, concentrations or numbers of individuals are denoted by [S] = s, [E] = e, [I] = i, [R] = r. Because of the conservation relation, s + i + e + r = C, the model has three independent variables. To take into account intrinsic stochastic effects, the SEIR model can be formulated as a renewal process 4 that is frequently used in theoretical epidemiology 8. To visualize fluctuations, we shall consider here the expectation values embedded in the one‐standard deviation band derived from numerical simulations of the chemical master equation of mechanism (3) 9. The results are shown in Figure 2: As expected the solution curves of the deterministic approach lie within the one‐standard deviation band but do not exactly coincide with the expectation values E(x), x ≡ s,e,i or r—exact coincidence can only be expected for first order or linear processes 10 and, indeed, the step (3a) is corresponding to a bimolecular second order reaction. The SEIR mechanism contains two‐step autocatalysis: S + I → E + I → 2 I resulting from (3a) and (3b). One special property of an autocatalytic system concerns the requirement of a non‐zero concentration of the autocatalyst as no reaction will take place otherwise. In the language of epidemiology this fact is trivial: There is no outbreak without infectious individuals. Autocatalysis gives also rise to a number of features, which are uncommon in conventional chemical kinetics. One property that is relevant for the problem of prediction will be discussed in detail in the next paragraph. It concerns the longtime result, which in chemistry is commonly a single state that does not depend on initial conditions. In case of autocatalysis, however, the final state can be a one‐dimensional (1D) manifold and the particular marginally stable stationary points depend on the initial values of the variables (Figure 3; see also a somewhat humoristic but mathematically serious analysis of the equilibria of epimemiological models and their stability see 11). In the SEIR and as well in the simpler susceptile‐infectious‐recoverd (SIR) model, the final outcome in the sense of the residual “susceptibles,” ${\lim }_{t\to \infty }\hspace{0.17em}S(t)\hspace{0.17em}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}{S}_{\infty }$, is a function of the number of initially infected people expressed by I(0).

Figure 2.

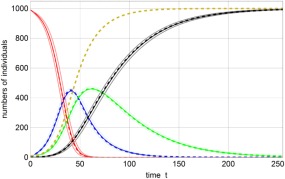
Solution curves of the SEIR model (3). Shown are the numbers of susceptible individuals S(t) (red), exposed individuals E(t) (blue), infectious individuals I(t) (green), and recovered or dead individuals R(t) (black). Expectation values <X(t)> (X ≡ S, E, I, R) are given in full color embedded in one‐standard deviation error bands, <X(t)> ± σ(X(t)), with the limits in light color. The dashed lines refer to the solutions of the ordinary differential equation (ODE) (4), x(t) with x ≡ s, e, i, r, and the yellow dashed curve represents d(t) = i(t) + r(t). The disease in this case affects the entire population. Parameters: N = 1000, β = 0.5, k = 0.05, γ = 0.025, which correspond to a high basic reproductive number of R ₀ = 20. Initial conditions: S(0) = 990, I(0) = 10.

Figure 3.

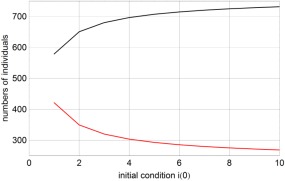
Dependence of the outcome of an epidemic on the number of initially infected individuals. The two curves represent the final number of susceptible and recovered individuals, ${\lim }_{t\to \infty }\hspace{0.17em}s(t)$ (red) and ${\lim }_{t\to \infty }\hspace{0.17em}r(t)$ (black) for different numbers of initially present infectious individuals i(0). The parameters were taken from the 1995 Ebola outbreak in Congo 14: β ₀ = 0.33, β ₁ = 0.09, τ = 100, t _h = 0.71, k = 0.189, and γ = 0.178 with time measured in days. A small population size, N = 1000, was chosen for the purpose of illustration. The critical value of the stationary number of susceptible is ${\overline{s}}_{\text{cr}}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}539.4$.

Next, we perform stationary state analysis of the SEIR model (4) and calculate the longtime solutions $(\overline{s}\hspace{0.17em},\hspace{0.17em}\overline{e}\hspace{0.17em},\hspace{0.17em}\overline{i}\hspace{0.17em},\hspace{0.17em}\overline{r})$ from the equations $\left(\frac{ds}{dt}\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}\frac{de}{dt}\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}\frac{di}{dt}\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}\frac{dr}{dt}\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em}\right)$. The result is not a single stationary state but a 1D manifold of states defined by

$$\overline{e}\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}\overline{i}\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em},\hspace{0.17em}\overline{s}\hspace{0.17em}+\hspace{0.17em}\overline{r}\hspace{0.17em}=\hspace{0.17em}N.$$ (5a)

The number of individuals, which are not infected by the disease is limited by $0\hspace{0.17em}\le \hspace{0.17em}\overline{s}\hspace{0.17em}<\hspace{0.17em}N$. Stability analysis of this 1D line of stationary points by means of the evaluation of the eigenvalues of the Jacobian matrix at the steady states yields three eigenvalues, one is zero and two are real:

$${\lambda }_0\hspace{0.17em}=\hspace{0.17em}0\hspace{0.17em},\hspace{1em}{\lambda }_{ 1,2}\hspace{0.17em}=\hspace{0.17em}\hspace{0.17em}-\frac{1}{2}\hspace{0.17em}\left( \hspace{0.17em}k\hspace{0.17em}+\hspace{0.17em}\gamma \hspace{0.17em}\mp \hspace{0.17em}\sqrt{{(k\hspace{0.17em}-\hspace{0.17em}\gamma )}^2\hspace{0.17em}+\hspace{0.17em}4\beta \hspace{0.17em}k\hspace{0.17em}\overline{s}\hspace{0.17em}}\hspace{0.17em}\right).$$ (5b)

The zero eigenvalue expresses marginal stability and concerns migration along the line of stationary states. The other two eigenvalues are both negative in the range $0\hspace{0.17em}\le \hspace{0.17em}\overline{s}\hspace{0.17em}<\hspace{0.17em}{\overline{s}}_{\text{cr}}$ with ${\overline{s}}_{\text{cr}}\hspace{0.17em}=\hspace{0.17em}\gamma \hspace{0.17em}N/\beta$ and depending on the initial conditions the longtime solution will lie somewhere in this range. An example is shown in Figure 3, the larger the initial number of infected individuals is, the smaller is $\overline{s}$, the number of people that remained unaffected by the epidemic (The parameter values for the calculations are taken from the 1995 Ebola epidemic in Congo 12).

In this context, it is illustrative to mention a result of the SIR model in the simplest version, which does not consider exposed individuals—as said above, S + I → 2 I and I → R with the two rate parameters β and γ. For simplicity, we replace the numbers of individuals by normalized variables s ⇒ s/C, i ⇒ i/C, r ⇒ r/C such that s + i + r = 1. The analysis of the system reveals again a one‐dimensional manifold of stationary points with $\overline{i}\hspace{0.17em}=\hspace{0.17em}0$ and $\overline{s}\hspace{0.17em}+\hspace{0.17em}\overline{r}\hspace{0.17em}=\hspace{0.17em}1.$ Stability analysis yields stable points in the range $0\hspace{0.17em}\le \hspace{0.17em}\overline{s}\hspace{0.17em}<\hspace{0.17em}{\overline{s}}_{\text{cr}}$ and unstable points for ${\overline{s}}_{\text{cr}}\hspace{0.17em}<\hspace{0.17em}\overline{s}\hspace{0.17em}\le \hspace{0.17em}1$, where ${\overline{s}}_{\text{cr}}\hspace{0.17em}=\hspace{0.17em}\gamma /\beta$. In Figure 4, it is shown how the initial ratio of susceptible to recovered or here better immune individuals determines the final number of people that were affected by the epidemic: The more susceptibles are initially present, the smaller is the number of individuals, which remain spared from the disease. Moreover, in the range $0\hspace{0.17em}\le \hspace{0.17em}\overline{s}\hspace{0.17em}<\hspace{0.17em}{\overline{s}}_{\text{cr}}$no epidemic can occur and this has a straightforward consequence for vaccination: If the fraction of immune people, r/(r + s), is above 1 −  ${\overline{s}}_{\text{cr}}$, the population cannot be invaded by the proliferating disease but, of course, the nonvaccinated individual can still be infected. From γ being larger than β follows ${\overline{s}}_{\text{cr}}\hspace{0.17em}>\hspace{0.17em}1$ and the population is stable in the whole range, $0\hspace{0.17em}\le \hspace{0.17em}s\hspace{0.17em}\le \hspace{0.17em}1$, and no outbreak can occur. The fraction of immune people is very hard to know a priori and this implies another uncertainty in modeling.

Figure 4.

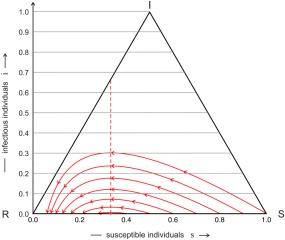
Trajectories of the simple SIR model. Trajectories of individual epidemics, ϑ(t), calculated by the simple SIR model are shown on the unit simplex S ₃, ϑ(t) = {s(t), i(t), r(t)} with s + i + r = 1. Every trajectory starts at t = 0 at the right end and progresses with increasing time to the left end that corresponds to the limit t → ∞. The initial conditions are given by s ₀ = α − δ, i ₀ = δ, and r ₀ = 1 − α, with δ = 0.001 and α = 1.0, 0.9, 0.8, 0.7, 0.6, 0.5, and 0.4, or in other words a population of α susceptible and 1 − α immune individuals is infected by a small fraction of diseased people. The number of infectious individual increases, passes through a maximum at ${\overline{s}}_{\text{cr}}\hspace{0.17em}=\hspace{0.17em}\gamma /\beta$, and for long times converges to lim_{t →∞} i(t) = 0, the disease has disappeared. Parameters: β = 3, γ = 1, and ${\overline{s}}_{\text{cr}}\hspace{0.17em}=\hspace{0.17em}1/3$.

The parameter β determines the rate of infection and may be controlled by successful intervention strategies. In modeling this can be taken into account using the parameter as a function of time 12

$$\beta (t)\hspace{0.17em}=\hspace{0.17em}\left\{\begin{array}{l}{\beta }_0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}t<\hspace{0.17em}\tau \\ {\beta }_1\hspace{0.17em}+\hspace{0.17em}({\beta }_0 - {\beta }_1)\hspace{0.17em}{e}^{- q (t - \tau )}\hspace{0.17em}\text{for} t\ge \hspace{0.17em}\tau \end{array}\right\}.$$ (6)

The parameter τ is the instant when the interventions start and q is the time constant of the implementation of the countermeasures. This approach is particularly appropriate for Ebola in developing countries since β ₁ is there much smaller than β ₀. The quantity, which is the key to modeling the course of an epidemic outbreak, is the basic reproduction number R ₀, which is a measure of the average number of secondary infections caused by a single primary case in a pool of mostly susceptible individuals 12. For R ₀ > 1, the epidemic is spreading whereas R ₀ < 1 implies that the infections are under control. The primary goal of politics and healthcare is to drive β(t) below one. The basic reproduction number in a population before intervention is simply given by R ₀ = β ₀/γ, and the relation to the critical fraction of susceptible individuals is ${\overline{s}}_{\text{cr}}/N$= γ/β ₀ =  $R_0^{-1}$. Although being a flexible and appropriate approximation for real situations, Eq. (6) provides an additional problem for the modelers: It contains three new parameters β _1, τ, and q that have to be derived from data and further information about the course of the epidemic.

Summarizing the current situation in modeling epidemics in view of the recent Ebola outbreak in West Africa we come to the main conclusions: (i) The epidemic provided a unique occasion for testing epidemiological models. (ii) Extrapolations from the phase of exponential growth to the final outcome—as rigorous and careful they might be 13—are very risky because they suffer not only from external uncertainties but also from intrinsic instabilities that are common in processes with autocatalytic steps. Elaborate statistics can substantially improve the situation and reduce the problem if enough and reliable data are available 5. Low robustness of the predictions results also from dynamical systems that are more complex than conventional chemical reaction networks. Simple models can, nevertheless, give important insights and help to understand complex relations.

In Table 1, finally we present some recent data in the light of the estimates of Ebola cases in early 2015 that were calculated to reach from several hundred thousand to even a million and more. Fortunately enough the severeness of the Ebola epidemic in West Africa so far has been overestimated by orders of magnitude. In addition, the dynamics of the epidemic was and is different in the three countries. At the beginning of March Liberia had reported no new case since 42 days but a few single cases were reported after that, whereas in Guinea and Sierra Leone the disease continues at a slowly down going rate.

Table 1.

Recent Updates of Ebola Victims in West Africa. The Data are Taken from International Resources 15, 16

Country		March 15, 2015	Confirmed Last Weeka	March 29, 2015	Confirmed Last Weeka
Guinea	Cases	3389	95	3492	57
	Deaths	2224		2314
Sierra Leone	Cases	11,751	55	11,974	25
	Deaths	3691		3799
Liberia	Cases	9526	0	9712	0
	Deaths	4264		4332
Total	Cases	24, 666	150	25,178	79
	Deaths	10, 179		10,445

^aThe numbers are the confirmed new Ebola cases with the last week before the date.

The recent Ebola outbreak is so well‐documented that it provides a unique opportunity for theoretical epidemiologists to test the existing and to develop new models. The take‐home lesson nevertheless is: whenever one cannot avoid extrapolating a process from the growth phase to saturation, special care in needed because the early data contain little information on the parameters that determine the late behavior. Complex dynamics may enlarge the uncertainties.