Figure 4.

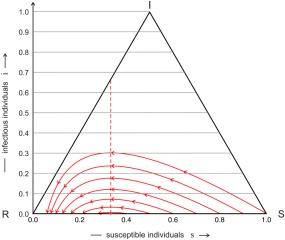
Trajectories of the simple SIR model. Trajectories of individual epidemics, ϑ(t), calculated by the simple SIR model are shown on the unit simplex S ₃, ϑ(t) = {s(t), i(t), r(t)} with s + i + r = 1. Every trajectory starts at t = 0 at the right end and progresses with increasing time to the left end that corresponds to the limit t → ∞. The initial conditions are given by s ₀ = α − δ, i ₀ = δ, and r ₀ = 1 − α, with δ = 0.001 and α = 1.0, 0.9, 0.8, 0.7, 0.6, 0.5, and 0.4, or in other words a population of α susceptible and 1 − α immune individuals is infected by a small fraction of diseased people. The number of infectious individual increases, passes through a maximum at ${\overline{s}}_{\text{cr}}\hspace{0.17em}=\hspace{0.17em}\gamma /\beta$, and for long times converges to lim_{t →∞} i(t) = 0, the disease has disappeared. Parameters: β = 3, γ = 1, and ${\overline{s}}_{\text{cr}}\hspace{0.17em}=\hspace{0.17em}1/3$.