Inverse probability weighting methods for Cox regression with right-truncated data

SUMMARY:

Right-truncated data arise when observations are ascertained retrospectively and only subjects who experience the event of interest by the time of sampling are selected. Such a selection scheme, without adjustment, leads to biased estimation of covariate effects in the Cox proportional hazards model. The existing methods for fitting the Cox model to right-truncated data, which are based on maximization of the likelihood or solving estimating equations with respect to both the baseline hazard function and the covariate effects, are numerically challenging. We consider two alternative simple methods based on inverse probability weighting (IPW) estimating equations, which allow consistent estimation of covariate effects under a positivity assumption and avoid estimation of baseline hazards. We discuss problems of identifiability and consistency that arise when positivity does not hold, and show that although the partial tests for null effects based on these IPW methods can be used in some settings even in the absence of positivity, they are not valid in general. We propose adjusted estimating equations that incorporate the probability of observation, when it is known from external sources, which results in consistent estimation. We compare the methods in simulations and apply them to analyses of HIV latency.

1. Introduction

Right-truncated survival data arise under retrospective sampling of subjects who have experienced the event of interest prior to the time of sampling. This offers an efficient alternative to prospective sampling, and is often used for registry data, from which investigators select all cases reported by a certain time. However, retrospective selection results in a sample with over-representation of shorter lifetimes, which, without adjustment, leads to biased estimation of the effects of factors related to the lifetime distribution. This is because the sampling mechanism distorts the joint distribution of lifetime and risk factors.

One example of right-truncated data is from a study of AIDS cases that resulted from contaminated blood transfusions (Lagakos, Barraj, and de Gruttola, 1988). Of interest was estimation of the distribution of the incubation period for AIDS, i.e., the time between HIV infection and onset of AIDS. However, only those who developed AIDS prior to sampling could be included. Thus, incubation time is right-truncated by the time from infection to ascertainment. The sampling of these data is described in the vignette of the accompanying R package coxrt (Vakulenko-Lagun et al., 2019). The question of primary interest is whether the incubation time depends on the age at HIV infection.

For nonparametric estimation of survival based on right-truncated data, only the conditional distribution of the target lifetime T in the observed support of T can be identified, and the proportion of those who fall in the unobservable region cannot be estimated. Lagakos et al. (1988), Kalbfleisch and Lawless (1989) and Jewell (1990) noted that invoking a parametric assumption for the distribution of T can help to solve this identifiability issue. However, such assumptions are not robust and might result in imprecise estimators, especially if the support of the observed lifetime is considerably truncated compared to the population support of T. Finkelstein, Moore, and Schoenfield (1993) showed that assuming the semi-parametric proportional hazards Cox model is enough to overcome the identifiability problem unless all covariate effects in this model are zero, in which case the Cox model reduces to a nonparametric model. Because of the interpretive appeal of the Cox regression model for survival data, we address inference and estimation based on this model in this paper.

While estimation of the Cox model is straightforward for left-truncated and right-censored data due to the natural alignment of the hazard function and associated risk sets with delayed entry, this is not the case for right-or doubly-truncated data (Mandel et al., 2018). Several approaches have been proposed for fitting the Cox regression to right-truncated data. Finkelstein et al. (1993), Tu, Meng, and Pagano (1993), Alioum and Commenges (1996) and Shen et al. (2017) all used the conditional likelihood given observed truncation times, which is a function of both covariate effects and baseline hazards. Finkelstein et al. (1993) and Alioum and Commenges (1996) maximized the likelihood with respect to both baseline hazard and covariate effects. This interweaving of nuisance parameters with parameters of interest is problematic; if covariate effects are non-zero, then the whole distribution of T can be estimated, while if covariate effects are all zero the setting becomes nonparametric and the identifiability issue arises. In addition, this direct maximization is computationally intensive and unstable, with the number of parameters growing with the sample size, and therefore this approach was recommended mostly for global and partial testing of covariate effects and not for their estimation (Finkelstein et al., 1993; Alioum and Commenges, 1996). Tu et al. (1993) used the expectation-maximization algorithm under the assumption that the support of observed lifetime is the same as the support of the original population variable (i.e.,“positivity”). Shen et al. (2017) assumed positivity as well, and used an iterative procedure for likelihood maximization; their simulation results indicate biased estimation for moderate and high probability of truncation. Shen and Liu (2017) used an unconditional likelihood for doubly-truncated data, but also assumed positivity, which may not hold for right-truncated data.

Kalbfleisch and Lawless (1991) and Gross and Huber-Carol (1992) suggested fitting the model in reverse time, i.e., transforming the times to τ – T for some large constant τ. This approach is attractive as it transforms a right-truncated setting into one that is left-truncated, and a simple risk-set adjustment based on a partial likelihood can be applied, and positivity is not required. However, the parameter estimates do not have interpretations as standard log hazard ratios, which limits the use of this approach to hypothesis testing. Shen et al. (2017) also used the reverse time procedure to fit the linear transformation model. However, they overcame the interpretation problem by expressing martingale estimating equations for reverse time in terms of the forward-time baseline hazard and regression coefficients. Drawbacks of this method are the need to solve simultaneously the equations for both baseline hazard and covariate effects and the requirement of positivity.

In this paper we adapt the inverse probability weighting (IPW) approaches of Mandel et al. (2018) and Rennert and Xie (2018) for doubly-truncated data to Cox regression for right-truncated data. In contrast to other approaches for right-truncated data, we do not need to estimate the baseline hazard. Right truncation, compared to double truncation, enables derivation of the asymptotic properties of estimators via established results (Wang, 1991). However, it also introduces new challenges, as having truncation only from the right side reveals the problem of violation of positivity, which is offset by the additional truncation from the left side under double truncation, and thus has not been noticed. Although the existing methods proposed for double truncation can be used for right-truncated data under positivity, they cannot be applied when positivity is violated.

Our contributions are: (a) comparison of two IPW methods, proposed for doubly-truncated data by Rennert and Xie (2018) and Mandel et al. (2018), in the setting of right truncation; (b) formal derivation of an analytical variance expression for the IPW estimator of Mandel et al. (2018) under right truncation, which is needed for settings in which simple bootstrap confidence intervals fail; (c) development of novel adjusted estimating equations that incorporate external information, when it is available, to correct for violation of the positivity assumption, which is the main obstacle in available computationally tractable regression methods for right-truncated data; (d) a new R-package coxrt (Vakulenko-Lagun et al., 2019) that implements our estimation and sensitivity analysis methods; (e) proof that IPW methods can be used for testing under violation of positivity when covariates are independent.

In Section 2 we present notation and the model, describe the identifiability and consistency problems that arise with right-truncated data, and introduce the positivity assumption that is required for consistent estimation. In Section 3 we describe the IPW estimating equations for the estimation of covariate effects. In Section 4 we present asymptotic properties. In Section 5 we propose a sensitivity analysis for the requisite positivity assumption. In Section 6 we present a simulation study of the IPW methods under violation of positivity and compare methods. In Section 7, we illustrate the methods through analyses of HIV incubation times.

2. Notation, identifiability and a positivity assumption

Denote by T the lifetime of interest in the target population, which starts at an initiating event and ends when the event of interest occurs, and denote by R the the right truncation time, which starts at the initiating event and ends at sampling. Under right truncation, pairs (T, R) are observed only if T < R. It is possible that the lifetimes T are additionally left-censored, but because this is uncommon in retrospective studies, we assume here that T is observed exactly. Finally, denote by Z a vector of covariates. The observed data are n triples $\left(R_i^{*},T_i^{*},Z_i^{*}\right),$ distributed as (R, T, Z) | T < R, where variables without an asterisk denote variables of interest in the target population, i.e., the population of interest. In the AIDS study it is the population of all people who were infected with HIV before treatment was available. We assume that (T, Z) are independent of R, and that the lifetime T in the target population follows the Cox proportional hazards model h(t; z) = h₀(t) exp(βz), where h₀(t) is an arbitrary baseline hazard that is left unspecified, and β is a vector of covariate effects, which is of interest.

In the absence of covariates, the density of T* is

$$f_{T^{*}}(t)=\frac{P(R>t)f_T(t)}{{\int }_0^{\infty }P(R>s)f_T(s)ds},$$ (1)

where f_T(t) is the density of T. Let $\tau =\inf \{t:P(T>t)=0\}\text{and}{r}_{*}=\inf \{r:P(R>r)=0\}$ denote the upper bounds of the supports of T and R, respectively. From (1), $f_{T^{*}}(t)$ is a weighted density of f_T(t), where the weight P(R > t) equals zero for t > r_*. If $\tau ⩽r_{*},F_T(t)=P(T⩽t)$ can be estimated nonparametrically. However, if τ > r_*, we can estimate only the conditional distribution $F_T(t)/F_T\left(r_{*}\right)\text{for}t\in \left[0,r_{*}\right],$ where the constant F_T(r_*) cannot be identified from the observed data (Lagakos et al., 1988). In order to solve this identifiability problem, it is often assumed, sometimes without justification, that F_T(r_*) = 1. We term the assumption F_T(r_*) = 1 the “positivity assumption,” since it means that the weight P(R > t) is positive for any t in the support of the original lifetime T. Given (1), this means that the support of observed T* is the same as the support of the original lifetime T.

The positivity assumption is required for consistent estimation of β in the Cox model using IPW estimating equations and is the cost of computational stability and interpretability. It is similar to the “overlap assumption” that is required for identifiability of a causal effect in the presence of confounders, and requires overlap between the confounder distributions in the treated and control subpopulations (e.g., Petersen et al., 2012). In our setting we do not deal with confounding bias, but rather with right truncation, which is a special case of selection bias. In Section 5 we propose estimating equations that can incorporate external knowledge about the proportion of truncated mass into the estimation, or alternatively, can be used for sensitivity analysis. We also prove that even under violation of positivity, partial testing of covariate effects can be conducted using the IPW methods if the covariates are independent, and in Section 6 we exhibit its invalidity for correlated covariates.

3. Estimation by IPW approaches

Double truncation occurs when a lifetime T_i is observed only if it falls within a subject-specific interval L_i < T_i < R_i Clearly, right truncation is a special case of double truncation with L_i = 0 for all i = 1,..., n. Estimating equations approaches were proposed for fitting the Cox model to doubly-truncated data by Mandel et al. (2018) and Rennert and Xie (2018). Both approaches employ inverse probability weights to correct for bias.

The equation proposed by Mandel et al. (2018) is motivated by Qin and Shen (2010) and is given by

$$U(\beta )=\sum _{i=1}^n\left\{Z_i^{*}-\frac{{\sum }_{j=1}^n{w}_j{Z}_j^{*}\exp \left(\beta Z_j^{*}\right)I\left(T_j^{*}⩾T_i^{*}\right)}{{\sum }_{j=1}^n{w}_j\exp \left(\beta Z_j^{*}\right)I\left(T_j^{*}⩾T_i^{*}\right)}\right\}=0,$$ (2)

where $w_j={\left\{S_R\left(T_j^{*}\right)\right\}}^{-1},S_R(t)=P(R>t)\text{and}I(.)$ is the indicator function. The weight w_j is the inverse of the probability of being sampled given $T=T_j^{*}.$ In practice, we replace w_j with ${\widehat{w}}_j={\left\{{\widehat{S}}_R\left(T_j^{*}\right)\right\}}^{-1}$ in (2) to obtain

$$\tilde{U}(\beta )=\sum _{i=1}^n\left\{Z_i^{*}-\frac{{\sum }_{j=1}^n{\widehat{w}}_j{Z}_j^{*}\exp \left(\beta Z_j^{*}\right)I\left(T_j^{*}⩾T_i^{*}\right)}{{\sum }_{j=1}^n{\widehat{w}}_j\exp \left(\beta Z_j^{*}\right)I\left(T_j^{*}⩾T_i^{*}\right)}\right\}=0,$$ (3)

where ${\widehat{S}}_R(t)$ is the Kaplan-Meier estimator of P(R > t), obtained from treating R* as left-truncated by T*. Under the assumption of independence between R and T, the Kaplan-Meier estimator ${\widehat{S}}_R(r)$ is uniformly consistent for S_R(r) on intervals [0, t] under a condition on the supports of R and T (Woodroofe, 1985, p.165) required for identifiability of S_R(r) on the whole support of R. Otherwise, only the conditional survival function $S_R(r)/S_R\left(T_{(1)}^{*}\right)$ is identifiable for $r>T_{(1)}^{*},\text{where}{T}_{(1)}^{*}=\min \left\{T_1^{*},\dots ,T_n^{*}\right\}.$ This does not present any problem for the IPW approaches, since the estimating equations remain the same whether $w_j=1/S_R\left(T_j^{*}\right)\text{or}{S}_R\left(T_{(1)}^{*}\right)/S_R\left(T_j^{*}\right).$

The estimating equation of Rennert and Xie (2018) is

$$\sum _{i=1}^n{\widehat{w}}_i\left\{Z_i^{*}-\frac{{\sum }_{j=1}^n{\widehat{w}}_j{Z}_j^{*}\exp \left(\beta Z_j^{*}\right)I\left(T_j^{*}⩾T_i^{*}\right)}{{\sum }_{j=1}^n{\widehat{w}}_j\exp \left(\beta Z_j^{*}\right)I\left(T_j^{*}⩾T_i^{*}\right)}\right\}=0.$$ (4)

Equations (3) and (4) are the same, except for the weight ${\widehat{w}}_i$ in the outer sum of (4).

The derivation of (3) begins with the equality

$$E\left(Z^{*}|T^{*}=t\right)=\frac{E_{Z^{*}}\left[Z^{*}\exp \left(\beta Z^{*}\right)P\left(T⩾t|Z^{*}\right)/E\left\{S_R(T)|Z^{*}\right\}\right]}{E_{Z^{*}}\left[\exp \left(\beta Z^{*}\right)P\left(T⩾t|Z^{*}\right)/E\left\{S_R(T)|Z^{*}\right\}\right]},$$

and then replaces $P\left(T⩾t|Z^{*}\right)/E\left\{S_R(T)|Z^{*}\right\}$ with an observed quantity that has the same expectation (under positivity):

$$E_{T^{*}|Z^{*}}\left\{\frac{I\left(T^{*}⩾t\right)}{S_R\left(T^{*}\right)}|Z^{*}=z\right\}=\frac{P(T⩾t|z)}{E\left\{S_R(T)|z\right\}}.$$ (5)

Additional details of the derivation of (3) can be found in Mandel et al. (2018) for doubly-truncated data or in Qin and Shen (2010) for length-biased and right-censored data. The derivation of (4) is motivated from a pseudo-population perspective, which treats each observation as a representative of unsampled observations from the target population and reweights the contributions of the sampled observations to reconstruct an unbiased population. This is similar in spirit to the estimator of Horvitz and Thompson (1952), which is used in survey sampling. For survey survival data, for which the weights are known, (4) was first suggested by Binder (1992). Interestingly, equation (3) can be re-expressed using time-varying weights ${\widehat{sw}}_j\left(T_i^{*}\right)={\widehat{S}}_R\left(T_i^{*}\right)/{\widehat{S}}_R\left(T_j^{*}\right):$

$$\tilde{U}(\beta )=\sum _{i=1}^n{\widehat{sw}}_i\left(T_i^{*}\right)\left\{Z_i^{*}-\frac{{\sum }_{j=1}^n{\widehat{sw}}_j\left(T_i^{*}\right)Z_j^{*}\exp \left(\beta Z_j^{*}\right)I\left(T_j^{*}⩾T_i^{*}\right)}{{\sum }_{j=1}^n{\widehat{sw}}_j\left(T_i^{*}\right)\exp \left(\beta Z_j^{*}\right)I\left(T_j^{*}⩾T_i^{*}\right)}\right\}=0.$$

This reveals that it can be interpreted also in the spirit of a pseudo-population obtained by reweighting each subject’s contribution at time $T_i^{*}$ by a “relative risk” of being selected when surviving $T_i^{*}$ versus $T_i^{*}$ time units. Thus, at each time point $T_i^{*}$, the weights of patients who are still at risk are re-calculated. Clearly, ${\widehat{sw}}_i\left(T_i^{*}\right)=1.$

In summary, both (3) and (4) create unbiased pseudo-populations, but these pseudo-populations are different. The weights in (4) of Rennert and Xie (2018) create a static population, while those of Mandel et al. (2018) create a “dynamic” population. The weights $\widehat{sw}$ are analogous to the stabilized weights introduced in the causal inference literature to correct for confounding bias and dependent censoring (Hernan, Brumback, and Robins, 2000). It was observed there that the stabilized weights both correct for confounding bias and reduce the variance. In Section 6 we show that the same holds in our context of selection bias. Wang (1996) studied the Cox model for length-biased data with no censoring and with a single covariate. Her estimator is obtained by solving estimating equations with a form similar to (4), but with known weights, and she proved that the optimal weight in the outer sum of the estimating equations is one. Our method requires estimation of the weights and enables multiple covariates, hence Wang’s proof does not apply, but her results are consistent with our finding of the superiority of (3) over (4). We use the label IPW-S for the approach based on (3), and IPW-NS for the approach based on (4).

We developed an R package coxrt (Vakulenko-Lagun et al., 2019) for estimation via (3). For estimation of β, coxph.RT uses the standard coxph function (from survival package) with an offset to incorporate weights that reweight the risk set appropriately. The function provides both analytical and bootstrap estimates for the asymptotic variance of $\widehat{\beta }.$ The package can be used for estimation under non-positivity and for sensitivity analyses (Section 5); this is implemented in the package function coxph.RT.a0, which uses the R package BB (Varadhan and Gilbert, 2009).

4. Asymptotic results

The consistency and asymptotic normality of $\widehat{\beta },$ the solution of (3), can be proved using Theorem A.1 in Mandel et al. (2018). However, the requisite uniform consistency and i.i.d. representation of the estimator of selection probability could not be established for doubly-truncated data. For right truncation, we are able to use the results of Wang (1991) to derive the asymptotic distribution of $\widehat{\beta }$ and an explicit expression for its asymptotic variance. The following theorem formally states the asymptotic properties of $\widehat{\beta }$. In addition to the regularity conditions typically required for the Cox model under random sampling, there must be no truncation of the support so that both estimated and true weights are positive in the whole support of T (Condition D-the positivity assumption). Web Appendix A contains the proof and Web Appendix B provides the associated analytical variance estimator.

Theorem 1:

Let β₀ be the true parameter and let $\widehat{\beta }$ be the solution of estimating equation (3). Under the positivity assumption and the standard regularity conditions for the Cox model (see conditions A-E in Web Appendix A), $\Vert \widehat{\beta }-{\beta }_0\Vert \to 0$ in probability and $\sqrt{n}\left(\widehat{\beta }-{\beta }_0\right)$ is asymptotically normal with mean 0 and a covariance matrix ${\Gamma }^{-1}\Sigma {\Gamma }^{-1},$ where $\Gamma \text{and}\Sigma$ are defined in Web Appendix A.

5. Adjustment of IPW methods for violation of positivity

Violation of positivity is common with right-truncated data and it cannot be identified by the observed data (Woodroofe, 1985). In practice, this assumption usually holds if r_* is sufficiently large. Even if the assumption that $P\left(T⩽r_{*}\right)=1$ is not reasonable, there are some options for hypothesis testing and estimation.

5.1. Testing

Interestingly, even when positivity does not hold the IPW estimator is still valid for partial hypothesis testing when the covariates are independent. Following Lin and Wei (1989), a valid test for H₀ : β₁ = 0 based on ${\widehat{\beta }}_1,$ the solution of (3), is available in the absence of positivity if the limit ${\beta }_1^{*}\text{of}{\widehat{\beta }}_1$ is still 0 under H₀.

PROPOSITION 2:

Suppose that Z₁ and Z₂ are independent vectors, and $h\left(t;z_1,z_2\right)=h_0(t)\exp \left({\beta }_1{z}_1+{\beta }_2{z}_2\right).$ Then in the absence of positivity (i.e., r_* < τ) and under Conditions 1 and 2 of Struthers and Kalbfleisch (1986), β₁ = 0 implies ${\beta }_1^{*}=0,$ and thus ${\widehat{\beta }}_1$ provides a valid test for β₁ = 0.

Conditions 1 and 2 from Struthers and Kalbfleisch (1986) are standard regularity conditions for consistency. We prove Proposition 2 in Web appendix C. Our R package coxrt implements the Wald test for testing partial hypotheses of H₀ : β₁ = 0. For dependent covariates and under violation of positivity, this test is not guaranteed to be valid; we illustrate this through an example in Section 6. An immediate corollary of Proposition 2 is that IPW approaches can be used to test global null hypotheses, for both dependent and independent covariates.

5.2. Estimation

For estimation, we propose an adjustment to the estimating equation (2) to accommodate the violation of positivity. This requires knowledge of the amount of truncated mass at one level of Z, possibly vector-valued, e.g., $a_0=P\left(T⩾r_{*}|Z=0\right).$ If a₀ is known and proportional hazards holds, the adjusted estimating equation will yield a consistent estimator of β. When a₀ is unknown, we suggest a sensitivity analysis with estimation of β for an interval of plausible values for a₀. This is particularly useful when this interval is small.

Equation (2) is biased if positivity does not hold as its derivation uses (5), which requires positivity. From the conditional density function of T*,

$$f_{T^{*}|Z^{*}}(t|z)=\frac{S_R(t)f_{T|Z}(t|z)}{E\left\{S_R(T)|Z=z\right\}},$$

it is clear that if the support of T in the population extends beyond that of R then the right tail of the distribution of T is completely unobserved and reweighting the sampled observations will not correct the bias. However, adding c to the left-hand side of (5) leads to an adjustment of (2) for violation of positivity. Our aim is to find c such that

$$E\left\{\frac{I\left(T^{*}⩾t\right)+c}{S_R\left(T^{*}\right)}|Z^{*}=z\right\}=\frac{P(T⩾t|z)}{E\left\{S_R(T)|Z=z\right\}}.$$

Then,

$$\begin{array}{l}E\left\{\frac{I\left(T^{*}⩾t\right)+c}{S_R\left(T^{*}\right)}|Z^{*}=z\right\}={\int }_t^{r_{*}}\frac{1}{S_R(s)}\frac{S_R(s)f_{T|Z}(s|z)}{E\left\{S_R(T)|Z=z\right\}}ds\\ +{\int }_0^{r_{*}}\frac{c}{S_R(s)}\frac{S_R(s)f_{T|Z}(s|z)}{E\left\{S_R(T)|Z=z\right\}}ds\\ =\frac{P(T⩾t|z)-P\left(T⩾r_{*}|z\right)}{E\left\{S_R(T)|Z=z\right\}}+\frac{c\left\{1-P\left(T⩾r_{*}|z\right)\right\}}{E\left\{S_R(T)|Z=z\right\}}.\end{array}$$

When $P\left(T⩾r_{*}|z\right)=0,$ the solution is c = 0. When $P\left(T⩾r_{*}|z\right)>0,c=\frac{P\left(T⩾r_{*}|z\right)}{1-P\left(T⩾r_{*}|z\right)}=\frac{S_T\left(r_{*}|z\right)}{1-S_T\left(r_{*}|z\right)},$ which is the odds of falling to the right of r_* given Z = z. The estimating equation (3), adjusted for non-positivity, is thus given by

$$\sum _{i=1}^n{\widehat{sw}}_i\left(T_i^{*}\right)\left[Z_i^{*}-\frac{{\sum }_{j=1}^n{\widehat{sw}}_j\left(T_i^{*}\right)Z_j^{*}\exp \left(\beta Z_j^{*}\right)\left\{I\left(T_j^{*}⩾T_i^{*}\right)+\frac{S_T\left(r_{*}|Z_j^{*}\right)}{1-S_{T_T}^{*}\left(r_{*}|Z_j\right)}\right\}}{{\sum }_{j=1}^n{\widehat{sw}}_j\left(T_i^{*}\right)\exp \left(\beta Z_j^{*}\right)\left\{I\left(T_j^{*}⩾T_i^{*}\right)+\frac{S_T\left(r_{*}|Z_j^{*}\right)}{1-S_T\left(r_{*}|Z_j^{*}\right)}\right\}}\right]=0.$$ (6)

Under the Cox model, $S_T\left(r_{*}|z\right)=S_T{\left(r_{*}|z=0\right)}^{\exp (\beta z)}=a_0^{\exp (\beta z)},$ so it suffices to know the amount of truncated mass for a single value of z, e.g., z = 0. In this case, (6) is given by

$$IPW-SA:\sum _{i=1}^n{\widehat{sw}}_i\left(T_i^{*}\right)\left[Z_i^{*}-\frac{{\sum }_{j=1}^n{\widehat{sw}}_j\left(T_i^{*}\right)Z_j^{*}\exp \left(\beta Z_j^{*}\right)\left\{I\left(T_j^{*}⩾T_i^{*}\right)+\frac{a_0^{\exp \left(\beta z_j^{*}\right)}}{1-a_0^{\exp \left(\beta Z_j^{*}\right)}}\right\}}{{\sum }_{j=1}^n{\widehat{sw}}_j\left(T_i^{*}\right)\exp \left(\beta Z_j^{*}\right)\left\{I\left(T_j^{*}⩾T_i^{*}\right)+\frac{a_0^{\exp \left(\beta Z_j^{*}\right)}}{1-a_0^{\exp \left(\beta Z_j^{*}\right)}}\right\}}\right]=0.$$ (7)

Sensitivity analysis involves estimation of β under different values of a₀. The estimating equation (4) can be adjusted for non-positivity using the same approach:

$$IPW-NSA:\sum _{i=1}^n{\widehat{w}}_i\left[Z_i^{*}-\frac{{\sum }_{j=1}^n{\widehat{w}}_j{Z}_j^{*}\exp \left(\beta Z_j^{*}\right)\left\{I\left(T_j^{*}⩾T_i^{*}\right)+\frac{a_0^{\exp \left(\beta Z_j^{*}\right)}}{1-a_0^{\exp \left(\beta Z_j^{*}\right)}}\right\}}{{\sum }_{j=1}^n{\widehat{w}}_j\exp \left(\beta Z_j^{*}\right)\left\{I\left(T_j^{*}⩾T_i^{*}\right)+\frac{a_0^{\exp \left(\beta Z_j^{*}\right)}}{1-a_0^{\exp \left(\beta Z_j^{*}\right)}}\right\}}\right]=0.$$ (8)

Finally, we note that the adjusted estimating equations (7) and (8) may not have solutions if the proportional hazards assumption does not hold, or if the true a₀ = 0 and we insert non-null a₀. It is impossible to distinguish between these cases using only truncated data.

6. Simulations

6.1. Comparisons among Shen et al. (2017), IPW-S, IPW-NS

Our first simulation experiment (Table 1) compares the two IPW estimators and the conditional maximum likelihood estimator (cMLE) and the estimating equation (EE) estimator proposed by Shen et al. (2017) using the settings from their Table 4 and including updated results received from the authors via personal communication. In particular, we assumed that $T|Z~Exp\left(e^{{\beta }_1{Z}_1+{\beta }_2{Z}_2}\right),R~Exp(\theta ),$ where θ = (2.5, 7.5,15) corresponds to three levels of truncation, 16%, 32% and 45%, P(Z₁ = i) = 0.25 for i = 1, 2, 3, 4, and Z₂ ~ Bern(0.5). As seen in Table 1, Shen’s cMLE is heavily biased. We thus do not consider it further. We were not able to include other methods in this comparison because software for their implementation is not available.

Table 1.

Comparison of approaches by Shen et al. (2016) with the IPW methods, using equations (3) and (4), and the unadjusted Cox regression that ignores truncation (UNADJ). bias, SD and SE are, respectively, the bias and, standard deviation of $\widehat{\beta },$ average of asymptotic estimators of $SE(\widehat{\beta }),$ where SE for IPW-S is an analytical estimate, and for IPW-NS is a bootstrap estimator of $SE(\widehat{\beta })$ based on bootstrap distribution with 500 replications. CP is a coverage probability of 95% confidence interval using normal approximation and SE for IPW-S, and it is a coverage probability of 95% confidence interval $\left({\widehat{\beta }}_{0.025}^{bs},{\widehat{\beta }}_{0.925}^{bs}\right)$ based on bootstrap distribution with 500 replications for IPW-NS. MSE is an empirical mean squared error. r₍₅₀₀₎ is an n^th-order statistic of $R_1^{*},\dots ,R_n^{*}$ in the samples with n = 500, ${\overline{r}}_{(500)}$ is an average of r₍₅₀₀₎ over 1000 samples. Results are based on 1000 replications.

		β1 = 1					β2 = 1
Light truncation: R ~ Exp(2.5), P(T > R) = 0.16, avg P(T > r(500)) = 0.0001, ${\overline{r}}_{(500)}$ = 2.79
	n	$\mathrm{bias}\left({\widehat{\beta }}_1\right)$	SD	SE	MSE	CP	$\mathrm{bias}\left({\widehat{\beta }}_2\right)$	SD	SE	MSE	CP
Shen-EE	100	−0.023	0.205	0.192	0.043	0.940	−0.025	0.404	0.381	0.164	0.939
	300	−0.015	0.116	0.107	0.014	0.943	−0.029	0.249	0.238	0.063	0.943
	500	−0.009	0.073	0.069	0.005	0.950	−0.011	0.178	0.173	0.032	0.946
Shen-cMLE	100	−0.093	0.116	0.108	0.022	0.937	−0.091	0.239	0.225	0.065	0.936
	300	−0.051	0.083	0.078	0.009	0.941	−0.051	0.151	0.143	0.025	0.942
	500	−0.012	0.053	0.050	0.003	0.947	−0.044	0.108	0.102	0.014	0.947
IPW-S	100	0.017	0.145	0.156	0.021	0.960	0.013	0.267	0.256	0.071	0.946
	300	0.000	0.080	0.090	0.006	0.976	0.000	0.153	0.150	0.023	0.942
	500	0.003	0.063	0.072	0.004	0.980	−0.003	0.120	0.118	0.014	0.950
IPW-NS	100	0.015	0.149	0.151	0.023	0.938	0.010	0.284	0.277	0.081	0.941
	300	0.000	0.084	0.085	0.007	0.951	0.001	0.169	0.158	0.029	0.935
	500	0.002	0.068	0.067	0.005	0.953	−0.002	0.136	0.125	0.018	0.933
UNADJ	500	−0.125	0.052	0.054	0.018	0.363	−0.134	0.096	0.096	0.027	0.699
Moderate truncation: R ~ Exp(7.5), P(T > R) = 0.32, avg P(T > r(500)) = 0 01, ${\overline{\mathrm{r}}}_{(500)}$ = 0.96
	n	$\mathrm{bias}\left({\widehat{\beta }}_1\right)$	SD	SE	MSE	CP	$\mathrm{bias}\left({\widehat{\beta }}_2\right)$	SD	SE	MSE	CP
Shen-EE	100	−0.033	0.227	0.214	0.053	0.938	−0.073	0.473	0.443	0.229	0.937
	300	−0.028	0.157	0.147	0.025	0.941	−0.051	0.291	0.274	0.087	0.941
	500	−0.023	0.106	0.097	0.012	0.944	−0.017	0.216	0.207	0.047	0.944
Shen-cMLE	100	−0.159	0.107	0.099	0.037	0.575	−0.163	0.246	0.218	0.087	0.826
	300	−0.114	0.086	0.072	0.020	0.658	−0.125	0.168	0.159	0.044	0.852
	500	−0.085	0.055	0.052	0.010	0.714	−0.096	0.112	0.106	0.022	0.883
IPW-S	100	−0.013	0.182	0.227	0.033	0.975	−0.026	0.317	0.323	0.101	0.948
	300	−0.019	0.113	0.136	0.013	0.977	−0.027	0.208	0.198	0.044	0.943
	500	−0.016	0.094	0.110	0.009	0.978	−0.029	0.167	0.159	0.029	0.945
IPW-NS	100	−0.027	0.205	0.181	0.043	0.938	−0.044	0.394	0.353	0.157	0.934
	300	−0.030	0.134	0.112	0.019	0.902	−0.040	0.286	0.228	0.084	0.910
	500	−0.029	0.116	0.092	0.014	0.892	−0.062	0.240	0.191	0.059	0.911
UNADJ	500	−0.259	0.052	0.053	0.070	0.003	−0.253	0.095	0.096	0.073	0.267
Heavy truncation: R ~ Exp (15), P(T > R) = 0.45, avg P(T > r(500)) = 0.04, ${\overline{\mathrm{r}}}_{(500)}$ = 0.49
	n	$\mathrm{bias}\left({\widehat{\beta }}_1\right)$	SD	SE	MSE	CP	$\mathrm{bias}\left({\widehat{\beta }}_2\right)$	SD	SE	MSE	CP
Shen-EE	100	−0.078	0.272	0.254	0.080	0.935	−0.085	0.519	0.487	0.277	0.935
	300	−0.034	0.185	0.174	0.035	0.939	−0.042	0.348	0.332	0.123	0.939
	500	−0.025	0.157	0.151	0.025	0.942	−0.036	0.287	0.271	0.084	0.942
Shen-cMLE	100	−0.181	0.117	0.109	0.046	0.285	−0.194	0.268	0.252	0.109	0.720
	300	−0.146	0.091	0.086	0.030	0.376	−0.152	0.176	0.164	0.054	0.765
	500	−0.107	0.068	0.064	0.016	0.442	−0.116	0.135	0.129	0.032	0.817
IPW-S	100	−0.076	0.208	0.305	0.049	0.970	−0.068	0.367	0.412	0.140	0.949
	300	−0.056	0.140	0.205	0.023	0.965	−0.060	0.242	0.280	0.062	0.949
	500	−0.045	0.124	0.184	0.017	0.960	−0.060	0.201	0.250	0.044	0.952
IPW-NS	100	−0.106	0.240	0.208	0.069	0.874	−0.103	0.480	0.407	0.241	0.912
	300	−0.086	0.173	0.138	0.037	0.834	−0.091	0.367	0.285	0.143	0.905
	500	−0.074	0.160	0.117	0.031	0.811	−0.096	0.334	0.249	0.120	0.888
UNADJ	500	−0.370	0.051	0.053	0.140	0.000	−0.343	0.092	0.096	0.126	0.048

Although theoretically this setting does not pose a problem of positivity, as both T and R have the same supports, in practice, heavier exponential truncation comes together with a near-zero chance of sampling longer lifetimes. For IPW methods, this translates into heavy weights. Although they are justifiable since they aim to compensate for the truncated observations, not every IPW estimator is robust to such a setting, and it is therefore important to examine the stability of the estimators in this scenario.

Comparison of IPW methods.

Overall, with heavier truncation, both IPW methods exhibit a slight bias that decreases with larger sample size. As expected (Robins, Hernan, and Brumback, 2000), large variability in selection probabilities, $S_R\left(T_j^{*}\right),$ may yield very large weights for a few subjects who will then have a large influence on the results. Fortunately, the use of stabilized weights can mitigate the instability problem, and reduce both bias and variance. For example, under heavy truncation, the relative efficiency of IPW-S to IPW-NS for β₂, defined as the ratio of mean squared errors (MSE), is 0.120/0.044 = 2.7 (for n = 500).

Stabilization of weights cannot fully remove the instability of this setting, in which the longer lifetimes are only rarely sampled. This is reflected in the upward bias of the analytical standard error (SE_a) of IPW-S. Nonetheless, the confidence intervals based on SE_a of IPW-S and normal approximation have coverage probabilities that are slightly conservative for β₁ and are very close to the nominal level for β₂. The percentile bootstrap-based confidence intervals result in low coverage probabilities (see Table 1 for IPW-NS and Web Table 2 for IPW-S) for both β₁ and β2, and therefore are not recommended for use.

Table 2.

An example showing that IPW-S approach, in general, cannot be used for partial testing when covariates are correlated and under violation of positivity. UNADJ - the naive use of the Cox regression that ignores truncation. The correlated covariates are $Z_1~N(0,1),P\left(Z_2=0|Z_1<0\right)=2/3=P\left(Z_2=1|Z_1>0\right).bias(\widehat{\beta })$ is the bias of estimates $\widehat{\beta }.$ SD is defined as in Table 1. SE_a is the analytical estimate of SE. size is the size of 0.05% test for H₀ : β₂ = 0 based on normal approximation and SE_a. The results are based on 1000 replications. *₋ results for IPW-SA are based on 200 replications. r₍₁₀₀₀₎ is an n^th-order statistic of $R_1^{*},\dots ,R_n^{*}$ in the samples with n = 1000.

	β1 = 2				β2 = 0
No violation of positivity assumption: R ~ Gamma(1.4, 0.27), P(T > R) = 0.15, average P(T > r(1000)) = 0.0005
	n	$\mathrm{bias}\left({\widehat{\beta }}_1\right)$	SD	SEa	$\mathrm{bias}\left({\widehat{\beta }}_2\right)$	SD	SEa	size
IPW-S	100	0.029	0.218	0.209	0.008	0.244	0.227	0.072
	300	0.013	0.115	0.116	−0.001	0.134	0.130	0.048
	500	0.010	0.092	0.090	0.004	0.107	0.101	0.062
	1000	0.001	0.065	0.064	−0.001	0.070	0.072	0.048
UNADJ	1000	−0.130	0.061	0.059	0.000	0.065	0.066	0.042
Light violation of positivity assumption: R ~ Unif[0, 1.5], P(T > R) = 0.562, average P(T > r(1000)) = 0.28, a0 = 0.11
	n	$\mathrm{bias}\left({\widehat{\beta }}_1\right)$	SD	SEa	$\mathrm{bias}\left({\widehat{\beta }}_2\right)$	SD	SEa	size
IPW-S	100	−0.263	0.246	0.225	−0.054	0.323	0.300	0.063
	300	−0.277	0.137	0.133	−0.046	0.201	0.189	0.069
	500	−0.284	0.108	0.104	−0.052	0.151	0.149	0.060
	1000	−0.286	0.080	0.076	−0.050	0.123	0.122	0.101
UNADJ	1000	−0.609	0.057	0.058	−0.063	0.074	0.068	0.173
Heavy violation of positivity assumption: R ~ Unif [0, 0.8], P(T > R) = 0.73, P(T > r(1000)) = 0.49, a0 = 0.527
	n	$\mathrm{bias}\left({\widehat{\beta }}_1\right)$	SD	SEa	$\mathrm{bias}\left({\widehat{\beta }}_2\right)$	SD	SEa	size
IPW-S	100	−0.539	0.274	0.287	−0.083	0.381	0.400	0.063
	300	−0.545	0.158	0.160	−0.086	0.233	0.223	0.065
	500	−0.554	0.124	0.133	−0.077	0.195	0.180	0.084
	1000	−0.551	0.091	0.092	−0.078	0.143	0.135	0.100
UNADJ	1000	−0.911	0.056	0.057	−0.070	0.071	0.069	0.176
*Under heavy violation of positivity using true a0 = 0.527
	n	$\mathrm{bias}\left({\widehat{\beta }}_1\right)$	SD		$\mathrm{bias}\left({\widehat{\beta }}_2\right)$	SD
IPW-SA	100	0.023	0.297		−0.055	0.430
	300	0.003	0.148		−0.040	0.272
	500	0.009	0.124		0.001	0.216
	1000	0.003	0.087		0.001	0.164

Comparison of Shen’s EE to IPW-S.

We compare Shen’s EE method to IPW-S since it is more efficient than IPW-NS. Over all three settings of truncation, IPW-S has lower empirical standard deviation (SD) and MSE than Shen’s EE method. For example, for light truncation and n = 100, the SD of IPW-S is 1.5 times lower than that of Shen’s EE method, and on the basis of MSEs, IPW-S is twice as efficient as Shen’s EE approach. Similar comparisons are observed for heavy truncation and n = 100.

In summary, the IPW-S approach exhibits the best performance in this simulation setting, which is challenging due to its finite sample near non-positivity. A simulation that compares IPW-S to IPW-NS in a stable scenario with positivity and no heavy weights is reported in Web Appendix D. In that setting, both IPW methods are unbiased, but IPW-S has lower variance and is approximately 1–2 times more efficient than IPW-NS. This confirms the superiority of IPW-S.

6.2. Simulations with non-positivity and correlated covariates

In Web Appendix C, we report results of a simulation that demonstrates that IPW-S can be used for testing in the absence of positivity in some cases that do not satisfy Proposition 2. However, in general, IPW-S cannot be used for testing when positivity does not hold and covariates are correlated. In this simulation (Table 2), lifetimes T followed Weibull proportional hazards regression $h(t;z)=(\kappa /\rho ){(t/\rho )}^{\kappa -1}\exp (\beta z)$ with shape parameter κ = 2 and scale parameter ρ =1, (β₁, β₂) = (2, 0), and covariates Z₁ ~ N(0,1) and $P\left(Z_2=0|Z_1<0\right)=2/3=P\left(Z_2=1|Z_1>0\right).$ Truncation times R were simulated from a Gamma distribution with shape=1.4 and scale=0.27 for the scenario with positivity, from Unif [0,1.5] for the scenario with light violation of positivity, and from Unif [0,0.8] for heavy violation of positivity. Overall, in this setting of correlated covariates, the greater the violation of positivity is, the larger the bias in $\widehat{{\beta }_1}\text{and}\widehat{{\beta }_2},$ which results in an inflated size of the test β₂ = 0. We also examined the performance of adjusted estimating equations IPW-SA under heavy violation of positivity when we plugged in the true value of a₀. As seen in the bottom of Table 2, the estimators of β₁ and β₂ are essentially unbiased.

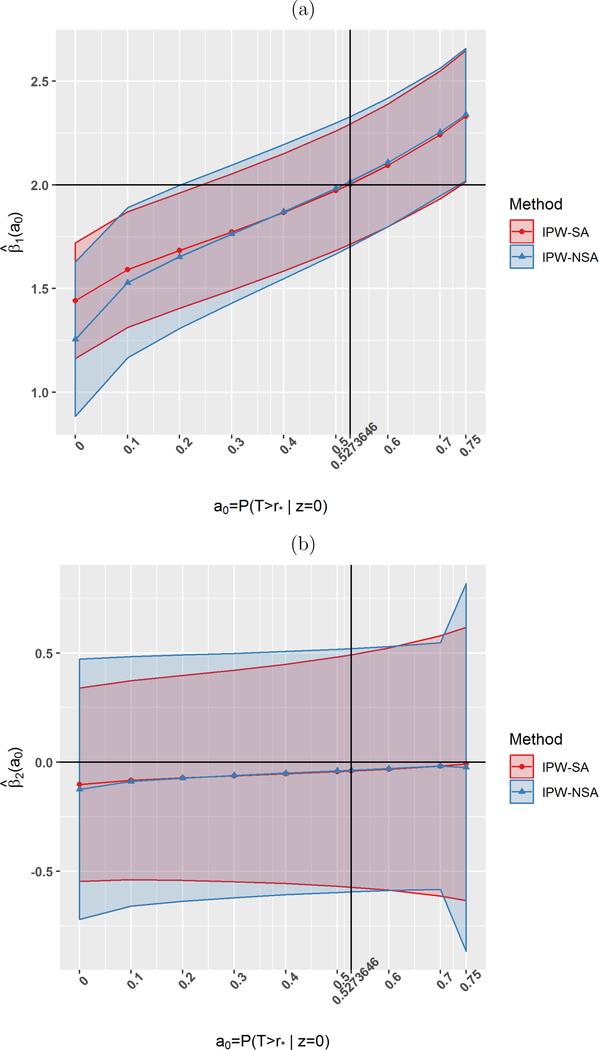
Next, we conducted simulations of our proposed sensitivity analysis under the setting of heavy violation of positivity. Figure 1 summarizes the results. For a generated sample, we estimated β₁ and β₂ for each hypothesized value of a₀ by solving equations IPW-SA and IPW-NSA. Figure 1 displays 95% confidence envelopes for β₁ and β₂ based on 200 repetitions. For the largest values of a₀ there were seven instances of non-convergence; these were excluded from the analyses. Figure 1 indicates that IPW-SA is less biased than IPW-NSA for β₁ for $a_0⩽0.3\text{and}\text{for}{\beta }_2\text{for}{a}_0⩽0.1,$ and both estimators exhibit similar bias for other values of a₀. For the true value of a₀ = 0.527, both IPW-SA and IPW-NSA yield unbiased estimators of β₁ and for β₂ for larger n (bottom of Table 2). The sensitivity analysis presented in Figure 1 is useful if something is known about a₀. For example, if it is known that a₀ is between 0.3 and 0.6, it can be concluded with 95% confidence that β₁ lies between 1.5 and 2.3. IPW-SA is slightly more efficient than IPW-NSA over the whole range of a₀.

Figure 1.

Simulations for sensitivity analysis under violation of positivity assumption with true value of $a_0=S_T\left(r_{*}|z_1=0,z_2=0\right)=\mathrm{0.527.}$ Based on 200 replications, sample size n = 300. This figure appears in color in the electronic version of this article, and any mention of color refers to that version.

7. AIDS data analysis

The data set on AIDS patients who were infected with HIV by contaminated blood transfusions is a classic example of right-truncated data (e.g., Wang, 1989, and the R-package gss). The data, collected by the Centers of Disease Control (CDC), include 295 patients who received transfusions and developed AIDS by June 30, 1986, the time of data extraction. The time of interest, T, is the incubation period of AIDS. The truncation time, R, is defined as the time between HIV infection and June 30, 1986. This data set has been used to exemplify right-truncated data by many authors (e.g., Lagakos et al., 1988; Kalbfleisch and Lawless, 1989; Wang, 1989; Alioum and Commenges, 1996; Shen et al., 2017). In fact, as pointed to us by a reviewer and noticed by Bilker and Wang (1996), the data are also left-truncated by the time from HIV infection to 1982, since AIDS was unknown prior to that time.

For comparison with Shen et al. (2017), which treats the data as right-truncated, we do so as well, and report our results in Section E of the Supporting Information. Our findings are similar to those of Shen et al. (2017). In order to illustrate our approach for truly right-truncated data, we used only those AIDS cases whose HIV infection occurred in 1983 or later; this ensures that the data are not subject to left truncation due to misdiagnosis of AIDS prior to 1982. This subset includes 116 subjects, of whom 22 were four years of age or younger and 58 were 60 or older. For the analysis, we replaced T = 0 with T = 0.5 for one subject, as done by Kalbfleisch and Lawless (1989). The maximum value of R in the sample is 3.4 years, whereas the median value of T, the AIDS induction period, is approximately 10 years (Alioum and Commenges, 1996). This implies that the positivity assumption does not hold for this data set. Due to non-positivity, we cannot estimate the probability of truncation, i.e., P(T > R).

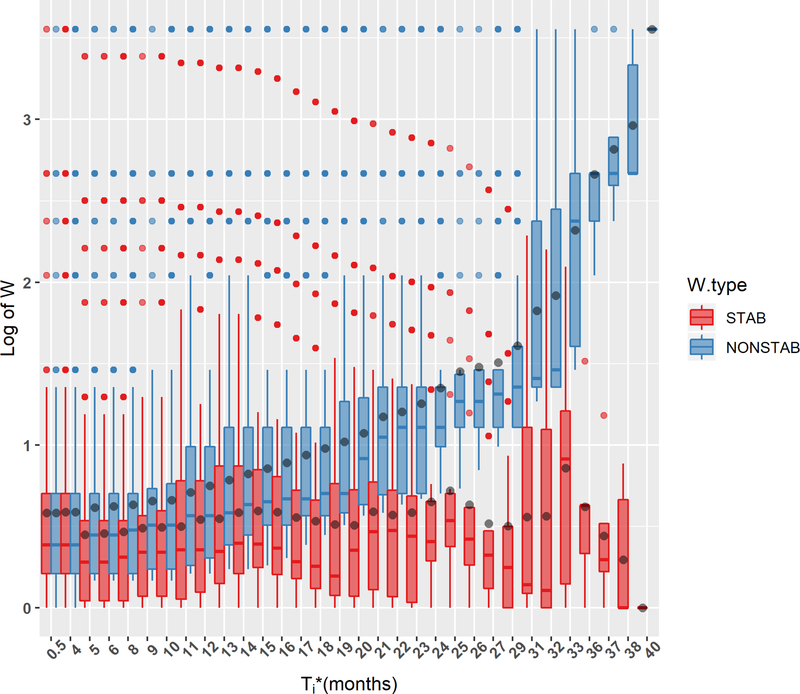
Figure 2 displays the distributions of weights as a function of time, for subjects who are still at risk at the given times. Since the weights are constructed from $S_R(.),$ a monotonically decreasing function, it follows that $1⩽{\widehat{sw}}_j(t)⩽{\widehat{w}}_j$ for all j and any t and that use of ${\widehat{sw}}_j$ versus ${\widehat{w}}_j$ can only improve stability. We observe that:

Figure 2.

Comparison of distributions of stabilized to nonstabilized weights for the right-truncated AIDS data set (based on 116 observations). The distributions of weights for patients who are at risk at selected time points $T_i^{*},$ are summarized through boxplots. Each box shows the mean (black dot), median (middle horizontal line) and quartiles (horizontal borders of a box). Vertical lines extend to the most extreme observations that do not exceed 1.5×IQR. More extreme observations that lie beyond 1.5×IQR are shown individually. This figure appears in color in the electronic version of this article, and any mention of color refers to that version.

1. The nonstabilized weights grow on average with time and shift toward the maximum weight observed in a sample, whereas the stabilized weights do not change on average over time.

2. While the maximum nonstabilized weights remain constant over time and influence estimation of the at-risk quantities (the inner sums in the estimating equations) during the whole time period, the most extreme stabilized weights decrease over time.

Both IPW methods require that R be independent of both T and Z. We did not detect dependence between R and T using the conditional Kendall’s tau test (Tsai, 1990) (τ = 0.07, p = 0.21). The covariates, Z, in this example are three age-at-infection categories as defined by Shen et al. (2017): 4 years of age or younger, older than 4 and 59 or younger, and older than 59 (the reference category). We tested independence between R and Z by fitting a Cox regression model to left-truncated R*. The estimated effect of $Z_1=\text{I}(\text{age}⩽4)$ is −0.15 (p = 0.53) and that of $Z_2=\text{I}(4<\text{age}⩽59)$ is −0.12 (p = 0.58). The results of the two IPW methods are shown in Table 3 and are similar. The hazards of developing AIDS for the youngest age group are more than 3 times than that of the oldest group. Under assumed positivity, IPW-S and IPW-NS behaved similarly and resulted in almost identical point and SE estimates. The analytical SE estimates for IPW-S and their bootstrap counterparts are similar in this example. We also analyzed the data ignoring the right truncation. This naive analysis considerably underestimates the effect of age and reinforces the importance of recognizing and adjusting for truncation.

Table 3.

Analysis of the right-truncated AIDS data based on 116 observations, assuming positivity. UNADJ - the naive use of the Cox regression that ignores truncation. SE_a is the analytical estimate of SE, SE_bs is a bootstrap-based estimate of SE, pvalue is calculated using normal approximation and SE_a, and pvalue_bs uses bootstrap distribution based on 1000 bootstrap replications.

results for 2 age indicators in the model
	covariate	$\widehat{\beta }$	SEa	SEbs	pvalue	pvaluebs
IPW-S	⩽ 4y	1.32	0.45	0.49	0.003	0.007
	4 – 59y	1.10	0.42	0.47	0.008	0.019
IPW-NS	⩽ 4y	1.33		0.49		0.007
	4 – 59y	1.15		0.49		0.018
UNADJ	⩽ 4y	0.71	0.28		0.010
	4 – 59y	0.55	0.21		0.009
results for 1 age indicator in the model
	covariate	$\widehat{\beta }$	SEa	SEbs	pvalue	pvaluebs
IPW-S	⩽ 59y	1.18	0.38	0.41	0.002	0.005
IPW-NS	⩽ 59y	1.21		0.43		0.006
UNADJ	⩽ 59y	0.60	0.19		0.001

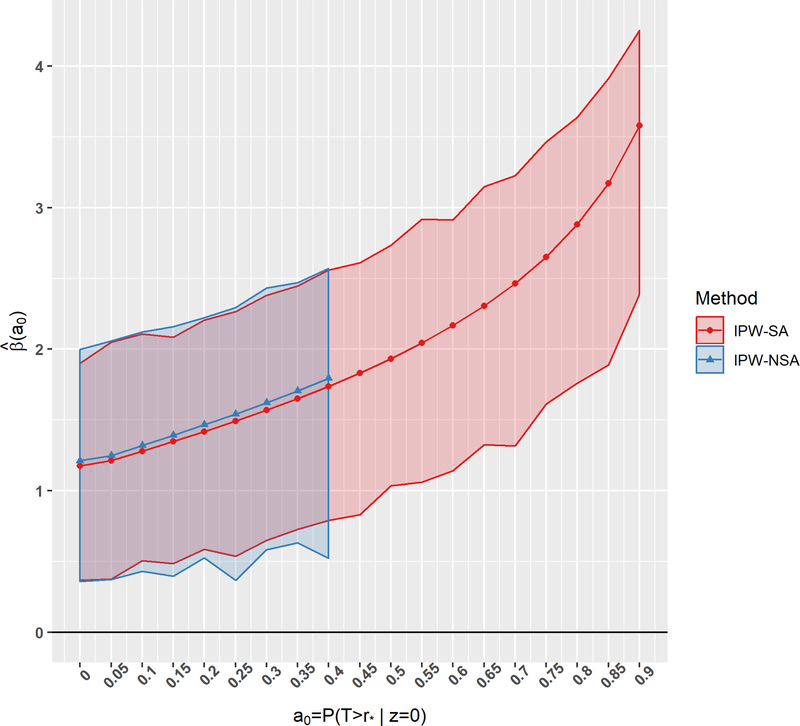
Since the magnitudes of the effects of Z₁ and Z₂ are similar under positivity (Table 3) and non-positivity (not shown), we reanalyzed the data using one age indicator $Z=\text{I}(\text{age}⩽\text{59)}$ (bottom of Table 3). We conducted sensitivity analyses of the positivity assumption for both IPW-SA and IPW-NSA (Figure 3). Equation IPW-NSA, while finding the point estimate, converged successfully only for $a_0⩽0.4,$ and for larger a₀ had numerous instances of divergence (Web Table 4). In contrast, equation IPW-SA converged successfully for all a₀ and had no divergence issues in bootstrap samples even for the extreme values of a₀ (Web Table 4). Based on IPW-SA, there is a large and significant effect of age $(⩽59\text{y}\text{vs}>59\text{y});\widehat{\beta }$ varies from 1.18 (95% CI is [0.36, 1.90]) for a₀ = 0 to 3.17 (95% CI is [1.89, 3.91]) for a₀ = 0.85.

Figure 3.

Sensitivity analysis for AIDS data based on 116 observations, with only one indicator of age: $z_1=\text{I}(\text{age}⩽59).$ The 95% confidence envelope is based on 1000 bootstrap replications. This figure appears in color in the electronic version of this article, and any mention of color refers to that version.

8. Discussion

We have considered two IPW methods for estimation of covariate effects under right truncation in the framework of the Cox model, which avoid estimation of baseline hazard. The stabilized weight version, IPW-S, demonstrated the best performance among all the existing methods for right-truncated data. This superiority, relative to all IPW methods, is theoretically proven by Wang (1996) in a similar setting of weighted estimating equations with known weights and a single covariate. We derived novel adjusted estimating equations IPW-SA to deal with violation of the requisite positivity condition. We derived an analytical variance formula, whose counterpart in the setting of double truncation is intractable. It offers an alternative to the simple bootstrap, which may fail under non-positivity and heavy truncation. To enable implementation of our methods, we developed the R package coxrt. For the Cox model, an alternative approach can be incorporation of knowledge on a₀ into the expectation-maximization procedure suggested by Tu et al. (1993).

The proposed methodology relies on independence between R and (T, Z). When T and R are independent only conditionally on Z, or when R depends on the covariates Z, the weights in (3) and (4) involve P(R > t | Z = z), which requires modeling for estimation. For example, the weight ${\widehat{sw}}_j\left(T_i^{*}\right)$ needs to be modified to, $\frac{{\widehat{S}}_R\left(T_i^{*},Z_j^{*}\right)}{{\widehat{S}}_R\left(T_j^{*},Z_j^{*}\right)},\text{where}{\widehat{S}}_R(t,z)=\widehat{P}(R>t|Z=z)$ is derived from a regression model for R* as left-truncated by T*. This is a topic for future research.

Regarding the assumption of proportional hazards, we hypothesize that if positivity holds, we can test this assumption using standard diagnostic tools developed for non-truncated survival data. In the absence of positivity, the proportional hazards assumption in the population cannot be tested using the observed data. In this case we can detect for violation of proportional hazards based on the conditional distribution function F(t)/F(r_*) in the interval [0, r_*]. Time-dependent covariates can relax the restrictive proportional hazards assumption and can easily be accommodated in all of our estimating equations.

Under independence between R and (T, Z) and positivity, our weights can be applied to any regression model for T|Z, such as additive hazards or accelerated failure time (AFT) models. As for the Cox model, an alternative model that is estimated using any standard inverse weighting approach that assumes F_T(r_*) = 1, i.e., positivity, will yield inconsistent estimates of the regression parameters if positivity does not hold.