Nonlinear voxel-based finite element model for strength assessment of healthy and metastatic proximal femurs

Abstract

Nonlinear finite element (FE) models can accurately quantify bone strength in healthy and metastatic femurs. However, their use in clinical practice is limited since state-of-the-art implementations using tetrahedral meshes involve a lot of manual work for which specific modelling software and engineering knowledge are required. Voxel-based meshes could enable the transition since they are robust and can be highly automated. Therefore, the aim of this work was to bridge the modelling gap between the tetrahedral and voxel-based approach. Specifically, we validated a nonlinear voxel-based FE method relative to experimental data from 20 femurs with and without artificial metastases that had been mechanically loaded until failure. CT scans of the femurs were segmented and automatically converted into a voxel-based mesh with hexahedral elements. Nonlinear material properties were implemented in an open-source linear voxel-based FE solver by adding an additional loop to the routine such that the material properties could be adapted after each increment. Bone strength, quantified as the maximum force in the force-displacement curve, was evaluated. The results were compared to a previously established nonlinear tetrahedral FE approach as well as to the experimentally measured bone strength. The voxel-based FE model predicted the experimental bone strength very well both for healthy (R² = 0.90, RMSE = 0.88 kN) and metastatic femurs (R² = 0.93, RMSE = 0.64 kN). The model precision and accuracy were very similar to the ones obtained with the tetrahedral model (R² = 0.90/0.93, RMSE = 0.90/0.64 kN for intact/metastatic respectively). The more intuitive voxel-based meshes thus quantified macroscale femoral strength equally well as state-of-the-art tetrahedral models. The robustness, high level of automation and time-efficiency (< 30 min) of the implemented workflow offer great potential for developing FE models to improve fracture risk prediction in clinical practice.

Highlights

• •A nonlinear voxel-based FE model was evaluated to assess femoral bone strength
• •Both healthy and metastatic femurs were evaluated
• •The FE models predicted bone strength with high accuracy and precision
• •Voxel-based and tetrahedral FE models showed similar accuracy and precision
• •An iterative routine enabled material nonlinearity in a linear FE solver

1. Introduction

Metastatic bone disease (MBD) is a secondary complication of cancer, which results when a primary tumor metastasizes to the skeleton. Bone is the third most common site of metastasis for a wide range of solid tumors, with up to 70% of metastatic prostate and breast cancer patients developing bone metastases (Fornetti et al., 2018). An important complication of MBD is that it damages and weakens bone, putting the patient at a greater risk for fracture (Coleman, 2006; Jawad and Scully, 2010). For these patients such fractures have severe consequences as bone healing is limited, even after adequate fracture fixation. Moreover, fractures strongly reduce the quality of life of these patients with an already limited life expectancy.

Radiologists and clinicians face the task of determining the probability of these fractures occurring to decide whether prophylactic surgery is necessary. Currently this decision is based on the subjective assessment of the clinical team, relying on clinical guidelines that have been shown to poorly predict fracture risk (Van der Linden et al., 2004; Tanck et al., 2009; Benca et al., 2016). The need for developing a more reliable clinical tool to objectively assess fracture risk in patients with MBD has been recognized for a long time (Derikx et al., 2015). A very promising technique is computed tomography (CT)-based finite element (FE) analysis which can simulate the mechanical behavior of bone under mechanical loading and quantify bone strength. A recent study by Derikx et al. showed that FE predictions outperform the predictions of clinicians (Derikx et al., 2012). They showed that clinicians were not able to rank femurs in terms of bone strength when using conventional radiographs as used in current clinical assessment. In contrast, the FE predictions showed very good correspondence with the experimentally measured bone strength of the cadaveric femurs.

To create a CT-based FE model from a CT scan of a femur, the scan is first segmented to extract a three-dimensional representation of the femur which is subsequently converted into a mesh. There are two main meshing techniques available (Lenaerts and Van Lenthe, 2009). The first one, geometry-based meshing, reconstructs the bone surface based on the contours of the segmented femur and subsequently builds a volumetric mesh with tetrahedral or hexahedral elements from it. The second approach, voxel-based meshing, directly converts the segmented voxel data into an FE model with brick elements. Currently, the vast majority of macroscale FE models of the proximal femur make use of geometry-based meshes to predict bone strength (Lenaerts and Van Lenthe, 2009). Only a limited number of studies have made use of voxel-based meshes. This trend is also observed for the application of FE models for fracture risk prediction in patients with bone metastases; tetrahedral element meshes have been used mostly in recent studies (Derikx et al., 2012; Yosibash et al., 2014; Alexander et al., 2013; Sternheim et al., 2018), while only a few older studies reported on voxel-based meshes (Tanck et al., 2009; Keyak et al., 2005; Spruijt et al., 2006). Yet, voxel-based meshes are very intuitive and can be generated in a quick and simple way. Furthermore, mesh generation can be fully automated without the risk of having bad quality, distorted elements no matter how complex the shape of the object (Charras and Guldberg, 2000), hence, it presents an efficient and robust methodology. The main disadvantage of a voxel-based mesh is the jagged representation of curved surfaces which may give rise to localized stress concentrations at the surface and thereby hamper a proper evaluation of bone failure.

Unlike the macroscale FE models, voxel-based meshes are already extensively used for evaluating bone stiffness for microstructural FE models of bone (Voide et al., 2008; van Lenthe et al., 2007) and bone-implant combinations (Steiner et al., 2017). It has been shown that tetrahedral and voxel-based meshes yield very similar results for these microscale models (Ulrich et al., 1998).

The goal of this study was to bridge the modelling gap between the tetrahedral and voxel-based approach on the macroscale level. We hypothesized that macroscale voxel-based FE models can achieve the same accuracy as tetrahedral models when quantifying strength of the proximal femur. The rationale for taking this approach is that it can be highly automated, is robust, and allows making use of the fast and memory-efficient FE solvers dedicated for voxel-based meshes, such as the open-source software ParOSol (Flaig, 2012). Especially with the focus on clinical implementation, these arguments become important. At present, clinical implementations of FE analyses are hampered since the workflow involves a lot of manual work for which specific modelling software and engineering knowledge are required (Benca et al., 2016; Derikx et al., 2015).

2. Methods

2.1. Dataset

To validate the nonlinear voxel-based FE method, data from a previously published study (Derikx et al., 2012) were used. In short, Derikx et al. conducted mechanical experiments on 10 pairs of fresh-frozen cadaver femurs. One femur of each pair was left intact (intact group), while the contralateral femur received one or more artificial cavities resembling metastatic bone lesions (metastatic group). Ethical approval for the collection of the specimens was granted by the Anatomical Department of Radboud umc. Each femur was CT scanned in a water basin on top of a solid calcium hydroxyapatite (CaHA) phantom (Image Analysis, Columbia, Kentucky). The following scanner settings were used: 120 kVp, 220 mAs, slice thickness 3 mm, pitch 1.5, spiral and standard reconstruction, in-plane resolution 0.9375 mm. Subsequently, the femurs were mechanically tested in single leg stance configuration by applying an increasing (10 N/s) axial force on the femur head until failure. A plastic cup (diameter 30 mm, polymethylene) was placed between the femur head and the loading plate to distribute the load. The distal ends of the femurs were embedded in PMMA and fixed using a distal ball-bearing and a sliding hinge, only allowing rotation around the anterior-posterior axis. From the CT scans, Derikx et al. developed an FE model with four-noded tetrahedral elements (mean edge length of approximately 2 mm) that mimicked the experimental set-up.

2.2. Finite element analysis

Using the CT images from Derikx et al., voxel-based FE models were created by reslicing the images into 2 mm sized, linear cubical voxels and subsequently converting them into a hexahedral mesh using an in-house voxel-to-element conversion approach. Hounsfield units were converted to bone density on a slice-by-slice basis using the calibration phantom as a reference. Any negative bone density estimate was set to 0 g/cm³. Material properties were assigned on an element-by-element basis as a function of bone density using the same relationships as Derikx et al. (Derikx et al., 2012), which modeled the nonlinear isotropic material behavior as defined by Keyak et al. (2005). Details on the applied material relationships are provided in supplementary material (S1). Due to differences in element characteristics a slight adaptation in the protocol that converts bone densities to FE elements was required. Specifically, at the outermost layer of elements, a threshold was applied that removed all surface elements with a CaHA-equivalent bone density smaller than 0.250 g/cm³ to account for partial volume effects from the CT scan. The threshold was chosen based on a sensitivity study where the threshold was varied from 0 to 0.400 g/cm³. Additionally, the bone densities were smoothed over the neighboring elements using an averaging method with Gaussian weights (σ = 1.27; support = 1).

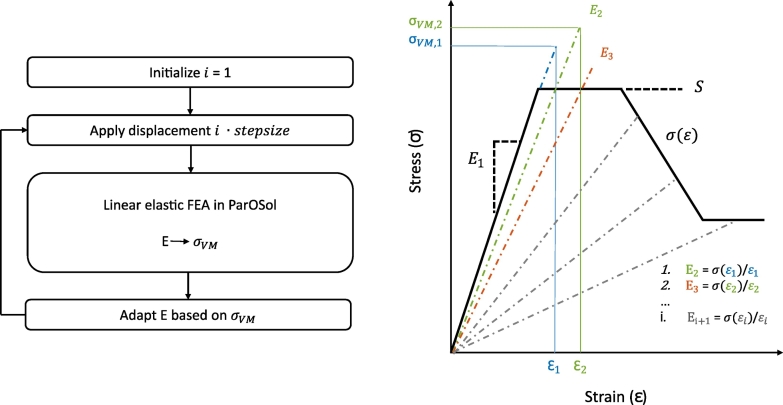
Boundary conditions mimicking the experimental setup were applied (Fig. 1). The orientation of the experimental coordinate system was extracted in the previous study based on a Roentgen Stereophotogrammetric Analysis (RSA) (Derikx et al., 2012). A loading cup was added at the proximal end with a diameter of 30 mm, a concave end that fits to the femur head and a Young's modulus of 2 GPa. A displacement was applied at the top nodes of the cup along the direction of the experimental z-axis. The surface elements of the femur head that were connected to this cup were assigned a Young's modulus of 20 GPa and a yield strength of 200 MPa to prevent severe distortion (Tanck et al., 2009). At the distal end, a stiff cylinder (diameter 40 mm, Young's moduli 200 GPa) was attached to the femur to mimic the distal embedding. Two nodes that lay on the experimental rotation axis were identified on the stiff cylinder and fully fixed. This ensured rotation along this axis (anterior-posterior direction), while translation and rotation along all other directions was restricted. The models were solved using the open-source software ParOSol (Flaig, 2012) (https://bitbucket.org/cflaig/parosol/src/default/), a dedicated voxel-based FE solver which is highly efficient and powerful in linear-elastic analyses. In order to capture the nonlinear material behavior with this linear FE solver, a method was implemented analogously to Steiner et al. (Steiner et al., 2014) by adding an additional loop to the routine such that after each increment, the material properties were adapted.

Fig. 1.

A voxel-based FE model (voxel-size 2 mm) was developed with boundary conditions mimicking the experimental set-up. Proximally, a load was applied on the top surface of a load cup (A). Distally, the embedding was mimicked as a stiff cylinder fixed at two points on the anterior-posterior (AP) axis to allow rotation along this axis (B).

2.3. Iterative routine for nonlinear material behavior

The iterative routine for capturing the nonlinear material behavior started with an initialization, in which a nonlinear stress-strain curve (Fig. 2) was defined for each element based on the material relations of Keyak et al. (2005) (supplementary material S1). In the first iteration, all elements were assigned their initial Young's modulus E₁ (Fig. 2) and a small displacement equal to a pre-defined step size was applied. Based on the Von Mises stress results from this linear FE simulation, the Young's moduli of the elements were adapted if needed. The next iteration then started from this adapted material model and the displacement was increased with one step size. This routine continued until a pre-defined maximal displacement was reached. Adaptation of the Young's moduli was necessary once an element entered the plastic phase, i.e. once the Von Mises stress was higher than the yield stress. The Young's modulus of the element was then reduced at every iteration such that it followed the material stress-strain curve (Fig. 2). The choice of the step size was a trade-off between accuracy and computation time. For this study, the step size was set at 0.025 mm, which means the displacement load increased with 0.025 mm at every iteration. The routine was scripted in Python and has been made available at GitHub (https://github.com/ameliesas/NonlinearRoutine).

Fig. 2.

The iterative routine for capturing nonlinear material behavior runs in a loop over the linear FE solver ParOSol. At each iteration the displacement load was increased with a pre-defined step size and based on the Von Mises stress (σ_VM) results the Young's moduli E were adapted if necessary. If σ_VM exceeded the yield strength S, the Young's modulus E was reduced at the next iteration such that it followed the material stress-strain curve σ(ε).

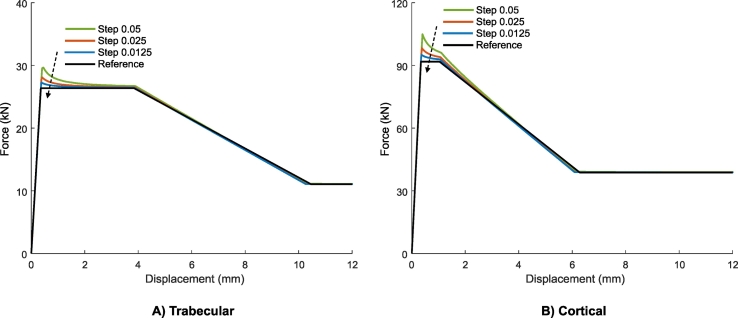
In order to validate this iterative routine, it was first applied to brick-shaped models (30 × 30 × 50 mm) with 2 mm voxel elements and a uniform density. A low stiffness model representing trabecular bone and a high stiffness model representing cortical bone properties were analyzed. The beams were loaded in a one-directional, unconfined compression. A displacement of 12 mm was applied at the top surface while the bottom surface was fixed in the direction of the applied displacement. The resulting force-displacement curves were extracted and compared against the theoretically expected piece-wise linear behavior that results from the material definition of Keyak et al. (2005).

2.4. Data analysis

The voxel-based FE model of the proximal femur was validated by comparing the failure force quantified by FE (F_FE) with the experimentally measured failure force (F_exp). In the FE model, the total reaction force was calculated as the sum of the reaction forces at all nodes on the top of the loading cup. Failure force was defined as the maximal reaction force in the loading direction. The relationship between F_FE and F_exp was computed with linear regression analysis, and the coefficient of determination (R²) and the root mean squared error (RSME) were calculated. RMSE is analogous to the standard deviation of the data around the regression line and thus provides a measure of model precision. The accuracy of the prediction was measured by the mean and standard deviation of the prediction error, calculated for each specimen as F_FE − F_exp. Bland–Altman plots were created to provide a graphical interpretation of the agreement between the experimental and FE calculated force values. Furthermore, the reduction in failure force as a result of the artificial lesions was calculated as the difference in failure force between each pair of femurs. The reduction in failure force quantified by the FE model was compared against the experimentally measured reduction. The same analysis was repeated for the results obtained with the tetrahedral FE model as published earlier (Derikx et al., 2012) to compare the model accuracy and precision. All statistical analyses were performed in MATLAB R2017a (MathWorks, Natick, MA) and p-values <0.05 were considered statistically significant. Finally, a qualitative validation was performed comparing the fracture locations in the FE model to the experimental fractures in the cadaver femurs.

3. Results

3.1. Beam model

The force-displacement curve of the unconfined compression tests as simulated with the iterative routine in ParOSol corresponded very well with the theoretical reference, except for a small overshoot at the sudden transition from linear to plastic behavior (Fig. 3). This overshoot was slightly larger for the cortical model compared to the trabecular one due to the steeper slope of the linear part (higher Young's modulus). The overshoot reduced when a smaller step size was selected.

Fig. 3.

The iterative routine that has been implemented to capture nonlinear material properties resulted in force-displacement curves for a simple beam model that corresponded very well with the theoretical reference solution. The overshoot at the transition from linear to plastic behavior reduced with a smaller step size.

3.2. Cadaver femurs

The failure force quantified by the voxel-based FE model in ParOSol corresponded very well with the experimental failure force, both for the intact and metastatic femurs. In the intact group, a strong linear relation (R² = 0.903, p <0.001, RMSE = 0.880 kN) was found between F_FE and F_exp (Fig. 4) with a slope not different from one and an intercept not different from zero. The prediction error indicated that the failure force was underestimated by an average of 0.54 kN (SD = 0.83 kN). Analogously in the metastatic group, a very good relation was found between F_FE and F_exp (R² = 0.928, p <0.001, RMSE = 0.645 kN) (Fig. 4) with again a slope not different from one and an intercept not different from 0. In contrast with the intact group, the FE model slightly overestimated the strength of the metastatic femurs by an average of 0.59 kN (SD = 0.64 kN). In both groups, the model precision and accuracy were very similar to the results obtained with the tetrahedral FE model (Table 1, Fig. 4). The regression lines and Bland-Altman plots were strongly corresponding (Fig. 4).

Fig. 4.

A strong linear relation was found between the predicted failure force by the nonlinear voxel-based FE model in ParOSol and the experimental failure force, both for the intact (A) and metastatic (B) group. Correlation graphs (left) and Bland-Altman plots (right) are depicted. The relationships were highly similar to the ones found with the nonlinear tetrahedral FE model.

Table 1.

Regression results between F_FE and F_exp for the voxel-based model and the tetrahedral model respectively.

	Regression (kN)	R2	p	RMSE (kN)	FFE − Fexp (μ ± SD; kN)
Intact
Voxel-based	y = 1.01 x – 0.62	0.903	<0.001	0.880	−0.54 ± 0.83
Tetrahedral	y = 1.00 x – 0.50	0.896	<0.001	0.901	−0.52 ± 0.85
Metastatic
Voxel-based	y = 0.91 x + 0.94	0.928	<0.001	0.645	0.59 ± 0.64
Tetrahedral	y = 0.95 x + 0.72	0.934	<0.001	0.642	0.54 ± 0.62

On average, the experimental failure force of a femur with an artificial metastatic lesion was 2.7 kN lower (SD = 2.0 kN) than that of an intact femur. The reduction in failure force quantified by the FE model was highly correlated with the experimental force reduction (R² = 0.92, p <0.001, RMSE = 0.590 kN) (Fig. 5). Furthermore, this relation was very similar to the relation found for the tetrahedral model (R² = 0.92, p <0.001, RMSE = 0.707 kN). The bias in the Bland-Altman plot was slightly larger compared to the tetrahedral model, but the limits of agreement were narrower indicating a higher precision (Fig. 5).

Fig. 5.

The voxel-based FE model accurately predicted the reduction in experimental failure force caused by an artificial metastatic lesion. The correlation graph (left) and Bland-Altman plot (right) are depicted. The relationship was highly similar to the one found with the nonlinear tetrahedral FE model.

The fracture locations indicated by the FE model corresponded better to the experimental fractures in the metastatic group than in the intact group. In the metastatic group, experimental fracture lines always passed through the lesion, as correctly indicated by the FE model in most cases (7/10). In the intact group, mostly intertrochanteric fractures occurred during the experiment while the FE model mainly indicated subcapital fractures (Fig. 6). The same discrepancy was observed with the tetrahedral FE models (Derikx et al., 2012).

Fig. 6.

The effective strains (EFF) in two representative FE models show a typical subcapital fracture line in an intact femur (A) and a fracture through the lesion in a metastatic femur with a lesion in the medial cortex (B). An arrow indicates the location of the center of the lesion.

The analysis was fully automated, except for the segmentation of the femur mask, the calibration phantom and the distal embedding. Model creation from the segmented CT scan up to the voxel-based FE mesh took around 2–3 min on a standard PC (Dell latitude 7480, Inter Core i7-7600U CPU 2.8 GHz, 16 GB RAM). The iterative FE simulation in ParOSol took around 20 min when parallelizing over eight cores on the CSCS supercomputer (Piz Daint, Intel Xeon CPU E5–2650 v3 2.3 GHz, 256 GB RAM) (Swiss National Supercomputing Centre, Lugano, Switzerland). The computation time of the FE simulation was highly related to the step size over which the load was increased at every iteration. It decreased linearly with an increasing step size, i.e. where the simulation at a step size of 0.025 mm was finished in approximately 20 min, the simulation at a step size of 0.05 mm took around 10 min; the latter caused a slight reduction in model precision (R² = 0.90/0.92, RMSE = 0.90/0.69 for intact/metastatic respectively). All models were solved without numerical problems. No convergence errors occurred with a convergence tolerance of 1e-11.

4. Discussion

In this study, we evaluated the ability of an efficient, nonlinear voxel-based FE model to assess bone strength in the proximal femur of healthy and metastatic patients. The voxel-based model showed a similar accuracy and precision in quantifying bone strength compared to a previously established tetrahedral FE model.

The need for a reliable clinical tool to predict fracture risk in metastatic patients has been recognized for a long time (Derikx et al., 2015). Currently clinicians often make use of guidelines for evaluating the impending fracture risk of the lesion based on conventional radiographs. One of the most commonly used methods is the Mirels' scoring system, where a score is assigned based on the type, size and location of the lesion and the amount of pain (Mirels, 1989). A high score is associated with an impending fracture and indicates the need for prophylactic surgery. Other often used guidelines suggest a circumferential cortical involvement >50% or an axial cortical gap >30 mm as a risk for fracture (Van der Linden et al., 2018). However, none of these guidelines have shown to be accurate enough to adequately predict fracture risk (Van der Linden et al., 2018). Potential causes of the failing accuracy are the ignorance of initial bone strength (Derikx et al., 2015) and specific location of the lesion within the bone (Benca et al., 2017), important aspects that CT-based FE models do incorporate for predicting fracture risk. Consequently, FE models have shown to be able to predict fracture risk much more accurately compared to clinicians (Derikx et al., 2012; Eggermont et al., 2018). CT-based FE modelling could therefore provide a useful additional support next to the existing clinical guidelines and general evaluation of the patient's health record, to improve fracture risk assessment.

However, FE models are currently hampered of entering clinical practice since they are too time-consuming, require expert knowledge and necessitate specific modelling software. The generation and calculation of an FE simulation model has been estimated to take about 8 h for a single femur (Benca et al., 2016; Derikx et al., 2012). To turn this method into a time- and cost-effective clinical tool, a high level of automation is necessary (Benca et al., 2016), the simulations should be robust and fast, and need to be able to run on a desktop PC or small workstation. This is where voxel-based models become of interest, since they allow a high level of automation, are robust for mesh distortion and allow the use of fast and memory-efficient voxel-based FE solvers. Therefore, we aimed to further develop the voxel-based FE approach and thereby enable the step towards clinical implementation. We developed a workflow which was highly automated and proceeded relatively fast. Starting from a segmented CT scan, the subsequent analysis was fully automated and finished in less than half an hour. The workflow also proved to be robust as no numerical problems occurred. Moreover, it makes use of the open-source software ParOSol, a dedicated voxel-based FE solver designed for memory efficiency (Flaig, 2012), which enables efficient simulating performance on a standard desktop PC.

We found a good agreement between the FE calculated and experimental failure load, both for intact (R² = 0.90, RMSE = 0.88 kN) and artificial metastatic femurs (R² = 0.93, RMSE = 0.64 kN). Furthermore, the FE models correctly predicted the reduction in failure load due to the artificial lesions (R² = 0.92, RMSE = 0.59 kN). The results were directly compared against the results from a previously established tetrahedral FE model (Derikx et al., 2012) (R² = 0.90/0.93, RMSE = 0.90/0.64 kN for intact/metastatic respectively) and proved to have almost identical results. The results in this study were also in line with the results from the voxel-based model of Keyak et al. (R² = 0.83–0.88) (Keyak et al., 2007), which could have been expected since our material model was based on their work. Only three small adjustments have been made, i.e. a smaller element size (2 mm versus 3 mm), a surface threshold to account for partial volume effects and an averaging method to smooth the density values. The regression analysis showed a slightly higher R² and a slope and intercept closer to 1 and 0 respectively. These small differences could have been caused by the adjustments made in comparison to Keyak's model, but might also be related to the differing datasets. Where this study evaluated specimens with artificial lytic lesions, Keyak et al. included specimens with real bone metastases. Under a similar rationale as our study, Benca et al. (2019) recently developed a voxel-based FE model (3 mm) to increase the level of automation in FE strength assessment of metastatic femurs. Analogously, it enabled them to perform a complete analysis in less than half an hour with minimal manual workload. However, the accuracy of Benca's voxel-based model was lower; they underestimated the failure load with a factor of two. This underestimation was likely caused by the differing material properties.

On the microscale level it has already been shown that tetrahedral and voxel-based meshes yield almost identical results (Ulrich et al., 1998). The same conclusion can now be drawn on the macroscale level, at least in the application of femoral fracture risk prediction. Although the focus of this study was on MBD patients, these results are also relevant for application in osteoporotic patients, since this patient group has an increased risk to sustain a fracture as well (Johnell and Kanis, 2006). Hence, they would also benefit from an accurate fracture risk assessment aiding clinicians in making a better informed decision on the question whether these patients should be treated prophylactically.

Voxel-based elements have mainly been used in linear FE analyses, for evaluating bone stiffness for highly-detailed and necessarily large-scale microstructural FE models of bone (Charras and Guldberg, 2000; Voide et al., 2008). Indeed, the FE solver ParOSol, which we used in this study, has been developed specifically for linear-elastic bone analyses, and did not include nonlinear material properties. For the application of femoral fracture prediction, Keyak (2001) however showed that nonlinear models provide a better precision compared to linear models. To enable this nonlinear material behavior in the solver, a method has been implemented in this study which adds an additional loop to ParOSol such that after each iteration, the material properties can be adapted if necessary. This nonlinear routine was made publicly available (https://github.com/ameliesas/NonlinearRoutine). The study proved that the method works very well for predicting fracture in the proximal femur, on the condition that an appropriately small iteration step was chosen. If the method would be used in different applications, an appropriate iteration step should be re-evaluated for the specific study since it depends on the model stiffness and loading conditions. Moreover, it should be noted that this study validated the nonlinear methodology only for the specific application of femoral strength assessment and can therefore not guarantee the same performance for all FE simulations. Especially for materials having a highly plastic behavior and undergoing large strains, the performance might deviate and additional validation studies should be performed. For predominantly elastic materials undergoing small strains such as bone, the method has shown to accurately quantify the onset of failure.

Although FE models have shown promising results, some challenges still remain before entering clinical practice. Even more automation is required to eliminate the need for expert knowledge and further reduce analysis time. Currently the segmentation step was still done manually. With the upcoming techniques and promising outcomes for automatic segmentation (Heimann and Meinzer, 2009; Cheng et al., 2013; Chu et al., 2015; Deniz et al., 2018), we believe that full automation should become possible. Clinical implementation would also require an improved patient-specific accuracy of the model. Although this study found a good overall correlation between the FE quantified and experimental bone strength, a relatively large under- or overestimation still occurs on the patient-specific level. Potential accuracy improvements could be expected with more complex anisotropic material properties (Kersh et al., 2013) compared to the isotropic material properties included in this model. Finally, large retro- or prospective studies should be conducted to show to the true predictive power of the CT-based FE models in a clinical setting. Such a prospective study has recently been set up (Eggermont et al., 2018; Eggermont et al., 2019) to compare the FE predicted fracture risk, measured as the ratio between failure load and body weight, between two groups of patients with fractured and non-fractured metastatic femoral lesions. The first results have recently been published and demonstrate an improved sensitivity in predicting fractures compared with clinical assessments (Eggermont et al., 2018; Eggermont et al., 2019). Future studies on a larger number of cases should confirm these preliminary findings.

Another limitation of the study was the use of cadaver femurs with artificial lytic metastases. The shape of the simulated lesions were simplified compared to actual metastatic lesions with an arbitrary shape. Actual lytic lesions will also likely affect the surrounding bone and often have a blastic component. Moreover, no information is available about bone material properties in cancer patients which might be different from the ones in healthy patients. These aspects might generate some uncertainty regarding the performance of our FE model in proximal femurs of real MBD patients.

The fracture lines in the FE models of the intact femurs differed from the observed experimental fractures. While the models mainly predicted subcapital fractures, intertrochanteric fractures mostly occurred in the experiments. The same discrepancy was observed with the tetrahedral FE models (Derikx et al., 2012) and is also in line with a previous study by Keyak et al. (2007), who observed a change in the modeled fracture location from the subcapital region (intact femur) to the lesion (metastatic femur). More complex anisotropic material properties might potentially improve the accuracy of modelling fracture location.

Finally, simplified loading conditions were applied in the model. One compressive force was applied instead of the full range of hip contact and muscle forces. Moreover, only a single-leg stance configuration was considered, instead of simulating multiple loading scenarios. Hence the models are not representative for all real life fractures. However, with the focus on validation, it was mainly important to reproduce the setup of the experiment.

To conclude, in this study, we evaluated the ability of a nonlinear voxel-based model to assess femoral strength in metastatic and healthy femurs. The results proved that this model matched the precision and accuracy of the more commonly used tetrahedral models. Such intuitive voxel-based models might simplify the step towards clinical implementation by ensuring high level of automation, robustness and time-efficiency. Although additional steps are still needed for entering clinical practice, we believe that CT-based FE modelling can become an important clinical tool for better fracture risk prediction in the near future. They can provide a more accurate, biomechanics-based support next to the current clinical evaluation methods, and thereby improve the clinician's decision process for prophylactic treatment.

Transparency document

Transparency document.

CRediT authorship contribution statement

Amelie Sas:Conceptualization, Methodology, Software, Validation, Formal analysis, Writing - original draft, Visualization, Project administration, Funding acquisition.Nicholas Ohs:Software, Writing - review & editing.Esther Tanck:Conceptualization, Validation, Resources, Writing - review & editing.G. Harry van Lenthe:Conceptualization, Methodology, Writing - review & editing, Supervision, Funding acquisition.

Declaration of competing interest

None.

Appendix A. Supplementary data

Supplementary material