Solitary wave solutions to some nonlinear fractional evolution equations in mathematical physics

Abstract

The objective of this article is to construct new and further general analytical wave solutions to some nonlinear evolution equations of fractional order in the sense of the modified Riemann-Liouville derivative relating to mathematical physics, namely, the space-time fractional Fokas equation, the time fractional nonlinear model equation and the space-time fractional (2 + 1)-dimensional breaking soliton equation by exerting a rather new mechanism $\left(G\text{'}/G,1/G\right)$ -expansion method. We use the fractional complex transformation and associate the fractional differential equations to the solvable integer order differential equations. A comprehensive class of new and broad-ranging exact traveling and solitary wave solutions are revealed in terms of trigonometric, rational and hyperbolic functions. The attained wave solutions are sketched graphically by using Mathematica and make a comparison to the results attained by the presented technique with other techniques in a comprehensive manner. It is notable that the method can be considered as a reduction of the reputed $\left(G\text{'}/G\right)$ -expansion method commenced by Wang et al. It is noticeable that, the two variable $\left(G\text{'}/G,1/G\right)$ -expansion method appears to be more reliable, straightforward, computerized and user-friendly.

Mathematics; Space-time fractional Fokas equation; time fractional (2 + 1)-dimensional nonlinear model; space-time fractional (2 + 1)-dimensional breaking soliton equation; $\left(G\text{'}/G,1/G\right)$ -expansion method; fractional derivative.

1. Introduction

Calculus of fractional order is one the growing fields of applied mathematics, mathematical physics and mathematical analysis whose concept was first initiated in 1695 [1], when Leibniz suggested the possibility of fractional derivatives for the first time. Since there was no such theory, the foundation of this subject was laid by Liouville in 1832 and the fractional derivative of a power function was established by Riemann in 1847 [2]. Fractional calculus is the generalization of classical order differentiation and integration and broadly depicts as a powerful tool for modeling complex systems, specifically for science and engineering. In the present time, it is remarkable that the study of explicit solitary wave solutions for nonlinear fractional partial differential equations (PDEs) plays a significant role due to their substantial application in the real world problems, especially in fractional dynamics, mathematical physics, mechanical engineering, plasma physics, signal processing, chemical physics, optical fibers, geochemistry, stochastic dynamical systems, nonlinear optics, systems identification, economics etc. In the recent past, a lot of attention has been received to finding the new and further general closed form exact wave solutions of fractional PDEs by many researchers. A good deal of potential symbolic computer programming tools have been employed for investigating appropriate solution to nonlinear fractional PDEs, namely, the first integral method [3, 4, 5], the modified simple equation method [6,7], the auxiliary equation method [8, 9, 10], the fractional sub-equation method [11, 12, 13, 14], the $\left(G\text{'}/G\right)$ -expansion method [15, 16, 17], the Lie-symmetry method [18], the Exp-function method [19, 20, 21, 22], the tanh-coth method [23], the generalized Kudryashov method [24, 25, 26, 27, 28, 29], the $\left(G\text{'}/G,1/G\right)$ -expansion method [30, 31, 32, 33, 34, 35, 36] etc. Recently, some researchers, like, Yasar and Giresunlu [37] achieved exact wave solutions to the space-time fractional Chan-Allen and the Klein-Gordon equation by implementing the $\left(G\text{'}/G,1/G\right)$ -expansion method. Alike, adopting the identical technique, Topsakal et al. [38] have established three different types of traveling wave solutions to the space-time fractional mBBM and the modified nonlinear Kawahara equations. Inspired by the ongoing research in the analogous topics, we extract the new and further general exact traveling and solitary wave solutions to some nonlinear fractional PDEs, stated earlier by suggesting the two variable $\left(G\text{'}/G,1/G\right)$ -expansion method, which can be regarded as the generalization of the original $\left(G\text{'}/G\right)$ -expansion method [39].

First of all, we consider the well-known space-time fractional Fokas equation which is a model for finite-amplitude wave packet in fluid dynamics. The standard form of this equation is [40]:

$$4\frac{{\partial }^{2\alpha }v}{\partial t^{\alpha }\partial x_1^{\alpha }}-\frac{{\partial }^{4\alpha }v}{\partial x_1^{3\alpha }\partial x_2^{\alpha }}+\frac{{\partial }^{4\alpha }v}{\partial x_1^{\alpha }\partial x_2^{3\alpha }}+12\frac{{\partial }^{\alpha }v{\partial }^{\alpha }v}{\partial x_1^{\alpha }\partial x_2^{\alpha }}+12v\frac{{\partial }^{2\alpha }v}{\partial x_1^{\alpha }\partial x_2^{\alpha }}-6\frac{{\partial }^{2\alpha }v}{\partial y_1^{\alpha }\partial y_2^{\alpha }}=0,t>0,0<\alpha \le 1$$ (1.1)

This is a transformed generalization of the (4 + 1)-dimensional Fokas equation [41,42],

$$\frac{{\partial }^{2}v}{\partial t\partial x_1}=\frac{1}{4}\frac{{\partial }^{4}v}{\partial x_1^3\partial x_2}-\frac{1}{4}\frac{{\partial }^{4}v}{\partial x_1^3\partial x_2}-\frac{3{\partial }^2\left(v^2\right)}{2\partial x_1\partial x_2}+\frac{3}{2}\frac{{\partial }^{2}v}{\partial y_1\partial y_2}$$ (1.2)

This equation is one of the new higher-dimensional nonlinear wave equations.

Many methods for solving the time fractional nonlinear Fokas equation have been employed currently. Wang et al. [41] derived the quasi-periodic and rouge wave solutions to the (4 + 1)-dimensional Fokas equation. Bilinearnization and new multi-soliton solutions for the (4 + 1)-dimensional Fokas equations have been established by Zhang et al. [42]. Zhang and Chen [43] obtained the Painleve integrability and new exact solutions to this equation. In [44] the authors derived the exact solutions to this equation by a new fractional sub-equation method. He [45] attained the exact solutions to the (4 + 1)-dimensional nonlinear Fokas equation using the extended F-expansion method and it's variant. Wazwaz [46] derived a variety of multiple-soliton solutions for the integrable (4 + 1)-dimensional Fokas equation. Li and Qiao [47] implemented the bifurcation and obtained traveling wave solutions to this equation. Gomez et al. [48] examined the exact solutions to the (4 + 1)-dimensional Fokas equation with variable coefficients. Lump-type solutions for the (4 + 1)-dimensional Fokas equation are investigated via symbolic computations by Cheng and Zhang [49]. Al-Amr and El-Ganaini [50] achieved new exact traveling wave solutions to the (4 + 1)-dimensional Fokas equation.

Secondly, we take into account the time fractional (2 + 1)-dimensional nonlinear model equation of the form [11,51,52],

$$\frac{{\partial }^{\alpha }v}{\partial t^{\alpha }}=\frac{{\partial }^2}{\partial x^2}\left(v^2\right)+\frac{{\partial }^2}{\partial y^2}\left(v^2\right)+h\left(v^2-r\right),t>0,0<\alpha \le 1$$ (1.3)

Here $\alpha$ is a parameter narrating the order of the fractional time derivative and h, r are real parameters. Several methods for solving the above time fractional nonlinear PDE have been implemented very recently [11,51,52].

Finally, we consider the space-time fractional (2 + 1)-dimensional breaking soliton equation [53]:

$$\{\begin{array}{l}\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}+a\frac{{\partial }^{3\alpha }u}{\partial x^{2\alpha }{y}^{\alpha }}+4au\frac{{\partial }^{\alpha }v}{\partial x^{\alpha }}+4a\frac{{\partial }^{\alpha }u}{\partial x^{\alpha }}v=0,\hfill \\ \frac{{\partial }^{\alpha }u}{\partial y^{\alpha }}-\frac{{\partial }^{\alpha }v}{\partial x^{\alpha }}=0,\hfill \end{array}$$ (1.4)

where $0<\alpha \le 1$. When $\alpha =1$, Eq. (1.4) is called the (2 + 1)-dimensional breaking soliton equations.

Various methods in order for solving the space-time fractional (2 + 1)-dimensional breaking soliton equations have been implemented lately. Yildirim and Yasar [54] studied the exact solutions to the (2 + 1)-dimensional breaking soliton equation. Osman [55] examined the multi-soliton solutions to the (2 + 1)-dimensional breaking soliton equation with variable coefficients in a graded-index waveguide. Breaking soliton equations and negative-order breaking soliton equations of typical and higher orders have been evaluated in [56]. Yildiz and Daghan [57] investigated solutions to the (2 + 1)-dimensional breaking soliton equation by using two different methods. Wang [58] suggested the analytical multi-soliton solutions to the (2 + 1)-dimensional breaking soliton equation. Symmetries of the (2 + 1)-dimensional breaking soliton equation have been used by the authors in [59]. Chen and Ma [60] introduced and investigated to extract exact solutions of non-traveling wave solutions for the (2 + 1)-dimensional breaking soliton system. Wazwaz [61] introduced the generalized (2 + 1)-dimensional breaking soliton equation. In [62] technologically advanced technique has been used to extract some exact solutions to the (2 + 1)-dimensional breaking soliton equation using the three-wave method. New multi-soliton solutions to the (2 + 1)-dimensional breaking soliton equations have been established in [63].

To the best our understanding, the space-time fractional nonlinear (4 + 1)-dimensional Fokas equation, the time fractional nonlinear model equation and the space-time fractional (2 + 1)-dimensional breaking soliton equation have not been searched by making use of the two variable $\left(G\text{'}/G,1/G\right)$ -expansion method. An exciting and incredibly dynamic field of research in the last two decades is the investigation of solitary wave solutions to the nonlinear fractional differential equations and the related issue is the development of closed form wave solutions to a broad class of nonlinear fractional equations. Therefore, the aim of this article is: we implement the two variable $\left(G\text{'}/G,1/G\right)$ -expansion method to extract exact and solitary wave solutions to the above stated nonlinear fractional differential equations.

The rest of this article is figured as follows: In section 2, definition and basic properties of the modified Riemann-Liouville fractional order derivative are provided. In section 3, we illustrate the sequence of the double variable $\left(G\text{'}/G,1/G\right)$ -expansion method. In section 4, we implement this technique to find new exact solitary wave solutions of the space-time fractional PDEs mentioned above. The nature of the solutions together with their graphical representation is provided in section 5. In section 6, we provide the results and discussion and finally in section 7, conclusions are given.

2. Description of the modified Riemann-Liouville fractional order derivative

There are several kinds of fractional differential operators in fractional calculus. In this article, we adopt the modified Riemann-Liouville derivative, the suitable and significant fractional differential operator.

Definition 1

Consider the Jumarie's modified Riemann-Liouville derivative of order $\alpha$ with the continuous function $f:R\to R$, $x\to f\left(x\right)$ is stated as [64]:

$$D_x^{\alpha }f\left(x\right)=\{\begin{array}{l}\frac{1}{\Gamma (-\alpha )}\underset{0}{\overset{x}{\int }}{(x-\eta )}^{-\alpha -1}\left(f\left(\eta \right)-f\left(0\right)\right)d\eta ,\alpha <0,\hfill \\ \frac{1}{\Gamma (1-\alpha )}\frac{d}{dx}\underset{0}{\overset{x}{\int }}{(x-\eta )}^{-\alpha }\left(f\left(\eta \right)-f\left(0\right)\right)d\eta ,0<\alpha <1,\hfill \\ {\left(f^{\left(n\right)}\left(x\right)\right)}^{\left(\alpha -n\right)},n\le \alpha \le n+1,n\ge 1\hfill \end{array}$$ (2.1)

where $"\Gamma "$ is the Gamma function and is defined by

$$\Gamma \left(\alpha \right)=\begin{array}{c}log\\ n\to \infty \end{array}\frac{n!n^{\alpha }}{\alpha \left(\alpha +1\right)\left(\alpha +2\right)\dots (\alpha +n)}$$ (2.2)

or

$$\Gamma \left(x\right)=\underset{0}{\overset{\infty }{\int }}{e}^{-t}{t}^{\left(x-1\right)}dx.$$ (2.3)

Definition 2

The Mittag-Leffler function with two parameters is defined as [65]:

$$E_{\alpha ,\beta }^{\left(x\right)}=\sum _{i=0}^{\infty }\frac{x^i}{\Gamma (\alpha i+\beta )},\mathfrak{R}e\left(\alpha \right)>0,\beta x\epsilon \mathbb{C}.$$ (2.4)

This function is utilized to examine the fractional PDEs as the exponential function in integer order.

For the sake of fractional derivative, some essential postulates which we use in this article provided in the underneath:

Postulate 1:

$$D_x^{\alpha }{x}^{\gamma }=\frac{\Gamma (1+\gamma )}{\Gamma (1+\gamma -\alpha )}{x}^{\gamma -\alpha },\gamma >0,$$ (2.5)

here $\gamma$ is a real number.

Postulate 2:

$$D_x^{\alpha }\left(Cf\left(x\right)\right)=C{D}_x^{\alpha }f\left(x\right),C=\text{Constant}.$$ (2.6)

Postulate 3:

$$D_x^{\alpha }\left(af\left(x\right)+bg\left(x\right)\right)=a{D}_x^{\alpha }f\left(x\right)+b{D}_x^{\alpha }g\left(x\right).$$ (2.7)

herein $a$ and $b$ are arbitrary constants.

Postulate 4:

$$D_x^{\alpha }f\left(\eta \right)=\frac{df}{d\eta }{D}_x^{\alpha }\left(\eta \right).$$ (2.8)

where $\eta =g\left(x\right)$.

3. The $\left(\mathit{G}\text{'}/\mathit{G},1/\mathit{G}\right)$ -expansion method

In this section, we explain the basic concept of the $\left(G\text{'}/G,1/G\right)$ -expansion method in order to attain the exact solitary wave solutions to the nonlinear fractional differential equations. For this, we assume the second-order linear ordinary differential equation (LODE) in $G=G\left(\eta \right)$ as

$$G^{\text{'}\text{'}}\left(\eta \right)+\lambda G\left(\eta \right)=\mu ,$$ (3.1)

where $\lambda$ and $\mu$ are arbitrary constants, $G^{\text{'}}$ is the derivative of $G$ and we undertake two rational functions $\varphi$ and $\psi$ as

$$\varphi =\frac{G^{\text{'}}\left(\eta \right)}{G\left(\eta \right)},\psi =\frac{1}{G\left(\eta \right)}.$$ (3.2)

Eqs. (3.1) and (3.2), yield

$${\varphi }^{\text{'}}=-{\varphi }^2+\mu \psi -\lambda ,{\psi }^{\text{'}}=-\varphi \psi ,$$ (3.3)

The solution of Eq. (3.1) is associated with the following three conditions:

Case 1

If $\lambda <0$, the general solution of Eq. (3.1) is

$$G\left(\eta \right)=A_1\sinh \left(\eta \sqrt{-\lambda }\right)+A_2\cosh \left(\eta \sqrt{-\lambda }\right)+\frac{\mu }{\lambda },$$ (3.4)

wherever $A_1$ and $A_2$ are two arbitrary constants. Therefore, from Eqs. 3.2), 3.3) and (3.4), it can be derived the following relation

$${\psi }^2=\frac{-\lambda }{{\lambda }^2\sigma +{\mu }^2}\left({\varphi }^2-2\mu \psi +\lambda \right),\text{where}\sigma =A_1^2-A_2^2.$$ (3.5)

Case 2

If $\lambda >0$, the general solution of Eq. (3.1) is

$$G\left(\eta \right)=A_1\sin \left(\eta \sqrt{\lambda }\right)+A_2\cos \left(\eta \sqrt{\lambda }\right)+\frac{\mu }{\lambda },$$ (3.6)

and using the techniques accepted above, from Eqs. 3.2), 3.3) and (3.6) the analogous relation is

$${\psi }^2=\frac{\lambda }{{\lambda }^2\sigma -{\mu }^2}\left({\varphi }^2-2\mu \psi +\lambda \right),\text{where}\sigma =A_1^2+A_2^2.$$ (3.7)

Case 3

If $\lambda =0$, the general solution of Eq. (3.1) is of the form

$$G\left(\eta \right)=\frac{\mu }{2}{\eta }^2+A_1\eta +A_2,$$ (3.8)

Consequently, we attain

$${\psi }^2=\frac{1}{A_1^2-2\mu A_2}\left({\varphi }^2-2\mu \psi \right).$$ (3.9)

Now, suppose the nonlinear fractional differential equation, say in two independent variables $x$ and $t$ is of the form

$$F\left(v,D_t^{\alpha }v,D_x^{\alpha }v,D_t^{\alpha }{D}_t^{\alpha }v,D_t^{\alpha }{D}_x^{\alpha }v,D_x^{\alpha }{D}_x^{\alpha }v,\dots \dots \dots \right)=0,$$ (3.10)

where $F$ is a polynomial in $v=v(x,t)$ and its various partial fractional derivatives. The main algorithm of the $\left(G\text{'}/G,1/G\right)$ -expansion method is presented stepwise:

First Step: Let us consider the traveling wave variable

$$v\left(x,t\right)=v\left(\eta \right),\eta =\frac{k{x}^{\alpha }}{\Gamma (1+\alpha )}+\frac{c{t}^{\alpha }}{\Gamma (1+\alpha )},$$ (3.11)

where k and c are the wave number and velocity respectively. Inserting (3.11) and the various fractional derivatives of $v=v(x,t)$ into (3.10), it transforms into the following ordinary differential equation (ODE):

$$H\left(v,v^{\text{'}},v^{\text{'}\text{'}},v^{\text{'}\text{'}\text{'}},\dots \dots \right)=0,$$ (3.12)

here $\text{'}$ refers to $\frac{d}{d\eta }$ and so on. If needed, we integrate Eq. (3.12) one or more times and assume the constant(s) of integration to be zero.

Second Step: According to the aforementioned technique, the exact solution of (3.12) can be revealed by a finite power series of two variables $\varphi$ and $\psi$ as follows:

$$v\left(\eta \right)=\sum _{i=0}^N{a}_i{\varphi }^i+\sum _{j=1}^N{b}_j{\varphi }^{j-1}\psi ,$$ (3.13)

where $a_i(i=\mathrm{0,1,2},\dots ,N)$ and $b_j(j=\mathrm{1,2},\dots ,N)$ are constantsto be determined afterward. The value of the positive integer $N$ can be found by the balancing principle.

Third Step: Substituting (3.13) into (3.12), also operating (3.3) and (3.5), it transforms into a polynomial in $\varphi$ and $\psi$, wherein the degree of $\psi$ is not greater than one. Equalizing all the coefficients of this polynomial to zero, yield a system of algebraic equations for $a_i(i=\mathrm{0,1,2},\dots ,N)$, $b_j(j=\mathrm{1,2},\dots ,N)$, $k$, $c$, $\mu$, $\lambda (\lambda <0)$, $A_1$ and $A_2$.

Fourth Step: We solve the system of equations attained in step 3 with the help of Mathematica and get the values of $a_i$, $b_j$, $k$, $c$, $\mu$, $\lambda (\lambda <0)$, $A_1$ and $A_2$. Setting these constants into solution (3.13), we ascertain different type of wave solutions to Eq. (3.10) presented by the hyperbolic functions.

Fifth Step: In the similar way, emulating step 3 and step 4, replacing Eq. (3.13) into (3.12), treating Eqs. (3.3) and (3.7) (or Eq. (3.3) and Eq. (3.9)), we attain the solution of Eq. (3.10) in terms of trigonometric functions (or by rational functions) as proceeding before. The details of the stated method are found in [30, 31, 32, 33, 34, 35, 36, 37] and the references therein.

4. Implementation of the introduced method

In this section, the two variable $\left(G\text{'}/G,1/G\right)$ -expansion method has been ascribed to establish abundant exact wave solutions to the nonlinear space-time fractional Fokas equation, the time fractional nonlinear model equation and the space-time fractional (2 + 1)-dimensional breaking soliton equation.

4.1. The space-time fractional Fokas equation

In this sub-section, the two variable $\left(G\text{'}/G,1/G\right)$ -expansion method is exerted to constitute the exact traveling and solitary wave solutions to the space-time fractional Fokas equation [43,44], stated in Eq. (1.1). For this equation, we take into account the subsequent wave transformation

$$v\left(x_1,x_2,y_1,y_2,t\right)=v\left(\eta \right),\eta =k_1\frac{x_1^{\alpha }}{\Gamma (1+\alpha )}+k_2\frac{x_2^{\alpha }}{\Gamma (1+\alpha )}+l_1\frac{y_1^{\alpha }}{\Gamma (1+\alpha )}+l_2\frac{y_2^{\alpha }}{\Gamma (1+\alpha )}+c\frac{t^{\alpha }}{\Gamma (1+\alpha )},$$ (4.1.1)

where k₁, k₂, l₁, l₂ and c are nonzero constants. Treating the properties of the modified Riemann-Liouville derivative and the wave transformation allow us to transform Eq. (1.1) into an ODE as

$$\left(4c{k}_1-6l_1{l}_2\right)v^{\text{'}}+\left(k_2^3{k}_1-k_1^3{k}_2\right)v^{\text{'}\text{'}\text{'}}+12k_1{k}_2\left(v{v}^{\text{'}}\right)=0,$$ (4.1.2)

where prime denotes the derivative with respect to $\eta$.

For Eq. (4.1.2), the balance number is N = 2, attained by balancing the highest order derivative $v^{\text{'}\text{'}\text{'}}$ with the nonlinear term of the highest order $v{v}^{\text{'}}$. For this value of N, the solution formula (3.13) becomes

$$v\left(\eta \right)=a_0+a_1\varphi +a_2{\varphi }^2+b_1\psi +b_2\varphi \psi ,$$ (4.1.3)

where a₀, a₁, a₂, b₁, b₂ are constants to be ascertained later. Therefore, the above designated three cases are employed as follows [30, 31, 32, 33, 34, 35, 36, 37]:

Case 1

When $\lambda <0$ (Hyperbolic function solutions)

When we substitute the value of $v\left(\eta \right)$ from (4.1.3) into Eq. (4.1.2), in addition to Eqs. (3.3) and (3.5), the left-hand side of Eq. (4.1.2) converts to a polynomial in φ and ψ. Setting each coefficient of the polynomial to zero yields a system of algebraic equations in a₀, a₁, a₂, b₁, b₂, μ, λ and σ. After solving the algebraic system, we obtain the subsequent values of the unknown constants:

$$a_1=0,a_2=\frac{1}{2}(k_1^2-k_2^2),b_1=\frac{1}{2}\mu (k_2^2-k_1^2),b_2=\pm \frac{\sqrt{{\mu }^2+{\lambda }^2\sigma }(k_2^2-k_1^2)}{2\sqrt{-\lambda }},c=\frac{-12a_0{k}_1{k}_2+5\lambda k_1^3{k}_2-5\lambda k_1{k}_2^3+6l_1{l}_2}{4k_1},$$ (4.1.4)

where a₀ is an arbitrary constant.

Setting the above values into the solution (4.1.3), we attain the exact solution of Eq. (1.1) as

$$v\left(\eta \right)=a_0+\frac{\mu (k_2^2-k_1^2)}{2\left(A_{1}sinh\left(\eta \sqrt{-\lambda }\right)+A_{2}cosh\left(\eta \sqrt{-\lambda }\right)+\frac{\mu }{\lambda }\right)}\pm \frac{\sqrt{{\mu }^2+{\lambda }^2\sigma }\left(A_{1}cosh\left(\eta \sqrt{-\lambda }\right)+A_{2}sinh\left(\eta \sqrt{-\lambda }\right)\right)(k_2^2-k_1^2)}{2{\left(A_{1}sinh\left(\eta \sqrt{-\lambda }\right)+A_{2}cosh\left(\eta \sqrt{-\lambda }\right)+\frac{\mu }{\lambda }\right)}^2}-\frac{\lambda {\left(A_{1}cosh\left(\eta \sqrt{-\lambda }\right)+A_{2}sinh\left(\eta \sqrt{-\lambda }\right)\right)}^2(k_1^2-k_2^2)}{2{\left(A_{1}sinh\left(\eta \sqrt{-\lambda }\right)+A_{2}cosh\left(\eta \sqrt{-\lambda }\right)+\frac{\mu }{\lambda }\right)}^2},$$ (4.1.5)

wherein $\sigma =A_1^2-A_2^2$ and

$$\eta =k_1\frac{x_1^{\alpha }}{\Gamma \left(1+\alpha \right)}+k_2\frac{x_2^{\alpha }}{\Gamma \left(1+\alpha \right)}+l_1\frac{y_1^{\alpha }}{\Gamma \left(1+\alpha \right)}+l_2\frac{y_2^{\alpha }}{\Gamma \left(1+\alpha \right)}+\left(\frac{-12a_0{k}_1{k}_2+5\lambda k_1^3{k}_2-5\lambda k_1{k}_2^3+6l_1{l}_2}{4k_1}\right)\frac{t^{\alpha }}{\Gamma \left(1+\alpha \right)}.$$

For special case, if we set A₂ = 0, μ = 0, A₁ ≠ 0 into (4.1.5), the solution turns into

$$v\left(\eta \right)=a_0+\frac{\lambda (k_1^2-k_2^2)}{2}\left(\mp coth\left(\eta \sqrt{-\lambda }\right)csch\left(\eta \sqrt{-\lambda }\right)-{\text{coth}}^2\left(\eta \sqrt{-\lambda }\right)\right).$$ (4.1.6)

Similarly, for other choices of the values of the parameters yield different solutions but for conciseness, the rest of the solutions have not documented here.

Case 2

When $\lambda >0$ (Trigonometric function solutions)

Similarly, as mentioned above in Case 1 and by solving the system of equations yields one set of value of arbitrary constants as follows:

$$a_1=0,a_2=\frac{1}{2}(k_1^2-k_2^2),b_1=\frac{1}{2}\mu (k_2^2-k_1^2),b_2=\mp \frac{\sqrt{{\lambda }^2\sigma -{\mu }^2}(k_2^2-k_1^2)}{2\sqrt{\lambda }},c=\frac{-12a_0{k}_1{k}_2+5\lambda k_1^3{k}_2-5\lambda k_1{k}_2^3+6l_1{l}_2}{4k_1},$$ (4.1.7)

where $a_0$ is an arbitrary constant.

Inserting the above values into solution (4.1.3), we found the exact solution of (1.1) as.

$$v\left(\eta \right)=a_0+\frac{\mu (k_2^2-k_1^2)}{2\left(A_{1}sin\left(\eta \sqrt{\lambda }\right)+A_{2}cos\left(\eta \sqrt{\lambda }\right)+\frac{\mu }{\lambda }\right)}\mp \frac{\sqrt{{\lambda }^2\sigma -{\mu }^2}\left(A_{1}cos\left(\eta \sqrt{\lambda }\right)-A_{2}sin\left(\eta \sqrt{\lambda }\right)\right)(k_2^2-k_1^2)}{2{\left(A_{1}sin\left(\eta \sqrt{\lambda }\right)+A_{2}cos\left(\eta \sqrt{\lambda }\right)+\frac{\mu }{\lambda }\right)}^2}+\frac{\lambda \left(A_{1}cos\left(\eta \sqrt{\lambda }\right)-A_{2}sin\left(\eta \sqrt{\lambda }\right)\right)(k_1^2-k_2^2)}{2{\left(A_{1}sin\left(\eta \sqrt{\lambda }\right)+A_{2}cos\left(\eta \sqrt{\lambda }\right)+\frac{\mu }{\lambda }\right)}^2},$$ (4.1.8)

where $\sigma =A_1^2+A_2^2$ and

$$\eta =k_1\frac{x_1^{\alpha }}{\Gamma (1+\alpha )}+k_2\frac{x_2^{\alpha }}{\Gamma (1+\alpha )}+l_1\frac{y_1^{\alpha }}{\Gamma (1+\alpha )}+l_2\frac{y_2^{\alpha }}{\Gamma (1+\alpha )}+\left(\frac{-12a_0{k}_1{k}_2+5\lambda k_1^3{k}_2-5\lambda k_1{k}_2^3+6l_1{l}_2}{4k_1}\right)\frac{t^{\alpha }}{\Gamma (1+\alpha )}.$$

Setting $A_1=0$, $\mu =0$ and $A_2\ne 0$ into solution (4.1.8), the periodic solution becomes

$$v\left(\eta \right)=a_0+\frac{\lambda (k_1^2-k_2^2)}{2}\left({\text{tan}}^2\left(\eta \sqrt{\lambda }\right)\mp tan\left(\eta \sqrt{\lambda }\right)sec\left(\eta \sqrt{\lambda }\right)\right).$$ (4.1.9)

Besides, setting $A_2=0$, $\mu =0$ and $A_1\ne 0$ into solution (4.1.8), we obtain the next solitary wave solution

$$v\left(\eta \right)=a_0+\frac{\lambda (k_1^2-k_2^2)}{2}\left({\text{cot}}^2\left(\eta \sqrt{\lambda }\right)\pm cot\left(\eta \sqrt{\lambda }\right)csc\left(\eta \sqrt{\lambda }\right)\right).$$ (4.1.10)

Case 3

When $\lambda =0$ (Rational function solution)

Using analogous steps, mentioned in Case 1 and solving the system of equations, we obtain the values of arbitrary constants as follows:

$$a_1=0,a_2=\frac{1}{2}(k_1^2-k_2^2),b_1=\frac{1}{2}\mu (k_2^2-k_1^2),b_2=-\frac{\left(k_2^2-k_1^2\right)\sqrt{A_1^2-2\mu A_2}}{2},c=-\frac{3\left(2a_0{k}_1{k}_2-l_1{l}_2\right)}{2k_1}$$ (4.1.11)

where $a_0$ is an arbitrary constant.

Using (4.1.11) into solution (4.1.3), we attain the new exact solution of Eq. (1.1) in the subsequent form

$$v\left(\eta \right)=\frac{a_0{\left(\mu {\eta }^2+2\eta A_1+2A_2\right)}^2+\left(2A_1^2+2A_1\left(\mu \eta +\sqrt{A_1^2-2\mu A_2}\right)+\mu \left(\eta \left(\mu \eta +2\sqrt{A_1^2-2\mu A_2}\right)-2A_2\right)\right)\left(k_1^2-k_2^2\right)}{{\left(\mu {\eta }^2+2\eta A_1+2A_2\right)}^2},$$ (4.1.12)

where

$$\eta =k_1\frac{x_1^{\alpha }}{\Gamma (1+\alpha )}+k_2\frac{x_2^{\alpha }}{\Gamma (1+\alpha )}+l_1\frac{y_1^{\alpha }}{\Gamma (1+\alpha )}+l_2\frac{y_2^{\alpha }}{\Gamma (1+\alpha )}-\left(\frac{3\left(2a_0{k}_1{k}_2-l_1{l}_2\right)}{2k_1}\right)\frac{t^{\alpha }}{\Gamma (1+\alpha )}.$$

Particularly, if we select $A_1=0$, $\mu =-1$ and $A_2\ne 0$ into (4.1.12), the solution takes the form

$$v\left(\eta \right)=a_0+\frac{(k_1^2-k_2^2)}{{\left(\eta +1\right)}^2}.$$ (4.1.13)

On the other hand, if we select $A_2=0$, $\mu =0$ and $A_1\ne 0$, we attain

$$v\left(\eta \right)=a_0+\frac{k_1^2-k_2^2}{{\eta }^2}.$$ (4.1.14)

4.2. The time fractional (2 + 1)-dimensional nonlinear model

To examine the fractional nonlinear model equation [11,51,52], stated in Eq. (1.3), we introduce the following traveling wave transformation

$$v\left(x,y,t\right)=v\left(\eta \right),$$ (4.2.1)

and

$$\eta =x+iy-\frac{c{t}^{\alpha }}{\text{Γ}\left(1+\alpha \right)},$$ (4.2.2)

where $c$ is the constant to be determined later. Substituting (4.2.2) into (4.2.1), we obtain the ODE as follows

$$c{v}^{\text{'}}+h{v}^2-hr=0.$$ (4.2.3)

The homogeneous balance principle between the highest order derivatives with highest order nonlinear term come out in (4.2.3), we ascertain the value of integer $N=1$. Thus, the solution formula (3.13) becomes

$$v\left(\eta \right)=a_0+a_1\varphi +b_1\psi .$$ (4.2.4)

wherever $a_0$, $a_1$ and $b_1$ are constants to be determined later.

Case 1

When $\lambda <0$ (Hyperbolic function solutions)

Substituting the value of $v\left(\eta \right)$ and its derivatives from (4.2.4) into (4.2.3) along with (3.3) and (3.5), we obtain a system of algebraic equations (for the sake of conciseness, the equations are not displayed here) whose solutions are as follows

Set 1:

$$a_0=0,a_1=\frac{\sqrt{r}}{\sqrt{-\lambda }},b_1=\mp \frac{\sqrt{r}\sqrt{{\mu }^2+{\lambda }^2\sigma }}{\lambda }\text{and}c=\frac{2h\sqrt{r}}{\sqrt{-\lambda }}.$$ (4.2.5)

Substituting the results into (4.2.4), we get the exact solution of (1.3) in the form

$$v\left(\eta \right)=\mp \frac{\sqrt{\text{r}}\sqrt{{\text{μ}}^2+{\text{λ}}^2\text{σ}}}{\text{λ}\left({\text{A}}_1\text{sinh}\left(\text{η}\sqrt{-\text{λ}}\right)+{\text{A}}_2\text{cosh}\left(\text{η}\sqrt{-\text{λ}}\right)+\frac{\text{μ}}{\text{λ}}\right)}+\frac{\sqrt{\text{r}}\left({\text{A}}_1\text{cosh}\left(\text{η}\sqrt{-\text{λ}}\right)+{\text{A}}_2\text{sinh}\left(\text{η}\sqrt{-\text{λ}}\right)\right)}{\left({\text{A}}_1\text{sinh}\left(\text{η}\sqrt{-\text{λ}}\right)+{\text{A}}_2\text{cosh}\left(\text{η}\sqrt{-\text{λ}}\right)+\frac{\text{μ}}{\text{λ}}\right)},$$ (4.2.6)

Here $\sigma =A_1^2-A_2^2$ and $\eta =x+iy-\left(\frac{2h\sqrt{r}}{\sqrt{-\lambda }}\right)\frac{t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}$.

For the particular solution, if we put $A_2=0$, $\mu =0$ and $A_1\ne 0$, the solitary wave solution is

$$v\left(x,y,t\right)=\sqrt{\text{r}}\{\text{coth}\left(\sqrt{-\text{λ}}\left(\text{x}+\text{iy}-\left(\frac{2\text{h}\sqrt{\text{r}}}{\sqrt{-\text{λ}}}\right)\frac{{\text{t}}^{\text{α}}}{\text{Γ}\left(1+\text{α}\right)}\right)\right)\mp \text{csch}\left(\sqrt{-\text{λ}}\left(\text{x}+\text{iy}-\left(\frac{2\text{h}\sqrt{\text{r}}}{\sqrt{-\text{λ}}}\right)\frac{{\text{t}}^{\text{α}}}{\text{Γ}\left(1+\text{α}\right)}\right)\right)\}.$$ (4.2.7)

Set 2:

$$a_0=0,a_1=-\frac{\sqrt{r}}{\sqrt{-\lambda }},b_1=\pm \frac{\sqrt{r}\sqrt{{\mu }^2+{\lambda }^2\sigma }}{\lambda },\text{and}c=-\frac{2h\sqrt{r}}{\sqrt{-\lambda }}.$$ (4.2.8)

Therefore, setting the above results into (4.2.4), the exact solution of Eq. (1.3) derives

$$v\left(\eta \right)=\pm \frac{\sqrt{\text{r}}\sqrt{{\text{μ}}^2+{\text{λ}}^2\text{σ}}}{\text{λ}\left({\text{A}}_1\text{sinh}\left(\text{η}\sqrt{-\text{λ}}\right)+{\text{A}}_2\text{cosh}\left(\text{η}\sqrt{-\text{λ}}\right)+\frac{\text{μ}}{\text{λ}}\right)}-\frac{\sqrt{\text{r}}\left({\text{A}}_1\text{cosh}\left(\text{η}\sqrt{-\text{λ}}\right)+{\text{A}}_2\text{sinh}\left(\text{η}\sqrt{-\text{λ}}\right)\right)}{\left({\text{A}}_1\text{sinh}\left(\text{η}\sqrt{-\text{λ}}\right)+{\text{A}}_2\text{cosh}\left(\text{η}\sqrt{-\text{λ}}\right)+\frac{\text{μ}}{\text{λ}}\right)},$$ (4.2.9)

Here $\sigma =A_1^2-A_2^2$ and $\eta =x+iy+\left(\frac{2h\sqrt{r}}{\sqrt{-\lambda }}\right)\frac{t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}.$

Particularly, for $A_2=0$, $\mu =0$ and $A_1\ne 0$, the solution becomes

$$v\left(x,y,t\right)=\sqrt{\text{r}}\{-coth\left(\sqrt{-\lambda }\left(x+iy+\left(\frac{2h\sqrt{r}}{\sqrt{\lambda }}\right)\frac{t^{\alpha }}{\Gamma \left(1+\alpha \right)}\right)\right)\pm \text{ }csch\left(\sqrt{-\lambda }\left(x+iy+\left(\frac{2h\sqrt{r}}{\sqrt{\lambda }}\right)\frac{t^{\alpha }}{\Gamma \left(1+\alpha \right)}\right)\right)\}.$$ (4.2.10)

Case 2

When $\lambda >0$ (Trigonometric function solutions)

In the similar way, embedding the value of $v\left(\eta \right)$ and its derivatives from (4.2.4) into (4.2.3) including (3.3) and (3.7) and solving the set of algebraic equations by Mathematica, it yields the following set of results.

Set 1:

$$a_0=0a_1=-\frac{\sqrt{-r}}{\sqrt{\lambda }}{b}_1=\mp \frac{\sqrt{r}\sqrt{{\mu }^2-{\lambda }^2\sigma }}{\lambda }\text{ and }c=-\frac{2h\sqrt{-r}}{\sqrt{\lambda }}.$$ (4.2.11)

Setting the above values into solution (4.2.4), we obtain the exact solution of Eq. (1.3) as

$$v\left(\eta \right)=\mp \frac{\sqrt{\text{r}}\sqrt{({\text{μ}}^2-{\text{λ}}^2\text{σ})}}{\text{λ}\left({\text{A}}_1\text{sin}\left(\text{η}\sqrt{\text{λ}}\right)+{\text{A}}_2\text{cos}\left(\text{η}\sqrt{\text{λ}}\right)+\frac{\text{μ}}{\text{λ}}\right)}-\frac{\sqrt{-\text{r}}\left({\text{A}}_1\text{cos}\left(\text{η}\sqrt{\text{λ}}\right)-{\text{A}}_2\text{sin}\left(\text{η}\sqrt{\text{λ}}\right)\right)}{\left({\text{A}}_1\text{sin}\left(\text{η}\sqrt{\text{λ}}\right)+{\text{A}}_2\text{cos}\left(\text{η}\sqrt{\text{λ}}\right)+\frac{\text{μ}}{\text{λ}}\right)},$$ (4.2.12)

where $\sigma =A_1^2+A_2^2$ and $\eta =x+iy+\left(\frac{2h\sqrt{-r}}{\sqrt{\lambda }}\right)\frac{t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}$.

Since $A_1$ and $A_2$ are free parameters, we may select $A_1=0$, $\mu =0$ and $A_2\ne 0$, the solitary wave solution is

$$v\left(x,y,t\right)=\sqrt{-\text{r}}\{\text{tan}\left(\sqrt{\text{λ}}\left(\text{x}+\text{iy}+\left(\frac{2\text{h}\sqrt{-\text{r}}}{\sqrt{\text{λ}}}\right)\frac{{\text{t}}^{\text{α}}}{\text{Γ}\left(1+\text{α}\right)}\right)\right)\mp \text{ sec}\left(\sqrt{\text{λ}}\left(\text{x}+\text{iy}+\left(\frac{2\text{h}\sqrt{-\text{r}}}{\sqrt{\text{λ}}}\right)\frac{{\text{t}}^{\text{α}}}{\text{Γ}\left(1+\text{α}\right)}\right)\right)\}.$$ (4.2.13)

Again, if we select $A_2=0$, $\mu =0$ and $A_1\ne 0$, the solitary wave solution is

$$v\left(x,y,t\right)=-\sqrt{-\text{r}}\{\text{cot}\left(\sqrt{\text{λ}}\left(\text{x}+\text{iy}+\left(\frac{2\text{h}\sqrt{-\text{r}}}{\sqrt{\text{λ}}}\right)\frac{{\text{t}}^{\text{α}}}{\text{Γ}\left(1+\text{α}\right)}\right)\right)\pm \text{ csc}\left(\sqrt{\text{λ}}\left(\text{x}+\text{iy}+\left(\frac{2\text{h}\sqrt{-\text{r}}}{\sqrt{\text{λ}}}\right)\frac{{\text{t}}^{\text{α}}}{\text{Γ}\left(1+\text{α}\right)}\right)\right)\}$$ (4.2.14)

Set 2:

$$a_0=0,\text{ }{a}_1=\frac{\sqrt{-r}}{\sqrt{\lambda }},\text{ }{b}_1=\pm \frac{\sqrt{r}\sqrt{{\mu }^2-{\lambda }^2\sigma }}{\lambda }\text{ and }c=\frac{2h\sqrt{-r}}{\sqrt{\lambda }}.$$ (4.2.15)

By means of the above values, the solution (4.2.4) of Eq. (1.3) is

$$v\left(\eta \right)=\pm \frac{\sqrt{\text{r}}\sqrt{({\text{μ}}^2-{\text{λ}}^2\text{σ})}}{\text{λ}\left({\text{A}}_1\text{sin}\left(\text{η}\sqrt{\text{λ}}\right)+{\text{A}}_2\text{cos}\left(\text{η}\sqrt{\text{λ}}\right)+\frac{\text{μ}}{\text{λ}}\right)}+\frac{\sqrt{-\text{r}}\left({\text{A}}_1\text{cos}\left(\text{η}\sqrt{\text{λ}}\right)-{\text{A}}_2\text{sin}\left(\text{η}\sqrt{\text{λ}}\right)\right)}{\left({\text{A}}_1\text{sin}\left(\text{η}\sqrt{\text{λ}}\right)+{\text{A}}_2\text{cos}\left(\text{η}\sqrt{\text{λ}}\right)+\frac{\text{μ}}{\text{λ}}\right)},$$ (4.2.16)

wherein $\sigma =A_1^2+A_2^2$ and $\eta =x+iy-\left(\frac{2h\sqrt{-r}}{\sqrt{\lambda }}\right)\frac{t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}$.

If we set $A_1=0$, $\mu =0$ and $A_2\ne 0$, the periodic solution (4.2.16) turns into

$$v\left(x,y,t\right)=-\sqrt{-\text{r}}\{\text{tan}\left(\sqrt{\text{λ}}\left(\text{x}+\text{iy}-\left(\frac{2\text{h}\sqrt{-\text{r}}}{\sqrt{\text{λ}}}\right)\frac{{\text{t}}^{\text{α}}}{\text{Γ}\left(1+\text{α}\right)}\right)\right)\mp \text{ sec}\left(\sqrt{\text{λ}}\left(\text{x}+\text{iy}-\left(\frac{2\text{h}\sqrt{-\text{r}}}{\sqrt{\text{λ}}}\right)\frac{{\text{t}}^{\text{α}}}{\text{Γ}\left(1+\text{α}\right)}\right)\right)\}.$$ (4.2.17)

On the other hand, if we put $A_2=0$, $\mu =0$ and $A_1\ne 0$, the periodic solution is

$$v\left(x,y,t\right)=\sqrt{-\text{r}}\{\text{cot}\left(\sqrt{\text{λ}}\left(\text{x}+\text{iy}-\left(\frac{2\text{h}\sqrt{-\text{r}}}{\sqrt{\text{λ}}}\right)\frac{{\text{t}}^{\text{α}}}{\text{Γ}\left(1+\text{α}\right)}\right)\right)\pm \text{ csc}\left(\sqrt{\text{λ}}\left(\text{x}+\text{iy}-\left(\frac{2\text{h}\sqrt{-\text{r}}}{\sqrt{\text{λ}}}\right)\frac{{\text{t}}^{\text{α}}}{\text{Γ}\left(1+\text{α}\right)}\right)\right)\}.$$ (4.2.18)

4.3. The space-time fractional (2 + 1)-dimensional breaking soliton equation

In this subsection, the space-time fractional (2 + 1)-dimensional breaking soliton equation [53], stated in Eq. (1.4) is investigated by putting in use the suggested method and ascertained various types of periodic and solitary wave solutions. To this end, we adopt the following transformation

$$u\left(x,y,t\right)=u\left(\eta \right)\text{, }v\left(x,y,t\right)=v\left(\eta \right).$$ (4.3.1)

$$\eta =\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{c{t}^{\alpha }}{\text{Γ}\left(1+\alpha \right),}$$ (4.3.2)

where $k$$w$, and $c$ are constants such that $k,w,c\ne 0$. Substituting the above transformation into (1.4), the nonlinear Eq. (1.4) becomes

$$-c{u}^{\text{'}}+a{k}^{2}w{u}^{\text{'}\text{'}\text{'}}+4aku{v}^{\text{'}}+4ak{u}^{\text{'}}v=0,w{u}^{\text{'}}-k{v}^{\text{'}}=0.$$ (4.3.3)

Integrating the second equation of (4.3.3) and letting the constant of integration to be zero, we attain

$$wu=kv,$$ (4.3.4)

Substituting (4.3.4) in the first equation of (4.3.3), yields

$$-c{u}^{\text{'}}+a{k}^{2}w{u}^{\text{'}\text{'}\text{'}}+8awu{u}^{\text{'}}=0.$$ (4.3.5)

Integrating the above equation once and ignoring the constant of integration, we obtain

$$-cu+a{k}^{2}w{u}^{\text{'}\text{'}}+4aw{u}^2=0.$$ (4.3.6)

By the homogeneous balance principle, balancing the highest order derivative $u^{\text{'}\text{'}}$ with the highest order nonlinear term $u^2$, we get $N=2$. So, the solution formula arrives

$$u\left(\eta \right)=a_0+a_1\varphi +a_2{\varphi }^2+b_1\psi +b_2\varphi \psi ,$$ (4.3.7)

wherein $a_0$, $a_1$, $a_2$, $b_1$, $b_2$ are constants to be calculated later.

Case 1

When $\lambda <0$ (Hyperbolic function solutions)

Using similar course of action stated in subsection 4.1 (Case 1), we obtain the values of the arbitrary constants as follows:

Set 1:

$$a_0=-\frac{k^2\lambda }{2},a_1=0,a_2=-\frac{3k^2}{4},b_1=\frac{3k^2\mu }{4},b_2=\pm \frac{3k^2\sqrt{{\mu }^2+{\lambda }^2\sigma }}{4\sqrt{-\lambda }},c=a{k}^{2}w\lambda ,$$ (4.3.8)

Making use of the solutions presented in (4.3.7), the exact solution of (1.4) is given by

$$u\left(\eta \right)=-\frac{k^2\lambda }{2}+\frac{3k^2\mu }{4\left(A_{1}sinh\left(\eta \sqrt{-\lambda }\right)+A_{2}cosh\left(\eta \sqrt{-\lambda }\right)+\frac{\mu }{\lambda }\right)}\pm \frac{3k^2\sqrt{{\mu }^2+{\lambda }^2\sigma }\left(A_{1}cosh\left(\eta \sqrt{-\lambda }\right)+A_{2}sinh\left(\eta \sqrt{-\lambda }\right)\right)}{4{\left(A_{1}sinh\left(\eta \sqrt{-\lambda }\right)+A_{2}cosh\left(\eta \sqrt{-\lambda }\right)+\frac{\mu }{\lambda }\right)}^2}+\frac{3k^2\lambda {\left(A_{1}cosh\left(\eta \sqrt{-\lambda }\right)+A_{2}sinh\left(\eta \sqrt{-\lambda }\right)\right)}^2}{4{\left(A_{1}sinh\left(\eta \sqrt{-\lambda }\right)+A_{2}cosh\left(\eta \sqrt{-\lambda }\right)+\frac{\mu }{\lambda }\right)}^2},$$ (4.3.9)

where $\sigma =A_1^2-A_2^2$ and $\eta =\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{a{k}^{2}w\lambda t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}$.

For particular case, if we set $A_2=0$, $\mu =0$ and $A_1\ne 0$, we found the soliton solutions as

$$u\left(\eta \right)=-\frac{k^2\lambda }{2}\left\{1\mp \frac{3}{2}coth\left(\eta \sqrt{-\lambda }\right)csch\left(\eta \sqrt{-\lambda }\right)-\frac{3}{2}cot{h}^2\left(\eta \sqrt{-\lambda }\right)\right\},$$ (4.3.10)

$$v\left(\eta \right)=-\frac{kw\lambda }{2}\left\{1\mp \frac{3}{2}coth\left(\eta \sqrt{-\lambda }\right)csch\left(\eta \sqrt{-\lambda }\right)-\frac{3}{2}cot{h}^2\left(\eta \sqrt{-\lambda }\right)\right\},$$ (4.3.11)

where $\eta =\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{a{k}^{2}w\lambda t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}$.

Set 2:

$$a_0=-\frac{3k^2\lambda }{4},a_1=0,a_2=-\frac{3k^2}{4},b_1=\frac{3k^2\mu }{4}{b}_2=\mp \frac{3k^2\sqrt{{\mu }^2+{\lambda }^2\sigma }}{4\sqrt{-\lambda }},c=-a{k}^{2}w\lambda ,$$ (4.3.12)

By means of the above values, the exact solution (4.3.7) of Eq. (1.4) turns into

$$u\left(\eta \right)=-\frac{3k^2\lambda }{4}+\frac{3k^2\mu }{4\left(A_{1}sinh\left(\eta \sqrt{-\lambda }\right)+A_{2}cosh\left(\eta \sqrt{-\lambda }\right)+\frac{\mu }{\lambda }\right)}\mp \frac{3k^2\sqrt{{\mu }^2+{\lambda }^2\sigma }\left(A_{1}cosh\left(\eta \sqrt{-\lambda }\right)+A_{2}sinh\left(\eta \sqrt{-\lambda }\right)\right)}{4{\left(A_{1}sinh\left(\eta \sqrt{-\lambda }\right)+A_{2}cosh\left(\eta \sqrt{-\lambda }\right)+\frac{\mu }{\lambda }\right)}^2}+\frac{3k^2\lambda {\left(A_{1}cosh\left(\eta \sqrt{-\lambda }\right)+A_{2}sinh\left(\eta \sqrt{-\lambda }\right)\right)}^2}{4{\left(A_{1}sinh\left(\eta \sqrt{-\lambda }\right)+A_{2}cosh\left(\eta \sqrt{-\lambda }\right)+\frac{\mu }{\lambda }\right)}^2}$$ (4.3.13)

wherein $\sigma =A_1^2-A_2^2$ and $\eta =\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{a{k}^{2}w\lambda t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}$.

Now, for $A_2=0$, $\mu =0$ and $A_1\ne 0$, we obtain the wave solution as follows

$$u\left(\eta \right)=\frac{3k^2\lambda }{4}\left\{\mp coth\left(\eta \sqrt{-\lambda }\right)csch\left(\eta \sqrt{-\lambda }\right)+cot{h}^2\left(\eta \sqrt{-\lambda }\right)-1\right\},$$ (4.3.14)

$$v\left(\eta \right)=\frac{3kw\lambda }{4}\left\{\mp \sqrt{\sigma }coth\left(\eta \sqrt{-\lambda }\right)csch\left(\eta \sqrt{-\lambda }\right)+cot{h}^2\left(\eta \sqrt{-\lambda }\right)-1\right\},$$ (4.3.15)

where $\sigma =A_1^2-A_2^2$ and $\eta =\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{a{k}^{2}w\lambda t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}$.

Case 2

When $\lambda >0$ (Trigonometric function solutions)

Correspondingly, the procedure described in subsection 4.1 (Case 2), the following results of the parameters will be derived:

Set 1:

$$a_0=\lambda a_2{a}_1=0b_1=-\mu a_2{b}_2=\mp \frac{a_2\sqrt{{\lambda }^2\sigma -{\mu }^2}}{\sqrt{\lambda }}k=-\frac{2\sqrt{a_2}}{\sqrt{-3}}c=\frac{4aw\lambda a_2}{3}$$ (4.3.16)

where $a_2$ is an arbitrary constant.

Therefore, the trigonometric function solution of Eq. (1.4) is

$$u\left(\eta \right)=\lambda a_2-\frac{\mu a_2}{\left(A_{1}sin\left(\eta \sqrt{\lambda }\right)+A_{2}cos\left(\eta \sqrt{\lambda }\right)+\frac{\mu }{\lambda }\right)}\mp \frac{a_2\sqrt{\left({\lambda }^2\sigma -{\mu }^2\right)}\left(A_{1}cos\left(\eta \sqrt{\lambda }\right)-A_{2}sin\left(\eta \sqrt{\lambda }\right)\right)}{{\left(A_{1}sin\left(\eta \sqrt{\lambda }\right)+A_{2}cos\left(\eta \sqrt{\lambda }\right)+\frac{\mu }{\lambda }\right)}^2}+\frac{\lambda a_2{\left(A_{1}cos\left(\eta \sqrt{\lambda }\right)-A_{2}sin\left(\eta \sqrt{\lambda }\right)\right)}^2}{{\left(A_{1}sin\left(\eta \sqrt{\lambda }\right)+A_{2}cos\left(\eta \sqrt{\lambda }\right)+\frac{\mu }{\lambda }\right)}^2}$$ (4.3.17)

where $\sigma =A_1^2+A_2^2$ and $\eta =\left(-\frac{2\sqrt{a_2}}{\sqrt{-3}}\right)\frac{x^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{4aw\lambda a_2{t}^{\alpha }}{3\text{Γ}\left(1+\alpha \right)}$.

For special case, if we set A₁ = 0, μ = 0 and A₂ ≠ 0, we obtain the soliton solution as

$$u\left(\eta \right)=\lambda a_2\left\{1\pm tan\left(\eta \sqrt{\lambda }\right)sec\left(\eta \sqrt{\lambda }\right)+ta{n}^2\left(\eta \sqrt{\lambda }\right)\right\}$$ (4.3.18)

$$v\left(\eta \right)=-\frac{w\lambda a_2^{1/2}\sqrt{-3}}{2}\left\{1\pm tan\left(\eta \sqrt{\lambda }\right)sec\left(\eta \sqrt{\lambda }\right)+ta{n}^2\left(\eta \sqrt{\lambda }\right)\right\}$$ (4.3.19)

Besides, if we set $A_2=0$, $\mu =0$ and $A_1\ne 0$, the soliton solution is

$$u\left(\eta \right)=\lambda a_2\left\{1\mp cot\left(\eta \sqrt{\lambda }\right)csc\left(\eta \sqrt{\lambda }\right)+co{t}^2\left(\eta \sqrt{\lambda }\right)\right\}$$ (4.3.20)

$$v\left(\eta \right)=-\frac{w\lambda a_2^{1/2}\sqrt{-3}}{2}\left\{1\mp cot\left(\eta \sqrt{\lambda }\right)csc\left(\eta \sqrt{\lambda }\right)+co{t}^2\left(\eta \sqrt{\lambda }\right)\right\}$$ (4.3.21)

Therefore, solutions 4.3.18), 4.3.19), 4.3.20), 4.3.21) are the trigonometric soliton solutions to the space-time breaking soliton equation, wherein $\sigma =A_1^2+A_2^2$ and $\eta =\left(-\frac{2\sqrt{a_2}}{\sqrt{-3}}\right)\frac{x^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{4aw\lambda a_2{t}^{\alpha }}{3\text{Γ}\left(1+\alpha \right)}$.

Set 2:

$$a_0=\frac{2\lambda a_2}{3}{a}_1=0b_1=-\mu a_2{b}_2=\pm \frac{a_2\sqrt{{\lambda }^2\sigma -{\mu }^2}}{\sqrt{\lambda }}k=\frac{2\sqrt{a_2}}{\sqrt{-3}}c=-\frac{4aw\lambda a_2}{3}$$ (4.3.22)

where $a_2$ is arbitrary constant.

Thus, for the above values of the parameters, the exact wave solution of Eq. (1.4) becomes

$$u\left(\eta \right)=\frac{2\lambda a_2}{3}-\frac{\mu a_2}{\left(A_{1}sin\left(\eta \sqrt{\lambda }\right)+A_{2}cos\left(\eta \sqrt{\lambda }\right)+\frac{\mu }{\lambda }\right)}\pm \frac{a_2\sqrt{{\lambda }^2\sigma -{\mu }^2}\left(A_{1}cos\left(\eta \sqrt{\lambda }\right)-A_{2}sin\left(\eta \sqrt{\lambda }\right)\right)}{{\left(A_{1}sin\left(\eta \sqrt{\lambda }\right)+A_{2}cos\left(\eta \sqrt{\lambda }\right)+\frac{\mu }{\lambda }\right)}^2}+\frac{\lambda a_2{\left(A_{1}cos\left(\eta \sqrt{\lambda }\right)-A_{2}sin\left(\eta \sqrt{\lambda }\right)\right)}^2}{{\left(A_{1}sin\left(\eta \sqrt{\lambda }\right)+A_{2}cos\left(\eta \sqrt{\lambda }\right)+\frac{\mu }{\lambda }\right)}^2}$$ (4.3.23)

where $\sigma =A_1^2+A_2^2$ and $\eta =\left(\frac{2\sqrt{a_2}}{\sqrt{-3}}\right)\frac{x^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{4aw\lambda a_2{t}^{\alpha }}{3\text{Γ}\left(1+\alpha \right)}$.

Since $A_1$, $A_2$ and $\mu$ are free parameters, we might choose randomly their values. If we choose $A_1=0$, $\mu =0$ and $A_2\ne 0$, the solution (4.3.23) reduces to the form

$$u\left(\eta \right)=\lambda a_2\left\{\frac{2}{3}\mp tan\left(\eta \sqrt{\lambda }\right)sec\left(\eta \sqrt{\lambda }\right)+ta{n}^2\left(\eta \sqrt{\lambda }\right)\right\}$$ (4.3.24)

$$\nu \left(n\right)=\frac{w\lambda a_2^{1/2}\sqrt{-3}}{2}\left\{\frac{2}{3}\mp tan\left(\eta \sqrt{\lambda }\right)sec\left(\eta \sqrt{\lambda }\right)+ta{n}^2\left(\eta \sqrt{\lambda }\right)\right\}$$ (4.3.25)

Moreover, if we choose $A_2=0$, $\mu =0$ and $A_1\ne 0$, we obtain

$$u\left(\eta \right)=\lambda a_2\left\{\frac{2}{3}\pm cot\left(\eta \sqrt{\lambda }\right)csc\left(\eta \sqrt{\lambda }\right)+co{t}^2\left(\eta \sqrt{\lambda }\right)\right\}$$ (4.3.26)

$$v\left(\eta \right)=\frac{w\lambda a_2^{1/2}\sqrt{-3}}{2}\left\{\frac{2}{3}\pm cot\left(\eta \sqrt{\lambda }\right)csc\left(\eta \sqrt{\lambda }\right)+co{t}^2\left(\eta \sqrt{\lambda }\right)\right\}$$ (4.3.27)

whereas $\sigma =A_1^2+A_2^2$ and $\eta =\left(\frac{2\sqrt{a_2}}{\sqrt{-3}}\right)\frac{x^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{4aw\lambda a_2{t}^{\alpha }}{3\text{Γ}\left(1+\alpha \right)}$.

Remark: All the above-mentioned solutions have been tested by substituting them back into the original equation via symbolic computer program Mathematica and found correct.

5. Graphical representations

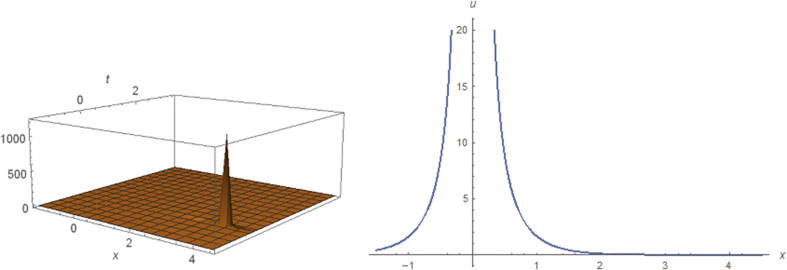
In this section, we briefly illustrate the physical significance and displayed graphical patterns of the achieved solutions to the space-time fractional Fokas equation, the time fractional nonlinear model equation and the space-time fractional (2 + 1)-dimensional breaking soliton equation. The solutions are derived in terms of hyperbolic, trigonometric and rational functions. Introducing several values of the free parameters, the general exact solutions of these equations are converted into different known shape waves, namely, kink, bell shape soliton, periodic soliton, singular solitons etc. Solutions (4.1.6) and (4.3.10) represent the soliton waves which are sketched in Figures 1 and 2 with the values $a_0=-1.4$, $k_1=-2.5$, $k_2=-3.4$, $l_1=-0.8$, $l_2=-0.3$, $\lambda =1$, $a=-1.2$, $k=-0.5$, $w=1.3$ and $\text{λ}=2$ within the intervals $-1.4\le x,t\le 4.4$ and $-2.5\le x,t\le 2.5$ respectively. For different values of the free parameters, the solutions (4.1.9), (4.1.10), (4.2.13), (4.3.20) are presented in Figures 3, 4, 5, and 6 which are periodic waves within the intervals $-3\le x\le 3$, $-1.2\le t\le 3.4$; $-5\le x\le 5$, $-2\le t\le 2$; $-2.5\le x,t\le 3.5$; $-5\le x\le 5$ and $-3\le t\le 3$ respectively. The solution (4.2.7) designate the kink shape soliton for $r=3$, $h=5$, $\lambda =-3$ within the interval$-5\le x\le 5$ and $-1\le t\le 1$ which is displayed in Figure 7. Moreover, solution (4.3.14) represents the multiple singular soliton type wave for the values $a=-3.5$, $k=-1.5$, $w=3.2$, $\lambda =3$ within the interval$-1.5\le x,t\le 4.5$which is shown in Fig. (8).

Figure 7.

Shape of solution (4.3.14) and its projection at $t=0$.

Figure 1.

Shape of solution (4.1.6) and its projection at $t=0$.

Figure 2.

Shape of solution (4.1.9) and its projection at $t=1$.

Figure 3.

Shape of solution (4.1.10) and its projection at $t=0$.

Figure 4.

Shape of solution (4.2.7) and its projection at $t=0$.

Figure 5.

Shape of solution (4.2.13) and its projection at $t=1$.

Figure 6.

Shape of solution (4.3.10) and its projection at $t=0$.

Figure 8.

Shape of solution (4.3.20) and its projection at $t=0$.

6. Results and discussion

The key accomplishment of an advanced method, namely the two variable $\left(G^{\text{'}}/G,1/G\right)$-expansion method is to emphasize new and further general exact solitary wave solutions in closed-form. In the attained solutions, since the parameters $A_1$ and $A_2$ receive various specific values, the traveling wave solutions convert into different solitary wave solutions. Setting $\mu =0$ and $b_j=0$, into (3.1) and (3.13) respectively, the two variable $\left(G^{\text{'}}/G,1/G\right)$-expansion method turns into the original $\left(G^{\text{'}}/G\right)$-expansion method. In Ref. [40], the solution of space-time fractional Fokas equation has been searched by introducing extended Kudryashov method and accomplished solutions which are only in the form of hyperbolic function. On the contrary, utilizing the two variable $\left(G^{\text{'}}/G,1/G\right)$-expansion method in this article, we obtain various types of solitary wave solutions which include the form of hyperbolic, trigonometric and rational functions. Also, placing various particular values of the parameters singular-soliton, kink and periodic solutions of fractional Fokas equation are found. In Ref. [51], Bekir and Guner investigated by the $\left(G^{\text{'}}/G\right)$-expansion method and obtained only eight exact wave solutions which are in the form of tanh and coth functions. But, by means of the $\left(G^{\text{'}}/G,1/G\right)$-expansion method, we have established twenty-four solutions including periodic, soliton, singular-kink solutions and presented hyperbolic, rational and trigonometric functions form. Besides, in Ref. [61] Guner searched the solution of space-time fractional (2 + 1)-dimensional breaking soliton equation and acquired only bright and singular soliton solutions by treating an ansatz method, which is the form of hyperbolic function solution. On the other hand, implementing advanced two variable $\left(G^{\text{'}}/G,1/G\right)$-expansion method, we have gained more general thirty solitary wave solutions including multiple-soliton, periodic and bell-shaped solutions, which have not been listed in the previous literature. We have also compared the obtained solutions with those obtained in [40,51,61], which are presented in Tables 1 2 and 3:

Table 1.

Comparison of the solutions to the space-time fractional Fokas equation.

Ege and Misirli's [40] solution

The obtained solutions

For $a_0=a_0,$$a_1=0$, $a_2=4k_2^2$, $a_4=-4k_2^2$, $k_1=0$, $l_1=0$ and $c=c$, then the hyperbolic solution of Eq. (4.5) becomes, $u_5\left(x_1,x_2,y_1,y_2,t\right)=a_0+\frac{k_2^2}{cos{h}^2\left[\frac{k_2{x}_2^{\alpha }+l_2{y}_2^{\alpha }+c{t}^{\alpha }}{\Gamma (1+\alpha )/2}\right]}$.

If $a_1=0$, $a_2=\frac{1}{2}(k_1^2-k_2^2)$, $b_1=\frac{1}{2}\mu (k_2^2-k_1^2)$, $b_2=\pm \frac{\sqrt{{\mu }^2+{\lambda }^2\sigma }(k_2^2-k_1^2)}{2\sqrt{-\lambda }}$, $c=\frac{-12a_0{k}_1{k}_2+5\lambda k_1^3{k}_2-5\lambda k_1{k}_2^3+6l_1{l}_2}{4k_1}$, the hyperbolic solution (4.1.6) is $v\left(\eta \right)=a_0+\frac{\lambda (k_1^2-k_2^2)}{2}\times \left(\mp coth\left(\eta \sqrt{-\lambda }\right)csch\left(\eta \sqrt{-\lambda }\right)-{\left(coth\left(\eta \sqrt{-\lambda }\right)\right)}^2\right)$

Table 2.

Comparison of the solutions to the time fractional nonlinear model.

Bekir and Guner's [51]solution

The obtained solutions

Particularly, if $C_1\ne 0$, $C_2=0$, $\lambda >0$, $\mu =0$ then the solution of hyperbolic form is $u_{\mathrm{1,2}}\left(x,y,t\right)=\pm \sqrt{r}tanh\frac{\lambda }{2}\left(x+iy+\frac{2h}{\text{Γ}\left(1+\alpha \right)}\sqrt{\frac{r}{{\lambda }^2-4\mu }}{t}^{\alpha }\right)$, Also, the trigonometric solution is $u_{\mathrm{1,2}}\left(x,y,t\right)=\pm \sqrt{r}cot\frac{\lambda }{2}\left(x+iy+\frac{2h}{\text{Γ}\left(1+\alpha \right)}\sqrt{\frac{r}{{\lambda }^2-4\mu }}{t}^{\alpha }\right)$.

For special s, if $A_2=0$, and $A_1\ne 0$, the hyperbolic solution is $v=\sqrt{r}\{coth\left(\sqrt{-\lambda }\left(x+iy-\left(\frac{2h\sqrt{r}}{\sqrt{-\lambda }}\right)\frac{t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}\right)\right)$ $\mp csch\left(\sqrt{-\lambda }\left(x+iy-\left(\frac{2h\sqrt{r}}{\sqrt{-\lambda }}\right)\frac{t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}\right)\right)\}$, and the trigonometric solution is $v=\sqrt{-r}\{cot\left(\sqrt{\lambda }\left(x+iy-\left(\frac{2h\sqrt{-r}}{\sqrt{\lambda }}\right)\frac{t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}\right)\right)$ $\pm csc\left(\sqrt{\lambda }\left(x+iy-\left(\frac{2h\sqrt{-r}}{\sqrt{\lambda }}\right)\frac{t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}\right)\right)\}$.

Table 3.

Comparison of the solutions to the space-time fractional (2 + 1)-dimensional breaking soliton equation.

Guner [61] solutions

The obtained solutions

For$A=\frac{3k^2}{2}$ and $c=4aw{k}^2$, then the non-topological solution of Eq. (42) takes into the form $u\left(x,y,t\right)=\frac{3k^2}{2}sec{h}^2\left(\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{4a{k}^{2}w{t}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}\right)$, and $v\left(x,y,t\right)=\frac{3kw}{2}sec{h}^2\left(\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{4a{k}^{2}w{t}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}\right)$,

Especially, if$A_2=0$, $\mu =0$ and $A_1\ne 0$, then the soliton solutions (4.3.14) and (4.3.15) become $u\left(x,y,t\right)=-\frac{k^2\lambda }{2}\left(\mp \frac{3}{2}coth\left(\left(\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{a{k}^{2}w\lambda t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}\right)\sqrt{-\lambda }\right)csch\left(\left(\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{a{k}^{2}w\lambda t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}\right)\sqrt{-\lambda }\right)-\frac{3}{2}{\left(coth\left(\left(\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{a{k}^{2}w\lambda t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}\right)\sqrt{-\lambda }\right)\right)}^2+1\right)$, and $v\left(x,y,t\right)=-\frac{kw\lambda }{2}\left(\mp \frac{3}{2}coth\left(\left(\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{a{k}^{2}w\lambda t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}\right)\sqrt{-\lambda }\right)csch\left(\left(\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{a{k}^{2}w\lambda t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}\right)\sqrt{-\lambda }\right)-\frac{3}{2}{\left(coth\left(\left(\frac{k{x}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}+\frac{w{y}^{\alpha }}{\text{Γ}\left(1+\alpha \right)}-\frac{a{k}^{2}w\lambda t^{\alpha }}{\text{Γ}\left(1+\alpha \right)}\right)\sqrt{-\lambda }\right)\right)}^2+1\right).$

From the above comparison, it is observed that all of the obtained solutions are completely fresh and general than the solutions existing in the literature.

7. Conclusion

In this article, the recently developed and generalized two variable $\left(G\text{'}/G,1/G\right)$-expansion method has been successfully implemented and derived functional closed-form exact traveling and solitary wave solutions to some nonlinear space-time fractional equations, namely, the fractional Fokas equation, the time fractional nonlinear model equation and the space-time fractional (2 + 1)-dimensional breaking soliton equation. By introducing different values of the free parameters the solutions convert into diverse expected soliton solutions, for instance, bell shape soliton, kink, periodic wave solution, compacton, etc. which are depicted graphically. It is important to notice that the new type of ascertained solutions has not been reported in the previous literature. The worked-out results assured that the presented method seems a promising and powerful mathematical tool that reduces the computational complication, durable and can be operative approach from the theoretical point of view. It is expected that the method can be frequently applied to examine various types of nonlinear fractional PDEs, which frequently emerges in the arena of nonlinear science and engineering.

Declarations

Author contribution statement

H. M. Shahadat Ali: Conceived and designed the analysis; Analyzed and interpreted the data; Wrote the paper.

M. A. Habib, M. Mamun Miah, M. Ali Akbar: Analyzed and interpreted the data; Wrote the paper.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Competing interest statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.