Mathematical model to reduce loop mediated isothermal amplification (LAMP) false‐positive diagnosis

Abstract

Loop mediated isothermal amplification (LAMP) is a nucleic acid amplification technique performed under isothermal conditions. The output of this amplification technique includes multiple different sizes of deoxyribonucleic acid (DNA) structures which are identified by a banding pattern on gel electrophoresis plots. Although this is a specific amplification technique, the complexity of the primer design and amplification still lead to the issue of obtaining false‐positive results, especially when a positive reading is determined solely by whether there is any banding pattern in the gel electrophoresis plot. Here, we first performed extensive LAMP experiments and evaluated the DNA structures using microchip electrophoresis. We then developed a mathematical model derived from the various components that make up an entire LAMP structure to predict the full LAMP structure size in base pairs. This model can be implemented by users to make predictions for specific, DNA size dependent, banding patterns on their gel electrophoresis plots. Each prediction is specific to the target sequence and primers used and therefore reduces incorrect diagnosis errors through identifying true‐positive and false‐positive results. This model was accurately tested with multiple primer sets in house and was also translatable to different DNA and RNA types in previously published literature. The mathematical model can ultimately be used to reduce false‐positive LAMP diagnosis errors for applications ranging from tuberculosis diagnostics to E. coli to numerous other infectious diseases.

Abbreviations

B3

backward outer primer

BIP

backward inner primer

F3

forward outer primer

FIP

forward inner primer

LAMP

loop mediated isothermal amplification

SARS

severe acute respiratory syndrome

1. Introduction

Nucleic acid sequences are an invaluable tool in diagnosing diseases and understanding an individual's genetic makeup. There are a variety of DNA amplification techniques used to increase the quantity of target DNA fragments for diagnostics. One commonly used method of DNA amplification is PCR. This technique works by using three different temperatures to amplify the DNA 1. Due to the restrictions that the temperature cycling needed to run PCR places on equipment and experimental setup, there has been an emphasis on developing DNA amplification techniques that can be performed at one temperature, or isothermally. Isothermal techniques to note are loop mediated isothermal amplification (LAMP), rolling circle amplification, and nucleic acid sequence‐based amplification. Rolling circle amplification works with a single stranded, circular DNA template and strand displacing DNA polymerase 2. The DNA polymerase performs strand‐displacing synthesis on the ssDNA and ‘rolls’ out a copy of the circular DNA under isothermal conditions 2, 3. Nucleic acid sequence‐based amplification is also executed under isothermal conditions but is a transcription‐based amplification procedure that copies single stranded RNA or DNA sequences 2, 4. Two RNA primers and three enzymes are used, and the procedure includes both an initiation phase and an amplification phase to create the final amplification product 2. Although these methods perform well under isothermal conditions, the focus of this mathematical model analysis is LAMP.

LAMP was discovered in 2000 by Notomi et al. and uses four to six primers to target six to eight primer binding sites within the target DNA 5. The primers include forward and backward inner primers (FIP and BIP), outer primers (F3 and B3), and loop primers. A detailed schematic of the LAMP process is outlined in Fig. 1. The LAMP process begins with a double stranded DNA template (Step 1). Next, the Bst DNA polymerase enzyme used in this reaction causes strand displacement by the forward inner primer (FIP) primer hybridizing F2 to the primer binding site at F2c (Step 2) 5. The inner primers are made up of two parts, one with the sense (5′ to 3′) and one with the antisense (3′ to 5′) strand complementary to the template DNA 5. Strand displacing DNA polymerase separates the dsDNA and creates a new copy of the template DNA starting from the inner primer 5. Hybridization of the forward outer primer (F3) to its respective primer binding site (F3c) then creates another new copy of the template while displacing the ssDNA created from the inner primer (Step 3) 5. Nucleotides are added to the F3 3′ end which releases the single strand of DNA including the FIP primer and the F1 and F1c sites are bound together using hydrogen bonds, creating a self‐hybridizing, single‐stranded loop (Step 4). This is then used as a template to repeat this process on the opposite end of the DNA structure with new, corresponding backward inner and outer primers, culminating in the production of a dumbbell structure (Steps 5–7) 5.

Figure 1.

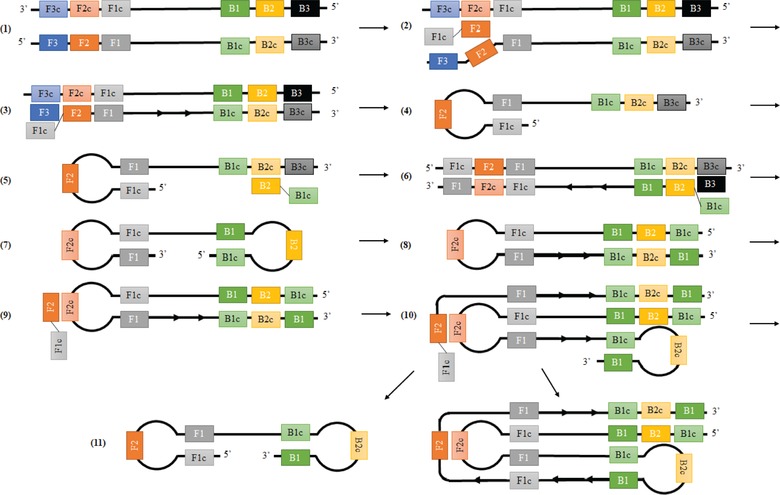
LAMP Dumbbell Formation (Steps 1–7) and LAMP Cycling (Steps 8–11) schematic using FIP binding sites (F1 and F2), F3 binding site, BIP binding sites (B1 and B2), and B3 binding site. All complement sequences are noted with a ‘c’ following the primer binding site name.

Next, LAMP cycling begins with extension from the 3′ end of the dumbbell structure, creating the first ‘stem and loop’ structure (Step 8). A new FIP primer binds to the F2c primer binding site (Step 9) and a new strand of DNA makes a copy of the stem and loop structure which creates a new loop between B1c and B1 primer binding sites (Step 10). Lastly, nucleotides are added to the 3′ end of DNA structure again which releases the newly created strand of DNA which will fold into a dumbbell structure and new stem and loop LAMP structure is also created which has an additional target sequence from the previous structure (Step 11). The newly created stem and loop DNA structure is used as another template for LAMP cycling using one inner primer at a time, either FIP or BIP 5. The overall result of LAMP can make 10⁹ copies of the target DNA when starting from a few copies within an hour 5. This efficient amplification is a major advantage of LAMP, as well as its ability to produce these DNA copies all under isothermal conditions.

Currently, LAMP has been widely used for infectious disease diagnostic applications where the researcher's main objective is to correctly identify positive and negative LAMP reactions to identify a specific disease 6, 7, 8. A positive LAMP reaction indicates that the target DNA sequence, representing a disease or other diagnosis such as human influenza viruses H1 or H3 9, has been amplified, and therefore identified in that sample. A negative LAMP reaction indicates that the sample does not contain that target sequence since it has not been identified and amplified in the reaction, therefore leading to a negative reaction and a negative diagnosis. Here, the focus is on better understanding the DNA structures that are created through this amplification technique since, unlike PCR, DNA copies created through LAMP are dissimilar in size. This investigation is done using mathematical modeling to predict the size of different DNA structures produced through LAMP using gel or microchip electrophoresis.

Mathematical modeling for LAMP has been used once previously to quantify the LAMP amplification process 10. This model uses the concentration versus time curves of LAMP experiments to determine the time‐to‐positive (T_p) of LAMP samples which is considered equivalent to the threshold cycling time in PCR reactions 10. Here, an alternative approach to better understand the amplification process is provided. This new mathematical model makes it possible to instead predict the banding pattern associated with positive LAMP samples during gel electrophoresis. A major benefit of this model is that it creates a user‐friendly prediction method for positive LAMP samples which allows for false‐positive reactions to be more easily identified and increases researchers’ understanding on different DNA products in the reaction.

The developed mathematical model fills a gap in the research on LAMP as a simple, easy to use tool that quickly recognizes false‐positive LAMP reactions. Since the stem and loop structures created through LAMP are complex in nature, creating this simple tool can be relatively difficult 11. In conventional PCR, researchers can predict the output DNA sizes of their amplified product in a true‐positive reaction based on the location of the forward and reverse primers on the template DNA. The complexity of the LAMP process has not allowed for that same predictive method. However, this mathematical model is a new tool that now allows researchers to make those same predictions for the sizes of the different amplified products produced through a true‐positive LAMP reaction based on the target and primer sizes. Similar to recognizing true‐positive reactions on gel electrophoresis plots for PCR, this model allows researchers to quickly recognize true‐positive and false‐positive amplification for LAMP because they will know what the correct banding pattern should be. Thus, if the gel electrophoresis plot shows an alternative banding pattern, the researchers can identify the sample as a false‐positive which can help to reduce the likelihood of an incorrect diagnosis. Current methods to reduce the chance of false‐positive LAMP reactions include optimizing LAMP reactions using multiple runs and techniques to find true positive results 12, 13 or using more intricate methods such as molecular beacons that only fluoresce when bound to target DNA or restriction enzyme digestions 5, 9, 14. Overall, this mathematical model helps to create a predictive method for researchers to implement into their LAMP experimental design that is of no extra cost to them, uses information already gathered during LAMP primer designing, and reduces the likelihood of false‐positive diagnosis.

2. Materials and methods

2.1. Template DNA

The LAMP analysis conducted in this study used M13mp18 (GenBank Accession #: X02513) as the template DNA. This is a double stranded phage vector that originated from bacteriophage M13 and was purchased from New England Biolabs (Ipswich, MA). It is a covalently closed circular DNA that contains 13 different restriction sites.

2.2. Primer design

The two sets of LAMP Primers (see Table 1) used in this study were designed from M13mp18 template DNA (New England Biolabs, Ipswich, MA). The EIKEN Primer Explorer version 5 software was used to generate the sequences for each FIP, F3, BIP, and backward outer primer (B3). The target positions of the primers are illustrated in Fig. 2. All the primers were then synthesized by Integrated DNA Technologies (Coralville, IA). Forward and backward loop primers were not originally used in this study to keep the LAMP procedure as simple as possible for this modeling application. Forward loop and backward loop primers were created and tested when evaluating the robustness of the model.

Table 1.

LAMP primers designed to be used with M13mp18 template DNA

Primer name	Length	Sequence (5′‐3′)
FIP‐1 (F1c + F2)	40‐mer	GCTATTACGCCAGCTGGCGAAGGAAAACCCTGGCGTTACC
BIP‐1 (B1c + B2)	38‐mer	CACCGATCGCCCTTCCCAACGCCGGAAACCAGGCAAAG
FIP‐2 (F1c + F2)	41‐mer	ACAACATACGAGCCGGAAGCAAGTTAGCTCACTCATTAGGC
BIP‐2 (B1c + B2)	42‐mer	ACACAGGAAACAGCTATGACCACAGGTCGACTCTAGAGGATC
F3‐1	20‐mer	CGTCGTTTTACAACGTCGTG
B3‐1	18‐mer	GCACTCCAGCCAGCTTTC
F3‐2	19‐mer	GCGCAACGCAATTAATGTG
B3‐2	18‐mer	GTAAAACGACGGCCAGTG
Forward loop	18‐mer	GCGAAAGGGGGATGTGCT
Backward loop	18‐mer	AGTTGCGCAGCCTGAATG

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

Figure 2.

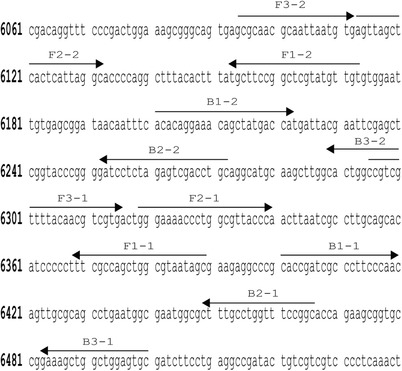
Schematic of LAMP primer sites within the M13mp18 template DNA.

2.3. LAMP reaction conditions

The LAMP reaction was conducted in a total volume of 25 µL and followed WarmStart® LAMP Kit (DNA & RNA) specifications (New England Biolabs, Ipswich, MA). The reaction mixture included 12.5 µL of NEB WarmStart LAMP 2X Master Mix which contains a combination of the enzymes Bst 2.0 WarmStart DNA Polymerase, WarmStart RTx Reverse Transcriptase, dNTPs, and MgSO₄. These enzymes were contained within an Isothermal Amplification Buffer optimized for LAMP and RT‐LAMP reactions according to the manufacturer. The exact concentration of these enzymes was not specified by NEB. The mixture also contained the following primers: 1.6 µM of FIP and BIP, and 0.2 µM of F3 and B3. Lastly, 9 µL of nuclease free water and 100 ng (1.28 × 10¹⁰ copies) of the M13mp18 target DNA was added to each LAMP reaction. Samples were heated to 67°C for 30 min, followed by a 5‐minute Bst 2.0 WarmStart DNA Polymerase inactivation step at 95°C.

2.4. Gel electrophoresis assessment of the LAMP product

Following every LAMP reaction, 1 µL of each sample was run through the Agilent Bioanalyzer 2100 machine with the Agilent DNA 1000 Kit and DNA Chip for On‐Chip‐Electrophoresis (Agilent Technologies, Santa Clara, CA). According to the Agilent DNA 1000 Kit Guide, the sensitivity of the kit is ± 5 base pairs (bps) with samples between 25 and 100 bps, ± 5% between 100 and 500 bps, and ± 10% between 500 and 1000 bps. The output of the Agilent Bioanalyzer 2100 is a gel electrophoresis plot, an electropherogram plot, and the concentration (ng/µL) and molarity (nmol/L) associated with each band or peak. The individual DNA sample concentrations at each band or peak were added together to find the overall concentration produced in the reaction.

2.5. Optimization of LAMP assay

Optimizing the LAMP procedure with the first set of LAMP primers (FIP‐1, BIP‐1, F3‐1, B3‐1) was required prior to LAMP product analysis. Optimization criteria included: creating a large amount of total LAMP product (∼30–50 ng/µL or more), creating a distinct banding pattern – represented by the lowest number of peaks on the electropherogram, and running the experiment in the least amount of time. The criteria were chosen to produce an abundant amount of DNA product with an easily identifiable banding pattern in an efficient amount of time. The variables tested during the optimization process were: adding a LAMP enzyme (Bst 2.0) inactivation temperature step, temperature, time, and temperature of LAMP enzyme inactivation step.

2.6. Development of mathematical model for base pair size analysis of LAMP structures

The DNA analysis tool used in this study was the Agilent Bioanalyzer 2100. This machine was essential for the novel evaluation and interpretation of LAMP products under varying conditions because it could give precise readouts for DNA structure. The Agilent Bioanalyzer 2100 device clearly demonstrated that the LAMP experiments led to distinct and relatively consistent products–within ∼10 bps–based on the DNA target sequence being used. Conventional gel electrophoresis does not provide specific base pair size outputs for each reaction, which is why this microchip electrophoresis machine was used in this study. The Bioanalyzer data also showed varying amounts of noise most likely caused by incomplete LAMP structures depending on the length of time and the temperature the test was run at. The most important analysis to note from the Bioanalyzer is the base pair sizes associated with the largest peaks on the electropherogram plots as these were the most common product sizes and the values used to create this mathematical model.

As previously noted, the main aim of this study was to provide users with a simple tool that can quickly recognize false‐positive LAMP reactions. This was approached through developing a mathematical model to easily create predictions for the sizes of different LAMP structures before performing any experiments. Thus, these predictions can be used to identify true‐positive and false‐positive LAMP reactions using gel electrophoresis banding pattern analysis.

The overall process of creating this model involved transforming the qualitative LAMP structure into a quantitative LAMP structure size. The first step of the model development was to identify how many times different primer binding sequences (F1, F2, F3, B1, B2, B3) appeared in the final LAMP product. This was important so that the size (bp) of each of these sequences could be multiplied by the number of times they appear in the final structure resulting in the overall structure size. Figure 1 shows that regardless of the number of target sequences, the final LAMP product will contain the same four primer binding sites: F1, F2, B1, and B2. Additionally, the sequences F_space (sequence between F1 and F2 sequences in forward inner primer), and B_space (sequence between B1 and B2 sequences in backward inner primer) will be in every final structure. Lastly, every LAMP structure will contain a specified amount of target sequences. The number of times each of these seven components appear in a LAMP structure is important when predicting the overall size. Therefore, different LAMP structures were evaluated to count the number of times each of these parts were found. Figure 1 was used for analyzing the Stem and Loop ×1 and Stem and Loop ×2 structures, and additional LAMP schematics by Notomi et al. 5 were used for structures up to Stem and Loop ×7 which contains 7 target sequences. Table 2 breaks down this quantitative analysis to show a population count for how many times each primer binding site, F_space, B_space, and target appears in each structure. These counts are consistent between any LAMP structures, irrespective of the diagnostic application. As amplification occurs, each cycle adds one target sequence and one primer binding site–either FIP (F1 and F2) or BIP (B1 and B2), depending on the structure that was amplified. Due to the self‐hybridizing loop that appears in the stem and loop structures, the addition of new primer binding sites during each amplification cycle can be complex to understand, therefore making Table 2 helpful in determining how many times each primer binding site appears for any given structure.

Table 2.

Quantitative analysis of the number of times six components of the LAMP structure appear in relation to the number of target sequences

Structure	Target	B2	Bspace	B1	F1	Fspace	F2
Stem and Loop ×1	1	1	1	1	2	1	1
Stem and Loop ×2	2	2	2	3	2	1	1
Stem and Loop ×3	3	2	2	3	4	2	2
Stem and Loop ×4	4	3	3	5	4	2	2
Stem and Loop ×5	5	3	3	5	6	3	3
Stem and Loop ×6	6	4	4	7	6	3	3
Stem and Loop ×7	7	4	4	7	8	4	4

B_space: sequence between B1 and B2 sequences in backward inner primer

F_space: sequence between F1 and F2 sequences in forward inner primer

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

Upon detailed analysis, Table 2 identifies a pattern obtained when comparing the number of times different primer binding sites and spaces appear in the LAMP structure to the number of target sequences. This pattern was essential in the development of the mathematical model. Also, as each amplification cycle adds either a FIP or BIP primer the model was split into two parts to account for this. It was also assumed that the loop of the stem and loop structure always included B2–part of the BIP primer–for developing this model. Therefore, an odd number of targets will end with the FIP primer represented by one equation, and an even number of targets will end with the BIP primer represented by a second equation. Each component of the final two equations was individually derived through relating the number of times a primer binding site appeared in a structure versus a target site. Equation (1) and (2) demonstrate how to relate the primer binding site B2 to the target for odd and even numbers of targets, respectively.

Equation (1) Number of B2 sequences in a LAMP Structure with an odd target number (x);

$$\mathrm{B}2\mathrm{Sequences}=\left(x\left(\frac{x-1}{2}\right)\right)$$ (1)

As an example, in a LAMP structure that has 3 target sequences, Equation (1) multiplies out to 2 when x = 3. This indicates that there are two B2 sequences in this structure and is confirmed again by Table 2. This equation will give the correct number of B2 sequences in all structures with an odd number of targets.

This equation derivation is repeated for B2 sequences when there is an even number of target sequences.

Equation (2) Number of B2 Sequences in a LAMP Structure with an even target number (x):

$$\mathrm{B}2\mathrm{Sequences}=\left(x-\left(\frac{x}{2}-1\right)\right)$$ (2)

This equation is tested using an example LAMP structure with 4 target sequences (x = 4). According to Equation (2), the structure will have three B2 sequences which corresponds with the value in Table 2. This evaluation is repeated for each of the six components of the LAMP structure (in Table 2) to relate the number of times they are repeated to the number of times the target sequence is present.

To convert the number of times each primer binding site appears in the equation to how many base pairs this will add to the overall structure, each of the values calculated in Equation (1), Equation (2) and subsequent derivations, were multiplied by the respective size (bp) of the primer binding site. This information is easily and immediately available to the user when creating specific LAMP primers. Using Fig. 2 for example, this shows the location of different primer binding sites in the target sequence so that each component of the LAMP structure can be identified, and the number of base pairs contained in that component can be counted. Then, in the final equations that calculate the overall structure sizes (bp) in this model, each of the individual primer binding site sizes will be inputted to the respective variable. One assumption made in this model is that the loops created in stem and loop structures are considered base pairs in this size estimation although they are single stranded nucleotides. Ultimately, following individual derivation for each component of the LAMP structure, two master equations are outputted: one that predicts the LAMP structure size (bp) with an odd number of target sequences (Equation (4)) and one that predicts the LAMP structure size (bp) with an even number of target sequences (Equation (5)). A breakdown of how to interpret these equations is first presented in Equation (3)

$$\begin{array}{c}\mathit{\text{LAMP}}\mathit{\text{Structure}}\mathit{\text{Size}}\left(\mathit{\text{bp}}\right)\hfill \\ =\left(\mathit{\text{B2}}\mathit{\text{sequence}}\mathit{\text{size}}+B_{space}\mathit{\text{sequence}}\mathit{\text{size}}\right)\hfill \\ \times \left(\mathit{\text{Number}}\mathit{\text{of}}\mathit{\text{times}}\mathit{\text{B2}}\mathit{\text{and}}{B}_{space}\mathit{\text{appear}}\mathit{\text{in}}\mathit{\text{the}}\mathit{\text{structure}}\right)\hfill \\ +\left(\mathit{\text{B1}}\mathit{\text{sequence}}\mathit{\text{size}}\right)\left(\mathit{\text{Number}}\mathit{\text{of}}\mathit{\text{times}}\mathit{\text{B1}}\mathit{\text{appears}}\mathit{\text{in}}\right.\hfill \\ \left.\mathit{\text{the}}\mathit{\text{structure}}\right)+\left(\mathit{\text{Target}}\mathit{\text{sequence}}\mathit{\text{size}}\right)\left(\mathit{\text{Number}}\mathit{\text{of}}\right.\hfill \\ \left.\mathit{\text{times}}\mathit{\text{the}}\mathit{\text{Target}}\mathit{\text{appears}}\mathit{\text{in}}\mathit{\text{the}}\mathit{\text{structure}}\right)\hfill \\ +\left(\mathit{\text{F1}}\mathit{\text{sequence}}\mathit{\text{size}}\right)\left(\mathit{\text{Number}}\mathit{\text{of}}\mathit{\text{times}}\mathit{\text{F1}}\mathit{\text{appears}}\right.\hfill \\ \left.\mathit{\text{in}}\mathit{\text{the}}\mathit{\text{structure}}\right)+\left(\mathit{\text{F2}}\mathit{\text{sequence}}\mathit{\text{size}}+F_{space}\right.\hfill \\ \left.\mathit{\text{sequence}}\mathit{\text{size}}\right)\left(\mathit{\text{Number}}\mathit{\text{of}}\mathit{\text{times}}\mathit{\text{F1}}\mathit{\text{and}}{F}_{space}\right.\hfill \\ \left.\mathit{\text{appear}}\mathit{\text{in}}\mathit{\text{the}}\mathit{\text{structure}}\right)\hfill \end{array}$$ (3)

Equation (4) LAMP structure size when there are an odd number of target sequences in structure:

$$\begin{array}{ccc}& & \mathit{\text{Structure}}\mathit{\text{Size}}\left(\mathit{\text{bp}}\right)\hfill \\ & & =\left(\mathit{\text{B2}}+\left(B_{space}\right)\right)\left(x-\left(\frac{x-1}{2}\right)\right)\hfill \\ & & +\left(\mathit{\text{B1}}\right)\left(x\right)+\mathit{\text{Target}}\left(x\right)+\left(\mathit{\text{F1}}\right)\left(x+1\right)\hfill \\ & & +\left(\mathit{\text{F2}}+\left(F_{space}\right)\right)\left(x-\left(\frac{x-1}{2}\right)\right)\hfill \end{array}$$ (4)

Equation (5) LAMP structure size when there are an even number of target sequences in structure:

$$\begin{array}{ccc}& & \mathit{\text{Structure}}\mathit{\text{Size}}\left(bp\right)\hfill \\ & & =\left(\mathit{\text{B2}}+\left(B_{space}\right)\right)\left(x-\left(\frac{x}{2}-1\right)\right)\hfill \\ & & +\left(\mathit{\text{B1}}\right)\left(x+1\right)+\mathit{\text{Target}}\left(x\right)+\left(F1\right)\left(x\right)\hfill \\ & & +\left(\mathit{\text{F2}}+\left(F_{space}\right)\right)\left(x-\frac{x}{2}\right)\hfill \end{array}$$ (5)

After deriving the LAMP structure size analysis model, it was tested using the optimized LAMP primer mix. Then it was verified by testing the robustness of the model through varying the concentration of input DNA, adding loop primers to the LAMP primer mix, creating a new set of LAMP primers, and testing against different types of DNA and RNA LAMP reactions recorded in the literature.

3. Results and discussion

3.1. Optimal LAMP assay

Results of optimization testing showed that running the experiment at 67°C created the largest amount of product (Fig. 3A). This optimized temperature can be explained by the melting temperature (T_m) of the FIP and BIP primers. At 70°C and 72.2°C, respectively, the temperature at which they anneal for amplification will be around 5°C below the T_m. Therefore, the range for the annealing temperature is between 65°C and 67.2°C, which includes the optimized temperature 15. The time optimization testing showed that the Bioanalyzer was able to analyze the amount of LAMP product produced after running the reaction for 30 minutes (Fig. 3B). A reason for this is that at 30 minutes, the amount of amplified DNA was now above the threshold of what the Bioanalyzer machine could recognize. Additionally, adding the heat inactivation step for the Bst enzyme at 95°C for 5 minutes helped to stop the reaction and, most likely, reduce the amount of secondary DNA structures which were interfering with the most prominent LAMP products during the control experiments. This heat inactivation step is not required for LAMP experiments but was important in this application to ensure the reaction was completely stopped after 30 minutes. The control procedure used as a comparison to the optimized assay was obtained from the WarmStart® LAMP Kit (DNA & RNA) specifications (New England Biolabs, Ipswich, MA). Figure 3C shows the difference in the total concentration of product produced between the control and final assays where an unpaired T‐test indicated a statistically significant difference in these results. This is the optimal LAMP assay for our application because there is a statistically significant larger amount of total DNA produced compared to the control, there are fewer distinct peaks based on base pair size as compared to the control (data not shown), and it was run in the shortest amount of time possible to still produce a substantial amount of amplified DNA. An electropherogram of the typical result of this LAMP reaction using the first set of primers (FIP‐1, BIP‐1, F3‐1, B3‐1) is seen in Fig. 3D.

Figure 3.

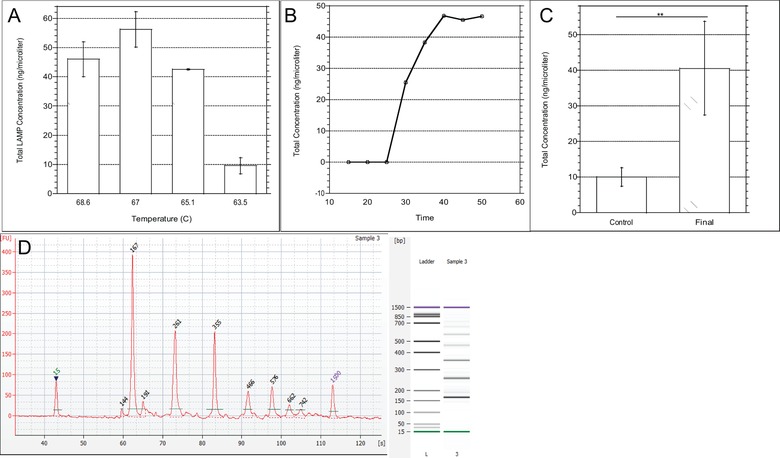
LAMP experimental results. (A) Comparison of LAMP Assay at different temperatures under same buffer conditions. (B) Comparison of LAMP Assay at different times under same buffer conditions. (C) Comparison of total amplified DNA under control conditions (65°C for 30 minutes) versus final optimized assay (67°C for 30 minutes, 95°C for 5 minutes). (D) Electropherogram of final optimized assay.

3.2. Robustness testing of the true‐positive banding pattern prediction mathematical model

Following the derivation of this model, different conditions were tested to evaluate how robust the model was at predicting the sizes of different LAMP structures. The first condition tested was the optimized set of LAMP primers containing only FIP, BIP, F3, and B3 primers in the primer mix and 100 ng of input DNA. Next, the concentration of input DNA was varied using the same set of primers. The concentrations tested were 50 ng, 200 ng, and 400 ng of input DNA. Following this test, another test was run with a new LAMP primer mix using the first set of LAMP primers plus forward loop and backward loop primers. Then, an additional set of FIP, BIP, F3, and B3 LAMP primers were created to test the model. Lastly, the model was applied to LAMP testing found in the literature to test it against different types of DNA and RNA.

The predicted shape values under each of these conditions were compared to the average base pair sizes of the largest peaks (highest DNA concentration) from the electropherograms of the LAMP experiments. Based on the sensitivity of the Agilent Bioanalyzer 2100 machine, the accepted error rate is ± 5% when the bp sizes are in the range of 100 and 500 bp or ± 10% when the bp size is between 500 and 1000 bp. An acceptable error range was then established for each predicted size value to assess the accuracy of the mathematical model to evaluate how the experimental data compared with the model's predictions.

3.2.1. Testing on optimized set of LAMP primers

Once the mathematical model was established, the next step was to test this model on the optimized LAMP assay. This process began with identifying the size and location of each primer and the number of nucleotides between them within the M13mp18 template DNA for the first primer set (Fig. 2 and Table 1). This information was readily available in the software used for LAMP primer design, so this did not create an extra evaluation step to use this model. Table 3 provides the given variable and corresponding base pair size for this first primer set and the outcome predicted DNA structure sizes exported from the mathematical model are listed under ‘Predicted Size (bp)’ in Table 4. When comparing the difference between the predicted size and the average structure size, 100% of the bp differences fell within this accepted range for each structure. The predicted versus actual structures sizes were also graphed and, using an unpaired T‐test, it was determined that six of the seven structures sizes did not have a statistically significant difference between the predicted and actual sizes, which is expected (Fig. 4A). Although, one structure did show a statistically significant difference between the predicted and actual values, seven out of the seven compared structures had a difference that was less than that of the sensitivity of the Bioanalyzer, which indicated the success of the predictions (Fig. 4A). Figure 4B shows an electropherogram of the optimized LAMP experiments and qualitatively presents what DNA structure is represented by each peak.

Table 3.

Variable inputs for mathematical model using LAMP Primer Set 1 and LAMP Primer Set 2

Variable	Base pair size inputs for LAMP primer Set 1	Base pair size inputs for LAMP primer set 2
F2	19	20
Fspace	30	20
F1c	21	21
Target	11	27
B1c	20	22
Bspace	28	29
B2	18	20

B_space: sequence between B1 and B2 sequences in backward inner primer

F_space: sequence between F1 and F2 sequences in forward inner primer

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

Table 4.

Predicted LAMP Structure Size versus Real LAMP Structure Size for optimized set of LAMP primers (Primer Set 1). n = 5

Structure	Predicted size (bp)	Average structure size (bp)	Difference (bp)
Stem and Loop, x = 1	168	172	4
Stem and Loop ×2, x = 2	265	263	2
Stem and Loop ×3, x = 3	367	354	13
Stem and Loop ×4, x = 4	464	461	3
Stem and Loop ×5, x = 5	566	572	6
Stem and Loop ×6, x = 6	663	666	3
Stem and Loop ×7, x = 7	765	768	3

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

Figure 4.

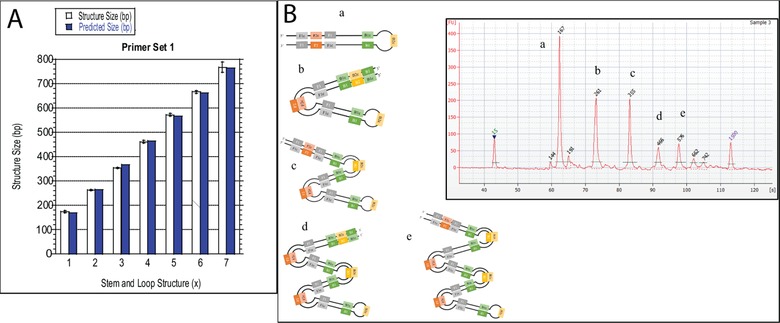
(A) Graphical comparison between the predicted and experimentally determined structure size and for every stem and loop structure size using the first set of LAMP primers. (B) Electropherogram of final LAMP Assay with corresponding structure sizes. Predicted peak sizes were (a) 168, (b) 265, (c) 367, (d) 464, (e) 566 which fall within 5% of the peak sizes produced by this assay. Each stem and loop structure produced has inverted repeats of the target sequence found between the forward and backward primer sections.

3.2.2. Effect of varying starting DNA concentrations

The original concentration of DNA used for the optimized set of LAMP primers experiments was 100 ng. The input DNA concentration was varied during the robustness testing. The different concentrations were 50 ng (6.39 × 10⁹ copies), 200 ng (2.56 × 10¹⁰ copies), and 400 ng (5.11 × 10¹⁰ copies). Copy number values are calculated based on the assumption that the average base pair weight is 650 Daltons. The same information from Table 3 for the first primer set and Predicted Sizes from Table 4 were used to assess the results of these experiments. In each of the three concentration groups, it was found that the Stem and Loop ×3 structure fell outside of the sensitivity of the Bioanalyzer with an average peak size of 345 bp for 50 ng, 344 bp for 200 ng, and 341 bp for 400 ng of input DNA where the predicted size is 367 bp with a sensitivity range of 18.35 bp. The Stem and Loop ×3 structure was also the only structure in the optimized LAMP primers testing to show a statistically significant difference between the predicted and actual values. One reason this specific structure may result in product sizes further from the predicted value is due to incomplete elongation of a new LAMP structure. This could be caused by annealing between alternatively inverted repeats in the same strand of DNA which would explain why the results show a slightly smaller size for this structure.

Additionally, with a starting concentration of 400 ng, the average structure size also fell outside of the range of the Bioanalyzer sensitivity at 438 bp where the predicted size is 464 bp which may also be explained by the same principles used for the Stem and Loop ×3 structure. Overall, it is hypothesized that concentration does not affect the validity of this model since each of these concentrations had a similar result with Stem and Loop ×3, although a starting concentration of 400 ng did produce an additional structure size outside of the sensitivity of the Bioanalyzer. One way to test how these specific structures fell outside of the respective predicted ranges would be to increase the experiment time to confirm all structure elongation has occurred.

3.2.3. Effect of including loop primers in the LAMP primer mix

The original LAMP primer design did not include loop primers so that the LAMP amplification could be kept as simple as possible for the predictive model development. But, to test the robustness of the model, researchers were interested in investigating the effect of adding these loop primers to the primer mix. The new loop primer mix used primers at a final concentration of 1.6 µM of FIP‐1 and BIP‐1, 0.2 µM of F3‐1 and B3‐1, and 0.4 µM of forward loop and backward loop primers (Table 1). The same predicted sizes from Table 4 were also used in this testing analysis. The result of adding the loop primers showed that 100% of the LAMP structures still fell within the range of the Bioanalyzer sensitivity, results are presented in Table 5. The only significant difference when using the loop primer mix was that each of these reactions also showed a peak on the electropherograms around 75 bp which is hypothesized to be caused by a primer dimer formation, caused by primers binding to themselves and amplifying. One reason why a primer dimer may be found when using the loop primer mix is because there is now a larger concentration of LAMP primers starting in the reaction, therefore it is possible that some may bind to each other, rather than existing LAMP structures.

Table 5.

Predicted LAMP structure size versus real LAMP structure size for loop primer mix testing. n = 4

Structure	Predicted Size (bp)	Average Structure Size (bp)	Difference (bp)
Stem and Loop, x = 1	168	169	1
Stem and Loop ×2, x = 2	265	261	4
Stem and Loop ×3, x = 3	367	355	12
Stem and Loop ×4, x = 4	464	466	2
Stem and Loop ×5, x = 5	566	577	11
Stem and Loop ×6, x = 6	663	668	5
Stem and Loop ×7, x = 7	765	749	16

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

3.2.4. Testing on new set of LAMP primers

To further confirm the validity of this mathematical model, a new set of LAMP primers were designed and tested (FIP‐2, BIP‐2, F3‐2, B3‐2, Table 1) while keeping all other testing conditions the same as the optimized LAMP primers testing. Using the length of the primers and their location in the M13mp18 DNA sequence (Fig. 2), each variable of the mathematical model was identified (Table 3 Primer Set 2) and predicted sizes were outputted (Table 6). Although this LAMP procedure was not optimized for this new primer set, the mathematical model still showed a 100% prediction accuracy when compared to the experimentally gathered structure sizes, still accounting for the same sensitivity of the Bioanalyzer machine. An example electropherogram of this data is presented in Fig. 5A and a graphical comparison of the predict and experimentally determined structure sizes is provided in Fig. 5B. Using these primers, only one of the structures showed no statistical significance for the difference between the predicted and actual value using an unpaired T‐test. This variation is to be expected though, because the experiment was not optimized for these primers and therefore the difference in the mean base pair sizes of the structures may be further apart than if the experiment was optimized. The model still does prove to be robust though because seven out of the seven structures tested did have a difference in size that was less than the sensitivity of the Bioanalyzer, which is how the success of this model is determined.

Table 6.

Predicted LAMP structure size versus real LAMP structure size for LAMP primer set 2. n = 5

Structure	Predicted size (bp)	Average structure size (bp)	Difference (bp)
Stem and Loop, x = 1	180	189	9
Stem and Loop ×2, x = 2	300	290	10
Stem and Loop ×3, x = 3	409	407	2
Stem and Loop ×4, x = 4	529	544	15
Stem and Loop ×5, x = 5	638	660	22
Stem and Loop ×6, x = 6	758	784	26

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

Figure 5.

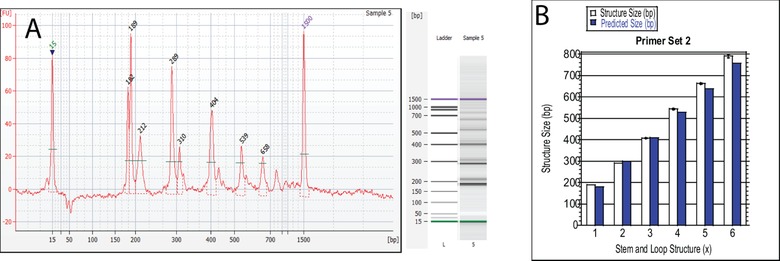
(A) Electropherogram of final LAMP Assay with Primer Set 2. (B) Graphical comparison between the predicted and experimentally determined structure size and for every stem and loop structure size.

3.2.5. Testing with LAMP experiments found in the literature

Following successful mathematical predictions using two different sets of LAMP primers and M13mp18 template DNA, this model was compared to LAMP data presented in current literature. Table 7 shows the results of this analysis. The given studies were chosen because they included a figure that showed the location of the LAMP primers in the DNA sequence used. This provided the input values for the mathematical model to make the size predictions. Additionally, there was a gel electrophoresis plot to compare the mathematically derived predictions to so that there could be an evaluation regarding whether the model worked or not. A benefit of using the Agilent Bioanalyzer 2100 for this study is that exact base pair values were exported for every peak, for every LAMP sample. In other literature on LAMP, most studies are not analyzed using an Agilent Bioanalyzer 2100, but with standard gel electrophoresis, therefore experimental values are written as an approximation if not otherwise specified by the author of that study. Even LAMP experiments analyzed with a Bioanalyzer did not provide exact sizes for the banding pattern. Overall, it was determined that the predicted sizes outputted from the mathematical model fall within the same accepted error range used in the previous testing. Therefore, this data shows that the developed mathematical model is translatable to many different diseases, to RT‐LAMP, and to different gel electrophoresis materials.

Table 7.

Result of mathematical modeling predictions for currently published LAMP experiments

Reference	DNA type	Gel type	Predicted sizes (bp)	Structure sizes (bp)
Notomi 5	M13mp18	2% agarose gel and followed by SYBR Green I stain	x = 1: 261 x = 2: 422 x = 3: 584 x = 4: 745 x = 5: 907 x = 6: 1068	x = 1: ∼270 x = 2: ∼440 x = 3: ∼600 x = 4: ∼800 (Fig. 3A , Lane 4) 5
Iwamoto 7	Genomic DNA from Mycobacterium tuberculosis	3% agarose gel and followed by ethidium bromide stain	x = 1: 157 x = 2: 249 x = 3: 342 x = 4: 434 x = 5: 527 x = 6: 619	x = 1: ∼150 x = 2: ∼250 x = 3: ∼350 x = 4: ∼450 (Fig. 2 Lane 1) 7
Iwamoto 7	Genomic DNA from Mycobacterium avium ATCC 25291	3% agarose gel and followed by ethidium bromide stain	x = 1: 174 x = 2: 273 x = 3: 375 x = 4: 474 x = 5: 576 x = 6: 675	x = 1: ∼165 x = 2: ∼285 x = 3: ∼390 x = 4: ∼490 (Fig. 2 Lane 6) 7
Iwamoto 7	Genomic DNA from Mycobacterium intracellular ATCC 13950	3% agarose gel and followed by ethidium bromide stain	x = 1: 180 x = 2: 300 x = 3: 411 x = 4: 531 x = 5: 642 x = 6: 762	x = 1: ∼180 x = 2: ∼275 x = 3: ∼395 x = 4: ∼500 (Fig. 2 Lane 11) 7
Thai 18	Severe Acute Respiratory Syndrome Coronavirus (SARS‐CoV)	3% agarose gel and followed by ethidium bromide stain	x = 1: 168 x = 2: 277 x = 3: 364 x = 4: 473 x = 5: 560 x = 6: 669	x = 1: ∼175 x = 2: ∼280 x = 3: ∼380 x = 4: ∼490 (Fig. 2 Lane 2) 18
Dukes 19	RT‐LAMP of Foot and Mouth Disease Virus Strain O UKG 35/2001	Agarose gel with Picogreen®	x = 1: 154 x = 2: 252 x = 3: 340 x = 4: 438 x = 5: 526 x = 6: 624	x = 1: ∼150 x = 2: ∼240 x = 3: ∼350 x = 4: ∼450 (Fig. 3 Lane 1) 19
Han 20	Plasmodium genus	3% agarose gel and followed by ethidium bromide stain	x = 1: 162 x = 2: 255 x = 3: 348 x = 4: 441 x = 5: 534 x = 6: 627	x = 1: ∼155 x = 2: ∼250 x = 3: ∼340 x = 4: ∼430 (Fig. 3 Lane 1) 20
Han 20	P. falciparum	3% agarose gel and followed by ethidium bromide stain	x = 1: 165 x = 2: 275 x = 3: 374 x = 4: 484 x = 5: 583 x = 6: 693	x = 1: ∼ 160 x = 2: ∼ 270 x = 3: ∼ 370 x = 4: ∼ 480 (Fig. 3 Lane 3) 20
Han 20	P. vivax	3% agarose gel and followed by ethidium bromide stain	x = 1: 165 x = 2: 269 x = 3: 364 x = 4: 468 x = 5: 563 x = 6: 667	x = 1: ∼ 160 x = 2: ∼ 260 x = 3: ∼ 350 x = 4: ∼ 450 (Fig. 3 Lane 5) 20
Han 20	P. malariae	3% agarose gel and followed by ethidium bromide stain	x = 1: 195 x = 2: 307 x = 3: 422 x = 4: 534 x = 5: 649 x = 6: 761	x = 1: ∼ 200 x = 2: ∼ 310 x = 3: ∼ 420 x = 4: ∼ 530 (Fig. 3 Lane 7) 20
Han 20	P. ovale	3% agarose gel and followed by ethidium bromide stain	x = 1: 183 x = 2: 304 x = 3: 404 x = 4: 525 x = 5: 625 x = 6: 746	x = 1: ∼ 175 x = 2: ∼ 290 x = 3: ∼ 390 x = 4: ∼ 510 (Fig. 3 Lane 9) 20

This article is being made freely available through PubMed Central as part of the COVID-19 public health emergency response. It can be used for unrestricted research re-use and analysis in any form or by any means with acknowledgement of the original source, for the duration of the public health emergency.

3.3. LAMP theoretical analysis

Following the true‐positive banding pattern prediction mathematical modeling, LAMP structures were also evaluated using the thermodynamic modeling software, MFold. Mfold is used to predict the folding and hybridization of single stranded nucleic acids 16. This was an important analytical tool because it was able to validate that the LAMP structures predicted from the DNA sequences in the mathematical model were also the most thermodynamically likely DNA structures. Input settings for the modeling software were a folding temperature at 67°C and Mg²⁺ concentration of 8 mM based on the composition of the LAMP WarmStart Mix being used in this reaction. From this technology the most likely structure was determined by the minimum ΔG (kcal/mol) or Gibbs free energy. ΔG is the amount of energy capable of doing work during a reaction where temperature and pressure are constant 17. If ΔG is a negative number, it releases free energy and the reaction is exergonic, and if the ΔG is positive it gains free energy and is an endergonic reaction 17. Equation (6) is used in the calculations for the thermodynamics of folding. Where ΔH is the change in enthalpy, T is temperature, and ΔS is the change in entropy.

$$\mathrm{\Delta }G=\mathrm{\Delta }H-T\mathrm{\Delta }S$$ (6)

Equation (7) provides the DNA folding thermodynamics for the stem and loop structure while Equation (8) repeats this analysis for Stem and Loop x2, both provided by the MFold software.

$$\mathrm{\Delta }G=\mathrm{\Delta }H-T\mathrm{\Delta }S=-78.30\frac{\mathrm{kcal}}{\mathrm{mol}}\mathrm{at}{67}^{\circ }\mathrm{C}$$ (7)

$$\mathrm{\Delta }G=\mathrm{\Delta }H-T\mathrm{\Delta }S=-153.44\frac{\mathrm{kcal}}{\mathrm{mol}}\mathrm{at}{67}^{\circ }\mathrm{C}$$ (8)

For both of these calculations the standard errors for this thermodynamic folding were roughly ± 5% for ΔG, ± 10% for ΔH, ± 11% for ΔS, 2–4°C for melting temperature (T).

A significant finding with MFold technology was that the stem and loop structures predicted (Fig. 6), were also the only possible structures created under these conditions according to this software under the 2‐state model, further validating this developed mathematical modeling tool. The simple 2‐state model means that the nucleic acid sequence is either folded in the configuration shown, or entirely single stranded 16. According to Zuker, to test the 2‐state model, the sequences can be refolded, using MFold, near the respective predicted T _m values, and if the new T _m is ‘significantly’ larger than the original, this would imply that the molecule can be refolded into another geometry at a larger T _m 16. To test whether these structures could be refolded into another geometry, the stem and loop and stem and loop ×2 sequences were rerun using MFold under the same conditions other than a new temperature setting at 95°C. The T _m values of the stem and loop and stem and loop ×2 structures during the first test were 95.2 and 97.8°C, respectively. These temperatures were near to the final heating temperature used experimentally, 95°C, so this temperature was selected for the new testing. The software results showed that both structures maintained the same thermodynamic folding with only a slight change in T _m. The stem and loop structure now had a ΔG of −3.19 kcal/mol at 95°C and T _m of 96.2°C. The stem and loop ×2 structure had a ΔG of −4.22 kcal/mol at 97.8°C and a T _m of 96.2°C. Due to the complexities of the LAMP structures and size constraints from the MFold modeling software, these were the only structures tested. However, this theoretical analysis strongly indicates that the predicted structures using DNA base pair size analysis are consistent with what is most likely to happen thermodynamically during single stranded nucleic acid folding and hybridization.

Figure 6.

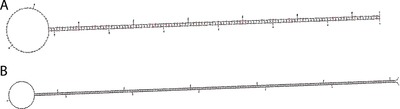
Output structures from MFold Modeling (A) Stem and Loop, (B) Stem and Loop ×2.

4. Concluding remarks

In summary, the model presented here correctly predicted the DNA structure sizes for various LAMP protocols from experimental data and primary literature examples. As LAMP has found a strong niche in diagnostic applications, it is essential that it is used accurately, and false‐positive diagnosis is avoided. This mathematical model can be used as a tool to easily validate positive diagnostic results using any set of LAMP primers because the correct banding pattern on a gel electrophoresis plot can now be predicted. Additionally, this model provides scientists with a stronger understanding of the various DNA structures being produced in their LAMP experiment. This model was validated using two sets of LAMP primers with 100% of the average DNA base pair sizes appearing within an accepted error margin of the LAMP predictions according to the sensitivity of the Agilent Bioanalyzer 2100 device. The model was also tested using different DNA concentrations, using loop primers, and using previously published literature of LAMP experiments with a similar level of accuracy. This model helps to fill a gap in the current LAMP research and provides an easy‐to‐use tool to efficiently and accurately identify a true‐positive LAMP reaction which can reduce false‐positive diagnosis.

The authors have declared no conflict of interest.