Mathematical deep learning for pose and binding affinity prediction and ranking in D3R Grand Challenges

Abstract

Advanced mathematics, such as multiscale weighted colored subgraph and element specific persistent homology, and machine learning including deep neural networks were integrated to construct mathematical deep learning models for pose and binding affinity prediction and ranking in the last two D3R Grand Challenges in computer-aided drug design and discovery. D3R Grand Challenge 2 focused on the pose prediction, binding affinity ranking and free energy prediction for Farnesoid X receptor ligands. Our models obtained the top place in absolute free energy prediction for free energy set 1 in stage 2. The latest competition, D3R Grand Challenge 3 (GC3), is considered as the most difficult challenge so far. It has five subchallenges involving Cathepsin S and five other kinase targets, namely VEGFR2, JAK2, p38-α, TIE2, and ABL1. There is a total of 26 official competitive tasks for GC3. Our predictions were ranked 1st in 10 out of these 26 tasks.

Introduction

With the availability of increasingly powerful computers and fast accumulating molecular and biomolecular datasets, one can dream of a possible scenario that all the major tasks of drug design and discovery can be conducted on computers [1–3]. Virtual screening (VS) is one of the most important aspects of computer-aid drug design (CADD) [4]. VS involves two stages, namely, the generation of different ligand conformations (i.e., poses) when a compound is docked to a target protein binding site, and the prediction of binding affinities. It is generally believed that the first stage can be well resolved by available techniques, such as molecular dynamics (MD), Monte Carlo (MC), and genetic algorithm (GA) [5–7]. However, The development of scoring function (SF) for binding affinity prediction with high accuracy still remains a formidable challenge. In general, current SFs can be classified into four different categories, namely force-field-based ones, knowledge-based ones, empirical-based ones and machine learning-based ones [8]. Among them, force-field-based SFs, such as COMBINE [9] and MedusaScore [10], emphasize the physical description of protein and ligand interactions in the solvent environment, including van der Walls (vdW), electrostatics, hydrogen bonding, solvation effect, etc. Typical Knowledge-based SFs represent the binding affinity as the linear sum of pairwise statistical potentials between receptor and ligand atoms. KECSA [11], PMF [12], DrugScore [13], and IT-Score [14] are some of the well-known examples. The empirical-based SFs, in fact, make use of multiple linear regression to construct a linear combination from different physical-descriptor components such as vdW interaction, hydrophobic, hydrogen bonding, desolvation, dipole, etc. The renowned candidates for empirical-based SFs include X-Score [15], PLP [16], and ChemScore [17], etc.

Recently, machine learning including deep learning has emerged as a major technique in CADD. By using advanced machine learning algorithms, such as random forest (RF) and deep convolutional neural network, the machine learning-based SFs can characterize the non-additive contributions of functional groups in protein–ligand binding interactions [18]. Such a characterization can help machine learning-based SFs consistently maintain their accuracy in binding affinity predictions for a variety of protein–ligand complexes [19–23]. However, the performance of machine learning-based SFs depends crucially on the training data quality and statistic distribution. Additionally, it also depends on selected features that might or might not accurately and completely describe the protein–ligand binding interactions. We assume that the intrinsic physics of interest of complex biomolecules and interactions lies on low-dimensional manifolds or subspaces embedded in a high-dimensional data space. Based on this hypothesis, we have recently proposed several low-dimensional mathematical models that dramatically reduce the structural complexity of protein–ligand complexes and give rise to surprisingly accurate predictions of various bimolecular properties. For example, we proposed a multiscale weighted colored graph (MWCG) model to simplify protein structures and analyze their flexibility [24]. The essential idea of this method is to use the graph theory to represent the interactions between atoms in a molecule in an element-level collective manner. The MWCG approach has been shown to be over 40% more accurate than the Gaussian network model on a set of 364 proteins [24].

In addition to graph theory simplification, we have also developed the topological abstraction of complex protein structures. In order to describe the topological changes such as the opening or closing of ion channels, the folding or unfolding of proteins, and the subtle change in binding site after the protein–ligand binding, we take the advantage of topological methods to study the connectivity of different molecular components in a space [25] which can represent important topological entities such as independent components, rings and higher dimension faces. However, since the conventional topology and homology are metric or coordinate free, they capture very little biomolecular geometric information and thus are unable to efficiently characterize biomolecular structures. Persistent homology (PH) is a new branch in algebraic topology. It embeds the geometric information into topological invariants. By changing a filtration parameter such as the radius of atoms PH creates a family of topological spaces for a given set of atoms. As a result, the topological properties of a given biomolecule can be systematically analyzed and recorded in terms of topological invariants, i.e., the so-called Betti numbers, over the filtration process. The resulting barcodes monitor the “birth” and “death” of isolated components, circles, and cavities at different geometric scales. The persistent homology framework together with practical algorithms was introduced by Edelsbrunner et al. [26] and formal mathematical theories were developed by Zomorodian and Carlsson [27]. A zeroth dimensional version was also introduced earlier under the name of size function by Frosini and Landi [28]. Primitive applications of PH to computational biology has been reported in the literature [29–31]. Recently, we have developed a variety of advanced PH models to analyze the topology–function relationship in protein folding and protein flexibility [32], quantitative predictions of curvature energies of fullerene isomers [33, 34], protein cavity detection [35], and the resolving ill-posed inverse problems in cryo-EM structure determination [36]. In 2015, we introduced some of the first combinations of PH and machine learning for protein structural classification [37]. Topological descriptors were further integrated with a variety of deep learning algorithms to achieve state-of-the-art analysis and prediction of protein folding stability change upon mutation [38], drug toxicity [39], aqueous solubility [40], partition coefficient [40], binding affinity [21, 22], and the virtual screening of active ligands and decoys [23].

In this paper, we report the performance of our mathematical deep learning models on pose and binding affinity prediction and ranking in the last two D3R Grand Challenges, namely D3R Grand Challenge 2 (GC2) and D3R Grand Challenge 3 (GC3). The GC2 was initiated in 2016 and consisted of two stages. The first stage asked participants to predict the crystallographic poses of 36 ligands for the target of farnesoid X receptor (FXR). In addition, there were affinity ranking task for all 102 compounds and absolute free energy prediction for two designated subsets of 18 and 15 small molecules. In the second stage, participants were asked again to submit the affinity ranking and free energy after the release of 36 crystal structures. In GC2, we employed our mathematical deep learning models to select the best poses from docking software generated poses for binding affinity ranking and prediction tasks. Our models achieved the top place in affinity ranking for the free energy set 1 in stage 2.

In addition, our results for the latest Grand Challenge, i.e., GC3, are presented in this paper. The third Grand Challenge, took place in 2017, is the largest in terms of the number of competitive tasks since 2015. It consisted of five subchallenges. Subchallenge 1 was about Cathepsin S. It comprised two stages with tasks the same as ones in the GC2. There were 24 ligands with crystal structures and their binding energies spread three orders of magnitude for 136 compounds. Subchallenge 2 focused on kinase selectivity. It has three kinase targets, namely VEGFR2, JAK2, and p38-α with their numbers of compounds being 85, 89, and 72, respectively. This subchallenge only asked participants to submit affinity ranking for each kinase dataset. Subchallenge 3 involved the binding affinity ranking and free energy prediction of target JAK2. It consisted of a relatively small dataset with 17 ligands having similar chemical structures. In subchallenge 4, there were 18 congeneric ligands with Kd values for kinase TIE2. In addition to asking for the affinity ranking of 18 compounds, subchallenge 4 asked participants to predict the free energies of two subsets with 4 and 6 compounds, respectively. The last subchallenge in GC3 concerned the binding affinity ranking of different mutants on protein ABL1. There were two compounds and five different mutation sites. Overall, our models performed well in GC3. Specifically, we obtained the first place in 10 out of a total of 26 predictive tasks.

Methods

In this section, we briefly describe our computation methods and algorithms developed for GC2 and GC3.

Ligand preparation

All ligands in Grand Challenges are provided in the SMILES string format. They are converted to the optimal 3D structures and protonated at pH 7.5 using LIGPREP tool in Schrödinger software [41]. Before employing Autodock Vina [42] for docking, Gasteiger partial charges were added to these ligands via MGLTools v1.5.6 [43].

Protein structures selection and preparation

Except for subchallenge 1, all the receptor structures in GC3 are supplied in the protein sequence format. We utilized the homology modeling task in Maestro of Schrödinger software [44] to obtain 3D structure predictions. In addition, we make use of the crystal structures available in the Protein Data Bank (PDB) for each protein family (see the supporting information for a complete list). These collected protein structures were prepared using the protein preparation wizard provided in Schrödinger package [41] with default parameters except enabling the FILLSIDECHAINS option.

Docking protocols

We use a number of docking protocols in GC2 and GC3. Among, a machine learning protocol was developed in our own lab. Motivated by earlier work [45], we carried out four different docking strategies, namely align-close, align-target, close-dock and cross-dock, to attain the best poses for binding affinity predictions. We also used induced fit docking (IFD) and unrestricted IFD in our pose predictions.

Protocol 1: machine learning based docking

We developed a machine learning-based scoring function to select the poses generated by GOLD [46], GLIDE [47], and Autodock Vina [42]. Given a ligand target, we at first formed a training data of complexes taken from the PDB. The criteria for such selections are based on the similarity coefficient, measured by fingerprint 2 (FP2) in Open Babel v2.3.1 [48], of ligand in the complex. Then, we utilized docking software packages such as GOLD, GLIDE, and Autodock Vina to re-dock ligands to protein in those selected complexes. A variety of docking poses was distributed into 10 different RMSD bins as follows: [0,1], (1,2], …, (9,10] Å. In each bin, we clustered decoys into 10 clusters based on their internal similarities. The docking poses having the smallest free energy were selected as the candidate for their clusters. As a result, one may end up with a total of 100 poses for each given complex. We employed all these decoy poses to form a training set with labels defined by their RMSDs. Our topological based deep learning models were utilized to learn this training set. Finally, we employed this established scoring function to re-rank the poses of the target ligand produced by docking software packages.

Protocol 2: align‑close

In the align-close method, we select ligand available in the PDB that has the highest chemical similarity to the target ligand. Here, the similarity score was measured by fingerprint 2 (FP2) in Open Babel v2.3.1 [48]. It is also noted that all the processed structures in this procedure were conducted in the Schrödinger suite 2017–4 [49]. A ligand was aligned to its similar candidates by the flexible ligand alignment task in Schrödinger’s Maestro [50, 51]. Then, the resulting aligned ligand is minimized to the co-crystal structure of the most similar ligand by Prime in Schödinger package [49, 52, 53].

Protocol 3: align‑target

In the align-target protocol, the homology modeling tool in Maestro was used to construct protein 3D structures from given sequences, and the aligned ligands obtained from the align-close procedure are minimized with respect to corresponding receptors.

Protocol 4: close‑dock

The fourth docking strategy is called as close-dock. Based on previous docking methods, one can identify the most similar structure in the PDB to a given D3R ligand. This procedure also gives us the corresponding co-crystal structure, i.e., the so-called closet receptor. In the close-dock approach, Autodock Vina is used to docki the target ligand to its corresponding closet receptor. The best pose is selected based on Autodock Vina’s energy scoring.

Protocol 5: cross‑dock

The next approach in our docking methods is named cross-dock. This is basically a cross docking method in which the close receptors are the co-crystal structures of the ligands having the similar chemical characteristics to the interested ligand. In the cross-docking procedure, we use Autodock Vina to dock the D3R ligands to their close receptors. Those poses that have the smallest binding energies are selected as the best poses.

Protocol 6: constraint‑IFD

Similarly to the align-target protocol, we used the homology modeling module in Maestro to generate 3D structure from a given sequence. For the docking procedure, we employed the induced fit docking (IFD) [54–56] in Maestro with restricting docking poses to the closet ligands with a tolerance of 3 Å. The best pose was selected due to the ranking from IFD.

Protocol 7: free‑IFD

This protocol is exactly the same protocol as Constraint-IFD except for no constraint during the run of induced-fit docking.

Multiscale weighted colored subgraph representation

Weighted colored subgraph (WCS) method describes intermolecular and intramolecular interactions as pairwise atomic correlations [24]. To apply the WCS for analyzing the protein–ligand interactions, we convert all the atoms and their pairwise interactions at the binding site of a protein–ligand complex with a cutoff distance d into a colored subgraph G(V^d, E) with vertices V^d and edge E. As such, the ith atom is labeled by its position r_i, element type α_i and co-crystal type β_i. Thus, we can express vertices V^d as

$$\begin{gathered} V^d=\{({\text{r}}_i,{\alpha }_i,{\beta }_i)|{\text{r}}_i\in {ℝ}^3,{\alpha }_i\in \mathcal{C},{\beta }_i\in \mathcal{S},\Vert {\text{r}}_i-{\text{r}}_j\Vert \\ <d\text{ for some }1\le j\le N\text{ such that }{\beta }_i+{\beta }_j=1,i=1,2,\dots ,N\}, \end{gathered}$$ (1)

where c = {C, N, O, S, P, F, Cl, Br, I} contains all the commonly occurring element types in a complex, and s = {0, 1} a bipartite graph label that if the ith atom belongs to protein then β_i = 0, otherwise β_i = 1. Hydrogen element is omitted since it does not present in the crystal structures of most protein–ligand complexes. To describe pairwise interactions between the protein and the ligand, we define an ordered colored set $\mathcal{P}=\left\{(\alpha ,0)\left({\alpha }^{\prime },1\right)\right\}$. Here, α ∈ {C, N, O, S} is a heavy atom in the protein, and α′ ∈ {C, N, O, S, P, F, Cl, Br, I} is a heavy atom in the ligand. With that setting, it is trivial to verify that set $\mathcal{P}$ has a total 36 partitions or subgraphs. For example, a partition ${\mathcal{P}}_1=\left\{(C,0)(O,1)\right\}$ contains all bipartite pairs CO in the complex with the first atom is a carbon in the protein and the second atom is an oxygen in the ligand. For each set of element pairs ${\mathcal{P}}_k$, k=1,2,…,36, a set of vertices, $V_{{\mathcal{P}}_k}$ is a subset of V^d containing all atoms that belong to a pair in ${\mathcal{P}}_k$. Therefore, the edges in such WCS describing potential pairwise atomic interactions are defined by

$$E_{{\mathcal{P}}_k}^{\sigma ,\tau ,\zeta }=\left\{{\mathrm{\Phi }}_{\tau ,\zeta }^{\sigma }\left(\Vert {\text{r}}_i-{\text{r}}_j\Vert \right)|\left(({\alpha }_i,{\beta }_i)({\alpha }_j,{\beta }_j)\right)\in {\mathcal{P}}_k;i,j=1,2,\dots ,N\right\},$$ (2)

where $\Vert {\text{r}}_i-{\text{r}}_j\Vert$ defines a Euclidean distance between ith and jth atoms, σ indicates the type of radial basic functions (e.g., σ = L for Lorentz kernel, σ = E for exponential kernel), τ is a scale distance factor between two atoms, and ζ is a parameter of power in the kernel (i.e., ζ = κ when σ = E, ζ = v when σ = L). The kernel ${\mathrm{\Phi }}_{\tau ,\zeta }^{\sigma }$ characterizes a pairwise correlation satisfying the following conditions

$${\mathrm{\Phi }}_{\tau ,\zeta }^{\sigma }\left(\Vert {\text{r}}_i-{\text{r}}_j\Vert \right)=1\text{as}\Vert {\text{r}}_i-{\text{r}}_j\Vert \to 0,$$ (3)

$${\mathrm{\Phi }}_{\tau ,\zeta }^{\sigma }\left(\Vert {\text{r}}_i-{\text{r}}_j\Vert \right)=0\text{as}\Vert {\text{r}}_i-{\text{r}}_j\Vert \to \infty .$$ (4)

Commonly used radial basis functions include generalized exponential functions

$${\mathrm{\Phi }}_{\tau ,x}^{\text{E}}=e^{-{\left(\Vert {\text{r}}_i-{\text{r}}_j\Vert /\tau (r_i+r_j)\right)}^{\kappa }},\kappa >0,$$ (5)

and generalized Lorentz functions

$${\mathrm{\Phi }}_{\tau ,v}^{\text{L}}\left(\Vert {\text{r}}_i-{\text{r}}_j\Vert \right)=\frac{1}{1+{\left(\Vert {\text{r}}_i-{\text{r}}_j\Vert /\tau (r_i+r_j)\right)}^v},v>0,$$ (6)

where r_i and r_j are, respectively, the van der Waals radius of the ith and jth atoms.

In the graph theory or network analysis, centrality is widely used to identify the most important nodes [57]. There are various types of centrality such as degree centrality [58], closeness centrality [59], harmonic centrality [60], etc. Specifically, while the degree centrality is measured as a number of edges upon a node, closeness and harmonic centralities depend on the length of edges and are defined as $1/{\sum }_j\Vert {\text{r}}_i-{\text{r}}_j\Vert$ and ${\sum }_{j}1/\Vert {\text{r}}_i-{\text{r}}_j\Vert$ respectively. Our centrality used in the current work is an extension of the harmonic formulation by our correlation functions

$$\begin{gathered} {\mu }_i^{k,\sigma ,\tau ,v}=\sum _{j=1}^{|V_{{\mathcal{P}}_k|}}{w}_{ij}{\mathrm{\Phi }}_{\tau ,v}^{\sigma }\left(\Vert {\text{r}}_i-{\text{r}}_j\Vert \right),(({\alpha }_i,{\beta }_i)({\alpha }_j,{\beta }_j))\in {\mathcal{P}}_k, \\ \forall i=1,2,\dots ,\left|V_{{\mathcal{P}}_k}\right|, \end{gathered}$$ (7)

where w_ij is a weight function assigned to each atomic pair. In the current work, we choose w_ij = 1 if β_i + β_j = 1, otherwise w_ij = 0, for all calculations to reduce dimension of the parameter space. To describe a centrality for the whole graph $G(V_{{\mathcal{P}}_k},E_{{\mathcal{P}}_k}^{\sigma ,\tau ,\zeta })$ we take into account a summation of the node’s centralities

$${\mu }^{k,\sigma ,\tau ,v}=\sum _{j=1}^{|V_{{\mathcal{P}}_k|}}{\mu }_j^{k,\sigma ,\tau ,v}$$ (8)

Since we have 36 choices of the set of weighted colored edges ${\mathcal{P}}_k$, we can obtain corresponding 36 bipartite subgraph centralities μ^k,σ,τ,v. By varying kernel parameters (σ, τ, v), one can achieve multiscale centralities for multiscale weighted colored subgraph (MWCS) [24]. For a two-scale WCS, we obtain a total of 72 descriptors for a protein–ligand complex.

Algebraic topology based molecular signature

The geometry of biomolecular systems together with the complex interaction patterns allows us to build topological spaces upon the systems which facilitate powerful topological analysis. The topological analysis provides us a description of the molecular system that captures a collection of key aspects of the system including the multiscale description of geometry, the characterization of interaction network in an arbitrary dimension, and the important physical and chemical information, which ensures the success of the downstream machine learning modeling. In this section, we first briefly describe the background of persistent homology. Then, we demonstrate how to apply it to biomolecular systems to obtain a rich but concise description.

Persistent homology

We describe the theory of persistent homology in the framework of simplicial homology in a geometric sense where topological spaces are represented by collections of points, edges, triangles, and their higher-dimensional counterparts. A k-simplex is a collection of (k + 1) affinely independent points in ${ℝ}^n$ with n ≥ k. If the vertices of a simplex is a subset of the vertices of another simplex, it is called a face of the other simplex. Simplices of various dimensions are building blocks of a simplicial complex which is a finite collection of simplices satisfying two conditions: (1) the faces of any simplex in the complex are also in the complex and (2) the intersection of two simplices in the complex is either empty or a common face of the two. A simplicial complex can be used to discretely represent or approximate a topological space. Given a simplicial complex X, a k-chain is a formal sum of all the k-simplices in X which is defined as

$$c=\sum _i{a}_i{\sigma }_i,$$ (9)

where σ_i is a k-simplex in X and a_i is a coefficient in a coefficient set of choice such as a finite field ${\mathbb{Z}}_p$ with a prime p. The set of all k-chains with the addition operator in the coefficient group forms a group called the kth chain group denoted C_k(X). The chain groups of different dimensions are connected by a collection of homeomorphisms called the boundary operators forming a chain complex,

$$\dots \stackrel{{\partial }_{i+1}}{\to }{\mathcal{C}}_i(X)\stackrel{{\partial }_i}{\to }{\mathcal{C}}_{i-1}(X)\stackrel{{\partial }_{i-1}}{\to }\dots \stackrel{{\partial }_2}{\to }{\mathcal{C}}_1(X)\stackrel{{\partial }_1}{\to }{\mathcal{C}}_0(X)\stackrel{{\partial }_0}{\to }0.$$ (10)

It suffices to define the boundary operator on simplices, and then, such a definition can be extended to general chains.

$${\partial }_k(\sigma )=\sum _{i=0}^k{(-1)}^i\left[v_0,\dots ,{\widehat{v}}_i,\dots ,v_k\right],$$ (11)

where v₀,…, v_k are vertices of the k-simplex σ and $\left[v_0,\dots ,{\widehat{v}}_i,\dots ,v_k\right]$ means the codim-1 face of σ be omitting the vertex v_i. The boundary operator has an important property that

$${\partial }_k\text{o}{\partial }_{k+1}=0.$$ (12)

With the boundary operators, we can define boundary groups and cycle groups which are subgroups of chain groups. The kth boundary group is defined to be the image of ∂_k+1 denoted ${\mathcal{B}}_k(X)=\text{Im}\left({\partial }_{k+1}\right)$. The kth cycle group is defined to be the kernel of ∂_k denoted ${\mathcal{Z}}_k(X)=\text{Ker}\left({\partial }_k\right)$. It can be seen that ${\mathcal{B}}_k(X)\subseteq {\mathcal{Z}}_k(X)$ following the property in Eq. (12). Then, the kth homology group is defined to be the quotient group

$${\mathcal{H}}_k(X)={\mathcal{Z}}_k(X)/{\mathcal{B}}_k(X).$$ (13)

Intuitively, the kth homology group contains elements associated to k dimensional holes which are not boundaries of (k + 1)-chains to characterize the topology.

The theory described above computes the homology of various dimensions of a topological space to obtain a multidimensional characterization of the space. However, this is not enough for the cases where the objects are also multiscale. Therefore, instead of only computing homology for a fixed topological space, we can build a sequence of subspaces of the topological space and track how homology evolves along this changing sequence. This sequence is called a filtration,

$$\varnothing =X_0\subseteq X_1\subseteq \cdots \subseteq X_{m-1}\subseteq X_m=X.$$ (14)

The filtration naturally induces an inclusion map connecting the homology groups of a certain dimension,

$${\mathcal{H}}_k\left(X_0\right)\to {\mathcal{H}}_k\left(X_1\right)\to \dots \to {\mathcal{H}}_k\left(X_{m-1}\right)\to {\mathcal{H}}_k\left(X_m\right).$$ (15)

Then for a homology generator $\delta \in {\mathcal{H}}_k\left(X_i\right)$, it is said to be born at i if it is not an image of the inclusion map from ${\mathcal{H}}_k\left(X_{i-1}\right)$ and it is said to die at i + 1 if it mapped to the empty set or another homology generator that is born before i by the inclusion map from ${\mathcal{H}}_k\left(X_i\right)$. Persistent homology tracks how these homology generators appear and disappear along the course of the filtration resulting in a robust multiscale description of the original topological space. The birth and death of each generator can be represented by a half-open interval starting at the birth time and stopping at the death time. There are several visualization methods for collections of such intervals such as barcodes and persistence diagrams.

Topological description of molecular systems

To describe molecular systems using persistent homology, the atoms can be regarded as vertices and different constructions of filtrations can reveal different topological aspects of the system.

To describe a complex protein geometry, an efficient filtration using alpha complex [61] can be employed. To build an alpha filtration, a Voronoi diagram is first generated for the collection of points representing the atoms in the system. The final frame of the topological spaces at the end of the course of filtration is constructed by including a k-simplex if there is a nonempty intersection of the (k + 1) Voronoi cells associated to its (k + 1) vertices. The filtration of the space can be constructed by associating a subcomplex to each value of a filtration parameter є. The subcomplex associated to є is defined as

$$X_{\text{alpha }}(ϵ)=\left\{\sigma \in X|\sigma =\left[v_0,\dots ,v_k\right],{\cap }_i\left(V(v_i)\cap B_{ϵ}(v_i)\right)\ne \varnothing \right\}$$ (16)

where V(v_i) is the Voronoi cell of v_i and B_є(v_i) is an є ball centered at v_i.

A more abstract construction of filtration via the Vietoris–Rips complex can be used to address other properties of the system such as protein–ligand interactions. Given a set of points with a pairwise distance (not necessarily satisfying triangular inequality), the subcomplex associated to a filtration parameter є is defined to be

$$X_{\text{Rips}}(ϵ)=\left\{\sigma \in X|\sigma =\left[v_0,\dots ,v_k\right],d(v_i,v_j)\le 2ϵ\text{ for }0\le i,j\le k\right\},$$ (17)

where d is the predefined distance function and X is the collection of all possible simplices. Tweaking the distance function can help emphasize on different properties of the system. For example, in a protein–ligand complex, setting the distance between an atom from the protein and an atom from the ligand to the Euclidean distance while setting the distance between atoms from the same molecule to infinity will emphasize the interaction pattern between two molecules [21]. Also, we can assign values between atoms according to a specific distance of interest by using kernel functions as distances [21]. We have proposed element specific persistent homology, which is a family of persistent homology groups defined on various topological subspaces, to encode physical interactions into various topological invariants [21, 38]. By computing persistent homology on the subsets of the atoms, we can extract different chemical information. For example, the element specific persistent homology computation on the collection of all carbon atoms describes the hydrophobic network or the structural basis of the molecule while computation on the nitrogen and oxygen atoms characterizes the hydrophilic networks [21]. For the characterization of small molecules, we can use a multilevel element specific persistent homology to both describe the covalent bonds and noncovalent interactions in the molecule [23].

The element specific persistent homology results (barcodes) can be paired with machine learning models in several ways. For example, Wasserstein metric can be applied to measure similarities among the barcodes of different proteins, which can be used with methods such as nearest neighbors and manifold learning [23]. The element specific persistent homology barcodes can also be turned into fixed length feature vectors by discretizing the range of barcode and counting the persistence, birth, and death events that fall in each subinterval. The statistics of element specific persistent homology barcodes can also be used for featurization [23]. These fixed length features can be used with powerful machine learning methods such as the ensemble of trees and deep learning neural networks [21, 22]. The barcodes can also be transformed to representations similar to images and used in a 1-dimensional or a 2-dimensional convolutional neural networks [22, 23].

Machine learning algorithms

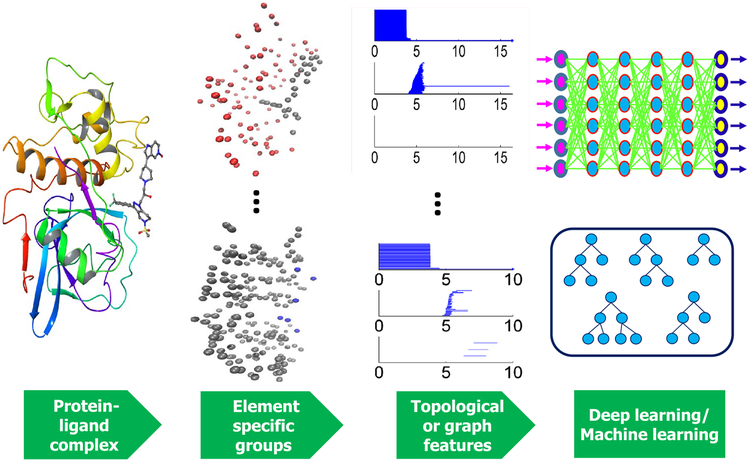
The machine learning methods used in our prediction fall into two categories, ensemble of trees and deep learning. A schematic illustration of our mathematical deep learning modeling is given in Fig. 1.

Fig. 1.

Illustration of mathematical learning prediction using deep learning and/or ensemble of trees

Ensemble of trees

The basic building block of this type of methods is a decision tree which identifies key features to make decisions at the nodes of the tree. Due to its simple structure, it is usually considered as a weak learner especially in the case of highly nonlinear problems or applications with high dimensional features. Ensemble of trees methods build models consisting of a collection of decision trees with the assumption that grouping the weak learners can improve the learning capability. We mainly used random forest and gradient boosting trees for our prediction. Random forest builds uncorrelated decision trees with each tree being trained on a resampling of the original training set (bootstrap). On the contrary, gradient boosting trees add one tree to the collection at a time along the direction of the steepest descent of the loss of the current collection. As these two models attempt to reduce error in two different ways, they behave differently in the bias-variance trade-off where the random forest is better at lowering bias and gradient boosting trees focus more on reducing variance. Therefore, a higher level bagging of models of different kinds can further improve the performance. The ensemble learning methods are also robust and overfitting can be reduced by learning partial problems. For example, each tree can be trained with a random subset of the training data and a subset of the features and the model complexity can be constrained by setting maximum tree depth. Both our graph theory based models [20, 62] and algebraic topology based models [21, 23] achieve top-class performance with the ensemble of trees methods.

Deep learning

When the feature is complex or there is some underlying dimension in the feature space, deep learning models can further imporve the performance of the predictor. For example, a spatial dimension associated to the filtration parameter lies in the persistent homology representation of protein–ligand systems. This enables the usage of the powerful convolutional neural networks (CNNs) which have been extremely successful in the field of computer vision and image analysis. The neural networks we used in the prediction are in the category of feedforward networks where the signal from the previous layer undergoes a linear transformation to the current layer, then the current layer applies a nonlinear activation function and sends the signal to the next layer. Classical deep neural networks are constructed by stacking fully connected layers where every pair of neurons in two adjacent layers are connected. Different rules of neuron connections and parameter sharing have resulted in a number of powerful deep learning models that flourish in various application domains. CNNs take advantage of the feature structure where there are spatial dimensions and only allow local connections with the parameters shared along the spatial dimensions which significantly lowers the dimension of the parameter space. Also, the flexibility of neural networks allows learning different but related tasks together by sharing layers, i.e., a type of multi-task learning. We applied convolutional neural networks and multi-task learning in our predictions which further advanced the capability of our models [22, 23].

To make use of both MWCG and algebraic topology features, we carried out two different schemes for the energy prediction. In the first approach, we used random forest to learn the biomolecular structure represented by MWCG, and used CNNs with topological features. The final predictions for this method was the consensus results between the energy values predicted by two aforementioned machine learning strategies. We name this method EP1. In the second approach, MWCG and topological features were mixed and fed into the CNNs model. The energy value predicted by these deep learning networks was submitted. We name this model EP2. We employed available PDBbind data sets (http://pdbbind.org.cn) as the training data.

Results and discussion

Here, we provide the results of our mathematical deep learning models in two recent Grand Challenges, i.e., GC2 and GC3.

Grand Challenge 3

There are five subchallenges in GC3 involving a total of 12 affinity prediction submissions and 2 pose prediction challenges, resulting in 26 different competitive tasks. Our submissions were ranked 1st in 10 of these 26 tasks as shown in Table 1 for additional information. While we employed align-close, align-target, close-dock and cross-dock protocols for pose generations in subchallenges 1–4, we applied constraint-IFD and free-IFD procedures for kinase mutants in subchallenge 5. The combination of MWCS and algebraic topological descriptors was utilized as the features in the random forest and deep learning methods. Also, we were interested in seeing how the docking features can enhance our mathematical descriptors by including the Autodock Vina scoring terms in some submissions. In fact, these additional docking features did not improve our available models. The following is the detailed discussion of our performance for each subchallenge task.

Table 1.

Overview of all 26 predictive tasks in D3R GC3

Dataset	Task	Best submission ID	Method description
Pose prediction
Cathepsin stage 1A	Pose prediction	5addj	DP 3
Cathepsin stage 1B	Pose prediction	Not participate
Affinity rankings excluding Kds > 10 μM
Cathepsin stage 1	Scoring	m7oq4	Pose prediction: DP 5, energy prediction: EP1
Cathepsin stage 1	Free energy ranking	4ekn8	Pose prediction: DP 5, energy prediction: EP1
Cathepsin stage 2	Scoring	yf20t	Pose prediction: DP 5, energy prediction: EP2
Cathepsin stage 2	Free energy ranking	8br4d	Pose prediction: DP 5, energy prediction: EP2
VEGFR2	Scoring	rtv8m	Pose prediction: DP 5, energy prediction: EP1
JAK2 SC	Scoring	2ozdx	Pose prediction: DP 2, energy prediction: EP2
P38-α	Scoring	msyrx	Pose prediction: DP 5, energy prediction: EP2
JAK2 SC3	Scoring	a6kw3	Pose prediction: DP 5, energy prediction: EP1
JAK2 SC3★	Free energy ranking	4u5ey	Pose prediction: DP 2, energy prediction: EP2
TIE2★	Scoring	uuihe	Pose prediction: DP 3, energy prediction: EP1
TIE2★	Free energy ranking	5g8ed	Pose prediction: DP 2, energy prediction: EP2
ABL1★	Scoring	rdn3k	Pose prediction: DP 6, energy prediction: EP2
Active/inactive classification
VEGFR2	Scoring	rtv8m	Pose prediction: DP 5, energy prediction: EP1
JAK2 SC	Scoring	pm8re	Pose prediction: DP 5, energy prediction: EP2
P38-α	Scoring	zwj2r	Pose prediction: DP 3, energy prediction: EP2
JAK2 SC3	Scoring	yqoad	Pose prediction: DP 3, energy prediction: EP1
JAK2 SC3★	Free energy ranking	70j6z	Pose prediction: DP 3, energy prediction: EP1
TIE2★	Scoring	uuihe	Pose prediction: DP 3, energy prediction: EP1
TIE2★	Free energy ranking	vwbp8	Pose prediction: DP 3, energy prediction: EP1
ABL1	Scoring	c4xt7	Pose prediction: DP 6, energy prediction: EP1
Affinity rankings for cocrystalized ligands
Cathepsin stage 1	Scoring	04kya	Pose prediction: DP 5, energy prediction: EP2
Cathepsin stage 1★	Free energy ranking	fomca	Pose prediction: DP 5, energy prediction: EP2
Cathepsin stage 2★	Scoring	6jekk	Pose prediction: DP 3, energy prediction: EP1
Cathepsin stage 2★	Free energy ranking	v4jv4	Pose prediction: DP 5, energy prediction: EP1

Our predictions were ranked 1st in the tasks marked by golden stars

DP docking protocol

Subchallenge 1

The protein target for this challenge is Cathepsin S. There are 24 ligand–protein co-crystal structures and 136 ligands having binding data (IC50s). There are two stages in this subchallenge. Stage 1 asks participants to submit pose predictions, affinity rankings, and energy predictions. Stage 2 asks similar tasks except for pose predictions. Co-crystal structures were released for the second stage.

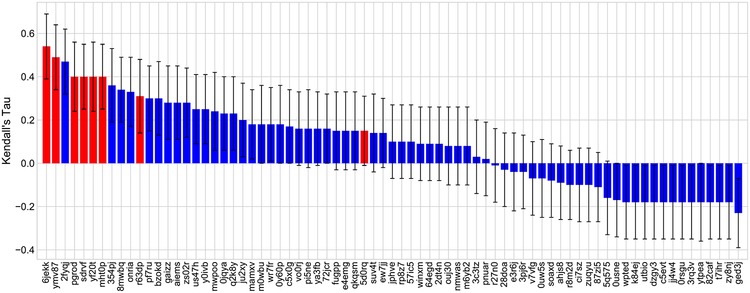
In order to examine the performances of scoring functions on the binding affinity when the ligand pose errors do not contribute to the final outcome, D3R organizers evaluated the accuracy of all submitted methods on 19 ligands having crystallographic poses. With this setting, our models attained the first places for the following tasks: free energy set in stage 1, scoring and free energy set in stage 2. It is worth mentioning that only stage 2 has the experimental structures. Stage 1 is still affected by the pose prediction errors. That explains why our predictors performed decently for scoring task in stage 1 with the best Kendall’s τ = 0.23, but they achieved a state-of-the-art result for the same task in stage 2 with the best Kendall’s τ = 0.54 (receipt ID 6jekk). Figure 2 depicts the ranking of all participants on the affinity ranking of 19 ligands in stage 2. The best free energy predictions on the ligands with experiment structures were also attained by our predictions. Particularly, in stage 1, our prediction with receipt ID fomca obtained RMSE_c = 0.33 kcal/mol. In stage 2, we accomplished RMSE_c = 0.29 kcal/mol with receipt ID v4jv4. Those results support that our mathematical deep learning models indeed gain a better performance when no pose prediction errors are involved.

Fig. 2.

Performance comparison of different submissions on affinity ranking of 19 ligands having crystallographic poses in stage 2 of subchallenge 1 of D3R GC3. All of our submissions are shown in the red color. Our best prediction having receipt ID 6jekk achieved the top performance with Kendall’s τ = 0.54

Subchallenge 2

In this subchallenge, there are 3 kinase families, namely VEGFR2, JAK2, and p38-α with number of ligands being 85, 89 and 72, respectively. The challenge is to rank affinities of all ligands in each kinase family. Our predictors do not perform well on these datasets. Our best result is the second place on the active/inactive classification of VERGFR2 set. Our best Matthews correlation coefficient (MCC) on such task is reported to be 0.48 from receipt ID rtv8m.

Subchallenge 3

The third subchallenge involves the kinase JAK2 which already appeared in the second one. However, this challenge only comprises 17 compounds with small changes in chemical structure. Subchallenge 3 consists of two tasks, namely affinity ranking and relative binding affinity predictions. We obtained the first place on the binding energy prediction with the centered RMSE as low as RMSE_c = 1.06 kcal/mol (receipt ID 4u5ey). On the affinity ranking, the performance of our models is unremarkable. However, we still manage to sit at the second place on the active/inactive classification with Mathew correlation coefficient = 0.23 with receipt ID yqoad.

Subchallenge 4

Similar to the third subchallenge, the fourth one consists of 18 ligands with small changes in chemical structures. However, the new protein family, TIE2, is considered. The tasks are still to give an affinity ranking for 18 ligands and absolute or relative binding energies for two subsets of 4 and 6 compounds. It is interesting to see that our model perform extremely well for the TIE2 dataset. We achieve the first place for all the evaluation metrics taken into account for this subchallenge. Specifically, for the affinity ranking excluding Kds > 10 μM, our model, receipt ID uuihe, produces the best Kendall’s τ and Spearman correlation coefficient among all of the participants with values being 0.57 and 0.76, respectively. When one is interested in active/inactive classification by including compounds having Kds > 10 μM, our model, receipt ID uuihe, is still ranked the first place with MCC = 0.78. On the absolute free energy predictions, the top results are still produced by our models. Specifically, on Set 1, our predictor with receipt ID vwbp8 was ranked the first place with MCC = 1.0. On Set 2, our model with receipt ID 5g8ed attained the RMSE_c = 1.02 kcal/mol which is the lowest among all submissions.

Subchallenge 5

The last subchallenge in the GC3 measures the accuracy of models on the binding affinity change prediction upon the mutation. ABL1 is the protein target for this subchallenge, and there are two compounds and five mutants. The challenge is to predict the ranking of all mutants for each of two ligands. Our models perform pretty decently for this task. Our best submission has receipt ID rdn3k which achieves the best Kendall’s tau (τ = 0.52) for affinity ranking excluding Kds > 10 μM.

Grand Challenge 2

The second Grand Challenge had 36 ligands with crystal structures and binding data for 102 ligands. All these compounds bind to the FXR target. The predictive tasks are the same as those of Subchallenge 1 in GC3. Specifically, GC2 consisted of two stages. The first stage included (i) pose prediction for 36 ligands; (ii) binding affinity ranking for 102 compounds; and (iii) absolute or relative free energy predictions for two subsets of 18 and 15 ligands, respectively. The second stage with released structures asked the same tasks as in the previous one except for the pose prediction.

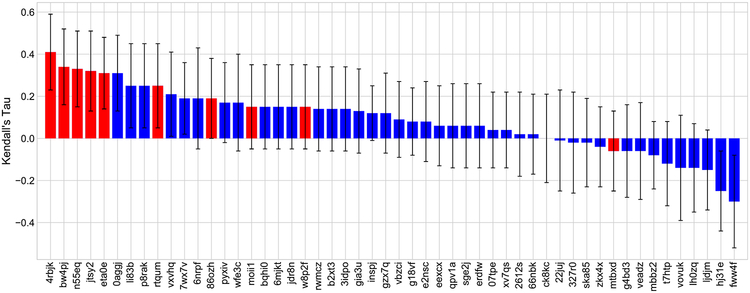
We employed the machine learning based scoring function to select the best poses for all prediction tasks, i.e., docking Protocol 1. The free energy values were predicted by scheme EP1. Although our pose ranking power was not impressive, the free energy predictions of our model performed pretty well. Specifically, our submission with receipt ID 5bvwx was ranked the second place in the free energy set 1 of stage 1 with RMSE_c = 0.68 kcal/mol. In stage 2, our models improved the accuracy of the energy prediction of compounds in the aforementioned free energy set. In fact, we obtained the first place in term of Kendall’s tau value (τ = 0.41) with receipt ID 4rbjk. That was also the highest Kendall’s tau value among all submissions in two stages for the free energy set 1. Figure 3 plots the performance of all submissions on the free energy set 1 in stage 2. Our submissions are highlighted in the red color.

Fig. 3.

Performance comparison of different submissions on free energy prediction for free energy set 1 in stage 2 of D3R GC2. All of our submissions are highlighted in the red color. Our best prediction having receipt ID 4rbjk achieved the top performance with Kendall’s τ = 0.41

Conclusion

In this work, we report the performances of our mathematical deep learning strategy on the binding affinity tasks in D3R GC2 and across five subchallenges in D3R GC3. The multiscale weighted colored graph and element specific persistent homology representations are the main descriptors in our models. We also employed a variety of machine learning algorithms including random forest and deep convolutional neural networks for the energy predictions. Overall, in GC2, our predictive models achieved the top place in free energy prediction for free energy set 1 in stage 2. In GC3, our submissions were ranked 1st in 10 out of 26 official evaluation tasks. These results confirm the predictive power and practical usage of our mathematical deep learning models in drug design and discovery. It is worthy to mention that the docking accuracy is still a bottleneck of our affinity prediction performance. We have tried a variety of docking protocols, namely align-close, align-target, close-dock, cross-dock, constraint-IFD, and free-IFD, for pose selection in GC3. However, none of them showed a dominant role in binding affinity accuracy. In addition, when one excludes the pose prediction error, Kendall’s tau of our model improves from 0.21 to 0.54 on the affinity ranking of compounds in Cathepsin S subchallenge. Therefore, the development of a state-of-the-art docking protocol is the major task in our roadmap to improve the accuracy of binding energy prediction when crystallographic structures are not available. Further improvement in the mathematical representations of protein–ligand binding using differential geometry is also under our consideration.