Prediction of leaf water potential and relative water content using terahertz radiation spectroscopy

Abstract

Increases in the frequency and severity of droughts across many regions worldwide necessitate an improved capacity to determine the water status of plants at organ, whole plant, canopy, and regional scales. Noninvasive methods have most potential for simultaneously improving basic water relations research and ground‐, flight‐, and space‐based sensing of water status, with applications in sustainability, food security, and conservation. The most frequently used methods to measure the most salient proxies of plant water status, that is, water mass per leaf area (WMA), relative water content (RWC), and leaf water potential (Ψ_leaf), require the excision of tissues and laboratory analysis, and have thus been limited to relatively low throughput and small study scales. Applications using electromagnetic radiation in the visible, infrared, and terahertz ranges can resolve the water status of canopies, yet heretofore have typically focused on statistical approaches to estimating RWC for leaves before and after severe dehydration, and few have predicted Ψ_leaf. Terahertz radiation has great promise to estimate leaf water status across the range of leaf dehydration important for the control of gas exchange and leaf survival. We demonstrate a refined method and physical model to predict WMA, RWC, and Ψ_leaf from terahertz transmission across a wide range of levels of dehydration for given leaves of three species, as well as across leaves of given species and across multiple species. These findings highlight the powerful potential and the outstanding challenges in applying in vivo terahertz spectrometry as a remote sensor of water status for a range of applications.

1. INTRODUCTION

Understanding plant responses to water is increasingly urgent given drought‐induced losses in crop productivity and tree mortality in many ecosystems worldwide (Allen et al., 2010; IPCC, 2014). Improving the capacity to determine tissue water status at organ, whole plant, canopy, and regional scales is necessary to resolve the drought responses and water requirements of crop and wild species, for food security and sustainability of agricultural and urban water use.

The most salient metrics of leaf water status at leaf scale are water mass per leaf area (WMA; numerically equal to the “leaf equivalent water thickness”; Tucker, 1980; Hunt & Rock, 1989; all terms and abbreviations summarized in Table 1), relative water content (RWC), and leaf water potential (Ψ_leaf; Jones, 2014). These indices are correlated for a given dehydrating leaf and provide different information. Whereas the WMA represents the absolute tissue water content normalized by leaf area, the RWC, normalized by the saturated water content, also provides information of cell volume shrinkage (Sack, John, & Buckley, 2018) and thereby captures more specifically the plant‐experienced water stress. Even more mechanistic insight is provided by Ψ_leaf, which enables quantification of the balance of osmotic and turgor pressures, and represents the driving force for water movement, enabling estimation of hydraulic conductances (Bartlett, Scoffoni, & Sack, 2012; Scoffoni et al., 2018; Scoffoni, McKown, Rawls, & Sack, 2012). However, typical methods for measuring these variables require the excision of tissues and laboratory analysis, either gravimetric in the case of WMA and RWC, or using the Scholander pressure chamber or psychrometry for Ψ_leaf, and thus, measurement of plant water status has often been limited to relatively low throughput and small study scales (Jones, 2014). By contrast, noninvasive methods have great potential for improving ground‐based and remote sensing in water relations research and their applications in agriculture and conservation, especially as WMA, RWC, and Ψ_leaf can in principle be estimated not only for leaves, but also at coarser scales, for whole canopies (Table S1). We present a refined method and physically based model to estimate WMA, RWC, and Ψ_leaf from terahertz radiation during mild, moderate, and severe leaf dehydration, for given leaves, across leaves of a given species, or across multiple species, validated for three species (Arabidopsis thaliana, Hedera canariensis, and Platanus racemosa; Table 2).

Table 1.

Terms, abbreviations, and definitions for terahertz spectroscopy and the measurement of leaf water status and underlying leaf structural and compositional variables

Term	Symbol	Units	Definitions and Significance
Terahertz spectroscopy
Terahertz time‐domain spectroscopy	THz‐TDS	–	System used to generate terahertz wavelength pulses and detect them after interaction with a sample to extract the time‐domain and frequency‐domain response of the sample
Peak field ratio	PFR	dBs	Ratio of transmitted terahertz radiation through sample to radiation transmitted through an empty system
Reference signal amplitude	E Ref	dBs	Peak electric field detected by the THz‐TDS system when no sample is placed in the system
Sample signal amplitude	E T	dBs	Peak electric field detected by the THz‐TDS system when a leaf sample is placed in the system
Absorption coefficient	α	m−1	Indication of the attenuation of radiation by a medium
Absorption coefficient of water	α w	m−1	Indication of the attenuation of radiation by water
Absorption coefficient of solid or dissolved leaf materials	α S	m−1	Indication of the attenuation of radiation by nonwater leaf materials
Reflectivity	R	unitless	Characteristic of a surface distinguishing its capacity to reflect incident radiation
Leaf water status and structural composition
Leaf water potential; predicted values	Ψleaf; $\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$	MPa	Water status variable indicating the bulk leaf average chemical potential of water within leaf cells
Osmotic potential	ΨS	MPa	Solute potential, determined by the concentration of cell solutes
Pressure potential	ΨP	MPa	Turgor pressure against the cell walls
Relative water content; predicted values	RWC; $\widehat{\text{RWC}}$	g∙g−1	Ratio of mass of leaf water to leaf water in saturated leaf
Water thickness	WT	m	Thickness of water within leaf
Water mass per area; predicted values	WMA; $\widehat{\text{WMA}}$	g∙m‐2	Mass of water within leaf per leaf area
Saturated water mass per area	SWMA	g∙m‐2	Mass of water within fully hydrated (saturated) leaf per leaf area
Saturated water content	SWC	g	Mass of water in fully hydrated (saturated) leaf
Leaf mass per area	LMA	g∙m‐2	Ratio of mass of dry leaf lamina to leaf area
Pressure–volume curve parameters
Water potential at turgor loss point	Ψtlp	MPa	The chemical potential of water within leaf cells at “wilting point”
Modulus of elasticity	ε	MPa	Stiffness of cell walls
Osmotic potential at full turgor	πo	MPa	Osmotic potential in cells at full turgor
Relative water content at turgor loss point	RWCtlp	g∙g−1	RWC at dehydration stage at which cells lose turgor

Table 2.

Species are listed with family, geographic origin, growth habit, and calculated pressure–volume curve parameters, including water potential at turgor loss point (Ψ_tlp), modulus of elasticity (ε), osmotic potential at full turgor (π _o), and the relative water content at turgor loss point (RWC_tlp)

Species	Family	Origin	Plant Habit	Ψtlp	ε	πo	RWCtlp
				MPa	MPa	MPa	%
Arabidopsis thaliana	Brassicaceae	Eurasia and Africa	Herbaceous	−0.41	0.26	−0.28	67.2
Hedera canariensis	Araliaceae	Canary Islands	Climber	−2.32	7.85	−1.71	78.3
Platanus racemosa	Platanaceae	Southern California	Tree	−1.39	9.69	−1.16	86.4

Water within a plant absorbs electromagnetic radiation across the visible, infrared, and terahertz wavelengths distinctly from other structural plant components (Jones, 2014; Knipling, 1970). Accordingly, many studies have shown correlations of radiation variables with leaf water status variables at the scale of individual leaves, whole plants, and forest stands (Table S1; Claudio et al., 2006; Cotrozzi et al., 2017; Danson, Steven, Malthus, & Clark, 1992; Hunt & Rock, 1989; Hunt, Rock, & Nobel, 1987; Peñuelas, Filella, Biel, Serrano, & Savé, 1993; Peñuelas & Inoue, 1999; Rapaport, Hochberg, Cochavi, Karnieli, & Rachmilevitch, 2017; Rapaport, Hochberg, Shoshany, Karnieli, & Rachmilevitch, 2015; Sancho‐Knapik et al., 2011). The power of these approaches at large scales is shown by the use of airborne hyperspectral or microwave data to detect canopy water content across large forest ranges (Asner et al., 2016; Rao, Anderegg, Sala, Martínez‐Vilalta, & Konings, 2019). Yet, heretofore, the bulk of studies has focused on statistical correlations of water status variables across well‐hydrated and strongly dehydrated leaves, without clear resolution for mildly to moderately dehydrated leaves (Table S1). Thus, further development is needed to sense WMA, RWC, and Ψ_leaf in mild and moderately dehydrated leaves, that is, in the important range of leaf dehydration for the control of gas exchange, between full turgor and turgor loss point (Bartlett, Klein, Jansen, Choat, & Sack, 2016; Trueba et al., 2019), as well as at stronger levels of dehydration below turgor loss point.

Electromagnetic radiation in the terahertz regime (loosely 100 GHz‐10 THz frequency range or 10–1,000 μm wavelength range) (Mittleman, Jacobsen, & Nuss, 1996) has exceptional promise for measuring plant water status and dynamics. Transitions between vibrational and rotational states of many polar molecules, such as water, fall in the terahertz region of the electromagnetic spectrum (Mittleman, Jacobsen, Neelamani, Baraniuk, & Nuss, 1998), and thus, terahertz wave propagation is very sensitive to the sample water content (Hecht, 2002; Rønne, Åstrand, & Keiding, 1999; Thrane, Jacobsen, Uhd Jepsen, & Keiding, 1995). In addition, terahertz radiation can offer higher resolution imaging compared with microwave frequencies. Imaging and spectroscopy at terahertz frequencies are harmless since the energy of the photon is very small, compared to lower‐wavelength radiation such as ultraviolet and X‐rays (Sun et al., 2011). Terahertz time‐domain spectroscopy (THz‐TDS) employs short pulses of electromagnetic radiation, which have a broad terahertz frequency range (Skoog, Holler, & Crouch, 2017). The transmitted and reflected pulses through and from the sample are detected to extract the time‐ and frequency‐domain responses (Yardimci, Cakmakyapan, Hemmati, & Jarrahi, 2017; Yardimci & Jarrahi, 2017). Because of these specifications, there has been great interest in predicting plant water status using THz‐TDS systems (Table S1; Hu & Nuss, 1995; Hadjiloucas, Karatzas, & Bowen, 1999; Jördens, Scheller, Breitenstein, Selmar, & Koch, 2009; Castro‐Camus, Palomar, & Covarrubias, 2013; Gente et al., 2013; Born et al., 2014; Gente, Rehn, & Koch, 2015; Santesteban et al., 2015; Baldacci et al., 2017; Gente et al., 2018). However, as for other wavelengths, previous terahertz studies have generally compared only well‐hydrated versus strongly dehydrated leaves in absolute water content (Born et al., 2014; Castro‐Camus et al., 2013; Gente et al., 2013; Jördens et al., 2009; Li et al., 2018), WMA (Baldacci et al., 2017; Gente et al., 2018), or Ψ_leaf (Hadjiloucas et al., 1999), with limited resolution for moderately dehydrated leaves. Physical models have been proposed to relate absolute water content or WMA to terahertz absorption (Gente et al., 2013; Jördens et al., 2009; Baldacci et al., 2017), but not yet extended to enable scaling to RWC and Ψ_leaf. Further, while it is important to follow individual leaves in their WMA, RWC, and Ψ_leaf during dehydration, tests are needed of whether the water status of multiple leaves of a species or different species can be estimated from generalized relationships of water status to terahertz radiation, as even for given species leaves can vary more than twofold in hydrated thickness and WMA independently of RWC and Ψ_leaf (Scoffoni, Vuong, Diep, Cochard, & Sack, 2014).

Our aim was to clarify the relationship between leaf terahertz spectroscopy responses and key water status variables, that is, WMA, RWC, and Ψ_leaf. We used a THz‐TDS system to characterize for given dehydrating leaves the terahertz transmission peak field ratio (PFR). We tested the hypothesis that a novel, physically based model, by which WMA would decline linearly with ln (PFR) (see Methods), can be applied to terahertz radiation for prediction of WMA, RWC, and Ψ_leaf during mild, moderate, and severe leaf dehydration. We also tested the ability to predict leaf water status from generalized equations across leaves of a given species, and across multiple species using physical relationships.

2. MATERIALS AND METHODS

2.1. Plant material and sample preparation

Measurements were conducted on three species diverse in phylogeny, habitat type, and responses to drought: Arabidopsis thaliana (Col‐0), Hedera canariensis, and Platanus racemosa (Table 2). Large individuals of climber H. canariensis, and tree P. racemosa were sampled on and around the campus of the University of California, Los Angeles. A. thaliana Col‐0, an annual herb, was grown in a climate‐controlled greenhouse at the University of California, Los Angeles (minimum, mean, and maximum values for temperature, 18.3, 22.4, 35.7°C; for relative humidity 8.3%, 44.4%, 83.8%; and for irradiance 1.2, 67.6, 1,300 μmol photons/m² s⁻¹). Seeds were cold‐acclimated at 4°C for three days and sown in pots (7.95 cm width × 12.4 cm length × 5.87 cm deep) in soil (1:1:2:1:1 mixture of washed plaster sand, loam, peat moss, perlite, vermiculite). After approximately a week, plants were thinned to one individual per pot, and plants were studied after 5–6 weeks of growth.

For H. canariensis and P. racemosa, shoots with at least six fully developed leaves were harvested in the afternoon of the day prior to measurements and transported to the laboratory in plastic bags with wet paper towels. From each shoot, two nodes were recut under deionized water, and shoots were rehydrated overnight under plastic. For A. thaliana, trays of potted individuals were watered to saturation with deionized water and sealed with a dark plastic cover and wet paper towels for overnight rehydration. Two leaves from each of 3 individuals of H. canariensis and P. racemosa, and one leaf from each of five individuals of A. thaliana (a sixth leaf was not successful) was used for measuring terahertz transmission and leaf water status during dehydration.

2.2. Terahertz time‐domain spectroscopy

A Ti:Sapphire laser (Coherent MIRA‐HP, Coherent Inc.) was used to generate femtosecond optical pulses at a 780 nm wavelength (Figure 1a). The beam of light was split into two, with the first beam used to pump a terahertz source to generate terahertz pulses, which were guided and focused on a terahertz detector, and the second beam passed through a linear delay stage to the terahertz detector. Plasmonic photoconductive nano‐antenna arrays were used as the terahertz source and detector to provide high‐power terahertz radiation and high terahertz detection sensitivity over a broad terahertz frequency range (Yardimci & Jarrahi, 2017; Yardimci, Yang, Berry, & Jarrahi, 2015). By moving the linear delay stage and changing the time delay between the optical pump and probe pulses incident on the terahertz source and detector, respectively, the time‐domain electric field profile of the terahertz pulses incident on the terahertz detector was resolved with a sub‐picosecond resolution over a 400 ps time‐window. Lock‐in detection was used to increase the signal‐to‐noise ratio of the resolved signal. To further increase the signal‐to‐noise ratio of the resolved signal, 10 time‐domain traces were captured and averaged. By taking the Fourier transform of the averaged time‐domain signal, the frequency‐domain data were obtained with a 2.5 GHz frequency resolution (Figure 1b). The THz‐TDS system used for the measurements reported in this work offered a 100‐dB dynamic range and a frequency range of 0.1–5.5 THz.

Figure 1.

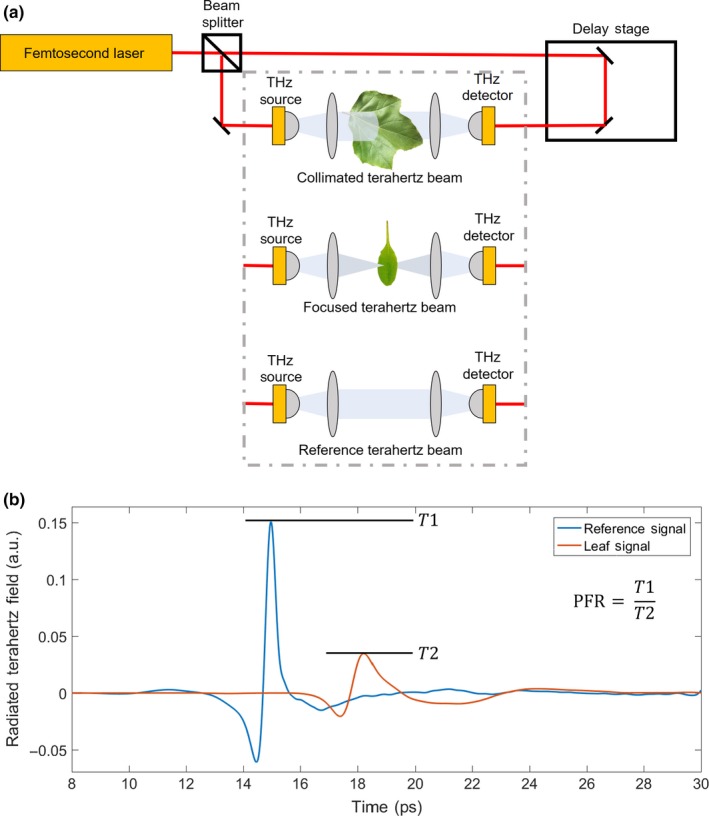
Schematic of the terahertz time‐domain spectroscopy and its output (THz‐TDS). The THz‐TDS system is based on a terahertz source that emits femtosecond pulses of light. These pulses of light were distributed between the terahertz source, where they were used for sample analyses, and the terahertz detector, where they were used for detecting the terahertz pulses that transmitted through the leaf samples. At the beginning of measurements, a reference signal was recorded. A delay stage was used to change the time delay between the light pulses that were incident on the terahertz source and detector to scan across the terahertz bandwidth. Hedera canariensis and Platanus racemosa samples were measured using a collimated terahertz beam, and Arabidopsis thaliana were measured using a focused terahertz beam (a). For each measurement, a time‐domain reference signal was recorded (E _Ref; blue curve) along with a signal transmitted through the leaf sample (E _Ref; red curve) (b)

2.3. Measurements of dehydrating leaves for terahertz transmission and leaf water status

Before starting measurements with the THz‐TDS system, a reference signal was acquired without placing any leaf samples on the terahertz beam path.

To determine the potential influence of variation in the angle of terahertz radiation incident on the leaf samples, leaves of H. canariensis were measured at 90°, perpendicular to the beam, as well as at ±5.0° off the perpendicular direction. We found negligible changes in the terahertz measurement results within this angle range.

Hydrated leaves were sealed in bags (Whirl‐Pak, Nasco, Fort Atkinson, WI, USA) that had been exhaled into to generate a moist, high CO₂ environment to minimize transpiration, and placed in a larger plastic bag with wet paper towels to equilibrate at least 30 min before weighing with an analytical balance (0.01 mg; MS205DU Mettler Toledo, Toledo, OH). Then, each leaf sample was placed on a motorized XY translation stage and the position of the leaf was adjusted such that a section of lamina between two secondary veins was exposed to the terahertz radiation which was incident on the adaxial leaf face. A collimated terahertz beam with ~1.5‐cm‐diameter beam spot size was used for the H. canariensis and P. racemosa leaves. The smaller and more fragile leaves of A. thaliana were placed on a glass slide to ensure proper alignment during dehydration, and the terahertz beam was focused to produce a ~3‐mm‐diameter beam spot size for the measurements (Figure 1a). Because A. thaliana samples were smaller than the beam from the terahertz source, reduction the beam size incident on the sample was necessary to avoid including radiation propagating through air around the leaf, which would have led to large errors in the extracted water status parameters, as the data analysis assumes that the entire terahertz radiation interacts with the leaf sample.

The measurements with the THz‐TDS system were repeated for each leaf during dehydration, with the position of the terahertz beam on the leaves marked to return to approximately the same spot for each measurement. However, given that leaves were removed from the system and replaced for repeated measurements, there were shifts in the exact position of the terahertz beam on the leaf sample in successive measurements; thus, for each dehydration stage, 25 measurements (at 1 mm steps) were made within the marked 5 × 5 mm² area for each H. canariensis and P. racemosa sample and averaged to improve the precision of the mean (Figure 2). Since a beam with much smaller spot size was incident on A. thaliana, 169 measurements (at 0.5 mm steps) were taken within a 6 × 6 mm² area. The THz‐TDS system can image the leaf surface with even greater resolution (Figure 3) but that requires significant measurement times, which may result in dehydration of excised tissues. After each THz‐TDS measurement, the leaf and bag were weighed with the analytical balance, and Ψ_leaf was determined with a pressure chamber (0.001 MPa resolution, Plant Moisture Stress Model 1000; PMS Instruments Co). Then, the leaves were bench dried on a fan to reduce Ψ_leaf by 0.1–0.2 MPa, and the terahertz measurements were repeated. Once at least two measurements were completed below the species’ previously published turgor loss point (Scoffoni et al., 2018, 2014), an image of the leaf was taken using a flatbed scanner (Epson Perfection 4490 Photo, Seiko Epson Corporation) and the leaf lamina area (LA) was determined using Fiji (Schindelin et al., 2012). After the experiment, the mass of the bag was determined and subtracted for calculation of fresh leaf mass (FM) values for each leaf dehydration stage.

Figure 2.

Terahertz transmission as a function of dehydration. Leaves were dehydrated to a range of leaf water potentials from full turgor to turgor loss point and beyond. At each measurement point for Hedera canariensis and Platanus racemosa, transmission of terahertz radiation through the leaf between major veins was characterized at 1‐mm steps. Depicted above are sequential images produced for a H. canariensis leaf at leaf water potential values of −0.28 to −2.10 MPa, illustrating an increase in the transmitted radiation with dehydration

Figure 3.

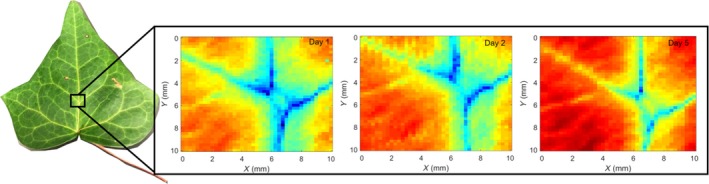
High‐resolution images of leaf water thickness during dehydration may be taken with the terahertz time‐domain spectroscopy system. Depicted are images of a Hedera canariensis leaf imaged after 1, 2, and 5 days of dehydration near major veins

Leaf dry mass (DM) was determined after oven drying for 48 hr at 70°C to enable determination of leaf mass per area (LMA):

$$\text{LMA}=\frac{\text{DM}}{\text{LA}}$$ (1)

For each leaf, the saturated mass (SM) was estimated as the intercept of standard major axis regression lines (Table S2) fitted for the relationship between the leaf water mass and Ψ_leaf (Sack & Pasquet‐kok, 2011). Then, RWC was determined for each stage of leaf dehydration as

$$\text{RWC}=\frac{\text{FM}-\text{DM}}{\text{SM}-\text{DM}}$$ (2)

And saturated water content (SWC) as:

$$\text{SWC}=\frac{\text{SM}}{\text{DM}}$$ (3)

Species‐specific pressure–volume curves were constructed using RWC and Ψ_leaf data for the leaves that had more than three data points more negative than turgor loss point, that is, for three leaves of H. canariensis and five leaves of P. racemosa. For A. thaliana, given the fewer data available for dehydration sequences of individual leaves, data for all six leaves were pooled together into an overall pressure–volume curve (Scoffoni et al., 2018). From the pressure–volume curves, parameters were extracted including turgor loss point (Ψ_tlp), osmotic potential at full turgor (π _o), and relative water content values at turgor loss point (RWC_tlp) (Sack & Pasquet‐kok, 2011). When “plateau effects” were detected during early dehydration, that is, minute changes in Ψ_leaf despite substantial declines of leaf water mass, representing the dehydration of water‐filled leaf airspaces, these points were removed before the estimation of pressure–volume parameters (Kubiske & Abrams, 1990).

A control was established to ensure that the change in the measured terahertz pulse during leaf dehydration was due to declining leaf water status, rather than simply associated with time duration. Thus, for H. canariensis, leaves that were maintained fully hydrated were measured over time (Figure 4). Shoots of H. canariensis were rehydrated, and then leaves were excised near the base of the petiole in a petri dish under filtered ultra‐pure degassed water (0.22 μm Thornton 200 CR; Millipore). The petioles were wrapped in parafilm and connected under filtered water to clear poly‐vinyl chloride tubing containing filtered water. Terahertz transmission measurements were recorded for these leaves at 1‐hr intervals for 4 hr. For each measurement, the leaves were removed, weighed for the determination of RWC, and reconnected to the tubing under water. Leaf dry mass was determined after oven drying for 48 hr at 70°C. No variation was found in terahertz absorption with time for the hydrated leaves (Figure 4).

Figure 4.

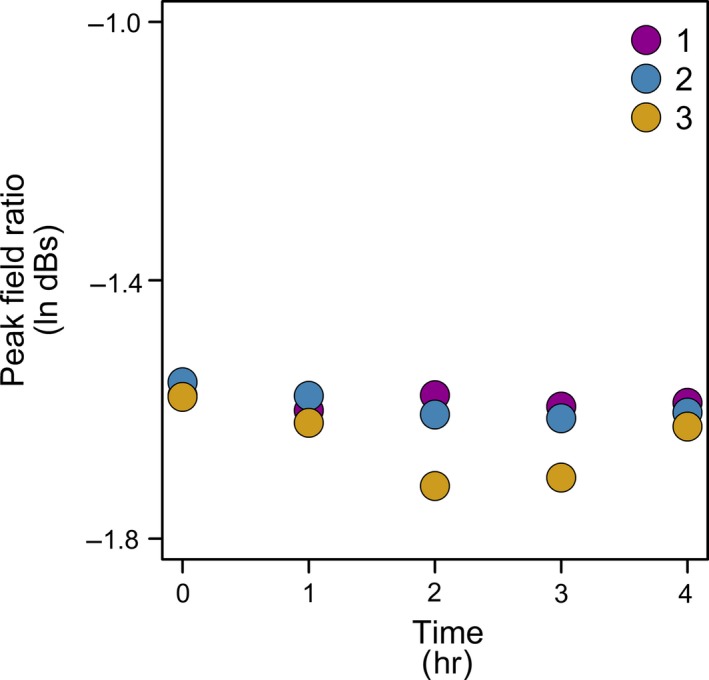
Testing for an influence of time on terahertz transmission for leaves maintained at full hydration. As a control, excised leaves were connected to a water source, while measurements were taken every hour for 4 hr, for H. canariensis (each symbol color represents a different leaf)

2.4. A physically based model for leaf water status from terahertz signal analysis

During the terahertz measurements, the electromagnetic radiation was partially reflected from the leaf surface and partially absorbed within the leaf. The absorbed terahertz radiation can be estimated by comparing the time‐domain reference signal with that obtained after transmission through the leaf. The peak field ratio (PFR) used to estimate leaf water status (Figure 1b) was calculated as:

$$\text{PFR}=\frac{max(E_{\mathrm{T}})}{max(E_{\text{Ref}})}$$ (4)

where E _Ref and E _T are the peak electric field amplitudes of the reference and transmitted terahertz signals through the leaf in the time domain (Hecht, 2002). The amplitude of the transmitted terahertz field has a strong dependence on the total absorbed power within the leaf over a broad terahertz frequency range. We note that the use of the PFR rather than other metrics, such as, for example, the power integrated over the time domain would not change our analysis as the values are dominated by the low‐frequency components of the terahertz pulse and, therefore, are strongly correlated, arising from the same absorption parameters. The relationship between the peak amplitudes of the reference and transmitted terahertz fields can be estimated as:

$$\left|E_{\mathrm{T}}\right|=\left|E_{\text{Ref}}\right|·\left|1-R\right|·e^{-\alpha d}$$ (5)

where R and α are, respectively, assumed to be the reflectivity and the absorption coefficient effective across the measured terahertz frequency band, and d to be the leaf thickness (Hecht, 2002). The absorption coefficient, α, has a strong dependence on the thickness of water within the leaf:

$$\alpha =\frac{\text{WT}·{\alpha }_{\mathrm{W}}+\text{VT}·{\alpha }_{\mathrm{V}}+\text{ST}·{\alpha }_{\mathrm{S}}}{\text{WT}+\text{VT}+\text{ST}}$$ (6)

where WT is the thickness of water in the leaf; VT is the thickness of the vapor‐saturated leaf airspaces; ST is the thickness of other nonair leaf materials; α _w, α _V, and α _s are the absorption coefficients of liquid water, vapor, and other nonwater (solid or dissolved) leaf materials. The absorption coefficients used in these equations were assumed to be an average value over terahertz frequency bandwidth of the THz‐TDS system used for these measurements. Combining Equations 5 and 6, with d = WT+VT + ST:

$$\begin{array}{c}\left|E_{\mathrm{T}}\right|=|E_{\text{Ref}}\left|·\right|1-\mathrm{R}|·{\mathrm{e}}^{-\left(\text{WT}·{\alpha }_{\mathrm{W}}+\text{VT}·{\alpha }_{\mathrm{V}}+\text{ST}·{\alpha }_{\mathrm{S}}\right)}\end{array}$$ (7)

To relate our measured PFR values to measured leaf water status, we divided both sides of Equation 7 by |E_Ref|, substituted PFR for $\frac{E_{\mathrm{T}}}{E_{\text{Ref}}}$ using Equation 4, and ln‐transformed both sides:

$$\begin{array}{c}\ln \left(\text{PFR}\right)=\ln \left(\left|1-R\right|\right)-\text{WT}·{\alpha }_{\mathrm{W}}-\text{VT}·{\alpha }_{\mathrm{V}}-\text{ST}·{\alpha }_{\mathrm{S}}\end{array}$$ (8)

We assumed that WT and VT were of similar magnitude, and α _V « α _W (Kindt & Schmuttenmaer, 1996; Rønne et al., 1999; Yang, Shutler, & Grischkowsky, 2011), and thus that $\text{VT}·{\alpha }_{\mathrm{V}}$ was negligible. Solving for WT:

$$\begin{array}{c}\text{WT}=\frac{-\ln \left(\text{PFR}\right)}{{\alpha }_{\mathrm{W}}}+\frac{\ln \left(\left|1-R\right|\right)-\text{ST}·{\alpha }_{\mathrm{S}}}{{\alpha }_{\mathrm{W}}}\end{array}$$ (9)

We assume that as a given leaf dehydrates, R remains constant, following (Sun et al., 2011), and further, that α _W, α _V, α _s, and α _S remain constant. Thus, WT can be predicted as a linear function of ln PFS in drying leaves.

$$\begin{array}{c}\text{WT}=\frac{-\ln \left(\text{PFR}\right)}{{\alpha }_{\mathrm{W}}}+c\end{array}$$ (10)

where c = $\frac{\ln \left(\left|1-R\right|\right)-\text{ST}·{\alpha }_{\mathrm{S}}}{{\alpha }_{\mathrm{W}}}$.

Notably, as the density of water = 1.0 g/cm³, and water thickness (WT) is equivalent to water volume per unit leaf area, WT is numerically equivalent to the total leaf water mass per area (WMA). Thus, for each leaf of a given species, we fitted lines for WMA as a linear function of $\ln \text{PFR}$ (Table 3).

$$\begin{array}{c}\text{WMA}=a·\ln \text{(PFR)}+b\end{array}$$ (11)

Table 3.

Ordinary least squares (OLS) regression model parameters with lower and upper confidence limits (CL) and tests of common slope (ANCOVA) among leaves. Relationships for each leaf, species, and across multiple species of water mass per area (WMA) with terahertz transmission (ln PFR) were tested and used to predict relative water content and leaf water potential. P‐values for individual leaves represent the fit of the linear model, and for common slopes, represent a test for the significance of variation in slope among individual leaves or among species

Species	Leaf	Slope (Lower CL, Upper CL)	Intercept (Lower CL, Upper CL)	R 2	p value
Arabidopsis thaliana	1	−343 (−656, −30.2)	−3.24 (−210, 203)	.88	.0421
	2	−332 (−566, −97.0)	−72.8 (−320, 174)	.83	.0205
	3	−223 (−263, −182)	19.7 (−8.57, 48.0)	.99	.0004
	4	−1002 (−1727, −277)	−521 (−1095, 49.9)	.95	.0277
	5	−312 (−582, −42.7)	−63.0 (−333, 207)	.93	.038
A. thaliana common slope					.0370
Hedera canariensis	1	−322 (−377, −268)	−211 (−286, −135)	.99	<.0001
	2	−300 (−496, −103)	−165 (−417, 87.8)	.82	.0130
	3	−179 (−193, −164)	−33.3 (−51.9, −14.6)	.99	<.0001
	4	−281 (−357, −205)	−114 (−203, −24.4)	.96	.001
	5	−340 (−664, −16.4)	−357 (−895, 181)	.59	.043
	6	−353 (−575, −132)	−3.45 (−721, 30.2)	.77	.009
H. canariensis common slope					.001
Platanus racemosa	1	−347 (−523, −172)	−139 (−311, 33.3)	.85	.005
	2	−128 (−164, −91.1)	13.0 (−33.9, 59.8)	.95	<.001
	3	−151 (−272, −30.6)	−9.70 (−149, 130)	.69	.025
	4	−97.1 (−110, −84.5)	16.9 (4.90, 29.0)	.98	<.0001
	5	−147 (−173, −122)	−27.3 (−49.5, 50.0)	.97	<.0001
	6	−89.5 (−107, −72.3)	39.4 (28.6, 50.2)	.96	<.0001
P. racemosa common slope					.003
Arabidopsis thaliana		−133 (−172, −96.5)	82.0 (−28.5, 44.9)	.55	1.28 × 10–5
Hedera canariensis		−91.7 (−135, −48.6)	90.3 (28.0, 153)	.34	.0001
Platanus racemosa		−245 (−339, −151)	90.0 (−71.7, 89.7)	.57	9.17 × 10–9
All species		−125	48.0	.37	2.25 × 10–12
All‐species common slope					.022

From these fitted lines, for each dehydration stage of each leaf, we predicted WMA values from PFR, that is, $\widehat{\text{WMA}}$. To predict the relative water content ($\widehat{\text{RWC}}$), we divided by the saturated water mass per area for each leaf (SWMA), where

$$\begin{array}{c}\widehat{\text{RWC}}=\frac{\widehat{\text{WMA}}}{\text{SWMA}}\end{array}$$ (12)

Notably,

$$\begin{array}{c}\text{SWMA}=\text{LMA}·\text{SWC}\end{array}$$ (13)

where SWC is the saturated water content, that is, the water mass in saturated leaf divided by leaf dry mass, and LMA is the leaf dry mass per area.

We then predicted $\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$ from $\widehat{\text{RWC}}$, using pressure–volume curve parameters derived from curves fitted according to pressure–volume theory (Sack et al., 2018). Ψ_leaf is the sum of the pressure potential (Ψ_P) and the solute potential (Ψ_S):

$$\begin{array}{c}{\mathrm{\Psi }}_{\text{leaf}}={\mathrm{\Psi }}_{\mathrm{S}}+{\mathrm{\Psi }}_{\mathrm{P}}\end{array}$$ (14)

and

$$\begin{array}{c}{\mathrm{\Psi }}_{\mathrm{S}}=\frac{{\pi }_{\mathrm{o}}·{\mathrm{\Psi }}_{\text{tlp}}\left(1-{\text{RWC}}_{\text{tlp}}\right)}{{\pi }_{\mathrm{o}}\left(1-\text{RWC}\right)+{\mathrm{\Psi }}_{\text{tlp}}\left(\text{RWC}-{\text{RWC}}_{\text{tlp}}\right)}\end{array}$$ (15)

where ${\pi }_{\mathrm{o}}$, RWC_tlp, and Ψ_tlp were determined from pressure–volume curves as described previously, and

$$\begin{array}{c}{\mathrm{\Psi }}_{\text{P}}=\left\{\begin{array}{cc}{\pi }_{\text{o}}·\left(\frac{\text{RWC}-{\text{RWC}}_{\text{tlp}}}{1-{\text{RWC}}_{\text{tlp}}}\right),\hfill & \text{if RWC}>{\text{RWC}}_{\text{tlp}}\\ 0,\hfill & \text{if RWC}<{\text{RWC}}_{\text{tlp}}\end{array}\right.\end{array}$$ (16)

Thus, using this physical model, $\widehat{\text{WMA}}$, $\widehat{\text{RWC}},$ and $\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$ were estimated from terahertz measurements during dehydration (Figure 5). Based on the relationship of water mass per area (WMA) to ln (PFR) (Equation 11), predictions are made of water mass per area ($\widehat{\text{WMA}}$). Then, relative water content ($\widehat{\text{RWC}}$) is estimated, accounting for saturated water mass per leaf area (SWMA), which is the product of leaf dry mass per area (LMA) and saturated water content (SWC) (Equations (12), (13). Finally, leaf water potential ($\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$) is estimated using pressure–volume curve (PV) parameters (Equations (14), (15), (16).

Figure 5.

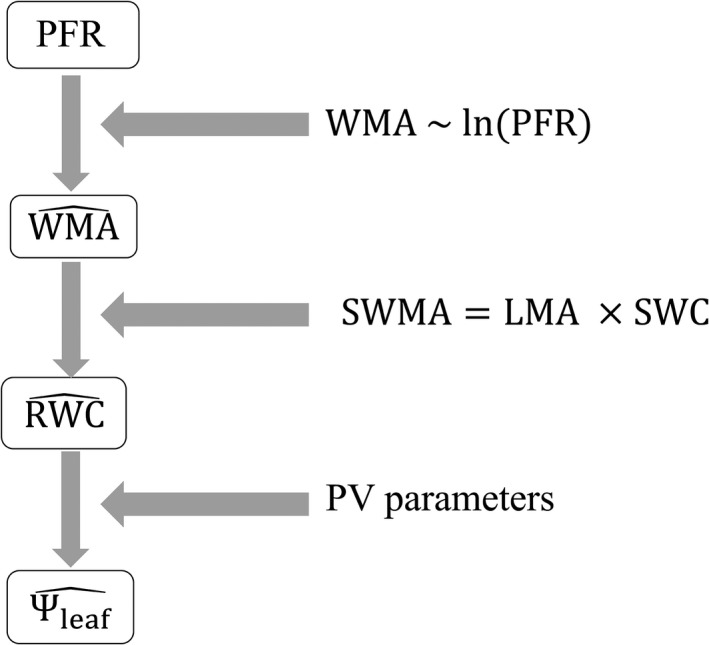
Flowchart illustrating the inputs to for the hierarchical prediction of water status variables from terahertz spectroscopy peak field ratio (PFR) and leaf traits (see Equations and Table 1 for further information about variables and symbols). Based on the relationship of water mass per area (WMA) to ln (PFR) for each dehydrating leaf, predictions are made of water mass per area ($\widehat{\text{WMA}}$). Then, relative water content ($\widehat{\text{RWC}}$) is estimated, accounting for saturated water mass per leaf area (SWMA), which is the product of leaf dry mass per area (LMA) and saturated water content (SWC). Finally, leaf water potential ($\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$) is estimated using pressure–volume curve (PV) parameters. These predictions were tested using the relationship of water mass per area (WMA) to ln (PFR) for individual leaves, or all leaves of given species, or across all leaves for the three species tested (Table 4)

2.5. Statistics

We used Pearson correlation coefficients (r) to test the strength of the association of variables, and the coefficient of determination (R ²) to express the goodness of fit of models to data (Sokal & Rohlf, 1995).

Applying the physically based model statistically, we used measured terahertz spectroscopy peak field ratio (PFR) to predict leaf water status variables, leaf water mass per area ($\widehat{\text{WMA}}$), relative water content ($\widehat{\text{RWC}}$), and leaf water potential ($\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$). Predictions were made for each individual leaf during dehydration (Table 4, left column), based on the relationship of water mass per area (WMA) to ln (PFR) for each dehydrating leaf, and from individual leaf values for saturated water mass per leaf area (SWMA) and species‐level mean pressure–volume curve (PV) parameters. Predictions were also tested using species‐level relationships of WMA to ln (PFR) (Table 4, middle column) and all‐species‐level relationships of WMA to ln (PFR) (Table 4, right column), using species‐level mean values for SWMA and PV parameters. We then tested how well these estimates corresponded to observed values of WMA, RWC, and Ψ_leaf.

Table 4.

Inputs for using measured terahertz spectroscopy peak field ratio (PFR) to predict leaf water status variables, water mass per area ($\widehat{\text{WMA}}$), relative water content ($\widehat{\text{RWC}}$), and leaf water potential ($\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$). Predictions were made for each individual leaf during dehydration ($\widehat{{\text{WMA}}_{\text{leaf}}}$, $\widehat{{\text{RWC}}_{\text{leaf}}}$ and $\widehat{{\mathrm{\Psi }}_{\text{leaf,leaf}}}$, left column), based on the relationship of water mass per area (WMA) to ln(PFR) for each dehydrating leaf, and from individual leaf values for saturated water mass per leaf area (SWMA) and species‐level mean pressure–volume curve (PV) parameters. Predictions were also tested using species‐level relationships of WMA to ln(PFR) ($\widehat{{\text{WMA}}_{\text{species}}}$, $\widehat{{\text{RWC}}_{\text{species}}},$ and $\widehat{{\mathrm{\Psi }}_{\text{leaf,species}}}$, middle column) and all‐species‐level relationships of WMA to ln(PFR) ($\widehat{{\text{WMA}}_{\text{all}}}$, $\widehat{{\text{RWC}}_{\text{all}}},$ and $\widehat{{\mathrm{\Psi }}_{\text{leaf,all}}}$, right column), using species‐level mean values for SWMA and PV parameters

	Individual leaf level prediction	Species‐level prediction	All‐species‐level prediction
$\widehat{\text{WMA}}$	$\widehat{{\text{WMA}}_{\text{leaf}}}$, from WMA ~ ln (PFR) relationship for each leaf	$\widehat{{\text{WMA}}_{\text{species}}}$, from WMA ~ ln (PFR) relationship for all leaves of given species	$\widehat{{\text{WMA}}_{\text{all}}}$, from WMA ~ ln (PFR) relationship for all leaves of all species
$\widehat{\text{RWC}}$	$\widehat{{\text{RWC}}_{\text{leaf}}}$, from $\widehat{{\text{WMA}}_{\text{leaf}}}$ and SWMA of each leaf	$\widehat{{\text{RWC}}_{\text{species}}}$, from $\widehat{{\text{WMA}}_{\text{species}}}$ and species‐level mean SWMA	$\widehat{{\text{RWC}}_{\text{all}}}$, from $\widehat{{\text{WMA}}_{\text{all}}}$ and species‐level mean SWMA
$\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$	$\widehat{{\mathrm{\Psi }}_{\text{leaf,leaf}}},$ from $\widehat{{\text{RWC}}_{\text{leaf}}}$ and species‐level mean P‐V parameters	$\widehat{{\mathrm{\Psi }}_{\text{leaf,species}}},$ from $\widehat{{\text{RWC}}_{\text{species}}}$ and species‐level mean P‐V parameters	$\widehat{{\mathrm{\Psi }}_{\text{leaf,all}}},$ from $\widehat{{\text{RWC}}_{\text{all}}}$ and species‐level mean P‐V parameters

To estimate the relationships of ln (PFR) to WMA at individual leaf, or species, or all‐species scale, we fitted lines using ordinary least squares (OLS) regression with the lm function in the stats R package (R Core Team, 2019). We tested for the similarity of slopes among leaves of each species in the relationships of ln (PFR) and WMA by performing an analysis of covariance (ANCOVA) (using SMATR; Warton, Wright, Falster, Westoby, 2006). Further, we tested for the similarity of slopes across species, considering all leaves of each species together.

In applying the hierarchical approach to prediction, from $\widehat{\text{WMA}}$ to $\widehat{\text{RWC}}$ to $\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$, outlier points that represented impossible values were removed for higher‐level predictions (Riazoshams, Midi, & Ghilagaber, 2019). Thus, when high outliers for $\widehat{\text{WMA}}$ from the fitted relationship of WMA to ln (PFR) led, when scaled by SWMA, to $\widehat{\text{RWC}}$ values that exceeded 1.0 g g⁻¹, and to $\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$ values that exceeded 0 MPa, or when extremely negative $\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$ were predicted from $\widehat{\text{RWC}}$ values far below the range of values in the PV curve, these $\widehat{\text{RWC}}$ and $\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$ values were removed for the estimation of predictive capacity. Altogether, for estimation of predictive capacity at the individual leaf level, values for 3 of 38 leaves were removed for H. canariensis and 1 of 42 leaves for P. racemosa; at the species level, 7 of 42 leaves for P. racemosa; and at the all‐species level, 8 of 38 leaves for H. canariensis, and 21 of 42 leaves for P. racemosa (Table S2).

We tested model predictions of leaf water status at leaf scale, at species scale and at all species scale, by plotting estimated against observed values, and calculating R ² and root mean square error (RMSE, in the same units as the predicted variable) as:

$$\begin{array}{c}\text{RMSE}=\sqrt{\overline{{\left(\text{observed}-\text{predicted}\right)}^2}}\end{array}$$ (17)

To compare the error in predicting different water status variables across scales, we also calculated a normalized RMSE (i.e., NRMSE; Botchkarev, 2018).

$$\begin{array}{c}\text{NRMSE}=\frac{\text{RMSE}}{y_{max}-y_{min}}\end{array}$$ (18)

3. RESULTS

3.1. Estimation of leaf water status variables using terahertz measurements

Terahertz measurements showed strong ability to predict all three leaf water status variables, supporting the physically based model for the relationship of WMA with ln (PFR). As leaf water status declined, terahertz transmission increased, and for individual leaves, the declines of WMA, RWC, and Ψ_leaf were associated with ln (PFR) across the range from full turgor to Ψ_tlp and below Ψ_tlp (Figure 6a–i; Table 3). Notably, the relationships for individual leaves of WMA, RWC and Ψ_leaf with ln (PFR) differed significantly in slopes and intercepts (Table 3). Despite the variation among leaves of given species, the relationship of WMA with ln (PFR) was strong combining leaves for given species, or even across species (Figure 7).

Figure 6.

Association of water status variables with the terahertz transmission peak field ratio for three species. Lines were fitted for each leaf during dehydration by ordinary least squares (OLS): water mass per area (WMA; a–c), relative water content (RWC; d–f), and leaf water potential (Ψ_leaf; g–i) (fitted line parameters in Table 3). p‐values all < .05; see values in Table 3

Figure 7.

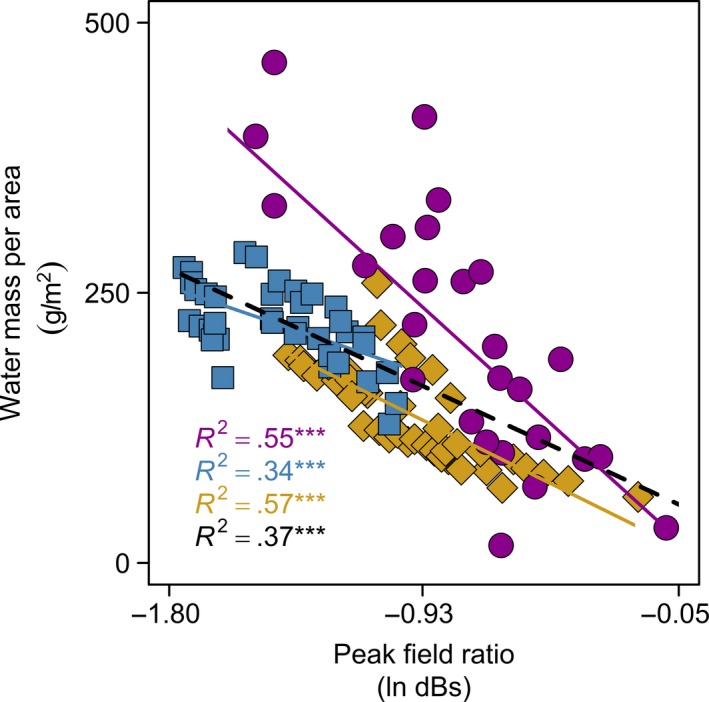
Association of water mass per area with the terahertz transmission peak field ratio, generalizing across leaves within and across three species. Each species’ measurement points, regression line, and ordinary least squares R ² values are presented: Arabidopsis thaliana, purple; Hedera canariensis, blue; Platanus racemosa, yellow; all species together, black. Statistical significance: *, p < .05; **, p < .01; ***, p < .001

Given these strong relationships, leaf water status variables could be predicted across scales, from individual leaf, to species, to all‐species, using our hierarchical approach to estimation (Table 4; Figure 5). Thus, for given leaves, or for a given species, or across all species, $\widehat{\text{WMA}}$ could be predicted from the relationship with ln (PFR) (Figure 8a‐d), relative water content ($\widehat{\text{RWC}}$) could be predicted by additionally including leaf‐ or species‐level means for saturated water mass per unit leaf area (SWMA) (Figure 8e‐h), and $\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$, by additionally including pressure–volume curve parameters (Figure 8i‐l). As expected, the error in predicting WMA, RWC, and Ψ_leaf increased across these scales of variation, that is, from individual leaf to species (Figure 8a–l). Further, the error increased from the prediction of $\widehat{\text{WMA}}$ and $\widehat{\text{RWC}}$ to $\widehat{{\mathrm{\Psi }}_{\text{leaf}}}$, as indicated by higher NRMSE values (Table 5; Figure 8a–l). The goodness of fit (i.e., significant R ² values) and predictive power (i.e., relatively low RMSE and NRMSE values; Table 5) signified strong potential for estimation of all three water status variables using the physically based model and hierarchical prediction approach within and across species (Table 4; Figure 5).

Figure 8.

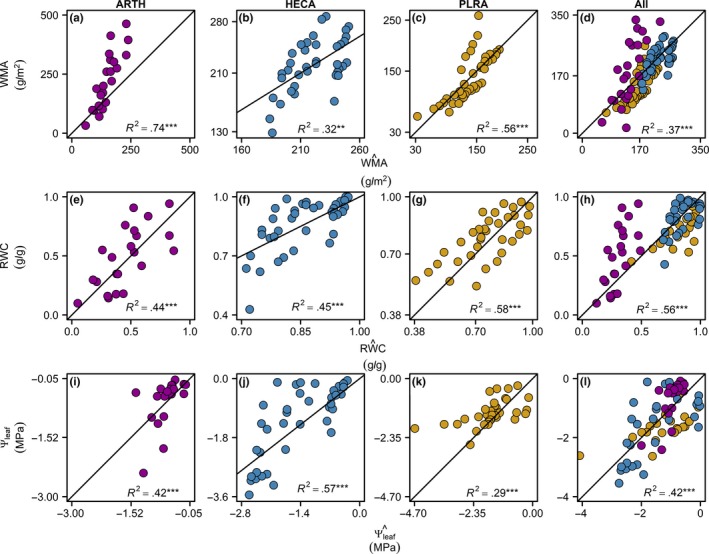
Species‐specific predictions of leaf water status using terahertz spectroscopy. Plots of observed values against predicted values for leaf water mass per area (WMA), relative water content (RWC), and leaf water potential (Ψ_leaf). Species‐level and all‐species‐level WMA were predicted for each measurement of PFR using species‐specific and all species regression parameters, respectively (Table S2). Statistical significance: not significant, ns; **, p < .01; ***, p < .001

Table 5.

Predictive power for the determination of water mass per area (WMA), relative water content (RWC), and leaf water potential (Ψ_leaf), from terahertz spectroscopy, including the root mean square error (RMSE), the R ², and the normalized RMSE (NRMSE), for individual leaves of each species (with minimum, mean [bold type], and maximum values reported), and using species‐specific relationships, and the all‐species relationship (Table 4; Figure 8)

Species code	Variable	RMSE (min‐mean‐max)	R 2 (min‐mean‐max)	NRMSE (min‐mean‐max)
Individual leaf‐level prediction
Arabidopsis thaliana	WMA	8.43–28.0–48.2	0.80–0.89–0.99	0.347–0.0942–0.123
	RWC	0.0254–0.0597–0.0981	0.80–0.89–0.99	0.0344–0.0940–0.123
	Ψleaf	0.0223–0.200–0.371	0.49–0.76–0.92	0.0762–0.130–0.235
Hedera canariensis	WMA	1.55–7.57–15.0	0.80–0.80–0.80	0.0199–0.104–0.193
	RWC	0.00670–0.0284–0.0553	0.80–0.80–0.80	0.0199–0.101–0.185
	Ψleaf	0.174–0.256–0.339	0.70–0.70–0.70	0.0665–0.112–0.170
Platanus racemosa	WMA	1.67–4.71–11.4	0.80–0.80–0.80	0.0410–0.0828–0.173
	RWC	0.0122–0.0246–0.0398	0.80–0.80–0.80	0.0411–0.0829–0.173
	Ψleaf	0.0680–0.170–0.225	0.70–0.70–0.70	0.0305–0.115–0.176
Species‐level prediction
Arabidopsis thaliana	WMA	58.7	0.74	0.136
	RWC	0.184	0.44	0.218
	Ψleaf	0.487	0.42	0.209
Hedera canariensis	WMA	28.9	0.32	0.182
	RWC	0.0935	0.45	0.164
	Ψleaf	0.703	0.57	0.202
Platanus racemosa	WMA	29.8	0.56	0.151
	RWC	0.0841	0.58	0.159
	Ψleaf	0.425	0.29	0.175
All‐species‐level prediction
All species	WMA	61.6	0.37	0.138
All species	RWC	0.151	0.56	0.159
All species	Ψleaf	0.700	0.42	0.201

4. DISCUSSION

We present strong relationships of leaf water status variables (WMA, RWC, and Ψ_leaf) to the transmission of terahertz radiation for three diverse species. Our work extends from previous studies that compared terahertz measurements to leaf water status variables for very well‐hydrated and strongly dehydrated leaves; we here show the strong association of terahertz absorption with water status within the range of operating leaf water status, that is, between full turgor and turgor loss point, and below. Further, previous work using terahertz radiation, and other parts of the electromagnetic spectrum, has tended to focus on the prediction of WMA (or “equivalent water thickness”) and RWC, and we show the extension of this prediction to Ψ_leaf. Our approach to hierarchical estimation using a physically based model enables the translation of terahertz measured PFR to all three water status variables, and this approach could be extended to the detection of leaf water status using other ranges of wavelengths.

Although many species have been previously studied for the association of spectroscopic variables with leaf water status, previous studies have tended to focus on individual dehydrating leaves (Table S1). Our findings indicate the potential to extend prediction across multiple leaves of given species, and even across multiple species, assuming knowledge of additional leaf traits, such as leaf mass per area (LMA), saturated water content (SWC), and pressure–volume parameters. This finding highlights the great potential for the expansion of the use of terahertz transmission to determine water status noninvasively for individual leaves, and also across canopies and indeed, mixed canopy ecosystems.

Despite this evident predictive power, we also noted outstanding challenges. We found that leaves varied in the slopes and intercepts of the relationship of WMA to ln (PFR), which reduced the predictive power for the general relationship for given species and the relationships across species. Indeed, due to this variation among leaves in their relationships, a number of impossible values were predicted for RWC and Ψ_leaf from the generalized relationships of WMA to ln (PFR) (see Methods, “Statistics”; Table S2). The variation in slopes indicates the potential for improving the physically based model. In the current formulation, the slopes of WMA versus ln (PFR) should simply represent the absorption coefficient of liquid water, expected to be constant. At least five effects might lead to variation in slopes. First, we did not account for the shrinkage of leaves during dehydration (Scoffoni et al., 2014), and such correction would likely slightly improve predictions. Second, we assumed that liquid water absorbs radiation as a single uniform layer, but it is unclear whether cellular structure would influence the effective absorption of water, especially given airspace shrinkage or expansion during dehydration. Third, in Equation 9 we assumed that the absorption of the “solid fraction” (i.e., absorption coefficient × thickness of solid fraction) was invariant with leaf dehydration, and, in applying Equation 11 across multiple leaves of given species and across leaves of different species, that this absorption is equivalent across leaves. This assumption would be moot if the solid fraction absorbs minimally, and, indeed, our tests have shown negligible absorption in completely dried leaves (data not shown). However, the absorption of pigments and other molecules may depend on leaf hydration state, as previous studies found that in hydrated leaves the chlorophyll and carotenoids also absorb substantially within the terahertz range of wavelengths (Qu, Zhang, Lian, & Kuang, 2017), and this absorption by pigments or other biomolecules or tissues (such as cuticle or leaf venation) could account for variation in relationships among leaves (Cotrozzi et al., 2017; Ollinger, 2011; Sims & Gamon, 2002), especially if it changes with leaf water status. Fourth, in generalizing Equation 11 we assumed that the reflectivity of the leaf (R) was constant. Previous work has shown comparatively minimal variation in reflectivity during leaf dehydration (Hadjiloucas et al., 1999; Sun et al., 2011), but no tests have been made comparing R for terahertz wavelengths among leaves of given species or across species. Thus, future work to clarify terahertz absorption in relation to variation in leaf structure and composition is ongoing in our laboratory and others (e.g., Born et al., 2014; Gente et al., 2018). Further technical improvements in the terahertz radiation technology might also increase precision, especially in the improvement of alignment of the terahertz beam spot on the leaf during measurements at different dehydration stages.

The ability to measure leaf water status nondestructively will engender numerous applications. Notably, the THz‐TDS system we used is a table‐top system containing large optical components in a laboratory setting. While such a system can be deployed in the field (Gente et al., 2018), the development of compact field‐ready systems have enormous potential, for example, as handheld devices or drone‐mounted instruments, for greenhouse and agricultural analyses, as have been developed for other applications in terahertz spectrometry such as tissue and chemical analyses (Humphreys et al., 2004; Sun et al., 2011). Under field settings, a system incorporating terahertz reflection measurements will be even more applicable to remote determination of leaf water status, for example, pinpointing when natural or crop canopies are approaching dangerous levels of drought, and enabling “need‐based” irrigation systems within crops and urban ecosystems for efficient water application (Jepsen, Cooke, & Koch, 2011). Recently, vegetation optical depth (VOD) as derived from microwave reflectance determined from airborne platforms has been used to estimate landscape‐scale relative water content or leaf area index (Momen et al., 2017; Rao et al., 2019). Given its ability to resolve Ψ_leaf across the leaf operating range, the application of terahertz spectroscopy in reflection mode would complement and enhance those remote sensing applications. Beyond the estimation of leaf water status, measurement of Ψ_leaf in addition to water flux rates enables the determination of hydraulic conductance, that is, the efficiency of water transport. If Ψ_leaf can be estimated nondestructively for leaves at predawn (as a proxy for soil water potential; Rao et al., 2019) and at mid‐day, alongside transpiration rates using gas exchange, thermal imagery, or sapflow systems (Lu & Zhuang, 2010), nondestructive measurements can be made of whole‐plant hydraulic conductance, enabling insights to address numerous unknowns and controversies in the field, for example, the strength of drought at which hydraulic decline occurs at plant scale (Delzon & Cochard, 2014). The opportunities that terahertz spectroscopy offers thus extend from the resolution of drought impacts and the design of systems for their mitigation, to the remote resolution of the dynamics of plant transport capacity.

CONFLICT OF INTEREST

The authors declare no conflict of interest associated with the work described in this manuscript.

AUTHOR CONTRIBUTIONS

All authors contributed to the design of the study. M.B., N.T.Y., and C.S. conducted data collection and analyses. M.B., N.T.Y., M.J., and L.S. wrote the manuscript with input from all authors.

Supporting information

 

Browne M, Yardimci NT, Scoffoni C, Jarrahi M, Sack L. Prediction of leaf water potential and relative water content using terahertz radiation spectroscopy. Plant Direct. 2020;4:1–16. 10.1002/pld3.197