Abstract

Experiments at the interface of quantum optics and chemistry have revealed that strong coupling between light and matter can substantially modify the chemical and physical properties of molecules and solids. While the theoretical description of such situations is usually based on nonrelativistic quantum electrodynamics, which contains quadratic light–matter coupling terms, it is commonplace to disregard these terms and restrict the treatment to purely bilinear couplings. In this work, we clarify the physical origin and the substantial impact of the most common quadratic terms, the diamagnetic and self-polarization terms, and highlight why neglecting them can lead to rather unphysical results. Specifically, we demonstrate their relevance by showing that neglecting these terms leads to the loss of gauge invariance, basis set dependence, disintegration (loss of bound states) of any system in the basis set limit, unphysical radiation of the ground state, and an artificial dependence on the static dipole. Besides providing important guidance for modeling of strongly coupled light–matter systems, the presented results also indicate conditions under which those effects might become accessible.
Keywords: ab initio quantum electrodynamics, strong light−matter coupling, electronic structure, polaritonic chemistry, quantum optics
Driven by substantial experimental progress in the field of cavity-modified chemistry,1−11 theoretical methods at the border between quantum-chemical ab initio methods and optics have become the focus of many recent investigations.12−58 The high complexity of a molecular system, which can undergo, e.g., chemical reactions or quantum phase transitions, coupled strongly to photons makes the use of some sort of approximation strategy necessary. A common approach is to use approximation strategies designed for atomic two-level-like systems in high-quality optical cavities59−61 and to apply them to the quite different situation of molecular systems. However, under the generalized conditions of cavity-modified chemistry, contributions in the theoretical description that are usually disregarded, e.g., quadratic terms describing the coupling between light and matter, can become important15,62,63and might even dominate the physical properties.13−16,64,65 While the existence of these quadratic terms is well-known,66−73 their origin, interpretation, and consequences are less clear, and when to include them has become the subject of recent intense discussions.15,40,62,74−82 Here we will elucidate these terms for the most relevant setting of cavity-modified chemistry (i.e., in the Coulomb gauge and in the long-wavelength limit), clarify their origins, physical interpretations, and consequences, and show under which conditions and for which observables they become relevant. This will also highlight the domain of applicability of common approximations that disregard these quadratic terms and at the same time indicate under which conditions substantial influence can be expected,12 accessible with ab initio techniques such as quantum-electrodynamic density functional theory (QEDFT).12,16,22,25,83 Before we do so, let us briefly outline the theory that we will consider and collect a set of fundamental conditions that we deem to be important for a reasonable theoretical description.
Any theory that we employ to model coupled light–matter systems should obey certain fundamental constraints. Which ones these are often depends on the specific situation being considered. For instance, in the case of high-energy physics, an adherence to special relativity (physical laws should be Lorentz-invariant) is paramount, and hence, the use of Dirac’s equation becomes necessary to capture the behavior of electrons. If we further want to ensure that all of the interactions among the electrons are local and our theory should stay invariant under local phase transformations, we find the Maxwell field coupled to Dirac’s momentum operator in a linear (minimal) fashion. However, the resulting theory—which, if quantized, is called quantum electrodynamics (QED) and perfectly describes high-energy scattering events—has many subtle issues.84 For low-energy physics, a simplified version, where instead of the relativistically invariant momentum the nonrelativistic momentum is employed, has been shown to be able to resolve many of these issues.73 The resulting theory of nonrelativistic QED (also sometimes called molecular QED69,72,85,86) is ideally suited to describe atoms, molecules, or solids interacting with the quantized light field.87−89 However, the coupling between light and matter is only defined up to a phase, and we need to make a specific choice for this phase, i.e., we need to fix a gauge. Changing the gauge or performing a local unitary transformation should not modify physical observables but merely affect their representation in terms of canonical coordinates. While gauge independence is respected by nonrelativistic QED, this constraint is specifically challenging for dimensionally reduced, simplified models.15,77,80,82 Besides gauge independence, nonrelativistic QED guarantees a set of further intuitive and essential conditions. For instance, it guarantees that the physical observables are independent of the chosen coordinate system (or, in more quantum-chemical terms, where a specific spatial basis is just one of many basis set choices, basis-set-independent), and it also guarantees the stability of matter, i.e., atoms and molecules are stable if coupled to the vacuum of the electromagnetic field.73 A direct consequence of this fundamental condition is that the combined ground state of light and matter has a zero transverse electric field expectation value. If this were not the case, the system could emit photons and lower its energy. To summarize, a few basic constraints to which we want a theory of light–matter interactions to adhere are the following: all physical observables should be independent of the gauge choice and the choice of coordinate system (e.g., it would be unphysical that the properties of atoms and molecules would depend on the choice of the origin of the laboratory reference frame); the theory should support stable ground states (or else we could not define equilibrium properties and identify specific atoms and molecules); and the coupled light–matter ground state should have a zero transverse electric field (or else the system would radiate and cascade into lower-energy states).
In From Microscopic to Macroscopic Maxwell’s Equations, we will introduce nonrelativistic QED and some of its unitarily equivalent realizations and highlight the physical implications of the associated transformations and further approximations that lead to nonrelativistic QED in the long-wavelength limit. In Necessity and Implications of Quadratic Couplings in the Dipole Approximation, we will illustrate that the aforementioned fundamental physical conditions will not be retained when the quadratic components are disregarded. Finally, in the Summary we will discuss implications and perspectives. We provide further details in the Appendix. In Fundamental Coupling of Light with Matter and the Emergence of Diamagnetism, we present the basic approximations leading to nonrelativistic QED. In The Power–Zienau–Wooley Gauge Transformation and Transverse Basis and Distributions, we provide additional details that complement our discussion regarding the Power–Zienau–Wooley transformation and transverse basis functions. In Spectral Features of Operators, we discuss some implications that go hand in hand with approximating operators. Our discussions will be presented first using a field-theoretical convention in which the four vector potential Aμ is given in volts and the four charge-current density jμ is given in coulombs per square meter per second and later in atomic units. By multiplying Aμ by 1/c we find the standard convention in terms of volt seconds per meter.
From Microscopic to Macroscopic Maxwell’s Equations
Classical electrodynamics is at the heart of QED. Consider for instance the inhomogeneous microscopic Maxwell equations:85
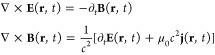 |
This representation of light–matter coupling is by no means unique, and many different formulations, such as the Riemann–Silberstein90,91 or macroscopic Maxwell’s equations, have been developed over the years. To arrive at the latter, let us first rewrite j = jb + jf, where jb is a bound current and jf a free current, and define the bound charge current as
where M is the magnetization
and P is the polarization of the matter system. If we
then define the displacement field D = ϵ0E + P and the magnetization field 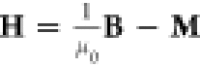 , we end up with
, we end up with
which takes the back-reaction of a given medium on the electromagnetic field into account by the constitutive equations. Clearly, the classical description of electromagnetic interactions can take different forms for which, without further simplifications, none is superior over the other. These forms deviate merely in their choice of canonical variables, the very same variables that will be quantized to reach QED. The electromagnetic field energy
| 1 |
is of quadratic form, and therefore, substituting D = ϵ0E + P into eq 1 will naturally lead to quadratic self-polarization (P2) and self-magnetization (M2) terms.
While many equivalent ways of formulating Maxwell’s equations exist, there will be accordingly also several (unitarily equivalent) forms of the resulting nonrelativistic QED Hamiltonian. Let us in the following see how this equivalence in QED is manifested. A relativistic quantization procedure with a subsequent nonrelativistic limit, as illustrated in Fundamental Coupling of Light with Matter and the Emergence of Diamagnetism, is indeed equivalent to introducing the covariant derivative for the electronic system and then quantizing the resulting gauge field.12,25,73 This minimal coupling procedure makes the invariance under local phase transformations Ψ′ = eiθ(r)Ψ explicit and, with the Coulomb gauge condition ∇·Â(r) = 0, fixes the local phase θ(r) uniquely. The momentum of each particle is shifted according to −iℏ∇ → −iℏ∇ – (q/c)Â(r), where q is the charge of the particle and the quantized vector potential is
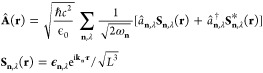 |
2 |
where we have defined the transverse polarization
vectors ϵn,λ for
mode and polarization (n, λ),92 and the creation and annihilation operators can be expressed
in terms of displacement coordinates 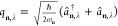 and their
conjugate momenta
and their
conjugate momenta 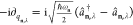 for harmonic oscillators with the allowed
frequencies ωn = c|kn|.
for harmonic oscillators with the allowed
frequencies ωn = c|kn|.
Then, with ĵ0(r) = cn̂(r) = c∑i=1Ne+Nnqiδ(r – ri), the nonrelativistic minimally coupled Hamiltonian (including Ne electrons and Nn nuclei) in the Coulomb gauge reads as
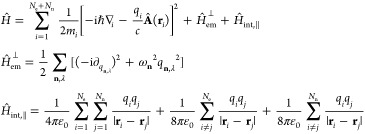 |
3 |
Each charged particle then evolves under the influence of the kinetic energy operator [−iℏ∇ – (q/c)Â(r)]2 and at the same time experiences the instantaneous longitudinal field (the Coulomb potential Ĥint,∥) created by all of the other charged particles. The nonrelativistic limit of the minimal coupling procedure therefore naturally leads to the appearance of a quadratic term (see also Fundamental Coupling of Light with Matter and the Emergence of Diamagnetism). This quadratic term provides the diamagnetic shift93 of the bare modes and introduces a lowest allowed frequency,94 which then removes the infrared divergence.73 It is therefore not a drawback to have this term.74 In contrast, it affects, for instance, optical spectroscopy,95,96 and it is responsible for diamagnetism97 and hence implies very important physical processes, such as the famous Meissner effect. Recent theoretical14,94,98 and experimental76 studies focused on ultrastrongly coupled light–matter dynamics as well as the prediction of enhanced electron–phonon coupling64,65,99 highlight the non-negligible influence of the collective diamagnetic shift.
Let us next for convenience assume linear polarization (i.e., ϵn,λ = ϵn,λ*) and, to connect to the more common formulation, switch to atomic units, such that ϵ0 = 1/4π, c = 1/α0, and the elementary charge (e) is equal to 1. There is a well-known procedure to connect to a Hamiltonian corresponding to the macroscopic Maxwell’s equation by employing the unitary Power–Zienau–Woolley (PZW) transformation (see also The Power–Zienau–Wooley Gauge Transformation):
for all charged particles contributing to the polarization,
where the jth nucleus has the effective positive charge Zj. This implies that all of the physical charges contribute to the bound current, such that jf = 0, ∇·D = ε0∇·E + ∇·P = 0, and therefore D = D⊥. However, since the vector potential operator is purely transverse, it also only couples to the transverse part of the polarization operator, which can be expressed in terms of the transverse δ distribution92 or we use the mode expansion of the vector potential directly. To do so, for notational simplicity we first introduce the abbreviation α ≡ (n, λ), and then we use the fact that the vector-valued functions Sn,λ(r) in eq 2 form a basis for the transverse square-integrable vector fields (see Transverse Basis and Distributions). With Sα(r) = ϵα·Sα(r), we find that
| 4 |
The resulting Hamiltonian29,69,72 has the advantage that it can be conveniently
expanded in multipoles of the interaction. We note, however, that
the validity of such an expansion depends critically on whether it
is considered as a perturbation of the wave function or to affect
the operator itself and subsequently its self-consistent solution
(see Spectral Features of Operators). The
mode expansion provides a consistent regularization such that terms
like P̂⊥2(r) are well-defined, a necessity
when multiplying δ distributions (see Transverse
Basis and Distributions). This avoids the usual auxiliary assumption
that some of these terms, which contribute to the polarization self-energy,
are only taken into account perturbatively.79 It furthermore highlights how the condition of transversality of
the Maxwell field also affects matter-only operators like the polarization.
So far, the only restriction we have employed is that we have considered
nonrelativistic particles. However, this simplification is usually
not yet enough to allow for practical calculations. In the following
we do not want to consider this more general case but rather assume
only dipole interactions. This approximation is very accurate provided
that the dominating modes of the photon field have wavelengths that
are large compared with the extent of the matter subsystem. In the
multipole form of the nonrelativistic QED Hamiltonian this means that
we discard the integration over s in our transformation
and the polarization operator.69 The Hamiltonian
we then find is the same as the one that we get if we approximate Â(r) ≈ Â(rmatter) for the bilinear and quadratic coupling
terms. This does not restrict the form of the cavity modes itself
but merely their spatial extension in relation to the matter subsystem.
In practice, where, e.g., an ensemble of molecules interacts with
the cavity mode, this simplification can become questionable. Such
an ensemble might extend over macroscopic scales such that individual
molecules will experience different couplings. For simplicity, in
the following we take rmatter = 0 such that Sα(0) is real and we can straightforwardly
perform the unitary PZW transformation (also called the length gauge
transformation) Ĥ = ÛĤÛ† with 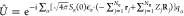 . We
accompany this by a canonical transformation
that swaps the photon coordinates and momenta (−i∂qα → −ωαpα, qα → −iωα–1∂pα) while preserving the commutation
relations.22 The nonrelativistic QED Hamiltonian
then reads as
. We
accompany this by a canonical transformation
that swaps the photon coordinates and momenta (−i∂qα → −ωαpα, qα → −iωα–1∂pα) while preserving the commutation
relations.22 The nonrelativistic QED Hamiltonian
then reads as
| 5 |
In eq 5, the nuclear Hamiltonian is
with the bare nuclear masses Mj. The electronic Hamiltonian is
with the bare electron mass me. The nuclear–electron interaction is given by
Furthermore, the photonic contribution for Mp modes is then given by
| 6 |
which incorporates the total dipole moment
of electrons and nuclei, i.e., R = −∑j=1Nerj + ∑j=1ZjRj. The resulting bilinear coupling or R itself
might be occasionally defined with the opposite sign as a consequence
of the inversion symmetry of eq 5. Even if we break the inversion symmetry of the matter Hamiltonian
as, e.g., in Coordinate System and Dipole Dependence
without Self-Polarization, the photonic symmetry pα ↔ −pα will retain the trivial connection between the two Hamiltonians
and their respective observables. In eq 6, Mp is a finite but arbitrarily
large number of photon modes that are the most relevant modes but
in principle run from the fundamental mode of our arbitrarily large
but for simplicity finite quantization volume up to a maximum sensible
frequency, e.g., an ultraviolet cutoff at the rest-mass energy of
the electrons (an extended discussion can be found in Transverse Basis and Distributions). The operator given by eq 6 contains the bilinear
matter–photon coupling and the quadratic dipole self-energy
term 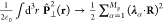 .
.
The fundamental light–matter coupling to mode α is then denoted by
| 7 |
which depends on the form
of the mode functions
and the chosen reference point for our matter subsystem.25,100 This can lead to an increase in the fundamental coupling to a specific
mode and is an inherent feature of the physical setup, e.g., the form
and nature of the cavity. In the following we will treat λα and the corresponding frequencies ωα as parameters that we can adopt freely to match different
physical situations, motivated by the recent experimental progress
to subwavelength effective cavity volumes.101,102 This also highlights that the self-energy term depending on λα is influenced directly by the properties
of the cavity, i.e, it obtains increasing relevance with decreasing
effective mode volume 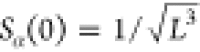 and
increasing number of participating
modes Mp.
and
increasing number of participating
modes Mp.
Importantly, since the PZW gauge is equivalent to Maxwell’s equation in matter as introduced earlier, we now work in terms of the purely transverse displacement field62,72,79
and the transverse polarization operator
By construction, the electric field operator in the PZW gauge, which no longer represents the conjugate momentum, becomes
| 8 |
The combination of the PZW and canonical momentum transformations changed our canonical operators B̂ ∝–i∂pα, D̂⊥ ∝ pα and consequentially the representation of our original creation and annihilation operators to
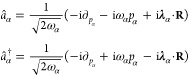 |
9 |
We might yet again define a new harmonic oscillator algebra solely in terms of our new canonical operators
to reach a potentially more familiar representation in terms of different âPZW and âPZW†. However, we have to consider then that the expression of physical observables in terms of creation and annihilation operators is not invariant under the PZW transformation, i.e., âPZW ≠ â. Special care has to be taken in how we interpret observables and design possible approximations, as otherwise unphysical consequences arise, as highlighted explicitly in Radiating Eigenstates without Self-Polarization. We also see that in accordance with the Maxwell’s equation in matter, by working with D̂⊥ we implicitly take into account the back-reaction (polarization) of matter on the electromagnetic field. The physical field is found with the constitutive relation of eq 8. Finally we note that the PZW transformation has removed the explicit diamagnetic contribution of the current, and the physical current is now equivalent to the paramagnetic current. However, the diamagnetic term has not vanished but is contained in the introduced phase of the coupled light–matter wave function.62
Let us clearly state a warning at this point. Unitary equivalence or gauge invariance, which implies that we obtain the same predictions in the Coulomb and PZW gauges, is only fulfilled when the full Hilbert space (full basis set) is considered. Any approximation in the molecular or photonic space will violate this equivalence and therefore result in deviating predictions.72,77,80,82,103 We remain with three different strategies. We can acknowledge this failure and focus on reasonable domains in which the predictions remain in reasonably close agreement, e.g., focus on resonant interactions.15,72 Alternatively, we can adjust the PZW transformation to compensate for the reduced space accordingly80 or consider as much of the space as possible, which leads us into the realm of first-principles cavity QED. This breakdown of gauge invariance can have very fundamental consequences, as the long-standing debate of the (non)existence of a Dicke super-radiant phase shows.63,104,105 Disregarding quadratic contributions (Â2/P̂⊥2) will consequentially merely allow perturbatively similar results to be obtained.
Finally, there is one subtle question left. If we consider many photon modes, they give rise to radiative losses, that is, they constitute the photon bath of the matter subsystem into which the excited states can dissipate their energy.50 Vacuum fluctuations give rise to effects like spontaneous emission, that is, turning the discrete eigenstates of the closed system described by a Schödinger equation into resonances with finite line width.50 Selecting furthermore only one or a very limited set of modes α will restrict retardation effects and can lead to unphysical superluminal transfer appearing in the (deep) ultrastrong coupling regime.106 In this work, however, we are not interested in lifetimes but in equilibrium states of the coupled light–matter system. In this case, instead of keeping many modes we can subsume the vacuum photon bath by renormalizing the bare masses me and Mj of the charged particles, i.e., we use the usual physical masses such as me = 1 in atomic units and keep only a few important modes that are enhanced with respect to the free-space vacuum.
We have seen that already several
approximations have to be employed
to arrive at the above Hamiltonian, which represents the usual starting
point for most considerations in cavity QED and cavity-modified chemistry.
Each approximation restricts its applicability, but the basic physical
constraints, i.e., gauge and coordinate system (basis set) independence,
existence of a ground state, and radiationless eigenstates, are as
of yet conserved. It is now the subject of the following sections
to emphasize that ignoring the transverse self-polarization term 1/2 ∑α=1Mp(λα·R)2 and/or the diamagnetic term 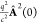 will inevitably break some of those fundamental
constraints. This by no means implies that perturbative treatments
that ignore these terms, either by restricting the Hilbert space of
the matter subsystem or by perturbation theory on top of free matter
observables, might not provide accurate predictions.15,77,107 However, it shows that care
has to be taken when the quadratic terms are disregarded.
will inevitably break some of those fundamental
constraints. This by no means implies that perturbative treatments
that ignore these terms, either by restricting the Hilbert space of
the matter subsystem or by perturbation theory on top of free matter
observables, might not provide accurate predictions.15,77,107 However, it shows that care
has to be taken when the quadratic terms are disregarded.
Necessity and Implications of Quadratic Couplings in the Dipole Approximation
Let us now consider concretely what happens if we discard the quadratic terms and which further physical constraints we violate. The example will be a simple molecular system, a slightly asymmetric one-dimensional Shin–Metiu model, coupled strongly to a single cavity mode, as illustrated in Figure 1. We subsume the rest of the photon bath in our description approximately into the physical masses of the electron and nuclei. The Shin–Metiu model features one nucleus moving in between two pinned nuclei with a total of one electron and is a paradigmatic model for nonadiabatic electron–nucleus coupling that gives rise to many interesting chemical processes. The Hamiltonian of this model with moving nuclear charge Z = +1 and removed vacuum shift ω/2 is given by
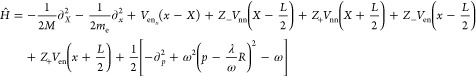 |
10 |
where R = −x + ZX is the total dipole moment and the electron–nuclear and nuclear–nuclear potentials are given by
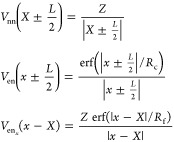 |
where erf(z) is the error
function. For the following calculations, we consider the parameter
values Z+ = 1, Z– = 1.05, M = 1836me, L = 18.8973, Rc = 2.8346, and Rf = 3.7795 with
electronic and nuclear spacings of Δx = 0.4 and ΔX = 0.04 between the
equidistant grid points and 40 photon number states. Furthermore,
we couple the electron and nucleus to a single cavity mode with the
frequency ω = 0.00231, which is resonant with the vibrational
excitation. We achieve ultrastrong vibrational coupling with 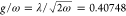 in atomic units, but by no means do the
following results qualitatively depend on the coupling or frequency.
The strength of the light–matter interaction solely determines
how quickly given effects will be visible, and the selected values
are close to those of previous publications in this field of research.
It is important to realize that the wavelength associated with this
frequency is 1.9724 × 105 Å = 19.724 μm
and thus differs by about 4 orders of magnitude from the size of the
computational box that is considered for the matter system (∼60
Å). Our example is thus safely within the validity of the long-wavelength
approximation when considering, e.g., one-dimensional cavities.
in atomic units, but by no means do the
following results qualitatively depend on the coupling or frequency.
The strength of the light–matter interaction solely determines
how quickly given effects will be visible, and the selected values
are close to those of previous publications in this field of research.
It is important to realize that the wavelength associated with this
frequency is 1.9724 × 105 Å = 19.724 μm
and thus differs by about 4 orders of magnitude from the size of the
computational box that is considered for the matter system (∼60
Å). Our example is thus safely within the validity of the long-wavelength
approximation when considering, e.g., one-dimensional cavities.
Figure 1.
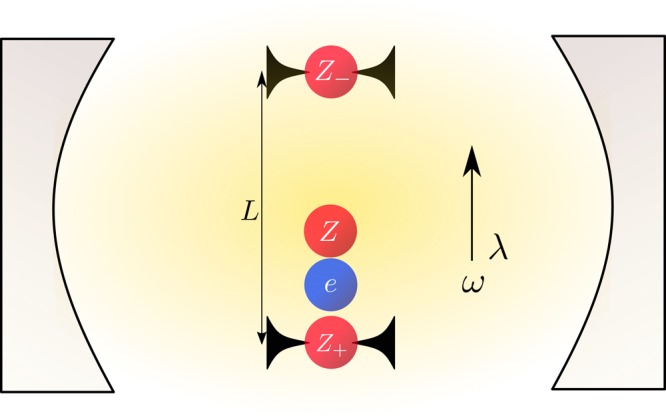
Illustration of the Shin–Metiu model inside the cavity. The two outer nuclei with the distance L and charges Z± are fixed in position, while the central nucleus and electron can move freely within one dimension.
No Bound Eigenstates without Self-Polarization
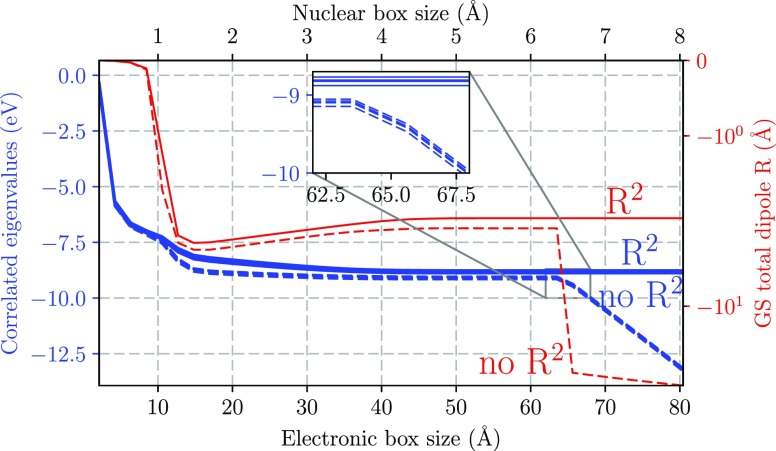
Let us start to investigate the most fundamental problem of discarding the quadratic term in the nonperturbative regime: the instability of the coupled system, i.e., the fact that electrons and nuclei fly apart if coupled even in the slightest to the photon field unless we restrict the Hilbert space.15,62 To illustrate this, we increase the simulation box stepwise by increasing the number of basis functions (grid points), keeping the other parameters fixed, and we present first the light–matter correlated energies as well as the total dipole moment in Figure 2. We find that when the space of allowed wave functions increases (i.e., approaching the basis set limit), the minimum-energy solution without the self-polarization term does not converge and minimizes the energy (dashed blue line) by increasing the total dipole moment (dashed red line). To put it differently, the system is torn apart, and electrons occupy one side of the simulation box while nuclei occupy the other.
Figure 2.
First four light–matter correlated eigenvalues with (blue, solid) and without (blue, dashed) the self-polarization contribution 1/2(λ·R)2 as well as the total dipole moment R = −x + ZX with (red, solid) and without (red, dashed) self-polarization. While observables start to be converged with a box size around 50 Å, without self-polarization the system starts to disintegrate already for slightly larger box sizes, as highlighted by the inset.
On the other hand, with the self-polarization term we see how we quickly approach the basis set limit, such that we have a basis-set-independent result (red and blue solid lines). The complete disintegration of the system without the self-polarization term happens at a critical box size that is just marginally larger than a box size leading to converged results when the self-polarization is included. As the box size is increased further, the energies resemble more and more those of an inverted shifted harmonic oscillator, which supports only scattering states.108 This illustrates that by a small (∼20%) variation of the simulation box we lose the physical character of the model and enter a nonphysical regime. How drastic this effect will be is given by the ratio of the quadratic potential energy 1/2(λ·R)2 to the energy needed to ionize the system from a given eigenstate, −εi (assuming noninteracting electrons for simplicity), such that a pure bilinear treatment would be perturbatively reasonable only for −(λ·R)2/2εi ≪ 1. In this sense, the common ratio of the coupling and excitation energies, g/ω, assuming resonance at ε2 – ε1 = ω, with a slight adjustment to
| 11 |
can be seen as an estimate
of how quickly
the given eigenstate i will become unstable without
the self-polarization component. The extension criterion shown in eq 11 can be motivated by
the single-particle Schrödinger equation 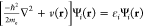 in the limit r →
∞, v(r) → 0, ∇2 → ∂r2, such that the long-range exponential
decay of the state
in the limit r →
∞, v(r) → 0, ∇2 → ∂r2, such that the long-range exponential
decay of the state 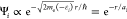 is
defined by its characteristic extension
is
defined by its characteristic extension 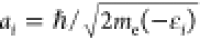 (e.g., the Bohr radius in the case of the
hydrogen atom). The simulation box has to be large enough to at least
fit the state i to an amount that we resolve an exponential
decay ∼e–1 (which is far from numerical convergence
in fact). This provides an estimate of the extension of the eigenstate
of interest and its associated self-polarization energy (λ·R)2 ≈ (λai)2 = −λ2/2εi. While this might provide
an orientation for theoretical calculations when instabilities are
to be expected without self-polarization, even before the system is
torn apart we see that the eigenvalues and the total dipole moment
differ noticeably as the basis set increases. Also, other observables
change without the self-polarization term, e.g., the nonperturbative
Rabi splitting. The observables with self-polarization remain completely
size-independent once a sufficient basis resolution is reached.
(e.g., the Bohr radius in the case of the
hydrogen atom). The simulation box has to be large enough to at least
fit the state i to an amount that we resolve an exponential
decay ∼e–1 (which is far from numerical convergence
in fact). This provides an estimate of the extension of the eigenstate
of interest and its associated self-polarization energy (λ·R)2 ≈ (λai)2 = −λ2/2εi. While this might provide
an orientation for theoretical calculations when instabilities are
to be expected without self-polarization, even before the system is
torn apart we see that the eigenvalues and the total dipole moment
differ noticeably as the basis set increases. Also, other observables
change without the self-polarization term, e.g., the nonperturbative
Rabi splitting. The observables with self-polarization remain completely
size-independent once a sufficient basis resolution is reached.
Let us illustrate how weakly bound states are affected with the
help of a second numerical example. We select a simple one-dimensional
soft-Coulomb hydrogen atom but screen the nuclear charge Z that binds the electron with 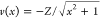 to Z = 1/20. We couple this system rather
weakly (g/ω = 0.006) with frequency ω
= 0.01368 in resonance with
its first excitation (when converged) and, as before, increase the
size of the simulation box stepwise. Figure 3 illustrates that although the ground state
is merely perturbatively affected up to 200 Å, the excited states
immediately turn into, for this case, unphysical scattering states.
As before, adding the self-polarization term results in the expected
spectrum, very much in contrast to the spectrum without the self-polarization
component. The extension criterion λ2/4εi2 leads to 0.0011 for the ground state and to 0.1664 for the first
excited state. While the ratio g/ω = 0.006
gives the impression of rather weak coupling, the extension criterion
provides a first indication that the excited states will be substantially
affected by the self-polarization component.
to Z = 1/20. We couple this system rather
weakly (g/ω = 0.006) with frequency ω
= 0.01368 in resonance with
its first excitation (when converged) and, as before, increase the
size of the simulation box stepwise. Figure 3 illustrates that although the ground state
is merely perturbatively affected up to 200 Å, the excited states
immediately turn into, for this case, unphysical scattering states.
As before, adding the self-polarization term results in the expected
spectrum, very much in contrast to the spectrum without the self-polarization
component. The extension criterion λ2/4εi2 leads to 0.0011 for the ground state and to 0.1664 for the first
excited state. While the ratio g/ω = 0.006
gives the impression of rather weak coupling, the extension criterion
provides a first indication that the excited states will be substantially
affected by the self-polarization component.
Figure 3.
First four light–matter correlated eigenvalues with (blue, solid) and without (red, dashed) the self-polarization contribution for the Rydberg-type weakly bound hydrogen model with grid spacing Δx = 0.8 and 120 photon number states. Until the box reaches a large extent (∼200 Å), the ground state without self-polarization deviatess merely slightly from the correct one. However, the excited states are relatively weakly bound and experience unphysical behavior (and therefore so do the spectra and all of observables involving excited states) even before entering a converged regime. The inset magnifies the unphysical crossover from physically bound into scattering states. The disintegration effect is qualitatively independent of the frequency.
While the bilinear interaction reduces the ground-state energy with increasing coupling, the self-polarization contribution counteracts this by an increase in energy and dominates for typical couplings the bilinear contribution, i.e., even the sign, and thus the qualitative behavior, of the energetic shift within the cavity can be altered depending on the presence/absence of the self-polarization.13,15 This qualitative change is also represented in spatial observables, i.e., the self-polarization term favors a reduced polarizability and thus focuses charge density in domains where charge is already present.14−16 The bilinear coupling, which furthermore scales with the frequency, is typically weaker affecting the ground state and features the contrary tendency, and their competition determines the qualitative distribution of charges inside the cavity.15,109 The resulting consequences can, e.g., include a reduced equilibrium bond length13,14 with an earlier onset of static correlation14 that could be steered on demand by controlling the polarization of the field and therefore implies interesting opportunities for chemical considerations and electronic devices.
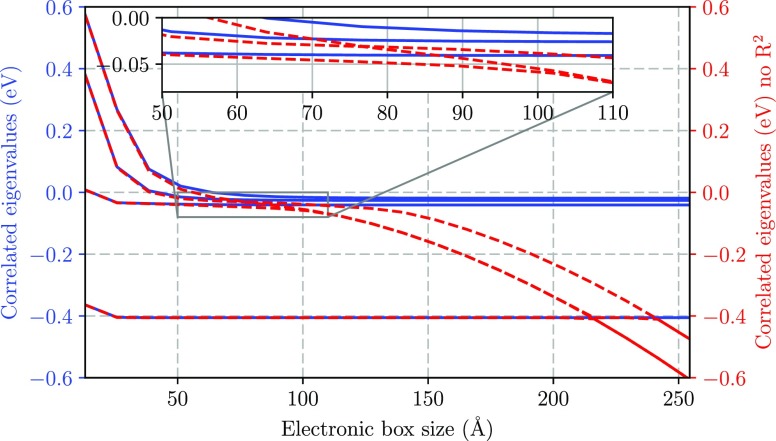
Let us briefly inspect how the same system behaves in the Coulomb gauge instead. Figure 4 illustrates the same correlated eigenvalues with increasing box size as in Figure 3. The Coulomb and PZW gauges lead to accurate agreement, with a numerical difference in energy of less than 10–7 eV for a box size of more than 40 Å, when both quadratic components are included. Omitting the diamagnetic term leads to a slight negative shift in the correlated eigenvalues and illustrates the relevance of the diamagnetic component, i.e., shifting the photonic excitations (also see Fundamental Coupling of Light with Matter and the Emergence of Diamagnetism). In the Coulomb gauge, couplings between higher excited states rescale lower matrix elements, demanding a well-converged set of electronic eigenstates, and therefore, the bilinear component accounts for the major effect of the self-polarization.15,77,82 We should recall, however, that the diamagnetic contribution scales with the amount of polarizable material and attains increasing importance as the frequency of the field decreases. In this sense, when the same investigation is performed with a 10 times smaller frequency, ω = 0.00137 = 0.0372 eV, the lowest excited states are photon replicas with an energy spacing of 0.0372 eV between the ground and first excited states with the diamagnetic contribution and 0.0254 eV without, highlighting a substantial deviation.
Figure 4.
First four light–matter correlated eigenvalues in the Coulomb gauge with (blue, solid) and without (red, dashed) the diamagnetic Â2(r) contribution for the Rydberg-type weakly bound hydrogen model (same parameters as Figure 3). Disregarding the quadratic (diamagnetic) term omits the diamagnetic shift that leads to accurate agreement between the two gauges. The inset magnifies the same region as in Figure 3. Recall that the diamagnetic contribution attains increasing impact as the frequency decreases and the amount of polarizable matter available increases.
As a side remark, we note that although the validity of the dipole approximation for high frequencies is questionable, the quadratic self-polarization term guarantees that the high-frequency photons are essentially decoupled from the matter subsystem. If only a purely linear coupling is assumed, then the UV behavior is completely wrong, as photons with arbitrarily high energies still interact with the matter subsystem.100
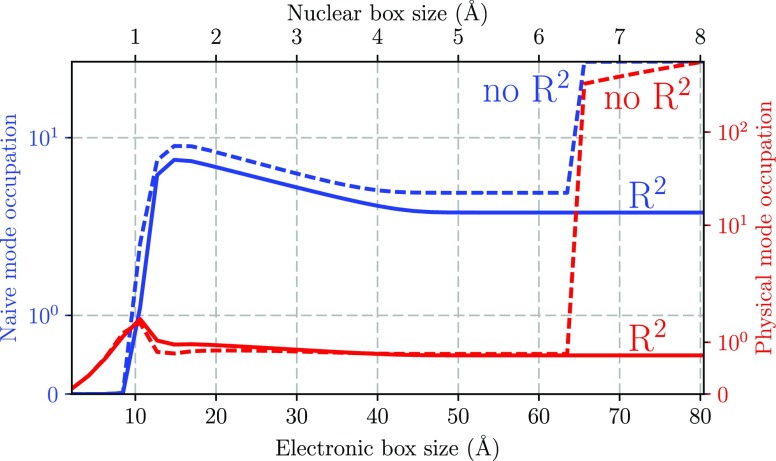
Radiating Eigenstates without Self-Polarization
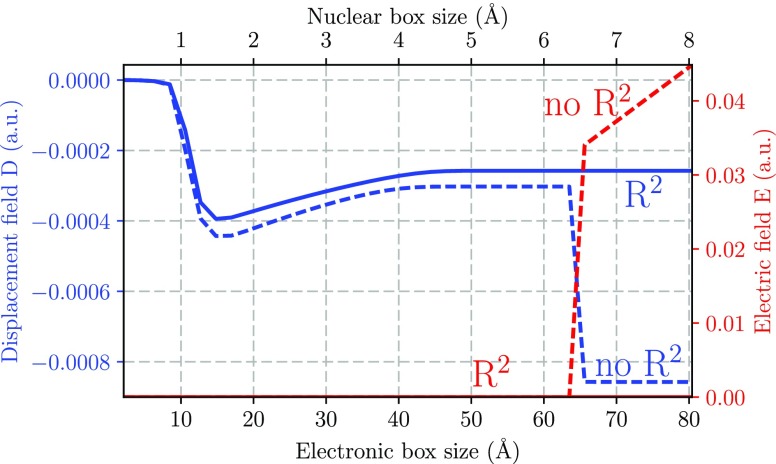
Let us look at another unphysical feature that appears when the self-polarization is neglected. In the case of the simple Rabi or Dicke model, where the particle is assumed to be perfectly localized (assuming effectively classical particles), the polarization is zero, and we can associate the expectation values of the modes in the PZW gauge with the electric field. However, if we consider an ab initio treatment, this is no longer the case, and we need to use the correct definition of the electric field given in eq 8. In Figure 5 we show the expectation values of the displacement and the electric field as we increase the number of basis functions. This is again the same as allowing the electrons and nuclei to extend over an ever-increasing spatial region, which is equivalent to exploring the full Hilbert space. Also in these observables we see that the system with the self-polarization term included leads to results that are independent of the simulation box size after roughly 45–50 Å (blue and red solid lines). When the box is extended only slightly to ∼60 Å, the system without the self-polarization disintegrates (blue and red dashed lines). By construction, the system with the self-polarization term always obeys the basic constraint of zero electric field, while the system with only bilinear coupling leads for large extensions to an eigenstate with nonzero electric field. This cannot be a physical ground state.
Figure 5.
Displacement fields (blue) and electric fields (red) for the Shin-Metiu model with (solid) and without (dashed) the self-polarization contribution. While the electric field is independent of the molecular convergence, and therefore even in a restricted subspace the system does not radiate and there is a well-defined equilibrium solution, the displacement field depends on the convergence of the molecular system.
Realizing the connection between the observable field and canonical momentum, let us turn our attention to the number of photons in the ground state. The photon number operator (the electromagnetic field occupation) is defined in the Coulomb gauge as
In the PZW gauge, these annihilation and creation operators are given by eq 9, and as a consequence, the number operator N̂ in that gauge is
As a result of the change of the conjugate momentum from the electric field to the displacement field, we see that the self-polarization enters the definition of the photon number operator when we work in the PZW gauge. Without surprise, this leads to different occupations as if we would naively use
and we illustrate this difference in Figure 6. The alleged occupation N′ (blue) is higher than the physical occupation N (red) caused by the permanent dipole. Only for two-level models such as the Rabi model do the two definitions agree.15 Upon comparison of Figures 5 and 6, it is instructive to observe that the behaviors of the displacement field D⊥ and the naive mode occupation N′ are qualitatively very similar, obtaining relevant nonzero values only after a sufficiently large numerical box size is reached. In contrast, the electric field E remains system-size-independent, and the physical mode occupation N adjusts merely quantitatively to the simulation box. Not surprisingly, ignoring the self-interaction contributions in general leads to different results for different gauge choices.
Figure 6.
Naive (N′, blue) and physical (N, red) photon occupations in the PZW gauge with (solid) and without (dashed) the self-polarization contribution during the self-consistent solution for the ground state of the Shin-Metiu model.
Coordinate System and Dipole Dependence without Self-Polarization
The Hamiltonian of eq 5 and its variants guarantee that all of the
physical observables
in equilibrium are independent of the chosen coordinate system. This
is obvious if we have a charge -neutral system, where the Hamiltonian
of eq 5 is completely
translationally invariant. This constraint is physically very reasonable
because without a spatial dependence (i.e., the manifestation of the
long-wavelength approximation), the electromagnetic field cannot break
the translational symmetry of the bare molecular system. If the system
is not charge-neutral, e.g., when we consider only electrons in an
external binding potential, we no longer have trivial translational
invariance. To see this, consider a shift of the origin of the coordinate
system along the polarization of the field such that the total dipole
moment operator R̂ is also shifted. It should be
noted that this also changes the origin of the cavity, as the long-wavelength
approximation enforces that all molecules see the same field (of the
now also shifted reference point) of the cavity. However, because
of the zero-electric-field condition of a physical ground state, we
explicitly know that the relation between the (shifted) dipole moment
expectation value ⟨R⟩ of the matter subsystem
and the expectation values of the displacement fields is 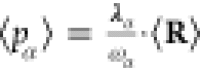 .15,25,62 If we then further re-express
the light–matter coupling with
fluctuation quantities ΔR = R –
⟨R⟩ such that eq 6 becomes
.15,25,62 If we then further re-express
the light–matter coupling with
fluctuation quantities ΔR = R –
⟨R⟩ such that eq 6 becomes
we find that at equilibrium the shifts cancel and the only remaining contribution in the Hamiltonian is given by the fluctuations around the mean values. Indeed, the equilibrium wave function in the new coordinate system is just the original wave function translated in space and the photon subsystem coherently shifted.
As a consequence, the light–matter-coupled system is invariant under shifts of the origin in equilibrium, and no physical observable has a dependence on the permanent dipole. The fact that the equilibrium properties of light–matter-coupled systems do not depend on a possible permanent dipole is merely a consequence of how particles couple to the transverse electromagnetic field: only currents can interact with photons. A permanent dipole only shifts the photonic displacement field, which is not a physical observable, and the permanent dipoles of molecules contribute only when the combined system is moved out of equilibrium.
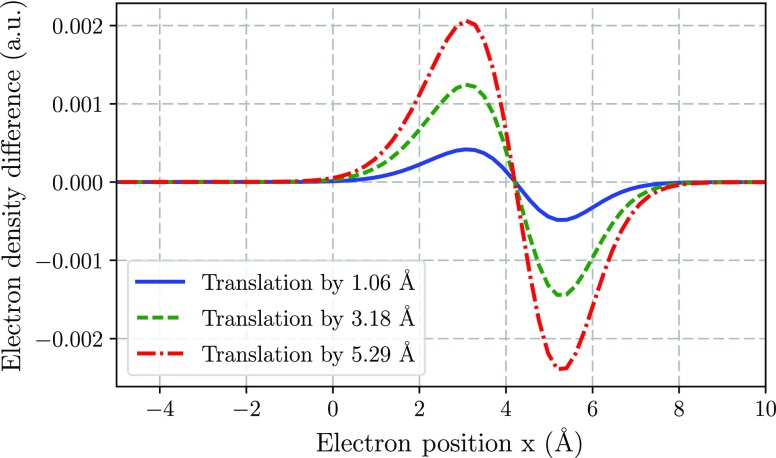
Only when the self-polarization term is neglected can an unphysical dependence on the permanent dipole in equilibrium arise. To illustrate that even for small systems and shifts this can have a large influence, we consider the Shin–Metiu model from before, but we slightly charge the complete system by using Z = +1.05e. We then perform a small shift x → x + μ in the coordinate system, solve the corresponding Shin–Metiu model, determine the ground-state electron density neμ(x), and then translate back to obtain ne(x – μ) and compare it with the original (unshifted) solution ne(x).
As expected, when the self-polarization is included, we just recover the old density, and neμ(x – μ) – ne(x) ≡ 0. In contrast, in Figure 7 we show the differences without the self-polarization and find an ever-increasing difference for larger μ (increasing permanent dipole moment). The behavior of the Shin–Metiu model without the self-polarization is clearly unphysical, since observables should not depend on the coordinate system. Any approximate method tailored to perform self-consistent calculations should respect the above coordinate-system independence by retaining the balance between bilinear and quadratic contributions. Consider for example the performance of the nonvariational Krieger–Li–Iafrate approximation for ab initio QEDFT presented in ref (16), which breaks this balance.
Figure 7.
Differences between the translated (by a shift μ) electron density neμ(x) and the electron density of the original system ne(x), i.e., ne(x – μ) – ne(x), without the self-polarization term. If the self-polarization is included the difference is always zero, i.e., the equilibrium physics remains independent of the coordinate system and the permanent dipole moment. In the Shin–Metiu model, the charge of the moving nucleus was slightly increased to Z = +1.05, and electronic and nuclear box sizes of 59.27 and 5.93 Å, respectively, were chosen (i.e., before any scattering states appear). All of the other parameter values remained as before.
It should be noticed that quadratic components also necessarily appear in other situations, i.e., they are indeed a quite general feature of nonrelativistic Hamiltonians. For example, if nuclear vibrations are approximated as phonon modes, the nonlinear Debye–Waller term, which is proportional to ∇k∇k′Ĥ, has to be added to the bilinear interaction.110,111 This term originates from the quadratic elements in a Born–Huang expansion15 with the very same physical effects as the quadratic components Â2 or P̂⊥2, e.g., enforcing translational invariance and renormalizing the excitation energies.
Collectivity, the Limit of the Dicke Model, and Plasmonic Systems
When considering a system of several molecules, we can separate their instantaneous interactions mediated by longitudinal and transverse polarization fields (in the PZW gauge) by ∫d3r P̂2 = ∫d3r P̂∥2 + P̂⊥. Here the first term on the right-hand side corresponds to the Coulomb interaction, and the second term corresponds to the self-polarization contribution.85 We can further approximately distinguish between situations where the wave functions of the different constituents overlap strongly and situations where there is no strong overlap. The former situation, often termed intramolecular, demands careful consideration of the Coulomb and self-polarization contributions simultaneously, where the Coulomb contribution dominates in most situations. The latter situation of contact-free interactions between matter subsystems, termed intermolecular, leads to a perturbative (dipolar approximation) cancellation of instantaneous interactions such that ∫d3r P̂A·P̂B ≈ 0, and we are left approximately with purely bilinear and retarded interactions between those separated matter subsystems.112 This situation, however, does not allow longitudinal or transverse interactions to be neglected when calculations are performed locally for one of the subsystems. A consistent calculation considering, for example, molecular rearrangements during chemical reactions due to the influence of cavity-mediated strong light–matter coupling will thus also demand a consistent treatment of Coulomb and self-polarization contributions.
If we now enter into the realm where instantaneous contributions to the intermolecular interaction cancel, it is often instructive to assume that indeed the local (i.e., subsystem) eigenstates are not affected by intermolecular interactions and do not need to be updated during the process. In this case we can perform the pinned-dipole approximation, which implies that each subsystem is localized at a specific position and distinguishable. Starting from eq 5, we can then recover the Dicke model by absorbing the self-polarization contribution perturbatively by renormalizing the mass of the particles (similar to the perturbative treatment of the Lamb shift) such that the effective interaction reduces to the common bilinear coupling.72 In the case of the pinned-dipole approximation, the bilinear coupling to the displacement field becomes equivalent to a coupling to the electric fields since the local polarization in Ê⊥ = 4π(D̂⊥ – P̂⊥) is zero by construction. To assume that the quantum subsystems are perfectly localized and distinguishable is in stark contrast to an ab initio quantum-mechanical description of molecules. Thus, applying the Dicke model to deduce the influence of strong coupling on the local molecular states calls for a very careful analysis of all of the applied approximations and their consequences. It furthermore permits physical features such as when charge distributions start to overlap, as is often the case in quantum-chemical calculations, leading to a dependence of the local observables on the surrounding (collective) ensemble.16
The occurrence
of quadratic (i.e., Debye–Waller) terms in
the electron–nuclear coupling highlights how general quadratic
components are in a nonrelativistic theory. More closely connected
to our current situation is the coupling to modes of a plasmonic environment.
In principle, if we describe the plasmonic environment as part of
the full system,113,114 the density oscillations of
the plasmonic environment are captured in an ab initio description
by the Coulomb interaction and the induced transverse photon field,
and hence, eq 5 is directly
applicable. Let us assume, however, that we are not interested in
a self-consistent calculation, can safely disregard contact terms
(i.e., ∫d3r P̂A·P̂B = 0), and rather
care about perturbative corrections. This consideration will lead
to van der Waals (dipole–dipole)-type interactions with different
scalings in terms of their intermolecular distance RAB, independent of the choice of Coulomb or PZW gauge.72 The consideration of large distances subject
to significant retardation is described by attractive Casimir–Polder
interactions,115,116 which scale as 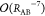 . For smaller RAB, retardation might
be omitted, and we would enter the realm of instantaneous
attractive interactions captured by the London dispersion potential,
which scale as
. For smaller RAB, retardation might
be omitted, and we would enter the realm of instantaneous
attractive interactions captured by the London dispersion potential,
which scale as 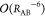 . While those considerations are well-tested
and allow for excellent perturbative results, they would not allow
a self-consistent calculation, as these forces would merely result
in a collapse of the wave function onto a singular point because of
its unbalanced attraction. Assuming for instance a set of harmonic
oscillators describing the plasmonic excitations coupled merely bilinearly
to the system of interest would introduce divergent forces proportional
to −∑αλα(λα·R).15 The Coulomb potential, wave function overlap,
and the Pauli principle give rise to repulsive components for small RAB, modeled for example by the empirical
. While those considerations are well-tested
and allow for excellent perturbative results, they would not allow
a self-consistent calculation, as these forces would merely result
in a collapse of the wave function onto a singular point because of
its unbalanced attraction. Assuming for instance a set of harmonic
oscillators describing the plasmonic excitations coupled merely bilinearly
to the system of interest would introduce divergent forces proportional
to −∑αλα(λα·R).15 The Coulomb potential, wave function overlap,
and the Pauli principle give rise to repulsive components for small RAB, modeled for example by the empirical 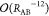 term of the Lennard-Jones potential or
the
term of the Lennard-Jones potential or
the 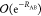 term
of the Buckingham potential. It is
therefore the higher-order components that ensure the stability of
matter. A self-consistent treatment of molecules in a plasmonic cavity,
which itself is modeled as, e.g., a simple harmonic oscillator,40,117 thus needs to include higher-order couplings to describe a stable
and physical system. Self-consistent calculations would therefore
demand extending the quasistatic approximation118−120 for plasmonic systems such that the plasmonic cluster responds to
the coupled molecule. This is precisely the physical origin of the
quadratic terms in QED, which allow the photonic or matter system
to respond to the coupling by adjusting their excitation energies.
For instance, the Â2 part can be subsumed
into adjusted mode frequencies and further defines a minimal frequency
(i.e., cures the infrared divergence), while the P̂⊥2 term
renormalizes the energies of the material, all within the long-wavelength
approximation. The very same effects should be present for a plasmonic
cavity when consistently quantized. Such effects are already observed
when ab initio calculations are performed with solely the longitudinal
Coulomb interaction.114 For small clusters,
and therefore a small effective volume and high coupling strength,
the modification of the response and volume due to the presence of
the coupled molecule is non-negligible and modifies the plasmonic
modes of the cluster. A purely bilinear coupling dictates entirely
different physics (see Spectral Features of Operators for a detailed discussion), violates all of the aforementioned basic
constraints, and leaves such a simplification as inherently perturbative.
While state-of-the-art models might provide insightful perturbative
results, the development of corrected models should obtain additional
interest, and ab initio calculations could prove beneficial to foster
this effort.
term
of the Buckingham potential. It is
therefore the higher-order components that ensure the stability of
matter. A self-consistent treatment of molecules in a plasmonic cavity,
which itself is modeled as, e.g., a simple harmonic oscillator,40,117 thus needs to include higher-order couplings to describe a stable
and physical system. Self-consistent calculations would therefore
demand extending the quasistatic approximation118−120 for plasmonic systems such that the plasmonic cluster responds to
the coupled molecule. This is precisely the physical origin of the
quadratic terms in QED, which allow the photonic or matter system
to respond to the coupling by adjusting their excitation energies.
For instance, the Â2 part can be subsumed
into adjusted mode frequencies and further defines a minimal frequency
(i.e., cures the infrared divergence), while the P̂⊥2 term
renormalizes the energies of the material, all within the long-wavelength
approximation. The very same effects should be present for a plasmonic
cavity when consistently quantized. Such effects are already observed
when ab initio calculations are performed with solely the longitudinal
Coulomb interaction.114 For small clusters,
and therefore a small effective volume and high coupling strength,
the modification of the response and volume due to the presence of
the coupled molecule is non-negligible and modifies the plasmonic
modes of the cluster. A purely bilinear coupling dictates entirely
different physics (see Spectral Features of Operators for a detailed discussion), violates all of the aforementioned basic
constraints, and leaves such a simplification as inherently perturbative.
While state-of-the-art models might provide insightful perturbative
results, the development of corrected models should obtain additional
interest, and ab initio calculations could prove beneficial to foster
this effort.
Summary
It is the very nature of physics that our descriptions are necessarily approximate and that every theory has its limitations and drawbacks. Moreover, even when we have seemingly very accurate theories like QED, we need to reduce their complexity by employing further approximations and assumptions to render them practical. For QED this was historically done by employing perturbation theory and/or restrictions to a minimal set of dynamical variables. Because of their clarity and elegance, the resulting simplified versions of QED are a very good starting point for further investigations, provide for good reasons a common language for a variety of subjects, and have provided tremendous insight over decades of research. Nevertheless, we need to be aware of the conditions under which these simplifications are valid and what their consequences are. With the recent experimental advances in combining quantum-optical, chemical, and materials science aspects121 and the subsequent merging of ab initio approaches with quantum-optical methods, it has become important to scrutinize these common assumptions.12
In this work, we have elucidated and illustrated the consequences of discarding quadratic terms that arise naturally in nonrelativistic QED. Omitting them breaks gauge invariance, introduces a dependence on the coordinate system (or basis set), leads to radiating ground states, introduces an artificial dependence on the total dipole moment, and in the basis set limit leads to disintegration of the complete system. However, many of these effects can be mitigated if one works perturbatively or restricts the parameter space. This is in accordance with many years of successful application of such approximations but also highlights their limits of applicability. However, estimates of their applicability, such as the extension criterion (eq 11) discussed in No Bound Eigenstates without Self-Polarization, nowadays become relevant for practical calculations. Certainly when strong coupling between light and matter modifies the local matter subsystem, as is suggested by recent experimental results,3,11,99,122−124 the quadratic terms can become important and determine the physical properties.
When looking beyond the simple Rabi splitting of spectral lines, which is the accepted indicator of the onset of strong coupling, other observables that contain further information about the matter subsystem should be able to highlight the necessity to modify the common Dicke or Rabi models, e.g., as demonstrated in ref (76). By consideration of photonic and matter observables at the same time, the dipole-approximated bilinear coupling can be further scrutinized, the influence of quadratic coupling terms can be revealed, and effects that are due to spatially inhomogeneous fields (beyond the long-wavelength approximation) can be observed. Furthermore, when the light–matter coupling causes bilinear, self-polarization, and Coulomb interactions to act on comparable energy scales, nonperturbative effects can be expected. At this point it is important to realize that this statement also holds spatially, i.e., that while a coupling might be considered small for certain bond lengths/extensions of the molecular system, at other parts or on other scales it might become substantial. The extension criterion (eq 11), which weighs the divergent forces (which increase with increasing spatial extension) against the ionization energy, is motivated precisely with this spirit in mind, providing the g/ω complementing parameter estimate. Consider for example the binding curve of a molecule. Probing the dissociative regime at large distances will change the ratio of the aforementioned contributions until van der Waals-type interactions containing retardation effects have to be considered, a problem that is also of chemical interest.125 Not just the equilibrium distance of molecules will change, but especially their behavior in the stretched configuration will be affected,13,14 a feature essential to describe chemical reactions. For relatively large systems, which are yet still small compared with the relevant wavelengths of the photon field, stronger effects would be expected. In the simple models presented here, we could have used a smaller coupling strength yet a spatially more extended system, and we would have found similar effects. Dynamics that probes the long-range part of potential energy surfaces should be affected more strongly, and this is especially true compared with dynamics due to classical external laser fields in the dipole approximation ignoring the self-polarization term. While our focus remained on the single-molecule limit, an additional essential scale of the system is represented by the number of charge carriers, amplifying the dipole moment, polarizability, and therefore the self-polarization contribution. Extended systems (e.g., solids and liquids) and molecular ensembles with charge contact (e.g., biomolecules) are therefore expected to experience quite sizable influences by quadratic components, i.e., perturbatively seen renormalizing photonic or matter excitations due to the collective light–matter interaction.15,62,75 Recent investigations of cavity-enhanced electron–phonon coupling64,65 and its role for superconductivity99 might indicate the substantial scientific impact of this realization. Exploring these situations where our theoretical descriptions begin to differ strongly thus holds promise to reveal further yet undiscovered effects.12
Acknowledgments
We thank S. Buhmann, J. Feist, A. Salam, and I. Tokatly for insightful discussions. This work was supported by the European Research Council (ERC-2015-AdG694097), by the Cluster of Excellence “Advanced Imaging of Matter” (AIM), Grupos Consolidados (IT1249-19), partially by Federal Ministry of Education and Research Grant RouTe-13N14839, and by SFB925 “Light Induced Dynamics and Control of Correlated Quantum Systems”.
Appendix
Fundamental Coupling of Light with Matter and the Emergence of Diamagnetism
Let us here briefly show how QED and its nonrelativistic limit can be set up starting from classical electrodynamics. In vector potential form, the microscopic description of the electromagnetic fields is given by
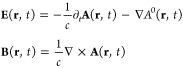 |
For later reference, we use the vacuum permeability
μ0 and vacuum permittivity ϵ0, which
are connected to the speed of light by 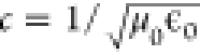 . If we then choose the Coulomb gauge condition
∇·A(r, t) = 0, which is most convenient in the nonrelativistic limit, the
energy of the classical electromagnetic field is given by the expression92
. If we then choose the Coulomb gauge condition
∇·A(r, t) = 0, which is most convenient in the nonrelativistic limit, the
energy of the classical electromagnetic field is given by the expression92
| 12 |
and the interaction among charged particles emerges via
| 13 |
where we have decomposed the electric field into a purely transverse part (polarized perpendicular to the propagation direction), E⊥(r, t) = −(1/c)∂tA(r, t), and a purely longitudinal part (polarized along the propagation direction), E∥(r, t) = −∇A0(r, t). The electromagnetic field is coupled to a charge current j(r, t) that obeys the continuity equation (1/c)∂tj0(r, t) = −∇·j(r, t). We therefore see that it is the moving charges via their combined charge current that induce and modify the electromagnetic fields.
The above decomposition is furthermore very convenient for singling out electrostatic contributions, which are given exclusively in terms of E∥ and j0. With the Poisson equation in full space, which determines the zero component of the electromagnetic vector potential,
the 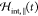 term
in eq 13 can be brought
into the form
term
in eq 13 can be brought
into the form
| 14 |
and thus
corresponds to the longitudinal Coulomb
interaction, which typically dominates the electronic structure of
condensed matter. If we are not in vacuum on all of 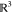 but instead have, e.g.,
boundaries with
certain boundary conditions, the Coulomb kernel
but instead have, e.g.,
boundaries with
certain boundary conditions, the Coulomb kernel 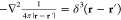 changes accordingly. This also changes
the Coulomb interaction among charged particles. For example, in the
case of cavity situations it can lead to the inclusion of mirror charges
depending on the selected gauge.112 Furthermore,
because of the Coulomb gauge condition, the first term on the right-hand
side of eq 13 is merely
coupling to the transverse part of the charge current and can thus
be rewritten as
changes accordingly. This also changes
the Coulomb interaction among charged particles. For example, in the
case of cavity situations it can lead to the inclusion of mirror charges
depending on the selected gauge.112 Furthermore,
because of the Coulomb gauge condition, the first term on the right-hand
side of eq 13 is merely
coupling to the transverse part of the charge current and can thus
be rewritten as
| 15 |
We have therefore divided the interaction due to coupling with a charge current into purely longitudinal (electrostatic) and purely transverse ones. To quantize the theory, we need to promote the classical vector potential to a quantum field Â(r), which is basically a sum of quantum harmonic oscillators25,92 (also see eq 2). The quantum fields include the transverse character via the transverse δ function δ⊥ij in the commutation relations between conjugate fields. We furthermore need to promote the classical charge current to the conserved charge current operators ĵ(r) and ĵ0(r) = cn̂(r) of the noninteracting matter subsystem.25,92 In this way, the total charge current of the quantized particles generates the quantized electromagnetic field, and at the same time the photon field modifies the movement of the quantized particles. Hence, QED becomes a self-consistent theory of light and matter, and equilibrium is reached when a force balance among the constituents is reached.
This clear procedure holds
true if we consider QED with Dirac particles
and thus the Dirac current. However, if we take the nonrelativistic
limit for the particles and thus also for the conserved charge current,
a subtlety arises with important consequences. When the positronic
degrees of freedom are expressed to first order in 1/mc2 in terms of the electronic components, a term that is
quadratic in the vector potential appears.25,126 This means that in eq 15, if we use the conserved current j(r, t) = jp(r, t) + jd(r, t) that consists of the paramagnetic current jp plus the diamagnetic current jd,97 a correction term of the form 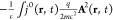 has to be added.25 This leads to the
appearance of a quadratic coupling term. This quadratic
term renders the coupling defined by eq 15 consistent with the
minimal coupling prescription also in the nonrelativistic limit (see
the usual minimal coupling form of eq 3). Indeed, this extra term is due to the explicit appearance
of the diamagnetic current contribution
has to be added.25 This leads to the
appearance of a quadratic coupling term. This quadratic
term renders the coupling defined by eq 15 consistent with the
minimal coupling prescription also in the nonrelativistic limit (see
the usual minimal coupling form of eq 3). Indeed, this extra term is due to the explicit appearance
of the diamagnetic current contribution 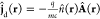 ,25,72,92 which in the
Dirac current arises only implicitly, as can be seen
by the Gordon decomposition.25,126 This quadratic coupling
term captures the effective photon–photon interaction due to
the discarded positronic degrees of freedom. A direct beneficial consequence
of this explicit diamagnetic term is that it removes the infrared
divergence of relativistic QED.73 This
can best be understood by considering the Heisenberg equation of motion,
which is analogous to the inhomogeneous microscopic Maxwell’s
equation,
,25,72,92 which in the
Dirac current arises only implicitly, as can be seen
by the Gordon decomposition.25,126 This quadratic coupling
term captures the effective photon–photon interaction due to
the discarded positronic degrees of freedom. A direct beneficial consequence
of this explicit diamagnetic term is that it removes the infrared
divergence of relativistic QED.73 This
can best be understood by considering the Heisenberg equation of motion,
which is analogous to the inhomogeneous microscopic Maxwell’s
equation,
| 16 |
where ĵ⊥(r) is the transverse part of the physical current operator ĵ(r) = ĵp(r) + ĵd(r). Grouping the diamagnetic current with the vector potential on the left-hand side shows that the mere existence of charged particles will modify the frequency of the bare fields (see also Necessity and Implications of Quadratic Couplings in the Dipole Approximation for the dipole case and recall the discussion in From Microscopic to Macroscopic Maxwell’s Equations).
Only when the longitudinal (eq 14) and transverse (eq 15) couplings are treated consistently can they provide a local interaction. However, in practice often only one of the two interactions is treated explicitly, depending on which properties of the combined light–matter system are of interest.12 Focusing on quantum mechanics (e.g., on the electronic structure, as is essential to describe chemical reactions), the transverse interaction is often omitted, and one merely implicitly considers the fluctuations in form of the physical mass.15,73 Quantum-optical considerations on the other hand typically focus on the description of the transverse fields and thus strongly simplify the electronic structure. The resulting quantum-optical models are designed to predict specific photonic observables and are consequentially limited in their predictability for the matter subsystem.14,15 Recent interest in strong light–matter interaction is calling now for a consistent treatment of those limits that have historically been perceived as complementary.
Under certain assumptions,
the diamagnetic term can indeed be absorbed
by a redefinition of the frequencies and polarizations of the field
modes.15,75,93,94 These redefinitions depend on the matter subsystem
(more specifically the number of charged particles) and lead to a
diamagnetic shift of the photon field, which can be observed experimentally.98,127,128 Since the difference between
the bare and diamagnetically dressed photonic quantities goes as 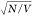 , where N is the total
number of particles and V is the quantization volume,
it is often argued93 that one can use the
bare quantities for finite systems. This is not entirely correct.
The same argument would predict that the coupling between light and
matter (see eq 7) would
be zero. The reason for nonzero coupling lies in the fact that as
the quantization volume becomes larger (approaching free space), the
number of modes in any frequency interval approaches infinity as well.
Thus, while the coupling to an individual mode indeed becomes zero,
the coupling to the continuum of modes is nonzero. Therefore, when
we keep individual modes in our theoretical description, we effectively
treat a small but finite frequency interval of modes. This frequency
interval can be related to the effective mode volume, since it gives
the spacing between the effective modes. Consequently, we also need
to dress the photon operators diamagnetically.
, where N is the total
number of particles and V is the quantization volume,
it is often argued93 that one can use the
bare quantities for finite systems. This is not entirely correct.
The same argument would predict that the coupling between light and
matter (see eq 7) would
be zero. The reason for nonzero coupling lies in the fact that as
the quantization volume becomes larger (approaching free space), the
number of modes in any frequency interval approaches infinity as well.
Thus, while the coupling to an individual mode indeed becomes zero,
the coupling to the continuum of modes is nonzero. Therefore, when
we keep individual modes in our theoretical description, we effectively
treat a small but finite frequency interval of modes. This frequency
interval can be related to the effective mode volume, since it gives
the spacing between the effective modes. Consequently, we also need
to dress the photon operators diamagnetically.
The Power–Zienau–Wooley Gauge Transformation
While here we performed the unitary PZW transformation after choosing the Coulomb gauge quantization, which leaves the vector potential operator invariant but leads to an adjusted conjugate photon field momentum and coupling, one can equivalently use the PZW (multipolar) gauge of the field to perform the quantization procedure.68 This gauge is connected to the Coulomb gauge by an adjustment of the phase of each particle by θ(r) = −qα0∫01r·A(sr) ds.68 This extra phase removes the explicit diamagnetic component from the physical current but also assigns a longitudinal component to the vector potential that can be associated with the Coulomb interaction. While the PZW gauge features purely transverse light–matter coupling, similar to the Coulomb gauge, it mixes light and matter degrees of freedom in accordance with the macroscopic Maxwell’s equations.66−68,79,85
Transverse Basis and Distributions
For an arbitrary cavity geometry, the vector-valued eigenfunctions can be very complicated, deviating from simple plane waves. Still, this basis Sα(r) is assumed to obey the condition ∇·Sα(r) = 0. In this case, we need to perform the mode expansion of the vector potential operator and the polarization operator with the corresponding modes. Selecting a basis defined the representation of the δ distribution and the according polarization. It is important to note that while there are many equivalent representations of the δ distribution, e.g., by using different basis sets Sα(r), multiplications of distributions are not uniquely defined.129,130 Indeed, the origin of the divergence in quantum field theories stems from the fact that (operator-valued) distributions are multiplied131 and a regularization and renormalization procedure needs to be employed to give a finite answer. The usual method of regularization is equivalent to introducing a cutoff in the mode expansion α, and hence, by keeping this explicit instead of working with an unspecified representation of the δ distribution we avoid nonuniqueness problems.79 We could straightaway also use the full infinite space,73 but this would just make the notation unnecessarily complicated, as the above Hamiltonian converges in the norm-resolvent sense to the infinite-space Hamiltonian for Mp → ∞.132 Hence, the above Hamiltonian can be made equivalent to the full infinite-space Hamiltonian if we increase the quantization volume.
Spectral Features of Operators
Most arguments for performing
a multipole expansion for a Hamiltonian are based on perturbation
theory, where local properties derived from a fixed wave function
only slightly depend on higher-order contributions of a perturbing
operator.72 However, this does not mean
that such arguments still apply for nonperturbative considerations,
i.e., when the operator itself is changed and we solve the resulting
equation self-consistently. Indeed, if we consider the influence of
such expansions on the Hamiltonian directly, the opposite is usually
true: the highest-order terms determine all of the basic properties.
An instructive example is a one-dimensional model atom with Ĥ = −∂x2/2 + v(x), where v(x) is some binding potential centered at x = 0 with v(x) → 0 for x →
∞. Its spectrum as a self-adjoint operator in 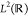 contains both bound states (eigenfunctions
exponentially localized around x = 0) and scattering
states (distributional eigenfunctions corresponding to the continuous
spectrum). In such cases, a harmonic approximation for certain ground-state
properties, v(x) ≈ v(0) + v′(0)x + v″(0)x2/2, is reasonable
(assuming v″(0) > 0), and the perturbative
influence of higher-order terms proportional to xn with n > 2 is minor.
However, if we consider the actual Hamiltonian and treat higher-order
terms proportional to xn nonperturbatively in
contains both bound states (eigenfunctions
exponentially localized around x = 0) and scattering
states (distributional eigenfunctions corresponding to the continuous
spectrum). In such cases, a harmonic approximation for certain ground-state
properties, v(x) ≈ v(0) + v′(0)x + v″(0)x2/2, is reasonable
(assuming v″(0) > 0), and the perturbative
influence of higher-order terms proportional to xn with n > 2 is minor.
However, if we consider the actual Hamiltonian and treat higher-order
terms proportional to xn nonperturbatively in  , we see that either we have an operator
that is unbounded from below (having no ground state) with a purely
continuous spectrum (no eigenfunctions but only scattering states)
for odd n(62) or bounded
from below with only bound states for even n (again
assuming that all v(n)(0) > 0). Thus, all of the basic properties are determined only
by
the highest order of n. We therefore find that an
expansion of an operator becomes meaningful only if we also indicate
whether we consider it perturbatively for a fixed wave function or
nonperturbatively. In this work, we focus on the nonperturbative situation.
Let us also mention that as an alternative to perturbation theory,
a nonperturbative consideration but on a different Hilbert space of
a restricted domain
, we see that either we have an operator
that is unbounded from below (having no ground state) with a purely
continuous spectrum (no eigenfunctions but only scattering states)
for odd n(62) or bounded
from below with only bound states for even n (again
assuming that all v(n)(0) > 0). Thus, all of the basic properties are determined only
by
the highest order of n. We therefore find that an
expansion of an operator becomes meaningful only if we also indicate
whether we consider it perturbatively for a fixed wave function or
nonperturbatively. In this work, we focus on the nonperturbative situation.
Let us also mention that as an alternative to perturbation theory,
a nonperturbative consideration but on a different Hilbert space of
a restricted domain 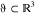 becomes possible, i.e., we consider the
operators on L2(ϑ) with appropriate
boundary conditions or on a restricted state space
becomes possible, i.e., we consider the
operators on L2(ϑ) with appropriate
boundary conditions or on a restricted state space 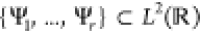 . As illustrated in Necessity
and Implications of Quadratic Couplings in the Dipole Approximation, this will render the restricted domain or subset a relevant parameter
for the theoretical prediction since the physical properties can then
crucially depend on this parameter.
. As illustrated in Necessity
and Implications of Quadratic Couplings in the Dipole Approximation, this will render the restricted domain or subset a relevant parameter
for the theoretical prediction since the physical properties can then
crucially depend on this parameter.
The authors declare no competing financial interest.
References
- Hutchison J. A.; Schwartz T.; Genet C.; Devaux E.; Ebbesen T. W. Modifying Chemical Landscapes by Coupling to Vacuum Fields. Angew. Chem., Int. Ed. 2012, 51, 1592–1596. 10.1002/anie.201107033. [DOI] [PubMed] [Google Scholar]
- Coles D. M.; Somaschi N.; Michetti P.; Clark C.; Lagoudakis P. G.; Savvidis P. G.; Lidzey D. G. Polariton-mediated energy transfer between organic dyes in a strongly coupled optical microcavity. Nat. Mater. 2014, 13, 712–719. 10.1038/nmat3950. [DOI] [PubMed] [Google Scholar]
- Thomas A.; George J.; Shalabney A.; Dryzhakov M.; Varma S. J.; Moran J.; Chervy T.; Zhong X.; Devaux E.; Genet C.; Hutchison J. A.; Ebbesen T. W. Ground-State Chemical Reactivity under Vibrational Coupling to the Vacuum Electromagnetic Field. Angew. Chem., Int. Ed. 2016, 55, 11462–11466. 10.1002/anie.201605504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong X.; Chervy T.; Zhang L.; Thomas A.; George J.; Genet C.; Hutchison J. A.; Ebbesen T. W. Energy Transfer between Spatially Separated Entangled Molecules. Angew. Chem., Int. Ed. 2017, 56, 9034–9038. 10.1002/anie.201703539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Munkhbat B.; Wersäll M.; Baranov D. G.; Antosiewicz T. J.; Shegai T. Suppression of photo-oxidation of organic chromophores by strong coupling to plasmonic nanoantennas. Sci. Adv. 2018, 4, eaas9552. 10.1126/sciadv.aas9552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiang B.; Ribeiro R. F.; Dunkelberger A. D.; Wang J.; Li Y.; Simpkins B. S.; Owrutsky J. C.; Yuen-Zhou J.; Xiong W. Two-dimensional infrared spectroscopy of vibrational polaritons. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, 4845–4850. 10.1073/pnas.1722063115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stranius K.; Hertzog M.; Börjesson K. Selective manipulation of electronically excited states through strong light–matter interactions. Nat. Commun. 2018, 9, 2273. 10.1038/s41467-018-04736-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang D.; Kelkar H.; Martin-Cano D.; Rattenbacher D.; Shkarin A.; Utikal T.; Götzinger S.; Sandoghdar V. Turning a molecule into a coherent two-level quantum system. Nat. Phys. 2019, 15, 483–489. 10.1038/s41567-019-0436-5. [DOI] [Google Scholar]
- Peters V. N.; Faruk M. O.; Asane J.; Alexander R.; Peters D. A.; Prayakarao S.; Rout S.; Noginov M. A. Effect of strong coupling on photodegradation of the semiconducting polymer P3HT. Optica 2019, 6, 318. 10.1364/OPTICA.6.000318. [DOI] [Google Scholar]
- Ojambati O. S.; Chikkaraddy R.; Deacon W. D.; Horton M.; Kos D.; Turek V. A.; Keyser U. F.; Baumberg J. J. Quantum electrodynamics at room temperature coupling a single vibrating molecule with a plasmonic nanocavity. Nat. Commun. 2019, 10, 1049. 10.1038/s41467-019-08611-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lather J.; Bhatt P.; Thomas A.; Ebbesen T. W.; George J. Cavity Catalysis by Cooperative Vibrational Strong Coupling of Reactant and Solvent Molecules. Angew. Chem., Int. Ed. 2019, 58, 10635–10638. 10.1002/anie.201905407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggenthaler M.; Tancogne-Dejean N.; Flick J.; Appel H.; Rubio A. From a quantum-electrodynamical light–matter description to novel spectroscopies. Nat. Rev. Chem. 2018, 2, 0118. 10.1038/s41570-018-0118. [DOI] [Google Scholar]
- Flick J.; Ruggenthaler M.; Appel H.; Rubio A. Atoms and molecules in cavities, from weak to strong coupling in quantum-electrodynamics (QED) chemistry. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, 3026–3034. 10.1073/pnas.1615509114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schäfer C.; Ruggenthaler M.; Appel H.; Rubio A. Modification of excitation and charge transfer in cavity quantum-electrodynamical chemistry. Proc. Natl. Acad. Sci. U. S. A. 2019, 116, 4883–4892. 10.1073/pnas.1814178116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schäfer C.; Ruggenthaler M.; Rubio A. Ab initio nonrelativistic quantum electrodynamics: Bridging quantum chemistry and quantum optics from weak to strong coupling. Phys. Rev. A: At., Mol., Opt. Phys. 2018, 98, 043801. 10.1103/PhysRevA.98.043801. [DOI] [Google Scholar]
- Flick J.; Schäfer C.; Ruggenthaler M.; Appel H.; Rubio A. Ab Initio Optimized Effective Potentials for Real Molecules in Optical Cavities: Photon Contributions to the Molecular Ground State. ACS Photonics 2018, 5, 992–1005. 10.1021/acsphotonics.7b01279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flick J.; Appel H.; Ruggenthaler M.; Rubio A. Cavity Born-Oppenheimer Approximation for Correlated Electron-Nuclear-Photon Systems. J. Chem. Theory Comput. 2017, 13, 1616–1625. 10.1021/acs.jctc.6b01126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agranovich V. M.; Litinskaia M.; Lidzey D. G. Cavity polaritons in microcavities containing disordered organic semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 67, 085311. 10.1103/PhysRevB.67.085311. [DOI] [Google Scholar]
- Michetti P.; La Rocca G. C. Polariton states in disordered organic microcavities. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 71, 115320. 10.1103/PhysRevB.71.115320. [DOI] [Google Scholar]
- Ruggenthaler M.; Mackenroth F.; Bauer D. Time-dependent Kohn–Sham approach to quantum electrodynamics. Phys. Rev. A: At., Mol., Opt. Phys. 2011, 84, 042107. 10.1103/PhysRevA.84.042107. [DOI] [Google Scholar]
- González-Tudela A.; Huidobro P. A.; Martín-Moreno L.; Tejedor C.; García-Vidal F. J. Theory of Strong Coupling between Quantum Emitters and Propagating Surface Plasmons. Phys. Rev. Lett. 2013, 110, 126801. 10.1103/PhysRevLett.110.126801. [DOI] [PubMed] [Google Scholar]
- Tokatly I. V. Time-Dependent Density Functional Theory for Many-Electron Systems Interacting with Cavity Photons. Phys. Rev. Lett. 2013, 110, 233001. 10.1103/PhysRevLett.110.233001. [DOI] [PubMed] [Google Scholar]
- Buhmann S. Y.Dispersion Forces I: Macroscopic Quantum Electrodynamics and Ground-State Casimir, Casimir–Polder and van der Waals Forces; Springer Tracts in Modern Physics, Vol. 247; Springer, 2012. [Google Scholar]
- Buhmann S. Y.Dispersion Forces II: Many-Body Effects, Excited Atoms, Finite Temperature and Quantum Friction; Springer Tracts in Modern Physics, Vol. 248; Springer, 2012. [Google Scholar]
- Ruggenthaler M.; Flick J.; Pellegrini C.; Appel H.; Tokatly I. V.; Rubio A. Quantum-electrodynamical density-functional theory: Bridging quantum optics and electronic-structure theory. Phys. Rev. A: At., Mol., Opt. Phys. 2014, 90, 012508. 10.1103/PhysRevA.90.012508. [DOI] [Google Scholar]
- Galego J.; Garcia-Vidal F. J.; Feist J. Cavity-Induced Modifications of Molecular Structure in the Strong-Coupling Regime. Phys. Rev. X 2015, 5, 041022. 10.1103/PhysRevX.5.041022. [DOI] [Google Scholar]
- del Pino J.; Feist J.; Garcia-Vidal F. J. Quantum theory of collective strong coupling of molecular vibrations with a microcavity mode. New J. Phys. 2015, 17, 053040. 10.1088/1367-2630/17/5/053040. [DOI] [Google Scholar]
- Schachenmayer J.; Genes C.; Tignone E.; Pupillo G. Cavity-Enhanced Transport of Excitons. Phys. Rev. Lett. 2015, 114, 196403. 10.1103/PhysRevLett.114.196403. [DOI] [PubMed] [Google Scholar]
- Salam A.Non-Relativistic QED Theory of the van der Waals Dispersion Interaction; Springer, 2016. [Google Scholar]
- Kowalewski M.; Bennett K.; Mukamel S. Cavity Femtochemistry: Manipulating Nonadiabatic Dynamics at Avoided Crossings. J. Phys. Chem. Lett. 2016, 7, 2050–2054. 10.1021/acs.jpclett.6b00864. [DOI] [PubMed] [Google Scholar]
- Herrera F.; Spano F. C. Cavity-Controlled Chemistry in Molecular Ensembles. Phys. Rev. Lett. 2016, 116, 238301. 10.1103/PhysRevLett.116.238301. [DOI] [PubMed] [Google Scholar]
- Zeb M. A.; Kirton P. G.; Keeling J. Exact States and Spectra of Vibrationally Dressed Polaritons. ACS Photonics 2018, 5, 249–257. 10.1021/acsphotonics.7b00916. [DOI] [Google Scholar]
- Luk H. L.; Feist J.; Toppari J. J.; Groenhof G. Multiscale Molecular Dynamics Simulations of Polaritonic Chemistry. J. Chem. Theory Comput. 2017, 13, 4324–4335. 10.1021/acs.jctc.7b00388. [DOI] [PubMed] [Google Scholar]
- De Liberato S. Virtual photons in the ground state of a dissipative system. Nat. Commun. 2017, 8, 1465. 10.1038/s41467-017-01504-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vendrell O. Collective Jahn–Teller Interactions through Light–Matter Coupling in a Cavity. Phys. Rev. Lett. 2018, 121, 253001. 10.1103/PhysRevLett.121.253001. [DOI] [PubMed] [Google Scholar]
- F. Ribeiro R.; Dunkelberger A. D.; Xiang B.; Xiong W.; Simpkins B. S.; Owrutsky J. C.; Yuen-Zhou J. Theory for Nonlinear Spectroscopy of Vibrational Polaritons. J. Phys. Chem. Lett. 2018, 9, 3766–3771. 10.1021/acs.jpclett.8b01176. [DOI] [PubMed] [Google Scholar]
- Hoffmann N. M.; Appel H.; Rubio A.; Maitra N. T. Light–matter interactions via the exact factorization approach. Eur. Phys. J. B 2018, 91, 180. 10.1140/epjb/e2018-90177-6. [DOI] [Google Scholar]
- Hagenmüller D.; Schütz S.; Schachenmayer J.; Genes C.; Pupillo G. Cavity-assisted mesoscopic transport of fermions: Coherent and dissipative dynamics. Phys. Rev. B: Condens. Matter Mater. Phys. 2018, 97, 205303. 10.1103/PhysRevB.97.205303. [DOI] [Google Scholar]
- Fregoni J.; Granucci G.; Coccia E.; Persico M.; Corni S. Manipulating azobenzene photoisomerization through strong light–molecule coupling. Nat. Commun. 2018, 9, 4688. 10.1038/s41467-018-06971-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galego J.; Climent C.; Garcia-Vidal F. J.; Feist J. Cavity Casimir–Polder Forces and Their Effects in Ground-State Chemical Reactivity. Phys. Rev. X 2019, 9, 021057. 10.1103/PhysRevX.9.021057. [DOI] [Google Scholar]
- del Pino J.; Schröder F. A. Y. N.; Chin A. W.; Feist J.; Garcia-Vidal F. J. Tensor Network Simulation of Non-Markovian Dynamics in Organic Polaritons. Phys. Rev. Lett. 2018, 121, 227401. 10.1103/PhysRevLett.121.227401. [DOI] [PubMed] [Google Scholar]
- Strathearn A.; Kirton P.; Kilda D.; Keeling J.; Lovett B. W. Efficient non-Markovian quantum dynamics using time-evolving matrix product operators. Nat. Commun. 2018, 9, 3322. 10.1038/s41467-018-05617-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abedi A.; Khosravi E.; Tokatly I. V. Shedding light on correlated electron–photon states using the exact factorization. Eur. Phys. J. B 2018, 91, 194. 10.1140/epjb/e2018-90243-1. [DOI] [Google Scholar]
- Hoffmann N. M.; Schäfer C.; Rubio A.; Kelly A.; Appel H. Capturing vacuum fluctuations and photon correlations in cavity quantum electrodynamics with multitrajectory Ehrenfest dynamics. Phys. Rev. A: At., Mol., Opt. Phys. 2019, 99, 063819. 10.1103/PhysRevA.99.063819. [DOI] [Google Scholar]
- Rivera N.; Flick J.; Narang P. Variational Theory of Nonrelativistic Quantum Electrodynamics. Phys. Rev. Lett. 2019, 122, 193603. 10.1103/PhysRevLett.122.193603. [DOI] [PubMed] [Google Scholar]
- Triana J. F.; Sanz-Vicario J. L. Revealing the Presence of Potential Crossings in Diatomics Induced by Quantum Cavity Radiation. Phys. Rev. Lett. 2019, 122, 063603. 10.1103/PhysRevLett.122.063603. [DOI] [PubMed] [Google Scholar]
- Reitz M.; Sommer C.; Genes C. Langevin Approach to Quantum Optics with Molecules. Phys. Rev. Lett. 2019, 122, 203602. 10.1103/PhysRevLett.122.203602. [DOI] [PubMed] [Google Scholar]
- Mordovina U.; Bungey C.; Appel H.; Knowles P. J.; Rubio A.; Manby F. R.. Polaritonic Coupled-Cluster Theory. arXiv (Physics.Chemical Physics), December 31, 2019, 1909.02401, ver. 2. https://arxiv.org/abs/1909.02401 (accessed 2019-11-20).
- Hoffmann N. M.; Schäfer C.; Säkkinen N.; Rubio A.; Appel H.; Kelly A. Benchmarking semiclassical and perturbative methods for real-time simulations of cavity-bound emission and interference. J. Chem. Phys. 2019, 151 (24), 244113. 10.1063/1.5128076. [DOI] [PubMed] [Google Scholar]
- Flick J.; Welakuh D. M.; Ruggenthaler M.; Appel H.; Rubio A. Light–Matter Response in Nonrelativistic Quantum Electrodynamics. ACS Photonics 2019, 6, 2757–2778. 10.1021/acsphotonics.9b00768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du M.; Martínez-Martínez L. A.; Ribeiro R. F.; Hu Z.; Menon V. M.; Yuen-Zhou J. Theory for polariton-assisted remote energy transfer. Chem. Sci. 2018, 9, 6659–6669. 10.1039/C8SC00171E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ribeiro R. F.; Martínez-Martínez L. A.; Du M.; Campos-Gonzalez-Angulo J.; Yuen-Zhou J. Polariton chemistry: controlling molecular dynamics with optical cavities. Chem. Sci. 2018, 9, 6325–6339. 10.1039/C8SC01043A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feist J.; Galego J.; Garcia-Vidal F. J. Polaritonic chemistry with organic molecules. ACS Photonics 2018, 5, 205–216. 10.1021/acsphotonics.7b00680. [DOI] [Google Scholar]
- Frisk Kockum A.; Miranowicz A.; De Liberato S.; Savasta S.; Nori F. Ultrastrong coupling between light and matter. Nat. Rev. Phys. 2019, 1, 19–40. 10.1038/s42254-018-0006-2. [DOI] [Google Scholar]
- Groenhof G.; Climent C.; Feist J.; Morozov D.; Toppari J. J. Tracking Polariton Relaxation with Multiscale Molecular Dynamics Simulations. J. Phys. Chem. Lett. 2019, 10, 5476–5483. 10.1021/acs.jpclett.9b02192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campos-Gonzalez-Angulo J. A.; Ribeiro R. F.; Yuen-Zhou J. Resonant catalysis of thermally activated chemical reactions with vibrational polaritons. Nat. Commun. 2019, 10, 4685. 10.1038/s41467-019-12636-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semenov A.; Nitzan A. Electron transfer in confined electromagnetic fields. J. Chem. Phys. 2019, 150, 174122. 10.1063/1.5095940. [DOI] [PubMed] [Google Scholar]
- Baranov D. G.; Munkhbat B.; Zhukova E.; Rousseaux B.; Bisht A.; Canales A.; Johansson G.; Antosiewicz T.; Shegai T.. Ultrastrong coupling between nanoparticle plasmons and cavity photons at ambient conditions. arXiv (Physics.Optics), December 16, 2019, 1912.07739, ver. 1. https://arxiv.org/abs/1912.07739 (accessed 2019-11-20). [DOI] [PMC free article] [PubMed]
- Dicke R. H. Coherence in Spontaneous Radiation Processes. Phys. Rev. 1954, 93, 99–110. 10.1103/PhysRev.93.99. [DOI] [Google Scholar]
- Jaynes E.; Cummings F. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. 10.1109/PROC.1963.1664. [DOI] [Google Scholar]
- Garraway B. M. The Dicke model in quantum optics: Dicke model revisited. Philos. Trans. R. Soc., A 2011, 369, 1137–1155. 10.1098/rsta.2010.0333. [DOI] [PubMed] [Google Scholar]
- Rokaj V.; Welakuh D. M.; Ruggenthaler M.; Rubio A. Light–matter interaction in the long-wavelength limit: no ground-state without dipole self-energy. J. Phys. B: At., Mol. Opt. Phys. 2018, 51, 034005. 10.1088/1361-6455/aa9c99. [DOI] [Google Scholar]
- Viehmann O.; von Delft J.; Marquardt F. Superradiant phase transitions and the standard description of circuit QED. Phys. Rev. Lett. 2011, 107, 113602. 10.1103/PhysRevLett.107.113602. [DOI] [PubMed] [Google Scholar]
- Sentef M. A.; Ruggenthaler M.; Rubio A. Cavity quantum-electrodynamical polaritonically enhanced electron–phonon coupling and its influence on superconductivity. Sci. Adv. 2018, 4, eaau6969. 10.1126/sciadv.aau6969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagenmüller D.; Schachenmayer J.; Genet C.; Ebbesen T. W.; Pupillo G. Enhancement of the Electron–Phonon Scattering Induced by Intrinsic Surface Plasmon–Phonon Polaritons. ACS Photonics 2019, 6, 1073–1081. 10.1021/acsphotonics.9b00268. [DOI] [Google Scholar]
- Power E. A.; Zienau S. Coulomb gauge in non-relativistic quantum electro-dynamics and the shape of spectral lines. Philos. Trans. R. Soc. London, Ser. A 1959, 251, 427–454. 10.1098/rsta.1959.0008. [DOI] [Google Scholar]
- Woolley R. Gauge invariant wave mechanics and the Power–Zienau–Woolley transformation. J. Phys. A: Math. Gen. 1980, 13, 2795. 10.1088/0305-4470/13/8/027. [DOI] [Google Scholar]
- Babiker M.; Loudon R. Derivation of the Power–Zienau–Woolley Hamiltonian in quantum electrodynamics by gauge transformation. Proc. R. Soc. London, Ser. A 1983, 385, 439–460. 10.1098/rspa.1983.0022. [DOI] [Google Scholar]
- Loudon R.The Quantum Theory of Light; Oxford Science Publications, 1988. [Google Scholar]
- Baxter C.; Babiker M.; Loudon R. Canonical approach to photon pressure. Phys. Rev. A: At., Mol., Opt. Phys. 1993, 47, 1278. 10.1103/PhysRevA.47.1278. [DOI] [PubMed] [Google Scholar]
- Lembessis V.; Babiker M.; Baxter C.; Loudon R. Theory of radiation forces and momenta for mobile atoms in light fields. Phys. Rev. A: At., Mol., Opt. Phys. 1993, 48, 1594. 10.1103/PhysRevA.48.1594. [DOI] [PubMed] [Google Scholar]
- Craig D.; Thirunamachandran T.. Molecular Quantum Electrodynamics: An Introduction to Radiation–Molecule Interactions; Dover Books on Chemistry Series; Dover Publications, 1998. [Google Scholar]
- Spohn H.Dynamics of Charged Particles and Their Radiation Field; Cambridge University Press, 2004. [Google Scholar]
- Vukics A.; Grießer T.; Domokos P. Elimination of the A-Square Problem from Cavity QED. Phys. Rev. Lett. 2014, 112, 073601. 10.1103/PhysRevLett.112.073601. [DOI] [PubMed] [Google Scholar]
- Todorov Y. Dipolar quantum electrodynamics theory of the three-dimensional electron gas. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 075115. 10.1103/PhysRevB.89.075115. [DOI] [Google Scholar]
- George J.; Chervy T.; Shalabney A.; Devaux E.; Hiura H.; Genet C.; Ebbesen T. W. Multiple Rabi Splittings under Ultrastrong Vibrational Coupling. Phys. Rev. Lett. 2016, 117, 153601. 10.1103/PhysRevLett.117.153601. [DOI] [PubMed] [Google Scholar]
- De Bernardis D.; Pilar P.; Jaako T.; De Liberato S.; Rabl P. Breakdown of gauge invariance in ultrastrong-coupling cavity QED. Phys. Rev. A: At., Mol., Opt. Phys. 2018, 98, 053819. 10.1103/PhysRevA.98.053819. [DOI] [Google Scholar]
- De Bernardis D.; Jaako T.; Rabl P. Cavity quantum electrodynamics in the nonperturbative regime. Phys. Rev. A: At., Mol., Opt. Phys. 2018, 97, 043820. 10.1103/PhysRevA.97.043820. [DOI] [Google Scholar]
- Andrews D. L.; Jones G. A.; Salam A.; Woolley R. G. Perspective: Quantum Hamiltonians for optical interactions. J. Chem. Phys. 2018, 148, 040901. 10.1063/1.5018399. [DOI] [PubMed] [Google Scholar]
- Di Stefano O.; Settineri A.; Macrì V.; Garziano L.; Stassi R.; Savasta S.; Nori F. Resolution of gauge ambiguities in ultrastrong-coupling cavity quantum electrodynamics. Nat. Phys. 2019, 15, 803–808. 10.1038/s41567-019-0534-4. [DOI] [Google Scholar]
- Hernández F.; Herrera F.. Multi-level quantum Rabi model for anharmonic vibrational polaritons. arXiv (Physics.Chemical Physics), June 11, 2019, 1906.04374, ver. 1. https://arxiv.org/abs/1906.04374 (accessed 2019-11-20). [DOI] [PubMed]
- Li J.; Golez D.; Mazza G.; Millis A.; Georges A.; Eckstein M.. Electromagnetic coupling in tight-binding models for strongly correlated light and matter. arXiv (Condensed Matter.Strongly Correlated Electrons), January 27, 2020, 2001.09726, ver. 1. https://arxiv.org/abs/2001.09726 (accessed 2019-11-20).
- Flick J.; Ruggenthaler M.; Appel H.; Rubio A. Kohn-Sham approach to quantum electrodynamical density-functional theory: Exact time-dependent effective potentials in real space. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 15285–15290. 10.1073/pnas.1518224112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baez J. C.; Segal I. E.; Zhou Z.. Introduction to Algebraic and Constructive Quantum Field Theory; Princeton University Press, 1992. [Google Scholar]
- Cohen-Tannoudji C.; Dupont-Roc J.; Grynberg G.. Photons and Atoms: Introduction to Quantum Electrodynamics; Wiley-VCH, 1997. [DOI] [PubMed] [Google Scholar]
- Salam A.Molecular Quantum Electrodynamics: Long-Range Intermolecular Interactions; Wiley, 2010. [Google Scholar]
- Bach V.; Fröhlich J.; Sigal I. M. Spectral Analysis for Systems of Atoms and Molecules Coupled to the Quantized Radiation Field. Commun. Math. Phys. 1999, 207, 249–290. 10.1007/s002200050726. [DOI] [Google Scholar]
- Dereziński J.; Jakšić V. Spectral Theory of Pauli–Fierz Operators. J. Funct. Anal. 2001, 180, 243–327. 10.1006/jfan.2000.3681. [DOI] [Google Scholar]
- Hidaka T.; Hiroshima F. Pauli–Fierz model with Kato-class potentials and exponential decays. Rev. Math. Phys. 2010, 22, 1181–1208. 10.1142/S0129055X10004181. [DOI] [Google Scholar]
- Gersten A. Maxwell’s Equations as the One-Photon Quantum Equation. Found. Phys. Lett. 1999, 12, 291–298. 10.1023/A:1021648704289. [DOI] [Google Scholar]
- Keller O.Quantum Theory of Near-Field Electrodynamics; Springer, 2011. [Google Scholar]
- Greiner W.; Reinhardt J.. Field Quantization; Springer, 1996. [Google Scholar]
- Faisal F. H.Theory of Multiphoton Processes; Springer, 1987. [Google Scholar]
- Rokaj V.; Penz M.; Sentef M. A.; Ruggenthaler M.; Rubio A. Quantum Electrodynamical Bloch Theory with Homogeneous Magnetic Fields. Phys. Rev. Lett. 2019, 123, 047202. 10.1103/PhysRevLett.123.047202. [DOI] [PubMed] [Google Scholar]
- Forbes K. A.; Bradshaw D. S.; Andrews D. L. Identifying diamagnetic interactions in scattering and nonlinear optics. Phys. Rev. A: At., Mol., Opt. Phys. 2016, 94, 033837. 10.1103/PhysRevA.94.033837. [DOI] [Google Scholar]
- Forbes K. A. Role of magnetic and diamagnetic interactions in molecular optics and scattering. Phys. Rev. A: At., Mol., Opt. Phys. 2018, 97, 053832. 10.1103/PhysRevA.97.053832. [DOI] [Google Scholar]
- Stefanucci G.; van Leeuwen R.. Nonequilibrium Many-Body Theory of Quantum Systems: A Modern Introduction; Cambridge University Press, 2013. [Google Scholar]
- Todorov Y.; Andrews A. M.; Colombelli R.; De Liberato S.; Ciuti C.; Klang P.; Strasser G.; Sirtori C. Ultrastrong Light–Matter Coupling Regime with Polariton Dots. Phys. Rev. Lett. 2010, 105, 196402. 10.1103/PhysRevLett.105.196402. [DOI] [PubMed] [Google Scholar]
- Thomas A.; Devaux E.; Nagarajan K.; Chervy T.; Seidel M.; Hagenmüller D.; Schütz S.; Schachenmayer J.; Genet C.; Pupillo G.; Ebbesen T. W.. Exploring Superconductivity under Strong Coupling with the Vacuum Electromagnetic Field. arXiv (Condensed Matter.Superconductivity), December 19, 2019, 1911.01459, ver. 2. https://arxiv.org/abs/1911.01459 (accessed 2019-11-20).
- Pellegrini C.; Flick J.; Tokatly I. V.; Appel H.; Rubio A. Optimized Effective Potential for Quantum Electrodynamical Time-Dependent Density Functional Theory. Phys. Rev. Lett. 2015, 115, 093001. 10.1103/PhysRevLett.115.093001. [DOI] [PubMed] [Google Scholar]
- Chikkaraddy R.; de Nijs B.; Benz F.; Barrow S. J.; Scherman O. A.; Rosta E.; Demetriadou A.; Fox P.; Hess O.; Baumberg J. J. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016, 535, 127–130. 10.1038/nature17974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baranov D. G.; Wersäll M.; Cuadra J.; Antosiewicz T. J.; Shegai T. Novel nanostructures and materials for strong light–matter interactions. ACS Photonics 2018, 5, 24–42. 10.1021/acsphotonics.7b00674. [DOI] [Google Scholar]
- Schäfer C.; Ruggenthaler M.; Rubio A. Ab initio nonrelativistic quantum electrodynamics: Bridging quantum chemistry and quantum optics from weak to strong coupling. Phys. Rev. A: At., Mol., Opt. Phys. 2018, 98, 043801. 10.1103/PhysRevA.98.043801. [DOI] [Google Scholar]
- Knight J. M.; Aharonov Y.; Hsieh G. T. C. Are super-radiant phase transitions possible?. Phys. Rev. A: At., Mol., Opt. Phys. 1978, 17, 1454–1462. 10.1103/PhysRevA.17.1454. [DOI] [Google Scholar]
- Vukics A.; Grießer T.; Domokos P. Fundamental limitation of ultrastrong coupling between light and atoms. Phys. Rev. A: At., Mol., Opt. Phys. 2015, 92, 043835. 10.1103/PhysRevA.92.043835. [DOI] [Google Scholar]
- Sánchez Muñoz C.; Nori F.; De Liberato S. Resolution of superluminal signalling in non-perturbative cavity quantum electrodynamics. Nat. Commun. 2018, 9, 1924. 10.1038/s41467-018-04339-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stokes A.; Nazir A. Gauge ambiguities imply Jaynes–Cummings physics remains valid in ultrastrong coupling QED. Nat. Commun. 2019, 10, 499. 10.1038/s41467-018-08101-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chruscinski D. Quantum mechanics of damped systems. J. Math. Phys. 2003, 44, 3718. 10.1063/1.1599074. [DOI] [Google Scholar]
- Buchholz F.; Theophilou I.; Nielsen S. E.; Ruggenthaler M.; Rubio A. Reduced density-matrix approach to strong matter-photon interaction. ACS Photonics 2019, 6, 2694–2711. 10.1021/acsphotonics.9b00648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antončík E. On the theory of temperature shift of the absorption curve in non-polar crystals. Czech. J. Phys. 1955, 5, 449–461. 10.1007/BF01687209. [DOI] [Google Scholar]
- Gonze X.; Boulanger P.; Côté M. Theoretical approaches to the temperature and zero-point motion effects on the electronic band structure. Ann. Phys. 2011, 523, 168–178. 10.1002/andp.201000100. [DOI] [Google Scholar]
- Power E.; Thirunamachandran T. Quantum electrodynamics in a cavity. Phys. Rev. A: At., Mol., Opt. Phys. 1982, 25, 2473. 10.1103/PhysRevA.25.2473. [DOI] [Google Scholar]
- Jestädt R.; Ruggenthaler M.; Oliveira M. J. T.; Rubio A.; Appel H. Light-matter interactions within the Ehrenfest–Maxwell–Pauli–Kohn–Sham framework: fundamentals, implementation, and nano-optical applications. Adv. Phys. 2019, 68 (4), 225–333. 10.1080/00018732.2019.1695875. [DOI] [Google Scholar]
- Rossi T. P.; Shegai T.; Erhart P.; Antosiewicz T. J. Strong plasmon-molecule coupling at the nanoscale revealed by first-principles modeling. Nat. Commun. 2019, 10, 3336. 10.1038/s41467-019-11315-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casimir H. B.; Polder D. The influence of retardation on the London-van der Waals forces. Phys. Rev. 1948, 73, 360. 10.1103/PhysRev.73.360. [DOI] [Google Scholar]
- Salam A. On the contribution of the diamagnetic coupling term to the two-body retarded dispersion interaction. J. Phys. B: At., Mol. Opt. Phys. 2000, 33, 2181. 10.1088/0953-4075/33/12/302. [DOI] [Google Scholar]
- Climent C.; Galego J.; Garcia-Vidal F. J.; Feist J. Plasmonic Nanocavities Enable Self-Induced Electrostatic Catalysis. Angew. Chem., Int. Ed. 2019, 58, 8698–8702. 10.1002/anie.201901926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Englman R.; Ruppin R. Optical lattice vibrations in finite ionic crystals: III. J. Phys. C: Solid State Phys. 1968, 1, 1515. 10.1088/0022-3719/1/6/307. [DOI] [Google Scholar]
- Brako R.; Hrnčević J.; Šunjić M. Curvature dependence of surface phonon and plasmon frequencies. Z. Phys. B: Condens. Matter Quanta 1975, 21, 193–201. 10.1007/BF01322251. [DOI] [Google Scholar]
- Alpeggiani F.; Andreani L. C. Quantum theory of surface plasmon polaritons: planar and spherical geometries. Plasmonics 2014, 9, 965–978. 10.1007/s11468-014-9703-6. [DOI] [Google Scholar]
- Ebbesen T. W. Hybrid Light–Matter States in a Molecular and Material Science Perspective. Acc. Chem. Res. 2016, 49, 2403–2412. 10.1021/acs.accounts.6b00295. [DOI] [PubMed] [Google Scholar]
- George J.; Shalabney A.; Hutchison J. A.; Genet C.; Ebbesen T. W. Liquid-Phase Vibrational Strong Coupling. J. Phys. Chem. Lett. 2015, 6, 1027–1031. 10.1021/acs.jpclett.5b00204. [DOI] [PubMed] [Google Scholar]
- Thomas A.; Lethuillier-Karl L.; Nagarajan K.; Vergauwe R. M. A.; George J.; Chervy T.; Shalabney A.; Devaux E.; Genet C.; Moran J.; Ebbesen T. W. Tilting a ground-state reactivity landscape by vibrational strong coupling. Science 2019, 363, 615–619. 10.1126/science.aau7742. [DOI] [PubMed] [Google Scholar]
- Damari R.; Weinberg O.; Krotkov D.; Demina N.; Akulov K.; Golombek A.; Schwartz T.; Fleischer S. Strong coupling of collective intermolecular vibrations in organic materials at terahertz frequencies. Nat. Commun. 2019, 10, 3248. 10.1038/s41467-019-11130-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson Y.; Hult E.; Rydberg H.; Apell P.; Lundqvist B. I.; Langreth D. C.. Electronic Density Functional Theory; Springer, 1998; pp 243–260. [Google Scholar]
- Engel E.; Dreizler R.. Density Functional Theory: An Advanced Course; Theoretical and Mathematical Physics; Springer, 2011. [Google Scholar]
- Li X.; Bamba M.; Zhang Q.; Fallahi S.; Gardner G. C.; Gao W.; Lou M.; Yoshioka K.; Manfra M. J.; Kono J. Vacuum Bloch–Siegert shift in Landau polaritons with ultra-high cooperativity. Nat. Photonics 2018, 12, 324–329. 10.1038/s41566-018-0153-0. [DOI] [Google Scholar]
- Paravicini-Bagliani G. L.; Appugliese F.; Richter E.; Valmorra F.; Keller J.; Beck M.; Bartolo N.; Rössler C.; Ihn T.; Ensslin K.; Ciuti C.; Scalari G.; Faist J. Magneto-transport controlled by Landau polariton states. Nat. Phys. 2019, 15, 186–190. 10.1038/s41567-018-0346-y. [DOI] [Google Scholar]
- Schwartz L. Sur l’impossibilite de la multiplication des distributions. C. R. Hebd. Seances Acad. Sci. 1954, 239, 847–848. [Google Scholar]
- Colombeau J. F.Elementary Introduction to New Generalized Functions; North-Holland Mathematics Studies, Vol. 113; North-Holland, 1985; p 103. [Google Scholar]
- Thirring W.Quantum Mathematical Physics: Atoms, Molecules and Large Systems; Springer Science & Business Media, 2013. [Google Scholar]
- Arai A.; Hirokawa M. On the existence and uniqueness of ground states of a generalized spin-boson model. J. Funct. Anal. 1997, 151, 455–503. 10.1006/jfan.1997.3140. [DOI] [Google Scholar]