Automatic Lumbar Spine Tracking Based on Siamese Convolutional Network

Abstract

Deep learning has demonstrated great success in various computer vision tasks. However, tracking the lumbar spine by digitalized video fluoroscopic imaging (DVFI), which can quantitatively analyze the motion mode of the spine to diagnose lumbar instability, has not yet been well developed due to the lack of steady and robust tracking method. The aim of this work is to automatically track lumbar vertebras with rotated bounding boxes in DVFI sequences. Instead of distinguishing vertebras using annotated lumbar images or sequences, we train a full-convolutional siamese neural network offline to learn generic image features with transfer learning. The siamese network is trained to learn a similarity function that compares the labeled target from the initial frame with the candidate patches from the current frame. The similarity function returns a high score if the two images depict the same object. Once learned, the similarity function is used to track a previously unseen object without any adapting online. Our tracker is performed by evaluating the candidate rotated patches sampled around the previous target’s position and presents rotated bounding boxes to locate the lumbar spine from L1 to L4. Results indicate that the proposed tracking method can track the lumbar vertebra steadily and robustly. The study demonstrates that the lumbar tracker based on siamese convolutional network can be trained successfully without annotated lumbar sequences.

Introduction

Lumbar spine instability, which is most likely related to the large number of patients with chronic low back pain, has been widely discussed [1–3]. Due to the characteristic change of lumbar instability, such as displacement and shaking compared with normal subjects, medical imaging technology has been used as an important diagnostic tool in clinical practice [4–6]. With the developing of medical technology, DVFI has been recommended for data acquisition of spine motion [7]. DVFI presents continuous imaging for the analysis of lumbar vertebra motion. Tracking the lumbar spine motion by DVFI, which can quantitatively analyze the motion mode of the spine to diagnose lumbar instability, has drawn great attention recently.

This paper presents a siamese convolutional neural network [8] with transfer learning to track the lumbar spine from L1 to L4. The strength of our method is that it does not require manually annotated lumbar spine training data. First, two convolutional network branches are trained on a recognized video dataset to learn generic representations. Siamese network is trained to learn a similarity function that compares the similarity between the contrast image and search images. Our tracker returns the high similarity value in the score map containing the position and rotation information. Second, it needs no online training and evaluates once in the larger search regions instead of several image patches. Third, by evaluating the search regions with different rotation transformation and adding a motion window, it can locate the lumbar spine precisely. The experiment shows that our method can receive a better accuracy than others.

The organization of this paper is scheduled as follow. In the “Related Works” section, we discuss previous related work on lumbar detection and tracking. The details of our proposed tracking lumbar method are introduced in the “Method” section. Experiment results tested on DVFI dataset and discussion are arranged in the “Experiment and Discussion” section. Finally, the conclusion is proposed in the “Conclusion” section.

Related Works

Several researches focus on automatically detect or track vertebras [9–12]. In previous studies, algorithms with support vector machine, classification forests, and other feature extraction methods show great performance on lumbar detection and tracking. ASBPF [4] utilizing a particle filter locates the vertebra-of-interest in every frame of the sequence. Based on automatic corner points of interest, Benjelloun et al. [10] develop an x-ray image segmentation approach to identify the location and the orientation of the cervical vertebrae. By combining local image features and semiglobal geometrical information, Oktay et al. [13] proposed a Markov-chain-like graphical model for localizing and labeling the lumbar vertebrae.

With the great power of feature representation, deep learning has been widely used in the tracking problem. DCIR [14] train a stacked denoising autoencoder offline to learn generic image features and train a classification neural network to track the target. TGPR [15] track object by using deep learning with Gaussian processes regression. The vector siamese convolutional network is introduced to track objects in [16]. Deep learning has also attracted great attention in medical image area [17]. Masudur et al. [13] proposed a novel shape-aware deep segmentation network to segment the vertebrae in x-ray image. Kim et al. [18] use annotated bounding boxes lumbar images to train networks for detecting lumbar vertebras. Han et al. [19] train the convolutional neural network (CNN) to segment cervical or lumbar vertebras with fully segmented lumbar images. Wang et al. [20] propose a siamese deep neural network approach comprising three identical subnetworks for multi-resolution analysis and detection of spinal metastasis.

However, most recent studies require fully segmented training data or annotated vertebras in the form of bounding boxes. Due to the lack of lumbar dataset with segmented labels or bounding boxes, lumbar tracker based on the deep learning is somewhat restricted on the accuracy of location [21]. Compared with these algorithms, our method does not require manually annotated lumbar spine training data. We train a siamese network with transfer learning to compare the similarity between the contrast image and search images. Furthermore, the lumbar is located with rotated bounding boxes for accurate tracking information.

Method

Method Overview

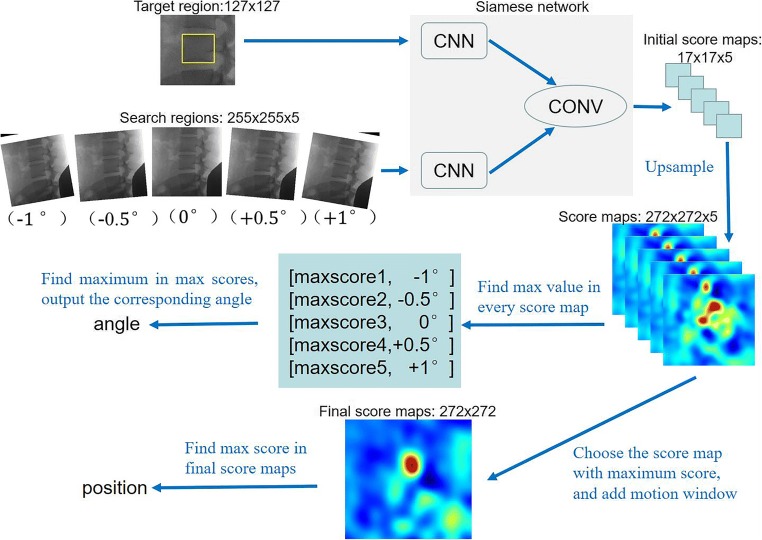
In this section, we describe our siamese network to track object directly from two image patches. The network input searches regions with different rotations from the current frame and a target region from the first frame and outputs the location and rotation angle of the predicted target, as shown in Fig. 1.

Fig. 1.

Our network architecture for tracking the spine motion. Net-A and Net-B share the parameters of the convolutional network and extract generic features to compare with each other, where the symbol “⊗” denotes a convolutional operation. The location and rotation angle of the target can be predicted by the index of the maximum in the final score map and score map respectively

Network Architecture

The architecture of our siamese network consists of two same CNN, named as Net-A and Net-B, as shown in Fig. 1. Both Net-A and Net-B share the same parameters of convolutional filters in order to reduce computation burden. In this model, we input the labeled target region and search region into Net-A and Net-B, respectively, which extract the high-level representations from the two image patches. Since our goal is to compare the labeled object with search regions, we need to compute the similarity of the two features maps result from two networks. To achieve this, the output of Net-A is used as a convolutional kernel to convolve with the feature maps result from Net-B.

In detail, the convolutional layers in our model, which is similar to the convolutional stage of the network of Krizhevsky et al. [22], consist of five convolutional layers and two max pooling layers. ReLU non-linearities follow every convolutional layer except for the fifth convolutional layer. The more detailed network settings is shown in Table 1.

Table 1.

Architecture of our convolutional network. Each network flow consists of 5 convolutional layers and 2 max pooling layers. The RELU activation function is used in all convolutional layers excluding the “conv5” layer

Layer	Filter	Stride	Net-A	Net-B
Input			127 × 127	255 × 255
Conv1	11 × 11	2	59 × 59 × 96	123 × 123 × 5
Pool1	3 × 3	2	29 × 29 × 96	61 × 61 × 5
Conv2	5 × 5	1	25 × 25 × 256	57 × 57 × 5
Pool2	3 × 3	2	12 × 12 × 256	28 × 28 × 5
Conv3	3 × 3	1	10 × 10 × 192	26 × 26 × 5
Conv4	3 × 3	1	8 × 8 × 192	24 × 24 × 5
Conv5	3 × 3	1	6 × 6 × 128	22 × 22 × 5

Input and Output

Overall, our siamese network is trained to learn the similarity between two image patches and successively output the location of the highest score. To find where the target object is located in a new frame, we need to prepare a true tracking target and some candidate patches for the network to compare.

Because of the fixed input size of our network, we crop and resize the image patch using bicubic interpolation. As the tracking target is labeled as a bounding box in the first frame, we crop and scale an image patch centered at the labeled object, as shown in Fig. 1. This crop is padded to allow the siamese network to receive some contextual information surrounding the object. Since objects tend to move smoothly through space between adjacent frames, we crop a larger search region X centered at the previous frame target location in the current frame. As long as the object is not moving too fast, it is very likely that the target will be located in the search region. If the size of target’s bounding box is denoted as (w, h), we crop the target region centering on the initial frame with size A × A which is defined as follows:

$$\left(w+p\right)\times \left(h+p\right)=A^2$$ 1

where p represents the padding which is equal to (w + h)/2. It is resized to 127 × 127 afterwards. In the same way, the search region is cropped on the current frame with double the size of the target region, and then resized in 255 × 255.

The network outputs score maps in which the coordinate of highest score locates the predicted target object. Note that the output of the network is not a single score or a vector but a score map as illustrated in Fig. 1. To achieve more accurate localization, we upsample the score map using bicubic interpolation with the magnification U. On the basis that the search region is center at the previous target position (x_t − 1, y_t − 1), the displacement $\stackrel{\rightharpoonup }{D}$ that the coordinate of the highest score relative to the center of search region, divided by the upsample magnificationU, multiplied by the stride of the network S, gives the new target position (x_t, y_t):

$$\left(x_t,y_t\right)=\left(x_{t-1},y_{t-1}\right)+\stackrel{\rightharpoonup }{D}/U\times S,$$ 2

Angle Estimation

In order to predict the rotated angle of the lumbar spine, our tracker evaluates the multiple rotations once by assembling a mini-batch of rotated regions. In detail, assume our tracker predicts the lumbar spine located in a rotated bounding box center at (x_t − 1, y_t − 1) with a width of W, a height of H, and an angle of α in the frame t − 1. In the next frame t, we crop a search region X_t center at (x_t − 1, y_t − 1). To get rotation information precisely, we generate a set of new search regions X_R = {X_t, T_αX_t} by rotating transformations, where $T_{\alpha }=\left\{T_{{\alpha }_1},T_{{\alpha }_2},\cdots ,T_{{\alpha }_K}\right\}$ is a family of K rotation transformations with $T_{{\partial }_k}$ denoting the rotation operation with the angle of α_k ∈ α, k = 1, …, K. Mathematically, each search region is associated with an (α), where α is the rotation angle. Similarly, the tracked object is determined by:

$$\left(x_t,y_t,{\alpha }_t\right)=\underset{x,y,\alpha }{argmax}{M}_k,\left(k=1,\dots ,K\right)$$ 3

where K is the number of search regions and also the number of core maps, and Mis the score map. (x_t, y_t) gives the center location of the tracked object and α_t gives the rotation angle.

As shown in Fig. 2, the target region and search regions are transferred into feature maps by CNN. Then, initial score maps are generated through a convolutional operation, which denote as conv. As we mentioned above, we upsample the initial score map using bicubic interpolation to obtain location and angle precisely. If target region and search regions are set as 127 × 127 × 1 and 255 × 255 × 5respectively, the score maps will be generated as 272 × 272 × 5. Note that five score maps correspond to the five search regions. We discover that the response score is dramatically increased when the target has the same orientation in the target region as in the search region. In this example, the highest response score in the map with (− 0.5°) is significantly higher than the top values in other maps.

Fig. 2.

Example of illustrating the rotated angle and position estimation

Loss Function

Assuming an image pair of target patch z and search patch x input the siamese network, the network will produce a map of scores g. Training positive and negative pairs with the ground-truth label y ∈ {+1, −1}, we adopt the logistic loss to define the whole loss of our network:

$$L\left(y,g\right)=\frac{1}{\mid M\mid }\sum _{m,n\in M}log\left(1+exp\left(-y_{\left(m,n\right)}{g}_{\left(m,n\right)}\right)\right),$$ 4

where g_(m, n) is the score of a single image pair and y_(m, n) ∈ {+1, −1} is its ground-truth label for each position (m, n) ∈ M in the score map. To obtain the parameters of network W, we apply Stochastic gradient descent (SGD) to the problem:

$$arg\underset{W}{min}\underset{\left(z,x,y\right)}{E}L\left(y,f\left(z,x;W\right)\right)$$ 5

Motion Window

Object targets tend to move smoothly through space between the adjacent frame. As long as the object is not moving too fast, the tracker should predict that the object will be located near the previous location. Considering the lumbar spine motion sequences with the attributes of in-plane rotation and scale invariation where the object size is fixed, we can further utilize the object’s motion information of previous status. That is to say, only the displacement and rotation are taken into consideration in our model. Inspired by the success of bounding-box regression model in [23], we model the frame t bounding box center (x_t, y_t) in the relative to the frame t − 1 bounding box center (x_t − 1, y_t − 1) as

$$x_t=x_{t-1}+w\cdot \mathit{\Delta x},$$ 6

$$y_t=y_{t-1}+h\cdot \mathit{\Delta y},$$ 7

where wand h are the width and height of the bounding box of the frame t − 1. The terms ∆x and ∆y denote the displacement of the bounding box relative to its width and height. In our training set, we discover that objects’ displacement can be modeled with a Gaussian distribution. We further introduce a motion window with the object’s motion information to increase the stability of our tracker. The motion window is added to the score map to encourage small motions and penalize large motions. In this paper, we model the motion window as follow:

$$G\left(\theta \right)=exp\left(-\frac{{\left(\theta -u\right)}^2}{2{\sigma }^2}\right),$$ 8

where G(θ) is the Gaussian distribution, and $u=\left(\frac{\mathit{\Delta x}}{2}\right),\left(\frac{\mathit{\Delta y}}{2}\right)$, σ = 50 in our experiments. And (Δx, Δy) denotes the displacement of the predicted target in previous frame.

Experiment and Discussion

DVFI Dataset

Our DVFI dataset comes from Department of Orthopedics Traumatology of Hong Kong University. The DVFI dataset consists of 47 sequences, about 14,000 frames with manual labeled rotated bounding box from L1 to L4, ranging from different age groups. Each frame contains 642 × 575 × 1 pixels. We use this dataset as a benchmark to test our proposed tracking algorithm with other state-of-art methods.

Experiment Setup

Training

We pick image pairs from the ImageNet Video dataset (ILSVRC) [24] by choosing frames with a small interval and performing crop procedure as described in Section 2.3. The target region and the search region are extracted from two frames of the same video. During training, the class of the object is ignored, and the scale of the object within each image are normalized. To train our network to be sensitive to rotation attribute, the rotation of the object within each image is forbidden. To handle the gray videos in our DVFI dataset, all the pairs are converted to grayscale during training.

In detail, our training videos come from ILSVRC [24] excluding the videos with the attributes of in-plane rotation, leading to a total of 65,000 frames. For each video, we choose each pair of frames within the nearest 30 frames and fed the cropped pair of target patches of 2× padding size to the network. The cropped target patches are resized to 127 × 127, and the cropped search patches are resized to 255 × 255. We apply SGD with momentum of 0.9 to train the network and set the weight decay γ to 0.0005; the learning rate is set to 1e−5. The model is trained for 20 epochs with a mini-batch size of 16.

Tracking

Considering the lumbar spine motion sequences with the attributes of in-plane rotation and scale invariation, we set the search regions of Net-B with different rotations and without scale variation. As we mentioned earlier, the initial object appearance computed once in the first frame is compared to a larger search region of the subsequent frames. We upsample the initial score map using bicubic interpolation with the magnification 16, from 17 × 17 to 272 × 272. A motion window is added to the score map for increasing the stability of our tracker. To handle rotation variations, we also search for the object over seven rotation transformations {‐2^o, −1^o, −0.5^o, 0, 0.5^o, 1^o, 2^o} based on the previous target status.

The proposed algorithm is implemented in MATLAB with MatConvNet [22]. All experiments are conducted on a machine with Intel Core i5-3470 at 3.2 GHz, 16 GB RAM, and a single NVIDIA GeForce GTX 1070 GPU. Our online tracking method operates at 31 FPS, when searching 7 rotations. This is because no backpropagation needed in our network when tracking.

Results and Evaluation

Since the DVFI dataset labeling includes the horizontal coordinate x, the vertical coordinate y, and the rotation angle α of the spine center, we utilize three tracking errors as the accuracy criterion. The tracking error Δω in a frame is defined as:

$$\mathit{\Delta \omega }={\omega }_m-{\omega }_{\mathit{gt}}$$ 9

where ω represents x, y, or α. Moreover, ω_m and ω_gt denote the ω from tracking algorithm and manually labeled results, respectively.

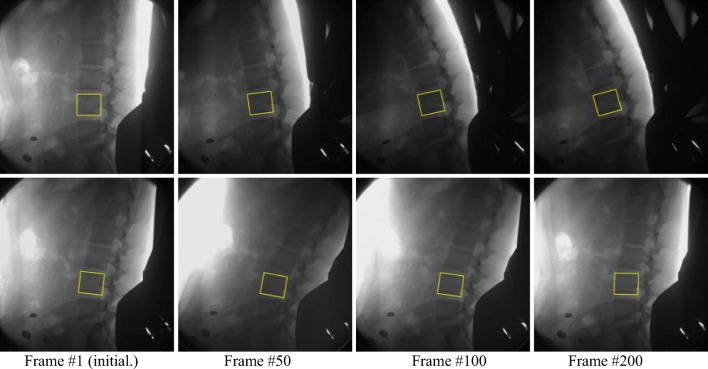
The results of our proposed method tracking one lumbar in two DVFI sequences are shown in Fig. 3. The tracked lumbar vertebrae targets are marked in the first frame to obtain their original status. Our tracker is robust to challenging situations of the lumbar spine motion by DVFI like cluttered background (row 1), illumination change (row 2), and the scenes with in-plane rotation (row 1, 2) in Fig. 3. Since the model is never updated online, thus the network outputs high scores for all the patches that are similar to the first appearance of the target.

Fig. 3.

Snapshots of our proposed method to track one lumbar. The snapshots have been taken at fixed frames (1, 50, 100, and 200) and the tracker is never re-initialized

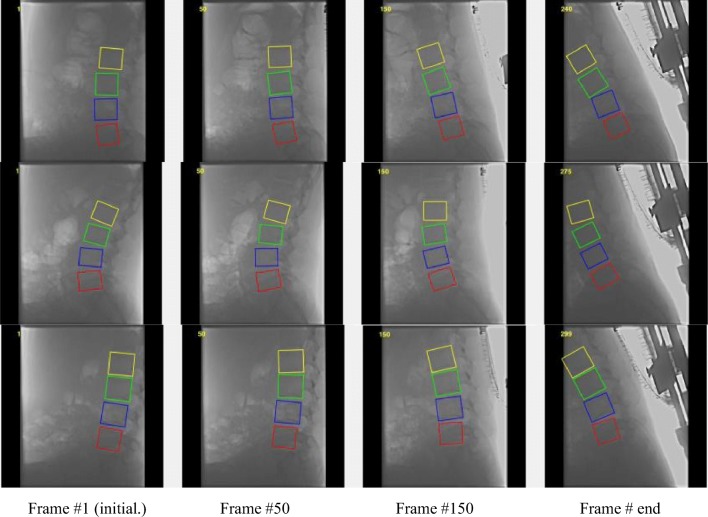
To analyze accuracy error, our tracking accuracy results in an example sequence by manual measurement is reported in Fig. 4. The tracking error in x- or y-direction shows the position pixel error at lumbar spine center from L1 to L4. And the tracking error in rotation angle, which the unit of vertical coordinate is π/360, represents the rotation angle error. It is obvious to see that the curve amplitude of the tracking for L3 is the largest of the tracked lumbar vertebrae. Despite this, the error is no more than three pixels in the x- or y-direction and the angle of 1°which is π/360. Furthermore, the tracking results of our method to locate lumbar from L1 to L4 is shown in Fig. 5. It proves that our proposed method can track the spine motion robustly in the example sequences.

Fig. 4.

Our tracking accuracy results in an example sequence. They are tracking error in x-direction, y-direction, and rotation angle, respectively

Fig. 5.

The tracking result of our proposed method to locate lumbar from L1 to L4 in three sequences from the DVFI dataset (the lumbar L1, L2, L3, and L4 represent the yellow, green, blue, and red color bounding box, respectively)

To further analyze performance, we evaluated our method with other three state-of-art trackers, ASBPF [4], DCIR [14], and TGPR [15] on the DVFI dataset benchmark. As mentioned above, our DVFI dataset consists of 47 sequences, about 14,000 frames. It is a common way to evaluate trackers which run them throughout test sequences with initialization from the ground truth in the first frame and calculate the average precision error. Table 2 shows the mean and variance of the tracking error by four tracking algorithms testing in our DVFI dataset. Due to DCIR [14] being not able to output the rotated bounding box, the angle accuracy of DCIR [14] is vacancy. As can be seen in Table 2, our tracker outperforms the other three algorithms on all accuracy criterion. In terms of displacement tracking error, our mean error is almost less than 2 pixels. We note that the mean error and variance dramatically increase when tracking failure occurs. It can be seen in the L4 mean error of TGPR [15] and L1 mean error of DCIR [14], which exceed one hundred pixels. For rotation angle error, our mean angle error is slightly more than 0.5° except that the mean angle error of L3 lumbar is 0.621. It is probably because the minimum rotation transformation is 0.5° in our search region rotating transformation stage.

Table 2.

Accuracy comparison with other algorithms

Methods	Lumbar name	Mean ± variance
		X-direction	Y-direction	Angle
Ours	L1	1.3 ± 2.04	− 1.23 ± 2.09	− 0.537 ± 0.60
	L2	− 1.27 ± 2.09	− 1.5 ± 2.08	− 0.516 ± 0.49
	L3	− 1.82 ± 3.17	− 2.08 ± 3.57	0.621 ± 0.47
	L4	− 1. 2 ± 1.04	− 1. 4 ± 1.04	− 0.509 ± 0.38
ASBPF [4]	L1	8.295 ± 705.88	17.494 ± 145.33	− 0.145 ± 0.02
	L2	23.041 ± 114.42	9.770 ± 52.30	1.474 ± 1.72
	L3	22.096 ± 37.48	0.409 ± 109.38	1.601 ± 2.16
	L4	− 9.301 ± 120.58	− 3.298 ± 121.21	2.739 ± 1.13
DCIR [23]	L1	118.931 ± 6990.6	1.558 ± 99.83	–
	L2	71.498 ± 4292.8	12.480 ± 248.12	–
	L3	52.248 ± 2061.7	13.919 ± 169.14	–
	L4	40.493 ± 1161.4	17.364 ± 338.92	–
TGPR [24]	L1	3.011 ± 5.71	− 3.785 ± 2.88	− 0.310 ± 0.33
	L2	2.549 ± 7.34	− 2.663 ± 3.14	1.662 ± 0.16
	L3	− 2.487 ± 2.11	− 4.124 ± 4.22	1.944 ± 0.44
	L4	− 260.051 ± 229.50	− 255.042 ± 217.30	1.997 ± 0.52

In order to explore the rotation angle limits of our tracker, we also test another 2 settings:{‐1^o ‐ 0.75^o, −0.5^o, −0.25^o, 0, 0.25^o, 0.5^o, 0.75^o, 1^o} and {−1^o, −0.3^o, −0.2^o, −0.1^o, 0, 0.1^o, 0.2^o, 0.3^o, 1^o} of the search region rotating transformations. However, it seems to be that the mean angle error does not decrease with the rotation transforming more precisely. It is probably because our training set is not enough for training CNN to distinguish the minimal scale rotation. We will study this problem by choosing the training set selectively in future work.

Conclusion

In this work, we proposed a siamese convolutional network for tracking the motion of the lumbar spine. The siamese convolutional network reformulates the tracking problem as similarity measurement between target and search regions. Once learned, the similarity measurement can be used to track a previously unseen object. Due to this, the proposed lumbar tracking method based on siamese network can be trained successfully without annotated lumbar spine sequences. By evaluating a mini-batch of rotated search regions, our tracker predicts the rotated angle of the lumbar spine robustly and preciously. The experiment results show that the proposed method can achieve an outstanding performance.