Sex differences in adult lifespan and aging rates of mortality across wild mammals

Significance

In human populations, women live longer than men. While it is commonly assumed that this pattern of long-lived females vs. short-lived males constitutes the rule in mammals, the magnitude of the sex differences in lifespan and increase of mortality rate with advancing age remain to be quantified. Here, we demonstrate that, in the wild, mammalian females live longer than males but we did not detect any sex differences in aging rates. Contrary to a widespread hypothesis, we reveal that sex differences in life history strategies do not detectably influence the magnitude of sex differences in either lifespan or aging rates. Instead, our findings suggest these differences are predominantly shaped by complex interactions between local environmental conditions and sex-specific reproductive costs.

Abstract

In human populations, women consistently outlive men, which suggests profound biological foundations for sex differences in survival. Quantifying whether such sex differences are also pervasive in wild mammals is a crucial challenge in both evolutionary biology and biogerontology. Here, we compile demographic data from 134 mammal populations, encompassing 101 species, to show that the female’s median lifespan is on average 18.6% longer than that of conspecific males, whereas in humans the female advantage is on average 7.8%. On the contrary, we do not find any consistent sex differences in aging rates. In addition, sex differences in median adult lifespan and aging rates are both highly variable across species. Our analyses suggest that the magnitude of sex differences in mammalian mortality patterns is likely shaped by local environmental conditions in interaction with the sex-specific costs of sexual selection.

In all countries worldwide, women live on average a longer life than men (1–3). This pattern of longer-lived women is consistent from the mid-18th century (when the first accurate birth records became available) until now (2, 4) and explains why about 90% of supercentenarians (i.e., people reaching 110 y old or more) are women. While social factors reinforce the gender gap in longevity (1), the greater survival prospects of women over men are observed even when both sexes share the same social habits (5). The female advantage in lifespan has thus been labeled as one of the most robust features of human biology (2). How much sexes differ in mortality patterns is a question of paramount importance associated with striking economical and biomedical implications (6, 7). Indeed, men and women show differences in the dynamics of age-associated diseases, which are currently increasing in prevalence due to a growing aging population (8).

It is usually assumed that female mammals generally live longer than males (9, 10). However, this belief is driven by studies performed across human populations, a small number of case studies on wild mammals, or records of mammals housed in captivity (11), where lifespan and aging patterns are often not representative of conspecifics in the wild (12). Identifying the evolutionary mechanisms underlying sex-specific mortality requires a thorough overview of the sex differences in lifespan across mammals in the wild, which has been lacking to date.

Dissimilarities in sex-chromosome content (i.e., heterogametic sex hypothesis) and asymmetric inheritance of mitochondrial DNA (i.e., the mother’s curse hypothesis) have been proposed to explain sex differences in mortality patterns (13–16). The first hypothesis suggests that within species the heterogametic sex (i.e., XY males in mammals) should suffer from impaired survival compared to the homogametic sex (13, 14), while the second proposes that the maternal inheritance of mitochondrial DNA should lead to the accumulation of mutations specifically deleterious for male’s fitness, notably in terms of increased mortality (15, 16). Until now, these hypotheses have been mostly investigated under laboratory conditions (17, 18), as the type of data required to tackle them (e.g., mitochondrial DNA mutation rate and transposable element content of the sex chromosomes; see ref. 13) has so far prevented any large-scale comparative analysis across mammalian species living in free-ranging conditions (16, 19).

These genetic mechanisms proposed to explain the evolution of sex differences in mortality patterns do not make any explicit distinction between the evolution of sex differences in lifespan and aging rate of mortality (i.e., defined as the exponential rate of increase of mortality risk with increasing age, hereafter “aging rate”; see also Table 1). Yet, these two demographic traits can be largely uncoupled, as recently shown by a comparative analysis revealing that although the observed variation in mammalian lifespan explained by the rate of aging increases with the species body mass, the aging rate never accounts for more than 50% of this variation (20). Therefore, while the above-mentioned evolutionary hypotheses (i.e., heterogametic sex and mother’s curse) could influence the evolution of sex differences in lifespan, they are not necessarily associated with the evolution of sex differences in the rate of aging. Overall, this emphasizes that studies investigating the direction and magnitude of sex differences in mortality patterns as well as the underlying mechanisms need to consider independently adult lifespan and rate of aging.

Table 1.

Mean percentage differences and mean log-transformed lifespan differences with 95% credibility intervals (CIs) between males and females of mammalian populations for four longevity metrics

Metrics	Mean percentage differences	Mean log-transformed differences	Lower CI	Upper CI	N
Median adult lifespan*	18.6	−0.171	−0.376	0.036	134
Adult life expectancy†	11.0	−0.104	−0.332	0.130	57
Adult lifespan 80%‡	18.6	−0.171	−0.333	−0.016	134
Maximum adult lifespan§	12.2	−0.115	−0.256	0.017	107

N corresponds to the number of populations included in the analyses. We focused on the adult stage to avoid any confounding effect of variation in juvenile mortality. We defined the adult life stage from the female age at first reproduction onward. The average difference across the four longevity metrics is 15.1%.

^*Age at which 50% of the individuals alive at the onset of adulthood were dead (i.e., when cumulative survivorship reaches 0.5).

^†Mean age at death of the individuals alive at the onset of adulthood.

^‡When 80% of the individuals alive at the onset of adulthood were dead (i.e., when cumulative survivorship reaches 0.2).

^§Oldest age reached by individuals alive at the onset of adulthood.

In his pioneering contribution to the evolutionary biology of aging, George C. Williams was the first to launch a theory including nine predictions to explain the evolution of aging. Among them, he proposed that the sex exposed to the highest level of environmentally driven adult mortality (i.e., mortality due to the interactive effects of both environment and genetic background; see ref. 21) should undergo a faster aging rate (22). Since then, the association between high adult mortality and faster aging rate has been discussed and refined (23), and factors such as condition-dependent mortality have been highlighted as moderators that can shape the relationship between adult mortality and aging rate in a sex-specific way (24). For instance, in wild boar (Sus scrofa), aging rates are similar between sexes despite a consistently higher mortality in males than in females throughout adulthood (25). It has been postulated that stronger condition-dependent mortality in males might cause a higher viability selection in this sex, ultimately buffering the expected occurrence of sex differences in aging rate (25).

From gamete production to parental care, males and females show striking differences in reproductive physiology and life history strategies. These differences are commonly proposed as determinants of the direction and magnitude of sex differences in aging rates of mortality observed in empirical studies (26, 27). In particular, the role played by sexual selection in shaping sex differences in mortality patterns has been intensively debated (9, 10, 26, 28). Males have been hypothesized to pay survival costs due to greater allocation to sexual competition in the form of the growth and maintenance of conspicuous sexual traits or through the expression of more risky behavior (9, 29), which should ultimately translate into a shorter adult lifespan and/or a faster rate of aging compared to females (22, 26, 27). A few comparative analyses have focused on the possible role of sexual selection in explaining sex differences in lifespan and in the rate of aging. However, these studies have made limited use of metrics that accurately assess the rate of aging (see ref. 28 for a review). Overall, evidence reported so far is equivocal at best (13, 28) and relies on small datasets (9, 10, 29) or on captive populations (28).

In the present study, we compile or reconstruct (e.g., in the case of capture–recapture studies; see Materials and Methods) age-specific mortality estimates for 134 populations of 101 species spanning the wide diversity of orders existing in mammals to quantify both the consistency and magnitude of sex differences in adult lifespan and aging rate. Taking advantage of this unique compilation of sex- and age-specific mortality estimates, we then perform a thorough evaluation of associations between proxies of sexual selection and sex differences in adult lifespan and aging rates observed across mammals.

Results and Discussion

We found that females have on average an adult median lifespan 18.6% longer than males in wild mammals, after synthesizing the most complete compilation of mammalian age- and sex-specific mortality estimates to date (Fig. 1 and Materials and Methods). The magnitude of sex differences in adult lifespan was robust with respect to four metrics of longevity commonly used (coefficient of variation: 26%; Table 1), although statistical significance was only reached for one metric (i.e., adult lifespan 80%; Table 1). The bias toward a longer lifespan for females was consistent across 60% of the populations included in our dataset whatever the lifespan metric analyzed (Dataset S3). We found that sex differences in adult median lifespan are also larger in longitudinal than in transversal studies (SI Appendix, Fig. S1). As individuals are closely monitored throughout their adult lifetime in longitudinal studies, these provide the most accurate demographic estimates (30), revealing that females live on average 20.3% longer than males (64 populations encompassing 50 species) in the best-studied populations. Although sex differences in adult median lifespan from culturally and geographically distinct human populations (Americans: 6.2%, Japanese: 5.1%, Swedish: 2.0%, Aché: 17.5%) are consistent with our estimates from nonhuman mammals, nonhuman females display a survival advantage greater than women in 66.4% of the sampled populations (Fig. 1).

Fig. 1.

Sex differences in adult lifespan across mammals. For a given population, the sex difference is measured as the ratio log[(Male adult lifespan)/(Female adult lifespan)]. Multiple bars for a given species represent estimates gathered from different populations. Orange bars correspond to longitudinal data, gray bars correspond to transversal data, and dark gray bars correspond to the human populations. The black dot corresponds to the overall effect for nonhuman mammals and is associated with its 95% credibility interval.

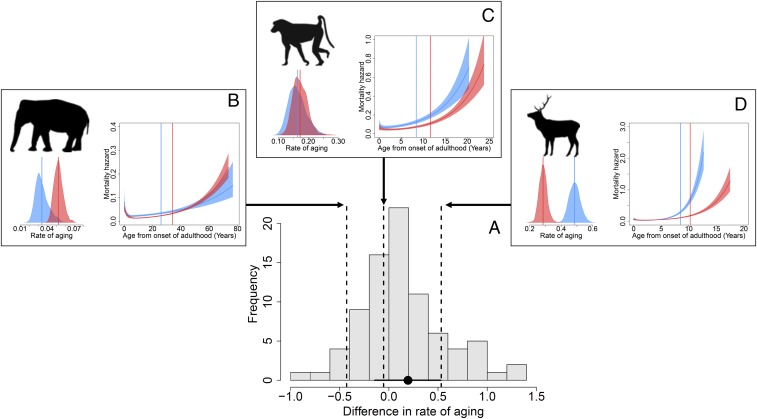
To investigate whether the direction and the magnitude of sex differences in the rate of aging were similar to those observed for the sex differences in adult lifespan, we estimated the rate of aging in populations where information on the distribution of ages at death was available (83 populations representing 66 species). Empirical evidence accumulated to date indicates that the onset of aging markedly varies across mammals and does not consistently start at the age of first reproduction (31). We thus estimated the rate of aging by fitting a Siler model (32), which does not require any assumption on when the onset of aging occurs, contrary to the commonly used Gompertz model (33). We did not find any consistent difference in aging rates between males and females (Table 2 and Fig. 2), even when our investigation was limited to longitudinal data (Table 2). The overall sex bias in adult lifespan we report across mammalian populations is therefore shaped by a multitude of sex-specific demographic features that characterize a species or a population but does not systematically involve a higher rate of aging in males. Thus, longer adult lifespan in females does not systematically involve a lower rate of aging but can simply result from lower mortality at all adult ages (20).

Table 2.

Mean of the posterior distribution of the difference between sexes in rate of mortality aging for longitudinal and transversal-dx data together (Materials and Methods) and longitudinal data only

Parameters	Mean	Lower CI	Upper CI	N
Rate of aging*	0.194	−0.144	0.529	83
Rate of aging* (longitudinal only)	0.215	−0.103	0.577	64

N corresponds to the number of populations included in the analyses. The mean sex difference is associated with the 95% credibility interval.

^*Exponential rate of mortality increase estimated from a Siler model fitted from the onset of adulthood (Materials and Methods).

Fig. 2.

Frequency distribution of the magnitude of sex differences in rate of aging across mammals in the wild (A). The black dot corresponds to the overall effect for nonhuman mammals and is associated with its 95% credibility interval. Patterns of age-specific changes in mortality rate for three mammalian populations are displayed. For each population the mortality curve with the vertical line representing the median adult lifespan and the posterior distribution of the aging rate b₁ are given in red for females and in blue for males. The mortality hazard corresponds to the instantaneous rate of mortality. In the three populations, adult females live on average longer than adult males. However, (B) in Asian elephant, Elephas maximus (Myanmar population), females have a higher aging rate; (C) in yellow baboon, Papio cynocephalus (Amboseli National Park population), no difference in aging rates is observed; and (D) in red deer, Cervus elaphus (Isle of Rum population), males show a higher rate of aging than females.

Such a decoupling between adult lifespan and rate of aging matches the human mortality pattern, because age-specific mortality in studied human populations increases at the same rate in both sexes even though women live on average longer than men (2, 6, 34). The absence of consistent sex differences in rates of aging we document here across wild populations of mammals does not preclude any potential sex differences in the rate of aging displayed by other phenotypic traits (e.g., fertility, reproductive performance, body mass, or components of the immune system), as illustrated by recent evidence that physiological and demographic aging patterns can be uncoupled in the wild (31, 35). However, age- and sex-specific data on physiological traits remain scarce, which currently prevents any large-scale investigation of sex differences in aging at the physiological level.

Sex differences in both adult lifespan and rate of aging are highly variable across species (coefficient of variation of 182% and 291% for adult lifespan and rate of aging, respectively; Figs. 1 and 2). Dissimilarities in sex-chromosome content is an influential explanation for sex differences in mortality (13, 14, 17), which suggests that within species the heterogametic sex (i.e., XY males in mammals) should suffer from impaired survival compared to the homogametic sex. While the exact biological mechanisms linking sex chromosomes and lifespan remain unclear (13), this hypothesis successfully explains the direction of sex ratio bias (potentially caused by sex differences in mortality) across tetrapods (36). However, our findings demonstrate that even within mammalian species that all share the same sex determination system, variation in the magnitude of sex differences in adult lifespan and rate of aging is particularly large. These between-species differences in mortality patterns were not explained by phylogenetic relatedness, which only weakly accounts for the variation observed in sex differences in adult lifespan (H² = 15%) or rate of aging (H² = 29%) across species. This contrasts with the estimations of analyses focused on males and females separately, which highlight that phylogenetic relatedness explains most of the variation in adult lifespan and rate of aging for a given sex (H² = 86% and H² = 85% for female and male adult lifespan, respectively; H² = 87% and H² = 88% for female and male rate of aging, respectively). These findings indicate that allometry [through the species-specific body size (37)] and pace of life [through the species-specific position along the slow–fast continuum (38)] that both closely track phylogenetic relatedness likely determine the mortality pattern observed within a given mammalian species (39) but have little influence on the difference between sexes in either adult lifespan or rate of aging. Overall the extant sexual dimorphism in survival metrics is mostly independent of phylogenetic relatedness and is thus shaped by other sources of variation (e.g., variation in environmental conditions among and within populations).

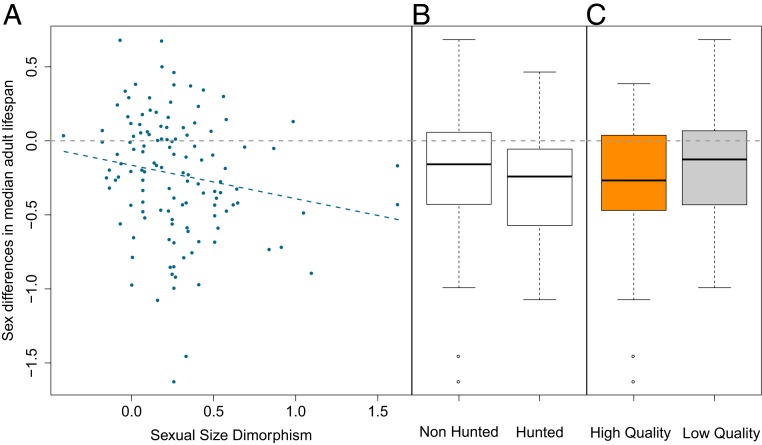
We then conducted additional analyses focused on sexual selection, which is commonly assumed to shape sexual dimorphism in mortality patterns (26, 28), using both sexual size dimorphism (SSD) and mating system as proxies of the strength of sexual selection (see ref. 40 and Materials and Methods). These broad-scale analyses on mammals in the wild reveal that SSD (but not mating system) is only weakly associated with the direction and magnitude of sex differences in adult lifespan (slope of −0.23 [95% credibility interval: −0.49; 0.04]; SI Appendix, Table S1 and Fig. 3) and is not associated with the rate of aging (SI Appendix, Table S2), which challenges the classic view that sexual selection is the major driver of sex differences in mortality patterns (9, 16, 27, 41). Moreover, these findings contrast with a previous comparative analysis performed on captive populations where sex differences in lifespan were unambiguously higher in polygynous than in monogamous ruminants (28). In zoological gardens, animals live in sheltered environments where environmentally driven mortality risks are buffered (e.g., through food provisioning or preventive veterinary medicine; see ref. 42). Therefore, the physiological costs associated with the evolution of a large body size and conspicuous sexual traits under natural conditions and over evolutionary times might be more likely to translate into a greater overall reduction in male survival, relative to females, since individuals living in zoos are protected from environmentally driven causes of death. In such captive conditions adaptations to sexual competition might be the main driver of sex differences in lifespan, since both sexes are sheltered from additional mortality sources linked to environmental severity that can influence lifespan in sex-dependent and -independent ways (28). By contrast, in the wild, we hypothesize that local environmental conditions and the myriad of associated mortality risks (e.g., climate harshness and pathogen richness) predominantly shape sex differences in adult lifespan and rate of aging by interacting with costs of sexual selection. More specifically, the substantial allocation of resources in males toward the growth and maintenance of secondary sexual traits might, everything else being equal, make males more vulnerable than females to harsh environmental conditions. For instance, sexual dimorphism is partly physiologically driven by a higher production of androgens in males, particularly during early adulthood (43), which directly controls the growth of many secondary sexual traits (e.g., ornaments and armaments) (13, 27). Circulating androgens also modulate immune performance and when present at high levels can impair some aspects of the immune defense (44), making males more susceptible to pathogens. Trophy hunting also constitutes one extreme example of environmental conditions (i.e., anthropogenic activities) that shape the magnitude of sex differences in mortality patterns across mammalian populations in the wild. Indeed, adult females from hunted populations (n = 21) tend to live longer relative to males than adult females from nonhunted populations (34.5% vs. 16.7%, respectively; Fig. 3). Finally, we cannot dismiss that sex differences in mortality patterns might also be influenced by interactions between local environmental conditions and the species-specific female reproductive tactics. For instance, females from promiscuous species, displaying multiple mating events during a single reproductive season, will be more likely to contract infectious diseases when the local environment is particularly rich in pathogens (45), which might be ultimately responsible for a shorter female lifespan or a stronger rate of aging. Overall, investigating how local environmental conditions and sex-specific life-history strategies interact to shape sex-specific mortality patterns across species and populations remains a challenging initiative as it requires fine-scale data on various environmental traits.

Fig. 3.

Effect of SSD (A), hunting (hunted vs. nonhunted populations) (B), and data quality (longitudinal–high quality vs. transversal–low quality) (C) on sex differences in median adult lifespan across mammals. The horizontal gray and dash line corresponds to the absence of sex differences in median adult lifespan.

In humans and laboratory rodents sex differences in mortality patterns extend to sex differences in frailty, neurological decline, and comorbidity (6). In laboratory mice and rats, the survival benefits associated with antiaging interventions (genetic or pharmacological) are also frequently sex-specific (6, 46). These sex-specific responses can be attributed to sex differences in physiological systems (e.g., hormonal profiles), which are also expected to modulate adult lifespan and aging (47). We propose that variation in the magnitude of sex differences in both adult lifespan and rate of aging in wild populations is likely a response to interactions between sex-specific physiological pathways and the diversity of environmental conditions met by mammals across the world. From an evolutionary perspective, sex-specific gene expression and physiological systems are the direct consequences of both natural and sexual selection pressures that have been exerted independently on males and females (27, 41, 48). For instance, sexual selection has led to the evolution of species with high sexual dimorphism for many phenotypic traits (e.g., body size) that differentially sensitize either sex to specific environmental conditions. This is particularly well illustrated by the three longitudinally monitored populations of bighorn sheep (Ovis canadensis) included in our dataset. In this polygynous ungulate, males and females show almost no difference in lifespan in the National Bison Range population where resources are consistently available. However, males live much shorter lives in Ram Mountain where winter severity is particularly pronounced, leading to marked sex differences in lifespan (49). Therefore, whether highly sexually dimorphic species living in the wild show marked sex differences in lifespan and aging rate of mortality is likely to depend on interactions between sex-specific genetic variation arising from a selection toward specific alleles that are associated in males with more extreme phenotypes (for physiological, morphological, and behavioral traits) and local conditions (e.g., pathogen richness), which can either exacerbate or buffer the magnitude of these sex differences (50). Albeit challenging, research programs that solve this complex network will undoubtedly provide innovative insights into the evolutionary roots and physiology underlying aging in both sexes.

Materials and Methods

Data Collection.

Age- and sex-specific mortality data were extracted from published life tables or graphs using WebPlotDigitizer (https://automeris.io/WebPlotDigitizer/). We limited our literature search to mortality or survival estimates published for both sexes for wild populations of mammals, for a total of 184 populations encompassing 128 species. Based on the methods used to estimate age-specific mortality in the initial source, we distinguished three main categories of study. The first type of study corresponds to age-specific mortality estimates obtained from the long-term monitoring of individuals marked during early life when age can be accurately assessed (i.e., longitudinal data). The second type of study corresponds to age-specific mortality estimates obtained from dead animals collected in the field [i.e., transversal data using the standard dx series (51)]. Finally, the third type of study corresponds to age-specific mortality estimates computed from the sampling of individuals alive in the population [i.e., transversal data using the standard lx series (51)]. For transversal data, population size has to be considered as constant or with a known growth rate and the distribution of ages of dead or alive individuals in the population as stable (51). Mortality estimates extracted from transversal data also depend on the precision of the methods used to assess the age of the individuals. Longitudinal data based on known-aged individuals regularly monitored by capture–recapture methods provide much more accurate estimates of age-specific mortality than transversal data (52). Sampled populations were also classified as hunted vs. nonhunted according to the information reported in the original publication. All data and associated references are provided in SI Appendix, Tables S1–S4.

To compare results obtained from wild populations to humans, we recovered age- and sex-specific mortality data from four human populations (all longitudinal). These data were extracted for three contemporary countries [Japan, Sweden and USA (53)] and for one hunter-gatherer population [Aché (54)]. We used a similar procedure (see Estimation of Adult Lifespan and Rate of Mortality Aging below) to compute adult lifespan and rate of aging in wild mammals and humans using 13 y of age as the onset of adulthood following reported data for the populations of Sweden, Japan, and the United States (55) and previous comparative analyses of mortality patterns (56). However, human estimates were only used in comparison with wild populations of mammals and were not included in the analysis.

For each species, we collected data on life-history traits that could explain sex differences in adult lifespan and aging rates. As both sexual selection and sociality have been suggested to influence sex-specific mortality (9, 57), we collected data on mating system, social system, and sex-specific body mass (to measure SSD). Following previous comparative studies in mammals (e.g., ref. 28), we classified the species in terms of mating (i.e., monogamous, polygynous, or promiscuous) and social (i.e., cooperative breeders vs. noncooperative breeders) systems. The intensity of sexual selection is expected to be smaller in monogamous species compared to polygynous and promiscuous species, which might reduce sex differences in mortality patterns (9). The intensity of SSD (i.e., increasingly larger males) is also increasing with the intensity of sexual selection (40) and is thus logically higher in polygynous than in monogamous mammals (58). In cooperative breeders, costs of reproduction are generally shared among females (59), which might also increase sex differences in mortality patterns through a reduced female mortality. For each life-history trait, we prioritized data recovered from the same population (see Datasets S1–S4 and associated references for each life-history trait used in the analysis).

Estimation of Adult Lifespan and Rate of Mortality Aging.

We excluded juvenile mortality because it is generally higher than adult mortality in mammals and can vary considerably among species and populations and even among years within the same population (60). To define the adulthood life stage, we used the species-specific female age at first reproduction as the onset of adulthood.

Rate of mortality aging.

For the longitudinal and transversal-dx data, the exact age at death of each individual was reported. The mortality rate at each age was estimated while accounting for differences in the number of individuals at risk. For instance, at old ages, mortality rates are typically computed from the few individuals that are still alive, which makes those rates less reliable than those at earlier ages. In a Gompertz model, aging is assumed to start at the species-specific age at first reproduction (22, 61), leading this model to represent a biological model of aging. However, empirical evidence suggests that the onset of aging is often delayed and shows considerable variation among mammals (31). Therefore, models that allow flexibility in the age at the onset of aging provide better fit than the Gompertz model fitted from the age of first reproduction. We thus fitted a Siler model on age-specific mortality data (32) for each population to obtain comparable metrics. The five-parameter Siler model is given by

$$\mathrm{\mu }\left(x\right)=a_0\text{exp}\left(-a_{1}x\right)+\hspace{0.17em}c\hspace{0.17em}+\hspace{0.17em}{b}_0\text{exp}\left(b_{1}x\right),$$ [1]

where a₀, a₁, c, b₀, b₁,and c ≥ 0 are the parameters of the mortality function and x the age in years. The first exponential function on the right-hand side of Eq. 1 corresponds to the decline in mortality in the early adult stage (e.g., subadult mortality), the c parameter provides the lower limit of mortality during the adult stage, and the second exponential function corresponds to the mortality increase during the senescent stage. As a metric of rate of aging we used the b₁ parameter of the Siler model (Eq. 1) that measures the exponential increase in mortality rate with age during the aging stage. This stage is defined from an onset of aging estimated from the analysis of the age-dependent mortality curve. The Siler model thus corresponds to a demographic model of aging. We restricted the analyses to populations that included at least 30 males and 30 females at the female age at first reproduction. To account for different sample size among ages we used the R package BaSTA (62). For transversal-lx data, we only had access to the age distribution for individuals alive. As the range of ages covered was quite low for some species (e.g., ref. 63), for example in weasels (Mustela nivalis), it was not possible to fit the Siler model using transversal-lx data and these populations were excluded from the rate of aging analysis.

Adult lifespan.

We estimated sex-specific median adult lifespan (in years) for populations from our dataset. We first defined adult survivorship as the cumulative survival conditioned on reaching adulthood, and thus, at the age of the onset of adulthood, adult survivorship is equal to 1. The median adult lifespan corresponds to the age when 50% of the individuals alive at the onset of adulthood were dead (i.e., when cumulative survivorship reaches 0.5). For the longitudinal and transversal-dx data, median lifespan was estimated from the Siler model by solving numerically the following equation:

$$e^{\left(\frac{a_0}{a_1}\left(e^{-a_{1}x}-1\right)-cx+\frac{b_0}{b_1}\left(1-e^{b_{1}x}\right)\right)}=\mathrm{0.5.}$$ [2]

For transversal-lx, we fitted a Gompertz model given by

$$\mathrm{\mu }\left(x\right)=a\hspace{0.17em}\text{exp}\left(b\hspace{0.17em}x\right)$$ [3]

on the observed distribution of ages among individuals alive where a > 0 and b ≥ 0 are the Gompertz parameters (33), with a representing the baseline mortality at the starting age and b the exponential rate of increase in mortality with age. As individuals for transversal-lx data are all sampled only once and are thus not monitored through their entire life, we took a larger sample size threshold for our selection procedure. Therefore, for transversal-lx data, we excluded populations when the sample size was below 50 individuals for at least one of the two sexes. For the transversal-lx data, median lifespan was estimated from the Gompertz model by solving numerically the following the equation:

$$e^{\frac{a}{b}\left(1-e^{bx}\right)}=\mathrm{0.5.}$$ [4]

To assess the accuracy of the adult lifespan estimate based on a Gompertz model fitted to the age distribution of animals alive, we also used this method to estimate adult lifespan from longitudinal and transversal-dx data. The correlation between estimates of adult lifespan obtained with the two methods (Siler vs. Gompertz models fitted to longitudinal and transversal-dx data only) was extremely high (R² = 0.99; SI Appendix, Fig. S1), which indicates that these two approaches did not influence the outcome of our analyses of adult lifespan. Moreover, to verify the robustness of our results, we analyzed sex differences in adult lifespan using three other metrics of longevity. For each population we computed the age when 80% of the individuals alive at the onset of adulthood were dead (i.e., when cumulative survivorship reaches 0.2, a metric also called adult lifespan 80%) and life expectancy at the onset of adulthood, which corresponds to the mean adult lifespan from the distribution of ages at death (using longitudinal and transversal-dx data with no censoring at old age). Finally, although it is highly sensitive to sample size (64), we also reported maximum adult lifespan for each sex because it is still the most often studied survival metric in comparative analyses of aging. Results obtained with the four longevity metrics are displayed in Table 1.

Statistical Analyses.

Adult lifespan.

For each population, we quantified sex differences in adult lifespan as the ratio between male and female adult lifespan on a log scale $\left(difference\hspace{0.17em}in\hspace{0.5em}adult\hspace{0.17em}lifespan=\log \left(\frac{adult\hspace{0.17em}lifespan\hspace{0.17em}male}{adult\hspace{0.17em}lifespan\hspace{0.17em}female}\right)\right)$. For the analysis of sex differences in adult lifespan, we ran a Bayesian hierarchical model using the package MCMCglmm (65) with the magnitude of sex differences in adult lifespan as the response variable. As species from our dataset were not independent because they share phylogenetic relatedness, we corrected all our analyses for phylogeny using the phylogenetic variance–covariance matrix extracted from a mammalian phylogenetic tree (66). Moreover, in some species (n = 21), estimates from several populations were available and the data from these populations were thus not independent. Therefore, we fitted the species independently of the phylogeny as a random effect because individuals from the same species can share different ecological characteristics, which are not necessarily linked to the phylogenetic relatedness. To test the sensitivity of the results to the priors, we used two sets of priors for the random effects in the model (uninformative inverse Whishart prior with nu = 0.02 and V = 1 and expanded prior with nu = 1 V = 1 alpha.nu = 0 alpha.V = 1,000). Models with different priors did not show any detectable difference [Gelman and Rubin’s convergence diagnostic was very close to 1 for each MCMC chain (67)]. From this model we were able to extract the percentage of the total variance explained by the phylogenetic effect (named phylogenetic heritability H²) (68). The value of H² can be interpreted as a direct equivalent to the phylogenetic signal (λ) of Pagel, with a value close to 1 meaning that there is a strong phylogenetic signal and a value close to 0 that there is no phylogenetic signal. For each parameter, we reported the mean of highest posterior density distribution, the lower and upper limits of the 95% credibility interval and sample size.

The first aim of our analyses was to estimate the average sex difference in adult lifespan across the whole set of mammals. We thus ran the model of sex differences in adult lifespan without any independent covariate or factor and found a longer adult lifespan for females in the dataset with an overall negative effect (see SI Appendix, Table S3 for all coefficients). In a second step, we tested whether some species-specific traits associated with sex-specific life history strategies and sexual competition (SSD, mating system, social system, sex-bias in dispersal) explained sex differences in adult lifespan observed across mammals. We included SSD (computed as the log-scaled ratio between male and female body mass) and the occurrence of sex-biased dispersal assessed through sex-biased individual detection (likely bias vs. unlikely bias). Indeed, in some mammalian populations, males are more difficult to detect than females because they wander at a much larger extent, by doing breeding dispersal and/or not defending a territory. Such lower male detection can lead to underestimates of male survival when not corrected for and thereby bias estimates of sex differences in adult lifespan and rate of aging. To overcome this problem, we considered that populations that are spatially constrained (e.g., living on island or in mountain ranges), monitored longitudinally, or of species where males defend a territory are unlikely to display biased estimates of sex differences in adult lifespan. On the other hand, populations of nonterritorial species (with an expected high breeding dispersal propensity) or without clear information on the mating tactic available in the literature are likely to display more biased estimates of sex differences in adult lifespan. For all of the models, we controlled for the potential confounding effect of the hunting status of the population (i.e., hunted vs. nonhunted) and of data quality (longitudinal vs. transversal data). All of the two-way interactions among these factors were included in candidate models.

To identify the model of sex differences in adult lifespan with highest support, we fitted different models with all of the possible combinations of variables from the full model (n = 19 models). These models were then ranked by the deviance information criterion (DIC) (69) (SI Appendix). The selected model included additive effects of hunting (i.e., sex differences in adult lifespan were highest in hunted populations) and data quality (i.e., higher sex differences occurred in adult lifespan with high-quality data; SI Appendix, Table S3 and Fig. 3).

The effect of both mating and social systems were tested on a population subset (n = 132 populations) because this information was lacking for some species. In addition, the social system was highly correlated to the mating system. Indeed, except for the four-striped grass mouse (Rhabdomys pumilio) (70) all cooperative breeders (n = 6) in our dataset were monogamous. We thus tested separately the influence of the mating and social systems, to avoid multicollinearities issues (71). The independent model including only mating system as a covariate did not reveal any effect on sex differences in adult lifespan (mean difference _{monogamous vs. polygynous} = 0.001 [−0.325; 0.318], mean difference _{monogamous vs. promiscuous} = 0.047 [−0.265; 0.392]). Similarly, the model including only social system did not reveal any detectable effect (mean difference _{cooperative vs. noncooperative breeder} = −0.015 [−0.366; 0.317]).

Rate of aging.

For each population, we computed sex differences in aging rates of mortality as the ratio between male and female rates of aging on a log scale $\left(difference\hspace{0.17em}inaging\hspace{0.17em}rate=\log \left(\frac{aging\hspace{0.17em}rate\hspace{0.17em}male}{aging\hspace{0.17em}rate\hspace{0.17em}female}\right)\right)$. We then followed the same procedure as used for sex differences in adult lifespan. We found no statistical support for consistent sex differences in aging rates across species (SI Appendix, Table S1). These results were qualitatively similar when using aging rates estimated from Gompertz models instead of Siler models (SI Appendix, Fig. S4). We performed a second set of analyses to test whether our set of life history traits can explain possible sex differences observed in aging rates across mammals. Similar to the analyses performed for sex differences in adult lifespan, we included SSD and potential sex-biased individual detection (SI Appendix, Table S3) and we controlled for possible confounding effects of hunting status and data quality. All of the two-way interactions between these variables were included in candidate models. We ranked all of the models based on their DIC score to identify the variables influencing sex differences in aging rates. The Null model was ranked first, revealing that none of these variables influenced the magnitude and the direction of sex differences in aging rates (SI Appendix, Table S4). Moreover, additional analyses did not reveal any effect of either mating or social system (mean difference _{monogamous vs. polygynous} = −0.04 [−0.48; 0.41], mean difference _{monogamous vs. promiscuous} = 0.01 [−0.45; 0.46], mean difference _{cooperative vs. noncooperative breeder} = −0.17 [−0.57; 0.23]).

Data Availability.

All data and code are provided in SI Appendix.