Extending the Latent Dirichlet Allocation model to presence/absence data: A case study on North American breeding birds and biogeographical shifts expected from climate change

Abstract

Understanding how species composition varies across space and time is fundamental to ecology. While multiple methods having been created to characterize this variation through the identification of groups of species that tend to co‐occur, most of these methods unfortunately are not able to represent gradual variation in species composition. The Latent Dirichlet Allocation (LDA) model is a mixed‐membership method that can represent gradual changes in community structure by delineating overlapping groups of species, but its use has been limited because it requires abundance data and requires users to a priori set the number of groups. We substantially extend LDA to accommodate widely available presence/absence data and to simultaneously determine the optimal number of groups. Using simulated data, we show that this model is able to accurately determine the true number of groups, estimate the underlying parameters, and fit with the data. We illustrate this method with data from the North American Breeding Bird Survey (BBS). Overall, our model identified 18 main bird groups, revealing striking spatial patterns for each group, many of which were closely associated with temperature and precipitation gradients. Furthermore, by comparing the estimated proportion of each group for two time periods (1997–2002 and 2010–2015), our results indicate that nine (of 18) breeding bird groups exhibited an expansion northward and contraction southward of their ranges, revealing subtle but important community‐level biodiversity changes at a continental scale that are consistent with those expected under climate change. Our proposed method is likely to find multiple uses in ecology, being a valuable addition to the toolkit of ecologists.

This article describes a new statistical method that can be used to understand the effect of global change phenomena on biodiversity based on high‐dimensional multivariate presence/absence data. We show how this method is able to automatically determine the number of species groups and fit the data well. Our case study reveals striking spatial patterns of breeding birds, some of which seem to be strongly constrained by temperature and rainfall, and subtle but important community‐level range shifts at a continental scale that may be associated with climate change.

1. INTRODUCTION

A major challenge in ecology is to understand how species assemblages, often composed by tens, hundreds, or even thousands of species, change in space and time and are influenced by environmental variables. Community ecologists rely heavily on a plethora of methods to analyze these high‐dimensional multivariate data (e.g., k‐means, hierarchical clustering, network methods, and model‐based approaches) (Bloomfield, Knerr, & Encinas‐Viso, 2017; Foster, Hill, & Lyons, 2017; Legendre & Legendre, 2012). Such approaches attempt to identify groups of species that tend to co‐occur in space and time. For example, in a spatial context, these approaches have attempted to identify geographic areas with similar taxa, areas that have been variously called “biogeographical regions” (Gonzales‐Orozco, Thornhill, Knerr, Laffan, & Miller, 2014), “bioregions” (Bloomfield et al., 2017), or “biogeographical modules” (Carstensen et al., 2012). Such bioregions have been argued to be important for understanding the role of history on community assemblages (Carstensen et al., 2012, 2013), interpreting ecological dynamics (Economo et al., 2015), and developing broad‐scale conservation strategies (Vilhena & Antonelli, 2015).

The Latent Dirichlet Allocation (LDA; not to be confused with linear discriminant analysis) model is a powerful model‐based method to decompose species assemblage data into groups of species that tend to co‐occur in space and/or time. The benefits of using this model include the ability to adequately represent uncertainty, accommodate missing data, and, perhaps most importantly, to describe sampling units as comprised of multiple groups (i.e., mixed‐membership [MM] units) (Valle, Baiser, Woodall, & Chazdon, 2014). Conceptually, the ability to describe sampling units as comprised of multiple groups has rarely been considered in previous methods (i.e., prior approaches are typically based on “hard” partitions) but may better honor community dynamics and may better characterize impacts of environmental change. For instance, biome transition zones, ecotones, and habitat edges are locations that are often comprised of a mix of species groups, providing sources for potentially novel species interactions (Gosz, 1993; Ries, Fletcher, Battin, & Sisk, 2004). Similarly, climate change is predicted to cause geographic shifts in species and communities, leading to the hypothesis of novel assemblages arising across space as climate and habitat changes (Urban et al., 2016; Williams & Jackson, 2007). In addition, most partitioning methods that delineate biogeographical regions or modules based on hard boundaries can lead to high uncertainty in boundary delineation—an issue that can be rectified by allowing groups to overlap. It is important to note that LDA allows for overlapping groups, but it does not require it to be present (i.e., if data do not support overlap, no overlap is estimated).

It is unfortunate that the LDA model, as currently developed, has been restricted to abundance data, which are often not available because accurate quantification of abundance can be very challenging and costly. In the absence of abundance data, researchers often have to rely on presence/absence data to understand species distributions and biodiversity patterns (Jones, 2011; Joseph, Field, Wilcox, & Possingham, 2006). Another limitation of the LDA model is that the number of groups has to be prespecified, requiring researchers to run LDA multiple times to then use some criterion (e.g., AIC) to choose the optimal number of groups (e.g., Valle et al., 2014), an approach that often can be computationally costly.

In this article, we substantially develop the LDA model to be able to fit the much more commonly available presence/absence data and to automatically determine the optimal number of groups. We start by describing our statistical model. Then, using simulated data, we show how our method automatically detects the optimal number of groups in the data, reliably estimates the underlying parameters, and better fits the data, outperforming other approaches. At last, we illustrate the novel insights gained using our method by analyzing a long‐term dataset collected on breeding birds in the United States and Canada (Breeding Bird Survey [BBS];Pardieck, Ziolkowski, Lutmerding, Campbell, & Hudson, 2017) to determine how environmental variables influence bird assemblages across the continent and how these assemblages are changing through time.

2. MATERIALS AND METHODS

2.1. Model description

The overall goal of our method is to identify the major patterns of species co‐occurrence in the data, each of which we define to be a distinct species group. We adopt the term species group (instead of “bioregion” or other related terms) because these major co‐occurrence patterns do not have to have a strong spatial pattern (although they often do), these groups can overlap in space, and proportion of groups can change through time. More specifically, our method characterizes each sampling unit l in terms of the proportion of the different groups (parameter vector ${\mathit{\theta }}_{\mathit{l}}$) and characterizes each group k in terms of the probability of the different species (parameter vector ${\mathit{\varphi }}_{\mathit{k}}$). For example, ${\mathit{\theta }}_{\mathit{l}}=\left[\begin{array}{c}0.1,0.8,0.1,0\end{array}\right]$ indicates that the second group dominates unit l and that the fourth group is absent. This example also illustrates that a given sampling unit can be comprised of multiple groups, which explains why these types of models are called mixed‐membership models. In the same way, ${\mathit{\varphi }}_{\mathit{k}}=\left[\begin{array}{c}0,0.8,0.8\end{array}\right]$ indicates that species 2 and 3 (but not species 1) are important species of group k. Note that a given species can have a high probability in more than one group. A more formal description of the statistical model is given below.

The data consist of a matrix filled with binary variables $x_{\mathit{isl}}$ (i.e., equal to one if species s was present in observation i and unit l and equal to zero otherwise). Notice that we assume that multiple observations might have been made for each species s and unit l, possibly due to temporally repeated measures or because multiple subsamples were measured within each unit l (e.g., a forest plot comprised of four subplots). Each of these binary variables has an associated latent group membership status $z_{\mathit{isl}}$. This variable indicates to which group species s in sampling unit l during observation i comes from.

We assume that each observation $x_{\mathit{isl}}$ comes from the following distribution, given that species s in unit l during observation i comes from group k ($z_{\mathit{isl}}=k$):

$$x_{\mathit{isl}}|z_{\mathit{isl}}=k\sim \text{Bernoulli}\left({\varphi }_{\mathit{sk}}\right),$$

where ${\varphi }_{\mathit{sk}}$ is the probability of observing species s if this species came from group k. Notice that $z_{\mathit{isl}}$ influences the distribution for $x_{\mathit{isl}}$ by determining the k subscript of the parameter $\varphi$. Next, we assume that the latent variable $z_{\mathit{isl}}$ comes from a multinomial distribution:

$$z_{\mathit{isl}}\sim \text{Multinomial}\left(n=1,p={\mathit{\theta }}_{\mathit{l}}\right),$$

where ${\mathit{\theta }}_{\mathit{l}}$ is a vector of probabilities that sum to one, and each element ${\theta }_{\mathit{lk}}$ consists of the probability of a species in unit l to have come from group k.

In relation to the priors for our parameters, we adopt a conjugate beta prior for ${\varphi }_{\mathit{sk}}$:

$${\varphi }_{\mathit{sk}}\sim \text{Beta}\left(a,b\right).$$

Throughout this article, we assume vague priors by setting a and b to 1. Building on the work of Dunson (2010) and Valle et al. (2017), we adopt a truncated stick‐breaking prior for ${\mathit{\theta }}_{\mathit{l}}$. This prior assumes that:

$$V_{\mathit{lk}}\sim \text{Beta}\left(1,\gamma \right)$$

for k = 1,…,K−1 and $\gamma >0$. We set the parameter for the last group to 1 (i.e., $V_{\mathit{lK}}=1$). With these parameters, we calculate ${\theta }_{\mathit{lk}}$ using the equation ${\theta }_{\mathit{lk}}=V_{\mathit{lk}}\prod _{p=1}^{k-1}\left(1-V_{\mathit{lp}}\right)$. Under this prior, ${\theta }_{\mathit{lk}}$ is a priori stochastically exponentially decreasing as long as $\gamma \le 1$ and smaller $\gamma$ tend to enforce greater sparseness (i.e., the existence of fewer groups). For most of the examples in this article, $\gamma$ was set to 0.1, which we have found to work well for multiple datasets. More details regarding this prior can be found in Supporting Information Appendix S1.

The benefit of this prior is that, if the data support fewer groups than specified by the user, it will tend to force these superfluous additional groups to be empty or to have very few latent variables $z_{\mathit{isl}}$ assigned to them, as illustrated in the simulation section below. This prior also helps to avoid label switching, a common problem in mixed‐membership and mixture models. Bayesian Markov chain Monte Carlo (MCMC) algorithms applied to these types of models sometimes mix poorly and can lead to nonsensical results if posterior distributions of parameters are summarized by their averages (Stephens, 2000). The label switching problem refers to the fact that the labels of the different groups can change (e.g., groups 1 and 2 can become groups 2 and 1, respectively) without changing the likelihood (i.e., the group labels are unidentifiable). Our truncated stick‐breaking prior helps to avoid the label switching problem by enforcing an ordering of the groups according to their overall proportions.

We fit the LDA using a Gibbs sampler. A more complete description of this model and the derivation of the full conditional distributions used within this Gibbs sampler are provided in Supporting Information Appendix S1. Supporting Information Appendix S2 contains a short tutorial describing how to fit the model using the code that we make publicly available, reproducing some of the simulated data results.

There are three important points regarding LDA that need to be emphasized. First, the proposed model can accommodate negative and positive correlations between species. To illustrate this, assume that there are just two species groups and two species, s and s’. Negative correlation between these species is captured by our model if, for example, ${\widehat{\varphi }}_s=\left[\begin{array}{c}1\\ 0\end{array}\right]$ and ${\widehat{\varphi }}_{s^{\prime }}=\left[\begin{array}{c}0\\ 1\end{array}\right]$. These parameter estimates indicate that, whenever a site has a high proportion of group 1, species s will have a high probability of occurring, whereas species s’ will tend to be absent. In the same way, whenever a site has a high proportion of group 2, species s’ will have a high probability of occurring but species s will tend to be absent, resulting in negative correlation. Positive correlation between these species is captured by our model if, for example, ${\widehat{\varphi }}_s=\left[\begin{array}{c}0.95\\ 0.1\end{array}\right]$ and ${\widehat{\varphi }}_{s^{\prime }}=\left[\begin{array}{c}0.8\\ 0.05\end{array}\right]$. These parameter estimates imply that, whenever a site has a high proportion of group 1, both species s and s’ will have a high probability of occurring. In the same way, whenever a site has a high proportion of group 2, both species s and s’ will have a high probability of being absent, inducing positive correlation.

Second, hard clustering methods that group locations with similar species composition (e.g., Kreft & Jetz, 2010) correspond in our model to vectors ${\mathit{\theta }}_{\mathit{l}}$ comprised of zeroes except for a single element which is equal to 1. In the same way, hard clustering methods that group species that tend to co‐occur (e.g., Azeria et al., 2009) correspond to vectors ${\mathit{\varphi }}_{\mathit{s}}$ comprised of zeroes except for a single element which is equal to 1. In other words, LDA can generate hard clustering results for locations and/or species if its parameters take on certain values but it can also represent mixed‐membership patterns, as illustrated with our simulations.

Third, there are two extreme situations for which the LDA parameters are not identifiable. If two groups have very similar species composition (i.e., similar ${\varphi }_{\mathit{ks}}$), then the model will have a hard time distinguishing these groups and not merging them into a single one. Similarly, if all locations have similar proportions of the different groups (i.e., similar ${\theta }_{\mathit{lk}}$), then all locations will have very similar species composition, regardless of how different the species groups are from a species composition perspective. This is due to the fact that the probability of observing species s for two locations p and q is given by $E\left(x_{\mathit{isp}}\right)={\mathit{\theta }}_{\mathit{p}}^{\mathit{T}}{\mathit{\varphi }}_{\mathit{s}}$ and $E\left(x_{\mathit{isq}}\right)={\mathit{\theta }}_{\mathit{q}}^{\mathit{T}}{\mathit{\varphi }}_{\mathit{s}}$, respectively. If ${\mathit{\theta }}_{\mathit{p}}^{\mathit{T}}\approx {\mathit{\theta }}_{\mathit{q}}^{\mathit{T}}$, then $E\left(x_{\mathit{isp}}\right)\approx E\left(x_{\mathit{isq}}\right)$ (see Supporting Information Appendix S1 for details). In this scenario, the algorithm might determine that a single species group dominates all locations instead of distinguishing the different species groups.

2.2. Simulated data and comparison of methods

We simulate data to evaluate the performance of the proposed model and to compare its results to those from other clustering methods. To avoid the identifiability problems described above, we generate parameters for all simulations such that each group completely dominates at least one location and that each group has at least one species that is never present in the other groups (ensuring distinct species composition of these groups).

2.2.1. Simulation set 1

We illustrate with simulated data how the truncated stick‐breaking prior can identify the optimal number of groups and how our algorithm can retrieve the true parameter values under a wide range of conditions. More specifically, the true number of groups K* was set to 3 and 10; the number of sampling units (i.e., locations) was set to 100 and 1000; the number of species was set to 50 and 200; and the number of observations per location was set to 5. Parameters were drawn randomly (i.e., ${\varphi }_{\mathit{sk}}\sim \text{Beta}\left(0.5,0.5\right)$ and ${\mathit{\theta }}_{\mathit{l}}\sim \text{Dirichlet}\left(0.1\right)$), and the identifiability assumptions described above were then imposed. We adopted a $\text{Beta}\left(0.5,0.5\right)$ distribution for ${\varphi }_{\mathit{sk}}$ because this distribution is likely to generate species groups that are more dissimilar in terms of species composition given that it is a U‐shaped symmetric distribution. We generated 10 datasets for each combination of these settings, totaling 80 datasets.

To fit these data, we assume a maximum of 20 groups (K = 20) and estimate the true number of groups K* by determining the number of groups that are not superfluous. Superfluous groups are defined to be those groups that are very uncommon across the entire region (i.e., ${\overline{\theta }}_{\mathit{lk}}<0.5$ for 99% of the locations, where ${\overline{\theta }}_{\mathit{lk}}$ is the mean of the posterior distribution). At last, we test the sensitivity of the modeling results to the prior by fitting these data with $\gamma$ set to 0.1 and 1.

2.2.2. Simulation set 2

We also compare LDA to other methods using simulated data. In these simulations, we assume data are available on 200 species over 1,000 locations, with five repeated observations per location. Furthermore, 3, 5, and 7 groups were used to generate these data. Because the goal is to compare inference from different methods, we set the parameters ${\theta }_{\mathit{lk}}$ in such a way that it allows for a straightforward visual appraisal of the advantages and limitations of the different methods. On the other hand, the parameters ${\varphi }_{\mathit{ks}}$ were randomly drawn from $\text{Beta}\left(0.5,0.5\right),$ and subsequently, the assumption regarding groups with distinct species composition was imposed.

When fitting LDA, we set the maximum number of groups to 20 and rely on the truncated stick‐breaking prior with $\gamma =0.1$ to uncover the correct number of groups. We compare and contrast inference from our model to that from competing approaches, including traditional hard clustering methods (i.e., hierarchical and k‐mean clustering) and mixture models (i.e., region of common profile (RCP) model; Foster et al., 2017; Lyons, Foster, & Keith, 2017). In particular, we compare how well LDA and these other clustering approaches estimate the true proportion of the different species groups and fit the data. Additional details regarding how these different methods were fit and how model fit was assessed are available in Supporting Information Appendix S3.

2.3. Breeding bird case study

2.3.1. Breeding Bird Survey (BBS) dataset

The Breeding Bird Survey is a long‐term program that monitors the status and trend of bird populations in North America. In brief, data are collected annually in June by trained participants along randomly established roadside routes approximately 39 km long with stops 0.8 km apart. At each stop, a 3‐min point count is conducted (Pardieck et al., 2017).

Because we were interested in spatial mapping of groups over time, we subset the data to the period 1997–2015, which had the greatest consistency in route surveys. Furthermore, we eliminated data from very rare and very common species, defined here as species that are present in <1% or more than 50% of the transect‐by‐year combinations, respectively. This resulted in the exclusion of 48% (rare species) and 3% (common species such as American Robin, Mourning Dove, and American Crow) of the species. The rationale for this decision is that species that are too rare tend to convey little information on groups while species that are common everywhere are likely to be important species in almost all groups, contributing little to discriminate between these groups. Similar decisions are made when other clustering methods are used in ecology (e.g., Azeria et al., 2009) and when the standard LDA is used for text‐mining, where both low‐ and high‐frequency words are often removed prior to running the model (Boyd‐Graber, Mimno, & Newman, 2014). Finally, the BBS actually records count data (rather than presence/absence) per stop in each route. However, because these counts may include the same individual observed multiple times and bird detection may vary by species and environmental conditions (e.g., weather or traffic noise), we decided to convert these data into presence/absence of each species per route. In total, the final dataset used for analysis contained information on 354 species and 4,397 routes, spread throughout Canada and the United States.

To determine whether these breeding bird groups have been shifting their spatial distribution over time, we divided our study period into two 6‐year periods: 1997–2002 and 2010–2015. Each route × period combination resulted in a distinct “sampling unit” (i.e., distinct row in our data matrix), and data from individual years within each time period were treated as repeated observations.

2.3.2. Climate datasets

To relate the spatial distribution of the identified groups to potential environmental drivers, we relied on freely available precipitation and temperature data from WorldClim version 2 (available at http://worldclim.org/version2) (Fick & Hijmans, 2017). These data consist of the 30‐years average climate information (from 1970 to 2000) for the month of June, covering the entire world.

2.3.3. Detecting the effect of climate change on breeding bird species composition

In an era of global change, an important feature of our method is that it is able to detect relatively subtle temporal changes in species composition. More specifically, we assessed whether group ranges had expanded north and contracted south. These are the patterns we a priori expected given warming temperatures and the strong influence of temperature on the spatial distribution of a range of taxonomic groups, including birds (Chen, Hill, Ohlemuller, Roy, & Thomas, 2011; Hitch & Leberg, 2007; Moritz et al., 2008; Parmesan & Yohe, 2003). To detect these patterns, we fit the model once to data from both time periods (instead of fitting the model separately for each time period). This enables the estimation of distinct sets of ${\theta }_{\mathit{lk}}$ for each time period (i.e., ${\theta }_{\mathit{lk}}^{\left(1997-2002\right)}$ and ${\theta }_{\mathit{lk}}^{\left(2010-2015\right)}$) but a single set of ${\varphi }_{\mathit{ks}}$. A group's range was defined to be the locations in which a focal group was present with a relatively high probability in 1997–2002 or 2010–2015 (i.e., ${\theta }_{\mathit{lk}}^{\left(1997-2002\right)}>0.05$ or ${\theta }_{\mathit{lk}}^{\left(2010-2015\right)}>0.05$). Based on parameter estimates from these locations, we estimated the Spearman correlation of the difference between current and past proportions of the focus group (i.e., ${\theta }_{\mathit{lk}}^{\left(2010-2015\right)}$‐${\theta }_{\mathit{lk}}^{\left(1997-2002\right)}$) and latitude.

2.4. Additional analyses and software details

We set the maximum number of groups to 20 for our case study. To interpolate the estimates of the proportion of different groups to unsampled areas, we relied on the inverse distance weighted (IDW) algorithm implemented in the package “gstat” (Graler, Pebesma, & Heuvelink, 2016; Pebesma, 2004). Interpolations were restricted to locations within one degree of a BBS route. Finally, our algorithm was programmed using a combination of C++ (through the Rcpp package; Eddelbuettel & Francois, 2011) and R code (R Core Team 2013). We provide a tutorial in the Supporting Information Appendix S2 for fitting this model.

3. RESULTS

3.1. Results from simulation set 1

Despite assuming the potential existence of a much higher number of groups (K = 20), our results reveal that the proposed model was generally able to estimate well the true number of groups (boxplots in Figure 1), except for datasets with few species and locations but many groups (i.e., 100 locations, 50 species, and 10 groups; Figure 1f). We also find a good correspondence between the true and estimated parameter values for most of the scenarios explored (scatterplots in Figure 1), with a slightly worse performance for data with few species but many groups (i.e., 50 species and 10 groups; Figure 1g,h). Taken together, these results suggest that, when the ratio of the number of species to the number of groups is small, there is likely to be less distinction between groups from a species composition perspective, making it a harder task to untangle these groups. Finally, in relation to the prior, we find that our results are broadly similar for $\gamma =0.1$ and $\gamma =1$. The main difference is that parameter estimates tended to be slightly worse when the true number of groups is 3 and $\gamma =1$ and when the true number of groups is 10 and $\gamma =0.1$ (results not shown), agreeing with our expectations. Because smaller $\gamma$ values induce greater sparseness, parameters are better estimated with $\gamma =0.1$ when simulations are based on sparse assumptions (i.e., simulations with three groups) versus when this is not true (i.e., simulations with 10 groups).

Figure 1.

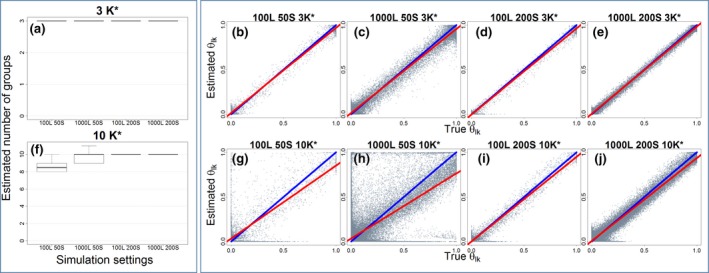
The Latent Dirichlet Allocation (LDA) estimates well the true number of groups (boxplots) and the ${\theta }_{\mathit{lk}}$ parameter values (scatterplots). Results from all 10 datasets in each simulation setting are displayed simultaneously, based on LDA with $\gamma$ set to 0.1. Top and bottom panels display results for three and 10 groups, respectively. Boxplots in panels (a) and (f) show the estimated number of groups (i.e., the number of groups deemed not to be superfluous), revealing that LDA can estimate well the true number of groups (K*) except for datasets with few locations (L), few species (S) but many groups (i.e., 100L 50S 10K*). Scatterplots (panels b–e and g–j) reveal that the ${\theta }_{\mathit{lk}}$ parameters can also be well estimated but there is considerable noise for datasets with few species but many groups (panels g and h). A 1:1 line and a linear regression line were added for reference (blue and red lines, respectively)

3.2. Results from simulation set 2

Our results reveal that the algorithm accurately estimates the proportion of the different groups in each location, regardless if MM units are present or not (left most and right most panels, respectively, in Figure 2). These results corroborate the observation that LDA encompasses hard clustering of sites and/or species as special cases. On the other hand, Figure 2 clearly reveals that hard clustering methods cannot represent these MM locations (k‐means and hierarchical clustering [HC] panels in Figure 2). Mixture model approaches such as RCP are sometimes perceived to be able to represent these gradual changes in the proportion of groups. However, our results reveal that, when applied to our simulated data, RCP tended to give transition regions that were too narrow (RCP panels in Figure 2). These model comparison results are particularly striking given that LDA was fitted assuming 20 potential groups, whereas results for the other methods were based on the assumption that the true number of groups was known. Notice that these figures illustrate how LDA can capture gradual changes in species composition associated with global change phenomena depending on what is being represented in the x‐axis. For instance, the x‐axis can represent a spatial gradient of anthropogenic forest disturbance (e.g., timber logging intensity or distance to forest edge) or can represent time (i.e., the same location sampled repeatedly through time, perhaps revealing the impact of climate change on species composition).

Figure 2.

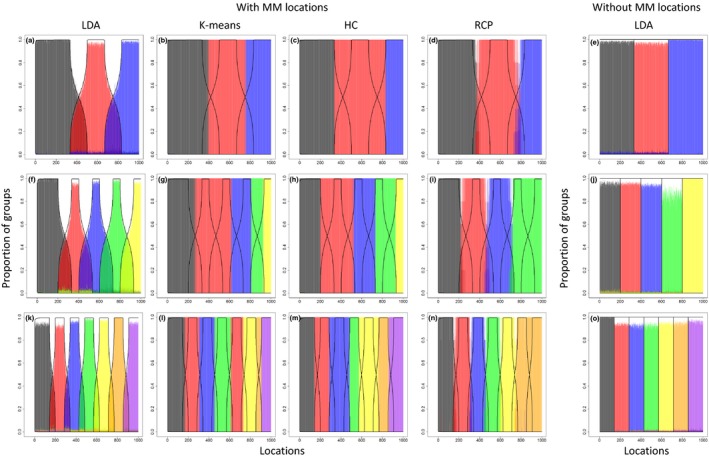
The extended Latent Dirichlet Allocation (LDA) method estimates well the true proportion of groups in each location (black lines) using simulated data with and without mixed‐membership (MM) locations. Results are shown separately for simulated data with 3, 5, and 7 groups (top to bottom). Left (panels a–d, f–i, k–n) and right (panels e, j, o) set of panels show results for simulated data with and without MM locations, respectively. Left to right panels for data with MM locations depict the results for LDA, k‐means clustering, hierarchical clustering (HC), and regions of common profile (RCP), respectively. For LDA, the proportion of groups corresponds to the ${\theta }_{\mathit{lk}}$ parameters. In all panels, the true proportion of each group is shown with thick black lines and the estimated proportions of each groups are shown with different colors and semitransparent vertical lines. For example, in the top set of panels with MM locations, the true proportion of each group for location 400 is equal to [0.54,0.46,0] whereas the estimated proportions were equal to [0.52,0.45,0.03] (LDA; a), [0,1,0] (K‐means; b), [0,1,0] (HC; c), and [0.2,0.8,0] (RCP; d)

Recall that the simulated data were generated with 3, 5, and 7 groups, but that the maximum number of groups when fitting LDA was set to 20. Our results suggest that the truncated stick‐breaking prior was able to correctly estimate the underlying true number of groups (boxplots in Figure 3) given that the estimated ${\theta }_{\mathit{lk}}$'s were shrunk toward zero for the superfluous groups (red boxes in Figure 3). We also find that all the other alternative methods required a much greater number of groups to fit the data as well as LDA when MM locations are present (line graphs in Figure 3). These results reveal that LDA achieves a much sparser representation of the data (based on the number of groups) without losing the ability to represent the inherent variability in the data. Although these results are expected, given the larger number of parameters in LDA, the ability to fit the data well with fewer groups is highly desirable from the user's perspective as the primary role of these methods is to reduce the dimensionality of biodiversity data. It is important to note that even in the absence of MM sampling units, LDA can still estimate well the true number of groups and has similar fit to the data as the other clustering approaches (results not shown). Finally, although Figures 2 and 3 are based on a single dataset, qualitatively similar results were found for multiple simulated datasets (a total of 10 datasets were simulated for each setting), revealing that these results were robust to variations in the simulated data.

Figure 3.

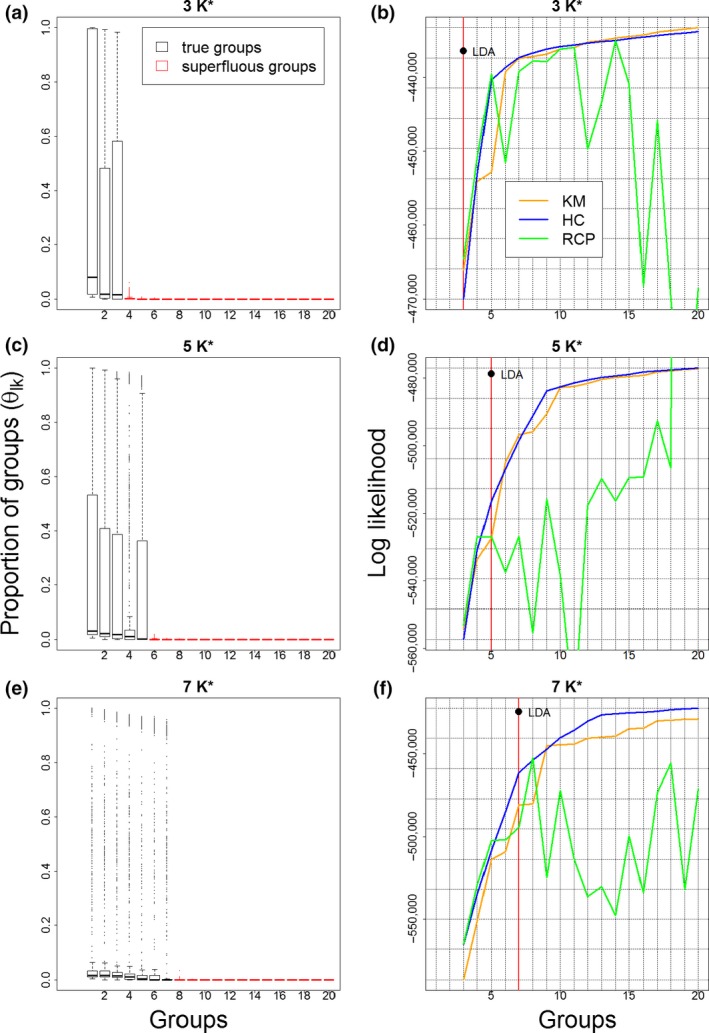
The extended Latent Dirichlet Allocation (LDA) method identifies the true number of groups (left panels) and fits the data better than other clustering approaches for data with MM locations (right panels). Results are shown separately for simulated data with 3, 5, and 7 groups (top to bottom). Boxplots depict the estimated proportion ${\theta }_{\mathit{lk}}$ of each group k for all locations l = 1,…,L. These boxplots emphasize how ${\theta }_{\mathit{lk}}$ for the irrelevant extra groups (red boxes) are shrunk to zero for all locations. Line graphs show the log likelihood, a measure of model fit for which larger values indicate better fit. These graphs reveal how other clustering approaches require a much greater number of groups to fit the data as well as LDA with fewer groups. Model fit results for LDA correspond to the posterior mean of the log likelihood. LDA results are shown with a single symbol because, differently from the other methods that were fitted multiple times with different number of groups, LDA was fitted just once using a maximum of 20 groups and the true number of groups was estimated (see corresponding boxplots). Details regarding how the log likelihood was calculated for the different methods are provided in Supporting Information Appendix S3

3.3. BBS case study

Overall, we identified 18 main breeding bird groups (of a maximum of 20) after eliminating groups that were very uncommon throughout the region (defined here as those for which ${\overline{\theta }}_{\mathit{lk}}$ was smaller than 0.5 for 99% of the locations, where ${\overline{\theta }}_{\mathit{lk}}$ denotes the posterior mean). An important test for any unsupervised method is if it is able to retrieve patterns that are widely acknowledged to exist by experts. Using the estimated group proportion for each location for the 2010–2015 period, we find striking spatial patterns (maps in Figure 4). Importantly, these spatial patterns generally agree well with other maps of bird communities (e.g., Bird Conservation Regions [BCR]; http://www.nabci.net/International/English/bird_conservation_regions.html), although we do not rely on other biotic (e.g., plants) and abiotic (e.g., soils, temperature, precipitation) data to fit the model. Despite these similarities, an important advantage of LDA is that, differently from BCR, it does not assume a sharp spatial delimitation of each bird group, a feature that may have potentially important implications for conservation.

Figure 4.

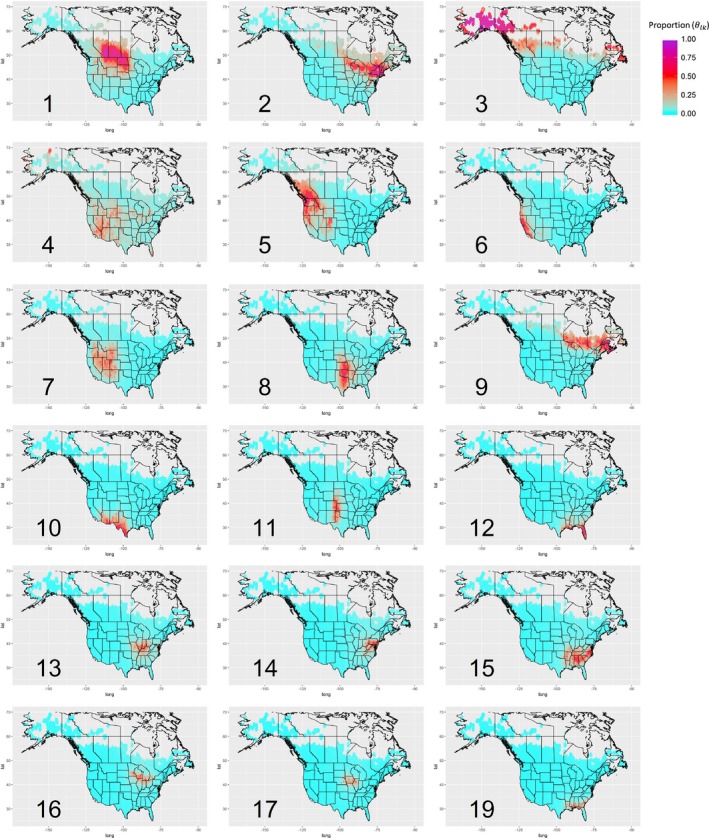
Breeding bird groups identified by LDA have a strong biogeographical pattern. Each panel depicts the interpolated proportion of each bird group (${\overline{\theta }}_{\mathit{lk}}$) based on the 2010–2015 parameter estimates. Species group identifiers are provided in the lower left corner

When examining more closely the spatial distribution of the breeding bird groups along the East coast, it is clear that groups 2, 9, 12, 14, 15, and 19 form rough latitudinal bands. To better illustrate this latitudinal pattern along the East coast, we interpolated the distribution of groups and plotted each group with a different color, revealing the regions that are dominated by each group as well as transition areas (Figure 5a). We find that the species that best distinguish these groups fall largely in line with the latitudinal variation in breeding ranges of common forest birds in the eastern United States, such as the least flycatchers and veeries in the northern group 9 and white‐eyed vireos and Carolina wrens in the southern group 15. Finally, group 12 captured wetland species common in Florida and the Gulf Coast such as the great egret.

Figure 5.

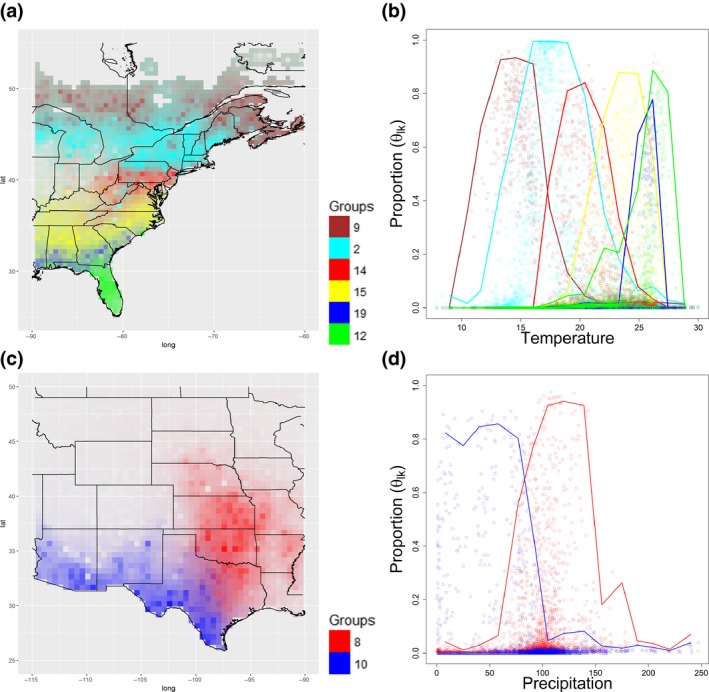
Biogeographical patterns of a subset of the species groups identified by LDA. The proportion of individual groups (given by the posterior mean ${\overline{\theta }}_{\mathit{lk}}$) is depicted in these panels. (a) displays the latitudinal bands formed by groups 2, 9, 12, 14, 15, and 19 along the East coast. (c) displays the spatial pattern of groups 8 and 10. In both (a) and (c), higher proportion of individual groups is depicted using more opaque (i.e., less transparent) colors and different groups are depicted with different colors. (b, d) reveals that average June temperature and precipitation gradients seem to strongly constrain the spatial distribution of these breeding bird groups, respectively. Circles represent the estimated proportion for each location and group while lines depict suitability envelopes. These envelopes were created by first defining equally spaced intervals on the x‐axis and then calculating the median x value and the 99% percentile of y within each interval and connecting these results. Notice that the same color scheme is used for right and left panels

Another interesting biogeographical pattern refers to groups 8 and 10 (Figure 5c), which seem to be divided along the middle of Texas, with several sites in this divide being characterized as transition areas comprised of mixed‐membership locations. This divide might be associated with the transition from Eastern Temperate Forests to the Great Plains. From a species composition perspective, we find that group 10 identifies species associated with desert environments (e.g., cactus wren and ash‐throated flycatcher), while group 8 identifies a mixture of short‐grass prairie birds (e.g., dickcissel) and species associated with open country environments with scattered trees and shrubs (e.g., eastern phoebe).

Besides these biogeographical patterns, we also highlight the ability of our algorithm in depicting how environmental gradients are linked to the proportion of each group. For instance, we display how the main East Coast groups (groups 2, 9, 12, 14, 15, and 19) are strongly constrained by average June temperatures (Figure 5b) and how the groups in Texas (groups 8 and 10) are constrained by average June precipitation (Figure 5d). These figures highlight that transition areas, either relative to precipitation or temperature, are often comprised of mixtures of groups. This pattern might arise because these areas are comprised of heterogeneous habitats and/or these areas are relatively homogeneous but with intermediate characteristics in comparison with sites with higher/lower precipitation or temperature. Regardless of the reason for this pattern, these areas are clearly suitable for multiple groups, an important characteristic that unfortunately cannot be captured with hard clustering methods.

3.3.1. Temporal patterns based on a comparison of ${\theta }_{\mathit{lk}}^{\left(1997-2002\right)}$ and ${\theta }_{\mathit{lk}}^{\left(2010-2015\right)}$

Although our results indicate that breeding bird groups have fairly consistent spatial distributions in both time periods (1997–2002 and 2010–2015; data not shown), we find statistically significant positive associations between latitude and changes in proportion between these two periods (${\theta }_{\mathit{lk}}^{\left(2010-2015\right)}$‐${\theta }_{\mathit{lk}}^{\left(1997-2002\right)}$) for nine groups (out of 18) using data from routes sampled during both of these time periods. This positive association reveals that increases in proportion tend to occur at higher latitudes whereas decreases are more likely at lower latitudes (Figure 6), supporting the hypothesis that breeding bird groups are increasingly expanding their range toward northern areas while contracting their range at southern boundaries. The remaining nine groups did not have a statistically significant association between latitude and changes in proportion. Although this analysis ignores uncertainty in parameter estimates for ${\theta }_{\mathit{lk}}^{\left(2010-2015\right)}$‐${\theta }_{\mathit{lk}}^{\left(1997-2002\right)}$, it is nevertheless useful in highlighting relatively subtle but important trends. In particular, these results agree with the patterns we a priori expected based on the warming environment, being robust to the threshold used to define a group's range (i.e., changing this threshold from 0.05 to 0.1 or 0.5 yielded several groups with statistically significant positive association with latitude, with the remaining groups having no statistically significant association).

Figure 6.

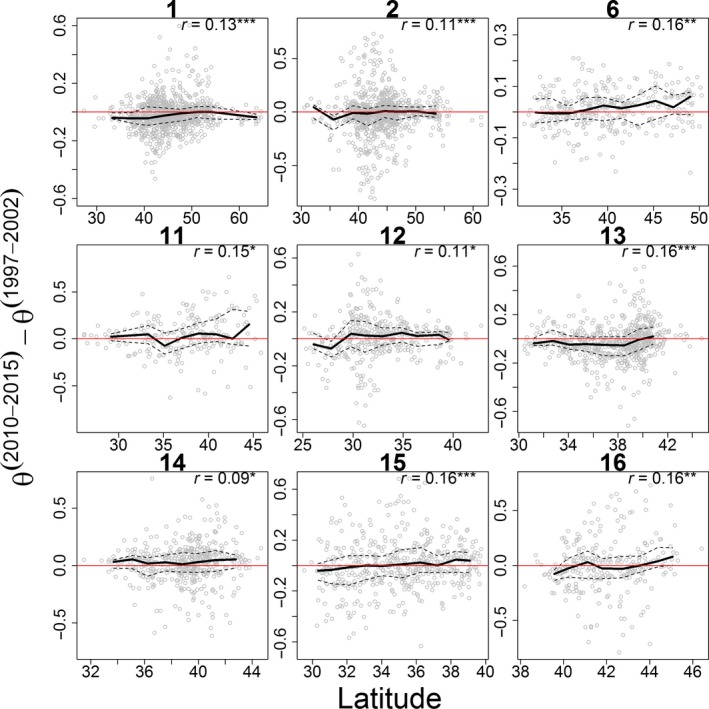
Species groups with a statistically significant association between latitude and change in group proportion (${\theta }^{\left(2010-2015\right)}-{\theta }^{\left(1997-2002\right)}$). Numbers in the title of each panel correspond to species group identifiers. Spearman's correlation coefficients between latitude and changes in proportion of each group between 1997–2002 and 2010–2015 are given in the upper right corner of each panel, and level of significance is indicated by asterisk (* 0.01 < p < 0.05, ** 0.001 < p < 0.01, *** p < 0.001). Trend lines were created by dividing the latitude range into 10 equally spaced bins and calculating the median (thick black line) and lower and upper quartiles (dashed black lines) for each bin. Bins with <10 observations were excluded. Results are based only on BBS routes within the range of each group, defined as locations for which ${\theta }_{\mathit{lk}}^{\left(1997-2002\right)}>0.05$ or ${\theta }_{\mathit{lk}}^{\left(2010-2015\right)}>0.05$

4. DISCUSSION

The Latent Dirichlet Allocation (LDA) model is a useful model for ecologists because it can more faithfully represent community dynamics and the impact of environmental change through the estimation of mixed‐membership sites (Valle et al., 2014). The standard LDA requires abundance data but, for many taxa, reliably estimating abundance is often very hard and costly (Ashelford, Chuzhanova, Fry, Jones, & Weightman, 2006; Joseph et al., 2006; Kembel, Wu, Eisen, & Green, 2012; Royle, 2004; Schloss, Gevers, & Westcott, 2011). For these reasons, presence/absence data are typically much more ubiquitous than abundance data, often enabling analysis at much larger spatial and temporal scales than that afforded by abundance data. Here, we have substantially developed the standard LDA model to enable the analysis of presence/absence data and we have demonstrated that novel insights can be gained using our method when applied to a continental‐scale wildlife dataset, with important implications for global change science.

Using the Breeding Bird Survey (BBS) dataset as a case study, we have shown how our method is able to uncover striking spatial and temporal patterns in bird groups. For example, we illustrate how these groups gradually change along a temperature gradient in the East Coast and a precipitation gradient in Texas. It has long been known that many bird species have strong relationships with abiotic gradients (Bowen, 1933), but how these gradients can explain entire groups of species has remained elusive. Furthermore, we find subtle but pervasive changes in bird group proportions, changes which follow the expected patterns based on climate change (e.g., Parmesan & Yohe, 2003). Half of the species groups (nine of 18) have expanded their northern range and shrunken their southern range. This pattern is consistent with species‐specific models of changes in bird distribution with climate change in the United States (e.g., Hitch & Leberg, 2007; La Sorte & Thompson, 2007). Our results expand on these findings by illustrating how entire groups are shifting their spatial distribution. Nevertheless, a more formal test that accounts for the multiple factors that influence the spatial distribution of birds will be required to ultimately confirm whether climate change is driving the spatial distribution shifts that we have detected.

An important limitation of the method that we have presented is that the identified groups do not change over time, even though their spatial distribution may vary. In other words, ${\theta }_{\mathit{lk}}$ may change with time but ${\varphi }_{\mathit{ks}}$ does not. This is particularly relevant in the context of climate change, where it is possible that the species composition of the groups themselves might be changing (Lurgi, Lopez, & Montoya, 2012; Stralberg et al., 2009; Urban et al., 2016). Another important limitation in this study is that the proposed model does not take into account imperfect detection, a pervasive issue for wildlife sampling (MacKenzie et al., 2002; Royle, 2004). This shortcoming can be partially attributed to inherent limitations in the BBS dataset, given that the estimation of detection probabilities requires very specific data types (e.g., repeated visits in occupancy models). It is also critical to highlight the importance of repeated observations per location given the relatively low information content in binary presence/absence data. Determining all the parameters in the proposed model, including the optimal number of groups, can be challenging in the absence of these repeated observations. Finally, although important broad‐scale patterns can be identified and novel insights gained from post hoc analysis of LDA model parameters, as illustrated with our case study, these results rely on a two‐stage analysis that does not take into uncertainty in the estimated parameters. Our ongoing work is focused on extending LDA to accommodate covariates through regression models built‐in to LDA so that uncertainty can be coherently propagated when performing more formal statistical tests and when making spatial and temporal predictions.

Community ecologists have traditionally relied on fitting clustering models with different numbers of clusters and choosing the optimal number of clusters using metrics such as AIC and BIC (Fraley & Raftery, 2007; Xu & Wunsch, 2005). Using simulated data, we have shown how the truncated stick‐breaking prior can aid the determination of the true number of groups. We acknowledge, however, that the modeler still has to specify the hyperparameter $\gamma$ and the maximum number of groups K. Using simulated data, we have found that setting $\gamma$ to 0.1 often works well and that our model often identifies K groups if the true number of groups is equal or larger than K. While this may be seen as an indication that K has to be increased when using real data, an extremely large number of groups defeats the purpose of dimension reduction, making it increasingly harder to visualize and interpret model outputs. Ultimately, we believe that the decision regarding the maximum number of groups K is a balance between what the data suggest and pragmatic considerations regarding how the results will be displayed and interpreted.

Our empirical example focused on large‐scale biogeographical patterns. Nevertheless, this method could also be applied in a landscape‐scale context, identifying spatial variation in community structure within general habitat types and across patches, or to analyze long‐term temporal changes in time‐series data of species composition (e.g., Christensen, Harris, & Ernest, 2018). Given the ubiquity of presence/absence data in community ecology, we believe that the extension of the Latent Dirichlet Allocation model developed here will see a much wider use, becoming an important addition to the toolkit of community ecologists.

AUTHOR CONTRIBUTIONS

DV wrote the first draft of the manuscript, developed the model and analyzed model results. PA contributed to the development of the model. QZ ran the alternative clustering methods for the simulated data. QZ and RF aided in the interpretation of BBS modeling results. All authors contributed substantially to revisions and gave final approval for publication.

Supporting information

 

 

 

Valle D, Albuquerque P, Zhao Q, Barberan A, Fletcher RJ Jr. Extending the Latent Dirichlet Allocation model to presence/absence data: A case study on North American breeding birds and biogeographical shifts expected from climate change. Glob Change Biol. 2018;24:5560–5572. 10.1111/gcb.14412