Effectiveness of the measures to flatten the epidemic curve of COVID-19. The case of Spain

Abstract

After the cases of COVID-19 skyrocketed, showing that it was no longer possible to contain the spread of the disease, the governments of many countries launched mitigation strategies, trying to slow the spread of the epidemic and flatten its curve. The Spanish Government adopted physical distancing measures on March 14; 13 days after the epidemic outbreak started its exponential growth. Our objective in this paper was to evaluate ex-ante (before the flattening of the curve) the effectiveness of the measures adopted by the Spanish Government to mitigate the COVID-19 epidemic. Our hypothesis was that the behavior of the epidemic curve is very similar in all countries. We employed a time series design, using information from January 17 to April 5, 2020 on the new daily COVID-19 cases from Spain, China and Italy. We specified two generalized linear mixed models (GLMM) with variable response from the Gaussian family (i.e. linear mixed models): one to explain the shape of the epidemic curve of accumulated cases and the other to estimate the effect of the intervention. Just one day after implementing the measures, the variation rate of accumulated cases decreased daily, on average, by 3.059 percentage points, (95% credibility interval: −5.371, −0.879). This reduction will be greater as time passes. The reduction in the variation rate of the accumulated cases, on the last day for which we have data, has reached 5.11 percentage points. The measures taken by the Spanish Government on March 14, 2020 to mitigate the epidemic curve of COVID-19 managed to flatten the curve and although they have not (yet) managed to enter the decrease phase, they are on the way to do so.

Graphical abstract

Highlights

• •After the COVID-19 cases skyrocketed, the Spanish government launched physical distancing.
• •The measures taken to mitigate the COVID-19 epidemic managed to flatten the curve.
• •The daily variation rate of accumulated cases decreased by 3.059 percentage points.
• •This reduction will be greater as time passes.

1. Introduction

As is known, the coronavirus disease 2019 (COVID-19), caused by infection with severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), dates back to December 29, 2019, when a cluster of pneumonia of unknown origin occurred in Wuhan, China (The 2019-nCoV Outbreak Joint Field Epidemiology Investigation Team, 2020). At the end of January, confirmed cases were concentrated in China (>7000), and in other countries there were only a few imported cases introduced through air travel (>70). However, in February several community outbreaks occurred in countries other than China, such as South Korea, Italy, Germany and Spain (ECDC, 2020a). On April 6, 2020, three months later, 1,244,421 confirmed cases of COVID-19 have been reported, including 68,976 deaths (ECDC, 2020b) with 49,71% of the cases (618,603) and 70,54% of the deaths (48,658) coming from Europe ECDC, 2020b. As of April 6, with 130,759 confirmed cases (10.51% of the world's total number of cases) and 12,418 deaths (18.00% of the world's total of deaths), Spain has become the country with the second-highest number of deaths (after Italy) and number of cases (after United States) (ECDC, 2020b).

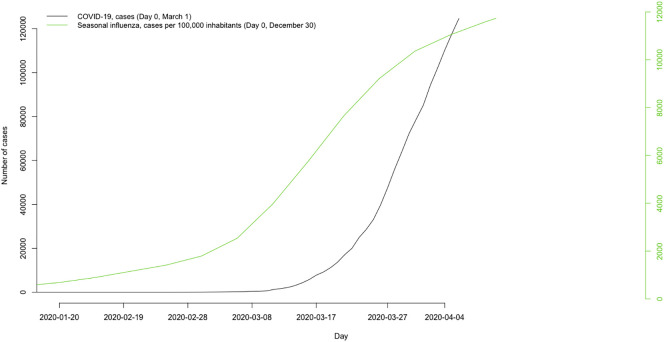
Although COVID-19 has the same symptoms as seasonal influenza, it differs in a number of ways. First, the SARS-CoV-2 has a much higher transmissibility, the reproduction number, R₀ (number of cases directly generated by one case) is estimated to be between 2.2 and 2.68 (Novel Coronavirus Pneumonia Emergency Response Epidemiology Team, 2020), while in the seasonal influenza virus R₀ is equal to 1.3 and 1.5 in the H1N1 influenza (SARS had an R₀ between 2 and 3 while the MERS R₀ is <1). See, for instance, Fig. 1 where it is observed that COVID-19 infections grow at much faster rate than seasonal influenza infections do. Second, the incidence in children is much lower. The mean age of patients with COVID-19 was 47 years (Novel Coronavirus Pneumonia Emergency Response Epidemiology Team, 2020), while that of influenza was 23.4 years (that of SARS was 39.9, while the median age of patients with MERS was 50 years). Third, the average incubation period for the SARS-CoV-2 is 4 days, with a range between 2 and 7 days (Novel Coronavirus Pneumonia Emergency Response Epidemiology Team, 2020), whereas the virus of the seasonal influenza virus has an average incubation period of 2 days and a range between 1 and 7 days (in SARS the average incubation period was 4.6 days, ranging between 2 and 14 days and in MERS 5.2 days, ranging between 2 and 13 days). Finally, the mortality rate is also much higher (2.3% in COVID-19 vs. 0.13% in seasonal influenza and 0.20% in H1N1 influenza) (Novel Coronavirus Pneumonia Emergency Response Epidemiology Team, 2020), although this rate should be interpreted with caution, since there is a significant underreporting of registered cases (ECDC, 2020a).

Fig. 1.

Accumulated confirmed cases of COVID 19 and seasonal influenza, Spain

Source: COVID-19: ECDC (https://www.ecdc.europa.eu/en/publications-data/download-todays-data-geographic-distribution-covid-19-cases-worldwide), Seasonal influenza: Influenza Surveillance System in Spain [in Spanish] (http://vgripe.isciii.es/inicio.do)

Day 0 corresponds to the epidemic outbreak: Coronavirus: The day that 20 cases were registered for the first time; Seasonal influenza: The week in which the global incidence rate of influenza was >54.6 cases per 100,000 inhabitants.

If the cases registered are represented in a sequence graph (that is, in the abscises time and the confirmed cases in ordinate) on a logarithmic scale, it can be seen that the epidemic outbreak begins its exponential growth (R₀ > 1) from the day they are registered 20 new cases are registered for the first time (for example in China this happened on January 22, in South Korea on February 20, in Italy on February 23, and in Spain on March 1).

In the early stages of the outbreak the governments of some countries tried a containment strategy. After the cases skyrocketed, showing that it was no longer possible to contain the spread of the disease, the governments of many countries launched mitigation and suppression strategies. Only China opted for a suppression strategy, one which aimed to reverse the epidemic by reducing the basic reproduction number to <1. On January 23 (just a day after the epidemic outbreak started its exponential growth), China took drastic actions, such as severe confinement involving quarantine measures affecting 60 million people, and strict limitations to travel. Other countries, however, have opted for a mitigation strategy, trying to slow but not stop the spread of the epidemic (flattening the epidemic curve, i.e. decreasing the peak of the epidemic). By slowing down the spread of the epidemic, the aim is to mitigate its effects on the health care system and on the social perception of the epidemic. South Korea introduced mass screening, localized quarantines, and a national mobile phone alert system to warn residents in districts or localities of the movements of affected individuals to detect possible outbreaks. Most countries have opted, to varying degrees, for physical distancing (also known as social distancing), which attempts to minimize close contact between people and thus slow down the spread of the epidemic. Physical distancing measures taken by governments include quarantines, travel restrictions, and the closure of schools, workplaces, stadiums, cinemas, theatres and restaurants. Furthermore, people themselves, either following the advice of their governments or obligatorily doing so to avoid fines, have adopted physical distancing methods by staying home, limiting travel, avoiding crowded areas, using non-contact greetings, and physically distancing themselves from others. Italy adopted these measures on March 7 in Lombardy and 11 other nearby provinces, and then in the rest of the country on March 12 (13 and 18 days after the epidemic outbreak started its exponential growth). Meanwhile, in Spain the measures were adopted for the whole country on March 14 (13 days after the epidemic outbreak started its exponential growth).

In Spain there has been some political controversy over whether these harsh measures are in fact sufficient to flatten the curve or if even more drastic measures (like the total lockdown of the Hubei province in China) are needed. Our objective in this paper was to evaluate ex-ante (before the flattening of the curve) the effectiveness of the measures adopted by the Spanish Government to mitigate the COVID-19 epidemic.

2. Methods

2.1. Design

We employed a time series design, using information from January 17 to April 5, 2020.

2.2. Variables

New daily COVID-19 cases from Spain, China and Italy. The data source was the European Center for Disease Prevention and Control (ECDC, 2020c).

2.3. Statistical analysis

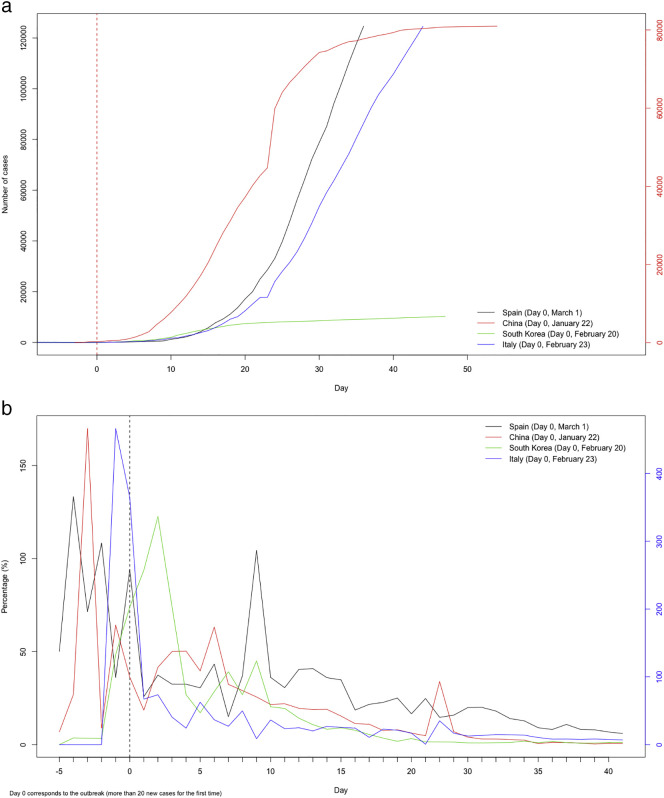
Our hypothesis was that the behavior of the epidemic curve is very similar in all countries. The problem is what variable to represent in that curve. Thus, the epidemic curve of new cases is not comparable between countries, since there is great variability in the diagnosis of the disease. For example, in Spain the diagnostic protocol established that routine diagnostic tests for coronaviruses should not be carried out on contacts, thus leaving mild and asymptomatic cases untested. However, in South Korea, performing as many tests as possible has been shown to be the key tool in curbing the virus. Nevertheless, the epidemic curve of the accumulated cases shows striking similarity between countries, especially once they are put on the same scale, defining day 0 as the outbreak of the epidemic (see Figs. 2 ). The shape of this curve can be estimated by the rate of variation of the represented variable.

Fig. 2.

(a) Accumulated confirmed cases of COVID 19

Source: COVID-19: ECDC (https://www.ecdc.europa.eu/en/publications-data/download-todays-data-geographic-distribution-covid-19-cases-worldwide) (b) Rate of variation of accumulated confirmed cases of COVID 19

Source: COVID-19: ECDC (https://www.ecdc.europa.eu/en/publications-data/download-todays-data-geographic-distribution-covid-19-cases-worldwide).

For this reason, as a response variable, we used the variation rate of the accumulated cases of COVID-19 in Spain, from February 25 to April 5, 2020 (until February 26, the number of cases accumulated in Spain did not reach two digits -specifically, only 7 cases had occurred-).

We specified two generalized linear mixed models (GLMM) with variable response from the Gaussian family (i.e. linear mixed models).

One to explain the shape of the epidemic curve of accumulated cases:

$$E\left(Y_t\right)={\eta }_t+{\tau }_t+f_1\left(X{1}_t\right)+f_2\left(X{2}_t\right)+f_3\left(X{3}_t\right)$$ (a)

where E() denoted expectation; Y_t the variation rate of the accumulated cases of COVID-19 in Spain; X1_t the variation rate of the accumulated cases in China; X2_t the variation rate of the accumulated cases in South Korea; X3_t the variation rate of the accumulated cases in Italy; η _t and τ _t denote two random effects indexed on time (t = 1, …, 88; with 1 on February 25, 2020), the first unstructured (independent and identically distributed random effects, iid) and the second structured (random walk of order two, rw2); and f_i() (i = 1,2,3) denoted structured random effects (random walk of order one, rw1) indexed on X_i (i = 1,2,3).

Following the terminology of the integrated nested Laplace approximations (INLA) approach (Rue et al., 2009; Rue et al., 2017), random effects were defined using a multivariate Gaussian distribution with a zero mean and precision matrix τΣ, where τ was a constant and Σ was a matrix that defined the dependence structure of the random effects. In unstructured random effects (iid) Σ was a diagonal matrix of 1 s; in random walk random effects Σ was defined assuming that increments (in random walk of order 1, rw1, Δu _i = u _t − u _t−1, in random walk of order 2, rw2, Δ² u _t = u _t − 2u _t−1 + u _t−2) followed a Gaussian distribution with zero mean and a constant precision τ (Gómez-Rubio, 2020).

Although both random walks (rw1 and rw2) are discrete latent effects, when, as in our case, they are indexed on a continuous variable they can be used as smoothers to model non-linear dependency on covariates in the linear predictor (i.e. the variation rates of the accumulated cases in China, South Korea and Italy). The curve of an rw2 is quite a bit smoother than that of an rw1.

That is, we assumed that the time evolution of the curve of accumulated cases presents a time dependency (structured time variability) with a non-linear behavior, possibly with unsystematic deviations (unstructured time variability), which resembles the time evolution of the curves of Italy and China and, to a lesser extent, South Korea (see Fig. 2a). We allowed the time evolution of these three curves to be nonlinear as well.

We specified another GLMM to estimate the effect of the intervention:

$$E\left(Y_t\right)={\eta }_t+{\tau }_t+{\tau }_t:M_{t-k}+\gamma M_{t-k}+f_1\left(X{1}_t\right)+f_2\left(X{2}_t\right)+f_3\left(X{3}_t\right)$$ (b)

where M_t denoted the intervention (1 from March 14, when the Spanish Government decreed the confinement of the population and 0 until March 13, included); k denoted lag (k = 0,1,2,3); γ was a parameter; τ _t : M _t denoted the interaction between the intervention and the structured temporal random effect; and the rest of variables and parameters were defined above.

Note that, we assumed that the effect of the intervention could have varied over time and that this effect may not be instantaneous but may occur with some delay.

Inferences were made following a Bayesian perspective, using the INLA approach (Rue et al., 2009; Rue et al., 2017). We used priors that penalize complexity (called PC priors). These priors are robust, in the sense that they do not have an impact on the results and, in addition, they have an epidemiological interpretation (Simpson et al., 2017).

The predictive accuracy of the models was evaluated using the Watanabe-Akaike information criterion (WAIC) (Watanabe, 2010) and the Deviance Information Criterion (Spiegelhalteer et al., 2002).

All analyses were made with the free statistical environment R (version 3.6.3) (R Core Team, 2020).

3. Results

Once the model (a) was estimated, we found that the epidemic curve of South Korea did not explain the temporal evolution of the rate of variation of the cases accumulated in Spain. In all cases, the 95% credibility interval of the random effects indexed with the rate of change for South Korea contained 1. Furthermore, both the WAIC and the DIC of the model with the South Korean curve were very similar to the model without this curve (WAIC -134.08 with South Korea and −134.59 without South Korea; DIC -130, 26 with South Korea and −130.96 without South Korea). For this reason, we re-specified models (a) and (b), omitting the South Korean curve.

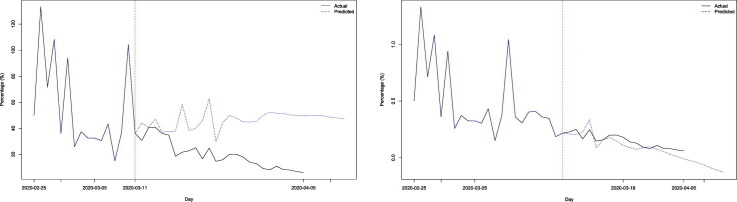
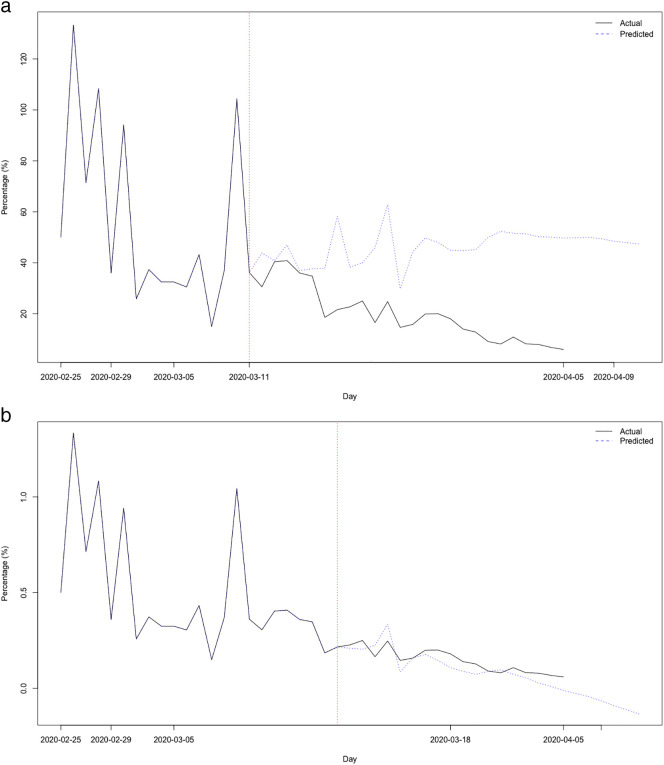
To evaluate the effect of the mitigation measures taken by the Spanish Government, we used both model (a) and model (b). Using model (a) we make predictions with two origins, one on March 11 (before the measurements) and another on March 18 (after the measurements). The results are shown in Table 1 and Fig. 3a and b. As can be seen both in the table and in the figures, the model with the origin before the intervention had an increasing trend, contrary to the real time evolution with its decreasing trend. In addition, observe how from the fourth day (March 15) they shoot up, distancing themselves from the real time evolution. Contrary to this, the predictions with origin after the intervention, have a decreasing trend as with the real evolution, and begin to differ from the real evolution, in a much smaller amount than the predictions with origin before the intervention, from the seventh day (25 of March).

Table 1.

New cases of COVID-19 in Spain. Actual and predicted with two origins, March 11 (before the intervention on March 14) and March 18 (after the intervention on March 14).

Date	Actual new cases	Predicted new cases
		Origin 11 March	Origin 18 March
March 12	501	719
March 13	864	861
March 14	1227	1561
March 15	1522	1802
March 16	2000	2516
March 17	1438	3465
March 18	1987	7380
March 19	2538	7672	2342
March 20	3431	11,096	2769
March 21	2833	17,810	3657
March 22	4946	35,589	6697
March 23	3646	27,454	2305
March 24	4517	52,879	4599
March 25	6584	85,171	5944
March 26	7937	124,017	5804
March 27	8578	171,887	4921
March 28	7851	248,213	4482
March 29	8189	362,050	4003
March 30	6549	525,372	5197
March 31	6398	844,427	5180
April 1	9222	1,325,889	4100
April 2	7719	1,991,211	2258
April 3	8102	2,937,484	2806
April 4	7472	4,399,395	2865
April 5	7026	6,551,768	2226

Fig. 3.

(a). Prediction of the variation rates of the cumulative cases of COVID-19 in Spain (%). Origin March 11 (before the intervention)

(b). Prediction of the variation rates of the cumulative cases of COVID-19 in Spain (%). Origin March 18 (after the intervention).

The estimation of the effect of the intervention, carried out with model (b) is shown in Table 2 . As we can see, the intervention had its effects one day late (delay 1 is the only one whose 95% credibility interval does not contain unity). As of March 15, the variation rate of accumulated cases decreased daily, on average, by 3.059 percentage points, (95% credibility interval: −5.371, −0.879). The reduction, when comparing before and after the intervention (calculated as reduction in delay 1 minus the counterfactual), was, on average, 5.186 percentage points each day.

Table 2.

Effect of the intervention, mitigation measures for the COVID-19 epidemic taken by the Government of Spain on March 14, on the variation rate of the accumulated cases.

Date	Estimated effect (95% credibility interval)
Lag 0	−0.265 (−59.67, 146.4)
Lag 1	−3.059 (−5.371,-0.879)
Lag 2	−0.431 (−2.756, 1.943)
Lag 3	−1.097 (−3.503, 1.322)
Lag 4	1.414 (−1.267, 4.382)
Lag 5
Contrafactual (no intervention)	2.127 (0.498,4.308)

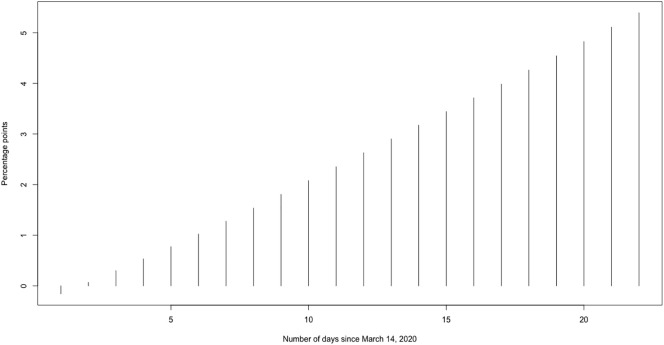
In Fig. 4 we can see that the reduction in the rate of variation of the accumulated cases increased from the day after the intervention (March 15), specifically from −0.32 percentage points to −5.11 percentage points.

Fig. 4.

Reduction of the rate of variation of cumulative cases of COVID-19 in Spain (percentage points).

4. Discussion

As we have estimated, the measures taken by the Spanish Government on March 14, 2020 to mitigate the epidemic curve of COVID-19 managed to flatten the curve and although they have not (yet) managed to enter the decrease phase, they are on the way to do so. In fact, just one day after implementing the measures, the variation rate of accumulated cases decreased daily, on average, by 3.059 percentage points, (95% credibility interval: −5.371, −0.879). This reduction will be greater as time passes. In this sense, we estimate that the reduction in the variation rate of the accumulated cases, on the last day in which we have data (April 5, three weeks after the intervention) has reached 5.11 percentage points.

An aspect that goes beyond our objective is which of the mitigation strategies that governments have taken has been the most effective. However, using our findings, we could provide some argument for the discussion. Thus, first, looking at Fig. 2a, it seems that the strategy adopted by South Korea has been the most effective, since it has managed to flatten the curve before any other country (between 10 and 15 days after the outbreak). In this same sense, we find that the curves that are most similar to Spain (still growing exponentially, i.e. with a reproductive number greater than one) are those of Italy and China in their first month of evolution (since the outbreak). As for whether confinement in Spain is not sufficient to flatten the curve and should therefore be tightened, our results seem to contradict it. We predict that the rate of change of cumulative cases will be zero (that is, the epidemic curve will flatten) in early April.

Our paper could have several limitations. First, estimates of new cases must be interpreted with some caution. It is important to note that under-registration occurs in Spain as a consequence of a lack of tests. It is very possible that when mass screening is carried out, the number of confirmed cases will increase, each time approaching the real incidence. However, we believe that our results on the variation of accumulated cases are much more reliable, since they are not based on the number of cases but on the shape of the epidemic curve, which is very similar in all the countries.

Second, our model performs well in the short term (a week at most), limiting it in making predictions about when the epidemic will peak. However, we are convinced of its usefulness in evaluating the measures that can be taken against the epidemic.

Funding

This paper received no funding.

Data availability

Data and code are available upon request to Marc Saez (marc.saez@udg.edu).

Ethics

Not applicable.

Authors' contribution

MS has the original idea for the paper. MS designed the study. The bibliographic search and the writing of the introduction were carried out by all the authors. The methods and statistical analysis were chosen and performed by MS. All authors created the tables and figures and wrote the results and the discussion. The writing and final editing was done by all authors. All authors reviewed and approved the manuscript.

CRediT authorship contribution statement

Marc Saez:Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing - original draft, Writing - review & editing, Visualization, Supervision.Aurelio Tobias:Software, Validation, Writing - original draft, Writing - review & editing, Visualization.Diego Varga:Software, Validation, Writing - original draft, Writing - review & editing, Visualization.Maria Antònia Barceló:Methodology, Software, Validation, Formal analysis, Investigation, Writing - original draft, Writing - review & editing, Visualization.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Editor: Jianmin Chen