Effect of lowest harmonic rank on fundamental-frequency difference limens varies with fundamental frequency

Abstract

This study investigated the relationship between fundamental frequency difference limens (F0DLs) and the lowest harmonic number present over a wide range of F0s (30–2000 Hz) for 12-component harmonic complex tones that were presented in either sine or random phase. For fundamental frequencies (F0s) between 100 and 400 Hz, a transition from low (∼1%) to high (∼5%) F0DLs occurred as the lowest harmonic number increased from about seven to ten, in line with earlier studies. At lower and higher F0s, the transition between low and high F0DLs occurred at lower harmonic numbers. The worsening performance at low F0s was reasonably well predicted by the expected decrease in spectral resolution below about 500 Hz. At higher F0s, the degradation in performance at lower harmonic numbers could not be predicted by changes in spectral resolution but remained relatively good (<2%–3%) in some conditions, even when all harmonics were above 8 kHz, confirming that F0 can be extracted from harmonics even when temporal envelope or fine-structure cues are weak or absent.

I. INTRODUCTION

Pitch is a fundamental perceptual property of many real-world sounds, including speech and music, and is crucial for the perceptual organization of sounds in an auditory scene. For most natural stimuli, the pitch is related to the fundamental frequency (F0) of the sound. For a simple stimulus like a harmonic complex tone, the perceived pitch corresponds to the F0 of the complex, irrespective of the presence of the F0 component in the complex. Considerable effort has gone into understanding which harmonics within a complex tone determine or dominate the overall pitch (Dai, 2000; Moore et al., 1985; Plomp, 1967). In most cases, it has been found that the low-numbered harmonics (N ≤ 6) dominate the pitch percept. Other studies have investigated how the harmonics present affect the accuracy of the pitch percept, quantified in terms of the F0 difference limen (F0DL) (Bernstein and Oxenham, 2003; Cullen and Long, 1986; Hoekstra, 1979; Houtsma and Smurzynski, 1990; Krumbholz et al., 2000; Ritsma, 1962; Ritsma and Hoekstra, 1974; Shackleton and Carlyon, 1994). Several studies have reported a relatively clear transition between low (good) F0DLs and high (poor) F0DLs, with plateau regions below and above the transition region (e.g., Bernstein and Oxenham, 2003, 2006a,b; Houtsma and Smurzynski, 1990). Based on the fact that F0DLs have been reported to depend on the phase relationships between harmonics above but not below this transition point, it has been proposed that the transition relates to the point at which harmonics are no longer spectrally resolved (e.g., Bernstein and Oxenham, 2006a,b; Houtsma and Smurzynski, 1990; Shackleton and Carlyon, 1994). However, there are situations where the presence of resolved harmonics is neither necessary (e.g., Bernstein and Oxenham, 2008; Graves and Oxenham, 2019) nor sufficient (Bernstein and Oxenham, 2003) to produce good F0DLs. Thus, it remains unclear whether harmonic resolvability per se, or something that is related to harmonic number, and therefore covaries with resolvability, explains the transition from good to poor F0DLs (e.g., Bernstein and Oxenham, 2005; de Cheveigné and Pressnitzer, 2006).

Ritsma and Hoekstra (1974) measured rate discrimination thresholds (RDTs) for filtered click trains with 1/3-octave fixed bandpass filters with center frequencies (Fc) between 1 and 8 kHz and repetition rates ranging from 20 to 2000 Hz. They found that for all conditions tested, performance deteriorated as the Fc increased from the 8th harmonic to the 20th harmonic, in a way that was broadly independent of Fc or repetition rate. The authors concluded that the decrease in ability to discriminate rates for Fc corresponding to harmonic numbers (N) greater than eight reflected the limits of spectral resolution in the cochlea. They suggested that frequency discrimination thresholds for the individual components limited performance for N < 8, whereas a temporal cue determined performance once thresholds reached a plateau for N > 20 and components were no longer spectrally resolved. In a later study, Cullen and Long (1986) tested five different repetition rates between 50 and 800 Hz, using high-pass filters with cutoff frequencies between 2.5 and 10 kHz. When thresholds were plotted as a function of N, their data were broadly consistent with those of Ritsma and Hoekstra (1974), with a transition from good to poor performance generally occurring for values of N between 10 and 20.

The studies of Ritsma and Hoekstra (1974) and Cullen and Long (1986) both used fixed bandpass filters. Although this kept the spectral envelope of the stimulus constant, it left open the possibility that listeners were able to use individual harmonics, rather than the pitch elicited by the F0, to complete the task. Indeed Ritsma and Hoekstra (1974) explicitly pointed out that their discrimination thresholds at high frequencies seemed to be unaffected by whether participants actually perceived the F0, or the “residue pitch,” and Cullen and Long (1986) noted the similarity between their F0DLs in these conditions and the frequency difference limens for pure tones in the same frequency region.

One way to avoid the possibility of listeners using individual harmonics, rather than the overall pitch, to perform F0 discrimination, is to rove the lowest harmonic present (e.g., Houtsma and Smurzynski, 1990). The roving makes the lowest harmonic an unreliable cue and therefore encourages listeners to use the overall pitch or F0 (Micheyl et al., 2010). Although this method may provide clearer evidence for the use of the F0, rather than individual harmonics, it has the potential disadvantage that the roving changes the timbre of the tone, which may prove distracting, thereby elevating thresholds (e.g., Allen and Oxenham, 2014). Bernstein and Oxenham (2006b) used a fixed bandpass filter and found roughly the same point of transition as an earlier study that had used a fixed number of harmonics and had roved the lowest harmonic present (Bernstein and Oxenham, 2003). However, this good correspondence between fixed-filter and roving-harmonic paradigms has only been established for F0s between about 100 and 200 Hz. It is not clear whether the same pattern of results would be found for higher or lower F0s, as all the previous studies with F0s below 100 Hz or above 200 Hz have used a filter with a fixed passband.

The purpose of this study was to investigate the relationship between F0DLs and the lowest harmonic number present in a harmonic complex tone over a wide range of F0s, while encouraging listeners to base their judgments on the pitch of the F0 by roving the lowest harmonic number present. Twelve consecutive harmonics were used to ensure a stable F0 percept that was not strongly influenced by the varying timbre (Houtsma and Smurzynski, 1990; Laguitton et al., 1998). In addition, the salience of potential spectral edge cues (Kohlrausch and Houtsma, 1992) was reduced by lowering the amplitude of the lowest and highest components in the complex and by embedding the complex tones in broadband noise.

II. METHODS

A. Participants

Eleven participants (eight female, three male) were tested, ranging in age from 18 to 30 years with audiometric thresholds no greater than 15 dB hearing level (HL) at octave frequencies from 250 to 8000 Hz. None of the participants reported a history of neurological or hearing deficits. Written informed consent was provided by each participant, and all participants were compensated for their time. The experiment was conducted at the University of Minnesota–Twin Cities. The protocol was approved by the University of Minnesota Institutional Review Board.

Each participant had to pass two screening tests to be eligible to take part in the actual experiment. The first screening test was to confirm audibility of the stimuli at the very low and very high frequencies. Detection thresholds for single pure tones were measured using an adaptive (two-down one-up) three-interval three-alternative forced-choice (3I3AFC) procedure in quiet for pure tones at 90 Hz, as well as at 12 and 16 kHz, in addition to the audiometric octave frequencies between 250 Hz and 8 kHz. Tone durations were 500 ms, including 20-ms raised-cosine onset and offset ramps. Detection thresholds at each frequency were measured twice and the mean of the two runs was calculated. To qualify for the study, a participant's detection thresholds had to be below 50 dB sound pressure level (SPL) at each frequency. Figure 1 shows the thresholds in quiet, averaged across the eleven participants.

FIG. 1.

Mean detection thresholds for pure tones in quiet. Error bars represent ±1 standard error (s.e.) across eleven participants.

The second screening test involved an F0-discrimination task with a mean F0 of 200 Hz to ensure that all the participants were able to discriminate F0s with a reasonable degree of accuracy, thereby ruling out conditions such as amusia. The F0DLs were measured over three runs for complex tones with an F0 of 200 Hz and harmonics 1–12 using an adaptive (three-down one-up) two-interval two-alternative forced-choice (2I2AFC) procedure. All tones were presented at 55 dB SPL per component. Participants were presented with two successive complex tones with durations of 300 ms, including 10-ms raised-cosine ramps, separated by an inter-stimulus interval of 500 ms, and were asked to judge which had the higher pitch or F0. Feedback was provided after each trial. All 11 participants had geometric mean F0DLs of less than 2% and were included in the main experiment. The main experiment involved measuring F0DLs for a large number of conditions (12 F0s with five different harmonic number cutoffs and two phase manipulations). Due to the length of the experiment, six of the 11 participants took part in the low-F0 experiment, which included F0s from 30 to 200 Hz and the other five took part in the high-F0 experiment, which included F0s from 200 to 2000 Hz.

B. Stimuli

All the stimuli were harmonic complex tones presented in a background of threshold equalizing noise (TEN) (Moore et al., 2000) with a bandwidth extending from 20 Hz to 20 kHz to prevent the detection of distortion products and to ensure that all the components were presented at approximately equal sensation level up to frequencies of 16 kHz. The F0s tested in the low-F0 experiment were 30, 40, 50, 70, 100, and 200 Hz; the F0s tested in the high-F0 experiment were 200, 280, 400, 800, 1120, 1600, and 2000 Hz. All stimuli consisted of ten consecutive harmonics presented at full amplitude of 55 dB SPL per component, spectrally flanked by two harmonics presented 6 dB lower (i.e., 49 dB SPL per component), for a total of 12 consecutive harmonics. The level was reduced for the edge components to reduce the salience of any potential edge-pitch cues (Kohlrausch and Houtsma, 1992), thereby helping listeners to focus on the F0. The nominal lowest harmonic number, N, presented at full amplitude was either 4, 7, 10, 13, or 16. The lowest harmonic present was roved across trials, such that the actual lowest harmonic number was N or N + 1. Therefore, in each trial, the lowest harmonic numbers for the two intervals were selected at random without replacement from these two possibilities. The components in each complex were added either in sine phase or in random phase, with new starting phases selected for each presentation. These two phase relationships were used because an effect of phase is thought to be indicative of the harmonics being spectrally unresolved in the auditory periphery (e.g., Bernstein and Oxenham, 2003; Houtsma and Smurzynski, 1990; Oxenham et al., 2009; Shackleton and Carlyon, 1994). The TEN was presented at a level of 45 dB SPL within the estimated equivalent rectangular bandwidth (ERB_N) of the auditory filter at 1 kHz (Glasberg and Moore, 1990), meaning that the full-amplitude components were presented at 10–15 dB above their masked thresholds in the TEN, which has been shown to be sufficient to mask potential distortion products (Oxenham et al., 2009; Oxenham et al., 2011). An additional (independent) TEN was lowpass filtered with a cutoff frequency half an octave below the nominal frequency of the lowest harmonic in each trial and was added at a level per ERB_N of 55 dB SPL. The duration of the tones was 500 ms, including 30-ms raised-cosine onset and offset ramps, and the inter-stimulus interval was 500 ms. The TEN was gated on 200 ms before the onset of the first tone and was gated off 100 ms after the offset of the second tone, also with 30-ms raised-cosine ramps.

C. Procedure

The experiments were conducted in a double-walled sound-attenuating booth. All stimuli were generated in matlab (The Mathworks, Natick, MA) via a 24-bit L22 soundcard (LynxStudio, Costa Mesa, CA) with a sampling rate of 48 kHz and were presented diotically via Sennheiser HD650 headphones. For all the tasks, thresholds were obtained using a 2I2AFC task with an adaptive three-down one-up procedure (Levitt, 1971). It has been shown that there is generally little difference between using 2AFC and 3AFC procedures to measure F0DLs, despite the fact that the 2AFC task involves labeling and the 3AFC task only requires the identification of a difference (Oxenham and Micheyl, 2013). In each trial, participants were presented with two intervals, each containing a complex tone, and were asked which interval contained the higher tone. The two complex tones had F0s that were geometrically centered around the nominal F0. The initial F0 difference (ΔF0) between the two intervals was 20%, relative to the lower of the two F0s. This value was increased or decreased by a factor of 1.41 after one incorrect or three consecutive correct responses, respectively. After the first four reversals in the adaptive procedure, the step size was reduced to a factor of 1.2 and the run continued for another six reversals. Feedback was provided after each trial. Threshold was defined as the geometric mean value of ΔF0 at the last six reversals. At least four such runs were completed by each participant in each condition. The order of conditions (F0s and N) was selected randomly for each participant and each repetition, so that each condition was run before any condition was repeated. The experiment took approximately six sessions of two hours each. The condition with F0 = 200 Hz was tested for both sets of participants to test for any differences between the two groups.

III. RESULTS

The mean data from all conditions are shown in the upper panels of Figs. 2 and 3, illustrating how F0DLs varied as a function of N across a range of reference F0s. Since the lowest full-amplitude harmonic was roved between N and N + 1, the average value of N is plotted on the abscissa. The dashed curves show the limit of performance that would be expected if participants based decisions on the frequency of the lowest harmonic (Bernstein and Oxenham, 2003; Moore et al., 2006; Oxenham et al., 2009). This limit is achieved when the F0s of the two intervals are so different that the lowest full-amplitude harmonic of the higher-F0 stimulus is always higher in frequency than the lowest full-amplitude harmonic of the lower-F0 stimulus, so that a response based on the frequency of the lowest harmonic (as opposed to the F0) is always correct [for more details and a derivation, see Oxenham et al. (2009)]. This limit assumes no coding noise and so represents the best possible performance that could be achieved based on the lowest full-amplitude harmonic present in the complex. Thus, F0DLs that fall below the dashed curve cannot be based entirely on the frequency of the lowest harmonic. For F0DLs that fall above the line, we cannot rule out the possibility that performance was based on the lowest frequency present, rather than the F0 itself, although that does not imply that the F0 was not used. The lower panels of Figs. 2 and 3 show the ratio between F0DLs in the sine-phase and random-phase conditions; a value greater than one indicates that F0DLs were higher (worse) in the random-phase than in the sine-phase condition, as would be expected in cases where performance is based on the temporal-envelope cues produced by unresolved harmonics (e.g., Houtsma and Smurzynski, 1990).

FIG. 2.

(Color online) Upper panels show F0DLs as a function of average lowest harmonic number (N) for F0s ranging from 30 to 50 Hz (left panel) and 70 to 200 Hz (right panel) for complexes in sine phase (filled symbols, solid lines) and random phase (open symbols, dashed lines). Lower panels show the ratio of the F0DLs for complexes in random and sine phase. Error bars represent ±1 s.e. across the six participants who completed the low-F0 experiment.

FIG. 3.

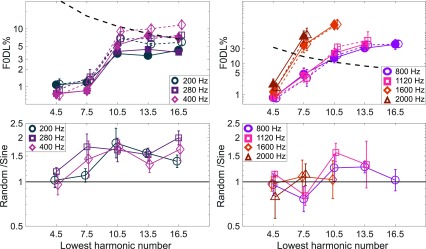
(Color online) Upper panels show F0DLs as a function of average lowest harmonic number (N) for F0s ranging from 200 to 400 Hz (left panel) and 800 to 2000 Hz (right panel) for complexes in sine phase (filled symbols, solid lines) and random phase (open symbols, dashed lines). Lower panels show the ratio of the F0DLs with complexes in random and sine phase. Error bars represent ±1 s.e. across the five participants who completed the high-F0 experiment.

Average F0DLs with F0 = 200 Hz (Fig. 2, upper right panel and Fig. 3, upper left panel) were analyzed first, as this was the only condition to be completed by all 11 participants and it is also one that has been tested extensively in earlier studies with roved lowest harmonic number (e.g., Bernstein and Oxenham, 2003; Houtsma and Smurzynski, 1990). In line with previous data, F0DLs were low (good) for low values of N and increased at higher values of N, with a relatively steep transition between 7.5 and 10.5, and a plateau of around 5% for higher values of N. A repeated-measures analysis of variance (ANOVA) was carried out on the log-transformed F0DLs, with N and component phase as within-subjects factors and participant group as a between-subjects factor. As expected, there was no significant main effect of group (F_1,9 = 0.01; p = 0.93), and no interaction between group and N (F_4,36 = 0.79; p = 0.535), between group and component phase (F_1,9 = 0.31; p = 0.59), or between group, N, and component phase (F_4,36 = 0.36; p = 0.84). The lack of an influence of group confirms that performance was similar between the two groups of participants for the conditions that they both undertook. There was a main effect of N (F_4,36 = 133.3; p < 0.001), reflecting lower F0DLs at low values of N and higher F0DLs at higher values of N. There was also a main effect of phase (F_1,9 = 39.7; p < 0.001) as well as a significant interaction between phase and N (F_4,36 = 6.16; p = 0.001). The effects of phase and N and their interaction, with phase effects only emerging at high values of N, where the components are spectrally unresolved, are consistent with earlier studies (Bernstein and Oxenham, 2003; Houtsma and Smurzynski, 1990; Shackleton and Carlyon, 1994).

A different pattern emerged at the lower F0s, below 100 Hz (Fig. 2, upper left panel). Performance was consistently poor with an F0 of 30 Hz, regardless of N. Nevertheless, F0DLs still fell below the dashed line, indicating that performance was likely based on F0 and not on the lower spectral edge of the stimulus. At 40 and 50 Hz, performance tended to be better at the lowest N (4.5) and plateau at N = 7.5, but remained poorer than observed at 100 or 200 Hz. Performance with an F0 of 70 Hz was intermediate between that observed at 50 and 100 Hz. As seen in the lower left panel of Fig. 2, no consistent effects of phase were seen for F0s from 30 to 70 Hz. However, effects of phase were observed at the higher values of N for F0s of 100 and 200 Hz, consistent with results from previous studies (Bernstein and Oxenham, 2003; Houtsma and Smurzynski, 1990). A repeated-measures ANOVA was carried out on the log-transformed F0DL values for all the low-F0 conditions, with within-subjects factors of lowest harmonic number (N), F0, and phase. There were significant main effects of F0 (F_5,25 = 69.5, p < 0.001) and N (F_4,20 = 129.2, p < 0.001) but not of phase (F_1,5 = 1.5, p = 0.26). Significant interactions were observed between phase and F0 (F_5,25 = 7.1, p = 0.006), phase and N (F_4,20 = 6.2; p = 0.014), and F0 and N (F_20,100= 22.5, p < 0.001). The three-way interaction was not significant (F_20,100 = 2.192; p = 0.112). Paired comparisons were carried out using Bonferroni correction. Post hoc comparisons for F0DLs as a factor of F0 indicated a significant difference (Bonferroni adjusted α = 0.05/15 = 0.0033) between F0DLs for the 30-Hz F0 and all other F0s (p < 0.001 in all cases), and a significant difference between F0DLs at 100 and 200 Hz and all other F0s (p < 0.001 in all cases). No differences were detected between 40 and 50 Hz, or between 100 and 200 Hz. Further post hoc tests on N revealed no differences between values of N of 10.5, 13.5, and 16.5 (p > 0.5 in all cases), confirming the apparent plateau in F0DLs at higher values of N. The F0DLs at N = 4.5 and N = 7.5 were significantly different both from each other and from all higher values of N (p < 0.005, Bonferroni adjusted α = 0.05/10 = 0.005), confirming the consistent increase in F0DLs overall from N = 4.5 to N = 10.5. The interaction between N and F0 presumably reflects the observation that the plateau of F0DLs with increasing N appears to occur earlier at lower F0 values (40 and 50 Hz), with roughly constant F0DLs at all values of N for the lowest F0 value (30 Hz). The interactions between N and phase and between F0 and phase presumably reflect the observation that phase effects only emerge at the higher values of N (> 10) and then primarily for the higher F0s (100 and 200 Hz).

For the F0s between 200 and 400 Hz (Fig. 3, upper left panel), the pattern of results remained roughly constant, with a clear transition in F0DLs occurring between N = 7.5 and N = 10.5, as was also observed at 100 and 200 Hz in the group data from the low F0s. Thus, it seems that the transition from good to poor F0DLs reported in the literature to occur around the 10th harmonic (Bernstein and Oxenham, 2003; Houtsma and Smurzynski, 1990; Shackleton and Carlyon, 1994) applies primarily to F0s between 100 and 400 Hz. At F0s higher than 400 Hz, performance remained relatively good at N = 4.5 for all F0s but became considerably poorer already at N = 7.5 (Fig. 3, right panel; note the large range of F0DLs on the ordinate). Indeed, for F0s of 1600 and 2000 Hz, only the conditions with N = 4.5 produced F0DLs below the dashed curve and so could not be based simply on the lowest harmonic present in the stimulus. For F0s of 800 and 1120 Hz, performance was still likely based on F0 comparisons for N = 7.5, but performance was already poorer than that observed for N = 4.5.

Because performance based unambiguously on F0 was limited to F0s below 800 Hz, these data were analyzed separately (Fig. 3, upper left panel). A repeated-measures ANOVA was carried out on the log-transformed F0DLs using only data from conditions with F0s of 200, 280, 400 Hz (N = 5), with within-participants factors of N, F0, and phase. There were significant main effects of F0 (F_2,8 = 8.92, p = 0.009), N (F_4,16 = 159.4, p < 0.001), and phase (F_1,4 = 39.2, p = 0.003). Significant interactions were observed between phase and N (F_4,16 = 5.5; p = 0.006), and between F0 and N (F_8,32 = 5.3, p < 0.001). No significant interaction was observed between phase and F0 (F_2,8 = 1.4, p = 0.424). Additionally, the three-way interaction was not significant (F_8,32 = 0.773; p = 0.629). Again, the interaction between N and phase is consistent with phase effects only emerging at higher values of N (> 10; lower left panel of Fig. 3). Paired comparisons were carried out using Bonferroni correction. Post hoc comparisons for F0DLs as a factor of F0 indicated a significant difference between F0DLs for the 400-Hz F0 and all other F0s (200 and 280) (p < 0.01, Bonferroni adjusted α = 0.05/3 = 0.0167). Further post hoc tests on N revealed no differences between values of N of 10.5, 13.5, and 16.5 (p > 0.05 in all cases), confirming the apparent plateau in F0DLs at higher values of N. The F0DLs at N = 4.5 and N = 7.5 were significantly different both from each other and from all higher values of N (p < 0.005, Bonferroni adjusted α = 0.05/10 = 0.005), confirming the consistent increase in F0DLs overall from N = 4.5 to N = 10.5. Unsurprisingly, no effects of phase were observed for F0s of 800 Hz and above, given that the envelope fluctuations at high repetition rates would probably not have been detectable (e.g., Burns and Viemeister, 1976; Kohlrausch et al., 2000).

Figure 4 replots the sine-phase data from all F0s. In the top panel, F0DLs are plotted as a function of N, as in Figs. 2 and 3. The results confirm that the transition from low to high F0DLs was not uniform as a function of N across the range of F0s tested here. Absolute frequency may play a role in determining F0DLs, particularly at the higher frequencies, where pure-tone frequency difference limens (FDLs) also worsen at frequencies above about 3–4 kHz (e.g., Moore, 1973). The F0DLs are plotted in the middle panel of Fig. 4 as a function corresponding to the absolute frequency of average value of N. Although the transition from low to high F0DLs is clearly not uniform in terms of absolute frequency, it is interesting that both the low and high plateaus in F0DL values follow similar shapes when plotted in these terms. Finally, to test whether the transition from low to high F0DLs is related to harmonic resolvability, the bottom panel of Fig. 4 shows F0DLs as a function of the auditory filter ERB, as estimated by Glasberg and Moore (1990), at the average value of lowest full-amplitude harmonic present (N), relative to the spacing of the harmonics (i.e., the F0). When plotted in this way, the transitions between low and high F0DLs line up more convincingly than when plotting the results as a function of N, with the exception of the higher values of F0 (800 Hz and higher), where performance is poorer than expected based on auditory filter bandwidths. The point above which all harmonics should begin to be spectrally unresolved occurs at approximately ERB_N/F0 = 1. Interestingly, in the case of the 30-Hz F0, poor performance would be predicted for all values of N tested, because the harmonics would be expected to be unresolved in all cases.

FIG. 4.

(Color online) Top panel shows F0DLs as a function of average lowest harmonic number (N) for F0s ranging from 30 to 2000 Hz. Middle panel shows F0DLs as a function of the frequency of the lowest harmonic. Bottom panel shows F0DLs as a function of ERB_N/F0. All the data are for complexes in sine phase. The filled symbols correspond to the data from the low-F0 experiment and the open symbols correspond to the data from the high-F0 experiment. Error bars represent ±1 s.e. across the participants in each experiment subset. Closed and open dark blue circles correspond to the data from the two participant groups at the common F0 of 200 Hz (denoted as 200-1 and 200-2 Hz in the legend).

IV. DISCUSSION

This study measured F0DLs as a function of F0 and lowest harmonic number over a wide range of F0s. In line with earlier studies in which the lowest harmonic present was roved (Bernstein and Oxenham, 2003; Houtsma and Smurzynski, 1990), for F0s between 100 and 400 Hz, F0DLs were low (good) and were independent of phase, so long as harmonics below the 10th were present. When only harmonics higher than the 10th were present, F0DLs were higher and displayed dependence on phase, with random-phase stimuli producing higher F0DLs than sine-phase stimuli. However, the pattern of results was different for F0s below that range, with progressively poorer performance at F0s of 70 Hz and below, and no phase dependence of F0DLs. In addition, the transition from low to high F0DLs with increasing N became less marked as the F0 decreased, and was nonexistent at the lowest F0 of 30 Hz. This outcome is consistent with the findings of Krumbholz et al. (2000), where no difference in F0DLs was observed with an F0 of 32 Hz for low-frequency cutoffs ranging from 0.2 to 0.8 kHz. Even poorer performance was observed by Krumbholz et al. (2000) at higher cutoff frequencies, corresponding to lowest harmonic numbers of 50 and above—conditions that were not tested here. Pressnitzer et al. (2001) and Krumbholz et al. (2000) reported that the lower limit of pitch, based on melody perception and F0DLs, was around 30 Hz (the lowest F0 tested here), and suggested that the limit reflected a temporal coding mechanism that was unable to process time intervals longer than about 33 ms (Licklider, 1951), corresponding to an F0 of 30 Hz.

Jackson and Moore (2013) attempted to determine the dominant region for pitch for complex tones with F0s of 50, 100, and 200 Hz. They varied the F0 of only a group of consecutive harmonics while keeping the other components in the complex fixed in frequency, reasoning that performance should be best when the varying components were in the dominant region for pitch. They found that performance varied much less as a function of the position of the varying harmonics at 50 Hz than at 200 Hz, to the extent that it was difficult to discern a clear transition or plateau in the data for the 50-Hz F0. Nevertheless, at 50 Hz, performance did seem to worsen between the 5th and 7th harmonic and remained roughly constant thereafter; in contrast at 200 Hz, performance worsened by more than an order of magnitude as the lowest varying harmonic increased from three to 11. Both the earlier plateau and the smaller range of performance at 50 Hz than at 200 Hz are consistent with the data from the present study, although a quantitative comparison is difficult, given the different nature of the stimuli.

For F0s higher than 400 Hz, F0DLs worsened with increasing N but remained good (1%–2%, although not as good as for lower F0s, where F0DLs were sometimes <1%) at the lowest N value of 4.5, even at the highest F0 of 2 kHz, where the fourth and fifth harmonics had frequencies of 8 and 10 kHz, respectively. The finding of relatively good F0DLs, even when all harmonics were at or above 6000 Hz, is consistent with earlier studies that reported usable pitch information (for F0DLs, pitch matching, and melody discrimination) for resolved harmonics (in the absence of temporal-envelope pitch), even when all harmonics were above the putative limits of phase locking in the auditory nerve (Lau et al., 2017; Oxenham et al., 2011). These findings also contradict the “existence region” of residue pitch proposed by Ritsma (1962, 1967) whereby only components below about 5–6 kHz elicited a percept corresponding to the F0. As seen in Fig. 4 (middle panel), F0DLs for the lowest conditions of N are still within the range of 1%–2% for lowest absolute frequencies up to about 8.5 kHz. As mentioned in earlier studies (Oxenham et al., 2011), this apparent discrepancy may arise due to the smaller number of harmonics used by Ritsma and to the lack of background noise in his study.

Poorer pitch perception with harmonic numbers greater than 8–10 has often been interpreted to be related to peripheral frequency selectivity and harmonic resolution (Bernstein and Oxenham, 2003; Houtsma and Smurzynski, 1990; Ritsma and Hoekstra, 1974; Shackleton and Carlyon, 1994). According to Glasberg and Moore's (1990) estimates of auditory filter bandwidths, ERB_N is roughly proportional to the filter's center frequency for frequencies above about 1000 Hz. Hence, if peripheral selectivity (and hence harmonic resolvability) was the sole factor determining F0DLs, we would expect the transition point between good and poor performance to remain roughly constant, when expressed in terms of N, at least when all the harmonics are above about 1000 Hz. It is possible that poorer performance, and earlier transitions from lower to higher F0DLs, at lower F0s (< 100 Hz) reflect poorer frequency selectivity at frequencies below 500 Hz. The bottom panel of Fig. 4 provides support for this hypothesis by showing that the transition between good and poor performance lines up reasonably well across all F0s lower than 800 Hz, when F0DLs are plotted as a function of the ERB_N relative to harmonic spacing (F0). However, if F0DLs are based on temporal-envelope cues associated with unresolved harmonics at the lowest F0s, it is not clear why changes in phase relations (from sine phase to random phase) did not strongly affect F0DLs for F0s lower than 100 Hz. It is possible that clearer phase effects would have been observed if the stimuli had been presented at a higher signal-to-noise ratio in the background noise.

Frequency selectivity alone cannot explain why performance degraded more rapidly with increasing N at F0s of 800 Hz and above. Indeed, according to more recent estimates of human frequency selectivity at low sound levels using non-simultaneous masking (Oxenham and Shera, 2003; Shera et al., 2002; Sumner et al., 2018), relative auditory filter bandwidth actually decreases (implying sharper filtering) with increasing center frequency, which would imply improved performance (i.e., increasing N at the transition from good to poor F0DLs) with increasing F0, i.e., the opposite of the results observed here (see Fig. 4, top and bottom panel). Poorer performance may be due to the effects of degraded auditory-nerve phase locking at high frequencies (e.g., Heinz et al., 2001; Moore and Ernst, 2012); however, such an account seems unlikely to explain how good F0DLs were still observed here and in earlier studies (Lau et al., 2017), even when the lowest frequency present exceeded 8 kHz (Verschooten et al., 2018). As suggested in earlier studies (Lau et al., 2017; Oxenham et al., 2011), it may be that poorer F0 sensitivity (and possibly greater susceptibility to interference through roving the lowest harmonic) is related to higher-level constraints that may arise due to less everyday exposure to such high F0s. We note that while performance remained good (1%–2%) for these high frequencies, it degraded somewhat with increasing absolute frequency above 5 kHz (Fig. 4, middle panel). This pattern is similar to the pure tone results of Moore (1973), where a similar degradation at high frequencies was observed, albeit at slightly lower frequencies than the current results. The improvement with added harmonics over simple pure tones is unlikely to be due to a simple integration of information; as shown by Lau et al. (2017), F0DLs for complex tones with high-frequency resolved harmonics are better than would be predicted by an optimal integration of information from each of the individual harmonics, suggesting instead a different pitch-based mechanism. Interestingly, thresholds in conditions with poorer performance (N ≥ 7.5) at the higher F0s also seemed to follow the same rising curve at lowest frequencies above about 5 kHz (Fig. 4, middle panel). Note, however, that these thresholds are the ones that also fall above the dashed curve in the upper panel of Fig. 4, suggesting that performance may have been based on the lower spectral edge rather than F0, so performance would be expected to follow that of high-frequency pure-tone frequency discrimination.

Our finding that the transition between good and poor F0DLs does not occur at a constant value of N across a wide range of F0s is not consistent with earlier data that measured F0DLs of filtered click trains as a function of the lower cut-off frequency of the filter (Cullen and Long, 1986; Ritsma and Hoekstra, 1974). In both of these earlier studies, rate discrimination thresholds (RDT) were measured for filtered click trains for a range of repetition rates and the transition was found to occur around N = 8–10 over a wide range of F0s. As mentioned in the Introduction, an important potential reason for this apparent discrepancy is the fact that the earlier studies did not rove the lowest harmonic present, which makes it difficult to rule out the possibility that performance was based on frequency discrimination of individual harmonics, rather than the F0 itself. Roving the lowest harmonic, as we did in the present study, reduces the possibility that listeners based their judgments on individual harmonics (Micheyl et al., 2010); however, the roving also introduces a possible “distraction” effect by varying the timbre between intervals (e.g., Allen and Oxenham, 2014). Our use of a relatively large number of harmonics (12), reduced-amplitude edge components, and a high level of background noise should have mitigated the distraction effect somewhat, but does not eliminate it.

These new data, showing a dependence on F0 of the transition from good to poor F0 discrimination as a function of N, provide new challenges for models of pitch perception. Although decreasing spectral resolution at low frequencies can likely explain the decrease in the value of N marking the transition between good and poor F0 discrimination at low F0s, it does not explain why phase effects are absent at low F0s, even though the harmonics should be clearly unresolved and temporal-envelope cues should be accessible. The decrease in the value of N marking the transition from good to poor F0 discrimination at high F0s (above 400 Hz) also cannot be explained in terms of changes in frequency selectivity, as the results are opposite to those predicted by the relatively sharper filters at high frequencies. They may be explained in part by poorer phase locking at the level of the auditory nerve, although a model of complex pitch perception based solely on timing information (e.g., Cariani and Delgutte, 1996; Meddis and O'Mard, 1997) would have difficulty explaining the ability of listeners to discriminate F0 in conditions where all the components fall above 8 kHz, and where little-or-no temporal-envelope information is present. Future models accounting for this pattern of results will likely need to incorporate the role of frequency selectivity and temporal sensitivity, as well as currently unspecified constraints on the ability of listeners to extract pitch from upper harmonics with high-frequency F0s.