Gaussian and Mixed Graphical Models as (multi-)omics data analysis tools

Abstract

Gaussian Graphical Models (GGMs) are tools to infer dependencies between biological variables. Popular applications are the reconstruction of gene, protein, and metabolite association networks. GGMs are an exploratory research tool that can be useful to discover interesting relations between genes (functional clusters) or to identify therapeutically interesting genes, but do not necessarily infer a network in the mechanistic sense. Although GGMs are well investigated from a theoretical and applied perspective, important extensions are not well known within the biological community. GGMs assume, for instance, multivariate normal distributed data. If this assumption is violated Mixed Graphical Models (MGMs) can be the better choice.

In this review we provide the theoretical foundations of GGMs, present extensions such as MGMs or multi-class GGMs, and illustrate how those methods can provide insight in biological mechanisms. We summarize several applications and present user-friendly estimation software.

1. Introduction

With the advent of high-throughput omics technologies an increased need for data analysis tools emerged to explore relationships between different biological readouts. These readouts can be, for instance, the expression levels of different genes, the presence of genomic variants, the accessibility of individual genomic regions (chromatin structure), or the abundances of single metabolites. In this context, naive correlation-based approaches were and are still widely used. Examples are the reconstruction of gene (Eisen et al., 1998; Aoki et al., 2007; Stuart et al., 2003; Obayashi and Kinoshita, 2009) and metabolite networks (Weckwerth et al., 2004; Camacho et al., 2005; Ursem et al., 2008; Rosato et al., 2018).

However, ordinary pair-wise correlation is only a measure of the marginal relationships between variables and so does not distinguish direct from indirect effects. Consequently, it is only a weak measure of dependency (Schäfer and Strimmer, 2004); if two variables are correlated, this does not necessarily imply that they are directly dependent on each other, as the observed correlation could be mediated by a third variable. This issue was already discussed by Pearson and Yule, as, for instance, reviewed in (Aldrich et al., 1995). In the context of gene networks, it was approached using first and second order partial correlations by (De La Fuente et al., 2004). These first or second order partial correlations are correlations between two genes that are corrected for the presence of either one or two genes.

Full order partial correlations are correlations between two variables corrected for all other variables under investigation. Thus, they allow to distinguish direct from indirect effects. Gaussian Graphical Models (GGMs) (Lauritzen, 1996; Bishop, 2006) provide a framework to estimate them. In contrast to pair-wise correlations, partial correlations measure the conditional dependencies between variables. These partial correlations can then be visualized as a network, in which nodes represent variables and edges the dependencies between them. Equally important, the absence of an edge corresponds to a conditional independency of two variables given the remaining variables.

This review will provide readers a general overview of GGMs and their extensions. We provide both the basic theory of GGMs and describe their scope of application in the analysis of omics data.

GGMs assume variables that follow a multivariate normal distribution. We will further discuss Mixed Graphical Models (MGMs) (Lauritzen, 1996), which allow the incorporation of, e.g., one set of variables following a Gaussian, and one set of variables following a multinomial distribution, simultaneously. We provide examples for the estimation and interpretation of both GGMs and MGMs, present available estimation and visualization software, and illustrate the strengths and weaknesses of the different methods.

As both standard GGMs and/or MGMs have, in recent years, been extended to account for compositeness of omics data (Kurtz et al., 2015), to include causality (Sedgewick et al., 2018), to take into account different sample groups, e.g., control vs. treated group (Danaher et al., 2014; Zhao et al., 2014), time-series experiments (Abegaz and Wit, 2013), or to include prior knowledge (Wang et al., 2013; Li and Jackson, 2015; Zuo et al., 2017; Yu et al., 2017; Manatakis et al., 2018), we will further review these novel concepts.

2. Conditional independence, partial correlations, Gaussian and Mixed Graphical Models

Throughout this section, we introduce the basic ideas of probabilistic graphical modeling. Here, the term “variable” can refer not only to any kind of biological readout, such as gene and protein expression levels, genomic variants, methylation levels, or metabolite concentrations, but also to demographic data such as sex, age, body-mass index, or other factors. A summary of all important statistical terms is given in Table 1.

Table 1:

Glossary of general terms in probabilistic graphical modeling.

General term	Short description
Pearson correlation	measure of linear relationship between two variables, can take values between −1 and 1
first/second order partial correlation	correlation between two variables corrected for presence of one/two other variables at a time, can take values between −1 and 1
full order partial correlation	correlation between two variables corrected for presence of all other variables under investigation, can take values between −1 and 1
probability distribution P(X = x)	gives the probability that a random variable X takes on the value x in an experiment
statistical independence	two random variables X and Y are statistically independent if the probability that X will take on the value x does not affect the probability that Y will take on the value y and vice versa
conditional independence	two random variables X and Y are conditionally independent given the random variable Z if the probability that X will take on the value x does not affect the probability that Y will take on the value y and vice versa given that Z equals z
probabilistic graphical model (PGM)	describes conditional dependency structure of a set of random variables and represents it in a graph
node/vertex	represents one variable in PGM
edge	represents conditional dependency between two vertices given all other vertices in PGM; absence of an edge encodes conditional independency between two vertices given all remaining vertices
neighbor of vertex vi	vertex which is adjacent, i.e. directly connected by an edge, to vertex vi
first order neighborhood of vertex vi	complete set of neighbors of vertex vi
precision matrix	encodes conditional dependencies of PGM, whereas 0 typically represents conditional independence between two vertices
Gaussian Graphical Model (GGM)	PGM with only Gaussian distributed variables
discrete Markov Random Field	PGM with only discrete variables
Mixed Graphical Model (MGM)	PGM with mixed variable types, typically Gaussian and categorical variables
parameter regularization	penalization of complex models to reduce risk of overfitting
overfitting	the estimated model too closely describes the underlying relationships in the training data and is not generalizable to independent data sets
probabilistic graphical model learning	determining the presence and strength of each individual edge in a PGM
probabilistic graphical model selection	selection of one specific PGM out of a set of estimated PGMs based on the optimization of a certain model selection criterion

2.1. Statistical independence and conditional independence

First, consider two random, discrete variables X and Y following a joint probability distribution P. P (X = x, Y = y) gives the probability that X will take on the value x, and Y the value y, respectively. X and Y are statistically independent if and only if their joint probability factorizes as

$$P\left(X=x,Y=y\right)=P\left(X=x\right)P\left(Y=y\right),$$ (1)

where P (X = x) and P (Y = y) are the marginal probability distributions of X and Y. This means that the probability that X will take on the value x does not affect the probability that Y will take on the value y and vice versa. For two random, continuous variables the analogous equation holds for the corresponding probability density functions, as illustrated in the Supplementary File 1.

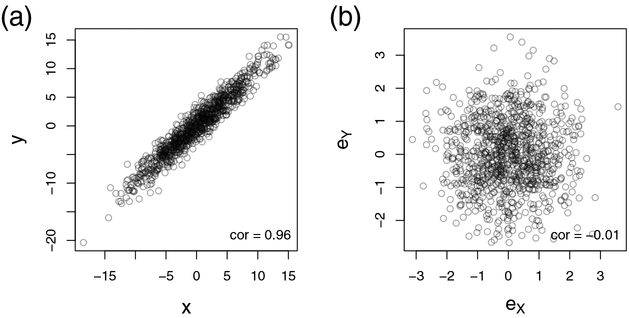
However, consider the case that X and Y are statistically dependent, i.e. the factorization in Eq. (1) does not hold. Now it is not a priori clear if this dependency is due to a direct relationship between the two variables or if it is mediated by a set of other random variables Z. For illustration, we simulated this scenario in the Supplementary File 1. The corresponding results are shown in Figure 1a and b. In Figure 1a we plot X versus Y and observe an excellent correlation, suggesting a direct association between X and Y. However, if we adjust for the third variable Z, this dependency completely diminishes, as shown in Figure 1b. Thus, the observed relationship between X and Y was only a consequence of their individual associations with Z.

Figure 1: Scatterplots before and after variable adjustment.

Figure (a) shows the scatterplot of 1000 measurements between two multivariate normal random variables X and Y. Figure (b) takes into account the effect of a third random variable Z, which is associated with both X and Y. Here, we calculated the residues e_X and e_Y after a linear regression of X with Z and of Y with Z. We observe that the correlation between X and Y in (a) can be entirely explained by variable Z as shown in Figure (b). The corresponding Pearson correlation coefficients are given in the lower right corners. Data were simulated from a three-dimensional multivariate normal distribution, (X, Y, Z)^T ~ N(0, Ω⁻¹), where the precision matrix Ω is defined by ω₁₁ = ω₂₂ = ω₃₃ = 1, ω₃₁ = ω₃₂ = ω₁₃ = ω₂₃ = −0.7 and 0 elsewhere, as outlined in the Supplementary File 1.

This example illustrates the need for more sophisticated measures of independence. Such a measure is conditional independency, which we introduce next. Assume that X, Y, and Z follow a joint probability distribution P. Then, X and Y are conditionally independent given Z if and only if

$$P\left(X=x,Y=y|Z=z\right)=P\left(X=x|Z=z\right)P\left(Y=y|Z=z\right).$$ (2)

Intuitively, this equation means that if we know the value of Z, then knowing the value of X does not provide any additional information about the value of Y, and vice versa. This statement also holds if Z is not just a third variable, but a set of variables. The mathematical notation for X is conditionally independent of Y given Z is X ⊥ Y |Z.

2.2. (Probabilistic) graphs as a visualization of conditional (in)dependencies

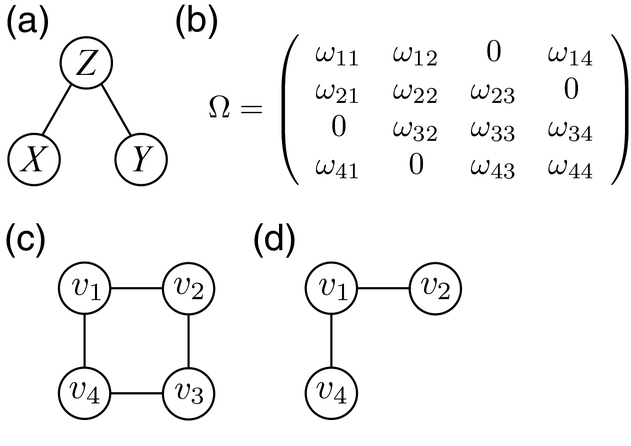
Conditional (in)dependencies can be visualized as probabilistic graphs, also called networks, as shown in Figure 2a. Here, nodes (vertices) represent variables and edges represent conditional dependencies. In example Figure 2a, there is an edge between X and Z, and between Y and Z, but no edge between X and Y. This can be translated to X ⊥ Y |Z. Thus, the graph is a visualization of the joint probability distribution of the observed data, where the conditional independence between two variables given the remaining variables corresponds to the absence of an edge.

Figure 2: Graphical representation of conditional independence.

Figure (a) illustrates the concept of conditional independence. Variables X and Y are conditionally independent given Z. Consequently, no edge is drawn between X and Y, while there is an edge between X and Z, and Y and Z. Figure (b) shows an exemplary precision matrix Ω. Figure (c) shows the corresponding network visualization, and (d) illustrates the first order neighborhood of the variable v₁, which includes the node itself and the two adjacent nodes v₂ and v₄.

2.3. Correlation vs. partial correlation

The Pearson correlation coefficient is defined as

$${\rho }_{XY}=\frac{\text{Cov}\left(X,Y\right)}{{\sigma }_X{\sigma }_Y},$$ (3)

where Cov(X, Y) is the covariance between X and Y, and σ_X and σ_Y are the standard deviations of X and Y. Pearson correlations take values from −1 to +1 and measure the linear relationship between two variables. If for example, the Pearson correlation coefficient between two variables is near +1, the increase in value of one variable is accompanied by the increase in value of the other variable and vice versa, as exemplified in Figure 1a. The statistical independence of two variables corresponds to a Pearson correlation coefficient equal to zero. Note, Pearson correlation is a measure of pair-wise relationships between two variables without considering the influence of other variables.

Here, we introduce the partial correlation coefficient ρ_{XY ·Z}, which measures the association between two random variables X and Y, controlling for a set of random variables Z. In other words, it measures the strength of an association between X and Y, taking into account effects of variables Z, which possibly explain this association. Thus, it is designed to distinguish between direct and indirect effects and therefore reflects conditional independencies.

Formally, for multivariate Gaussian variables conditional independence corresponds to a partial correlation coefficient equal to zero,

$$X\perp Y|Z\iff {\rho }_{XY\cdot Z}=0,$$ (4)

and conditional dependence to a non-zero partial correlation coefficient,

$$X\cancel{\perp }Y|Z\iff {\rho }_{XY\cdot Z}\ne 0.$$ (5)

In fact, if we calculate the sample Pearson correlation coefficient between the residues from the linear regression of X on Z and the residues from the linear regression of Y on Z shown in Fig. 1b, this corresponds to an estimate of the partial correlation coefficient ρ_{XY ·Z}.

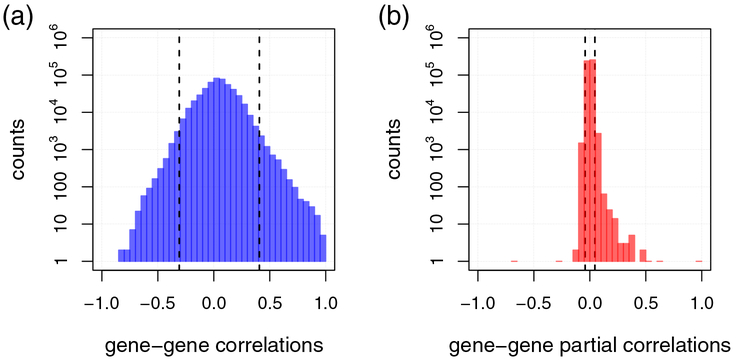
In Figure 3, we compare estimated gene-gene Pearson correlation coefficients with their respective full order partial correlation coefficients for single-cell RNA sequencing data of melanoma metastases (Tirosh et al., 2016). Figure 3a shows the distribution of Pearson correlation coefficients, where we observe a high proportion of both correlated (and anti-correlated) genes. The highest (lowest) percentile (> 99% and < 1%) has correlations > 0.41 (< −0.31), as shown by the dashed black lines. Thus, directly or indirectly all genes are more or less correlated, making correlation a weak measure of dependency: although a vanishing correlation suggests independence, high correlation is not a strong indicator of dependence.

Figure 3: Distribution of gene-gene Pearson correlations and full order partial correlations.

Figure (a) shows the distribution of gene-gene Pearson’s correlation coefficients estimated for single-cell RNA sequencing data of melanoma metastases from Tirosh et al. (2016). Figure (b) shows the corresponding distribution of full order partial correlations estimated using the R package GeneNet (Schaefer et al., 2015). The black dashed lines in (a) mark the highest and lowest percentile (99% and 1%) of (anti-)correlations. In (b), the corresponding lines are shown for partial correlations. Notice that for both (a) and (b) the y-axis is on log-scale.

The corresponding distribution of partial correlations is shown in Figure 3b. Partial correlations can take the same values as correlations, i.e., ranging from −1 to 1. In our example, the lowest partial correlation is ρ = −0.66 and the highest is ρ = 0.97, which is roughly concordant with Figure 3a. The obvious difference is that the distribution of partial correlations is much tighter (see also the highest and lowest percentiles shown as black dashed lines). In contrast to correlation, a vanishing partial correlation is not a strong indicator of independence, but high partial correlation is a strong indicator of dependence.

2.4. Gaussian Graphical Models

For multivariate normal data X = (X₁, …, X_p) ~ N(μ, Σ) with mean vector μ = (μ¹, …, μ^p)^T and the positive definite covariance matrix

$$\Sigma =\left(\begin{array}{rrr}\hfill {\sigma }^{11}& \hfill \dots & \hfill {\sigma }^{1p}\\ \hfill ⋮& \hfill \ddots & \hfill ⋮\\ \hfill {\sigma }^{p1}& \hfill \dots & \hfill {\sigma }^{pp}\end{array}\right),$$

the partial correlation coefficient ${\rho }_{X_i{X}_j\cdot \text{rest}}$ between X_i and X_j given all remaining variables is related to the precision matrix Ω = (ω_ij) =Σ⁻¹ by (Lauritzen, 1996)

$${\rho }_{X_i{X}_j\cdot \text{rest}}=-\frac{{\omega }_{ij}}{\sqrt{{\omega }_{ii}{\omega }_{jj}}}.$$ (6)

This relation is also visualized in Figure 2b to d. Figure 2b shows an exemplary precision matrix Ω for four variables v₁ to v₄. Here, an entry of ω_ij = 0 indicates conditional independence, corresponding to a zero partial correlation coefficient ${\rho }_{X_i{X}_j\cdot \text{rest}}$. A non-zero entry ω_ij corresponds to non-zero partial correlation. A Gaussian Graphical Model (GGM) represents this conditional dependency structure in a graph, where the nodes correspond to multivariate normal distributed variables, and edges between these variables represent conditional dependencies or non-zero partial correlation coefficients. The corresponding network is shown in Figure 2c. Here v₁ and v₂, as well as v₁ and v₄ are adjacent to each other, i.e., they are connected by one direct edge in the GGM. Since there are no other variables adjacent to v₁, they also form the (first-order) neighborhood of v₁ shown in Figure 2d.

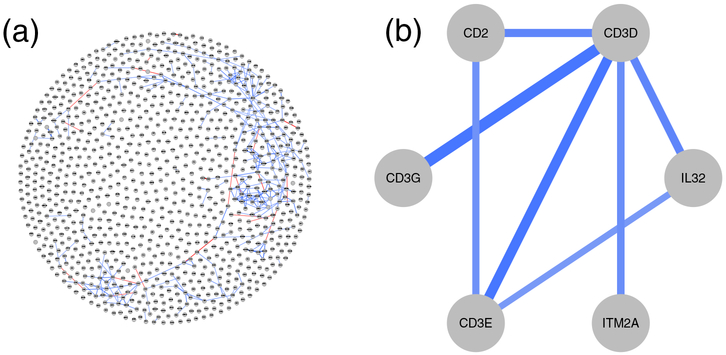
The GGM estimated for the single-cell data set from the previous section is represented as a graph in Figure 4a. Here, the edge corresponds to a significant partial correlation coefficient ranging from −1 (red) to +1 (blue), and the edge strength is encoded by the width and transparency of the edge. An example of a first order neighborhood is shown in Figure 4b for the gene CD3D.

Figure 4: Gaussian Graphical Model for single-cell RNA sequencing data of melanoma metastases (Tirosh et al., 2016).

Figure (a) displays the complete GGM with nodes representing the 1,000 most abundant genes in the data set and edges representing significant (q-value < 0.05) full order partial correlations. The strength of an association is reflected by the edge intensity from strong positive (dark blue) to strong negative association (dark red). Figure (b) displays the first order neighborhood of CD3D, which encodes a protein of the T-cell receptor/CD3 complex. The corresponding R code to reproduce the results is given in the Supplementary File 1.

2.5. Model overfitting and solutions

A GGM is defined by the set of variables or nodes it incorporates, and the respective edge weights between these nodes. Estimating the strength of each individual edge in the graph based on a training data set is referred to as “model learning/training or estimation”. For a given set of p different variables, one has to estimate, in total, p × (p − 1)/2 possible edges, a number which grows rapidly with increasing p. GGMs can be estimated by inverting the covariance matrix Σ, however, this is not possible if the number of variables p exceeds the number of distinct training samples N. Then, the covariance matrix does not have full rank and cannot be inverted. This can be a significant problem in omics data analysis, where the number of variables can be orders of magnitudes larger than the number of samples profiled, i.e., p ≫ N.

In case the covariance matrix cannot be inverted, other methods based on, e.g., parameter regularization can overcome this problem. These regularization techniques penalize complex models and therefore reduce the risk of overfitting the training data. In case of overfitting, the estimated model too closely describes the underlying relationships in the training data and is not generalizable to independent data sets. Thus, estimated edges might only reflect noise in the training data and not the true underlying probability density function.

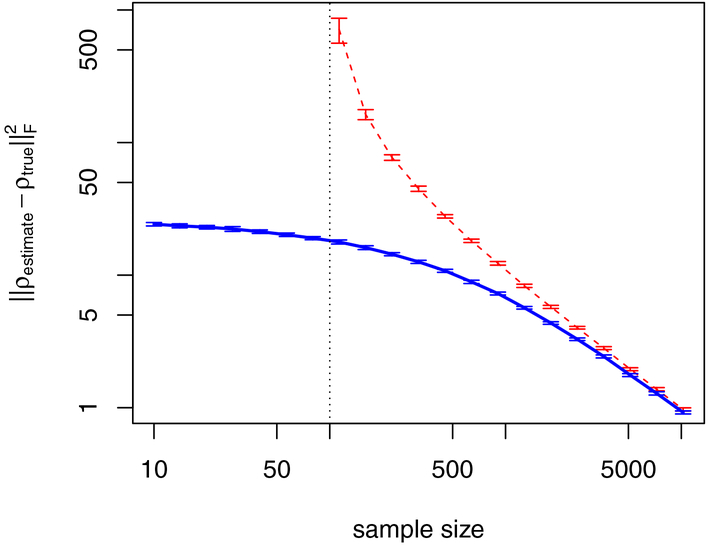
The problem of overfitting is not only present if p exceeds N. Figure 5 illustrates how the reliability of the partial correlation estimates depends on the number of measurements for a simulation study with 100 variables and 248 true edges (5% of all possible edges). Here, we contrast different sample sizes with the deviation of the partial correlation estimate from the ground truth, calculated as ${\Vert {\rho }_{\text{estimate}}-{\rho }_{\text{true}}\Vert }_F^2$, where ρ_estimate is the estimated partial correlation matrix, ρ_true the corresponding ground truth, and ||.||_F the Frobenius norm. The red line shows the results for partial correlation estimates using the standard matrix inversion of subsection 2.4. These estimates can only be calculated for N > p, as indicated by the black dotted line at N = p. Near to this boundary, the estimation accuracy is most compromised and the deviation shows a peak.

Figure 5: Partial correlation estimation accuracy.

We simulated data for p = 100 variables and 248 true edges (5% of all possible edges) for different sample sizes. The y-axis gives the deviation between partial correlation estimates and the ground truth, calculated as ${\Vert {\rho }_{\text{estimate}}-{\rho }_{\text{true}}\Vert }_F^2$, where ρ_estimate is the estimate, ρ_true the ground truth, and ||.||_F the Frobenius norm. Here, the red curve is the estimate obtained from covariance matrix inversion, which is only possible for sample sizes N > p. N = p is indicated by the vertical black dotted line. The blue line shows the corresponding result using the covariance shrinkage approach of Schaefer et al. (2015). We observe that covariance shrinkage provides estimates for sample sizes N < p and that estimates improve considerably for moderate sample sizes N > p. Note that both axes are on a logarithmic scale.

There is a variety of techniques that reduce overfitting by parameter regularization and improve partial correlation estimates for small and moderate sample sizes. These are, for instance, a node-wise regression approach for neighborhood selection (Meinshausen et al., 2006) based on the least absolute shrinkage and selection operator (LASSO, l₁) (Tibshirani, 1996), a covariance shrinkage approach (Schäfer and Strimmer, 2005), a joint sparse regression model to perform neighborhood selection for all nodes simultaneously (SPACE) (Peng et al., 2009), a penalized maximum likelihood approach (Yuan and Lin, 2007; Banerjee et al., 2008; Friedman et al., 2008), and a bivariate nodewise-scaled LASSO method called asymptotic normal thresholding (ANT) algorithm (Ren et al., 2015).

These regularization methods assume that the training samples are independent. There are both non-sparse and sparse regularization methods. The latter, e.g., LASSO-based methods, assume that the underlying true network is sparse, i.e., that only a small number of all possible edges between the nodes is in fact unequal to zero. Such sparse networks are also easier to interpret than (almost) fully connected networks. Here, penalty parameters calibrate the sparseness of the model. These parameters, however, are usually not known a priori and have to be determined. There are different strategies to estimate them, such as using the (extended) Bayesian information criterion ((E)BIC) (Yuan and Lin, 2007; Foygel and Drton, 2010), cross-validation (Krämer et al., 2009), stability selection based methods (Liu et al., 2010; Meinshausen and Bühlmann, 2010; Shah and Samworth, 2013), or according to the method suggested by Meinshausen et al. (2006). Alternatively, there are non-sparse estimation methods as, for instance, covariance shrinkage. Here, the partial correlations can be thresholded, as proposed for instance by Schäfer and Strimmer (2005). P-values are calculated for the partial correlations, and subsequently corrected for multiple testing Schäfer et al. (2006). Then, partial correlations are only considered significant and drawn as an edge, if they fall below some pre-defined threshold.

We demonstrate how partial correlation estimates can be improved by regularization methods exemplarily for covariance shrinkage in Figure 5. The corresponding estimation accuracy is shown as a blue line. We observe that overfitting is reduced substantially compared to the standard estimate shown as a red dashed line and that it provides also estimates for N < p. For large sample sizes, both methods provide equally reliable estimates.

All proposed methods to reduce overfitting exhibit both advantages and disadvantages. Regularization algorithms based on the LASSO method try to maximize specificity, i.e., they try to reduce the number of false positive edges. As a consequence, however, they might increase the number of false negatives and estimate very sparse networks in case of small sample sizes (Epskamp and Fried, 2018), which do not correctly reflect the underlying ground truth. Nevertheless, LASSO regularization yields edge weights which are exactly zero, thus there is no need for post-hoc thresholding or significance testing. Covariance shrinkage, in contrast, has the disadvantage that it does not provide a sparse estimate of the partial correlation matrix. Instead, the estimated partial correlations are thresholded post-hoc. However, the regularization parameter for covariance shrinkage can be estimated analytically (Ledoit and Wolf, 2003), rendering this approach computationally efficient.

Likewise, various pros and cons can be reported for the different penalty parameter estimation methods. The (E)BIC has shown excellent performance in case the underlying networks are sparse (Foygel and Drton, 2010), but it requires the manual setting of an additional hyperparameter. The cross-validation approach determines the optimal penalization parameter according to the maximum log-likelihood in cross-validation. This approach has the disadvantage that it can be computationally expensive and, as shown for the node-wise LASSO approach (Meinshausen et al., 2006), does not lead to a consistent model selection. In stability selection, the stability of estimated edge weights is assessed across different random subsampling runs for a set of penalty parameters, and the smallest penalty parameter which makes a graph sparse and stable across the different subsamples is chosen (Liu et al., 2010). Similar to cross-validation, the subsampling routine increases computation time. For a thorough introduction and discussion of regularized graphical models including an extensive R tutorial, we refer the interested reader to (Epskamp and Fried, 2018).

2.6. Mixed Graphical Models

GGMs are an instance of undirected graphical models, where variables are assumed to be multivariate normal distributed. Another classical instance is the Ising model or discrete Markov Random Field (MRF), in which variables are assumed to be discrete. Complex omics data, frequently combined with phenotypical data, often contain continuous, discrete, and count variables. Mixed Graphical Models (MGMs) combine, e.g., the characteristics of Gaussian Graphical and the Ising model, allowing such combined data to be effectively analyzed (Lauritzen, 1996). In general, MGMs are probabilistic graphical models, which reflect the joint probability density function of a set of variables following two or more different data distributions. They describe the conditional dependency structure of, for example, one set of variables following a Gaussian, and one set of variables following a multinomial distribution, simultaneously. Another example would be the joint distribution of a set of Gaussian variables, a set of multinomial variables, and a set of Poisson variables. In the popular case of an MGM incorporating both Gaussian and multinomial variables, three different edge types reflecting conditional dependencies, can be distinguished: edges between two Gaussian variables, edges between two multinomial variables, as well as edges connecting a Gaussian and a multinomial variable. Several scaleable algorithms for MGMs have been proposed (Lee and Hastie, 2015; Cheng et al., 2017; Yang et al., 2014; Chen et al., 2014; Fellinghauer et al., 2013). Analogously to GGMs, the problem of model overfitting also exists for MGMs, especially in the context of omics data sets. Similar strategies based on parameter regularization have been proposed for MGMs, including approaches based on the pseudo-log-likelihood in combination with l₁- and group LASSO penalty terms (Lee and Hastie, 2015; Sedgewick et al., 2016), or node-wise LASSO regressions (Haslbeck and Waldorp, 2016).

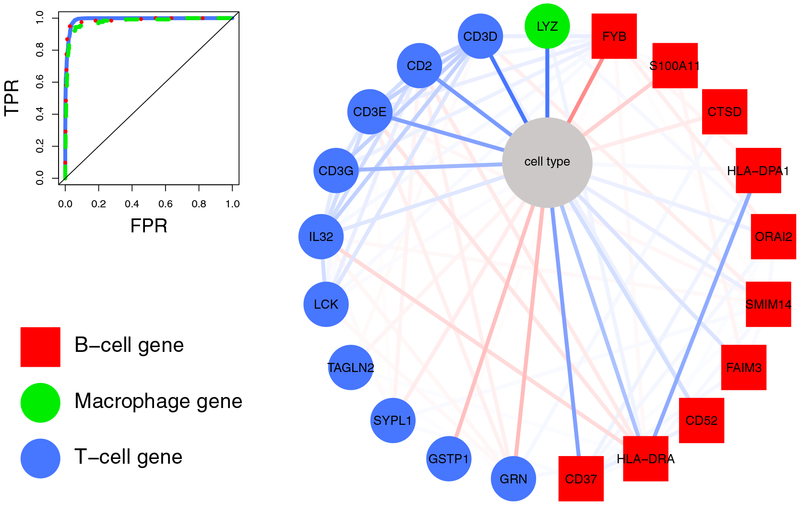
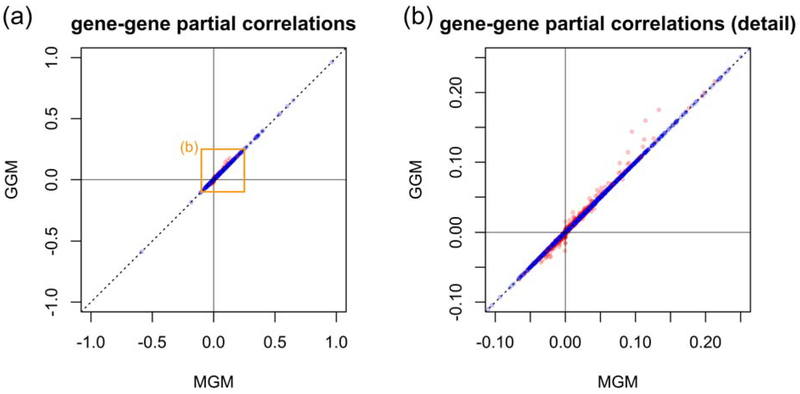
For illustration purposes, we present here an application to the single-cell RNA sequencing dataset of melanoma metastases introduced earlier. Here, we included, in addition to the continuous gene-expression levels, a categorical variable that encodes the respective cell type. This variable contains the following categories: malignant/unknown, T cell, B cell, macrophage, endothelial cell, cancer associated fibroblast (CAF), and natural killer (NK) cell. As baseline level, we chose malignant/unknown. We trained the MGM analogous to (Altenbuchinger et al. 2019) and the model was selected according to BIC. Figure 6 shows the first order neighborhood of the variable “cell type”. Typical cell type specific genes are directly connected to the “cell type” node. Importantly, the presence of additional variables, here the cell type, influences the estimated gene-gene partial correlations, as shown in Figure 7. Here, we contrast the gene-gene partial correlations estimated by the GGM (y-axis) with those estimated by the MGM (x-axis). Although the majority coincides, as indicated by a correlation between GGM and MGM estimates of ~ 1.0, there are several gene pairs which acquire different partial correlations, as shown in detail in Figure 7b. Interestingly, genes, which are directly connected to the cell-type node, are frequently affected, as shown by the red circles. Thus, taking into account possible confounding variables, such as the cell type, can change the estimated graphs.

Figure 6: First order neighborhood of the node “cell type”.

The right figure shows the neighborhood of the categorical variable “cell type”. Edge intensity reflects the strength of an association from strong positive (dark blue) to strong negative association (dark red). The node color indicates if the selected gene is specific for B cells (red squares), macrophages (green circles), and T cells (blue circles). T-cell genes are, e.g., CD3D, CD3E, CD3G, which encode proteins of the T-cell receptor-CD3 complex, CD2, that encodes a surface antigen present on all peripheral blood T cells, and Interleukin 32 (IL32), which encodes a cytokine increased in the activation of T cells. B-cell related genes (red) are, e.g., CD37, which encodes a cell-surface protein whose expression is restricted to cells of the immune system, with highest expression in mature B cells, and HLA-DRA, which is one of the HLA class II alpha chain paralogues that is expressed in antigen presenting cells. The only selected macrophage gene was Lysozyme (LYZ). Lysozymes are associated with the monozyte-macrophage system and enhance the activity of immunoagents. The corresponding classification performance in differentiating T and B cells, and macrophages from the remaining cells is shown in the upper left corner.

Figure 7: Partial correlation estimates GGM versus MGM.

Figure (a) compares the partial correlations estimated using a GGM (y-axis) with those estimated using a MGM that additionally contains the cell type as a discrete node (x-axis). For better comparability, we estimated both the GGM and MGM as described in Altenbuchinger et al. (2019). Figure (b) shows the orange area indicated in (a). Red circles correspond to genes that are directly connected to the cell-type node in the MGM approach.

It is also important to note that, once we have specified the joint probability, or equivalently, when we have learned the GGM/MGM, we can use it to calculate the likelihood of an observed value, given the neighboring variables. Similarly, we can use the joint probability to predict unobserved variables. This is illustrated in the upper left corner of Figure 6, where we give the performance to correctly classify B and T cells, and macrophages in a one-versus-all classification based on the first order neighborhood of the node “cell type”. For this aspect see also Friedman (2004) and Altenbuchinger et al. (2019).

3. Software for model learning and network visualization

Numerous softwares and especially R-packages for GGM and MGM calculation are publicly available. Table 2 provides an overview of published model estimation software including the implemented parameter estimation and model selection strategies.

Table 2:

(a) Gaussian and (b) Mixed Graphical Model estimation softwares as well as (c) recent extensions thereof. Abbreviations: AIC: Akaike information criterion, ANT: asymptotic normal thresholding, BIC: Bayesian Information Criterion, CPSS: complementary pairs stability selection, CV: cross-validation, EBIC: extended Bayesian Information Criterion, FDR: false discovery rate, mBIC: modified Bayesian Information Criterion, mVAR: mixed Vector Autoregressive, RIC: rotation information criterion, SCAD: smoothly clipped absolute deviation, STARS: stability approach to regularization selection, StEPS: Stable Edge-specific Penalty Selection.

(a) Gaussian Graphical Models
Method name	Software name	Reference	Parameter estimation	Model selection	Features	Availability
Graphical Lasso	glasso	Friedman et al. (2008)	l1 penalized maximum likelihood inference of inverse covariance matrix	-	computationally efficient and sparse solution	R package https://CRAN.R-project.org/package=glasso
	GGMselect	Giraud et al. (2009)	6 different methods: C01 (Wille and Buhlmann, 2006); node-wise regression (Meinshausen et al., 2006); adaptive l1 penalty (Zou, 2006); combination of C01 and node-wise regression; combination of C01, node-wise regression, and adaptive l1 penalty; quasi-exhaustive combination of neighborhood selection with different parameter combination rules	minimization of penalized empirical risk (Giraud et al., 2008)	selection of penalization parameter(s) of any graph estimation procedure and comparison of any collection of estimation procedures possible	R package https://CRAN.R-project.org/package=GGMselect
Sparse Partial Correlation Estimation	space	Peng et al. (2009)	joint sparse regression model to simultaneously perform neighborhood selection for all nodes	BIC-type criterion (Peng et al., 2009)	method specifically designed for p ≫ N scenario, particularly powerful for hub identification	R package https://CRAN.R-project.org/package=space
	qgraph	Epskamp et al. (2012)	graphical LASSO	EBIC or local FDR	allows estimation of GGMs, graph visualization and analysis	R package https://CRAN.R-project.org/package=qgraph
High-Dimensional Undirected Graph Estimation	huge	Zhao et al. (2015)	neighborhood selection (Meinshausen et al., 2006) or graphical LASSO, further acceleration by lossy screening rule preselecting neighborhood of each node via thresholding sample correlation	STARS (Liu et al., 2010), RIC, or EBIC for glasso	integrates data preprocessing, neighborhood screening, graph estimation, and model selection techniques into one pipeline	R package https://CRAN.R-project.org/package=huge
Covariance Shrinkage	GeneNet	Schaefer et al. (2015)	analytic shrinkage estimation of covariance and (partial) correlation matrices	parameter calibration according to (Ledoit and Wolf, 2003) and significance thresholding using the local FDR	very efficient, no parameter tuning, also suitable for dynamic (partial) correlations (Opgen-Rhein and Strimmer, 2006)	R package https://CRAN.R-project.org/package=GeneNet
	XMRF	Wan et al. (2016)	neighborhood selection (Meinshausen et al., 2006) for GGMs	stability selection (Meinshausen and Bühlmann, 2010) and STARS (Liu et al., 2010)	allows estimation of GGMs, lsing models, and Poisson family graphical models	R package https://CRAN.R-project.org/package=XMRF
	FastGGM	Wang et al. (2016)	ANT algorithm (Ren et al., 2015)	-	efficient, tuning-free GGM estimation for large variable sets, supplies p-values and confidence intervals for estimated edges	R package http://www.pitt.edu/~wec47/fastGGM.html
	SILGGM	Zhang et al. (2018)	4 different methods: ANT algorithm (Ren et al., 2015), de-sparsified node-wise scaled LASSO (Jankova and van de Geer, 2017), de-sparsified graphical LASSO (Jankova et al., 2015), and (scaled) LASSO GGM estimation with FDR control (Liu et al., 2013)	FDR multiple testing	provides confidence intervals, z-scores, and p-values for estimated edges, faster than FastGGM	R package https://CRAN.R-project.org/package=SILGGM
	GeNeCK	Zhang et al. (2019)	neighborhood selection, GeneNet, space, glasso, glasso-SF (Liu and Ihler, 2011), Bayesian-glasso (Wang et al., 2012), ESPACE, and EGLASSO for GGMs	p-value thresholding for ensemble-based network aggregation method (Zhong et al., 2014)	ensemble-based network aggregation method (Zhong et al., 2014) allows combination of networks reconstructed by different methods	web server http://lce.biohpc.swmed.edu/geneck/
(b) Mixed Graphical Models
Method name	Software name	Reference	Parameter estimation	Model selection	Features	Availability
Graphical Random Forests		(Fellinghauer et al., 2013)	individual nonlinear regressions with Random Forests	stability selection (Meinshausen and Bühlmann, 2010)	appropriate edge ranking among mixed data types based on Random Forest’s variable importance measure	R code https://ars.els-cdn.com/content/image/1-s2.0-S0167947313000789-mmc1.zip
		Chen et al. (2014)	node-wise penalized conditional likelihood	BIC	MGM estimation for Gaussian, Bernoulli, and Poisson variables	R code on github https://github.com/ChenShizhe/MixedGraphicalModels
		Lee and Hastie (2015)	maximum pseudo-log-likelihood with calibrated weighting scheme for penalization		MGM estimation for p ≫ N scenario with individually weighted penalization for each edge type	Matlab code https://jasondlee88.github.io/learningmgm.html
	mgm	Haslbeck and Waldorp (2016)	node-wise neighborhood selection by penalized (default: l1, also supports elastic net penalty (Zou and Hastie, 2005)) multinomial logistic regression in case of discrete response node and linear regression in case of Gaussian response node	EBIC or CV	estimation of k-order MGM and mVAR models in high-dimensional data, Gaussian, categorical, and Poisson data, also time-varying MGMs and mVAR models, allows to compute predictions and node-wise errors from these models and to assess model stability via resampling	R package https://CRAN.R-project.org/package=mgm
(c) Extensions of GGMs and MGMs
Method name	Software name	Reference	Parameter estimation	Model selection	Features	Availability
Sparse Time Series Chain Graphical Models	SparseTSCGM	Abegaz and Wit (2013)	penalized maximum likelihood inference with SCAD penalty	BIC or CV	estimation of time series chain graphical models	R package https://CRAN.R-project.org/package=SparseTSCGM
Sparse Inverse Covariance Estimation for Ecological Association Inference	SpiecEasi	Kurtz et al. (2015)	neighborhood selection or glasso	STARS	GGM estimation for compositional data	R package https://github.com/zdkl23/SpiecEasi
prior Lasso	pLasso	Wang et al. (2013)	neighborhood selection	mBIC or pBIC (Wang et al., 2013)	incorporation of prior knowledge in GGM estimation	Matlab code https://nba.uth.tmc.edu/homepage/liu/pLasso/
weighted graphical lasso	wglasso	Li and Jackson (2015)	graphical Lasso	BIC	incorporation of prior knowledge in GGM estimation	R code on github https://github.com/bioops/wglasso
differentially weighted graphical lasso	dwglasso	Zuo et al. (2017)	glasso	CV	wglasso for two groups and subsequent differential network score calculation for each variable	R code on github https://github.com/Hurricanerl989/dwgLASS0-R-codes
ESPACE/EGLASSO	espace	Yu et al. (2017)	extension of SPACE/graphical Lasso with additional tuning parameter to individually change penalization of hub gene edges	GIC (Yu et al., 2015)	allows incorporation of prior biological knowledge about hub genes to improve model estimation	R package for ESPACE https://sites.google.com/site/dhyeonyu/software
Joint Graphical Lasso	JGL	Danaher et al. (2014)	graphical Lasso with two penalty functions: Fused Graphical Lasso (FGL), employs fused penalty to encourage inverse covariance matrices to be similar across classes, and Group Graphical Lasso (GGL), which encourages similar network structure between classes	AIC	jointly estimates multiple graphical models corresponding to distinct but related conditions (multi-class GGMs)	R package https://CRAN.R-project.org/package=JGL
	CausalMGM	Sedgewick et al. (2018)	penalized maximum pseudo-likelihood method of (Lee and Hastie, 2015) with different sparsity penalties for each edge type (Sedgewick et al., 2016), PC- and CPC-algorithm (Colombo and Maathuis, 2014) for directionality search	StEPS (Sedgewick et al., 2016) and CPSS (Shah and Sam worth, 2013)	estimation of both undirected and directed MGMs	R package https://CRAN.R-project.org/package=causalMGM

Likewise many software packages for the visualization of graphs exist. One of the most popular open-source desktop applications is Cytoscape (Shannon et al., 2003). It allows easy visualization and network analysis, and is constantly extended by the community. For R users, the package igraph (Csardi et al., 2006) offers a large range of network visualization and analysis tools, including interactive plotting. A direct translation of igraph network objects to Cytoscape is conveniently enabled by the R-package RCy3 (Ono et al., 2015). Another user-friendly visualization and network analysis R-package is qgraph (Epskamp et al., 2012), which also allows the direct conversion of qgraph objects into igraph objects. visNetwork (Almende et al., 2016), threejs (Lewis, 2017), and networkD3 (Gandrud et al., 2015) facilitate interactive javascript network visualizations. In Python, networks can be analyzed and visualized using tools such as NetworkX (Hagberg et al., 2008).

4. Applications of Gaussian Graphical Models and its extensions in omics sciences

Gaussian Graphical Models and extensions thereof are frequently applied in omics data analysis. Here, we give several examples to illustrate the scope of applications, without the intention of being complete.

4.1. Gaussian Graphical Models in single omics data analysis

Reverse engineering of gene-regulatory networks.

A popular application of GGMs is in the inference of biochemical pathways and gene regulatory networks. De La Fuente et al. (2004) were among the first to propose the use of partial correlation networks to infer biochemical interactions from large-scale observational datasets. They applied this method to microarray data of Saccharomyces cerevisiae, identified sub-networks containing a high proportion of functionally related genes, and generated new hypotheses about the biological function of several genes.

Wille et al. (2004) modified the GGM by only considering small sub-networks of three genes at a time to explore the dependence between two of the genes conditioned on the third. They applied this approach to reconstruct two isoprenoid pathways in Arabidopsis thaliana and to identify candidate genes for cross-talk between these pathways.

Werhli et al. (2006) compared pairwise correlation networks, GGMs, and Bayesian networks to reconstruct gene-regulatory networks. They report a better performance of GGMs and Bayesian networks in comparison to pairwise correlation networks for Gaussian observational data, but no significant differences between GGMs and Bayesian networks in general. For interventional data from gene knockout and over-expression experiments, Bayesian networks outperformed the other two methods.

Ma et al. (2007) used GeneNet to reveal locally coherent subnetworks in Arabidopsis thaliana, which could be related to biochemical pathways, cell wall metabolism, and cold responses. Since these subnetworks also incorporated genes with unknown functions, Ma et al. (2007) suggested to employ gene networks reconstructed by GGMs as hypothesis generating tools for future studies on plant metabolism and stress response.

Xue et al. (2015) reconstructed a regulatory network of paracrine signals from single-cell data. They investigated the role of paracrine signaling in cytokine secretion by macrophages in response to stimulation of Toll-like receptor 4 (TLR4) with lipopolysaccharide (LPS). In this context, a GGM on single-cell data defined a regulatory network of paracrine signals, which could be experimentally validated through neutralization of individual cytokines by antibodies. Here, Tumor necrosis factor-α (TNF-α) turned out to be the most influential cytokine, which was necessary, but not sufficient, for secretion of interleukin-6 (IL-6) and IL-10.

Tissue-specific regulatory networks of transcription and splicing.

Saha et al. (2017) proposed a GGM-based framework to construct Transcriptome-Wide Networks (TWNs). These TWNs combine total gene expression levels with relative isoform abundances within one sparse network that potentially covers the interplay between splicing regulation and transcription. This method was applied to RNA sequencing data from the Genotype-Tissue Expression (GTEx) project to build tissue-specific TWNs. The authors identified several hubs that were enriched for splicing and RNA binding genes. They further screened for tissue-specific edges and identified 10 groups of related tissues.

Identification of gene signatures to predict survival benefit through therapeutic intervention for patients with resected non-small cell lung cancer.

Tang et al. (2013) constructed a gene expression network using the SPACE method on a set of genes associated with survival time in a multivariate Cox model adjusted for age, cancer stage, and sample processing site. In this survival-associated gene network, they identified 18 hub genes and combined them into a multivariate signature which was subsequently assessed in several independent datasets across different microarray platforms. Interestingly, the 18-hub-gene-signature outperformed a signature comprising the 18 top-ranked genes of the initial Cox survival analysis as well as a signature comprising all genes significantly associated with survival time. The authors investigated possible reasons for the performance gain of the 18-hub-gene signature by analyzing the information content of the individual gene signatures. Here, the 18-hub-gene signature comprised genes with less information redundancy than the 18-top-ranked-gene signature and thus was able to capture more patient variability. In a second step, 12 out of these 18 hub genes were identified to be either synthetic lethal or to have genetic alterations in lung cancer based on literature. The predictive performance for adjuvant chemotherapy response of this 12-gene-signature was subsequently tested in two independent cohorts across two microarray platforms.

Gaussian Graphical Models in the analysis of high-grade serous ovarian cancer.

Svoboda et al. (2018) constructed GGMs of different sparsity from mRNA expression data of the organic anion transporters encoded by SLCO genes. The network sparsity was calibrated by varying the penalty parameter and the corresponding gene networks were summarized by first principal components. These principal components were subsequently used together with all single gene expression values not summarized in the network and clinicopathological parameters, to explain variation in patient’s overall survival. The model with the highest percentage of explained variation was finally selected, which incorporated two putative co-regulated networks ABCB2/ABCB3/ABCC4/HER2 and ABCC3/SLCO2B1. The first subnetwork was suggested to be important for immune regulation, whereas the latter appeared to be relevant for estrogen turnover.

Metabolite - metabolite association networks and the reconstruction of metabolic reactions and pathways from observational data.

One of the first applications of partial correlation networks in metabolomics was done by Ursem et al. (2008), where associations between metabolites across tomato genotypes were investigated. Here, partial correlation networks were compared with correlation networks. The authors identified both consistent metabolite - metabolite associations and distinct associations that differed between both measures.

Similar to the different applications of GGMs for the reconstruction of gene regulatory networks, several studies used GGMs to reconstruct metabolic biochemical pathways from observational data. Çakır et al. (2009) systematically investigated the inference power of different pathway reconstruction methods for various in silico steady state data sets. They simulated three different data sets based on the threonine synthesis pathway of Escherichia coli, the glycolysis pathway of Saccharomyces cerevisiae, and the central metabolism pathway of Escherichia coli, and perturbed the data taking into account enzymatic, intrinsic, and environmental variability. The authors assessed the ability to reconstruct metabolic pathways of conditioned networks (including both first-order partial correlation networks and GGMs), and relevance networks based on Pearson correlation or entropy-based mutual information. Here, conditioned networks were superior compared to relevance networks, which was attributed to their ability to distinguish direct from indirect effects.

A systematic evaluation of the reconstruction performance of GGMs in comparison to Pearson correlation relevance networks for many different metabolic reactions on both simulated and real metabolic data sets was done by Krumsiek et al. (2011). The GGM inferred from a large-scale population based serum data set displayed a modular structure with respect to different metabolite classes, and appeared to be robust against the choice of samples and even sample size as long as N > p for covariance matrix inversion. They further illustrated that high partial correlation coefficients corresponded to known metabolic reactions in their analysis.

Prediction of unknown Immunoglobulin G glycosylation reactions.

Besides the application of GGMs for the reconstruction of metabolic pathways, they were further used to infer reactions in the Immunoglobulin G (IgG) glycosylation pathway (Benedetti et al., 2017). The authors could show that edges of a GGM, calculated from plasma IgG glycomics data, mostly reflected enzymatic steps in the known IgG glycosylation pathway. They predicted 22 new biochemical reactions based on the GGM and tested those with a genome-wide association study in an independent cohort as well as different in vitro experiments. They could experimentally validate that at least one predicted reaction occurs in vitro and that one rejected reaction does not occur.

Network differences between individual subpopulations.

Valcárcel et al. (2011) compared partial correlation networks of nuclear magnetic resonance (NMR)-based lipoprotein subclasses of a large cohort of 4,406 individuals with normal fasting glucose to a cohort of 531 subjects with prediabetes. They discovered several changes in lipoprotein metabolism related to diabetic dyslipidemias.

4.2. Gaussian Graphical Models in multiomics data integration

Identification of unknown metabolites with Gaussian Graphical Models incorporating genetic and metabolic information.

To facilitate the identification of yet unidentified metabolites from untargeted metabolomic measurements in a large-scale population based study, Krumsiek et al. (2012) combined a genome-wide association analysis of 655,658 genotyped single-nucleotide polymorphisms (SNPs) on concentrations of serum metabolites with a GGM derived from both identified and unidentified metabolites and literature based metabolic pathway information. They were able to experimentally confirm nine specific metabolite identity predictions.

Integrating the genome with the metabolome in obesity research.

Valcárcel et al. (2014) combined a differential GGM network approach with a genome-wide correlation analysis to study the effect of genetic variants on the metabolome. The authors constructed two metabolite association networks for obese and for normal weight individuals using GeneNet. They assessed differences between the two networks by permutation tests and constructed a differential network, where edges represent significantly different metabolite partial correlations between the two physiological groups. In a second step, a genome-wide correlation analysis identified genetic variants associated with metabolic network differences. The authors validated their approach, called genome metabolome integrated network analysis (GEMINi), in simulation studies covering a large range of data variation. This approach revealed similar patterns of metabolic network differences across two independent cohorts. The genome-wide correlation analysis of 318,443 SNPs with metabolite network differences revealed 24 loci significantly associated with differences in associations between total lipids in medium very-low-density lipoprotein particles (VLDL) and very-large VLDL.

Investigating the effects of diet induced weight changes on adipose tissue.

Montastier et al. (2015) investigated the interactions among bio-clinical information, fatty acid as well as mRNA levels in adipose tissue of women following a weight-reducing diet program. For each dataset, intra-omic networks were calculated utilizing GGMs, and a combined network across the different omics layers was achieved by regularized canonical correlation analysis. A subsequent comparison of network component clusters highlighted the central role of myristoleic acid, a minor adipose tissue fatty acid not provided by food, in fat mass reduction.

4.3. Applications of Mixed Graphical Models with (multi-)omics data

Identification of molecular pathways that underlie age-related diseases and associated comorbidities.

Graphical Random Forests were employed to integrate preselected epigenomics, transcriptomics, glycomics, and metabolomics data known to be associated with chronological age with various disease phenotypes in 510 women of the TwinsUK cohort (Zierer et al., 2016). Seven individual network modules were identified, representing distinct aspects of aging, namely gene expression, lung function, arthritis, bone density, fat and lean mass related variables, as well as liver and kidney function. They were connected by distinct hubs such as urate that connects renal function with body composition and obesity, or oxytocin, that connects body composition and inflammation. These hubs might represent molecular markers of the aging process and might drive disease comorbidities.

Data integration in the context of chronic kidney disease.

Altenbuchinger et al. (2019) used MGMs for an integrative analysis of NMR metabolic fingerprints with comprehensive patient data, such as clinical, phenotypic, and demographic parameters from the German Chronic Kidney Disease (GCKD) study (Eckardt et al., 2011; Titze et al., 2014). Here, the MGM was used to estimate the joint probability of this complex feature space including, in total, 879 different variables. It was shown that the model provides associations that remain robust with respect to subsequent covariate adjustment. Thus, MGMs were not primarily used to gain insights into the underlying biochemical reactions and pathways. They were used as a data screening tool that returns meaningful associations, which also persist if the data are analyzed epidemiologically accounting for confounding variables selected based on expert knowledge. Using the MGM, the authors identified associations between cardiac arrhythmia and trimethylamine-N-oxide (TMAO), as well as cardiac infarction and TMAO. These associations persisted after appropriate covariate adjustment. Interestingly, the MGM revealed associations which remained hidden or underestimated in univariate screening approaches. For instance, alcohol consumption was one of the least prominent risk factors of gout in a univariate screening analysis, but was almost the strongest risk factor according to the MGM and even surpassed male gender as risk factor. Moreover, the authors demonstrated the predictive power of linear signatures derived from the first order MGM neighborhoods of various discrete and continuous nodes.

Causal MGMs for chronic lung disease diagnosis and prognosis.

In (Sedgewick et al., 2018) the authors used a causal extension of MGMs to analyze disease diagnosis and progression in a clinical data set from patients with chronic obstructive pulmonary disease (COPD). Using this approach, they confirmed known causal relationships and proposed factors that potentially affect the longitudinal lung function decline of COPD patients.

Identification of gene pathways associated with breast cancer.

In (Manatakis et al., 2018) MGMs were extended to incorporate prior knowledge. This method was used to identify gene pathways differentially regulated between receptor positive (Luminal A and B subtypes) and receptor negative (HER2 and Triple-Negative) breast cancer subtypes.

5. Extensions of Gaussian Graphical Models

5.1. Modeling network differences between Gaussian Graphical Models

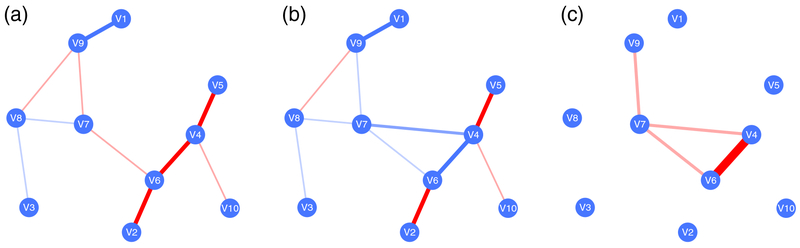
Networks can differ between phenotypes or diseases. For example, in cancerous tissue other cellular processes are carried out than in healthy tissue, which is also reflected in the underlying transcriptional networks. GGMs were extended by several authors to incorporate network differences (Danaher et al., 2014; Zhao et al., 2014). The basic concept is illustrated in Figure 8. Figure (a) and (b) show two partial covariance networks, corresponding to two different phenotypes A and B, with precision matrices ${\Omega }_A={\Sigma }_A^{-1}$ and ${\Omega }_B={\Sigma }_B^{-1}$ respectively. Figure (c) shows the difference Ω_A − Ω_B, which can be understood as the differential partial covariance network. Thus, we investigate the differential wiring of networks.

Figure 8: Differential networks.

Figure (a) shows an example network Ω_A, corresponding to phenotype A, (b) shows the corresponding network of phenotype B. Both networks share similarities, but differ in selected edges, yielding the differential network Ω_A − Ω_B in (c). Blue edges encode positive associations and red edges negative associations.

In (Danaher et al., 2014), these differential networks were estimated using a penalized log-likelihood, where both edge weights and edge weight differences were penalized by two distinct penalty parameters. While the first penalty induces sparseness in edges, the second enforces edge weights to be equal among the compared sample groups. As a consequence, both edge differences and edge weights are modeled simultaneously. Thus, information is shared across sample groups. As an example application, the differential network was estimated from epithelial cells sampled from patients with lung cancer versus those of controls.

In (Zhao et al., 2014), a similar method was applied to study stage III and IV ovarian cancers, where the differential networks were built between molecular tumor subtypes.

5.2. Graphical Models with prior knowledge

The estimation of GGMs can be improved by taking advantage of prior biological knowledge. Such prior knowledge can be based on known relationships between variables such as a functional association between two genes or a biochemical pathway directly connecting two metabolites. Usually, a priori known edges are assigned a lower weight in a penalized regression setup, which increases the likelihood of being recovered. Several authors suggested algorithms: Wang et al. (2013) modify the node-wise neighborhood selection method of Meinshausen et al. (2006), Li and Jackson (2015) and Zuo et al. (2017) the graphical LASSO algorithm, and Yu et al. (2017) the SPACE method.

The incorporation of prior knowledge in the MGM estimation procedure was proposed by Manatakis et al. (2018). This method, called piMGM, is also able to score the reliability of provided prior information, thus enabling the identification of gene pathways, which appear to be active in a specific data set.

5.3. Learning gene networks under SNP perturbations

In (Zhang and Kim, 2014), gene regulatory networks were estimated using a GGM based approach, called Conditional Gaussian Graphical Model (CGGM), that learns the network along with expression quantitative trait loci (eQTLs). Those were considered as naturally-occurring perturbations of the gene regulatory system. The model provides a characterization of how the direct genetic perturbations propagate through the gene network to perturb other genes indirectly. A successor of this method, called Perturb-Net, models the gene network that modulates the influence of SNPs on phenotypes, using again SNPs as naturally occurring perturbation of a biological system (McCarter et al., 2018).

5.4. Prediction of protein residue-residue contacts by inverse covariance estimation

Protein structure prediction is one of the essential problems in molecular biology. Here, information about amino acid residues which are in contact with each other can substantially reduce the computational complexity. Multiple-sequence alignment (MSA) can be used to predict these contacts, since correlated mutations can be indicative of residue-residue contacts: given a contacting residue is mutated, its partner will more likely be mutated to a complementary amino acid. Otherwise, it would perturb the contact. In this context, measures of correlation based on binary amino acid variables are used (Halabi et al., 2009). However, correlation does not distinguish direct from indirect effects, i.e. a direct coupling between residue A and B, and residue B and C can result in an observed correlation between A and C. Thus, it is natural to use partial correlations which allow to distinguish these indirect from direct couplings. The seminal work in this context is (Jones et al., 2011). Here, the graphical LASSO algorithm (Friedman et al., 2008) was used in combination with a shrinking of the sample covariance as, e.g., in (Schäfer and Strimmer, 2005), to improve the convergence of the graphical LASSO. This method, called PSICOV, substantially improved predictions compared to the best performing normalized mutual information approach.

5.5. Graphical models for repeated multivariate time-series data

So far, we restricted our discussion on stationary graphical models meaning that we estimated the dependency structure between variables measured at one time-point in different samples (cross-sectional). In contrast, time-series experiments repeatedly measure variables in individual samples at multiple time-points such as in prospective cohort studies that include multiple repeated measurements at regular intervals. Graphical models of time-series data can provide information about dynamic or delayed interactions and contemporaneous interactions amongst genes, metabolites, or any other omics trait. Therefore, time-series chain graphical models (TSCGMs), as proposed by Abegaz and Wit (2013), combine GGMs for stationary undirected interactions at one time-point and dynamic Bayesian networks for dynamic or delayed directed interactions from one time-point to a consecutive time-point. Abegaz and Wit (2013) employed the TSCGM to explore regulatory networks of mammary gland gene expression in mice and circadian gene expression in Arabidopsis thaliana.

5.6. Sparse and compositionally robust Inference of Gaussian Graphical Models

Most omics measurements are not quantitative: we do not measure the number of RNAs in a specimen but only something which is proportional to this number. This proportionality factor depends on a number of factors such as sequencing depths, sensitivity of the technology, and quality of the material. That makes data “compositional” meaning that we only measure compositions. In studies of microbial communities (16S ribosomal RNA (rRNA) sequencing), this property received particular attention (Lin et al., 2014; Altenbuchinger et al., 2017a), although it applies similarly to other omics read outs, such as transcriptomics and metabolomics (Zacharias et al., 2017; Altenbuchinger et al., 2017b). In Kurtz et al. (2015), SPIEC-EASI (SParse InversE Covariance Estimation for Ecological Association Inference) was proposed, which is a statistical method for the compositionally robust inference of microbial ecological networks. SPIEC-EASI combines data transformations developed for compositional data analysis with Gaussian graphical modeling. SPIEC-EASI was demonstrated to outperform state-of-the-art methods with respect to edge recovery under a variety of scenarios. Moreover, it predicted previously unknown microbial associations using data from the American Gut project (AGP; http://americangut.org).

6. Summary and conclusion

GGMs are among the most popular methods to infer networks from omics data. Their estimation was approached by various strategies. Software for GGM inference and visualization is readily available as R and Python packages or as stand-alone software or interface. In fact, they became standard analysis tools. Reasons are that they have a straightforward interpretation as conditional independences, which allows to distinguish direct from indirect effects, they can be used for realistic data simulation (Emmert-Streib et al., 2019), and they are computationally efficient.

GGMs are also extended in various aspects, which are less well known to the community. Those allow, for instance, to incorporate other data types (MGMs and CGGMs), to account for compositeness of omics data, to include causality, to estimate GGMs over different categories (or phenotypes), and to include prior knowledge such as biochemical pathways. Here, we gave (1) the theoretical background of GGMs to allow the computational biologist/statistician to apply and to interpret GGMs in a cautious way, (2) we presented extensions that could be the better choice for his/her biological problem, and (3) we illustrated the scope of possible applications. GGMs are likely to play a key role in the analysis of upcoming omics data, and they will be the backbone of upcoming methods that are adapted to new biological problems. Here, we hoped to stimulate this process of applications and developments of GGMs.

Highlights.

• Gaussian Graphical Models (GGMs) infer statistical dependencies between variables.

• They are popular tools for omics data analysis.

• A general overview of GGMs and Mixed Graphical Models (MGMs) is provided.

• Their scope of application in the analysis of omics data is described.

• Important extensions of GGMs and MGMs are reviewed.