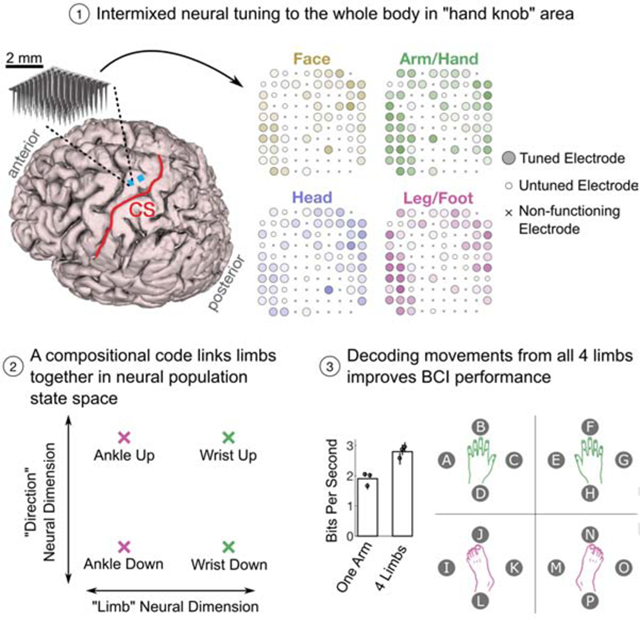
Summary
Decades after the motor homunculus was first proposed, it is still unknown how different body parts are intermixed and interrelated in human motor cortical areas at single-neuron resolution. Using multi-unit recordings, we studied how face, head, arm and leg movements are represented in hand knob area of premotor cortex (precentral gyrus) in people with tetraplegia. Contrary to traditional expectations, we found strong representation of all movements and a partially “compositional” neural code that linked together all four limbs. The code consisted of: (1) a limb-coding component representing the limb-to-be-moved, and (2) a movement-coding component where analogous movements from each limb (e.g. hand grasp and toe curl) were represented similarly. Compositional coding might facilitate skill transfer across limbs and provides a useful framework for thinking about how the motor system constructs movement. Finally, we leveraged these results to create a whole-body intracortical brain-computer interface that spreads targets across all limbs.
In Brief
Willett et al. show that “hand knob” area of premotor cortex in people with tetraplegia is tuned to the entire body and contains a compositional code that links all four limbs together. This coding may potentially facilitate skill transfer and a discrete brain-computer interface can accurately decode all four limbs.
Graphical Abstract
Introduction
Knowing how different body parts are topographically mapped onto motor cortex is central to understanding the motor cortical system. Neural activity in human motor cortex, including Brodmann area 4 (BA4) in central sulcus and adjacent Brodmann area 6 (BA6) on precentral gyrus, is traditionally thought to have macroscopic somatotopy. In this view, face, arm and leg movements are represented in distinct areas of cortex but individual muscles within any one body area may be mixed (e.g. wrist and finger movements may overlap within arm area) (Schieber, 2001). Classical stimulation studies in great apes and humans suggest an orderly arrangement of body parts along precentral gyrus, with little intermixing between face, arm and leg within any one individual (Leyton and Sherrington, 1917; Penfield and Boldrey, 1937; Penfield and Rasmussen, 1950). fMRI studies also support the idea of an orderly map with largely separate face, arm and leg areas along the precentral gyrus (caudal BA6) and the anterior bank of the central sulcus (BA4) (Lotze et al., 2000; Meier et al., 2008), as do electrocortiographic recordings in the high gamma band above precentral gyrus (albeit with occasional exceptions) (Crone et al., 1998a, 1998b; Ganguly et al., 2009; Miller et al., 2007; Ruescher et al., 2013). Nevertheless, the level of mixed representation within any one area of human precentral gyrus has not yet been quantified at single neuron resolution.
Here, we revisit motor somatotopy using microelectrode array recordings from hand knob area of precentral gyrus (Yousry et al., 1997) while two participants in the BrainGate2 pilot clinical trial made (or attempted) a variety of face, head, leg and arm movements. Surprisingly, we found strong neural tuning to all tested movements, contradicting traditional views on human motor cortical organization. In light of this new evidence of intermixed whole-body tuning, combined with prior anatomical evidence that places dorsal precentral gyrus in Brodmann area 6 and links it to macaque premotor area PMd [e.g. (White et al., 1997; Rizzolatti et al., 1998)], we refer to human precentral gyrus as premotor cortex in this manuscript (see Discussion for more details).
Our new finding of whole-body tuning in human premotor cortex presents a unique opportunity to investigate how each body part is neurally coded in relation to the others, which could shed light on its functional role. It also presents an opportunity to improve brain-computer interfaces (BCIs) by enabling whole-body decoding from microelectrode arrays in a single brain area. Along these lines, this manuscript is structured into three parts: (1) demonstrating tuning to the whole body in hand area of premotor cortex, (2) building on this finding to investigate the structure of the neural code for the whole body, and (3) translating this finding to BCIs to help people with paralysis.
Prior work in humans and macaques sets some expectations for how different body parts might be neurally coded in relation to each other. Previous fMRI and ECoG studies on human precentral gyrus found that matching movements of the ipsilateral and contralateral arms have similar (correlated) neural representations (Diedrichsen et al., 2013; Wiestler et al., 2014; Jin et al., 2016; Fujiwara et al., 2017; Bundy et al., 2018). Macaque studies also show a correlated representation of ipsilateral and contralateral reaching movements (Cisek et al., 2003) that changes during bimanual movements (Rokni et al., 2003). Here, we study not only how ipsilateral and contralateral arm movements are related, but also how leg movements are related to arm movements. Examining all four limbs together reveals a “compositional” neural code that links homologous movements of different limbs (e.g. links wrist movements to ankle movements, as well as ipsilateral wrist movements to contralateral ones).
The compositional code has a two-part structure where movements are coded in partial independence of the limb to be moved. One potential function of such a representation is to enable the transfer of motor skills between different limbs [as shown in (Kelso and Zanone, 2002; Christou and Rodriguez, 2008; Morris et al., 2009; Shea et al., 2011)]; motor skill could be learned in movement-coding components of the neural activity and then transferred to another limb by changing only the limb-coding component. We call the code “compositional” since the limb and movement components are “composed” (summed together) to specify the motor action. Recently, compositionality has also been suggested to underlie the representation of task rules in prefrontal areas (Reverberi et al., 2012; Yang et al., 2019).
In the last part of the manuscript, we demonstrate a discrete intracortical BCI that decodes movements across all four limbs from only a single brain area. We show that this whole-body BCI improves information throughput relative to a single-effector approach. This result substantially opens up the space of what intracortical BCIs can do and explore, as current systems are limited to placing microelectrodes in only a few brain areas [e.g. (Hochberg et al., 2012; Collinger et al., 2013; Aflalo et al., 2015; Bouton et al., 2016; Pandarinath et al., 2017; Ajiboye et al., 2017)].
Results
Intermixed Tuning to the Whole Body in Hand Premotor Cortex
Face, Head, and Contralateral Arm & Leg Movements
We used microelectrode array recordings from participants T5 and T7 to assess tuning to attempted movements of the face (mouth, tongue, facial muscles and speaking), head (head turning and tilting), contralateral arm (shoulder, elbow, wrist and fingers) and contralateral leg (hip, knee, ankle, and toes) in hand knob area of precentral gyrus. Participant T5 had a C4 spinal cord injury and was paralyzed from the neck down; he could move his face and head, but most attempted arm and leg movements resulted in little or no motion. Participant T7 had ALS and could move all joints tested, although some of his arm movements were limited due to weakness (see Table S2 for neurologic exam results).
In this experiment, T5 and T7 made (or attempted to make) movements in sync with visual cues displayed on a computer screen (Figure 1A). T5 completed an instructed delay version of the task where each trial randomly cued one of 32 possible movements spanning the face, head, arm and legs. For face and head movements, T5 was instructed to move normally; for arm and leg movements, T5 was instructed to attempt to move as if he were not paralyzed. T7, whose more limited data was collected earlier in a different study (and who is no longer enrolled), completed an alternating paired movement task with a block design. Each block tested a different movement pair, during which T7 alternated between making each of the paired movements every 3 seconds.
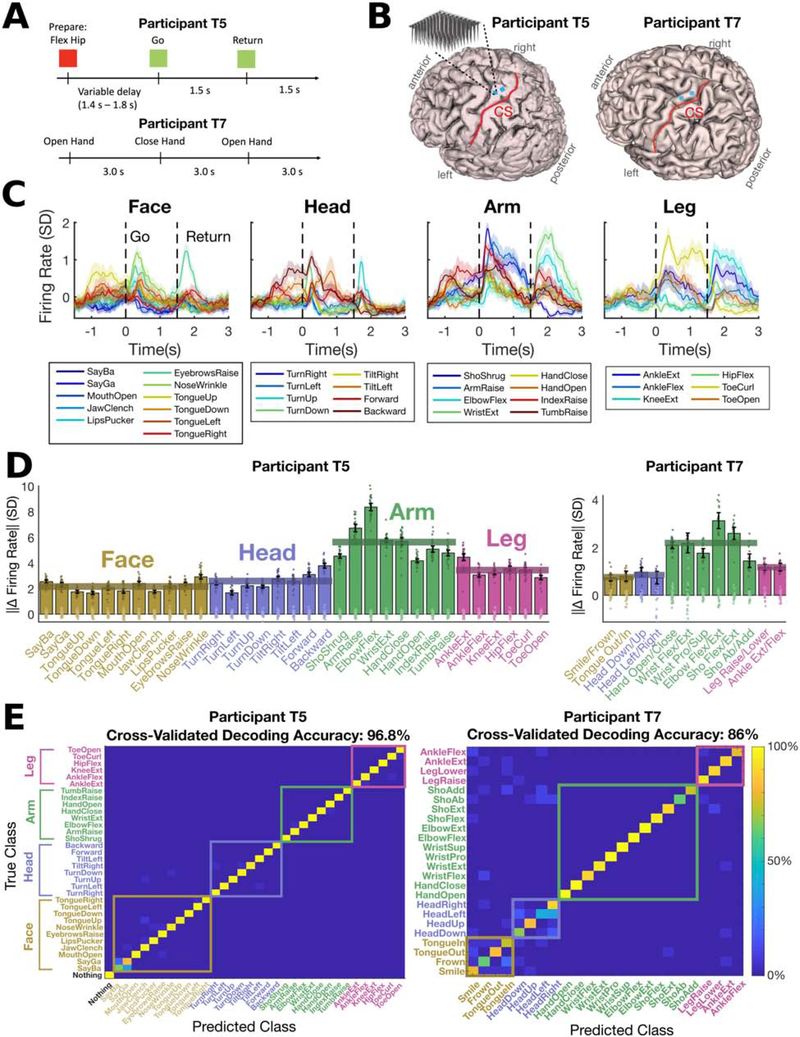
Figure 1. Separable and robust neural modulation for face, head, and contralateral arm & leg movements in hand knob area.
(A) Neural activity was recorded while participants T5 and T7 completed cued movement tasks that instructed them to make (or attempt to make) movements of the face, head arm and leg in sync with text appearing on a computer monitor.
(B) Participants’ MRI-derived brain anatomy and microelectrode array locations. Microelectrode array locations were determined by co-registration of postoperative CT images with preoperative MRI images.
(C) The mean firing rate recorded for each cued movement is shown for an example electrode from participant T5. Shaded regions indicate 95% CIs. Neural activity was denoised by convolving with a Gaussian smoothing kernel (30 ms sd).
(D) The size of the neural modulation for each movement was quantified by comparing to a baseline “do nothing” condition (in participant T5) or by comparing to its paired movement (T7). Each bar indicates the size (Euclidean norm) of the mean change in firing rate across the neural population (with a 95% CI). Each dot corresponds to the cross-validated projection of a single trial’s firing rate vector onto the “difference” axis. For T5, light dots represent the “do nothing” condition and dark dots represent the given movement. For T7, dark and light dots represent different movements of the given pair. Statistically significant modulation was observed for all movements (no confidence intervals contain 0). Translucent horizontal bars indicate the mean bar height for each movement type.
(E) A Gaussian naive Bayes classifier was used to classify each trial’s movement using the firing rate in a window from 200 to 600 ms (T5) or 200 to 1600 ms (T7) after the go cue. Confusion matrices are shown from offline cross-validated performance results; each entry (i, j) in the matrix is colored according to the percentage of trials where movement j was decoded (out of all trials where movement i was cued).
Despite recording from microelectrode arrays placed in hand knob region of precentral gyrus (Figure 1B), we found strong neural tuning to all tested movements, including those of the face, head and leg. Figure 1C shows an example electrode from T5 that was tuned to all movement categories. Here, and in most other results, we analyzed binned threshold crossing rates (i.e. multi-unit “firing rates”) for each microelectrode (although Figure S3, mentioned below, reports single unit results). Analyzing multi-unit threshold crossings allowed us to leverage information from more electrodes, since many electrodes recorded activity from multiple neurons that could not be precisely distinguished. Recent results indicate that neural population structure can be accurately estimated from threshold crossing rates alone (Trautmann et al., 2019). Binned threshold crossing rates were z-scored by subtracting the mean firing rate and dividing by the bin-by-bin standard deviation of the firing rate (and are reported in units of standard deviation, SD).
In Figure 1D we summarize the population-level neural modulation observed for each individual movement (T5) or pair of movements (T7) across all microelectrodes. For participant T5, we quantified modulation size by computing the magnitude (Euclidean norm) of the difference between mean firing rates observed during a “do nothing” control condition and mean rates observed during the movement of interest. Modulation size was estimated in a cross-validated way to reduce bias (see Methods). For participant T7, we computed the difference between the mean rates observed for each pair of movements. Mean rates were computed for each trial in a time window 200 to 600 ms after the go cue (T5) or 200 to 1600 ms after the go cue (T7). Figure 1D shows robust modulation for each tested movement in both participants (the clusters of single trial firing rates are clearly separable and the confidence intervals are far from zero). Tuning to arm movement was the strongest in both participants (p<1e-3; see Methods), with tuning to non-arm movements 38% (face), 46% (head) and 61% (leg) as large as arm movement tuning in T5, and 38% (face), 34% (head) and 53% (leg) as large in T7.
Next, we tested whether each movement was neurally distinguishable from other movements by using a cross-validated naive Bayes classifier to decode the movement on each trial. High classification accuracies (Figure 1E) confirm that tuning to each movement was unique and separable (as opposed to being caused by a generic signal that was the same for all movements). In Figure S1, we plot the neural activity in the top neural dimensions found using principal components analysis (PCA) to illustrate that activity is rich and multi-dimensional for all movement types.
Finally, we searched for somatotopy across the microelectrode arrays and saw no clear patterns; tuning to all four movement types was highly intermixed and many electrodes were tuned to multiple movement types (Figure S2). We also analyzed well-isolated, spike-sorted single neurons and found that they were frequently tuned to multiple movement types as well (Figure S3). In Figures S2–S3, we also report firing rate statistics in raw units of Hz.
Ipsilateral Arm & Leg Movements
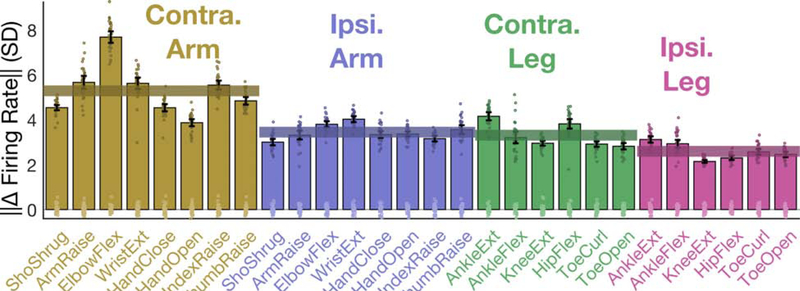
Next, we assessed tuning to ipsilateral attempted arm and leg movements in participant T5 (Figure 2). Our remaining results are based on data from T5, who is currently enrolled in the trial. Figure 2 shows that firing rates changed two-thirds as much for ipsilateral movement as compared to contralateral movement (65% as much for the arm, 78% as much for the leg). Tuning to ipsilateral movements was separable and robust. A cross-validated naive Bayes classifier could decode movements with 97.4% accuracy (amongst all movements shown in Figure 2) using a 200 to 600 ms window after the go cue.
Figure 2. Modulation for ipsilateral vs. contralateral arm and leg movements.
The size of the neural modulation for each attempted movement was quantified by comparing to a baseline “do nothing” condition. Each bar indicates the size (Euclidean norm) of the mean change in neural population activity (with a 95% CI) and each dot corresponds to the cross-validated projection of a single trial’s neural activity onto the “difference” axis. Translucent horizontal bars indicate the mean bar height for each attempted movement type.
A Compositional Code for Arm & Leg Movements
Isolated Movements of Single Effectors
Next, we probed the population-level structure of the whole-body tuning shown above, starting first with the relationship between ipsilateral and contralateral movements. We were guided by prior single unit recordings in macaques (Cisek et al., 2003; Rokni et al., 2003) and fMRI and ECoG studies in people (Bundy et al., 2018; Diedrichsen et al., 2013; Jin et al., 2016) which found that ipsilateral and contralateral movements had correlated representations in motor cortex. If this is the case, we hypothesized there should also exist laterality-related neural dimensions which code for the side of the body independently of the movement details. Laterality dimensions would help downstream areas distinguish between contralateral and ipsilateral movement. This kind of “compositional” neural code, defined by correlated movement-coding dimensions and separate effector-coding dimensions, is distinct from a muscle-like representation. In a muscle-like representation, contralateral and ipsilateral movements would exist in largely orthogonal neural dimensions and hence be uncorrelated [as recently found in macaque primary motor cortex (Ames and Churchland, 2019; Heming et al., 2019)], since the muscles are largely non-overlapping.
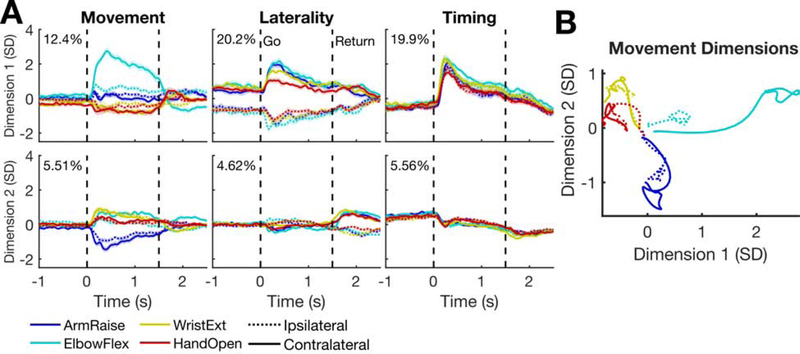
We used demixed PCA (dPCA) (Kobak et al., 2016) to visualize where the neural activity falls on the spectrum between muscle-like and compositional. dPCA decomposes neural data into a set of dimensions that each explain variance related to one marginalization of the data. We marginalized the data according to three factors: time, laterality, and movement. In the movement marginalization, we included the main effect of the movement condition as well as the interaction between movement and laterality. If the muscle-like hypothesis holds, there should be small laterality dimensions and large movement dimensions in which activity is dissimilar for matching movements on opposite sides of the body. On the other hand, for compositional coding, there should be a large laterality dimension (in addition to large movement dimensions), and activity in the movement dimensions should be similar for matching movements on opposite sides of the body.
The dPCA results (Figure 3) appear more consistent with the compositional coding hypothesis. There is a large laterality dimension coding for body side independently of the movement itself (Figure 3A, middle column). Additionally, activity in the movement dimensions (Figure 3A, left column) is similar for any given movement (e.g. wrist extension) regardless of which side of the body it is on (Figure 3B).
Figure 3. The neural population code relating ipsilateral to contralateral movements.
(A) To reveal how the ipsilateral and contralateral movements are represented in relation to each other, demixed PCA was applied to a set of four example attempted arm movements (taken from the dataset shown in Figure 2). Each panel shows the mean activity for a single dimension and each column shows dimensions related to a particular factor (marginalization). Each trace shows the mean activity for a single condition and the shaded regions indicate 95% CIs. The percent variance explained by each dimension is indicated in the top left.
(B) The mean activity through time in the first two movement dimensions is plotted as a trajectory for each condition. The dashed lines lie mostly near the solid lines and travel in the same direction, indicating that activity for a given movement is similar across sides of the body.
The dPCA analysis is a helpful visualization of the overall neural structure, but is not definitive proof of a compositional code. Next, we test for compositionality using more comprehensive analyses. We also expand the scope beyond ipsilateral vs. contralateral movements to consider the possibility of a compositional code linking the arms to the legs.
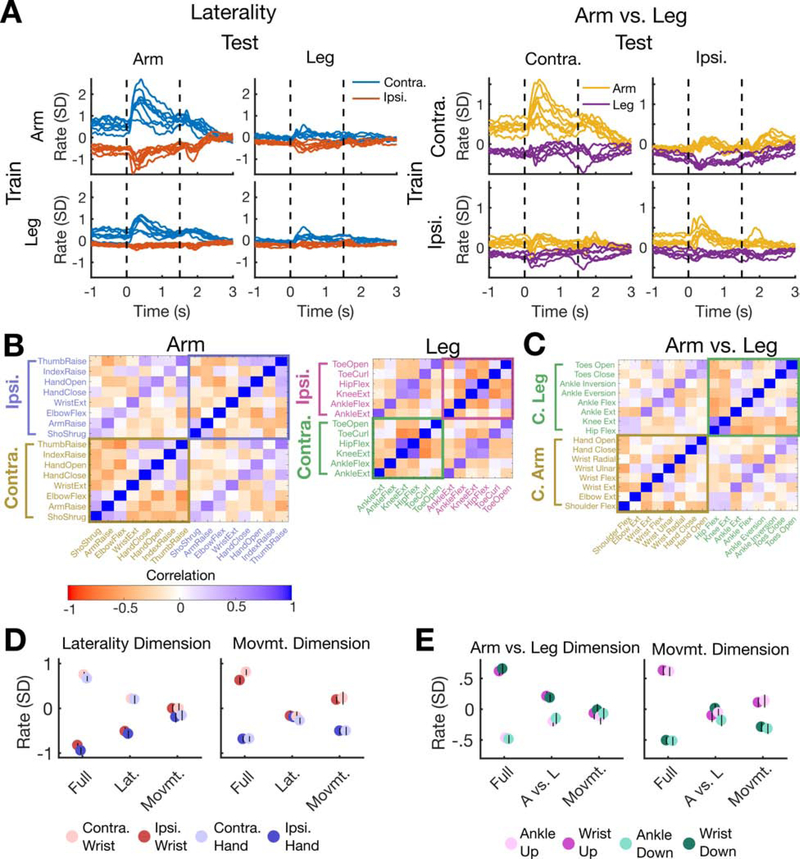
First, we used cross-validation to confirm that the laterality dimension revealed in Figure 3A was consistent for held-out movements that were not used to find it. Figure 4A shows that activity in the laterality dimension correctly separates attempted movements made on opposite sides of the body even for held-out movements (diagonal panels) and for held out effectors (arm or leg, off-diagonal panels). We also used cross-validated dPCA to search for a putative “arm vs. leg” dimension that codes for whether a movement was attempted with the arm or the leg (independently of the movement details or laterality). Results indicate the presence of a robust arm vs. leg dimension in addition to a laterality dimension.
Figure 4. A compositional code that links together all four limbs.
(A) A cross-validation analysis demonstrates the existence of neural dimensions that code for laterality (left vs. right side of the body) and effector (arm vs. leg). Each dimension was identified using only a subset of the data (rows) and then applied to all data (columns). In diagonal panels (e.g. train on arm and test on arm), each individual movement was held out (that is, each movement’s trace was made using dimensions found using other movements only).
(B) Each square (i,j) of the correlation matrices indicates the Pearson correlation between the mean firing rate vector of movement i and that of movement j. The off-diagonal banding shows that ipsilateral and contralateral movements were correlated with each other, for both the arm (left) and leg (right).
(C) Correlations between pairs of contralateral arm and leg movements were computed to reveal a surprising pattern: homologous movements of the arm and leg are correlated (e.g. hand opening and closing is uniquely correlated with toe opening and closing, as indicated by the off-diagonal band)..
(D) Neural activity in laterality-coding and movement-coding dimensions is partially active during an instructed delay period where only the laterality or the movement is specified. Each panel corresponds to a different neural dimension. Each circle indicates the mean (and its black line indicates the 95% CI) of activity in each dimension in the case where the full movement is specified (Full), only the laterality is specified (Lat.), or only the movement is specified (Movmt.). A 300 ms time window preceding the go cue was used for analysis.
(E) Same as in D, showing results from a different experiment testing the partial preparation of arm vs. leg (wrist vs. ankle) and movement direction.
Next, we quantified the correlations between firing rate vectors observed for arm and leg movements on opposite sides of the body (Figure 4B). First, firing rates were averaged across trials in a 200 to 600 ms window after the go cue and concatenated across electrodes into a vector. Then, the effect of the laterality dimension was removed by subtracting the mean firing rate within each laterality (otherwise, all movements on opposite sides of the body would appear negatively correlated). Finally, the correlation (Pearson’s r) between the firing rate vectors for each movement pair was computed. We observed a consistently positive correlation between matching ipsilateral and contralateral movements for both the arms and legs (indicated by the off-diagonal bands in Figure 4B). Correlation values for matching movements, such as contralateral vs. ipsilateral wrist extension, were statistically significantly greater than those for non-matching movements, such as contralateral wrist extension vs. ipsilateral elbow flexion (mean r=0.52 vs. r=−0.07 for the arm, p<1e-9; r=0.73 vs. r=−0.14 for the leg, p<1e-08; significance assessed with a t-test). All correlations were computed with cross-validation to reduce bias (see Methods).
Surprisingly, homologous movements of the arm and leg were also more correlated than non-homologous movements (e.g. hand grasp and toe curl are positively correlated, while hand close and ankle inversion are not, as shown in the off-diagonal band in Figure 4C). Correlations between homologous movements were statistically significantly greater than for non-homologous movements (mean r=0.48 vs. r=−0.06, p<1e-9). We also confirmed this result for a more limited set of four arm and leg movements in participant T7 (mean r=0.22 vs. r=−0.07, p=0.0036). These homologous correlations, along with the arm vs. leg dimension shown in Figure 4A, extend the compositional code to pairs of arm and leg movements.
In Figure S4, we examined the neural representation of directional movement (as opposed to single-joint movement) and found that it was also correlated across all four limbs. Interestingly, directional movements were correlated in an intrinsic coordinate frame (where mirrored joint movements were correlated) as opposed to an extrinsic frame (where movements in the same spatial direction would be correlated), placing precentral gyrus at an intermediate level of motor abstraction.
To exhaustively test that both aspects of compositionality (shared movement-coding and independent effector-coding) were indeed non-trivial properties of the data and well above chance, we performed additional shuffle controls (Figure S5) which confirmed their significance.
Finally, we examined compositionality through the lens of motor preparation. We reasoned that if compositionality was indeed the result of independently specifying the movement and the limb-to-be-moved, then neural activity in limb-coding or movement-coding dimensions should be able to be prepared by itself in the case of partial information (e.g. when only the limb, but not the movement, is cued in an instructed delay task). We tested this idea with a partial cue task. We found that when only the movement is specified during the delay period (i.e. “wrist extension” or “hand close” instead of “right wrist extension” or “left hand close”), activity in the movement dimension partially codes for the upcoming movement while activity in the laterality dimension doesn’t change (Figure 4D, right panel). Likewise, when only the laterality is specified (i.e. “left” or “right”), activity in the laterality dimension codes for the upcoming side of the body while activity in the movement dimension doesn’t change (Figure 4D, left panel). This result also holds for partial specification of arm vs. leg and movement direction (Figure 4E). By examining the single trial distributions of preparatory activity (Figure S6), we confirmed that the neural activity is consistent with partial preparation as opposed to a mixture of full preparation and no preparation.
Simultaneous Movement of Two Effectors
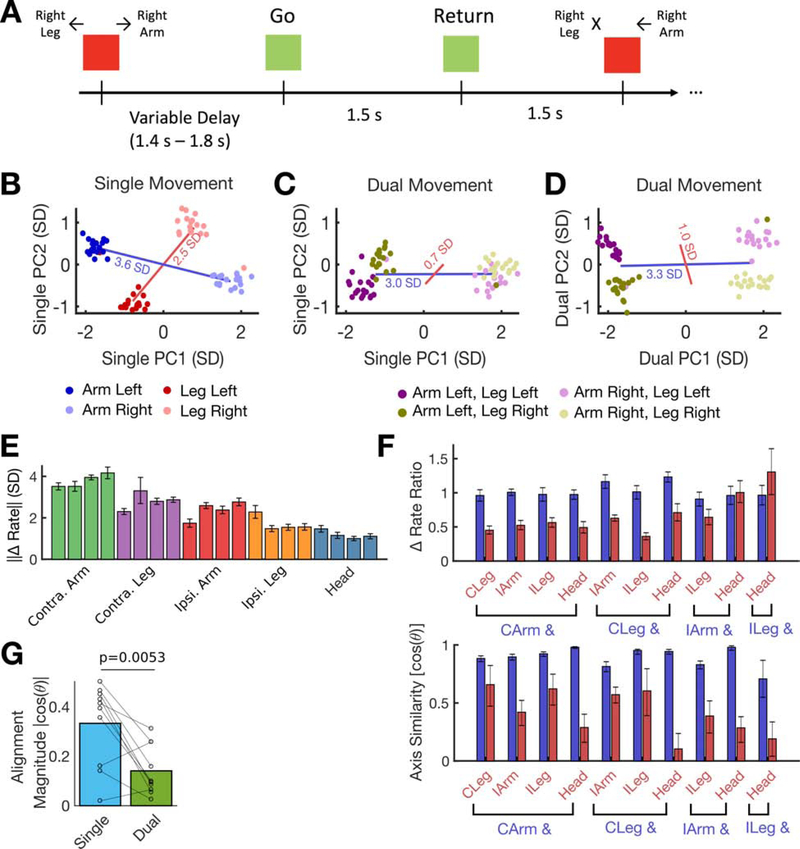
We further tested the idea of compositionality by examining how neural activity changes when two effectors are moved simultaneously. Since a movement code that is shared across effectors cannot simultaneously specify two different movements, we hypothesized that the code should change during dual movement. Prior work on bimanual reaching in macaques showed a decorrelation and suppression of ipsilateral-related neural activity during bimanual reaches (Rokni et al., 2003). To investigate this possibility, we tested all pairings of the following five effectors: left arm, right arm, left leg, right leg, and head. For each effector pair, we used an instructed delay cued movement task (Figure 5A) to probe the neural representation of left and right directional movements made either in isolation or simultaneously. For all pairs, we observed separable neural tuning to each of the four simultaneous movement conditions. A cross-validated naive Bayes classifier was able to distinguish between these conditions with an accuracy ranging from 86.1% to 100% (mean=95% across all pairs) using firing rates within a 200 to 1000 ms window after the go cue.
Figure 5. Departure from compositionality during dual movement: suppression and decorrelation effects.
(A) An instructed delay task was used to probe the neural representation of dual (multi-effector) movement. In this example experiment, participant T5 attempted to move his contralateral arm and leg to the left or right either simultaneously (e.g. the first illustrated movement) or individually (e.g. the second illustrated movement).
(B) Example single trial firing rates vectors during the “go” period are plotted in the top two neural dimensions that show differences in firing rate due to movement direction. Red and blue lines connect their respective cluster means and their lengths are a measure of tuning strength.
(C) Firing rates observed during dual movement are plotted in the same dimensions used in B. Leg modulation is considerably weakened in this space (the red line is smaller than in B). Red and blue lines show the distance between the dark and light clusters (blue, arm movement) and the purple and gold clusters (red, leg movement).
(D) The data in C is plotted in the top two principal components that describe the dual movement data. The leg modulation appears larger, indicating that its axis of representation has changed relative to single movement.
(E) Each bar depicts, for a single experiment, the mean change (± 95% CI) of firing rate observed during single movement for each effector (e.g. the blue and red lines in B).
(F) The ratio of dual/single modulation (top) and the change in axis during dual movement (bottom) is shown for each individual experiment. Each pair of bars is from a separate experiment with two different body parts. The blue bar corresponds to whichever body part of the two tested that had the largest modulation in E. Results show that the “secondary” effector (red bar) almost always decreased its modulation more sharply during simultaneous movement (top) and changed its axis of representation more (bottom).
(G) The alignment between each pair of effectors is summarized for the single and dual movement contexts. Each circle shows data from a single pair and lines connect matching pairs. Bar heights indicate the mean across all pairs. A paired t-test reveals a statistically significant difference in alignment between the single and dual contexts, meaning that the effectors become less correlated during dual movement (p=0.0053; 0.33 vs. 0.14).
Figure 5B shows example data from one effector pairing (contralateral arm and leg). To visualize the neural activity, firing rate vectors were computed for each trial using a 200 ms to 1000 ms time window after the go cue. Then, two neural dimensions were found in which to visualize these vectors by using PCA to highlight tuning to movement direction (see Methods). The example data shows clear and separable firing rate clusters for each movement when the effectors are moved in isolation.
Next, we used these same two dimensions to visualize the neural activity observed during dual movement (Figure 5C). Interestingly, the neural representation of arm movement appears largely intact (blue line is similar) while the representation of leg movement shrinks considerably in this space (red line is smaller). This could be because the axis of representation has changed and no longer aligns with the single movement PCs. In Figure 5D we show the same activity but in neural dimensions that best explain dual movement (found again using PCA). Although the modulation for leg movement is still smaller than in Figure 5B, it is enlarged relative to Figure 5C, indicating that both the modulation size has decreased and the axis of representation has shifted.
We then summarized the effects observed in Figure 5B–D across all effector pairings (Figure 5E–F). Figure 5E summarizes the change in firing rate when each effector is moved separately (e.g. the red and blue lines in Figure 5B). Contralateral arm movements cause the largest firing rate changes, followed by the contralateral leg, ipsilateral arm, ipsilateral leg and head. We then quantified how the modulation size changed during dual movement (Figure 5F, top panel). To measure how it changed, we divided the modulation size during dual movement (length of the lines in Figure 5D) by the modulation size during single movement (length of the lines in Figure 5B). Values less than 1 indicate that neural activity was attenuated. For most pairings, the neural representation of the “primary” effector (blue bars) stays relatively constant while the representation of the “secondary” effector (red bars) is attenuated.
We found the same pattern for the change in axis (Figure 5F, bottom panel); the primary effector mostly retains its axis of representation while the secondary effector’s axis changes more. The change in axis was defined by the cosine of the angle between the single movement axis and the dual movement axis. On average, this change caused the two effectors to become less correlated with each other during dual movement (Figure 5G). These suppression and decorrelation effects might facilitate independent dual-effector control by keeping the somatotopically dominant activity free from interference.
A Whole-Body Discrete Decoding BCI that Increases Information Throughput
Current intracortical BCIs (iBCIs) are limited to recording from a small number of locations [e.g. (Hochberg et al., 2012; Collinger et al., 2013; Aflalo et al., 2015; Bouton et al., 2016; Pandarinath et al., 2017; Ajiboye et al., 2017)], making it difficult to record from the arm and leg areas of precentral gyrus across both hemispheres. The results above, which show strong whole-body tuning in just one patch of cortex, make it possible for current iBCIs to decode movements from all four limbs. One context where this could be useful is to enable accurate selection from a large number of items by mapping movements from different limbs to different items. This could be better than using the contralateral arm alone, since neural activity patterns from other limbs might be more distinct from each other.
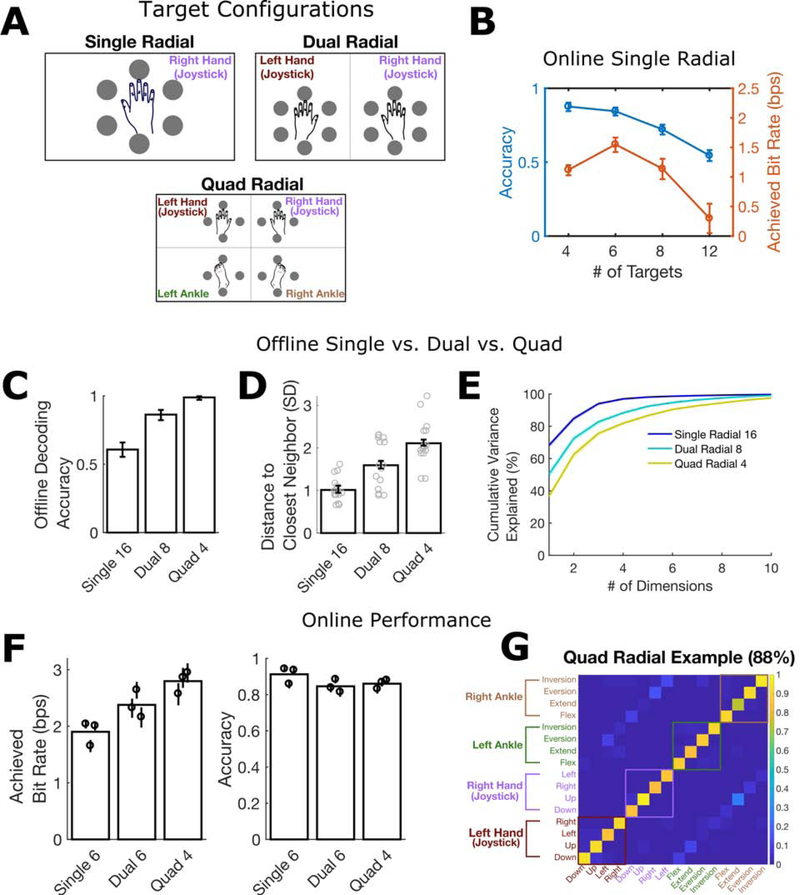
We tested this idea with a discrete iBCI that decoded, in closed-loop, which of a set of N movements was attempted by the user. A Gaussian naïve Bayes classifier was used to decode the movement (using a single time window of neural activity). We focused on directional movements made by the wrists (as if pointing a joystick) and ankles (pointing the foot), consistent with prior work on discrete iBCIs that decoded directional movements (Musallam et al., 2004; Santhanam et al., 2006). Figure 6A shows the three target configurations tested. For each trial, a target would illuminate and T5 had exactly one second to identify the target and perform the indicated movement. At the end of one second, the movement was decoded and a sound played indicating to T5 whether the decoder was successful. The next target then appeared immediately.
Figure 6. Spreading targets across multiple effectors increases the accuracy and throughput of a discrete BCI.
(A) Target configurations. Each target was associated with a specific attempted movement.
(B) Online discrete decoding performance for a single contralateral effector (right wrist) as a function of the number of radially spaced targets. Bit rate and accuracy decline if more than 6 targets are used.
(C) Offline decoding accuracy increases as targets are spread across more effectors (mean and 95% CI shown).
(D) As the number of effectors increases, the distance of each target to its closest neighbor in neural population state space increases (each gray dot corresponds to a single target and indicates the distance to its closest neighbor in neural population state space). Bars and error bars show the means ± 95% CIs.
(E) The dimensionality of the neural activity increases with the number of effectors. Cumulative variance explained is plotted (mean ± 95% CI) as a function of the number of PCA components used to explain the neural activity across all targets.
(F) Online decoder performance for the target layouts in A. The achieved bitrate increases with the number of effectors, even when the number of targets is optimized for each layout (see Methods). Each circle shows the mean performance (± 95% CI) during a single session; bar heights show the mean across all sessions.
(G) Example confusion matrix from the online Quad Radial task. Each entry (i, j) in the matrix is colored according to the fraction of trials where movement j was decoded (out of all trials where movement i was cued). Off-diagonal banding shows that most errors were made when classifying between matching hand and foot movements.
First, we motivate the need for using multiple effectors by showing how information throughput [measured with “achieved bit rate” (Nuyujukian et al., 2015)] and decoding accuracy varies as a function of the number of targets when only a single effector is used (Figure 6B). After just 6 targets, accuracy and bit rate start to decrease. Next, we tested offline whether spreading out 16 targets across multiple effectors could increase performance (Figure 6 C–E). When spread across all four limbs (4 targets per limb), accuracy was near 100% (Figure 6C). The improvement in accuracy was a result of increasing the distance between each target in neural population state space (Figure 6D) and increasing the dimensionality of the neural population space spanned by the targets (Figure 6E). We then confirmed online that information throughput was higher when using multiple effectors. Even when using an optimized number of targets for each layout (see Methods), the four-limb layout performed substantially better (Figure 6F). Decoding errors mostly confused matching targets from the arm and leg on the same side of the body (Figure 6G), likely due to their correlated representation (as shown in Figure 4). Supplemental Video 1 shows example trials.
Finally, we explored spreading targets across more body parts than just the wrists and ankles (including the elbow, knee, hip, toes, and fingers). Supplemental Video 2 shows that high decoding accuracies (mean of 95%) can be achieved across 32 targets in this manner, as long as T5 is given more time to recognize the target and prepare the movement.
Discussion
Representation of the Whole Body in Hand Knob Area of Human Precentral Gyrus
How different body parts are topographically mapped onto motor cortical areas is fundamental to understanding the motor system. Although prior work has addressed this question in humans using electrical stimulation [e.g. (Penfield and Boldrey, 1937; Penfield and Rasmussen, 1950)] and low-resolution recording technologies [e.g. ECoG and fMRI (Crone et al., 1998a; Miller et al., 2007; Meier et al., 2008)], single neuron data has been lacking. Using microelectrode recordings, we found the surprising result that there was strong neural tuning to face, head, arm and leg movements intermixed in hand knob area of precentral gyrus. While it was previously recognized that nearby body parts within the arm, leg or face area of precentral gyrus may overlap (e.g. wrist and fingers may overlap), prior work in humans has largely supported the idea of separate areas for the arm, leg and face on precentral gyrus (Penfield and Boldrey, 1937; Miller et al., 2007; Meier et al., 2008). Our finding of intermixed whole-body tuning overturns this prior expectation and illustrates that single neurons may differ substantially from what electrical stimulation or low-resolution activity might predict.
In our view, anatomical studies convincingly argue that a great majority of the precentral gyrus belongs to the caudal portion of Brodmann area 6, a premotor area (as opposed to Brodmann area 4, primary motor cortex) (Rademacher et al., 1993; Geyer et al., 1996; White et al., 1997; Rademacher et al., 2001; Geyer, 2004). This modern perspective is somewhat at odds with Brodmann’s original illustrations, where area 4 was drawn as occupying a large amount of the surface of precentral gyrus (Brodmann, 1909). More recent studies show that area 4 only emerges from the central sulcus quite medially (in leg region) and is mostly confined to the area above the superior frontal sulcus in a wedge shape (Rademacher et al., 1993, 2001; White et al., 1997).
Given that our recordings are likely from premotor cortex, it is natural to ask: would the intermixed tuning we showed here also hold in primary cortex (in the central sulcus)? Prior work in macaques provides some guidance on this issue. Dorsal precentral gyrus, where our arrays were implanted, has been proposed to be homologous to macaque area F2 (PMd) (Genon et al., 2017, 2018; Geyer et al., 2000; Rizzolatti et al., 1998; Zilles et al., 1995). From this perspective, many of our results match previous results from macaque studies, including a large correlation in PMd activity between contralateral and ipsilateral reaching movements (but not in M1) (Cisek et al., 2003; Ames and Churchland, 2019; Heming et al., 2019), and mixed arm and leg representations in PMd (but not in M1) (Kurata, 1989). The close match between our results and macaque PMd provides compelling evidence of homology between human dorsal precentral gyrus and macaque PMd at single neuron and multi-unit resolution, and suggests that Brodmann area 4 in humans likely contains more somatotopically segregated (and less compositional) movement representations. However, only neural recordings from human central sulcus can provide a definitive answer.
Importantly, both participants had chronic tetraplegia (T7 had ALS and T5 had high level spinal cord injury), which raises the question of how whole-body tuning might generalize to people without tetraplegia. One would expect cortical remapping to occur after spinal cord injury; however, current models of remapping predict that the most adjacent intact body parts (in this case face and head) should become more dominant (Qi et al., 2000). Instead, we found in participant T5 that the arm and leg were more strongly represented than the face and head, suggesting that remapping may be limited in precentral gyrus. We also observed similar proportions of population-level tuning for face, head, arm and leg movements in participant T7, who had ALS, giving further confidence that intermixed tuning was not caused by remapping. Nevertheless, only neural recordings from able-bodied people can provide a definitive answer.
One additional consideration is the possibility that some of the whole-body tuning we observed was caused by small, inadvertent movements of the contralateral arm. However, we believe this is an unlikely explanation of our results. First, small generic movements of the contralateral arm induced by effort are unlikely to explain the rich, high-dimensional structure in the data (e.g. compositional coding). Second, BCI decoding performance increased when decoding additional effectors (due to better neural separability of the movements), which would not occur if tuning to the other effectors was caused by small, inadvertent movement of the contralateral arm.
A Compositional Neural Code for Movement
In one participant (T5), we characterized the structure of the neural code for movements across the whole body in one area of premotor cortex. We found that arm and leg movements were represented in a correlated way. Movements of the same body part on opposite sides of the body, and homologous movements of the arm and leg (e.g. hand grasp and toe curl), were significantly correlated in neural dimensions that coded for movement type. In other neural dimensions, the limb itself was represented largely independently of the movement. Together, activity in these neural dimensions forms a partially “compositional” code for movement that differs from a muscle-like representation.
Compositionality provides a new conceptual framework for thinking about how the motor cortical system constructs movement. It can also explain why the entire body is represented in a single area of premotor cortex, since a whole-body compositional code might be useful for transferring motor skills to different limbs. Based on our findings, we propose a concrete neural mechanism for skill transfer that works as follows. Neural activity in movement-coding neural dimensions could be optimized through learning to produce the correct patterns to accomplish the task. Then, the skill could be transferred to another limb by changing only the activity in limb-coding dimensions, causing the movement activity to re-route to different muscles. We schematize this idea in Figure 7 and further concretize it with a neural network model (presented in Figure S7) that is capable of transferring motor skills across the arms using a compositional code. Behaviorally, motor skills such as sequences, rhythms and trajectories have been demonstrated to transfer from one arm to the other (Latash, 1999; Criscimagna-Hemminger et al., 2003; Shea et al., 2011), from one leg to the other (Morris et al., 2009), and from the arms to the legs (Christou and Rodriguez, 2008; Kelso and Zanone, 2002; Savin and Morton, 2008).
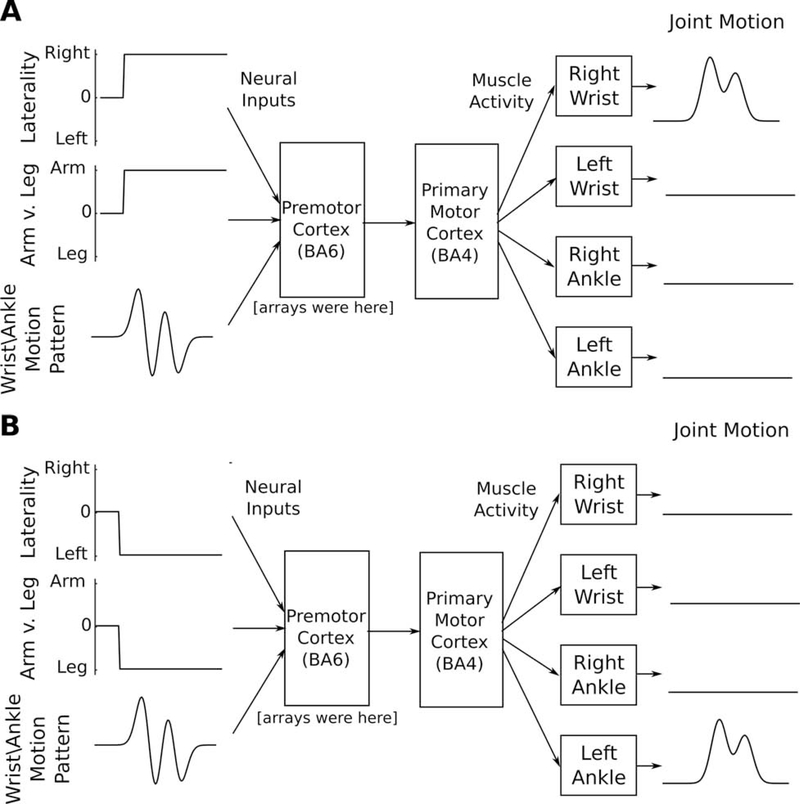
Figure 7. A compositional neural code may facilitate the transfer of motor skills across limbs.
(A) We speculate that premotor cortex (the site of our arrays) might receive input from upstream areas in the form of a “compositional” representation of movement where the limb is specified somewhat independently of the motion details. In this example, activity in the “laterality” and “arm vs. leg” input streams specify which of the four limbs should move, and activity in the “wrist/ankle motion pattern” input stream specifies the motion that should be performed (at a wrist or ankle joint). Premotor cortex and primary motor cortex would then convert this representation into limb-specific muscle patterns to achieve a desired joint motion.
(B) The same motion pattern could be transferred to any other wrist or ankle by changing activity only in the “laterality” and “arm vs. leg” dimensions, achieving immediate transfer without requiring relearning.
See Figure S7 for a concrete implementation of this hypothesis in a neural network model.
We hypothesize that precentral gyrus might be an intermediate node that helps transform a compositional representation of movement inherited from upstream areas into a more muscle-like representation required for motor control. Such an “in-between” role could explain why neural activity in precentral gyrus was not fully compositional in the sense that correlations values were always less than one (they typically ranged from 0.5 to 0.7). Consistent with such a role, we also observed that the movement code shared across effectors was represented in an intrinsic coordinate frame (Figure S4). We expect that more rostral areas might encode motor actions in visuospatial coordinates or in more abstract codes that could enable skill transfer between non-homologous effectors.
Our results are consistent with previous fMRI and ECoG studies that found a correlated representation of ipsilateral and contralateral finger/arm movements on precentral gyrus (Bundy et al., 2018; Diedrichsen et al., 2013; Jin et al., 2016) and an intrinsic, effector-independent code for finger movements (Wiestler et al., 2014). A recent microelectrode study of human parietal cortex also found a correlated representation of ipsilateral and contralateral hand and shoulder movements (Zhang et al., 2017). Our study puts these results into a larger context of a two-part compositional coding scheme that includes all four limbs and contains a limb-coding component in addition to correlated movement-coding components. We also showed that neural activity in movement dimensions can be prepared independently of neural activity in limb-coding dimensions, lending more support to the idea of independent specification of the movement and the limb-to-be-moved.
We further tested the idea of compositionality by examining how neural activity changed when two effectors were moved simultaneously. Since a shared movement code cannot simultaneously specify two different movements, we predicted that the code would change during dual movement. Results showed that during dual movement, the neural representation for the secondary effector was suppressed and its tuning changed, becoming less correlated with the primary effector. Our results are consistent with prior behavioral work suggesting that bimanual movements are coded separately from unimanual movements (Nozaki et al., 2006; Yokoi et al., 2016),fMRI studies in people (Diedrichsen et al., 2013), and electrode recordings in macaques that also showed changes in neural tuning for bimanual arm movements (Ifft et al., 2013; Rokni et al., 2003). This study extends these findings to a broader set of effector pairings, revealing a rank ordering of effectors that determines which effector’s representation remains intact during simultaneous movement.
Our compositional coding results focused on the arms and legs. Future work is needed to test whether the representation of head and face movements also shares a common structure with arm and leg movements, and thus whether compositionality can explain the presence of head and face related activity in arm/hand area of premotor cortex. One could imagine that motor skills such as timing and intensity (e.g. finger-tapping vs. nose-wrinkling a certain rhythm) might indeed be able to be transferred between the face and the limbs, necessitating a movement code with shared representations between the limbs and the face. However, skills that are more tied to the morphology of the extremities would likely require a unique representation.
Motor skill transfer is an intriguing hypothesis that could explain why all four limbs are represented in one area of premotor cortex; however, it is not the only possible explanation. One alternative is that the observed activity is an epiphenomenon of “overflow” activity from connected networks that control other body parts. However, the idea of overflow by itself cannot explain why we observed compositional structure (wherein homologous body parts had linked representations, effector-related activity could be prepared independently of movement-related activity, etc.). It is also unclear why motor cortical activity would overflow to connected regions to such a large degree with no functional purpose. Nevertheless, future work is needed to test whether the compositional code is causally involved with movement construction as opposed to epiphenomenal.
Related to the idea of neural overflow is the behavioral finding of “motor overflow”: the phenomenon that arm or leg movements are sometimes accompanied by small, unintended mirror movements of the opposite arm or leg, even in healthy adults (Hoy et al., 2004). Compositional coding offers an explanation for this phenomenon. An incomplete transformation between a compositional code and muscle activity could cause the effector-independent movement command to leak to unintended effectors, resulting in homologous limbs making small mirror movements. One concrete prediction of our theory is that motor overflow should be observed from the arm to the leg, and vice versa, since these limbs are linked together in the compositional code. We are unaware of any studies which test this behavioral prediction in adults, although it has been observed in infants (Soska et al., 2012).
Whole-Body Intracortical Brain-Computer Interfaces
Our findings have important implications for intracortical brain-computer interfaces (iBCIs), since they open up the opportunity to decode movements across the entire body from just a small area of precentral gyrus. We showed that a discrete target selection iBCI could successfully decode targets across all four limbs accurately enough to improve performance relative to a single-effector approach. Using more limbs increased the neural separability of targets, enabling more targets to be presented (up to 32 targets at 95% accuracy, Supplemental Video 2). While promising, it is important to note that our iBCI system was intended only as a proof-of-concept to demonstrate the potential of whole-body decoding. It does not constitute a complete, clinically viable system that is robust enough to recalibrate rapidly as neural features change [e.g. (Jarosiewicz et al., 2015)], or to automatically switch off during task disengagement, which are important challenges to overcome for real-world deployment.
Here, we demonstrated one use case for whole-body decoding: discrete target selection. Other use cases could be to map multiple movements to different kinds of clicks for general purpose computer use (e.g. curl left toes for left click, curl right toes for right click, etc.), or even to restore continuous control of leg and arm movements across both sides of the body. While whole-body decoding could also be achieved by placing electrodes across the entire precentral gyrus of both hemispheres, this is a much more difficult surgical and technical proposition.
One potential limitation of decoding the whole body from a single area is the suppression of activity related to secondary effectors during simultaneous movement (i.e. Figure 5). Nevertheless, simultaneous movements can still be decoded (we observed a mean offline decoding accuracy of 95% across all pairs of simultaneous movement). Moving forward, our results provide important design considerations for future iBCIs which must consider the tradeoff between additional microelectrode placement and multi-effector decoding performance.
STAR Methods
Lead Contact and Materials Availability
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Frank Willett (fwillett@stanford.edu). This study did not generate new unique reagents.
Experimental Model and Subject Details
This study includes data from two participants (identified as T5 and T7), who gave informed consent and were enrolled in the BrainGate2 Neural Interface System clinical trial (ClinicalTrials.gov Identifier: NCT00912041, registered June 3, 2009). This pilot clinical trial was approved under an Investigational Device Exemption (IDE) by the US Food and Drug Administration (Investigational Device Exemption #G090003). Permission was also granted by the Institutional Review Boards of University Hospitals (protocol #04–12-17), Stanford University (protocol #20804), Partners Healthcare/Massachusetts General Hospital (2011P001036), Providence VA Medical Center (2011–009), and Brown University (0809992560). All research was performed in accordance with relevant guidelines/regulations.
Participant T7 was a right-handed man, 53 years old at the time of data collection, who was diagnosed with Amyotrophic Lateral Sclerosis (ALS) and had resultant motor impairment (functional rating scale ALSFRS-R of 17). In July 2013, T7 was implanted with two 96 channel intracortical microelectrode arrays (Blackrock Microsystems, Salt Lake City, UT) in the hand knob area of dominant precentral gyrus (1.5-mm length). Data are reported from post-implant day 24. At the time of data collection, T7 retained movement of the arm, leg, face and head. T7 was able to extend and flex the knee and ankle normally, and make all requested head and face movements normally, but had more limited range of motion in the arm and leg for some movements (Table S2 reports neurologic exam results). T7 is no longer enrolled in the trial and the data from T7 were collected before the present study was conceived.
Participant T5 is a right-handed man, 65 years old at the time of data collection, with a C4 ASIA C spinal cord injury that occurred approximately 9 years prior to study enrollment. In August 2016, participant T5 was implanted with two 96 channel intracortical microelectrode arrays (Blackrock Microsystems, Salt Lake City, UT) in the hand knob area of dominant precentral gyrus (1.5-mm length). Data are reported from post-implant days 579–961 (Table S1). T5 retained full movement of the head and face and the ability to shrug his shoulders. Below the injury, T5 retained some very limited voluntary motion of the arms and legs that was largely restricted to the left elbow. Some micromotions of the right and left hands were also visible, along with extremely small but reliable twitching of the feet and toes (Table S2 reports neurologic exam results).
The hand knob area in both participants was identified by pre-operative magnetic resonance imaging (MRI). Figure 1 shows array placement locations registered to MRI-derived brain anatomy.
Method Details
Session Structure and Cued Movement Tasks
Neural data was recorded in 3–5 hour “sessions” on scheduled days. During the sessions, participants sat upright in a wheelchair that supported their backs and legs. A computer monitor placed in front of the participants displayed text and/or colored shapes to indicate which movement to make and when. Data was collected in a series of 2–10 minute “blocks” consisting of an uninterrupted series of cued movements; in between these blocks, participants were encouraged to rest as needed. The software required for running the experimental tasks, recording data, and implementing the closed-loop decoding system was developed using MATLAB & Simulink (MathWorks).
The data from participant T7 were collected in a single session consisting of a series of 2-minute blocks containing 20 repetitions of one set of paired movements. These paired movements were designed to engage the same joint(s) but in different directions; for example: hand open/close, wrist flexion/extension, head left/right, etc. Every three seconds, the text on the screen alternated to instruct the other paired movement (e.g. as in Figure 1A) and T7 responded as soon as he was able.
The data from T5 were collected across 19 sessions (Table S1). All sessions followed a simple instructed delay paradigm (like that shown in Figure 1A) except for the closed-loop discrete decoding sessions (described in their own section below). For text-cued tasks (Figures 1–5), during the instructed delay period a red square and text appeared in the center of the screen indicating to T5 that he should prepare to make the specified movement. The instructed delay period lasted a random amount of time that was drawn from an exponential distribution; values that fell outside of a minimum/maximum range were re-drawn. Maximum and minimum delay times varied from session to session but were within 1.4 to 3 seconds. After the delay time, the square turned green and the text indicating the movement changed to “Go”, at which point T5 made the movement immediately. T5 was told to continue attempting to make the movement (for arm & leg movements) or to hold the posture of the completed movement (for face & head movements) until the text changed to “Return”, at which point T5 relaxed and returned to a neutral posture. The movement and return periods lasted 1.5 seconds each. The spatially cued movement task (Figure S4) followed the same structure, but used colored targets instead of text to specify which movement was supposed to be made (as shown in Figure S4A).
Neural Data Processing
Neural signals were recorded from the microelectrode arrays using the NeuroPort™ system (Blackrock Microsystems) [(Hochberg 2006) describes the basic setup]. Neural signals were analog filtered from 0.3 Hz to 7.5 kHz and digitized at 30 kHz (250 nV resolution). Next, a common average reference filter was applied that subtracted the average signal across the array from every electrode in order to reduce common mode noise. Finally, a digital bandpass filter from 250 to 3000 Hz was applied to each electrode before spike detection.
For threshold crossing detection, we used a −4.5 × RMS threshold applied to each electrode, where RMS is the electrode-specific root mean square (standard deviation) of the voltage time series recorded on that electrode. For the analysis of waveform-sorted single neurons (which was only done for Figure S3), neurons were sorted manually using Plexon Offline Spike Sorter v3. Only waveform clusters that appeared in an unambiguous, highly separable cluster in principal component space were included.
Threshold crossing times (and single-unit spike times) were binned into 10 ms bins (for T5) or 20 ms bins (for T7) and z-scored to ensure that electrodes with high firing rates did not overly influence the population-level results. Different bin widths were used for T5 and T7 because the task data was collected with different computer systems at different sampling rates. Z-scoring was accomplished by first subtracting, in a block-wise manner, the mean count over all bins within each block. Subtracting the mean within each block helps to counteract slow drifts in the firing rate of electrodes and was especially important for the T7 data, since it was collected in a block-wise fashion. For this dataset, mean subtraction ensures that spurious drifts in firing rate did not artificially inflate the classification performance shown in Figure 1E (by helping to distinguish movements from different blocks). After mean-subtraction, the binned counts were divided by the sample standard deviation computed using all bins across all blocks.
Finally, electrodes with firing rates < 1 HZ over all time steps were excluded from further analysis in order to denoise population-level results. For some analyses (e.g. dPCA in Figure 3), the binned spike count time series were convolved with a Gaussian kernel (sd = 30 ms) to reduce high frequency noise.
Gaussian Naïve Bayes Classification
For both offline (e.g. Figure 1E) and online classification (Figure 6 F–G), we used a Gaussian naïve Bayes classifier to classify firing rate vectors. We chose to use a Gaussian naïve Bayes classifier because it is a simple and straightforward method that performed well enough to demonstrate our key points. It is possible that more advanced decoding architectures may improve performance even further.
Firing rate vectors were computed by counting the number of threshold crossings that occurred within a fixed window of time for each electrode and then dividing by the window width. To classify the firing rate vectors, we computed the log likelihood of observing that vector for each possible class and then chose the class with the largest log likelihood. We assumed that each element of the firing rate vector was normally distributed and was statistically independent from each other element. We also assumed that the variance of each Gaussian distribution was the same across all classes. Under these assumptions, the following quantity is proportional to the log likelihood of observing firing rate vector x under the class Ck (Bishop, 2006):
Here, N is the number of electrodes, xi is the ith element of the firing rate vector x (corresponding to electrode i’s firing rate), ui,k is the mean for electrode i under class k, and σi is the standard deviation for electrode i (under all classes). To classify, we computed this quantity for each class and chose the class with the largest value. The class-specific means were estimated using the sample mean across all available training data; likewise, the variances were estimated using the pooled variances across all classes.
Closed-Loop Discrete Decoding
All closed-loop discrete decoding experiments used a “time-locked” trial structure where each trial lasted for 1 second and no pauses occurred between trials. At the end of each trial, the closed-loop discrete decoding system classified the participant’s attempted movement. If the movement was correctly classified, a “success” sound played; otherwise, a “failure” sound played. After each trial ended, a new target appeared and the next trial began immediately (see Supplemental Videos 1 and 2 for example trials).
We used a Gaussian naïve Bayes classifier (defined above) to classify mean firing rate vectors computed using a fixed window of time for each trial. This window was optimized for each task and session as part of the process of calibrating the classifier; the window typically fell between 300 to 1000 ms. To optimize the window, we performed an offline grid search across all possible start and end times for the window in 50 ms increments from 0 ms to 1000 ms. Ten-fold cross-validation was used to estimate the achieved bit rate that would result from using each window. The window with the largest achieved bit rate was then chosen.
For each online discrete decoding session, one or two target configurations were tested. For each target configuration, one 5 minute open-loop block of data was first collected with which to calibrate an initial classifier. Then, we proceeded with a series of 5 minute closed-loop blocks to allow participant T5 to practice with that target configuration. After each closed-loop block, we re-calibrated the classifier using the preceding two blocks of data. We continued until we determined that T5’s performance had plateaued and he was comfortable with the task. After this decision was made, we collected a series of five, 3-minute “performance” blocks with the classifier held fixed; the average accuracy and achieved bit rate obtained during these blocks were reported in Figure 6. In addition to the sessions reported here, T5 benefitted from 6 additional sessions of practice wherein we developed/tested the BCI system and tried different target configurations.
Achieved bit rate is a conservative, clinically-motivated metric of information throughput (Nuyujukian et al., 2015) and was computed with the following formula:
where N is the number of targets, Sc is the number of correct selections, Si is the number of incorrect selections, and t is the total time elapsed. Achieved bit rate assumes that every incorrect selection must be followed by the correct selection of a delete key to undo the error, thus heavily penalizing low accuracies that would be hard for participants to work with in practice.
For the online results in Figure 6 F–G, we used an offline simulation to find the optimal number of targets for each layout in order to maximize the achieved bit rate. To do so, we used an exploratory offline dataset with all four effectors (right & left hand, right & left foot) and with eight targets per effector. We then fit a simple linear encoding model of target direction to each effector, using only the data corresponding to that effector’s movements:
Here, f is the N × 1 firing rate vector for a single trial, Ek is an N × 3 matrix of mean firing rates (first column) and directional tuning coefficients (second and third columns) for effector k, θ is the angle of the target, ε is an N × 1 noise vector, and a is a scalar gain factor. Each element of ε is normally distributed with covariance matrix Σk. Ek was fit to the data using least squares regression for each effector independently, and Σk was estimated using the sample error covariance of the linear model. To counteract overfitting in Ek (which could overestimate the amount of tuning present), we searched for the gain factor a which led to the best match in predicted accuracy for the number of targets present in the exploratory dataset (eight). These a values were < 1 and downweighed the tuning.
Once the model was fit, we varied the number of possible targets from 2 to 10. For each target layout, we simulated a new set of trials using the model and predicted decoder performance by applying a Gaussian naïve Bayes classifier to the simulated data using ten-fold cross-validation. Using this method, we predicted that the optimal number of targets was equal to 6 for a single effector (right hand only), 6 each for two effectors (right & left hand), and 4 each for four effectors (right & left hand, right & left foot) when the trial time was constrained to be one second. Encouragingly, the optimal number of targets predicted by this method for a single effector (6) matched online data (Figure 6b).
Quantification and Statistical Analysis
The quantitative methods used for data analysis are detailed below in this section, organized mainly by the Figure for which they were used. Statistical analyses are reported in the Results and also described in detail below in this section. In general, 95% confidence intervals and/or p-values < 0.05 were used to define statistical significance. We used t-tests to compare the means of two distributions. We used bootstrap resampling, jackknifing or parametric assumptions of normality to generate 95% confidence intervals of the mean. Quantitative approaches were not used to determine if the data met the assumptions of the t-tests or normality. The statistical units and N for each test are detailed below.
Cross-Validated Estimator of Neural Distance
Measuring the distance between two distributions of firing rate vectors is useful for quantifying the amount of neural modulation caused by a particular movement. However, measuring this in an unbiased way in the presence of noise is a nontrivial problem. Here, we motivate the problem and describe the methods we used to obtain conservative estimates of distance that substantially reduce bias by using cross-validation (see our code repository https://github.com/fwillett/cvVectorStats for an implementation and simulated tests that validate the approach).
To understand the problem, consider the measurements in Figure 1C. The bar heights reflect the distance between two multivariate distributions: a distribution of firing rate vectors corresponding to the “do nothing” condition (distribution 1), and a distribution of firing rate vectors corresponding to the movement in question (distribution 2). Let us denote the firing rate vector observed on trial i for distribution 1 as xi1 and for distribution 2 as xi2. The sample means are
The sample means differ from the true means u1 and u2 by some sampling error. As a result, the difference in sample means also contains error: for some error vector ε.
One simple method for estimating the distance between distributions 1 and 2 would be to take the Euclidean norm of the difference in sample means: . However, the sampling error inherent in causes this metric to be biased upwards. Expanding terms, we have: , which is larger than on average since ε · ε > 0. One intuitive way to see this is to consider the case where distribution 1 and distribution 2 are identical. The sample means for each distribution will always differ from each other (due to sampling error), and hence there will always be some positive distance between them even though the true difference in means is zero.
Fortunately, there is a straightforward way to achieve a practically bias-free estimate of distance. First, by following the approach laid out in (Allefeld and Haynes, 2014), we can estimate the squared distance by averaging together a series of unbiased estimates, each made by using leave-one-out trials. The following is an unbiased estimate of the squared distance:
Here, is the sample estimate of the difference in means using only the pair of samples from trial i and is the sample estimate of the difference in means using all trials except i. Note that this cross-validation technique has also been used elsewhere as part of the “crossnobis” estimator (Diedrichsen and Kriegeskorte, 2017).
Since and contain no overlapping trials, they are statistically independent from each other. Statistical independence implies that the expectation of their product is equal to the product of their expectation. Taking the expectation, we can show that it is an unbiased measure:
Note that this cross-validation approach will work for computing the squared norm of any vector quantity in an unbiased way. For example, could be a vector of coefficients from a linear tuning model or, more simply, the mean of a single distribution.
Although squared distance can be used as a measure of neural modulation, we find ordinary (Euclidean) distance to be a much more intuitive metric (e.g. when using Euclidean distance, if the neural distance is twice as large, then there is twice as much firing rate change). Unfortunately, taking the square root of the above quantity does not immediately yield an unbiased measure of Euclidean distance, since it can be negative. Nevertheless, it is possible to construct a conservative, largely unbiased estimator of Euclidean distance by taking the square root of the absolute value while preserving the sign: . This square root estimator substantially reduces (practically eliminates) bias and is far more robust to sampling error than a naïve approach of taking the Euclidean norm of the sample estimate. We found that except in cases of very high sampling error, the square root estimator’s expectation was equal to the true value. Importantly, in cases where some bias was present, the estimator was conservative (see https://github.com/fwillett/cvVectorStats for simulations); since it is conservative, significantly positive distances can be safely interpreted as meaningful differences in neural activity.
Note that above method assumes that there are an equal number of observations from each distribution (N observations from each), but the same technique can be applied for unequal numbers of observations by splitting the data into folds of varying sizes (https://github.com/fwillett/cvVectorStats).
Cross-Validated Angles and Correlations
In the above section, we described our approach for reducing bias when estimating the distance between two firing rate distributions. We also extended this approach to reduce the bias of correlation and angle measurements, which we describe here (see our code repository at https://github.com/fwillett/cvVectorStats for an implementation and simulated tests that validate the approach).
When computing the angle between mean firing rate vectors (in Figure 5F–G), the sample estimate is:
Here, and are the sample estimates of the mean firing rate vectors for distribution 1 and 2. The problem here is that and are biased upwards because they contain sampling error. This causes cos θ to appear smaller than it truly is, making the vectors appear more dissimilar. The larger the uncertainty (smaller sample sizes or smaller vectors), the greater this effect will be.
By replacing and with bias-reduced estimators of vector norm, this effect can be eliminated. For example, as shown in the above section, can be estimated in an unbiased way by computing , where is the sample estimate of u1 using only trial i and is the sample estimate of u1 using all trials except i. can then be estimated by applying the sign-preserving square root transform.
The same technique of substituting bias-reduced estimators into the denominator can be applied to greatly reduce bias when estimating correlations between vector means (as in Figure 4) or vectors of tuning coefficients (as in Figure S4). To see this, note that the equation estimates the correlation between two u1 and u2 as long as and are taken to be the sample estimates of the centered vectors.
Figure 1 Methods
The datasets presented in this figure (10.22.2018 and 08.23.2013) consisted of 32 trials per movement for T5 and 19 trials per movement for T7.
In Figure 1C, 95% confidence intervals of the mean were computed by assuming that the data are normally distributed.
In Figure 1D, we used the bias-reducing, cross-validated estimator of distance to compute the height of each bar. To compute the confidence intervals, we used a jackknife procedure as described in (Severiano et al., 2011). We found that the jackknife confidence intervals produced more accurate confidence intervals than bootstrapping (which we confirmed via simulation), since the cross-validated distance metric is biased upwards when resampling identical data points (because identical data points are more aligned with each other). This effect is similar to that noted in (Severiano et al., 2011), where the jackknife was also found to outperform the bootstrap.
In Figure 1D, the small circles represent single trial firing rate vectors projected onto a “difference axis” consisting of the difference between two distributions of firing rate vectors. For T5, the two distributions correspond to the “do nothing” control condition and the movement condition of interest. The light circles are the single trial projections of the “do nothing” activity onto this axis and the dark circles are the single trial projections of the movement activity. For T7, the two distributions correspond to each of the paired movements for the pair of interest, and the light and dark circles each correspond to one of the movements in the pair. The small circles were jittered along the x-axis for ease of visualization.
We used cross-validation to project each trial’s firing rate vector onto a line connecting the two distributions in question. For each trial, we first estimated the line connecting the two distributions using all other trials by computing , where is the sample mean for distribution 1, is the sample mean for distribution 2, and d is the scalar distance between the distributions found using the cross-validated estimator. We then projected the held-out trial’s firing rate vector onto v by using the dot product.
Using the data in Figure 1D, we performed t-tests to determine whether the changes in firing rate evoked by arm movements were statistically significantly larger than those evoked by non-arm movements. For T5, enough movements were tested so that we could perform independent, two-sample t-tests for each movement category (using the mean Δ firing rate magnitude for each movement as the statistical unit, i.e. the bar height for each bar in Figure 1D). The arm modulation (N=8 arm data points) was statistically significantly larger than the face (p<1e-06, N=11 face data points), head (p<1e-04, N=8 head data points), and leg (p=0.003, N=6 leg data points) modulation. For T7, only two movement pairs each were tested for the face, head, and leg categories, making statistical comparison underpowered on a per-category basis. However, lumping together all non-arm movements (for a total of 6 arm data points and 6 non-arm data points) showed a statistically significant difference from arm movements when using a two-sample t-test (p<1e-3).
For Figure 1E (offline classification), we used the firing rates in a window between 200–600 ms (T5) or 200–1600 ms (T7) after the go cue as input into the classifier. For T7, we found that since there was temporal variation in activity throughout the movement, classification performance could be improved by including multiple time windows of firing rates for each electrode in the feature vector. We split the 200 to 1600 ms time window into two smaller windows (200 to 800 and 800 to 1600) and included the activity in each of these windows for each electrode as input to the classifier (effectively doubling the number of inputs). This wasn’t necessary for the T5 dataset as performance was already saturated with a single window.
Note that, due to the block design of T7’s data, we pre-processed the neural data to remove differences in firing rate means from block to block that could spuriously increase classification performance (see above section “Neural Data Processing”).
Figure 2 Methods
Figure 2 was created in the same way as Figure 1D, detailed above. Figure 2’s dataset (12.05.2018) consisted of 30 trials per movement.
Figure 3 Methods
Figure 3 used the same dataset as the one shown in Figure 2 (12.05.2018; 30 trials per movement).
We used the most recent version of demixed principal components analysis (Kobak et al., 2016) [https://github.com/machenslab/dPCA] with the default parameters, including using an optimization procedure to find the best regularization factor. Demixed principal components analysis (dPCA) is an optimization technique that decomposes neural data into a sum of neural dimensions that express variance related only to certain variables in the experiment. This decomposition gives an interpretable and comprehensive overview of the structure in the neural data as it relates to the experimentally manipulated variables. Here, we briefly summarize dPCA as it was applied to our data [refer to (Kobak et al., 2016) for a complete description].
Demixed PCA begins with splitting the data into marginalizations in an ANOVA-like manner. Considering first just a single electrode, we can put this electrode’s binned firing rate data into a four-dimensional data tensor the laterality condition, and k is the trial. By averaging across trials, we can obtain the trial-averaged, three-dimensional data tensor .
We can now define the following marginalizations of the trial-averaged data tensor. In the following equations, when a subscripted index is replaced with a dot, it means to average over that dimension:
The left-hand side of the above equations are the marginalizations and the right-hand side shows how to compute them. Note that the trial-averaged data tensor can be written as a sum of the marginalizations, since they define a complete decomposition of the data:
Next, each marginalization can be “unrolled” into a row-vector of length TML by tiling the marginalization appropriately (where T is the number of time steps, M is the number of movement conditions, and L=2 is the number of body sides). Once unrolled, this marginalization can be “stacked” vertically across all electrodes to yield a matrix of size N × TML that describes the entire neural population’s marginalization.
After computing the marginalizations, demixed PCA then attempts to find neural dimensions that “readout” certain sets of the marginalizations on a single-trial basis. For example, we can group together the and marginalizations by adding together their matrices XL and XTL, yielding an N × TML matrix of laterality-related signals in the neural population. Demixed PCA then tries to find neural dimensions that will map single trial recordings to the marginalization matrix. To do so, first the marginalization matrix must be expanded to tile across all single trials, yielding a matrix of size N × TMLK (where K is the number of trials). Demixed PCA then uses the following loss function:
Here, is the trial-averaged marginalization set of interest (in this example, XL + XTL) tiled across all trials, X is a matrix containing the single-trial data (also of size N × TMLK), and D and F are decoder and encoder matrices (of size C × N and N × C) that readout the single trial activity into C signals and then re-encode them back into the N-dimensional neural activity.
For the analysis in Figure 3A, we grouped the marginalizations as follows for ease of interpretation: movement , laterality , and time . Figure 2B shows the top readout dimensions (rows of DϕX in order of variance explained) for each marginalization group. Each line depicts the average across trials and the shaded regions depict 95% confidence intervals.
Confidence intervals were found using a cross-validated version of dPCA. Specifically, for each trial, we performed dPCA on all remaining trials to find the readout dimensions Dϕ and then applied them to the held-out trial. After doing this for each held-out trial, we then estimated the means and 95% CIs using the held-out readouts. CIs were computed by assuming that the data were normally distributed. Cross-validation ensures that any result found is not due to overfitting the decoder matrices to noise in the data. One potential issue with this cross-validation approach is that the sign of the readout dimensions can sometimes change for each held-out trial; to counteract this, we corrected for any sign flips by finding the sign that best matched the readout dimensions found for the first held-out trial (match quality was assessed with the dot product). This problem is discussed in general in (Milan and Whittaker, 1995).
Figure 4 Methods
In Fig4A, we used a cross-validation approach to verify that the laterality and arm vs. leg dimensions found by dPCA generalized to new movements. To do so, we took two approaches: a held-out “single movement” approach and a held-out “movement set” approach. In the single movement approach (diagonal panels in Figure 4A), we used leave-one-out cross-validation for each single movement condition. That is, for each movement, we applied dPCA to all other movements in order to find the top component for reading out the laterality or arm vs. leg marginalization. We then applied this component to the held-out condition. In the movement set approach (off-diagonal panels in Figure 4A), we held out an entire set of movements corresponding to a different limb (or laterality). The results show that the laterality and arm vs. leg components generalize both across movement conditions and across different sides of the body and effectors.
For Figure 4B–C we used the cross-validated correlation metric (described above in “Cross-Validated Angles and Correlations”) to compute the correlation between pairs of mean firing rate vectors associated with each movement condition. Figure 4B uses data collected in session 12.05.2018 (the same as in Figure 2 and 3; 30 trials per movement), while Figure 4C used a different dataset designed specifically to contain many pairs of homologous arm and leg movements (11.19.2018; 20 trials per movement). Before computing the correlations, we subtracted the average firing rate within each laterality (Figure 4B) or within each effector (Figure 4C). Otherwise, correlations would be predominately negative across all movements due to the presence of large laterality and arm vs. leg dimensions (shown in Figure 4A). For example, for Figure 4B, we computed the mean firing rate vector across all ipsilateral movements (vector I) and contralateral movements (vector C). Vector I was subtracted from all ipsilateral movement conditions and vector C was subtracted from all contralateral movement conditions to remove the effect of the laterality dimension.
To test for correlations between homologous arm and leg movements in T7, we leveraged the following movement pairs that were present in T7’s dataset (shown in Figure 1D): (Arm Raise & Leg Raise), (Arm Lower & Leg Lower), (Wrist Flex & Ankle Flex), (Wrist Extend & Ankle Extend). Using these pairs, we computed a 4×4 correlation matrix with the same methods we used for T5, yielding 4 homologous correlation values and 12 non-homologous correlation values. A two-sample t-test with these two distributions indicated statistical significance between them (p=0.0036, with an average Pearson’s r=0.22 for homologous movements vs. an average Pearson’s r=−0.07 for non-homologous movements).
Figure 4D–E contains data from two separate sessions (12.10.2018 and 03.27.2019, 18 trials per movement condition) designed to test whether partially specified movements could elicit preparatory activity in dimensions corresponding only to the partially specified information. In the partial laterality cueing experiment (Figure 4D), there were four movements tested: contralateral wrist extension, ipsilateral wrist extension, contralateral hand grasp, and ipsilateral hand grasp. During the instructed delay period, the upcoming movement could either be fully cued (with both the laterality & movement specified by text on the screen), laterality-cued (with only the laterality specified), or movement-cued (with only the movement specified), with equal probability of each. In the partially cued conditions, when the go cue was given, the text on the screen changed to specify the missing piece of information so that the movement could be attempted.
For example, for a movement-cued trial for contralateral wrist extension, during the delay period a red square appeared in the center of the screen and the text above it was: “Wrist”. Then, during the go period, the square turned green and the text changed to: “Right”. Displaying “Right” instead of “Right Wrist” during the go period ensured that T5 must remember the partially specified piece of information (and cannot simply skip movement preparation, waiting until the go cue to read the text).
The partial arm vs. leg cueing experiment (Figure 4E) had an analogous design with the following four movements: wrist up (extension), wrist down (flexion), ankle up (dorsiflexion), and ankle down (plantarflexion). During the instructed delay period, the upcoming movement could either be fully cued (with both the effector & movement direction specified by text on the screen), effector-cued (with only the “wrist” or “ankle” specified) or movement-cued (with only the movement direction specified).
To analyze the data from the partial cue experiment, the data was first smoothed (convolved with a Gaussian kernel, width = 60 ms std) and marginalized according to either movement type or laterality (for the first experiment), or movement direction or effector (for the second experiment). We then applied demixed PCA to a time window of the data beginning 1 second before the go cue and ending at the go cue (see the section above on Figure 2 for an explanation of dPCA and marginalization). The demixed PCA components were found using only the fully cued trials.
To make Figure 4D–E (and Figure S6), we used the dPCA component for each marginalization that explained the most variance. The means and confidence intervals plotted in Figure 4D–E were found by first averaging the activity in each dPCA dimension across a 300 ms time window for each trial. This yields a single value for each trial; these values were then averaged for each condition and confidence intervals were fit by assuming a normal distribution. We used unsmoothed neural data for this portion of the analysis so that only data that was strictly contained within the 300 ms window was used.
Figure 5 Methods
This figure used a series of ten paired effector experiments collected across three sessions (03.19.2018, 03.21.2018, 04.02.2018; 18 trials per movement condition).
To find the neural dimensions used to visualize the activity in Figure 5B–D, we first computed a firing rate vector for each trial containing each electrode’s firing rate within a window from 200 to 1000 ms after the go cue. For Figure 5B, in order to find neural dimensions for visualization, we first averaged these firing rate vectors within each single-movement condition to obtain four average vectors: f1A, f1B, f2A, f2B (for effectors 1 & 2 and movement directions A & B). We then subtracted the average firing rate vector within each effector to remove the differences in firing rates caused by effector alone. That is, we computed mean-subtracted vectors:
We then applied PCA to the mean-subtracted vectors , , , to find the two components that explained the most variance in these vectors. Finally, we used these two components to project the single trial firing rate vectors into a two-dimensional space for visualization. Note that applying PCA to the mean-subtracted vectors ensures that the PCA components capture differences in firing rate that are related to movement direction. Otherwise, PCA would find a large “effector” dimension (like that shown in Figure 3A) and the direction-related activity would not be as visible in the first two dimensions.
For Figure 5D, in order to find the dual movement neural dimensions for visualization, we first averaged the single trial firing rate vectors within each dual-movement condition to obtain four average vectors: gAA, gAB, gBA, gBB (for movement directions A & B). We then applied PCA directly to these vectors without mean-subtraction. No mean subtraction was necessary in this case because both effectors were active for all movements; thus, there is no possibility of finding dimensions that are related to the effector being moved and not the direction it is moving in.
When applying PCA for Figure 5B–D, we used cross-validation to ensure that the clustering observed was not due to overfitting noise in the data. Specifically, for each trial, we performed PCA on all remaining trials to find the top principal components and then projected the held-out trial into those dimensions. Cross-validation ensures that any result found is not due to overfitting to noise in the data. One potential issue with this cross-validation approach is that the sign of the readout dimensions can sometimes change for each held-out trial; to counteract this, we corrected for any sign flips by finding the sign that best matched the PCA dimensions found for the first held-out trial (match quality was assessed with the dot product). This problem is discussed in general in (Milan and Whittaker, 1995).
For Figure 5E and the top panel of Figure 5F (dual/single ratio), we used the cross-validated estimator of distance (see above section “Cross-Validated Estimator of Neural Distance”). For the bottom panel of Figure 5F (change in angle), we used the cross-validated estimator of vector angle (see above section “Cross-Validated Angles and Correlations”). When computing angles and distances for Figure 5E–F, the full-dimensional space of all electrodes was used (i.e. not just the top two principal components shown in Figure 5B–D). To compute the 95% CIs of the mean for each bar, jackknifing was used (Severiano et al., 2011); see above section “Figure 1 Methods” for more details.
For Figure 5G, each circle denotes, for a single pair of effectors, the absolute value of the cosine of the angle between each effector’s axis of representation. This “alignment magnitude” metric denotes the strength of the correlation between that pair’s neural representation. As in Figure 5F, the angle was computed using cross-validation to reduce bias. There are ten data points, one for each effector pair. The alignment magnitude was computed separately for the single movement context (where the axes of representation where estimated during single-effector movement, e.g. Figure 5B) and the dual movement context (where the axes were estimated during dual-effector movement, e.g. Figure 5D). Bar heights indicate the mean across all ten data points, and lines connect matching effector pairs. A paired t-test reveals a statistically significant difference in alignment between the single and dual contexts (p=0.0053; 0.33 vs. 0.14).
Figure 6 Methods
Data for Figure 6B was collected in a single session (11.05.2018; 540 trials per layout) where multiple target layouts were tested. For each target layout, T5 first completed a 4 minute “open-loop” block where he made the cued movements but they were not decoded in real-time. This block was used to calibrated an initial decoder. T5 then completed a 4 minute “practice” closed-loop block using the initial decoder. Next, a new decoder was calibrated by combining data from the open-loop and closed-loop block. Finally, T5 completed a series of three, 4 minute “performance” closed-loop blocks using that decoder; performance form these blocks was reported in Figure 6B.
Data for Figure 6C–E was collected in a separate session (01.07.2019; 355 trials per layout). In this session, T5 completed a series of 15 open-loop blocks with three target layouts (5 blocks each, 71 trials per block): radial 16 single-effector (right hand joystick), radial 8 dual-effector (left & right hand joystick), and radial 4 quad-effector (left & right hand, left & right feet). Each block lasted 5 minutes. The blocks were interleaved in sets of 3 blocks each (1 for each layout).
The 95% confidence intervals of the mean shown in Figure 6D were computed by bootstrap resampling individual trials (not targets). The 95% CIs in Figure 6E were also computed by bootstrap resampling individual trials.
To compute the dimensionality of the neural activity as shown in Figure 6E, we first averaged the time-varying neural activity across trials to produce a trial-averaged, three-dimensional firing rate data tensor XNxTxM where N is the number of electrodes, T is the number of time bins, and M is the number of movements. We then “unrolled” the last two dimensions of this tensor to yield a two-dimensional matrix XNxTM; PCA was then applied to this matrix to find the cumulative variance explained by increasing numbers of N-dimensional components.
Data for Figure 6F was collected in a series of 7 sessions (see above section “Closed-Loop Discrete Decoding” for details about the session structure and decoder). Table S1 lists each individual session. The 95% confidence intervals of the mean shown in Figure 6F were computed by bootstrap resampling individual trials.
Figure S1 Methods
To make this figure, we did a PCA-type analysis within each movement category using the data shown in Figure 1 (datasets 10.22.2018 and 08.23.2013). First, the mean time-varying response of each electrode across all movements within a particular category was subtracted off. This eliminates any generic signal that varies across time but is otherwise the same across all movements, making movement-specific tuning easier to see. Next, we averaged the mean-subtracted neural activity across trials to produce a trial-averaged, three-dimensional firing rate data tensor XNxTxM where N is the number of electrodes, T is the number of time bins, and M is the number of movements within a movement category. We then “unrolled” the last two dimensions of this tensor to yield a two-dimensional matrix XNxTM; PCA was then applied to this matrix to find the top 3 neural dimensions (principal components) that explained the most variance. The mean-subtracted neural activity was then projected into these three components and plotted above.
To generate confidence intervals, we used bootstrap resampling (percentile method, 200 re-samplings). One potential issue with applying resampling techniques to PCA is that, if multiple dimensions contain similar amounts of variance, the principle components can change order, rotate, or flip their signs from resampling to resampling, causing the confidence intervals to be much wider than they should be. To counteract this, we applied a Procrustes analysis to each resampling’s principal components to solve for a small 5×5 rotation matrix to align the first five principal components to a reference set computed on all the data. This problem (and solution method) is discussed in general in (Milan and Whittaker, 1995).
Figure S2 Methods
The array maps in Figure S2A were created using the two datasets shown in Figure 1 (10.22.2018 and 08.23.2013). To assess statistical significance and compute FVAF scores, firing rates were first computed for each trial within a 200 to 600 ms window for T5 and 200 to 1600 ms window for T7 (matching Figure 1). Next, we grouped trials into four movement sets (Head, Face, Arm and Leg) as in Figure 1. To assess the statistical significance of tuning to a movement set on a given electrode, we performed a 1-way ANOVA on all trials within that movement set. Each individual movement cue within the set was considered its own group. If the p-value was less than 0.001, the electrode was considered significantly tuned.
To compute FVAF scores for each electrode and movement set, we used the following equations:
Here, SSTOT is the total variance (sum of squares), SSMOV is the movement-related variance, N is the total number of trials across all movements within the set, fi is the firing rate for trial i, is the average firing rate across all movements within the set, and is the average firing rate for the particular movement cued on trial i. FVAF values range from 0 (no movement-related variance) to 1 (all variance is movement-related). T7’s FVAF shading range was reduced to 0.5 to increase visibility of the colors (since the maximum FVAF value for T7’s dataset was 0.52).
To assess statistical significance for T5’s matrix in (B), we performed a two-sample t-test comparing each movement’s firing rates to the “Do Nothing” firing rates. For T7, we performed a two-sample t-test to compare the firing rates corresponding to each movement of a movement pair. For both analyses, the electrode was considered significantly tuned if the p-value was less than 0.001. Black horizontal bars indicate cluster ranges computed via k-means clustering with the number of clusters set to 4. Results show a diversity of electrodes with both sparse and broad movement tuning characteristics.
The bar plots in (C) were created by summing the number of significantly tuned electrode channels for each movement set as computed via the ANOVA analysis performed in (A).
To make the pie charts in (D), the p-values from the ANOVA analysis in (A) were used to compute how many movement categories each functioning electrode was tuned to (i.e. by counting the number of p-values less than 0.001).
To make the scatter plots in (E), first, for each electrode, the mean change in firing rate was computed for each movement separately. The cross-validated distance estimator was used to estimate the magnitude of the firing rate change. Then, the absolute change in firing rates were averaged across all movements within a movement category to produce four numbers per electrode: mean change for arm, head, face and leg. Then, pairs of these numbers were plotted against each other as scatter plots, where each circle corresponds to a single electrode.
Figure S3 Methods
The datasets analyzed in this figure are the same as those analyzed in Figure 1 (datasets 10.22.2018 and 08.23.2013). The firing rates for the PSTHs were smoothed with a Gaussian kernel (30 ms std for T5 and 60 ms std for T7). The statistical significance of movement tuning was assessed with a 1-way ANOVA (for movement category) or a two-sample t-test (for individual movements) with a p-value threshold of 0.001, using the same methods as described above for Figure S2.
Figure S4 Methods
Figures 1–4 assess neural modulation largely to movements around a single joint. In Figure S4, we assessed how movement direction is represented across different effectors. Our goal was to determine whether a shared representation of direction exists across effectors and to characterize its coordinate frame. Participant T5 completed an instructed delay, spatially cued movement task which randomly cued one of eight directional movements from one of four effectors (Figure S4A). Two datasets were collected (02.13.2019, 24 trials per target; 12.05.2018, 26 trials per target), each testing a different set of effectors (hands and feet, SFig 4B–D; arms and legs, SFig 4E).
We first confirmed that neural activity was linearly tuned to movement direction [as expected from previous work (Georgopoulos et al., 1982)] by plotting the mean firing rates for each movement in the first two principal components (in a time window between 200 to 1000 ms after the go cue). PCA was applied in a cross-validated manner to ensure an unbiased result (explained in more detail below). The neural activity forms a ring which matches the geometry of the targets for each of the four body parts tested and is indicative of linear tuning to direction (Figure S4B).
To make Figure S4B, we used PCA to find, for each effector separately, the two highest-variance neural dimensions that best explained across-target variance. To do so, we first computed a firing rate vector for each trial containing each electrode’s firing rate within a window from 200 to 1000 ms after the go cue. Next, we averaged these firing rate vectors within each target to obtain eight target-averaged vectors. We then applied PCA to these target-averaged vectors to obtain the top two neural dimensions that best explained across-target variance. Finally, we then projected each trial’s firing rate vector onto these components to obtain the single-trial dots shown in Figure S4B. These were then rotated using a Procrustes analysis to align with the target geometry (i.e. a single rotation matrix was found that best mapped the neural activity to the target locations; this matrix had no ability to shear or skew the firing rates).
When applying PCA, we used a leave-one-out cross-validation approach. For each trial, the top two neural dimensions were found using all other trials; the held-out trial was then projected onto those neural dimensions. One potential issue with a cross-validation approach for PCA is that the sign of the PCs can sometimes change for each held-out trial; to counteract this, we corrected for any sign flips by finding the sign that best matched the PCA dimensions found for the first held-out trial (match quality was assessed with the dot product). This problem is discussed in general in (Milan and Whittaker, 1995).
Next, to assess how neural tuning to movement direction was correlated across different body parts, we first fit a linear tuning model for each body part separately to obtain horizontal and vertical tuning coefficients (preferred directions) for each electrode. Then, we correlated these horizontal and vertical coefficients separately between each different body part to see if a representation of movement direction was shared across body parts (Figure S4D–E). If an “extrinsic” (visuospatial) representation were shared, then both the horizontal and vertical coefficients should be positively correlated. On the other hand, if an “intrinsic” (joint or muscle-related) representation were shared, then the vertical coefficients should be positively correlated in all cases (since these correspond to the same joint movements), while the horizontal coefficients should be negatively correlated across different sides of the body (since these correspond to opposite joint movements) but positively correlated on the same side of the body. For example, the joint movement made when pointing the right hand towards the right is the opposite of that made when pointing the left hand towards the right; if neural activity is primarily intrinsic (representing the joint movement), then it will be negatively correlated across these two conditions.
We found that, across both the wrists and ankles (Figure S4D) and the arms and legs (Figure S4E), the pattern of correlations was more consistent with a shared intrinsic representation (mean r=0.50 for cases of matching joint movements, mean r=−0.34 for cases of opposite joint movements, p=1.4e-17). Statistical significance was assessed with a two-sample t-test that compared correlation values for matching joint movements (N=8) to correlation values for opposite joint movements (N=4). This result indicates that a shared representation of direction does indeed exist across effectors in precentral gyrus, and that this representation lies at an intermediate level of motor abstraction.
Tuning coefficients were found using the following model:
Here, f is the N × 1 firing rate vector for a single trial, Ek is an N × 3 matrix of mean firing rates (first column) and directional tuning coefficients (second and third columns) for effector k, θ is the angle of the target, and ε is an N × 1 noise vector. Ek was fit using ordinary least squares regression using all trials from effector k. Correlations were computed by calculating Pearson’s r using matching columns of Ek for pairs different effectors.
When computing the correlation between vectors of linear tuning coefficients, we used cross-validation (employing the principles described above in “Cross-Validated Angles and Correlations”). To do so, the coefficient vector magnitudes were estimated by fitting the encoding model separately for held-out and held-in data. We then took the dot product between held-out and held-in vectors to estimate the magnitude term in the correlation equation (see cvOLS in our code repository for an implementation).
Figure S5 Methods
We developed shuffle controls to demonstrate two points with further rigor: (1) that both the movement correlations and the movement-independent effector coding we observed are significantly above chance, and (2) the fact that homologous movements are correlated does not automatically imply the existence of significant effector-coding, and vice versa. Our shuffle controls examine how the variance explained by different marginalizations of the data changes when structure in the data is destroyed by shuffling across certain factors (see the above section “Figure 3 Methods” for a detailed description of how to compute marginalizations of the data).
To test for effector-coding, we shuffled the effector labels corresponding to each condition. For example, for a dataset consisting of ipsilateral and contralateral arm movements (e.g. Figure 4B), each condition has a particular movement (e.g. elbow flex, hand close, etc.) and a particular effector (ipsilateral arm or contralateral arm). For each movement, we can randomly swap the effector labels for the corresponding pair of conditions relating to that movement. Then, we test if this shuffling significantly decreases the amount of variance captured by the effector marginalization of the neural data. If it does, this is quantitative proof of significant (i.e. above chance) effector-related, movement-independent variance. Note that this shuffle control does not affect the correlations between homologous movements.
Likewise, to test for movement correlations, we shuffle the movement labels within each effector. This breaks the association between homologous movements by re-pairing them in a random way, but keeps intact the effector that each movement belongs to, preserving any consistent effector code. We then test if this shuffling decreases the amount of variance captured by the movement marginalization as compared to the movement × effector interaction marginalization. If it does, this quantitatively shows that the shared movement variance is larger than chance.
In Figure S5A, we show the results of applying these shuffle controls to three sets of movements studied in this manuscript: ipsilateral arm and contralateral arm (top row; dataset 12.05.2018), ipsilateral leg and contralateral leg (middle row; dataset 12.05.2018), and contralateral arm and contralateral leg (bottom row; dataset 11.19.2018).
Each set of movements has two shuffle distributions associated with it: an effector shuffle distribution (left) and a movement shuffle distribution (right). The statistic we compute to test for effector-coding is a variance ratio: Var{E} / (Var{M} + Var{M × E})), where Var{E} is the variance captured by the effector marginalization, Var{M} is the variance of the movement marginalization, and Var{M × E} is the variance of the movement × effector interaction marginalization. The larger this value is, the larger the effector signal is. The statistic we compute to test for movement correlations is Var{M} / Var{M × E}. If this ratio is larger than 1, there is more shared variance across effectors than unique variance.
The results from Figure S5A show that for each real dataset, both the effector-coding property and the movement correlation property are significantly above chance (the real variance ratio is always the largest ratio as compared to all other shufflings of the data).
In addition to applying these shuffle controls to the real data, we also apply them to four simple models to demonstrate that movement correlations and effector coding are independent properties. Neither of these properties imply the other or are trivial artifacts of our data analysis process or movement tuning in general. The models are defined as follows:
In the “random” model, each movement’s neural representation (i.e. mean firing rate vector) is a random vector with each element drawn from a Gaussian distribution; this model shows neither movement correlations nor effector-coding.
In the “movement correlations” model, each movement’s neural representation is the sum of a movement-specific “shared” vector which is the same across both effectors and a “private” vector which is drawn randomly within each movement. This model shows movement correlations but not effector-coding.
In the “effector coding” model, each movement’s neural representation is the sum of a “private” vector which is drawn randomly for each movement and an “effector” vector which is effector-specific and constant across all movements within an effector. This model shows effector-coding but not movement correlation.
Finally, in the “movement correlations + effector coding” model, each movement’s neural representation is the sum of a “private” random vector, a movement-specific “shared vector” which is the same across both effectors, and an “effector” vector which is the same across all movements within an effector. This model shows both effector-coding and movement correlation.
The results of applying the shuffle controls to the four models are shown above in Figure S5B. The results show that effector-coding and movement correlation properties are independent properties, neither of which imply the other. This also demonstrates that the shuffle controls are capable of correctly testing for the existence of each property.
Figure S6 Methods
See the above section “Figure 4 Methods” for details about the partial preparation experiment and dPCA methods.
Figure S7 Methods
First, we trained a recurrent neural network model (“controller RNN”) to control two simulated arms by using standard gradient descent techniques (Figure S7A). Each arm is a planar, two-link mechanical arm model (as if reaching in the transverse plane across a table top). The controller RNN takes as input a compositional representation of movement velocity and outputs the shoulder and elbow joint torque needed to make that movement. The controller RNN can be loosely thought of as representing lower motor cortical areas [e.g. primary motor cortex (M1) and dorsocaudal premotor cortex (PMd)] which might take as input a compositional representation of movement and convert it into the lower-level motor outputs necessary to execute that movement.
To demonstrate that this architecture can enable skill transfer, we simulated the process of learning a motor skill by training a pattern-generating RNN to generate a time series of joint velocities that, when given as input to the controller RNN, make the left arm trace a circle (Figure S7B). The pattern-generating RNN was trained only with the left arm; that is, the laterality input to the controller RNN was fixed to represent the left arm only. To demonstrate that the skill can be transferred to the right arm post-learning, we changed only the laterality input to the controller RNN to represent the right arm while keeping the pattern-generating RNN the same. The results indicate successful transfer of the circle-drawing skill to the right arm (Figure S7C).
Next, we examined the neural tuning properties of the controller RNN and compared them to a “direct mapping” RNN that is equally capable of controlling the simulated arms but that does not use a compositional movement code. In Figure S7D, we illustrate the architecture of the direct mapping RNN. Instead of taking as input a representation of shoulder and elbow velocity that is shared across both arms, it receives separate shoulder and elbow velocity inputs for each arm. This architecture is incapable of implementing skill transfer, since it has no mechanism for flexibly re-routing joint velocity inputs for one arm into joint torques for the other arm.
To compare the neural tuning between the compositional RNN and the direct RNN, we first collected synthetic “radial 8” data from both RNNs and both arms (Figure S7E). Each RNN was given joint velocity inputs that specified a reaching movement in one of eight radial directions [a minimum-jerk trajectory was used to specify the movement (Flash and Hogan, 1985)]. Data was collected one reach and one arm at a time (20 repetitions per movement). The corresponding neural activity from each movement was concatenated and saved for analysis
Examining the neural activity, we found that both the compositional RNN and the direct RNN show a high degree of overlapping neural tuning for both arms (Figure S7F). In fact, 100% of the neurons in both networks showed statistically significant tuning to movements in both arms (as assessed with a 1-way ANOVA for each arm, see below). Despite both networks showing highly overlapping and intermixed tuning, the neural representations were very different. As expected, the compositional RNN contained a compositional representation of movement consistent with what we observed in the real data, with positive neural correlations between matching movements across the arms (Figure S7G) and a consistent, movement-independent neural representation of the effector (Figure S7H). On the other hand, the direct RNN exhibited neither of these properties. Matching movements across the arms had no neural similarity (Figure S7G) and demixed PCA was unable to find a neural dimension that consistently represented the effector independently of the movement (Figure S7H). These results illustrate that tuning to multiple effectors is not sufficient for skill transfer nor does it imply a compositional code for movement.
Neural Network Methods
We used a basic RNN models with the following dynamics:
Here, σh is the hyperbolic tangent function, h(t) is the RNN’s hidden state vector (neural activity) at time step t, x(t) is the input vector, y(t) is the output vector, ε(t) is a Gaussian noise vector (sd = 0.01), Wh, Uh, Wy, bh and by are weight matrices and bias vectors, and a0 and a1 are scalars that define the range of outputs (which was −30 to 30 N m for the controller RNN and −20 to 20 rad/s for the pattern-generating RNN).
The RNNs were trained using backpropagation through time using the Adam method (Kingma and Ba, 2014). Networks were trained for 2000 iterations using minibatches of 64 trials. We used TensorFlow v1 (Abadi et al., 2016) to implement both the RNNs and the planar arm models, enabling backpropagation through both the arms and the RNNs in series. Each time step was 10 ms long.
Controller RNNs were trained to convert randomly generated time series of joint velocity inputs into arm motion that matches the joint velocities. The RNNs were trained to minimize the squared error between the target joint velocities and the arms’ actual joint velocities:
Here, is the left arm’s joint velocity vector, is the right arm’s joint velocity vector, is the target joint velocity vector for the right arm, and is the target joint velocity for velocity inputs when the laterality input matches that arm, otherwise they were equal to zero. For the direct RNN, the target velocity vectors were always equal to the joint velocity inputs.
For each 3 second trial of each minibatch, joint velocity and laterality input time series were randomly generated. Each time series consisted of one or more bouts of instructed movement with an exponentially distributed duration (mean = 0.5 s). For each bout, the arm to be moved was randomly chosen and, if the network was compositional, the laterality input was fixed to −1 (for the left arm) or 1 (for the right arm). Then, joint velocity inputs for the chosen arm were generated by convolving white noise (sd=8) with a Gaussian kernel (sd=100 ms) and subtracting a line connecting the first and last points (so that the time series would begin and end at zero).
In addition to velocity squared error, we used the following additional regularizing costs:
Here, the first term corresponds to L2 weight decay, the second term penalizes large activations, and the third term penalizes rapid changes in output torque (τ(t) is the RNN’s output torque vector for time step t).
Implementation of the planar arm physics in TensorFlow is relatively straightforward since two-link arm mechanics can be expressed in closed-form with a relatively small number of terms [e.g. (Fagg et al., 1997; Uno et al., 1989)]. Approximate solutions were obtained using Euler integration. The parameters of the arm were as follows for each link: mass (1.86 kg, 1.53 kg), center of mass (0.18 m, 0.18 m), moment of inertia (0.013 kg m2, 0.02 kg m2), and length (0.29 m, 0.235 m).
When training the pattern-generating network, the controller network weights were held fixed. The pattern-generating network was trained with the following cost function:
Here, px(t) and py(t) are the X and Y coordinates of the left hand. This cost function computes the error between the position of the left hand and a circular trajectory. We also used the same weight and activation regularization terms described above for the controller networks.
Modulation Depth and Tuning
To compute modulation depth for each artificial neuron (Figure S7F), first the mean activation of each neuron was computed for each movement by averaging over all 20 repetitions. Activations were averaged over a 250 ms bin beginning at movement onset. Then, for each neuron and each arm, the maximum and minimum mean activations were found. The modulation depth was then computed as the difference between the maximum and minimum activations.
To test for statistical significance of tuning to each arm, we performed a 1-way ANOVA for each neuron and each arm (consisting of 8 groups of 20 observations). A p-value < 0.001 was considered significant. Under this criterion, all neurons in both the compositional and direct networks were significantly tuned to both arms.
Supplemental Video 2 Methods
The decoding methods used for the 32-target layout were the same as those described for Figure 6, except that an additional two second instructed delay period was added before each trial to inform T5 of the upcoming target. This allowed T5 enough time to recognize and prepare the movement. During this time, the target appeared red. After the delay period, the target turned blue and T5 had one second to make the movement. The discrete decoder used data only from this one second movement period to classify the movement. We found that, without the delay period, T5 could not recognize the movement quickly enough and perform it correctly within the allotted time.
We collected closed-loop data for the 32-target layout on three different days. Accuracy was high (mean of 95% across all three sessions) but the achieved bit rate is relatively low (mean of 1.5 bps) because of the additional two second delay period. Without the two second delay period, the bit rate would have been 4.52 bps, suggesting that high bit rates are possible if the user can learn to select between a large number of movements quickly.
Supplementary Material
Figure S1. Neural population activity for each movement category is rich and multi-dimensional. Related to Figure 1.
Each subpanel shows the neural activity in one neural dimension found using PCA (using the data shown in Figure 1). Each line in a panel shows the mean response to a given movement cue and shaded regions depict 95% confidence intervals. Within each column (movement set) only the neural responses for the movement cues within that set are shown (for ease of visualization). Results show that there is distinguishable neural activity (non-overlapping confidence intervals) between movements for all four movement sets and both participants. This holds true for all three neural dimensions, indicating that the movement-specific activity is strongly multi-dimensional. Note that, unlike T5, T7 performed a set of periodic paired movements (e.g. open hand, close hand, open hand, etc.). The vertical dashed lines for T7 show the paired movement “switch” time.
Figure S2. Tuning to face, head, arm and leg movements is intermixed within electrodes and has no clear somatotopic pattern. Related to Figure 1.
(A) The strength of each electrodes’ tuning to each category of movements is indicated with a shaded color (darker colors indicate more tuning). Tuning strength was quantified by computing the fraction of total firing rate variance accounted for by changes in firing rate due to the movement conditions. Crosses indicate “non-functioning” electrodes (mean firing rate < 1 Hz). Small white circles indicate channels that had no significant tuning to that movement category. Broad spatial tuning to all movement categories can be seen across all arrays. Additionally, tuning strength to particular movement categories does not appear to have clear gradients matching the expected somatotopy (where face, head, arm and leg tuning should proceed laterally to medially in that order), with the possible exception of leg tuning in T7.
(B) Matrices indicating whether an electrode was significantly tuned to each individual movement. A colored cell within a matrix (i,j) indicates significant tuning of electrode channel i to movement j. The cell color corresponds to the associated movement category. X-axis labels have been limited to the movement set names for brevity. For T5, significant tuning was assessed by comparing the firing rates for each movement against the “Do Nothing” condition. For T7, significant tuning was assessed by comparing movements within each movement pair. P-values < 0.001 were considered significant. For visualization, rows were re-ordered according to a clustering analysis (black horizontal bars indicate cluster ranges).
(C) Bar plots indicate the number of electrodes that were significantly tuned to each movement category as computed in A. Results show a greater preference for arm tuning in T7 as compared to T5.
(D) Pie charts summarize the number of electrodes that had statistically significant tuning to each possible number of movement sets (from 0 to 4). In both participants, many electrodes are tuned to more than one movement set.
(E) Scatter plots indicate the mean absolute change in firing rate of each electrode for two movement sets. In both participants (T5 in top row, T7 in bottom row), most electrodes showed a greater mean change in firing rate for movements within the Arm movement class in comparison to other (Face, Head, Leg) movement classes. T5’s change in firing rates were computed relative to the “Do Nothing” condition serving as a point of comparison. T7’s change in firing rates were computed by comparing to each cued movement’s paired movement.
(F) Histograms indicate the baseline firing rate measured on each electrode channel. For T5, baseline is defined as the “Do Nothing” condition. For T7, baseline firing rates were computed by taking the mean firing rate across all time bins and across all paired movements cued.
Figure S3. Sorted single units are tuned to multiple movement categories. Related to Figure 1.
(A) PSTHs for two example sorted units from participant T5. Lines show the mean firing rate and shaded regions indicate 95% CIs of the mean (computed by assuming the data is normally distributed). The responses show broad tuning to a variety of movements across the body.
(B) PSTHs for an example sorted unit from T7. Unlike T5, T7 performed a set of periodic paired movements (e.g. open hand, close hand, open hand, etc.). The vertical dashed lines show the paired movement “switch” time. Since these data were collected in a block-wise fashion (with each block testing a different movement pair), we plotted each pair separately for ease of visualization. This particular unit is strongly tuned to both the arm and the leg.
(C) Matrices indicating whether a single unit was significantly tuned to each movement (computed as in Figure S2).
(D) Bar plots indicate the number of units that were significantly tuned to each movement set. (determined as in Figure S2).
(E) Pie charts summarize the number of single units that had statistically significant tuning to each possible number of movement sets (from 0 to 4). Most of T5’s sorted units modulated significantly to all four sets of movements, whereas most of T7’s sorted units had significant modulation to one or two sets of movements. This difference might be due in part to the fact that more movements were tested in T5 (especially non-arm movements) and more trials were collected (32 vs. 18 per movement).
(F) Scatter plots indicate the mean absolute change in firing rate of each sorted unit for each movement set, computed as in Figure S2.
(G) Histograms indicate the baseline firing rate measured on each sorted unit, computed as in Figure S2
Figure S4. The representation of movement direction across the arms and legs is shared in an intrinsic frame. Related to Figure 4.
(A) An instructed delay, spatially cued movement task was used to probe the neural representation of directional movements across different effectors. The task illustrated here cues directional movements of the hand (as if pointing a joystick) and foot (pointing the ankles) on both sides of the body.
(B) Mean (large circles) and single trial (small circles) averaged firing rates during the “go” period of a radial 8 directional movement task are plotted in the first two dimensions found by principal components analysis (PCA). The dimensions are rotated to align with the targets and thus are labeled as “rPC1” and “rPC2”.
(C) Illustration of how horizontal movements in the same extrinsic direction (left image) require opposite joint movements while vertical movements in the same direction (right image) require identical joint movements. Hands are depicted making joystick pointing movements (matching T5’s instructions).
(D,E) Directional tuning was correlated across effectors in the horizontal and vertical directions. Each smaller square (i,j) indicates the correlation coefficient between the horizontal or vertical tuning coefficients that were fit to each body part i and j separately using a linear model. In the vertical direction, the directional tuning across all effectors is positively correlated. In the horizontal direction, however, effectors on opposite sides of the body are negatively correlated, indicating that movement direction is intrinsically represented. Movement in the horizontal direction on opposite sides of the body requires opposite joint movements to move in the same extrinsic direction. See Methods for more details.
Figure S5. Shuffle controls demonstrate that the compositional coding properties we observed are quantitatively meaningful. Related to Figure 4.
(A) Shuffle controls demonstrate that both properties of the compositional code (movement correlations, right column, and effector coding, left column) are quantitatively meaningful properties of the data. Each row of panels is a different dataset. To test for significant effector-coding, we shuffled the effector labels corresponding to each movement condition. Shuffled datasets (blue histogram) have significantly less variance in the effector marginalization than the true data. To test for significant movement correlations, we shuffled the movement labels within each effector. Shuffled datasets have significantly less variance in the movement marginalization than the true data. See Methods for details.
(B) Shuffle controls applied to four simulated models (each row corresponds to a different model) demonstrate that movement correlations and effector coding are truly independent properties, neither of which imply the other or are trivial properties of movement tuning in general. See Methods for details.
Supplemental Figure 6. Single trial firing rates during the partially cued movement task show patterns consistent with genuine partial preparation. Related to Figure 4.
Single trial distributions of neural activity during the instructed delay period of the partially cued movement task show patterns consistent with genuine partial preparation as opposed to a mixture of full preparation and no preparation.
(A, B) Single trial distributions of neural activity for the partially cued laterality and movement task; each panel depicts different partially cued distributions for ease of visualization. Each dot shows the neural activity in the laterality and movement dimensions in a 300 ms window just prior to the go cue. Each color corresponds to a different cue. If the partial preparation we observed during the partially-cued trials were an artifact of T5 deciding sometimes to prepare one of the two potential upcoming movements (e.g. preparing either the right wrist or the right hand movement once the right side of the body was cued), and other times to prepare nothing, we would expect to see dots from the “right” partial cue condition (light blue dots in panel A) to occupy either the right hand distribution (purple dots), right wrist distribution (gold dots), or the “do nothing” distribution (black dots). Instead, the distribution appears to be in a genuinely different and “in-between” location that cannot be explained by a Gaussian mixture distribution composed of the fully-specified and “do nothing” distributions.
(C, D) Single trial distributions of neural activity for the partially cued arm vs. leg and movement task, depicted as in (A, B). Similar to the distributions for the laterality task, the partially-cued distributions appear to lie in “in-between” locations that cannot be explained by sometimes fully preparing possible upcoming movements and sometimes preparing nothing.
Supplemental Figure 7. A neural network model of motor skill transfer using a compositional code. Related to Figure 7.
To demonstrate our proposed mechanism of motor skill transfer in a concrete way, we built a neural network model that can implement skill transfer using the compositional representation of movement we schematized in Figure 7. The model also demonstrates that single neurons being tuned to multiple body parts is not, by itself, sufficient to facilitate skill transfer. Only certain representations of movement (e.g. a compositional code) can enable skill transfer.
(A) We used gradient descent to optimize a recurrent neural network (RNN) to translate a compositional representation of movement into the joint torques needed to execute that movement. The RNN (“Controller Network”) takes as input desired shoulder and elbow velocities and a “laterality” signal which declares which arm should make the specified movement. The RNN outputs shoulder and elbow joint torques for each of the two arms (“left arm” and “right arm”, which are each identical two-link planar arms). In this example, the RNN is fed a shoulder velocity pulse first for the left arm, then for the right arm. The joint torques output by the RNN correctly execute the desired movements (shown on the right).
(B) To demonstrate that this RNN is capable of implementing skill transfer, we trained a “pattern network” RNN to output joint velocities that make the left arm generate a circle movement when placed in series with the controller RNN. The pattern network RNN is trained with the left arm only (training is indicated with a bold arrow across the pattern RNN).
(C) To transfer the learned skill, the weights of the pattern and controller RNNs are held fixed while the laterality input is changed. The skill successfully transfers to the right arm.
(D) We trained a controller RNN with a non-compositional architecture (“direct mapping” controller network) to demonstrate how neural tuning is shaped by the compositional representation of movement. The direct RNN receives as input a non-compositional representation of arm joint velocities (with separate input channels for each arm), but otherwise is trained in the same way as the compositional RNN.
(E) To compare the neural tuning between the compositional and direct RNNs, we first collected synthetic “radial 8” data from both arms and both RNNs. Example reaches are shown indicating successful completion of the radial 8 task by both RNNs.
(F) The modulation depths are plotted for each neuron in the compositional RNN (left) and the direct RNN (right). Modulation depth was defined as the maximum minus the minimum firing rate observed across the eight reaching movement conditions. Results show a high degree of overlapping tuning for both arms; that is, many neurons have high modulation depths for both arms.
(G) For each of the eight movements, the corresponding firing rate vectors were correlated across the arms for the compositional and direct networks (as done in Figure 4), revealing correlated movement representations in the compositional network but not the direct network.
(H) Demixed PCA was used to find neural dimensions that express variance related to the effector (i.e. left vs. right arm), as done in Fig. 4. dPCA finds a consistent representation of movement laterality in the compositional network but not the direct network.
Supplemental Video 1. Related to Figure 6. Real-time, discrete neural decoding of attempted movements from among 16 possible directional movements spanning the wrists and ankles.
Supplemental Video 2. Related to Figure 6. Real-time, discrete neural decoding of attempted movements from among 32 possible movements spanning the hands, arms, feet, and legs from both sides of the body.
“Hand knob” area of premotor cortex is tuned to the entire body
A compositional neural code links matching movements from all 4 limbs together
Separate coding of the movement and limb-to-be-moved may facilitate skill transfer
A discrete BCI can accurately decode movements of all 4 limbs from hand knob
Acknowledgements
We thank participants T5 and T7 and their caregivers for their dedicated contributions to this research, N. Lam for administrative support, and J. Simeral and B. Sorice for data collection with T7.
This work was supported by the following awards to LRH: Office of Research and Development, Rehabilitation R and D Service, Department of Veterans Affairs N9288C, N2864C, A2295R, B6453R, the Executive Committee on Research of Massachusetts General Hospital, and NIDCD R01DC009899 and NINDS U01NS098968. The following awards to JMH and KVS: Larry and Pamela Garlick, Samuel and Betsy Reeves, the Wu Tsai Neuroscience Institute at Stanford, and NIDCD R01DC014034. The following awards to KVS: Simons Foundation Collaboration on the Global Brain 543045 and the Howard Hughes Medical Institute. The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.
Footnotes
Declaration of interests
JMH is a consultant for Neuralink Inc., Proteus Biomedical and Boston Scientific, and serves on the Medical Advisory Board of Enspire DBS. KVS is a consultant for Neuralink Inc. and is on the Scientific Advisory Boards of CTRL-Labs Inc., MIND-X Inc., Inscopix Inc., and Heal Inc. All other authors have no competing interests.
Data and Code Availability
Data are available upon request to the Lead Contact, Frank Willett (fwillett@stanford.edu). Custom MATLAB code for cross-validated estimation of neural distance, angle and correlation is available at https://github.com/fwillett/cvVectorStats.
Additional Resources
ClinicalTrials.gov Identifier: NCT00912041, registered June 3, 2009.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abadi M, Agarwal A, Barham P, Brevdo E, Chen Z, Citro C, Corrado GS, Davis A, Dean J, Devin M, et al. (2016). TensorFlow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. ArXiv160304467 Cs. [Google Scholar]
- Aflalo T, Kellis S, Klaes C, Lee B, Shi Y, Pejsa K, Shanfield K, Hayes-Jackson S, Aisen M, Heck C, et al. (2015). Decoding motor imagery from the posterior parietal cortex of a tetraplegic human. Science 348, 906–910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ajiboye AB, Willett FR, Young DR, Memberg WD, Murphy BA, Miller JP, Walter BL, Sweet JA, Hoyen HA, Keith MW, et al. (2017). Restoration of reaching and grasping movements through brain-controlled muscle stimulation in a person with tetraplegia: a proof-of-concept demonstration. The Lancet 389, 1821–1830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allefeld C, and Haynes J-D (2014). Searchlight-based multi-voxel pattern analysis of fMRI by cross-validated MANOVA. NeuroImage 89, 345–357. [DOI] [PubMed] [Google Scholar]
- Ames KC, and Churchland MM (2019). Motor cortex signals for each arm are mixed across hemispheres and neurons yet partitioned within the population response. ELife 8, e46159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bishop CM (2006). Pattern Recognition and Machine Learning (Springer; ). [Google Scholar]
- Bouton CE, Shaikhouni A, Annetta NV, Bockbrader MA, Friedenberg DA, Nielson DM, Sharma G, Sederberg PB, Glenn BC, Mysiw WJ, et al. (2016). Restoring cortical control of functional movement in a human with quadriplegia. Nature 533, 247–250. [DOI] [PubMed] [Google Scholar]
- Brodmann K (1909). Vergleichende Lokalisationslehre der Grosshirnrinde in ihren Prinzipien dargestellt auf Grund des Zellenbaues (Leipzig: Barth: ). [Google Scholar]
- Bundy DT, Szrama N, Pahwa M, and Leuthardt EC (2018). Unilateral, 3D Arm Movement Kinematics Are Encoded in Ipsilateral Human Cortex. J. Neurosci. 38, 10042–10056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christou EA, and Rodriguez TM (2008). Time but not Force Is Transferred Between Ipsilateral Upper and Lower Limbs. J. Mot. Behav. 40, 186–189. [DOI] [PubMed] [Google Scholar]
- Cisek P, Crammond DJ, and Kalaska JF (2003). Neural Activity in Primary Motor and Dorsal Premotor Cortex In Reaching Tasks With the Contralateral Versus Ipsilateral Arm. J. Neurophysiol. 89, 922–942. [DOI] [PubMed] [Google Scholar]
- Collinger JL, Wodlinger B, Downey JE, Wang W, Tyler-Kabara EC, Weber DJ, McMorland AJ, Velliste M, Boninger ML, and Schwartz AB (2013). High-performance neuroprosthetic control by an individual with tetraplegia. The Lancet 381, 557–564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Criscimagna-Hemminger SE, Donchin O, Gazzaniga MS, and Shadmehr R (2003). Learned Dynamics of Reaching Movements Generalize From Dominant to Nondominant Arm. J. Neurophysiol. 89, 168–176. [DOI] [PubMed] [Google Scholar]
- Crone NE, Miglioretti DL, Gordon B, Sieracki JM, Wilson MT, Uematsu S, and Lesser RP (1998a). Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis. I. Alpha and beta event-related desynchronization. Brain 121, 2271–2299. [DOI] [PubMed] [Google Scholar]
- Crone NE, Miglioretti DL, Gordon B, and Lesser RP (1998b). Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis. II. Event-related synchronization in the gamma band. Brain 121, 2301–2315. [DOI] [PubMed] [Google Scholar]
- Diedrichsen J, and Kriegeskorte N (2017). Representational models: A common framework for understanding encoding, pattern-component, and representational-similarity analysis. PLOS Comput. Biol. 13, e1005508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diedrichsen J, Wiestler T, and Krakauer JW (2013). Two Distinct Ipsilateral Cortical Representations for Individuated Finger Movements. Cereb. Cortex 23, 1362–1377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fagg AH, Sitkoff N, Barto AG, and Houk JC (1997). Cerebellar learning for control of a two-link arm in muscle space. In 1997 IEEE International Conference on Robotics and Automation, 1997. Proceedings, pp. 2638–2644 vol.3. [Google Scholar]
- Flash T, and Hogan N (1985). The coordination of arm movements: an experimentally confirmed mathematical model. J. Neurosci. 5, 1688–1703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujiwara Y, Matsumoto R, Nakae T, Usami K, Matsuhashi M, Kikuchi T, Yoshida K, Kunieda T, Miyamoto S, Mima T, et al. (2017). Neural pattern similarity between contra- and ipsilateral movements in high-frequency band of human electrocorticograms. NeuroImage 147, 302–313. [DOI] [PubMed] [Google Scholar]
- Ganguly K, Secundo L, Ranade G, Orsborn A, Chang EF, Dimitrov DF, Wallis JD, Barbaro NM, Knight RT, and Carmena JM (2009). Cortical Representation of Ipsilateral Arm Movements in Monkey and Man. J. Neurosci. 29, 12948–12956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genon S, Li H, Fan L, Müller VI, Cieslik EC, Hoffstaedter F, Reid AT, Langner R, Grefkes C, Fox PT, et al. (2017). The Right Dorsal Premotor Mosaic: Organization, Functions, and Connectivity. Cereb. Cortex N. Y. NY 27, 2095–2110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genon S, Reid A, Li H, Fan L, Müller VI, Cieslik EC, Hoffstaedter F, Langner R, Grefkes C, Laird AR, et al. (2018). The heterogeneity of the left dorsal premotor cortex evidenced by multimodal connectivity-based parcellation and functional characterization. NeuroImage 170, 400–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Georgopoulos AP, Kalaska JF, Caminiti R, and Massey JT (1982). On the relations between the direction of two-dimensional arm movements and cell discharge in primate motor cortex. J. Neurosci. 2, 1527–1537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geyer S (2004). The Microstructural Border Between the Motor and the Cognitive Domain in the Human Cerebral Cortex (Berlin Heidelberg: Springer-Verlag; ). [DOI] [PubMed] [Google Scholar]
- Geyer S, Ledberg A, Schleicher A, Kinomura S, Schormann T, Bürgel U, Klingberg T, Larsson J, Zilles K, and Roland PE (1996). Two different areas within the primary motor cortex of man. Nature 382, 805–807. [DOI] [PubMed] [Google Scholar]
- Geyer S, Matelli M, Luppino G, and Zilles K (2000). Functional neuroanatomy of the primate isocortical motor system. Anat. Embryol. (Berl.) 202, 443–474. [DOI] [PubMed] [Google Scholar]
- Heming EA, Cross KP, Takei T, Cook DJ, and Scott SH (2019). Independent representations of ipsilateral and contralateral limbs in primary motor cortex. ELife 8, e48190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hochberg LR, Bacher D, Jarosiewicz B, Masse NY, Simeral JD, Vogel J, Haddadin S, Liu J, Cash SS, Smagt P. van der, et al. (2012). Reach and grasp by people with tetraplegia using a neurally controlled robotic arm. Nature 485, 372–375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoy KE, Fitzgerald PB, Bradshaw JL, Armatas CA, and Georgiou-Karistianis N (2004). Investigating the cortical origins of motor overflow. Brain Res. Rev. 46, 315–327. [DOI] [PubMed] [Google Scholar]
- Ifft PJ, Shokur S, Li Z, Lebedev MA, and Nicolelis MAL (2013). A brain-machine interface enables bimanual arm movements in monkeys. Sci. Transl. Med. 5, 210ra154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarosiewicz B, Sarma AA, Bacher D, Masse NY, Simeral JD, Sorice B, Oakley EM, Blabe C, Pandarinath C, Gilja V, et al. (2015). Virtual typing by people with tetraplegia using a self-calibrating intracortical brain-computer interface. Sci. Transl. Med. 7, 313ra179–313ra179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin Y, Lu M, Wang X, Zhang S, Zhu J, and Zheng X (2016). Electrocorticographic signals comparison in sensorimotor cortex between contralateral and ipsilateral hand movements. In 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), pp. 1544–1547. [DOI] [PubMed] [Google Scholar]
- Kelso J. a. S., and Zanone PG (2002). Coordination dynamics of learning and transfer across different effector systems. J. Exp. Psychol. Hum. Percept. Perform. 28, 776–797. [PubMed] [Google Scholar]
- Kingma DP, and Ba J (2014). Adam: A Method for Stochastic Optimization. ArXiv14126980 Cs. [Google Scholar]
- Kobak D, Brendel W, Constantinidis C, Feierstein CE, Kepecs A, Mainen ZF, Qi X-L, Romo R, Uchida N, and Machens CK (2016). Demixed principal component analysis of neural population data. ELife 5, e10989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurata K (1989). Distribution of neurons with set- and movement-related activity before hand and foot movements in the premotor cortex of rhesus monkeys. Exp. Brain Res. 77, 245–256. [DOI] [PubMed] [Google Scholar]
- Latash ML (1999). Mirror Writing: Learning, Transfer, and Implications for Internal Inverse Models. J. Mot. Behav. 31, 107–111. [DOI] [PubMed] [Google Scholar]
- Leyton ASF, and Sherrington CS (1917). Observations on the Excitable Cortex of the Chimpanzee, Orang-Utan, and Gorilla. Q. J. Exp. Physiol. 11, 135–222. [Google Scholar]
- Lotze M, Erb M, Flor H, Huelsmann E, Godde B, and Grodd W (2000). fMRI Evaluation of Somatotopic Representation in Human Primary Motor Cortex. NeuroImage 11, 473–481. [DOI] [PubMed] [Google Scholar]
- Meier JD, Aflalo TN, Kastner S, and Graziano MSA (2008). Complex organization of human primary motor cortex: a high-resolution fMRI study. J. Neurophysiol. 100, 1800–1812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milan L, and Whittaker J (1995). Application of the Parametric Bootstrap to Models that Incorporate a Singular Value Decomposition. J. R. Stat. Soc. Ser. C Appl. Stat. 44, 31–49. [Google Scholar]
- Miller KJ, Leuthardt EC, Schalk G, Rao RPN, Anderson NR, Moran DW, Miller JW, and Ojemann JG (2007). Spectral Changes in Cortical Surface Potentials during Motor Movement. J. Neurosci. 27, 2424–2432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris T, Newby NA, Wininger M, and Craelius W (2009). Inter-limb transfer of learned ankle movements. Exp. Brain Res. 192, 33–42. [DOI] [PubMed] [Google Scholar]
- Musallam S, Corneil BD, Greger B, Scherberger H, and Andersen RA (2004). Cognitive Control Signals for Neural Prosthetics. Science 305, 258–262. [DOI] [PubMed] [Google Scholar]
- Nozaki D, Kurtzer I, and Scott SH (2006). Limited transfer of learning between unimanual and bimanual skills within the same limb. Nat. Neurosci. 9, 1364–1366. [DOI] [PubMed] [Google Scholar]
- Nuyujukian P, Fan JM, Kao JC, Ryu SI, and Shenoy KV (2015). A high-performance keyboard neural prosthesis enabled by task optimization. IEEE Trans. Biomed. Eng. 62, 21–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pandarinath C, Nuyujukian P, Blabe CH, Sorice BL, Saab J, Willett FR, Hochberg LR, Shenoy KV, and Henderson JM (2017). High performance communication by people with paralysis using an intracortical brain-computer interface. ELife 6, e18554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penfield W, and Boldrey E (1937). Somatic motor and sensory representation in the cerebral cortex of man as studied by electrical stimulation. Brain J. Neurol. 60, 389–443. [Google Scholar]
- Penfield W, and Rasmussen T (1950). The cerebral cortex of man; a clinical study of localization of function (Oxford, England: Macmillan; ). [Google Scholar]
- Qi H-X, Stepniewska I, and Kaas JH (2000). Reorganization of Primary Motor Cortex in Adult Macaque Monkeys With Long-Standing Amputations. J. Neurophysiol. 84, 2133–2147. [DOI] [PubMed] [Google Scholar]
- Rademacher J, Caviness VS, Steinmetz H, and Galaburda AM (1993). Topographical Variation of the Human Primary Cortices: Implications for Neuroimaging, Brain Mapping, and Neurobiology. Cereb. Cortex 3, 313–329. [DOI] [PubMed] [Google Scholar]
- Rademacher J, Bürgel U, Geyer S, Schormann T, Schleicher A, Freund H-J, and Zilles K (2001). Variability and asymmetry in the human precentral motor systemA cytoarchitectonic and myeloarchitectonic brain mapping study. Brain 124, 2232–2258. [DOI] [PubMed] [Google Scholar]
- Reverberi C, Görgen K, and Haynes J-D (2012). Compositionality of Rule Representations in Human Prefrontal Cortex. Cereb. Cortex 22, 1237–1246. [DOI] [PubMed] [Google Scholar]
- Rizzolatti G, Luppino G, and Matelli M (1998). The organization of the cortical motor system: new concepts. Electroencephalogr. Clin. Neurophysiol. 106, 283–296. [DOI] [PubMed] [Google Scholar]
- Rokni U, Steinberg O, Vaadia E, and Sompolinsky H (2003). Cortical Representation of Bimanual Movements. J. Neurosci. 23, 11577–11586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruescher J, Iljina O, Altenmüller D-M, Aertsen A, Schulze-Bonhage A, and Ball T (2013). Somatotopic mapping of natural upper- and lower-extremity movements and speech production with high gamma electrocorticography. NeuroImage 81, 164–177. [DOI] [PubMed] [Google Scholar]
- Santhanam G, Ryu SI, Yu BM, Afshar A, and Shenoy KV (2006). A high-performance brain–computer interface. Nature 442, 195–198. [DOI] [PubMed] [Google Scholar]
- Savin DN, and Morton SM (2008). Asymmetric generalization between the arm and leg following prism-induced visuomotor adaptation. Exp. Brain Res. 186, 175–182. [DOI] [PubMed] [Google Scholar]
- Schieber MH (2001). Constraints on somatotopic organization in the primary motor cortex. J. Neurophysiol. 86, 2125–2143. [DOI] [PubMed] [Google Scholar]
- Severiano A, Carriço JA, Robinson DA, Ramirez M, and Pinto FR (2011). Evaluation of Jackknife and Bootstrap for Defining Confidence Intervals for Pairwise Agreement Measures. PLOS ONE 6, e19539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shea CH, Kovacs AJ, and Panzer S (2011). The Coding and Inter-Manual Transfer of Movement Sequences. Front. Psychol 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soska KC, Galeon MA, and Adolph KE (2012). On the other hand: Overflow movements of infants’ hands and legs during unimanual object exploration. Dev. Psychobiol. 54, 372–382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trautmann EM, Stavisky SD, Lahiri S, Ames KC, Kaufman MT, O’Shea DJ, Vyas S, Sun X, Ryu SI, Ganguli S, et al. (2019). Accurate Estimation of Neural Population Dynamics without Spike Sorting. Neuron 103, 292–308.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uno Y, Kawato M, and Suzuki R (1989). Formation and control of optimal trajectory in human multijoint arm movement. Biol. Cybern. 61, 89–101. [DOI] [PubMed] [Google Scholar]
- White LE, Andrews TJ, Hulette C, Richards A, Groelle M, Paydarfar J, and Purves D (1997). Structure of the human sensorimotor system. I: Morphology and cytoarchitecture of the central sulcus. Cereb. Cortex 7, 18–30. [DOI] [PubMed] [Google Scholar]
- Wiestler T, Waters-Metenier S, and Diedrichsen J (2014). Effector-independent motor sequence representations exist in extrinsic and intrinsic reference frames. J. Neurosci. Off. J. Soc. Neurosci. 34, 5054–5064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang GR, Joglekar MR, Song HF, Newsome WT, and Wang X-J (2019). Task representations in neural networks trained to perform many cognitive tasks. Nat. Neurosci. 22, 297–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yokoi A, Bai W, and Diedrichsen J (2016). Restricted transfer of learning between unimanual and bimanual finger sequences. J. Neurophysiol. 117, 1043–1051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yousry TA, Schmid UD, Alkadhi H, Schmidt D, Peraud A, Buettner A, and Winkler P (1997). Localization of the motor hand area to a knob on the precentral gyrus. A new landmark. Brain 120, 141–157. [DOI] [PubMed] [Google Scholar]
- Zhang CY, Aflalo T, Revechkis B, Rosario ER, Ouellette D, Pouratian N, and Andersen RA (2017). Partially Mixed Selectivity in Human Posterior Parietal Association Cortex. Neuron 95, 697–708.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zilles K, Schlaug G, Matelli M, Luppino G, Schleicher A, Qü M, Dabringhaus A, Seitz R, and Roland PE (1995). Mapping of human and macaque sensorimotor areas by integrating architectonic, transmitter receptor, MRI and PET data. J. Anat. 187 (Pt 3), 515–537. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1. Neural population activity for each movement category is rich and multi-dimensional. Related to Figure 1.
Each subpanel shows the neural activity in one neural dimension found using PCA (using the data shown in Figure 1). Each line in a panel shows the mean response to a given movement cue and shaded regions depict 95% confidence intervals. Within each column (movement set) only the neural responses for the movement cues within that set are shown (for ease of visualization). Results show that there is distinguishable neural activity (non-overlapping confidence intervals) between movements for all four movement sets and both participants. This holds true for all three neural dimensions, indicating that the movement-specific activity is strongly multi-dimensional. Note that, unlike T5, T7 performed a set of periodic paired movements (e.g. open hand, close hand, open hand, etc.). The vertical dashed lines for T7 show the paired movement “switch” time.
Figure S2. Tuning to face, head, arm and leg movements is intermixed within electrodes and has no clear somatotopic pattern. Related to Figure 1.
(A) The strength of each electrodes’ tuning to each category of movements is indicated with a shaded color (darker colors indicate more tuning). Tuning strength was quantified by computing the fraction of total firing rate variance accounted for by changes in firing rate due to the movement conditions. Crosses indicate “non-functioning” electrodes (mean firing rate < 1 Hz). Small white circles indicate channels that had no significant tuning to that movement category. Broad spatial tuning to all movement categories can be seen across all arrays. Additionally, tuning strength to particular movement categories does not appear to have clear gradients matching the expected somatotopy (where face, head, arm and leg tuning should proceed laterally to medially in that order), with the possible exception of leg tuning in T7.
(B) Matrices indicating whether an electrode was significantly tuned to each individual movement. A colored cell within a matrix (i,j) indicates significant tuning of electrode channel i to movement j. The cell color corresponds to the associated movement category. X-axis labels have been limited to the movement set names for brevity. For T5, significant tuning was assessed by comparing the firing rates for each movement against the “Do Nothing” condition. For T7, significant tuning was assessed by comparing movements within each movement pair. P-values < 0.001 were considered significant. For visualization, rows were re-ordered according to a clustering analysis (black horizontal bars indicate cluster ranges).
(C) Bar plots indicate the number of electrodes that were significantly tuned to each movement category as computed in A. Results show a greater preference for arm tuning in T7 as compared to T5.
(D) Pie charts summarize the number of electrodes that had statistically significant tuning to each possible number of movement sets (from 0 to 4). In both participants, many electrodes are tuned to more than one movement set.
(E) Scatter plots indicate the mean absolute change in firing rate of each electrode for two movement sets. In both participants (T5 in top row, T7 in bottom row), most electrodes showed a greater mean change in firing rate for movements within the Arm movement class in comparison to other (Face, Head, Leg) movement classes. T5’s change in firing rates were computed relative to the “Do Nothing” condition serving as a point of comparison. T7’s change in firing rates were computed by comparing to each cued movement’s paired movement.
(F) Histograms indicate the baseline firing rate measured on each electrode channel. For T5, baseline is defined as the “Do Nothing” condition. For T7, baseline firing rates were computed by taking the mean firing rate across all time bins and across all paired movements cued.
Figure S3. Sorted single units are tuned to multiple movement categories. Related to Figure 1.
(A) PSTHs for two example sorted units from participant T5. Lines show the mean firing rate and shaded regions indicate 95% CIs of the mean (computed by assuming the data is normally distributed). The responses show broad tuning to a variety of movements across the body.
(B) PSTHs for an example sorted unit from T7. Unlike T5, T7 performed a set of periodic paired movements (e.g. open hand, close hand, open hand, etc.). The vertical dashed lines show the paired movement “switch” time. Since these data were collected in a block-wise fashion (with each block testing a different movement pair), we plotted each pair separately for ease of visualization. This particular unit is strongly tuned to both the arm and the leg.
(C) Matrices indicating whether a single unit was significantly tuned to each movement (computed as in Figure S2).
(D) Bar plots indicate the number of units that were significantly tuned to each movement set. (determined as in Figure S2).
(E) Pie charts summarize the number of single units that had statistically significant tuning to each possible number of movement sets (from 0 to 4). Most of T5’s sorted units modulated significantly to all four sets of movements, whereas most of T7’s sorted units had significant modulation to one or two sets of movements. This difference might be due in part to the fact that more movements were tested in T5 (especially non-arm movements) and more trials were collected (32 vs. 18 per movement).
(F) Scatter plots indicate the mean absolute change in firing rate of each sorted unit for each movement set, computed as in Figure S2.
(G) Histograms indicate the baseline firing rate measured on each sorted unit, computed as in Figure S2
Figure S4. The representation of movement direction across the arms and legs is shared in an intrinsic frame. Related to Figure 4.
(A) An instructed delay, spatially cued movement task was used to probe the neural representation of directional movements across different effectors. The task illustrated here cues directional movements of the hand (as if pointing a joystick) and foot (pointing the ankles) on both sides of the body.
(B) Mean (large circles) and single trial (small circles) averaged firing rates during the “go” period of a radial 8 directional movement task are plotted in the first two dimensions found by principal components analysis (PCA). The dimensions are rotated to align with the targets and thus are labeled as “rPC1” and “rPC2”.
(C) Illustration of how horizontal movements in the same extrinsic direction (left image) require opposite joint movements while vertical movements in the same direction (right image) require identical joint movements. Hands are depicted making joystick pointing movements (matching T5’s instructions).
(D,E) Directional tuning was correlated across effectors in the horizontal and vertical directions. Each smaller square (i,j) indicates the correlation coefficient between the horizontal or vertical tuning coefficients that were fit to each body part i and j separately using a linear model. In the vertical direction, the directional tuning across all effectors is positively correlated. In the horizontal direction, however, effectors on opposite sides of the body are negatively correlated, indicating that movement direction is intrinsically represented. Movement in the horizontal direction on opposite sides of the body requires opposite joint movements to move in the same extrinsic direction. See Methods for more details.
Figure S5. Shuffle controls demonstrate that the compositional coding properties we observed are quantitatively meaningful. Related to Figure 4.
(A) Shuffle controls demonstrate that both properties of the compositional code (movement correlations, right column, and effector coding, left column) are quantitatively meaningful properties of the data. Each row of panels is a different dataset. To test for significant effector-coding, we shuffled the effector labels corresponding to each movement condition. Shuffled datasets (blue histogram) have significantly less variance in the effector marginalization than the true data. To test for significant movement correlations, we shuffled the movement labels within each effector. Shuffled datasets have significantly less variance in the movement marginalization than the true data. See Methods for details.
(B) Shuffle controls applied to four simulated models (each row corresponds to a different model) demonstrate that movement correlations and effector coding are truly independent properties, neither of which imply the other or are trivial properties of movement tuning in general. See Methods for details.
Supplemental Figure 6. Single trial firing rates during the partially cued movement task show patterns consistent with genuine partial preparation. Related to Figure 4.
Single trial distributions of neural activity during the instructed delay period of the partially cued movement task show patterns consistent with genuine partial preparation as opposed to a mixture of full preparation and no preparation.
(A, B) Single trial distributions of neural activity for the partially cued laterality and movement task; each panel depicts different partially cued distributions for ease of visualization. Each dot shows the neural activity in the laterality and movement dimensions in a 300 ms window just prior to the go cue. Each color corresponds to a different cue. If the partial preparation we observed during the partially-cued trials were an artifact of T5 deciding sometimes to prepare one of the two potential upcoming movements (e.g. preparing either the right wrist or the right hand movement once the right side of the body was cued), and other times to prepare nothing, we would expect to see dots from the “right” partial cue condition (light blue dots in panel A) to occupy either the right hand distribution (purple dots), right wrist distribution (gold dots), or the “do nothing” distribution (black dots). Instead, the distribution appears to be in a genuinely different and “in-between” location that cannot be explained by a Gaussian mixture distribution composed of the fully-specified and “do nothing” distributions.
(C, D) Single trial distributions of neural activity for the partially cued arm vs. leg and movement task, depicted as in (A, B). Similar to the distributions for the laterality task, the partially-cued distributions appear to lie in “in-between” locations that cannot be explained by sometimes fully preparing possible upcoming movements and sometimes preparing nothing.
Supplemental Figure 7. A neural network model of motor skill transfer using a compositional code. Related to Figure 7.
To demonstrate our proposed mechanism of motor skill transfer in a concrete way, we built a neural network model that can implement skill transfer using the compositional representation of movement we schematized in Figure 7. The model also demonstrates that single neurons being tuned to multiple body parts is not, by itself, sufficient to facilitate skill transfer. Only certain representations of movement (e.g. a compositional code) can enable skill transfer.
(A) We used gradient descent to optimize a recurrent neural network (RNN) to translate a compositional representation of movement into the joint torques needed to execute that movement. The RNN (“Controller Network”) takes as input desired shoulder and elbow velocities and a “laterality” signal which declares which arm should make the specified movement. The RNN outputs shoulder and elbow joint torques for each of the two arms (“left arm” and “right arm”, which are each identical two-link planar arms). In this example, the RNN is fed a shoulder velocity pulse first for the left arm, then for the right arm. The joint torques output by the RNN correctly execute the desired movements (shown on the right).
(B) To demonstrate that this RNN is capable of implementing skill transfer, we trained a “pattern network” RNN to output joint velocities that make the left arm generate a circle movement when placed in series with the controller RNN. The pattern network RNN is trained with the left arm only (training is indicated with a bold arrow across the pattern RNN).
(C) To transfer the learned skill, the weights of the pattern and controller RNNs are held fixed while the laterality input is changed. The skill successfully transfers to the right arm.
(D) We trained a controller RNN with a non-compositional architecture (“direct mapping” controller network) to demonstrate how neural tuning is shaped by the compositional representation of movement. The direct RNN receives as input a non-compositional representation of arm joint velocities (with separate input channels for each arm), but otherwise is trained in the same way as the compositional RNN.
(E) To compare the neural tuning between the compositional and direct RNNs, we first collected synthetic “radial 8” data from both arms and both RNNs. Example reaches are shown indicating successful completion of the radial 8 task by both RNNs.
(F) The modulation depths are plotted for each neuron in the compositional RNN (left) and the direct RNN (right). Modulation depth was defined as the maximum minus the minimum firing rate observed across the eight reaching movement conditions. Results show a high degree of overlapping tuning for both arms; that is, many neurons have high modulation depths for both arms.
(G) For each of the eight movements, the corresponding firing rate vectors were correlated across the arms for the compositional and direct networks (as done in Figure 4), revealing correlated movement representations in the compositional network but not the direct network.
(H) Demixed PCA was used to find neural dimensions that express variance related to the effector (i.e. left vs. right arm), as done in Fig. 4. dPCA finds a consistent representation of movement laterality in the compositional network but not the direct network.
Supplemental Video 1. Related to Figure 6. Real-time, discrete neural decoding of attempted movements from among 16 possible directional movements spanning the wrists and ankles.
Supplemental Video 2. Related to Figure 6. Real-time, discrete neural decoding of attempted movements from among 32 possible movements spanning the hands, arms, feet, and legs from both sides of the body.