What Does the Machine Learn? Knowledge Representations of Chemical Reactivity

Abstract

In a departure from conventional chemical approaches, data-driven models of chemical reactions have recently been shown to be statistically successful using machine learning. These models, however, are largely black box in character and have not provided the kind of chemical insights that historically advanced the field of chemistry. To examine the knowledgebase of machine-learning models—what does the machine learn—this article deconstructs black-box machine-learning models of a diverse chemical reaction data set. Through experimentation with chemical representations and modeling techniques, the analysis provides insights into the nature of how statistical accuracy can arise, even when the model lacks informative physical principles. By peeling back the layers of these complicated models we arrive at a minimal, chemically intuitive model (and no machine learning involved). This model is based on systematic reaction-type classification and Evans-Polanyi relationships within reaction types which are easily visualized and interpreted. Through exploring this simple model, we gain deeper understanding of the data set and uncover a means for expert interactions to improve the model’s reliability.

Graphical Abstract

INTRODUCTION

A great deal of excitement has been growing among physical scientists and engineers about machine learning. This excitement stems from a host of interesting examples from the data science field, including widely reported advances in image recognition, artificial intelligence in games, and natural language processing that have demonstrated extremely high levels of performance and even abilities beyond expert human capabilities. Substantial efforts have therefore been made to bring the tools of machine learning to bear upon the physical sciences,^1–5 with some of the most interesting chemical applications being in the areas of reactions and synthesis.^6–10 Chemistry, however, is traditionally driven by a combination of concepts and data, with its own heuristics, models, and hypothesis-making approach to research. It is our view that the contrast in approach between purely data-driven research and concept-driven research begs questions such as the following. What is the machine’s representation of knowledge? What does the machine learn? It is these questions that will lead to more effective synergies between machine learning and the chemical sciences as useful answers will involve explainable and interpretable concepts, not merely machine abstraction and black-box decision making. The intent of this article is to provide some preliminary indications of how current-generation machine-learning tools operate on chemical data, in partial answer to these two questions. Our emphasis will be on application to computer prediction of chemical reactions, a key target for recent generations of machine-learning methods.

The potential for computers to assist in synthesis has a long history, dating back to original proposals by E. J. Corey in the 1960s.^11–13 These ideas were focused on the possibility for expert systems to encode known chemical principles into a systematic framework for predicting synthetic routes. Expert systems, however, fell out of favor due to the tedious encoding of rules and the rule exceptions required to maintain usability and accuracy across a diversity of reaction types. While recent efforts have challenged this conclusion,¹⁴ the manual efforts needed to construct quality expert systems have by no means decreased. Alternatively, machine-learning methodologies give the appearance of being particularly fit for encoding chemical reaction data without substantial human intervention and tinkering. To date, millions of reactions have been reported and are available in online databases, motivating recent efforts to use methods such as neural networks to build predictive tools for synthesis planning.^15–22

Nonlinear regressions, which include deep neural networks,^23–27 form the basis for machine learning to represent complex relationships between input and output variables.²⁸ These methods can represent arbitrarily complex maps between any number of input variables and output results²⁹ and can simply be applied to data, often with excellent statistical results. Since expert understanding of the meaning behind the data is not needed, the application of nonlinear regressions to encode chemical reactions is vastly different than applying expert systems (i.e., where specific rules are manually encoded and easily understood). In the specific case of neural networks, “hidden layers” constitute the intermediate representations that are used to make predictions. While these layers may well encode concepts and heuristics, they are indeed hidden and do not provide transparent or interpretable reasons for decisions made by the network. In other popular nonlinear techniques, “kernel” functions are used, where similarity between pairs of data points determines the structure of the predictions. Kernels are relatively interpretable compared to the hidden layers of neural networks, as similarity in the feature space is the core concept that can be understood.

To improve interpretability, data scientists might make use of input features that are comprehensible to chemists.³⁰ Typical machine-learning features involve graph-based features^31–34 (e.g., based on covalent attachments in molecules), strings (e.g., SMILES³⁵), hashing, or substructure analysis, and these techniques have been widely used in drug design applications. Metrics such as Tanimoto distances,³¹ which are measures of similarity between molecules, provide some grounding to chemical concepts but are otherwise not trivial to interpret. In contrast, atomic charges or orbital energies derived from quantum chemistry, for instance, might be used alongside conventional physical organic descriptors^36,37 to capture chemical principles in quantitative form.^38,39 Progress in this area is useful and ongoing, but more insight is needed into the relationship between the physical content of these features and how machine-learning models make use of the features.

Whereas machines have no prior expectations of the meaning of input features, chemists are clearly the opposite.⁴⁰ Chemists use explainable, physical features to make pre dictions, and they have strong expectations about how their models should behave based on these features.⁴¹ In the case of a polar reaction, an atom with a high positive charge might be expected to react with an atom of large negative charge due to Coulomb interactions. This fundamental physical interaction is described by chemists in terms of electronegativity and bond polarity, which are chemically specific descriptors that are highly useful for predicting the reaction outcome. Due to these relationships, invoking atomic charge as a descriptor brings in a wealth of expectations for an expert chemist due to their knowledge of firmly established physical laws.

Machine-learning models thus face a significant challenge in providing advances in chemical reactions (Figure 1), as it is not obvious how they are rooted in physical reality or whether they use chemical features in a way that in any way resembles chemical thought. In the machine-learning world, it is known that neural networks focus on distinctly different regions of images compared to humans when recognizing objects⁴² and yet still reach high accuracy. In the text that follows, this issue is investigated in detail by examining a data set of chemical reactions with two qualitatively distinct, powerful machine-learning methods. In short, we will show deep neural network and support machine (SVM) models to be quantitatively accurate but missing a basic, qualitative representation of physical principles. Using this knowledge, it will be shown that a well-known, interpretable chemical principle better describes this data set and even provides higher quantitative accuracy than machine learning. On the basis of these results, Figure 1 outlines our viewpoint of the relationship between current-generation machine-learning methods and chemical methods. This figure will be discussed in more detail in the Discussion section after the main results of this study.

Figure 1.

Overview of the status of machine learning for chemical reactions. Popular deep neural networks are shown in the middle row, where the internal “hidden” representations are hoped to be equivalent to the third row. In the third row, principles behind the predictions are chemically intuitive concepts.

FIRST CHALLENGE: REPRESENTING CHEMICAL DATA

For algorithmic techniques to learn relationships between chemical properties and reaction outcomes,^{38,39,43–48} the representation of those features is vitally important. A basic principle used here and elsewhere^15,16 is to consider reactions as being composed of bond-breaking and bond-forming events. This places the features squarely into the chemical domain and automatically injects accepted chemical principles into the choice of representation: chemical bonding is an a priori accepted concept that does not need to be “learned” by the machine. This assumption in turn allows each reaction to be expressed in terms of atom-centered properties (possibly including neighboring atoms, next neighbors, etc.), such that characteristics of the features are dominated by the properties of the reactive atoms. The choice of reactive-atom-centered properties therefore gives a list (a vector) of real numbers that specify a particular reaction. Many choices are conceivable for this feature list.

To represent an atom, one approach is to consider features of the molecular graph centered on the (reactive) atom (Scheme 1). Prior efforts in this area have used graphs in a similar way, where in some contexts the assignment of this graph is a key step to classify reactions¹⁹ and in others graphs are key frameworks for the ranking of reactions.^15,16,21,22 To form such graphs in the present context, the atomic number, number of covalent bonds, and formal hybridization can be used, where hybridization can usually be inferred from the former two properties. To build a more detailed picture of the atomic environment, these three features can also be added for the atom’s neighbors or next neighbors as appropriate. While the features themselves are easy to determine, a number of atoms are involved in any particular reaction. The order of these atoms in a feature vector may influence a machine-learning algorithm’s results, so in this work the ordering of the atoms is standardized according to a prescription given in the Computational Details section.

Scheme 1.

Atomic Representations Based on Atomic Connectivity and First-Principles Computation^a

^aSimilar features are available through the neighbors to the central atom, allowing more contextual information to inform the model.

Atomistic simulations can also be used to derive the properties of atoms and molecules using procedures that are now considered routine. These techniques can provide a wealth of chemically relevant information, for instance, energies and shapes of molecular and atomic orbitals, atomic charges, molecular multipole moments, and excitation energies. While more expensive to calculate than graphical features, these features are expected to provide more precise, physically meaningful information compared to purely graphical features. In this work, charges and effective hybridization (i.e., a measure of s/p character for an atom) from natural bond order⁴⁹ (NBO) calculations are specifically considered as chemically informative atomic features.

In addition to graphical and quantum-chemical features, the energy of the reaction is a particularly informative feature for predicting reaction outcome. The energy of reaction (ΔE) is simple to compute with quantum chemistry and provides a basic thermodynamic principle that directly relates to reaction outcome: increasingly positive energies of reaction correspond to a reduction in reactivity. ΔE for a single reaction can be found in seconds to minutes on modern computers, and the activation energy, which will be the focus of the predictions herein, costs at least an order of magnitude more computational time, even with advanced algorithms for its evaluation.^50,51

RELATIONSHIPS BETWEEN REPRESENTATIONS

To understand how choices of feature representations affect the ability for machine learning to predict reaction outcomes, a machine-learning model was set up based on two databases of chemical reactions (723 elementary steps and 3862 elementary steps). These reactions—described further in the Computational Details—come from first-principles atomistic simulations of reaction pathways.^52,53 The simulations cover two reaction classes: one of interest to atmospheric chemistry^54–57 and the other to CO reduction chemistry.^58–60 2 The choice of this data set allows two significant advantages over other data sets: (1) Activation energies are available for feasible as well as infeasible reactions and (2) noise and uncertainties are decreased, as all data points were generated with the same simulation method. In summary, the two data sets include a host of polar and radical reactions involving unimolecular and bimolecular elementary steps. While we report primarily on the first data set in this article, the Supporting Information will show that the second data set behaves similarly to the first, with little differences in statistical errors and interpretation compared to the first data set.

Two types of regression techniques were chosen as nonlinear machine-learning models for further study: neural networks (NNs) and SVM. Both are considered powerful tools with strong theoretical foundations^29,61 in the machine-learning community, but the SVM provides simpler, less ambiguous choices of model setup compared to NNs. Vitally, the NN approach is believed to be able to form internal features that represent the core quantities for accurate predictions. To test this hypothesis, a number of network topologies were constructed and tested with the most generalizable model being presented in the main text (see Supporting Information for full details). These methods are therefore expected to predict activation energies for chemical reactions to high accuracy, assuming that the input feature representation is meaningful. In addition, the least-squares (LS) variant of SVM—LS-SVM²⁹—can provide error bars on all predictions, giving it an internal validation metric to gauge generalizability.

For the first round of machine-learning modeling, graphical features of reactive atoms, augmented by the energy of reaction, were utilized as features for the NN and the SVM. Upon cross-validation and testing on data points outside of the training set, a good correlation (NN: R² = 0.88. SVM: R² = 0.87) is found between quantum chemical activation energies (E_a) and machine-learning estimates of the same quantities (Figure 2, left). While higher R² values have been found for larger data sets with millions of data points (e.g., potential energies from quantum chemistry),^63,64 these R² values are more typical of machine-learning studies of chemical reactions.⁶⁵ The Supporting Information shows the error distribution for SVM matches the expected error distribution over the entire data set (Figure S2), indicating that these error estimates are reliable. Similar models without graphical features or energy of reaction showed much lower R² values (Figure S2). In short, NN and LS-SVM using the chemically relevant graphical and reaction energy features provided quantitative estimates for activation energies that it was not trained on and reasonable estimates of uncertainties in the LS-SVM case. By these statistical metrics, NN and SVM are each successful at learning activation barriers from first-principles simulations.

Figure 2.

Comparison of graphical and quantum chemical feature sets in deep neural network modeling.

Next, the quantum chemically derived atomic charges were used as features in place of the graphical features (Figure 2, right). Being sensitive to the electronic structure of the reactive molecules and atoms, these charges should in principle be more detailed descriptors than graphical features. The quantum chemical features performed similarly to purely graphical features in terms of test set R² (SVM: 0.84 vs 0.87. NN: 0.84 vs 0.88). Correlations between the predicted and the actual error (Figure S2) further show that LS-SVM can predict the activation energies just as well using either graphical or quantum chemical features with consistent uncertainties. While the NN provided a slight advantage using graphical features compared to the atomic charges, the difference was not dramatic.

The similar utility of graphical and electronic features suggests that the two sets contain similar information. We hypothesized that one feature set implies the other: the atomic connectivity around each reactive atom dictates the physical charge. To test this hypothesis, all molecules in the benchmark set were collected and specific atom types extracted based on the graphical features. For example, a trivalent, sp² carbon would be one atom type, distinct from a tetravalent, sp³ carbon. Atomic charges across this set were averaged on an atom-type by atom-type basis, yielding a lookup table that maps atom type to a characteristic charge (Figure 3). The mean change in charge associated with this averaging is small (0.05 au vs the original charges), suggesting that the charge assignments are reasonable.

Figure 3.

Method for generating the average charge features. First, the reactant molecules are collected and charges are computed for all atoms. For each atom in all of these reactants, atoms with equivalent connectivity are aggregated and their partial charges averaged. Mean charges are used for all atoms of each respective type in machine learning.

The NN and SVM models trained on the graphically derived electronic properties of atoms (Figure 4, top left) show similar prediction accuracy for SVM (R² = 0.83) and slightly worse for NN (R² = 0.80). This similarity suggests that the graph implicitly contains sufficient information to reproduce meaningful electronic features, which in turn work well in building effective NN and SVM models. For the purposes of predicting activation energy in the benchmark set of reactions, these qualitatively different feature sets appear to be equally successful. Up until this point, the NN and SVM modeling of elementary chemical reactions of main group elements is performing well and has no obvious deficiencies.

Figure 4.

(Top left) NN results using electronic features derived from graphical features. (Top right) NN results based on random values of atomic charges. There is no physical meaning to these charges in the sense that they have no value in representing Coulomb interactions. (Bottom) One-hot encoding of reaction types using graphical atomic features.

DECONSTRUCTION OF MACHINE MODEL MAKING

At this point in our study important insight has been gained with respect to representing chemical information. When expert chemists look at a 2D chemical structure (e.g., a ChemDraw), deep properties are inferred based on their knowledge, intuition, and experiences. Chemists can identify reactive centers, hypothesize the most likely transformations to occur, and propose experiments to reduce uncertainty in challenging cases.^66,67 This expert skill is the concept-centered approach mentioned in the Introduction, which relies on the physical properties inferred from the 2D structure (for example, atomic charge).

Since a 2D chemical structure is equivalent to its graph, one might suppose that the machine is inferring principles and properties in a way similar to the expert. The graph implies electronic features, which are the same physical properties that dictate chemical reactivity. While this is easy to imagine and is the hoped-for goal of machine learning, such principles are by no means necessary for nonlinear machine-learning tools to provide quantitative accuracy. Not only could the machine develop an entirely alternative viewpoint not held by chemists, it could also be making predictions using properties an expert would consider physically incorrect.

The second possibility appears to be closer to the truth. As the next numerical experiment, the machine-learning models were built using random values of atomic charge. Instead of using (physically meaningful) average values of charge from graphically derived atom types, each atom type was assigned to a random number from a standard Gaussian distribution. Using the randomized “charges”, the two machine-learning models performed similarly to the previous models, with R² = 0.86 for SVM and R² = 0.80 for NN, showing approximately equal quantitative accuracy (Figure 4). The atomic charge used by SVM therefore must be a label, not a physical measure; increasing or decreasing this number does not reflect a varying chemical environment but simply a renaming of the label. Adjacency or proximity between two of these charges holds no particular meaning, as the random charges have no particular relationship with physical charge.

REESTABLISHING CHEMICAL CONCEPTS

If electronic or graphical features of atoms are simply labels, it is likely that using “good” labels would yield a somewhat better procedure. An improvement in accuracy should result because the charges might be mistakenly seen by the NN or SVM to be “ordered” (−0.2 < −0.1 < 0.0 < 0.1), which is unrealistic given that the actual ordering is random. A good labeling procedure would not entail any artificial ordering, and this can be done with one-hot encoding. This encoding entails constructing a set of features with values of 0 or 1, where each feature is treated independently of the others. A single one-hot feature corresponds to a particular assignment of atom type based on the graph, just like in the feature-averaging strategy discussed above (but with no charge assignment).

A small increase in machine-learning predictive performance is observed when using one-hot encoded atom types, giving a test set R² of 0.87 (NN) and 0.89 (SVM) (Figure 4). This R² is slightly higher than that of the random features and close to or better than the best-case models with the other feature types (0.88 NN and 0.87 SVM). This result suggests that the machine-learning models using labels of atomic type appear to be fully sufficient to reach quantitative accuracy. The implications of this simplified feature representation are important to understanding nonlinear regressions in machine learning and will thus be further discussed.

The high accuracy achieved using one-hot labels challenges whether machine learning requires quantitative physical principles as underlying features for making accurate predictions. Recall that the reaction feature vector is simply a composite of the atomic features of reactive atoms, augmented by the energy of reaction. Where graphical features and properties derived from quantum chemistry remain close to basic principles such as periodic trends, covalency, and electronic structure, atom labels contain no such properties. A one-hot encoding of a 3-valent carbon is equally different from a 2-valent carbon or a hydrogen in an O–H bond. In other words, all one hots are unique labels with no special relationships to each other, much less physical relationships. This uniqueness means that (in the feature set) a pair of atom types of the same element are just as different from each other as a pair of atom types with different elements! Periodic trends, bonding patterns, and electronic properties are lost to such atom labels that do not contain this information.

To push this hypothesis even further, a k-nearest neighbors model was applied to the data set using the base graphical features. With K = 2, predictions are made by assuming that the average of the two most closely related data points gives the unknown data point. In this case, an R² of 0.86 on the test sets was achieved with the one-hot encoding feature set (Figure S3). This surprising result suggests that machine learning is doing little more than memorizing,⁶⁸ as predictions are made to reasonably high accuracy by mere similarity with training data points. No believable trends in physical properties are possible using only pairs of data points.

The analysis so far (Figure 5 and statistically summarized in Table S2supp) suggests that the nonlinear regressions of this work are largely agnostic to the underlying feature representations (with the exception of the energy of reaction, which is important and thus we will focus on this shortly). The Supporting Information shows analysis of a larger data set with 1 order of magnitude additional data points (3862); no qualitative change in outcome was observed, and only minor differences in quantitative accuracy were found. We therefore ask whether a highly simplified representation of chemical information may be just as effective as the machine learning. When atomic features are represented by simple labels, reaction types therefore are just composites of these labels. Incidentally, chemists have worked with labeled reaction types for centuries: they are called named reactions. For each reaction type, simple relationships have been developed to relate the molecular properties to the reaction rate. This approach will provide a much more transparent picture of reactions than nonlinear regression.

Figure 5.

Comparison of three machine-learning approaches using various representations of the underlying features. Each filled circle is an R² on a cross-validated test set, so there are 5 R² values per method/feature combination.

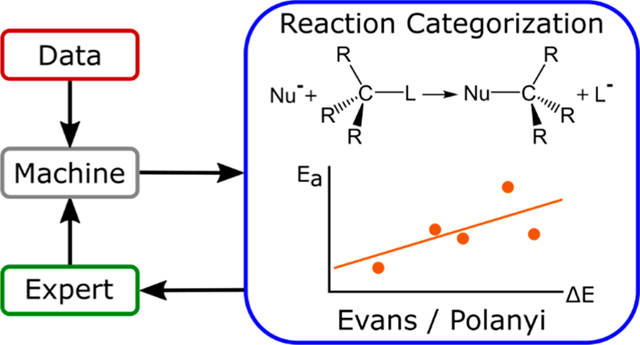
EVANS-POLANYI RELATIONSHIPS

At this point, it is clear that machine learning views reactions categorically rather than by any deeper physical relationship. The well-known Evans-Polanyi relationship can also do the same, where a linear trend between the activation energy and the energy of reaction is constructed. The statistical errors on the top-10 most prevalent reaction types are shown in Table 1. In this data set certain reaction types appear repeatedly, and the trends in reactivity fit well to the linear relationship (first row). The SVM model is able to perform almost as well as the Evans-Polanyi relationship for the same reactions, with an overall RMSE about 6% higher. The NN model is similar, at 5% higher overall error than the Evans-Polanyi relationship. This trend remains when analyzing the full data set, shown in Figure 6, which affirms that the Evans-Polanyi relationship is slightly numerically improved over the SVM and NN models. See the Supporting Information, Figure S8, showing that the same picture holds when analyzing the second data set, which was generated using density functional theory.

Table 1.

Comparison of Statistical Accuracy of the Evans-Polanyi Relationship Compared to SVM and NN for Common Reaction Types (RMSE, kcal/mol)^a

	1	2	3	4	5	6	7	8	9	10	total
Evans–Polanyi relationship	5.00	4.98	4.69	4.86	5.12	4.13	6.63	9.09	6.12	1.99	5.35
one-hot SVM	5.69	6.41	4.45	5.70	4.64	4.67	6.12	7.34	7.24	2.56	5.68
one-hot DNN	5.71	5.93	5.84	4.73	4.13	5.01	5.54	8.42	5.90	3.07	5.62
no. of data points	44	39	26	21	18	15	15	15	15	15	223

^aEvans-Polanyi relationship errors are based on leave-one-out cross validation with RMSE reported for the hold-out points.

Figure 6.

Error distributions for all data set 1 reaction types with at least 3 data points. Green triangles are mean values.

Figure 7 shows a hydrolysis reaction as an interesting example (reaction type 1 of Table 1). The Evans-Polanyi relationship on these 44 data points gives an R² of 0.74 and provides a simple interpretation: water-assisted elimination of ROH at an sp³ carbon has barriers that trend with the energy of reaction. While this statement is not particularly profound, it is easily constructed and can be performed for any reaction type represented by at least two points in the data set. Further analysis of the data in Figure 7 (top), however, shows this reaction is somewhat more nuanced. While in the original feature set rings were not identified, these were found to be important. The data points of Figure 7 therefore divide themselves into two sets: (A) reactions without 4-membered rings and (B) reactions involving 4-membered ring breakup. The B reactions break the 4-membered ring, release significant strain, and sit to the left of the other data points in Figure 7 (lower ΔE). In region B, the Evans-Polanyi relationship has a nearly flat slope. Removing these data points increases the R² of the A region to 0.81, indicating an improved linear fit. Predicting A and B data regions separately gives an overall RMSE of 3.37 kcal/mol compared to 4.40 kcal/mol for the original, single Evans-Polanyi relationship.

Figure 7.

(Top) Example of the Evans-Polanyi relationship from a reaction type with many examples in the data set. (Bottom) Bimodal Evans-Polanyi relationship for a second reaction type. Dashed green lines represent the (poor) linear fits when including all data points.

The Evans-Polanyi relationship can break down within specific sets of reactions, giving an indication that the chemistry is more complex than originally envisioned.⁶⁹ For example, an Evans-Polanyi relationship plot with a multi-modal structure suggests that there are significant mechanistic differences within the reaction type.⁷⁰ One such “bad” Evans-Polanyi relationship was easily identified within the data set.

The reaction type of Figure 7 (bottom) illustrates this point well (reaction type 9 of Table 1). The single-line relationship is poor (R² = 0.39), and 3 points on the left appear to be well separated from the points on the right. While this is insufficient data for statistical significance, mechanistic differences are responsible for the bimodal structure in this example. Examining the individual reactions revealed that the 3 data points differed qualitatively from the others and involved release of strain from a 4-membered ring. This shifted the reaction energies (ΔE) significantly downward for elementary steps that otherwise had the same reaction classification. Dividing the two cases based on the ring-release criterion provides two Evans-Polanyi relationships with R² of 0.98 and 0.73, indicating good fits to the linear relationships.

DISCUSSION

The above results and analysis of a chemical reaction data set highlight a certain tension between machine-learning and chemical approaches. Whereas chemistry usually seeks explanations based on the physical properties—and inherently cares whether those physical properties are real—machine-learning approaches can reach their criteria for success (test-set statistical accuracy) without achieving a convincing relationship to chemical principles.^68,71 While the machine approach could in theory provide physical relationships, there is no reason to believe this will come automatically with currently available algorithms, which are agnostic to expert knowledge. In the cases examined above, it is reasonable to conclude the machine-learning models do little more than memorize values from clusters of data points, where those clusters happened to be similar reaction types.

This limitation applies just as well to similarity-based SVM models as to deep NN machine-learning tools. In the latter case, NNs provide no obvious correspondence between their hidden representations and chemical concepts, though in principle these hidden representations could be valuable. Such a valuable hidden representation, however, is clearly not present when formed in the two data sets of this study, as the NN was unable to generalize its predictions beyond the specific reaction types that appeared in the input vector.

The two questions posed in the Introduction (what is the machine’s representation of knowledge and what does the machine learn) can be succinctly answered, at least in the case of the NN and SVM models used herein. Since NN and SVM recognize similarity between data points, it does not appear to greatly matter what form the input data comes in. Since the features can take many forms and still discriminate between reaction classes, these features need not be physically grounded. SVM therefore learns to recognize reaction types based on similarity within an abstract feature space. The NN performs similarly, does not provide any additional general-izability, and does so in a less transparent manner. While it is possible that machine learning through NNs can provide improved representations of chemistry with larger data sets, no improvement in statistical accuracy was found on a second data set with 3862 reactions (see Supporting Information, especially Figure S8).

Despite these concerns, however, machine learning still has strong abilities. It can operate directly on data and quickly give quantitative accuracy, in contrast to the chemical approach which relies on existing knowledge and highly developed insight. Certain questions of value therefore deserve further consideration.

1. Does the method solve an unsolved chemical problem or does it simply reproduce what is known?

2. Does the method offer clear advantages in time to solution compared to existing approaches?

3. Does the method provide transferable chemical insight, where transferable refers to the ability to work well outside of the current data set?

In our opinion, contemporary approaches used by expert chemists address points 1 and 3. New approaches for handling chemical problems are being developed by domain scientists for 2. In the area of chemical reactions, some progress has been made using machine learning to achieve 2 as well but not necessarily 1 and a few examples of 3 within specific domains.^3,72 While there remains a lot of room for new machine-learning approaches for chemical problems that may perform at a much higher level, one fundamental difficulty remains.

Figure 1 compared three types of models for relating data to predicted outcomes. The first most closely resembles expert procedures, where knowledge is represented in precise, explainable concepts developed over years of experience. These concepts are clearly understood, and chemists know the contexts in which each concept may be applied. In many cases, simple mathematical expressions can be written down that show the relationship between the physical properties and the outcome of interest (i.e., Table 1 and Figure 6). In the second case (in the middle of Figure 1), machine learning performs a complicated transformation of raw features into a hidden representation, which in turns leads to quantitative predictions. The second case provides no clear interpretation of how it obtains its high accuracy, and this is essentially what is expected of current-generation machine-learning methods. In the third case shown at the bottom of Figure 1, an idealized machine-learning setup takes raw chemical features (e.g., graphs) and relates them to concepts that are recognizable to chemists. This represents an automatic reduction in dimensionality of the feature set into more concise features that are primarily predictive of outcome. While this is a beautiful procedure, more work will be needed to achieve such a goal.

While these three procedures may seem like three equivalent means to the same end, in practice this is far from the truth. The two procedures using interpretable features employ a low-dimensionality, transferable representation of the chemical information, which is an incredibly important advantage (Figure 7). With a low-dimensionality representation, predictive accuracy can be obtained with exponentially fewer data points compared to a high-dimensionality representation.⁷³ Consider, for instance, the (linear) Evans-Polanyi relationship: given perhaps 3 data points, the data can be fit and predictions made. An SVM or neural network with an input feature vector of dimension 10 can do little to nothing with 3 data points. In addition, chemical principles are backed up by physical considerations, making them much more likely to be transferable outside of the current training/test set. For example, in polar reactions the Coulomb relationship states that positive and negative charges attract, leading to faster reactions (and physical charges are required to capture this relationship in full). Physical models built directly from physical features will therefore be the most generalizable predictive tools.

The low-dimensionality representation of knowledge expressly used by expert chemists allows them to operate in uncertain domains and make considerable progress in developing new chemical reactions. Machine learning in high-dimensional spaces is, on the other hand, unlikely to provide any value for new chemistries where the number of data points is low. The concern raised in question 3 seems to require low dimensionality and an underlying physicality in models and feature space, which deviates substantially from contemporary machine-learning methods.

CONCLUSIONS

The present investigation started with an analysis of feature representations (Figure 8) for machine learning of chemical reaction barrier heights. Atomic labels that lacked physical trends were found to be the basis for which the model made its predictions, and recognition of reaction types was the full basis for this model. This analysis showed that the machine-learning method was simply recalling reaction types, and we therefore give a tentative, weak answer to “what does the machine learn?” The machine learns to recognize the reaction types that were already encoded directly in the input features.

Figure 8.

Summary of feature experimentation steps. All feature types produce similar results in deep neural network or SVM regression, including random atomic charge assignments and one-hot labels. Machine-learning algorithms treat all atom types as completely unique and essentially unrelated to one another.

The machine-learning model was subsequently replaced by a simple, well-known chemical principle called the Evans-Polanyi relationship. Statistically, the linear Evans-Polanyi model slightly outperformed the nonlinear machine-learning models (by about 5% RMSE) and provided a simple interpretation of the results. This low-dimensionality model (2 parameters per reaction type) is algorithmically and conceptually easier to apply and can be evaluated using chemical principles, making it transferable to new reactions within the same class. While Evans-Polanyi relationships are not expected to be universal,^69,70 they provide a metric for reactivity that can be easily applied and tested and give a starting point for more complex models to be proposed.

The interpretable superiority—alongside reasonable statistical accuracy—of a simple chemical relationship compared to nonlinear machine regression suggests that deeper analysis is needed of machine-learning methods for chemical sciences.⁷¹ The approaches should not be used as black boxes, and careful investigations are required to reveal whether simpler, more easily interpreted methods could replace the complex workings of these machines. It should be recalled that machine-learning tools have seen their greatest benefits when working with giant data sets that are not well understood. Chemical research is not necessarily in this limit: chemists understand their data and do not necessarily have available millions of poorly understood data points that are ripe for machine-learning models.

COMPUTATIONAL DETAILS

Reaction Representations.

To represent a reaction, which involves bond-forming and/or -breaking events, the representations of the two atoms involved in the bond were concatenated. Consistency in ordering is important to ensuring that driving coordinates involving the same atoms are treated appropriately when algorithmically learning. Therefore, the atoms’ representations were sorted in descending order, which provides a unique representation. Due to this ordering, however, if two driving coordinates share an atom in common, it is possible that the two driving coordinates will appear to have no atoms in common.

Representing a reaction using a collection of bond changes is somewhat complex, however, due to the two types of driving coordinates (formed and broken bonds) and a variable number of driving coordinates of each type. Therefore, separate representations for the sets of formed and broken bonds were created and concatenated. For each type’s representation we utilized pooling to generate a fixed length representation from a variable number of driving coordinates (Scheme 2). Min, mean, and max pooling were tested as each of these seems plausibly important in conveying chemical meaning, with mean pooling not utilized in the final feature representation. Our representation also tested a few reaction level features in addition to the aggregate atomic representations. These were the number of bonds formed, number of bonds broken, and ΔE of the reaction (the former two were not used in the final machine-learning strategy). While obtaining ΔE requires geometry optimizations, this step is much lower in computational cost than optimizing a reaction path including its associated transition state.⁵¹ The various atomic feature sets examined in the main text are denoted in Table 2.

Scheme 2.

Graphical Feature Vector for Machine-Learning Applications^a

^aWhile more complicated feature vectors were examined (e.g., including nearest neighbor atom descriptors), none showed substantial improvement over this simple choice. See the Supporting Information for additional test cases.

Table 2.

Feature Sets for Atomic Representations

feature set	description	size of atom representation	overall feature set size (8n + 1)
one hot	one-hot encoded atom type (atom type determined by base graphical representation)	5 (no. of atom types in PM6 data set)	41
base graphical	atomic no. and coordination no.	2	17
partial charge	effective atomic charge	1	9
graphical → partial charge	average partial charge of all atoms of an atom’s type	1	9
graphical → random	random real number is drawn from a normal distribution for each atom type; this number is used to represent all atoms of this type	1	9

Data Set.

The Z-Struct reaction discovery method^74–76 was used to combinatorically propose intramolecular and inter-molecular reactions between small-molecule reactants, which include carbon, hydrogen, and oxygen (Scheme 3, data set 1). Even with these relatively simple reactants, the full extent of elementary reactions that may appear when the species are combined is unknown, due to the significant number of plausible changes in chemical bonding. On the basis of their relevance to atmospheric chemistries^54–57 and the difficulty in studying the host of possibilities using experiment, details of these reactions are best provided via first-principles simulation. For this study, a systematic simulation approach was used to generate this set of possibilities. Specifically, the Z-Struct technique used the Growing String Method (GSM)⁵¹ to search for reaction paths with optimized transition states for each proposed reaction (thousands of possibilities). Postprocessing scripts then attempted to include only reactions that were unique and well-converged single elementary steps. Machine-learning tests exposed a few (<10) outliers that passed the automated filters but were clearly incorrect and were manually removed. The PM6 method as implemented in MOPAC^77–79 was used as the underlying potential energy surface. The resulting data set contained 723 unique reactions from 6 original reactants. This data set is openly available online at https://github.com/ZimmermanGroup/reactivity-ml-data along with the data set of the next paragraph.

Scheme 3.

Reactants Involved in Data Set 1 and Data Set 2^a

^aResults in this paper from data set 1, with data set 2 analyzed in the Supporting Information.

To confirm the scalability of the methodology to a larger, higher quality data set, a second set of reactant molecules was examined (Scheme 3, data set 2). This larger, more chemically complicated set of reactants was examined at the density functional theory (B3LYP/6–31G**) level using the same ZStruct/GSM strategy to generate a second data set of reactions. Data set 2 includes nitrogen and boron in addition to carbon, oxygen, and hydrogen, so many types of reactions were possible, and nearly one-half of the reactions were the only reaction of their type. These single-instance reactions were removed, leaving 3862 reactions in data set 2. For analysis on this data set, see the Supporting Information. No qualitatively significant changes were observed compared to data set 1.

Machine-Learning Pipeline.

For the machine-learning pipeline, each feature set was extracted from the data set to give the aggregate reaction representation including the relevant atomic representation of reactive atoms and reaction level features. The features were standardized to zero mean and unitary standard deviation except in the case of one-hot encoding, in which the atomic representation was one-hot encoded and the energy of reaction was scaled to a standard deviation of 3 to balance its influence. This reaction representation was provided as input into an LS-SVM⁶² with radial basis function kernel that can compute confidence intervals. Since the data set size is relatively small by machine-learning standards, cross-validation was used to tune hyperparameters and generate generalization predictions on all data points. For final predictions, 5-fold cross validation was used for all models. For nearest neighbors, no hyperparameters were trained by cross validation. For SVM, within each split of the outer cross validation, hyperparameters for the test set were chosen using 3-fold cross validation within the training folds. Deep NN training was more resource intensive, so hyperparameters were chosen globally by 3-fold cross validation on the entire data set. In the final 5-fold cross validation weights and biases were trained only on training folds, but the globally chosen hyperparameters were used for all folds. Data were leaked into the models through comparisons between classes of algorithms and feature sets. Examining extreme outliers in early predictions uncovered a few clearly invalid data points (e.g., reaction profile lacking a single, defined transition state) that evaded automated filters for validating the data generation process, so these data points were removed manually. These extreme outliers were a result of reaction pathways passing through high-energy intermediates (e.g., multiradicals) that could not be effectively treated by the quantum chemical methods and were obviously nonsense pathways upon examination. Additionally, since R² is sensitive to outliers and can be dominated by a single extreme outlier, when generating the plots and metrics above, all predictions were clipped into the interval [0, 200] kcal/mol. This clipping was performed only after the “nonsense” pathways were removed and was necessary due to the machine-learning tools occasionally predicting barriers outside of a sensible range (i.e., 0–200 kcal/mol).

For the charge averaging in Figure 3, the charges for all reactive atoms in all driving coordinates in all reactions in the data set were grouped into atom types by element and coordination number. Within each atom type, the mean of all charges of all atoms of each type was computed and the charge of each atom within the type was set to this mean charge. This counting strategy implies that, for example, if there are more methanediol reactions involving the hydroxyl hydrogen than the alkyl hydrogen then the charge on the hydroxyl hydrogen will be effectively weighted heavier in the charge averaging.