On the Characterization of Interstitial Fluid Flow in the Skeletal Muscle Endomysium

Abstract

In this paper, the interstitial fluid flow in skeletal muscle endomysium was examined using an in-situ indentation testing in combination with theoretical modeling. The objective was to understand the transport properties of the three-dimensional and highly hierarchical muscular interstitial matrices, which play important roles in muscle-bone cross-talk and signaling during musculoskeletal development and maintenance. Gastrocnemius muscles from four 3-month old calves were harvested and subjected to a creeping test using a custom-designed device. The experiments, in combination with an anatomy-based theoretical model, were used to capture the spatial-temporal response of the skeletal muscle to external impacts. For the first time, the detailed load-induced interstitial fluid pressurization in the muscle endomyseal space was obtained. The relative contribution from the solid muscle fibers and the interstitial fluid to the temporal loading response was captured. The paper presented herein provides important information regarding the mechanical environment within the muscle tissue, which could help the future study of muscle’s response to forces and its subsequent signaling to surrounding tissues in vivo.

1. Introduction

Muscles and bones, serving as a functional unit enabling body’s locomotion, are believed to communicate mechanically and biochemically during musculoskeletal development and maintenance [1,2]. As muscle is electrically stimulated and muscle fibers contract, muscle-residing cells are found to secret many signaling factors (termed myokines) [3], including growth factors (e.g., insulin-like growth factor-1, fibroblast growth factor-2, and transforming growth factor-β), cytokines (e.g., interleukins-6, and -15), and other small signaling molecules (e.g., prostaglandin E2). These myokines may act on neighboring organs, including bone, where receptors for these myokines were found [4]. Both in vivo and in vitro studies support that myokines are involved in bone formation and repair [5–7]. For example, in a recent study, myokines secreted by skeletal muscles were shown to protect osteocytes from glucocorticoid-induced apoptosis through the activation of Wnt/β-catenin pathway, and the protective effect was greatly enhanced when the muscle was electrically stimulated [8]. However, the transport processes of myokines from muscle to adjacent bone tissue remain poorly understood.

The extracellular space within the muscle tissue, such as endomysium, epimysium, and perimysium [9], forms an extensive hierarchal pore system that could regulate the transport process of cytokines. The permeability of such a pore system not only affects the molecular diffusion within muscle but also determines the magnitude of fluid pressurization and convection of myokines in mechanically stimulated muscles. In a recent study [10], fluorescent microspheres (0.1-0.2 microns in diameter) were injected in the skeletal muscle to evaluate interstitial fluid movement. However, quantitative transport measurements were not performed, possibly due to the relatively large size of the microspheres and their steric exclusion interactions with the extracellular matrix (ECM). Previous reports have also developed various approaches using micropuncture [11], catheters with pressure transducers [12] [13] [14] [15], and capsule implantation [16], to measure fluid pressure in the bulk of normal muscle (mean value of approximately −0.12 mm Hg) [13], and confirm the elevation of interstitial pressure in tumor tissues [14]. However, the spatial distribution of interstitial fluid pressure build-up in muscle under mechanical loading and its relationship to the extracellular matrix porosity remain to be determined.

In the current study, an in-situ indentation test of bovine skeletal muscle samples was performed, during which the time-varying displacement of the indenter tip and the reaction force were measured simultaneously. The morphology of bovine skeletal muscle was analyzed to derive the Darcy permeability at the endomysium level. The strain-dependent compaction of the skeletal muscle under loading was experimentally imaged and subsequently accounted for in a novel anatomy-based theoretical model of muscle permeability. Combining the theoretical model and the in-situ indentation test, the relative contribution of reaction force from both the solid muscle fibers and interstitial fluid pressure to the muscle’s overall reaction to indentation was dissected for the first time. In particular, the spatial-temporal distribution of load-induced interstitial fluid pressure and fluid flow field within muscle were obtained. The results provide important information regarding the mechanical environment for the muscle tissue, which could inform future studies of loading-induced muscle functions and transport of myokines.

2. Materials and Methods

Indentation test

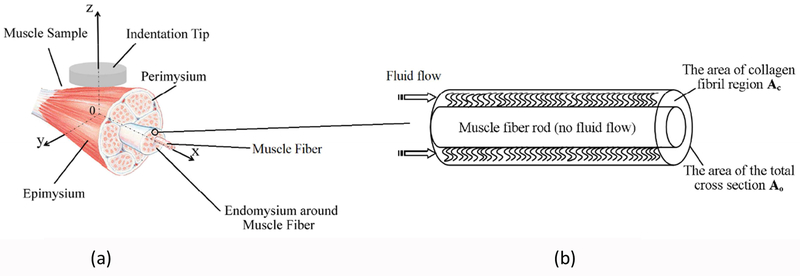
Knee joints with intact surrounding soft tissues from four 3-month-old calves were obtained from a local abattoir (Green Village, NJ) within 24h of sacrifice. Gastrocnemius muscle strips (15 mm x 15 mm x 5 mm) were dissected approximately 30 mm distal from the medial head. The samples were equilibrated in 1x PBS supplemented with a cocktail of proteinase inhibitors (PBS-PI solution) [17] for 2-3 hours. The sample, immersed in the PBS-PI solution, was subjected to a creep test using a custom-designed indenter (Figure 1). A rigid indentation tip (diameter = 1.6 mm) was brought to contact with the gastrocnemius muscle perpendicularly to the muscle fibers with a small tare loading (~2 mN) for 5 min (Figure 1). The piezo actuator (P602.8SL, Physik Instrumente) was then instructed to apply a step load of 5 mN, and the load was maintained for 90 min. The 5mN load applied through the indentation tip was estimated to induce a local stress of 2.5kPa and a strain level of ~10% (assuming 25kPa of muscle bulk modulus), which are close to physiological strains (~16%-18%) experienced by human gastrocnemius muscle fascicle during backward downhill walking [18] and by rabbits hindlimb muscles during in vivo stretch-shortening cycle experiment [19]. The reaction force and indentation depth experienced by the indenter tip were simultaneously recorded digitally via the load cell and position sensor of the actuator (Figure 1). The thickness of the muscle (~5 mm) was measured using a needle technique [17]. The apparent bulk strain was then calculated as the ratio of the final creeping depth over the thickness of the muscle. The mean value of the average strain was ~8.6%.

Figure 1.

(Left) A custom-designed indentation device and the testing setup on muscle samples. The muscle sample was hydrated in a water bath (containing PBS and proteinase inhibitors) mounted on a ball head, which could be adjusted so that the indenter tip (1.6 mm diameter) was perpendicular to the muscle surface. The tip was lowered to contact the muscle surface using both coarse and fine adjustments. The piezoelectric actuator was instructed to apply a step load of 5mN, while the deformation history was monitored in real time. (Right) Bovine gastrocnemius muscle was glued on top of a rigid aluminum block with its center being indented vertically and the muscle fibers being arranged horizontally.

Imaging of skeletal muscle under compression

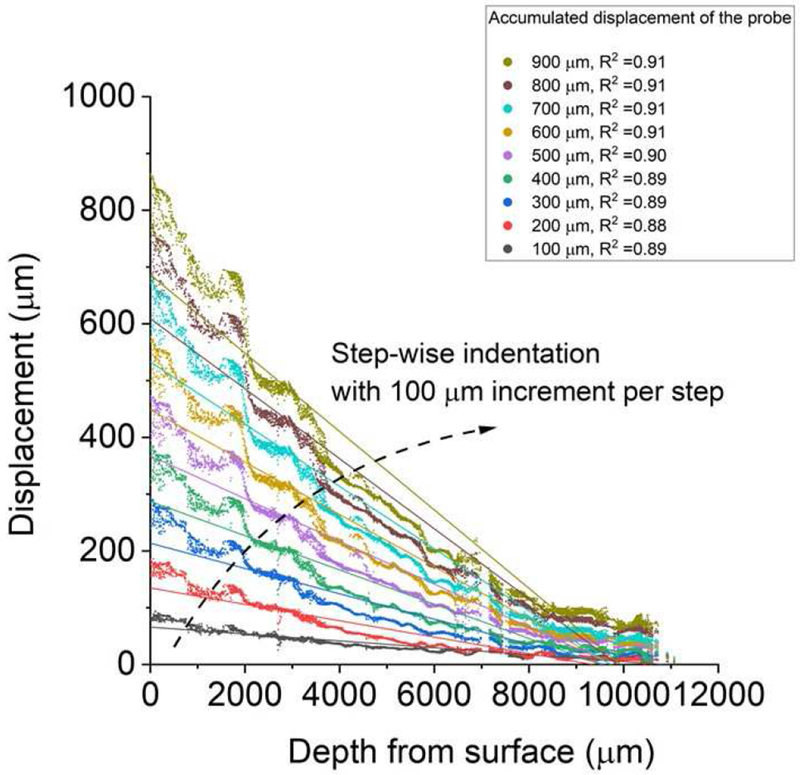
To understand the spatial pattern of muscle deformations underneath the indenter, we subjected bovine gastrocnemius muscle samples of approximately 11 mm x 11 mm x 10 mm size to a quasi-static step-wise compression (0.1 mm per step for a total 0.9 mm displacement) using a semi-cylindrically shaped indenter with a halved circle as its cross-section (0.5 mm diameter, Figure 2). The axially flat surface was placed facing down on the cover glass above the imaging objective, while the front tip of the indenter was in contact with the muscle sample and advanced at a step of 0.1mm from the surface (right side) towards the depth of the muscle (fixed surface, Figure 2). Prior to compression, the muscle sample was stained with a nuclear stain (Hoechest 33342, ThermoFisher Scientific, MA, USA) and visualized under a confocal microscope (Zeiss LSM510, Zeiss, NY) with a 5X objective lens (Zeiss EC Plan-Neofluar, N.A of 0.16). For the step-wise indentation, the indenter was instructed to advance 100 μm per step over a period of 1 s. During the 60 s holding period between two adjacent steps, multiple images were captured and later stitched (using an image correlation method and MATLAB codes) to map the entire thickness of the muscle sample. The experiment was stopped when the muscle surface was indented 900 μm from its initial position. A KLT tracking algorithm[20] implemented in MATLAB was applied to our recordings, where thousands of features (points) were automatically selected along the tissue depths below the indenter, and their locations were tracked in the subsequent series of indentation images. The displacement from its initial position for each tracking point was calculated, and the pattern of the displacement vs. tissue depth was identified using linear regression analysis.

Figure 2.

Direct imaging and tracking indentation-induced muscle deformation as a function of tissue location and the indentation depth. (a) A muscle sample was compressed up to 0.9 mm with an indenter in a cross-fiber fashion while the entire depth of the muscle was imaged with a confocal microscope. (b) Muscle samples were labeled with Hoechst nuclear staining (blue), and the images below show the compaction of the muscle tissue prior to (upper) and post indentation (lower). A total of 4679 points (green) at various depths from muscle surface (red, dotted line) underneath the indenter (light blue) were selected as representative tissue features and their locations in the time series of confocal images were tracked using MATLAB.

3. Theoretical Model

Force balance

To model the reaction of the skeletal muscle to the external impact, a novel theoretical approach was developed. The muscle tissue was modeled as a biphasic material, consisting of solid muscle fibers and interstitial fluid in the ECM [21]. Both phases contribute to the force response of the muscle sample when it is under external compression. The muscle fibers were modeled as solid with a negligible flow of cytosol fluid, because of the much faster fluid pressure relaxation within the skeletal muscle cells (diameter of ~50 μm) in comparison with that in the endomysium extracellular space (gap < 2 μm). As detailed below, the morphology of the bovine skeletal muscle suggested a relatively small permeability of the extracellular space, making most of the resistance that the fluid encounters as it flows out of the compressed muscle sample arise from the extracellular matrix. Hence, fluid pressurization mainly occurs in the endomysium extracellular matrix.

During the creeping phase (>200 s after initiation of the loading), the compression of the muscle sample occurred slowly (indenter velocity < 0.4 μm/s, as shown in the Results section), the inertia effect was thus neglected. The force balance requires that the applied load to the muscle sample equals the sum of the reaction force from the solid muscle fibers and the generated interstitial fluid force, as follows,

$$F_{Total\_applied}=F_{Fluids}+F_{Solid}.$$ (1)

Solid model

The average strain of the samples was ~8.6% in the current study. Thus, the solid structure was simplified as a quasi-linear material following a standard stress-strain relationship,

$$\sigma =\overline{E}·\epsilon .$$ (2)

where σ is the uniaxial force per unit area (σ= F_solid/A_t where A_t is the contact area of the indenter tip); ε is the strain of muscle samples; $\overline{E}$ is Young’s modulus of muscle samples. Previous studies by Collinsworth et al. [22] and Mathur et al. [23] used atomic force microscopy (AFM) and estimated $\overline{E}$ of murine skeletal muscle to be in the range of 10.2 to 49.3 kPa [22] and 21.2 to 28.2 kPa [23], respectively. It is noted that the strain used in [22] and [23] was calculated using the displacement of the AFM indenter probe, including the combined effects of extracellular pore deformation and muscle fiber compression.

Fluid flow model

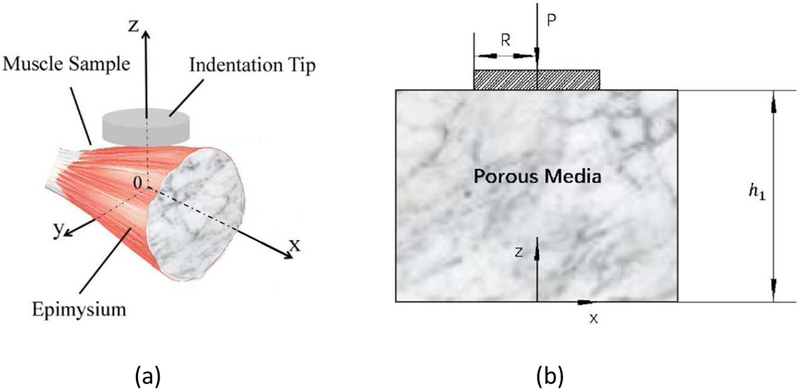
As for fluid pressurization, the skeletal muscle under indentation was modeled to account for the local compression and the resultant permeability change of the muscle ECM (Figure 3). The schematic of the problem is shown in Figure 3a, where a cylindrical probe with a flat end compresses a muscle sample perpendicularly (z-axis) to the fiber direction (x-axis), resulting in interstitial fluid flow within the endomysium space, along the muscle fibers. It is noted that, as the muscle is compressed by the flat indenter tip, the fluid flow in the random, porous endomysium surrounding each of the muscle fiber is three-dimensional, while macroscopically, the fluid is forced out in the axial (x-) direction.

Figure 3.

(a). The sketch of the theoretical model of fluid flow in muscle under a cross-fiber indentation. (b) The sketch of a repeating unit of muscle fiber with surrounding endomysium consisted of fine collagen-like fibrils.

We use a consolidation theory [24–27] to describe the fluid flow in which the entire muscle sample is treated as a porous media. Fluid flow through the porous media, governed by Darcy’s law, encounters resistance from the solid structures, which is expressed as a distributed body force (Darcy’s term). The obtained velocity field is a continuous field, meaning the velocity obtained from Darcy’s law is not the velocity in the isolated pores but the average velocity over a cross section area that includes both pores and solid structures. For example, if one examines the interstitial fluid flow pattern in the skeleton muscle, where a muscle fiber is surrounded by randomly distributed fibrils in the endomysium space, as shown in Figure 3b. The fluid flow in the annular conduit whose cross-section area is A_c, leads to a volume flow rate, Q. If Q is averaged in the overall cross section area of the unit, A₀, one obtains an average velocity for the entire unit. Considering there are numerous repeats of this type of unit, the flow field is equivalent to a continuous flow field where the velocity is an average velocity over the cross-section area of a flow unit that includes both pores and solids.

Hence, the indentation process described in Figure 3 is equivalent to an indentation on an effective porous media, as shown in Figure 4. The porosity of the porous media, ϕ, refers to the ratio of the volume of the pore space (fluid space), V_pore, to the volume of the muscle sample. For example, in Figure 3b, the porosity of the effective porous media, ϕ, is the ratio of V_pore, to the entire volume of the flow unit whose cross-sectional area is A₀. It is not the porosity of the endomysium, ϕ_em, because the latter is the ratio of V_pore to the volume of the conduit whose cross-section area is A_c. Similarly, the permeability of the porous media area shown in Figure 4, $\overline{K_P}$, is an effective permeability, not the permeability of the endomysium space, K_Pem.

Figure 4.

The sketch of the theoretical model of fluid flow in an effective porous media. (b) The cross-section in the x-z plane of Figure 4a.

As imaged in the preceding section and detailed in the Results section, indentation at a speed of 0.01mm/s introduced spatially uniformed compaction of the muscle tissue. Due to the slow creeping speed of muscle samples during indentation, the muscle sample is modelled to be compressed uniformly, and at any instant, a quasi-steady condition is immediately established [24–27]. In this model, the initial thickness of the skeletal muscle sample, H, is a constant as determined by the running condition. The motion of the indenter tip causes the deformation of the muscle sample. At any instant, the porous layer thickness is h₁, as shown in Figure 4. Thus, h₁ is a function of time. It is noted that the compression of the muscle sample arises from both the change in the pore size and the compression of the solid structure. We can view the problem as, pore size the change leads to the porous layer thickness to be h(t) (not shown in Figure 4), while the solid structure deformation contributes to the rest h₁(t)-h(t), at any instant. Obviously, if there is no deformation of the solid fiber, then h₁(t)=h(t). Here the time, t, is a parameter due to the quasi-steady assumption. It is noted that only the change in the pore size leads to pore pressure generation and relaxation. Thus h, instead of h₁, is used in the fluids modelling.

The porosity of the porous muscle, ϕ, at any instant, is then obtained [24–27],

$$\varphi =1-\frac{H}{h}·(1-{\varphi }_0)$$ (3)

where ϕ₀ is the initial porosity of the porous media.

The continuity equation for the fluid flow inside the deforming porous layer is given by Equation (4a) and the momentum equation, i.e., Darcy’s law, is given by Equation (4b) [24–27],

$$\{\begin{array}{l}\nabla \cdot (\rho u+\rho \varphi u_{\mathit{solid}})+\frac{\partial (\rho \varphi )}{\partial t}=0.\\ u=-\frac{\overline{K_P}}{\text{μ}}\cdot \nabla P.\end{array}$$ (4a)(4b)

where ρ is the density of the interstitial fluids, u is the relative velocity of the interstitial fluid with respective to the solid structure, which, in the majority of the muscle sampler, is along the x direction and represents the average fluid velocity over the cross-section of a muscle fiber calculation unit. u_solid is the velocity vector of the solid phase, whose components in the x and y direction are assumed to be zero and component in the z direction varies linearly from the indenter tip velocity at z=h₁ to zero at z=0; P is the pressure distribution in the region; μ is the dynamic viscosity of fluid; $\overline{K_{\text{p}}}$ is the effective permeability of the muscle sample, which will be determined later. It is noted that there is no time-dependent term in the momentum Equation (4b) because of the quasi-steady assumption.

Owing to the axis-symmetry of the geometry and the vertical compression motion without tilting, the boundary conditions of no flow are applied at the center line of the muscle sample (x=0) is given by

$$\frac{\partial P}{\partial x}{|}_{x=0}=0.$$ (5)

As the porosity of the material has a sudden change at the edge of the indenter tip, the fluid pressure will release very quickly to the undeformed surroundings [25,28]. The surrounding muscle tissue presents extra resistance for the fluid to relax and contributes to the pressurization underneath the indenter tip. The fluid pressure on the edge of the indenter tip, P*, is assumed to be uniform vertically at each time step [28].

$$P{|}_{x\to R}=P^{*}.$$ (6)

To determine P*, if the distance from the edge of the indenter tip to the outer edge of the muscle sample is L and a simple plug flow is assumed along the fiber axial direction in the surrounding undeformed muscle region, then $P^{\ast }=\left(u_x{|}_{x=R}\cdot \mu \cdot L\right)/\overline{K_P}$, where $u_x{|}_{x=R}$ is the axial velocity at the edge of the indenter tip, and $\overline{K_{\text{P}}}$ is the undeformed effective permeability of the muscle sample. $u_x{|}_{x=R}$ can be obtained by equating the amount of fluid displaced by the indenter tip to the amount of fluid flowing into the undeformed muscle sample,$-R\cdot \frac{dh}{dt}=h\cdot u_x{|}_{x=R}$, where R is the local radius of the indenter tip at a given y position.

No fluid flow is allowed at the bottom surface facing the impermeable block (z=0),

$$u_z{|}_{z=0}=-\frac{\overline{K_p}}{\mu }\frac{\partial P}{\partial z}=0.$$ (7)

The no-penetration condition also requires that the flow has a uniform downward average velocity the same as that of the indenter probe. Thus, the relative velocity between the fluid and the solid is zero at z=h.

$$u_z{|}_{z=h}=0.$$ (8)

Again, h, instead of h₁, is used to estimate the pressure boundary condition.

Effective permeability of skeletal muscle, $\overline{K_{\text{p}}}$

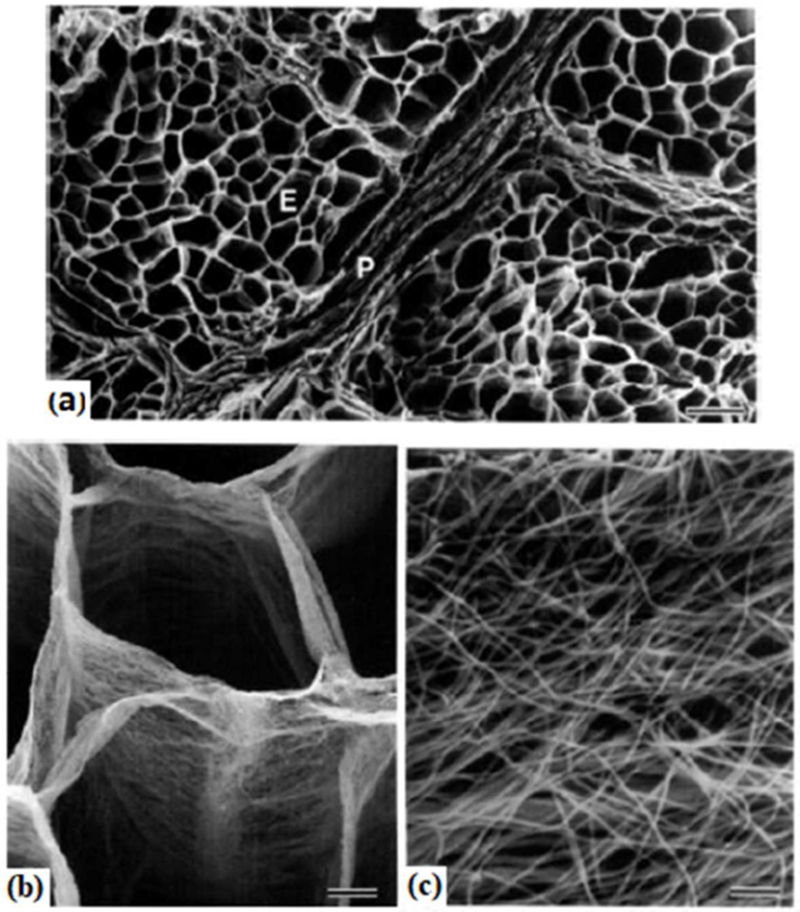
To estimate the permeability, $\overline{K_{\text{P}}}$ of the skeletal muscle sample, a morphology-based approach was adopted by analyzing the high resolution transmit electron microscopic (TEM) images of the endomysium of cow skeletal muscles [29]. Figure 5a shows the cross-section of the extracellular matrix surrounding muscle fibers, which have been removed chemically and shown as voids. The cylindrical sheaths of the endomysium around individual muscle fibers are ~60-100 μm in outer diameter, with a thickness of a few microns (Figure 5b). Randomly distributed fibrils of ~50 nm in diameter (obtained from image analysis measurement) fill the space enclosed by the thin sheath of the endomysium (Figure 5c)[29]. The initial porosity of the endomysium, ϕ_em, before compression, estimated as the areal fraction of the voids (black) in Figure 5c using custom MATLAB^© codes, varied between 0.35 (selected grayscale <25 as black on the scale of 255), and 0.55 (selected grayscale <55 as black on the scale of 255) depending on the threshold for voids. The median value of this range, 0.45, was selected to be the initial porosity of the endomysium space, ϕ_em0.

Figure 5.

Scanning electron micrographs of intramuscular connective tissue of treated bovine semitendinosus muscle using the cell-maceration method. (a) The endomysium, E, is a cylindrical sheath housing individual muscle fiber, and the perimysium, P, is composed of several layers of collagen sheets.

Bar=100μm. (b) Endomysial sheaths are membranous. Bar=10 μm. (c) A closer view of endomysium shows the random arrangement of fibrils (possibly collagen). Bar=500 nm. The figure is reproduced with permission [29]

As shown in Figure 3b, the interstitial flow in the repeating unit of the skeletal muscle can be simplified as, a muscle fiber located at the center of the repeating unit, and the interstitial fluid was only flowing through the annular endomysium space that is filled with randomly distributed fibrils. The permeability of the endomysium space, K_Pem, can be obtained from the correlation for fluid flow through a highly porous, random, fibrous material [30],

$$\frac{K_{pem}}{a^2}=\frac{0.219-22.13{\varphi }_{em}+10.849{\varphi }^2+10.995{{\varphi }_{\mathit{em}}}^3-21.906(1-{\varphi }_{em})\mathit{ln}(1-{\varphi }_{em})}{48{(1-{\varphi }_{em})}^2}$$ (9)

where a is the fiber diameter, and ϕ_em is the porosity of the endomysium space, which changes during the indentation process, ${\varphi }_{em}=1-\frac{H}{h}\cdot \left(1-{\varphi }_{em0}\right).$ The diameter of fibrils in the endomysium, a=50 nm, and the initial porosity of endomysium, ϕ_em0=0.45, have been obtained as described above. The permeability of the annular endomysium region, K_Pem, is then expressed in terms of the instantaneous value of h, based on Equation (9).

In theoretical modelling, we use an effective media approach. As described earlier in Figure 3b, the fluid flow in the endomysium surrounding the muscle fiber leads to a volume flow rate, Q = v_emA_c, where v_em is the fluid velocity in the collagen fibrils whose permeability is K_Pem and cross-sectional area is A_c. This flow is equivalent to an average flow through an effective porous media whose permeability is $\overline{K_{\text{P}}}$ and the cross-sectional area is A_o. Thus, Q = u_xA₀ where u_x is the effective velocity averaged across A₀. Applying Darcy’s law, $v_{em}=\frac{K_{pem}}{\text{μ}}\frac{dP}{dx}\text{and }{u}_x=\frac{\overline{K_p}}{\text{μ}}\frac{dP}{dx}.$ For the same pressure gradient, $\frac{dP}{dx}$, the effective Darcy permeability of the local muscle fiber unit enclosed by the endomysial sheath, $\overline{K_p}$, can be obtained,

$$\overline{K_p}=\frac{A_c}{A_0}\cdot K_{pem}$$ (10)

Three regions containing multiple endomysial sheaths were selected in Figure 5a, and the areal fraction of endomysium (white) was measured using MATLAB^© code. The mean value of A_c/ A_o was determined to be 0.75.

Parameters and numerical methods

In Equation (1), ε is the bulk strain experienced by the indented muscle sample, which is obtained from the experimentally recorded displacement of the indenter probe; F_{Total_applied} is the total applied load on the indenter probe, which is known as 5 mN; and F_Fluids is the integration of the fluid pressure underneath the indenter tip. As described earlier, the fluid pressure distribution depends on the change of the pore size, or equivalently the value of h, which, however, is not explicitly given. On the other hand, with the total applied force, F_{Total_applied} and the bulk strain of the muscle sample, ε, given, if Young’s modulus of the skeletal muscle sample $\overline{E}$ is chosen based on the values reported [22,23], the total lifting force from the interstitial fluid, F_Fluids is solely determined. One can use the obtained F_Fluids to back calculate the value of h, which is further used to predict the pore pressure distribution inside the muscle sample.

The back-calculation of h from F_Fluids is achieved through an iterative numerical scheme. Numerical methods are adopted because of the complexity of the loading and flow patterns in the system. The loading surface is circular; the dominant flow is along the x-axis, while fluid flow inside the endomysium is in both the axial, x direction and vertical, z direction. The existence of the epimysium eliminates the fluid flow in the y direction. The governing equation, Equation (4), subject to the boundary conditions, Equations (5–8), are solved using the finite difference method, where the spatial steps in z-direction and x-direction are chosen to be 0.05 mm and 0.04 mm, respectively. To begin the iteration, a trial value of h is used in Equation (3) to obtain the instantaneous porosity of the porous media, ϕ, which is then substituted into Equations (9) and (10) to obtain the effective permeability $\overline{K_p}$. The effective permeability, $\overline{K_p}$, is then substituted in Equations (4) to (8) to predict the fluid pressure distribution and the corresponding total lifting force from the interstitial fluid. A shooting method is used, meaning various values of h are tested, but only one of them satisfies Equation (1), based on the chosen value of $\overline{E}$. The corresponding h is then solely determined.

Model outputs:

As described earlier, for a given Young’s modulus of muscle, $\overline{E}$, F_Fluids is uniquely determined to back calculate the value of h, and the corresponding interstitial pressure/velocity field. However, only when $\overline{E}$ is chosen in a certain range, the physically meaningful value of h can be obtained numerically. Thus, the first output of the model would be the lifting force from both the fluid and the solid phase of the muscle sample when Young’s modulus of the muscle is chosen in the range that leads to a meaningful solution of h. The percentage of fluid vs. solid support as the function of time is presented. Next, for a representative value of $\overline{E}$, the temporal compaction of the endomysium porosity and its effect on tissue permeability, as well as the spatiotemporal profiles of the interstitial fluid pressure and velocity distribution underneath the indenter tip are readily derived from the model. Furthermore, to reveal the effects of the loading induced interstitial fluid on the muscle cells, the velocity of the fluid flow within the microscopic endomysium space is calculated by scaling the flow cross-sectional area. Briefly, the solution of Equation (4), subject to the B.Cs (Equations (5–8)) provides the bulk interstitial flow velocity along the muscle fiber, u_x, based on the overall cross-sectional area of the tissue unit, A_o (Figure 3b). The fluid velocity along the fiber direction within the endomysium is then scaled as v_em = u_x (A_o/A_c) (Figure 3b), which is applied to estimate the shear stress, τ, acting on a muscle fiber of a cylindrical shape suspended in a Darcy media [31], τ=μv_em,/(K_pem)^1/2. K_pem is the permeability of the ECM given by Equation (9).

4. Representative Results

Results for Bovine Sample Indentation Tests (Figure 1)

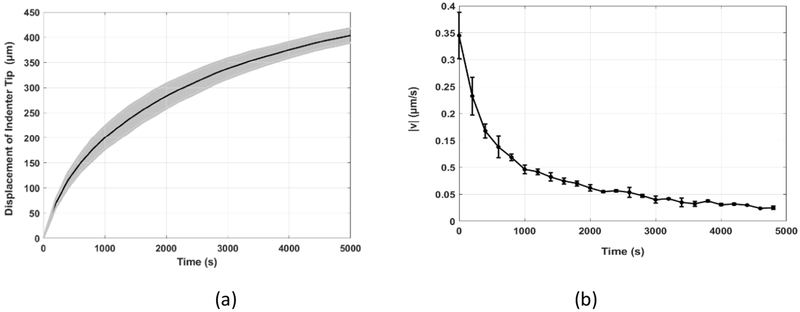
The displacement of the indenter tip, d, was recorded by the actuator’s internal sensor. The raw data shows that there was a rapid compression at the very beginning of the indentation process, due to the collapse of the large perimysium space, as shown in Figure 4a. This initial collapse, which occurred within 200 s with corresponding compression of the muscle sample being 200 μm, was discounted in the theoretical model for the prediction of the interstitial fluid flow, because it is the much smaller endomysium space, instead of the large perimysium, that provides the resistance for the fluid flow and the resultant lift generation. The displacement of the indenter tip, without the initial collapse, is shown in Figure 6a. The time duration was counted from the moment the step load of 5 mN was applied to the indenter tip. The initial position of the indenter was at the top layer of the muscle sample (~5 mm). The indenter tip traveled 0.43 mm downward, compressing the muscle sample underneath. Note that the indentation depth was much smaller than the thickness of the sample. The grey shadow, surrounding the solid black line, shows the deviation of the experimental data. The time derivative of the displacement data indicates the velocity of the indenter tip, v, as shown in Figure 6b.

Figure 6.

(a) The displacement history and (b) the velocity of the indenter tip

Location-dependent Displacement Based on the Imaging of Skeletal Muscle under Compression (Figure 2)

The microscopical image of skeletal muscle under indentation showed that the accumulated displacements for the tracking points within bovine muscle tissue increases with the indentation steps (0.01mm per step) while decreases for deeper tissues away from the indentation surface (Figure 7). Please note that the indenter moved at much slower speeds during the creeping test (< 0.4 μm/s, Figure 6b) than the speed (0.01mm/s) used in the imaging test (Figure 2). A total of four samples were imaged, and all demonstrated a nearly linear behavior of muscle compaction under indentation, as shown in the representative result (Figure 7).

Figure 7.

A spatially uniformed compaction of muscle tissue under quasi-static compression. In a representative test, the displacement (μm) for those tracking points shows a roughly linear relationship with their original (without indentation) depth from the muscle surface at discrete indentation steps (100 μm per step for a total of 900 μm penetration).

The Prediction of the Fluid Pressure in the muscle under Compression

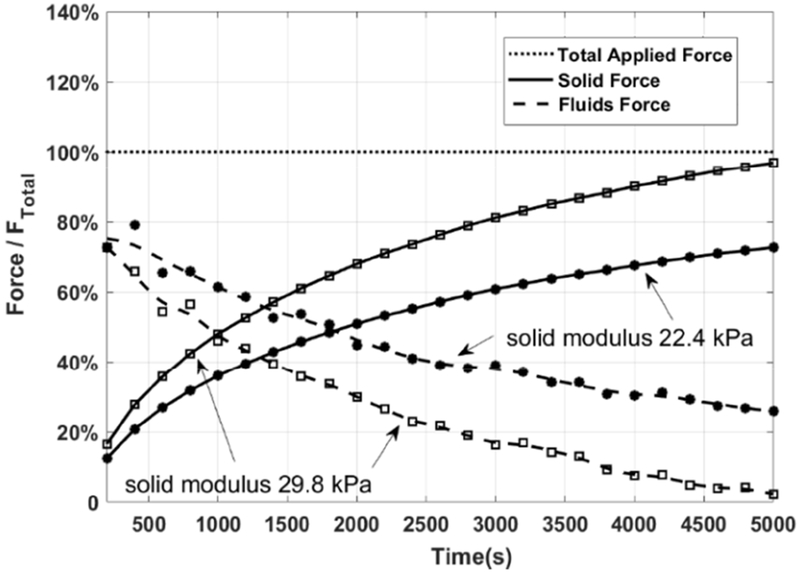
Figure 8 shows the lifting force from both the solid structure and the interstitial fluids during the indentation process, when Young’s modulus of the skeletal muscle, $\overline{E}$, is chosen in the range of 22.4~29.8 kPa. We tried the entire span of suggested values [22,23] of $\overline{E}$, and noticed that only when 22.4 kPa< $\overline{E}$ <29.8 kPa, there was a solution for the fluid pressure distribution. This figure is obtained from the theoretical prediction. The only input parameter with uncertainty is the total strain, which is calculated by the experimental displacement measurement. Thus, the curves in this figure have the same error range as Figure 6a.

Figure 8.

The relative contribution of fluid and solid phases to the total force response of muscle during the compression

The solid force, shown as solid lines in Figure 8, is relatively small at the beginning of the compression process (<20% total force) and becomes the dominant support at the later stage of the indentation process (>60% total force). The solid force reached 50% of the total force at t=1100 s when $\overline{E}$ =29.8 kPa, while t= 1900 s when E =22.4 kPa. Towards the end of the compression process, the solid force offered by the muscle fibers can be up to 75~95% of the total applied force. One can find that more solid phase support is predicted if the effective Young’s modulus, $\overline{E}$, is larger.

The fluid force shown as dash lines in Figure 8 is quite similar to that of the velocity of the indenter tip, Figure 6b. This is because the faster the compression is, the less time there is for the fluids to escape and thus the higher-pressure build-up [24–28,32,33]. One finds that the generated fluid pressure is the main support force at the beginning of the compression process because the velocity of the indenter tip was high and much of the interstitial fluid is still trapped inside the pores. As time goes on, the lifting force from the fluid decreases monotonically with the transiently trapped fluid leaving the compressed muscle sample. More fluid force is generated if the solid fiber is softer. Very importantly, one notices that, even though the compression duration is long, and the indentation speed is slow, the interstitial fluid pressure still contributes significantly to the overall reaction force, especially in the earlier stage of the indentation process. This is because the flow is confined in the endomysium among the tightly arranged muscle fiber bundles, and the thin, dense endomysium presents tremendous resistance for the interstitial fluid flow out of the compressed muscle sample, as evidenced in Figure 9.

Figure 9.

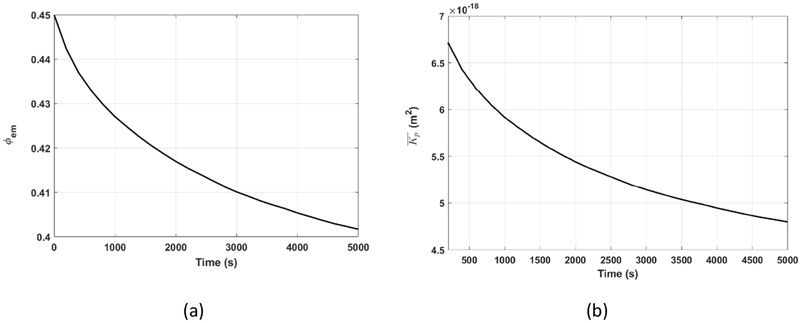
(a) The porosity of the endomysium (b)The effective permeability of the skeletal muscle during the compression

Figure 9 shows the change of the porosity of the endomysium, (a), and the change of the effective permeability of the skeletal muscle, (b), during the indentation process when $\overline{E}$ =29.8 kPa. Figure 7 indicates that the muscle sample is compressed uniformly. Thus, at any instant, both the porosity of the endomysium, ϕ, and the effective permeability, $\overline{K_p}$, of the muscle sample are uniform. $\overline{K_p}$ decreases with the compression of the muscle sample. The porosity and effective permeability changed from its initial value, 0.45 and 6.7×10⁻¹⁸m² to the lowest value, 0.4 and 4.8×10⁻¹⁸ m², respectively, at the end of the compression process. The very small and ever-decreasing effective permeability indicates the very high and ever-increasing difficulty for the interstitial fluid to flow out of the compressed muscle sample, which is the reason for the fluid pressure generation, even for the very slow creeping indentation test.

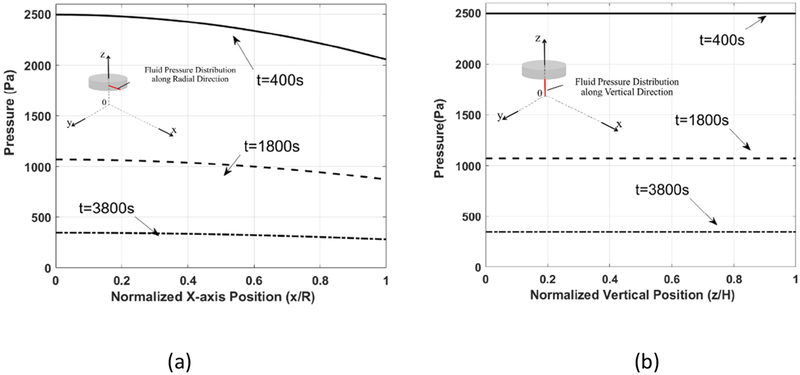
The fluid pressure distribution underneath the indenter tip, when $\overline{E}$ =29.8 kPa, in the fiber axis (x-) direction at y=0, z=h₁ is shown in Figure 10a. It shows that, at any instant, e.g., t= 400 s, the highest value of fluid pressure occurs at the center of the indenter tip. It decreases monotonically as x increases, when x=R where R is the radius of the indenter tip, the pressure reaches its minimum value. The generated fluid pressure increased to a higher value at the early stage and then decreased during the compression process. The maximum values of the fluid pressure are 2496 Pa at t = 400 s, 1071 Pa at t=1800 s, and 346 Pa at t=3800 s. As shown in Figure 6b, the indentation speed at the earlier stage of the compression process, e.g., t=400 s, is higher than that of a later stage of the compression. Faster compression leads to higher pressure generation.

Figure 10.

The fluid pressure generation at (a) a normalized x-axis position (x/R) for z=h₁ y=0 and (b) a normalized height(z/H) for y=0, x=0

The fluid pressure generation in the vertical direction at x=0, y=0, when $\overline{E}$ =29.8 kPa, is shown in Figure 10b. At any instant, the change of fluid pressure in the vertical direction is very small because the fluid and the solid structures are displaced together by the indenter tip, meanwhile the epimysium eliminates any relative fluid velocity in the z direction. Therefore, the motion of the indenter tip forces the interstitial fluid to flow downward[34–37], which is then diverted into two streams due to the existence of the impermeable substrate. Overall, higher pressure is generated at the earlier stage of the indentation, consistent with the observation in Figure 10a.

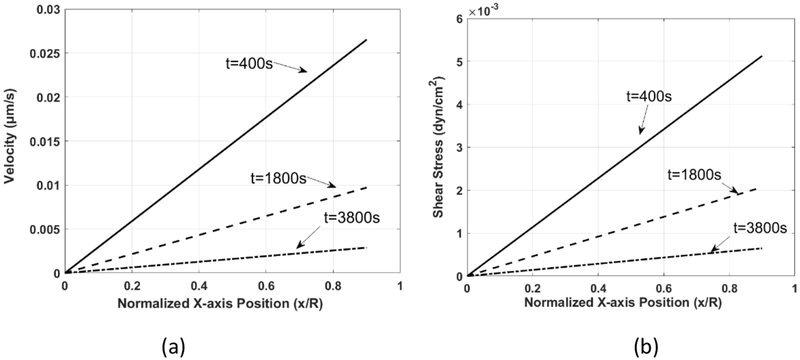
The fluid velocity along the muscle fiber axis, v_em, within the endomysium, and the resulting wall shear stress, τ, on the membrane of the muscle fiber, immediately underneath the indenter tip (z=h₁, y=0) are shown in Figure 11. Higher fluid velocity and associated shear stress are observed at the earlier stage of the indentation process. The maximum value of the velocity and corresponding shear stress along the muscle fibers array are 0.027 μm /s and 0.005 dyne/cm² for t= 400 s, 0.010μm /s and 0.002 dyne/cm² for t = 1800s, and 0.0006 μm/s and 0.001 dyne/cm², for t = 3800 s, respectively. Due to the mass conservation, the fluid velocity increases as x/R changes from 0 to 1; accordingly, the fluid shear stress increases as well because the muscle sample is compressed uniformly, and there is no change of gap height as x/R increases from 0 to 1.

Figure 11.

(a) The fluid velocity along the fiber axis, v_em, and (b) shear stress within the endomysium of the skeletal muscle, at the top of the muscle sample, z=h₁, y=0.

5. Discussion

Skeletal muscle is a porous material, consisted of tightly packed muscle fibers and the extensive extracellular space filled with collagen-like fibrils and interstitial fluid. Under compression, the fluid could be transiently trapped inside the extracellular pores, and its subsequent flow out of the compressed region is hindered because of the hydrodynamic resistance from the solid matrix, leading to pressure built up. In the past decade, extensive studies have been performed on the lift generation inside a soft porous media [25–28,30,33,38–41], which has demonstrated the significant role of the transiently trapped fluid for the proper functions of many biological systems, from red cells moving in a capillary to knee joints lubrication, etc. However, interstitial fluid flow inside a skeletal muscle, although very important, was not well studied.

In the current study, we develop a novel theoretical frame work to capture the fluid pressurization and the solid lifting force during an indentation process. The experiment provides the applied constant loading and records the indentation speeds, which are used as the input parameters of the theory. The outputs of the theory are the pressurization of the interstitial fluid as well as the lifting force from the muscle fibers during the indentation process, which are difficult to obtain experimentally due to the fact that, (1) any measurements of interstitial pressure using pressure sensors are invasive and thus affect the fluid flow environment; (2) there is lack of method to isolate the solid lifting force because no matter how slow the indentation speed is, there is always fluid pressurization due to the very small permeability of the endomysium space. As compared to the well-established poroelastic theory [42] that requires the knowledge of the constitutive equation of the fiber matrix and is typically applied to systems with small deformation, the consolidation theory presented herein separates the fluid flow in the pores and the deformation of the solid phase. Because fluid flow is driven by the moving upper boundary, knowledge of the solid phase constitutive equation is not necessary for modelling the fluid flow. This model allows us to capture the flow within the indented muscle as the pores undergoing non-uniformed depth-dependent compression, a conceptual improvement from the previous modeling of homogeneous and isotropic porous media. The results from this work fill the gap of knowledge in the literature.

The morphology-based model developed in the present study provides a novel in situ approach to quantify the transport properties of heterogeneous soft tissues like skeletal muscle. The model accounts for not only the macroscopic features (tightly packed and highly oriented muscle fibers) and microscopic anatomical characteristics (endomysium with random fine fibrils), but also the nonlinear behaviors of pore compaction under compression. Combining this model with indentation testing, we measured the Darcy permeability of the skeletal muscle, a key parameter that governs fluid flow inside a porous media. There are a few techniques available to measure fluid or solute permeability in biological tissues. A common method is to drive fluid flow through a thin slice of tissue mounted between a two-compartment chamber under a predefined pressure gradient or flow rate, such as those performed in bone, intervertebral disc, and periosteum samples [43–45]. The tested samples must be uniform in thickness, and a well-sealed contact should be maintained between the sample and chamber holder to avoid leaking artifacts. These strict requirements limit the application of this technique on samples of irregular shapes or heterogeneous properties. In addition, various imaging techniques using fluorescent probes have been used to study the solute permeability of various tissues. Direct observations of probe penetration into the periosteum in situ allowed the measurement of effective diffusivity of fluorescent probes in the tissue [46]. Washing out of pre-permeated tracers have been used to derive diffusivities and convection of tracers in cartilage samples [47]. Furthermore, with perturbation methods such as Fluorescent Recovery After Photobleaching (FRAP) and Fluorescence Loss Induced by Photobleaching (FLIP), the permeability of tracers in cartilage [48], tendon [49], TMJ disc [50], bone [51], calcified cartilage [52] have been successfully quantified. Despite the versatile applications of these imaging methods, the outcomes are tracer diffusivity instead of Darcy permeability. Also, the requirement of perfusing fluorescent probes in the tissues and limited imaging depths makes it challenging to apply the imaging techniques on denser and bulky tissues like skeletal muscles. Mechanical testing has been applied to derive hydraulic permeability in cartilage in combination with indentation and poroelasticity theory [17,53]. As illustrated in the present study, the advantages of our approach include no need of fluorescent probes or imaging (compared with the imaging approaches) and no need for pre-sectioning the samples (compared with the chamber approaches). It is also more anatomically and physiologically accurate by fully considering the fiber orientations in the skeletal muscle, and taking into account the strain-dependent character of the permeability in the skeletal muscle.

The effective permeability $\overline{{\text{K}}_{\text{p}}}$ of bovine skeletal muscles obtained in this study is in the range of 4.8 to 6.7×10⁻¹⁸ m². Although solute and hydraulic permeability of smooth muscles surrounding blood vessels has been extensively studied in the literature [54,55], few data are available on skeletal muscle permeability. A recent study, utilizing the chamber approach, measured the bulk Darcy permeability of rabbit skeletal muscles to be ~7.4×10⁻¹⁴ m², and the permeability was found insensitive to muscle fiber orientation and external compression [56], in contrast to our finding where 5 mN compression of the indenter (2.2 kPa) resulted in 30% decrease of the Darcy permeability. The inconsistency of the two results may be due to the differences in species (rabbit vs. cow) and muscle location (shoulder vs. knee). Most likely, the chamber approach may test the fluid flow over a relatively large area of samples, where larger additional ECM spaces such as perimysium might have impacted the results more than the smaller endomysium spaces. In our study, the initial rapid collapse of the muscle sample due to the collapse of the perimysium was not considered in the theoretical model because our focus was on the interstitial pressurization which mainly occurred in the endomysium spaces. More work is needed to study the hierarchy of the pore system in the muscle. Nevertheless, our measured permeability is consistent with the numerical simulations of smooth muscle layers around the capillary wall by Tada and Tarbell [57], where $\overline{{\text{K}}_{\text{p}}}=1.432\times {10}^{-18}{\text{m}}^2$, and the value used by Wang and Tarbell [58], where $\overline{{\text{K}}_{\text{p}}}=1.2\times {10}^{-18}{\text{m}}^2$.

The quantitative data of the present study allow qualitative comparisons of the transport across all barriers involved in the transport of myokines to reach target bone tissues. The permeability of bovine skeletal muscles (order of 10⁻¹⁸ m²) is one order of magnitude smaller than that of bone periosteum (2-5×10⁻¹⁷m²)[45]. Plus, the characteristic transport distance for muscle (20 mm for bovine gastrocnemius) is over 10-fold larger than that for periosteum (1 mm bovine species) [45,46]. Thus, the muscle will present a more effective resistance for the interstitial muscle-bone cross-talk than the periosteum. This simple analysis suggests that both muscle interstitium and bone periosteum may affect the transport of the myokines during potential bone-muscle cross-talk, and the muscle presents a dominant barrier than the bone. These effects will depend on the sizes of the signaling molecules, as demonstrated in the sieving effects of bone periosteum [46].

Our model, incorporating the endomysium microstructure, allows us to better understand the interstitial fluid pressure and velocity in muscle, especially the mechanical signals such as flow induced shear stress experienced by muscle cells. For example, eccentric exercises were found to induce elevated intramuscular pressure at the level of 10 kPa [59]. Our model predicts 0.03 μm s⁻¹ of the fluid velocity and 0.005 dyn/cm² of wall shear stress on muscle membrane under the indentation pressure of 2.49 kPa. Therefore, it is reasonable to extrapolate that the pressure-driven fluid velocity in the human skeletal muscle under eccentric exercises is ~ 0.12 μm s⁻¹, which is within the reported velocity range of interstitial flows (from 0.1 to 1.0 μm s⁻¹) in normal tissues [60,61]. In this case, the muscle cells would be exposed to ~0.02 dyn/cm² of shear stress, which has been shown to activate skeletal muscle activity [62], and influence the functions of vascular smooth muscle cells and fibroblasts [31]. Although skeletal muscle is well known to be mechanosensitive, and its tension and compression properties have been extensively studied [63–66], the interstitial fluid environment surrounding the muscle cells has not been fully characterized until now. The comprehensive experimental and theoretical framework presented herein allows us to capture the critical flow behavior and thus the shear stress distribution inside a skeletal muscle. It helps to advance our understanding of muscle mechanotransduction process and how muscle interacts with neighboring tissues like bone.

There are several limitations to the current study. Firstly, all the muscles were tested postmortem without active muscle contractions typically seen in vivo. Therefore, the data reported here are mainly on the passive behaviors of muscles. Secondly, due to the nature of the experiments, the preparation and testing period was long (3.5-4.5 hours). Despite the use of proteinase inhibitors to slow down the degradation process, structural and material property changes might have occurred, such as stiffening of the tissue [67]. Care should be taken when extrapolating these in vitro results to in vivo conditions.

6. Conclusion

This study provides the first quantitative estimations of Darcy permeability of skeletal muscles and predicts the microscopic interstitial fluid field inside the skeletal muscles under compression. The developed tools and the findings from the study will help the future study of muscle mechanotransduction and muscle-bone cross-talk, which may lead to possible new targets for treating musculoskeletal diseases and defects.

NOMENCLATURE

a

The collagen fibril diameter

v

The velocity of the moving tip in the indentation test

u

The relative velocity of fluids

u_solid

The velocity vector of the solid phase

u_x

The average fluid velocity over the cross-section of a muscle fiber unit, A₀

v_em

The fluid velocity in the endomysial space filled with collagen fibrils

A_c

The cross-section area of collagen fibril region of a muscle fiber unit

A_o

The overall cross-section of a muscle fiber unit

A_t

The contact area of the indenter tip

$\overline{E}$

Effective Young’s modulus of muscle samples

H

The initial thickness of the skeletal muscle sample before the indentation test

h₁

The time-dependent porous layer thickness during the indentation process

h

The time-dependent porous layer thickness due to the pore size change during the indentation process

F_{total_applied}

The total applied force

F_Fluids

The total lifting force from the interstitial fluid

$\overline{K_p}$

The effective permeability of the skeletal muscle

K_Pem

The permeability of the endomysium space

P

The fluid pressure distribution

P*

The fluid pressure at the edge of the indenter tip

R

The radius of the indenter tip

ϕ

The effective porosity of the skeletal muscle

ϕ₀

The initial effective porosity of the porous media

ϕ_em

The porosity of the endomysium space

ϕ_em0

The initial porosity of the endomysium space

μ

The dynamic viscosity of the fluids

ρ

The density of the interstitial fluids

ε

The total strain of the muscle sample during the indentation process

σ

The uniaxial force per unit area, σ= F_solid/A_t