Network and cellular mechanisms underlying heterogeneous excitatory/inhibitory balanced states

Abstract

Recent work has explored spatio-temporal relationships between excitatory (E) and inhibitory (I) signaling within neural networks, and the effect of these relationships on network activity patterns. Data from these studies have indicated that excitation and inhibition are maintained at a similar level across long time periods, and that excitatory and inhibitory currents may be tightly synchronized. Disruption of this balance - leading to an aberrant E/I ratio - is implicated in various brain pathologies. However, a thorough characterization of the relationship between E and I currents in experimental settings is largely impossible, due to their tight regulation at multiple cellular and network levels. Here we use biophysical neural network models to investigate the emergence and properties of balanced states by heterogeneous mechanisms. Our results show that a network can homeostatically regulate the E/I ratio through interactions among multiple cellular and network factors, including average firing rates, synaptic weights and average neural depolarization levels in excitatory/inhibitory populations. Complex and competing interactions between firing rates and depolarization levels allow these factors to alternately dominate network dynamics in different synaptic weight regimes. This leads to the emergence of distinct mechanisms responsible for determining a balanced state and its dynamical correlate. Our analysis provides a comprehensive picture of how E/I ratio changes when manipulating specific network properties, and identifies the mechanisms regulating E/I balance. These results provide a framework to explain the diverse, and in some cases, contradictory experimental observations on the E/I state in different brain states and conditions.

Graphical Abstract

Network can homeostatically regulate the E/I ratio and net postsynaptic current through interactions among multiple cellular and network factors, including average firing rates, synaptic weights and average neural depolarization levels in excitatory/inhibitory neuronal populations, leading to the emergence of distinct mechanisms responsible for determining a balanced E/I state and its dynamical correlate. This in turn leads to emergence of multiple balance states having different dynamical properties.

Introduction

Since it was first proposed that excitatory/inhibitory (E/I) balance emerges within brain networks (van Vreeswijk & Sompolinsky, 1996), a large body of theoretical and experimental work has focused on clarifying its regulation and possible role in maintaining desired spatio-temporal activity states (Deneve & Machens, 2016). Co-occurring E/I responses have been observed for many modalities, e.g., in auditory cortex (D’Amour & Froemke 2015; Wehr & Zador, 2003), visual cortex (Liu et al., 2009; Tan et al., 2013), and olfactory cortex (Poo & Isaacson, 2009, Stettler & Axel, 2009). Besides activity evoked by stimuli, balanced excitation and inhibition also appears to be present during spontaneous brain activity (Graupner & Reyes, 2013; Murphy & Miller, 2009) and may play a critical role in generating certain brain rhythms (Atallah & Scanziani 2009).

Despite these experimental findings, two questions remain unresolved. First, how does E/I balance contribute to the spatio-temporal patterning of neuronal microcircuit activity? Second, what are the underlying mechanisms promoting E/I balance across brain networks? E/I input to neurons was initially proposed to balance only over long timescales, leading to the notion of “loose E/I balance” with specific statistics of the firing patterns (Brunel 2000; Rudolph et al., 2007; Salinas & Their, 2000; van Vreeswijk, 1998). This idea was challenged by experimental phenomena, such as efficient coding of irregular spiking, and the correlation of membrane potentials between neurons responding to similar stimuli (Cohen & Kohn, 2011; Gentet et al., 2010; Yu J, Ferster 2010), which cannot be explained by loose interactions of E/I cells (Deneve & Machens, 2016). More recent findings have demonstrated that inhibition can closely track excitation at a millisecond timescale, leaving only a brief window of disinhibition for neurons to fire. This “tight balance” has been observed in brain regions such as somatosensory cortex (Okun & Lampl 2008), hippocampus and piriform cortex, as well as in vitro (Atallah & Scanziani 2009) and in computational simulations (Renart et al.,2010). Indeed, disinhibition is thought to be significant in learning and memory (Letzkus et al., 2015).

The interaction of recurrent inhibitory and excitatory circuits also regulates the occurrence of cortical up- and down- states ( Haider et al., 2006; Shu et al., 2003), and it was shown that different levels of correlation between excitation and inhibition can emerge from the same neuronal circuitry, depending on the specific cortical state - with correlations observed to be lower during anesthesia than during states exhibiting up- and down-state activity (Tan et al., 2013).

One roadblock to understanding the regulation and function of E/I balance is a lack of technical ability to experimentally quantify E/I ratios. It is impossible to simultaneously measure the excitatory and inhibitory post synaptic currents (EPSCs and IPSCs) at every neuron across a network. Several indirect experimental quantifications (for example cell-wise measurement of excitatory and inhibitory conductance obtained from whole-cell recording) have also been used ( Landau et al. 2016; Monier et al., 2008; Tan et al., 2013; Wehr & Zador, 2003; Xue et al., 2014). Although each of these capture characteristics of E/I balance in some way, none of them quantifies all of the features that simultaneously contribute to E/I balance. Further, such measurements can only infer E/I ratio from a selected subset of neurons, which may not accurately represent E/I ratios at the network level.

To investigate E/I balance in a network and its dynamical correlates, we use a computational model network composed of biophysical neurons, and quantify E/I ratio as the ratio between mean levels of total EPSC and IPSC across the network. By systematically varying parameters, we show that a network can homeostatically regulate E/I ratio over a wide range of E/I levels and reach asymptotic balance states after evolving for a period of time. These balanced states are generated by multiple, heterogeneous cellular and network mechanisms. We particularly analyze the multiple E=I balanced states to show that synaptic conductance levels, average firing rates and average membrane potential levels contribute to the E/I ratio in a distinct manner, thus defining different mechanisms governing E/I balance. These results demonstrate that E/I ratio states are not achieved by varying the excitation (or inhibition) in the network monotonically, but instead can be achieved by different combinations in a non-monotonic way, and result in a diverse range of network dynamics.

Materials and Methods

Neuron Model

Modified Hodgkin-Huxley Model

The model networks in these studies consist of biophysical Hodgkin-Huxley-type (Stiefel K et al., 2009) single compartment neurons with the following equation defining the overall dynamics of neuronal currents for the i-th neuron:

$$C\frac{d{V}_i}{dt}=-g_{Na}{m}_{\infty }^{3}h\left(V_i-V_{Na}\right)-g_{Kdr}{n}^4\left(V_i-V_K\right)-g_L\left(V_i-V_L\right)+I_i^{drive}-I_i^{syn}$$

Each neuron receives an external applied current, $I_i^{drive}$, consisting of both a constant subthreshold current and external noise. To simulate neuronal heterogeneity, each cell receives a random subthreshold current chosen from a Gaussian distribution centered around −0.2 μA/cm² with a deviation of 0.1 μA/cm². External noise is modeled by the delivery of brief (0.05ms), square, 30uA/cm² current pulses, at intervals dictated by a Poisson process (with an average frequency of 40 Hz except Figure 6; we additionally tested effects of different noise frequencies in Fig. S2 in supplemental material). The kinetics of neuronal Na⁺ conductance are governed by the steady state activation function

$$m_{\infty }\left(V\right)={\left\{1+\exp \left[\frac{-V-30.0}{9.5}\right]\right\}}^{-1},$$

and the inactivation gating equation

$$\frac{dh}{dt}=\left(h_{\infty }\left(V\right)-h\right)/{\tau }_h\left(V\right),$$

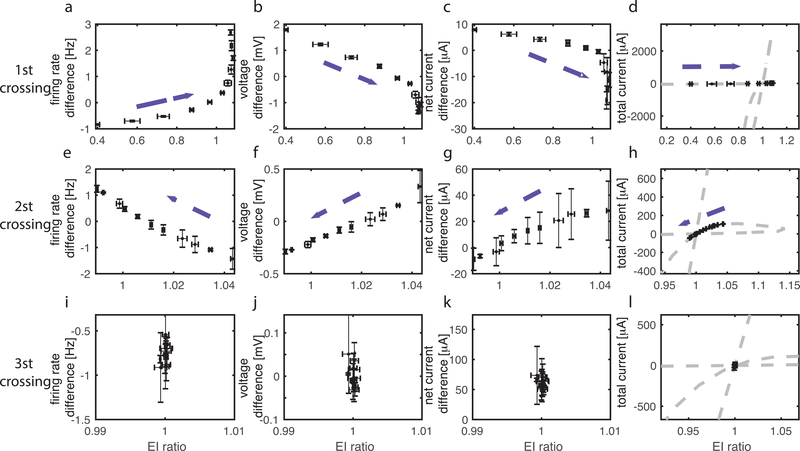
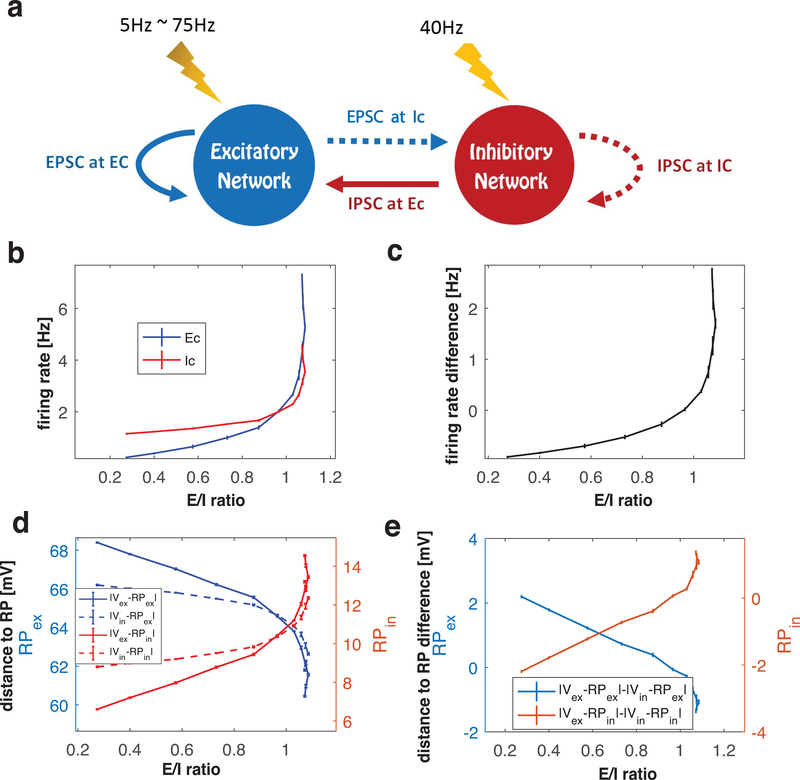
Figure 6.

Comparison of network dynamics at the first (top row), second (middle row) and third (bottom row) crossings of the E=I balanced state. Three different values of w_E are chosen to place the network at the respective E=I balanced. For each value of w_E, the frequency of noise events to the E cells is varied between 5 and 75Hz while the noise event frequency to the I cells is kept at 40Hz (dashed arrows indicate direction of change of the variables indicated with increasing noise frequency). Trajectories of E/I ratio values and: (a, e, i) firing frequency difference between the E and I cells; (b, f, j) absolute value of mean voltage difference between the E and I cells; (c, g, k) “net current difference” (see text for description) between the E and I cells; and (d, h, l) total current (E-I).

with $h_{\infty }\left(V\right)={\left\{1+\exp \left[\frac{V+53.0}{7.0}\right]\right\}}^{-1}$, and ${\tau }_h\left(V\right)=0.37+2.78{\left\{1+\exp \left[\frac{V+40.5}{6.0}\right]\right\}}^{-1}$.

Neuronal K⁺ conductance is gated by the variable n, which evolves in time according to the equation

$$\frac{dn}{dt}=\left(n_{\infty }\left(V\right)-n\right)/{\tau }_n\left(V\right),$$

with $n_{\infty }\left(V\right)={\left\{1+\exp \left[\frac{-V-30.0}{10.0}\right]\right\}}^{-1}$, and ${\tau }_n\left(V\right)=0.37+1.85{\left\{1+\exp \left[\frac{V+27.0}{15.0}\right]\right\}}^{-1}.$ In addition, the leak conductance is given by g_L=0.02mS/cm². Other parameters are set to g_Na=24.0 mS/cm², g_Kdr=3.0 mS/cm², V_Na=55.0mV, V_K=−90.0mV, and V_L=−60.0mV. This model exhibits Type 1 dynamics in terms of phase response curves and current-frequency relation (Smeal et al., 2010). Ignoring (important) mathematical details of cell level excitability properties (Ermentrout, 1996), the type of membrane excitability determines the capacity for neurons in the network to synchronize, with networks consisting of type 2 neurons exhibiting significantly increased capacity to synchronize (Boggard et al., 2009; Smeal et al., 2010). This becomes an additional important consideration when dealing with emergence of E/I balance. Here we concentrate predominantly on cell (population) activation as the variable driving changes in E/I balance, hence the choice of Type 1 excitability.

Network simulation

Networks contain 2000 neurons, 1000 with excitatory (E) synapses and 1000 with inhibitory (I) synapses. While this ratio is not physiological we found that our results do not depend on it as the ratio of cells is offset by the number of connections originating from the given cell type. For the main results, neurons were randomly connected with connectivity probability 3% (i.e. providing on average ~60 connections per cell).

In separate simulations, when investigating the role of network topology on the evolution of E/I balance, we applied the Watts-Strogatz framework to obtain Small World network connectivity (Watts & Strogatz, 1998) to a two-layer network composed of interconnected 1-D rings of excitatory (E) neurons and inhibitory (I) neurons. For this network configuration, each neuron is initially connected to 3% of their nearest neighbors in each layer. Connectivity structure is varied by rewiring each E and I connection to a randomly chosen post-synaptic target neuron with probability given by the rewiring parameter rp_E and rp_I, respectively. In this way we can easily control the network topology with more local excitation or inhibition depending on specific values of rp_E and rp_I.

Synaptic current transmitted from neuron j to neuron i at time t is given by

$$I_{ij}^{syn}=w\text{exp}\left(-\frac{t-t_j}{\tau }\right)\left(V_i-E_{syn}\right)$$

where t_j is the timing of the presynaptic spike in neuron j. The parameter w refers to the synaptic weight, where excitatory (w_E) and inhibitory (w_I) weights are changed separately. The reversal potential E_syn is 0mV for excitatory synaptic current and −75mV for inhibitory synaptic current. Synaptic current decay rate τ is set to be 0.5ms for both synapse types, simulating fast AMPA-like and GABA-A-like synaptic currents. Therefore, the total synaptic current to neuron i at time t is $I_i^{syn}={\sum }_{j\in {\text{Γ}}_i}{I}_{ij}^{syn}$, where ${\text{Γ}}_i$ is the set of pre-synaptic neurons to neuron i.

The dynamics of the network is numerically integrated by a fourth-order Runge-Kutta method with a time step 0.05ms. Total simulation time is 3 seconds, and the results shown are averages over 5 simulations.

Mean Phase Coherence (MPC) measurement

The firing pattern and synchronization of neuron spike trains generated in the network are quantified by the Mean Phase Coherence (MPC) (Mormann, 2004). For the k-th spike in the spike train generated by neuron j denoted as t_j,k, its relative phase to the spike train generated by neuron i is given by ${\theta }_{jik}=2\pi \left(\frac{t_{j,k}-t_{i,k}}{t_{i,k+1}-t_{i,k}}\right)$, where t_i,k is the timestamp of the nearest spike prior to t_j,k in spike train i and t_i+1,k is the nearest spike following t_j,k. The phase coherence of spike train j to spike train i is defined as ${\sigma }_{j,i}=\left|\frac{1}{N}{\sum }_{k=1}^N{e}^{i{\theta }_{jik}}\right|$, where N is the total number of spikes in train j. This pairwise mean phase coherence takes on values between 0 and 1, with 0 indicating completely random firing, and 1 indicating stable phase locking.

Quantification of E/I ratio

At each time step, the total E and I synaptic current in the network is recorded. The mean E (or I) current is calculated by averaging these values over the whole time of the recording. We quantify the E/I ratio of the network as the ratio of mean E to mean I synaptic current, measured during time period T: $\frac{E}{I}=\frac{{\int }_0^T{\sum }_i{\sum }_j{\sum }_k{w}_E\exp \left[\frac{t_{j,k}-t}{\tau }\right]\left(V_i\left(t\right)-E_{syn}^E\right)dt}{{\int }_0^T{\sum }_i{\sum }_j{\sum }_k{w}_I\text{exp}\left[\frac{t_{j,k}-t}{\tau }\right]\left(V_i\left(t\right)-E_{syn}^I\right)dt}$, where k denotes the spike number occurring in the j-th pre-synaptic cell, j sums over all connected E cells in the numerator and over all connected I cells in the denominator, and i sums over all cells in the network.

In addition, we quantify the difference of synaptic currents or total current, calculated by subtracting the mean inhibitory current from the mean excitatory current, as this quantity is more directly connected to neuronal activity. The E=I balanced state is given by E/I ratio equals to 1 and zero total current.

Quantification of tightness of balance

The E/I ratio only quantifies the relative values of the excitatory and inhibitory synaptic currents averaged across the simulation. To further investigate the temporal relationship between the two currents and the tightness of balance, we calculated the cross correlation of the I_E and I_I currents time traces, given by $I_X\left(t\right)={\sum }_i{\sum }_j{\sum }_k{w}_X\exp \left[\frac{t_{j,k}-t}{\tau }\right]\left(V_i\left(t\right)-E_{syn}^X\right)$ where X=E,I and j sums over pre-synaptic neurons of type X and k sums over pre-synaptic spikes occurring before time t. By definition, loose balance corresponds to equal average amounts of excitatory and inhibitory current during a period of time, but without showing significant correlation between the current traces. Tight balance, on the other hand, is characterized by significant temporal correlation where fluctuations in inhibitory current closely follow the fluctuations in excitatory current (Deneve & Machens, 2016; Hennequin et al., 2017).

Results

Here we investigate emergence of global asymptotic balance between excitatory and inhibitory currents in mixed excitatory-inhibitory neural networks. We vary the relative level of excitation and inhibition by changing the structural network parameters (i.e. synaptic weights) or neuronal input levels.

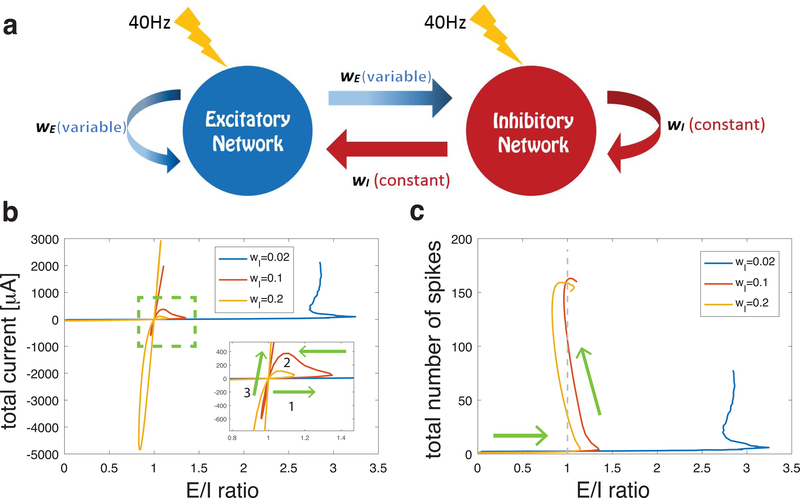
First, we manipulated E/I ratio in a randomly connected network by varying synaptic weights (Fig. 1a) - for a fixed inhibitory synaptic weight w_I, the excitatory synaptic weight w_E was increased from 0 mS/cm² up to about 3 times the value of w_I. For each value of w_E, we allow network dynamics to evolve to an asymptotic stable state, and then compute E/I ratio and total current (i.e. sum of excitatory – inhibitory currents; E – I) during a 3s time window. The curves in Fig. 1b track the relationship between E/I ratio values and total current values as w_E was increased. Each data point on the curve represents one asymptotic E/I ratio for a specific value of w_E. As evident in the figure, the E/I ratio does not monotonically increase as w_E is increased, but can switch between excitation-dominant (E/I ratio > 1 and positive total current) or inhibition-dominant (E/I ratio < 1 and negative total current) regimes and cross the E=I balanced state (E/I ratio = 1 and zero total current) multiple times. Furthermore, the same value of E/I ratio can correspond to different values of total current with different network dynamics and firing patterns. The results show that the E/I level of the network cannot be represented comprehensively by either E/I ratio or total current alone, but requires both measures in a 2-D phase space. We demonstrate that this behavior is robust under a broad range of network parameters such as connectivity density (Fig. 2a), ratio of excitatory cells (Fig. 2b), and various connectivity parameters (Fig. 2c and d). We have also tested the behavior of the network against different noise frequencies (Fig. S3 in supplemental material) and two different neuronal models (Fig. S4 and Fig. S5 in supplemental material) obtaining qualitatively the same results indicating that this pattern of E/I regulation is general and applies to different neural systems. In the following sections, we give detailed characterizations of how network dynamics are governed by firing rates, synaptic weights, and neural membrane potentials, and at the E=I balanced state identify the mechanisms accounting for each balanced state regime by exploring the relationship between each dynamical characteristic and network E/I level. The turning points on the E/I trajectory split the balance states into three different regimes with different governing mechanisms. We study the three regimes by taking the three E=I balance states as examples. Finally, to test the universality of the results against network connectivity structure, we investigate how different network topologies affect the changes in E/I ratio and the occurrence of multiple balanced states as synaptic weights are varied. The consistency of the results demonstrates that our framework applies to a wide range of networks in a generic way.

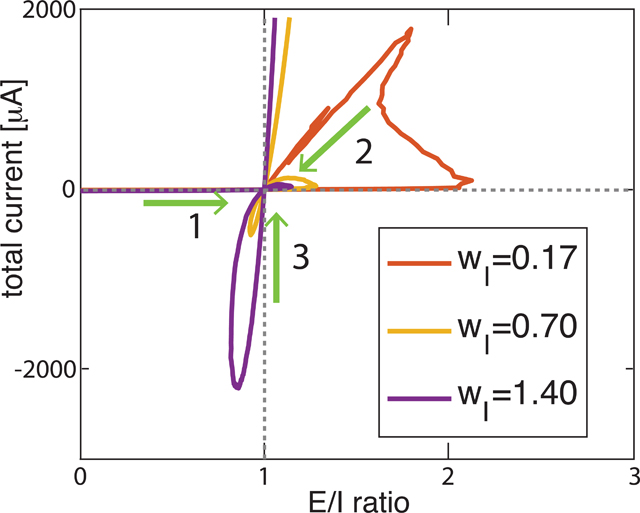
Figure 1.

(a) Schematic of network structure illustrating synaptic interactions from inhibitory cells (red) with fixed synaptic weight w_I and from excitatory cells (blue) with varied synaptic weight w_E. Lightning bolts represent the external noisy stimuli with average frequency 40 Hz applied to each neuron in the network. (b) Relationship between E/I ratio values and E-I current difference (total current) values in asymptotic balance states as excitatory synaptic weight w_E was monotonically increased (arrows show direction of relative change with increasing w_E). Four trajectory curves correspond to 4 values of inhibitory synaptic weight w_I (given in legend in mS/cm2). Inset in panel b shows a close-up of the asymptotic E=I balanced state (i.e. when E/I ratio is near 1 and total current is near 0) with two trajectories (violet and yellow) that crossed this balanced state 3 times. (c) Trajectory curves of E/I ratio values and network spiking activity values (in Hz computed during the 1.5s simulation in the asymptotic balance state), as excitatory synaptic weight w_E was systematically increased for the 4 values of w_I (arrows show direction of change with increasing w_E). For two trajectories (violet and yellow) although the E/I ratio oscillated above and below 1, spiking rates continued to increase as w_E was increased.

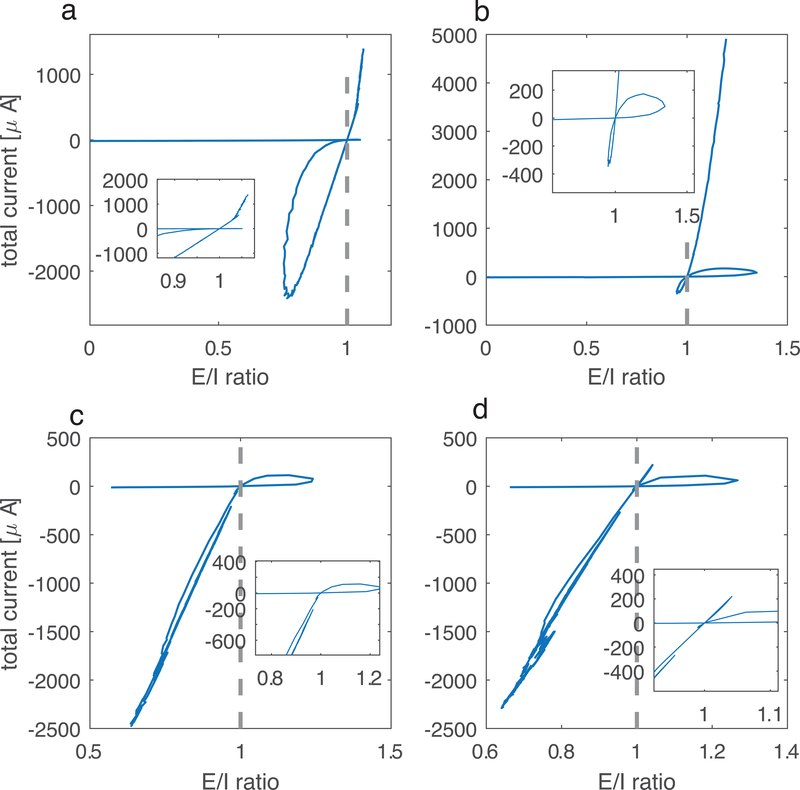
Figure 2.

Trajectories of E/I ratio and total current values for networks with additional parameter changes addressing aspects of biological realism display the same qualitative behavior. Comparing with Figure 1b, the value of one parameter is changed in each panel while other parameters stay the same as original simulation. Inhibitory weight w_I is adjusted accordingly to show the appropriate E/I ratio range. a) random network with increased connectivity density (20% vs 3%, w_I=0.2mS/cm²); b) 80% excitatory cells and 20% inhibitory cells (w_I=2.8mS/cm²); c) different values for the four types of synapses, w_EE is varied, w_EI = 0.35mS/cm², w_IE = 0.5mS/ cm², w_II = 0.7 mS/ cm²; d) same as panel e) but the values for w_EI and w_IE are reversed: w_EI = 0.5mS/ cm², w_IE = 0.35mS/ cm², w_II = 0.7 mS/cm².

Network E/I trajectory crosses the E=I balanced states up to three times in response to varying synaptic weights.

We first investigated how the E/I ratio evolves as a function of excitatory coupling for networks having different levels of overall coupling strength. The trajectory curves in Fig. 1b show the relationship between E/I ratio and total current values in asymptotic balance states as w_E was increased for 3 different values of w_I; we adjusted w_E accordingly to obtain the same E/I ratios. For each w_I value, initially, when w_E = 0 mS/cm², the E/I ratio was 0 and the total current fluctuated near zero. As w_E increased, E/I ratios increased but current differences remained small as the network passed through an E=I asymptotic balanced state. For each value of w_I, the E=I balanced state was reached for different values of w_E. Fig. 1c shows how total spike numbers in the network (during the 3s simulation in the asymptotic balance state) varied with E/I ratio as w_E was systematically increased. When w_E ~ 0 mS/cm² (and network activity was driven only by noise), network activity remained low in all networks as they crossed the E=I balanced state for the first time.

For networks with weak inhibitory connectivity (blue and red curves), as w_E increased and E/I ratios increased significantly past the E=I balance point, excitatory synaptic current rapidly overtook the networks’ dynamics and increased network firing rates. In the network with weakest inhibition (blue curve), E/I ratio saturated around 3, and the network remained in an excitation-dominant regime (positive E/I ratio). For networks with stronger inhibitory connectivity (red and yellow curves), two loops emerge in the trajectory curves: after crossing the E=I balanced state for the first time (inset, arrow 1), as w_E increased further, the trajectories turned around (arrow 2) and the networks crossed the E=I balanced state for a second time. As w_E continued to increase, the networks entered an inhibition-dominant regime (E/I ratio < 1, negative total current). However, upon further increases in w_E, E/I ratios increased, leading to a third crossing of the E=I balanced state. Network firing rates continued to increase during these subsequent crossings of the E=I balanced state. As shown in Fig. 1c, the networks generally showed higher spike rates with higher w_E, while the E/I ratio oscillated around 1. For the highest values of w_E, the networks remained in the excitation dominant regime with increasing total current and network firing.

The surprising finding that E/I ratio repeatedly returns to 1 as excitatory current increases, suggests, somewhat counterintuitively, that higher excitatory coupling may actually result in lower E/I ratio and total current in the network - increasing excitatory current can drive increases in inhibition, leading to non-monotonic changes in E/I ratio. A similarly counterintuitive effect was documented by (Tsodyks et al., 1997) where increases in inhibitory inputs to a neuronal network lead higher overall firing-rates (as observed here, Fig. 1b). For networks with strong inhibitory connectivity, we observe the formation of two loops in the trajectory curves, one in the excitation-dominant regime (i.e., E/I ratio is greater than one) and one in an inhibition-dominant regime (i.e., E/I ratio is below one). This shows that states exhibiting a particular E/I balance are not unique, but correspond to a set of network states with differential dynamical properties.

To validate the generality of the non-monotonic E/I trajectories, we also analyzed networks with different parameters, to consider various possible biological realisms (Fig. 2). Compared to the trajectory in Fig. 1b, the qualitative pattern stays the same for all the new parameter combinations, connectivity density, the excitatory to inhibitory cell number ratio, asymmetry in various connection strengths, and finally different neuronal formalisms. The only additional modification made in these simulations was to adjust the value of w_I accordingly to maintain trajectories in the appropriate range. First, as the sparsity of connectivity of the brain networks can vary from region to region, we investigated whether the effect averages out with higher network connectivity (Fig. 2a).

As it has been measured that the percentage of excitatory cells in the mammalian cortex is around 80% (Braitenberg & Schuz, 1991), we modified the cell ratio accordingly - this case is shown in Fig. 2b.

In the original simulations (Fig. 1), we set w_EE = w_EI = w_E, w_II = w_IE = w_I. As there is no evidence demonstrating that the excitatory (or inhibitory) synaptic weights are the same for synapses targeting excitatory and inhibitory populations, we applied different values for w_EE, w_EI, w_IE, w_II (Fig. 2c and 2d) and tested cases where w_EI>w_IE and w_EI<w_IE.

In supplemental material we further investigate universality of the observed result as we change frequency of the applied noise to every neuron (Fig. S3) and, finally, to validate that results are not due to the cellular properties of a specific neuron model, we simulated networks of Wang-Buzaki neurons (Wang & Buzsáki, 1996) in Fig. S4, and integrate-and fire neurons (Fig. S5).

It is evident that all the E/I trajectories under different parameter values display the same qualitative shape, indicating that the dynamic properties and the mechanisms in our framework are robust and are not constrained by some specific parameters of our models. Therefore, in the following discussion, we consider the network/cell parameters described in the yellow curve of Fig. 1b to illustrate results and analyze mechanisms.

Network firing patterns are different in the three E/I balance regimes.

We next investigated the differences in network dynamics at the E = I balanced states. As we will show below, the three different balance regimes, separated by the turning points of the two loops of the trajectory curves, are governed by qualitatively distinct mechanisms.

To better understand the differences in dynamics between E/I balanced states, we focused on a network with moderate inhibition (w_I = 0.2 mS/cm², yellow curve in Fig. 1b, c) that showed three crossings through E/I =1. We chose the three values of w_E at which the network resides at (or near) the E=I balance point (Fig. 3a–c). Fig. 3 shows network firing raster plots (second row), distributions of pairwise mean phase coherences (MPC, third row), and pairwise relative phases (fourth row) between all synaptically connected neurons near the three E=I states.

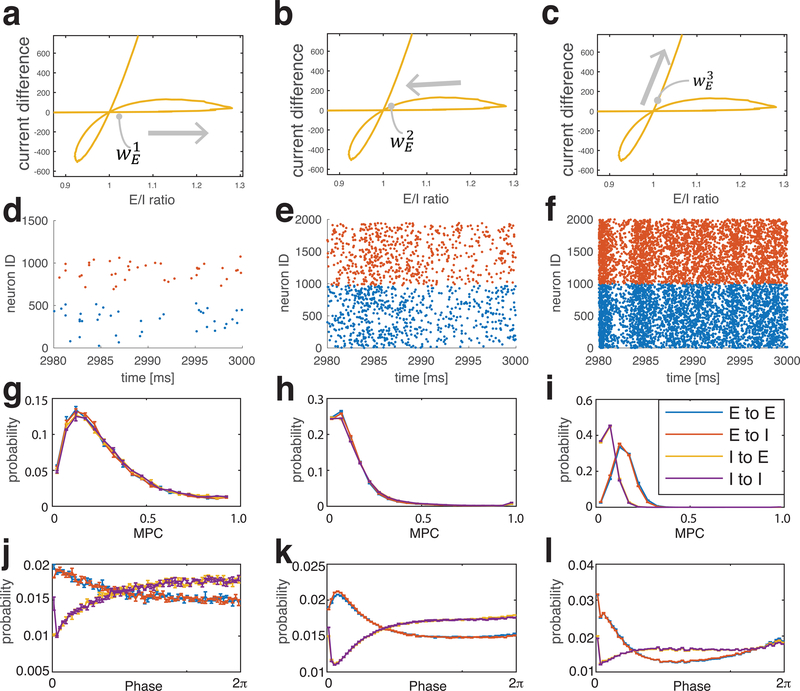
Figure 3.

Firing patterns near three E=I balanced states for a network with wI = 0.2 mS/cm2. The excitatory weight, w_E is chosen near the balanced state as marked on panels (a-c). (d-f) spike raster plot; (g-i) distribution of pairwise Mean Phase Coherences (MPCs) and (j-l) distribution of pairwise relative phases of neuronal firing computed near each balanced state. Mean Phase Coherences (MPC) (g-i) and relative phases (j-l) are computed only for pairs of synaptically connected neurons. The pairs are separated into four groups depending on the synaptic connections between them: excitatory to excitatory (E-E), excitatory to inhibitory (E-I), inhibitory to excitatory (I-E), inhibitory to inhibitory (I-I).

For the first crossing of the E=I balanced state (left column), the system displayed random, sparse firing (Fig. 3d), driven principally by external noisy stimuli (see calculation distributions of coefficient of variation of interspike intervals for every neuron and the distributions of mean ISI themselves, Fig. 1S in supplemental data). The MPC distributions almost overlapped (Fig. 3g) for the four types of synaptically-connected cells (excitatory to excitatory (E-E), excitatory to inhibitory (E-I), inhibitory to excitatory (I-E), inhibitory to inhibitory (I-I)), and reflect no significant phase locking between the cell populations. The distribution of relative phases (Fig. 3j) for excitatory (E) pre-synaptic cells peaked at low values of phase, while it was at its minimum for inhibitory pre-synaptic cells at these phases. This is intuitive in that E neurons tend to promote firing in post-synaptic cells, leading to small relative phases, while I neurons tend to suppress post-synaptic cell firing, thus inhibiting post-synaptic firing at small phases. These probabilities, however decay quickly (exponentially) to base value.

Network firing activity was greater at the second crossing of the E=I balanced state (Fig. 3e, also see Fig. S1 in supplemental material), but the firing pattern remained largely random. The distributions of pairwise MPCs (Fig. 3h) started to separate for the different types of synaptic connections between cells. Separation of the E-E and E-I pair groups (blue and red curves) to larger MPC values compared to the I-E and I-I pair groups (yellow and violet curves) means that neurons fired somewhat more coherently when pre-synaptic neurons were excitatory. The differences in the profiles of the pairwise phase distributions (Fig. 3k) between pairs with E pre-synaptic neurons (blue and red curves) and pairs with I pre-synaptic neurons (yellow and violet curves) was maintained and solidified compared to the first crossing, reflecting the formation of more regular, causal firing patterns.

At the third crossing, network firing activity was high and some degree of synchronization started to emerge (Fig. 3f and Fig. S1 in supplemental material). The significant separation in MPC distributions (Fig. 3i) between pair groups with E pre-synaptic cells (blue and red curves) compared to I pre-synaptic cells (yellow and violet curves) points to higher coherence with E pre-synaptic neurons. Relative phases (Fig. 3l) when pre-synaptic E cells are shifted towards 0 and 2π, indicating some degree of synchronization in the network. The larger peak in the distribution at 0 compared to 2π reflects a causal relationship in firing without synchronization. The phases for I pre-synaptic neurons, on the other hand, show a similar dip for low phase values as observed near the other balanced states without any significant change for higher phase values.

In summary, a significant separation in the distributions for both pairwise MPC and relative phases for E pre-synaptic cells and I pre-synaptic cells appeared gradually from the first crossing (Fig. 3g, j) to the third crossing (Fig. 3i, l), indicating a transition from a sparse and random firing pattern to a more organized and causal firing pattern. While the trend appears at the second crossing, it is more distinct at the third crossing where relative phases are clustered around 0 when pre-synaptic cells are excitatory, indicating causal initiation of post-synaptic firing. The rightward shift in MPC values from the first to the third crossing is further evidence for an increase in the coherence of the firing pattern.

Detailed dynamics at the E=I balanced states: first crossing.

Next, to understand the cellular and network mechanisms underlying regulation of network dynamics at E=I balanced states, we separately considered the factors that influence the E/I ratio on both the cellular and network level. Here, conceptually, we can consider total synaptic current as consisting of the product of three factors: 1) the number of synaptic events (which is dictated by the overall firing activity of E or I cells), 2) the strength of synaptic events (governed by synaptic weight parameters), and 3) the driving force of synaptic current (dictated by the difference between the mean membrane voltage of the post-synaptic cells and the current’s reversal potential). Thus, we can represent the E/I ratio by the following expression:

$$\frac{E}{I}=\frac{total{I}_E^{syn}}{total{I}_I^{syn}}\cong \frac{excitatorypopulationfrequency}{inhibitorypopulationfrequency}\times \frac{w_E}{w_I}\times \frac{{\sum }_i{\overline{V}}_i-E_E^{syn}}{{\sum }_i{\overline{V}}_i-E_I^{syn}},$$

where ${\overline{V}}_i$ is mean membrane potential of the i-th cell and i sums over all cells in the network. In our results in Fig. 1 and Fig. 3, we varied synaptic weights w_E and w_I, which induced changes in the other factors, altered the level of firing activity, and changed membrane potential. In an attempt to disentangle the interactions among these factors, we implemented a different method to manipulate E/I ratio in the network. To do this, w_E and w_I are fixed at specific values near an E=I balanced state, and E/I ratio is varied by changing the frequency of external stimuli (random, pulse like events) to E cells in the network. The frequency of these events was varied between 5 and 75 Hz, while noise event frequency to I cells was maintained at 40Hz (Fig. 4a). Since here the synaptic weights are fixed, crossing through the E=I balanced state is caused by changes in the other two factors (i.e. spike frequency and mean voltage difference between cell membrane potential and reversal potential in above equation). Therefore, we monitored mean synaptic currents, firing rates, and the mean membrane potential of cells in the network to further characterize the three balanced states displayed in the network with moderate inhibition (w_I = 0.2 mS/cm²) from Fig. 3. We start with a detailed analysis of the first crossing of the E=I balanced state.

Figure 4.

Analysis of network factors contributing to E/I balance at the first crossing of the E=I balanced state. (a) Schematic of alternate method to change E/I ratio. Synaptic weights are fixed near the E=I balanced state and frequency of noisy external stimuli to the excitatory (E) cells is varied (see text for details). (b) Relationship between E/I ratio values and mean firing rates of the excitatory (E, blue curve) and inhibitory (I, red curve) cell populations as noise event frequency to the E cells is increased. (c) Difference between blue and red curves in (b). (d) Relationship between E/I ratio values and the difference between the mean membrane potentials of the excitatory (${\overline{\mathit{V}}}_{\mathit{E}}$) and inhibitory (${\overline{\mathit{V}}}_{\mathit{I}}$) cell populations, and the reversal potentials of the excitatory (${\mathit{E}}_{\mathit{E}}^{\mathit{syn}}$) and inhibitory (${\mathit{E}}_{\mathit{I}}^{\mathit{syn}}$) synaptic currents as noisy event frequency to the E cells is increased. Blue (red) curves show distances from ${\mathit{E}}_{\mathit{E}}^{\mathit{syn}}({\mathit{E}}_{\mathit{I}}^{\mathit{syn}})$. (e) Difference of distance curves shown in (d).

We set w_E to a value such that the network sits just below the first E=I balanced state. Fig. 4b shows the relationship between the E/I ratio and the mean firing rates of the E and I cells as the noise event frequency to the E cells was increased from 5 to 75 Hz. At the lowest noise frequency, E/I ratio was low (~ 0.2) and E cells (blue curve) fired less than I cells (red curve). As the noise frequency was increased, E/I ratio increased, with the firing rate of E cells (blue curve) increasing more than that of I cells (red curve), which were also increased as a result of greater excitatory synaptic activity in the network. As the E=I balanced state was approached (i.e. with increasing noise frequency), E cell firing rates surpassed I cell firing rates and the difference in firing rates (Fig. 4c) between E and I cells moved from negative values to positive values.

To track the efficacy of the synaptic currents due to increased firing in the network, we computed the mean membrane potential of E and I cell populations, ${\overline{V}}_E$ and ${\overline{V}}_I$, respectively during simulations with increasing noise frequency. Fig. 4d shows the difference between mean membrane potentials and the reversal potentials (i.e. distance to RP) of E (blue curves, left vertical axis) and I (red curves, right vertical axis) synaptic currents, $E_E^{syn}$ and $E_I^{syn}$, respectively. Due to increasing firing activity in the network, mean membrane potentials of both E and I cell populations were depolarized, resulting in their voltage values closer to $E_E^{syn}$ and farther from $E_I^{syn}$ for both populations. The E cell population depolarized at a higher rate (as a function of increasing noise frequency) than the I cell population with increasing noise frequency (as shown in Fig. 4d and e). The difference between mean voltages and $E_E^{syn}$, $\left|{\overline{V}}_E-E_E^{syn}\right|-\left|{\overline{V}}_I-E_E^{syn}\right|$, transitioned from positive values to negative values as noise frequency increased (blue curve). The difference between mean voltages and $E_I^{syn}$ showed opposite behavior (red curve).

Based on these data, we conclude that the first balanced state is achieved in the network by increased firing rates of the excitatory cell population relative to the inhibitory cell population. However, this difference in firing rates is partially compensated by a decrease in the efficacy of excitatory synaptic currents in the network, due to decreased voltage difference between membrane potential and reversal potential. The results shown in Fig. 4d suggest that EPSCs and IPSCs are differentially distributed to E and I cell populations. We next took a closer look at this.

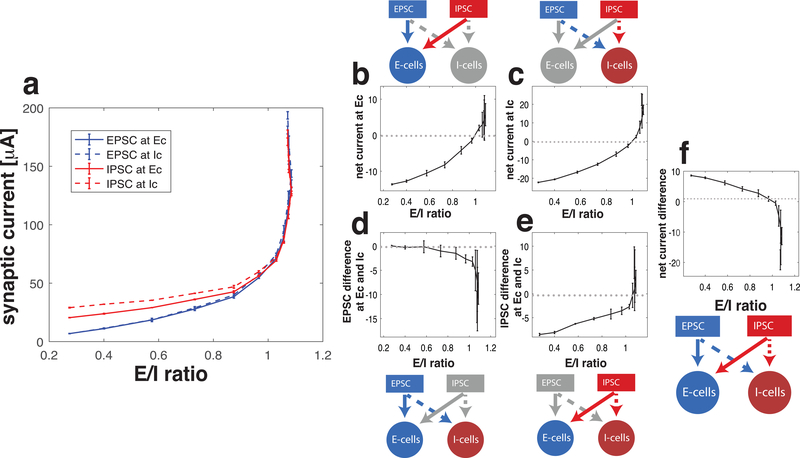
In the E=I balanced state, mean total EPSC and mean total IPSC are equal in the network. However, excitatory and inhibitory synaptic currents are not necessarily uniformly distributed among E and I cell populations. Here we analyze the relative magnitudes of the four types of post-synaptic currents: excitatory current to E cells (EPSC at E cells), excitatory current to I cells (EPSC at I cells), inhibitory currents to E cells (IPSC at E cells), inhibitory currents to I cells (IPSC at I cells), where “EPSC” and “IPSC” refer to mean total synaptic current arriving at the post-synaptic population (Fig 5a). As the noise frequency in E cells was increased and the E/I ratio passed through the E=I balanced state, all four types of synaptic current increased. At the E=I balanced state, the difference between total EPSC and total IPSC (values of blue curves – values of red curves when E/I ratio is 1) is zero. To identify the relative distribution of synaptic currents in the network, we next considered what we call the “net current difference” which we defined in two different ways, as follows.

Figure 5.

Distribution of synaptic current in the network at the first crossing of the balanced state. (a) Trajectories of the four different types of mean total synaptic currents, Excitatory Post Synaptic Current (EPSC) at excitatory cells (blue solid), EPSC at inhibitory cells (blue dash), Inhibitory Post Synaptic Current (IPSC) at excitatory cells (red solid) and IPSC at inhibitory cells (red dash) as E/I ratio is varied by increasing the frequency of noise events to the excitatory cell population. The relative distribution of excitatory and inhibitory currents to the excitatory and inhibitory cell populations is displayed in two different ways (b and c, or d and e). The color and pattern of the arrows in the diagrams are consistent with the curves in panel a. (b) Net synaptic current received by E cells, which is the difference of EPSC and IPSC at E cells (difference between blue and red solid curves in panel a). (c) Net synaptic current received by I cells, which is difference between EPSC and IPSC at I cells (difference between blue and red dashed curves in panel a). (d) Difference of EPSC received by the E cells and the I cells (difference between blue solid and blue dashed curves in panel a). (e) Difference of IPSC received by E cells and I cells (difference between red solid and red dashed curves in panel a). (f) Difference of the net currents shown in (b) and (c) indicating which population received more net current, or equivalently difference of currents shown in (d) and (e) indicating which type of current is more distributed in E cells compared to I cells.

First, we computed the net synaptic current received by E cells and I cells separately (Fig. 5b, c). To do this we separately calculated the net synaptic current received by E-cells as (EPSC at E cells) – (IPSC at E cells) (Fig. 5b), and the net synaptic current received by I-cells as (EPSC at I cells) – (IPSC at I cells) (Fig. 5c). As the noise frequency in excitatory cells increased and E/I ratio crossed through the E=I balanced state, net synaptic current to both cell populations increased from negative values to positive values reflecting a greater increase in the excitatory synaptic current received by both populations compared to inhibitory synaptic current. We then compute a “net current difference” by subtracting the net synaptic current curves in Fig. 5b and 5c (Fig. 5f). This net current difference shows that the synaptic currents to the inhibitory cell population dominate at this crossing of the E=I balanced state: below the E=I balanced state, IPSC at I cells is greater than IPSC at E cells. As the E=I balanced state is crossed, EPSC at I cells is greater than EPSC at E cells.

Second, we compared the relative magnitudes of EPSCs and IPSCs received by the two cell populations (Fig. 5d, e). This alternate way takes the point of view of the synaptic current in the network. We computed the difference between EPSC received by E cells and I cells: (EPSC at E cells) – (EPSC at I cells) (Fig. 5d), and the difference between the amount of inhibitory synaptic current received by E and I cells (IPSC at E cells) – (IPSC at I cells) (Fig. 5e). Below the E=I balanced state, the I cells receive more inhibitory current while the excitatory current is roughly evenly distributed, but as the noise frequency to E cells increases, EPSC at I cells exceeds that at E cells. The difference of the curves in these two panels yields the “net current difference” in Fig. 5f.

Thus, a characteristic of this E=I balanced state is that increased activity of E cells drives the network into an excitation-dominant regime, in which E cells increase their firing rates relative to I cells. While the efficacy of EPSC in the network decreases due to reductions in driving force (i.e., due to overall depolarized membrane potentials), as the E=I balanced state is crossed, EPSC dominates over IPSC (Fig. 5b and c). At the E=I balanced state, I cells receive more EPSC than E cells (Fig. 5d) and beyond the E=I balanced state, in the excitation-dominant regime, E cells receive more IPSC than I cells (Fig. 5e).

Detailed dynamics at the E=I balanced states: comparison of dynamics at the three balanced states

We next extended this analysis to compare network dynamics at all three crossings of the E=I balanced states (Fig. 6). Near each, we chose a value of w_E and increased E cells’ noise frequency to vary the E/I ratio. For each w_E value, we examined the trajectory of the E/I ratio and the difference in firing rates between E and I cells (first column, similar to Fig. 4c), and the difference between the absolute value of the mean membrane potentials of E and I cells (second column, similar to Fig. 4e). This latter value directly affects the relative voltage distance of the two cell populations to EPSC and IPSC reversal potentials. We also assessed the trajectory of the E/I ratio vs. net current difference (as in Fig. 5f; third column; arrows indicate the direction of change as noise frequency increases) and vs. total current (E-I) in the network (as in Fig. 1a; fourth column).

Additionally, in Fig. S3 of supplemental data we show that changes due to increasing noise frequency follow the same path as those due to increasing w_E (blue, black and yellow). At the first crossing (top row), trajectories for different w_E values almost overlap, suggesting that the state of the network is determined by the relative frequency of cell population firing. At the 2nd crossing (middle row), trajectories for different synaptic weights occupy different intervals of E/I ratio values, but all show the same trends as noise frequency increases. This suggests that noise and internal synaptic interactions together control network dynamics. Finally, at the 3^rd crossing (bottom row), synaptic weight has a much greater effect on E/I ratio as trajectories remain essentially at fixed E/I values as noise frequency increases. In this case, external drive does not strongly affect network dynamics due to strong synaptic interactions (caused by high w_E values) in this regime.

As, at each of the three crossings of the E=I balanced state, the trajectories for different w_E values (Fig. S3) are similar with increasing noise frequency, indicating a qualitative consistency of effects, we focused on properties of one trajectory (black) for each crossing (Fig 6). The trajectory through the first crossing of the E=I balanced state (Fig. 6, top row) replicates the results shown in Fig. 4c, 4e (blue curve), and 5f, respectively. Near the second crossing (middle row), initially the frequency of I cells is higher than that of E cells. As E cells’ noise frequency increases, their firing frequency increases relative to that of I cells, resulting in smaller firing rate differences (Fig. 6e). This results in depolarization of both cell types in the network, evidenced by smaller differences in mean voltage between E and I populations (Fig. 6f). Depolarization causes the EPSC driving force to decrease and consequently, the IPSC driving force to increase, overall decreasing EPSCs and increasing IPSCs. This change is not uniform, however, as E cells depolarize more than I cells (i.e. $\left|{\overline{V}}_E\right|-\left|{\overline{V}}_I\right|$ becomes negative). These two effects result in overall decrease of net current difference (Fig. 6g), due to a) increased depolarization of E cells vs. I cells, and b) the increase in inhibitory current in the network resulting from depolarization of both cell types (Fig. 6h). Hence, at the second crossing of the E=I balanced state, either increased spiking of E cells or increases in excitatory synaptic weight act to push total network inhibition to be dominant. As we show below, membrane potential depolarization means that decreased EPSC driving force and increased IPSC driving force may be responsible for an overall decrease in EPSC efficacy in the network at the crossing of this balanced state.

At the third crossing of the E=I balanced state (third row), increasing noise frequency to E cells has smaller effects on E/I ratio than changes in w_E (see also blue to black to yellow data points in Fig. S3). At this balanced state, E cells and I cells have similar firing rates (Fig. 6i) with I cells only slightly more depolarized than E cells (Fig. 6j). However, the w_E/w_I ratio skews the current significantly towards EPSC domination within the network. Moreover, as shown below (Fig. 8), greater synchrony of firing patterns emerges in this state, driving the network toward balanced firing rates. Thus, similar to the first crossing of the E=I balanced state, increases in excitatory synaptic activity (due to weight increases) act to push the network from the inhibition dominant regime into the excitation dominant regime.

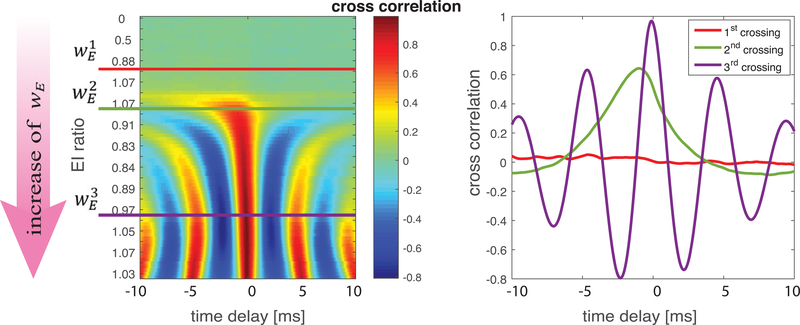
Figure 8.

Temporal relationship of total excitatory and inhibitory synaptic currents. Cross-correlation (a, color) of the time traces of the total excitatory and inhibitory synaptic currents as w_E is varied (direction of arrow) driving the network across the three balanced states indicated by $w_E^1$ (red curve), $w_E^2$ (green curves) and $w_E^3$ (violet curves). b) Cross correlation traces between the E and I currents at the three crossings of the balanced state. Negative delay indicates excitation leads inhibition.

Detailed dynamics at the E=I balanced states: Competition between the firing rate ratio and the depolarization ratio.

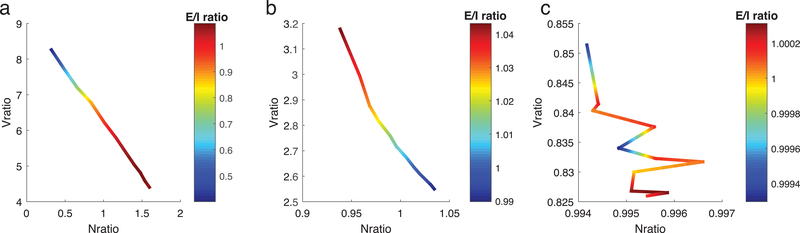
The primary distinction between the first and second crossings of the E=I balanced state is illustrated by relating the changes in total current (E-I, Fig. 6, last column) with changes in firing rate differences (first column) and membrane potential differences (second column) between E and I populations. At both crossings, increases in firing rate difference occur with decreases of voltage difference. However, at the first crossing total current increases mirroring the change in firing rate difference; in contrast, at the second crossing total current decreases in response to the change in voltage difference. This suggests that E/I ratio actually depends on competition between two opposing constraints: the ratio of firing rates of E and I cells (which we refer to as Nratio), and the ratio of driving forces for EPSCs and IPSCs (which we refer to as Vratio). Fig. 7 displays the trajectories of Nratio (x-axis) and Vratio (y-axis) for the three crossings, with E/I ratio values indicated by color. Here, as in Fig. 6, w_E is constant and trajectories show changes in response to systematically increasing the frequency of noise events to E cells.

Figure 7.

The contribution of changes in E and I firing rates (Nratio) and excitatory and inhibitory synaptic current driving forces (Vratio) to changes in E/I ratio. Values for w_E are fixed near each balanced state (a: first crossing, b: second crossing, c: third crossing) and frequency of noise events to E cells is increased to vary E/I ratio (color of curves). Curves show relationships between values of the ratio of E to I cell average firing rates (Nratio, x-axis) and values of the ratio of differences between average membrane potentials and reversal potentials of the excitatory and inhibitory synaptic currents (Vratio, y-axis) at each value of E/I ratio. At the first crossing (a), increasing E/I ratio mirrors increasing Nratio while at the 2^nd crossing it mirrors increasing Vratio.

At the first crossing (Fig. 7a), E/I ratio increases mirror Nratio increases. At the same time, Vratio decreases, meaning that the change in E/I ratio is driven by Nratio in this regime. However, this relationship is reversed at the second crossing (Fig. 7b), with increasing E/I ratio mirroring increasing Vratio (while Nratio decreases). On the other hand, at the third crossing (Fig. 7c) there is no clear relationship between E/I ratio and either Nratio or Vratio. In this case E/I ratio is minimally affected by external noise frequency, and oscillates near 1 (note the change in color scale). Taken together, these findings show that the change of E/I ratio in the network can result from different mechanisms, depending on the relative change of firing rates and depolarization levels of E and I populations.

Detailed dynamics at the E=I balanced states: Quantification of tightness of E/I balance.

The E/I ratio measures the relative amounts of total EPSC and IPSC in the network across a period of time, but it does not indicate the temporal relationship between variations in these currents. To analyze differences in the temporal occurrence of EPSC and IPSC at the three balanced states, we calculated the cross-correlation of the time traces of total EPSC and total IPSC for a range of w_E values in a network with moderate inhibition (w_I = 0.2 mS/cm²) (Fig. 8). As w_E increased driving the network across all three balanced states (Fig. 8a), stronger correlations and multiple peaks emerged, and the temporal delay between EPSC and subsequent IPSC decreased.

Cross-correlations at the three balanced states are shown in Fig. 8b. The first balanced state (red curve) displays a loose temporal relationship (corresponding to “loose E/I balance”) (Deneve & Machens, 2016), with no significant correlations between the two currents over time. In contrast, the second balanced state (green curve) shows “tight E/I balance” with a single peak in the correlation offset at a negative value indicating EPSC leading IPSC on a millisecond timescale. The third balanced state (violet curve) shows even tighter correlation, with a shorter delay and stronger correlation between the currents. Additionally, the appearance of multiple peaks in the correlation indicate that global oscillatory dynamics have emerged in the network.

Network topology affects the E/I ratio trajectory when changing synaptic weights.

Finally, to test the robustness of these different E/I balanced states, we varied the connectivity structure of the network (Fig. 9). We constructed a two-layer network (one E cell layer and one I cell layer), with synaptic connections both between and within layers. We started with nearest neighbor connections (2.5% connectivity density), then systematically varied inter-layer and intra-layer connectivity structure by defining synapse rewiring probabilities (rp_E and rp_I) which dictate the degree in randomness in re-wiring of E and I synapses, respectively. In Fig. 9 we consider nine different connectivity combinations: local excitation (rp_E=0, first column), small-world excitation (rp_E=0.2, middle column) and random excitation (rp_E=1, last column) with local inhibition (rp_I=0, blue curves), small-world inhibition (rp_I=0.2, red curves) and random inhibition (rp_I=1, yellow curves).

Figure 9.

Trajectory curves of E/I ratio values and total current (E-I) values (top row), and network firing rate values (bottom row) as excitatory synaptic strength increases for networks with different connectivity structures. Networks are composed of one layer of excitatory cells and one layer of inhibitory cells, which are connected within and between layers with 2.5% connectivity probability. The synapse rewiring parameter for excitatory (rp_E) and inhibitory (rp_I) synapses are changed separately, resulting in different network topologies. Excitatory synaptic strength, w_E, increases from 0 while inhibitory synaptic strength w_I =0.7mS/cm2 stays constant. In all panels, different curves show results for different inhibitory connectivity structures (blue: local inhibition, rp_I=0; red: small world inhibition, rp_I=0.2; yellow: global inhibition, rp_I=1). Columns show results for different excitatory connectivity structures: (a, d) local excitation (rpE=0); (b, e) small world excitation (rp_E=0.2); (c, f) global excitation (rp_E=1).

As in Fig. 1, as w_E increases (with moderate inhibition w_I = 0.2 mS/cm²), the trajectories of E/I ratio values (x-axis) and total current (E-I) values (top row, y-axis) cross through the E=I balanced state up to three times as network firing rates (bottom row, y-axis) show non-monotonic changes. When E connections are local (first column), the connectivity pattern of I synapses can have a large effect. For local or small-world inhibitory synaptic connectivity (blue and red curves), the E/I ratio trajectories are similar as with completely random connectivity - with three crossings of the E=I balanced state as w_E is increased. However, with random inhibitory synaptic connectivity (yellow curves), resulting in global inhibition in the network, only two crossings of the E=I balanced state occurred. Furthermore, the network remained in the inhibition-dominant regime for high w_E. This is due to the fact that EPSCs excite the I cell population only locally, while the global IPSCs can suppress firing effectively, evidenced by the flat portion of the firing rate trajectory (Fig. 9d, yellow curve). When E synapses have small-world (middle column) and random (right column) connectivity structure, three crossings of the E=I balanced state occur regardless of the inhibitory synaptic structure. Here the global component of excitation, generated by random excitatory connections, offsets the effects of inhibitory synaptic connectivity. For random excitatory connectivity (c), the trajectory curves almost overlap for all inhibitory connectivity structures, while with small-world excitatory connectivity (b), the trajectory curves are modulated by inhibitory connectivity structure.

Discussion

Here we provide a schematic picture of the cellular and network mechanisms that determine changes of E/I ratio in a biophysical neural network model. Our results show that neurons and networks have a homeostatic capability to regulate the balance for excitation and inhibition via competitive contributions between firing rates and the voltage difference between membrane potential and the respective reversal potentials across a relatively wide range of network excitation levels. This homeostatic effect is particularly evident at the second E=I balanced state, where increased activity of E cells invokes increased IPSC in the network. On the other hand, we show that the dynamical mechanisms regulating a network toward balanced excitation and inhibition can change depending on the relative amount of excitation in the network, placing the system in diverse dynamical regimes. Specifically, at the first crossing of the E=I balanced state (when excitation in the network is low), firing rates of E cells drive changes in the E/I ratio, while at the second crossing (with higher excitation), E/I ratio is influenced by the efficacy of postsynaptic currents, which is determined by the voltage difference between membrane potential and the respective reversal potentials. Thus, our present data suggest that there is no universal E=I balanced state as defined by a single mechanism. Rather, our results show that the dynamics towards a balanced state is driven by the interaction of both network activity and cellular depolarization levels. Further, our results show that experimental measurement of single specific cellular or network properties, such as ratios of conductances (Monier et al., 2008) or PSC conductances alone (Wehr & Zador, 2003; Xue et al., 2014), may provide inadequate information about the true E/I ratio of the system. This is because the true E/I ratio results from combined (and interdependent) effects of firing rates, membrane depolarization, and synaptic weights.

Tightness of temporal correlation between excitation and inhibition (Fig. 8) is another important and experimentally measurable dynamical property providing information about the system’s activity regime. In our model, only the first crossing of the E=I balance point has low correlation between excitation and inhibition (i.e. “loose balance”) while the other two are tightly correlated (i.e. “tight balance”). This observation may provide an explanation for the emergence of the two types of balance. Loose balance emerges in a relatively low coupling regime and the variation in the relative strength of excitation and inhibition is driven predominantly by external input. This, in turn, results in a similar average level of E and I currents but no correlation. On the other hand, tight balance is due to recurrent interaction between excitatory and inhibitory synapses, which results in significant temporal correlation between the two currents. As depicted in Fig. 8, as excitatory synaptic weight w_E increased, the correlation between the two currents developed and the temporal delay between them decreased. Here the specific dynamical regime in which the network resides may be especially important, as it has been postulated that balanced excitatory transients may play an important role in amplification of neural activity patterns (Hennequin et al., 2014; Kremkow et al., 2010; Murphy & Miller, 2009).

In our model, the first balance state provides conditions for temporally long balanced states during which such excitatory transients can occur whereas the two other balance states limit this temporal window to a couple of milliseconds. We, however, except for correlation analysis of E-I currents, did not study the emergence of such transients in our networks, as all our results are averaged over relatively long simulation runs. We speculate that the first balance state would be characterized by relatively long and spatially extended transients, while the duration and spatial extent at the other two balance states would be limited. However, in the second and third balance stat, the emergence of synchrony and temporal codes (in contrast to rate coding) could play an important role in pattern transmission (Kumar et al., 2010). Because here we specifically concentrated on networks composed of neurons with Type I membrane excitability (which impedes formation of synchronous clusters), the role of synchrony is necessarily limited. Future experiments will assess the emergence of synchrony in E/I balanced states in networks composed of neurons having Type 2 membrane excitability.

Finally, network connection topology may also affect the dynamics of E/I ratio and the pattern of E/I regulation. This is most clearly observed when excitation is kept local in the network. As shown in Fig. 9a, increasing randomness (i.e. scope) of inhibitory connections significantly alters how E/I ratio changes when increasing excitatory synaptic weight. In this case for high excitatory weight network remains in the inhibition dominant regime. However, the general mechanism of regulation stays the same as our framework, i.e. E/I ratio depends on the relative contribution between firing rates and depolarization level. While these studies provide insight on how the dynamics of excitatory and inhibitory currents change as a function of spatial distribution and extent of excitation and inhibition, we don’t directly study effects of structural or input heterogeneities on the local emergence of E/I balance. Such heterogeneities and clustering by themselves were shown to prevent emergence of detailed E/I balance and emergence of both fast spiking variability and slow firing rate fluctuations (Landau et al., 2016; Litwin-Kumar & Doiron, 2012). However, because E/I balance is critical for invariant computation in neural networks (Marino et al., 2005), it may be preserved in the face of network heterogeneity via homeostatic plasticity in inhibitory synapses and spike-frequency adaptation (Landau et al., 2016).

A critical question is how the brain regulates the balance between excitation and inhibition on local and/or global levels. This question has been addressed by other studies showing that inhibitory homeostatic plasticity can play a critical role in regulating and controlling E/I balance on diverse spatio-temporal scales (Hennequin et al., 2017; Landau et al., 2016; Litwin-Kumar & Doiron, 2014; Sprekeler, 2017). However, our results potentially reconcile a number of other discrepant experimental observations. For example, one recent study suggested that E/I ratios are pushed towards an inhibition dominant regime during wakefulness, when compared with the same brain network under anesthesia (Haider & Hausser, 2013). However, other experiments have found that excitation and inhibition are at similar levels when comparing sleep states and wakefulness (Chellappa et al., 2016; Ly et al., 2016; Niell & Stryker, 2010). These discrepancies may have profound implications for how the brain processes information. For example, the reported features of tuning curves for excitation and inhibition (i.e., in response to variations in external sensory stimuli) vary across studies. Similar tuning curves are observed in some experiments (Runyan et al., 2010; Wehr & Zador, 2003; Zhou et al., 2014) while others have found either wider tuning (Niell & Stryker, 2010; Kerlin, et al.,2010) or narrower tuning (Sun et al., 2013) for inhibition, as compared to excitation. We speculate that these discrepancies in experimental findings may result from differing contributions of firing rate and membrane depolarization between experiments, which push the networks under study into different balanced state realizations.

Together, our results point to complex interactions between excitatory and inhibitory currents in the balanced network regime. Our characterization of the repertoire of diverse balanced states provides a theoretical framework for experimental studies quantifying E/I balance and characterizing network interactions in various brain states and modalities.

Abbreviations:

E

excitatory

I

inhibitory

E/I

excitatory/inhibitory

EPSC

excitatory post synaptic current

IPSC

inhibitory postsynaptic current

MPC

mean phase coherence